Multiscale Modelling of Lytic Polysaccharide Monooxygenases

Abstract

Lytic polysaccharide monooxygenase (LPMO) enzymes have attracted considerable attention owing to their ability to enhance polysaccharide depolymerization, making them interesting with respect to production of biofuel from cellulose. LPMOs are metalloenzymes that contain a mononuclear copper active site, capable of activating dioxygen. However, many details of this activation are unclear. Some aspects of the mechanism have previously been investigated from a computational angle. Yet, either these studies have employed only molecular mechanics (MM), which are inaccurate for metal active sites, or they have described only the active site with quantum mechanics (QM) and neglected the effect of the protein. Here, we employ hybrid QM and MM (QM/MM) methods to investigate the first steps of the LPMO mechanism, which is reduction of Cu^II to Cu^I and the formation of a Cu^II–superoxide complex. In the latter complex, the superoxide can bind either in an equatorial or an axial position. For both steps, we obtain structures that are markedly different from previous suggestions, based on small QM-cluster calculations. Our calculations show that the equatorial isomer of the superoxide complex is over 60 kJ/mol more stable than the axial isomer because it is stabilized by interactions with a second-coordination-sphere glutamine residue, suggesting a possible role for this residue. The coordination of superoxide in this manner agrees with recent experimental suggestions.

1. Introduction

Employing cellulose in biofuel production can make this advancing technology a highly competitive alternative to fossil fuels. As a major component of biomass, cellulose is inexpensive and the most abundant polysaccharide on earth.¹ However, the application of cellulose in biofuel production requires its degradation into smaller sugars, which has been shown to be a major obstacle, requiring both hydrolytic enzymes and thermal work. This remarkable stability is caused by its structure, involving very long glucan chains, which are composed of glucose monomers, coupled together by β-1,4 glycosidic linkages. The glucan chains interact with each other by an extensive network of inter- and intramolecular hydrogen bonds involving the three hydroxyl groups of each glucose monomer, which limits the accessibility of hydrolytic enzymes to the glycosidic linkages.^2,3

Lately, a class of fungal and bacterial enzymes called lytic polysaccharide monooxygenases (LPMOs) have attracted considerable attention owing to their ability to enhance polysaccharide depolymerization, thereby providing a route to efficient conversion of cellulose into fermentable sugars.⁴⁻⁶ The first industrial applications have already been seen for ethanol production.⁷ Initially, LPMO enzymes^9,10 were assumed to be solely hydrolytic and were classified as belonging to the glycoside hydrolase 61 (GH61) and carbohydrate-binding modules 33 (CBM33) families. Initial reports questioning whether GH61 indeed were hydrolases were published in 2008,¹¹ and in 2010, Harris et al.¹² showed that an LPMO from the GH61 family significantly enhanced cellulase activity (a few earlier reports are also known from the patent literature^13,14). The exact role of LPMOs was demonstrated later in 2010 by Vaaje-Kolstad et al.,¹⁵ who showed that a bacterial LPMO belonging to the CBM33 family exhibited an oxidative mechanism. Importantly, these studies suggested the involvement of a metal, although the nature of this metal was not immediately elucidated. Yet, it was clear that the LPMOs employed a common mechanism, different from the traditional glycoside hydrolases, and the enzymes are today reclassified as auxiliary activity enzymes AA9 (formerly GH61) and AA10 (formerly CBM33).¹⁶ From X-ray crystallography and electron paramagnetic resonance (EPR) spectroscopy, Quinlan et al.⁸ was able to show that LPMOs employ copper in the active site, which solved the initial confusion concerning the metal site.^11,12,15 Later, several other reports confirmed that both AA9 and AA10 enzymes contain a single copper ion.^8,17−24

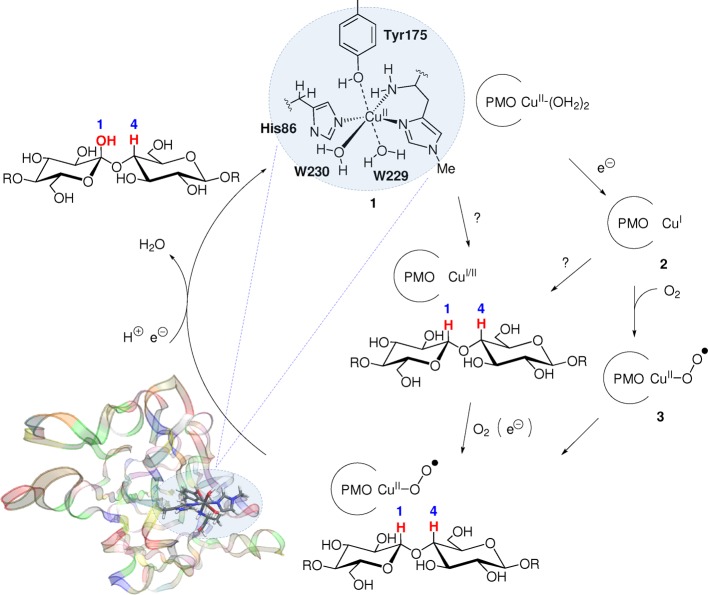
The active site of an AA9 enzyme is shown in Figure 1, together with a putative mechanism.¹⁷ For the resting state, 1, the first coordination sphere is distorted octahedral and comprises a weakly coordinated tyrosine, two water molecules, and an unusual histidine brace composed of two histidine residues, coordinating through the imidazole group. One of these is the N-terminal residue, which also coordinates through the terminal NH₂ group,⁸ as also seen in the particulate methane monooxygenases.²⁵ Notably, a peculiar methylation of this N-terminal histidine has been observed in many fungal LPMO structures,^8,11,26−29 although its role is unclear because the nonmethylated enzyme is also catalytically active.^28,29

Figure 1.

Active site and putative mechanism of a fungal LPMO (bacterial LPMOs lack the axial tyrosine residue but are likely to work through a similar mechanism). The order of events (electron transfer, substrate uptake, and O₂ coordination) is not clarified as suggested by the different possible paths. Residue numbers refer to the enzyme from Thermoascus aurantiacus (PDB 2YET).⁸

EPR spectroscopy⁸ has shown that 1 contains a Cu^II ion.³⁰ The EPR spectra provide an important complement to X-ray structures because Cu is known to be photoreduced in the X-ray beam. In fact, it is likely that most LPMO crystal structures have contained a mixture of Cu^II and Cu^I.^4,5,29 The reduction gives rise to a lowering of the coordination number, and many AA10 structures have been reported to have an approximate T-shaped coordination environment, indicating that the metal site contains a Cu^I ion.^4,21,31

The mechanism of the LPMOs is far from clarified, and even the order of reduction, substrate binding, and O₂ uptake is unknown, as suggested by Figure 1. A complicating factor is that there is much sequence variation within the LPMO family,^32,33 and different LPMOs might employ slightly different mechanisms. For instance, the axial tyrosine (Tyr175 in Figure 1) is replaced by phenylalanine in most AA10 LPMOs. A different mechanism could explain the differing substrate preferences among the LPMOs: fungal AA9 enzymes oxidize cellulose,^8,12,17,18 whereas AA10 enzymes oxidize both cellulose^20,34,35 and chitin.^15,20,34 Fungal LPMOs that break down chitin or starch have also been identified and are classified as AA11³⁶ and AA13,^37,38 respectively.

Apart from varying preferences with respect to substrate, LPMOs also have different regioselectivity: some oxidize only the C1 atom of the glycoside linkage, others oxidize only the C4 atom, whereas still others can oxidize both C1 and C4. This has led to a subclassification of the AA9 family, in that enzymes belonging to the LPMO type 1 subfamily are C1 specific, those belonging to LPMO type 2 are C4 specific, and those belonging to LPMO type 3 oxidize both C1 and C4.³⁹ Bacterial LPMOs (AA10) were initially thought to be C1 specific^15,20,35 until a C4-specific counterexample was identified.³⁴

Although the insight gained from experimental studies has been paramount, it has often been complemented by computational chemistry. For instance, the interaction between a fungal LPMO and cellulose has been studied using molecular dynamics methods,^29,40 whereas the structural change upon Cu^II reduction (1 → 2 in Figure 1) has been studied using X-ray diffraction and X-ray absorption, combined with density functional theory (DFT).^31,41 The copper superoxide intermediate (3) has also been the target of multiple combined theoretical and experimental studies and has played a central role in mechanistic suggestions so far. This intermediate is believed to either directly abstract a hydrogen from the substrate⁵ or function as a precursor for a more reactive copper–oxyl species that is involved in hydrogen abstraction.⁴²

The coordination of O₂ to Cu in 3 may give rise to two isomers because there are two possible coordination sites for O₂ (although this complication has often been overlooked). One study⁴² suggested that O₂ binds in an axial position, trans to Tyr175, replacing W229 (see Figure 1), whereas a combined spectroscopic and computational study suggested that O₂ instead binds equatorially,⁴¹ replacing W230. However, each study investigated only one of the two isomers. Furthermore, all previous computation studies on LPMOs have been carried out using small models of the active site,^31,41,42 although it has been shown that the protein environment is crucial for accurate structures and energetics in studies on transition-metal enzymes.⁴³⁻⁵¹

In this study, we investigated the reduction of the LPMO active site from 1 to 2 and the two isomers of 3. We include the protein environment with the combined quantum mechanics and molecular mechanics (QM/MM) methodology.⁵²⁻⁵⁵ Using our QM/MM protocol, we can show that the small cluster models of the active site employed previously can give rise to large errors in the obtained structures.

2. Results

We start this section by discussing whether our computational protocol can reproduce the observed^31,41 decrease in coordination number when Cu^II is reduced to Cu^I (section 2.1). We then proceed to discuss the O₂ bound states (section 2.2).

2.1. Structural Changes When the Resting State Is Reduced

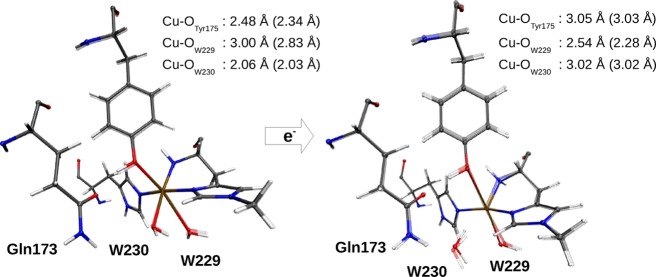
The optimized structures and selected Cu–ligand distances of 1 and 2 are shown in Figure 2. The bond distances are compared with the computational results from the literature and with bond distances from a number of crystal structures in Table 1.

Figure 2.

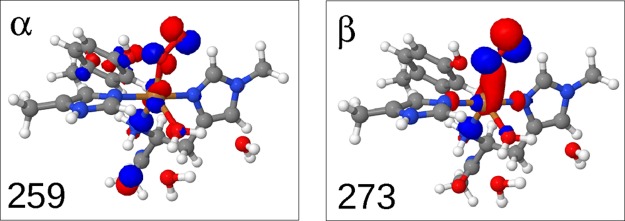
Structural changes upon reduction of 1 to 2. Both figures contain an overlay of structures obtained with the def2-SV(P) (transparent) and def2-TZVPD basis sets. The selected bond distances are for the def2-TZVPD basis set, with those of the def2-SV(P) basis set in parentheses. The second-sphere Gln173 residue is also included.

Table 1. Cu–Ligand Bond Lengths (Å) for the Active Site of LPMO.

state	Cun	(spin)	Cu–NHis86ε	Cu–NHisl	Cu–NHis1δ	Cu–OTyr175	Cu–OW229	Cu–OW230
1fixed	CuII	S = 1/2	2.02	2.07	1.98	2.80	2.28	2.11
1free	CuII	S = 1/2	2.03	2.03	1.99	2.34	2.83	2.03
1free,a	CuII	S = 1/2	2.02	2.02	1.97	2.48	3.00	2.06
1free,b	CuII	S = 1/2	2.04	1.98	2.02	2.47	2.96	2.07
1(42)	CuII	S = 1/2	1.99	2.08	1.99	3.08		2.33
1(31),c	CuI	S = 1/2	1.99	2.07	1.98		2.22	2.12
2fixed	CuI	S = 0	1.97	2.11	1.99	2.87	2.30	3.01
2free	CuI	S = 0	1.95	2.08	1.96	3.03	2.28	3.02
2free,a	CuI	S = 0	1.93	2.09	1.93	3.05	2.54	3.03
2free,b	CuI	S = 0	1.97	1.97	1.95	2.90	2.74	3.04
2(42)	CuI	S = 0	1.93	2.14	1.93	4.37	2.19
2(41)	CuI	S = 0	1.91	2.27	1.91	3.23	3.32	3.11
2(31),c	CuI	S = 0	1.98	2.18	1.98
2YET(8)	CuI/II	S = 0, 1/2	2.32	2.10	2.43	2.80	2.65	2.23
3ZUD(8)	CuI/II	S = 0, 1/2	2.03	2.20	1.91	2.92	2.89
4EIR(27)	CuI/II	S = 0, 1/2	1.99	2.25	1.92	2.76		1.84
5ACF(56)	CuI/II	S = 0, 1/2	2.06	1.88	2.16	2.47
4ALC(31),c	CuII	S = 1/2	1.97	2.12	1.99		2.21	2.19
4ALT(31),c	CuI	S = 0	1.91	2.19	1.94

^aOptimized with TPSS-D3/def2-TZVPD.

^bOptimized with B3LYP-D3/def2-TZVPD.

^cThis is from an AA10 LPMO enzyme, whose reduction in the X-ray beam has been carefully followed.

We start by discussing the results obtained with TPSS/def2-SV(P) and system 2 relaxed (entries 1^free and 2^free in Table 1). Despite the reduction of the Cu ion, the lengths of the three Cu–N bonds do not change by more than 0.08 Å, which emphasizes the fact that the active site is constructed to accommodate both Cu^II and Cu^I. Furthermore, the effect of reducing Cu^II to Cu^I is an elongation of the Cu–O bonds of Tyr175 and the equatorial water molecule (W230) to 3.0 Å. Meanwhile, the Cu–O bond to the other water molecule shortens from 2.8 to 2.3 Å. Therefore, the Cu ion becomes essentially four-coordinated, rather than 5- or 6-coordinated (octahedral).

Considering these small differences in the Cu–N bonds lengths upon reduction, it is surprising that the calculated distances reproduce the distances in the starting crystal structure (2YET⁸) so poorly: those to the side-chain imidazole rings are 0.3–0.5 Å too short. We, therefore, optimized structures with the larger def2-TZVPD basis set, both with the TPSS and B3LYP functionals. However, as can be seen in Table 1, this did not lead to any major changes in the Cu–N bond lengths. In particular, those to the histidine side chains changed by less than 0.05 Å. A comparison with a range of other crystal LPMO structures (also in Table 1) shows that the Cu–N^δ bonds in the 2YET are highly untypical, being 0.3–0.5 Å too long. If we instead compare with the other crystal structures, the calculated Cu–N bond lengths fall well within the range observed in the crystal structures, with a maximum difference of 0.10 Å for the Cu–N_His1 in the oxidized state and 0.05 Å for the other distances compared with the average of the five crystal structures.

Comparison of structures with the surrounding protein (system 2) fixed or free to relax (fixed or free structures in Table 1) shows that there are only small differences for the reduced state 2 (up to 0.03 Å except for the weak bond to Tyr175, which changes by 0.16 Å). However, for the oxidized state (1), much larger changes are seen: the bond length to Tyr175 decreases from 2.80 to 2.34 Å, whereas that to the axial water molecule increases by almost the same amount, that is, from 2.28 to 2.83 Å. This indicates that the crystal structure represents a predominantly reduced state (with a long bond to Tyr175) and that fixing the junction at the C^β atoms of Tyr175 is too restrictive to model the full flexibility of this residue during the reduction. As will be discussed in section 2.2, it is also too restrictive to describe the distance in the intermediate 3. Therefore, we generally expect large differences in this bond distance when compared with various vacuum studies, where it is customary to fix C^β to its initial location from the crystal structure, and this is indeed the case (as will be discussed below). The Tyr175 residue has recently been speculated to have implications for the LMPO mechanism,⁵⁶ and the Cu–O distances are therefore crucial, but it should also be remembered that axial bonds in Cu complexes are weak and extremely flexible (i.e., the distance to Cu can vary a lot at a minimal expense in energy).⁵⁷⁻⁵⁹ This was reflected in the rather large variation of these bond lengths in the structures optimized with different basis sets and DFT functionals (up to 0.5 Å) and in the various crystal structures (up to 0.7 Å) as can be seen in Table 1.

Our structures for 1 and 2 are mostly in agreement with the results from previous computational studies^31,41,42 (also included in Table 1). The Cu–N distances agree, except that the Cu–N_His1 distance in the reduced state (2) is somewhat shorter (1.97–2.11 Å in our structures, compared with 2.14–2.27 Å in the previous studies). All of these studies also suggest that the coordination number of the Cu ion decreases when it is reduced, as expected. However, these studies differ in their predictions regarding which of the three prospective O ligands bind and at what distance. For the oxidized state (1), all studies agree that the equatorial water molecule binds strongly, although the Cu–O distance is ∼0.2 Å longer in the study by Kim et al.⁴² than those in the other studies. Both Kim et al.⁴² and Gudmundsson et al.³¹ also suggested that the second water molecule coordinates to Cu (although ref (42) does not report the bond distance to the axial water molecule) in agreement with our result with a fixed surrounding. However, when we allow the protein to relax, we instead find that Tyr175 coordinates weakly to Cu, whereas the axial water molecule practically dissociates.

For the reduced state (2), all studies agree that both Tyr175 and the equatorial water molecule effectively dissociate. However, for the axial water molecule, the results differ. Kim et al.⁴² suggested that it binds rather strongly at a Cu–O distance of 2.19 Å, whereas the other two studies indicated that it also dissociates.^31,41 Our results are intermediate: with the def2-SV(P) basis set, we obtain a rather short Cu–O bond of ∼2.2 Å. However, with the larger def2-TZVPD basis set, and especially with the B3LYP functional, the Cu–O bond becomes appreciably longer, 2.54 and 2.74 Å, respectively.

Clearly, this reflects the flexibility of the weak Cu–O bonds, as mentioned above.⁵⁷⁻⁵⁹ These bond lengths are determined more by interactions with the surrounding protein than by the Cu–O interaction. Therefore, it is likely that our QM/MM results, with an explicit account of the surroundings, give more accurate results. However, it is clear that these bonds are sensitive to the theoretical treatment, as our results indicate and as has been pointed out before.⁴¹

2.2. Copper–Superoxide Intermediates

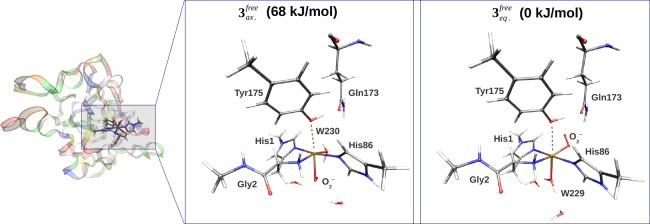
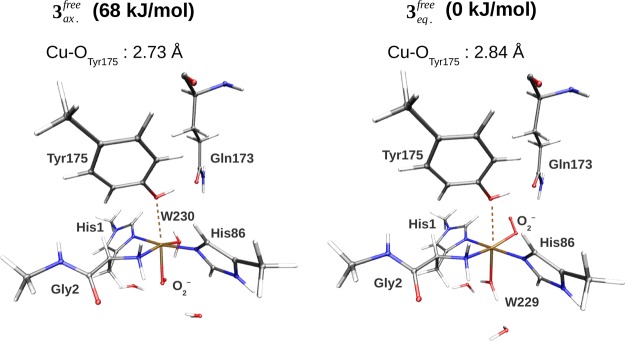
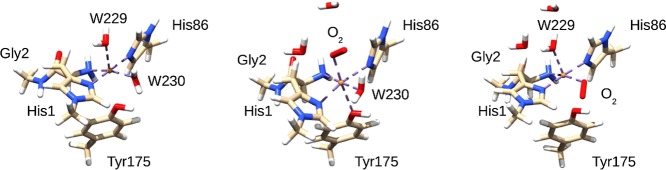
Next, we discuss the nature of the Cu^II–superoxide adduct, 3. It is expected to form through the binding of O₂ to the reduced active site (see Figure 1). As mentioned above, there are two possible isomers (3_eq or 3_ax) of this complex, depending on whether O₂ replaces the equatorial or the axial water molecule. At variance with the previous studies, we have studied both isomers. The optimized structures and selected bond distances of the two isomers are shown in Figure 3 and Table 2, whereas the energy difference between them is shown in the upper part of Table 3.

Figure 3.

Comparison of the axial and equatorial isomers of 3, showing also the Gln173 residue that can interact with O₂^–. The structures were optimized in the triplet states (S = 1) with the TPSS-D3 functional and the def2-SV(P) basis set. The corresponding bond lengths are shown in Table 2.

Table 2. Cu–Ligand Bond Lengths (Å) for the Active Site of LPMO^a.

method	spin	Cu–NHis86ε	Cu–NHis1	Cu–NHis1δ	Cu–OTyr175	Cu–O2	Cu–OW
3eqfixed	S = 1	2.06	2.15	2.01	2.89	2.04	2.24
3eqfree	S = 1	2.06	2.13	2.00	2.84	2.04	2.29
3eqfree,b	S = 1	2.06	2.12	2.00	2.94	2.01	2.40
3eqfree,c	S = 1	2.08	2.11	2.01	2.84	1.99	2.46
ref (41)	S = 1	1.98	2.09	1.97	3.35	1.98	3.76
3eqfixed	S = 0	2.06	2.15	2.01	2.87	2.02	2.24
3eqfree	S = 0	2.06	2.12	2.00	2.82	2.03	2.30
3axfixed	S = 1	2.31	2.05	2.15	2.58	2.09	2.10
3axfree	S = 1	2.11	2.02	2.05	2.73	2.29	2.03
ref (42)	S = 1	1.98	2.18	1.98	3.82	1.96	2.33
3axfixed	S = 0	2.31	2.04	2.14	2.57	2.10	2.08
3axfree	S = 0	2.08	2.03	2.03	2.71	2.30	2.02
ref (42)	S = 0	1.98	2.16	1.98	3.80	1.96	2.30

^aThe results were obtained with the TPSS-D3 functional and the def2-SV(P) basis set, unless otherwise specified. The Cu–O_W distance corresponds to that of Cu–O_W229 for 3_eq and Cu–O_W230 for 3_ax.

^bOptimized with TPSS-D3/def2-TZVPD.

^cOptimized with B3LYP-D3/def2-TZVPD.

Table 3. Energy Difference ΔE = E(3_ax) – E(3_eq) and Spin-State Splittings ΔE = E^S(3) – E^T(3) in kJ/mol^a.

state	func	spin	ΔEQM/MM	ΔEQM+ptch	ΔEQM	ΔEMM	ΔEbig-QM
3fix	TPSS-D3	S = 1	63.4	76.5	74.9	–4.4
3free	TPSS-D3	S = 1	67.8	51.0	65.5	–14.6	87.7
3axfree	TPSS-D3	S = 1,0	4.2	5.4	2.7	–1.2
3axfree	B3LYP-D3	S = 1,0	–0.7	0.8	2.8	–1.2
3eqfree	TPSS-D3	S = 1,0	12.5	10.6	14.0	2.0	10.5
3eqfree	B3LYP-D3	S = 1,0	13.2	11.2	16.5	2.0

^aΔE_QM/MM and ΔE_QM+ptch are defined in eq 1 and ΔE_QM/MM = E_MM123 – E_MM1 from the same equation. E_QM is the energy of the QM system, without any point-charge model. E_big-QM is the big-QM energy. All energies were calculated or extrapolated (ΔE_big-QM) with the def2-TZVPP basis set on structures optimized using QM/MM using the def2-SV(P) basis set. In ΔE_big-QM, 10.8 kJ/mol (3^free) or −1.3 kJ/mol (3_eq^free) of the total energy is a correction obtained as the difference between def2-TZVPP and def2-SV(P) calculations on the QM systems in Figure 6.

Our results clearly show that the equatorial isomer is most stable. The QM/MM calculations predict an energy difference of 68 kJ/mol. This is in agreement with the observation in the previous section that the equatorial water molecule effectively dissociates when the oxidized enzyme is reduced, providing a free coordinate site to the O₂ molecule. The point charges, representing the environment, give a contribution of 15 kJ/mol (the difference between ΔE_QM+ptch and ΔE_QM). The electrostatic contribution from the protein is thus nonnegligible, yet not very large. The contributions from the MM force field are of a similar magnitude, but of an opposite sign, and accordingly, the vacuum result (ΔE_QM) is close to the QM/MM result (ΔE_QM/MM). We additionally carried out a big-QM calculation that included all residues within 5 Å of the active site. This gave an energy difference of 77 kJ/mol with the def2-SV(P) basis set. An estimate of the effect of increasing the basis set size to def2-TZVPP can be obtained from the difference between def2-SV(P) and def2-TZVPP for the smaller QM system. This effect is 11 kJ/mol, resulting in the total difference of 88 kJ/mol, given in Table 3.

It should be noted that the protein significantly influences the structures. As for the resting states 1 and 2, previous computational studies on 3 imposed restrictions during the structure optimization (by freezing selected atoms) to mimic this protein effect. We compare both isomers with the previously calculated results in Table 2, and in both cases, we find that the structures differ significantly. In particular, we find large differences in the Cu–O distance to Tyr175, although it is long in all structures (2.57–2.94 Å in our structures but 3.35–3.82 Å in the previous studies; see refs (41) and (42)).

Both Cu^II and O₂^– have one unpaired electron. These two electrons can either couple ferromagnetically in a triplet state or antiferromagnetically in a singlet state. We have studied both states, and it can be seen from Table 2 that the structures for the two spin states are almost identical. The energy differences between the two spin states are reported in the lower part of Table 3. For 3_eq, the triplet is most stable. The energy difference is 13 kJ/mol, both with the TPSS and with the B3LYP functionals, and the big-QM result is only 2 kJ/mol lower. This is in reasonable agreement with the 19 kJ/mol obtained in a previous study,⁴¹ which is remarkable considering the large differences in the obtained structures.

For the axial isomer, the singlet–triplet energy splittings calculated with the QM region and a point-charge model of the environment (ΔE_QM+ptch) are 5 kJ/mol for TPSS and 1 kJ/mol for B3LYP, which means that the two spin states are essentially degenerate. In fact, adding the MM energy of −1 kJ/mol (giving ΔE_QM/MM) is enough to make the singlet the ground state at the B3LYP level. Thus, it is not possible to settle which of the two spin states is the most stable for the axial isomer within the accuracy of current methods. Our spin-splitting energy estimates for 3_ax are somewhat lower than the 19 kJ/mol that was obtained in the study by Kim et al.⁴²

3. Discussion

The spectroscopic, crystallographic, and computational studies have suggested that the reduction of 1 to 2 is accompanied by a decrease in the coordination number of the Cu atom. This is confirmed in our calculations, but the individual structures for 1 and 2 are rather different from those obtained in previous computational studies that have neglected the protein environment. We can confirm a previous suggestion that a large basis set is required before a significant bond elongation of the axial water molecule (W229) is obtained. However, even with large basis sets, we find that this water molecule is still weakly coordinated. We also find large differences in our structures of 3 compared with the previous calculations on smaller active-site models. Here, we highlight that 3_eq is not 4-coordinate, as has been suggested;⁵ instead, our structures indicate that the axial water molecule remains coordinated to the Cu ion, although with a rather long distance (2.24–2.46 Å), the length of which is sensitive to the DFT method and the basis set (see Table 2).

In most suggestions for the reaction mechanism of LPMOs, the substrate has been hydroxylated at either C1 or C4,^5,17,18,42 starting with a hydrogen abstraction from the substrate. The Cu–superoxide complex, [Cu^IIO₂]⁺, is involved either by directly abstracting a hydrogen atom from the substrate^17,18 or as a precursor for an Cu–oxyl radical, which then abstracts the hydrogen.⁴² The fact that the superoxide can have both axial and equatorial isomers has not been considered in any quantitative studies, although it was noted by Beeson et al.,⁵ who suggested that the axial isomer would be unstable, based on a Jahn–Teller distortion argument. Our calculations show that the axial isomer is stable, but they also confirm and quantify that the axial isomer is significantly less stable than the equatorial one (the difference is more than 60 kJ/mol). There are two sources of stabilization of the equatorial isomer. One is that the equatorial isomer is stabilized by interactions between the superoxide and the second-coordination-sphere Gln173 residue (2.24 Å away), showing a possible role for this highly conserved residue (see Figure 3). Another source is that the equatorial coordination of O₂^– provides a better possibility for π-interaction with the Cu 3d orbitals. The orbitals involved for 3_eq are shown in Figure 4, and more extensive molecular orbital plots for 3_eq and 3_ax are shown in Figures S1 and S2. From these figures, it can be seen that stabilizing d_π–O_π interactions are completely absent for 3_ax.

Figure 4.

Pair of molecular orbitals for 3_eq, involved in the Cu 3d_π–O_π interaction with the O₂^– π orbitals.

Mechanistic insights have so far been hampered by the lack of crystal structures including a bound substrate, which is difficult to obtain owing to the low solubility of cellulose and chitin. However, very recently, LPMOs that target smaller (soluble) oligosaccharides as substrates have been discovered, and a crystal structure for a (C4-specific) LPMO complexed with cellotriose and cellohexose have been reported.⁵⁶ In the LPMO–oligosaccharide complex, a Cl^– ion occupies the equatorial binding site, and it is suggested that this is the binding site of O₂, in agreement with our results. However, note that the LPMO reported in ref (56) has a rather different protein scaffold compared with that of the protein investigated here, and the inclusion of substrate, therefore, cannot be carried out by simple means (e.g., overlaying C_α-atoms). In this study, we have rather employed a protein that is either identical or bears close resemblance to those used in previous computational studies, and we can thus more directly compare the computational approaches. The large differences in the obtained structures compared with those from previous computations strongly indicate that an inclusion of the protein matrix is pivotal. Although the binding of the substrate may affect the active site, the large energy difference between axial and equatorial isomers found here indicates that the equatorial superoxide adduct is the active species or a precursor. Finally, we should emphasize that we cannot at the present state rule out that the active species is a Cu–oxyl complex as suggested in ref (42).

4. Conclusions

We have presented the first QM/MM calculations on an LPMO enzyme, based on the AA9 enzyme from Thermoascus aurantiacus. We investigated the resting state (1), its reduced form (2), and the Cu–superoxide complex (3). For all intermediates, the calculated structures are significantly different from those obtained in previous computational studies, where the protein environment was neglected. For 3, there exist two possible isomers, and in this study, we have found that one of these (with an equatorial O₂^– ligand) is much more stable than the other (more than 60 kJ/mol). Our further studies on the LPMO mechanism will therefore focus on this intermediate or intermediates derived from this one. Moreover, our future studies will also include the LPMO–substrate complexes, employing the same QM/MM computational protocol employed here. This will allow us to investigate the reactivity of both the superoxide intermediate (3) and Cu–oxyl complexes.

5. Computational Methods

5.1. Protein Setup

The starting coordinates were taken from the 1.5 Å resolution X-ray structure from Thermoascus aurantiacus, which belongs to the fungal LPMO (type 3) family.^5,8 This structure shows the protein in the resting state, possibly with a partly reduced active-site Cu ion. The structure is deposited in the protein data bank (2YET) and was also employed in a previous computational study.⁴² The structure is a dimer that contains 462 amino acids and 625 crystal water molecules, amounting to 4199 atoms in total. Here, we consider only the monomer (chain A), and the remainder of this paper always refers to chain A, unless explicitly specified.

The crystal structure contains eight amino acids with alternative conformations, namely Asp10, Met25, Ser26, Asn27, Leu41, Ser117, Gln167, and Lys214. We selected the conformation with the highest occupation or the first conformation if they had the same occupation numbers. Hydrogen atoms were added using the Maestro protein preparation tools.⁶⁰ For the titratable residues (2 arginine, 5 lysine, 7 histidine, 14 aspartate, and 5 glutamate residues), the Maestro program employs the PROPKA program⁶¹ to estimate pK_a values. The individual residues were visually inspected, and their solvent exposure and hydrogen-bond network were assessed. In this study, all arginine and lysine were protonated (+1), whereas the aspartate and glutamate residues were in their carboxylate forms (−1).

The histidine residues have two possible protonation sites, and in the following, we denote histidines as HIE (N^ε2 protonated), HID (N^δ1 protonated), or HIP (both nitrogens protonated). The first (N-terminal) histidine is a special case because the imidazole ring is methylated on the N^ε2 atom, whereas N^δ1 coordinates to the Cu ion. For the remaining histidine residues, we employed the protonation states HIE57, HID86, HIP87, HID158, HIP164, and HIP201. The N^δ1 atom of HIE57 receives a hydrogen bond from the backbone NH group of Arg58, HID86 coordinates to Cu through N^ε2, and HIP87 forms a salt bridge from H^δ1 to the carboxylate group of Asp132 and a hydrogen bond to a crystal water through H^ε2. HID158 forms a hydrogen bond to the carbonyl oxygen of Asn92 through H^δ1, whereas the N^ε2 atom accepts a hydrogen bond from the side-chain indole NH group of Trp79. HIP164 and HIP201 are solvent-exposed on the surface of the protein. With this charge assignment, the total charge of the protein in the resting state (1) was −7.

The protein contains four cysteine residues that are cross-linked by disulfide bridges in the pairs Cys56–Cys178 and Cys97–Cys101. The carboxy-terminal residue Gly228 was missing from the X-ray analysis and was left out from the calculations. The X-ray structure contained one glycerol and four acetate molecules, which were all removed.

5.2. RESP Charges

Restrained electrostatic potential (RESP) charges for the metal center and its first coordination sphere were obtained by fitting to the electrostatic potential (ESP). The employed structure was taken from the protein (see Figure 5); it includes all ligands coordinating to the Cu ion in any of the studied complexes, and only hydrogen atoms were optimized, employing the TPSS functional⁶² together with a def2-SV(P) basis set.^63,64 All calculations in this section were carried out with a development version of Turbomole 7.0⁶⁵ (modified to write the ESP points). The ESP points were sampled using Merz–Kollman scheme,^66,67 using default radii for all atoms⁶⁷ and 2.0 Å for Cu.⁶⁸ They were employed by the resp program (a part of the Amber⁶⁹ package) to calculate the RESP charges.

Figure 5.

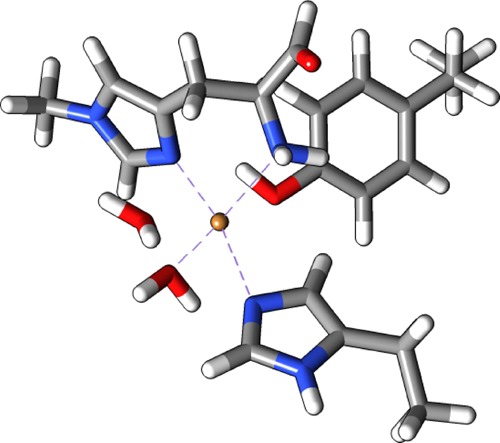
Structure used to obtain RESP charges for 1.

5.3. Equilibration

The system described in section 5.1 was equilibrated by simulated annealing using the Amber⁶⁹ software. The protein was immersed in a sphere of TIP3P water molecules with a radius of 40 Å, generated by the tLeAP program in the Amber suite. Heavy atoms in the protein and crystal water molecules were kept fixed at their crystal-structure positions. During the first 200 ps, the system was heated up to 370 K. This was followed by cooling from 370 to 0 K over 400 ps. The temperature was regulated using the Berendsen thermostat,⁷⁰ using a time constant that varied during the simulation: 0.2 ps during the first 200 ps, 1.0 ps during the next 200 ps, 0.5 ps during the following 100 ps, and 0.05 ps during the last 100 ps, leading to a total simulation time of 600 ps. The simulations used a time step of 0.5 fs. Finally, the system was subjected to a 10 000-step minimization.

5.4. QM/MM Calculations

The equilibrated system (section 5.3) was employed in the QM/MM calculations, employing the ComQum program.^71,72 This program combines the QM software Turbomole 7.0⁶⁵ and the MM program Amber 14.⁶⁹ In ComQum, the simulated system is divided into three subsystems, labeled systems 1, 2, and 3. System 1 is described using a QM method (here, DFT). Systems 2 and 3 are both described using an MM force field. System 2 is defined as all atoms within 6 Å of any atom in system 1. In the following, we use the label “free” for calculations in which the coordinates of the atoms in system 2 are optimized. In calculations labeled “fixed”, these are kept fixed. System 3 contains the remaining protein and solvent atoms and is always kept fixed at the equilibrated structure. When there is a bond between systems 1 and 2 (a junction), the hydrogen link-atom approach was employed: the QM region is capped with hydrogen atoms (hydrogen link atoms), the positions of which are linearly related to the corresponding carbon atoms (carbon link atoms) in the full system.^73,74

The total energy of the system is calculated as

1

E_QM+ptch is the QM energy of system 1, including hydrogen link atoms and a point-charge model of systems 2 and 3 (with point charges taken from the Amber force field and excluding only the carbon link atoms).⁴⁴E_MM123 is the total MM energy of the full system (but with the charges of the QM system zeroed), and E_MM1 is the MM energy of system 1 (still with zeroed charges).

In our study, we focused on the three states 1, 2, and 3 in Figure 1. For 3, we considered two possible isomers with the superoxide ion binding in either the axial or the equatorial position, denoted as 3_ax and 3_eq. Both isomers of 3 may attain either a triplet state or an antiferromagnetically coupled (open-shell) singlet state. The latter was calculated to be a broken-symmetry state.⁷⁵

The QM region always included the first coordination sphere, that is, the imidazole ring of His86 and the phenol ring of Tyr175, both capped with a hydrogen atom (replacing C^α). The whole terminal histidine residue and parts of the next amino-acid (Gly2; junction at the carbonyl C atom) were included. The QM regions are shown in Figure 6.

Figure 6.

The QM systems employed for 1, 3_ax, and 3_eq. Model 2 employed the same QM system as 1 (but with a reduced copper ion), and the same QM system is employed for triplet and singlet variants of 3.

For both isomers of 3, we included two solvent molecules in the QM region, in addition to the water molecule coordinating to Cu^II. This decision was made based on initial calculations, in which they were absent. The initial calculations showed that the energy difference between the isomers was dominated by van der Waals energy from the MM calculations (amounting to over 80 kJ/mol). By decomposing the energy into contributions from individual residues, it was shown that the large change in the van der Waals energy was almost exclusively caused by the two solvent water molecules. To shift this large energy contribution to the more accurate QM part of the energy, we decided to include these two solvent molecules in the QM system. As expected, this lowered the energy change associated with the MM part to around 17 kJ/mol.

In our initial setup, we noted that the side chain of Gln173 was flipped by the Maestro preparation tools. It was located in the second coordination sphere at the hydrogen-bonding distance of both Tyr175 and one of the Cu-bound water molecules (2.7–2.8 Å distance between the heavy atoms). Therefore, we decided to perform an optimization both in the flipped (1a) and original (1b) conformations. The latter conformation was employed in the study by Kim et al.,⁴² which was performed in vacuum, but included parts of the second coordination sphere. In conformation 1b and the crystal structure, the side-chain carbonyl group of Gln173 can receive a hydrogen bond from the Tyr175 OH group and another from the Cu-bound water molecule. In the other conformation, the side-chain NH₂ group instead donates a hydrogen bond to Tyr175, but it cannot donate any hydrogen bond to the water molecule. Therefore, 1b is favored by about 30 kJ/mol, even when calculated on a structure equilibrated for the 1a state where the hydrogen bonding networks around the Gln173 NH₂ group are somewhat unfavorable for 1b. We will, therefore, focus on the conformation in 1b from this point on. To ensure that the hydrogen network around the Gln173 NH₂ was sufficiently relaxed, the structure was re-equilibrated, and the QM/MM optimization of 1 was carried out from this re-equilibrated structure. The starting structures for 2 and 3 were built from 1, by reducing the charge of the QM region (2) and replacing W229 (3_ax) or W230 (3_eq) with O₂.

The structure optimizations employed the def2-SV(P) basis set^63,64 and the dispersion-corrected TPSS-D3 functional^62,76 with Becke–Johnson damping.⁷⁷ All reported energies were obtained from these structures by single-point calculations with the more accurate def2-TZVPP basis set⁶³ and including the entire protein (systems 2 and 3), represented by point charges (the effect of increasing the basis set is usually around 1 kJ/mol for energy differences). In the case of 3, we also tried the B3LYP/def2-TZVPP combination (with the same structures). It was previously emphasized that basis sets of at least triple-zeta quality are required to model the structure of 2.⁴¹ For states 1, 2, and 3_eq, we, therefore, probed the quality of the TPSS-D3/def2-SV(P) structures by increasing the basis set to def2-TZVPD or replacing the TPSS-D3 functional with B3LYP-D3.⁷⁸⁻⁸⁰ For both 1 and 2, the basis-set effect was significant for the Cu–O bonds (as discussed in more detail in section 2). For 3, the effect is smaller, and here the def2-SV(P) basis set is sufficient to obtain reliable QM/MM structures.

It should be emphasized that the relaxation of system 2 was found to have a significant influence on the obtained structure, also within the first coordination sphere. Consequently, we have, in general focused on the results obtained with a relaxed system 2. The effect of relaxing system 2 will shortly be discussed for intermediates 1 and 2 in section 2.1. Otherwise, results with a fixed system 2 are included in the tables for comparison but not thoroughly discussed.

5.5. Big-QM Calculations

The use of a point-charge model for the environment can be somewhat inaccurate and for other metalloenzymes, it has been advocated to improve the QM/MM energies with single-point energy calculations with larger QM systems based on the QM/MM optimized structures.^45,46 Following refs (45) and (46), we have, therefore, defined a large QM system composed of all residues within 5.0 Å of the active site, as shown in Figure 1. In addition, junctions were moved at least three residues away from the active site and we included the only two buried charged residues in the protein, Arg157 and Glu159, which form a salt bridge, rather close to the active site (Glu159 was actually included already with the 5 Å criterion). The total system had a charge of +3 and was composed of 628 atoms. Around this system, we employed a conductorlike screening model (COSMO)⁸¹ with a dielectric constant of ε = 4.0. The calculations employed the TPSS method and the def2-SV(P) basis set, based on the structures obtained with the same specifications (note that this is sufficient for 3, as described in the previous section). The big-QM energy was enhanced with a DFT-D3 dispersion correction, calculated for the same big-QM region with Becke–Johnson damping, third-order terms, and default parameters for the TPSS functional. Finally, the energies were extrapolated to the def2-TZVPP basis set using two QM calculations on the normal QM system.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.6b00521.

• Coordinates for the optimized protein-free structures and more detailed molecular orbital plots for intermediate 3 (PDF)

The authors declare no competing financial interest.