Excited-State Proton Transfer of Phenol Cyanine Picolinium Photoacid

Abstract

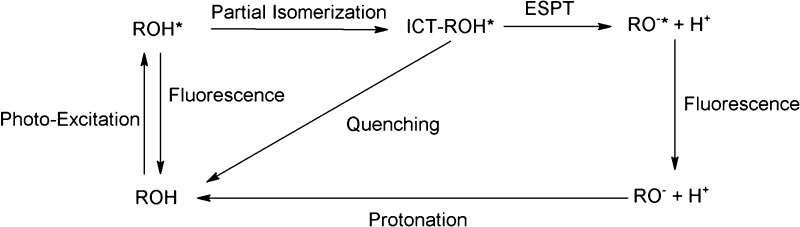
Steady-state and time-resolved fluorescence techniques as well as quantum-mechanical calculations were used to study the photophysics and photochemistry of a newly synthesized photoacid—the phenol cyanine picolinium salt. We found that the nonradiative rate constant k_nr of the excited protonated form of the photoacid is larger than that of the excited-state proton transfer (ESPT) to the solvent, k_ESPT. We estimate that the quantum efficiency of the ESPT process is about 0.16. The nonradiative process is explained by a partial trans–cis isomerization reaction, which leads to the formation of a “dark” excited state that can cross to the ground state by nonadiabatic coupling. Moreover, the ESPT process is coupled to the photo-isomerization reaction, as this latter reaction enhances the photoacidity of the studied compound, as a result of photoinduced charge transfer. To prevent trans–cis isomerization of the cyanine bridge, we conducted experiments of PCyP adsorbed on cellulose in the presence of water. We found that the steady-state fluorescence intensity increased by about a factor of 50 and the lifetime of the ROH band increased by the same factor. The fluorescence intensity of the RO^– band with respect to that of the ROH band was the same as in aqueous solution. This explains why inhibiting the photo-isomerization reaction by adsorbing the PCyP on cellulose does not lead to a higher ESPT rate.

Introduction

Photoacids are compounds that are weak acids in their ground electronic state and much stronger acids in their first excited singlet electronic state. Usually, the ground-state pK_a values are in the range of 5–10, whereas their excited-state pK_a^* can vary from −8 to 3. When time-resolved techniques are employed to study the photoacidity of a photoacid, the excited-state proton transfer (ESPT) rate constant is evaluated from the decay of the protonated form of the photoacid or from the rise time of the deprotonated-form signal. The ESPT rate constant, k_PT, of photoacids varies from 10¹³ s^–1 (τ_PT ≈ 100 fs) to 10⁸ s^–1 (τ_PT = 10 ns).

Photoacids can be classified into four groups. Regime I includes the weak photoacids with pK_a^* ≥ 0.4. These photoacids can transfer a proton to water as a solvent within the excited-state lifetime but not to alcohols such as methanol or higher alkanols. The second regime includes stronger photoacids of which the pK_a values are in the range of −4 ≤ pK_a^* ≤ 0.4. These photoacids can undergo an ESPT process not only to water but also to other protic solvents such as alcohols and dimethyl sulfoxide. The third group (regime III) includes even stronger photoacids with pK_a values of about −5. The rate of the ESPT process is of the order of translation and orientation time of protic solvents. The ESPT rate depends on the motion of the solvent because the solvent is the proton acceptor and the barrier height, and the motion along the reaction coordinate in the Marcus description of the electron- and proton-transfer reactions depends on the solvent coordinate.¹ This regime is referred to as the “solvent-controlled ESPT rate”. In water, the solvent-controlled ESPT rate constant is about 10¹² s^–1 because the solvent-reorientation time of water is ∼1 ps. The fourth class (regime IV) is the “beyond-the-solvent-controlled” regime. The pK_a^* of photoacids in this regime is <−6.5, and the ESPT rate constant, k_PT, is >10¹² s^–1. The fastest recorded ESPT rate is that of quinone cyanine 9 (QCy9), for which k_PT ≈ 10¹³ s^–1 (τ_PT ≈ 100 fs).²

Photoacids have been studied extensively for the last 50 years by steady-state methods and time-resolved techniques.³⁻¹⁸ These techniques are frequently used in the study of photoacids and the ESPT rate. More recently, transient infrared spectroscopy has provided more structure-accurate information on the ESPT process.⁷⁻⁹

In the current work, we have focused our attention on a newly synthesized photoacid, as shown in Scheme 1a—the PCyP salt. This photoacid has an ultrafast ESPT rate constant that competes with a nonradiative process to the ground state which would prevent a large quantum yield of the ESPT process. In this article, we also compare the photoprotolytic properties of the current photoacid, the PCyP compound, with two other stronger photoacids based on the same structure—the phenol benzoate cyanine picolinium salt and the CBCyP salt.^19,20 Both are shown in Scheme 1.

Scheme 1. Molecular Structure of (a) Phenol Cyanine Picolinium (PCyP) (b) Benzoate Cyanine Picolinium (BCyP) and (c) Chlorophenol Benzoate Cyanine Picolinium (CBCyP).

Results and Discussion

Figure 1a,b shows the steady-state fluorescence excitation and emission spectra of PCyP in slightly acidic (pH ≈ 6) H₂O and in basic H₂O solution (pH ≈ 10).

Figure 1.

(a) Normalized steady-state excitation and emission spectra of PCyP in slightly acidic H₂O, collected at λ = 540 nm and excited at λ = 370 nm, respectively. (b) Normalized steady-state excitation and emission spectra of PCyP in basic pH H₂O, excited at λ = 410 nm and λ = 480 nm, respectively.

At pH ≈ 6, the ground-state PCyP photoacid is in the protonated ROH form. The excitation-spectrum maximum is at ∼370 nm and the emission-spectrum maximum is at ∼524 nm. We assign these maxima to the absorption and emission ROH bands. At 650 nm, there is a signal buried in the ROH fluorescence tail which we assign to the RO^– band that originates from the excited-state proton transfer (ESPT) to the solvent. Figure 1b shows the excitation and emission spectra of PCyP photoacid in basic aqueous solution at pH ≈ 10. The excitation-spectrum maximum is at about 530 nm, and the fluorescence spectrum maximum is at ∼650 nm. The intensity of the steady-state fluorescence spectrum of the ROH fluorescence is about four times that of the RO^– fluorescence.

Figure 2a,b shows, on linear and semilogarithmic scales, the time-resolved fluorescence of PCyP in slightly acidic (pH ≈ 6) aqueous solution.

Figure 2.

Time-resolved emission of PCyP in slightly acidic (pH ≈ 6) aqueous solution, measured over the wavelength range of 470–650 nm, shown on a (a) linear scale and a (b) semilog scale; (c) only 630 and 650 nm (RO^– band) are displayed.

The signals were acquired by the fluorescence upconversion technique at several wavelengths over the spectral range of 470–650 nm. The normalized signal between 470 and 550 nm overlaps the ROH steady-state fluorescence band. The decay of the signals is nonexponential with short-, intermediate-, and long-time components. We used a multiexponential function to fit the experimental signals. The fit parameters are given in Table S1a in the Supporting Information section.

At low wavelengths, ≤490 nm, the short-time component has a decay time of ∼160 fs and an amplitude of about 0.6. At higher wavelengths, ≥500 nm, the decay time of the short-time component is about 220 fs, and its amplitude decreases as the fluorescence-monitored wavelength increases to about 0.27 at 580 nm. The intermediate-time component ranges from 700 fs at the low wavelength to about 1000 fs at 530 nm. The amplitude of the intermediate component increases with the wavelength increase. The amplitude of the long-time component increases with the increasing wavelength. The time constant is about 6 ps. At high wavelengths, >610 nm, the signal shows rise components followed by a nearly exponential decay (Figure 2c). These signals overlap the RO^– fluorescence band. The rise component fits the short- and intermediate-time components of the ROH time-resolved signals. The decay time of the RO^– signal is about 6 ps (τ₃ in Table S1 of the Supporting Information).

Figure 3 shows the steady-state excitation and fluorescence spectra of PCyP in D₂O in neutral pH (3a) and basic solutions (pH ≈ 11) (3b).

Figure 3.

a) Normalized steady-state emission (excited at λ = 400 nm) and excitation (collected at λ = 540 nm) spectra of PCyP in acidic D₂O. (b) Normalized steady-state emission (excited at λ = 460 nm) and excitation (collected at λ = 640 nm) spectra of PCyP in basic D₂O.

The steady-state excitation and emission spectra are similar to those obtained in H₂O. The maximum of the ROH excitation spectrum is at about 370 nm, and the fluorescence maximum is at about 524 nm. At ∼650 nm, the RO^– band is scarcely seen when the ROD ground-state form is excited in neutral D₂O. The RO^– band seen in Figure 3a arises as a consequence of the ESPT process. Because the RO^– form has a very short lifetime (∼12 ps) and the emission cross section is rather small, the overall steady-state fluorescence band intensity of the RO^– band is small. In basic solution, the RO^– excitation band in D₂O has the same shape and position as in H₂O and the fluorescence band is similar to that in H₂O.

Figure 4 shows the time-resolved fluorescence signals of PCyP in neutral D₂O solution measured over the spectral range of 470–650 nm.

Figure 4.

Time-resolved emission of PCyP in D₂O, measured over the wavelength range of 470–650 nm, shown on a (a) linear scale and a (b) semilog scale.

The normalized signal decay is nonexponential at short wavelengths (<590 nm). We fit the signals in that spectral range by a three-exponent fit function. The signal-fit parameters are given in Table S1b in the Supporting Information section. The decay time of the short-time component is about 280 fs while that of H₂O is shorter, 170 fs at λ < 500 nm. The decay time of the intermediate-time component in D₂O is about 1200 fs versus 700 fs in H₂O at short (<500 nm) wavelengths. The decay time of the long-time component in D₂O is about 12 ps versus 6 ps in H₂O. At long wavelengths (>610 nm), the signals of PCyP in D₂O (as also in H₂O) show two distinct rise components of 200 and 1200 fs followed by an exponential decay with a time constant of ∼12 ps, which we assign to the fluorescence decay of the RO^– form of PCyP in D₂O. The rise-component fit of the RO^– form approximately matches the two shorter decay components of the ROH form of PCyP in D₂O. The time-resolved fluorescence signals of PCyP in D₂O support the fact that an ESPT process takes place when the ROD form is excited.

Figure 5 shows the time-resolved fluorescence on linear and semilogarithmic scales of H₂O and D₂O at four wavelengths.

Figure 5.

Time-resolved emission of PCyP in H₂O and D₂O shown on a linear scale, measured at wavelengths of (a) 480 and (c) 500 nm and on a semilog scale, measured at wavelengths of (b) 480 (d) 500 nm.

Each panel shows two signals, that of H₂O and of D₂O at a certain wavelength. At short wavelengths, (<550 nm), the main contribution to the signal arises from the decay of the ROH form. The decay is governed by the ESPT process, and its rate is smaller in D₂O, as seen in the signals displayed in the panels. Table S2 in the Supporting Information section provides the values of the average decay time of the signals of PCyP in H₂O and D₂O, where , and I_F(λ,t) is normalized.

As seen in Table S2, τ_av^λ is higher in D₂O. The kinetic isotope effect (KIE) can be approximated by the simple relation

The average value of the KIE at short wavelengths, (≤530 nm), is 1.87.

With the Förster-cycle calculation,²¹ one can estimate the change in acidity upon excitation of the molecule. This calculation is based on the positions of the optical absorption or emission bands of the protonated and deprotonated forms of a photoacid. The energy cycle leads to a simple relation between band positions and change in acidity in the excited state with respect to the ground-state pK_a.

1

2

where C is a factor of universal constants

3

Δν is the difference between the positions of the ROH* and RO^–* bands given in wavenumber units (cm^–1). Δν for the fluorescence band peaks of ROH and RO^– forms of PCyP is 3700 cm^–1 and pK_a is about 6.7. The pK_a^* for these values is about −1.1. Δν calculated from the ROH and RO^– absorption spectra maxima is ∼4090 cm^–1 and the pK_a is slightly more negative (∼−1.8).

Comparison of Three Phenol Cyanine Picolinium Salt Photoacids

Figure 6 shows the steady-state fluorescence spectra of the recently synthesized three PCyP photoacids shown in Scheme 1. The pH of the aqueous solution was slightly acidic (5 < pH < 6), and the ROH form of the photoacid was excited.

Figure 6.

Steady-state fluorescence spectra of PCyP, BCyP, and CBCyP, shown in Scheme 1.

The steady-state fluorescence intensity ratio I_RO^–/I_ROH of the RO^– and ROH bands for CBCyP is the largest of the three. The BCyP is intermediate and for the currently studied photoacid, the PCyP, the fluorescence ratio is the smallest. Weller²² used a qualitative equation to estimate the ESPT rate constant from the steady-state fluorescence spectrum

4

where I_RO^– and I_ROH are the intensities of the RO^– and ROH fluorescence bands of the steady-state spectrum, and τ_F is the lifetime of the RO^– band. The equation is more accurate when and the oscillator strengths of both S₁ → S₀ transitions are the same. In fact, the RO^– fluorescence band intensity is so small in PCyP that it is buried in the tail of the ROH fluorescence. The steady-state fluorescence intensity of the RO^– band depends on the oscillator strength of the S₁ → S₀ transition, the nonradiative rates of both ROH and RO^– forms of the photoacid and the ESPT rate. When the nonradiative rate of the ROH form of a photoacid is higher than the ESPT rate, the ESPT quantum yield is small.

Figure 7 shows, on linear and semilog scales, the time-resolved fluorescence signal of the ROH form of the three PCyP photoacids measured at 480 and 500 nm.

Figure 7.

Time-resolved emission of PCyP, BCyP, and CBCyP (shown in Scheme 1) in aqueous solution, measured at a wavelength of 480 nm near the ROH peak: (a) linear scale (b) semilog scale and at 500 nm (c) linear scale (d) semilog scale.

At 500 nm, the average decay time, τ_av = ∫I(t) dt, is 310 fs for CBCyP, 900 fs for BCyP, and > 3000 fs for the PCyP. The signals for the decay of all the three compounds are nonexponential and could be fitted by four exponentials. For chlorobenzoate, the amplitude of the major component at 500 nm is about 0.83, and the decay time is about 165 fs. The amplitude of the second time component is about 0.1, and the decay time is about 500 fs. For the benzoate compound, the amplitude of the major component at 500 nm is about 0.74, and the decay time is about 380 fs. The second component has an amplitude of 0.19 and a lifetime of ∼1.4 ps. For the phenol (PCyP) compound, the major component at 500 nm has an amplitude of ∼0.44 and a lifetime of 220 fs. The second time component has an amplitude of ∼0.44 and a lifetime of 750 fs. The third time component at 500 nm has an amplitude of ∼0.12 and a lifetime of about 6 ps.

As seen in Figure 7, for the chlorobenzoate and the benzoate compounds, the amplitude of the third time component, with a long decay time, is much smaller than that of the phenol (PCyP) analog. The nonexponential decay of the fluorescence of PCyP arises from processes that are nonexponential and faster than the ESPT process. Solvation dynamics are nonexponential. Maroncelli et al.²³ have studied this process and found that they can fit the time-dependent (TD) red shift of coumarin 153 in many solvents by the four exponential fit function that spans from about 100 fs to tens of picoseconds in alcohols. The PCyP molecule has a floppy cyanine bridge that tends to twist after excitation to the first excited singlet state. This process is also nonexponential. These processes in PCyP are faster than the ESPT process and therefore the nonexponential fluorescence decay.

Figure 8 shows the time-resolved fluorescence of the ROH form of chlorobenzoate cyanine picolinium (CBCyP) in the spectral range of 470–530 nm. The signals are almost the same. This fact indicates that the ESPT takes place before solvation and half-twist of the cyanine bridge take place.

Figure 8.

Time-resolved fluorescence of CBCyP in slightly acidic (pH ≈ 6) H₂O, monitored at several wavelengths over the spectral range of 470–530 nm.

We suspect that for the PCyP compound, the third time component of 6 ps is the actual combined rate constant of the nonradiative and ESPT processes. The signal of PCyP at short times is assigned to the solvent response of the molecule. An ESPT process is also taking place during the solvation time, but the ESPT efficiency is much lower than that of the two analog compounds, the chlorobenzoate and the benzoate. The main process of the excited state of the PCyP compound is a nonradiative process. We conclude that because the steady-state fluorescence spectrum almost lacks the RO^– fluorescence band, the ESPT efficiency is very low, and we estimate it to be about 16%.

The overall fluorescence-decay rate constant of the ROH band is

5

The three major processes are

6

where k_nr and k_r are the nonradiative and radiative rate constants. The ESPT efficiency is given by

7

If k_r ≪ k_nr, k_ESPT and k_nr = 5k_ESPT, then .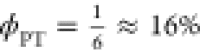

The signals at short times (τ < 1 ps) are strongly influenced by solvation processes and trans–cis isomerization that leads to a nonradiative process. From an examination of the steady-state fluorescence spectra of the three analog compounds, it is seen that the chlorobenzoate compound (CBCyP) has a band-intensity ratio (I_RO^–/I_ROH) of ∼6, whereas for the benzoate compound (BCyP), I_RO^–/I_ROH ≈ 1.5 and for the phenol compound, (PCyP), I_RO^–/I_ROH < 0.12. If we assume that the oscillator strengths of the ROH and RO^– bands, as well as the nonradiative rates, are similar for all three compounds, then k_ESPT for the CBCyP is six times that of BCyP and that of PCyP is smaller than that of CBCyP by a factor of about 36.

Figure 9 shows the time-resolved fluorescence signals of the RO^– form in D₂O of the three photoacids measured at 650 nm, near the band peak of the RO^– fluorescence.

Figure 9.

Time-resolved emission of PCyP, BCyP, and CBCyP (shown in Scheme 1) in D₂O, measured at 650 nm, near the RO^– peak: (a) linear scale (b) semilog scale.

Figure 9 shows that the time-resolved fluorescence signal of the RO^– form of the three photoacids in D₂O is similar at short times of ∼8 ps and that the rise time and decay of the signals are about the same. As a result of band overlap, the signals measured at 650 nm also contain a contribution of the signal of the ROH form because the oscillator strength of the ROH form is much greater than that of the RO^– form that has the character of a charge-transfer state which carries much lower oscillator strength.

PCyP Adsorbed on Cellulose

Figure 10 shows the steady-state fluorescence spectra of PCyP adsorbed on cellulose powder of 20 μm.

Figure 10.

Steady-state fluorescence spectra of two PCyP samples adsorbed on cellulose powder of 20 μm. One sample is in water and the other is semidry.

The samples were excited at 390 nm, near the maximum of the S₀ → S₁ absorption band. The spectra were measured at the front-surface excitation and fluorescence collection mode. The first sample is that of the semidry sample after the PCyP was sprayed by 30 μL of methanol solution on the cellulose powder that was glued on a silica disc of 40 mm diameter. The spectrum lacks the fluorescence band of the deprotonated RO^– form. The second spectrum is of PCyP adsorbed on cellulose powder of 50 mg sprayed with 50 μL of water. The spectrum of this sample clearly shows the emission band of the RO^– form with a band maximum at 650 nm.

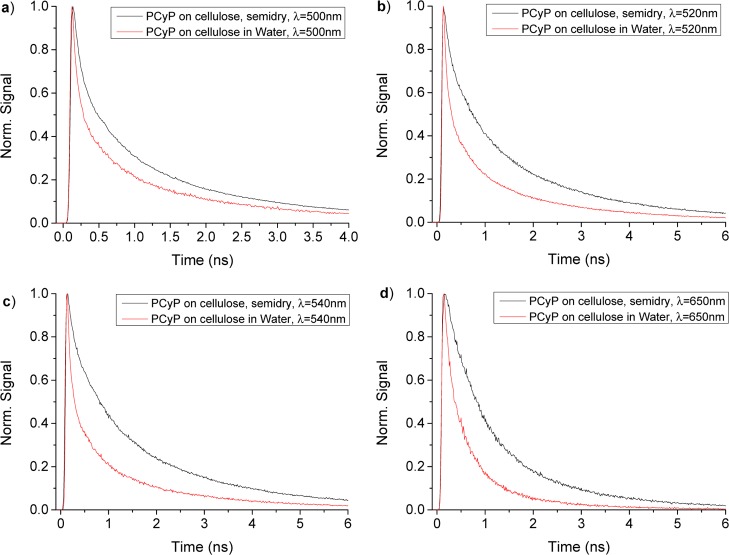
Figure 11 shows the time-resolved fluorescence of PCyP adsorbed on cellulose measured by the time-correlated single-photon-count (TCSPC) technique.

Figure 11.

Time-resolved fluorescence signals of PCyP adsorbed on cellulose, in 50 μL of water and in a semidry condition, measured by the TCSPC technique at wavelengths of (a) 500, (b) 520, (c) 540, and (d) 650 nm.

The signal intensities are about 100-fold more intense than in solution. Each panel in the figure displays two measurements made, at a particular wavelength, of PCyP adsorbed on semidry cellulose after spraying 30 μL of methanol solution of PCyP on 50 mg of cellulose. The second sample shows the TCSPC signal of PCyP after the addition of 50 μL of water to the semidry PCyP cellulose samples.

The decay of the fluorescence signals of the PCyP adsorbed on cellulose with and without water is nonexponential. When water is added to the samples, the average lifetime of the fluorescence is much shorter than is the case for the semidry samples. Table 1 provides the values of τ_av in nanoseconds of the semidry samples and the samples containing water.

Table 1. Average Lifetimes (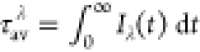) of Fluorescence of PCyP Adsorbed on Cellulose in Water and in Semidry Conditions, at Several Wavelengths in the Range of 480–650 nm.

wavelength (nm)	τav (ns) of PCyP on cellulose (semidry)	τav (ns) of PCyP on cellulose (water added)
480	0.955	0.698
500	1.024	0.724
520	1.347	0.743
540	1.440	0.753
560	1.493	0.771
580	1.272
650	1.163	0.520

The most important achievement of the study of time-resolved fluorescence of PCyP adsorbed on cellulose has been to show that a nonradiative process occurs in PCyP in solution at a rapid rate for both the ROH and RO^– forms of the photoacid. In previous studies of molecular rotors adsorbed on cellulose,²⁴ we were able to reduce the nonradiative process of molecular rotors such as thioflavin-T (ThT) and auramine-O (AuO). The molecular rotors have a short fluorescence lifetime of a few picoseconds in liquids with viscosities of 1–10 cP.²⁵ The lifetime of ThT and AuO is linear with the solvent viscosity. When adsorbed on cellulose, the ThT lifetime is about 1.6 ns and the fluorescence quantum yield increases by a factor of 1000 when compared with ethanol solution where τ_av(490 nm) ≈ 2 ps.

When water is added to cellulose, the ESPT to water takes place. In a previous work, we presented an ESPT study of 8-hydroxy-1,3,6-pyrenetrisulfonate (HPTS) adsorbed on cellulose.^26,27 There are two kinds of water in wet cellulose, water adsorbed on the skeleton of the polysaccharide and water in small pools next to the polysaccharide skeleton.^28,29 We found that for HPTS, the ESPT process has two rate constants. We assigned the larger ESPT rate to the proton transfer to the water pool and the smaller rate to water adsorbed on the polysaccharide skeleton. The time-resolved signals of PCyP adsorbed on wet cellulose also show a bimodal decay that could be assigned, as in the case of HPTS, to two kinds of ESPT rates to the two water domains next to wet cellulose.

To summarize this subsection, the protonated ROH form of PCyP in H₂O undergoes two processes in the excited state, a nonradiative process due to the trans–cis isomerization of the cyanine bridge and the ESPT process. The higher rate constant is that of the nonradiative process, and therefore, the ESPT efficiency is about 0.16, as in bulk water. We expected to find that upon adsorption of PCyP on cellulose, the fluorescence intensity ratio I_RO^–/I_ROH in the steady-state spectrum would increase approximately tenfold because the k_ESPT rate would be about the same as in water, but k_nr would be lower by at least a factor of ten. We find instead a rather small increase in I_RO^–/I_ROH when PCyP is adsorbed on cellulose. Both the ROH and RO^– average lifetimes increase by a factor of 100. From the steady-state and time-resolved fluorescence results, we conclude that the ESPT process is coupled to the isomerization, and the ESPT rate, k_PT, slows when k_nr does. QM computation studies that are described below indeed show the coupling of the ESPT process and the cis–trans isomerization process.

When PCyP is adsorbed on cellulose, the potential barrier ΔG^† of both excited-state processes, the nonradiative and the ESPT processes, increases and the reaction rate of both processes decreases by a factor of about 100. In water solution, the potential barrier for an ESPT process is low because ΔG of the ESPT reaction in liquid solution is low or negative. The concept of the free-energy relation between ΔG and ΔG^† is part of the Marcus electron-transfer theory. When the RO^– of a photoacid is stabilized and ΔG is negative, then ΔG^† is low. This takes place when the negative charge of the phenolate is reduced by intramolecular charge rearrangement and the electron density on the oxygen of the phenolate is transferred to the picolinium positive moiety through the conjugate cyanine bridge. Our recent finding is that the electron density is reduced only when trans–cis isomerization occurs. We suggest that the electrons of the cyanine bridge are delocalized when trans–cis isomerization takes place, and this enables the rearrangement of the electric charge. The end result for PCyP is a negative ΔG and small ΔG^† for the ESPT process and a high k_ESPT in water and small k_ESPT when adsorbed on cellulose.

Computation Results

The C₅–C₈–C₉–C₁₀ dihedral angle of PCyP (numbering can be seen in Figure 12A) has a minimum potential at 179.7° in the S₀ state in the aqueous phase. To analyze the potential role of trans–cis isomerization in the fluorescence quenching of this molecule, a relaxed scan was made by decreasing the C₅–C₈–C₉–C₁₀ dihedral angle by 9°/step. The energies of the S₀ and S₁ states are shown in Figure 12B.

Figure 12.

Chemical structure and atom numbering of PCyP (A). Energetic profile of the trans–cis isomerization reaction (B). Oscillator strength of the S₁ state as a function of dihedral-angle variation (C). The arrows in Figure 12B indicate the possible pathway for S₁ → S₀ de-excitation.

S₀ trans–cis isomerization is unfavorable, as there is a high reaction barrier of 55.6 kcal·mol^–1, which occurs at a dihedral angle of 62.7°. Moreover, no structure is more energetically stable than the initial one with a dihedral angle of 179.7°. In fact, the structures more energetically close to the initial one are the ones with dihedral angles of 8.7° and −0.3°, which are still less stable than that of the reactant by 3.8 kcal·mol^–1. Nevertheless, after the energy barrier is overcome, the relative S₀ energies decrease continuously without the presence of another energy barrier. It should be noted that the S₀ potential curve is asymmetric. However, this is because the two moieties connected by the cyanine bridge (picolinium and phenol) are not symmetric. Also, as can be seen in Figure 13, while the reactant structure has these two moieties far apart, the trans–cis isomerization makes them closer.

Figure 13.

Molecular structures of PCyP with a C₅–C₈–C₉–C₁₀ dihedral angle of 179.7° (A), 62.7° (B), and −0.3° (C).

In contrast to the ground state, the trans–cis isomerization reaction appears to be favorable in the S₁ state. The energy barrier is only 16.5 kcal·mol^–1, and the structures with dihedral angles of 71.7° and 62.7° are more stable than the initial structure (with a dihedral angle of 179.7°) by 16.1 and 8.3 kcal·mol^–1, respectively. If implicit solvation is modeled with the SMD model instead, which includes nonelectrostatic terms in the calculation,³⁰ this energy barrier decreases to 15.2 kcal·mol^–1. It should be noted that the S₁ energy barrier is reached earlier in the reaction (corresponding to a dihedral angle of 80.7°) than the S₀ barrier (corresponding to a dihedral angle of 62.7°). Also, between the structures with dihedral angles of 71.7° and 53.7°, there is another S₁ energy barrier. So, after the reaction reaches the structure with a dihedral angle of 71.7°, the reaction cannot proceed in either direction, with this structure acting as a S₁ energy minimum. From the dihedral angle of 71.7°, there is an S₁ energy barrier of 23.8 kcal·mol^–1 toward smaller dihedral angles and another of 32.6 kcal·mol^–1 toward larger dihedral angles. Thus, our calculations indicate that the ring-rotation reaction is favorable in the S₁ state but apparently only between dihedral angles of ∼180° and ∼70°. As a result, the trans–cis isomerization is not fully achieved in the S₁ state.

Figure 14A presents the S₁ electrostatic potential (ESP) atomic charges³¹ for the picolinium, cyanine, and phenol moieties of PCyP. Up until the energy barrier, the ESP charges of the cyanine moiety change very little, indicating that this moiety has a small role in the trans–cis isomerization. That is not the case for the picolinium and the phenol moieties, as there is an intramolecular charge transfer (ICT) between them. There is a transfer of negative charge of about −0.104e from the picolinium to the phenol group, up until the energy barrier is reached. Also notable is the ICT process occurring between all three moieties, starting from the vicinities of the S₁ energy barrier to the S₁ energy minimum (the structure with a dihedral angle of 71.7°). There is a significant transfer of negative charge from the phenol to both the cyanine bridge and the picolinium moiety. From that point on, there are some other processes of ICT, which should not be relevant, as our calculations indicated that the reaction cannot reach structures with dihedral angles smaller than ∼70°.

Figure 14.

(A) ESP charge transfer between picolinium, cyanine, and phenol moieties of PCyP, as a function of dihedral-angle variation. (B) Difference between the ESP charge of the hydroxyl oxygen in the S₁ and S₀ states, as a function of dihedral-angle variation.

For explaining the fluorescence-quenching mechanism of PCyP and its derivatives, the most important region of the S₁ potential–energy–surface (PES) is that which follows the energy barrier at a dihedral angle of 80.7°, namely, the structure with a C₅–C₈–C₉–C₁₀ dihedral angle of 71.7° (Figure 12). While the S₀–S₁ energy gap for the other structures varies between 53.4 and 84.8 kcal·mol^–1, this gap for two structures is significantly smaller: 13.9 (dihedral angle of 71.7°) and 15.2 (dihedral angle of 62.7°) kcal·mol^–1. This small S₀–S₁ energy gap indicates that both states are nearly degenerated, and so allow the identification of a S₁ → S₀ de-excitation pathway: nonadiabatic coupling between the S₀ and S₁ states, as a result of rotation of a C₅–C₈–C₉–C₁₀ dihedral angle (Figure 12B). Moreover, as the point of nonadiabatic coupling (dihedral angle of 71.7°) is reached earlier in the reaction than the S₀ energy barrier (dihedral angle of 62.7°), upon S₁ → S₀ de-excitation, the reaction should proceed energetically toward the PCyP reactant structure (dihedral angle of 179.7°). This is visually displayed by the arrows in Figure 12B.

While smaller S₀–S₁ energy gaps might be expected for the identification of a region for nonadiabatic coupling, reports in the literature indicate that multireference calculations will surely predict smaller energy gaps between S₀ and S₁.³²⁻⁴¹ In different systems, while TD-DFT calculations predict S₀–S₁ energy gaps of the magnitude obtained here (about 14 kcal·mol^–1), multireference calculations identified the presence of conical intersections or nonadiabatic coupling (S₀–S₁ energy gap lower than 5 kcal·mol^–1).³²⁻⁴¹ This results from the role of multireference correlation in systems where S₀ and S₁ are degenerated/nearly degenerated.^40,41 The energetic error present in the TD-DFT calculations may arise from spin contamination in the reference state.^32,33 However, while multireference methods are obviously important to obtain more quantitative pictures of systems such as these, they may be too computationally demanding to employ in situations where solvation and more structurally complex systems are involved. Thus, we have employed a long-range corrected hybrid exchange–correlation density functional (ωB97XD), which performs well for predicting local, CT, and Rydberg excitation.^44,56 This type of approach can provide quite accurate qualitative pictures for systems presenting S₀–S₁ degeneracy.³²⁻³⁵

While the other structures are all closed-shell species, the structures with dihedral angles of 71.7° and 62.7° are not. In fact, in the S₀ state, they possess a (S²) value of 0.1240 (dihedral angle of 71.7°) and 0.3982 (dihedral angle of 62.7°).

Another factor of interest is the variation of the oscillator strength as a function of the C₅–C₈–C₉–C₁₀ dihedral angle (Figure 12C). While the oscillator strength is high upon photoexcitation (1.24 at a dihedral angle of 179.7°), it decreases with lowering of the dihedral-angle value. In fact, it reaches a value of 0.04 (a very large decrease by a factor of ∼30 in the oscillator strength) in the structure with the dihedral angle of 71.7° (the structure with the lowest S₀–S₁ energy gap and which corresponds to the S₁ energetic minimum). Thus, even if we do not take into account the de-excitation pathway based on nonadiabatic coupling, the trans–cis isomerization in itself provides another explanation for the fluorescence quenching: the arrival at a structure for which the S₁ state is a “dark” state. Compared with the initial structure possessing a C₅–C₈–C₉–C₁₀ dihedral angle of 179.7°, the structure with a dihedral angle of 71.7° is clearly an ICT state (Figure 14A). There is the transfer of negative charge (−0.280e) from the phenol groups to the picolinium (−0.074e) and to the cyanine moieties (−0.206e). Thus, while the cyanine bridge appears not to be of such importance for the evolution of the reaction toward the S₁ energy barrier, it is important for the formation of the “dark” ICT state.

If the trans–cis isomerization reaction of PCyP explains the fluorescence quenching of this molecule and provides a competing pathway for ESPT, adsorbing PCyP on cellulose should increase the fluorescence intensity and favor the ESPT reaction. However, this was not observed experimentally (see Figures 10 and 11). The steady-state fluorescence intensity of both emission bands of PCyP increased by a factor of 100, but the I_RO^–/I_ROH did not increase by much. Thus, these data suggest that the ESPT reaction is linked to the trans–cis isomerization reaction, and so, decreasing the yield of the latter reaction (by adsorbing PCyP on cellulose) should also affect the photoacidity of the phenol group.

The source of enhanced photoacidity of a given molecule is explained by the anionic side of the ESPT reaction.^11,42 That is, photoinduced charge transfer reduces the negative charge on the hydroxyl oxygen (in comparison with the S₀ state), making it a weaker base in the excited state and energetically stabilizing the anion form of the photoacid.

Figure 14B shows the difference between the ESP atomic charge of the hydroxyl oxygen in the S₁ and S₀ states, as a function of the C₅–C₈–C₉–C₁₀ dihedral angle. This atom is always more electronegative in the S₀ than in the S₁ state, making it a weaker base in the excited state. However, while the difference in the reactant structure (dihedral angle of 179.7°) is 0.068e, this difference decreases with decreasing values of the dihedral angle, reaching a value of only 0.001e in the “dark” ICT state (dihedral angle of 71.7°). Thus, the rotation of the C₅–C₈–C₉–C₁₀ dihedral angle prevents the ESPT reaction, up to a dihedral angle of 71.7°, by diminishing the difference in basicity of the hydroxyl oxygen between the S₁ and S₀ states. From the dihedral angle of 71.7° on, there is a significant increase in the difference in electronegativity, reaching a value of 0.104e at a dihedral angle of 8.7°. At this point, the hydroxyl oxygen is a significantly weaker base in the S₁ state than in the S₀ state, theoretically enabling the ESPT reaction. However, the dihedral angle of 8.7° is reached only after fluorescence quenching has occurred.

Thus, in conclusion, the ESPT process is linked to the trans–cis isomerization, as is the rotation of the C₅–C₈–C₉–C₁₀ dihedral angle that enables the ESPT by making the hydroxyl oxygen a significantly weaker base in the S₁ state. Nevertheless, this only occurs after fluorescence quenching which, in practice, means that the ESPT reaction does not occur. As the ESPT reaction is dependent on the trans–cis isomerization, decreasing the yield of the latter process also decreases the yield of the former, which explains the results obtained in cellulose.

We also calculated the trans–cis isomerization of anionic PCyP in implicit water (Figure 15A). The reaction is not favored in the S₀ state, with no structure being energetically more stable than the reactant (dihedral angle of 179.8°). This is similar to what was observed earlier for the neutral species. Nevertheless, the S₀ energy barrier for anionic PCyP (27.2 kcal·mol^–1) is smaller by 28.3 kcal·mol^–1 than the one for the neutral species (55.6 kcal·mol^–1). This decrease may be due to the approximation between the cationic picolinium and anionic phenolate moieties during the reaction, leading to favorable electrostatic interactions. In the isomerization reaction of anionic PCyP, no open-shell structures were found. Contrary to the neutral species, the S₁ trans–cis isomerization is not energetically favored (Figure 15A). While the energy barrier is only 16.2 kcal·mol^–1, all remaining structures are less stable than the reactant by at least 6.9 kcal·mol^–1. Nevertheless, the oscillator strength of the Franck–Condon S₁ state decreases with the decreasing dihedral angle (Figure 15B), the same as for the neutral species.

Figure 15.

(A) Energetic profile of the trans–cis isomerization reaction for anionic PCyP. (B) Oscillator strength of the S₁ state as a function of dihedral-angle variation. (C) ESP charge transfer between picolinium, cyanine, and phenol moieties of anionic PCyP, as a function of dihedral-angle variation. (D) ESP charge of the hydroxyl oxygen in the S₁ state as a function of dihedral-angle variation.

The S₁ ESP charge transfer between the picolinium, cyanine, and phenol moieties (as a function of the C₅–C₈–C₉–C₁₀ dihedral angle) is presented in Figure 15C. These results show that the trans–cis isomerization of anionic PCyP is the result of ICT processes, mainly between the picolinium and phenolate moieties. First, there is the ICT of negative charge from the picolinium moiety to the phenolate ring, up until the S₁ energy barrier is reached. After this point, the reaction is dominated by reverse negative-charge transfer, from the phenolate to picolinium. The S₁ ESP charge of the phenolate oxygen is also affected by these ICT processes (Figure 15C). There is an increase of 0.042e in the negative charge from the reactant to the energy barrier. From that barrier on, the negative charge decreases by 0.167e.

It should be noted that our calculations of the neutral trans–cis isomerization indicated that the possibility of ESPT exists only for C₅–C₈–C₉–C₁₀ dihedral angles smaller than 70° (Figure 14). The calculations for the anionic reaction showed that in dihedral angles of that magnitude, there is an ICT of negative charge from the phenolate to the picolinium moiety (Figure 15C). Moreover, the negative charge of the phenolate oxygen decreases significantly in this region (Figure 15D). Thus, these ICT processes should stabilize the RO^– species, leading to a negative ΔG and low ΔG^†. By contrast, for dihedral angles higher than 70°, ΔG should be positive and ΔG^† high, leading to a low k_PT. This shows that the ESPT reaction of PCyP is coupled to the trans–cis isomerization, namely, the ICT processes resulting from the latter reaction.

To obtain more information about the ESPT process, we have modeled two PT reactions from PCyP to a single water molecule. In these reactions, the dihedral angle of PCyP is constrained to be either 8.7° (Figure 16A) or 179.7° (Figure 16B). The calculations indicate that PCyP is a photoacid with either of these dihedral angles, as the S₁ energy barrier is significantly lower (by ∼10 kcal·mol^–1) than its corresponding S₀ barrier, for the two dihedral angles. Nevertheless, our calculations support our previous conclusions in which the ESPT reaction is more favorable with dihedral angles lower than 70°. While the ESPT reaction with a dihedral angle of 179.7° leads to an energy increase of 15.3 kcal·mol^–1, with a dihedral angle of 8.7°, the reaction proceeds with an increase of only 13.8 kcal·mol^–1.

Figure 16.

Energetic profile of the ESPT from PCyP to a single water molecule, with dihedral angles of (A) 8.7° and (B) 179.7°. S₁ ESP charge transfer between picolinium, cyanine, phenolate, water molecule, and the phenol hydroxy hydrogen, with dihedral angles of (C) 8.7° and (D) 179.7°.

The ESPT reaction with a dihedral angle of 179.7° proceeds by the transfer of negative charge (−0.290e) from the water molecule to the PCyP molecule (Figure 16D). This negative charge is positioned mainly on the cyanine bridge (−0.138e) and on the phenol hydrogen (−0.082e), followed by the picolinium (−0.051e) and phenolate (−0.019e) moieties. This charge-transfer behavior shows some differences from what was observed for the ESPT reaction with a dihedral angle of 8.7° (Figure 16C). This reaction still proceeds with negative-charge transfer (−0.277e) from the water molecule to PCyP but receives the charge differently. The negative charge is positioned mainly on the phenolate (−0.136e) moiety and on the cyanine bridge (−0.108e), but little on the picolinium moiety (−0.058e). In this case, the phenol hydrogen does not receive negative charge but transfers it to the other moieties of PCyP (−0.025e). The fact that the phenolate moiety is the main receiver of negative charge can be explained by its proximity to the positively charged picolinium moiety, with the negative charge being important for creating attractive electrostatic interactions. These results also indicate that the cyanine bridge has a role as an electron reservoir in the ESPT reactions of PCyP. It should also be noted that as both ESPT reactions are based on charge-transfer processes, they should be negatively affected when PCyP is adsorbed on cellulose (which has a low dielectric constant). This should help explain why I_RO^–/I_ROH did not increase by much when PCyP was adsorbed on cellulose, especially because PCyP has a dihedral angle of 179°, at which a higher degree of charge transfer takes place.

Main Findings

Main Findings of Experimental Results

• 1.The ESPT rate constant of PCyP to water is smaller than 10¹¹ s^–1.
• 2.The nonradiative rate of the ROH form is higher than the ESPT rate.
• 3.We estimate the quantum efficiency of the proton transfer to water to be about 0.1.

Main Findings of QM Calculations

• 1.The fluorescence-quenching mechanism is explained by a partial trans–cis isomerization reaction with a dihedral rotation from 179.7° to 71.7°.
• 2.This reaction leads to the formation of a “dark” S₁ state and to a de-excitation pathway caused by nonadiabatic coupling between the S₀ and S₁ states.
• 3.The “dark” S₁ state is an ICT state, with negative-charge transfer from the phenol group to the picolinium and cyanine moieties.
• 4.The partial trans–cis isomerization is governed by an initial negative-charge transfer from the picolinium moiety to the phenol group, followed by back charge transfer.
• 5.The ESPT reaction is coupled to the trans–cis isomerization, as the photoacidity of these molecules is enhanced by the isomerization reaction. This is explained by charge-transfer processes, which make the anionic species a weaker base in the excited-state, thereby stabilizing it.
• 6.The higher k_ESPT of CBCyP is explained by the electron-withdrawing character of its substituents. They should impair the back charge transfer from phenol to picolinium (an essential step for the trans–cis isomerization), thereby disrupting the latter reaction and blocking the reaction competing with the ESPT reaction.

Time Sequence of Events of PCyP in S₁

In the photoacid CBCyP (see Scheme 1c) with pK_a^* ≈ −7, the ESPT occurs prior to solvation and half-twist of the cyanine bridge. The proton transfer constant, τ_PT ≈ 170 fs.

In the photoacid BCyP (see Scheme 1b) with pK_a^* ≈ −5, the solvation controls the ESPT rate with τ_PT ≈ 2 ps.

In the photoacid PCyP with pK_a^* ≈ −1.5, the ESPT time constant is small and estimated to be τ_PT ≈ 2 × 10^–10 s^–1.

The time sequence of events for PCyP in the S₁ state based on the TD-DFT calculations and the low quantum yield of the ESPT process (based on Figure 6) is as follows:

• 1.Solvation in H₂O takes place on 1 ps time-scale.
• 2.Half-twist from ∼180° to 72° takes place on the same time-scale.
• 3.nonradiative S₁ → S₀ at 72° takes place (see Figure 2) in about 10^–11 s.
• 4.The large reduction in the oscillator strength at 72° should take place within 1 ps.
• 5.From the quantum yield of the ESPT (see Figure 6), the ESPT time constant is estimated to be 2 × 10^–10 s^–1.

Scheme 2 shows schematically the major events of PCyP in the first excited singlet state.

Scheme 2. Schematic Depiction of the Photoprotolytic Cycle of PCyP.

CBCyP Computation

The data regarding the charge-transfer reorganization associated with the trans–cis isomerization enable us to explain why CBCyP has a high k_ESPT (∼6.2 × 10¹² s^–1), as opposed to PCyP (<10¹¹ s^–1). The structural difference between CBCyP and PCyP is the presence of two electron-withdrawing substituents (chlorine and an acetoxy group) in the phenol moiety of the former molecule, which is expected to decrease the electron density of the phenol. According the charge density measured for PCyP (Figure 14A), the S₁ trans–cis isomerization is initiated by transfer of negative charge from picolinium to phenol, which leads to a continuous increase in energy until the activation barrier is reached (Figure 12A). This step should be favored for CBCyP, given the electron-depleted character of its phenol moiety because of the electron-withdrawing character of its substituents. However, the next step in the S₁ trans–cis isomerization is charge transfer from phenol to the picolinium moiety, which leads to a continuous decrease in energy until the S₁ energy minimum is reached. Because of the expected electron-depleted nature of the phenol moiety, this charge-transfer step should not be very efficient, a fact which prevents reaching the S₁ minimum. Thus, the electron-withdrawing substituents present in the phenol of CBCyP are expected to disrupt the S₁ trans–cis isomerization reaction and so block the pathway competing with the ESPT reaction. As a result of the limited competition provided by the trans–cis isomerization, the k_ESPT for CBCyP is expected to increase.

The presence of these electron-withdrawing substituents on the phenol moiety of CBCyP should also increase the k_ESPT by affecting the ESPT reaction directly. As already noted, the enhanced photoacidity results from photoinduced charge transfer that stabilizes the anionic (RO^–) form in the excited state make it a weaker base.^11,42 This is achieved by delocalizing the negative charge from the phenolate moiety to the remaining molecule. By introducing electron-withdrawing substituents to the phenol moiety of CBCyP, the electron density of the phenolate moiety is decreased and delocalized throughout the molecule, thereby stabilizing the anion in the S₁ state.

Summary and Conclusions

In this work, we studied the photoprotolytic properties of a newly synthesized photoacid, the PCyP salt, shown in Scheme 1a. We used steady-state and time-resolved fluorescence techniques in this study. When the ground-state ROH form is excited by light at ∼380 nm (the ROH absorption-band peak), the steady-state fluorescence spectrum of PCyP consists of a strong band of the ROH form and a much weaker band of the RO^– form. The RO^– fluorescence is also weak when the RO^– form of the PCyP is directly excited in basic solution (pH > pK_a). We find that the fluorescence of the ROH is about five times stronger than that of the RO^– band when the ROH is excited at pH < pK_a. We therefore conclude that the nonradiative rate constant of the ROH form is about five times that of the ESPT process.

The time-resolved fluorescence shown in Figure 2 shows that the signal shape is wavelength-dependent. The shorter the monitored wavelength, the shorter the average lifetime given by 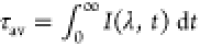. The decay of the signal is nonexponential within the ROH-band wavelength range of 470 < λ < 560 nm. We explain the wavelength dependence of the signal’s shape by a large TD red band shift. This red shift is due to an excited-state solvation process and trans–cis isomerization that leads to a nonradiative process. During these two processes, the transition dipole moment, S₁ → S₀, decreases and the fluorescence intensity decreases. The ESPT rate constant for the PCyP photoacid is smaller than the nonradiative rate, and therefore, the efficiency of the ESPT process is rather low. We estimate that the ESPT rate is smaller than the nonradiative rate by a factor of five, and therefore, the time-resolved signals of the ROH form mimic the red band shift and the trans–cis isomerization and not the ESPT process.

In this article, we also compare the photoprotolytic rates of the PCyP with two other analog compounds, also shown in Scheme 1: the phenol BCyP and the chlorobenzoate cyanine picolinium (CBCyP). The CBCyP compound is a very strong photoacid with a pK_a^* of −6.5 and k_ESPT ≈ 6 × 10¹² s^–1 and τ_ESPT ≈ 170 fs. The time-resolved fluorescence signals are almost identical at all wavelengths of the ROH bands. This is because the ESPT rate is higher than the solvation and the trans–cis processes. The BCyP compound has a smaller ESPT rate constant of about 0.5 × 10¹² s^–1. The ESPT rate is controlled by the solvation dynamics. Therefore, the time-resolved fluorescence is wavelength-dependent because the ESPT process is controlled by the solvation dynamics.

Materials and Methods

Syntheses and General Techniques

The syntheses of the three PCyP salts are described in the Supporting Information section.

Spectroscopy

Fresh solutions of PCyP were used in all measurements. HPLC-grade or analytical-grade solvents were used in this study. All solvents were purchased from Sigma-Aldrich and used as received.

The time-resolved fluorescence was measured by the upconversion technique. The fluorescence of PCyP shown in Scheme 1 was studied in H₂O and in D₂O at room temperature. The laser used for the fluorescence upconversion was a cavity-dumped Ti:sapphire femtosecond laser (Mira, Coherent), which provides short, 120 fs, pulses at about 800 nm. The cavity dumper operated with the low repetition rate of 800 kHz. The upconversion system is a commercial system (FOG-100, CDP, Russia). The samples were excited by second-harmonic-generation pulses of ∼8 mW at wavelengths of 390–420 nm on average. The time response of the upconversion system is determined by the Raman–Stokes line of water, red-shifted by 3600 cm^–1. We found that the full width at half-maximum (fwhm) of the signal is 280 fs and the time resolution is about 100 fs. To avoid photodegradation, samples were placed in a rotating optical cell and rotated at a frequency of 10 Hz. Sample degradation was minimal and did not affect the profile of the signal decay.

For the TCSPC measurements, we used, for sample excitation, the same laser as was used for the fluorescence upconversion system. The TCSPC detection system was based on a Hamamatsu 3809U multichannel plate photomultiplier and an Edinburgh Instruments TCC 900 integrated TCSPC system. The time response of the instrument was approximately 40 ps fwhm. The excitation-pulse energy was reduced by neutral-density filters to about 10 pJ. Experiments were carried out on solutions at concentrations of about 0.5 mM.

The steady-state fluorescence and excitation spectra were measured by a HORIBA Jobin Yvon FluoroMax-3 fluorescence spectrofluorometer.

QM Computational Methods

All calculations were made with the Gaussian 09 program package.⁴³ Geometry optimizations and vibrational calculations were made at the ωB97XD/6-31+G(d,p) level of theory.⁴⁴ The trans–cis isomerization reaction was modeled by performing a relaxed PES scan, with geometry optimization at each point. This PES scan was also performed at the ωB97XD/6-31+G(d,p) level of theory.

The energies of the ground state (S₀) were corrected by performing single-point energy calculations at the ωB97XD/6-311+G(2d,p) level of theory. The PES of the first singlet excited state (S₁) was evaluated by constructing the respective Franck–Condon curves. These are constructed by obtaining the TD⁴⁵ ωB97XD/6-311+G(2d,p) vertical excitation energies at the respective S₀ structures. The validity of constructing Franck–Condon curves arises from the idea that the absorption process can provide valuable insight into the fluorescent properties of a molecule. It should be noted that the absorption spectrum often reflects the main features of the emissive state, differing only by a red shift that occurs as a result of geometrical relaxation of the molecule,⁴⁶⁻⁴⁸ and so, this approach has been used routinely, with good results in the study of photochemical reactions.⁴⁹⁻⁵⁴

All optimization, frequency, and PES scan calculations were performed in implicit water, which was modeled by the use of the integral equation formalism implicit solvation model (IEFPCM).⁵⁵ ωB97XD is a long-range-corrected functional and was chosen because of good results in local n → π*, π → π*, charge-transfer, and Rydberg states.⁵⁶

Closed-shell systems were treated with a restricted (R) approach, whereas open-shell systems were treated with an unrestricted (U) approach and broken-symmetry technology (which mixes the highest occupied molecular orbital and lowest unoccupied molecular orbital).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.7b01888.

• Syntheses and general techniques, multiexponential function fit parameter tables for time-resolved fluorescence of PCyP in H₂O and D₂O, and fluorescence upconversion values of phenol picolinium in H₂O and D₂O (PDF)

The authors declare no competing financial interest.