Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2018 Feb 8;3(2):1653–1662. doi: 10.1021/acsomega.7b01895

Empirical Conversion of pKa Values between Different Solvents and Interpretation of the Parameters: Application to Water, Acetonitrile, Dimethyl Sulfoxide, and Methanol

Emanuele Rossini †,‡, Art D Bochevarov §, Ernst Walter Knapp †,*
PMCID: PMC6641400  PMID: 31458485

Abstract

graphic file with name ao-2017-01895v_0003.jpg

An empirical conversion method (ECM) that transforms pKa values of arbitrary organic compounds from one solvent to the other is introduced. We demonstrate the method’s usefulness and performance on pKa conversions involving water and organic solvents acetonitrile (MeCN), dimethyl sulfoxide (Me2SO), and methanol (MeOH). We focus on the pKa conversion from the known reference value in water to the other three organic solvents, although such a conversion can also be performed between any pair of the considered solvents. The ECM works with an additive parameter that is specific to a solvent and a molecular family (essentially characterized by a functional group that is titrated). We formally show that the method can be formulated with a single additive parameter, and that the extra multiplicative parameter used in other works is not required. The values of the additive parameter are determined from known pKa data, and their interpretation is provided on the basis of physicochemical concepts. The data set of known pKa values is augmented with pKa values computed with the recently introduced electrostatic transform method, whose validity is demonstrated. For a validation of our method, we consider pKa conversions for two data sets of titratable compounds. The first data set involves 81 relatively small molecules belonging to 19 different molecular families, with the pKa data available in all four considered solvents. The second data set involves 76 titratable molecules from 5 additional molecular families. These molecules are typically larger, and their experimental pKa values are available only in Me2SO and water. The validation tests show that the agreement between the experimental pKa data and the ECM predictions is generally good, with absolute errors often on the order of 0.5 pH units. The presence of a few outliers is rationalized, and observed trends with respect to molecular families are discussed.

Introduction

The acid dissociation constant Ka measures the strength of an acid in a solution. It is a key quantity for the functionality of molecules with variable protonation. For practical purposes, one uses the negative decadic logarithm of Ka, also known as pKa. The determination of this quantity, performed in different protic and aprotic solvents, is particularly important for both applied and fundamental physicochemical sciences.1−3

The pKa value also plays a central role in drug discovery. This value influences solubility, membrane permeability, clearance, and binding of a drug molecule to the target protein.4−9 About two-third of the approved pharmaceutical compounds contain ionizable groups, usually in the pH range between 3 and 11 with a maximum at 8.5.5 Before a drug can exercise its function in the living cell environment, it has to penetrate the cytoplasmic membrane, which is structurally composed of a lipid bilayer. The inside of such cell membranes is much less polar than water. Charged compounds are generally better soluble in water than in apolar solvents, whereas charge-neutral compounds are better soluble in apolar solvents. The lipophilicity is maximized for a protonation form with zero charge,6 and therefore it is this form of a molecule that can penetrate the membrane most efficiently.

The pKa value of a drug is important for passive renal tubular reabsorption.10−12 Many drugs are either weak acids or bases. Their clearance and absorption behavior depends on urine pH that can vary from 4.5 to 8.0. Whereas weakly acidic drugs are reabsorbed from acidic urine, weakly basic drugs tend to be reinternalized in basic urine. Hence, by knowing the pKa of the drug molecule, one can more effectively predict the clearance and its tubular reabsorption process as a function of pH. For all these reasons, the design of successful drug compounds could greatly benefit from a fast and accurate methodology to predict the pKa of a molecule in apolar nonaqueous solvents.

There are different approaches for computing or predicting the pKa values ranging from empirical methods to ab initio methods. The latter employ quantum chemistry usually combined with electrostatics and occasionally also with molecular dynamics (MD). A recent work on proton solvation in different solvents13 provides an overview of such pKa computations for organic compounds. The empirical methods, on the other hand, relate their pKa to specific features of titratable molecules like molecular structure, semiempirical molecular orbital theory, atomic charges, philicity, and others.14−22

It is demonstrated that converting the computed pKa values of a set of 34 titratable compounds among the organic solvents acetonitrile (MeCN), dimethyl sulfoxide (Me2SO), and tetrahydrofuran can be essentially performed with an additive shift parameter that depends only on the two solvents but not on the nature of the molecules.23 For dimethyl sulfoxide (DMSO), it is demonstrated that the computed pKa values agree very well with the measured values such that this conversion should be also valid among experimental pKa values. These results suggest that for the mentioned organic solvents, only a solvent specific shift parameter is necessary, and that specific solute–solvent interactions have no influence on the pKa values. In an earlier work,24 the experimental pKa values in water and methanol are compared for a much larger set of molecules. It is found that essentially an additive shift parameter is necessary for converting the pKa values between the two solvents. However, it is necessary to use different values of the shift parameter for different groups of molecules. This may be partly due to the much larger set of considered molecules but also due the involvement of water, which has a stronger interaction with charged solutes.

Here, we introduce a fully empirical approach that converts the pKa values known in aqueous solution to pKa values of the same compound in other solvents. A key feature of our approach is the assignment of a titratable molecule to a specific family of titratable molecular groups. The molecular families of compounds follow the categorization scheme defined in ref (25). These families are selected according to the degree of homogeneity among the chemical functional groups characterizing their components, which can influence the pKa values of their titratable groups. To convert a pKa value between two solvents, one needs a single additive shift parameter for each molecular family and pair of solvents. Such families of titratable molecular groups are previously used in the context of empirical prediction of pKa values in aqueous solvent,25,26 and family-specific linear functions serve for interconversion between the estimated pKa values.

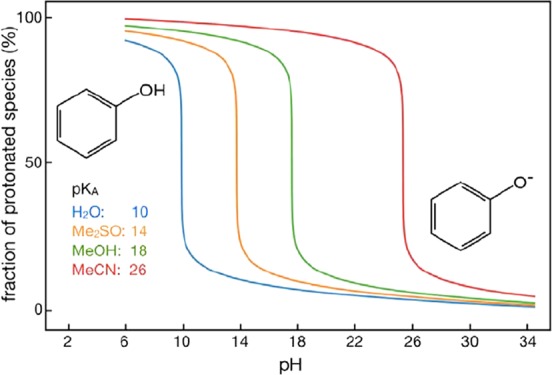
Solvent molecules can either possess or not possess polar hydrogen atoms, and the corresponding solvents are called protic or aprotic, respectively. One of the most typical protic solvents is water, which involves only polar hydrogens. Acetonitrile (MeCN) and dimethyl sulfoxide (Me2SO) constitute typical aprotic solvents. These are pharmacologically relevant solvents because they are of lower polarity and can therefore mimic the interior of the membranes, which need to be penetrated by drug molecules to reach their targets. On the other hand, methanol (MeOH) possesses both polar and nonpolar hydrogens and is therefore a solvent that is neither protic nor aprotic. Products of methanol oxidation are toxic in living cells. However, methanol can be considered as a model system that mimics the situation in a living cell consisting of a mixture of water with a high concentration of proteins and organic molecules that are neither protic nor aprotic.

In the present study, we consider two data sets. The first data set focuses on titratable compounds of small size, for which measured pKa values are known in water and preferentially also in several of the considered three organic solvents. This data set is provided in Tables S1–S7 in the Supporting Information. It comprises 81 titratable compounds assigned to 19 different families (Figure 1). The 81 chosen titratable compounds are typical members of their molecular families. For this data set, 87 measured pKa values are available in the three considered organic solvents. In 107 cases, where no measured pKa values are available for some organic solvents, we compute them by the electrostatic transform method (ETM) using the measured pKa values in other solvents.27 To demonstrate the validity of the ETM, the pKa values are computed in 35 cases and compared with the known measured pKa values, yielding a root mean square deviation pKa value (pKa-RMSD) of 0.77 pH units.

Figure 1.

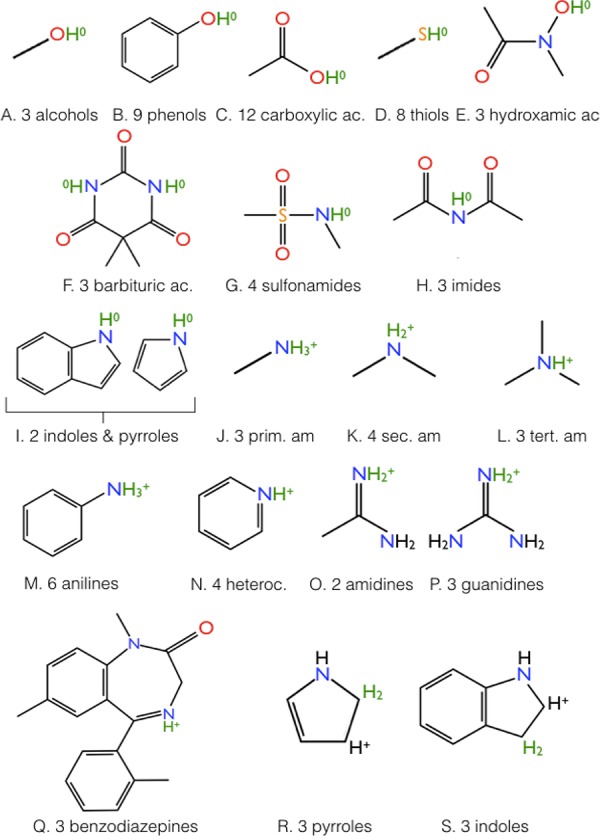
Figure 1

Open in a new tab

First data set of titratable molecules involves 81 molecules in nineteen different molecular families (A–S). The detailed data are listed in Tables S1–S7 of the Supporting Information. The number of molecules of a specific family is given after the one-letter family name. The molecules are displayed in the protonated state with titratable protons in green color, whereas the other polar hydrogens are displayed in black. For the families O and P only one resonance structure is shown, but, all displayed hydrogen atoms are equivalent and titratable. Nonpolar hydrogens are not displayed. For the families R and S protonation of the carbon atom C2 and C3, respectively, converts the double bond between the two carbon atoms to a single bond. As a consequence the excess positive charge is localizes at the carbon atom, which is not protonated. The formal charge localized at the titratable hydrogen is denoted as a superscript. Oxygen, nitrogen, and sulfur atoms are highlighted in red, blue, and yellow color, respectively.

We also provide the pKa values in water obtained with the Jaguar pKa prediction method (JPM),28,29 which is based on the work of Friesner et al.25 JPM assembles a reference pKa value from gas phase and solution phase energies of protonated and deprotonated species, using the density functional theory B3LYP as implemented in Jaguar. The predicted pKa value is obtained from the reference pKa value with a linear regression scheme involving adjustable parameters for different molecular families. In the present work, the pKa values in water obtained with the JPM are used as reference values for converting them to the pKa values in the other solvents. The JPM predictions serve as a substitute for measured pKa values in water because the pKa values of the JPM are readily available for practically all different types of titratable molecules. The parameters of the presently proposed empirical conversion method (ECM) are determined by matching the pKa values with 87 measured and 107 pKa values computed with the electrostatic transform method (ETM). The quality of the ECM is evaluated by comparing the measured pKa values and those computed with ETM, with the corresponding ones obtained through ECM.

The second data set involves 76 titratable compounds belonging to 5 different additional molecular families. These molecules are generally of larger size. Here, the measured pKa values are mainly available in DMSO only. The corresponding pKa values in DMSO are predicted with Jaguar whenever possible. The measured pKa values in DMSO are used to compute the pKa values in water through ETM. Subsequently, the measured and ETM pKa values are used to establish the ECM for the five molecular families. The same operation is performed employing the measured pKa values in DMSO and the pKa values in water obtained with the JPM.26 Here, the quality of the ECM is evaluated by comparing the ECM pKa values in water with the corresponding ETM and JPM pKa values.

Methods

Basic Theory of pKa Computation

Through the years, many different approaches have been developed for computing or predicting the pKa value of a molecule in different solvents. Among these methods, there is a popular strategy based on the exploitation of a thermodynamic cycle that describes the process of proton dissociation.30−33 In such a cycle, gas and solvent phases are considered. The gas-phase free energy of deprotonation (i.e., the proton affinity) is computed as

graphic file with name ao-2017-01895v_m001.jpg 1

where Ggas(M) is the gas-phase free energy of molecular species M. The gas-phase free energy of the proton in the standard state T = 298.15 K and 1 mol/L is given as34,35

graphic file with name ao-2017-01895v_m002.jpg 2

The difference in solvation free energies of the deprotonated (A– + H+) and protonated (AH) molecular species given by

graphic file with name ao-2017-01895v_m003.jpg 3

describes the influence of the solvent environment on the energetics of the protonation process. If the nonelectrostatic part of the binding free energy of a proton to a solute molecule does not depend on the particular solvent environment, which is often the case, the energetics of a protonation process in a solvent environment can be described as the sum of free energy differences in the gas-phase and solvent yielding with eqs 1 and 3

graphic file with name ao-2017-01895v_m004.jpg 4

According to a thermodynamic relation, the resulting free energy difference can be used to evaluate the pKa value31−33

graphic file with name ao-2017-01895v_m005.jpg 5

Empirical pKa Conversion Method (ECM)

We seek a simple molecular family specific function gf, with parameters to be optimized, that converts the pKa value of a compound Yf belonging to family f from solvent j (which, in the present case, is water) to one of the three considered organic solvents i

graphic file with name ao-2017-01895v_m006.jpg 6

This problem is related to the electrostatic transform method (ETM), which was recently introduced.27 With the ETM, the measured or computed pKa value of a titratable compound Y can be transformed from one solvent (j) to another (i) using only contributions from solvation energies of the two considered solvents according to the following relation

graphic file with name ao-2017-01895v_m007.jpg 7

The terms ΔGsolv(Y) = Gsolv(Y–) – Gsolv(YH) in eq 7 are the electrostatically computed differences of solvation free energies (deprotonated minus protonated) of compound Y and Gsolv(U+, i) together with Gsolv(H+, j) are the free energies of proton solvation of the two solvents (i and j). In the following text, the energy differences ΔGsolv(Y, i) – ΔGsolv(Y, j) are tabulated in pH units.

In the ETM methodology,27 atomic partial charges of a molecule are determined by matching the electrostatic potential generated by the electronic wave function and the nuclear charges with the electrostatic potential from atomic point charges using the restrained electrostatic potential procedure.36,37 The electronic wave function of the geometry optimized molecule is computed with the B3LYP functional in combination with the double-ζ basis set 6-31G. Finally, the electrostatic solvation energies of the protonated and deprotonated molecular species are computed by solving the Poisson equation with the program SOLVATE, from the program suit MEAD.38,39

The ETM works properly under the following three conditions: (1) variations in the molecular conformations in the environment that can be either a liquid or even the gas phase do no influence the pKa value or do not even occur. (2) The charge pattern of protonated and deprotonated molecular species does not depend on the environment, i.e., the charge distribution is the same in the gas phase and different solvents. (3) The nonelectrostatic part of the energy difference between protonated and deprotonated molecular species does not depend on the environment, i.e., it is the same in gas phase or different solvents. Under these conditions, the ETM procedure has been proven to work with an accuracy of 0.7 pH units when applied to transform pKa values of compounds between water, MeCN, Me2SO, and MeOH.27 However, it should be noted that these conditions might not be satisfied for some titratable compounds considered in the present study.

The strategy to transform pKa values from one environment to another is also performed for titratable residues in proteins.40−50 In this case, the pKa values are transformed from aqueous solution to the corresponding protein environment, which is represented by the atomic point charges embedded in a low dielectric medium. The accuracy of the computed pKa values in proteins is typically in the range of 1 pH unit or above, where one critical source of error is the uncertainty in the atomic coordinates of the protein model. This is particularly the case if the protein model is solely based on the crystal structures. Alternating the protein crystal structures by modeling51,52 or molecular dynamics (MD) simulations53 helps reduce the pKa-RMSD, which for MD simulations is significantly below 1 pH unit.

Empirical schemes have already been used for converting measured pKa values between different solvents. They were applied to a set of phenols (Ph) using multiplicative (A = 1.68) and additive (B = 9.80) parameters54 converting the pKa values from water (WAT) to acetonitrile (ACN) according to

graphic file with name ao-2017-01895v_m008.jpg 8

A linear transformation is also used to convert approximately computed pKa values for water25,29,55−57 and acetonitrile40 into pKa values comparable to experiment. Thereby, the parameter A compensates mainly for deficiencies of the quantum chemically computed energies and the electrostatic solvation energies, whereas the additive parameter B accounts mainly for the lack or insufficient accuracy of vibrational energies, entropy, and proton solvation energy.27

The ETM and its eq 7(27) demonstrates that no multiplicative factor like A in eq 8 is necessary to convert pKa values between different solvents, if the pKa value of the reference solvent is precise. In other work, it is demonstrated that the pKa values can be converted between different organic solvents with eq 8 with a multiplicative factor A close to unity.23,24 Therefore, we advocate the use of the simplified linear function

graphic file with name ao-2017-01895v_m009.jpg 9

to convert the pKa value of a compound Yf belonging to the molecular family f from the solvent j to the solvent i. Test computations show no detectable improvement if the more general linear function, eq 8, was used.

The validity of the electrostatic transform method (ETM) requires that the molecular conformation and the atomic partial charges be the same in gas phase and solutions. In contrast, the empirical conversion method (ECM), eq 9, is more general and can account for such dependencies as well as for solvent-dependent shifts in the electronic energies, if they are the same for the considered molecular family. The accuracy of the ECM depends on the appropriate choice of the molecular families and can be improved by using more molecular families.

Results and Discussion

First Data Set of Titratable Molecules

Let us begin with an application of our method to the first data set of titratable molecules, shown in Figure 1. Our empirical conversion method (ECM) will be used to transform the pKa values from water to three organic solvents: acetonitrile (MeCN), dimethyl sulfoxide (Me2SO), and methanol (MeOH). As reference pKa values in water, we use the pKa values computed with the Jaguar pKa prediction method (JPM), alternatively referred to as simply Jaguar. The pKa values computed with Jaguar apply a semiempirical scheme where an approximate “raw” pKa value is converted by a linear function with adjustable parameters that depend on a molecular family. These reference pKa values are used to optimize the parameters ΔpKaf of eq 9. For comparison, we also provide the corresponding experimental pKa values in water. The deviation between the measured pKa values in water and those predicted by Jaguar varies for the 19 different molecular families of the first data set, but is on the average less than 0.5 pH units for the considered titratable molecules. However, for some families in some solvents, it can be larger. Detailed data are given in Tables S1–S7 of the Supporting Information.

In this study, the ECM, eq 9, is established for 81 titratable compounds of the first data set represented by the nineteen different molecular families from Figure 1. The additive parameters ΔpKaf are optimized by fitting the pKa values of the ECM to the measured benchmark pKa values for the three organic solvents using the predicted JPM pKa values in water as a basis. For pure Me2SO, the measured pKa values are available for many organic compounds (37 for the considered set of titratable compounds).58 However, there are fewer measured pKa values available for the pure solvents of MeCN (23 for the considered set of titratable compounds) and MeOH (27 for the considered set of titratable compounds). In the two latter solvents, the pKa measurements are often performed in mixtures with water. However, the pKa values measured in mixtures with water may be biased by water molecules clustering around the polar atoms of the titratable groups. Hence, such measurements are not considered for the set of benchmark pKa values.

For seven molecular families [barbituric acids (F), imides (H), amidines (O), guanidines (P), benzodiazepines (Q), pyrroles C (R), and indoles C (S)], the measured pKa values are not available in any of the three considered organic solvents. Therefore, to enlarge the database of benchmark pKa values for the first data set and obtain a more representative set of known pKa values for the three organic solvents, the ETM27 is applied. The accuracy of this method is generally high and allows optimizing the parameters on a larger set of benchmark pKa values to convert the pKa values between the three organic solvents. However, the ETM has a limited range of applicability, as discussed above. Therefore, we apply it to small molecules, where the gas-phase geometry is the same as in solutions. We also make sure that the computed atomic partial charges determined in vacuum are appropriate for the solution phase.

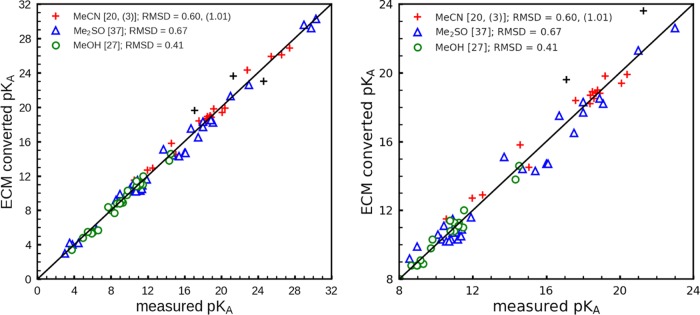
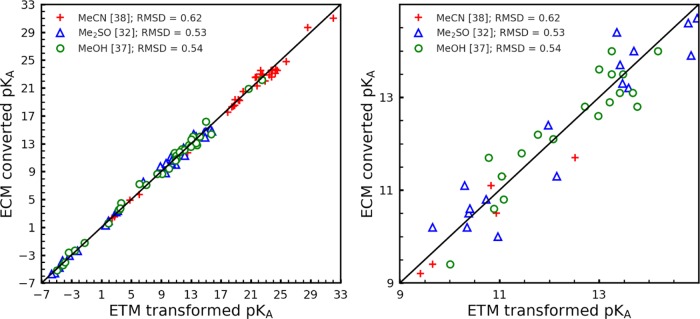
In Figure 2, the ECM pKa values are plotted versus the measured values. The pKa-RMSD values are 0.60, 0.67, 0.41 pH units for 20 (excluding 3 outliers), 37, and 27 measured pKa values in acetonitrile, dimethyl sulfoxide, and methanol, respectively. In Figure 3, the ECM pKa values are displayed versus the pKa values computed with the ETM27 that uses the measured pKa values in water for the transformation to the other solvents. In this case, the pKa-RMSD values are 0.62, 0.53, 0.54 pH units for 38, 32, 37 transformed pKa values in acetonitrile, dimethyl sulfoxide, and methanol, respectively. Hence, the pKa-RMSD values between empirically converted pKa values and pKa values obtained with the ETM are nearly as small as the pKa-RMSD values between empirically converted and experimental pKa values, which demonstrates the quality of the pKa values obtained with ECM.

Figure 2.

Figure 2

Open in a new tab

Correlation diagram for the empirical conversion method (ECM). ECM versus measured pKa values are plotted for the first data set. The ECM pKa values are evaluated according to eq 9 using the pKa values in water obtained with the Jaguar pKa prediction method (JPM)28,29 as the basis. The three outliers for MeCN are denoted by black crosses (+). The numerical values of the pKa are listed in Tables S1–S7 of the Supporting Information. The left part of the figure displays all of the data. The right part is a close-up that focuses on the center pH interval.

Figure 3.

Figure 3

Open in a new tab

Correlation diagram for the empirical conversion method (ECM). ECM pKa values are plotted versus with the electrostatic transform method (ETM)27 computed pKa values for the first data set. The ECM pKa values are evaluated according to eq 9 using the pKa values in water obtained with the Jaguar pKa prediction method (JPM)28,29 as the basis. The ETM uses the measured pKa values in water for the transformation to other solvents. The numerical values of the pKa are listed in Tables S1–S7 of the Supporting Information. The left part of the figure displays all of the data. The right part is a close-up that focuses on the center pH interval.

The values of the empirical pKa shift parameters ΔpKaf that appear in eq 9 are listed in Table 1 for the nineteen considered molecular families. They describe the family (f) specific shifts of the pKa values in water to obtain the pKa values in the other three organic solvents. For MeCN the shift parameters of the pKa values (ΔpKaf) are systematically larger by about 8 pH units compared to the corresponding values for Me2SO. This is due to the difference in proton solvation energies relative to the value in water. The proton solvation energies are −255.1, −266.4, and −265.9 kcal/mol for MeCN, Me2SO, and MeOH, respectively.13 They correlate with the pKa values that these solvent molecules have in aqueous solution.13 In water the corresponding proton solvation energy determined by matching computed and measured pKa values for a suitable set of titratable organic molecules is −266.3 kcal/mol.13 This value is slightly lower than the consensus value of −265.9 kcal/mol.59,60 The differences of the proton solvation energies relative to the value in water are 11.2, −0.1, and 0.4 kcal/mol for MeCN, Me2SO, and MeOH, respectively. Converting these energy values into pH units by means of eq 5, we obtain at T = 298 K the values 8.22, −0.07, and 0.29 for MeCN, Me2SO, and MeOH, respectively. These values where subtracted from the pKa shift parameter ΔpKaf yielding the values in the last three columns of Table 1. They show the contributions to the pKa shift parameter [ΔpKa] relative to water, which are due to the solvation energy differences of the deprotonated and protonated molecular species. According to eq 7, the solvation energy difference corresponding to the pKa shift between water and another solvent (solv) is given by

graphic file with name ao-2017-01895v_m010.jpg 10

The corresponding contribution to the pKa shift relative to water without the contribution from proton solvation is

graphic file with name ao-2017-01895v_m011.jpg 11

The nineteen molecular families of the first data set, Figure 1, can be split into two groups. The molecules of the first group (A–I) possess a neutrally charged titratable group in the protonated state with a single proton attached to oxygen, sulfur, or nitrogen atoms. The molecules of the second group (J–Q) possess a positively charged titratable group in the protonated state with a proton attached to nitrogen or an additional proton attached to carbon.

Table 1. Parameters that Shift pKa Values from Water to MeCN, Me2SO, and MeOH for the First Data Set of Nineteen Molecular Families as Depicted in Figure 1a.

    ΔpKa, eq 9, relative to water
 [ΔpKa], eq 11, relative to water without proton solvation
No. molecular family MeCN Me2SO MeOH MeCN Me2SO MeOH
A 3 alcoholsb 13.20 13.27
B 9 phenols 16.30 7.90 4.00 8.08 7.97 3.71
C 12 carboxylic acids 15.50 7.20 5.00 7.28 7.27 4.71
D 8 thiols 12.70 3.70 2.20 4.48 3.77 1.91
E 3 hydroxamic acids 15.00 6.60 5.00 6.78 6.67 4.71
F 3 barbituric acids 15.40 6.50 4.70 7.18 6.57 4.41
G 4 sulfonamides 12.80 4.50 4.20 4.58 4.57 3.91
H 3 imides 15.00 5.70 4.10 6.78 5.77 3.81
I 2 indoles and pyrroles N 14.20 5.80 5.40 5.98 5.87 5.11
               
J 3 primary amines 7.70 –0.50 0.30 –0.52 –0.43 0.01
K 4 secondary amines 7.90 0.20 0.20 –0.32 0.27 –0.09
L 3 tertiary amines 8.30 –0.40 0.20 0.08 –0.33 –0.09
M 6 anilines 6.80 –0.70 0.80 –1.42 –0.63 0.51
N 4 heterocycles 7.70 –1.00 0.30 –0.52 –0.93 0.01
O 2 amidines 9.90 1.80 1.20 1.68 1.87 0.91
P 3 guanidines 9.50 1.40 0.60 1.28 1.47 0.31
Q 3 benzodiazepines 7.30 –0.60 –0.30 –0.92 –0.53 –0.59
R 3 pyrroles (C-2 prot.) 6.60 –1.50 –0.30 –1.62 –1.43 –0.59
S 3 indoles (C-3 prot.) 6.90 –1.10 –0.30 –1.32 –1.03 –0.59
               
  first group B–I 14.70 6.00 4.20 6.48 6.07 3.91
  second group J–S 7.80 –0.30 0.30 –0.42 –0.23 0.01
Open in a new tab
a

The first column denotes the family by single letter code and gives the number of compounds considered for this family. The first three columns with numbers list the shift of pKa values (ΔpKa) in MeCN, Me2SO, and MeOH relative to the values in water. In the last three columns, the contributions from the proton solvation energies (in pH units: 8.22, −0.07, and 0.29 for MeCN, Me2SO, and MeOH, respectively) were subtracted from ΔpKa yielding [ΔpKa], eq 11. The last two lines contain the pKa shift parameters, if only two groups of families are considered as described in text.

b

No experimental pKa values are available in MeCN and MeOH and the electrostatic transform method (ETM) fails to yield proper values.

For the first group of nine molecular families (A–I), the values of solvation energy differences ΔΔGsolv(A–/AH) [defined by eq 10] and consequently also [ΔpKa] (defined by eq 11 and listed in Table 1) are significantly positive. This indicates that deprotonation in one of the three considered organic solvents is energetically less favorable than in water. This is due to the fact that in the negatively charged deprotonated state, the molecules are better solvated in the protic solvent water than in the aprotic solvents acetonitrile and dimethyl sulfoxide. Because methanol is neither protic nor aprotic, the corresponding values of [ΔpKa] are less positive for methanol.

For the other ten molecular families (J–S) belonging to the second group of families, the [ΔpKa] values are generally close to zero, yielding shift parameters ΔpKa that depend mainly on the proton solvation energy. These molecular families have two common features. (i) In the protonated state, they have a positively charged titratable group. (ii) The titratable atom is either nitrogen or carbon to which several hydrogen atoms are attached (except for tertiary amines, family K), and so they possess generally less polar titratable groups than the molecules of the first group of molecular families. Therefore, the solvation energies of these molecules differ less between protic and aprotic solvents than for molecules belonging to the first group.

Simplified pKa Prediction Model that Ignores Detailed Molecular Family Dependencies

In contrast to the pKa prediction model that requires the use of nineteen molecular families for applying the electrostatic conversion method (ECM) to the first data set, a very approximate scheme may use just two different sets of molecular families. However, one cannot dispense with the dependence on the solvent because the pKa shift parameters [ΔpKa] are systematically larger for MeCN than for Me2SO and MeOH. The first set involves the families B to I, where the pKa shift parameters are generally large (Table 1). What is common about these titratable compounds is that their titratable group is charge neutral in the protonated state. The family of alcohols (A) is excluded because for them, the necessary ΔpKa values (albeit available only for Me2SO) are considerably larger than for other compounds. This difference may correlate with the fact that the ETM fails to provide proper pKa values for this family. A reason for this failure could be solvent-specific interactions that are not included in an electrostatic continuum model of the solvent. The second set comprises the molecular families J–S (Table 1). Here, the pKa shift parameters [ΔpKa] are small for all three organic solvents. These compounds are similar in that their titratable group is positively charged in the protonated state and involves a nitrogen or carbon atom to which several hydrogen atoms are attached in the protonated state. The corresponding values of the pKa shift parameters are listed in the last two lines of Table 1. The overall pKa-RMSDs for all three considered organic solvents are 1.37 and 0.96 for the first and second set of molecular families, respectively, which is reasonably small to serve as a rough approximation.

Second Data Set of Titratable Molecules

The second data set involves 76 titratable molecules from 5 specific families (Figure 4). It is of high interest to know the pKa values of these compounds in water. Unfortunately, experimental pKa values for this data set are scarce and practically only available for DMSO. The majority of these molecules are of larger size and are more flexible than the molecules from the first data set. Therefore, the pKa values computed with the electrostatic transform method (ETM) are not necessarily as reliable as for the first data set. But the ETM is nevertheless a practical tool to obtain estimates of the pKa values in water. In addition to ETM, the Jaguar prediction scheme is also applied for obtaining the pKa values in water. Both sets of pKa values in water are used to establish alternative ECM for the pKa values in water. For two families (cyano- and keto-compounds), the Jaguar prediction scheme is applicable in DMSO. A comparison of these predicted pKa values with the measured pKa values yielded pKa-RMSD of 1.32 and 1.85 pH units for the families of cyano- and keto-compounds, respectively. However, it should be noted that the Jaguar prediction scheme for DMSO is still in preliminary stage of development and needs to be improved. Detailed data are listed in Tables S8–S12 of the Supporting Information. The correlation diagram between ECM (converted) and ETM (transformed) pKa values is shown in Figure 5 for all five molecular families of the second data set. If the outliers are discarded, then the pKa-RMSDs differ by less than 0.8 pH units.

Figure 4.

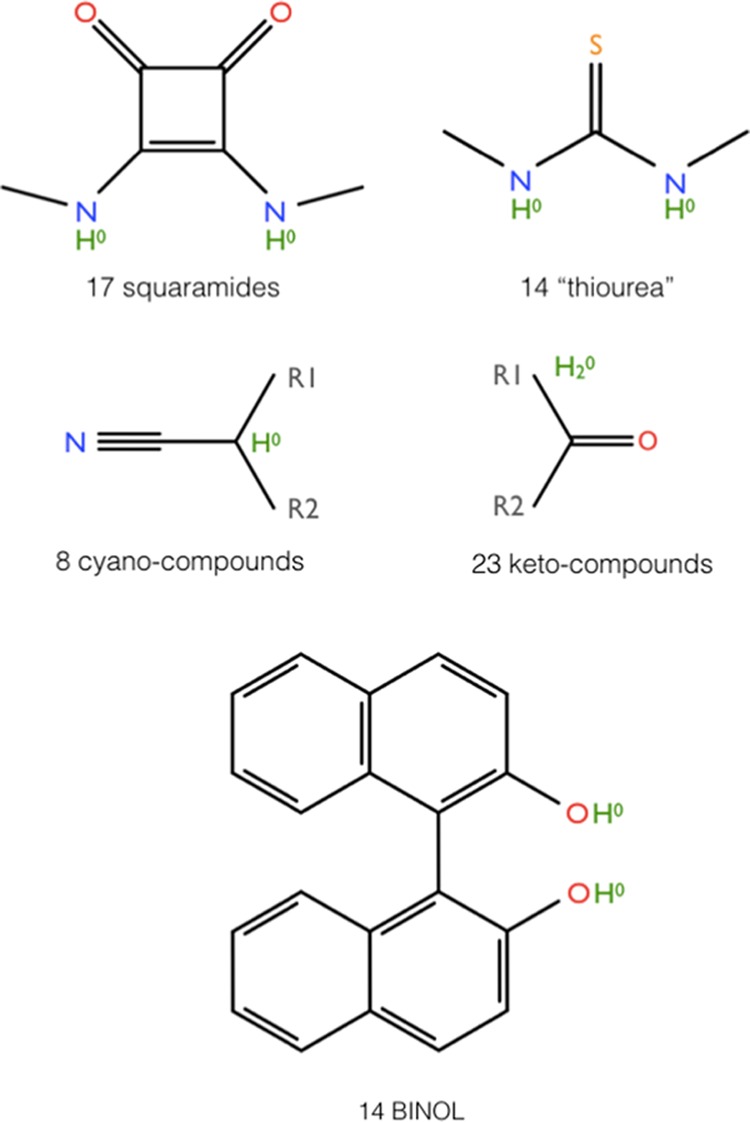
Figure 4

Open in a new tab

The second data set of titratable molecules involves 76 molecules in 5 different molecular families displayed in the protonated state. The detailed data are listed in Tables S8–S12 of the Supporting Information. The number of molecules of a specific family is given before the family name. Titratable hydrogens carry the formal charge zero for all five families and are shown in green. Oxygen, nitrogen, and sulfur atoms are highlighted in red, blue, and yellow, respectively.

Figure 5.

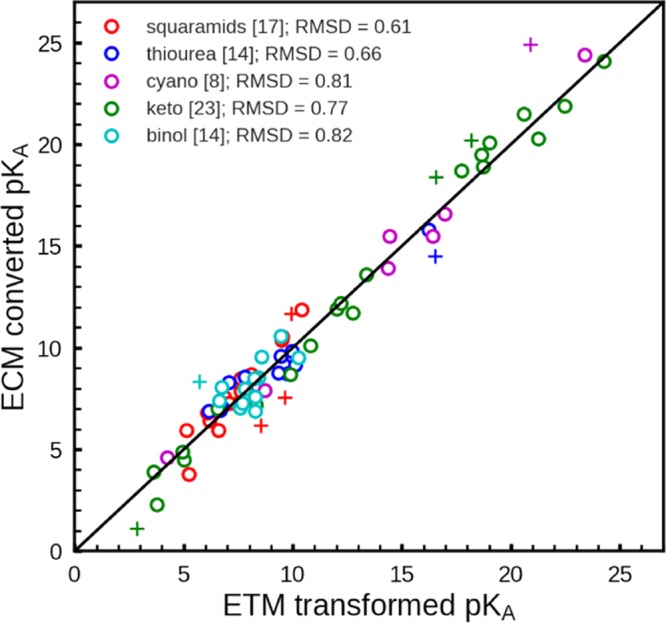
Figure 5

Open in a new tab

Correlation diagram for the empirical conversion method (ECM). ECM (converted) pKa values are plotted versus the electrostatic transform method (ETM)27 computed pKa values for the second data set. The latter are based on measured pKa values in DMSO. The ECM pKa values are evaluated according to eq 9 using preliminary pKa values in DMSO obtained with the Jaguar pKa prediction method (JPM)28,29 as the basis. The number of compounds for the individual molecular families is given in the rectangular brackets. Outliers where the pKa values differ by more than 1.5 pH units are denoted with “+”. The numerical values of the pKa are listed in Tables S8–S12 of the Supporting Information.

The titratable groups in the molecules of the second data set carry for all five molecular families zero formal charge (Figure 4). For the molecular families squaramides, thiourea, and BINOL, the titratable hydrogen is attached to nitrogen or oxygen. These molecular families are therefore analogous to the families A–I of the first data set (Figure 1), where the values of [ΔpKa], eq 11, are significantly larger than zero. Because the proton solvation energy is nearly the same for water and DMSO, the shift parameters ΔpKa involving also proton solvation are nearly equal to the shift parameters [ΔpKa] without proton solvation. Hence, for the same reason as described before, we expect significantly positive values of the shift parameters, ΔpKa. This is indeed the case (see Table 2).

Table 2. Parameters Shifting pKa Values from Water to Me2SO for the Second Data Set Consisting of Five Molecular Families as Depicted in Figure 4a.

    ΔpKa, eq 9, relative to water
No. molecular family based on ETM based on JPM
17 squaramides 4.60 4.50
14 thiourea-compounds 3.70 1.40
8 cyano-compounds 6.40 6.00
23 keto-compounds 6.30 6.20
14 BINOL-compounds 2.40 2.60
Open in a new tab
a

The first column gives the number of compounds considered for the corresponding molecular family. The last two columns contain the values of the pKa shift parameter ΔpKa. They convert the pKa values from water to Me2SO according to eq 9. In this application, the shift parameters are determined by converting the measured pKa values in Me2SO to the corresponding values in water. The third column contains the values of ΔpKa obtained by using the pKa values in water that were computed with the electrostatic transform method (ETM), whereas in the last column ΔpKa are obtained using the pKa values in water computed with the Jaguar pKa prediction method (JPM).

The other two molecular families of cyano- and keto-compounds have the titratable hydrogen attached to carbon atom. They should therefore be analogous to the molecular families R and S of the first data set, where the [ΔpKa] parameters are close to zero. But, for the cyano- and keto-compounds, the pKa shift parameter ΔpKa adopts values above 6 pH units. Hence, the deprotonated cyano- and keto-compounds must be much more polar than the deprotonated indoles and pyrroles (molecular families R and S). In the latter case, the carbon atoms are part of an aromatic ring system, which may be responsible for lower polarity of the deprotonated state of these compounds. However, another difference is the formal charge of the titratable group in the protonated state. This charge is positive for the molecular families R and S of the first data set, but neutral for the cyano- and keto-compounds of the second data set, which is in analogy to the molecular families A–I of the first data set. Therefore, the cyano- and keto-compounds are indeed more polar in the deprotonated state than the deprotonated pyrroles and indoles of the molecular families R and S, which explains the large values of the pKa shift parameters ΔpKa.

Comparing the values of the shift parameters for the molecular families of the second data set by using the ETM or the JPM pKa values in water, we obtain practically the same values except for the thiourea compounds (Table 2). This general agreement demonstrates the reliability of the computed pKa values in water. However, for thiourea, the shift parameters deviate by 2.3 pH units, which is considerable. Unfortunately, no measured pKa values in water are available for thiourea compounds to resolve this discrepancy. These deviations may be connected with the sulfur atomic radii of 2.00 and 2.18 Å used in water and DMSO,13,27 respectively, which have not yet been tested sufficiently carefully.

For cyano- and keto-compounds, the measured pKa values in water are available in a few cases. We also found the measured pKa values in water for four different keto-compounds (Table S10 of the Supporting Information). Except for cyclobutanone, the measured pKa values agree well with the corresponding values obtained by ETM and JPM, supporting our approach to establish the empirical conversion method (ECM) with the pKa values in water obtained with ETM and JPM. For cyano-compounds, we found only two measured pKa values. These are 25.061 and 11.262 for CH3CN and CH2(CN)2, respectively (Table S10 of the Supporting Information). These values deviate considerably from 20.89 and 4.25 computed with ETM or 19.23 and 7.96 obtained with JPM, respectively. Interestingly, the ECM pKa values for CH3CN in water are 24.90 and 25.30, if based on the ETM or JPM pKa values in water, respectively. Hence, the ensemble of molecules considered for the family of cyano-compounds makes sure that the ECM estimate of the pKa value of CH3CN is appropriate. However, this is not the case for the pKa value of CH2(CN)2, where the pKa values in water estimated with ECM are 4.60 and 5.00, if based on the ETM or JPM pKa values in water, respectively. According to the measured pKa values of CH2(CN)2 in DMSO (11.2) and water (11.0), which are practically equal, [CH(CN)2]− should solvate equally well or even better (because CH2(CN)2 is aprotic as is DMSO) in DMSO than in water. On the other hand, the measured pKa values of CH3CN in water (31.3) and DMSO (25.0) suggest that [CH2CN]− solvates better in water than in DMSO. Hence, the measured pKa value of CH2(CN)2 in water being practically equal to the value in DMSO is not very plausible.

Summary

The empirical pKa conversion method (ECM) predicts the pKa values of titratable compounds in organic solvents using known pKa values in water. The concept of the ECM, which uses a molecular family dependent parameterization, seems to work also for large and even flexible molecules. This indicates that the dependencies of pKa values on molecular conformations and interactions of the titratable group with other functional molecular groups within the solute molecule are moderate at least for the molecules studied in this work. The ECM procedure uses a single additive shift parameter. It is explained why an additional multiplicative shift parameter is not useful. Two data sets of titratable molecules are considered. The first data set involves 19 different molecular families with 81 different titratable compounds. Molecular family and solvent-specific additive pKa shift parameters ΔpKa are evaluated relative to the pKa values in water, which, in their turn, are obtained with the Jaguar pKa prediction method (JPM)28,29 for the solvents acetonitrile, dimethyl sulfoxide, and methanol (Table 1). The additive pKa shift parameters are optimized using 87 measured and 107 pKa values that are computed with the electrostatic transform method (ETM).27 The ETM may also be very useful in extending the ECM of the present work to other solvents where the database of measured pKa values is small. By combining the pKa shift parameters ΔpKa of Table 1 additively, pKa values can be converted between arbitrary pairs of solvents involving water, DMSO, acetonitrile, and methanol. The average accuracy of the ECM pKa values is found to be about 0.5 pH units. The agreement between the measured and the ETM computed pKa values demonstrates the usefulness of this method, which can be employed to enlarge the database of known pKa values for different solvents.

An analysis of the additive parameters shifting the water pKa value of a molecule to the corresponding values in other solvents reveals that there are two categories of molecules: very polar molecules involving preferentially titratable oxygen and nitrogen with a single hydrogen attached and less polar molecules involving either titratable nitrogen with several hydrogens attached or carbon atoms. The first category involves molecules with solvation energies that disfavor deprotonation in aprotic organic solvents compared to water. The molecules from the second category have solvation energy differences between protonated and deprotonated species, which are about the same in water and different organic solvents.

The second data set of titratable molecules involves five molecular families with 76 molecules. Most of these molecules are considerably larger than the molecules of the first data set. Here, the measured pKa values are available essentially only for DMSO. The pKa shift parameters between water and DMSO are optimized by using computed pKa values in water obtained with ETM or JPM. These two sets of shift parameters agreed well except for the family thiourea demonstrating the validity of the ECM for the other four families (Table 2). In the few cases where the measured pKa values in water are available, the computed pKa values agree with the corresponding measured values except in one case (the keto-compound cyclobutanone) where the measured pKa value is doubtful.

Acknowledgments

This work is supported by the German Science Foundation (DFG), Sfb1078, project C2.

Glossary

Abbreviations

MeCN

acetonitrile

Me2SO (DMSO)

dimethyl sulfoxide

ECM

empirical conversion method

ETM

electrostatic transform method

JPM

Jaguar pKa prediction method

MD

molecular dynamics

pKa-RMSD

pKa root mean square deviation

RESP

Restrained Electrostatic Potential

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.7b01895.

  • Detailed data of measured and computed pKa values shown in Figures 2, 3, and 5 (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao7b01895_si_001.pdf (216.8KB, pdf)

References

  1. Mamy L.; Patureau D.; Barriuso E.; Bedos C.; Bessac F.; Louchart X.; Martin-Laurent F.; Miege C.; Benoit P. Prediction of the Fate of Organic Compounds in the Environment from Their Molecular Properties: A Review. Crit. Rev. Environ. Sci. Technol. 2015, 45, 1277–1377. 10.1080/10643389.2014.955627. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Katritzky A. R.; Kuanar M.; Slavov S.; Hall C. D.; Karelson M.; Kahn I.; Dobchev D. A. Quantitative Correlation of Physical and Chemical Properties with Chemical Structure: Utility for Prediction. Chem. Rev. 2010, 110, 5714–5789. 10.1021/cr900238d. [DOI] [PubMed] [Google Scholar]
  3. Nieto-Draghi C.; Fayet G.; Creton B.; Rozanska X.; Rotureau P.; de Hemptinne J.-C.; Ungerer P.; Rousseau B.; Adamo C. A General Guidebook for the Theoretical Prediction of Physicochemical Properties of Chemicals for Regulatory Purposes. Chem. Rev. 2015, 115, 13093–13164. 10.1021/acs.chemrev.5b00215. [DOI] [PubMed] [Google Scholar]
  4. Kerns E. H.; Di L.. Drug-like Properties: Concepts, Structure Design and Methods from ADME to Toxicity Optimization, 2013; Vol. 53.
  5. Manallack D. T. The pKa Distribution of Drugs: Application to Drug Discovery. Perspect. Med. Chem. 2007, 1, 25–38. 10.1177/1177391X0700100003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Manallack D. T.; Prankerd R. J.; Yuriev E.; Oprea T. I.; Chalmers D. K. The Significance of Acid/base Properties in Drug Discovery. Chem. Soc. Rev. 2013, 42, 485–496. 10.1039/C2CS35348B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Diaz D.; Ford K. A.; Hartley D. P.; Harstad E. B.; Cain G. R.; Achilles-Poon K.; Nguyen T.; Peng J.; Zheng Z.; Merchant M.; et al. Pharmacokinetic Drivers of Toxicity for Basic Molecules: Strategy to Lower pKa Results in Decreased Tissue Exposure and Toxicity for a Small Molecule Met Inhibitor. Toxicol. Appl. Pharmacol. 2013, 266, 86–94. 10.1016/j.taap.2012.10.026. [DOI] [PubMed] [Google Scholar]
  8. Charifson P. S.; Walters W. P. Acidic and Basic Drugs in Medicinal Chemistry: A Perspective. J. Med. Chem. 2014, 9701–9717. 10.1021/jm501000a. [DOI] [PubMed] [Google Scholar]
  9. Petukh M.; Stefl S.; Alexov E. The Role of Protonation States in Ligand-Receptor Recognition and Binding. Curr. Pharm. Des. 2013, 19, 4182–4190. 10.2174/1381612811319230004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Roch-Ramel F.; Besseghir K.; Murer H.. Renal Excretion and Tubular Transport of Organic Anions and Cations. In Handbook of Physiology: A Critical, Comprehensive Presentation of Physiological Knowledge and Concepts; American Physiological Society, 1992; pp 2189–2262. [Google Scholar]
  11. Ullrich K. J. Specificity of Transporters for “organic Anions and Cations” in the Kidney. Biochim. Biophys. Acta 1994, 1197, 45–62. 10.1016/0304-4157(94)90018-3. [DOI] [PubMed] [Google Scholar]
  12. Inui K.-I.; Masuda S.; Saito H. Cellular and Molecular Aspects of Drug Transport in the Kidney. Kidney Int. 2000, 58, 944–958. 10.1046/j.1523-1755.2000.00251.x. [DOI] [PubMed] [Google Scholar]
  13. Rossini E.; Knapp E. W. Proton Solvation in Protic and Aprotic Solvents. J. Comput. Chem. 2016, 37, 1082–1091. 10.1002/jcc.24297. [DOI] [PubMed] [Google Scholar]
  14. Tehan B. G.; Lloyd E. J.; Wong M. G.; Pitt W. R.; Montana J. G.; Manallack D. T.; Gancia E. Estimation of pKa Using Semiempirical Molecular Orbital Methods. Part 1: Application to Phenols and Carboxylic Acids. Quant. Struct.-Act. Relat. 2002, 21, 457–472. . [DOI] [Google Scholar]
  15. Tehan B. G.; Lloyd E. J.; Wong M. G.; Pitt W. R.; Gancia E.; Manallack D. T. Estimation of pKa Using Semiempirical Molecular Orbital Methods. Part 2: Application to Amines, Anilines and Various Nitrogen Containing Heterocyclic Compounds. Quant. Struct.-Act. Relat. 2002, 21, 473–485. . [DOI] [Google Scholar]
  16. Parthasarathi R.; Padmanabhan J.; Elango M.; Chitra K.; Subramanian V.; Chattaraj P. K. pKa Prediction Using Group Philicity. J. Phys. Chem. A 2006, 110, 6540–6544. 10.1021/jp055849m. [DOI] [PubMed] [Google Scholar]
  17. Jover J.; Bosque R.; Sales J. Neural Network Based QSPR Study for Predicting pKa of Phenols in Different Solvents. QSAR Comb. Sci. 2007, 26, 385–397. 10.1002/qsar.200610088. [DOI] [Google Scholar]
  18. Meloun M.; Bordovská S. Benchmarking and Validating Algorithms That Estimate pKa Values of Drugs Based on Their Molecular Structures. Anal. Bioanal. Chem. 2007, 389, 1267–1281. 10.1007/s00216-007-1502-x. [DOI] [PubMed] [Google Scholar]
  19. Rupp M.; Körner R.; Tetko I. V. Estimation of Acid Dissociation Constants Using Graph Kernels. Mol. Inform. 2010, 29, 731–740. 10.1002/minf.201000072. [DOI] [PubMed] [Google Scholar]
  20. Ščavničar A.; Balaban A. T.; Pompe M. Application of Variable Anti-Connectivity Index to Active Sites. Modelling pKa Values of Aliphatic Monocarboxylic Acids. SAR QSAR Environ. Res. 2013, 24, 553–563. 10.1080/1062936X.2012.751552. [DOI] [PubMed] [Google Scholar]
  21. Ugur I.; Marion A.; Parant S.; Jensen J. H.; Monard G. Rationalization of the pKa Values of Alcohols and Thiols Using Atomic Charge Descriptors and Its Application to the Prediction of Amino Acid pKa’s. J. Chem. Inf. Model. 2014, 54, 2200–2213. 10.1021/ci500079w. [DOI] [PubMed] [Google Scholar]
  22. Rupp M.; Ramakrishnan R.; von Lilienfeld O. A. Machine Learning for Quantum Mechanical Properties of Atoms in Molecules. J. Phys. Chem. Lett. 2015, 6, 3309–3313. 10.1021/acs.jpclett.5b01456. [DOI] [Google Scholar]
  23. Ding F.; Smith J. M.; Wang H. First-Principles Calculation of pKa Values for Organic Acids in Nonaqueous Solution. J. Org. Chem. 2009, 74, 2679–2691. 10.1021/jo802641r. [DOI] [PubMed] [Google Scholar]
  24. Rived F.; Rosés M.; Bosch E. Dissociation Constants of Neutral and Charged Acids in Methyl Alcohol. The Acid Strength Resolution. Anal. Chim. Acta 1998, 374, 309–324. 10.1016/S0003-2670(98)00418-8. [DOI] [Google Scholar]
  25. Klicić J. J.; Friesner R. A.; Liu S.-Y.; Guida W. C. Accurate Prediction of Acidity Constants in Aqueous Solution via Density Functional Theory and Self-Consistent Reaction Field Methods. J. Phys. Chem. A 2002, 106, 1327–1335. 10.1021/jp012533f. [DOI] [Google Scholar]
  26. Skolidis G.; Hansen K.; Sanguinetti G.; Rupp M. Multi-Task Learning for pKa Prediction. J. Comput. Aided. Mol. Des. 2012, 26, 883–895. 10.1007/s10822-012-9582-x. [DOI] [PubMed] [Google Scholar]
  27. Rossini E.; Netz R. R.; Knapp E. W. Computing pKa Values in Different Solvents by Electrostatic Transformation. J. Comput.-Aided Mol. Des. 2016, 12, 3360–3369. 10.1021/acs.jctc.6b00446. [DOI] [PubMed] [Google Scholar]
  28. Bochevarov A. D.; Harder E.; Hughes T. F.; Greenwood J. R.; Braden D. A.; Philipp D. M.; Rinaldo D.; Halls M. D.; Zhang J.; Friesner R. A. Jaguar: A High-Performance Quantum Chemistry Software Program with Strengths in Life and Materials Sciences. Int. J. Quantum Chem. 2013, 113, 2110–2142. 10.1002/qua.24481. [DOI] [Google Scholar]
  29. Bochevarov A. D.; Watson M. A.; Greenwood J. R.; Philipp D. M. Multiconformation, Density Functional Theory-Based pKa Prediction in Application to Large, Flexible Organic Molecules with Diverse Functional Groups. J. Chem. Theory Comput. 2016, 12, 6001–6019. 10.1021/acs.jctc.6b00805. [DOI] [PubMed] [Google Scholar]
  30. Kang Y. K.; Nemethy G.; Scheraga H. A. Free Energies of Hydration of Solute Molecules. 3. Application of the Hydration Shell Model to Charged Organic Molecules. J. Phys. Chem. 1987, 91, 4118–4120. 10.1021/j100299a034. [DOI] [Google Scholar]
  31. Jorgensen W. L.; Briggs J. M.; Gao J. A Priori Calculations of pKa’s for Organic Compounds in Water. The pKa of Ethane. J. Am. Chem. Soc. 1987, 109, 6857–6858. 10.1021/ja00256a053. [DOI] [Google Scholar]
  32. Jorgensen W. L.; Briggs J. M. A Priori pKa Calculations and the Hydration of Organic Anions. J. Am. Chem. Soc. 1989, 111, 4190–4197. 10.1021/ja00194a007. [DOI] [Google Scholar]
  33. Lim C.; Bashford D.; Karplus M. Absolute pKa Calculations with Continuum Dielectric Methods. J. Phys. Chem. A 1991, 95, 5610–5620. 10.1021/j100167a045. [DOI] [Google Scholar]
  34. Kelly C. P.; Cramer C. J.; Truhlar D. G. Aqueous Solvation Free Energies of Ions and Ion-Water Clusters Based on an Accurate Value for the Absolute Aqueous Solvation Free Energy of the Proton. J. Phys. Chem. B 2006, 110, 16066–16081. 10.1021/jp063552y. [DOI] [PubMed] [Google Scholar]
  35. Rossini E.; Knapp E. W. Protonation Equilibria of Transition Metal Complexes: From Model Systems toward the Mn-Complex in Photosystem II. Coord. Chem. Rev. 2017, 345, 16–30. 10.1016/j.ccr.2017.02.017. [DOI] [Google Scholar]
  36. Besler B. H.; Merz K. M.; Kollman P. A. Atomic Charges Derived from Semiempirical Methods. J. Comput. Chem. 1990, 11, 431–439. 10.1002/jcc.540110404. [DOI] [Google Scholar]
  37. Bayly C. I.; Cieplak P.; Cornell W.; Kollman P. A. A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: The RESP Model. J. Phys. Chem. 1993, 97, 10269–10280. 10.1021/j100142a004. [DOI] [Google Scholar]
  38. Bashford D.; Gerwert K. Electrostatic Calculations of the pKa Values of Ionizable Groups in Bacteriorhodopsin. J. Mol. Biol. 1992, 224, 473–486. 10.1016/0022-2836(92)91009-E. [DOI] [PubMed] [Google Scholar]
  39. Bashford D.; Case D. A.; Dalvit C.; Tennant L.; Wright P. E. Electrostatic Calculations of Side-Chain pKa Values in Myoglobin and Comparison with NMR Data for Histidines. Biochemistry 1993, 32, 8045–8056. 10.1021/bi00082a027. [DOI] [PubMed] [Google Scholar]
  40. Bashford D.; Karplus M. pKa’s of Ionizable Groups in Proteins: Atomic Detail from a Continuum Electrostatic Model. Biochemistry 1990, 29, 10219–10225. 10.1021/bi00496a010. [DOI] [PubMed] [Google Scholar]
  41. Gunner M. R.; Honig B. Electrostatic Control of Midpoint Potentials in the Cytochrome Subunit of the Rhodopseudomonas Viridis Reaction Center. Proc. Natl. Acad. Sci. U.S.A. 1991, 88, 9151–9155. 10.1073/pnas.88.20.9151. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Karshikoff A. A Simple Algorithm for the Calculation of Multiple Site Titration Curves. Protein Eng., Des. Sel. 1995, 8, 243–248. 10.1093/protein/8.3.243. [DOI] [PubMed] [Google Scholar]
  43. Demchuk E.; Wade R. C. Improving the Continuum Dielectric Approach to Calculating pKas of Ionizable Groups in Proteins. J. Phys. Chem. 1996, 100, 17373–17387. 10.1021/jp960111d. [DOI] [Google Scholar]
  44. Mehler E. L. Self-Consistent, Free Energy Based Approximation to Calculate pH Dependent Electrostatic Effects in Proteins. J. Phys. Chem. 1996, 100, 16006–16018. 10.1021/jp9537926. [DOI] [Google Scholar]
  45. Sham Y. Y.; Chu Z. T.; Warshel A. Consistent Calculations of pKa’s of Ionizable Residues in Proteins: Semi-Microscopic and Microscopic Approaches. J. Phys. Chem. B 1997, 101, 4458–4472. 10.1021/jp963412w. [DOI] [Google Scholar]
  46. Schaefer M.; Sommer M.; Karplus M. pH-Dependence of Protein Stability: Absolute Electrostatic Free Energy Differences. J. Phys. Chem. B 1997, 101, 1663–1683. 10.1021/jp962972s. [DOI] [Google Scholar]
  47. Ullmann G. M.; Knapp E. W. Electrostatic Models for Computing Protonation and Redox Equilibria in Proteins. Eur. Biophys. J. 1999, 28, 533–551. 10.1007/s002490050236. [DOI] [PubMed] [Google Scholar]
  48. Alexov E.; Mehler E. L.; Baker N.; Baptista A. M.; Huang Y.; Milletti F.; Erik Nielsen J.; Farrell D.; Carstensen T.; Olsson M. H. M.; et al. Progress in the Prediction of pKa Values in Proteins. Proteins: Struct., Funct., Bioinf. 2011, 79, 3260–3275. 10.1002/prot.23189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Ullmann G. M.; Bombarda E. PKa Values and Redox Potentials of Proteins. What Do They Mean?. Biol. Chem. 2013, 394, 611–619. 10.1515/hsz-2012-0329. [DOI] [PubMed] [Google Scholar]
  50. Lin Y.-L.; Aleksandrov A.; Simonson T.; Roux B. An Overview of Electrostatic Free Energy Computations for Solutions and Proteins. J. Chem. Theory Comput. 2014, 10, 2690–2709. 10.1021/ct500195p. [DOI] [PubMed] [Google Scholar]
  51. Kieseritzky G.; Knapp E. W. Optimizing pKa Computation in Proteins with pH Adapted Conformations. Proteins: Struct., Funct., Bioinf. 2008, 71, 1335–1348. 10.1002/prot.21820. [DOI] [PubMed] [Google Scholar]
  52. Sakalli I.; Knapp E. W. pKa in Proteins Solving the Poisson-Boltzmann Equation with Finite Elements. J. Comput. Chem. 2015, 36, 2147–2157. 10.1002/jcc.24053. [DOI] [PubMed] [Google Scholar]
  53. Meyer T.; Knapp E. W. pKa Values in Proteins Determined by Electrostatics Applied to Molecular Dynamics Trajectories. J. Chem. Theory Comput. 2015, 11, 2827–2840. 10.1021/acs.jctc.5b00123. [DOI] [PubMed] [Google Scholar]
  54. Nicoleti C. R.; Marini V. G.; Zimmermann L. M.; Machado V. G. Anionic Chromogenic Chemosensors Highly Selective for Fluoride or Cyanide Based on 4-(4-Nitrobenzylideneamine)phenol. J. Braz. Chem. Soc. 2012, 23, 1488–1500. 10.1590/S0103-50532012005000007. [DOI] [Google Scholar]
  55. Klamt A.; Eckert F.; Diedenhofen M.; Beck M. E. First Principles Calculations of Aqueous pKa Values for Organic and Inorganic Acids Using COSMO-RS Reveal an Inconsistency in the Slope of the pKa Scale. J. Phys. Chem. A 2003, 107, 9380–9386. 10.1021/jp034688o. [DOI] [PubMed] [Google Scholar]
  56. Eckert F.; Klamt A. Accurate Prediction of Basicity in Aqueous Solution with COSMO-RS. J. Comput. Chem. 2006, 27, 11–19. 10.1002/jcc.20309. [DOI] [PubMed] [Google Scholar]
  57. Muckerman J. T.; Skone J. H.; Ning M.; Wasada-Tsutsui Y. Toward the Accurate Calculation of pKa Values in Water and Acetonitrile. Biochim. Biophys. Acta 2013, 1827, 882–891. 10.1016/j.bbabio.2013.03.011. [DOI] [PubMed] [Google Scholar]
  58. Bordwell pKa Table http://www.chem.wisc.edu/areas/reich/pkatable/.
  59. Alongi K. S.; Shields G. C. Theoretical Calculations of Acid Dissociation Constants: A Review Article. Annu. Rep. Comput. Chem. 2010, 6, 113–138. 10.1016/s1574-1400(10)06008-1. [DOI] [Google Scholar]
  60. Camaioni D. M.; Schwerdtfeger C. A. Comment on “accurate Experimental Values for the Free Energies of Hydration of H+, OH−, and H3O+.”. J. Phys. Chem. A 2005, 109, 10795–10797. 10.1021/jp054088k. [DOI] [PubMed] [Google Scholar]
  61. Pearson R. G.; Dillon R. L. Rates of Ionization of Pseudo Acids. IV. Relation between Rates and Equilibria. J. Am. Chem. Soc. 1953, 75, 2439–2443. 10.1021/ja01106a048. [DOI] [Google Scholar]
  62. Wada M.; Mitsunobu O. Intermolecular Dehydration between Alcohols and Active Hydrogen Compounds by Means of Diethyl Azodicarboxylate and Triphenylphosphine. Tetrahedron Lett. 1972, 13, 1279–1282. 10.1016/S0040-4039(01)84567-6. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao7b01895_si_001.pdf (216.8KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES