Prediction of Accurate Binding Modes Using Combination of Classical and Accelerated Molecular Dynamics and Free-Energy Perturbation Calculations: An Application to Toxicity Studies

Abstract

Estimating the correct binding modes of ligands in protein–ligand complexes is crucial not only in the drug discovery process but also for elucidating potential toxicity mechanisms. In the current paper, we propose a computational modeling workflow using the combination of docking, classical molecular dynamics (cMD), accelerated molecular dynamics (aMD) and free-energy perturbation (FEP+ protocol) for identification of possible ligand binding modes. It was applied for investigation of selected perfluorocarboxyl acids (PFCAs) in the PPARγ nuclear receptor. Although both regular and induced fit docking failed to reproduce the experimentally determined binding mode of the ligands when docked into a non-native X-ray structure, cMD and aMD simulations successfully identified the most probable binding conformations. Moreover, multiple binding modes were identified for all of these compounds and the shorter-chain PFCAs continuously moved between a few energetically favorable binding conformations. On the basis of MD predictions of binding conformations, we applied the default and also redesigned FEP+ sampling protocols, which accurately reproduced experimental differences in the binding energies. Thus, the preliminary MD simulations can also provide helpful information about correct setup of the FEP+ calculations. These results show that the PFCA binding modes were accurately predicted and that the FEP+ protocol can be used to estimate free energies of binding of flexible ligands that are not typical druglike compounds. Our in silico workflow revealed the specific ligand–residue interactions within the ligand binding domain and the main characteristics of the PFCAs, and it was concluded that these compounds are week PPARγ partial agonists. This work also suggests a common pipeline for identification of ligand binding modes, ligand–protein dynamics description, and relative free-energy calculations.

Introduction

The field of computer-aided drug discovery comprises a large variety of simulation techniques (molecular docking to free-energy perturbations (FEPs)) with different capabilities and complexities. These approaches have proven their usefulness in other research areas than in silico drug design, such as toxicology studies, but have not been applied extensively within this field to date. Such atomic-level simulations can significantly improve our understanding on how interactions between chemical compounds and proteins play a role regarding various adverse effects. Moreover, the combined use of different computational tools to form general pipelines is not well established. Both these aspects are addressed in the present work.

Although docking techniques have proven to be highly useful for predicting realistic ligand binding modes within specific protein targets, such approaches can, however, fail to identify relevant binding modes mainly within large and flexible ligand binding domains (LBDs), where the protein dynamics cannot be neglected,¹⁻⁴ for instance, in cases where conformations of individual amino acid residues within the LBD are determining whether a specific binding mode is possible or not. In contrast to docking methods, classical molecular dynamics (cMD), as well as advanced sampling methods, such as accelerated molecular dynamics (aMD) and metadynamics, provide atomic-level description of both the protein and ligand dynamics. These MD methods have shown to be reliable tools for exploring the free-energy conformational space of the ligand–protein complex. In particular, such methods model the structural and dynamical properties of the protein receptor at a submillisecond time scale, thereby offering much better sampling of the possible binding modes and identification of the most energetically favorable ligand–protein complex conformations.⁴

The prediction of a most probable binding mode is also a critical step in preparing free-energy calculations, and in particular, calculations using the FEP+ protocol.⁵ Due to increased GPU computational power, the applications of FEP have become very popular in both conventional lead and fragment optimization during the last couple of years.^5,6 Generally, published FEP calculations have showed highly significant correlation between calculated and experimental binding free energies with average errors in the range of 1 kcal/mol.⁵ The FEP+ calculations are based on MD simulations and therefore explicitly consider both the enthalpy and entropy effects of the conformational flexibility of the ligand, as well as desolvation effects within the LBD. This is done through the use of a molecular mechanics (MM) force field (FF) to describe the molecular interactions on the atomic scale and to model realistic environment of the protein binding site through the inclusion of explicit water solvent molecules. Such calculations are powerful tools for improving estimation of the docking scoring functions, which are often used for binding affinity predictions, as they are highly computational efficient compared to traditional molecular dynamics (MD)-based approaches such as molecular mechanics/generalized born surface area (MM/GBSA). However, detection of the most probable binding mode of one compound is a crucial step for the correct setup of the FEP calculations.^5,6 This is because typically all compounds are aligned prior to the FEP execution. Thus, without some knowledge of the possible binding modes, the FEP calculations are often impossible to perform. In cases where the binding modes of the ligands are unknown, preliminary MD studies can provide a helpful tool for both refinement of the docking protocol and the starting/alignment pose for FEP simulations, i.e., better bridging the docking and FEP calculations. Moreover, knowledge about the protein dynamics, such as the identification of residues that are significant for, e.g., ligand–flexible loop interactions within the LBD, may further improve the FEP+ protocol, for example, by including these residues in the so-called replica exchange solute tempering (REST) region, where more detailed sampling is made.⁷ If multiple stable possible binding poses are known for a series of compounds, free-energy calculations can be set up to rigorously treat their contributions to the binding free energy as well.⁸

Perfluorinated carboxyl acids (PFCAs) are an important group of perfluorinated substances, as well as highly persistent degradation products of polyfluorinated substances.^9,10 Poly- and perfluorinated substances have a wide spectrum of industrial and consumer applications due to their excellent surfactant properties and resistance to degradation. These substances are, for instance, used in coatings that keep food from sticking to food packaging material made of paper and board; in fabrics, furniture, carpets, and leather to make them repellent to stains; as well as in some firefighting foams and pesticides.⁹ Due to their wide application, high persistence, and affinity for biomolecules, these compounds are widely found in humans and biota.¹⁰⁻¹² Studies have explicitly shown a variety of adverse effects related to perfluorinated substances. Perfluorooctanoic acid (PFOA) and perfluorooctanesulfonic acid (PFOS), the two most applied compounds among these substances, are documented to be toxic to liver, kidney, and neurons; to induce tumors; and to affect fetal development, the hormonal system, immune responses, and regulation of fatty acid storage and glucose metabolism.^9,12−15 Both PFOS and PFOA are documented to potentially cause nongenotoxic carcinogenesis.¹⁵

The PFCAs and other perfluorinated alkylic acids (PFAAs) are documented to bind to and/or interact with many proteins, potentially interfering with their normal physiological function. This includes serum albumin that acts as blood fatty acid transporter system,¹⁶ and proteins highly expressed in the liver, such as liver fatty acid binding protein, which is responsible for fatty acid uptake, transport, and metabolism¹⁷ and peroxisome proliferator-activated receptors α and γ (PPARα and PPARγ).¹⁸⁻²¹ PPARα is highly important in the regulation of fatty acid metabolism in the liver, whereas PPARγ regulates glucose metabolism and storage of fatty acids. Through regulation of physiological processes, the three PPAR subtypes, PPARα, β/δ, and γ, have impact not only on lipid homeostasis and adipogenesis but also on inflammation, carcinogenesis, reproduction, and fetal development.^14,15,22 Interactions with these proteins are potentially linked to the observed liver toxicity and the influence on fatty acid storage and glucose metabolism caused by PFAAs, as well as the large accumulation of such compounds in liver tissue.

Various studies have documented that using different in silico methodologies in concert for identifying possible binding modes and for generating more accurate binding energy predictions has in many cases provided significantly improved understanding of the molecular mechanisms of action as well as provided better basis for interpretation of available experimental data.^4,23−28

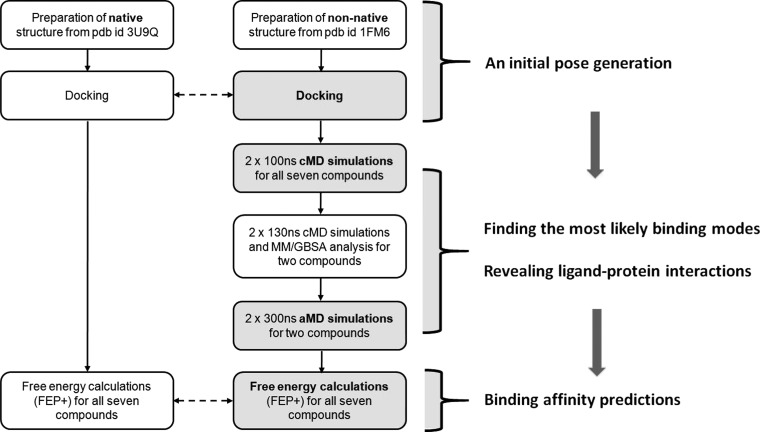
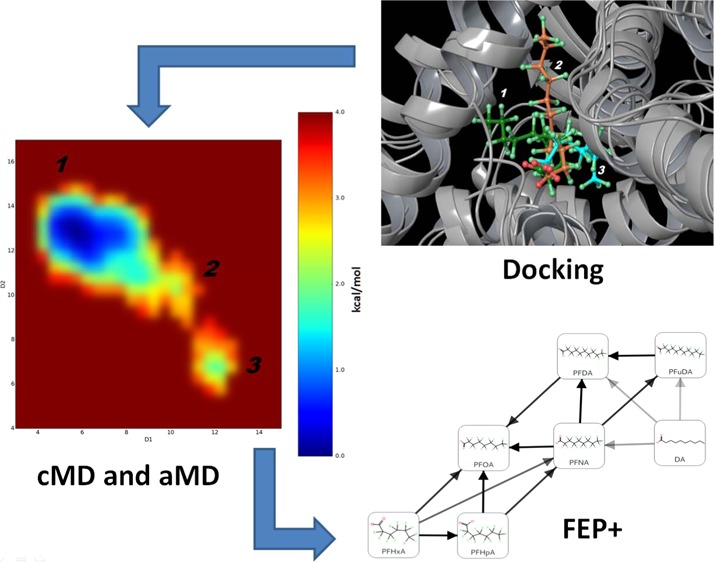
In the present study, we propose a workflow for identification of ligand binding modes, ligand–protein dynamics description, and relative free-energy calculations for proteins with flexible LBDs (Figure 1). The proposed workflow combines several computational tools, such as docking, classical MD (cMD), accelerated MD (aMD), and the free-energy perturbations (FEP+ protocol). This workflow was used to investigate possible binding modes and characteristics of the interactions of PFCAs within the PPARγ receptor. The PPARγ receptor has a large and flexible ligand binding domain (LBD) and is associated with various adverse effects,²⁹ and PFCAs have been identified as weak PPARγ binders.¹² PFCAs, like PFAAs in general, are nondrug-like compounds causing a wide variety of adverse effects⁹ that are highly persistent within the human organism.¹⁰

Figure 1.

Illustration of the proposed workflow, highlighting each step of the computational protocol and the information provided by each computational method.

Different binding conformations have been observed in the large LBD of PPARγ receptor. Decanoic acid (DA) and rosaglitazone bind in different parts of the LBD, as observed by X-ray crystallographic studies. Multiple ligand binding modes are also possible.^3,4,30 On the other hand, the interactions of PFCA compounds within protein targets are poorly understood. Both ligand flexibility and solvation/desolvation effects may play an important role for PFCAs, as these compounds contain a long fluorinated tail that does not form hydrogen bonds with the protein residues within the LBD. In this way, PFCAs differ significantly from typical druglike molecules. Thus, one of the goals of this study was also to explore whether a rigorous free-energy approach, such as FEP+, is suitable to describe such ligands.

Results and Discussion

Binding Pocket and Docking Analyses

The PPARγ ligand binding domain (LBD) X-ray structures with protein data bank (pdb) codes 3U9Q and 1FM6 were downloaded and prepared for modeling. The two X-ray structures, co-crystallized with decanoic acid (DA) and rosiglitazone, respectively, suggest two possible binding modes for ligands within the PPARγ LBD despite their highly similar protein conformations (root-mean-square deviation (RMSD) of 1.2 Å). In both binding modes, ligands are H-bonded to the His323 protein residue. Among these two ligands, only the smaller DA fits into the lipophilic cavity surrounded by protein residues Phe363, Phe360, Phe282, Ile281, Leu356, and Leu353, whereas the rosiglitazone molecule adopts a kinked binding mode occupying the channel connecting the binding pocket to the solvent medium.

The X-ray structure analysis suggests a size limit for compounds that can adopt a DA-like binding mode. This was further investigated for a series of PFCAs by conducting ligand docking calculations. Flexible re-docking of the DA molecule into the PPARγ LBD of pdb structure 3U9Q reproduced the observed ligand binding geometry of DA with high accuracy (all-atom RMSD 1.7 Å). Flexible docking of the PFCAs with chain lengths of 6–8 carbon atoms yielded binding modes in which the ligands occupied the same position as DA; these results agree with the previous docking experiments by Zhang et al.¹² The docked poses for PFCAs with chain lengths of 9–12 carbon atoms superimposed better with the rosiglitazone ligand. For PFCA chain lengths of 14, 16, and 18 carbon atoms, which are PPARγ binders, no docked poses were found and they were not included in the further analysis. A special treatment of the LBD is required to accommodate these larger ligands, which is interesting but out of the scope of the current study topic. If the PFCAs were docked using constrained placement of the first 6 carbon atoms to within 1 Å of those of DA, docked poses could only be obtained for PFCAs with chain length of 6–10 carbon atoms.

When docking the PFCAs in the binding pocket of the pdb structure 1FM6 (rosiglitazone), the docked poses obtained for PFCAs of chain lengths of 6–12 and 14 carbon atoms, all superimpose well with a position similar to the observed position of the rosiglitazone ligand. Furthermore, the experimentally known binding mode of DA was not reproduced when DA was docked into the 1FM6 pdb structure. Furthermore, the binding energies of DA and the PFCAs were not scored correctly.

It was observed that PFOA, with a chain length of 8 carbon atoms, showed a much more negative Glide XP score than perfluoroundecanoic acid (PFuDA), with a chain length of 11 carbon atoms, which does not correspond to available experimental data for the binding energies for these compounds.¹² This suggests that ligand binding modes of PFCAs within PPARγ can vary depending on not only ligand size but also small but significant changes in the receptor structure, causing the ligand to bind in an alternative site within the LBD. In particular, the conformation of the Phe363 residue within the 1FM6 pdb structure LBD was seen to restrict the DA binding pocket from being occupied. Hence, it seems that the flexibility of the individual amino acid residues within the LBD is an important factor that cannot be neglected when investigating binding modes within PPARγ. Similar results have been obtained previously for several partial agonists as well as for antagonists.^3,4,30

In an attempt to overcoming this problem, we used the induced fit docking approach (IFD)³¹ to dock DA into the 1FM6 pbd structure. Despite that the flexibility of the Phe363 residue was considered and several conformations for this residue were obtained, all 18 docking poses retrieved failed to reproduce the experimentally observed binding mode of DA. The same problem using IFD has recently been described for another set of PPARγ ligands, and in such cases, the combination of IFD and an advanced sampling approach, metadynamics,³² was suggested to overcome the problem and to find the most probable ligand binding modes.³³

Considering that the experimentally observed binding mode of DA was only reproduced when DA was docked into the 3U9Q pdb structure, but not when docked into the 1FM6 pbd structure, these results strongly suggest that the application of docking techniques alone is not sufficient to identify the most probably binding modes of the studied PFCAs within the PPARγ LBD. This is an example where the docking approach has a problem not only with the ligands scoring but also in the reproduction of the compounds’ correct binding poses.

Binding Mode Identification by Classical Molecular Dynamics (cMD)

Six PFCAs containing 6–11 carbon atoms were selected for further analysis. These six ligands and DA are listed in Table S1 and their two-dimensional (2D) molecular structures and key physical parameters can be also found.

In an attempt to identify the binding modes of the ligands in Table S1 more accurately, a set of classical molecular dynamics (cMD) simulations were made. As an input for these runs, we used the conformations of the ligands as docked into the non-native structure (the LBD structure as co-crystallized with rosiglitazone (pdb id: 1FM6)) for all of the MD simulations. This was done to avoid any bias toward the DA binding mode and also to correctly reproduce a scenario where only one X-ray structure might be available. In addition, cMD simulations were carried for DA and the computed binding mode of DA was compared to the experimentally observed binding conformation within the 3U9Q X-ray structure.

Initially, two independent 100 ns long simulations were executed for each of the studied ligands (1.4 μs simulation time in total), in each case referred to as MD runs 1 and 2, respectively. We focused particularly on exploring the binding mode and dynamics of the PFuDA ligand as an example of a PFCA, for which the docking results, using both the X-ray structures with pdb id 3U9Q and 1FM6, indicated a binding mode similar to the one of rosiglitazone and not to the one of DA. Also, PFuDA exhibited the strongest experimental binding affinity in the human PPARγ-LBD according to the study by Zhang et al.¹²

In contrast to the docking studies using the 1FM6 pdb structure, the experimental binding conformation of DA was reproduced well by these simulations. The averaged structure of the PFuDA–PPARγ complex obtained by the cMD simulations has an RMSD of 1.8 Å compared to the experimental X-ray structure of DA co-crystallized in PPARγ. It was noted that in both MD runs 1 and 2 for PFuDA, the Phe363 residue did shift its conformation. Consequently, for a large part of the simulation time, the PFuDA ligand adopted a binding mode similar to the binding mode observed for the co-crystallized DA within the 3U9Q pdb structure, labeled binding mode 1 (see Figure S1). For periods of the simulation time, PFuDA even overlapped with the experimentally observed position of the DA skeleton.

During MD run 1, the PFuDA ligand changed its initial orientation and after about only 20 ns approached an intermediate state, named binding mode 2, and then after the 50 ns of the simulation entered a relatively stable position in binding mode 1 (Figures 2A and S2A). An RMSD of PFuDA about 2.7 Å compared to the initial docking position was observed during MD run 1. In MD run 2, the ligand adopted the DA binding mode (binding mode 1) faster than that in MD run 1, and this binding mode was the only stable one observed during almost all MD run 2. However, during the last 20 ns of this run, PFuDA adopted a new conformation and a binding mode, similar to the one of rosiglitazone, labeled herein as binding mode 3 (Figure S2B).

Figure 2.

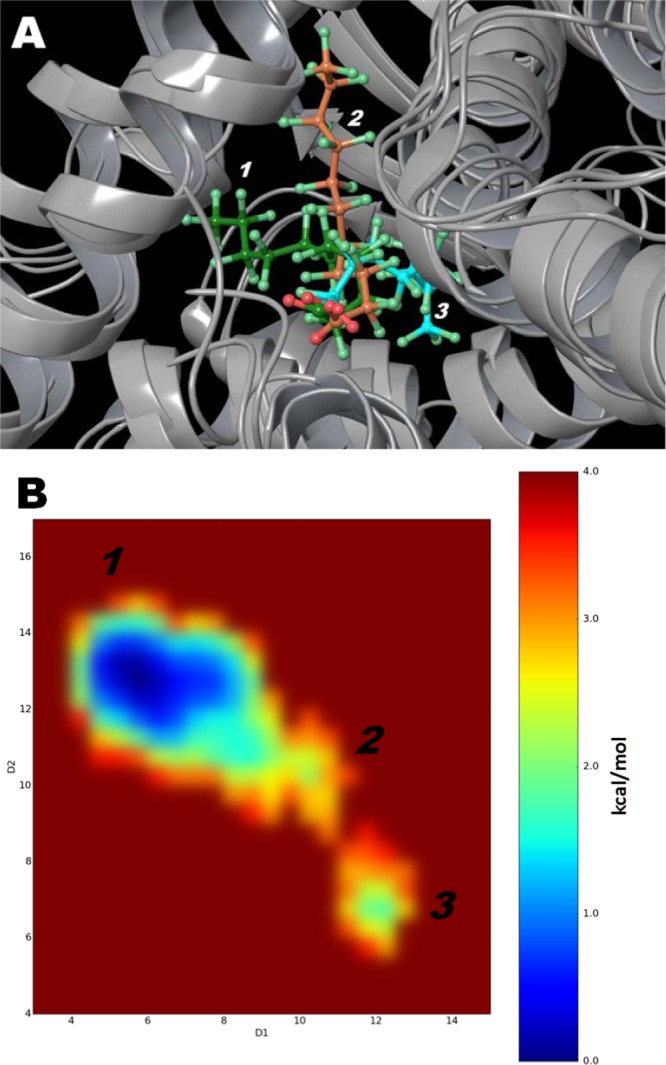
(A) Binding modes for PFuDA detected by cMD simulations. Binding modes 1, 2, and 3 are displayed in green, orange, and blue, respectively. (B) Difference in free energies between detected conformations of PFuDA in kcal/mol, determined by cMD simulations (2 × 130 ns), which also represents their populations and probability of existence. D1 and D2 coordinates are the distances in angstrom between the carbon atom of the CF₃ group (the end of ligand) and the Cα atoms of Phe282 (helix 3) and Tyr473 (helix 5), respectively.

The simulations performed for the ligands listed in Table S1 showed that the shorter-chain PFCAs of 6–8 carbon atoms (PFHxA, PFHpA, and PFOA) were much more flexible than PFuDA and continuously moved from one binding mode to another (Figures 3 and S3). The initial cMD simulations indicate that these three ligands do not establish a stable complex in the DA binding pocket, nor at the rosiglitazone binding site. On the other hand, the dynamics of PFNA and PFDA were more similar to the dynamics of PFuDA. Like PFuDA, PFNA and PFDA did predominantly bind in the same cavity as DA (binding mode 1).

Figure 3.

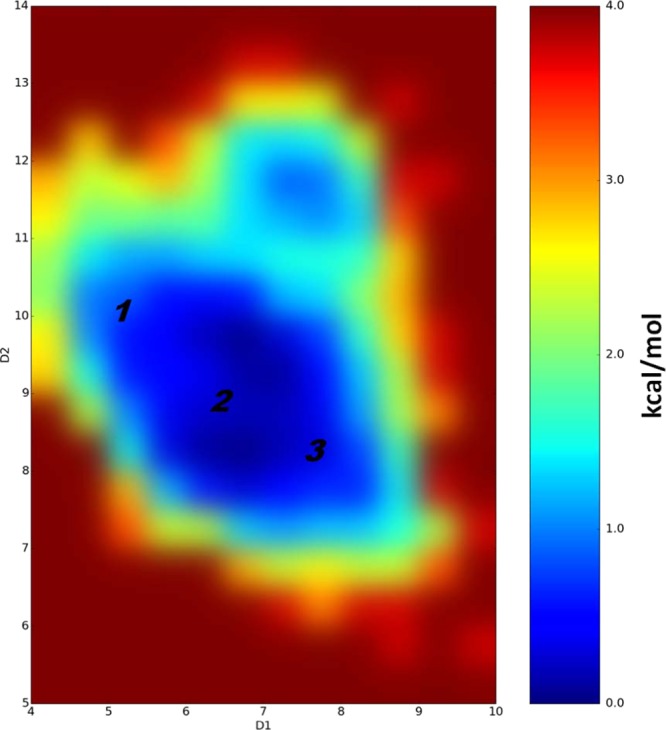
Difference in free energies between detected conformations of PFHpA (in kcal/mol) determined by performed cMD simulations, which also represents their populations and probability of existence. D1 and D2 coordinates are the distances in angstrom between the carbon atom of the CF₃ group (the end of ligand) and the Cα atoms of Phe282 (helix 3) and Tyr473 (helix 5), respectively. Note that the difference in free energies between detected PFHpA conformations is less than 1 kcal/mol.

Thus, according to these cMD simulations, all six PFCA ligands exhibit significant dynamical behavior and ability to change from one binding mode to another. This is particularity the case for the shorter-chain PFCAs. Also, the carboxyl group and adjacent atoms have a relatively constant position for all six PFCAs, but the fluorinated chain moves significantly within the LBD.

Detailed Study of the PFuDA Ligand–Protein Interactions

The observed dynamic behavior of fluctuating periodically between binding modes 1 and 3 was investigated in greater detail for two of the ligands, PFuDA and PFHpA. These two binding modes and the intermediate binding mode 2 are illustrated for PFuDA in Figure 2A. To investigate whether other conformations might be possible, as well as to estimate the probability of the identified binding modes and estimate the difference in their free energies, a new set of cMD (2 × 130 ns) additional runs were executed for each of these two PFCAs.

Free-energy plots were constructed based on these simulations. To describe the movement of PFuDA in the PPARγ LBD, we choose as coordinates the distances between the C atom of the CF₃ group (the end of ligand) and the Cα atoms of Phe282 (helix 3) and Tyr473 (helix 5). To compare the results obtained for PFuDA to the dynamics of the carbon atom of the CF₃ group of a PFCA with shorter chain length, corresponding analysis was made for PFHpA.

The free-energy plot shown in Figure 2B confirms that in principle three possible binding modes are possible for the PFuDA ligand. The most populated binding mode is binding mode 1, which is similar to the binding mode observed for DA. Binding mode 3 was much less populated and has free energy that is 1.8 kcal/mol higher than that of binding mode 1 according to the simulation results. The intermediate state, binding mode 2, displays a spread position range movement with free energy of about 2.0 kcal/mol higher than that of binding mode 1. Also, two highly similar conformations, separated by 0.5 kcal/mol, were observed inside the lowest free-energy well for binding mode 1.

Thus, the conclusion of these calculations is that PFuDA, as other PPARγ partial agonists and antagonists,^3,4,30 does not have a unique binding mode, but instead multiple binding conformations representing the ligand dynamics within the LBD. Indeed, according to the simulation results, the PFuDA ligand spent most of the time in the lower free-energy state (about 91.5% of the simulation time in binding mode 1, vs 3.6 and 4.9% of the time in binding modes 2 and 3, respectively). These data are in agreement to our previous studies on other ligand–PPARγ complexes^3,4 as well as to NMR experiments.³⁰

According to the simulation results, the PFHpA ligand had much higher probability of entering binding mode positions 2 and 3, and all binding modes were equally populated and no significant energy barriers were seen between binding modes 1, 2, and 3 in our analysis (see Figure 3).

On the basis of the above results, binding mode 1 was identified as the most probable PFuDA conformation within the PPARγ LBD and the ligand–residue interactions were described in detail. Similarly to DA and many other PPARγ agonists the carboxyl group forms a salt bridge with Ser289, His323, Tyr473, and His449. Averaged life times of these bonds, assessed on the basis of the combination of the two MD trajectories, were 64, 92, 39, and 94%, respectively. One of the main differences between the two MD runs was that PFuDA formed very stable bond with Ser289 in the first 130 ns MD run (Figure S4), but the H-bond with His449 was predominant in the second MD 130 ns run (Figure 4A,B). In both simulations, the hydrogen bonds with Tyr473 and His323 were very stable. The remaining ligand–protein interactions were almost identical in the two MD runs (see Figures 4B and S4).

Figure 4.

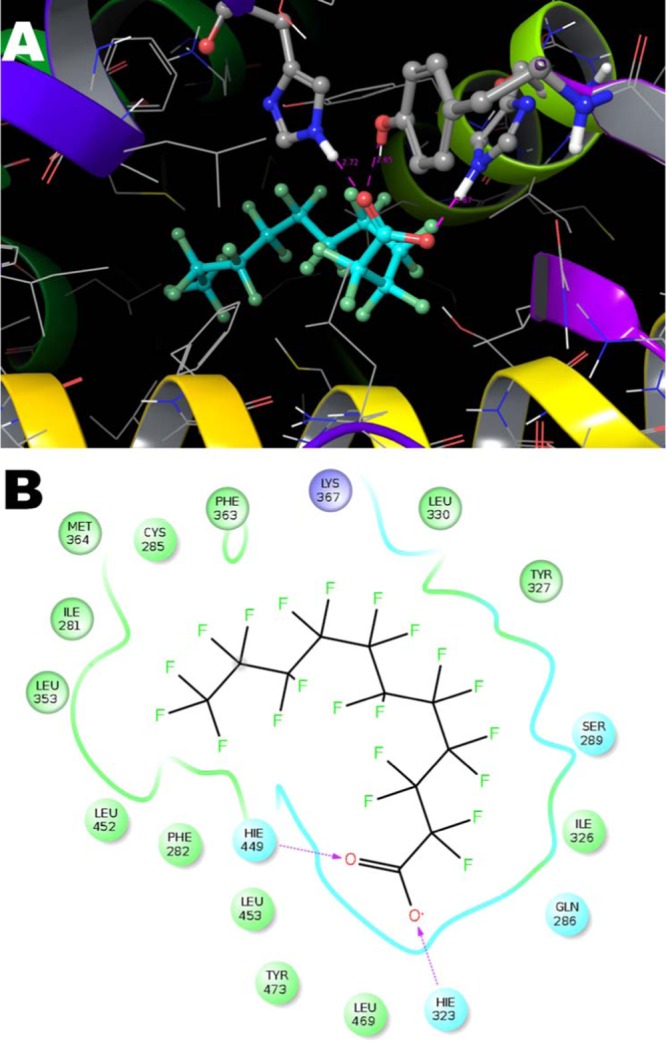
Representation of detected PFuDA–receptor interactions in the most populated binding mode (binding mode 1) determined by a cMD simulation (second 130 ns run) illustrated by (A) three-dimensional (3D) and (B) 2D illustrations. The H-bonds are marked with dotted lines, and the blue and green spheres show the areas of electrostatic and hydrophobic interactions, respectively.

These results also demonstrate that for the PFCAs investigated the docking scoring function cannot rank compounds correctly, due to not only some insufficiency in the scoring, but because in docking, at least with presently used techniques, only one docking pose is used for the scoring and thus the dynamics is neglected.

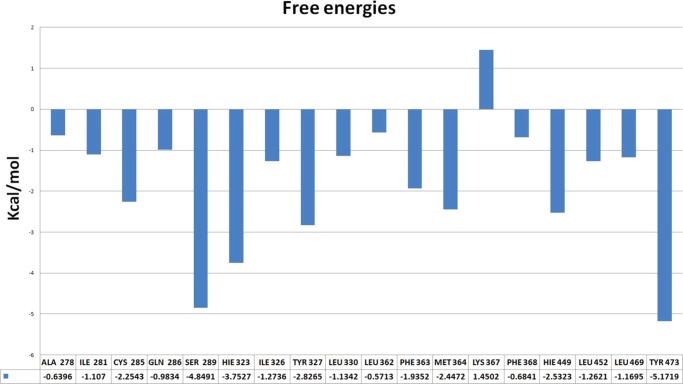
Finally, to measure the contribution of the individual residues, the MM/GBSA decomposition analysis was performed for PFuDA (Figure 5). Although the analyses of the ligand–residue interactions in the above section are based on the trajectory averaged and minimized, i.e., on static PFuDA conformations, the MD-based decomposition considers the contribution of protein residues in all possible binding modes. As one can expect, the residues involved in the salt bridge (Ser289, His323, Tyr473, and His449) have the largest negative contributions to the free energy, −4.8, −3.7, −5.2, and −2.5 kcal/mol, respectively. However, interactions with the Cys285, Tyr327, Phe363, and Met364 residues also contribute favorably to the binding, with contributions between −2 and −3 kcal/mol. It is interesting to note that the Lys367 residue has a contribution of +1.5 kcal/mol and thus this interaction has a negative contribution with respect to binding. This explains why the DA binding mode (binding mode 1) is the preferable one, especially for the ligands with longer chains, where the repulsive interactions with Lys367 are more significant and restrict the frequency of the realization of binding modes 2 and 3.

Figure 5.

Most significant interactions between PFuDA and receptor residues in binding mode 1, presented as free energies (in kcal/mol), as they were detected by MM/GBSA decomposition approach during all executed cMD runs.

Multiple Binding Mode Study by Accelerated Molecular Dynamics (aMD) Study

Above results clearly suggest multiple binding modes for the studied compounds; thus, to study in detail the possible conformational changes of both the ligands and the LBD at a microseconds time range, we used the accelerated molecular dynamics (aMD) enhanced sampling approach. Two 300 ns long aMD simulations were executed for PFuDA and PFOA, which represent the ligands with longer and middle chain length.

As an aMD simulation carried out for 100–200 ns provides information on the dynamics of a system that corresponds to a cMD simulation of 1 μs, the aMD method gives us the opportunity to study the dynamics of the two ligands within the LBD on a much longer time scale than is possible when only using cMD. A drawback is that the free energies estimated with the aMD simulation method are significantly less accurate than those obtained with cMD. As a result, some error in the free energy can be seen in an aMD simulation, and this needs to be considered in the interpretation of the obtained results.

In the case of PFuDA, two large free-energy minima and an intermediate state were sampled, where each of the two large free-energy minima contain two separate minima (Figure 6). Considering the uncertainty associated with the aMD simulation technique, it was concluded that the binding modes 1–3 in Figure 6 correspond to the binding modes identified by the cMD simulation (Figure 2B). The additional energy minima, binding modes 1′ and 3′, identified in the aMD simulation were not sampled in the cMD simulations. This can be illustrated by dividing the free-energy map in Figure 6 into two parts, areas A and B, where it can be seen that area A is similar to the map obtained in the cMD simulations (Figure 2B).

Figure 6.

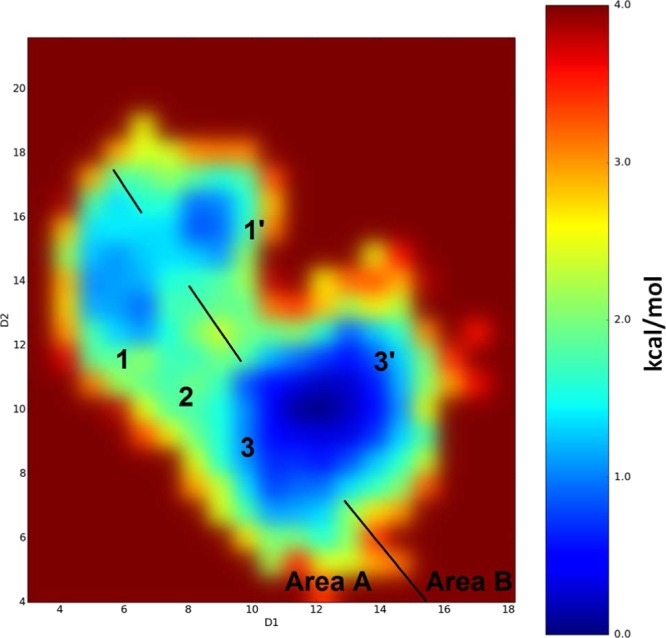
Binding modes detected for the PFuDA ligand retrieved by aMD calculations and corresponding reweighted free energies (in kcal/mol) obtained by these simulations. D1 and D2 coordinates are the distances in angstrom between the carbon atom of the CF₃ group (the end of ligand) and the Cα atoms of Phe282 (helix 3) and Tyr473 (helix 5), respectively. Note that some deviations between both D1 and D2 coordinates can be expected during the aMD simulations due to the larger variations in the receptor structure.

The free-energy difference between binding modes 3′ and 3 determined based on the aMD simulations was less than 1 kcal/mol. The free-energy difference between these two binding modes is thus insignificant, considering the uncertainty of the aMD simulations. The conformations of binding modes 1′ and 3′ within area B in Figure 6 are similar to the corresponding conformations of binding modes 1 and 3, respectively, but shifted by 1–2 Å in their positions. In binding mode 1′, PFuDA adopted more planar conformation, which is similar to the one observed for DA, but the ligand was moved away from helix 12 (H12) to the other end of the DA pocket. Binding mode 3′ was situated in the opposite corner of the LBD in a surface cavity between helices 3 and 5, which is close to a possible entrance/exit gate to the LBD (see Figure 6). It has been shown in previous studies that the enhanced sampling methods are capable, without any guidance, of recovering the binding path of a ligand entering an LBD.³⁴ Thus, we consider it likely that the accelerated dynamics sampled the movement of the PFuDA ligand, thereby not only capturing the binding modes of PFuDA, but also detecting a likely path that the ligand follows to reach the LBD or to move from one binding mode to another. For PFuDA, we suggest that conformation 3′ located at the receptor surface between helices 3, 4, and 5 describes the binding path the ligand follows when entering the LBD, but not a real binding mode within the LBD.

According to the aMD simulation results, H12 of the PPARγ LBD was not stabilized in its full agonist conformation. The detected conformations of H12 were more similar to those in the apo receptor, as seen both in X-ray data and in our previous aMD simulations.^4,35 The same has also been observed for other partial agonists.³⁰ However, in contrast to the apo form, where the agonist and antagonist H12 conformations were almost equally populated,³⁵ no antagonist-like H12 orientations were captured during the present aMD simulation of the PFuDA–PPARγ complex. Thus, according to the aMD results, the PFuDA movement affected the LBD secondary structure, and the PPARγ receptor was partially stabilized by the PFuDA ligand, probably due to the ligand’s weak binding capability. This observation is supported by experimental data, which have shown that the ligand PFuDA affects the protein structure.¹²

PFOA exhibited a similar behavior to PFHxA, PFHpA, and PFOA in the cMD simulations, where these ligands constantly flip between binding modes 1, 2, and 3 (see Figure S5). The free-energy map generated by the cMD simulation for PFHpA (Figure 3) and the free-energy map obtained from the aMD simulation for PFOA (Figure S5) are similar.

For PFOA, which is a weak binder, H12 entered a conformation similar to that of the apo form and adopted an antagonist conformation as well (see Figure S6). However, according to the simulation, the antagonist conformation is less populated than was seen in previous aMD studies for other ligands,^4,35 demonstrating that even weak ligand binding provides some PPARγ stability. According to the aMD enhanced sampling in an antagonist receptor conformation or the apo from, the PFOA ligand can form stable H-bonds also with Tyr327 and Lys367 due to disruption of the typical hydrogen bond network that is seen for all agonists.

The results for both compounds studied showed that the receptor dynamics is similar to that of the apo form, i.e., the compounds did not stabilize the PPARγ in a full agonist state, which agrees well with the experimentally observed transactivation energies.³⁷ For instance, it has been shown that DA has no effect on the hydrogen/deuterium exchange of PPARγ despite its binding within the LBD, providing experimental evidence that DA does not have the same ability as rosiglitazone to stabilize the AF-2 receptor region. As a consequence, DA has reduced ability to act as a full agonist.³⁶ Similarly, the above observations for PFuDA and PFOA provide atomic-level data that can explain why the PFCA-mediated transactivation of human PPARγ was only detected at concentrations of 18 μM and higher.³⁷

Free-Energy Calculations (FEP+)

Only compounds with overall known binding modes can be studied in free-energy calculations by the FEP+ (free-energy perturbation) methodology. On the basis of our cMD and aMD results, the 3U9Q pdb structure for the PPARγ LBD and the DA binding mode was initially selected for these calculations. An FEP map was prepared for the seven ligands listed in Tables 1 and S1, i.e., the PFCAs with 6–11 carbon atoms (PFHxA, PFHpA, PFOA, PFNA, PFDA, and PFuDA), as well as DA. All of the selected PFCAs can fit into the same binding pocket and enter similar binding mode to DA according to the cMD simulations presented above.

Table 1. FEP+ Calculation Results^a.

ligand name abbreviation	ligand name	experimental activity (μM)	experimental ΔG values	predicted ΔG values
PFHxA	perfluorohexanoic acid	n.d.		–1.76
PFHpA	perfluoroheptanoic acid	1330	–3.92	–2.92
PFOA	perfluorooctanoic acid	300	–4.80	–4.22
PFNA	perfluorononaic acid	155	–5.20	–6.01
PFDA	perfluorodecanoic acid	84	–5.56	–6.26
PFuDA	perfluoroundecanoic acid	58	–5.78	–5.93
DA	decanoic acid	1521	–3.84	–3.77

^aExperimental activity (K_d) data taken from ref (12). Predicted ΔG values were obtained by shifting the calculated ΔΔG values by a uniform constant to minimize mean unsigned error (MUE) to experiment.

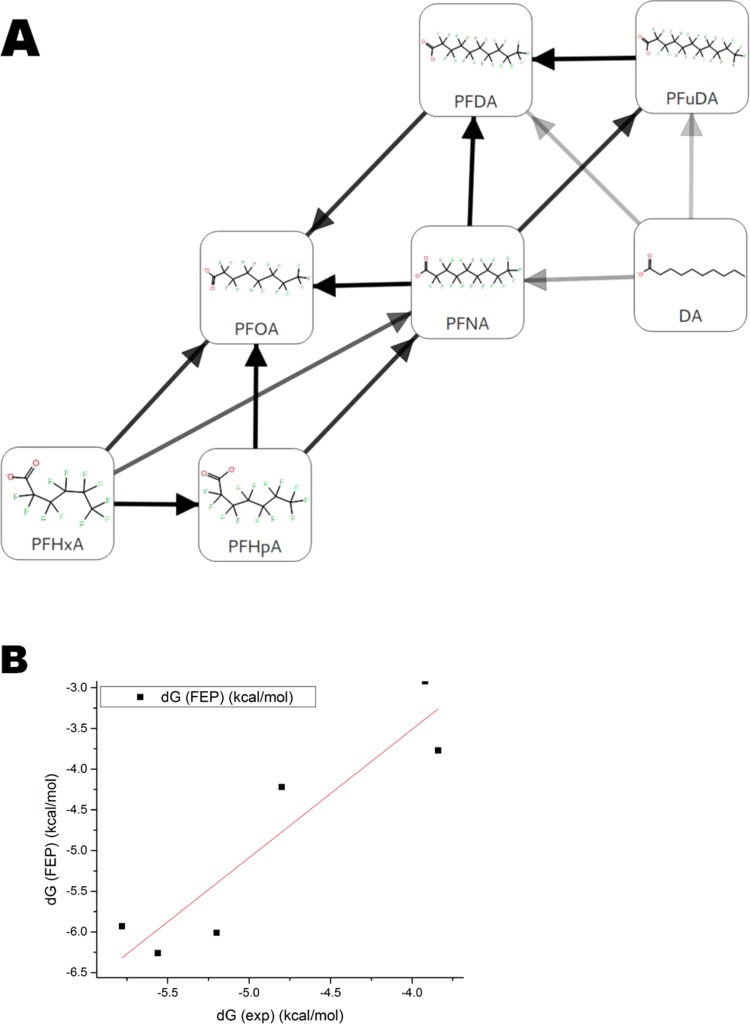
The six PFCA ligands were prealigned with their heavy atoms on top of the corresponding heavy atoms in the co-crystallized structure of DA (pdb id: 3U9Q). The FEP+ protocol was run on the resulting transformation map, and the resulting relative ΔΔG values (with respect to an arbitrary zero) were shifted by a uniform constant to minimize their mean unsigned error with the experimental values, yielding estimated ΔG values. This shift does not change the obtained information and only serves for easier comparison of computed and experimental data.

The computed ΔG values agree well with experimental free energies computed from the K_d values from Zhang et al.,¹² with a correlation coefficient (R² value) of 0.86 and a root-mean-square error (RMSE) of 1.0 kcal/mol between the experimental and predicted values (Figure 7A,B and Table 1). The estimated prediction errors lie in the range of 0.2–0.5 kcal/mol, and the average hysteresis over all free-energy cycles is 0.5 kcal/mol (Table 1). The FEP+ calculations correctly predict the trend of increasing ligand free energy of binding with increasing chain length, as well as the gain in the free energy due to perfluoration.

Figure 7.

(A) FEP transformation map for seven ligands. Each line represents one free-energy calculation conducted in both solvated and receptor-bound states. Connections have been automatically created with multiple pathways connecting each pair of compounds to obtain redundancy in the calculations as well as connecting compounds that have the largest maximum common substructure possible. (B) Correlation obtained by comparing FEP+ and experimental results with linear regression line.

Next, we run an FEP+ calculation based on the rosiglitazone binding mode and the 1FM6 pdb structure, but it was not possible to reproduce the experimental binding affinities by these calculations. In particular, this was noted for transformations from DA to both shorter- and longer-chain PFCA transformations. The gain in the free energy due to perfluoration was also overestimated. The mean unsigned error (MUE) was higher than 1.3 kcal/mol, and the RMSE was 1.8 kcal/mol (Figure S7). We carefully examined the obtained MD trajectories and found that the conformation of the Phe363 residue could not change, which restricted the longer-chain ligands (PFNA, PFDA, and PFuDA) from entering the DA binding mode. On the other hand, the FEP+ predications for the shorter-chain PFCAs (PFHxA, PFHpA, and PFOA) were similar to those retrieved from the FEP+ simulation for the 3U9Q structure. These results illustrate that the three shorter-chain ligands are less sensitive to the alignment into the DA mode (binding mode 1) than the longer-chain ligands. Our interpretation is that this is due to the lower-energy barriers between and consequently frequent shifts between binding modes 1, 2, and 3 observed in the cMD and aMD simulations.

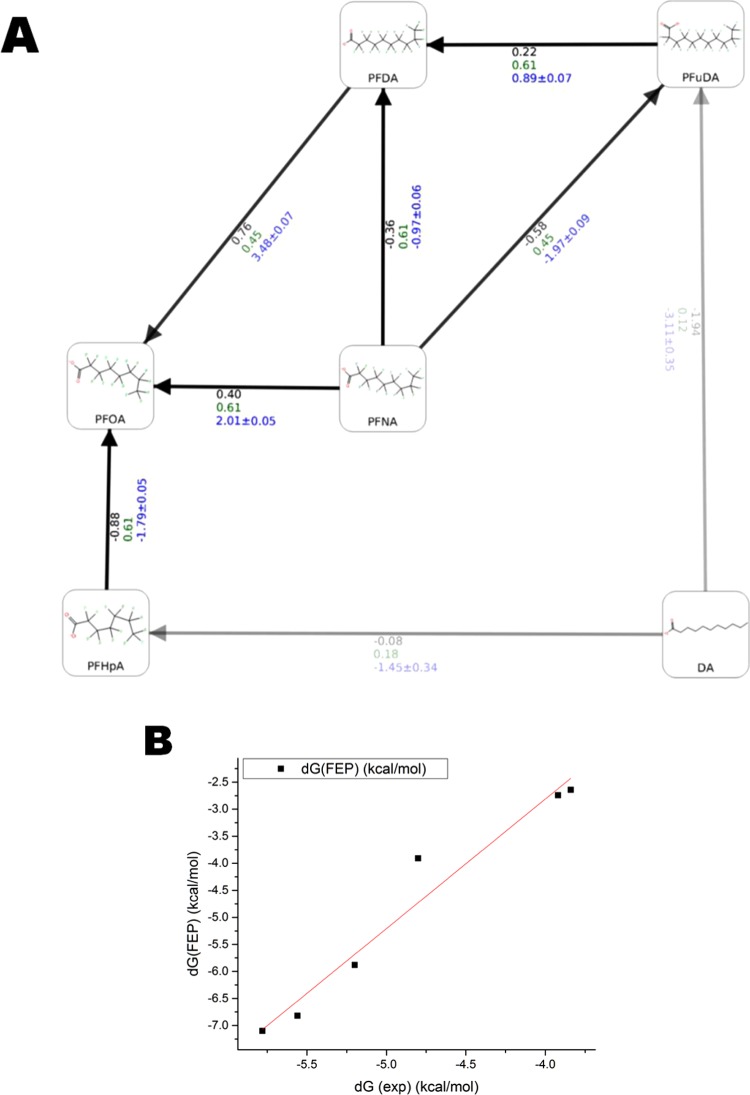
A new set of calculations was made with the same seven ligands and the same parameters, but using the center of the clustered PFuDA ligand–PPARγ structure obtained in the cMD runs as a template instead of the experimental DA–PPARγ complex. It was examined whether basing the FEP+ calculations on the simulated PFuDA binding mode, which is similar to the experimentally observed DA conformation, can reproduce the experimental free energies accurately. The standard FEP+ protocol (0.24 ns pre-REST and 5 ns REST simulations) could not describe the individual permutations giving errors up to 7 kcal/mol (Figure S8). This was mainly due to the significant changes in receptor structure provoked by the conformational change of PFuDA from the rosiglitazone binding mode (binding mode 3) to the DA binding mode (binding mode 1) (Figure S1). Thus, the FEP+ procedure was modified and the pre-REST and REST steps were increased to 2 × 10 and 8 ns/λ, respectively. The FEP+ results obtained by these calculations provided a reasonable RMSE value of 1.23 kcal/mol (MUE = 0.96 kcal/mol) and R² = 0.96 (Figure 8A,B). It is also notable that six of six ligands were correctly ranked, and for all perturbations, the signs of calculated ΔG values were in agreement to the experimental data.

Figure 8.

FEP+ results based on the cMD-derived structure of the PFuDA–PPARγ complex and redesigned FEP+ protocol. (A) Predicted ΔΔG values for each individual permutation used. The ligand similarity and experimental and computed ΔΔG (kcal/mol) values are written in green, black, and blue, respectively. The similarity was calculated with the FEP+ mapper tool. (B) Linear regression between the experimental and predicted ΔG values.

We are currently working on the improvement of FEP+ sampling protocol for FEP calculations based on MD-derived and flexible structures, and a paper about this topic is in preparation. Moreover, the use of MD-retrieved structures after simulation of the shorter-chain ligands showed that they do not significantly affect the LBD residues conformations and were well handled by the regular FEP+ protocol (data not shown).

Mechanism of Action

According to the results presented in the paper by Zhang et al.,¹² which were based only on docking analysis, the PFCAs with chain lengths of 4–10 carbon atoms bind within the same binding cavity as DA, thus occupying binding mode 1. Instead, the fluorinated chain of PFCAs containing 11 or more carbon atoms is mostly located outside this cavity. In contrast, our simulations revealed that more than one binding mode are possible for the six PFCAs studied herein within the large PPARγ LBD. The longer-chain ligands (PFNA, PFDA, and PFuDA containing 9–11 carbon atoms) did predominantly occupy a binding mode similar to the one experimentally observed for DA (binding mode 1) and to a lesser degree a binding mode similar to the one experimentally observed for rosiglitazone (binding mode 3). For the shorter-chain ligands studied (PFHxA, PFHpA, and PFOA containing 6–8 carbon atoms), the fluorinated tail moved quite flexibly within the LBD during the simulations. Consequently, these compounds shifted continuously from one binding mode to another.

Further, in the docking studies by Zhang et al.,¹² the hydrophilic heads of PFCAs up to the chain length of 14 carbon atoms all formed hydrogen bonds (H-bonds) with the Ser289, His449, and Tyr473 residues, and like DA, PFDA and PFuDA formed a H-bond with His323 as well. PFHxDA and PFOcDA, with chain lengths of 16 and 18 carbon atoms, respectively, only formed H-bonds with His449 and Tyr473. The cMD studies made for PFCAs with 6–11 carbon atoms as a part of this study gave corresponding results, and a detailed analysis of the free-energy contribution of the PFuDA ligand interactions with LBD residues by the MM/GBSA approach identified Ser289, Tyr473, and His323 to be the residues with the strongest contribution to the free energy of binding for PFuDA (Figure 5). Thus, both the docking and the cMD simulations confirm that the position of the hydrophilic head is stable within the human PPARγ LBD due the hydrogen bonding.

The flexibility of the fluorinated tails of the PFCAs, and particularly of those with shorter chain length, within the LBD, and the tendency of PFHxA, PFHpA, and PFOA to flip continuously between different binding modes observed in the cMD and aMD simulations must be interpreted such that no one binding mode is significantly more energetically favorable for these compounds and that the energy barrier to flip from one binding mode to another is low. The fluorinated tails have a strong internal symmetry, and the fluorine atoms do not form H-bonds with the surrounding protein residues. The interactions between the fluorinated tails and the LBD are thus probably highly governed by an entropic factor, which might be the driving force governing the rapid shift from one binding mode to another observed in the MD simulations. The energy barriers between the binding modes of PFHpA and PFOA are low according to the free-energy diagrams generated by the MD simulations (Figures 3 and S5) but clearly visible on the corresponding diagram for PFuDA (Figure 2B). Our hypothesis is that PFuDA fits tightly into the DA binding pocket, resulting in a higher-energy barrier to flip the fluorinated tail into the other binding modes.

Detailed analysis of the binding modes of PFuDA and PFOA based on the aMD simulations revealed that helix 12 (H12) was not stabilized in a full agonist position but adopted conformations more similar to those in the apo form.³⁵ Thus, according to our results, these compounds should only have some partial agonist activity, which agrees well with the experimental transactivation data. The limited data available on transactivation on human PPARγ caused by PFCA showed that PFOA and perfluorinated dodecanoic acid (PFDDA) have the strongest transactivation (c20% values of 20 and 18 μM, respectively) among the studied PFCAs.³⁷ No data were given for PFuDA. The experimental c20% values for PFHxA, PFHpA, and PFDA are in the range of 43–57 μM, and for PFNA, the test result was >100 μM; according to these results, these four PFCAs do not activate the human PPARγ transcription factor. PFOA and PFDDA are classified as weak PPARγ activators, both of which have similar potency. This is in contrast to the human PPARα, where PFOA and PFHpA cause the strongest transactivation among these compounds (c20% values of 0.9 and 5.3 μM, respectively),^37,38 but the PPARα receptor has a significantly smaller binding cavity than PPARγ.

Conclusions

The results from the current study demonstrate that the use of molecular dynamics simulations and enhanced sampled techniques is highly recommended after ligand docking procedure when searching for relevant ligand binding modes within large and flexible LBDs. Recent studies document that ligands show multiple binding modes within LBDs, such as the PPARγ receptor. In addition to the PFCAs studied herein, this is the case for several other PPARγ partial agonists and antagonists.^4,30 Approaches such as aMD, metadynamics, etc. can capture these binding conformations, detail their populations, and describe the dynamics of both the ligand and the receptor. However, more detailed studies should be performed on the barostat choice because according to our preliminary results one should employ the Monte Carlo (MC) barostat, which is presently the default choice in the Amber software, with caution.

The use of free-energy calculations like the FEP+ protocol in combination with cMD and aMD can distinguish the most probable binding modes and score the ligands adequately, given that the ligands can be aligned in a correct way during the design of the FEP computations. Thus, the MD simulations are highly desirable before the execution of FEP+ calculations, as demonstrated for the PFCAs studied (chain length of 6–11 carbon atoms). Moreover, in the current work, we showed that the FEP+ approach works well for PFCAs, which are compounds with physical–chemical properties that are very different from typical druglike molecules and where the interactions by the fluorinated tail is governed by entropic rather than enthalpic forces.

Using the proposed in silico workflow for ligand binding mode searching, ligand–protein dynamics description, and relative free-energy calculations, the most probable PFCA binding conformations and ligand–residue interactions were determined. It was illustrated that the fluorinated tail shows highly dynamic behavior for the shorter-chain PFCAs studied (6–8 carbon atoms) and that the flexibility becomes less pronounced for the PFCAs of 9–11 carbon atoms, which fill out the binding pocket, where DA is known to bind.

The influence of two of the PFCAs (PFOA and PFuDA) on the secondary structure of the PPARγ LBD was investigated by aMD, and according to that analysis, these two ligands partly stabilized the conformation of helix 12, thus potentially acting as partial rather than full agonists. The partial agonist activity of PFOA has been confirmed in a transactivation study, PFuDA was not tested, but perfluorododecanoic acid (PFDDA) showed transactivation activity as well.³⁷ The partial agonist potential is likely to contribute to some of the adverse effects related to lipid homeostasis, adipogenesis, inflammation, and liver toxicity that are observed for chemicals such as PFOA. PPARγ is known to be involved in the regulation of glucose metabolism and storage of fatty acids and to be significantly expressed in the liver. Although PFCAs are only weak binders and some of them are weak activators, the accumulation of such compounds in the human organism increases their concentration level in different protein receptors. In turn, this can increase the probability of these compounds being present in sufficiently high concentrations to cause adverse effects, for example, by hindering fatty acids to enter these proteins for transport and other physiological functions.

Computational Methods

Protein Preparation and Ligand Docking

Protein structures were downloaded from protein data bank (pdb).³⁹ In this study, both the DA (pdb id: 3U9Q) and rosiglitazone (pdb id: 1FM6) structures were used. The X-ray structure preparation for subsequent modeling was conducted with the protein preparation wizard,⁴⁰ which adds missing atoms and optimizes the H-bond network by assigning tautomer/ionization states, sampling water orientations, and flipping Asn, Gln, and His residues in the plane of their π-systems. Finally, restrained energy minimizations were conducted to conclude the system preparation. All resolved crystal water molecules were maintained. Ligand 3D structures were sketched manually and transformed into low-energy 3D structures using LigPrep version 3.5. Docking calculations to place compounds into the PPARγ ligand binding domain were performed with Glide version 6.4 with default parameters. Induced fit docking (IFD)³¹ was also performed using both the default settings and either an increased accuracy to XP docking mode or enhanced sampling option. This was done to investigate if other docking poses were obtained when using a docking method where the flexibility of specific residues could be considered.

Note about Force Field (FF) and Barostat Choice for the Sampling of Ligand Binding Modes during MD Simulations

The FEP+ tools in this work are implemented in the software that uses the OPLS3 FF, and the enhanced MD-based sampling tools used are implemented in the Amber suite that uses the Amber14SB FF. The Amber14SB and OPLS3 FFs are supposed to offer reasonably similar descriptions ligand–protein interactions. Also the main objective of the study is to develop a workflow that uses different computational tools in concert for identifying relevant binding modes and determining free energies of the ligand–protein complexes. It should be noted that all of the ligand–protein structures obtained by the Amber FF were reoptimized and then well equilibrated by the OPLS3 FF before carrying out the FEP calculations.

To obtain the constants needed for the aMD boost parameters, the averaged dihedral and potential energies, one needs initially to perform a regular cMD simulation. In Amber 14 and latter versions, a new Monte Carlo (MC) barostat has been implemented, which speeds up calculations up to 20% and is considered to be more rigorous. However, during these cMD runs, we observed different ligands dynamics behavior. For the PPARγ ligands studied in this work (Table S1), and in particular for DA and PFuDA, the DA binding mode was not obtained with the MC barostat method when using the non-native LBD structure (as co-crystallized with rosiglitazone (pdb id: 1FM6)) as a starting point. In six additional 100 ns long cMD runs for the PFuDA ligand using both the MC and Berendsen barostats, e.g., three runs for each barostat, the DA binding mode was obtained for PFuDA when applying the Amber14SB FF with the Berendsen barostat. However, all simulations performed with the MC barostat failed to reproduce the DA binding mode and indicated that the rosiglitazone binding mode (which was the initial conformation) is energetically more favorable. A similar behavior was observed when we employed OPLS3 FF in a frame of the Desmond software using the default simulation protocol.

One possible explanation of this is that the pmemd.cuda (the GPU version of Amber 14 software) does not compute the virial when using the MC barostat. As a consequence of these observations, the Amber14SB FF was used along with the Berendsen barostat in all of the MD simulations presented in the work.

Classical Molecular Dynamics (cMD)

Classical molecular dynamics (cMD) was carried out using the Amber 14 program and the Amber14SB force field.⁴¹ Initially, the systems were energy-minimized in two steps. First, only the water molecules and ions were minimized in 6000 steps while keeping the protein and ligand structures restricted by weak harmonic constrains of 2 kcal/mol Ų. Second, a 6000 step minimization with the conjugate gradient method on the whole system was performed. Furthermore, the simulated systems were gradually heated from 0 to 310 K for 50 ps (NVT ensemble) and equilibrated for 3 ns (NPT ensemble). The production runs were performed at 310 K in an NPT ensemble. Temperature regulation was done by using a Langevin thermostat with a collision frequency of 2 ps^–1, and pressure regulation via Berendsen barostats. The time step of the simulations was 2 fs with a nonbonded cutoff of 8 Å using the SHAKE algorithm⁴² and the particle-mesh Ewald method.⁴³ For each of the studied PFCAs and for DA (seven compounds listed in Table S1 in the Supporting Information), two independent 100 ns long simulations were executed (1.4 μs total simulation time for all of the systems). Moreover, for two of the ligands, 2 × 130 ns additional runs were also performed (see Results and Discussion for details).

Accelerated Molecular Dynamics (aMD)

Accelerated molecular dynamics (aMD) simulations provide the possibility to sample the conformational space in much greater detail and to detect the local energy minima that remain hidden in the cMD calculations.^44,45 Moreover, aMD simulations can boost the sampling by up to 2000 times compared to cMD.⁴⁴ Thus, one can consider that the sampling performed by a 300 ns aMD trajectory might be equal to that of several microseconds of cMD simulation. aMD modifies the energy landscape by adding a boost potential ΔV(r) to the original potential energy surface when V(r) is below a predefined energy level E, as defined in eq 1.

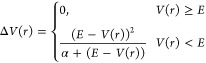1

In general, this approach also allows the canonical average of an observable calculated from configurations sampled and the modified potential energy surface to be fully mapped.^46,47

All of the aMD calculations were performed using the Amber 14 molecular modeling package and the Amber14SB force field.⁴¹ The production runs were performed at 310 K in an NPT ensemble. Temperature regulation was done using a Langevin thermostat with a collision frequency of 2 ps^–1, and pressure regulation via Berendsen barostat. The time step of the simulations was 2 fs with a nonbonded cutoff of 8 Å using the SHAKE algorithm⁴² and the particle-mesh Ewald method.⁴³

To simultaneously enhance the sampling of the internal and diffusive degrees of freedom, a dual-boosting approach based on separate dihedral and total boost potentials was employed.⁴⁴⁻⁴⁶ This method may be compromised by the increased statistical noise, but was also successfully applied in similar studies.^4,35,48 The selections of the boost parameters E and α for the dihedral boost (E_d and α_d) and for the total boost (E_p and α_p) were based on the corresponding average dihedral energy and total potential energy obtained from the combined cMD production runs (2 × 100 ns for each ligand). The dihedral boost parameter, E_d, was set equal to the average dihedral energy obtained from the cMD simulation plus an approximate energy contribution of N_sr × 3.5 kcal/mol residue to account for the degrees of freedom, where N_sr is the number of protein residues. The α_d parameter was then set equal to 0.2 × N_sr × 3.5 kcal/mol/residue. For the total boost parameter, E_p, the value was set to be equal to the average total potential energy obtained from the cMD simulation plus 0.2 × N_tot, where N_tot is the total number of atoms in the simulated system. The α_p parameter was simply set equal to 0.2 × N_tot.⁴¹

Two 300 ns long production aMD runs were performed on both the PFuDA and PFOA ligand–receptor complexes.

Reweighting of biased aMD frames is an important procedure and was performed based on the Maclaurin series expansion scheme up to the tenth order. The reweighting procedure has been recently discussed and described in several studies.^46,47 For the free-energy plots, the distances between the carbon atom of the CF₃ group (the end of ligand) and the C_α atoms of Phe282 (helix 3) and Tyr473 (helix 5) were chosen as coordinates. As the fluorinated tail of these compounds was seen to move quite flexibly within the LBD, the carbon in the CF₃ group at the end of the fluorinated tail was seen as the best choice to describe the flexibility of these ligands.

Finally, convergence analyses were performed by the RMS average correlations method⁴⁹ and the Kullback–Leibler divergence⁵⁰ in the way that was well documented in previous works.^4,35,48−50

MM/GBSA Calculations

The ligand–residue free energies of binding calculations were performed by the molecular mechanics/generalized born surface area (MM/GBSA) method using the MMPBSA.py script included in the AmberTools 15 package.^41,51 This method was successfully used in numerous studies and the methodology was widely described previously.^3,48,51−53 In this study, the free energies were calculated for each frame extracted from the MD trajectory with an interval of 10 ps. The entropy term was neglected. The binding free energy of a ligand can of course not rigorously be decomposed into atomic or residue contributions. Nevertheless, MM/GBSA approaches offer an approximate energy decomposition that, despite being somewhat arbitrary, can offer qualitative insights when a series of highly similar ligands are analyzed using the same decomposition scheme.

Free-Energy Calculations (FEP+)

All calculations have been conducted using the Schrödinger molecular modeling suite.⁵⁴ Free-energy perturbation calculations were performed using the FEP+ methodology, which combines the accurate modern OPLS3 force field,⁵⁵ GPU-enabled high-speed molecular dynamics simulations with Desmond version 3.9,⁵⁶ the REST algorithm for locally enhanced sampling,⁵⁷ a cycle-closure correction⁵⁸ to incorporate redundant information into free-energy estimates, and the FEP Mapper tool to automate setup and analysis of the calculations. The force-field builder tool was used to test if accurate OPLS3 force-field torsional parameters for all molecules were available.

The FEP+ calculations based on the X-ray structures, performed with the pdb id structures 3U9Q and 1FM6, were conducted using the default protocols: The systems were solvated in an orthogonal box of SPC water molecules with buffer widths (minimum distance between box edge and any solute atom) of 5 Å for the complex and 10 Å for the solvent simulations. The full systems were relaxed and equilibrated using the default Desmond relaxation protocol, consisting of an energy minimization with restraints on the solute and then 12 ps length simulations at 10 K using an NVT ensemble, followed by an NPT ensemble. After that, the restrained system was equilibrated at room temperature using the NPT ensemble. Finally, a 240 ps room-temperature NPT ensemble simulation was conducted. Production simulations in the NPT ensemble lasted 5 ns for both the complex and the solvent systems. A total of 12 λ windows were used for all of the 5 ns long FEP/REST calculations. Replica exchanges between neighboring λ windows were attempted every 1.2 ps. For a more detailed description of the free-energy calculation protocol employed, see the Supporting Information of Wang et al.⁵

For the FEP+ calculations based on MD-derived structures, an improved and new protocol was employed, which is described in detail in a different study. Briefly, we used the structures obtained with the help of cluster analysis and the most populated PFuDA conformation identified in the cMD simulations based on pdb id 1FM6, which was minimized by the OPLS3 FF and used as a template for all other ligands during the design of the FEP+ procedure. For these FEP+ simulations, we employed 2 × 10 ns/λ pre-REST and 8 ns/λ REST calculations.

The convergence was closely monitored. No significant changes in the free energy were observed after 3 and 5 ns simulation times for templates derived from X-ray analyses and MD-generated structures, respectively. More details and discussions are found in the Free-Energy Calculations (FEP+) section of Results and Discussion section. All calculations were run on Nvidia Kepler and Pascal architecture GPUs.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b00123.

• Ligand names, 2D graphs (Table S1); comparison between the binding mode of DA and PFuDA (Figure S1); RMSD of the PFuDA ligand (Figure S2); free energy map of the PFOA (Figure S3); PFuDA ligand–receptor interactions for cMD (Figure S4); reweighted free energy map of the PFOA (Figure S5); antagonist H12 conformation (Figure S6); FEP+ results (Figures S7 and S8) (PDF)

• Structural files (regular and induced fit docking outputs, first and last MD frames from cMD run 1 on PFuDA) (PDB)(PDB)(PDB)(PDB)

• Movement of PFuDA ligand (Movie S1) (AVI)

The authors declare no competing financial interest.