Abstract
Conformational characteristics of poly(ethylene carbonate) (PEC) and poly(propylene carbonate) (PPC) have been revealed via molecular orbital (MO) calculations and nuclear magnetic resonance (NMR) experiments on model compounds with the same bond sequences as those of the polycarbonates. Bond conformations derived from the MO calculations on the models were in exact agreement with those from the NMR experiments. Both PEC and PPC were indicated to adopt distorted conformations including a number of gauche bonds and cover themselves with negative charges, thus failing to form a regular packing and remaining amorphous. The MO data were applied to the refined rotational isomeric state (RIS) calculations to yield configurational properties such as the characteristic ratio, its temperature coefficient, the configurational entropy, and average geometrical parameters of unperturbed PEC and PPC chains. In the RIS calculations on PPC, the regio- and stereosequences were generated according to the Bernoulli trial or Markov stochastic process. In consequence, it was shown that the configurational properties of PPC do not depend significantly on its regio- and stereoregularities. The internal energy contribution to rubberlike chain elasticity, calculated from the temperature coefficient of the characteristic ratio, has indicated the possibility that PEC and PPC will behave as elastomers. The practical applications and potential utilizations of the polycarbonates are discussed on the basis of the conformational characteristics and configurational properties.
Introduction
If noxious fumes generated in industrial processes were dispersed into the atmosphere, animals including human beings and plants would be seriously injured or, at their worst, killed. However, chemists have settled such problems by fixing the gases in solids. For example, in alkali industries, gaseous chlorine generated in sodium production has been chemically changed to useful polymers such as poly(vinyl chloride).1 As another example, one may mention carbon dioxide. Of course, carbon dioxide itself is not necessarily a harmful substance but, on the contrary, a nutrient source indispensable for plants. To suppress the global warming, however, we have been strongly required to control the amount of atmospheric carbon dioxide.
In 1969, Inoue, Koinuma, and Tsuruta2,3 reported a reaction scheme to synthesize poly(alkyl carbonate)s, that is, alternating copolymers of epoxides with carbon dioxide (Scheme 1). In the reaction, carbon dioxide, the most inactive (i.e., thermodynamically dead) carbon source, is utilized. Because of the growing worldwide interest in global warming, polymer chemists and engineers have been paying particular attention to polycarbonates. If carbon dioxide emitted from combustion of natural gas, petroleum, and coal can be effectively absorbed on basic polymers such as poly(ethylene imine)4−6 and its derivatives7 and analogues,8 the polycarbonates may be produced from the collected gas, and consequently, CO2 fixation will be realized.
Scheme 1. Synthesis of Aliphatic Polycarbonates from Epoxides and Carbon Dioxide: R = H, Poly(ethylene carbonate) (PEC) and R = CH3, Poly(propylene carbonate) (PPC).
Of the aliphatic polycarbonates, PEC (Figure 1) and PPC were synthesized early2,3 but have not been easy to use either as hard plastics or as flexible rubbers because glass transitions of PEC and PPC occur around room temperature (ca. 20 °C) and human body temperature (35–40 °C), respectively.9 Therefore, the polycarbonates will become hard in cold areas (or seasons) but flexible in hot ones.
Figure 1.

(a) PEC and (b) PPC. The bonds are designated as shown, and x is the degree of polymerization. To facilitate the refined rotational isomeric state (RIS) calculations, the polymeric chains have been assumed to be terminated by a methyl group.
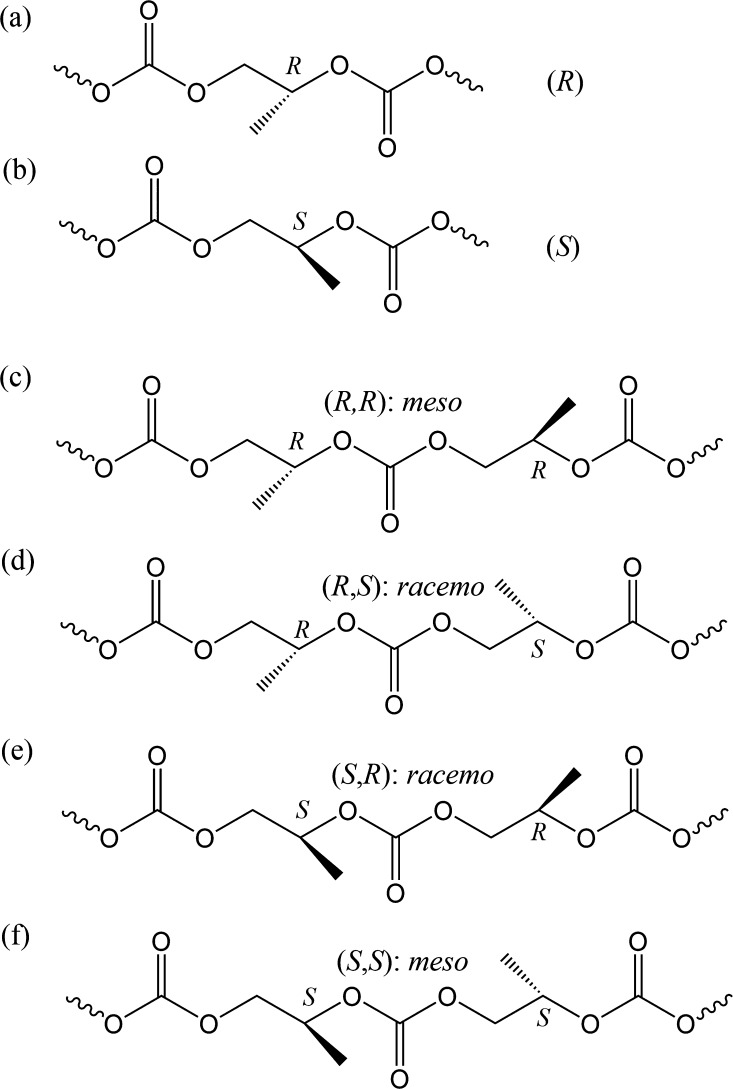
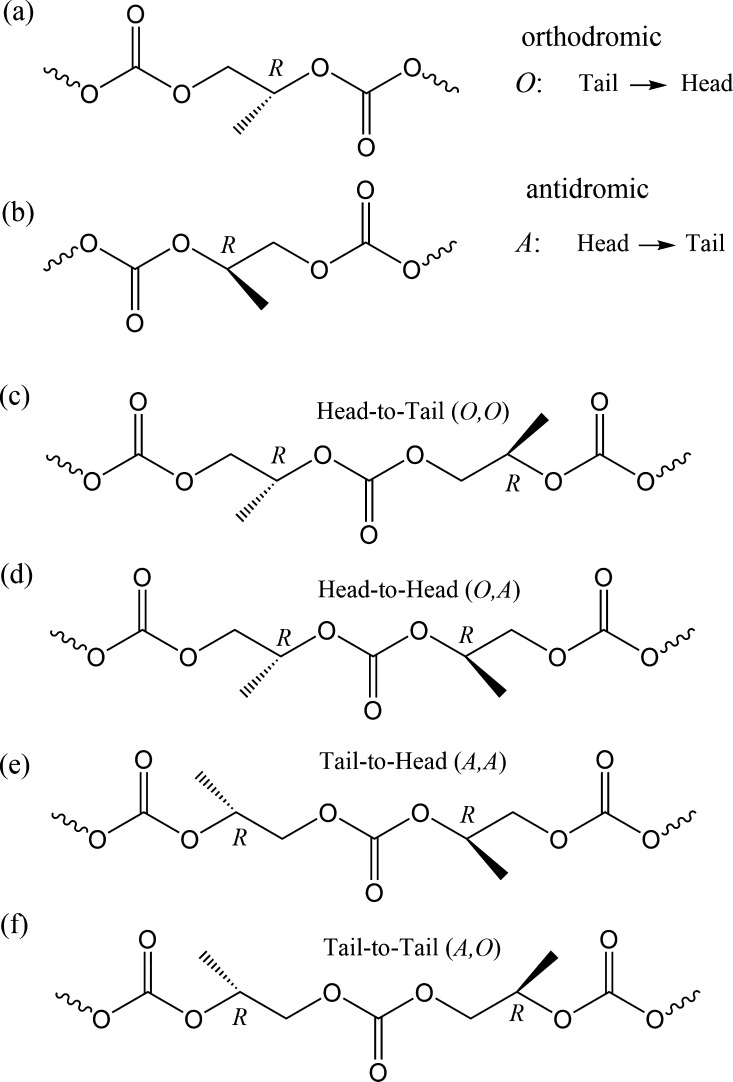
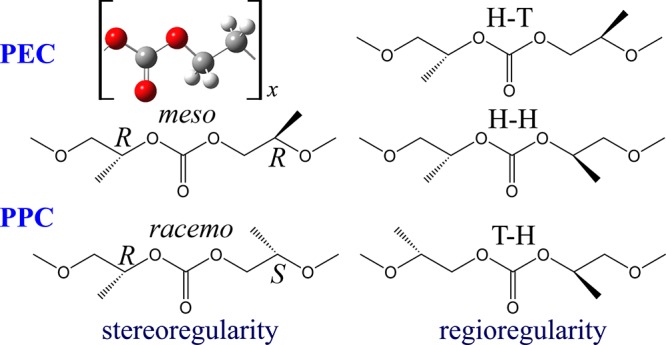
Inasmuch as PPC has an asymmetric carbon atom in the repeating unit, its primary structure is determined by two kinds of configurations: stereo- and regioisomerizations. The former means the existence of (R)- and (S)-isomers (see Figure 2). The latter means the formation of three kinds of linkages between the monomeric units: head-to-tail (abbreviated as H–T), head-to-head (H–H), and tail-to-tail (T–T) (see Figure 3). For these reasons, polymer chemists have challenged to develop stereospecific catalysts for controlling its regio- and stereoregularities,10−22 in expectation that fully regular PPCs might crystallize and exhibit so large an elastic modulus and so high a glass transition temperature (Tg) as to be used as hard plastics.
Figure 2.
Stereosequences of PPC: (a) (R)- and (b) (S)-isomers; (c) (R,R)-, (d) (R,S)-, (e) (S,R)-, and (f) (S,S)-diads. (R,R)- and (S,S)-diad combinations are designated as meso, and (R,S)- and (S,R)-diad ones as racemo. When the polymeric chain is composed of only meso (racemo) couplings, the stereoregularity is termed isotactic (syndiotactic).
Figure 3.
Regiosequences of PPC. Definition of (a) orthodromic (O) and (b) antidromic (A) directions. Four possible combinations of (O)- and (A)-directions between neighboring units: (c) (O,O), head-to-tail (H–T); (d) (O,A), head-to-head (H–H); (e) (A,A), tail-to-head (T–H); and (f) (A,O), tail-to-tail (T–T). The tail-to-head linkage is included in H–T; therefore, the three expressions, H–T, H–H, and T–T, are used herein.
According to a cardinal principle of polymer science and molecular biology, “higher-order structures, physical properties, and functions of a polymer originate from its primary structure”; it is of fundamental importance to reveal the conformational characteristics of PEC and PPC and, furthermore, to evaluate their configurational properties. This is the prime aim of this study. The conformational analysis of model compounds with the same bond sequences as those of the polycarbonates, ethylene glycol bis(methyl carbonate) (E_model, Figure 4) for PEC and propylene glycol bis(methyl carbonate) (P_model) for PPC, has been carried out by molecular orbital (MO) calculations and nuclear magnetic resonance (NMR) experiments. The MO energies and geometrical parameters were introduced into the refined RIS scheme23 to yield configurational properties of the two polycarbonates. Then, stochastic processes based on the Bernoulli trial and first-order Markov chain24,25 were employed to generate regio- and stereosequences of PPC to elucidate how its properties depend on the two kinds of configurations. Herein, the procedures and results are described in detail. On the basis of the structural information thus established, physical properties, practical uses, and potential applications of PEC and PPC are discussed.
Figure 4.
Model compounds of PEC and PPC: (a) for PEC, ethane-1,2-diyl dimethyl bis(carbonate) (E_model) and (b) for PPC, dimethyl propane-1,2-diyl bis(carbonate) (P_model). As indicated, the bonds are designated, and the methylene and methine protons are labeled for NMR analysis. (R)- and (S)-P_models yield the identical NMR spectra; therefore, (R)-P_model is exclusively employed herein.
Results and Discussion
NMR Experiments
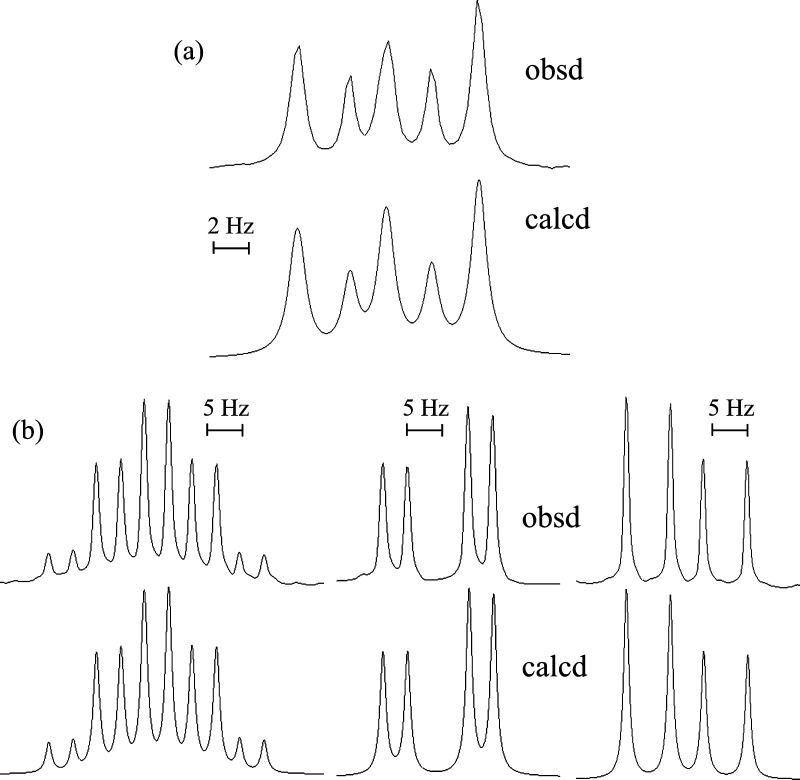
Figure 5a shows 1H NMR satellite peaks observed from the naturally abundant 13CH2 group of the E_model. The spectrum simulation reproduced the observation well and yielded the JHH and J′HH values. In Table 1, the two vicinal couplings are given for each NMR solvent and temperature. As explained in the “Methods” section, the pt and pg values were derived from eqs 8 and 9 with the two sets of JT and JG. The sum of pt and pg, thus obtained was slightly different from unity and hence divided by the sum to fulfill eq 10. The pt values of bond 5 (Table 2) are so small as to indicate a strong gauche preference of the CH2–CH2 bond, and the pt value tends to increase with temperature and decrease slightly with solvent polarity.
Figure 5.
Observed (above) and calculated (below) 1H NMR spectra: (a) satellite from the CH2 group of the E_model dissolved in dimethyl-d6 sulfoxide (DMSO-d6) at 25 °C; (b) HC (left), HA (middle), and HB (right) of the P_model dissolved in CDCl3 at 25 °C. For the proton symbols of the P_model, see Figure 4.
Table 1. Observed NMR Vicinal 1H–1H Coupling Constants of E_Modela.
| solvent | permittivity | temp (°C) | JHH | JHH′ |
|---|---|---|---|---|
| chloroform-d | 4.8 | 15 | 6.46 | 2.70 |
| 25 | 6.46 | 2.81 | ||
| 35 | 6.46 | 2.89 | ||
| 45 | 6.45 | 2.97 | ||
| 55 | 6.44 | 3.05 | ||
| acetone-d6 | 20.7 | 15 | 6.52 | 2.60 |
| 25 | 6.49 | 2.65 | ||
| 35 | 6.49 | 2.70 | ||
| 45 | 6.48 | 2.76 | ||
| methanol-d4 | 32.7 | 15 | 6.48 | 2.58 |
| 25 | 6.47 | 2.61 | ||
| 35 | 6.46 | 2.67 | ||
| 45 | 6.46 | 2.75 | ||
| 55 | 6.46 | 2.82 | ||
| DMSO-d6 | 46.7 | 25 | 6.49 | 2.48 |
| 35 | 6.49 | 2.53 | ||
| 45 | 6.48 | 2.60 | ||
| 55 | 6.47 | 2.69 |
In Hz.
Table 2. Trans Fractions (pt’s) of E_Model: Comparison between MO Calculations and NMR Experiments.
| bond 5 |
|||||
|---|---|---|---|---|---|
| bond 4 (6) | NMR |
||||
| medium | temp (°C) | MO | MO | set A | set B |
| gas | 15 | 0.39 | 0.12 | ||
| 25 | 0.39 | 0.12 | |||
| 35 | 0.39 | 0.13 | |||
| 45 | 0.39 | 0.13 | |||
| 55 | 0.38 | 0.14 | |||
| chloroform | 15 | 0.51 | 0.06 | 0.01 | 0.05 |
| 25 | 0.50 | 0.07 | 0.02 | 0.06 | |
| 35 | 0.50 | 0.07 | 0.03 | 0.07 | |
| 45 | 0.49 | 0.07 | 0.04 | 0.08 | |
| 55 | 0.49 | 0.08 | 0.04 | 0.08 | |
| acetone | 15 | 0.55 | 0.04 | 0.00 | 0.04 |
| 25 | 0.54 | 0.05 | 0.01 | 0.05 | |
| 35 | 0.53 | 0.05 | 0.02 | 0.05 | |
| 45 | 0.53 | 0.05 | 0.02 | 0.06 | |
| methanol | 15 | 0.55 | 0.04 | 0.00 | 0.04 |
| 25 | 0.55 | 0.04 | 0.01 | 0.04 | |
| 35 | 0.54 | 0.05 | 0.01 | 0.05 | |
| 45 | 0.53 | 0.05 | 0.02 | 0.06 | |
| 55 | 0.53 | 0.06 | 0.03 | 0.06 | |
| DMSO | 25 | 0.55 | 0.04 | ∼0.00 | 0.03 |
| 35 | 0.54 | 0.05 | ∼0.00 | 0.03 | |
| 45 | 0.54 | 0.05 | 0.01 | 0.04 | |
| 55 | 0.53 | 0.06 | 0.01 | 0.05 | |
In Figure 5b, 1H NMR spectra observed from HA, HB, and HC of the P_model are shown, together with the spectrum simulations. The obtained JAB and JBC values (Table 3) were substituted into eqs 11 and 12 to yield the bond conformations as shown in Table 4. The magnitude relation of pt ≪ pg– < pg+ always holds regardless of the solvent and temperature.
Table 3. Observed NMR Vicinal 1H–1H Coupling Constants of P_Modela.
| solvent | temp (°C) | JAC | JBC |
|---|---|---|---|
| chloroform-d | 15 | 6.85 | 3.32 |
| 25 | 6.80 | 3.34 | |
| 35 | 6.71 | 3.43 | |
| 45 | 6.60 | 3.51 | |
| 55 | 6.58 | 3.55 | |
| acetone-d6 | 15 | 6.82 | 3.06 |
| 25 | 6.75 | 3.11 | |
| 35 | 6.68 | 3.16 | |
| 45 | 6.66 | 3.20 | |
| methanol-d4 | 15 | 6.80 | 3.10 |
| 25 | 6.77 | 3.15 | |
| 35 | 6.75 | 3.21 | |
| 45 | 6.70 | 3.25 | |
| 55 | 6.65 | 3.31 | |
| DMSO-d6 | 25 | 6.76 | 2.93 |
| 35 | 6.70 | 2.96 | |
| 45 | 6.66 | 3.00 | |
| 55 | 6.60 | 3.04 |
In Hz.
Table 4. Bond Conformations of (R)-P_Model Determined from NMR Experiments.
| bond 5 |
|||||||
|---|---|---|---|---|---|---|---|
| set A |
set B |
||||||
| solvent | temp (°C) | pt | pg+ | pg– | pt | pg+ | pg– |
| chloroform | 15 | 0.10 | 0.59 | 0.31 | 0.11 | 0.50 | 0.39 |
| 25 | 0.11 | 0.58 | 0.31 | 0.11 | 0.50 | 0.39 | |
| 35 | 0.12 | 0.57 | 0.31 | 0.12 | 0.49 | 0.39 | |
| 45 | 0.13 | 0.56 | 0.31 | 0.13 | 0.48 | 0.39 | |
| 55 | 0.14 | 0.55 | 0.31 | 0.14 | 0.47 | 0.39 | |
| acetone | 15 | 0.07 | 0.56 | 0.37 | 0.08 | 0.50 | 0.42 |
| 25 | 0.08 | 0.55 | 0.37 | 0.09 | 0.49 | 0.42 | |
| 35 | 0.08 | 0.54 | 0.38 | 0.10 | 0.48 | 0.42 | |
| 45 | 0.09 | 0.53 | 0.38 | 0.10 | 0.48 | 0.42 | |
| methanol | 15 | 0.08 | 0.55 | 0.37 | 0.09 | 0.49 | 0.42 |
| 25 | 0.08 | 0.55 | 0.37 | 0.09 | 0.49 | 0.42 | |
| 35 | 0.09 | 0.55 | 0.36 | 0.10 | 0.49 | 0.41 | |
| 45 | 0.10 | 0.54 | 0.36 | 0.11 | 0.48 | 0.41 | |
| 55 | 0.10 | 0.54 | 0.36 | 0.11 | 0.48 | 0.41 | |
| DMSO | 25 | 0.05 | 0.55 | 0.40 | 0.07 | 0.49 | 0.44 |
| 35 | 0.06 | 0.54 | 0.40 | 0.07 | 0.49 | 0.44 | |
| 45 | 0.06 | 0.54 | 0.40 | 0.08 | 0.48 | 0.44 | |
| 55 | 0.07 | 0.53 | 0.40 | 0.08 | 0.47 | 0.45 | |
MO Calculations
Table 5 shows conformer free energies of the E_model. Of the eight conformers that the B3LYP optimization gave, the most stable conformation is tg+t (Figure 6a), indicating a gauche preference of the central CH2–CH2 bond. It has been found that the aromatic and aliphatic esters with the C(=O)–O–CH2–CH2–O–C(=O) bond sequence show strong gauche preferences in the central CH2–CH2 bond. The free energies of the tgt conformation were evaluated as, for example, −1.1 kcal mol–1 for poly(ethylene terephthalate) (PET)26 and −1.2 kcal mol–1 for poly(ethylene succinate) (PES).27 These ΔGk values are comparable to that of PEC (Table 5). Therefore, it can be concluded that the tgt stability is inherent in the C(=O)–O–CH2–CH2–O–C(=O) sequence of the esters. The ttg+ conformer also has a small free energy of 0.1–0.3 kcal mol–1 as compared with that of poly(ethylene oxide) (PEO) (1.3 kcal mol–1).28−30 It is also known that the ttg conformations of PET and PES have relatively small ΔGk values of 0.5 and 0.3 kcal mol–1, respectively.26,27 In the ttg+ conformation (Figure 6b), a short C=O···C–H contact (2.40 Å) can be found between the carbonyl and methylene groups via the gauche O–CH2 bond, and the involved O=C–O–CH2–C–H atoms lie on a plane. The above results indicate that the PEC chain tends to adopt distorted structures with a number of gauche bonds. In Table 2, the bond conformations calculated from the ΔGk values are listed. As for the CH2–CH2 bond, the MO calculations agree satisfactorily with set A and exactly with set B. These facts show the reliability of the MO energies.
Table 5. Conformer Free Energies (ΔGk’s) of Model Compounds of PEC and PEO, Evaluated by Ab Initio MO Calculationsa.
| |
PECb |
PEOc | |||||||
|---|---|---|---|---|---|---|---|---|---|
| k | conformationd | gas | chloroform | acetone | methanol | DMSO | gas | ||
| 1 | t | t | t | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | t | t | g+ | 0.11 | 0.23 | 0.28 | 0.29 | 0.29 | 1.31 |
| 3 | t | g+ | t | –0.81 | –1.35 | –1.59 | –1.62 | –1.64 | 0.19 (−0.08e) |
| 4 | t | g+ | g+ | –0.59 | –1.00 | –1.20 | –1.23 | –1.25 | 1.28 |
| 5 | t | g+ | g– | (absent)f | 0.26 | ||||
| 6 | g+ | t | g+ | 1.90 | 1.89 | 1.85 | 1.84 | 1.84 | 2.74 |
| 7 | g+ | t | g– | 0.59 | 0.82 | 0.87 | 0.88 | 0.88 | 2.61 |
| 8 | g+ | g+ | g+ | –0.42 | –0.45 | –0.48 | –0.49 | –0.49 | 2.27 |
| 9 | g+ | g+ | g– | –0.72 | –0.81 | –0.89 | –0.90 | –0.91 | 1.88 |
| 10 | g+ | g– | g+ | (absent)f | 1.77 | ||||
In kcal mol–1, relative to the all-trans conformation.
From E_model, at the MP2/6-311+G(2d,p)//B3LYP/6-311+G(2d,p) level.
From 1,2-dimethoxyethane, at the MP2/6-311++G(3df,3pd)//HF/6-31G(d) level.30
In the O–CH2–CH2–O bond sequence.
At the CH2–CH2 bond of the central unit of triglyme.30
Local minimum of the potential was not found by the geometrical optimization.
Figure 6.
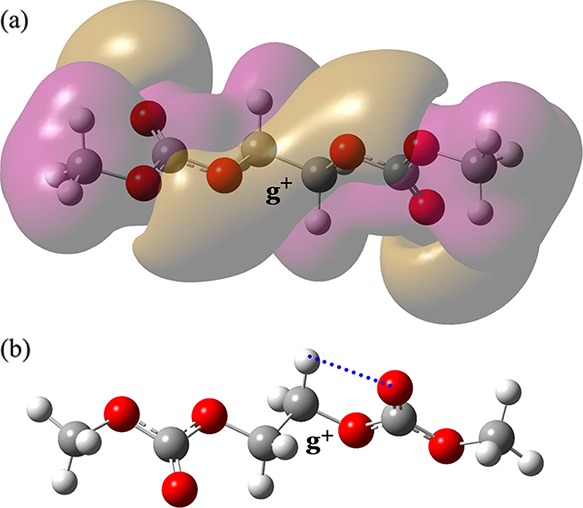
E_model: (a) tg+t, electrostatic potential distribution and (b) ttg+, an intramolecular C=O···H–C close contact (dotted line) with the O···H distance of 2.40 Å.
Table 6 shows the ΔGk values of P_model. Its asymmetric carbon renders the 27 (=33) conformers unique and irreducible, and the pendent methyl group gives rise to intramolecular steric repulsions; however, P_model exhibits the conformational preferences and intramolecular interactions similar to those found for the E_model. A number of conformers have negative ΔGk’s. In particular, those of g+g+t and tg+t and g+g–g– are largely negative; therefore, PPC will also adopt distorted structures. The bond conformations of P_model, calculated from the ΔGk values, are listed in Table 7. For the CH2–CH(CH3) bond, the magnitude relation pt ≪ pg– < pg+ holds, thus being consistent with the NMR analysis. On the basis of the good agreement between theory and experiment, we advanced to the refined RIS calculations on PEC and PPC with the ΔGk energies and geometrical parameters (Tables S1 and S2, Supporting Information) of the models.
Table 6. Conformer Free Energies (ΔGk’s) of PPC and Poly(propylene oxide) (PPO), Evaluated by Ab Initio MO Calculationsa.
| |
PPCb |
PPOc | |||||||
|---|---|---|---|---|---|---|---|---|---|
| k | conformationd | gas | chloroform | acetone | methanol | DMSO | gas | ||
| 1 | t | t | t | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | t | t | g+ | 2.22 | 2.36 | 2.41 | 2.42 | 2.42 | 3.20 |
| 3 | t | t | g– | –0.15 | –0.18 | –0.18 | –0.18 | –0.18 | 0.43 |
| 4 | t | g+ | t | –0.47 | –1.07 | –1.31 | –1.34 | –1.36 | 0.62 |
| 5 | t | g+ | g+ | 2.28 | 1.82 | 1.58 | 1.55 | 1.53 | 3.80 |
| 6 | t | g+ | g– | (absent)e | –0.20 | ||||
| 7 | t | g– | t | –0.06 | –0.58 | –0.84 | –0.88 | –0.90 | 1.57 |
| 8 | t | g– | g+ | 5.06 | 4.32 | 3.91 | 3.85 | 3.82 | 2.18 |
| 9 | t | g– | g– | –0.22 | –0.70 | –0.95 | –0.98 | –1.00 | 1.38 |
| 10 | g+ | t | t | (absent)e | (absent)e | ||||
| 11 | g+ | t | g+ | (absent)e | (absent)e | ||||
| 12 | g+ | t | g– | (absent)e | (absent)e | ||||
| 13 | g+ | g+ | t | –0.78 | –1.22 | –1.39 | –1.42 | –1.43 | 2.30 |
| 14 | g+ | g+ | g+ | 2.02 | 2.02 | 2.01 | 2.00 | 2.00 | 4.02 |
| 15 | g+ | g+ | g– | 2.19 | 1.13 | 0.69 | 0.62 | 0.59 | 1.34 |
| 16 | g+ | g– | t | (absent)e | 0.99 | ||||
| 17 | g+ | g– | g+ | (absent)e | (absent)e | ||||
| 18 | g+ | g– | g– | –0.59 | –0.78 | –0.90 | –0.92 | –0.93 | 1.51 |
| 19 | g– | t | t | 0.12 | 0.18 | 0.20 | 0.20 | 0.20 | 1.25 |
| 20 | g– | t | g+ | 2.64 | 2.86 | 2.91 | 2.92 | 2.92 | 4.46 |
| 21 | g– | t | g– | (absent)e | 1.87 | ||||
| 22 | g– | g+ | t | (absent)e | 0.80 | ||||
| 23 | g– | g+ | g+ | 2.28 | 2.12 | 1.98 | 1.96 | 1.95 | 4.28 |
| 24 | g– | g+ | g– | (absent)e | (absent)e | ||||
| 25 | g– | g– | t | 0.33 | –0.11 | –0.34 | –0.37 | –0.39 | (absent)e |
| 26 | g– | g– | g+ | 5.14 | 4.73 | 4.48 | 4.44 | 4.42 | (absent)e |
| 27 | g– | g– | g– | 0.13 | –0.13 | –0.27 | –0.29 | –0.30 | (absent)e |
In kcal mol–1, relative to the all-trans conformation.
From (R)-P_model, at the MP2/6-311+G(2d,p)//B3LYP/6-311+G(2d,p) level.
From (R)-1,2-dimethoxypropane, at the MP2/6-31+G(d)//HF/6-31G(d) level.31
In the O–CH2–CH(CH3)–O bond sequence.
Local minimum of the potential was not found by the geometrical optimization.
Table 7. Bond Conformation of (R)-P_Model, Evaluated from MO Calculations.
| bond 4 |
bond 5 |
bond 6 |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| medium | temp (°C) | pt | pg+ | pg– | pt | pg+ | pg– | pt | pg+ | pg– |
| gas | 15 | 0.44 | 0.42 | 0.14 | 0.19 | 0.39 | 0.42 | 0.60 | 0.01 | 0.39 |
| 25 | 0.45 | 0.41 | 0.14 | 0.20 | 0.38 | 0.42 | 0.59 | 0.01 | 0.40 | |
| 35 | 0.45 | 0.40 | 0.15 | 0.20 | 0.38 | 0.42 | 0.59 | 0.01 | 0.40 | |
| 45 | 0.45 | 0.40 | 0.15 | 0.21 | 0.37 | 0.42 | 0.59 | 0.01 | 0.40 | |
| 55 | 0.46 | 0.39 | 0.15 | 0.21 | 0.37 | 0.42 | 0.59 | 0.01 | 0.40 | |
| chloroform | 15 | 0.49 | 0.41 | 0.10 | 0.10 | 0.49 | 0.41 | 0.67 | 0.00 | 0.33 |
| 25 | 0.49 | 0.40 | 0.11 | 0.11 | 0.48 | 0.41 | 0.67 | 0.00 | 0.33 | |
| 35 | 0.49 | 0.40 | 0.11 | 0.11 | 0.48 | 0.41 | 0.66 | 0.01 | 0.33 | |
| 45 | 0.49 | 0.39 | 0.12 | 0.11 | 0.47 | 0.42 | 0.65 | 0.01 | 0.34 | |
| 55 | 0.49 | 0.39 | 0.12 | 0.12 | 0.46 | 0.42 | 0.65 | 0.01 | 0.34 | |
| acetone | 15 | 0.51 | 0.39 | 0.10 | 0.07 | 0.51 | 0.42 | 0.68 | 0.00 | 0.32 |
| 25 | 0.51 | 0.39 | 0.10 | 0.08 | 0.50 | 0.42 | 0.68 | 0.00 | 0.32 | |
| 35 | 0.51 | 0.38 | 0.11 | 0.08 | 0.49 | 0.43 | 0.67 | 0.01 | 0.32 | |
| 45 | 0.51 | 0.38 | 0.11 | 0.09 | 0.48 | 0.43 | 0.67 | 0.01 | 0.32 | |
| methanol | 15 | 0.51 | 0.39 | 0.10 | 0.07 | 0.51 | 0.42 | 0.69 | 0.00 | 0.31 |
| 25 | 0.52 | 0.38 | 0.10 | 0.07 | 0.50 | 0.43 | 0.68 | 0.00 | 0.32 | |
| 35 | 0.52 | 0.38 | 0.10 | 0.08 | 0.49 | 0.43 | 0.67 | 0.01 | 0.32 | |
| 45 | 0.52 | 0.37 | 0.11 | 0.08 | 0.48 | 0.44 | 0.67 | 0.01 | 0.32 | |
| 55 | 0.52 | 0.37 | 0.11 | 0.08 | 0.48 | 0.44 | 0.66 | 0.01 | 0.33 | |
| DMSO | 25 | 0.52 | 0.38 | 0.10 | 0.07 | 0.50 | 0.43 | 0.68 | 0.00 | 0.32 |
| 35 | 0.52 | 0.38 | 0.10 | 0.08 | 0.49 | 0.43 | 0.67 | 0.01 | 0.32 | |
| 45 | 0.52 | 0.37 | 0.11 | 0.08 | 0.48 | 0.44 | 0.67 | 0.01 | 0.32 | |
| 55 | 0.52 | 0.37 | 0.11 | 0.08 | 0.48 | 0.44 | 0.66 | 0.01 | 0.33 | |
Refined RIS Calculations
The characteristic ratios (⟨r2⟩0/nl2), its temperature coefficients (dln⟨r2⟩0/dT), configurational entropies (Sconf), and averaged geometrical parameters of unperturbed PEC and PPC chains at 25 °C are presented in Table 8. The PPC chain was assumed to be isotactic and include only the H–T linkage. The temperature coefficient at T0 was calculated by the finite-difference method
| 1 |
where T0 and ΔT were set equal to 298.15 K (25 °C) and 1.00 K, respectively.
Table 8. Configurational Properties and Averaged Geometrical Parameters of PEC and Isotactic (R)-PPC at 25 °C, Evaluated from the Refined RIS Calculations with MO Parameters Including Solvent Effects.
| gas | chloroform | acetone | methanol | DMSO | |
|---|---|---|---|---|---|
| PEC | |||||
| ⟨r2⟩0/nl2 | 2.42 | 2.52 | 2.54 | 2.54 | 2.54 |
| dln⟨r2⟩0/dT × 103 (K–1) | 0.32 | –0.12 | –0.25 | –0.26 | –0.27 |
| Sconf (cal K–1 mol–1) | 5.51 | 5.16 | 4.97 | 4.94 | 4.93 |
| fU/f × 103 | 95 | –35 | –73 | –78 | –80 |
| geometrya (chloroform) | bond | l̅ | θ̅ | 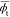 |
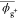 |
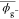 |
|---|---|---|---|---|---|---|
| a | 1.339 | 107.9 | 0.0 | |||
| b | 1.339 | 115.5 | 0.0 | |||
| c | 1.440 | 110.0 | 0.0 | 95.5 | –95.5 | |
| d | 1.510 | 110.0 | 0.0 | 111.9 | –111.9 | |
| e | 1.440 | 115.5 | 0.0 | 95.5 | –95.5 |
| gas | chloroform | acetone | methanol | DMSO | |
|---|---|---|---|---|---|
| Isotactic(R)-PPCof100%H–T | |||||
| ⟨r2⟩0/nl2 | 2.36 | 2.26 | 2.26 | 2.26 | 2.26 |
| dln⟨r2⟩0/dT × 103 (K–1) | 1.07 | 0.44 | 0.24 | 0.20 | 0.18 |
| Sconf (cal K–1 mol–1) | 4.34 | 4.12 | 4.05 | 4.04 | 4.03 |
| fU/f × 103 | 320 | 130 | 72 | 60 | 52 |
| geometrya (chloroform) | bond | l̅ | θ̅ | 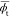 |
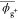 |
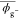 |
|---|---|---|---|---|---|---|
| a | 1.337 | 107.9 | 0.0 | |||
| b | 1.340 | 115.5 | –0.1 | |||
| c | 1.440 | 110.1 | 0.1 | 87.7 | –72.3 | |
| d | 1.517 | 107.3 | 3.4 | 111.9 | –113.0 | |
| e | 1.453 | 116.5 | –31.0 | 116.5 | –96.8 |
Geometrical parameters averaged
at 25 °C with the MO energies on the chloroform solution. Symbols: l̅, averaged bond length (in Å); θ̅,
averaged bond angle (in deg); 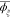 , average dihedral angle (in deg) of the
ξ conformation.
, average dihedral angle (in deg) of the
ξ conformation.
The ⟨r2⟩0/nl2 values are 2.42–2.54 (PEC) and 2.26–2.36 (PPC), much smaller than those of PEO (5.2 at 34.5 °C),29,32,33 PPO (6.0 at 50 °C),31,34 and polyethylene (6.4–8.3 around 140 °C).35−39 This is because both PEC and PPC have strong preferences for gauche conformations. The dln⟨r2⟩0/dT values of PEC and PPC show solvent dependence; the values decrease with increasing solvent polarity. The temperature coefficient of PEC changes its sign between gas and chloroform, whereas that of PPC always stays positive. These results will be discussed in the “Mechanical Properties” section.
The configurational entropy (often termed conformational entropy) can be calculated from
| 2 |
where R is the gas constant, x is the degree of polymerization, T is the absolute temperature, and Z is the partition function of the whole chain. At a phase transition such as melting, the Sconf value corresponds to the entropy change at constant volume and is related to that ((ΔS)p) at constant pressure and that (ΔSv) due to the volume change (ΔV) by40,41
| 3 |
where ΔSv = (α/β)ΔV with α and β being the thermal expansion coefficient and isothermal compressibility, respectively. The Sconf/(ΔS)p ratio has been estimated as, for example, 0.8–0.9 for polyethers and polythioethers42 and 0.5–0.7 for polyesters,27 while amorphous elastomers exhibit comparatively small Sconf/(ΔS)p values such as 0.5 (natural rubber) and 0.6 (gutta percha).41 Therefore, amorphous PEC and PPC would also have somewhat smaller Sconf/(ΔS)p ratios than those of semicrystalline polymers.
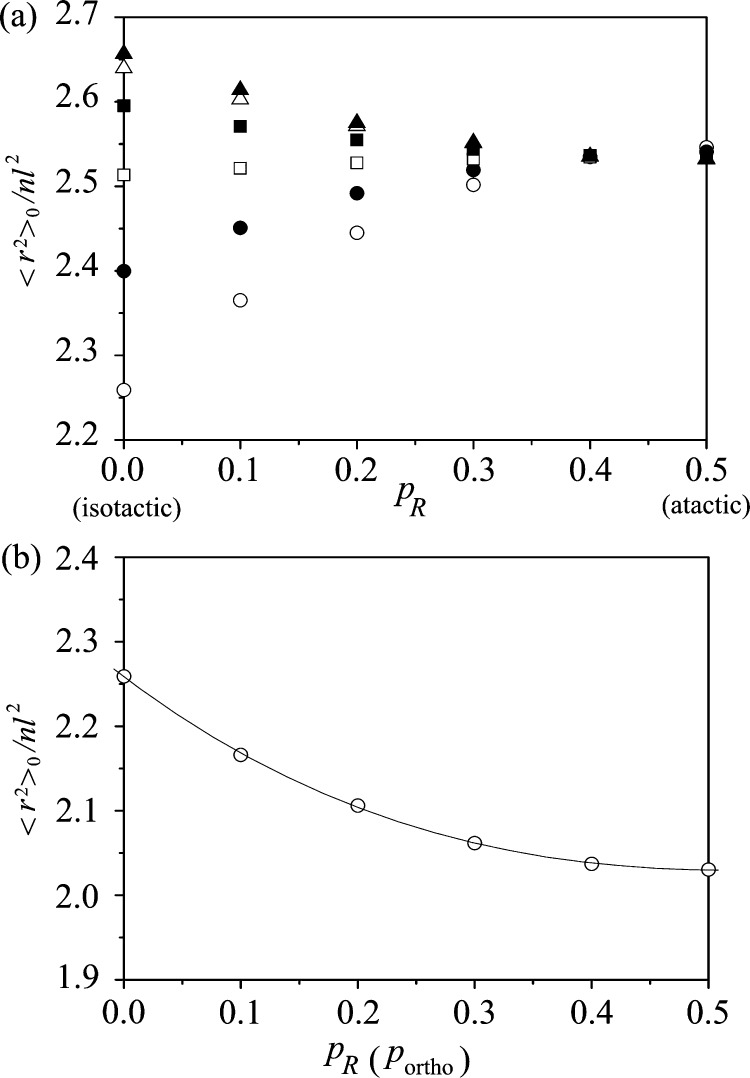
The characteristic ratios of the PPC chains with different regio- and stereosequences were also calculated. Then, the ΔGk values on the chloroform solution were employed because the dielectric constant (ca. 3) of PPC43 is comparatively close to that (4.8) of chloroform; the RIS calculations are expected to represent the amorphous PPC chain. According to the Bernoulli trial, the ⟨r2⟩0/nl2 value of the infinite PPC chain (degree of polymerization x = ∞) was calculated as a function of portho and pR, as shown in Figure 7a. The portho and pR values change at an interval of 0.1. The stereoinversion ((R) → (S) or (S) → (R)) and regioinversion ((O) → (A) or (A) → (O)) were assumed to occur independently of each other (the independent-event model). In the Bernoulli trial, the calculated quantities f(p)’s always satisfy f(portho) = f(1 – portho) and f(pR) = f(1 – pR) (see Table S3, Supporting Information); thus, the f(p) is symmetric with respect to portho = 0.5 and pR = 0.5. The average of f(portho) and f(1 – portho) is given in Table 8. Similarly, in the Markov process, such symmetries were considered, and the average values were adopted.
Figure 7.
Characteristic ratios (⟨r2⟩0/nl2’s) of PPC, derived from the refined RIS calculations with the Bernoulli trial. (a) (Independent-event model) the regio- and stereosequences were generated independently of each other, and the ⟨r2⟩0/nl2’ values are plotted against pR for different portho and (pH–T, pH–H, pT–T) values: 0.0 and (1.00, 0.00, 0.00) (open circle); 0.10 and (0.82, 0.09, 0.09) (filled circle); 0.20 and (0.68, 0.16, 0.16) (open square); 0.30 and (0.58, 0.21, 0.21) (filled square); 0.40 and (0.52, 0.24, 0.24) (open triangle); and 0.50 and (0.50, 0.25, 0.25) (filled triangle). (b) (Synchronous model) the regio- and stereoforms are changed synchronously: (O,R) → (A,S), (A,R) → (O,S), (O,S) → (A,R), or (A,S) → (O,R). The solid line represents a cubic function fitted to the calculated date (open circle).
In Figure 7a, therefore, the ⟨r2⟩0/nl2 value is plotted within ranges of 0.0 ≤ portho ≤ 0.5 and 0.0 ≤ pR ≤ 0.5. When pR = 0.0 (isotactic), the characteristic ratio increases from 2.26 to 2.66 with increasing portho. In the range of pR = 0.4–0.5 (atactic), the plotted data overlap each other at ⟨r2⟩0/nl2 ≈ 2.54; the stereochemically irregular PPC chains have almost the same average dimension independently of the regioregularity. It should be noted that the Bernoulli trial cannot generate the syndiotactic chain.
Most of the synthesized PPC chains keep the chirality of propylene oxide and include the H–T linkage predominantly. However, propylene oxide rarely undergoes abnormal ring-opening, and consequently, the PPC chain randomly includes adjoining H–H and T–T linkages, between which the chiral form is different from those of the neighbors;14,21 therefore, both stereoinversion (R) → (S) or (S) → (R) and regioinversion (O) → (A) or (A) → (O) occur simultaneously. However, the probability of the defect stays as small as several percent. Thus, the configuration of the PPC chain with the defects may be represented by the Bernoulli trial in which both regio- and stereoinversions are synchronized (the synchronous model). In Figure 7b, the characteristic ratios thus calculated are plotted as a function of pR (=portho). The plot is also symmetric with respect to pR = 0.5 and portho = 0.5. The curve can be seen to decrease gradually with an increase in pR; the synchronous inversions tend to render the PPC chain more contracted. However, the change in ⟨r2⟩0/nl2 between pR = 0.0 and 0.5 is ca. 10%.
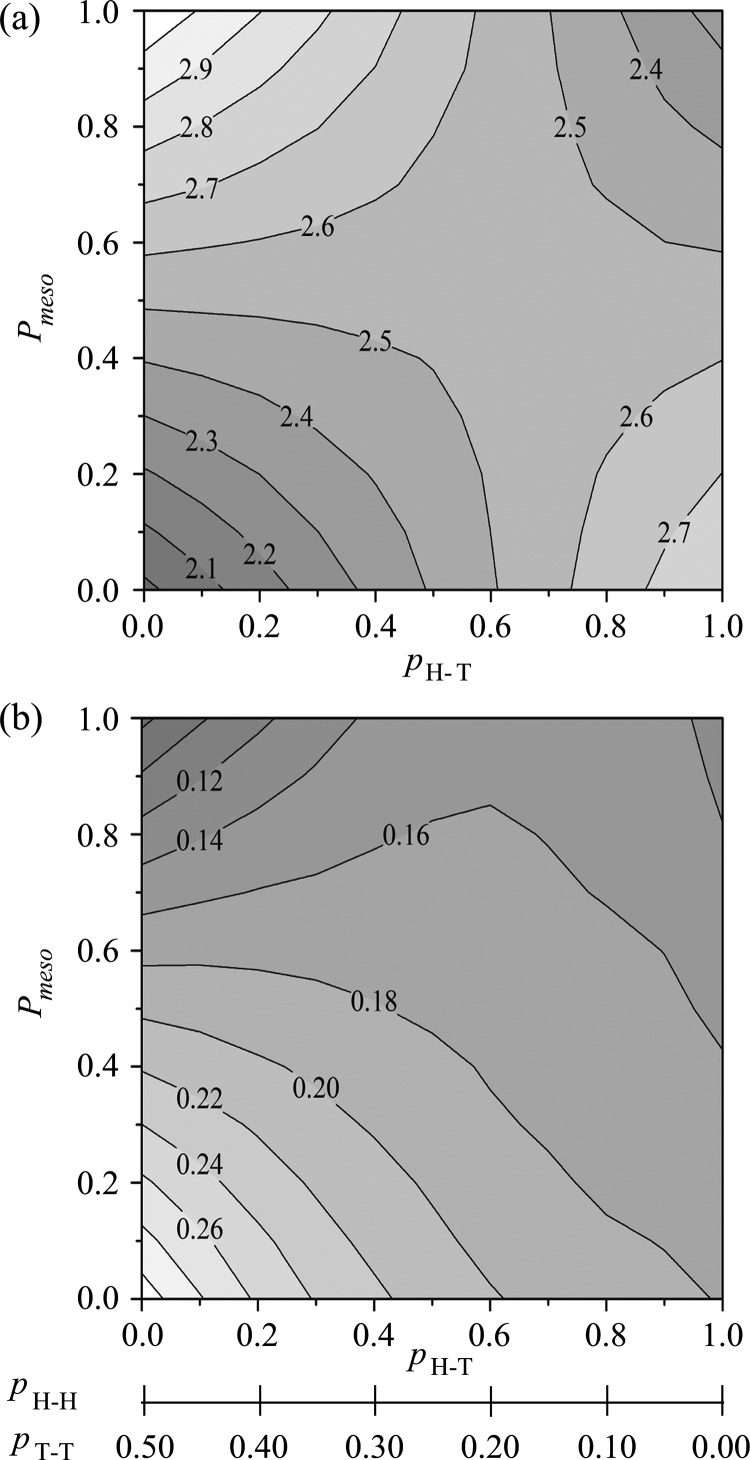
In Figure 8a, the ⟨r2⟩0/nl2 values calculated according to the Markov process are shown as a function of pH–T and pmeso. Then, the pH–T and pmeso values were changed from zero to unity at intervals of 0.1, and the contour lines in Figure 8 were drawn by interpolating the two-dimensional data meshes. In pmeso = 0.0 (syndiotactic), the ⟨r2⟩0/nl2 value increases from 1.98 to 2.80 with increasing pH–T, whereas, in pmeso = 1.0 (isotactic), it decreases from 3.08 to 2.26. Therefore, its maximum can be found at pmeso = 1.0 and pH–T = 0.0: either (O,R)- and (A,R)-units or (O,S)- and (A,S)-units are arranged alternately. The minimum ⟨r2⟩0/nl2 (≈2.0) is essentially equal to that (≈2.0) of the above synchronous model of pR = portho = 0.5 and located at the origin, pmeso = pH−Τ = 0.0, where either (O,R)- and (A,S)-units or (A,R)- and (O,S)-units are arranged alternately (the synchronous inversions).
Figure 8.
(a) ⟨r2⟩0/nl2 and (b) fU/f values (displayed numerically on the maps) of PPC with different regio- and stereosequences, derived from the refined RIS calculations with the Markov stochastic process and plotted as two-dimensional contour plots against pH–T and pmeso.
Characteristics of the Polycarbonate Chains
It is known that PEO crystallizes in the tgt conformation.44 As our MO calculations indicate, PEC is also most stabilized in this conformation. Nevertheless, PEC is an amorphous polymer. Figure 6a shows the charge distribution of E_model whose O–CH2–CH2–O bonds lie in the tgt state. The carbonate group with three oxygen atoms draws electrons, and the negative charge appears to be distributed helically on the molecular surface. Accordingly, the PEC chains repel each other and fail to form a regular packing. This may be an origin of its amorphous nature. In addition, as shown above, PEC and PPC strongly prefer distorted conformations including a number of gauche bonds. This is also an origin.
For liquid crystalline polycarbonates, the geometrical characters of the carbonate linkage were revealed.45 The O–C(=O)–O group lies on a plane, and the O–C–O and C(=O)–O–C angles were determined to be 108° and 118.3°, respectively; therefore, the mesogenic cores can scarcely be arranged in parallel with each other, and hence this structural distortion affects the stability of the liquid crystalline phase. The present study has evaluated bond angles of bonds a and b of PEC and PPC to be 107.9° and 115.5°, respectively (Table 8). In these two polycarbonates, therefore, the linearity of the chain backbone would be unattainable even though they were in the all-trans form. This may also be a reason for their amorphous nature.
Inasmuch as amorphous PEC and PPC chains lie in near unperturbed states, the refined RIS calculations can provide reliable insights into their solid-state properties as well as solution (melt) properties. Because of the distorted conformations, PEC and PPC exhibit the characteristic ratios smaller than those of common linear polymers. The RIS calculations with the Markov chain showed that the characteristic ratio of PPC does not depend significantly on the regio- and stereoregularities. The reason may be explained as follows. The carbonate group separates the neighboring rotatable O–CH2–CH(CH3)–O parts with two rigid O–C(=O)–O bonds; therefore, the conformational correlations can be only weakly transmitted to the adjacent monomeric unit, and hence the individual units are allowed to change the conformation nearly independently of the neighbors. As far as PPC is concerned, the regio- and stereoregularities have no significant effects on the spatial configuration and probably on the other physical properties.
Mechanical Properties
Flory et al. thermodynamically revealed the requirement for rubberlike elasticity of polymers.46−51 On this basis, we can discuss whether amorphous PEC and PPC will exhibit rubberlike chain elasticity.
The tension (f) of an elastomer is composed of two terms due to internal-energy (U) and entropy (S) changes46
| 4 |
where
| 5 |
and
| 6 |
with T, V, and L being the absolute temperature, volume, and length, respectively. The fU/f ratio is expressed as a function of the temperature coefficient of the mean square end-to-end distance by47−50
| 7 |
Although intermolecular interactions occur in rubberlike materials, these interactions have been assumed to be independent of the configurations of the network chains. In other words, it is well-established that rubberlike elasticity is principally of intramolecular origin.48,50,52 Therefore, we are allowed to discuss the possibility that the two polycarbonates will act as elastomers, on the basis of eq 7, which can be evaluated from the refined RIS calculations.
The fU/f ratios of PEC and isotactic PPC of 100% H–T linkage at 25 °C were evaluated from the dln⟨r2⟩0/dT values (in Table 8). The PEC chain has a positive value of 0.095 in the gas phase but negatives of −0.035 to −0.080 in the solvents, whereas PPC always shows positive values (0.32–0.052). For both polycarbonates, the fU/f ratio tends to decrease with increasing medium polarity. The sign of fU/f can be related to conformational changes during chain deformation as follows.
It is known that polyethylene shows negative fU/f values of ca. −0.4.47,49,50 Its CH2–CH2 bond prefers the trans conformation, and the trans-gauche energy difference is 0.4–0.5 kcal mol–1.35,53 As temperature increases (ΔT > 0), the trans conformations partly change to distorted gauche states of higher energy, and hence the chain dimension decreases (Δ⟨r2⟩0 < 0, ΔL < 0, and ΔU > 0), accordingly, dln⟨r2⟩0/dT < 0, ΔU/ΔL ≈ (∂U/∂L) < 0, and fU/f < 0. The negative fU/f works against the entropic elasticity because the fS term must always be positive.
The PPC chain gives positive fU/f values. This is because, in contrast to polyethylene, PPC by nature chooses distorted conformations such as g+g+t, g+g–g–, tg+t, tg–g–, and tg–t. As the temperature is increased, the distortion is released by the gauche-to-trans change, and hence, the chain is extended: dln⟨r2⟩0/dT > 0. The stretching (contraction) of the PPC chain increases (decreases) the internal energy: (∂U/∂L) > 0, therefore, fU/f > 0. The conformational characteristic of PPC supports its entropic elasticity. On the other hand, PEC changes the sign of fU/f, depending on the surroundings. It is well-known that elastomers give positive fU/f values: cis-1,4-polybutadiene (0.10–0.17), polydimethylsiloxane (0.13–0.30), and natural rubber (0.12–0.18).50 Therefore, the PPC chain may be more likely than PEC to behave as an elastomer.
The fU/f ratios of PPC were calculated according to the Markov model as a function of pH–T and pmeso. In Figure 8b, the data are also plotted as a two-dimensional contour map. The maximum fU/f value (0.311) is found at the origin (pH–T = pmeso = 0), where the minimum characteristic ratio was predicted above, and the PPC chain is a perfect alternating copolymer of either (O,R)- and (A,S)-monomers or (O,S)- and (A,R)-monomers. The minimum fU/f (0.075) is indicated to be located at the left top corner (pH–T = 0 and pmeso = 1), where the maximum ⟨r2⟩0/nl2 was suggested, and the PPC chain is an alternating copolymer of either (O,R)- and (A,R)-units or (O,S)- and (A,S)-units. These facts suggest an inverse correlation between fU/f and ⟨r2⟩0/nl2, that is, between the rubberlike elasticity and the chain dimension.
It has been reported that PEC with a low Tg of ca. 10 °C behaves as an elastomer at room temperature with an elongation at break greater than 600% and completely recovers to the initial length after removal of the load.54 On the other hand, mechanical properties of PPC are more complicated owing to its higher Tg of 35–42 °C. Although PPC is brittle below 20 °C, an effective plasticizer (10 wt % of 1,6-bis(methyl urethane)hexane) was found to reduce Tg of PPC significantly and improve the mechanical properties: elongation at break, ca. 700% and tensile strength, 30 MPa.55 In addition, PPC was mixed with rubbery polyurethane particles (30 wt %) to show an impact strength of as much as 228.3 J m–1.56 When amorphous PPC was blended and fixed by graft polymerization with poly(β-hydroxybutyrate-co-hydroxyvalerate) (PHBV) (PHBV/PPC = 30:70 in weight), the composite materials exhibited a marked elongation at break of 1300%.57 In addition, block copolymers of PPC with poly(ethylene glycol), having weight-average molecular weights of 81 000 and 225 000, were shown to be stretchable up to 870 and 720%, respectively, even though the PPC alone was so brittle as to be broken at only a 7% extension.58 Accordingly, effective processing such as copolymerization, cross-linking, blending, and plasticizing for PEC and PPC will reveal their potential mechanical properties.
On Applications of PEC and PPC
Another expectable utilization of PEC and PPC is ion-conductive polymer electrolytes. As a representative polymer for this purpose, we can mention PEO. It is known that PEO is capable of changing the conformational preference according to the environment.29,30,59 In the gas phase or nonpolar media, the energy difference between ttt and tgt states in the O–CH2–CH2–O bonds is close to null. In polar solvents, however, the tgt conformation will be more stable than ttt by over 1.0 kcal mol–1. As found for crown ethers,60 the PEO chain adopts the tgt conformation and captures a cation such as alkali metal ions. Inasmuch as PEO is semicrystalline, the cations will be trapped only in the amorphous phase and on the crystallite surface. The ionic conductivity of PEO is reported to be on the order of 10–8 to 10–7 S cm–1.61
The present study has shown that the tg+t and tg+g+ conformations of PEC are more stable in ΔGk than those of PEO. Therefore, the O–CH2–CH2–O bond sequence as well as the electronegative carbonate group (see Figure 6a) can readily capture, for example, Li+ ion. In addition, PEC and PPC are completely amorphous, and hence most monomeric units are ready to accept Li+ ions. Compared with PEO, therefore, PEC can interact with much more inorganic salts, and its ionic conductivity is as high as ∼10–4 S cm–1.61,62 As can be seen from Table 6, stable conformations in the O–CH2–C*H(CH3)–O bond sequence of P_model are tg+t, g+g+t, tg–g–, and g+g–g–, and hence amorphous PPC can also capture Li+ ion effectually. For a PPC/Li6.76La3Zr1.75Ta0.25O12 composite, the following electric characteristics have been reported: ionic conductivity, 5.2 × 10–4 S cm–1; electrochemical window, 4.6 V; and ionic transference number, 0.75.63 The green polymers produced from carbon dioxide would be future ion-conductive electrolytes to illuminate the world.
Conclusions
Conformational characteristics and configurational properties of PEC and PPC have been elucidated by the methodology based on MO calculations, NMR experiments, and RIS calculations. Both PEC and PPC were found to strongly prefer distorted conformations including a number of gauche states. In the RIS calculations on PPC, the Bernoulli and Markov stochastic processes were employed to generate its regio- and stereosequences, and its configurational properties were shown not to depend significantly on the regio- and stereosequences. The physical properties, practical uses, and potential applications of the two polycarbonates have been discussed in terms of the structural information thus obtained. In conclusion, as a result of the detailed computational characterization, it is preferable that PEC and PPC should be prepared at low costs so as to give high yields without paying particular attention to the regio- and stereoregularities, processed so as to lower the glass transition temperatures, and used as high-value added flexible functional materials.
Methods
Synthesis of Model Compounds
Methyl chloroformate (9.7 mL, 0.125 mol), dissolved in chloroform (12.5 mL), was added dropwise under argon atmosphere to ethylene glycol (2.8 mL, 0.05 mol) and pyridine (20 mL), and the mixture was stirred at 0 °C for 3 h and then at room temperature overnight.64 The reaction mixture was acidified to pH = 2 with hydrochloric acid (20 mL) and underwent extraction twice with chloroform (15 mL × 2). The organic layer was washed thrice with saturated solution of sodium bicarbonate (30 mL × 3) and dried over anhydrous sodium sulfate (ca. 10 g) overnight. The solution was filtrated and condensed on a rotary evaporator. The residue was dried in vacuo at 35 °C for 3 h to yield ethylene glycol bis(methyl carbonate) (E_model) (yield, 86%).
Propylene glycol bis(methyl carbonate) (P_model) was synthesized similarly except that propylene glycol was used instead of ethylene glycol. The yield was 50%.
NMR Measurements
Proton NMR spectra were recorded at 500 MHz on a JEOL JNM-ECA500 spectrometer in the Center for Analytical Instrumentation of Chiba University. The sample temperature was increased stepwise from 15 or 25 °C to 45 or 55 °C at intervals of 10 °C. Free induction decays (FIDs) were accumulated under the following conditions: scan, 32–128; 45° pulse width, 5.7 μs; acquisition time, 4.4 s; and recycle delay, 4 s. The FID was fully zero-filled prior to the Fourier transform to yield enough digital resolution in Hz for the subsequent analysis. The NMR solvents were chloroform-d, acetone-d6, methanol-d4, and dimethyl-d6 sulfoxide (DMSO-d6), and 5 mm NMR sample tubes were used. The obtained spectra were simulated with the gNMR program65 to yield 1H chemical shifts and 1H–1H coupling constants.
NMR Analysis
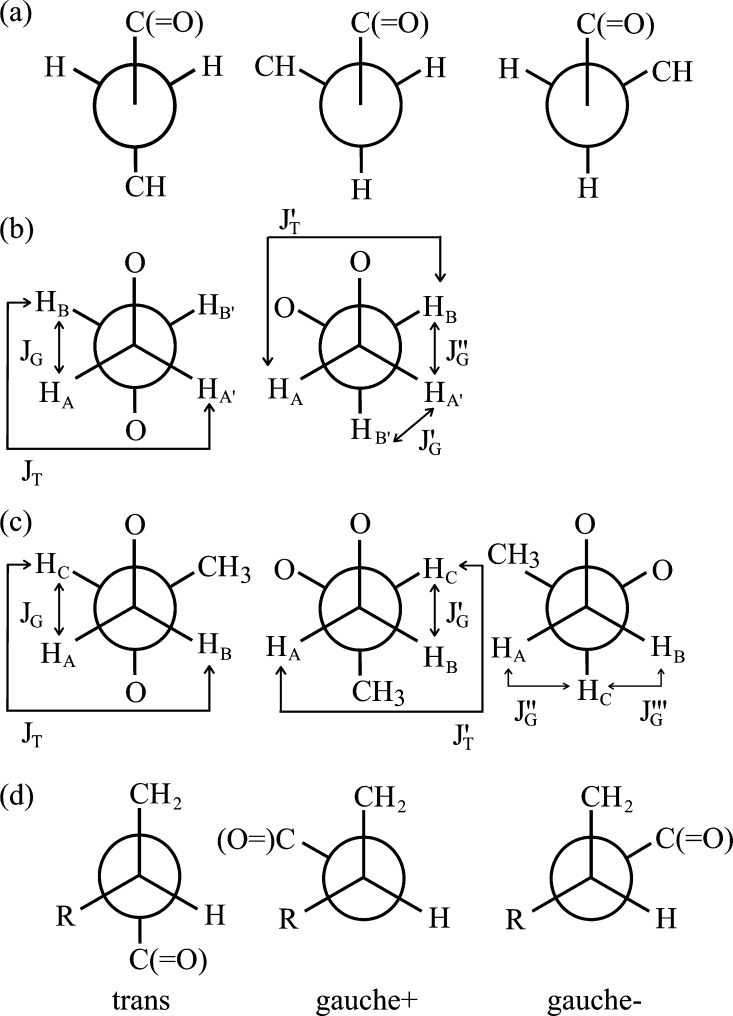
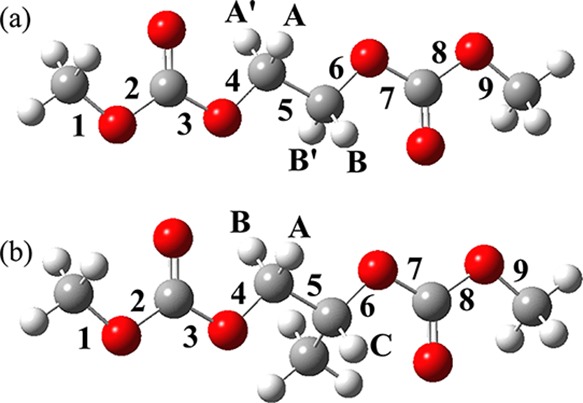
Vicinal 1H–1H coupling constants (JHH and J′HH) observed from the methylene protons, A, A′, B, and B′ of E_model (see Figures 4 and 9) can be expressed as weight averages of JT’s and JG’s
| 8 |
and
| 9 |
where the weights, pt and pg, are trans and gauche fractions of the CH2–CH2 bond, respectively. By definition, we have
| 10 |
where pg+ = pg– = pg/2.
Figure 9.
Rotamers around bonds (a) 4 of E_model and P_model, (b) 5 of E_model, (c) 5 of (R)-P_model, and (d) 6 of E_ (R = H) and (R)-P_ (R = CH3) models. For the bond numbers, see Figure 4. The vicinal JT and JG couplings used in eqs 8, 9, 11, and 12 are defined as illustrated.
There is the possibility that P_model is either (R)- or (S)-isomer, but both give the identical NMR spectra. Therefore, although we employed its racemic mixture in NMR measurements, we are allowed to analyze the observed spectra with either isomeric model. Herein, the (R)-P_model is used throughout. Vicinal coupling constants between the methylene (A or B) and methine (C) protons are expressed as
| 11 |
and
| 12 |
For JT’s and JG’s, see Figure 9. The trans, gauche+, and gauche– fractions fulfill
| 13 |
It should be noted that the gauche+ and gauche– states are not equivalent: pg+ ≠ pg–. Substitution of the observed J values into the above equations yields pt and pg of E_model or pt, pg+, and pg– of P_model, if the JT and JG values are given beforehand. This study has adopted two sets of JT and JG: set A, JT’s = 9.87 and JG’s = 2.54 Hz for the chloroform solution and JT’s = 10.25 and JG’s = 2.52 Hz for the acetone, methanol, and DMSO solutions (taken from those of cis-2,6-dimethyl-1,4-dioxane66); set B, JT’s = 11.4 and JG’s = 2.3 Hz (optimized for 1,2-dimethoxyethane28).
Molecular Orbital Calculations
MO calculations on the model compounds were carried out with the Gaussian 09 program67 installed on an HPC Systems 5000-Z800 computer. For each conformer, the molecular geometry was fully optimized at the B3LYP/6-311+G(2d,p) level under the tight convergence, and thermochemical energies at 25 °C and 1 atm were also computed by the frequency calculation at the same level. Furthermore, the electronic energy was calculated at the MP2/6-311+G(2d,p) level for the optimized geometry. The conformer free energy was obtained from the MP2 electronic energy and the B3LYP thermochemical correction term to the Gibbs free energy, being expressed as the difference (ΔGk, k: conformer) from that of the all-trans conformation. The solvent effect on the MP2 electronic energy was evaluated by the polarizable continuum model using the integral equation formalism variant.68
Rotational Isomeric State Calculation
The refined RIS scheme23,35,69 was applied to PEC and PPC. The refined RIS scheme has been developed so as to change both conformational energy and geometrical parameters with conformations of the neighboring as well as current bonds to yield accurate results. The statistical weight matrices of PEC and PPC were formulated on the basis of the chemical structures shown in Figure 1 and as presented in Appendices A and B (Supporting Information). The geometrical parameters of PEC and PPC were chosen from the optimized structures of E_model and P_model, respectively, being tabulated in Tables S1 and S2 (Supporting Information).
Conventionally, the C*H(CH3) and CH2 parts of PPC have been termed head and tail, respectively. Herein, the CH2 → C*H(CH3) (tail → head) and C*H(CH3) → CH2 (head → tail) directions are designated as orthodromic (O) and antidromic (A), respectively (see Figure 3). However, this definition is not absolute: if the (O)-isomer is turned around 180° with respect to a line perpendicular to the chain axis, it becomes the (A)-isomer. Nevertheless, the RIS scheme requires us to determine the moving direction for the matrix multiplication. For example, when the monomer (propylene oxide + carbonate) has the O direction and (R)-chiral center, it is represented herein as (O,R)-monomer. The OO, OA, AA, and AO combinations between monomers form H–T, H–H, T–H, and T–T linkages, respectively, as illustrated in Figure 3. Inasmuch as the H–T and T–H linkages are identical, the regiosequences expressed in the O and A manner can be rewritten in terms of H–T, H–H, and T–T.
If we obtain conformer free energies of (O,R)-monomer of PPC and formulate its statistical weight matrices Uj’s (j: bond number), we can derive Uj’s of (O,S)-, and (A,R)-, and (A,S)-monomers by proper matrix operations as shown in Appendix B (Supporting Information). From the optimized geometrical parameters of (O,R)-monomer (Table S2, Supporting Information), we can also derive those of the other three isomers.
To arrange the stereo- and regiosequences of the PPC chain, we have adopted two stochastic processes: the Bernoulli trial and the first-order Markov chain.24,25 In the Bernoulli trial, a random number was generated between zero and unity. When the number was smaller than or equal to the given pR value, the next repeating unit was (R)-isomer. Otherwise, (S)-isomer was selected. Here, pR represents the (R)-isomeric probability. The regiosequences were determined similarly with the O probability (portho) instead of pR. The operation was repeated up to a given degree (x) of polymerization over a given number (nc) of chains. Fractions of the regio- (H–T, H–H, and T–T) and stereosequences (diad, meso, and racemo; triad, mm, mr, rm, and rr) were calculated as a function of pR and portho, according to the Bernoulli trial as given in Table S3 (Supporting Information).
In the Markov process, a random number was generated within the range of zero to unity. When the value was smaller or equal to pmeso (or pH–T), the same optical isomer (direction) as that of the preceding monomer was added. Otherwise, the other isomer (orientation) was added. Here, pmeso and pH–T are probabilities of meso diad and H–T linkage, respectively. This operation was repeated x × nc times as above. Fractions of the regio- and stereosequences based on the Markov chain are also listed in Table S3 (Supporting Information).
In accordance with the stereo- and regiosequences of the PPC chains thus generated, the super generator matrices Hβα’s (α = R or S and β = O or A)23 were chosen, arranged, and multiplied sequentially to yield the configurational properties and thermodynamic quantities for the individual chains. The final outcomes were the averages over all of the nc chains. In our previous study on poly(lactide)s,70 fluctuations in data resulting from the stochastic processes were found to decrease with increasing number (x × nc) of trials. When x = nc = 300, the accuracy and reproducibility were fully satisfactory. Therefore, this study has generally employed x = nc = 300, except when the data on the infinite chain (x = ∞) were determined from the extrapolation of the datum versus x–1 plot. Then, the x and nc values were set as 100 ≤ x ≤ 300 and nc = 300.
Acknowledgments
This study was partially supported by the Grants-in-Aid for Scientific Research (C) (16K05906) from the Japan Society for the Promotion of Science.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.7b00964.
Statistical weight matrices of PEC; statistical weight matrices of PPC; geometrical parameters of PEC; geometrical parameters of PPC; and fractions of reigo- and stereosequences in Bernoulli and Markov statistics for PPC (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Patrick S. G.Practical Guide to Polyvinyl Chloride; Rapra Technology: Shawbury, U.K., 2005; Chapter 2. [Google Scholar]
- Inoue S.; Koinuma H.; Tsuruta T. Copolymerization of carbon dioxide and epoxide. J. Polym. Sci., Part B: Polym. Lett. 1969, 7, 287–292. 10.1002/pol.1969.110070408. [DOI] [Google Scholar]
- Inoue S.; Koinuma H.; Tsuruta T. Copolymerization of carbon dioxide and epoxide with organometallic compounds. Makromol. Chem. 1969, 130, 210–220. 10.1002/macp.1969.021300112. [DOI] [Google Scholar]
- Lin Y.; Yan Q.; Kong C.; Chen L. Polyethyleneimine incorporated metal-organic frameworks adsorbent for highly selective CO2 capture. Sci. Rep. 2013, 3, 1859. 10.1038/srep01859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W.; Liu H.; Sun C.; Drage T. C.; Snape C. E. Capturing CO2 from ambient air using a polyethyleneimine–silica adsorbent in fluidized beds. Chem. Eng. Sci. 2014, 116, 306–316. 10.1016/j.ces.2014.05.018. [DOI] [Google Scholar]
- Sasanuma Y.; Hattori S.; Imazu S.; Ikeda S.; Kaizuka T.; Iijima T.; Sawanobori M.; Azam M. A.; Law R. V.; Steinke J. H. G. Conformational analysis of poly(ethylene imine) and its model compounds: rotational and inversional isomerizations and intramolecular and intermolecular hydrogen bonds. Macromolecules 2004, 37, 9169–9183. 10.1021/ma0401222. [DOI] [Google Scholar]
- Fukuda Y.; Abe D.; Tanaka Y.; Uchida J.; Suzuki N.; Miyai T.; Sasanuma Y. Solution properties of poly(N-methylethylene imine), a highly hydrophilic polycation. Polym. J. 2016, 48, 1065–1072. 10.1038/pj.2016.71. [DOI] [Google Scholar]
- Sasanuma Y.; Teramae F.; Yamashita H.; Hamano I.; Hattori S. Conformational analysis of poly(trimethylene imine) and poly(N-methyltrimethylene imine) by the rotational isomeric state scheme with up to fourth-order intramolecular interactions. Macromolecules 2005, 38, 3519–3532. 10.1021/ma050130y. [DOI] [Google Scholar]
- Udipi K.; Gillham J. K. Poly(ethylene carbonate) and poly(propylene carbonate): Transitions and thermomechanical spectra. J. Appl. Polym. Sci. 1974, 18, 1575–1580. 10.1002/app.1974.070180525. [DOI] [Google Scholar]
- Chisholm M. H.; Navarro-Llobet D.; Zhou Z. Poly(propylene carbonate). 1. More about poly(propylene carbonate) formed from the copolymerization of propylene oxide and carbon dioxide employing a zinc glutarate catalyst. Macromolecules 2002, 35, 6494–6504. 10.1021/ma020348+. [DOI] [Google Scholar]
- Allen S. D.; Moore D. R.; Lobkovsky E. B.; Coates G. W. High-activity, single-site catalysts for the alternating copolymerization of CO2 and propylene oxide. J. Am. Chem. Soc. 2002, 124, 14284–14285. 10.1021/ja028071g. [DOI] [PubMed] [Google Scholar]
- Qin Z.; Thomas C. M.; Lee S.; Coates G. W. Cobalt-based complexes for the copolymerization of propylene oxide and CO2: Active and selective catalysts for polycarbonate synthesis. Angew. Chem., Int. Ed. 2003, 42, 5484–5487. 10.1002/anie.200352605. [DOI] [PubMed] [Google Scholar]
- Quan Z.; Min J.; Zhou Q.; Xie D.; Liu J.; Wang X.; Zhao X.; Wang F. Synthesis and properties of carbon dioxide—epoxides copolymers from rare earth metal catalyst. Macromol. Symp. 2003, 195, 281–286. 10.1002/masy.200390135. [DOI] [Google Scholar]
- Chisholm M. H.; Zhou Z. Concerning the mechanism of the ring opening of propylene oxide in the copolymerization of propylene oxide and carbon dioxide to give poly(propylene carbonate). J. Am. Chem. Soc. 2004, 126, 11030–11039. 10.1021/ja0394232. [DOI] [PubMed] [Google Scholar]
- Lu X.-B.; Wang Y. Highly active, binary catalyst systems for the alternating copolymerization of CO2 and epoxides under mild conditions. Angew. Chem., Int. Ed. 2004, 43, 3574–3577. 10.1002/anie.200453998. [DOI] [PubMed] [Google Scholar]
- Coates G. W.; Moore D. R. Discrete metal-based catalysts for the copolymerization of CO2 and epoxides: Discovery, reactivity, optimization, and mechanism. Angew. Chem., Int. Ed. 2004, 43, 6618–6639. 10.1002/anie.200460442. [DOI] [PubMed] [Google Scholar]
- Darensbourg D. J. Making plastics from carbon dioxide: Salen metal complexes as catalysts for the production of polycarbonates from epoxides and CO2. Chem. Rev. 2007, 107, 2388–2410. 10.1021/cr068363q. [DOI] [PubMed] [Google Scholar]
- Luinstra G. A. Poly(propylene carbonate), old copolymers of propylene oxide and carbon dioxide with new interests: Catalysis and material properties. Polym. Rev. 2008, 48, 192–219. 10.1080/15583720701834240. [DOI] [Google Scholar]
- Nakano K.; Kobayashi K.; Nozaki K. Tetravalent metal complexes as a new family of catalysts for copolymerization of epoxides with carbon dioxide. J. Am. Chem. Soc. 2011, 133, 10720–10723. 10.1021/ja203382q. [DOI] [PubMed] [Google Scholar]
- Nakano K.; Hashimoto S.; Nakamura M.; Kamada T.; Nozaki K. Stereocomplex of poly(propylene carbonate): Synthesis of stereogradient poly(propylene carbonate) by regio- and enantioselective copolymerization of propylene oxide with carbon dioxide. Angew. Chem., Int. Ed. 2011, 50, 4868–4871. 10.1002/anie.201007958. [DOI] [PubMed] [Google Scholar]
- Salmeia K. A.; Vagin S.; Anderson C. E.; Rieger B. Poly(propylene carbonate): Insight into the microstructure and enantioselective ring-opening mechanism. Macromolecules 2012, 45, 8604–8613. 10.1021/ma301916r. [DOI] [Google Scholar]
- Nakano K.; Kobayashi K.; Ohkawara T.; Imoto H.; Nozaki K. Copolymerization of epoxides with carbon dioxide catalyzed by iron–corrole complexes: Synthesis of a crystalline copolymer. J. Am. Chem. Soc. 2013, 135, 8456–8459. 10.1021/ja4028633. [DOI] [PubMed] [Google Scholar]
- Sasanuma Y.; Asai S.; Kumagai R. Conformational characteristics and configurational properties of poly(ethylene oxide-alt-ethylene sulfide). Macromolecules 2007, 40, 3488–3497. 10.1021/ma070065n. [DOI] [Google Scholar]
- Taylor H. M.; Karlin S.. An Introduction To Stochastic Modeling, 3rd ed.; Academic Press: San Diego, 1998. [Google Scholar]
- Melsa J. L.; Sage A. P.. An Introduction To Probability & Stochastic Processes; Dover Publications: Mineola, New York, USA, 2013. [Google Scholar]
- Sasanuma Y. Conformational characteristics, configurational properties, and thermodynamic characteristics of poly(ethylene terephthalate) and poly(ethylene-2,6-naphthalate). Macromolecules 2009, 42, 2854–2862. 10.1021/ma802804n. [DOI] [Google Scholar]
- Sasanuma Y.; Nonaka Y.; Yamaguchi Y. Conformational characteristics and configurational properties of poly(ethylene succinate) and poly(butylene succinate) and structure–property–function relationships of representative biodegradable polyesters. Polymer 2015, 56, 327–339. 10.1016/j.polymer.2014.11.003. [DOI] [Google Scholar]
- Tasaki K.; Abe A. NMR studies and conformational energy calculations of 1,2-dimethoxyethane and poly(oxyethylene). Polym. J. 1985, 17, 641–655. 10.1295/polymj.17.641. [DOI] [Google Scholar]
- Sasanuma Y.; Ohta H.; Touma I.; Matoba H.; Hayashi Y.; Kaito A. Conformational characteristics of poly(ethylene sulfide) and poly(ethylene oxide): Solvent dependence of attractive and repulsive gauche effects. Macromolecules 2002, 35, 3748–3761. , and references cited therein 10.1021/ma012027o. [DOI] [Google Scholar]
- Sasanuma Y.; Sugita K. The attractive gauche effect of ethylene oxides. Polym. J. 2006, 38, 983–988. 10.1295/polymj.pj2006018. [DOI] [Google Scholar]
- Sasanuma Y. Conformational analysis of poly(propylene oxide) and its model compound 1,2-dimethoxypropane. Macromolecules 1995, 28, 8629–8638. , and references cited therein 10.1021/ma00129a023. [DOI] [Google Scholar]
- Abe A.; Mark J. E. Conformational energies and the random-coil dimensions and dipole moments of the polyoxides CH3O[(CH2)yO]xCH3. J. Am. Chem. Soc. 1976, 98, 6468–6476. 10.1021/ja00437a006. [DOI] [Google Scholar]
- Kawaguchi S.; Imai G.; Suzuki J.; Miyahara A.; Kitano T.; Ito K. Aqueous solution properties of oligo- and poly(ethylene oxide) by static light scattering and intrinsic viscosity. Polymer 1997, 38, 2885–2891. 10.1016/s0032-3861(96)00859-2. [DOI] [Google Scholar]
- Allen G.; Booth C.; Price C. III—The unperturbed dimensions of poly(propylene oxide). Polymer 1967, 8, 397–401. 10.1016/0032-3861(67)90040-7. [DOI] [Google Scholar]
- Flory P. J.Statistical Mechanics of Chain Molecules; Wiley & Sons: New York, USA, 1969. [Google Scholar]
- Lieser G.; Fischer E. W.; Ibel K. Conformation of polyethylene molecules in the melt as revealed by small-angle neutron scattering. J. Polym. Sci., Part C: Polym. Lett. 1975, 13, 39–43. 10.1002/pol.1975.130130107. [DOI] [Google Scholar]
- Schelten J.; Ballard D. G. H.; Wignall G. D.; Longman G.; Schmatz W. Small-angle neutron scattering studies of molten and crystalline polyethylene. Polymer 1976, 17, 751–757. 10.1016/0032-3861(76)90028-8. [DOI] [Google Scholar]
- Mandelkern L.; Alamo R. G. In Polymer Data Handbook; Mark J. E., Ed.; Oxford University Press: New York, USA, 1999; pp 493–507. [Google Scholar]
- Fetters L. J.; Lohse D. J.; Colby R. H. In Physical Properties of Polymer Handbook, 2nd ed.; Mark J. E., Ed.; Springer: New York, USA, 1999; pp 447–454. [Google Scholar]
- Abe A.; Takeda T.; Hiejima T. Role of conformation entropy in determining the phase transitions of polymeric systems. Macromol. Symp. 2000, 152, 255–265. . [DOI] [Google Scholar]
- Mandelkern L.Crystallization of Polymers Volume 1 Equilibrium Concepts, 2nd ed.; Cambridge University Press: New York, USA, 2002; Chapter 6. [Google Scholar]
- Sasanuma Y.; Watanabe A. Conformational characteristics of poly(trimethylene sulfide) and structure–property relationships of representative polysulfides and polyethers. Macromolecules 2006, 39, 1646–1656. 10.1021/ma0523623. [DOI] [Google Scholar]
- Luinstra G. A.; Borchardt E. Material properties of poly(propylene carbonates). Adv. Polym. Sci. 2012, 245, 29–48. 10.1007/12_2011_126. [DOI] [Google Scholar]
- Takahashi Y.; Tadokoro H. Structural studies of polyethers, (-(CH2)m-O-)n. X. Crystal structure of poly(ethylene oxide). Macromolecules 1973, 6, 672–675. 10.1021/ma60035a005. [DOI] [Google Scholar]
- Abe A.; Furuya H.; Nam S. Y.; Okamoto S. Thermodynamics and molecular ordering of carbonate-type dimer liquid crystals with emphasis on the geometrical characteristics of the linking group. Acta Polym. 1995, 46, 437–444. 10.1002/actp.1995.010460606. [DOI] [Google Scholar]
- Flory P. J.Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Flory P. J.; Hoeve C. A. J.; Ciferri A. Influence of bond angle restrictions on polymer elasticity. J. Polym. Sci. 1959, 34, 337–347. 10.1002/pol.1959.1203412726. [DOI] [Google Scholar]
- Flory P. J.; Ciferri A.; Hoeve C. A. J. The thermodynamic analysis of thermoelastic measurements on high elastic materials. J. Polym. Sci. 1960, 45, 235–236. 10.1002/pol.1960.1204514527. [DOI] [Google Scholar]
- Ciferri A.; Hoeve C. A. J.; Flory P. J. Stress-temperature coefficients of polymer networks and the conformational energy of polymer chains. J. Am. Chem. Soc. 1961, 83, 1015–1022. 10.1021/ja01466a001. [DOI] [Google Scholar]
- Mark J. E. Thermoelastic results on rubberlike networks and their bearing on the foundations of elasticity theory. Macromol. Rev. 1976, 11, 135–159. 10.1002/pol.1976.230110104. [DOI] [Google Scholar]
- Mark J. E. Rubber Elasticity. J. Chem. Educ. 1981, 58, 898–903. 10.1021/ed058p898. [DOI] [Google Scholar]
- Flory P. J. Molecular interpretation of rubber elasticity. Charles Goodyear Medal Address—1968. Rubber Chem. Technol. 1968, 41, G41–G48. 10.5254/1.3547224. [DOI] [Google Scholar]
- Abe A.; Jernigan R. L.; Flory P. J. Conformational energies of n-alkanes and the random configuration of higher homologs including polymethylene. J. Am. Chem. Soc. 1966, 88, 631–639. 10.1021/ja00956a001. [DOI] [Google Scholar]
- Thorat S. D.; Phillips P. J.; Semenov V.; Gakh A. Physical properties of aliphatic polycarbonates made from CO2 and epoxides. J. Appl. Polym. Sci. 2003, 89, 1163–1176. 10.1002/app.12355. [DOI] [Google Scholar]
- Chen L.; Qin Y.; Wang X.; Zhao X.; Wang F. Plasticizing while toughening and reinforcing poly(propylene carbonate) using low molecular weight urethane: Role of hydrogen-bonding interaction. Polymer 2011, 52, 4873–4880. 10.1016/j.polymer.2011.08.025. [DOI] [Google Scholar]
- Ren G.; Miao Y.; Qiao L.; Qin Y.; Wang X.; Wang F. Toughening of amorphous poly(propylene carbonate) by rubbery CO2-based polyurethane: Transition from brittle to ductile. RSC Adv. 2015, 5, 49979–49986. 10.1039/c5ra07142a. [DOI] [Google Scholar]
- Li J.; Lai M. F.; Liu J. J. Control and development of crystallinity and morphology in poly(β-hydroxybutyrate-co-β-hydroxyvalerate)/poly(propylene carbonate) blends. J. Appl. Polym. Sci. 2005, 98, 1427–1436. 10.1002/app.22117. [DOI] [Google Scholar]
- Cyriac A.; Lee S. H.; Lee B. Y. Connection of polymer chains using diepoxide in CO2/propylene oxide copolymerizations. Polym. Chem. 2011, 2, 950–956. 10.1039/c0py00365d. [DOI] [Google Scholar]
- Abe A.; Furuya H.; Mitra M. K.; Hiejima T. The polyoxyethylene chain—on the origin of its conformational flexibility. Comput. Theor. Polym. Sci. 1998, 8, 253–258. 10.1016/s1089-3156(98)00046-4. [DOI] [Google Scholar]
- Pedersen C. J. Cyclic polyethers and their complexes with metal salts. J. Am. Chem. Soc. 1967, 89, 7017–7036. 10.1021/ja01002a035. [DOI] [Google Scholar]
- Tominaga Y.; Yamazaki K. Fast Li-ion conduction in poly(ethylene carbonate)-based electrolytes and composites filled with TiO2 nanoparticles. Chem. Commun. 2014, 50, 4448–4450. 10.1039/c3cc49588d. [DOI] [PubMed] [Google Scholar]
- Tominaga Y. Ion-conductive polymer electrolytes based on poly(ethylene carbonate) and its derivatives. Polym. J. 2017, 49, 291–299. 10.1038/pj.2016.115. [DOI] [Google Scholar]
- Zhang J.; Zang X.; Wen H.; Dong T.; Chai J.; Li Y.; Chen B.; Zhao J.; Dong S.; Ma J.; Yue L.; Liu Z.; Guo X.; Cui G.; Chen L. High-voltage and free-standing poly(propylene carbonate)/Li6.75La3Zr1.75Ta0.25O12 composite solid electrolyte for wide temperature range and flexible solid lithium ion battery. J. Mater. Chem. A 2017, 5, 4940–4948. 10.1039/c6ta10066j. [DOI] [Google Scholar]
- Jeromin G. E.Production of carbonate esters from alcohol and chloroformate, used as perfumes and aroma agents. German Patent DE 19802198A1, 1999.
- Budzelaar P. H.gNMR, Version 5.0; IvorySoft & Adept Scientific plc: Letchworth, U.K., 2004.
- Sasanuma Y. Solvent effect on the conformation of 1,2-dimethoxypropane. J. Phys. Chem. 1994, 98, 13486–13488. 10.1021/j100102a010. [DOI] [Google Scholar]
- Frisch M. J.; et al. Gaussian 09, Revision B01; Gaussian Inc: Wallingford CT, USA, 2009.
- Cancès E.; Mennucci B.; Tomasi J. A new integral equation formalism for the polarizable continuum model: theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. 10.1063/1.474659. [DOI] [Google Scholar]
- Mattice W. L.; Suter U. W.. Conformational Theory of Large Molecules: The Rotational Isomeric State Model in Macromolecular Systems; Wiley-Interscience: New York, USA, 1994. [Google Scholar]
- Sasanuma Y.; Touge D. Configurational statistics of poly(L-lactide) and poly(DL-lactide) chains. Polymer 2014, 55, 1901–1911. 10.1016/j.polymer.2014.01.059. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.