Redox control on nitrogen isotope fractionation during planetary core formation

Significance

The origin and evolution of Earth’s nitrogen is often discussed by comparing the large variation of N-isotopic compositions among Earth’s building blocks (chondrites) to the signatures of various terrestrial reservoirs. Here, we demonstrate that planetary differentiation processes, such as core formation, may have significantly modified the N-isotopic composition of the proto-Earth. During core–mantle differentiation, a significant amount of isotopically light N entered Earth’s core, producing an isotopic fractionation much larger than has been observed for other geochemical tracers of core formation. The magnitude of N-isotopic fractionation varies significantly as a function of the redox history of the early Earth. Therefore, distinct N-isotopic ratios among Earth’s reservoirs or between planetary bodies may reflect different planetary evolution processes as opposed to different N sources.

Abstract

The present-day nitrogen isotopic compositions of Earth’s surficial (¹⁵N-enriched) and deep reservoirs (¹⁵N-depleted) differ significantly. This distribution can neither be explained by modern mantle degassing nor recycling via subduction zones. As the effect of planetary differentiation on the behavior of N isotopes is poorly understood, we experimentally determined N-isotopic fractionations during metal–silicate partitioning (analogous to planetary core formation) over a large range of oxygen fugacities (ΔIW −3.1 < logfO₂ < ΔIW −0.5, where ΔIW is the logarithmic difference between experimental oxygen fugacity [fO₂] conditions and that imposed by the coexistence of iron and wüstite) at 1 GPa and 1,400 °C. We developed an in situ analytical method to measure the N-elemental and -isotopic compositions of experimental run products composed of Fe–C–N metal alloys and basaltic melts. Our results show substantial N-isotopic fractionations between metal alloys and silicate glasses, i.e., from −257 ± 22‰ to −49 ± 1‰ over 3 log units of fO₂. These large fractionations under reduced conditions can be explained by the large difference between N bonding in metal alloys (Fe–N) and in silicate glasses (as molecular N₂ and NH complexes). We show that the δ¹⁵N value of the silicate mantle could have increased by ∼20‰ during core formation due to N segregation into the core.

The bulk silicate Earth is the largest nitrogen reservoir on Earth, containing 3 to 11 times more N (27 ± 16 × 10¹⁸ kg N) than the present-day atmosphere (4 × 10¹⁸ kg N or the present atmospheric nitrogen abundance [PAN]) (1). In particular, Earth’s mantle is estimated to contain 6 PAN (up to 24 × 10¹⁸ kg N) (1), which is 12 times more than the continental crust (0.5 PAN) (1). The 2 stable isotopes of nitrogen, ¹⁴N and ¹⁵N (∼99.6% and ∼0.4% of present atmospheric N₂, respectively), are used to trace fluxes between surface and deep-Earth reservoirs. N stable isotopic compositions are conventionally normalized to the present atmospheric value and reported as follows:

$${\text{δ}}^{15}\text{N}\left[\text{‰}\right]=\mathrm{1,000}\cdot \left[\left(\frac{{}^{15}\text{N}/{}^{14}\text{N}_{\text{sample}}}{{}^{15}\text{N}/{}^{14}\text{N}_{{\text{atmN}}_2}}\right)-1\right]\mathrm{.}$$ [1]

The current N-isotopic distribution among terrestrial reservoirs shows an unexplained difference (2) between the ¹⁵N-depleted mantle [δ¹⁵N = −5 ± 2‰ in diamonds and midocean ridge basalts (MORBs) (3)] and the ¹⁵N-enriched surface [δ¹⁵N = +6‰ in sediments, and 0‰ (by definition) in the present-day atmosphere (4)]. Contradictory to these observations, diffusion-controlled N₂ degassing (5) of the mantle is expected to preferentially segregate ¹⁴N into the atmosphere (Graham’s law), which would enrich the mantle in ¹⁵N. Equilibrium degassing of MORBs modeled by Rayleigh distillation (5, 6) enriches the residual melt in ¹⁵N, but this fractionation is limited to 1 to 1.5‰ (7). Recycling (subduction) of surficial material is expected to increase the δ¹⁵N value of the mantle because sediments and altered continental crust are enriched in ¹⁵N (3) by biological processes [i.e., N fixation pathways and N cycling within microbial communities (e.g., refs. 8 and 9)] and metamorphism-related devolatilization of N (4), respectively. Marty and Dauphas (7) proposed that the mantle’s N-isotopic signature corresponds to that of recycled Archean sediments; this hypothesis has been actively debated (10) because the δ¹⁵N values of ancient sediments are highly variable [−6.2 to +13‰ (8)]. Hence, neither degassing processes nor recycling can explain the mantle’s N-isotopic signature relative to the atmosphere (3).

An alternative explanation of the mantle’s N-isotopic signature is the heterogeneous accretion of the Earth from materials with δ¹⁵N values as low as −40‰ (11), the lowest value measured on Earth in deep diamonds (12). Indeed, the low δ¹⁵N values of enstatite chondrites [−45 to −15‰ (13)] compared with carbonaceous chondrites [+15 to +55‰ (14)] suggest an enstatite chondrite origin of Earth’s nitrogen (11, 12). After accretion, planetary differentiation processes could have modified the initial N budget and isotopic signature of the mantle. Core–mantle differentiation, magma ocean solidification/crystallization, and magma ocean degassing are key stages of early planetary evolution. These 3 processes could potentially result in N-isotopic fractionations sufficient to explain the large differences in current δ¹⁵N values among the distinct terrestrial reservoirs (3).

Recent studies have revealed that a significant fraction of N could have been segregated into the core during the late stages of core formation (15–22). Investigation of the effect of core formation on the evolution of the bulk mantle δ¹⁵N value requires knowledge of the N-isotopic fractionation factors between metal and silicate phases. Li et al. (16) measured the ¹⁵N/¹⁴N fractionation between metal and basaltic glasses (∆¹⁵N^{metal-silicate} = δ¹⁵N^metal − δ¹⁵N^silicate) at 1.5 to 7 GPa and 1,600 to 1,800 °C. They showed that during metal–silicate segregation, the silicate melt is enriched in ¹⁵N by 3.5 ± 2.5‰ relative to the coexisting liquid Fe–C–N metal alloy. These experimental results are consistent with an equilibrium isotopic fractionation, which causes the lighter isotope to be enriched in the most reduced phase (23). However, the large uncertainties on their isotopic fractionation factors (typically 2.5‰) preclude any definitive conclusion on the effect of metal–silicate N segregation. Additionally, the relatively narrow range of oxygen fugacities (fO₂, reported as the logarithmic difference between experimental fO₂ conditions and the iron–wüstite buffer [IW]) explored by Li et al. [ΔIW −0.11 to −0.35 (16)] presumably corresponds only to the latest stage of core–mantle differentiation (24). Although the fO₂ conditions of Earth’s core formation are still debated (e.g., refs. 25–27), recent models acknowledge that the Earth accreted from highly reduced materials (typically around ΔIW −5) and that its fO₂ increased throughout the late stages of accretion and core–mantle differentiation (reaching ΔIW −2 to IW during the late stages of the magma ocean; refs. 24, 26, and 28). Recent studies have shown fO₂ to be the main control on N partitioning during metal–silicate segregation (17–22) because it determines the N speciation in the silicate phase (17, 29). N speciation, in turn, is expected to dictate ∆¹⁵N^{metal-silicate} (29). The magnitude of isotopic fractionations is proportional to the difference in bond stiffness and vibration modes between equilibrated phases (30, 31), i.e., ∆¹⁵N^{metal-silicate} is determined by the bonding of N in the metal (as Fe–N) and silicate melt [as N–N vs. N–H complexes depending on fO₂ conditions (29)]. Therefore, fO₂ is expected to play a fundamental role in the evolution of the δ¹⁵N value of Earth’s mantle, and thus in the establishment of the observed difference between surficial and deep N-isotopic signatures.

In this study, we investigated the redox effect on N-isotopic fractionation during metal–silicate N partitioning in samples quenched at 1 GPa and 1,400 °C in a piston-cylinder (Laboratoire Magmas et Volcans, Clermont-Ferrand, France). We explored fO₂ conditions ranging from Fe–FeO equilibrium (IW) to ΔIW −3 (i.e., 3 orders of magnitude more reducing), consistent with the inferred conditions of core formation (32). The duration of the experiments was 6 h, which is sufficient to reach compositional equilibrium (17). The starting material compositions comprised a Fe-rich haplo-basalt [similar to the Humphrey basalt composition of Dalou et al. (17) and Armstrong et al. (33)] to promote the segregation of large metal blobs under reducing conditions, and a haplo-andesite composition similar to that used by Zhang et al. (34). These mafic to intermediate compositions were chosen as analogs of planetary magma ocean compositions (35). The fO₂ of the samples was changed (not controlled) by adding 0.5 to 4 wt% Si₃N₄ [a reducing agent (17)] to the starting compositions. To “spike” the samples in ¹⁵N, we used mixtures of Si₃¹⁴N₄ and Si₃¹⁵N₄ as the N source. Si₃¹⁴N₄ was synthetized by Si nitridation using flowing N₂ in a Nabertherm 1-atm furnace, whereas isotopically enriched Si₃¹⁵N₄ (∼95% ¹⁵N) was prepared as described by Leonova et al. (36). Mixtures of Si₃¹⁴N₄ and Si₃¹⁵N₄ were used to obtain variable initial ¹⁵N/¹⁴N ratios (between 0.1 and 8; Table 1) in the starting materials to assess the effect of ¹⁵N spiking. Experimental procedures are described in SI Appendix, section S1.

Table 1.

Redox conditions, N elemental and isotopic compositions of the samples, and calculated N elemental and isotopic fractionations

Sample	fO2 (ΔIW)	[N]silicate, ppm)	[N]metal, ppm	DNmetal-silicate	15N/14N initial*	${\text{δ}}^{15}{\mathrm{N}}_{\text{norm}}^{\mathrm{silicate}}$, ‰	${\mathrm{\delta }}^{15}{\mathrm{N}}_{\mathrm{norm}}^{\mathrm{metal}}$, ‰	αmetal-silicate	∆15Nmetal-silicate, ‰	[H2O]silicate, wt%†
HB01	−3.13	186 ± 2	28 ± 3	0.2 ± 0.2	0.09 ± 0.01	72 ± 10	−171 ± 28	0.77 ± 0.09	−257 ± 22	0.20 ± 0.04
HB05	−0.45	235 ± 36	1,571 ± 1,287‡	7 ± 2	0.67 ± 0.07	23 ± 3	−27 ± 4	0.95 ± 0.02	−49 ± 1	0.267 ± 0.002
HB15	−1.40	420 ± 22	682 ± 267	1.6 ± 0.8	8.0 ± 0.8	25 ± 4	−88 ± 13	0.89 ± 0.05	−116 ± 6	0.13 ± 0.03
HB3	−1.46	448 ± 5	1,493 ± 149	3.3 ± 0.2	0.80 ± 0.08	36 ± 5	−95 ± 13	0.87 ± 0.01	−135 ± 1	0.13 ± 0.09
HB4	−1.21	493 ± 12	1,488 ± 14	3.02 ± 0.05	0.85 ± 0.08	16 ± 2	−70 ± 10	0.92 ± 0.01	−89 ± 1	0.13 ± 0.03
A05	−2.15	855 ± 18	669 ± 126	0.8 ± 0.4	0.67 ± 0.07	11 ± 2	−14 ± 2	0.976 ± 0.002	−25 ± 1	0.19 ± 0.01

Reported errors are 2σ SDs.

^*Estimated from the addition of ¹⁴Si₃N₄ and ¹⁵Si₃N₄ to the starting material. SDs on ${\text{δ}}^{15}{\text{N}}_{\mathrm{norm}}$ were estimated from weighing uncertainties related to the addition of Si₃N₄ to the starting material, and thus are larger than α^{metal-silicate} and ∆¹⁵N^{metal-silicate} (‰), which were directly determined from SIMS measurements.

^†Analyzed by SIMS (1280 HR2) following the method of Sobolev et al. (37). Details of the measurement conditions and standards are given in SI Appendix, section S1.

^‡Large error due to C heterogeneities, likely graphite microinclusions, in the metal blobs.

Silicate- and Metal-Phase Nitrogen Analyses

Previous studies of N partitioning between metal and silicate phases (15, 17–22, 38) presented N abundance data obtained by electron probe microanalysis (EPMA). This in situ analytical method allows measuring N contents in metal alloys and silicate glasses in a polished section of an experimental charge with a detection limit as low as 0.03 wt% (17, 39) but is not adapted to isotopic measurements. Noble gas mass spectrometry enables bulk N-isotopic analyses (16) but, in our case, can only provide phase-specific isotopic compositions if the silicate glass and metal blobs are physically separated and measured independently, a challenging task depending on the sample texture (SI Appendix, Fig. S1).

We thus developed a method for in situ measurement of the N concentrations and isotopic compositions of quenched silicate and metal alloy phases by secondary ion mass spectrometry (SIMS) using the CAMECA IMS 1280 HR2 and 1270 at the Centre de Recherches Pétrographiques et Géochimiques (Nancy, France). Following the analytical protocol of Füri et al. (40), nitrogen isotopes in silicate glasses were measured with the IMS 1280 HR2 by spot analyses of ¹⁴N¹⁶O⁻ and ¹⁵N¹⁶O⁻ secondary molecular ions at mass numbers 30 and 31, respectively, at a nominal mass resolution m/Δm = 14,000 using a Cs⁺ primary ion beam with a current of ∼10 nA. A suite of reference glasses with known ¹⁴N contents (40, 41) was used to determine the nitrogen concentration of each sample based on the ¹⁴N¹⁶O⁻ count rate normalized by the ¹⁶O₂^– signal (SI Appendix, section S1). The nitrogen and carbon abundances and ¹⁵N/¹⁴N and ¹³C/¹²C ratios of metal phases were measured on the IMS 1270 using a Cs⁺ primary ion beam with a current of ∼2.4 nA. The size of the primary beam was set to ∼5 µm to analyze metal blobs 10 to 65 µm in diameter. Carbon concentrations were measured as ¹²C₂^–, whereas nitrogen isotopes were measured as ¹²C¹⁴N⁻ and ¹²C¹⁵N⁻ at mass numbers 26 and 27, respectively, with a mass resolution of 8,000. Nitrogen elemental abundances were determined using the ¹²C¹⁴N⁻/¹²C₂⁻ ratio (42, 43). Owing to the low Si solubility in metals at the studied pressure–temperature (P–T) and fO₂ conditions (17), ²⁸Si⁻ was analyzed to monitor for potential silicate contamination during analyses. In parallel to the SIMS measurements, the nitrogen contents and ¹⁵N/¹⁴N ratios of reference silicate glasses (40) and metal reference materials were determined independently by noble gas mass spectrometry (SI Appendix, section S1). The use of ¹⁵N-spiked samples allowed us to determine the ¹⁵N/¹⁴N ratios in the silicate and metal phases with average analytical uncertainties of 0.1‰ and 5.5‰, respectively. However, this uncertainty reached 91‰ for metal alloys in sample HB01, likely due to its highly heterogeneous C distribution.

Raman spectroscopic analyses were performed to determine N speciation in silicate glasses and metal alloy blobs (SI Appendix, section S1).

Sample Description

Experimental run products were composed of graphite-saturated mafic glass, close to the melt composition expected during a magma ocean stage (35), coexisting with variable amounts of an iron carbide metallic phase (SI Appendix, section S1 and Fig. S1). Among the experiments run, 6 samples had metal blobs of sufficient diameter (>7 µm) to permit SIMS analysis (SI Appendix, Fig. S1 and Table 1): only the data from these samples are presented herein. Silicate melts quenched to form large glass pools that were well separated from metal domains. Both silicate glasses and Fe–C–N alloys were compositionally homogeneous at the scale of EPMA analyses (∼2 μm for metals; SI Appendix, section S1 and Tables S1 and S2). Along with Fe, the Pt and Si concentrations in the metal phases of all samples were measured by EPMA, which revealed Si contents below the detection limit and low amounts of Pt (<0.7 wt%). The major element compositions of silicate glasses and metal alloys determined by EPMA are presented in SI Appendix, Tables S1 and S2, respectively.

Table 1 presents sample oxygen fugacities, expressed as log f_O2 (ΔIW), as estimated from the equilibrium reaction:

$${\text{FeO}}_{\text{silicate}\hspace{0.17em}\text{melt}}={\text{Fe}}_{\text{liquid}\hspace{0.17em}\text{metal}}+1/2{\text{O}}_2\mathrm{.}$$ [2]

Following this equilibrium, the fO₂ of each sample was calculated according to the method described in Dalou et al. (17), i.e., using the relationship between the mole fractions of FeO in the silicate melt $\left(X_{\text{FeO}}^{\text{melt}}\right)$ and Fe in the liquid metal $\left(X_{\text{Fe}}^{\text{alloy}}\right)$, the associated activity coefficients (${\gamma }_{\text{FeO}}^{\text{melt}}$ and ${\gamma }_{\text{Fe}}^{\text{alloy}}$, respectively), and the equilibrium constant, K, of the reaction (44):

$${\text{log}}_{10}f{\text{O}}_2=\frac{2}{\ln \left(10\right)}\cdot \left[\ln \left(\frac{X_{\text{FeO}}^{\text{melt}}}{X_{\text{Fe}}^{\text{alloy}}}\right)-\ln \left({\gamma }_{\text{Fe}}^{\text{alloy}}\right)+\ln \left({\gamma }_{\text{FeO}}^{\text{melt}}\right)-\ln K\right]\mathrm{.}$$ [3]

As described by Dalou et al. (17) and Grewal et al. (21, 22), we accounted for the effect of N and C on ${\gamma }_{\text{Fe}}^{\text{alloy}}$ by extending the Wagner ε formalism (45) for nonideal interactions in liquid Fe alloys (46) via the MetalAct metal activity calculator (47), and we assumed ${\gamma }_{\text{FeO}}^{\text{melt}}$ = 1.2 (48). Moreover, to permit direct comparison with the IW buffer, which is referenced to solid Fe metal, the activity coefficient of Fe was adjusted following the method of Stanley et al. (49). Finally, the resulting fO₂ was compared with the IW buffer as determined by Zhang et al. (50). This calculation was applied to our samples and all literature data presented for comparison in the figures. The fO₂ of our samples spanned from ΔIW −0.45 to −3.13.

We noted a significant loss of N (up to 75%) between the N added to the starting material and the total N measured in our experimental products. Speelmanns et al. (19, 20) observed a similar N loss during their experiments and suggested that N was lost to the graphite capsules enclosing their samples. Nonetheless, no significant difference in N loss is observed in N-partitioning experiments using single graphite (this study) or double platinum–graphite capsules (22). The samples showed no signs of vapor bubbles in the silicate glasses or metal alloy blobs. Although we cannot rule out the possible presence of submicroscopic bubbles in these phases, we assume that our experiments were N-vapor saturated and that N was lost to pores in the graphite capsules during the experiments. Therefore, the measured elemental and isotopic N fractionations between the metal and silicate phases occurred in an open system. The effect of N loss on N-isotopic fractionation is discussed in the following section.

The reported N and C contents and N-isotopic ratios and their associated SDs (2σ) were averaged from 2 to 6 analyses per sample (SI Appendix, Tables S2 and S3). Nitrogen and carbon contents in metal alloys are homogeneous within most samples, with SDs below 22% and 2% (2σ), respectively. The N contents of silicate glasses in each sample were homogeneous with a SD below 9%. As observed by Dalou et al. (17) and Füri et al. (40), the glasses contained micrometer-sized graphite inclusions, causing highly variable C signals over the course of an analysis and between distinct areas. Given that silicate glass N contents and isotopic compositions were measured as ¹⁴N¹⁶O⁻/¹⁶O₂⁻ and ¹⁵N¹⁶O⁻/¹⁴N¹⁶O⁻ instead of ¹²C¹⁴N⁻/¹²C₂⁻ and ¹²C¹⁵N⁻/¹²C¹⁴N⁻, this variability does not affect our N-elemental and -isotopic analyses (40). In samples for which metal blobs were large enough to perform multiple measurements (up to 4 analyses in HB05 and HB3, and 6 in HB4), homogeneous N-isotopic ratios were observed across the metal blobs, with SDs below 2% (2σ; SI Appendix, Table S3). Nitrogen contents in silicate glasses and metal alloy blobs are presented in Table 1, and carbon contents in metal phases in SI Appendix, Table S2.

It is very difficult to ensure that isotopic equilibrium is attained during isotope fractionation experiments that do not allow application of the “3-isotope method” (51). At temperatures from 1,600 °C to 1,800 °C, Li et al. (16) performed a series of experiments with increasing equilibration times between 30 and 120 min to ensure that isotopic equilibrium was attained. To promote isotopic equilibrium at 1,400 °C, we extended the run periods of our experiments to 6 h. Moreover, the homogeneity of N contents and ¹⁵N/¹⁴N ratios of the metal blobs and silicate glasses (SI Appendix, Table S3) strongly suggests that both chemical and isotopic equilibria were attained during our experiments.

fO₂ Control on N Partitioning Between Metal and Silicate Phases

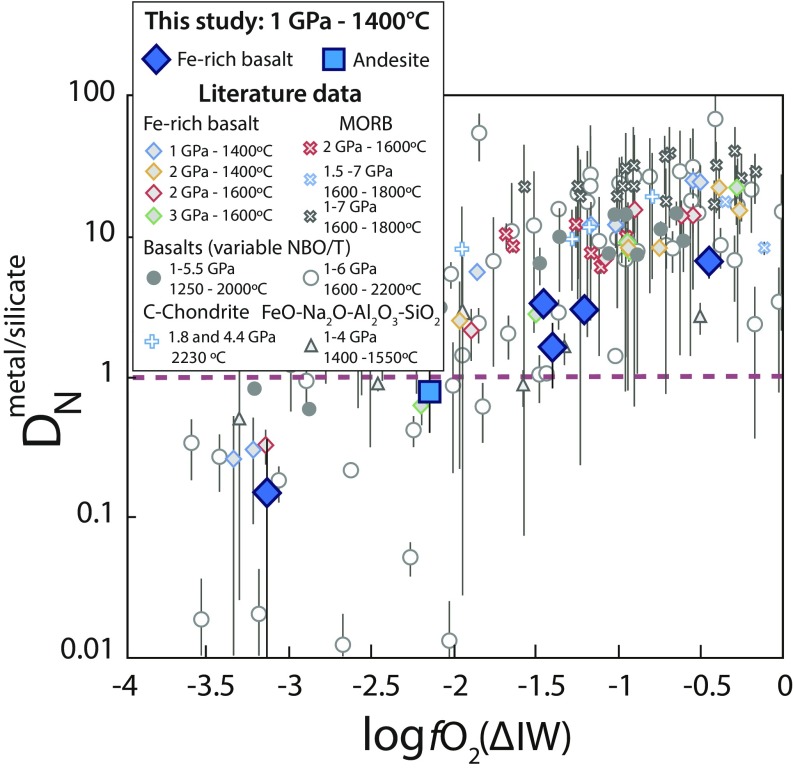
Nitrogen partition coefficients between the metal and silicate phases, D_N^{metal-silicate}, were calculated as D_N^{metal-silicate} = C_N^metal/C_N^silicate, where C_N^metal and C_N^silicate are the average N contents (wt%) of the metal alloys and silicate glasses, respectively (Table 1). With decreasing fO₂ from ΔIW −0.45 to −3.13, D_N^{metal-silicate} decreases from 7 ± 2 to 0.2 ± 0.2, consistent with previous experimentally determined partition coefficients (15–22, 52, 53) (Fig. 1). Despite highly variable experimental parameters between studies (melt composition, P, and T), which produce scatter in the data trend (22), fO₂ remains the key parameter controlling N partitioning between the metal and silicate phases (17). D_N^{metal-silicate} decreases with decreasing fO₂ due to the stabilization of N species in more reduced silicate melts (17).

Fig. 1.

D_N^{metal-silicate} as a function of fO_2. Large symbols represent D_N^{metal-silicate} values from this study, and small symbols are results from several previous studies: diamonds and red x’s (17), blue x’s (16), black x’s (21), gray circles (20), empty circles (22), triangles (18, 37, 50, 51), and blue crosses (15). All fO₂ values were recalculated following the procedure described in the text. Following this calculation, only 2 of the 4 samples from Li et al. (16) have log fO₂ < ΔIW. Error bars represent 2σ SDs. P–T conditions have only a small effect on D_N^{metal-silicate} and explain the scatter among the overall decreasing trend with decreasing fO₂. Our data measured using SIMS (Fe-rich basalt and andesite) are in agreement with previously published D_N^{metal-silicate} values measured by EPMA.

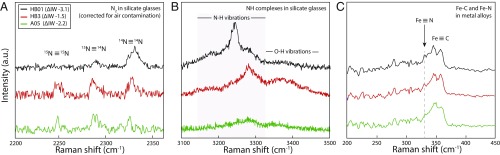
In glasses, Raman spectroscopic analysis revealed that nitrogen is dissolved as N₂ and NH complexes (Fig. 2 A and B). At near-constant water content (Table 1), the ratio of NH to OH complexes (NH/OH, as determined from the Raman peak areas) increases with decreasing fO₂ (54), reflecting the increased N solubility in silicate glasses at more reducing conditions (17, 53). We note that vibrations associated with NH complexes are more intense in the Raman spectra of Fe-rich basalt samples (noted HB) than in the andesite A05 (Fig. 2B). Increased melt polymerization is known to increase N solubility and decrease the proportion of NH relative to N₂, i.e., the NH/N₂ ratio (29, 55). Therefore, the melt structure of sample A05 (more polymerized than the Fe-rich basalt glasses) favors N dissolution in the form of N₂ rather than NH complexes (Fig. 2 A and B). Overall, decreasing fO₂ has 2 effects: it increases both melt polymerization (due to increasing metal precipitation; SI Appendix, section S2) and the NH/N₂ ratio. Among the HB samples, we observe that the change of fO₂ primarily controls the NH/N₂ ratio, whereas at constant fO₂, melt polymerization governs the NH/N₂ ratio in silicate glasses (29).

Fig. 2.

Representative normalized Raman spectra of N species in silicate glasses and metal alloys of samples HB01, HB3, and A05: (A) N₂ isotopomers in silicate glasses, (B) NH complexes in silicate glasses, and (C) Fe–N bonds in metal alloys. The Raman shifts of N species are significantly different depending on speciation (N₂ versus NH complexes) and whether N is dissolved in metal alloy or silicate glass. Details of our Raman analysis are presented in SI Appendix, section S1.

Under nominally anhydrous conditions, N is assumed to chemically dissolve as nitride ions (N³⁻) in reduced melts (below ΔIW −1.3) at 1 atm (56). The vibration mode of Si–N (near 800 cm⁻¹, ref. 57) is in the range of the dominant Si–O vibrations in silicate glasses. We therefore cannot ascertain the presence or absence of nitride species in our glasses by Raman spectroscopy.

Metal-Silicate N Isotopic Fractionation (∆¹⁵N^{metal-silicate})

The N-isotopic compositions of metal alloys $\left({}^{15}\text{N}/{}^{14}\text{N}^{\text{metal}}\right)$ and silicate glasses $\left({}^{15}\text{N}/{}^{14}\text{N}^{\text{silicate}}\right)$ in the Fe-rich basalts and haplo-andesite were determined via SIMS. The N-isotopic ratios, ${}^{15}\text{N}/{}^{14}\text{N}^p$, where p denotes the phase, were normalized to the initial N-isotopic composition of the starting material, ${}^{15}\text{N}/{}^{14}\text{N}^{\text{initial}}$, which ranged from 0.09 ± 0.01 to 8.0 ± 0.1 (Table 1). The normalized isotopic compositions are represented as follows:

$${\text{δ}}^{15}{\text{N}}_{\mathrm{norm}}^p\left[\text{‰}\right]=\mathrm{1,000}\cdot \left[\left(\frac{{}^{15}\text{N}/{}^{14}\text{N}^p}{{}^{15}\text{N}/{}^{14}\text{N}^{\text{initial}}}\right)-1\right].$$ [4]

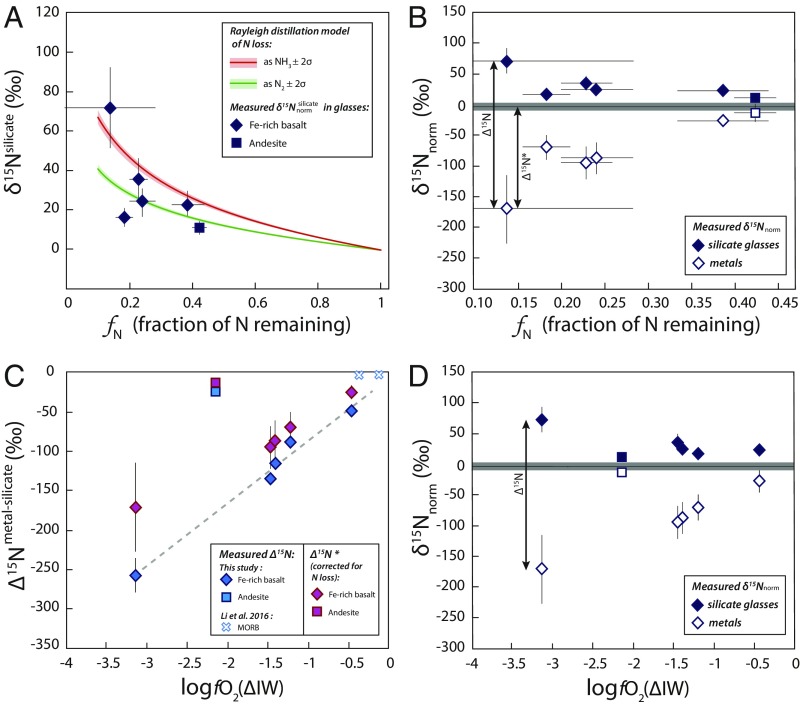
Although these normalized values were not calculated relative to the atmospheric N-isotopic composition and are not directly comparable to δ¹⁵N values measured in natural samples (40), they represent the magnitude of the observed change in the isotopic composition of each phase during the experiments. Fig. 3A reveals that N loss (in the form of N₂, NH₃, or both) by Rayleigh distillation during the experiments could increase the δ¹⁵N^silicate values of the melt and may explain the positive ${\text{δ}}^{15}{\text{N}}_{\text{norm}}^{\text{silicate}}$ values measured in the silicate glasses (Fig. 3B). In contrast, ${\text{δ}}^{15}{\text{N}}_{\text{norm}}^{\text{metal}}$ is clearly negative compared with the initial δ¹⁵N value (i.e., δ¹⁵N_norm = 0‰), suggesting that the metal phase becomes enriched in ¹⁴N during its segregation (Fig. 3B). Therefore, the observed positive ${\text{δ}}^{15}{\text{N}}_{\text{norm}}^{\text{silicate}}$ values may result from N loss from the experiments and/or ¹⁴N depletion during N partitioning into the metal phase.

Fig. 3.

Effect of N loss (A and B) and fO₂ (C and D) on N-isotopic fractionation ∆¹⁵N^{metal-silicate}. (A) Modeled effect of N loss by Rayleigh distillation on the δ¹⁵N_norm values of silicate glasses as a function of f_N, the fraction of N remaining in the sample at the end of the experiments compared with the initial N content of the starting materials. The ${\text{δ}}^{15}{\mathrm{N}}_{\text{norm}}^{\mathrm{silicate}}$ values represent measured ¹⁵N/¹⁴N^silicate ratios normalized to the initial ¹⁵N/¹⁴N ratio of the starting material (see text and Table 1). Rayleigh distillation was modeled for N₂ loss (green curve) and NH₃ loss (red curve) as ${\text{δ}}^{15}{\text{N}}^{\text{silicate}}=\mathrm{1,000}\cdot \left(f_{\text{N}}^{\left(\left(1/\alpha \right)-1\right)}-1\right)$, where α is the fractionation factor approximated here by $\sqrt{\left[m\left({}^{15}\text{N}\right)+m\left({}^{14}\text{N}\right)\right]/m\left({}^{14}\text{N}_2\right)}$ = 1.02 for N₂ loss and by $\sqrt{\left[m\left({}^{15}\text{N}\right)+3\cdot m\left(\text{H}\right)\right]/\left[m\left({}^{14}\text{N}\right)+3\cdot m\left(\text{H}\right)\right]}$ = 1.03 for NH₃ loss. The positive δ¹⁵N values measured in our silicate glasses can be explained by the Rayleigh distillation model, suggesting that N loss may have increased the δ¹⁵N values of the silicate glasses. (B) Evolution of δ¹⁵N in the silicate glasses (closed symbols) and in the metal blobs (open symbols) as a function of f_N. The δ¹⁵N_norm values represent measured ¹⁵N/¹⁴N^p ratios (p representing the metallic or silicate phase) normalized to the initial ¹⁵N/¹⁴N ratio of the starting material (see text and Table 1), and the gray line at 0‰ represents the initial δ¹⁵N_norm value. The difference between the δ¹⁵N values measured in the metal and the silicate phases (δ¹⁵N^metal − δ¹⁵N^silicate) approximates the calculated ∆¹⁵N^{metal-silicate} values. Considering that positive ${\text{δ}}^{15}{\mathrm{N}}_{\text{norm}}^{\mathrm{silicate}}$ values may have been produced by N loss, the difference between the initial ${\text{δ}}^{15}{\mathrm{N}}_{\text{norm}}$ (0‰) and the ${\text{δ}}^{15}{\mathrm{N}}_{\text{norm}}^{\mathrm{metal}}$ values corresponds to ∆¹⁵N*, the N-isotopic fractionation corrected for N loss. (C) ∆¹⁵N^{metal-silicate} as a function of fO₂, showing both calculated ∆¹⁵N^{metal-silicate} (blue symbols) and ∆¹⁵N* (purple symbols). The small blue x's are reproduced from Li et al. (16), with fO₂ values recalculated following the procedure described in the text. Error bars represent 2σ SDs. Whereas the uncertainties on ∆¹⁵N^{metal-silicate} are determined from the SDs on ¹⁵N/¹⁴N ratios measured by SIMS, the larger uncertainties on f_N, δ¹⁵N_norm values, and ∆¹⁵N* are derived from the weighing uncertainties associated with the addition of Si₃¹⁴N₄ and Si₃¹⁵N₄ to the starting materials. The dashed line represents a linear regression (r² > 0.9) on the ∆¹⁵N^{metal-silicate} values measured in Fe-rich basalt. ∆¹⁵N^{metal-silicate} data describe 2 trends that can be explained by compositionally dependent differences in N speciation in the silicate glasses (see text). (D) Evolution of δ¹⁵N_norm in the silicate glasses and metal blobs as a function of fO₂. This plot shows that positive ${\text{δ}}^{15}{\mathrm{N}}_{\text{norm}}^{\mathrm{silicate}}$ values can also be produced by N-isotopic fractionation during metal segregation from the melt via the formation of ¹⁴N–Fe bonds in the metal from ¹⁴N in NH complexes in the melt. This process becomes more important as the fO₂ decreases due to the increasing stabilization of NH complexes in the melt under more reducing conditions.

The N-isotopic fractionations between metal and silicate in the samples (Table 1 and Fig. 3C) were calculated from the ${}^{15}\text{N}/{}^{14}\text{N}^{\text{metal}}$ and ${}^{15}\text{N}/{}^{14}\text{N}^{\text{silicate}}$ ratios measured by ion probe as follows:

$${\mathrm{\Delta }}^{15}{\text{N}}^{\text{metal}-\text{silicate}}\approx \mathrm{1,000}\cdot \ln \left(\frac{{}^{15}\text{N}/{}^{14}\text{N}^{\text{metal}}}{{}^{15}\text{N}/{}^{14}\text{N}^{\text{silicate}}}\right).$$ [5]

They decrease from −49 ± 1‰ to −257 ± 22‰ with decreasing fO₂ from ∆IW −0.45 to −3.13. Such negative N-isotopic fractionations are in accord with equilibrium fractionation, during which the lightest isotopes favor bonds in the most reduced phase (23, 56), here as Fe–N (Fig. 2C). As the metal segregates from the silicate melt at isotopic equilibrium, it more favorably forms ¹⁴N–Fe bonds than ¹⁵N–Fe bonds, thereby depleting the silicate melt in ¹⁴N; this process may increase the ${\text{δ}}^{15}{\text{N}}_{\text{norm}}^{\text{silicate}}$ values. Alternatively, assuming that Rayleigh distillation alone produced the positive ${\text{δ}}^{15}{\text{N}}_{\text{norm}}^{\text{silicate}}$ values observed in Fig. 3 A and B, then, when corrected for this process, ${\text{δ}}^{15}{\text{N}}_{\text{norm}}^{\text{silicate}}$ can be assumed to remain at 0‰ during N partitioning into the metal phase. In this scenario, N-isotopic fractionations corrected for N loss, expressed as ${\mathrm{\Delta }}^{15}{\mathrm{N}}^{\ast }={\text{δ}}^{15}{\mathrm{N}}_{\text{norm}}^{\mathrm{metal}}-{\text{δ}}^{15}{\mathrm{N}}_{\text{norm}}^{\mathrm{silicate}}$ with ${\text{δ}}^{15}{\mathrm{N}}_{\text{norm}}^{\mathrm{silicate}}$ corrected to 0‰ (Fig. 3B), decrease from −27 ± 4‰ to −171 ± 28‰ with decreasing fO₂ from ∆IW −0.45 to −3.13 (Fig. 3C). Following this reasoning, ∆¹⁵N^{metal-silicate} and ∆¹⁵N* represent the maximum and minimum bounds on metal–silicate N-isotopic fractionation in our experiments, respectively.

The ∆¹⁵N^{metal-silicate} and ∆¹⁵N* values from this study are significantly lower than those obtained by Li et al. [∆¹⁵N^{metal-silicate} between 1.1 ± 2.8‰ and −5.5 ± 2.3‰ (16)]. This difference may be explained by the different P–T conditions of the 2 studies, although the results of Li et al. (16) show no pressure or temperature dependence over 1.5 to 7 GPa and 1,600 to 1,800 °C. It is, however, questionable that they do not observe any temperature effect on ∆¹⁵N^{metal-silicate} since, by definition, fractionation factors are inversely proportional to temperature (e.g., refs. 23 and 58). In addition, our large N-isotopic fractionations cannot be explained by ¹⁵N spiking of our samples. As has been shown for H isotopic fractionation (59), ∆¹⁵N^{metal-silicate} values are not dependent on the initial ¹⁵N/¹⁴N ratios of the experiments (Table 1). Instead, fO₂ is the key parameter differing between the 2 studies. The fO₂ of the samples of Li et al. (16) were between ∆IW −0.11 and −0.35, whereas the fO₂ of our samples varies from ∆IW −0.45 to −3.13. This observation implies an effect of fO₂ on ∆¹⁵N^{metal-silicate}.

These large N-isotopic fractionation values are comparable to estimates of H metal–silicate isotopic fractionation [between −55 and −285‰, modeled based on chondritic and mantle-like D/H values and H solubility in metal and silicate phases (60)], although, to our knowledge, no experimental data on metal–silicate fractionation are available for hydrogen or carbon isotopes. There are, however, experimental data available on H- and C-isotopic fractionations during other high-temperature magmatic processes. For instance, hydration or dehydration of silicate melts and nominally anhydrous minerals produces δD variations of up to 550‰ at 1,000 °C (61). During aqueous fluid–silicate melt interaction, H- and C-isotopic fractionations can reach 150‰ at 750 °C (56, 62–64). Among other isotope tracers of core formation, i.e., isotopes of heavier siderophile elements such as Si, Fe, Mo, Cr, Cu, and Ni (65), sulfur is the most comparable to N in terms of mass, solubility in reduced melts (66), and volatile behavior. However, experimentally determined metal–silicate S isotopic fractionation factors, ∆³⁴S^{metal-silicate}, are only on the order of 0.1 to 1.2‰ between ∆IW −0.6 and −4.1 (67). Although the mass difference between N isotopes is 2.5 times larger than that between S isotopes, this difference is insufficient to explain the vast difference between the metal–silicate isotopic fractionations of N and S.

The Effects of fO₂ and N Speciation on ∆¹⁵N^{metal-silicate}

Following Bigeleisen and Mayer (30) and Urey (31), mass-dependent N-isotopic fractionation can be expressed as follows:

$${\mathrm{\Delta }}^{15}{\text{N}}^{\text{metal}-\text{silicate}}\propto \mathrm{1,000}\cdot \left(\frac{\mathrm{\Delta }m}{m_{14}{m}_{15}}\frac{\mathrm{\Delta }{F}^{\text{metal}-\text{silicate}}}{T^2}\right),$$ [6]

where m₁₄ and m₁₅ are the atomic masses of ¹⁴N and ¹⁵N, respectively, Δm is their mass difference, $\mathrm{\Delta }{F}^{\text{metal}-\text{silicate}}$ is the difference between the force constants acting on the isotopes in the metallic phase and the silicate melt ($\mathrm{\Delta }{F}^{\text{metal}-\text{silicate}}=F_{\text{N}}^{\text{metal}}-F_{\text{N}}^{\text{silicate}}$, with $F_{\text{N}}^{\text{metal}}$ and $F_{\text{N}}^{\text{silicate}}$ the effective force constants that depend on the chemical bond stiffness of N bonds in the metallic phase and silicate glass, respectively), and T is temperature in kelvin. In this study, at constant T, $\mathrm{\Delta }{F}^{\text{metal}-\text{silicate}}$ is the only variable in the above equation acting on the N-isotopic fractionation between metal alloy and silicate melt, along with fO₂ variations. This parameter is related to vibrational frequency, v_N, (30, 51), following:

$$v_{\text{N}}^p=\frac{1}{2\pi }{\left(\frac{F_{\text{N}}^p}{{\mu }_{\text{N}}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\mathrm{,}$$ [7]

where v_N was determined from the Raman vibration modes of N species in the metallic phases and the silicate glasses (Fig. 2) and µ_N is the reduced mass of the N-bearing molecule, calculated for N–H as µ(N–H) = [m_N × m_H/(m_N + m_H)], with m_N and m_H being the atomic masses of N and H, respectively. More details on the principles and factors controlling stable isotopic fractionations can be found in Schauble (23) and Young et al. (51). Nitrogen dissolves in silicate glasses as molecular nitrogen (N₂) and NH complexes, and as Fe–N in metal alloys. N₂ has 3 isotopomers, ¹⁵N≡¹⁵N, ¹⁵N≡¹⁴N, and ¹⁴N≡¹⁴N, with vibration modes in silicate glasses at 2,251, 2,287, and 2,326 cm⁻¹, respectively (Fig. 2A) (55), whereas the vibration mode of gaseous ¹⁴N≡¹⁴N is at 2,331 cm⁻¹ (68). The vibration modes of NH complexes are between 3,180 and 3,350 cm⁻¹ (Fig. 2B) (e.g., refs. 41 and 69). Fe–N vibrations in metal alloys are distinctly different, occurring at 338 cm⁻¹ (Fig. 2C) (70). In comparison, S dissolves in metal alloys as Fe–S with vibration modes at 310 and 360 cm⁻¹, and in silicate melts as Fe–, Mg–, and Ca–S with vibration modes between 285 and 350 cm⁻¹ (66). Although the vibration modes of complexes involving N or S have been determined for quenched silicate and metal, their equivalents in silicate melts and liquid metals at HP–HT are expected to vary only by a few cm⁻¹, as shown by Mysen (71) for the N₂ vibration mode in silicate melts and aqueous fluids. The observed vibration modes are directly related to the reduced masses µ_N and µ_S of the bonds formed by N and S, respectively, in the metal and silicate phases. As the relevant N bonds have very different reduced masses [µ(N–H) = 1 a.m.u., µ(N≡N) = 7 a.m.u., and µ(Fe–N) = 11 a.m.u.], the bonding of N with ions of very different masses directly produces large differences in the force constants (i.e., ∆F^{metal-silicate}) acting on N isotopes in the 2 phases. In comparison, the smaller ∆F^{metal-silicate} values for S isotopes should result from the similar reduced masses of S bonds [µ(Mg–S) = 14 a.m.u., µ(Ca–S) = 18 a.m.u., and µ(Fe–S) = 20 a.m.u.]. Therefore, we conclude that the observed large N-isotopic fractionations relative to those of S are a consequence of the distinct N speciation between the metallic phase and the silicate melt.

The difference in vibrational frequencies and reduced masses between the metal and silicate phases is higher when N is dissolved as N–H complexes (e.g., NH₃) than as molecular N₂. The basic equation for equilibrium isotopic fractionation for stable isotopes, derived from Bigeleisen and Mayer (30), Urey (31), and Young et al. (51), can be expressed as follows:

$${\mathrm{\Delta }}^{15}{\text{N}}^{\text{metal}-\text{silicate}}=\frac{\mathrm{1,000}}{24}\cdot {\left(\frac{h}{k_{b}T}\right)}^2\left(\frac{\mathrm{\Delta }m}{m_{14}{m}_{15}}\right)\times \left[\left(v_{\text{N}}^{{\text{metal}}^2}-v_{\text{N}}^{{\text{silicate}}^2}\right)\left({\mu }_{\text{N}}^{\text{metal}}-{\mu }_{\text{N}}^{\text{silicate}}\right)\right],$$ [8]

where h is Planck’s constant (in joules per kelvin), k_b is the Boltzmann constant (in joules per hertz), T is temperature in kelvin, and $v_{\text{N}}^{\text{metal}}$ and $v_{\text{N}}^{\text{silicate}}$ denote the Raman vibration modes (in hertz) for the metal and silicate phases, respectively. From Eq. 8, we estimate ${\mathrm{\Delta }}^{15}{\text{N}}^{\text{metal}-\text{silicate}}$ to be −4 to −24‰ for N dissolved as N₂ or NH₃ in the silicate glass, respectively. Eq. 8 only considers N speciation differences between phases and assumes the absence of N interactions between molecular groups within each metal or silicate phase (e.g., different structural units). In general, however, this assumption is not valid for silicate melts because strong intermolecular bonds influence isotopic exchanges, thereby leading to a significant underestimation of the isotopic fractionation between distinct phases (e.g., refs. 59, 67, 72, and 73). However, this calculation shows that larger N-isotopic fractionations between the metal and silicate phases are produced depending on whether N is dissolved as N–H complexes or as molecular N₂. Accordingly, we can assume that higher NH/N₂ ratios in the melt produce larger metal–silicate N-isotopic fractionations than when N is present in the melt mainly as N₂. The increasing stabilization of NH complexes with decreasing fO₂ (Fig. 2B) therefore increases the observed metal–silicate N-isotopic fractionation among HB samples (Fig. 3C and SI Appendix, Fig. S5). In contrast, the ∆¹⁵N^{metal-silicate} value of A05, −25 ± 1‰, is significantly smaller than those of the Fe-rich basalts at equal fO₂ values (Fig. 3). This discrepancy may be explained by the lower NH/N₂ ratio of the andesite compared with that of the Fe-rich basalts.

Although not observed in our glasses, N dissolution as nitrides in the silicate melt would lead to smaller metal–silicate N-isotopic fractionation than for N dissolved as N₂ or N–H complexes, given the small difference in vibration modes between Fe–N in metals and Si–N in silicates ($v_{\text{N}}^{\text{metal}}-v_{\text{N}}^{\text{silicate}}=$ 462 cm^–1).

Nitrogen Isotopic Fractionation during Core Formation

N partitioning data (this study; refs. 15–22, 38, 52, and 53) show that, during terrestrial core–mantle differentiation, a fraction of N must have been removed from the magma ocean into the core-forming metals (Fig. 1). This N segregation produced an isotopic fractionation that depleted the metallic phase and enriched the silicate mantle in ¹⁵N and was fundamentally dependent on the fO₂ conditions of the proto-mantle. Recent models (24, 28, 74) propose that the Earth accreted from small and highly reduced materials (∆IW −5) during the first stages of its formation (60 to 70% of its mass), then from larger and more oxidized bodies (∆IW −2) toward the end of accretion. Thus, the studied fO₂ range (∆IW −3.1 to −0.5) represents plausible conditions of metal–silicate equilibration during the later stages of accretion and core formation (24, 74). During progressive oxidation from ∆IW −3.1 to −0.5, while the fraction of Earth’s N increased in core-forming materials, the N-isotopic fractionation between the segregating metal and the silicate mantle would likely have decreased. These concurrent processes can be modeled using an equilibrium model of Earth’s core–mantle differentiation (16). We adapted an equilibrium model of core formation that assumes complete equilibrium between the silicate mantle and the forming core (16) to account for progressive metal–silicate equilibration. This progressive equilibration is represented by the ratio of the masses of the silicate mantle and the bulk Earth (BE), $m^{\text{mantle}}/m^{\text{BE}}$, which varied between 1 (precore) and 0.67 (present-day Earth). The total mass $M_{\text{N}}$ of N in the silicate mantle or BE is calculated from the following:

$$M_{\text{N}}^{\text{mantle},\hspace{0.17em}\text{BE}}=C_{\text{N}}^{\text{mantle},\hspace{0.17em}\text{BE}}\cdot m^{\text{mantle},\hspace{0.17em}\text{BE}}\mathrm{,}$$ [9]

where $C_{\text{N}}^{\text{mantle},\hspace{0.17em}\text{BE}}$ is the N concentration in the mantle or BE, with

$$C_{\text{N}}^{\text{mantle}}=C_{\text{N}}^{\text{BE}}\cdot \left[{\left(m^{\text{mantle}}/m^{\text{BE}}\right)}^{\left(D_{\text{N}}^{\text{metal}-\text{silicate}}-1\right)}\right].$$ [10]

The evolution of the N-isotopic composition of the mantle ${\text{δ}}^{15}{\text{N}}_{\text{mantle}}$ during core formation is expressed as follows:

$${\text{δ}}^{15}{\text{N}}_{\text{mantle}}={\text{δ}}^{15}{\text{N}}_{\text{BE}}-{\mathrm{\Delta }}^{15}{\text{N}}^{\text{metal}-\text{silicate}}\cdot \left(1-\frac{M_{\text{N}}^{\text{mantle}}}{M_{\text{N}}^{\text{BE}}}\right).$$ [11]

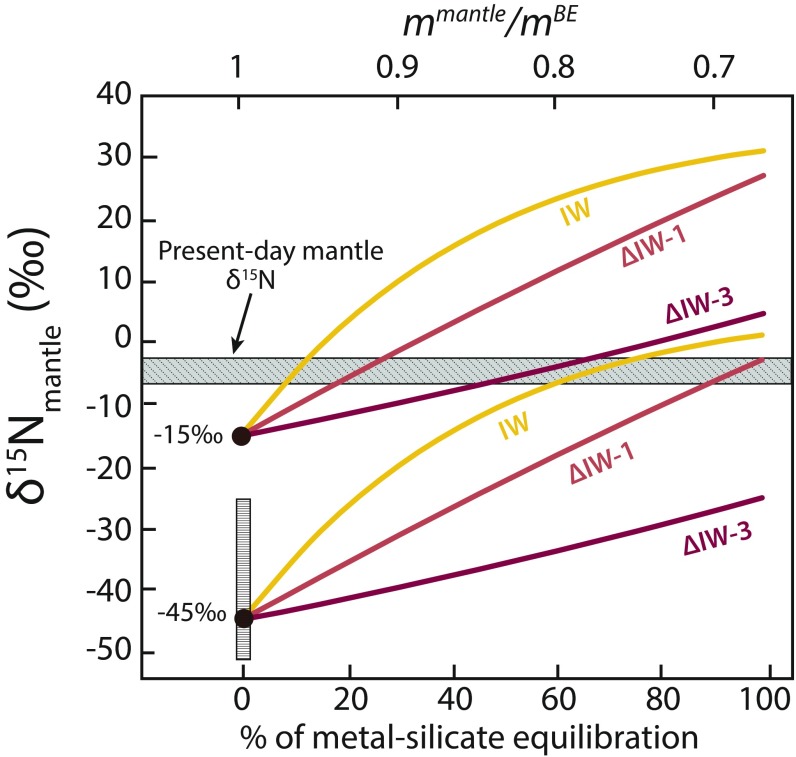
This model is primarily dependent on the N-isotopic composition of the BE, ${\text{δ}}^{15}{\text{N}}_{\text{BE}}$, and, to a lesser extent, $C_{\text{N}}^{\text{BE}}$, necessitating assumptions regarding the nature of the accreting bodies that formed the Earth. Considering an enstatite chondrite origin for Earth’s N (11) and assuming no N was lost during accretion, the $C_{\text{N}}^{\text{BE}}$ value of the proto-Earth was 160 ppm (75). For ${\text{δ}}^{15}{\text{N}}_{\text{BE}}$, we chose to explore the 2 most extreme δ¹⁵N values measured in enstatite chondrites: −45 and −15‰ (13). Over the fO₂ range ∆IW −3.1 to −0.5 (i.e., using the N partition coefficients and isotopic fractionation values derived from our experiments), a proto-Earth with a ${\text{δ}}^{15}{\text{N}}_{\text{BE}}$ value of −45‰ would result in a ${\text{δ}}^{15}{\text{N}}_{\text{mantle}}$ value between −25 and +1‰ at the end of core formation depending on the fO₂, whereas a ${\text{δ}}^{15}{\text{N}}_{\text{BE}}$ value of −15‰ would result in a ${\text{δ}}^{15}{\text{N}}_{\text{mantle}}$ value between +5 and +31‰ (Fig. 4). The modeled trend is linear at ∆IW −3 but logarithmic at IW, such that the difference between the 2 trends increases to a maximum of ∼27‰ at ∼60% metal–silicate equilibration, and then decreases to ∼20‰ at 100% metal–silicate equilibration (Fig. 4). This simple model demonstrates that the present-day mantle’s δ¹⁵N value of −5‰ could have been produced by core–mantle differentiation, assuming that enstatite chondrites are Earth’s primary building blocks and the source of terrestrial N (or if ${\text{δ}}^{15}{\text{N}}_{\text{BE}}$ was between −51 and −25‰; Fig. 4). Nevertheless, the outcome of this model is mainly controlled by the value of ${\text{δ}}^{15}{\text{N}}_{\text{BE}}$ (Fig. 4) and therefore the source of Earth’s N, which remains a matter of debate (5, 76).

Fig. 4.

Modeled δ¹⁵N values of the silicate proto-mantle during core formation as a function of core–mantle equilibration and fO₂ conditions of the magma ocean. We explored 2 different ${\text{δ}}^{15}{\text{N}}_{\text{BE}}$ values: the lowest (−45‰) and highest (−15‰) ${\text{δ}}^{15}\text{N}$ values measured in enstatite chondrites (13). The respective values used for D_N^{metal-silicate} and ∆¹⁵N^{metal-silicate} were 7 and −49‰ at IW, 3.02 and −89‰ at ∆IW −1, and 0.2 and −257‰ at ∆IW −3.1 (Table 1). The present-day ${\text{δ}}^{15}\text{N}$ value of the mantle is −5 ± 2‰ (gray bar; the thickness of the bar represents the 2σ SD), based on a compilation from diamonds and MORBs (3). This model assumes that ∆¹⁵N^{metal-silicate} was not affected by Rayleigh distillation during the experiments, and thus only considers that the mantle’s ${\text{δ}}^{15}\text{N}$ value was modified by core–mantle fractionation without accounting for the effect of degassing. After 30% core–mantle (metal–silicate) equilibration, the modeled fO₂ variations account for a difference in the mantle δ¹⁵N value of up to 27‰. The vertical bar between −51 and −25‰ represents the plausible range of δ¹⁵N values of Earth’s building blocks necessary to produce the present-day δ¹⁵N_mantle value of −5 ± 2‰ at fO₂ conditions between ∆IW −3 and −0.5, assuming that core formation is the only process that fractionated N isotopes during the Earth’s early history. At ∆IW −3.1, assuming a ${\text{δ}}^{15}{\text{N}}_{\text{BE}}$ value of −25‰ for Earth’s building blocks, complete metal–silicate equilibration is required to reach the present-day δ¹⁵N_mantle value. In contrast, at IW, conditions under which N is siderophile, the present-day δ¹⁵N_mantle value is attained at 60% metal–silicate equilibration from any source of N with a ${\text{δ}}^{15}{\text{N}}_{\text{BE}}$ ≥ −45‰.

On the Origin(s) and Evolution of Terrestrial N

Because the N-isotopic signatures of solar system objects and reservoirs are highly variable (77), N isotopes are key tracers of the source of terrestrial volatiles. Among chondrites, only enstatite chondrites have negative δ¹⁵N values [−45 to −15‰ (13)]. This fact led Javoy et al. (5) to suggest that enstatite chondrites are the source of Earth’s N. An enstatite chondrite-like δ¹⁵N value of the proto-Earth is consistent with the scenario presented by Li et al. (16) and herein: N segregation into the core during proto-Earth differentiation could have increased the δ¹⁵N value of the silicate mantle from very negative values (as low as −45‰) to −5‰. In addition, the range of δ¹⁵N values in Archean diamonds is similar to that of present-day diamonds and MORBs (11), suggesting that the mantle acquired its δ¹⁵N value of −5‰ before the Archean (16). This would support the idea of a very negative proto-Earth δ¹⁵N signature, similar to that of enstatite chondrites, and the subsequent enrichment of the mantle in ¹⁵N by an early process, for instance core formation (16), possibly combined with magma ocean degassing and/or N recycling (7).

Nitrogen degassing (as N₂ or NH₃; Fig. 3A) from the magma ocean to the primitive atmosphere could also have increased the δ¹⁵N_mantle value from an enstatite chondrite N-isotopic signature to the present-day value. Considering the highest reported δ¹⁵N value for enstatite chondrites (−15‰), only 30% of magma ocean degassing is required to increase δ¹⁵N_mantle by 10‰ to the present-day value of −5‰ assuming a Graham’s law relationship (Fig. 3A). On the other hand, from an enstatite chondrite δ¹⁵N value of −45‰, more than 75% of the initial N of the Earth needs to be degassed to increase δ¹⁵N_mantle by 40‰ to the present-day value (Fig. 3A). Considering the low solubility of N₂ at low pressure under reduced conditions [<0.2 ppm at 1 atm between ΔIW −2 and IW (56)], large fractions of the proto-Earth’s initial N content could have been degassed from a reduced magma ocean (e.g., refs. 20 and 35). However, these considerations are dependent on N solubility variations with fO₂ and fH₂ (which control the stabilization of NH complexes and thus N solubility) in mafic to ultramafic melts, for which data are sparse. In comparison, N recycling via subduction is insufficient to increase δ¹⁵N_mantle by more than 5‰, even if subduction was initiated 4 Ga (78). As both magma ocean degassing and core formation may have increased the δ¹⁵N value of the magma ocean, the source of terrestrial N might have had a N-isotopic signature significantly more negative than −45‰.

The very low δ¹⁵N values of some Archean diamonds [−25 to −39‰, compared with −12 to +6‰ in most other Archean diamonds (12, 79)] have been suggested to represent relics of primordial N that have been preserved in an undegassed reservoir. The existence of such a primitive, undegassed mantle reservoir has been proposed to explain the low ⁴He/³He and ²¹Ne/²²Ne [i.e., low (U+Th)/³He and (U+Th)/²²Ne] values of ocean island basalts (OIBs) [see review by Moreira (80)], as well as the preservation of a chondritic Xe component in the deep mantle (81). However, OIBs, typically associated with mantle plumes, exhibit high δ¹⁵N values (around +2‰) akin to surficial N-isotopic compositions (7), suggesting that at least some of the N in OIBs is derived from recycled surficial N. The low δ¹⁵N signature of the inferred undegassed reservoir responsible for Archean diamonds must have somehow been maintained during metal–silicate fractionation and core formation. The stable isotopic (i.e., δ¹³C) signature of diamonds can vary widely as a result of the redox state of the C–O–H–N fluids/melts from which they form (82, 83). Therefore, the extremely low δ¹⁵N values of some Archean diamonds (12, 79) may similarly reflect fO₂ heterogeneities in the Archean mantle, although the effects of fO₂ on N speciation and isotopic fractionation in diamonds remain unknown (82).

Another possible origin of terrestrial N arises from the combined study of N isotopes and noble gases among solar system bodies. Based on the solar-like Ne isotopic composition of the mantle, Marty (76) discussed the possibility that the mantle has preserved some solar N. This scenario implies that precursor grains accreted during Earth’s formation were first irradiated by the solar wind and preserved their solar volatile isotopic signature during Earth’s accretion and differentiation [δ¹⁵N_IFSW ≤ −240‰; IFSW: implantation-fractionated solar wind (84, 85)]. Alternatively, a primordial solar atmosphere could have been captured by Earth’s gravity and dissolved into the early magma ocean [δ¹⁵N_solar = −383‰ (e.g., ref. 86)]. Assuming a solar-like source of N for the proto-Earth, the mantle’s N must have been significantly enriched in ¹⁵N by N-isotopic fractionation during core–mantle differentiation, during magma ocean degassing (as N₂ and/or NH₃; Fig. 3A), and/or by the delivery of carbonaceous chondrites [δ¹⁵N_CC = +15 to +55‰ (14)] during late accretion and the addition of the late veneer.

Conclusions

We studied metal–silicate N-isotopic fractionation over a fO₂ range consistent with the inferred conditions of Earth’s core formation. Our results reveal large N-isotopic fractionations over fO₂ conditions spanning 3 orders of magnitude. Such large fractionations can be explained by the vastly different N bonds formed in metal and silicate phases. The particularity of N, compared with other isotope tracers of core formation, is that it forms N₂ molecules or NH complexes in silicate melts, whereas it bonds as Fe–N in metal alloys. The strong dependence of N-isotopic fractionation on fO₂ conditions is a consequence of the increased solubility of NH complexes in silicate melts under increasingly reducing conditions. We also demonstrated that the NH/N₂ ratio and the N-isotopic fractionation depend on melt composition. Planetary magma oceans are expected to be mafic (close to our Fe-rich basalts) to ultramafic. Ultramafic melts (SiO₂-poor and MgO-rich) are difficult to quench from HP–HT to ambient conditions. Therefore, to advance our understanding of the effect of melt composition on N speciation and isotopic fractionation for extrapolation to such ultramafic melts at core-forming reduced conditions, experimental studies need to be performed using silicate melts spanning a large range of polymerization degrees.

Metal–silicate N partitioning coefficients increase significantly with increasing P–T conditions (22) because N solubility in metal blobs increases (15). How P–T conditions affect N₂ and NH solubility in silicate melts, and thereby metal–silicate N-isotopic fractionation, remains to be experimentally constrained over a wide range of P–T conditions. Although isotopic fractionations decrease with increasing temperature [Δ¹⁵N ∝ 1/T² (20, 21)], an increase of pressure over tens of gigapascals should increase isotopic fractionations by increasing bond stiffness (51). However, how pressure affects bond stiffness in silicate glasses versus in metal alloys remains to be studied. At P–T conditions more representative of core–mantle equilibration in the terrestrial magma ocean [0 to 40 GPa and 2,000 to 3,000 K (87)], the magnitude of N-isotopic fractionation is expected to be smaller than determined in this study since the effect of T should dominate that of P. Thanks to our analytical developments, the N-content and -isotopic ratios of small phases (<15 µm in diameter) can now be measured in high-pressure (>10-GPa) experimental samples, which will allow the determination of N-isotopic fractionations at P–T conditions more representative of core–magma ocean equilibration conditions.

We have highlighted the fundamental effect of fO₂ on the evolution of the mantle’s δ¹⁵N value during core formation. We showed that fO₂ variations of 3 log units can produce a δ¹⁵N variation of >20‰ in the silicate mantle after only 30% metal–silicate equilibration (Fig. 4). The magnitude of the N-isotopic fractionation observed here during metal–silicate segregation, larger fractionations under more reducing conditions, suggests that large N-isotopic fractionations could have also occurred during other high-temperature stages of Earth’s formation, such as accretion and magma ocean crystallization and/or degassing.