High-frequency microrheology in 3D reveals mismatch between cytoskeletal and extracellular matrix mechanics

Significance

Mechanical homeostasis describes how cells sense physical cues from the microenvironment and concomitantly remodel both the cytoskeleton and the surrounding extracellular matrix (ECM). However, the nature of the dynamic coupling between microscale cell and ECM mechanics remains poorly understood. Here we investigate whether cells mechanically adapt to distinct microenvironments. We determined that tumor cells are mechanically plastic to adapt to many environments. This mechanical mismatch holds for multiple perturbations of the cytoskeletal architecture and in 2 different surrogate ECM hydrogels mimicking breast and brain microenvironments. Our data also obey laws similar to those used to model rheological properties of polymers. Linking these mathematical parameters to biophysical factors will move us closer to exploiting mechanics as a cancer biomarker.

Abstract

Mechanical homeostasis describes how cells sense physical cues from the microenvironment and concomitantly remodel both the cytoskeleton and the surrounding extracellular matrix (ECM). Such feedback is thought to be essential to healthy development and maintenance of tissue. However, the nature of the dynamic coupling between microscale cell and ECM mechanics remains poorly understood. Here we investigate how and whether cells remodel their cortex and basement membrane to adapt to their microenvironment. We measured both intracellular and extracellular viscoelasticity, generating a full factorial dataset on 5 cell lines in 2 ECMs subjected to 4 cytoskeletal drug treatments at 2 time points. Nonmalignant breast epithelial cells show a similar viscoelasticity to that measured for the local ECM when cultured in 3D laminin-rich ECM. In contrast, the malignant counterpart is stiffer than the local environment. We confirmed that other mammary cancer cells embedded in tissue-mimetic hydrogels are nearly 4-fold stiffer than the surrounding ECM. Perturbation of actomyosin did not yield uniform responses but instead depended on the cell type and chemistry of the hydrogel. The observed viscoelasticity of both ECM and cells were well described by power laws in a frequency range that governs single filament cytoskeletal dynamics. Remarkably, the intracellular and extracellular power law parameters for the entire dataset collectively fall onto 2 parallel master curves described by just 2 parameters. Our work shows that tumor cells are mechanically plastic to adapt to many environments and reveals dynamical scaling behavior in the microscale mechanical responses of both cells and ECM.

Mechanotransduction is a process by which cells sense external forces that directly modulate biochemical signaling and ultimately drive cell fate decisions (1, 2). Cells in turn respond with contractile forces to remodel physical properties of the surrounding extracellular matrix (ECM) biopolymers (3, 4). Thus, force generation depends on both external and internal factors. Moreover, plasticity of mechanical adaptation may be one of the key properties for disseminated tumor cells to colonize new organs (5, 6). Externally, cells encounter organ-specific cues such as the physicochemical properties of the ECM within a given microenvironment (1, 7, 8). The physical properties of the ECM depend on the chemical composition, concentration, and cross-linking of biopolymers (9). Internally, cells adopt various mechanical phenotypes (1, 7, 8). The mechanical phenotype of a cell is dominated by its cytoskeletal architecture and the proteins and organelles that regulate it (7).

Bulk and microscale rheology have elucidated that both cells and ECM typically exhibit a combination of elastic (“solid-like”) and viscous (“liquid-like”) mechanical responses, i.e., viscoelasticity (1, 10). This complex behavior depends on both a material’s intrinsic properties and on the frequency of the applied force (1, 7, 9). Thus, ECM can behave like a liquid on one time scale but like a solid on another. This is important in determining how cells maintain shape when subjected to external forces in different physical conditions. Moreover, intracellular viscoelasticity plays a role in diffusion and chemical reactions inside the cell. However, the details of how intracellular and ECM mechanical properties interrelate at the microscale remain elusive (10, 11). Simply, do cells modulate their internal viscoelasticity to match the surrounding ECM? Would this coupling be different for malignant cells compared with normal cells? Finally, would it depend on the chemistry of the ECM? Cytoskeletal elements contribute to the mechanical properties of cells (1, 7, 8). Thus, cytoskeletal rearrangements may contribute to the plasticity of mechanical adaptation.

Formulaic explanations allow us to draw from our understanding of non-Newtonian fluids to model rheological properties of tissue (12–14). One property of tissues that emerges from non-Newtonian fluid mechanics is that viscoelasticity (complex moduli [G′*]) obeys frequency-dependent power laws, |G*(ω)| = Aω^B, where the dependence B varies for different frequency regimes and different cell types (12–16). Gaining a mechanistic understanding of how these dynamics influence physiological and pathological mechanobiology thus requires quantitative measurements of cells and ECM in context.

To interrogate the dynamics of cell–ECM mechanical adaptation, we employ broadband frequency optical tweezer (OT)-based active microrheology to directly measure the mechanical properties of 3D-embedded cells and the surrounding ECM with near simultaneity. We determined that, while normal cells’ viscoelasticity closely matches that of the surrounding ECM, malignant cells are significantly stiffer than the surrounding ECM. This mechanical mismatch holds for multiple perturbations of the cytoskeletal architecture and in 2 different surrogate ECM hydrogels mimicking breast and brain microenvironments. The cell and ECM complex moduli all exhibit power law frequency dependence in the high-frequency range (400 to 15,000 oscillations/s). We show that the fit parameters of these power laws obey a simple empirical master relation and collapse onto parallel intracellular and extracellular master curves. These observations suggest that perhaps deeper principles related to critical phenomena may govern the mechanical dynamics of these complex cell–ECM systems.

Results

Optical Trap-Based Active Microrheology to Probe Mechanical Coupling of Cells Embedded in 3D ECM with the Surrounding ECM.

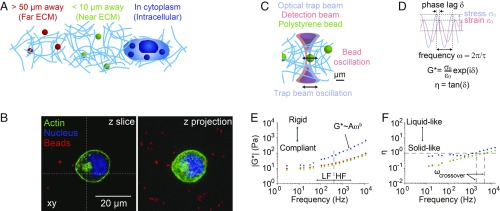
Polystyrene beads serve as local mechanical sensors distributed within cells and in the surrounding ECM (Fig. 1 A and B). Live imaging revealed that these 1-μm diameter beads were randomly distributed with respect to the actin cytoskeleton and the nucleus (Fig. 1B and Movie S1). Image-based colocalization analysis showed a mixed distribution where some of the beads were encapsulated within lysosomes with the remainder randomly dispersed within the cytoplasm (SI Appendix, Fig. S1). Using optical tweezers, we then sinusoidally oscillate each bead in the optical trap over a range of frequencies from 3 to 15,000 Hz, and simultaneously track the nanometer displacements of the bead via back focal plane interferometry. Correlating the trap and bead positions yields the local viscoelasticity in terms of the complex modulus, G*. The complex modulus, G* = |G*|exp(iδ) = G′ + iG″, can be deconvolved into magnitude |G*| = (G′² + G″²)^1/2 and η = G″/G′ which encode the rigidity and hysteresivity of the material in the immediate vicinity of the measured bead, respectively (Fig. 1 C and D). For purely elastic materials, the phase lag between bead and trap motion δ = 0 (in radians), and for purely viscous materials, δ = π/2; for viscoelastic materials, 0 > δ > π/2. Fig. 1 E and F show the microscale frequency-dependent rigidity and hysteresivity (in terms of |G*| and η) for MCF7 nontumorigenic human mammary epithelial cancer cells embedded in 3D laminin-rich ECM (lrECM, Matrigel). We configured our custom optical setup to measure 20 frequencies at once (by multiplexing), reducing collection time to ∼2 min per bead (including piezo centering and in situ calibrations of the optical trap stiffness and detector sensitivity) and allowing near-simultaneous measurement of intracellular and extracellular mechanical properties (SI Appendix). To assess short-range and long-range remodeling, we measured ECM mechanical responses at distinct regions from the cell membrane: within 10 μm of the cell membrane (“near-ECM”) and greater than 50 μm of the cell membrane (“far-ECM”).

Fig. 1.

Optical trap-based active microrheology inside cells embedded in 3D ECM and in surrounding ECM. (A) Experimental schematic. One micron beads inside cells and in the surrounding 3D ECM serve as local mechanical sensors. (B) Confocal micrographs of an MCF7 cell embedded in lrECM showing distribution of beads. (C) Schematic of optical trap measurements. (D) Dynamic mechanical parameters obtained from oscillating the trap while tracking bead motion. (E) Complex modulus |G*| gives material’s microscale rigidity and depends on frequency, with power law behavior at high frequencies, where A and b are the power law fit parameters. Low-frequency (LF) and high-frequency (HF) regimes are indicated. (F) Hysteresivity η gives material’s microscale viscoelastic properties, with η = 0 for purely elastic materials, η infinite for purely viscous materials, and η = 1 for semifluid materials. The crossover frequency ω_crossover is the frequency at which the hysteresivity η reaches a value of 1. Power law coefficients (A) and exponents (B) and 95% confidence intervals are as follows. Intracellular: A = 0.78 (0.36, 1.20), b = 0.70 (0.64, 0.76); near-ECM: A = 0.92 (0.60, 1.23), b = 0.46 (0.42, 0.49); far-ECM: A = 1.01 (0.60, 1.41), b = 0.47 (0.43, 0.52).

On a logarithmic scale, a power law y = Ax^b appears as a straight line with slope b and intercept y = A at x = 1. Drawing on polymer physics, we can further classify the cell rheological properties by examining the power law frequency dependence |G*| ∝ ω^b. Flexible polymer networks are predicted to have complex moduli with b = 0.5, whereas b = 0.75 for semiflexible polymers (16). We observed that for high frequencies (400 to 15,000 Hz), the magnitudes |G*| of cells, near-ECM and far-ECM each fit to power laws with different exponents (i.e., slopes) b ranging from 0.46 to 0.70 (SI Appendix, Fig. S11E). In contrast, |G*| shows a flat plateau at lower frequencies. The terminal relaxation crossover frequency, ω_crossover, indicates when the material properties transition from solid-like to liquid-like and occurs at η = 1, as shown by the intersecting dashed lines (Fig. 1F). The intracellular ω_crossover is ∼2 kHz, while it is ∼7 kHz for both near-ECM and far-ECM, indicating the intracellular mechanics transition from more elastic to more viscous behavior at much lower frequencies than the ECM.

Cells Tune Intracellular Mechanical Properties in Response to 2D vs. 3D Culture Conditions.

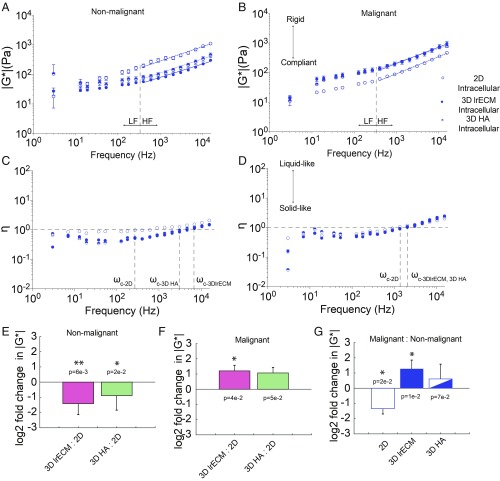
We then asked how intracellular mechanics change as a function of malignancy. Using 2 isogenic pairs of mammary cancer cells, one pair that mimics the transition from nonmalignant to invasive cancer (MCF10A vs. MCF10-CA1) and a second pair that displays dormant and proliferative phenotypes (D2.0R vs. D2.A1), we first probed changes in intracellular mechanics for 2D vs. 3D culture methods (17–20). Fig. 2 shows data for normal MCF10A and malignant MCF10-CA1 cells. While normal cells are significantly stiffer in 2D than 3D (Fig. 2 A, B, and E), malignant cells are significantly stiffer in 3D than 2D (Fig. 2 A, B, and F). Normal cells are significantly stiffer than malignant cells when cultured on 2D tissue substrates (Fig. 2 A, B, and G). However, when cultured in 3D lrECM, the converse is true (Fig. 2 A, B, and G).

Fig. 2.

Intracellular mechanical properties depend on extracellular mechanical cues. (A and B) Intracellular |G*| (mean ± SE) vs. frequency of nonmalignant MCF10A cells (A) and malignant MCF10-CA1 cells (B) adherent to 2D glass substrates (open circles), embedded in 3D lrECM (closed circles), and embedded in 3D HA (half-open circles). (C and D) Intracellular η (mean ± SE) vs. frequency of nonmalignant MCF10A cells (C) and malignant MCF10-CA1 cells (D) adherent to 2D glass substrates (open circles), embedded in 3D lrECM (closed circles), and embedded in 3D HA (half-open circles). Intersections with the horizontal dashed line at η = 1 of the vertical lines occur at crossover frequencies ω_c. (E and F) Log2 ratios of |G*(ω)| in 3D ECM vs. on 2D substrates for nonmalignant MCF10A cells (E) and malignant MCF10-CA1 cells (F) (mean ± SD, averaged across frequency). (G) Log2 ratios of |G*(ω)| for malignant MCF10-CA1 cells vs. nonmalignant MCF10A cells. Power law coefficients (A) and exponents (B) and 95% confidence intervals are as follows: Nonmalignant cells in 2D: A = 11.74 (4.74, 18.74), b = 0.47 (0.40, 0.54); malignant cells in 2D: A = 1.14 (0.72, 1.55), b = 0.62 (0.58, 0.66); nonmalignant cells in 3D lrECM: A = 2.36 (0.91, 3.81), b = 0.49 (0.42, 0.56); malignant cells in 3D lrECM: A = 2.39 (1.21, 3.56), b = 0.62 (0.57, 0.68); nonmalignant cells in 3D HA: A = 2.26 (1.06, 3.46), b = 0.54 (0.48, 0.60); malignant cells in 3D HA: A = 6.36 (2.90, 9.81), b = 0.50 (0.44, 0.56). P values from 2-way ANOVA are shown above or below each bar in E–G (*P < 0.05 and **P < 0.01).

Next, we tested adaptation to a different ECM environment by embedding cells in 3D hyaluronic acid (HA) hydrogels with mechanical properties tuned to match those of the lrECM. We determined that both cell types (MCF10A and CA1s) show similar stiffness in 3D HA and lrECM (Fig. 2 A, B, and E–G). Interestingly, nonmalignant cells behaved more like flexible polymers (b = 0.5), with exponents b ranging ∼0.47 to 0.54 when cultured for all conditions. Malignant cells also had exponents b ∼ 0.50 in 3D HA, but behaved more like semiflexible polymers (b = 0.75) on 2D and in 3D lrECM, with exponents b ∼ 0.62.

For the isogenic pair of dormant and proliferative clones, we found that the stiffness of the dormant clone (D2.0R) does not change significantly in response to the microenvironment, but instead remains very similar in 2D, 3D lrECM, and 3D HA (SI Appendix, Fig. S2). Conversely, the aggressive clone (D2.A1) is indistinguishable in 3D lrECM, but significantly stiffer in 2D, and nearly 10-fold more compliant in 3D HA (SI Appendix, Fig. S2). These results demonstrate that the mechanical malignant phenotype depends on microenvironmental context.

Cells Are More Liquid-Like When Cultured in 2D vs. 3D Culture Conditions.

How cancer cells move or maintain shape in response to external or endogenous force depends on the resistance to deformation (i.e., rigidity) as well as the time dependence of the deformation (i.e., hysteresivity). We assessed if cells became more liquid-like or solid-like based on culture conditions. All cell types were found to be viscoelastic, with hysteresivity η ranging between 0.44 and 2.07 in 2D and 0.16 and 2.48 in 3D (Fig. 2 C and D). We determined that both the nonmalignant and malignant cells are more viscous (liquid-like) when cultured in 2D than in 3D, as the crossover frequency, ω_crossover, is lower. The nonmalignant cells are also significantly less viscous in 3D lrECM than in 3D HA. Overall, malignant cell hysteresivity is much less responsive to changes in the microenvironment than normal counterparts.

Malignant Cells in 3D Culture Show a Mismatch between Intracellular and ECM Mechanical Properties.

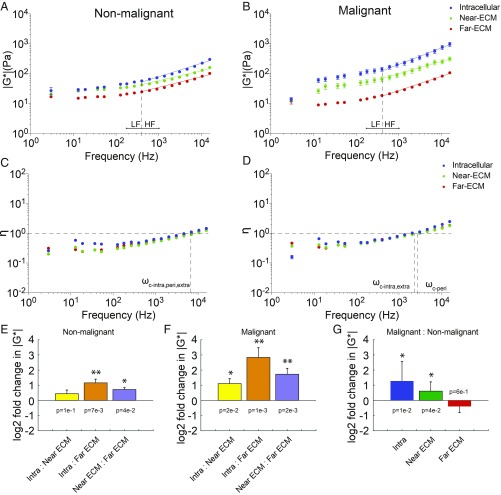
Having established that the internal mechanical properties of normal and cancer cells respond differently to different environments, we utilized optical trap-based active microrheology to address cell–ECM mechanical adaptation in the context of malignancy. In conjunction with the intracellular measurements, we directly interrogated the ECM mechanical properties both near to (<10 µm) and far from (>50 µm) embedded cells. As expected, the lrECM behaves like a flexible polymer (exponents b ∼ 0.5). The distant ECM for nonmalignant vs. malignant cells is also indistinguishable. We determined that the intracellular complex modulus |G*| of nonmalignant MCF10A cells matched the local ECM stiffness, but the cells were significantly stiffer than the more distant ECM (P = 0.007). This is due at least in part to remodeling of the local ECM, which is significantly stiffer than distant ECM (Fig. 3 A and E). The intracellular and extracellular hysteresivity are the same (Fig. 3C). In contrast, there was a significant mismatch between the malignant cells and both local ECM and distant ECM (Fig. 3 B and F). This mismatch persists despite drastic remodeling of the local ECM, whereby the local ECM around malignant cells is significantly stiffer than distant ECM. Indeed, it is also stiffer than the local ECM around the nonmalignant cells. Rather, the mismatch is explained by the fact that malignant cells are over 2-fold stiffer than nonmalignant cells in 3D lrECM (Fig. 3G). Interestingly, the hysteresivity is greater for malignant cells and surrounding ECM than nonmalignant cells, and malignant cells become more viscous than the ECM at the highest frequencies (Fig. 3 C and D).

Fig. 3.

Matching and mismatching of intracellular and extracellular matrix (near and far 3D lrECM) mechanical properties. (A and B) Intracellular |G*| (mean ± SE) vs. frequency of nonmalignant MCF10A cells (A) and malignant MCF10-CA1 cells embedded in 3D lrECM (blue circles), of the surrounding matrix <10 µm away from the cell (green circles), and of the matrix >50 µm away from any cell (red circles). Intracellular data are a repeat of Fig. 2 for clarity. Blue, green, and red lines of best fit to the power law model |G*(ω)| = Aω^b for intracellular, near-ECM, and far-ECM, respectively, are fitted to the mean values at high frequencies (past the vertical dashed line at 400 Hz). Low-frequency (LF) and high-frequency (HF) regimes are indicated. (C and D) Intracellular η (mean ± SE) vs. frequency of nonmalignant MCF10A cells (C) and malignant MCF10-CA1 cells (D) embedded in 3D lrECM (blue circles), of the surrounding matrix <10 µm away from the cell (green circles), and of the matrix >50 µm away from any cell (red circles). Intersections with the horizontal dashed line at η = 1 of the vertical lines occur at crossover frequencies ω_c. (E and F) Log2 ratios of intracellular vs. extracellular |G*(ω)| in 3D lrECM for nonmalignant MCF10A cells (E) and malignant MCF10-CA1 cells (F) (mean ± SD, averaged across frequency). (G) Log2 ratios of intracellular and extracellular |G*(ω)| for malignant MCF10-CA1 cells vs. nonmalignant MCF10A cells. Power law coefficients (A) and exponents (B) and 95% confidence intervals are as follows: Nonmalignant cells in 3D lrECM: A = 2.36 (0.91,3.81), b = 0.49 (0.42, 0.56); nonmalignant cells’ near-ECM: A = 3.32 (2.11, 4.52), b = 0.40 (0.35, 0.44); nonmalignant cells’ far-ECM: A = 1.58 (0.98, 2.18), b = 0.43 (0.38, 0.47); malignant cells in 3D lrECM: A = 2.39 (1.21, 3.56), b = 0.62 (0.57, 0.68); malignant cells’ near-ECM: A = 4.38 (2.64, 6.11), b = 0.44 (0.40, 0.49); malignant cells’ far-ECM: A = 0.64 (0.41, 0.86), b = 0.52 (0.49, 0.57). P values from 2-way ANOVA are shown above or below each bar in E–G (*P < 0.05 and **P < 0.01).

The increased stiffness of malignant vs. nonmalignant cells in 3D lrECM may be due to altered actomyosin machinery that regulates cytoskeletal architecture and generates the contractile forces cells exert to remodel the microenvironment (2, 7, 8). ECM remodeling occurs on the time scale of hours. To probe the dynamics of intracellular and extracellular mechanical remodeling, we conducted measurements after 24 h. Compared with initial measurements (within 4 h of embedding), malignant cell stiffness significantly decreases while nonmalignant cell stiffness increases slightly (SI Appendix, Fig. S3). Moreover, the local ECM stiffness drops to match the distant ECM by this time for both cell lines. Therefore, malignant and nonmalignant cells mechanically adapt to the microenvironment dynamically, so the choice of measurement time is critical.

ECM Chemistry and Cytoskeletal Perturbation Modulate Intracellular Mechanical Adaptation and ECM Remodeling.

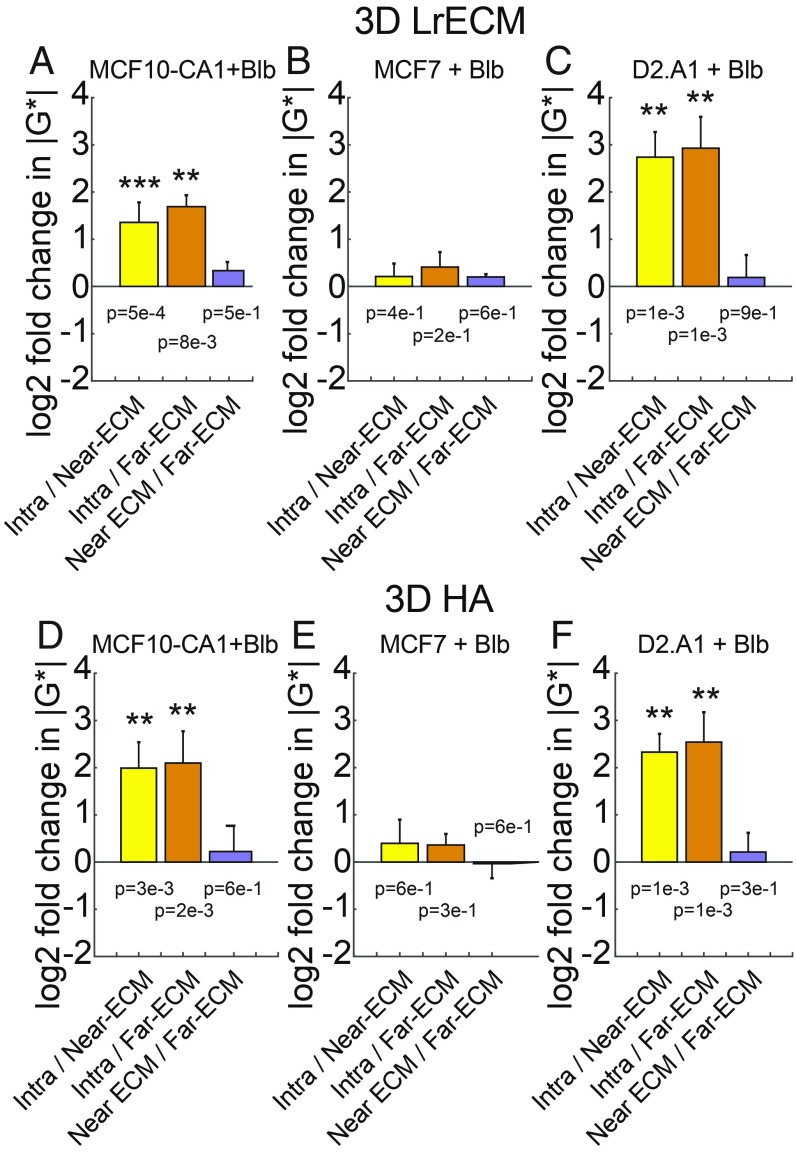
To better understand the role of actomyosin cytoskeletal contractility in driving these dynamic changes, we next examined how intracellular and ECM mechanical properties changed in response to treatment with inhibitors of Myosin II (blebbistatin), ROCK (Y-27632), and protein phosphatases (calyculin A). We first conducted live imaging to confirm that these modulations of the actin cytoskeletal architecture did not affect the distribution of beads inside the cell compared with vehicle controls (Movies S2 and S3). Fig. 4 compares intracellular vs. extracellular and drug vs. control for MCF10-CA1, MCF7, and D2.A1 cells treated with 10 µM blebbistatin embedded in lrECM and HA. For both lrECM and HA, the ECM stiffness near blebbistatin-treated cells differed insignificantly from distant ECM, indicating a loss of ECM remodeling ability. The more benign MCF7 cell stiffness drops compared with control, matching the ECM stiffness. The more aggressive MCF10A-CA1 and D2.A1 cells both remain significantly stiffer than the surrounding ECM despite blebbistatin treatment. Compared with controls, MCF10-CA1 cell stiffness drops in lrECM but not HA, while D2.A1 cell stiffness increases in lrECM and HA (Fig. 4 A–F and SI Appendix, Fig. S4). Taken together, these comparisons show that cell and ECM mechanics are affected by complex interactions between drug type, cell type, ECM type, and the time of measurement after embedding.

Fig. 4.

Effects of actomyosin contractility inhibitor blebbistatin on intracellular and extracellular mechanics. (A–C) Log2 ratios of intracellular vs. extracellular |G*(ω)| for MCF10-CA1 cells (A), MCF7 cells (B), and D2.A1 cells (C) embedded in 3D lrECM treated with blebbistatin. (D–F) Log2 ratios of intracellular vs. extracellular |G*(ω)| for MCF10-CA1 cells (D), MCF7 cells (E), and D2.A1 cells (F) embedded in 3D HA treated with blebbistatin. (J–L) Log2 ratios of blebbistatin-treated vs. untreated control |G*(ω)| for MCF10-CA1 cells (J), MCF7 cells (K), and D2.A1 cells (L) embedded in 3D HA. P values from 2-way ANOVA are shown above or below each bar in A–F (**P < 0.01 and ***P < 0.001).

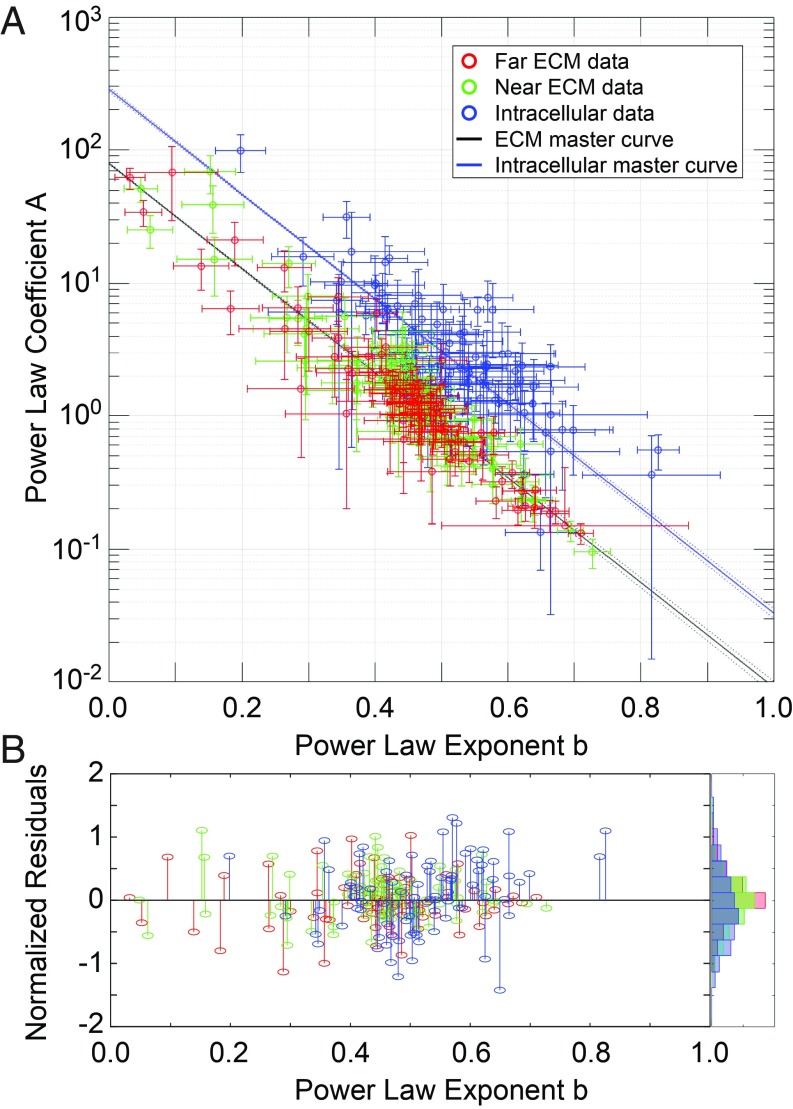
Complex Modulus Power Laws Collapse onto Parallel Master Curves.

In total, we measured the intracellular and extracellular (near-ECM and far-ECM) viscoelasticity of 5 cell lines in 2 ECMs subjected to 4 drug treatments at 2 time points, generating a very large full-factorial dataset comprising 240 distinct conditions. We found at high frequencies >400 Hz, all of the data follow power laws, |G*(ω)|_i = A_iω^bi for each condition i, with exponents b ranging from ∼0.2 to 0.8 (SI Appendix, Figs. S5 and S6). Such power law behavior is said to be scale-free (scale-invariant). We next inspected the power law behavior by plotting the coefficients A against the exponents b for the entire dataset. Remarkably, when all data are plotted together (Fig. 5A), the intracellular |G*| data points cluster along a line defined by a simple empirical master relation, A_i = exp((α − b_i)/β), which is fully described by 2 hyperparameters, α and β. Furthermore, the extracellular data (both near-ECM and far-ECM data combined) also cluster along a line defined by the same relation. The 2 master curves appear parallel because they share a common value for β, i.e., β*. Differing values of α account for the vertical shift that corresponds to the observed mechanical mismatch, with intracellular |G*| generally stiffer than extracellular |G*| across all conditions (α_cell > α_ECM). Normalized residuals to the fits are shown in Fig. 5B.

Fig. 5.

Power law fit parameters fall on master curves. Five cell lines (MCF10A, MCF10-CA1, MCF7, D2.A1, and D2.0R) were measured in 2 ECMs (3D lrECM and 3D HA), at 2 time points (0 to 4 h and 24 to 28 h after embedding), under 4 drug treatment conditions (untreated, +10 µM blebbistatin, +10 µM Y27632, +10 nM calyculin A). For each experiment, at least 3 individually prepared samples were measured. For each sample, at least 3 cells were measured. For each cell, at least 3 intracellular beads, 3 beads in near-ECM (within 10 µm from the cell) and 3 beads in far-ECM (at least 50 µm from the nearest cell) were measured. For each bead, 7 technical replicates were measured at 20 frequencies each. |G*| values were calculated from each replicate, and all replicates were pooled for each condition to calculate mean |G*| values at each frequency. For each condition, the mean G* values at high frequencies (>400 Hz) were fit to a power law |G*(ω)| = Aω^b. (A) Plot of all of the fit parameters from each condition, with all intracellular data plotted in blue, all near-ECM data plotted in green, and all far-ECM data plotted in red. Error bars represent the 95% confidence intervals of the fit. All intracellular data were then fit to a master relation A_i = exp((α − b_i)/β), where the A_i and the b_i are the power law coefficient (A) and exponent (B) of the ith experimental condition (such as, e.g., near-ECM of D2.A1 cells in 3D HA at 24 to 28 h treated with 10 µM Y27632), and α and β are global parameters of the master relation. The data were split into 2 groups to fit the master relations. The intracellular data were fit separately, giving α_intra and β_intra (solid blue line). Separate fits of near- and far-ECM data showed very similar values for α and β, so they were combined and fit together to give α_extra and β_extra (solid black line). Dashed lines show prediction bounds at 95% confidence. (B) Normalized residuals (1 − b_fit/b) of each data point to its respective fit line, with a normalized histogram plotted at the right.

We also found that for all cells and ECM conditions, the hysteresivity η follows a power law η(ω) = A₂ω^b2 in the same high-frequency regime (400 to 15,000 oscillations/s), with exponents ranging ∼0.2 to 0.8 that vary with cell type, gel type, and drug treatment (SI Appendix, Figs. S7 and S8). Furthermore, the power law fit parameters for the η data also follow their own master relation of the same form, which is parallel to the other 2 (β = β*) (SI Appendix, Fig. S9). Taken together, these G* and η power laws present a mathematical model that differs from the structural damping model of the soft glassy rheology (SGR) theoretical framework (12, 13). Residual analysis shows that the power laws fit our data better than the structural damping model (SI Appendix).

To investigate what may physically govern the values of α and β, we conducted additional measurements on reference samples (unoccupied by cells) of lrECM and HA and more heavily chemically cross-linked HA. These samples were probed over a range of stress amplitudes by varying the optical trapping beam power, and over a range of strain amplitudes by varying the displacement amplitude of the optical trap during oscillations. The data from each material measured at all stress and strain amplitudes still cluster along the same master curves (SI Appendix, Fig. S10). Thus, α and β are not governed merely by the experimental conditions of the measuring apparatus, but by the intrinsic biomaterial properties.

Discussion

Reciprocal mechanical cross-talk between cells and the surrounding ECM milieu plays essential roles in both homeostatic maintenance of normal tissue and malignant transformation of the tumor microenvironment (5, 11, 21–23). The mechanical properties of cells and ECM, and mechanical interactions between them, are also critical for motile cells encountering new environments, e.g., immune cells surveilling inflammation sites or tumor cells colonizing metastatic sites. However, the mechanics of cells in 3D ECM remain poorly understood at the microscale. Here, we probed embedded cells and the surrounding ECM with near simultaneity to determine whether and how single cells modulate intracellular mechanical properties to match those of 3D ECM microenvironments. For a suite of malignant cell lines, but not normal counterpart cells, we found a mismatch between intracellular and local ECM mechanical properties, in the presence and absence of actomyosin perturbations. In addition, the mechanical properties of normal and cancer cells, as well as the ECM, consistently show power law frequency dependence on the time scales of single filament dynamics. Although it was not apparent a priori, we also showed that these power laws follow a master relation that persists for different cell types, ECMs, and pharmacological inhibitions.

Recently, there has been an increased focus on using mechanical properties as a potential therapeutic target (24, 25). Can knowledge of cell and tissue mechanics be exploited as a prognostic or diagnostic metric with added value to standard testing? Importantly, interpreting how mechanical phenotype relates to malignancy depends on the length scale at which the measurement is performed. For example, increased ECM deposition and polymer cross-linking concomitant with malignant transformation manifest increased bulk tissue stiffness as observed in macroscale measurements (21, 26–29). In contrast, in vitro and ex vivo studies indicate individual cancer cells (microscale) are softer than their normal counterparts, a trait that is thought to be required for dissemination from the primary organ (30, 31). Our work shows that microscale mechanics of both normal and cancer cells are heavily context dependent. They dynamically adjust themselves and their surroundings over time, involving complex interactions between ECM chemistry and actomyosin contractility. Our work highlights the plasticity of mechanical adaptation of cancer cells to diverse 3D ECM hydrogels and demonstrates that a comprehensive understanding of cell mechanics in specific tissue microenvironments will prove essential for new clinical strategies to successfully leverage cancer mechanobiology. The 3D lrECM culture allows us to interrogate one aspect of the in vivo microenvironment. However, direct correlation to matching in vivo mechanical properties of the tissue will need to be performed as some of the physiologically relevant cues are not present in our in vitro models.

The notion of mechanical homeostasis suggests that cells establish rheological properties in a dynamic equilibrium with the environment (3, 8, 24). One idea is that cells may adopt a mechanical phenotype that “matches” the external tissue mechanics. But the conditions under which cells either succeed or fail to “stiffness-match” the ECM have not yet been studied in vivo or in physiologic microenvironments (24, 32, 33). Here, we showed that normal MCF10A cells stiffness-match by slightly stiffening the local ECM, while MCF10-CA1 tumor cells drastically stiffen the local ECM but are themselves much stiffer than normal counterparts and thus fail to stiffness-match. This would suggest tumor cells need not match the physical properties of the 3D ECM microenvironment, but measurements at 24 h highlight the fact that adaptation occurs over time, and the situation is not so simple. Here, we looked at the earliest stages of adaptation in this system well before proliferation and extensive remodeling. However, it remains to be seen how cells mechanically adapt within multicellular structures during acinar or tumor formation in 3D under physiological conditions that mimic contributions from stromal cells in vivo.

Normal and malignant cells cultured on 2D substrates obey different scaling laws in the kilohertz regime dominated by the dynamics of single cytoskeletal filaments (34). We build on this finding and determine that in response to different culture conditions, both normal and cancer cells may adopt glassy, flexible, or semiflexible dynamics as per high-frequency scaling laws with exponents ranging from 0.2 to 0.8 (12–14). Earlier pioneering work on soft glassy rheology applied concepts of universality to the behavior of various normal cells cultured in 2D despite different pharmacological treatments, in terms of a single parameter. While our data do not span the full 5 decades required to establish universality, our large dataset enabled us to recognize the emergence of a robust master relationship between the power law coefficients A and exponents b that links all of the dynamical scaling laws. This simple empirical framework reduces the data dimensionality of the coupled mechanical responses of cells and ECM—despite the complexity, heterogeneity, and details—down to just one parameter (α) and one constant (β*). We believe this could potentially shed light on critical phenomena in living cells and other biomaterials. Linking these mathematical parameters to biophysical factors will move us closer to exploiting mechanics as a cancer biomarker.

Methods

Cell Preparation.

To visualize actin dynamics of cells embedded in 3D matrices, MCF7 cells were plated in 24-well plates, with 50,000 cells/well in 1 mL/well of growth medium (DMEM, 10% FBS, 1% P/S, 1% l-glut). The following day, seeding media was removed, and cells were incubated with 0.5 mL/well of growth media containing an ibidi TagGFP2 rAV-CMV-LifeAct adenoviral vector (ibidi, Martinsried, Germany, catalog no. 60121) at a multiplicity of infection (MOI) of 30. After a 4-h incubation, medium containing virus was removed and replaced with fresh growth medium. After an additional 48 h, cells were seeded in matrices. Briefly, cells were detached with 10 mM EDTA in PBS containing 1 μg/mL Hoechst 33342 (Thermo Fisher Scientific, Waltham, MA, catalog no. H3570) at 37 °C, resuspended in growth medium, spun down at 1,000 rpm for 5 min, and resuspended at 1.5 × 10⁶ cells/mL in growth medium. Cells were mixed with red fluorescent 1-μm diameter polystyrene beads at a ratio of 50 μL stock beads per 500 μL cell suspension. Cells were incubated with beads for 1 h at 37 °C. The cell/bead mixture was then mixed with laminin-rich ECM Matrigel or hyaluronic acid at a ratio of 66 μL of cell/bead mixture per 300 μL Matrigel. Per well, 300 μL of the cell/bead/matrix mixture was plated in glass-bottom dishes (WillCo, Amsterdam, The Netherlands, catalog no. GWST-5040) and incubated at 37 °C for 1 h. After matrix gelation, 3 mL/well of media (with or without pharmacological agents) was added, and cells were imaged during the 0- to 4-h or 24- to 28-h measurement windows.

Pharmacological Inhibition.

Drug solutions were prepared as follows: (±)-blebbistatin (CAS 674289–55-5, Calbiochem), calyculin A (CAS 101932–71-2, Calbiochem), and Y27632 dihydrochloride (CAS 129830–38-2, Mitsubishi Pharma Company) were suspended in DMSO (CAS 67–68-5, Sigma) and stock solutions were prepared according to manufacturer specifications. Stock solutions or DMSO alone were diluted in growth medium to concentrations of 10 µM blebbistatin, 10 nM calyculin A, 10 µM Y27632, or 1:1,000 wt/vol DMSO, respectively.

Data Processing.

Experiments were controlled using custom LabVIEW programs. Data were analyzed and plotted using custom MATLAB and Prism programs. Vector graphic layouts were assembled for the figures using Adobe Illustrator. For experimental details on how optical trap data are collected and processed, see SI Appendix.

Data Analysis and Statistics.

Samples for each condition were measured in triplicate. For each measured sample, at least 30 cells were measured. In total, a range of 80 to 460 beads per condition were measured. Data were analyzed using custom MATLAB programs. All P values noted parenthetically in the text are from 2-way ANOVA (grouped against frequency) with Tukey’s honestly significant difference post hoc test. For the log2 fold-change plots, the mean/mean ratios were taken at each frequency, converted to log2, and then averaged (mean ± SD). For details and statistics on power law and master curve fitting, see SI Appendix.

Full methods are available in SI Appendix.