Bilingual phonological awareness: Construct validation of Grade 1 Spanish-speaking English learners

Abstract

This study investigated the dimensionality of bilingual phonological awareness (PA) in English and Spanish by replicating Branum-Martin et al.’s (2006) kindergarten model in Grade 1, and presents alternatives to modeling clustered data. English and Spanish tasks were administered to 1,586 first grade Spanish-speaking English learners. Four distinct approaches to confirmatory factor analysis (CFA) models were examined: (a) uncentered student-level data, (b) student-level data centered at the classroom means, (c) classroom-level data, and (d) multilevel CFA. Results indicated that while the multilevel CFA provided the most comprehensive view of the data, the multi-level student-level estimates were not appreciably different from estimates based on student-level data centered at the classroom means, and multi-level classroom-level estimates were comparable to estimates based on the analysis of classroom means. Importantly, English and Spanish PA were statistically separable at the student-level, but minimally distinct (r = .86) and slightly less correlated than what has been reported for kindergarten (r=.93). At the classroom level, the correlation was moderate (r=.51), and substantially reduced compared to kindergarten (r=.83). The distinction at the classroom-level between kindergarten and Grade 1 imply that instruction differentiates the abilities across languages at the classroom-level, but less so at the student-level.

Phonological awareness

Phonological awareness (PA), defined as the ability to identify and manipulate linguistic sounds apart from their meanings, is a fundamental skill in learning to read not only alphabetic languages with varying degrees of phoneme-to-grapheme correspondence such as English and Spanish (National Reading Panel, 2000), but also non-alphabetic languages with no immediate correspondence between phoneme and symbol, such as Chinese (cf. Chan & Siegel, 2001; Ho & Bryant, 1997; Hu & Catts, 1998). The role of PA in literacy acquisition and reading development has been studied extensively since the early 1980s, generally focusing on the relation between PA at the phoneme level (Gough & Hillinger, 1980), or at the level of speech units, such as onsets and rimes (Goswami, 1993), and reading measured as decoding (Wagner et al., 1997). This work has provided evidence of a relation between PA and reading ability, demonstrating that the more phonologically aware children are, the better they tend to be at reading (Adams, 1990; Wagner et al., 1997).

PA appears to have a similar relation with reading within many languages that vary both in terms of genetic distance as well as the transparency of their writing systems such as Spanish (Signorini, 1997), Greek (Rothou, Padeliadu, & Sideridis, 2013), Korean, and Chinese (Branum-Martin, Tao, & Garnaat, 2015). Nonetheless, research on how PA affects literacy across languages indicates that the typologies of the languages being acquired (such as the granularity of the writing system and grapheme-phoneme matching consistency) affect how children construct meaning from print (cf. Ziegler & Goswami, 2005; 2006). Taken together, these findings indicate that while PA is an important skill for learning how to read irrespective of the language and the writing system involved, the path to acquiring literacy skills is – to some extent – driven by factors specific to the language, including the peculiarities of the writing system and oral language input. These issues present critical challenges for children learning more than one language, especially if they are learning to read and write in both languages.

Research on bilingualism – including learning how to read and write in multiple languages – has received increased attention in the US in recent years (e.g., August & Hakuta, 1996; August & Shanahan, 2006; Branum-Martin, Tao, Garnaat, Bunta, & Francis, 2012; Branum-Martin, Tao, Garnaat, 2015), fueled, at least in part, by growing awareness of the economic and social advantages of multi-lingualism, which is reflected in the large number of states presently offering the Seal of Biliteracy to high school students who graduate with proficiency in two or more languages (in May of 2017, 26 states offer the seal and 13 more states are in early or later stages of adopting it). A longstanding question in the bilingual literature is that of transfer of skill across languages. Expectations about cross-language transfer have been one of the foundational elements behind arguments in favor of bilingual education for ELs in the early grades (Francis, Lesaux, & August, 2006; Genessee, et al., 2006). The questions of cross-language transfer and bilingual development have also led to research examining cross-language correlations among measures of achievement and ability.

Studies investigating children learning two languages show that PA skills in the first and second language correlate highly with each other, appear to transfer cross-linguistically, and predict word reading development in both languages (Cummins, 2004; Geva & Wang, 2001; Riccio et al., 2001). For example, PA in Spanish has been found to relate to English word reading (Lindsey, Manis, & Bailey, 2003), English reading achievement (Goldenberg et al., 2014), and English reading fluency (Riccio et al., 2001). However, Branum-Martin et al. (2012) found that the role of PA differed across various languages by features of those languages and also by features of the speakers. Using a meta-analysis of 101 correlations from 38 published studies, these authors found that the PA tasks in English were correlated with similar tasks in Spanish, other alphabetic languages, and even non-alphabetic languages (such as Chinese), but the correlations differed based on the non-English language. Among the factors influencing the correlations was linguistic grain size, a theory which stipulates that the acquisition of fluent word reading skills is governed by the size of orthographic units at which consistent sound representations can be expected by the learner, the writing system of the language, and the consistency with which the spoken language and writing system match (Ziegler & Goswami, 2005; 2006). In addition to the differences in the written orthographies, salient features of the oral langue (such as syllable structures or phoneme inventories) will to some extent affect the degree of PA development across languages even prior to literacy instruction. The degree of awareness is related to sensitivity to different grain size of the phonology. For example, in languages that have different syllable structures such as Czech and English, speakers were found to vary in the grain size of their phonological sensitivity. Czech has a higher variety of complex syllabic onsets compared to English, and therefore Czech-speaking children tend to have a better performance on complex consonant cluster tasks than English-speaking children. English-speaking children, however, have a higher awareness of simple onsets in oral tasks (Caravolas & Bruck, 1993). Thus, it appears amount that having robust PA is generally beneficial for acquiring literacy skills in a variety of languages. Importantly, problems in PA will impede the acquisition of literacy skills in all alphabetic languages, but how these problems in PA manifest themselves in early literacy skills varies across languages, depending on variables such as linguistic grain size, or orthographic transparency.

Dimensionality of Phonological Awareness

Various tasks have been used to measure the construct of PA. These tasks range from measuring an individuals’ ability to recognize and manipulate phonemes within words (e.g., blending phonemes into words, segmenting words into phonemes, and deleting individual phonemes) to identifying and manipulating larger linguistic units of words (e.g., syllables, onsets, and rimes). In the midst of this diversity of tasks, there have been studies that have explicitly investigated the dimensionality of PA (Anthony et al., 2002; Høien et al., 1995; Muter, Hulme, Snowling, & Taylor, 1997; Schatschneider et al., 1999; Wagner et al., 1993), and some studies that have investigated the dimensionality of PA across languages (Branum-Martin et al., 2006; Branum-Martin et al., 2012; 2015). To date, only Branum-Martin et al. (2006) have investigated this question in multiple languages simultaneously while also taking into account the impact of clustering of students into classrooms on the assessment of dimensionality.

The dimensionality of PA was first considered from the perspective of the diverse methods used to assess it. Yopp (1988) claimed that the construct of PA consists of two highly related factors that are different based on the number of cognitive operations that they require, namely, rhyming and segmentation ability. Similarly, Muter, Hulme, Snowling, and Taylor (1997) conducted a longitudinal study and found phoneme segmentation and rhyming to be two distinct factors, which remained stable over time. Høien et al. (1995) found three basic factors to characterize PA, namely, a phoneme, a syllable, and a rhyming factor, which were also significant predictors of early word decoding ability. In early research (Wagner et al., 1993) that led to development of the Comprehensive Test of Phonological Processes (CTOPP) (Wagner, Torgesen, & Rashotte, 1999), PA tasks were characterized in terms of Analysis and Synthesis, reflecting whether the task required the individual to break down words into their constituent sounds (Analysis), or integrate distinct sounds into linguistic wholes (Synthesis). Schatschneider et al. (1999), showed that this distinction could be made on the basis of the face validity of the tasks used to measure PA, but that the two types of tasks did not identify two distinct phonological constructs. Rather, the different task types were, if you will, two sides of the same coin, or two approaches to tapping the same ability. Anthony et al. (2002) reached a similar conclusion by modeling the performance on eight PA tasks in younger (2- and 3-year-olds) and older preschool children (4- and 5-year-olds). Such contradictory findings (i.e., unidimensionality vs. multidimensionality of PA) may be the result of linguistic complexity or failure to account for task difficulty of the various PA tasks in some of the factor analytic research. While all of these earlier studies were restricted to native speakers of either English or Norwegian, the more recent studies (Anthony et al., 2002; Schatschneider et al., 1999) among them are distinguished from the earlier studies of dimensionality by their use of confirmatory factor analysis (CFA) rather than exploratory factor analysis (EFA), and the use of explicit hypothesis tests related to dimensionality, while also taking into account the confounding influence of shared method variance across tasks using the same method.

The unidimensionality of PA among monolinguals raises the possibility that PA represents a unitary construct regardless of the language in which PA is assessed. That is to say, PA is a general language ability that undergirds the acquisition of literacy in any alphabetic language, and that the choice of language in which to assess PA is more a matter of convenience than necessity. In other words, the ability that allows an individual to identify and manipulate sounds in the speech stream of the language that they speak is the same ability that would allow them to identify and manipulate the sounds in the speech stream of any language to which they are exposed. Extending the question of dimensionality beyond the methods used in a single language to assess unidimensionality across languages has important implications for theories of language development and the identification of children at risk for reading disabilities when children speak a language other than the language of the society.

Branum-Martin et al. (2006) were the first to examine the question of dimensionality across languages. They used the CTOPP in English and a measure of PA in Spanish that was similar in design to the CTOPP in English in order to examine the dimensionality of PA in English and Spanish among Spanish-speaking language minority kindergarten students in the US. The other unique element of the Branum-Martin et al. (2006) study was their use of multi-level confirmatory factor analysis to remove the effects of clustering on the student level covariances in order to model the covariance among PA and reading measures at both the student- and classroom-levels simultaneously. They concluded that the data were consistent with the idea of a single construct that reaches across languages and reflects the ability of individuals to identify and manipulate sounds in the speech stream regardless of the language in which stimuli are presented. Although their test of unidimensionality was rejected, the two PA factors correlated .93 at the student level and .83 at the classroom level, suggesting that the two are, at best, minimally distinct.

Regardless of the dimesionality of PA within and across languages, acquisition of literacy is multi-determined. Many factors contribute to children’s ability to read and write in their first and second languages, some of which are related to the child, while others are related to the environment, such as the classroom, which includes the teacher, the language(s) of instruction, the methods of instruction, the other students in the classroom, and so on. The high degree of relatedness between the PA constructs in English and Spanish at the classroom level in Branum-Martin et al. (2006) indicates that classrooms that tended to be high functioning in English PA also tended to be high functioning in Spanish PA. At the classroom level, correlations between PA and decoding were also strong within- and across-languages. These correlations inform us about how the students are organized for instruction at the classroom level in these transitional bilingual education classrooms.

Student versus Classroom Effects

Although learning by a particular child may be conceptualized as an individual phenomenon, it typically occurs within a classroom context delivered by a teacher with the children’s peers also present and interacting with her. Classroom effects (mean differences across classrooms) may include influences from the teachers’ instruction, the classroom language environment (i.e., type of language program), curriculum, the demographics of the school, and the processes that govern the selection of students into specific teachers’ classrooms. More specifically, when it comes to Spanish-speaking ELs the type of bilingual instructional program (i.e., English immersion, transitional, maintenance, and dual language) and the factors that determine students’ placement into these programs (e.g., the student’s level of proficiency in English as compared to Spanish) are major sources of classroom differences. Regardless of the type of instructional program, classrooms will differ systematically from one another in the amount of instruction students receive in a particular language. For example, when instruction is predominantly in Spanish, Spanish-speaking ELs students might be expected to have higher mean performances on Spanish tasks and possibly lower mean performance on English tasks. However, if Spanish-speaking ELs receive instruction in both English and Spanish, one might expect lower English and Spanish mean performance in these classrooms relative to classrooms focusing exclusively on English or exclusively on Spanish, but more consistent performance across Spanish and English on average in comparison to those same classrooms (Branum-Martin et al., 2009).

In the current study, we extend the study of Branum-Martin et al. (2006) and examine the dimensionality of PA among Spanish-speaking ELs in transitional bilingual programs in grade 1. In this context, students’ performance is a function of both student ability, the classroom, and instructional context. One way to account for classroom effects on student performance is through application of multilevel models (i.e., simultaneously modeling classrooms and students as different levels of the design as in Branum-Martin et al., 2006). While multilevel models have been widely used in educational contexts (Baker, 1990), few studies have used this approach when examining the dimensionality of constructs such as PA (Branum-Martin et al., 2006).

The purpose of this study was to investigate the dimensionality of PA in English and Spanish among Spanish-speaking ELs in grade 1 while also considering the impact of the clustering of students into classrooms on inferences about dimensionality. Because clustering is often ignored in psychometric research, we considered the impact of clustering on inferences about dimensionality by using four different approaches to estimating the CFA models that were based on the findings of Branum-Martin et al. (2006). Specifically, we compared four distinct approaches to addressing the issue of clustering. Approaches 1–3 treated the data as single-level (see Figure 1A) with Approach 1 ignoring clustering, Approach 2 controlling clustering through classroom level centering of student-level data, and Approach 3 analyzing data at the classroom level only. Approach 4 used a multi-level model (see Figure 1B) similar to Branum-Martin et al. (2006). We considered these different approaches in an effort to understand the contributions that clustering may have played in previous examinations of the dimensionality of PA, most of which have used Approach 1, but also to assess the utility of controlling clustering in psychometric research through group-level centering.

Figure 1.

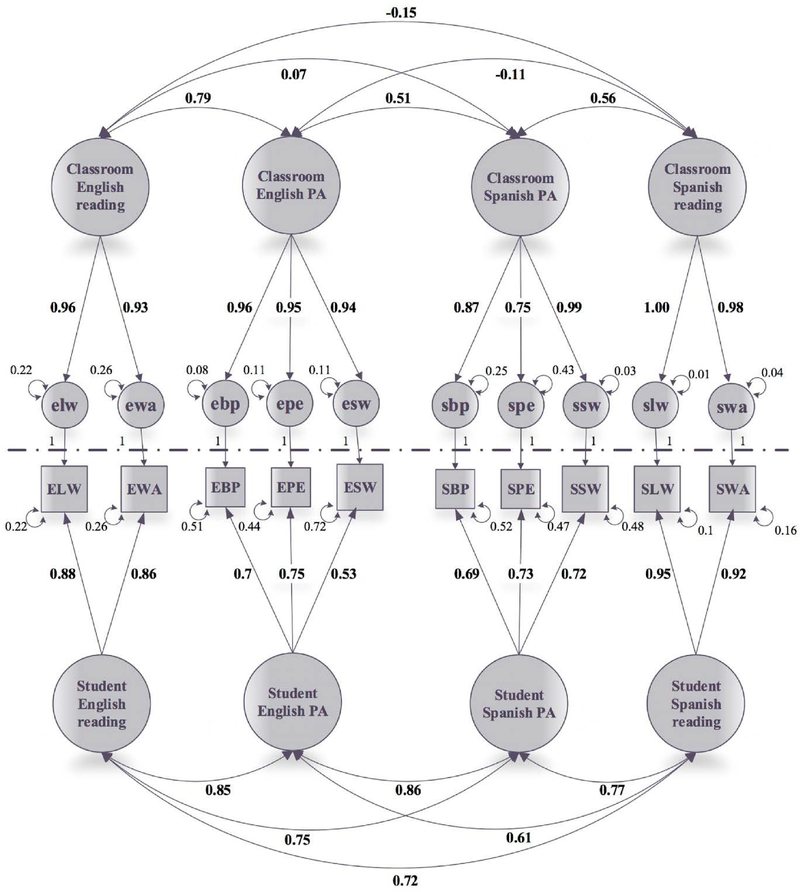
Path diagrams for single level-CFA with language specific PA factors (panel A) and multilevel-CFA with language specific PA factors at both the student- and the classroom-level (panel B). Both models allowed for shared method variance, but the method correlations are not shown. EBP= English blending phonemes; EPE= English phoneme elision; ESW= English segmenting words; SBP= Spanish blending phonemes SPE= Spanish phoneme elision; SSW= Spanish segmenting words; ELW= English letter-word identification; EWA= English word attack; SLW= Spanish letter-word identification; and SWA= Spanish word attack.

With each approach we began by estimating the final model presented by Branum-Martin et al. (2006), which specified that PA tasks have a unitary underlying construct in each language, but represent distinct, but correlated constructs across languages. We relied on model parameter estimates to determine if the more restrictive models should be fit. For example, the one-factor structure (i.e., English and Spanish PA define a single factor) used in Branum-Martin et al. (2006) can be viewed as nested within their final model. Conceptually, the one factor model is obtained from the final model by constraining the correlation between the factors to 1.0 and constraining all correlations with other factors to be equal between the English and Spanish PA factors. Thus, a confidence interval around the correlation between Spanish and English PA that excludes 1.0 would indicate that the less complex, one-factor model would fit more poorly than the final model (see Francis, Fletcher, & Rourke, 1988 for a more detailed discussion).

It is instructive to consider how these approaches relate to the multi-level approach used in Approach 4. In essence, Approach 1 combines the student-level and classroom-level components of Approach 4 and analyzes covariances that are a mixture of covariances among classroom means (Approach 3) and covariances among students’ within-classrooms (Approach 2). In contrast, Approach 2 attempts to estimate the student-level model of Approach 4 while ignoring the between-class component of Approach 4, whereas Approach 3 attempts to estimate the between-class model of Approach 4, while ignoring the student-level (i.e., the within-class) component. Approach 4 is the most statistically defensible, but can be challenging to estimate in many measurement contexts, specifically because Approach 4 requires a large sample of classrooms to estimate the between-class component of the model. Moreover, the between-class component of the model can be difficult to estimate if the model is complex, even if the number of classrooms is reasonably large (e.g., 125–150). In these cases, it is important to have alternatives to the full multi-level approach (i.e., Approach 4) that are not biased by the combining of student-level (i.e., within-class) and classroom-level (i.e., between-class) covariances that occurs under Approach 1. Although each of these approaches (2 and 3) ignores one dimension of the data, it is possible that they allow us to obtain a reasonable approximation to the model from the respective level of Approach 4, without explicitly modeling the covariation at the other level. If so, these approaches could have implications for dealing with data that have more complex clustering, such as three and four level data.

We expected that PA tasks would represent a unitary construct in English and Spanish in grade 1 at the student level. We further expected that Approach 1 would differ substantially from the student level model of Approach 4, whereas Approach 2 would be consistent with the student level estimates of Approach 4, and Approach 3 would be consistent with the classroom level estimates of Approach 4. We further expected that parameter estimates and dimensionality from Approaches 2 and 3 would be consistent with Approach 4, but standard errors would be biased downward (i.e., standard errors were expected to be too small).

Method

Participants

The participants included 1,586 ELs from 130 grade 1 classrooms, studying in transitional bilingual education programs located in urban California, urban Texas, and nonurban Texas. In transitional bilingual programs, literacy and academic content is taught through the child’s first language, along with instruction in English oral language development. These programs prepare students to transfer to English-only programs either early in elementary school (grade 3 or before), or later (typically in grade 4) to ensure the mastery of their first language before transitioning to English-only programs (Slavin, Madden, Calderón, Chamberlain, & Hennessy, 2011). In the present study, none of the grade 1 students had been transitioned into English only instruction, but classrooms varied in the extent of English and Spanish literacy instruction.

This study utilized existing data from three separate studies within a larger program of research. Study 1, was a cross-sectional study in which ELs from kindergarten to grade 3 were selected to participate at a single time point during the 2001–02 or 2002–03 school years. Study 2 was a longitudinal study in which ELs were recruited in kindergarten and followed through the end of grade 2. Students in Study 2 were in grade 1 in the 2003–2004 academic year. Finally, Study 3 was also a longitudinal study in which ELs were again recruited in kindergarten, but in this case were followed into grade 3. Students in Study 3 were in grade 1 in the 2005–2006 academic year. Because studies 2 and 3 were interested in classroom instruction in addition to student progress and development, both of these studies augmented their samples in the follow-up years to make up for student attrition from one year to the next. In all three studies, students were assessed on a variety of reading and language skills in the fall and spring of each year. The present study used a systematic merging procedure to construct a final dataset comprised of measures that were common across the three studies in the spring of grade 1. That is, we restricted the present analyses to measures of reading and phonological awareness that were administered in English and Spanish between the first week of February and the first week of June. Each child contributed only a single observation to the dataset. The final dataset included slightly more males (51.13%) than females with a mean age of 7.22 years (SD = 0.41) and all participants were Hispanic. The number of students within each class ranged from 5 to 21, with an average classroom size of twelve.

Measures

Phonological Awareness (PA)

PA in English was measured using the Comprehensive Tests of Phonological Processes (CTOPP; Wagner, Torgesen, & Rashotte, 1999). This battery consists of seven individually administered subtests, which are designed to assess students’ ability to blend, segment, and categorize units of speech. To measure phonological processes in Spanish, we used the Test of Phonological Processes in Spanish (TOPPS), which was created as part of study 1 to parallel the CTOPP, so that the two measures were developmentally comparable while the latter measure was linguistically appropriate to measure PA in Spanish. Thus, the two measures included the same subtests and the same numbers of items per subtest, and individual items on the TOPPS were designed to be similar to the corresponding item on the CTOPP in terms of the number of phonemes, and the location and type of manipulation.

Since the purpose of the current study was to extend Branum-Martin et al. (2006) to grade 1, the English and Spanish CTOPP subtests that were used included blending phonemes into words, blending phonemes into non-words, phoneme elision, and segmenting words into phonemes. The total raw score for these subtests is the total number of correct items up to the ceiling rule of three incorrect items. Internal consistency estimates for the English subtests for 6–7-year-old children as reported by Wagner et al. (1999) ranged from 0.83 to 0.92.

Blending phonemes into words (BPW) measures children’s ability to combine phonological units (syllables, phonemes, onsets-rimes) to make real words. In this task, the child listens to a series of audio recorded phonological units, and is asked to blend the phonological units in order to form a word. For example, the child would hear two separate syllables “gar” and “den,” and would have to blend the phonological units and say “garden.” This test consisted of 18 test items and six practice items. The internal consistency estimates calculated in the present study was .75 for both English and Spanish subtests.

Blending phonemes into non-words (BPN) is similar to the BPW but requires the child to blend phonological units into pronounceable non-words. For example, the child would hear two separate syllables “nim” and “di,” and would have to blend the items and say “nimdi.” The internal consistency estimates calculated for the current sample was .75 for both English and Spanish subtests.

The raw English BPW and BPN correlated at .73, and the Spanish BPW and BPN correlated at .77. Therefore, to stay consistent with the models used in Branum-Martin et al. (2006) a single blending phoneme composite variable was created separately for English and Spanish (EBP and SBP, respectively) by averaging BPW and BPN. It is important to note that since both measures were on the same scale there was no need to use z scores.

Phoneme elision (PE) measures the extent to which a child can say a word, then say what is left after dropping out designated sounds. An example would be to say, “fold,” and then say the word without the /f/, in which case the correct response would be “old.” This subtest is made up of 20 test items (4 practice items). The internal consistency for the current sample was .74 and .73 for English and Spanish, respectively.

Segmenting words (SW) measures a child’s ability to say the separate phonemes that make up a word. The examiner would ask the child to say “fan” and then to say it one sound at a time, the correct response would be “f-a-n.” This subtest is made up of 20 test items (4 practice items). The internal consistency estimates for the current sample was .75 for English and .74 for Spanish subtests.

Related reading skills

The Woodcock letter-word identification and word attack measures in English (WJ: Woodcock, 1989) and Spanish (WJM: Woodcock & Muñoz-Sandoval, 1995) are used in the study to represent the level of students’ decoding ability. These measures are used in the models as a way to increase the discriminant power to show how certain phonological measures may be distinct from one another.

Letter-word identification (LWID) assesses the child’s ability to decode isolated words of varying difficulty. In this subtest, students are required to first identify letters, which are presented in large type, and then to pronounce the presented words correctly. Internal consistency estimates for first graders as reported by WJ and WJM are .95 and .91, respectively. The internal consistency estimates in the present study were .71 and .72 for English and Spanish, respectively.

Word attack (WA) measures a child’s skill to apply phonic and structural analysis skills to pronounce printed pseudo words that are not contained in the lexicon. In this subtest students are required to read combinations of letters that follow English (or Spanish in the case of the Woodcock-Muñoz) orthographic rules, but are either low frequency or nonsense words. Internal consistency estimates for first graders as reported by WJ and WJM are .96 and .91, respectively. The internal consistency estimates in the present study were .7 and .68 for English and Spanish, respectively.

Analytic Procedure

Approach 1 – Uncentered Student-Level Data

Approach 1 fit a single-level CFA using the total groups covariance matrix, which is the covariance matrix based on uncentered student-level data. This approach ignores the hierarchical structure of the data (see Figure 1A). Ignoring the clustering of students in classrooms could bias the estimation of factor loadings, the estimation of error variances, the correlations among factors, and the standard errors of all model parameters. Covariances among measures under this approach are a function of both the within- and between-classroom covariances. To obtain standard errors that are robust to non-normality and non-independence we used maximum likelihood estimation with robust standard errors (MLR) and specified the sampling as complex (TYPE=COMPLEX), with classroom as the clustering unit. This approach adjusts the standard errors for non-independence, but does not attempt to model covaration at the classroom level.

Approach 2: Analysis of Student-level Data Centered at the Classroom Mean

This model uses the same single-level CFA model as Approach 1, but controls for between-classroom effects on the covariances by removing the observed classroom means (discussed below) from the individuals’ scores on the tests. This approach attempts to estimate the factor structure at the student-level from Approach 4 without the complexity of fitting the multi-level model. As in Approach 1, in order to obtain standard errors that are robust to non-normality and non-independence, we used MLR estimation and specified the sampling as COMPLEX, with classroom as the clustering unit. As with Approach 1, using MLR estimation in Approach 2 with TYPE=COMPLEX yielded standard errors that were robust to non-normality and non-independence, while not attempting to model covaration at the classroom level. Using MLR without TYPE=COMPLEX would have yielded standard errors robust to non-normality, but not robust to non-independence, and would have yielded standard errors that were too small.

Approach 3: Analysis of the Between-classroom covariance matrix

This approach also fits a single-level CFA model, but at the classroom- rather than at the student-level. The observed classroom-means for the PA and reading tasks were computed within each class. The model in Figure 1 A is then fit to the covariances among these means. This approach is expected to approximate the between-classroom model of the multilevel model of Approach 4. For Approach 3 we used MLR estimation, but did not specify the TYPE as COMPLEX.

Approach 4: Multilevel-CFA

This approach was used by Branum-Martin et al. (2006) and involves fitting a two-level CFA model to the data with separate English and Spanish constructs at each level. This approach provides evidence about the dimensionality of PA at the student- and classroom-levels, simultaneously. More specifically, at the student-level, student deviations from the classroom means on the English and Spanish tasks are related to their respective language-specific latent variable. At the classroom-level, the classroom means of the English and Spanish tasks are related to their respective language-specific latent variable. Furthermore, the English and Spanish PA and reading factors were allowed to correlate both at the student- and classroom-level, but not across levels. The parameter estimates at each level reflect how the traits are reflective of the latent construct at that level.

The models fit under each approach included five variables in each language, for a total of 10 observed variables: three PA scores in English and Spanish, and two reading scores in English and Spanish. In Approach 4, each variable is essentially represented as two independent parts – the classroom mean and the student deviations from the classroom mean. The English and Spanish tasks (observed measures) are related to their respective language-specific latent variable as reflected in Figure 1A (Approaches 1–3) and Figure 1B (Approach 4). Furthermore, the four factors (language-specific PA and reading factors) were allowed to correlate. As previously mentioned, the reading measures were used to increase the discriminant power of the models.

In order to deal with missing data, full information maximum likelihood (FIML) estimation was used because it produces unbiased parameter estimates and standard errors (Enders & Bandalos, 2001) under the assumption that the data are missing at random. As in the other approaches, we used MLR estimation, which provides maximum likelihood estimates and standard errors that are robust to non-normality. For Approach 4, we specify the type of analysis as two-level, which allows modeling at both the student and classroom levels simultaneously. Furthermore, for all approaches, we relaxed the model in Figure 1A/1B to allow for correlated errors of measurement for phonological and reading measures based on the same method across languages (e.g., EBP to SBP; ESW to SSW; EPE to SPE; ELW to SLW; and EWA to SWA). These correlations account for shared method variance, which if left unaccounted for could lead to inflation of the correlation between the English and Spanish PA latent variables. All models were fit in Mplus 7.2 (Muthen & Muthen, 2014).

To assess the dimensionality of PA within and across languages we examined indices of model fit and model parameter estimates. The CFA model fit indices indicate the degree to which a hypothesized model accurately represents relations among the observed variables. As recommended by Hu and Bentler (1999) we used different indices to examine model fit including: (a) the chi-square statistic (${\chi }^2$); (b) Comparative Fit Index (CFI); (c) Tucker-Lewis Index (TLI); (d) Root Mean Square Error of Approximation (RMSEA); and (e) Standardized Root Square Mean Residual (SRMR). Values of 0.95 and above are considered an excellent fit for CFI and TLI, while values of .08 or less are considered an adequate fit for RMSEA and SRMR (Schreiber, Nora, Stage, Barlow, King, 2006). An important aspect of the model comparison is the comparability of parameter estimates obtained through Approaches 1–3 to the corresponding student- and classroom-level estimates from Approach 4.

Results

Descriptive Statistics

Table 1 presents a correlation matrix and descriptive statistics of the English and Spanish PA tasks and the reading measures at the student- (below the diagonal) and classroom-levels (above the diagonal). The purpose of this table was to depict the student versus classroom effects (as discussed previously), highlighting how performances on the different tasks were considerably different at the two levels. The student- and classroom-level correlations were estimated using an unconstrained model (i.e., all variables freely correlated within the student- and classroom-levels) in Mplus.

Table 1.

Descriptive Statistics at the Student- and Classroom-Level.

	1	2	3	4	5	6	7	8	9	10
1. EBP	–	0.91	0.90	0.70	0.54	0.42	0.75	0.76	−0.11	−0.03
2. EPE	0.49	–	0.88	0.53	0.67	0.37	0.85	0.78	0.02	0.07
3. ESW	0.49	0.35	–	0.61	0.50	0.44	0.69	0.72	−0.12	−0.01
4. SBP	0.74	0.42	0.44	–	0.66	0.82	0.25	0.27	0.32	0.37
5. SPE	0.39	0.65	0.27	0.44	–	0.71	0.49	0.35	0.56	0.58
6. SSW	0.53	0.39	0.42	0.63	0.47	–	0.08	0.07	0.58	0.62
7. ELW	0.49	0.61	0.36	0.40	0.57	0.43	–	0.91	−0.03	0.02
8. EWA	0.45	0.59	0.35	0.41	0.53	0.42	0.76	–	−0.10	−0.02
9. SLW	0.34	0.48	0.24	0.45	0.58	0.51	0.56	0.59	–	0.98
10. SWA	0.36	0.49	0.24	0.44	0.57	0.51	0.57	0.61	0.87	–
Mean	10.16	7.65	8.27	11.92	9.78	13.75	431.93	470.19	487.61	489.96
classroom SD	1.78	2.26	2.26	1.61	2.78	2.86	20.47	10.84	26.17	14.2
student SD	3.36	4.72	4.17	3.55	6.06	5.40	38.70	18.74	43.74	25.75
Intraclass Correlation	0.25	0.18	0.26	0.15	0.14	0.25	0.23	0.32	0.33	0.28

Note. Classroom-level correlations appear above the diagonal and student-level correlations appear below the diagonal. Means, standard deviations and intraclass correlations appear at the bottom of the table. EBP= English blending phonemes; EPE= English phoneme elision; ESW= English segmenting words; SBP= Spanish blending phonemes SPE= Spanish phoneme elision; SSW= Spanish segmenting words; ELW= English letter-word identification; EWA= English word attack; SLW= Spanish letter-word identification; and SWA= Spanish word attack.

The bottom section of Table 1 provides the means, student- and classroom-level standard deviations, and the intra-class correlations (i.e., the ratio of the variance in classroom means to the total variance). The classroom standard deviation for a measure indicates the extent to which the classroom means vary around the grand mean for that measure, and the student standard deviation indicates the extent to which the scores for students within a classroom deviate from the classroom mean for that measure pooled across all classrooms. The intra-class correlation tells us the proportion of the total variance in student scores that arises from differences between the classrooms. The variances of the phonological tasks in English and Spanish were not very different at the classroom-level, however they appeared to be higher at the student-level, as expected (i.e., sample means vary less than individual scores), especially for the Spanish phoneme elision (SPE) and segmenting word (SSW) tasks. The variances of the Spanish reading measures were higher than the English reading measures, both at the classroom- and student-level. Across the PA tasks, the ICCs ranged between .14 and .26, indicating that 14% to 26% of the variance in PA scores is attributable to differences between classrooms. In contrast, ICCs for English reading measures were .23 and .32, and for Spanish reading measures were .33 and .28 for Letter Word and Word Attack, respectively. Comparing the ICCs from grade 1 to those reported by Branum-Martin et al. (2006) for kindergarten (.17 to .27 for Spanish PA, .20 to .26 for English PA, and .26 for both English and Spanish Reading) it appears that the effects of clustering may be slightly more pronounced in grade 1 for Reading. Regardless of the difference between kindergarten and grade 1, the grade 1 ICCs for PA and for Reading indicate substantial between-class variation, necessitating the need to account for the effects of clustering in analyses, because ignoring clustering would ultimately result in biased standard errors (Raudenbush, & Bryk, 2001) and possibly in biased parameter estimates.

In multivariate contexts, clustering can affect not only standard errors of parameter estimates, but may also affect the parameter estimates themselves because clustering can affect the covariances/correlations among measures, such that covariances/correlations that ignore clustering may be quite different from covariances/correlations that take clustering into account. The correlation matrix (top section of Table 1) shows that at the student-level (i.e., below the diagonal in the top of Table 1) the PA tasks were moderately related both in English (.35 – .49) and Spanish (.44 – .63) and the reading measures were highly correlated at .76 in English and .87 in Spanish. At the classroom-level (i.e., above the diagonal) the correlations among measures within domain were considerably higher than at the student-level for the English (.88 – .91) and Spanish (.66 – .82) PA tasks, and reading measures (.91 and .98, for English and Spanish respectively). The higher correlations at the classroom-level indicated that clustering was pronounced at grade 1, and perhaps somewhat more so than Branum-Martin et al. (2006) found in kindergarten (classroom correlations of .77 to .87 for English PA; .61to .88 for Spanish PA). Branum-Martin et al. (2006) reported a single composite reading measure in English and Spanish, so within language correlations for reading were not reported. The most striking difference between the student-level correlations and the classroom-level correlations is also the largest difference between the grade 1 data in Table 1 and the kindergarten data reported in Branum-Martin et al. (2006); namely, the very small and slightly negative correlation at the classroom-level between English and Spanish reading measures in grade 1. These correlations were uniformly positive and moderate at the student-level in grade 1, and at both the student- and classroom-levels in kindergarten. This difference between the student- and classroom-level relations, and the shift between kindergarten and grade 1 suggest an effect of instruction on class-mean performance that differs across measures, or a change from kindergarten to grade 1 in the stratification of students into classrooms, possibly based on their Spanish and/or English proficiency.

Most importantly, the magnitude of these clustering effects and the different pattern of cross-language correlations at the student and classroom levels suggest that the clustering of students into classrooms cannot be ignored in psychometric analyses. At the same time, the ubiquity of psychometric analyses that ignore clustering and the number of psychometric studies carried out in school contexts where the number of clusters is too small for multi-level psychometric analyses highlights the need for alternatives to the full, multi-level CFA of Approach 4.

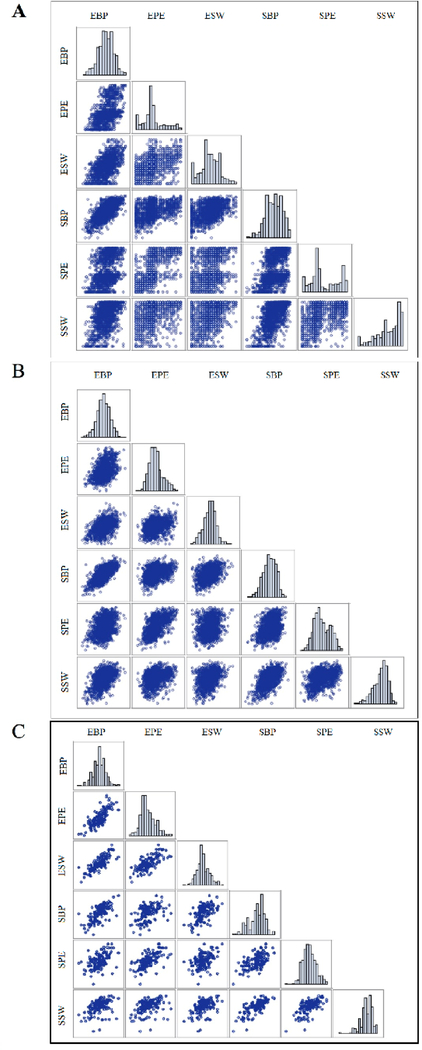
Figure 2 is a set of three scatter-plot matrices, which provides a graphical representation of the correlation matrix of the PA tasks for the datasets that represent the different approaches: Approach 1 - uncentered student-level data (Figure 2A), Approach 2 - student-level data after controlling for clustering by centering at the classroom mean (Figure 2B), and Approach 3 –classroom means (Figure 2C). Figures 2B and 2C together represent the multi-level data for Approach 4. When clustering is ignored (Figure 2A) the correlation matrix reflects a complex mixture of the substantial covariation that is due to covariation at the student level within classrooms, as well as the substantial covariation that exists between classrooms. However, when clustering is accounted for (Figures 2B and 2C), the bivariate scatter plots in each cell of the matrices appear more bivariate normal than when clustering is not taken into consideration and the magnitude of the relation in each two-dimensional plot is much easier to discern. Thus, the covariation in the uncentered student-level raw scores reflects both the covariation that exists between students because of the covariation in the classroom means and the covariation at the student-level within classrooms because of the tendency for a student to be above or below the classroom means for all measures. If these two sources of covariation differ from one another, and/or are affected by different determinants, then analysis of the uncentered student-level data (Approach 1) might be expected to lead to over-estimating the dimensionality of the data, and miss-estimation of the factor loadings, factor variances and covariances, and the variance of measurement errors.

Figure 2.

Correlation matrixes of Spanish and English PA using total scores (panel A), within-classroom scores adjusted for classroom mean variation (Panel B), and classroom means (Panel C). Panel A shows substantial amount of variation in the total scores that is due to the combination of variation between students within classrooms and variation between the classrooms. Panel B has less variation because it has adjusted for the between-classroom variation by removing the classroom means. There are less points in panel C because the panel depicts the classroom means variation. EBP= English blending phonemes; EPE= English phoneme elision; ESW= English segmenting words; SBP= Spanish blending phonemes SPE= Spanish phoneme elision; SSW= Spanish segmenting words.

Model Estimation and Assessment of Fit for the Four Approaches

The fit indices from the four analyses are displayed in Table 2. While the CFI and TLI indices for Approach 1 indicated reasonable fit (.95 and .90 respectively), the RMSEA and SRMR indices (.10 and .055, respectively) suggested otherwise, although SRMR is not too far outside the expected range for well-fitting models (SRMR < .05). Thus, it is not obvious from the global fit measures that Approach 1 has failed in any substantial way. However, if one examines the parameter estimates in Table 3, one sees quickly that factor loadings for Approach 1 are inflated relative to the student level factor loadings under Approach 4. The reason for this inflation in Approach 1 is the slightly higher factor loadings for any given measure at the classroom level (see Approach 3 estimates and classroom level estimates in Approach 4) as compared to the student-level (see Approach 2 estimates and the student level estimates in Approach 4). When all of this covariation is attributed to the student level in Approach 1, estimates become inflated.

Table 2.

Global Model Fit Indices

Approaches	Chi-Square (df)	RMSEA	CFI	TLI	SRMR
Approach 1: Total score matrix	437.161 (24)	.10	.95	.90	.06
Approach 2: Within-student matrix	346.517 (24)	.09	.96	.92	.05
Approach 3: Between-classroom matrix	95.708 (24)	.15	.94	.89	.08
Approach 4: Multilevel-CFA model	494.396 (48)	.08	.95	.91	.05 (Within) .12 (Between)
Approach 41: Multilevel-CFA model saturated at the within level.	9.703(24)	.04	.99	.97	.003 (Within) .01 (Between)
Approach 4: Multilevel-CFA model saturated at the between level.	423.205(24)	.10	.96	.83	.05 (Within) .02 (Between)

Note. Degrees of freedom appear in parentheses. RMSEA = root mean square error of approximation, CFI = comparative fit index, TLI = Tucker-Lewis Index; and SRMR = standardized root mean square residual.

¹The last two models in Table 2 fit Model 4 with a saturated model at the student or classroom level in order to isolate the lack of fit at the alternate level (Ryu & West, 2009). These models and their fit to the data are discussed later in the text.

Table 3.

Standardized Parameter Estimates for the Single- and Multilevel-CFA Models

Factor Loading
	Approach 1	Approach 2	Approach 3	Approach 4
				Within-level	Between-level
English PA Factor by:
EBP	.777 (.022)	.698 (.028)	.907 (.023)	.699 (.027)	.958 (.025)
EPE	.753 (.022)	.729 (.024)	.839 (.032)	.745 (.023)	.946 (.038)
ESW	.648 (.027)	.535 (.030)	.860 (.028)	.532 (.030)	.942 (.035)
Spanish PA Factor by:
SBP	.735 (.025)	.692 (.030)	.835 (.034)	.691 (.030)	.866 (.056)
SPE	.704 (.028)	.715 (.026)	.728 (.047)	.727 (.025)	.752 (.073)
SSW	.783 (.025)	.725 (.031)	.898 (.031)	.724 (.031)	.986 (.045)
English Reading by:
ELW	.909 (.011)	.881 (.012)	.935 (.021)	.884 (.012)	.964 (.026)
EWA	.864 (.013)	.848 (.013)	.909 (.024)	.860 (.012)	.929 (.028)
Spanish Reading by:
SLW	.949 (.010)	.945 (.010)	.963 (.022)	.947 (.010)	.996 (.022)
SWA	.941 (.010)	.909 (.011)	.944 (.023)	.917 (.011)	.982 (.023)
English PA Factor with:
Spanish PA Factor	.798 (.025)	.855 (.017)	.626 (.064)	.857 (.017)	.505 (.135)
English Reading	.819 (.023)	.840 (.023)	.781 (.044)	.845 (.022)	.789 (.052)
Spanish Reading	.437 (.047)	.597 (.031)	.057 (.095)	.608 (.030)	−.113 (.141)
Spanish PA Factor with:
English Reading	.618 (.040)	.738 (.032)	.255 (.097)*	.746 (.030)	.072 (.163)
Spanish Reading	.700 (.038)	.766 (.027)	.594 (.067)	.773 (.026)	.558 (.131)
English Reading with:
Spanish Reading	.539 (.042)	.713 (.021)	.110 (.093)	.717 (.021)	−.148 (.131)
Correlated residuals:
EBP with SBP	.611 (.029)	.618 (.030)	.627 (.082)	.621 (.029)	.856 (.191)
EPE with SPE	.448 (.036)	.391 (.035)	.546 (.075)	.386 (.036)	.877 (.242)
ESW with SSW	.163 (.046)	.177 (.041)	.121 (.142)	.189 (.040)	−.035 (.987)
ELW with SLW	−.007 (.073)	−.130 (.081)	.095 (.235)	−.126 (.080)	.798 (1.820)
EWA with SWA	.128 (.055)*	.137 (.046)	.001 (.188)	.134 (.048)*	.205 (.260)

Note. Standard errors appear in parentheses. The top section of the table provides the standardized factor loadings for the four models. The bottom section of the table provides the correlations between the factors for the four models. EBP= English blending phonemes; EPE= English phoneme elision; ESW= English segmenting words; SBP= Spanish blending phonemes SPE= Spanish phoneme elision; SSW= Spanish segmenting words; ELW= English letter-word identification; EWA= English word attack; SLW= Spanish letter-word identification; and SWA= Spanish word attack.

^*Statistically significant at p<.05

bolded entries are not statistically significant at p < .05, all other elements are statistically significant a p < .001.

Examination of the factor correlations reveals a somewhat different picture, namely, the factor correlations in Approach 1 are underestimated relative to the factor correlations in Approach 2 and the student-level factor correlations in Approach 4. This result suggests that factors are more “distinct” when analysis is based on Approach 1, and could lead to over-extraction of factors in some contexts. The source driving this reduction is apparent from the factor correlations in Approach 3 and the estimates of factor correlations at the classroom-level in Approach 4. If one examines the factor correlations in Approach 3, or the classroom level correlations in Approach 4 in comparison to the factor correlations in Approach 2, or the student-level factor correlations in Approach 4 one sees that the factor correlations at the classroom level are smaller than the correlations at the student level. Hence, the correlations under Approach 1 are diminished relative to Approach 2 and the student level estimates in Approach 4, as the Approach 1 correlations are a weighted combination of the student and classroom correlations in Approach 4.

Global model fit statistics for Approach 2 suggest that the model generally fits the data well. Fitting the model under Approach 2 yielded a smaller chi-square value than Approach 1 (i.e., smaller values indicate better fit, although values are not strictly comparable across the four approaches since the models are being fit to different data) ($\mathrm{A}\mathrm{p}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{ }2 {\chi }^2\left(24\right)=346.5, p<.001$), and thus variation in the distributional properties of the data will affect the scaling of the chi-square statistic across the different data sets. What is compelling about Approach 2 is how closely the parameter estimates of Approach 2 approximate the student-level estimates of Approach 4, which is a more challenging approach to modeling the relations among the measures. While the model parameter estimates are quite close to the student-level estimates of Approach 4, the standard errors of Approach 2 would have been too small, if we had ignored the non-independence across students that results from their nesting within classrooms. If we had estimated the model under Approach 1 or Approach 2 without specifying that the TYPE=COMPLEX, we would have obtained standard errors that had been too small. In fact, failing to specify TYPE=COMPLEX under Approach 2 would have yielded standard errors that were 57% to 92% as large as the corresponding standard errors under Approach 4. On average, the standard errors for Approach 2 would have been only 77% as large as those for the student level under Approach 4 had we used MLR estimation, but not specified TYPE=COMPLEX. These are not trivial differences. However, as one can see from the standard errors under Approach 2 in Table 2, using MLR estimation and TYPE=COMPLEX yields standard errors that are quite close to the standard errors at the student level under Approach 4. In fact, on average these standard errors are just slightly larger (about 2% larger) than the standard errors from the student level for Approach 4. This difference in the standard errors is relatively small in comparison to the magnitude of the parameter estimate itself in virtually every case. Thus, it is not clear that inferences based on Approach 2 would be negatively impacted, at least in the current situation, provided that MLR estimation is used with TYPE=COMPLEX to make the standard errors robust to non-normality and non-independence of observations. Failure to use this option would produce an unacceptable underestimation of the standard errors compared to multi-level CFA.

Approach 3 had somewhat poorer fit compared to the other models. Specifically, although the chi-square value was smaller for the same degrees of freedom of Approaches 1 and 2 (${\mathrm{A}\mathrm{p}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{ }3 \chi }^2\left(24\right)=95.7, p<.001$), other global fit statistics suggested problems with the model when fit to the covariances among the classroom means (RMSEA = .15; SRMR = .08; TLI = .89). Lack of fit from Approach 3 could reflect problems stemming from the smaller sample size used in this approach (i.e., the number of classrooms was much smaller than the number of students), heterogeneity in the number of students per classroom, which implies that means for some classrooms are estimated with greater precision than others, or differences among the schools and communities that differentially impact the classroom means and affect their conformity to the psychometric model.

The poor fit of Approach 3 as compared to Approach 2 has implications for the lack of fit in Approach 4, namely that lack of fit stems from the model for the covariances among the classroom means more so than from the model at the student-level. This inference is supported by the RMSR for the classroom level under Approach 4, but other global fit information under Approach 4 is not specific to one level. In fact, a potential advantage to fitting the model to the separate student and classroom covariances in Approaches 2 and 3 is that one obtains global fit indices like RMSEA, CFI, and TLI and chi-square fit statistics separately for the student and classroom levels in contrast to the multi-level model estimated under Approach 4, where the global fit statistics are influenced by lack of fit at both levels. Moreover, fit statistics in multi-level CFA tends to be driven by lack of fit at the student level (Pornprasermanit, Lee, & Preacher, 2014), although it is possible to isolate the lack of fit in multi-level CFA by fitting a saturated model at the student level, and vice versa (Ryu & West, 2009), provided that the model does not contain random slopes, which is the case in the present model. Fitting such a saturated model at the student level in Approach 4 changes the model fit statistics to ${\chi }^2\left(24\right)$ = 90.7, RMSEA = .04, CFI = .993, TLI = .972, and SRMR = .098. When we fit a saturated model at the classroom-level to isolate the lack of fit at the student level, the corresponding values are ${\chi }^2\left(24\right)$ = 423.2, RMSEA = .102, CFI = .955, TLI = .832, and SRMR = .052. These statistics present somewhat conflicting views of the quality of the model fit at the student and classroom levels, with RMSEA, CFI, and TLI suggesting a well-fitting model at the classroom level, and CFI and SRMR suggesting a well-fitting model at the student level.

Discussion

The purpose of this study was to examine the dimensionality of PA in English and Spanish among Spanish-speaking ELs by replicating the final model presented in Branum-Martin et al. (2006) and examined alternatives to modeling clustered data. Prior to discussing the results an important distinction needs to be made with regards to the interpretation of the student- and classroom-level latent constructs (factors). While student-level constructs reflect student abilities and how they responded on various measured variables controlling for the classroom context, the same cannot be said about the classroom-level constructs. The grouping dimension (in this case the classrooms) reflects the instructional context, which is comprised of instructional effects as well as other classroom related factors such as the effects of the teachers, factors related to the stratification of students into classrooms, the demographics of the school, and so forth. Together these factors influence the classroom means and the covariances among those means, and thereby the classroom-level factor correlations. Due to the simple descriptive design of the current study, it was not possible to disentangle these confounding effects from one another. Therefore, the classroom-level latent constructs in this study are interpreted as instructional context effects at an organizational level for students across different classrooms as they relate to the many factors that distinguish one classroom from another. Simply put, classrooms do not have abilities in and of themselves, rather our measures of classroom ability reflect the aggregate abilities of the students in those classrooms and the myriad of factors that affect student performance in the aggregate.

While, Branum-Martin et al. examined the dimensionality of PA with ELs in kindergarten, we looked at the nature of the construct in grade 1 and found similar results. Specifically, English and Spanish PA were statistically separable across languages at both levels; however, they tended to overlap considerably at the student-level (.86²=74%), but to a lesser extent at the classroom-level (.51²=26%). In other words, although the skills represent unique constructs in each language, the constructs are minimally distinct at the student level, reflecting the inherent nature of PA as a language general ability, but are somewhat more distinct at the classroom level as instruction tends to differentiate the abilities in the two languages from one another across students in different classrooms.

The medium-high correlations between English and Spanish PA factors at the student- and classroom-level indicated that students with high PA in one language also had high PA in the other. However, comparing the English and Spanish PA factor correlations in grade 1 to that of kindergarten, it was apparent that the constructs were less closely related in grade 1, especially at the classroom-level. This change in the correlation across languages may suggest that as children become readers, they may approach PA tasks differently. Prior to receiving reading instruction, children may tend to process PA tasks perceptually; however, once they are able to read and spell they start to process the tasks based on the representation of the word (Anthony & Francis, 2005). For example, in grade 1 children may be approaching phoneme elision as a decoding rather than as a phonemic task. As a result, PA tasks seem to be purer measures of phonological abilities prior to receiving instruction on reading. The lack of relation between the classroom-level PA and reading factors across languages in grade 1 in contrast to the significant and positive correlations in kindergarten may suggest that literacy instruction is altering the relationship between PA and reading across languages at the classroom level. The fact that the cross-language relations between PA and reading remain strong and positive at the student level, while differing at the classroom-level relative to the kindergarten study is consistent with the idea that the grade 1 classrooms were mainly providing instruction in Spanish and to a lesser extent in English. This difference in time allocation to Spanish and English would be expected to impact the magnitude of the correlation at the classroom-level, and thus the relation between PA and reading at that level. The fact that this pattern of correlation is only observed at the classroom-level may imply that ELs are applying their PA and decoding skills to both languages and approaching the English and Spanish tasks similarly. Alternatively, the different patterns of correlation observed in the two studies may indicate that the factors affecting stratification of students into classrooms differs across kindergarten and grade 1. Decomposing these relations into student- and classroom-level relations over longer time frames and in longitudinal designs would provide a stronger basis for differentiating instructional effects from stratification effects, especially using designs with multiple occasions of measurement per year.

In this study, we also examined possible ways of modeling aggregated data by comparing four distinct approaches to fitting the CFA models in clustered contexts. Approach 1 ignored the clustered structure of the data. As a result, the model fit and parameter estimates reflected the combined influence of within- and between-classroom relations across measures. Essentially, parameter estimates are a weighted average of the estimates from the within- and between-classroom factor structures and factor covariances. Although attributed entirely to the relations among students, because Approach 1 involves only student-level data, the student-level variances and covariances in this “total-groups” covariance matrix reflect both the relations that exist at the student-level within classrooms, and the covariances among classroom means. This finding is not surprising as other research studies have also shown that using conventional CFA for clustered data produces results that reflect neither the student-level nor classroom-level structure, with the degree of departure from the student-level model reflecting the degree to which the ICC’s (i.e., variances and covariances at the classroom-level) depart from zero and/or are different from the student level variances and covariances (Dyer, Hanges, & Hall, 2005; Muthen, 1994; Pornprasertmanit & Preacher, 2014).

Approaches 2 and 3 are a more direct attempt to estimate the student-level and classroom-level model, respectively, by analyzing student-level data centered within classrooms in Approach 2 and by analyzing covariation among the classroom means in Approach 3. Despite the lack of model fit in Approach 3, the parameter estimates from Approach 3 were similar to the between-classroom estimates from the multi-level analysis in Approach 4. Across the board, factor loadings for Approach 3 are smaller than the estimates at the between-level under Approach 4. This difference likely reflects the fact that the multi-level approach differentially weights classrooms based on the number of students per classroom; classrooms with more students provide more information about variation at the classroom level and this differential precision is taken into account in estimation in Approach 4, but not in Approach 3. If the number of students per classroom were equal across classrooms, the estimates from Approach 3 would have matched the between classroom estimates from Approach 4 (Muthen, 1989; 1990; 1994; Yuan & Bentler, 2007). It is possible that applying weights at the classroom-level could reduce the difference between the estimates of the two approaches, but to our knowledge this alternative has not been investigated for CFA models.

In contrast to Approach 3, estimates and standard errors from Approach 2 were quite similar to the student-level estimates from Approach 4. Approach 2 was a pure within-class model because it adjusted for differences in the classroom means. Muthen (1994) and Pornprasertmanit, Lee, and Preacher (2014) also reported a similar pattern of parameter estimates. It is important to note that comparability of the standard errors requires MLR estimation with the specification that TYPE=COMPLEX in Mplus so that standard errors are robust to violations of independence. Thus, while there are clear advantages to estimating CFA models for clustered data using multilevel-CFA (i.e., Approach 4), it is possible to estimate the student-level model quite well using student-level data centered at the classroom mean.

At the same time, it is incorrect to view the covariation at the student level after centering as reflecting the “true” covariation among students. Covariation at the student level after centering at the classroom mean tells us how abilities are related absent the influence of classrooms, and the factors associated with the grouping of students into classrooms. Classrooms and the factors that contribute to the grouping of students into classrooms are real sources of covariation in students’ scores, but these factors need not conform to the psychological reality at the student level as reflected in the psychometric properties of the test at the student-level.

Factor analytic models were originally introduced as a way to uncover the latent human abilities that underlie test scores. To the extent that these abilities are independent of factors that influence the performance of students clustered for instruction (e.g., the grouping of students for instruction, or the instruction itself), then the student-level estimates of Approach 2 and Approach 4 reflect the latent structure of these human abilities. To the extent that abilities are influenced by factors that relate to the grouping of students into classrooms, either causally or spuriously, then the dimensions underlying test performance are not fully represented by the student-level factors alone. Regardless, there is no reason to expect the dimensions operating at the group level to parallel those dimensions operating at the student level. Observing a different structure at the classroom and student levels is not a cause for alarm that would indicate that the tests do not measure what they purport to measure. Rather, such differences signal the existence of dimensions that influence the performance of groups of individuals that differ from those that influence the individuals without regard to grouping. Focusing only on covariation at the student level presents an incomplete picture of the latent dimensions that influence student performance because some of these influences affect the performance of all children who are grouped together for instruction, while other dimensions influence the performance of all children regardless of their being grouped together for instruction. Only the multi-level CFA can properly differentiate the dimensions that operate at each level.

Limitations

While the current study addressed some of the limitations of Branum-Martin et al. (2006) by having a larger sample size and more classrooms to fit the CFA models, it is limited in a number of ways. The current study is limited to investigating a single language subgroup (i.e., Spanish-speaking ELs in an English-speaking context) and did not examine the dimensionality of PA across different language subgroups or linguistic contexts. Also, the study was limited to four geographical regions in the U.S., specifically southern California, and central, southeastern, and south central Texas and was limited to grade 1 ELs in Transitional Bilingual classrooms. Therefore, the generalizability of our findings can only be made to populations that are similar to the one on which this study was based. Future studies are needed to extend the current approach to a more diverse sample that is representative of the larger population of ELs and to other linguistic contexts.

A second limitation of the current investigation is that we did not attempt to separate classroom-level covariation from school-level covariation. The multilevel-CFA model (Approach 4) had a poor fit at the classroom-level, which could be the result of instructional differences across the classrooms and how students were grouped into the transitional bilingual programs, or possible differences at the school-level, which were left uncontrolled and unexamined in the present study. In essence, the problems that affected the total group covariance (Approach 1) are potentially affecting the classroom-level covariances in Approach 3 and the between-classroom model of Approach 4. Specifically, the classroom covariances are a mixture of the school-level covariances and the classroom-covariances. This problem does not stem so much from school mean differences, but from school differences in the relations across measures. If schools differ in the factors they consider when placing students into different types of bilingual programs, these differences could lead to differences in the relations across measures at the classroom-level when schools are ignored. School-differences in instructional effects on reading and/or phonological awareness, or school differences in emphasis on Spanish versus English outcomes could also result in classroom-level differences across schools in the covariance among the measures used in this study. These factors are only examples as possible ways in which school-level factors might have affected covariation at the classroom-level and are not intended to represent an exhaustive list.

Finally, this study used a cross-sectional design and looked at end-of-year PA and reading scores. Consequently, the study covered a narrow developmental range. An important extension of this study would examine the bilingual constructs of PA and reading longitudinally, both within grades and across a longer developmental period. Extending the model to multiple grade years for the same students would significantly complicate the model because students change classrooms and possibly instructional programs over time. Even if students remain in the same instructional programs, the changing of classrooms complicates the model because students are now cross-classified rather than nested within teachers. While the possibility of examining the effects of different classrooms, amount of instruction in English, and program effects is appealing and the examination of change using students as their own longitudinal controls might help to disentangle the effects of instruction from selection effects for explaining classroom-level covariation, there are significant challenges to estimating the CFA model in the longitudinal, cross-classified context.

Implications

The current study has implications for research and practice. One implication for bilingual research is that classroom differences, types of bilingual instructional program, and instructional effects beyond program type can affect student performance, and these influences cannot be ignored in studies of EL students. Furthermore, student-level effects need to be examined separately from school and classroom effects. As evidenced in the present study, these effects can differ from one another, may have different determinants, and may even be opposite in sign. The ways that schools place students into classrooms, and in particular into instructional programs, can induce covariation at the classroom-level that is distinct from covariation at the student-level. Such differential covariation at the student- and classroom-level complicates the evaluation of instructional effects, program types, and student abilities, as well as cross-language transfer. Also, this differential covariation can complicate the investigation of cross-level moderators, such as characteristics that alter the effects of school and classroom.

Furthermore, in psychometric studies that are carried out in school contexts where the number of clusters is too small or the statistical model is too complex, the between-component (classroom-level) of the model can be difficult to estimate. In such cases instead of ignoring the clusters, researchers can use approaches 2 (for the within part of model) and 3 (for the between part of the model) to get fairly comparable results to approach 4. Although, approaches 2 and 3 ignore one dimension of the data, they provided comparable estimates to the model from the respective level of approach 4 without explicitly modeling the covariation at the other level provided that standard errors were properly estimated to take into account non-independence of observations.

In practice, the amount and type of instruction, as well as the language in which instruction is delivered may vary across classrooms even when classrooms are ostensibly delivering instruction under a common program model. The current study did not attempt to incorporate measures of classroom instruction to account for variation at the classroom level, but it is clear from the intra-class correlations that substantial variability exists at the classroom level. That covariation in measures also exists at the classroom level and the fact that this covariation is substantial in size suggest at least the possibility that instruction delivery within a program model can influence relations across abilities. The magnitude of the classroom covariances and the differences observed between the student and classroom levels, as well as the differences in these grade 1 classrooms in comparison to the kindergarten classrooms studied in Branum-Martin et al. (2006) are consistent with findings from other research that have focused on effects of instruction for EL students. While our study did not explicitly address the factors that affect student placement into instructional programs, the positive covariation that exists in student abilities across languages in both kindergarten (Branum-Martin et al., 2006) and in grade 1 (present study) suggest that placement of students into program types based on English versus Spanish proficiency may be misguided. Differences in proficiencies across languages likely reflect prior experience with each language more than language ability. While such differences may be relevant for instructional placements, instruction will also contribute to the future development of abilities in each language, and goals for bilingual competence in language and literacy should also be considered in program placements. As the number of EL students in US schools and the number of language minority students in schools worldwide continues to increase, understanding how abilities relate at the student-, classroom-, and school-levels, and how factors relate across levels will remain important questions for researchers and practitioners.

Figure 3.

Path diagram of multilevel-CFA. The parameter estimates at the student (bottom section of the diagram) and classroom-level (top section of the diagram) are provided. Shared method correlations are not provided. EBP(ebp)= English blending phonemes; EPE(epe)= English phoneme elision; ESW(esw)= English segmenting words; SBP(sbp)= Spanish blending phonemes SPE(spe)= Spanish phoneme elision; SSW(ssw)= Spanish segmenting words; ELW(elw)= English letter-word identification; EWA(ewa)= English word attack; SLW(slw)= Spanish letter-word identification; and SWA(swa)= Spanish word attack.