A Data Analysis Method for Using Longitudinal Binary Outcome Data From a SMART to Compare Adaptive Interventions

Abstract

Sequential multiple assignment randomized trials (SMARTs) are a useful and increasingly popular approach for gathering information to inform the construction of adaptive interventions to treat psychological and behavioral health conditions. Until recently, analysis methods for data from SMART designs considered only a single measurement of the outcome of interest when comparing the efficacy of adaptive interventions. Lu and co-workers (2016) proposed a method for considering repeated outcome measurements to incorporate information about the longitudinal trajectory of change. While their proposed method can be applied to many kinds of outcome variables, they focused mainly on linear models for normally distributed outcomes. Practical guidelines and extensions are required to implement this methodology with other types of repeated outcome measures common in behavioral research. In this paper we discuss implementation of this method with repeated binary outcomes. We explain how to compare adaptive interventions in terms of various summaries of repeated binary outcome measures, including average outcome (area under the curve) and delayed effects. The method is illustrated using an empirical example from a SMART study to develop an adaptive intervention for engaging alcohol- and cocaine-dependent patients in treatment. Monte Carlo simulations are provided to demonstrate the good performance of the proposed technique.

There has been increased interest in recent years in the development of adaptive interventions (AIs). AIs are evidence-based treatment protocols that specify how information about the participant’s progress in the course of the intervention (e.g., early signs of non-response or poor adherence) should be used to modify aspects of the type, dosage, intensity, or delivery modality of an intervention. AIs are often motivated by evidence indicating that a particular intervention option (e.g., a particular type, intensity, scope, or delivery modality of treatment) is not beneficial for a sizable portion of the target population. Further, it is often possible to identify early in the course of an intervention those individuals for whom an intervention option would ultimately not be beneficial (Almirall & Chronis-Tuscano, 2016) and hence offer an alternative that would be more helpful for them. Adaptive interventions play an important role in various domains of behavioral research, including clinical psychology (Connell, Dishion, Yasui, & Kavanagh, 2007), education (Connor et al., 2011), organizational behavior (Eden, 2015), and health behavior change (Nahum-Shani, Hekler, & Spruijt-Metz, 2015; Almirall, Nahum-Shani, Sherwood, & Murphy, 2014).

The Sequential Multiple Assignment Randomized Trial (SMART) (Murphy, 2005) is an experimental design that can aid in the development of effective AIs. A SMART includes multiple stages of randomizations, where each stage is designed to address scientific questions concerning the selection and individualization of intervention options at a given decision point. The uptake of SMART studies in behavioral research is increasing rapidly (Almirall et al., 2016; Gunlicks-Stoessel, Mufson, Westervelt, Almirall, & Murphy, 2016; Naar-King et al., 2016; Page et al., 2016).

While there are various forms of SMARTs (Nahum-Shani et al., 2012), a prototypical SMART includes two stages of randomizations. At the first stage, each individual is randomized to one of two initial intervention options, but then the second stage of randomization is restricted to participants who are showing early signs of insufficient progress, referred to as early non-responders. That is, early non-responders are re-randomized to second-stage intervention options (e.g., to two different rescue treatments), whereas responders are not re-randomized. Depending on the study design, responders often either continue with the initial intervention, or transition to a less intense or less costly intervention option. Designing the study such that different intervention options are offered to early responders versus early non-responders leads to several AIs that are embedded in the SMART by design. Each embedded AI is operationalized by a relatively simple decision rule that recommends a particular initial intervention option for all individuals in the target population, and then a different subsequent intervention option for early non-responders versus early responders. Many SMART studies are motivated by scientific questions concerning the comparison of these embedded AIs.

The use of data from a prototypical SMART to compare embedded AIs requires careful consideration of the unique features of the SMART (Nahum-Shani et al., 2012). Nahum-Shani and colleagues (2012) suggested that embedded AIs could be compared in an unbiased and efficient manner using weighting and replication. Recently, Lu and colleagues (2016) extended this methodology for use with repeated outcome measures arising from a SMART. By capitalizing on both the key features of the SMART and the key features of longitudinal data, the method developed by Lu and colleagues (2016) enables researchers to better understand the process by which the effect of an AI unfolds over time and possibly to improve statistical efficiency (i.e., to obtain smaller standard errors in the comparison of embedded AIs).

While the theorems provided by Lu and colleagues (2016) are applicable to various types of outcomes, the examples used to illustrate the methodology, as well as the simulation studies conducted to evaluate its performance, assumed that the repeated outcome of interest is continuous. Kidwell and colleagues (2018) use a weighting and replication approach with a binary outcome, but not for longitudinal data. The goal of the current manuscript is to further extend this work by discussing practical implications pertaining to the use of this methodology in a setting where the repeated outcome measure of interest is binary. Binary outcomes are very common in behavioral research, such as in studies of drug use, alcohol and smoking (Hedeker et al., 2007) and in studies of learning and memory (Vuorre & Bolger, 2017). However, they present several challenges in the analysis of longitudinal data. For example, some estimands of interest, such as the area under the curve (AUC), will no longer be linear combinations of model parameters as they would be in a linear model with continuous outcomes. Therefore, the proposed methodology represents an important step in expanding the toolbox of data analysis methods behavioral scientists can employ with SMART study data.

We begin by providing a brief review of the method of Lu and colleagues (2016) for repeated continuous outcome measures, including key modeling considerations and estimation features. We then provide an extension to a setting in which the outcome is binary and discuss how to estimate important quantities, such as binary outcomes averaged over time and delayed effects. Simulation studies are provided to evaluate the performance of this extension in terms of bias, efficiency, and confidence interval coverage and also to investigate the extent to which efficiency is improved when implementing the method in various ways. Throughout, data from the ENGAGE SMART study (McKay et al., 2015) will be used for illustration. The goal of ENGAGE is to inform the development of an adaptive intervention for re-engaging alcohol and cocaine dependent patients in intensive outpatient programs (IOPs).

Empirical Example: ENGAGE SMART Study

The ENGAGE experiment was motivated by the need to develop an AI for re-engaging cocaine and alcohol dependent patients in IOPs and improving substance use outcomes in this high risk group. The first purpose of this study was to determine whether it is better, at the first intervention stage, to offer a brief, phone-based motivational interviewing (MI) session that focuses on helping the individual re-engage in their IOP or to offer a brief phone-based MI session that focuses on helping the individual make a personal choice among various available treatment options, including (in addition to IOP), individual cognitive-behavioral therapy (CBT), telephone-based stepped care, and medication management (see McKay et al., 2015). The two types of phone-based MI sessions are denoted MI-IOP and MI-PC, respectively. The second purpose of the study was to determine whether the better second-stage course of action for participants who do not respond to the initial outreach efforts is to offer MI-PC or to offer no further phone-based MI contact (abbreviated NFC for no further contact, although patients were still allowed to continue treatment in the outpatient program if they re-engaged on their own).

The experimental design is illustrated in Table 1; it involved 6 cells, labeled A-F and assigned via sequential randomization as follows. Cocaine- and alcohol- dependent individuals were recruited when they entered treatment at the IOP, and their treatment attendance was tracked for 8 weeks. Those who failed to engage in treatment early in the program were randomized with equal probability to either MI-IOP or MI-PC. At the end of the second month, participants showing signs of non-response (i.e., continued disengagement in treatment) were re-randomized to either MI-PC or NFC, whereas all participants showing signs of response received no further contact (i.e., responders were not re-randomized).

Table 1.

Adaptive Interventions in the ENGAGE SMART

Adaptive Intervention				Cells (Fig. 1)
	Stage 1	Response Status	Stage 2
Later Choice (A1=−1, A2=1)	MI-IOP	Responder	NFC	A, B
		Non-responder	MI-PC
No Choice (A1=−1, A2=−1)	MI-IOP	Responder	NFC	A, C
		Non-responder	NFC
Choice Throughout (A1=1, A2=1)	MI-PC	Responder	NFC	D, E
		Non-responder	MI-PC
Initial Choice (A1=1, A2=−1)	MI-PC	Responder	NFC	D, F
		Non-responder	NFC

The multiple, sequential randomizations in ENGAGE—i.e., the stage 1 randomization among all participants, and the stage 2 randomization, which was restricted to non-responders—give rise to 4 embedded sequences of treatments, which are summarized in Table 1. Note that an adaptive intervention is a protocol that recommends how to sequence and individualize intervention options, where the term ‘individualization’ refers to offering different intervention options to different sub-groups comprising the target population (e.g., to responders vs. non-responders). Since an adaptive intervention specifies how to treat each sub-group, outcome information from individuals in each of the sub-groups (e.g., both responders and non-responders) is consistent with, and can be used to evaluate, the adaptive intervention. In the ENGAGE SMART, one of the embedded AIs recommends offering MI-IOP initially, and then MI-PC for non-responders and NFC for responders. We refer to this adaptive intervention as later choice, as it offers personal choice only during the second stage (to non-responders). Consistent with this adaptive intervention are individuals who were offered MI-IOP initially, and then MI-PC if they did not respond (subgroup b in Figure 1) and NFC if they responded (subgroup a in Figure 1). The second adaptive intervention embedded in ENGAGE recommends offering MI-PC initially, and then MI-PC for non-responders and NFC for responders. We refer to this adaptive intervention as choice throughout, since personal choice is facilitated initially (to all individuals who enter the re-engagement program), as well as subsequently (to non-responders). Consistent with this adaptive intervention are individuals who were offered MI-PC initially, and then MI-PC if they did not respond (subgroup e in Figure 1) and NFC if they responded (subgroup d in Figure 1). ENGAGE also includes two other embedded interventions, which are actually non-adaptive in that the same second-stage intervention option (no further contact; NFC) is offered to both early non-responders and early responders. One of them begins with MI-IOP and the other with MI-PC. We refer to the former as no choice, since personal choice is not facilitated at either stage of the intervention. Consistent with no choice are individuals, who were offered MI-IOP initially, and then NFC if they did not respond (subgroup c in Figure 1) or if they responded (subgroup a in Figure 1). We refer to the later as initial choice, since personal choice is facilitated only at the first stage of the intervention. Consistent with initial choice are individuals who were offered MI-PC initially and then NFC if they did not respond (subgroup f in Figure 1) or if they responded (subgroup d in Figure 1). As noted earlier, both no choice and initial choice are non-adaptive (because they involve treating participants in the same manner regardless of responder status), but are still considered here as adaptive interventions for ease of presentation. Of course, a SMART can be designed such that all four embedded sequences are adaptive, namely such that non-responders and responders are treated differently in all embedded sequences (see example in Pelham et al., 2016).

Figure 1.

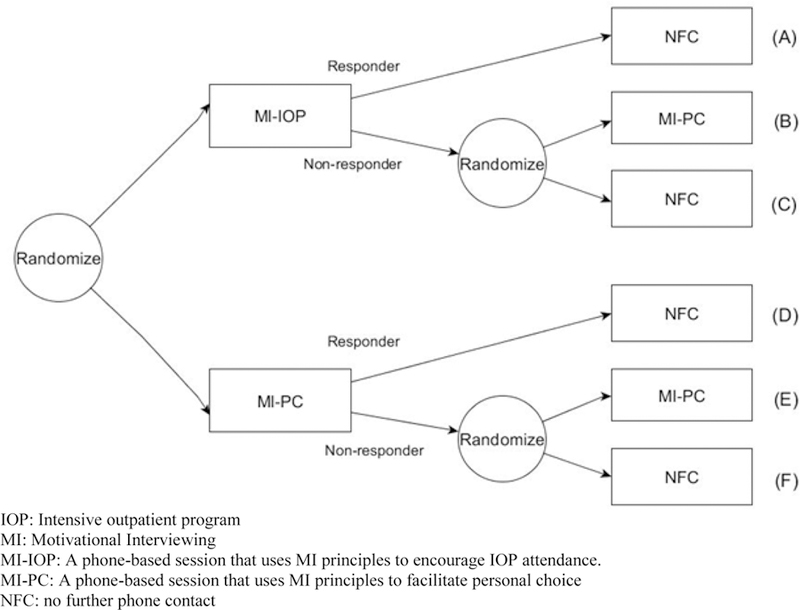
Randomization structure of ENGAGE SMART study.

Timeline follow-back assessments obtained approximately monthly over six months were summarized to obtain monthly measurements of drinking and cocaine use behaviors. The goal is to use these repeated measurements to compare the adaptive interventions (AIs) embedded in this SMART. The methodology discussed here can be easily extended to enable the use of additional measurement occasions before and after exposure to second-stage intervention options.

Denote the observable data for subjects in this SMART by $\left(\mathit{\text{X}},Y_1,A_1,Y_2,A_2,Y_3,Y_4,Y_5,Y_6\right)$, where $Y_t$ is the outcome measured at month t; $A_1$ and $A_2$ are the randomly assigned first- and second-stage intervention options, respectively; and $\mathit{\text{X}}$ is a vector of baseline measures obtained prior to the initial randomization (e.g., age, gender). Let $A_1$ denote the indicator for the first-stage intervention options, coded −1 for MI-IOP and +1 for MI-PC, and $A_2$ denote the indicator for the second-stage intervention options for non-responders, coded −1 for NFC and +1 for MI-PC. $A_2$ is left undefined for responders because they were not re-randomized; all responders receive NFC. Throughout, we assume the dataset is in a long form, such that each participant has six observations (rows in the dataset) corresponding to the six measurement occasions. In this paper, we also assume equal timing of observations, relative to each other and to the randomization times, across subjects; however, this assumption can be relaxed.

In the following section, we discuss how such repeated outcome data can be used to compare embedded AIs, following the method proposed by Lu and colleagues (2016). We present the procedure in six steps.

Comparing Adaptive Interventions With Repeated Outcome Measures

For each step, we provide a general conceptual overview. We then explain, when relevant, the modifications required for the case of binary rather than numerical outcome variables.

Step One: Create the Assigned Weights.

In a prototypical SMART such as ENGAGE, outcome data from early non-responders is under-represented, by design, in the sample average of each embedded AI. This is because only early non-responders are re-randomized to subsequent intervention options and hence are split into two subgroups, whereas early responders are not re-randomized and hence are not split into two subgroups. Using standard regression methods to compare the embedded AIs in such a setting will result in biased estimates (see details in Nahum-Shani et al., 2012; Lu et al., 2016). Hence, weights are used to correct for this imbalance. Because the randomization probabilities are known, one option is to assign a weight based on these known probabilities, namely the inverse of the randomization probability. In the case of ENGAGE, participants were randomized with equal probability (0.5) to either of the two first-stage intervention options, and then non-responders were re-randomized with equal probability (0.5) to the second-stage intervention options. Hence, by design, a non-responder would have 0.5×0.5=0.25 chance of being assigned to a particular AI, whereas a responder would have a 0.5 chance. Capitalizing on these known probabilities, the assigned weights would be $w_i=1/0.25=4$ for non-responders and $w_i=1/0.5=2$ for responders.

An alternative to using known weights as described above is to estimate the weights by using covariates that might be correlated with the repeated outcome measures. This approach, which has the potential to asymptotically improve efficiency of the estimator (Brumback, 2009; Hernan, Brumback, & Robins, 2002; Hirano, Imbens, & Ridder, 2003), can be employed in the current setting by conducting two logistic regressions to estimate the probability of assignment to the first- and second-stage intervention options respectively. To estimate the probability of assignment to the first-stage intervention options, the indicator for the first-stage intervention options $\left(A_1\right)$ can be regressed on covariates that are measured prior to the first-stage randomization (e.g., baseline information) and that are thought to correlate with the repeated outcomes. To estimate the probability of assignment to the second-stage intervention options among non-responders, the indicator for the second-stage intervention options $\left(A_2\right)$ among non-responders can be regressed on covariates that are measured prior to the second-stage randomization and that are thought to correlate with the repeated outcomes. The covariates for predicting A₂ could include both the baseline information and time-varying information obtained during the first intervention stage. Based on these logistic regressions, an estimated probability of assignment for first-stage and second-stage intervention options can be obtained for each individual. Multiplying the two probabilities yields the estimated weight for each individual.

The weights are reminiscent of inverse-probability of treatment weighting in causal inference (Robins, 1986); in addition, in observational study analyses, such weights must be estimated, which is reminiscent of the second approach to weighting discussed above. However, the goal of the estimated weights is not to correct for imbalance in how individuals are distributed across the assigned treatments, as is usually the case in the analysis of observational studies (Harder, Stuart, & Anthony, 2010; Rosenbaum & Rubin, 1983; Schafer & Kang, 2008). Indeed, in ENGAGE, treatment assignment probabilities at each stage are known, by design: all individuals at baseline (e.g., regardless of baseline severity or history of treatment) are assigned with equal probability to either initial MI-IOP or initial MI-PC; all responders are assigned ‘no further contact’ in the second-stage; and all non-responders (e.g., regardless of severity) are assigned with equal probability to either second-stage MI-PC or second-stage NFC. Rather, the goal of estimating the weights is to improve efficiency (see Hirano, Imbens, and Ridder 2003, Lu et al., 2016).

Step Two: Restructure the Dataset.

In a prototypical SMART, observations from early responders are consistent with more than one embedded AI (see details in Nahum-Shani et al., 2012). Since data from a particular responding individual can be used to estimate the mean outcome under multiple embedded AIs, familiar regression procedures in standard statistical software (e.g., SAS, R, SPSS) cannot be directly employed to simultaneously compare all embedded AIs (see Nahum-Shani et al., 2012; Lu et al., 2016). For example, in ENGAGE, responders to MI-IOP provide outcomes that are consistent with two interventions: later choice (which recommends MI-IOP initially and then MI-PC for non-responders and NFC for responders), and no choice (which recommends MI-IOP initially and then NFC for both non-responders and responders). Responders to MI-PC also provide outcomes that are consistent with two interventions: choice throughout (which recommends MI-PC initially and then MI-PC for non-responders), and initial choice (which recommends MI-PC initially and then NFC for both non-responders and responders). Hence, in order to estimate the mean outcome under all four AIs embedded in the ENGAGE SMART study simultaneously, outcome data from each responder should be used twice (to inform two estimated means).This can be done by restructuring the data in the following manner.

In the original long-form dataset, each participant in the ENGAGE study has six observations, one per measurement occasion. For each responder, each of the three observations is then replicated, so that instead of one observation per measurement occasion, the new dataset includes two identical observations per measurement occasion. $A_2$ is set to 1 in one of the replicated observations, and we set $A_2$ to −1 in the other replicated observation. Note that $A_2$ is missing in the original dataset for responders, since responders were not re-randomized to second-stage intervention options.

For example, suppose that the original data included 40 responders and 50 non-responders, each with 6 observations (for each of the 6 measurement occasions), namely 240 observations for responders and 300 observations for non-responders. Then the new dataset will include 480 observations for responders (2 identical observations for each of the 6 measurement occasions, for each of the 40 responders) as well as the same 300 observations for non-responders as before. Replicating observations of responders in that manner enables investigators to conveniently “reuse” repeated outcome measures from each responding individual to investigate the performance of two embedded AIs using one fitted regression model. As before, the new dataset should contain a variable providing the weights (either known or estimated) for each observation.

Step Three: Specify a Model.

To facilitate comparison of the AIs, it is helpful to specify a model for how individuals change over time in the course of a given AI. As an example, consider a piecewise linear model, which can be used with the new weighted and replicated dataset to compare the four embedded AIs. The outcome variable can change over time, and the rate of change over time might vary before and after the re-randomization to second-stage intervention options. Because of this potential change, the time variable $t$ is partitioned into two variables: number of months $S_1\left(t\right)$ spent in stage 1 (i.e., before re-randomization) and number of months $S_2\left(t\right)$ spent in stage 2 (i.e., following re-randomization).

For example, suppose that the first randomization is made at the same time as the first outcome measurement $Y_1$. Then for $t=1$, we would set $S_1\left(1\right)=0$ and $S_2\left(1\right)=0$ because no time has elapsed in treatment yet. Next, suppose that the second measurement occasion $Y_2$ has occurred 1 month following the first-stage randomization and immediately before the second-stage randomization. Hence, for $t=2$, $S_1\left(2\right)=1$ and $S_2\left(2\right)=0$ because one time unit has elapsed since the first randomization, but the second randomization has not occurred yet. The second randomization occurs at $t=2$, so $t=3$ corresponds to $S_1\left(3\right)=1$ and $S_2\left(3\right)=1$. $S_1$ is truncated at 1 because the first phase of the study lasted 1 time unit; thus, for $t\ge 3$, we would set $S_1=1$ and $S_2=t-2$.

It is important to code the time variables $S_1$ and $S_2$ in a way which reflects the design of the study as closely as possible. In many SMART studies, the first measurement $Y_1$ is a baseline measurement which is observed before the first action is applied. However, ENGAGE was somewhat unusual in that $A_1$ was assigned half a month before $Y_1$ was observed; this is explained further in the empirical analysis section below. Therefore, in the empirical data analysis we actually coded $S_1\left(1\right)=0.5$ instead of $S_1\left(1\right)=0$. For $t\ge 2$, we code $S_1\left(t\right)=1.5$ and $S_2\left(t\right)=t-2$.

For either coding of $S_1$ and $S_2$, a straightforward piecewise model is therefore

$$\begin{gathered} g\left(E\left[Y_t|\mathit{\text{X}},A_1,A_2\right]\right)={\beta }_0+\left({\beta }_{S1}+{\beta }_{A1S1}{A}_1\right)S_1\left(t\right)+\left({\beta }_{S2}+{\beta }_{S2A1}{A}_1+{\beta }_{S2A2}{A}_2+ \\ {\beta }_{S2A1A2}{A}_1{A}_2\right)S_2\left(t\right)+{\mathbf{\phi }}^{\text{T}}\mathit{\text{X}}, \end{gathered}$$ (1)

where $g()$ is the appropriate link function (identity link function in the case of a numerical outcome variable, logit link in the case of a binary outcome variable), $Y_t$ is the primary outcome at time (i.e., at measurement occasion), $\mathit{\text{X}}$ is a vector of baseline measures included in the regression models as mean-centered covariates, and $\mathbf{\phi }$ is a vector of regression coefficients expressing the effects of the baseline measures $\mathit{\text{X}}$. The quantity ${\beta }_{S1}+{\beta }_{A1S1}{A}_1$ expresses the expected change in the outcome during the first intervention stage, that is, the effect of increasing $S_1\left(t\right)$ from 0 to 1. Likewise, the quantity ${\beta }_{S2}+{\beta }_{S2A1}{A}_1+{\beta }_{S2A2}{A}_2+{\beta }_{S2A1A2}{A}_1{A}_2$ expresses the expected change during the second intervention stage.

Model (1) could be expanded in several ways. For example, the trajectory during the second phase could be allowed to be quadratic by including terms for $S_2^2$ in addition to $S_2$. However, we use the simple form (1) in this paper.

There are two important features in this piecewise model that accommodate the unique features of longitudinal data arising from a SMART. First, the effect of time (i.e., the expected change in the outcome) during the first intervention stage is allowed to vary only as a function of the first-stage intervention options $\left(A_1\right)$, whereas the effect of time during the second stage is allowed to vary as a function of both the first-stage $\left(A_1\right)$ and second-stage $\left(A_2\right)$ intervention options. In other words, model (1) respects the sequencing of the measurement occasions relative to the sequencing of the intervention options, enabling outcome measurements at each stage to be predicted only by intervention options that were introduced prior to that stage. Second, rather than modeling the effect of time as linear throughout the study, Model (1) accommodates a possible deflection in this effect at the end of month 2 because this is the point at which the intervention might be modified for non-responders. Lu and colleagues (2016) discussed the bias which would be incurred by failing to properly account for these features when using repeated outcome measures arising from a SMART to compare embedded AIs.

Step Four: Estimate the Coefficients in the Selected Model.

In order to estimate the model in Equation (1), building on the work of Lu and colleagues (2016), we use a weighted regression procedure, solving

$$\mathbf{0}={\sum }_{i=1}^N{\sum }_{\left(a_1,a_2\right)}{w}_i{c}_{i,a_1,a_2}{\mathbf{\text{D}}}_{i,a_1,a_2}^T{\mathbf{\text{V}}}_{i,a_1,a_2}^{-1}\left({\mathbf{\text{Y}}}_i-{\mathbf{\mu }}_{i,a_1,a_2}\right)$$ (2)

to estimate the regression coefficients. The notation in this expression is explained below. Further technical details are provided in Appendix A, and sample code in SAS and R is provided in the online supplement Appendix B (https://github.com/dziakj1/BinaryLongitudinalSmart). Let $c_{i,a_1,a_2}$ be the indicator function, which is 1 if the observed AI for an individual $i$ is consistent with an underlying sequence $\left(a_1,a_2\right)$ and 0 otherwise. Note that in this context, $c_{i,a_1,a_2}$ is a prespecified, known function of the observed data; it is not estimated or imputed. In particular, in a SMART like ENGAGE, where only non-responders are re-randomized to $A_2$, $c_{i,a_1,a_2}$ is defined as follows:

$$c_{i,a_1,a_2}=\{\begin{array}{cc}1\text{\hspace{0.17em}if}& A_{1i}=a_1,R_i=1\\ 1\text{\hspace{0.17em}if}& A_{1i}=a_1,R_i=0,A_{2i}=a_2\\ 0& \text{otherwise}\end{array}$$

where $A_{1i}$ is the first-stage treatment given to participant $i$, $R_i$ is the early response status indicator, taking the values 1 for responders and 0 for non-responders, and $A_{2i}$ is the first-stage treatment given to participant $i$ (which here is only observed, and only used, if $R_i=1$.)

Let ${\mathit{\text{Y}}}_i$ be the T-vector of observed outcomes at the $T$ measurement occasions for subject i. Let ${\mathit{\text{Z}}}_{a_1,a_2}$ be a T×p coded matrix expressing the p covariates in the marginal model for ${\mathit{\text{Y}}}_i$, assuming that the underlying sequence $(a_1,a_2)$ is followed. The value of p depends on the complexity of the longitudinal model. If Model (1) is used and there are no baseline covariates, then p = 7, corresponding to the intercept and the six covariates $S_1,A_1{S}_1,S_2,A_1{S}_2,A_2{S}_2,A_1{A}_2{S}_2$. If there are additional covariates ${\mathit{\text{X}}}_i$, they can be represented by including an additional entries of ${\mathit{\text{Z}}}_{a_1,a_2}$ and expanding the notation to ${\mathit{\text{Z}}}_{i,a_1,a_2}$ to allow the values of the covariates to vary among participants receiving the same AI. For generality, we will continue to use the $i$ subscript for the $\mathit{\text{Z}}$ matrix, with the understanding if there are no baseline covariates, ${\mathit{\text{Z}}}_{i,a_1,a_2}$ will actually be the same for all participants receiving the same AI. Next, ${\mathbf{\mu }}_{i,a_1,a_2}=\text{E}\left({\mathit{\text{Y}}}_i|{\mathit{\text{Z}}}_{i,a_1,a_2}\right)$, which is the T-vector of expected values of the outcome variable at the different measurement occasions under $(a_1,a_2)$. As usual in generalized estimating equations, it is assumed that $\text{E}\left(Y_{it}|{\mathit{\text{Z}}}_{i,a_1,a_2,t}\right)=\mu \left({\mathit{\text{Z}}}_{i,a_1,a_2,t}\mathbf{\beta }\right)$ for a known function $\mu (\cdot )$ and unknown parameter vector $\mathbf{\beta }$. $w_i$ represents the weight assigned to individual $i$ as described earlier in the first step. ${\mathbf{\text{D}}}_{i,a_1,a_2}$ is a T×p matrix of derivatives whose (t,p)^th entry is $\frac{\partial }{\partial {\mathbf{\beta }}_{\mathit{\text{p}}}}{\mu }_{i,a_1,a_2,t}$. Finally, ${\mathbf{\text{V}}}_{i,a_1,a_2}$ is a T×T matrix which serves as a working estimate of the covariance matrix of ${\mathbf{\text{Y}}}_i$ under sequence $\left(a_1,a_2\right)$, that is, of $\text{Cov}\left({\mathbf{\text{Y}}}_i|{\mathit{\text{Z}}}_{i,a_1,a_2}\right)$. In particular, ${\mathbf{\text{V}}}_{i,a_1,a_2}$ is treated as being equal to ${\mathbf{\text{M}}}_{i,a_1,a_2}^{1/2}{\mathbf{\text{R}}}_{a_1,a_2}{\mathbf{\text{M}}}_{i,a_1,a_2}^{1/2}$, with ${\mathbf{\text{R}}}_{a_1,a_2}$ being a working correlation matrix and ${\mathbf{\text{M}}}_{i,a_1,a_2}$ being a T×T diagonal matrix of marginal variances $M_{tt}=\text{Var}\left(Y_{it}|{\mathit{\text{Z}}}_{a_1,a_2,t}\right)$.

Equation (2) is similar to the generalized estimating equation (GEE) estimator (Liang & Zeger 1986). As in classic GEE, the solution $\widehat{\mathbf{\beta }}$ obtained by solving equation (1) is unbiased for the true value of $\mathbf{\beta }$ regardless of the working structure for ${\mathbf{\text{V}}}_{i,a_1,a_2}$. To estimate the standard errors for $\widehat{\mathbf{\beta }}$, Lu and colleagues (2016) recommend a sandwich estimator (discussed in detail in Appendix A) and recommend a way of adjusting the sandwich estimator in the presence of estimated weights.

Step four for a normally distributed outcome.

The equation in (2) applies to many possible outcome distributions. In the case of a normally distributed outcome with an identity link function, ${\mathbf{\mu }}_{i,a_1,a_2}={\mathbf{\text{Z}}}_{i,a_1,a_2}\mathbf{\beta }$, so that ${\mathbf{\text{D}}}_{i,a_1,a_2}={\mathbf{\text{Z}}}_{i,a_1,a_2}$. Under the working assumption of homoskedasticity over measurement times and AIs, equation (2) would simplify to

$$\mathbf{0}={\sum }_{i=1}^N{\sum }_{\left(a_1,a_2\right)}{w}_i{c}_{i,a_1,a_2}{\mathbf{\text{Z}}}_{i,a_1,a_2}^T{\mathbf{\text{R}}}_{a_1,a_2}^{-1}\left({\mathbf{\text{Y}}}_i-{\mathbf{\text{Z}}}_{i,a_1,a_2}\mathbf{\beta }\right).$$ (3)

Below, we discuss the details of how equation (2) can be applied to repeated binary outcome measures with logit link.

Step four for a binary outcome.

In the case of a binary outcome with a logit link function,

$$\begin{array}{cc}{\mu }_{i,a_1,a_2,t}& =\mu \left({\mathit{\text{Z}}}_{i,a_1,a_2,t}\mathbf{\beta }\right)={\text{logit}}^{-1}\left({\mathit{\text{Z}}}_{i,a_1,a_2,t}\mathbf{\beta }\right)\hfill \\ ⬚& =\left(\text{exp}\left({\mathit{\text{Z}}}_{i,a_1,a_2,t}\mathbf{\beta }\right)\right)/\left(1+\text{exp}\left({\mathit{\text{Z}}}_{i,a_1,a_2,t}\mathbf{\beta }\right)\right)\hfill \end{array}$$

After some algebra, ${\mathbf{\text{D}}}_{i,a_1,a_2}={\mathbf{\text{Z}}}_{i,a_1,a_2}^T{\mathbf{\text{M}}}_{i,a_1,a_2}$, where ${\mathbf{\text{M}}}_{i,a_1,a_2}$ is a diagonal matrix of the marginal variances ${\mu }_{i,a_1,a_2,t}\left(1-{\mu }_{i,a_1,a_2,t}\right)$. Then (2) becomes

$$\mathbf{0}={\sum }_{i=1}^N{\sum }_{\left(a_1,a_2\right)}{w}_i{c}_{i,a_1,a_2}{\mathbf{\text{Z}}}_{i,a_1,a_2}^T{\mathbf{\text{M}}}_{i,a_1,a_2}^{1/2}{\mathbf{\text{R}}}^{-1}{\mathbf{\text{M}}}_{i,a_1,a_2}^{-1/2}\left({\mathbf{\text{Y}}}_i-{\mathbf{\mu }}_{i,a_1,a_2}\right).$$ (4)

When comparing equations (3) and (4), recall that ${\mathbf{\mu }}_{i,a_1,a_2}$ is defined differently in each because of the different link function. If working independence is being used so that R is the identity matrix, then (4) simplifies to

$$\mathbf{0}={\sum }_{i=1}^N{\sum }_{\left(a_1,a_2\right)}{w}_i{c}_{i,a_1,a_2}{\mathbf{\text{Z}}}_{i,a_1,a_2}^T\left({\mathbf{\text{Y}}}_i-{\mathbf{\mu }}_{i,a_1,a_2}\right).$$ (5)

Note that the empirical analysis in this paper uses autoregressive (AR-1) structure for the R matrix, so the simplified form (5) does not apply. The simulation study discussed later compares three different working structures, including independence and AR-1.

Step Five: Choose Which Contrast to Estimate.

Various estimands can be used to compare embedded AIs with repeated outcome measures arising from a SMART. Four estimands that are likely to be of high clinical or theoretical importance and that are relatively straightforward to interpret are the following: (a) the expected outcome at end of study, (b) the stage-specific slopes, (c) the AUC from baseline to end of study, and (d) the delayed effect of stage one treatment option during stage two.

The first estimand of interest is the expected end-of-study outcome. The expected outcome at the end of the study under a given embedded AI $(a_1,a_2)$ is simply the probability $E_{a_1,a_2}\left[Y_t\right]$ for the largest observed value of $t$, which is 6 in our example. We abbreviate this as ${\pi }_6$. The contrast between two AIs $(a_1,a_2)$ and $(a_1^{\text{'}},a_2^{\text{'}})$ in terms of end-of-study outcome is therefore $E_{a_1,a_2}\left[Y_6\right]-E_{a_1^{\text{'}},a_2^{\text{'}}}\left[Y_6\right]$, which we abbreviate as ${\pi }_6-{\pi }_6^{\text{'}}$. Note that the prime symbol $\text{'}$ is used here to mean “other,” not “derivative of.” The values of ${\pi }_t$ for a given AI $(a_1,a_2)$ are obtained from ${\eta }_t=\text{logit}({\pi }_t)$ calculated as the right-hand side of Model 1.

Even for an estimand as simple as the end-of-study outcome, the binary nature of the outcome means that choices have to be made. First, the researcher must decide whether the scale of measurement for the estimand of interest will be in terms of probability, odds, or log odds. That is, instead of the difference in probabilities ${\pi }_6-{\pi }_6^{\text{'}}$, one could alternatively use an odds ratio $(\frac{{\pi }_6}{1-{\pi }_6})/(\frac{{\pi }_6^{\text{'}}}{1-{\pi }_6^{\text{'}}})$, or simply ${\eta }_t$ itself, which is the logarithm of the odds ratio. Odds ratios and log odds ratios can give more emphasis to rare events than probabilities do. For example, a difference in success proportions of .01 versus .03 represents the same effect size on the probability scale as a difference of .51 versus .53, but the odds ratios are not the same: 3.06 for the first comparison and only 1.08 for the second. However, probabilities, odds or log odds are each valid ways to compare AIs on a binary outcome. The log odds ratio (logit) scale has the advantage that the estimand is a linear function of the regression coefficients. However, in some cases, the actual probabilities are more interpretable. Fortunately, because the probability, odds, and log odds are all monotonically related, the comparison between a pair of AIs in terms of an outcome at a given time point will always have the same sign regardless of the scale of measure.

Another decision involves the pre-randomization (baseline) covariates. If the probabilities or odds are being used as the outcome metric, then covariates will not cancel out when comparing outcomes between AIs, even if they are set to the same level. This is because the estimand of interest is no longer a linear function of the regression coefficients. Mathematically, ${\text{logit}}^{-1}\left({\mathit{\text{Z}}}_i\mathbf{\beta }\right)-{\text{logit}}^{-1}\left({\mathit{\text{Z}}}_{i^{\text{'}}}\mathbf{\beta }\right)\ne {\text{logit}}^{-1}\left(({\mathit{\text{Z}}}_i-{\mathit{\text{Z}}}_{i^{\text{'}}})\mathbf{\beta }\right)$ even though ${\mathit{\text{Z}}}_i\mathbf{\beta }-{\mathit{\text{Z}}}_{i^{\text{'}}}\mathbf{\beta }=\left({\mathit{\text{Z}}}_i-{\mathit{\text{Z}}}_{i^{\text{'}}}\right)\mathbf{\beta }$. Therefore, the size of the difference in outcomes depends on the value assumed for the baseline covariates, even if this value is assumed to be the same for both AIs. As an extreme example, if the value chosen for the baseline covariates predicts a very high success probability, then there may be less room left for the choice of AI to have a practically significant effect. Thus, if an outcome scale other than log odds is being used, it is necessary to choose a level at which to fix each baseline covariate for purposes of calculating the fitted values.

The second estimand of interest is the slope during stage 1 or during stage 2, which is directly related to the expected improvement or decline in the outcome of interest during that stage. A researcher may be interested in making an inference on a slope for a particular AI (e.g., whether statistically significant change is expected during a stage) or on a contrast between two AIs in terms of corresponding slopes (e.g., whether one intervention causes quicker improvement than another during the initial stage). As in the case of a comparison of point outcomes, a researcher can choose between estimating the slope on the probability scale, the odds scale, or the log odds scale. It is not clear which scale is the most interpretable, but the log odds scale is much easier to use. This is because differences in slopes on the log odds scale can be expressed as simple linear combinations of regression coefficients. Using the piecewise model specified by expression (1) with the logit link function, the first-stage slope on the log odds scale for AI $(a_1,a_2)$ is ${\beta }_{S_1}+{\beta }_{S_1{A}_1}{a}_1$, and the second-stage slope on the log odds scale for AI $(a_1,a_2)$ is ${\beta }_{S_2}+{\beta }_{S_2{A}_1}{a}_1+{\beta }_{S_2{A}_2}{a}_2+{\beta }_{S_2{A}_1{A}_2}{a}_1{a}_2$. Differences between interventions can be calculated accordingly. For example, the difference in first-stage slopes between AIs $(+1,a_2)$ and $(-1,a_2^{\text{'}})$ is $\left({\beta }_{S_1}+{\beta }_{S_1{A}_1}\right)-\left({\beta }_{S_1}-{\beta }_{S_1{A}_1}\right)=2{\beta }_{S_1{A}_1}$, again on the log-odds scale. Differences in second-stage slopes can be calculated similarly. For example, the difference in second-stage slopes between AI’s $(+1,+1)$ and $(-1,+1)$ is $\left({\beta }_{S_2}+{\beta }_{S_2{A}_1}+{\beta }_{S_2{A}_2}+{\beta }_{S_2{A}_1{A}_2}\right)-\left({\beta }_{S_2}-{\beta }_{S_2{A}_1}+{\beta }_{S_2{A}_2}-{\beta }_{S_2{A}_1{A}_2}\right)=2\left({\beta }_{S_2{A}_1}+{\beta }_{S_2{A}_1{A}_2}\right)$, and the difference in second-stage slopes between AI’s $(+1,+1)$ and $(-1,-1)$ is $\left({\beta }_{S_2}+{\beta }_{S_2{A}_1}+{\beta }_{S_2{A}_2}+{\beta }_{S_2{A}_1{A}_2}\right)-\left({\beta }_{S_2}-{\beta }_{S_2{A}_1}-{\beta }_{S_2{A}_2}+{\beta }_{S_2{A}_1{A}_2}\right)=2\left({\beta }_{S_2{A}_1}+{\beta }_{S_2{A}_2}\right)$.

Another reason why the log-odds scale is easier to interpret is that Model (1) only assumes that the trajectory within each stage is linear on the log-odds scale, not that it is linear on the odds or raw probability scale; generally it could not be linear on more than one of these scales, except in the special case where it is zero on all of them. We consider slopes only on the log-odds scale in this paper.

The third estimand, the area under the curve (AUC), is a summary which takes into account measurements at all time points, not only the last one (Fekedulegn et al., 2007), so it is useful when the participants’ experiences over the course of the trial are of interest rather than only the final endpoint. One limitation is that the AUC by itself does not completely describe the process. Because it essentially averages the time points, it does not distinguish a trajectory that rises and falls from one that simply maintains flat at a medium level. Thus, the AUC is not a replacement for the stage-specific slope. The investigator may choose to estimate the AUC of probabilities, odds, or log odds as a function over time. The AUC of probabilities is somewhat more interpretable because it can be rescaled to yield an estimate of the average probability $E\left(Y|A_1,A_2\right)$ over time. Therefore, it may be best to use the probability scale for comparing AUC’s for binary outcomes. However, as with time-specific outcomes, this requires specifying a particular level of each baseline covariate at which to compare the difference in estimated AUC’s.

The AUC of the probability curve is a weighted sum of fitted probabilities, with weights determined by the number and spacing of time points. In particular, it is supposed that the outcome probability $\pi \left(t\right)$ is a smooth function of time $t$, and define AUC as the integral of $\pi \left(t\right)$ over the time interval from the beginning to the end of the study. Because $\pi \left(t\right)$ is only observed at integer time points ${\pi }_1=\pi \left(1\right)$, ${\pi }_2=\pi \left(2\right)$, etc., we interpolate by assuming $\pi \left(t\right)$ is linear between time points. The resulting formula turns out to be a weighted sum of the probabilities ${\pi }_t$. To see this, consider our example with six evenly spaced time points. The AUC between times 1 and 2 can be approximated as a trapezoid of base width $2-1=1$ and height ${\pi }_1$ on the left leg and ${\pi }_2$ on the right leg; the area of this trapezoid is $\frac{1}{2}{\pi }_1+\frac{1}{2}{\pi }_2$. Similarly, the AUC is $\frac{1}{2}{\pi }_2+\frac{1}{2}{\pi }_3$ between times 2 and 3, $\frac{1}{2}{\pi }_3+\frac{1}{2}{\pi }_4$ between times 3 and 4, $\frac{1}{2}{\pi }_4+\frac{1}{2}{\pi }_5$, between times 4 and 5, and $\frac{1}{2}{\pi }_5+\frac{1}{2}{\pi }_6$ between times 5 and 6. The total AUC is the sum of AUCs of these 5 trapezoids, namely $\frac{1}{2}{\pi }_1+{\pi }_2+{\pi }_3+{\pi }_4+{\pi }_5+\frac{1}{2}{\pi }_6$. Each of the ${\pi }_t$ values can be obtained for each embedded AI as a fitted value from Model (1).

The AUC is proportional to the average of the probability function over the duration of the study. Let us write the estimated successful outcome probability at time $t$ as $\pi \left(t\right)$ instead of ${\pi }_t$ to emphasize that we are temporarily imagining time as continuous, interpolating between the observed times. Then applying the law of iterated expectation and assuming $t$ is randomly selected from a uniform random distribution over the 5-unit interval from 1 to 6, we have $\text{E}\left(Y\right)=\text{E}\left(\text{E}\left(Y|t\right)\right)=\frac{1}{6-1}{\int }_1^6\pi \left(t\right)dt=\frac{1}{5}\text{AUC}$. Although dividing by the length of the time interval is necessary in order to interpret the $\text{AUC}$ as an average probability, all of the AIs have the same time interval length, so tests of the differences between AUCs are equivalent to tests of the differences between $\frac{1}{5}\text{AUC}$. We call this rescaled AUC the “time-averaged AUC” because of its interpretability as an estimated average probability over time.

A fourth estimand of interest when comparing the change processes expected for each AI is the delayed effect. The delayed effect measures the difference between a long-term and a short-term effect. This is actually a difference in differences, which is a kind of statistical interaction: in other words, it is the difference between the long-term difference and the short-term difference between the expected outcomes of two AIs. The delayed effect of one AI $(a_1,a_2)$ relative to another AI $(a_1^{\text{'}},a_2^{\text{'}})$ can be operationally defined as the difference between the contrasts in a long-term outcome (e.g., following second-stage randomization) and the contrasts in a short-term outcome (e.g., prior to second-stage randomization). In the ENGAGE example, it would be reasonable to take time 2 as the short-term outcome (because the re-randomization was done then) and time 6 as the long-term outcome (because it is the last follow-up). That is, the delayed effect in that example is $({\pi }_6-{\pi }_6^{\text{'}})-({\pi }_2-{\pi }_2^{\text{'}})$. If the absolute value of the delayed effect is large, it means that the short term effect (i.e., when only first-stage options are introduced) of one AI compared to another is significantly different from its long-term effect (i.e., when subsequent intervention options are introduced). One could also compare two AIs at different follow-up times after the second randomization (e.g., times 3 versus 6 instead of 2 versus 6) depending on the scientific questions of interest.

Step Six: Use the Fitted Model to Estimate the Contrasts of Primary Interest.

Regardless of the estimand(s) chosen, they can all be calculated from the coefficients of Model (1). We work through this step for the case of a contrast in AUCs of the probabilities over time. As argued above, it seems more informative and interpretable to focus on the AUC for the expected outcome (e.g., abstinence) probabilities rather than the AUC for the expected log odds of the outcome. However, the contrasts in probabilities and their standard errors takes some extra work to compute because it is not a linear function of the model parameters. Recall that if estimands of interest can be expressed as a linear combination of regression coefficients, namely $\mathbf{\text{L}}\widehat{\mathbf{\beta }}$, then their standard errors can be computed using the identity $\text{Cov}\left(\mathbf{\text{L}}\widehat{\mathbf{\beta }}\right)=\mathbf{L}\text{Cov}(\widehat{\mathbf{\beta }}){\mathbf{\text{L}}}^T$. Thus, standard errors in this case would be the square roots of the diagonal entries of $\text{Cov}\left(\mathbf{\text{L}}\widehat{\mathbf{\beta }}\right)$. Such an $\mathbf{\text{L}}$ can be constructed for the AUC of the mean of a linear model, or in the AUC of the log odds of a logistic model, but not for the AUC of the probability in a logistic model. Because of this, some additional work is required in order to obtain estimates and standard errors for AUCs, or for contrasts of AUCs, in the binary case.

Using the law of iterated expectation, the value of ${\pi }_t$ for AI $(a_1,a_2)$ can be calculated as

$$\begin{array}{cc}E\left(Y_t|a_1,a_2\right)=& P\left(R=0|A_1=a_1\right)E\left(Y_t|A_1=a_1,A_2=a_2,R=0\right)+\hfill \\ ⬚& P\left(R=1|A_1=a_1\right)E\left(Y_t|A_1=a_1,A_2=a_2,R=1\right)\hfill \end{array}$$

using the fitted values for $E\left(Y_t|A_1,A_2,R\right)$ from the longitudinal analysis and using the empirical proportions of responders and non-responders in each first-stage treatment group for $P\left(R|A_1\right)$. These can be used to easily compute the point estimate

$$\widehat{\text{AUC}}=\frac{1}{2}{\widehat{\pi }}_1+{\widehat{\pi }}_2+{\widehat{\pi }}_3+{\widehat{\pi }}_4+{\widehat{\pi }}_5+\frac{1}{2}{\widehat{\pi }}_6$$

for AI $(a_1,a_2)$. However, it remains necessary to compute the error variance for $\widehat{\text{AUC}}$ for each AI. Notice that the log odds ${\widehat{\eta }}_t$ at time $t$ are given by the right-hand side of Model (1) and are a linear combination of regression coefficients. If there are no baseline coordinates, then Model (1) gives $\mathbf{\eta }=\mathbf{\text{L}}\mathbf{\beta }$, where $\mathbf{\text{L}}$ is a matrix whose $t$^th row is

$$\left[1,S_1\left(t\right),S_2\left(t\right),S_1\left(t\right)a_1,S_2\left(t\right)a_1,S_2\left(t\right)a_2,S_2\left(t\right)a_1{a}_2\right],$$

and where $\mathbf{\beta }={\left[{\beta }_0,{\beta }_{\text{S}1},{\beta }_{S2},{\beta }_{S1A1},{\beta }_{S2A1},{\beta }_{S2A2},{\beta }_{S2A1A2}\right]}^T$. If there are baseline covariates, then reference values must be chosen for them. The specified AUC estimate will be the expected value for a hypothetical participant with those values.

Recall that for the ENGAGE dataset we set $S_1=0.5$ and $S_2=0$ for $t=1$, and set $S_1=1.5$ and $S_2=t-2$ for $t>1$, because the randomizations were assumed to have been performed at $t=0.5$ and $t=2$ instead of $t=1$ and $t=2$, counting the first outcome measurement time as $t=1$. Therefore, for a given AI $(a_1,a_2)$, the matrix of linear coefficients, without baseline covariates, is

$$\mathit{\text{L}}(a_1,a_2)=\left[\begin{array}{ccccccc}1& 0.5& 0& 0.5a_1& 0& 0& 0\\ 1& 1.5& 0& 1.5a_1& 0& 0& 0\\ 1& 1.5& 1& 1.5a_1& a_1& a_2& a_1{a}_2\\ 1& 1.5& 2& 1.5a_1& 2a_1& 2a_2& 2a_1{a}_2\\ 1& 1.5& 3& 1.5a_1& 3a_1& 3a_2& 3a_1{a}_2\\ 1& 1.5& 4& 1.5a_1& 4a_1& 4a_2& 4a_1{a}_2\end{array}\right],$$

Note that if the first randomization had been at $t=1$, as is more usual in SMART trials, the matrix would have been

$$\mathit{\text{L}}(a_1,a_2)=\left[\begin{array}{ccccccc}1& 0& 0& 0& 0& 0& 0\\ 1& 1& 0& a_1& 0& 0& 0\\ 1& 1& 1& a_1& a_1& a_2& a_1{a}_2\\ 1& 1& 2& a_1& 2a_1& 2a_2& 2a_1{a}_2\\ 1& 1& 3& a_1& 3a_1& 3a_2& 3a_1{a}_2\\ 1& 1& 4& a_1& 4a_1& 4a_2& 4a_1{a}_2\end{array}\right].$$

In either case, baseline covariates can be included by appending additional columns of constants to $\mathit{\text{L}}$, representing the level at which each covariate is hypothetically fixed for obtaining the fitted values of the estimands.

Cramér’s delta method (Taylor linearization) shows that $\widehat{\mathbf{\eta }}=\mathbf{\text{L}}\widehat{\mathbf{\beta }}$ is asymptotically unbiased for $\mathbf{\eta }=\mathbf{\text{L}}\mathbf{\beta }$ with asymptotic covariance $\mathbf{L}\text{Cov}(\widehat{\mathbf{\beta }}){\mathbf{\text{L}}}^T$. Going a step further, notice that $\widehat{\text{AUC}}$ can be rewritten as

$$\widehat{\text{AUC}}{=}_{+{\text{logit}}^{-1}\left({\widehat{\eta }}_4\right)+{\text{logit}}^{-1}\left({\widehat{\eta }}_5\right)+\frac{1}{2}{\text{logit}}^{-1}\left({\widehat{\eta }}_6\right).}^{\frac{1}{2}{\text{logit}}^{-1}\left({\widehat{\eta }}_1\right)+{\text{logit}}^{-1}\left({\widehat{\eta }}_2\right)+{\text{logit}}^{-1}\left({\widehat{\eta }}_3\right)}$$

Therefore, Cramér’s delta method shows that $\widehat{\text{AUC}}$ is an asymptotically unbiased estimate of $\text{AUC}$ and that this estimator has asymptotic variance ${\left(\frac{\partial \text{AUC}}{\partial \eta }\right)}^T\left(\text{Cov}\left(\widehat{\mathbf{\eta }}\right)\right)\left(\frac{\partial \text{AUC}}{\partial \eta }\right)$. Because $\frac{\partial {\pi }_t}{\partial {\eta }_t}={\pi }_t\left(1-{\pi }_t\right)$, we have $\frac{\partial \text{AUC}}{\partial {\eta }_t}=\frac{1}{2}{\pi }_t\left(1-{\pi }_t\right)$ for $t=1$ or 6, and $\frac{\partial \text{AUC}}{\partial {\eta }_1}={\pi }_t\left(1-{\pi }_t\right)$ for $t=2,3,4,\text{or\hspace{0.17em}}5$. Thus, the asymptotic variance estimate of $\widehat{\text{AUC}}$ is

$$\text{Var}\left(\widehat{\text{AUC}}\right)={\mathit{\text{d}}}^T\mathbf{L}\text{Cov}\left(\widehat{\mathbf{\beta }}\right){\mathbf{\text{L}}}^T\mathit{\text{d}}\hspace{1em}\text{with}\hspace{1em}\mathit{\text{d}}=\left[\begin{array}{c}\frac{1}{2}{\widehat{\pi }}_1\left(1-{\widehat{\pi }}_1\right)\\ {\widehat{\pi }}_2\left(1-{\widehat{\pi }}_2\right)\\ {\widehat{\pi }}_3\left(1-{\widehat{\pi }}_3\right)\\ {\widehat{\pi }}_4\left(1-{\widehat{\pi }}_4\right)\\ {\widehat{\pi }}_5\left(1-{\widehat{\pi }}_5\right)\\ \frac{1}{2}{\widehat{\pi }}_6\left(1-{\widehat{\pi }}_6\right)\end{array}\right].$$

We are actually interested not only in AUC for one AI, but in contrasts of the AUC under pairs of possible embedded AIs. In particular, let $\text{AUC}(a_1,a_2)$ be the AUC for AI $(a_1,a_2)$. We are interested in estimating $\text{DIFF}=\text{AUC}(a_1,a_2)-\text{AUC}(a_1^{\text{'}},a_2^{\text{'}})$ for some pair of AI $(a_1,a_2)$ and AI $(a_1^{\text{'}},a_2^{\text{'}})$. This can be written as

$$\begin{array}{cc}\text{DIFF}=& \text{AUC}(a_1,a_2)-\text{AUC}(a_1^{\prime },a_2^{\prime })\\ =& \left(\frac{1}{2}{\pi }_1+{\pi }_2+{\pi }_3+{\pi }_4+{\pi }_5+\frac{1}{2}{\pi }_6\right)-\left(\frac{1}{2}{\pi }_1^{\prime }+{\pi }_2^{\prime }+{\pi }_3^{\prime }+{\pi }_4^{\prime }+{\pi }_5^{\prime }+\frac{1}{2}{\pi }_6^{\prime }\right)\\ =& \frac{1}{2}{\text{logit}}^{-1}({\eta }_1)+{\text{logit}}^{-1}({\eta }_2)+{\text{logit}}^{-1}({\eta }_3)+{\text{logit}}^{-1}({\eta }_4)+{\text{logit}}^{-1}({\eta }_5)+\frac{1}{2}{\text{logit}}^{-1}({\eta }_6)\\ ⬚& -\frac{1}{2}{\text{logit}}^{-1}({\eta }_1^{\prime })-{\text{logit}}^{-1}({\eta }_2^{\prime })-{\text{logit}}^{-1}({\eta }_3^{\prime })-{\text{logit}}^{-1}({\eta }_4^{\prime })-{\text{logit}}^{-1}({\eta }_5^{\prime })-\frac{1}{2}{\text{logit}}^{-1}({\eta }_6^{\prime }).\end{array}$$

where $\mathbf{\eta }$ and ${\mathbf{\eta }}^{\prime }$ are the 6-vectors of ${\eta }_t$ and ${\eta }_t^{\prime }$ values. The estimate $\widehat{\text{DIFF}}$ is obtained using the estimates ${\widehat{\eta }}_t$ and ${\widehat{\eta }}_t^{\prime }$ from Model (6), and Cramér’s delta method can be used in the same way as before to estimate $\text{Var}(\widehat{\text{DIFF}})$. First, $\left[\begin{array}{c}\widehat{\mathbf{\eta }}\\ {\widehat{\mathbf{\eta }}}^{\prime }\end{array}\right]=\left[\begin{array}{l}\mathbf{\text{L}}\\ {\mathbf{\text{L}}}^{\prime }\end{array}\right]\widehat{\mathbf{\beta }}$, where L and ${\mathbf{\text{L}}}^{\prime }$ are abbreviations for $\mathbf{\text{L}}(a_1,a_2)$ and $\mathbf{\text{L}}(a_1^{\prime },a_2^{\prime })$. Therefore, $\text{Cov}(\left[\begin{array}{l}\widehat{\mathbf{\eta }}\\ {\widehat{\mathbf{\eta }}}^{\prime }\end{array}\right])=\left[\begin{array}{l}\mathbf{\text{L}}\\ -{\mathbf{\text{L}}}^{\prime }\end{array}\right]\text{Cov}(\widehat{\mathbf{\beta }}){\left[\begin{array}{l}\mathbf{\text{L}}\\ -{\mathbf{\text{L}}}^{\prime }\end{array}\right]}^T=\left[\begin{array}{l}\mathbf{\text{L}}\\ {\mathbf{\text{L}}}^{\prime }\end{array}\right]\text{Cov}(\widehat{\mathbf{\beta }}){\left[\begin{array}{l}\mathbf{\text{L}}\\ {\mathbf{\text{L}}}^{\prime }\end{array}\right]}^T$. Going a step further, the asymptotic variance of $\widehat{\text{DIFF}}$ is therefore

$$\begin{array}{cc}\text{Var}(\widehat{\text{DIFF}})=& {\left[\begin{array}{l}\mathit{\text{d}}\\ {\mathit{\text{d}}}^{\prime }\end{array}\right]}^T\left(\text{Cov}\left(\left[\begin{array}{l}\widehat{\mathbf{\eta }}\\ {\widehat{\mathbf{\eta }}}^{\prime }\end{array}\right]\right)\right)\left[\begin{array}{l}\mathit{\text{d}}\\ {\mathit{\text{d}}}^{\prime }\end{array}\right]\\ ⬚& ={\left[\begin{array}{l}\mathit{\text{d}}\\ {\mathit{\text{d}}}^{\prime }\end{array}\right]}^T\left[\begin{array}{l}\mathbf{\text{L}}\\ {\mathbf{\text{L}}}^{\prime }\end{array}\right]\left(\text{Cov}(\widehat{\mathbf{\beta }})\right){\left[\begin{array}{l}\mathbf{\text{L}}\\ {\mathbf{\text{L}}}^{\prime }\end{array}\right]}^T\left[\begin{array}{l}\mathit{\text{d}}\\ {\mathit{\text{d}}}^{\prime }\end{array}\right],\end{array}$$

where $\mathit{\text{d}}=\frac{\partial \widehat{\text{DIFF}}}{\partial \widehat{\mathbf{\eta }}}$ and ${\mathit{\text{d}}}^{\prime }=\frac{\partial \widehat{\text{DIFF}}}{\partial {\widehat{\mathbf{\eta }}}^{\prime }}$, again using $\prime$ to represent “other,” not “derivative of.” Recall that by the properties of the logistic function, $\frac{\partial }{\partial {\eta }_t}{\text{logit}}^{-1}\left({\eta }_t\right)={\pi }_t\left(1-{\pi }_t\right)$ so that

$$\mathit{\text{d}}=\left[\begin{array}{c}+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\widehat{\pi }}_1\left(1-{\widehat{\pi }}_1\right)\\ {\widehat{\pi }}_2\left(1-{\widehat{\pi }}_2\right)\\ {\widehat{\pi }}_3\left(1-{\widehat{\pi }}_3\right)\\ {\widehat{\pi }}_4\left(1-{\widehat{\pi }}_4\right)\\ {\widehat{\pi }}_5\left(1-{\widehat{\pi }}_5\right)\\ \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\widehat{\pi }}_6\left(1-{\widehat{\pi }}_6\right)\end{array}\right].$$

The asymptotic standard error of $\widehat{\text{DIFF}}$ is then obtained as $\sqrt{\text{Var}(\widehat{\text{DIFF}})}$. The form of $\text{Var}(\widehat{\text{AUC}})$ or $\text{Var}(\widehat{\text{DIFF}})$ as a function of $\text{Cov}(\widehat{\mathbf{\beta }})$ does not depend on whether the known or estimated form of the weights are used, because $\widehat{\text{AUC}}$ and $\widehat{\text{DIFF}}$ remain the same functions of $\widehat{\mathbf{\beta }}$. However, Lu and colleagues (2016) recommended an adjustment to $\text{Cov}(\widehat{\mathbf{\beta }})$ itself if weights are estimated; this is summarized in Appendix A.

Another possibility for estimating standard errors, rather than using the asymptotic covariance matrix and Cramér’s delta method, would be to use a bootstrapping approach. We have not explored this possibility here. The bootstrapping procedure would have to be done before applying the weighting and replication procedure.

Empirical Data Analysis

The previous section outlined a six-step procedure for obtaining estimates and standard errors for comparisons of important estimands under particular AIs. We now present the results of the proposed analysis with the ENGAGE SMART data. In the ENGAGE study, individuals entered an IOP and their engagement with the IOP was monitored. After at least two weeks in the IOP, if their engagement with the IOP was suboptimal, they were randomized to one of the two initial engagement strategies described earlier, namely either MI-IOP or MI-PC, which are represented by the two levels of $A_1$. In total, 273 individuals were randomized to MI-PC (n=137) and MI-IOP (n=136). Two months following IOP entry, participants who were classified as non-responders were re-randomized to levels of $A_2$, namely MI-PC (n=57) and NFC (n=53), as described earlier. Weekly timeline followback (TLFB) assessments over a 6 month period were summarized to obtain monthly measurements of whether (=1) or not (=0) the individual was abstinent one, two, three, four, five and six months after the beginning of the IOP. The monthly measurements of the abstinence binary outcome are denoted $Y_1,Y_2,Y_3,Y_4,Y_5,$ and $Y_6$, respectively. In sum, an approximate representative time course would be as follows: $A_1$ was assigned at least half a month after IOP entry, $Y_1$ was assessed one month after IOP entry, $Y_2$ was assessed two months after IOP entry, $A_2$ was assigned among non-responders two months after IOP entry, and $Y_3,Y_4,Y_5$ and $Y_6$ were assessed 3, 4, 5 and 6 months following IOP entry, respectively.

As mentioned earlier, there was no measurement of monthly abstinence at the exact time of the first randomization; rather, a baseline measure of alcohol/cocaine use in the month prior to IOP entry (i.e., $t=0$) was obtained. Including abstinence at $t=0$ as a repeated measure would have required an assumption of a linear trajectory between abstinence at program entry and abstinence at the end of month 1. This would not be realistic because the assignment of $A_1$ in the middle of this interval could cause a change in trajectory. Hence, the baseline measure of alcohol or cocaine use prior to IOP entry was treated as a covariate rather than a repeated measure.

Our analysis focuses on the comparison between two of the four embedded AIs, choice throughout (1, 1) and later choice (−1, 1), using two binary outcomes, which were analyzed separately. The first is cocaine abstinence in a given month, coded 1 if the individual reported no cocaine use days during the month and 0 if the individual reported one or more cocaine use days during the month. The second is alcohol abstinence over a month, coded 1 if the individual reported no drinking days during the month and 0 if the individual reported one or more drinking days during the month. In both models, we included gender (effect-coded as 1 for male and −1 for female) as a covariate. Additionally, the number of cocaine use days at baseline (i.e., in the month prior to IOP entry) was included as a covariate in the model for cocaine abstinence, and the number of alcohol use days at baseline was included as a covariate in the model for alcohol abstinence. The resulting model for each substance was

$$\begin{gathered} {\eta }_t=\text{logit}\left({\pi }_t\right)={\beta }_0+{\phi }_1{X}_1+{\phi }_2{X}_2+\left({\beta }_{S1}+{\beta }_{A1S1}{A}_1\right)S_1\left(t\right)+({\beta }_{S2}+{\beta }_{S2A1}{A}_1 \\ +{\beta }_{S2A2}{A}_2+{\beta }_{S2A1A2}{A}_1{A}_2)S_2\left(t\right), \end{gathered}$$ (7)

where $X_1$ and $X_2$ represent gender and baseline use days for that substance.

There were some missing data due to study dropout (n=68) or skipping a study assessment (n=22). For illustrative purposes, we present here the analyses with complete cases (n =183). The data was weighted and replicated as described earlier. Estimated (rather than true) weights were used in the analysis. Specifically, the following covariates were used to predict first-stage treatment assignment: baseline diagnosis with alcohol dependence, cocaine dependence, or both (three-level categorical variable coded into two dummy-coded variables where “both” is the reference category), gender, age, and the baseline number of substance use days (cocaine use days when the outcome is cocaine abstinence; alcohol use days when outcome is alcohol abstinence). The following covariates were used to predict second-stage treatment assignment: baseline diagnosis with alcohol dependence, cocaine dependence, or both; gender; age; baseline number of substance use days; and month 1 abstinence. An autoregressive (AR-1) working correlation matrix was assumed.

The method described above was implemented using the R software package (R Core Team, 2017). R code is available in the online supplementary Appendix B. Tables 2 (for cocaine abstinence) and 3 (for alcohol abstinence) present the estimated regression coefficients for model (7), as well as estimated linear combinations of these coefficients that are of scientific interest; these include the estimated differences between choice throughout (1,1) and later choice (−1, 1) AIs in terms of time-specific outcomes, stage-specific slopes, AUCs, and delayed effects.

Table 2:

Results for Cocaine Abstinence (Binary outcome 1=abstinence, 0=non-abstinence).

		Estimate	SE	95% CI
				LL	UL
Intercept		1.94**	0.30	1.36	2.52
Gender (male=1;female=−1)		−0.02	0.17	−0.36	0.31
Number of cocaine use days over 28 days preceding baseline		−0.11**	0.02	−0.14	−0.08
S1		−0.45**	0.17	−0.79	−0.10
S2		0.10*	0.05	0.00	0.20
S1*A1		0.16	0.10	−0.04	0.36
S2*A1		−0.13**	0.05	−0.23	−0.03
S2*A2		0.03	0.02	−0.01	0.08
S2*A1*A2		−0.04	0.03	−0.10	0.02
Time-Specific Outcomes
Month 1	Choice Throughout (1, 1)	0.84	0.03	0.79	0.90
	Later Choice (−1, 1)	0.82	0.03	0.76	0.88
	Difference (1, 1) vs. (−1,1)	0.02	0.01	−0.01	0.05
Month 2	Choice Throughout (1, 1)	0.80	0.04	0.72	0.88
	Later Choice (−1, 1)	0.71	0.05	0.62	0.80
	Difference (1, 1) vs. (−1,1)	0.09	0.06	−0.02	0.20
Month 3	Choice Throughout (1, 1)	0.79	0.04	0.72	0.86
	Later Choice (−1, 1)	0.77	0.04	0.70	0.84
	Difference (1, 1) vs. (−1,1)	0.02	0.05	−0.07	0.12
Month 4	Choice Throughout (1, 1)	0.79	0.04	0.72	0.86
	Later Choice (−1, 1)	0.82	0.03	0.75	0.89
	Difference (1, 1) vs. (−1,1)	−0.03	0.05	−0.12	0.06
Month 5	Choice Throughout (1, 1)	0.78	0.04	0.70	0.86
	Later Choice (−1, 1)	0.86	0.03	0.79	0.93
	Difference (1, 1) vs. (−1,1)	−0.08	0.05	−0.18	0.03
Month 6	Choice Throughout (1, 1)	0.78	0.05	0.68	0.88
	Later Choice (−1, 1)	0.89	0.03	0.83	0.96
	Difference (1, 1) vs. (−1,1)	−0.11†	0.06	−0.23	0.00
Slopes (Log-odds scale)
Stage 1	Choice Throughout (1, 1)	−0.29	0.20	−0.68	0.10
	Later Choice (−1, 1)	−0.60**	0.21	−1.01	−0.20
	Difference (1, 1) vs. (−1,1)	0.31	0.21	−0.09	0.72
Stage 2	Choice Throughout (1, 1)	−0.03	0.08	−0.20	0.13
	Later Choice (−1, 1)	0.30**	0.09	0.13	0.47
	Difference (1, 1) vs. (−1,1)	−0.33**	0.13	−0.58	−0.09
Areas Under the Curve (AUC)
Time-averaged AUC	Choice Throughout (1, 1)	0.79	0.03	0.73	0.86
	Later Choice (−1, 1)	0.80	0.03	0.74	0.87
	Difference (1,1) vs. (−1, 1)	−0.01	0.04	−0.09	0.07
Delayed Effects
Delayed Effect	In terms of Time-Specific Outcomes: (1,1) vs.(−1, 1)	−0.20**	0.08	−0.35	−0.05
	In terms of AUC: (1, 1) vs. (−1, 1)	−0.15	0.16	−0.46	0.16

Notes:

^†p≤0.10

^*p≤0.05

^**p≤0.01. CI=95% Confidence Interval; LL=Lower Limit UL=Upper Limit SE=Standard Error

Figures 2 and 3 present the estimated probability of abstinence over time under each of the embedded AIs in ENGAGE based on Model (7). Note that the relatively higher expected rates of cocaine abstinence (Figure 2) compared to alcohol abstinence (Figure 3) might be in part due to the slightly higher percentage of alcohol dependent individuals in the sample.

Figure 2.

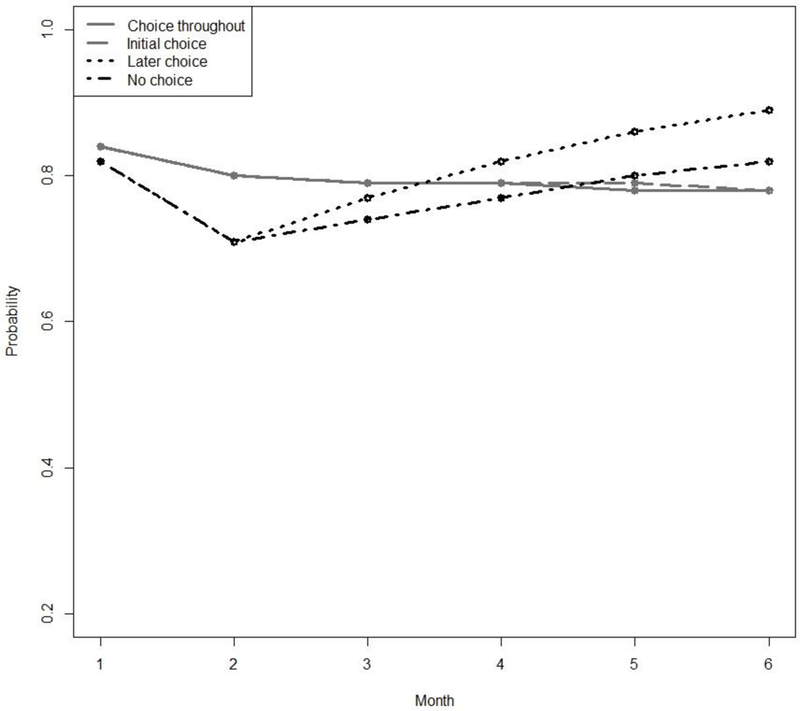
Estimated Probabilities of Cocaine Abstinence for each of the 4 Adaptive Interventions Embedded in the ENGAGE SMART.

Figure 3.

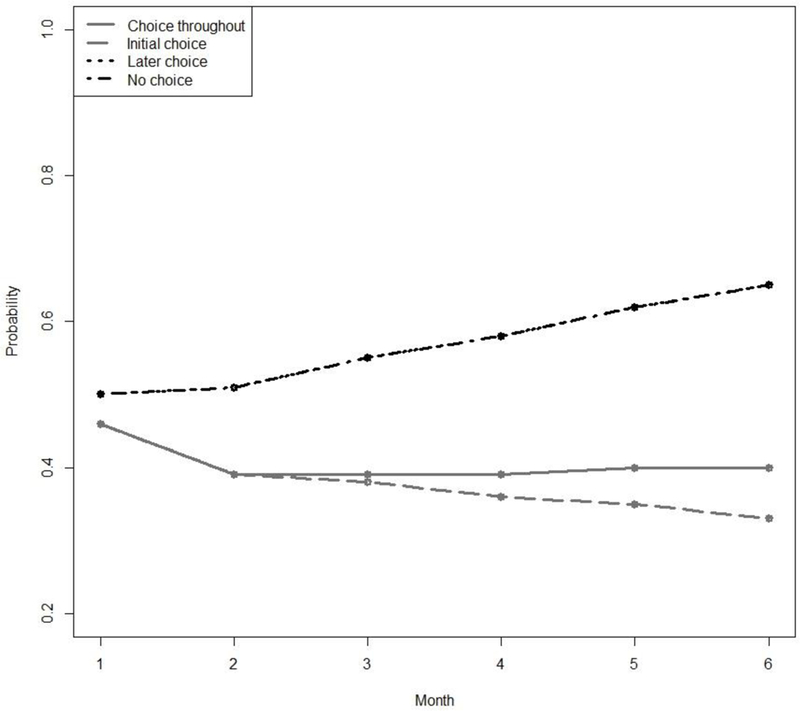
Estimated Probabilities of Alcohol Abstinence for each of the 4 Adaptive Interventions Embedded in the ENGAGE SMART. The “later choice” and “no choice” trajectories are almost identical and therefore overlap in the figure.

For cocaine abstinence, the results in Table 2 indicate that the coefficient for $S_1({\widehat{\beta }}_{S_1}=-.45,SE=.17,p\le .01)$, the coefficient for $S_2({\widehat{\beta }}_{S_2}=.10,SE=.05,p<.05)$, and the interaction between $A_1$ and $S_2({\widehat{\beta }}_{S_2{A}_1}=-.13,\text{SE}=.05,p\le .01)$ are significantly different from zero. Other coefficients of interest (i.e., ${\widehat{\beta }}_{S_1{A}_1},{\widehat{\beta }}_{S_2{A}_2},$ and ${\widehat{\beta }}_{S_1{A}_1{A}_2}$) are not significantly different from zero. This means that on average, the probability of cocaine abstinence decreases during stage 1 (because ${\widehat{\beta }}_{S_1}$ is negative and significantly different from zero) and increases during stage 2 (because ${\widehat{\beta }}_{S_2}$ is positive and significantly different from zero). Moreover, stage 2 slope varies by first-stage intervention options (because ${\widehat{\beta }}_{S_2{A}_1}$ is significantly different from zero).

The difference between the choice-throughout (1,1) and the later-choice (−1, 1) AIs depends on time, as can be seen in Table 2. While both embedded AIs produce similar abstinence probabilities at months 1 to 5 (e.g., estimated probabilities at month 5: .78 and .86, respectively, difference=−.08, SE = .05, ns), choice throughout produces lower probability of abstinence compared to later choice at month 6 (estimated probabilities .78 and .89, respectively, difference = −.11, SE = .06, p < .10). Further, the process by which outcomes unfold over time differs substantially between these two AIs. Specifically, there is evidence of a delayed effect based on time-specific outcomes (estimate = −.20, SE = .08, p ≤ .01). The nature of this delayed effect is illustrated in Figure 2.

During the first stage, the later-choice AI is significantly associated with decreases in the probability of abstinence (stage 1 slope = −.60, SE = .21, p < .01) relative to the choice-throughout AI. However, this trend is reversed after the second-stage intervention options are introduced. Specifically, during stage 2, the later choice AI is associated with increased probability of abstinence (stage 2 slope = .30, SE = .09, p < .01). On the other hand, choice throughout is not associated with significant changes in abstinence during stage 1 (estimated stage 1 slope = −.29, SE = .20, ns), or stage 2 (estimated stage 2 slope= −.03, SE = .08, ns). In other words, the later-choice AI leads to decrease in abstinence during the first stage, followed by increase in abstinence during the second stage, whereas the choice-throughout AI does not produce significant changes in abstinence.

For alcohol abstinence, none of the model coefficients of interest, considered individually, were significantly different from zero. However, as in the case of cocaine abstinence, the results indicate that the difference between the choice-throughout AI (1, 1) and the later choice AI (−1, 1) depends on time. As can be seen in Table 3, compared to the choice-throughout AI, the later-choice AI is associated with significantly higher abstinence probability at month 3 (estimated difference = −.13, SE = 0.05, p ≤ .01) and month 6 (estimated difference = −.20, SE = .07, p < .01). However, the two AIs are marginally different at month 1 (estimated difference = −.03, SE = .02, p < .10) and month 2 (estimated difference = −.11, SE = .06, p < .10). In other words, the advantage of later choice over choice-throughout in promoting alcohol abstinence increases in magnitude over time. In terms of overall time-averaged AUC, later choice (estimated average AUC = .57, SE = .05, p < .01) was significantly more successful (estimated difference = −.17, SE = .06, p < .01) than choice throughout (estimated average AUC = .40, SE = .05, p < .01). However, there is also evidence of a delayed effect in terms of AUC (estimate = −.55, SE = .18, p < .01). The nature of this delayed effect is illustrated in Figure 3.

Table 3.

Results for Alcohol Abstinence (Binary outcome 1=abstinence, 0=non-abstinence).

		Estimate	SE	95% CI
				LL	UL
Intercept		0.47*	0.23	0.03	0.91
Gender (male=1; female=−1)		0.06	0.15	−0.23	0.35
Number of alcohol use days over 28 days preceding baseline		−0.52**	0.11	−0.73	−0.32
S1		−0.14	0.15	−0.44	0.16
S2		0.06	0.05	−0.04	0.16
S1*A1		−0.16†	0.09	−0.35	0.02
S2*A1		−0.09†	0.05	−0.19	0.01
S2*A2		0.02	0.02	−0.03	0.07
S2*A1*A2		0.02	0.03	−0.03	0.07
Time-specific Outcomes
Month 1	Choice throughout (1, 1)	0.46	0.05	0.37	0.56
	Later choice (−1, 1)	0.50	0.05	0.40	0.61
	Difference (1, 1) vs. (−1,1)	−0.03†	0.02	−0.07	0.00
Month 2	Choice throughout (1, 1)	0.39	0.05	0.29	0.49
	Later choice (−1, 1)	0.51	0.06	0.39	0.64
	Difference (1, 1) vs. (−1,1)	−0.11†	0.06	−0.23	0.01
Month 3	Choice throughout (1, 1)	0.39	0.05	0.30	0.48
	Later choice (−1, 1)	0.55	0.06	0.44	0.66
	Difference (1, 1) vs. (−1,1)	−0.13**	0.05	−0.23	−0.03
Month 4	Choice throughout (1, 1)	0.39	0.05	0.30	0.49
	Later choice (−1, 1)	0.58	0.06	0.47	0.70
	Difference (1, 1) vs. (−1,1)	−0.16**	0.05	−0.26	−0.06
Month 5	Choice throughout (1, 1)	0.40	0.05	0.29	0.50
	Later choice (−1, 1)	0.62	0.07	0.49	0.75
	Difference (1, 1) vs. (−1,1)	−0.18**	0.06	−0.30	−0.06
Month 6	Choice throughout (1, 1)	0.40	0.07	0.27	0.53
	Later choice (−1, 1)	0.65	0.08	0.50	0.80
	Difference (1, 1) vs. (−1,1)	−0.20**	0.07	−0.34	−0.05
Slopes (Log-odds scale)
Stage 1	Choice throughout (1, 1)	−0.30†	0.17	−0.64	0.04
	Later choice (−1, 1)	0.03	0.19	−0.34	0.39
	Difference (1, 1) vs. (−1,1)	−0.33†	0.19	−0.70	0.04
Stage 2	Choice throughout (1, 1)	0.01	0.07	−0.14	0.15
	Later choice (−1, 1)	0.15	0.09	−0.03	0.32
	Difference (1, 1) vs. (−1,1)	−0.14	0.12	−0.37	0.10
Areas under the curve (AUC)
Time-averaged average AUC	Choice throughout ( 1 , 1 )	0.40	0.05	0.31	0.49
	Later choice (−1, 1)	0.57	0.05	0.46	0.67
	Difference (1,1) vs. (−1, 1)	−0.17**	0.06	−0.28	−0.06
Delayed Effects
Delayed effect	In terms of time-specific outcomes: ( 1 , 1 ) vs.( −1, 1 )	−0.09	0.09	−0.27	0.09
	In terms of AUC’s: (1, 1) vs. (−1, 1)	−0.55**	0.18	−0.90	−0.20

Notes:

^†p≤0.10

^*p≤0.05

^**p≤0.01. CI=95% Confidence Interval; LL=Lower Limit UL=Upper Limit SE=Standard Error

Estimates of stage 1 and stage 2 slopes in Table 3 show that the later choice AI is not associated with significant changes in abstinence (none of the estimated slopes in stages 1 or 2 are significantly different from zero), whereas the choice-throughout AI is associated with near-significant reduction in abstinence in stage 1 (estimate = −.30, SE = .17, p < .10) but not in stage 2 (estimate = .01, SE = .07, ns). Further, in terms of stage-specific AUCs, the difference in stage 1 AUC between choice throughout and later choice is near-significant (estimated difference = −.07, SE = .04, p < .10), while the difference in stage 2 AUC in favor of later choice is larger in magnitude and significantly different from zero (estimated difference = −.62, SE = .20, p < .01). In other words, the advantage of later choice over the choice throughout in terms of alcohol abstinence unfolds over time and is more pronounced after second-stage intervention options are introduced.

This empirical analysis shows that interesting results can be obtained by analyzing longitudinal binary from a SMART trial. The formulas proposed and used here for estimating contrasts and standard errors for binary data are applications of Cramér’s delta method (Taylor linearization; see Ferguson, 1996) and therefore are expected to perform well asymptotically, but it is important to use simulations to investigate their performance with datasets of realistic sample size and realistic features. In simulations, the true parameter values are known, so the accuracy of the technique under different scenarios can be measured.

Simulation Study

Lu and colleagues (2016) conducted simulation studies to study the performance of the weight and replicate strategy for longitudinal SMART data but only considered the case of normally distributed outcomes. The simulation presented in this section achieves two important advances over existing simulations. First, this simulation uses a logistic model with binary outcome instead of a linear model. The amount of efficiency gained by correctly specifying the working correlation structure and/or by using estimated (rather than known) weights is unknown in such a setting. Second, the response indicator $R$ in the simulations conducted by Lu and colleagues (2016) was generated independently of the outcome variable $Y$, which is somewhat unrealistic and might have implications on the performance of the proposed method. In the current simulation, $R$ is allowed to be correlated with $Y$. In the next subsection we specify the questions motivating the simulation study.

Motivating Questions

We conducted a factorial simulation study to address four questions concerning the performance of the proposed method in estimating contrasts of AUCs for the expected value of a binary outcome variable between a pair of embedded AIs in a prototypical SMART design as described above. The five questions are as follows. First, are the estimates for contrasts unbiased? Second, are confidence intervals for contrasts valid in the sense of having nominal coverage? That is, assuming the parameter estimates are unbiased for the true parameters, are the standard errors also unbiased for the true standard errors? Third, how greatly are the standard errors and the statistical power affected by the true correlation structure, the working correlation structure, and the form of weighting (known or estimated weights)? Fourth, are the estimates for the marginal correlation parameters accurate? Finally, does sample size impact the answers to the previous four questions?

Data-Generating Model

For the main simulation experiment, we assume that each dataset comes from a SMART study similar to the ENGAGE example presented earlier, with six equally spaced measurement occasions. Each simulated dataset in the main simulation study consists of 250 individuals; however, a follow-up study was done allowing 100, 150, or 400 individuals for some conditions. For each of the 24 scenarios described below, 2000 simulated datasets were generated and analyzed using R software (R Core Team, 2015).

Each of four true correlation structures was used for the correlation of $Y_t$ within individuals. The first three were independence, exchangeable correlation (equicorrelation), and autoregressive of order one (AR-1) (see, e.g., Liang & Zeger, 1986). A value of $\rho =0.50$ was used as the true data-generating value of the correlation parameter (the highest off-diagonal correlation coefficient) for all non-independent correlation structures. Specifically, under independence working correlation, the correlation matrix is the diagonal matrix (all off-diagonal elements are zero) so the $\rho$ parameter is not used. For exchangeable working correlation, all observations are equally correlated regardless of time order:

$$\text{Corr}\left(\left[\begin{array}{l}{Y}_1\\ Y_2\\ Y_3\\ Y_4\\ Y_5\\ Y_6\end{array}\right]\right)=\left[\begin{array}{cccccc}1& \rho & \rho & \rho & \rho & \rho \\ \rho & 1& \rho & \rho & \rho & \rho \\ \rho & \rho & 1& \rho & \rho & \rho \\ \rho & \rho & \rho & 1& \rho & \rho \\ \rho & \rho & \rho & \rho & 1& \rho \\ \rho & \rho & \rho & \rho & \rho & 1\end{array}\right].$$

For AR-1 working correlation, observations which are closer in time are more highly correlated:

$$\text{Corr}\left(\left[\begin{array}{l}{Y}_1\\ Y_2\\ Y_3\\ Y_4\\ Y_5\\ Y_6\end{array}\right]\right)=\left[\begin{array}{cccccc}1& \rho & {\rho }^2& {\rho }^3& {\rho }^4& {\rho }^5\\ \rho & 1& \rho & {\rho }^2& {\rho }^3& {\rho }^4\\ {\rho }^2& \rho & 1& \rho & {\rho }^2& {\rho }^3\\ {\rho }^3& {\rho }^2& \rho & 1& \rho & {\rho }^2\\ {\rho }^4& {\rho }^3& {\rho }^2& \rho & 1& \rho \\ {\rho }^5& {\rho }^4& {\rho }^3& {\rho }^2& \rho & 1\end{array}\right].$$

Recall that generally ${\rho }^2\le \rho$, as $0\le \rho \le 1$. Additionally, to try to assess robustness to unexpected correlation structures, an intentionally strange and unrealistic data-generating structure was also implemented, which we call a “checkerboard” pattern:

$$\text{Corr}\left(\left[\begin{array}{l}{Y}_1\\ Y_2\\ Y_3\\ Y_4\\ Y_5\\ Y_6\end{array}\right]\right)=\left[\begin{array}{cccccc}1& 0& \rho & 0& \rho & 0\\ 0& 1& 0& \rho & 0& \rho \\ \rho & 0& 1& 0& \rho & 0\\ 0& \rho & 0& 1& 0& \rho \\ \rho & 0& \rho & 0& 1& 0\\ 0& \rho & 0& \rho & 0& 1\end{array}\right].$$

Each of three working correlation structures was used for the fitted analysis model: independence, exchangeable, or AR-1. A working checkerboard structure was not used, as it would not be used in practice. Lastly, weights were either treated as known or were estimated using the data. This defines $4\times 3\times 2$ scenarios.

The data-generating model was intended to be similar to Model (7). However, it is impossible to simulate data from Model (7) directly because Model (7) is a marginal model, both in the sense of not requiring a model of the exact structure of the within-subject correlation and also of not requiring a model of the relationship of Y to R. This use of a marginal model was deliberate, because it corresponded directly to the scientific question. That is, it was of interest to determine which AI has the best performance in general, without knowing in advance what a particular participant’s response status or outcome history would be. However, the relationships which Model (7) did not specify for purposes of analyzing data, must still be specified in some way in order to simulate data. That is, the data-generating model must be richer than the data-analytic model in that it should specify a precise correlation structure and a realistic scenario for the connection between the response status $R$ and the outcome $Y$. It would be possible to set $R$ to relate to $Y_t$ only for $t>2$, that is, set response status to impact the outcome only after $R$ is known. However, we decided to also allow $R$ to relate to $Y_1$ and $Y_2$ because $R$ is not randomized and is presumably dependent on various latent or observed characteristics which were partly set prior to observing $R$.

To generate the data, the values of two hypothetical baseline covariates were first randomly generated for each participant. These covariates were effect-coded gender $X_1$ simulated as equally likely to be −1 or +1, and baseline use days $X_2$, simulated as 1 plus a Poisson distribution with mean 7.7. The value of $A_1$ for each participant was then randomly generated, equally likely to be −1 or +1, independent of the baseline covariates. $R$ was then generated depending on $A_1$, such that $P(R=1|A_1=+1)=0.71$ and $P(R=1|A_1=-1)=0.65$. For individuals with $R=0$ (i.e., non-responders), a value of $A_2$ was generated, again equally likely to be −1 or +1. The values for the $Y_t$ were generated to have probabilities given by and marginal correlations given by a prespecified true correlation structure. This was done using

$$\begin{array}{cc}{\text{logit}}^{-1}\left(P(Y_t=1)\right)=& 0.687+0.041X_1-0.052X_2+0.236R+\\ ⬚& \left(-0.490-0.068A_1+0.555R-0.201A_{1}R\right)S_1\left(t\right)+\\ ⬚& \left(0.163-0.140A_1-0.120R+0.040A_2+0.058A_1{A}_2+0.141A_{1}R\right)S_2\left(t\right),\end{array}$$ (8)

the R package bindata (Leisch, Weingessel & Hornik, 2012). Lu and co-workers (2016) simulated $Y_t$ from a model similar to (8), except that their simulation used a normally distributed $Y_t$ and did not allow $Y_1$ to be directly associated with $R$ The regression coefficients values and other numerical constants for this model were set using an initial data analysis on the alcohol data from the ENGAGE study. They are not the same as the estimated coefficients for the marginal model because of the different model and parameterization being used.

Performance Measures

Because there are four embedded AIs, there are a total of $\left(\begin{array}{l}4\\ 2\end{array}\right)=6$ unique pairwise contrasts between their AUC values. For each simulated dataset within each scenario and for each of the six pairwise contrasts between the AUC values listed in the lower part of Table 3, an estimate was calculated using the method described earlier in this paper and was compared to the true value. A standard error for the contrast was also calculated. These were used to create the following four performance measures.

Absolute bias.

The absolute bias for the contrast in AUCs for AIs $\left(a_1,a_2\right)$ and $\left(a_1^{\prime },a_2^{\prime }\right)$ was calculated as the absolute value of the average difference between the true and estimated values, that is,

$$\left|\frac{1}{2000}{\sum }_{S=1}^{2000}\left(({\widehat{AUC}}_{a_1,a_2,S}-{\widehat{AUC}}_{a_1^{\prime },a_2^{\prime },S})-(AU{C}_{a_1,a_2}-AU{C}_{a_1^{\prime },a_2^{\prime }})\right)\right|,$$

where ${\widehat{AUC}}_{a_1,a_2,S}$ represents the estimate in simulation $s$ for the area under the curve of AI $\left(a_1,a_2\right)$, and $AU{C}_{a_1,a_2}$ represents the corresponding true value. Note that it is often more informative to report signed bias, rather than absolute bias, because signed bias indicates direction. However, because we averaged the performance across the contrasts of interests in our analysis before making conclusions about overall estimation performance, we used absolute bias in order to avoid the risk of cancelling out errors in opposite directions for different contrasts.

Root mean squared error (RMSE).

Similarly to the above, the RMSE for each contrast was calculated as the square root of the average of the squared values of the difference between the true and estimated values; that is,

$$\sqrt{\frac{1}{2000}\sum _{S=1}^{2000}{\left(({\widehat{AUC}}_{a_1,a_2,s}-{\widehat{AUC}}_{a_1^{\prime },a_2^{\prime },s})-(AU{C}_{a_1,a_2}-AU{C}_{a_1^{\prime },a_2^{\prime }})\right)}^2}.$$

The average estimated standard error was also calculated for comparison; it should be approximately the same as the RMSE if it is an unbiased estimate of sampling variability.

Confidence interval coverage.

The coverage for each contrast was calculated as the proportion of simulations in which a nominally 95% confidence interval using the estimate and standard error obtained included the true value of the contrast.

Statistical power.

The statistical power for a contrast was calculated as the proportion of simulations in which a z-test at $\alpha =.05$, based on the estimate and standard error for each contrast, excluded zero. Unlike the other measures, this was computed only for the four contrasts that had true absolute values above 0.1. This is because it is not expected, and perhaps not desirable, to have high power for a contrast whose true value is practically zero.

Each performance measure was calculated for each of the six contrasts separately (or over the four nonnegligible contrasts in the case of statistical power) and then averaged across all six contrasts to achieve a single aggregate measure.

Results

Performance measures for estimated weights were extremely similar to those for known weights, so only the results for known weights are described here. Findings for the four questions described earlier are given below. With respect to the first motivating question, which concerned, bias, we found estimates of the pairwise contrasts in time-averaged AUCs for AIs to be essentially unbiased. The simulated absolute bias was less than .005 in all scenarios. This was the case regardless of true and working correlation structure. With respect to the second motivating question, which concerned coverage, we found the simulated coverage for the pairwise contrasts to be approximately 95% for nominal 95% confidence intervals, suggesting that the confidence intervals were working well. This was the case regardless of true and working correlation structure. The third question concerned the effect of the correlation structure. The results in Table 4 show that in situations where the true structure was non-independent, the estimates tended to be more accurate and power tended to be higher when a non-independent working structure was used in the analysis.

Table 4.

Effects of True and Working Correlation Structure on Accuracy and Power of Pairwise AUC Comparisons

Average Root Mean Squared Error
		Fitted Structure
True Structure	Indep.	Exch.	AR-1
Independence	0.0239	0.0239	0.0239
Exchangeable	0.0393	0.0334	0.0362
AR-1	0.0340	0.0337	0.0326
Checkerboard	0.0304	0.0290	0.0304
Power for Nonnegligible Contrasts
		Fitted Structure
True Structure	Indep.	Exch.	AR-1
Independence	0.9990	0.9990	0.9989
Exchangeable	0.8241	0.9275	0.8789
AR-1	0.9225	0.9293	0.9426
Checkerboard	0.9650	0.9756	0.9659

Our fourth motivating question concerned the accuracy of estimating the correlation parameter. Table 5 shows the average estimated values for the correlation parameter; note that the true value is $\rho =0.5$. This table shows that when the working correlation structure was correctly specified, the method-of-moments estimate of the correlation parameter averages very close to 0.50 and thus had little or no bias. Of course, when the structure is incorrectly specified, there is no reason to expect the correlation estimate to converge to any particular meaningful value (Crowder, 1995), and in fact estimates tended to be much smaller than 0.50.

Table 5.

Average Estimated Correlation Parameters

Known Weights
		Fitted Structure
True Structure	Indep.	Exch.	AR-1
Independence	0.000	0.027	0.031
Exchangeable	0.000	0.508	0.511
AR-1	0.000	0.285	0.512
Checkerboard	0.000	0.219	0.029

Finally, with respect to sample size, the simulation results reported so far were based on sample sizes of n=250, approximately that of the ENGAGE SMART experiment. Repeating a few scenarios (AR-1 true correlation with working AR-1 or working independence correlation) using sample sizes of 150 or 400 instead of 250 showed (see Table 6) improvement in power and RMSE as n increased. Still, power was found to be reasonably good even for the smaller value of n. Coverage for nominal 95% confidence intervals was quite close to 95% regardless of n.

Table 6.

Effect of Sample Size on Accuracy, Coverage and Power of Pairwise AUC Comparisons with AR-1 True Structure

Sample	Working	Bias	RMSE	Coverage	Power
Size	Structure
100	Independence	0.001	0.055	0.949	0.517
	AR-1	0.001	0.053	0.949	0.571
150	Independence	0.001	0.043	0.956	0.729
	AR-1	0.001	0.041	0.953	0.781
250	Independence	0.000	0.034	0.954	0.923
	AR-1	0.000	0.033	0.953	0.943
400	Independence	−0.001	0.028	0.947	0.990
	AR-1	−0.001	0.027	0.946	0.994

Discussion

This manuscript provides practical guidelines and extensions to enable behavioral scientists to use repeated binary outcome data arising from a SMART to compare AIs. Although the method proposed by Lu and colleagues (2016) for analyzing repeated outcome data from SMART studies is general enough to be applicable to many kinds of outcome variables, it was originally illustrated and evaluated mainly for use with linear models for normally distributed outcomes. In this manuscript we have addressed several important questions that arise concerning the performance and utility of applying this method when the repeated outcome of interest is binary. Following a comprehensive review of this method, we provided guidelines for implementation in a binary outcome setting and highlighted the extensions required to enable the comparison of AIs in terms of various summaries of repeated binary outcome measures, including average outcome (AUC), stage-specific slopes, and delayed effects. An empirical example from a SMART study to develop an AI for engaging alcohol- and cocaine- dependent patients in treatment is used to illustrate the proposed method and highlight its scientific yield.

The empirical data analysis used to illustrate the methodology highlights the scientific gains associated with comparing AIs in terms of repeated binary outcome measures, as opposed to focusing on end-of-study outcome. Focusing on two embedded AIs of primary scientific interest, namely later choice and choice throughout, we found that the process by which outcomes unfold over time differs substantially between these two AIs. For example, in terms of cocaine abstinence, the AI that consisted of no choice early with choice later for non-responders (i.e., later choice) led to substantial decreases in the probability of abstinence (during the first stage), before leading to substantial increases in the probability of abstinence (during the second stage). On the other hand, choice throughout produced consistent abstinence probabilities during both stage 1 and stage 2. Simply comparing the two AIs in terms of the outcome at month 6 would lead to the conclusion that later choice should be selected, given that it is associated with higher probability of abstinence at the end of the study. While the current analysis still suggests that later choice is likely to be better or at least no worse than choice throughout, the longitudinal analysis provides additional insight into the likely course of change under each AI. In particular, an analysis focusing only on the final outcome would ignore the substantial decrease in the probability of abstinence during the first stage of later choice. Such reduction may have practical and clinical significance, especially because it suggests that further improvements to the later-choice AI should be considered in order to prevent such decline. For example, the researcher might introduce another phone contact between months 1 and 2. Moreover, in some clinical settings and other chronic disorders, consistent response, albeit modest, is sometimes better than sharp fluctuations. The course of improvement induced by the sequence of intervention options is important in selecting an AI, as it would allow clinicians and patients to weight short-term and long-term treatment goals when selecting an AI, rather than focusing on long-term improvement alone.

The results of Monte Carlo simulations were also presented to address questions concerning the performance of the proposed technique for analyzing repeated binary outcome measures arising from a SMART. The simulations employed a logistic model with binary repeated outcome measurements, as well as more realistic scenarios than those used by Lu and colleagues (2016), the proposed method performed well. Specifically, the method produces unbiased estimates as well as valid confidence intervals for the contrasts of interest. Statistical efficiency was higher (i.e., RMSE was lower and power was higher) when the correlation structure was correctly specified.

Limitations and Directions for Future Research

Contrary to hypothesis, the current simulation did not find any performance advantage for estimated weights. This was also contrary to findings from preliminary simulations (not shown) with three instead of six measurement waves. In these simulations, although estimated weights did not improve the performance over known weights when the correlation structure was misspecified, they prevented the efficiency loss that would otherwise have occurred from misspecified correlation. It is not clear why the current simulation did not find a similar result, and it is not clear whether or how the difference in performance is related to the number of waves. Additional research is required to systematically address these questions. In the future, there are some possible ways in which further methodological research might expand the usefulness of estimated weights in the context of the weighting and replication method. First, in the context of reducing bias in observational studies, estimating the weights using machine learning methods is sometimes preferable to using logistic regression (Lee, Lessler, and Stuart, 2010). Second, although developed in the context of reducing bias in observational studies, methods for ensuring double robustness (see Davidian, Tsiatis & Leon, 2005; Jonsson Funk et al., 2010) can also be used to improve efficiency in the comparison of AIs with data arising from a SMART (see Ertefaie et al., 2015).

The example repeated measures model described in this tutorial article, namely Model (1), is only one of various ways to model the mean trajectory for the AIs embedded in a SMART like ENGAGE. Other longitudinal models are also possible, which can accommodate (or approximately accommodate) the features of SMARTs like ENGAGE. For example, the marginal mean trajectories need not be linear functions of time (e.g., they could be quadratic or otherwise curvilinear if there are enough measurements per stage). Methods for selecting the best model for longitudinal data arising from a SMART is one area of future research.

In the illustrative analysis presented here, we used a complete-case approach, removing missing data. However, it would often be better in practice to use multiple imputation (see Schafer, 1999; Lang & Little, 2018). Shortreed and co-authors (2014) described an approach to multiple imputation for longitudinal data arising from a SMART. Future methodological research may focus on better understanding alternatives to handling missing data in the context of different types of SMART designs and analyses. In the context of the weighting and replication method, it would be appropriate to impute the missing data before weighting and replicating, rather than after.

Model (1) is design-specific in that it is constructed for SMART studies, such as ENGAGE, in which all individuals are randomized to two initial intervention options, and only non-responders are re-randomized to two other options. In such a design, as described earlier, there are four embedded AIs. Many SMART studies are of this type (e.g., Gunlicks-Stoessel et al., 2016; Naar-King et al., 2016; Pelham et al., 2016), but other types of SMARTs also exist (e.g., Lei, Nahum-Shani, Lynch, Oslin & Murphy, 2012). For some of these different designs, a different repeated measures model would be needed. For example, in some designs everyone is re-randomized, including responders, and the randomization options available to responders differ from those available for non-responders. In such a design, there would be eight embedded AIs rather than four, and the model would have to be adapted for this. Another form of adjustment would be appropriate if there were large differences between participants in either the spacing of randomizations (i.e., the length of stage 1 or of stage 2), or in the spacing of measurements within stage. For example, a second-stage intervention might take place at one of a range of different time points depending on when the individual shows signs of early non-response. In this case, it might be beneficial to use a model that accounts for the time at which the individual transitioned to the second stage of the intervention. Several SMART design scenarios of increasing complexity are discussed by Lu and colleagues (Lu et al., 2016), along with suggested ways to model repeated outcome measurements from such trials. If measurement timing is indeed subject-specific, then it may be necessary to define some of the estimands of interest more carefully and use a different approach to computing them. For example, the formula for the AUC would depend on the time spacing, so perhaps in that situation the AUC should be treated as different for each subject, and an overall average could be calculated.

The development of mixed-effects models for use with binary data from a prototypical SMART (e.g., ENGAGE) represents another important direction for future research. Mixed-effects models are common in the analysis of repeated outcome measures arising from conventional randomized trials. Such models are often used because the variability of person-specific trends over time is of interest, rather than simply the mean trend (Bauer, Preacher, & Gil, 2006; Singer, 1998; Singer & Willett, 2003). Subject-specific effects can be included in models with binary and other non-normal outcomes in addition to normal outcomes.

The repeated outcome measure of interest in the current manuscript was binary, simply reflecting abstinence versus any nonzero level of use. However, in many areas of behavioral research, particularly addictions (e.g., drug-use, alcohol-use), the outcomes of interest are counts, such as the number of drug-use occasions per week or month. An important outcome in the context of the ENGAGE SMART could be the monthly number of cocaine use days. Although this outcome is a count, it might not be sufficiently well modeled by simply approximating it as a Poisson distribution, namely by using Model (1) with the log link function and the Poisson variance function. This is because, as compared to a Poisson distribution, the distribution of a count outcome is likely to have a larger number of zeroes (e.g., many person-months with no days of cocaine use). This occurs commonly in count data on substance use and other behavioral health variables. The analysis of longitudinal zero-inflated count outcomes arising from a SMART is associated with additional challenges, as the outcome at any given month for a person is considered to be a result of two distinct processes. The first process concerns person-months that have no cocaine-use days because the person has either quit or has never begun using cocaine. The second process concerns person-months in which cocaine may or may not be used; these person-months may result in cocaine use (i.e., 1 or more days of cocaine use) or not (i.e., no cocaine use days). In contrast to the single model used for the binary repeated outcome measures (Model 1), a mixture-model approach is typically recommended for zero-inflated data in order to model both processes (see, e.g., Buu, Li, Tan, & Zucker, 2012, Hu, Pavlicova, & Nunes, 2011, Olsen & Schafer, 2001; Yau, Wang & Lee, 2003). Extending the proposed method to enable the comparison of adaptive interventions in terms of zero-inflated outcome data arising from a SMART represents an important direction for future research.

In this paper we have considered only a relatively small number of repeated measurements. In many settings there may be advantages to using many repeated measurements (i.e., intensive longitudinal data; Walls & Schafer, 2006). We conjecture that the methods used in this paper would also be valid in such settings, although further simulation studies are necessary in order to explore this further. However, to make full use of intensive longitudinal data, somewhat more complicated models are likely to be beneficial. In particular, if there are many observations per stage, it would not make sense to simply assume that the trajectory of change within the stage must have a simple shape such as linearity. Also, if the number of observations per participant is large and the number of participants is small, then misspecification of the correlation structure may have a larger impact than it had in this paper (see Crowder, 1995). For relatively simple estimands such as end-of-study outcome, previous work with clustered data suggests that it is likely to be much more beneficial to increase the number of participants than to increase the number of observations per participant (see, e.g., Dziak, Nahum-Shani, and Collins, 2012). However, if short-term changes are of interest, then it is necessary to measure the outcome intensively (see Collins et al., 2002).

Conclusion

The goal of this manuscript was to provide practical guidelines and extensions to enable the use of repeated binary outcome measures arising from a SMART to compare AIs. Various estimands that summarize the repeated binary outcome measures in different ways, including AUC, slopes, and delayed effects, have been discussed to operationalize the difference between the AIs. For illustrative purposes, we used longitudinal binary data from a single SMART study (ENGAGE) to demonstrate how these various summaries can be obtained and estimated. This does not imply that all summaries should be tested; an investigator should select the appropriate summaries a priori based on the primary scientific questions motivating the SMART study. The method of Lu and colleagues (2016) for analyzing repeated outcome measures from a SMART was shown to perform well in the setting of binary outcome measures.

Appendix A: Standard Error Estimator

As usual, standard errors for the parameters in Model (1) can be obtained as the square roots of the diagonal entries on a covariance matrix of the estimated regression parameters. Let

$${\mathbf{\text{U}}}_i(\widehat{\mathbf{\beta }})={\sum }_{\left(a_1,a_2\right)}{w}_i{c}_{i,a_1,a_2}{\mathbf{\text{D}}}_{i,a_1,a_2}^T{\mathbf{\text{V}}}_{i,a_1,a_2}^{-1}\left({\mathbf{\text{Y}}}_i-{\mathbf{\mu }}_{i,a_1,a_2}\right)$$

be the score function for $\mathbf{\beta }$ (the vector that is set to 0 to solve the estimating equation), so that ${\sum }_{i=1}^N{\mathbf{\text{U}}}_i$ is the right-hand side of (1).

Let ${\mathbf{\text{g}}}_i\left(\widehat{\mathbf{\gamma }}\right)$ be the combined score function for the logistic regression equations predicting the treatment assignment probabilities, where $\widehat{\mathbf{\gamma }}$ are the estimated logistic regression parameters for the model predicting these probabilities. Then Lu and colleagues (2016; online appendix page 5) recommend the following sandwich estimator for the covariance of the estimated regression parameters:

$$\widehat{\text{Cov}}\left(\widehat{\mathbf{\beta }}\right)={\mathbf{\text{J}}}^{-1}\mathbf{\text{I}}{\mathbf{\text{J}}}^{-1},$$ (7)

where

$$\mathbf{\text{J}}=\frac{1}{N}{\sum }_{i=1}^N{\sum }_{\left(a_1,a_2\right)}{w}_i{c}_{i,a_1,a_2}{\mathbf{\text{D}}}_{i,a_1,a_2}^T{\mathbf{\text{V}}}_{i,a_1,a_2}^{-1}{\mathbf{\text{D}}}_{i,a_1,a_2}$$

is the naive model-based information matrix, and

$$\mathbf{\text{I}}=\frac{1}{N}{\sum }_{i=1}^N{\mathbf{\text{U}}}_i{\mathbf{\text{U}}}_i^T-\left(\frac{1}{N}{\sum }_{i=1}^N{\mathbf{\text{U}}}_i{\mathbf{\text{g}}}_i^T\right){\left(\frac{1}{N}{\sum }_{i=1}^N{\mathbf{\text{g}}}_i{\mathbf{\text{g}}}_i^T\right)}^{-1}\left(\frac{1}{N}{\sum }_{i=1}^N{\mathbf{\text{U}}}_i{\mathbf{\text{g}}}_i^T\right)$$

is the empirical covariance matrix of ${\mathbf{\text{U}}}_i$ after adjusting for the use of estimated weights. The second term attempts to estimate the reduction in error caused by using estimated weights; for a more conservative estimate of variance, the second term of the expression for $\mathbf{\text{I}}$ could be ignored. Also, if known weights are used, the usual GEE sandwich estimator could be used, which is similar to (7) but uses simply $\mathbf{\text{I}}=\frac{1}{N}{\sum }_{i=1}^N{\mathbf{\text{U}}}_i{\mathbf{\text{U}}}_i^T$.

The logistic regression score function ${\mathbf{\text{g}}}_i$ does not depend on the distribution of $\mathbf{\text{Y}}$ because it predicts the treatment assignments, rather than predicting $\mathbf{\text{Y}}$. The “bread” of the sandwich, ${\mathbf{\text{J}}}^{-1}$, which is also the naive model-based covariance estimator, does depend on the link function, in the way that is usual for GEE. For a continuous outcome,

$$\mathbf{\text{J}}=\frac{1}{N}{\sum }_{i=1}^N{\sum }_{\left(a_1,a_2\right)}{w}_i{c}_{i,a_1,a_2}{\sigma }_{a_1,a_2}^{-2}{\mathbf{\text{Z}}}_{i,a_1,a_2}^T{\mathbf{\text{R}}}_{a_1,a_2}^{-1}{\mathbf{\text{Z}}}_{i,a_1,a_2}.$$

For a binary outcome,

$$\mathbf{\text{J}}=\frac{1}{N}{\sum }_{i=1}^N{\sum }_{\left(a_1,a_2\right)}{c}_{i,a_1,a_2}{w}_i{\mathbf{\text{Z}}}_{i,a_1,a_2}^T{\mathbf{\text{M}}}_{a_1,a_2}^{1/2}{\mathbf{\text{R}}}_{a_1,a_2}^{-1}{\mathbf{\text{M}}}_{a_1,a_2}^{1/2}{\mathbf{\text{Z}}}_{i,a_1,a_2},$$

where ${\mathbf{\text{M}}}_{a_1,a_2}$ is a diagonal matrix with entries ${\mu }_{a_1,a_2,t}\left(1-{\mu }_{a_1,a_2,t}\right)$.

Appendix B provides sample code for fitting models in R (R Core Team, 2015) and SAS (SAS Institute, 2008) and is available as an online supplement.