Accuracy and Feasibility of High-Speed Dual Fluoroscopy and Model-based Tracking to Measure In-vivo Ankle Arthrokinematics

1. Introduction

The ankle joint complex consists of soft-tissue and the tibiotalar, tibiofibular and talo-calcaneal joints. Working in synergy, these structures provide stable, six degree-of-freedom motion. As a result, the ankle experiences relatively low rates of osteoarthritis (OA). Nevertheless, abnormal biomechanics, caused by mal-alignment, ligamentous tears, or trauma may accelerate OA, especially at the tibiotalar and subtalar (i.e., talo-calcaneal) interfaces [1, 2].

The tibiotalar and subtalar joints serve independent roles, but motion/constraint of one is likely tied with the other as evidenced by the occurrence of subtalar OA following tibiotalar arthrodesis [3]. Accurate measurements of tibiotalar and subtalar kinematics in the normal, pathological, and post-operative ankle could elucidate the pathomechanics of ankle OA. However, in the absence of a suitable location to place a skin marker about the talus, skin marker motion analysis requires one to assume that the calcaneus and talus are coupled. Intra-cortical pins with reflective markers have independently tracked the tibia, talus, and calcaneus [4, 5], but this approach is highly invasive. Other studies have used single plane fluoroscopy to study in-vivo motions of the ankle [6–8]. However, out-of-plane motions, such as axial rotation of the subtalar joint, cannot be accurately measured with single plane fluoroscopy [9]. Dual fluoroscopy (DF), on the other hand, can reconstruct three-dimensional (3D) positions of bones. Most DF studies have analyzed quasi-static motion, where DF images were acquired with the subject’s ankle in a fixed position of gait at a pre-defined load [10–13]. Although two dynamic ankle studies have been performed using DF [14, 15], the dynamic accuracy was not reported. Other ankle DF studies assumed the kinematic accuracy of joints such as the knee [12, 14], but independent validation studies are recommended for each DF system, joint, and activity [16].

To dynamically measure in-vivo ankle kinematics during load-bearing activities, we have coupled a high-speed DF system with an instrumented treadmill. Model-based markerless tracking (MBT) is then used to align 3D bone surface models with fluoroscopic images to quantify motion in-vivo. Our first objective was to quantify the accuracy of our high-speed DF system and MBT to measure and visualize articulation (i.e. arthrokinematics) of the tibiotalar and subtalar joints during dynamic motion. The second objective was to demonstrate the feasibility of the protocol for measuring in-vivo ankle arthrokinematics of a normal volunteer during treadmill gait.

2. Methods

2.1. Specimen Preparation.

Two fresh-frozen cadaver specimens (mid-tibia to toe-tips) were obtained: a right and left ankle/foot from a 52 year-old male and 81 year-old female, respectively. Screening radiographs ruled out OA. Four 2 mm steel beads were implanted in the cortex of the tibia, talus and calcaneus. A 10 mm diameter metal rod was fit into the tibial shaft.

2.2. Dual Fluoroscopy System Setup and Calibration.

A custom DF system consisting of two x-ray emitters, 12” image intensifiers, and high-speed cameras [17] was positioned around a dual-belt instrumented treadmill (Bertec, Columbus, OH) (Figure 1). Specimens were placed in the shared field of view (FOV) (Figure 1). The image space was calibrated using an acrylic cube with 19 beads [17].

Figure 1:

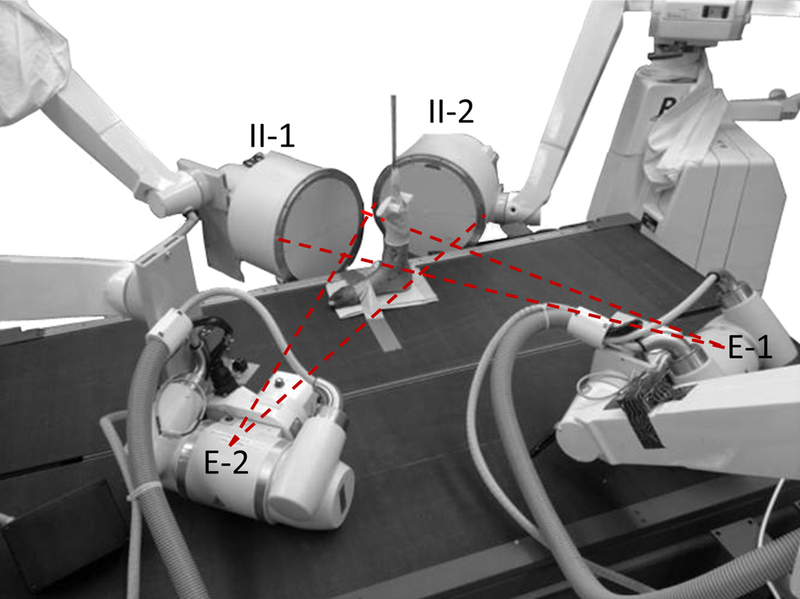
Custom dual fluoroscopy system positioned around a dual-belt instrumented treadmill to image in-vivo articulation of the subtalar and tibiotalar joints. The specimen was placed in the combined field of view of both fluoroscopes. Dashed lines represent projected x-ray beam. E=emitter, II=image intensifier.

2.3. Simulation of Rotational Profiles and Gait.

Ankle range of motion (ROM) was simulated about three axes of rotation: dorsi-plantar flexion, inversion-eversion and internal-external rotation by manipulating the implanted tibia rod with the toes taped to the stationary treadmill. DF images were acquired at 100 Hz. Gait, moderated by the instrumented treadmill, was simulated at 0.5 m/s and 1.0 m/s by lifting and lowering the tibia rod as DF images were captured at 300 Hz. As the entire gait cycle could not be viewed within the combined DF FOV, heel-strike and toe-off were captured separately. Here, ‘heel-strike’ began prior to contact between the heel and treadmill and ended during early midstance; ‘toe-off’ began during late midstance and ended during early swing. Continuous fluoroscopy was obtained at 67–75 kV and 1.3–2.0 mA, with 608×600 camera resolution at 1000 μs exposure for all trials. Two trials were captured of each activity.

2.4. CT and 3D Model Generation.

Specimens were scanned using computed tomography (CT) (Emotion, Siemens Medical Solutions, Malvern, Pa) at 0.75mm slice thickness, 256 mm FOV, 512×512 matrix, 130 kV, 140 mAs. Specimens were placed in the CT scanner such that the angle between the foot and tibial shaft was approximately 90°. The tibia, talus, and calcaneus were segmented semi-automatically from CT images (Amira 5.5, Visage Imaging, San Diego, CA) to produce a 3D surface reconstruction of each bone.

2.5. Bead Tracking with Dynamic Radiostereometric Analysis.

Three beads in each bone, visible throughout the activity, were identified. The positions of the three beads were tracked using dynamic radiostereometric analysis (DRSA) to serve as the reference standard. In optimal conditions (beads embedded in acrylic), bias and precision for DRSA using our DF system was 0.017 and 0.113 mm, respectively [17]. Beads were automatically segmented and fit to a sphere to quantify each centroid. Centroid locations were smoothed with a 4th-order low-pass Butterworth filter with a cutoff frequency of 10 Hz, selected using a residual analysis method [18].

2.6. Measurement of Bead Position with Model-Based Markerless Tracking.

MBT was performed using validated software [19]. Briefly, digitally reconstructed radiographs (DRRs) were generated via ray-traced projection through the bone CT volumes. To eliminate potential prejudice of the MBT software, beads were masked from the CT images by replacing pixel intensities at the beads with those of adjacent trabecular bone. Tibia, talus, and calcaneus bone positions were then calculated for each DF video frame by optimizing pixel intensity agreement between the DRRs and fluoroscope images. The mean difference in inter-bead distance between the two methods quantified bias whereas the standard deviation of the differences between the methods defined precision.

2.7. Definition of Anatomical Coordinate Systems

To convert raw positions quantified by DF to joint kinematics, coordinate systems were defined using anatomical landmarks visible on the bone 3D surfaces. Each 3D surface reconstruction was loaded into PostView [20] to select landmarks semi-automatically for the definition of anatomical coordinate systems as follows:

1. Tibia. The superior-inferior (SI) axis coincided with the axis of a cylinder fit to the tibia shaft. The origin was defined as the intersection point between the SI axis and tibial plafond. Perpendicular to the SI axis, the temporary medial-lateral (ML) axis was defined parallel to the axis of a cylinder fit to the tibia plafond surface, through the origin. The anterior-posterior (AP) axis was the cross product of the SI and temporary ML axes. Taking the cross product of the SI and AP axes yielded the final ML axis.

2. Talus. The surface of the trochlea tali was fit to a cylinder with the midpoint of the cylinder’s axis defining the origin. The ML, AP and SI axes were parallel to those of the tibia, but passed through the talus origin.

3. Calcaneus. A line was defined between the furthest surface nodes on the lateral side of the posterior articulating surface and the medial edge of the middle articulating surface. The origin was the closest surface node on the calcaneal articulating region to the midpoint of this line. The ML, AP and SI axes were parallel to those of the tibia, but passed through the calcaneal origin.

2.8. Validation of Model-Based Markerless Tracking and Data Analysis

2.8.1. Bead Positions

The Euclidean distance and the distance along each DF axis between bead centroids were calculated for MBT and DRSA. With DRSA as the standard, the mean and standard deviation of the inter-bead distances was calculated across subjects and trials for all frames. The mean distance and standard deviation of the distance represented the positional bias and precision of MBT, respectively.

2.8.2. Joint Angles and Translations

All bone movements were originally recorded in the DF coordinate system. Thus, a series of transformation matrices (S-Figure 1) were required to relate the bone movements in the DF system to the anatomical coordinate systems defined in Section 2.7.

First, transformation matrices were defined between the tibia (B), talus (L) and calcaneus (C) anatomical coordinate systems (_an) and the coordinate system of the CT scanner (CT). For the tibia, talus and calcaneus the transformations from the anatomical to CT coordinate systems were represented as:

B_an/CT

L_an/CT

C_an/CT

The anatomical coordinate systems were not tracked directly in MBT or DRSA. Instead, technical coordinate systems were established for each bone and tracking method as follows:

MBT.

For MBT, the CT volume was cropped to each bone. The corners of each cropped CT volume established a technical coordinate system for each bone (_{Tech_MBT}). The transformations from technical to CT coordinate systems (CT) were as follows:

CT/B _{Tech_MBT}

CT/L _{Tech_MBT}

CT/C _{Tech_MBT}

For each fluoroscopy frame, the position and orientation of each bone was defined by a transformation from its technical coordinate system in CT to its corresponding location in DF coordinates (DF) as determined by MBT:

B _{Tech_MBT} /DF

L _{Tech_MBT} /DF

C _{Tech_MBT} /DF

DRSA.

For DRSA, the centroid locations were identified in the CT coordinate system (CT). These centroid locations established a technical coordinate system for each bone (_{Tech_DRSA}). The transformations from CT to the technical systems were as follows:

CT/B _{Tech_DRSA}

CT/L _{Tech_DRSA}

CT/C _{Tech_DRSA}

In each fluoroscopy frame, bead centroids were defined by a transformation from its technical coordinate system in CT to its corresponding location in DF coordinates (DF) as determined by DRSA:

B _{Tech_DRSA} /DF

L _{Tech_DRSA} /DF

C _{Tech_DRSA} /DF

The transformation matrices defined above were combined to relate the DF to anatomical coordinate system. This transformation for the tibia, for example, was:

B_an /DF = B_an/CT × CT/B _Tech × B _Tech/DF

Transformation matrices were used in conjunction with the Grood and Suntay method to determine joint angles (plantar/dorsiflexion, internal/external rotation and inversion/eversion) between the tibia and talus, talus and calcaneus, and tibia and calcaneus [21]. Joint angles were determined using overall transformations from the proximal to distal bone. For example, from tibia to talus:

B_an /L_an = B_an /CT × CT/B _Tech × B _Tech/DF × DF/L_Tech × L_Tech /CT × CT/L_an

Joint angles were calculated for both MBT and DRSA tracking results; differences were used to evaluate MBT errors. Angular bias and precision was quantified as the average difference and standard deviation of the differences between methods, respectively when considering all trials, specimens and frames together.

Translations were determined by converting the anatomical coordinate system and joint center of each bone in the CT coordinate system to DF coordinates. The vector between joint centers was projected onto each axis of the proximal bone to quantify translations; results were reported as movement in the ML, AP or SI directions of the more proximal bone. The mean and standard deviation of the differences in joint translations between DRSA and MBT tracking quantified translational bias and precision, respectively.

2.8.3. Bone-to-Bone Distance

Bone-to-bone distance was calculated between opposing surfaces in PostView for every tenth frame, and plotted in color. Distances were calculated using kinematics quantified by both MBT and DRSA separately; differences between the two methods across trials and specimens were compared for those surface nodes of the 3D reconstructions in the tibiotalar and subtalar articulating regions as a root mean square (RMS) difference.

2.9. Feasibility Application to a Live Human Subject

One female volunteer (28 years-old, 172 cm, 63.5kg, BMI=21.5) with no history of foot and ankle pain or pathology was recruited under ethics board approval and informed consent (IRB#65620). Screening radiographs ruled out abnormalities. The volunteer walked on the instrumented treadmill at 0.5 m/s and 1.0 m/s as DF images were acquired of the right ankle. Fluoroscope settings were 62–66 kV and 1.4–1.8 mA, with 608×600 camera resolution at 300 Hz and 1500 μs exposure. Heel-strike and toe-off events were imaged separately. Total fluoroscopy time was 31 seconds, including all trials. The subject ambulated for at least 30 seconds prior to DF acquisition to stabilize gait; at least 2 minutes of rest occurred between trials the two trials acquired for each activity.

A CT scan was acquired of the volunteer;s right ankle/foot (SOMATOM Definition AS, Siemens Medical Solutions, Malvern, PA) at 1.0mm slice thickness, 322 mm FOV, 512×512 matrix, 100 kV, 73 mAs. Processing of the data followed procedures above. ROM was calculated as the absolute value of the minimum subtracted from the maximum over each activity and trial for heel-strike and toe-off trials separately. ROM over the trials, within an activity, was averaged. Changes in bone-to-bone distance were qualitatively analyzed.

3. Results

The mean Euclidean bias of MBT (± standard deviation) across all trials and specimens was 0.31±0.09 mm, 0.41±0.17 mm, and 0.50±0.23 mm for the tibia, talus and calcaneus, respectively. The mean MBT Euclidean precision across all trials and specimens for the tibia, talus, and calcaneus was 0.15±0.07 mm, 0.19±0.07 mm, and 0.20±0.10 mm, respectively. Mean Euclidean bias and precision did not exceed 0.80 mm and 0.37 mm, respectively (S-Table 1).

Across all trials and specimens, the mean angular bias of MBT did not exceed 1.68° (S-Table 2). Translational bias did not exceed 0.47 mm (S-Table 3). Joint angles and translations calculated by MBT closely matched those calculated by DRSA (Figure 2). The mean rotational and translational bias was 0.25±0.81° and 0.03±0.35 mm, respectively when averaging all specimens, joints, and trials. The mean rotational and translational precision was 0.63±0.28° and 0.30±0.12 mm, respectively when averaging all specimens, joints, and trials. Mean RMS error for the bone-to-bone distance measurements for the tibiotalar and subtalar joints was 0.39±0.22 mm and 0.55±0.18 mm, respectively (S-Table 4).

Figure 2:

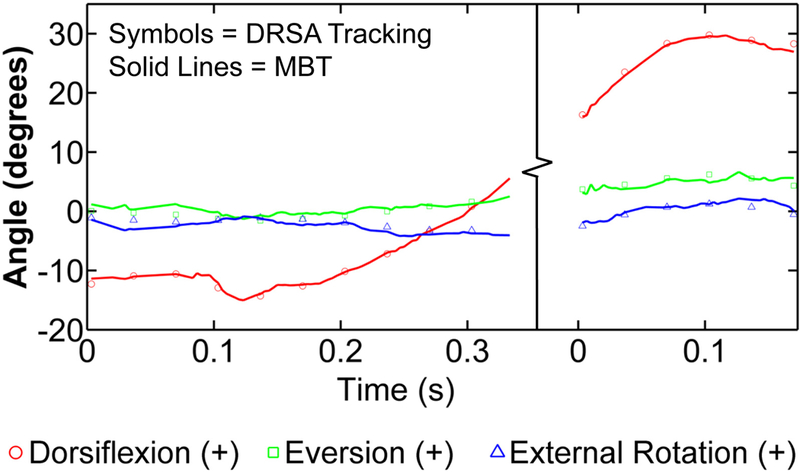
Plots of the joint angles from the heel-strike and toe-off trials of the first specimen were combined to recreate the gait cycle. The single markers represent joint angle values determined through digital radiostereometric analysis and are plotted every 10 frames. The solid, lines demonstrate the results obtained through model-based tracking, plotted for every frame.

Tibiotalar and subtalar ROM for the volunteer (Figure 3) during heel-strike was 11.19±1.38° and 2.83±0.84° respectively, for dorsi-/plantar flexion (S-Table 5). Tibiotalar and subtalar ROM during toe-off was 8.98±4.45°and 6.82±1.58°, respectively for dorsi-/plantar flexion. During heel-strike, the tibiotalar and subtalar joints experienced 3.19±1.45° and 3.04±0.91° of internal/external rotation ROM, respectively. Internal/external rotation ROM during toe-off was 3.59±2.07° for the tibiotalar joint and 3.93±1.16° for the subtalar joint. During heel-strike, tibiotalar and subtalar inversion/eversion ROM was 1.47±0.44° and 4.74±1.01°, respectively. During toe-off, inversion/eversion ROM for the tibiotalar and subtalar joints was 3.82±1.28° and 15.51±3.80°, respectively. The average tibiotalar displacement for the volunteer ranged from 0.39±0.06‒0.61±0.25 mm during heel-strike and 0.82±0.28‒0.89±0.38 mm during toe-off (S-Table 5). Average subtalar displacement ranged from 0.83±0.44‒1.34±0.15 mm during heel-strike and from 0.88±0.37‒2.37±0.47 mm during toe-off.

Figure 3:

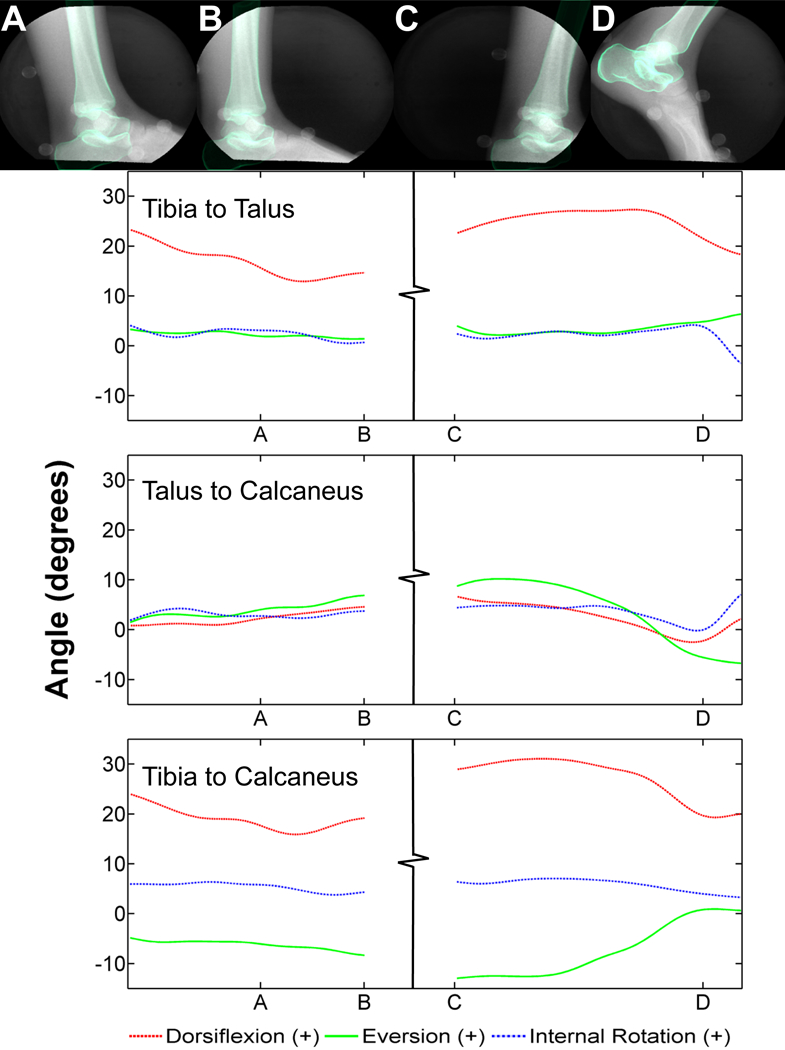
Heel-strike and toe-off trials for the normal volunteer. Fluoroscopic images overlaid with the digitally reconstructed radiographs of each bone from specific time points of each trial (top row): A) heel-strike, B) early midstance, C) late midstance, D) toe-off. Each corresponds with the identified time points A-D on the graphs below. Joint angles between the tibia and talus (second row), talus and calcaneus (third row) and tibia and calcaneus (bottom row).

Bone-to-bone distance varied across gait (Figure 4). During initial heel-strike, bone-to-bone distance immediately decreased at the medial subtalar joint (S-Video 1). Bone-to-bone distance at the tibiotalar joint decreased at the medial talus from late mid-stance to actual toe-off (S-Video 2).

Figure 4:

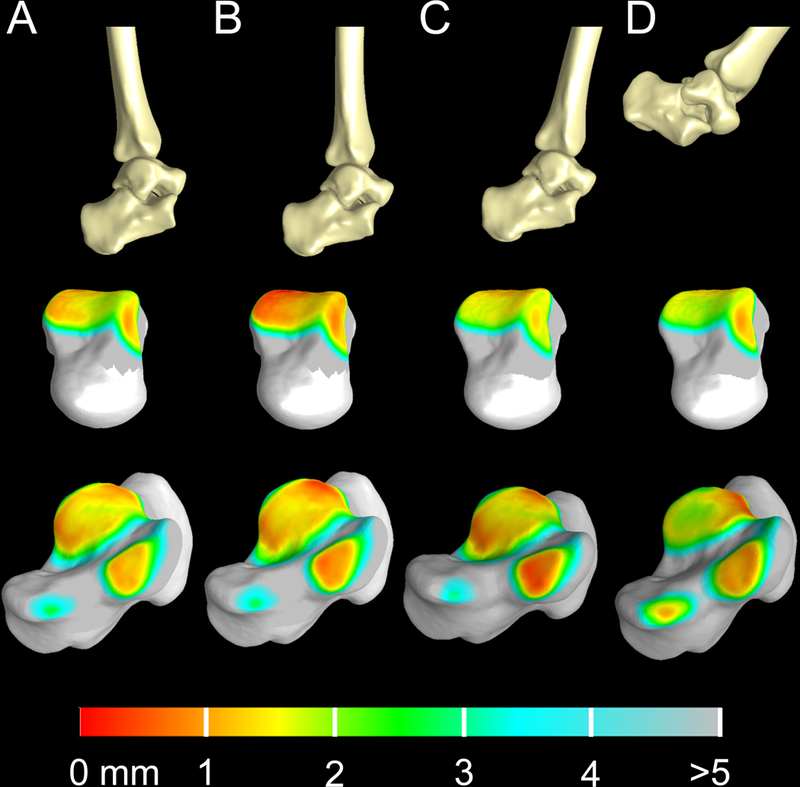
Three dimensional bone models of the tibia, talus and calcaneus throughout the gait cycle and the corresponding bone-to-bone distance fringe plots for the tibiotalar and subtalar joints. Top row: three-dimensional bone reconstruction of the ankle joint during heel-strike (A), early midstance (B), late midstance (C) and toe-off (D) per the identified time points in Figure 3. Middle row: color fringe plots of bone-to-bone distance for the tibiotalar joint displayed on the talus at time points A-D. Bottom row: color fringe plots of bone-to-bone distance for the subtalar joint displayed on the calcaneus at time points A-D.

4. Discussion

Though the DF system described herein was previously validated for the hip [17], we deemed it necessary to conduct an ankle validation study given substantial differences in bone morphology and motion between the hip and ankle. Here, DF and MBT could quantify subtalar and tibiotalar kinematics to mean errors less than 1 mm and 1°. We also successfully applied the protocol to a living subject, quantifying joint angles, translations, and bone-to-bone distances for the subtalar and tibiotalar joints independently.

Most ankle DF studies have been quasi-static [10–14], and none have validated the dynamic accuracy [10–15]. While we cannot directly compare our validation results to prior work, our data are similar to an ankle DF validation study conducted under quasi-static loading (Table 1). Statistics were not used to compare contributions of the subtalar and tibiotalar to the overall arc of motion at the ankle, but results from the feasibility study are comparable to the literature (S-Table 5) [12, 15]. For the volunteer, the mean change in subtalar inversion/eversion during toe-off in our subject was approximately five times that of the tibiotalar joint (15.51±3.80° versus 3.82±1.28°), strengthening the belief that the subtalar joint is primarily responsible for this motion as previously postulated (e.g., Yamaguchi et al.) [7, 12]. Still, the tibiotalar joint offered inversion/eversion, a phenomenon that will be explored in future studies.

Table 1:

Comparison of model-based tracking mean bias and precision from the present study with a study by Caputo et al.

	Present Study	Caputo et al.,2009
Mean Translational Bias (mm)	0.03	0.04
Mean Translational Precision (mm)	0.12	0.11
Mean Rotational Bias (°)	0.16	0.2
Mean Rotational Precision (°)	0.78	0.1

The mean translational ROM for the tibiotalar joint of the volunteer was 0.39±0.06‒0.89±0.38 mm, indicating that this joint is rather restricted in its positional movement. Conversely, the subtalar joint demonstrated considerably more translational movement at 0.83±0.44‒2.37±0.47 mm. Constraint of the subtalar joint could therefore require the tibiotalar joint to undergo increased translational movement, providing a quantitative explanation for tibiotalar OA following subtalar arthrodesis. Future work is necessary to confirm these findings.

In our study, the image intensifiers of the DF system were positioned below the treadmill to visualize both the subtalar and tibiotalar joints. As a result, portions of the bones were not visible in the DF images for the entire trial (e.g. caudal aspect of the calcaneus in Figure 3). One need not have the entire bone visible to perform MBT, but the accuracy could be influenced when defining features are not visible. We found similar accuracy values between the three bones, overall and on a frame-by-frame basis (Figure 2), suggesting that lowering of the DF system did not have a substantial effect. Still, caution should be exercised when using MBT to measure spatial positions of bones that fall outside the FOV.

Our study had limitations. First, cadavers were manipulated to simulate gait; the resulting kinematic profile was expected to differ from living subjects. We therefore chose to also quantify the accuracy of MBT for activities that would likely induce larger ROM than gait: dorsi-/plantar-flexion, inversion/eversion and internal/external rotation. Second, although the use of a treadmill prohibited us from imaging the entire gait cycle, we believe our results for dynamic motion is more representative than quasi-static motion [10–13]. Finally, radiation is a potential limitation. The total estimated dose equivalent (EDE) for the volunteer did not exceed 0.12 mSv. The risk to benefit ratio of utilizing DF and MBT should be carefully assessed.

In conclusion, we demonstrated that DF and MBT can accurately quantify tibiotalar and subtalar kinematics during dynamic motions. By visualizing what may be subtle differences in tibiotalar kinematics and bone-to-bone distance, we believe DF and MBT will serve as a valuable tool to study ankle pathomechanics. The applied methodologies may serve other motion analysis studies, for example, to validate, standardize, or calibrate gait models.

Supplementary Material

S Vid 1

Oblique medial perspective of subtalar joint bone-to-bone distance during treadmill walking at 1.0 m/s during heel-strike. Bone-to-bone distance immediately decreased on the medial aspect of the subtalar joint during actual heel-strike (S-Video 1).

S Vid 2

Oblique lateral perspective of tibiotalar joint bone-to-bone distance during treadmill walking at 1.0 m/s during toe-off. Bone-to-bone distance decreased on the medial talus, especially toward actual toe-off (S-Video 2).

S Fig 1

Coordinate systems used to convert bone motions captured by dual fluoroscopy (DF) to clinical joint angles and translations for both model-based markerless tracking (MBT) (top row) and dynamic radiostereometric analysis (DRSA) (bottom row). Each bone has an anatomical coordinate system (An) within the overall computed tomography coordinate system (CT) (left column), while bone movement is visualized within the DF coordinate system (DF) (right column) as shown here for the tibia.