Abstract
First-principles density functional theory calculations are performed to study the stability and electronic properties of hydrogenated and fluorinated two-dimensional sp3 boron phosphide (BP) and boron arsenide (BAs). As expected, the phonon dispersion spectrum and phonon density of states of hydrogenated and fluorinated BX (X = P, As) systems are found to be different, which can be attributed to the different masses of hydrogen and fluorine. Hydrogenated BX systems bear larger and indirect band gaps and are found to be different from fluorinated BX systems. These derivatives can be utilized in hydrogen storage applications and ultrafast electronic devices. Finally, we investigated the stability and electronic properties of stacked bilayers of functionalized BP. Interestingly, we found that these systems display strong interlayer interactions, which impart strong stability. In contrast with the electronic properties determined for the fluorinated/hydrogenated monolayers, we found that the electronic properties of these bilayers can finely be tuned to a narrow gap semiconductor, metallic or nearly semimetallic one by selecting a suitable arrangement of layers. Moreover, the nearly linear dispersion of the conduction band edge and the heavy-, light-hole bands are the interesting characteristics. Furthermore, the exceptional values of effective masses assure the fast electronic transport, making this material very attractive to construct electronic devices.
1. Introduction
The groundbreaking scotch tape experiment of successful isolation of graphene opened a new research area of two-dimensional (2D) materials.1 Since then, many 2D materials are predicted by density functional theory (DFT) calculations followed by their experimental synthesis. Furthermore, modification of the existing materials can lead to some exciting properties, especially in the case of graphene.2−5 The chemical modification of graphene is a common practice for which radicals such as hydrogen (H),6−8 oxygen (O),9 fluorine,10−12 and so forth are adsorbed on graphene. These adsorbates can take the form of an irregular pattern in graphene oxide2 or systematic motifs in hydrogenated graphene (graphane)3,7,8 and fluorinated graphene10−12 (fluorographene).5 Moreover, these modifications can significantly alter the electronic properties of graphene as both graphane and fluorographene are considered to be wide band gap semiconductors. However, the list is not limited to that because new/modified materials come with a number of applications, thus causing the advancement of the present technologies.13−16 Some of these materials with exceptional properties include (but are not limited to) stanene,17,18 Nb2O3,19 plumbene,20 arsenene,21 and silicene.22,23
Soon after the exfoliation of graphene, the synthesis of monolayer III–V binary compounds became a sizzling area of research with a particular interest toward the hexagonal boron nitride (h-BN).24−32 By virtue of its wide band gap, h-BN has lots of potential applications in nanoelectronics to be used as a dielectric material, ultraviolet light emitter, and oxidation-resistant coating.13−21
Another III–V binary compound that joined the league is hexagonal boron phosphide (h-BP).24,33 Despite the fact that it is not yet synthesized experimentally, it is already in the focus of theoretical studies. The geometric structure of h-BP is identical to that of graphene and h-BN, whereas two heterogeneous species (B and P) share the unit cell causing the breaking of symmetry and resulting in a band gap opening of 0.82–1.81 eV depending on the employed level of theory. Another material that is analogous to h-BP is hexagonal boron arsenide (h-BAs)34 having a band gap opening of 0.71 eV at local density approximation and 1.24 eV at GW0 levels of theory. Both these systems are found to be stable as predicted by the phonon dispersion spectrum. In this paper, we study the hydrogenation and fluorination of 2D BP and BAs, their effects on stability, and structural and electronic properties with the help of DFT calculations. To the best of our knowledge, the literature lacks such an investigation. In the following, we demonstrate that these systems display unique stability and electronic properties, which can be fine-tuned when fluorinated and hydrogenated BX layers are stacked, X = P, As.
2. Results and Discussion
Initially, we optimized h-BP and h-BAs to check the validity of our computational procedure. The bond lengths and lattice parameters were in good agreement with the previous studies.24,33 We also reproduced the band structures by employing the Γ–M–K–Γ path showing excellent agreement with the reported literature. In the next step, we studied the hydrogenation and fluorination of BX in chair conformation as this is the most favorable configuration in the case of graphane and fluorographene.11 After the introduction of these radicals, the planar BX structures are altered to the puckered ones. The very same happens to graphene by the addition of these radicals.
2.1. Structural Properties
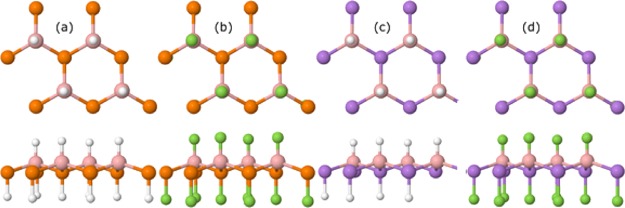
In the case of H–BP/F–BP, the lattice parameters and B–P bond lengths are found to be 3.199 Å/3.272 Å and 1.93 Å/1.99 Å, respectively. The distances of H from B and P are found to be 1.22 and 1.43 Å, respectively. The F–B bond length is found to be 1.39 Å, whereas the F–P bond length is as large as 1.61 Å. The H/F–P distance is almost 0.21 Å larger than the H/F–B distance. As discussed above, these structures are no longer planar and, therefore, we calculated the buckling height difference and found that B–P is 0.56 and 0.628 Å apart, in the case of H–BP and F–BP, respectively. Additionally, the lattice parameters and B–As bond lengths are calculated to be 3.414 Å/3.499 Å and 2.06 Å/2.12 Å for H–BAs and F–BAs, respectively. These larger lattice parameters (in comparison with the BP ones) can be attributed to the bigger covalent radius of As. The difference in the lattice parameters of H–BP and F–BP is 0.073 Å, whereas in the case of H–BAs and F–BAs, this difference is a bit larger (0.085 Å). Furthermore, the H–B (1.21 Å) and H–As (1.53 Å) bonds are smaller than the F–B (1.39 Å) and F–As (1.77 Å) bonds. In addition to this, the height between B and As is found to be 0.6 and 0.636 Å in H–BAs and F–BAs, respectively. It should be noted that both the sides of BX were functionalized, so there is no need to introduce a substrate. However, in the case where the use of a substrate is necessary, help can be taken from a very nice literature reported recently.35 All these geometric structures can be seen in Figure 1.
Figure 1.
Top and side view of (a) H–BP, (b) F–BP, (c) H–BAs, and (d) F–BAs derivatives.
2.2. Cohesive Strength
In order to assess the strength of these derivatives, cohesive energies are calculated and compared with the pristine BX cases. The expression used is given as
where nx and Ex are the number and gas-phase energy of the atom type x, whereas N is the total number of atoms in the simulation box. Finally, Etot is the total energy of the system under study. It is found that fluorination causes a minor reduction in the cohesive energy (CE) of BP in comparison with the pristine cases, whereas for BAs, fluorination increases the CE. On the contrary, hydrogenation significantly reduces the CE by 0.86 and 0.60 eV for BP and BAs, respectively. The CE analysis shows that the fluorinated derivatives can be equally stable as compared to their parent compounds. The summary of cohesive energies and formation energies (FEs) is shown in Table 1.
Table 1. Cohesive Strength (eV/atom), Formation Energies (eV), and Band Gaps (eV) Calculated at Different Levels of Theory.
| system | CE vdW-DF | CE M06-L | formation energy M06-L | gap (vdW-DF) | gap (HSEH1PBE) |
|---|---|---|---|---|---|
| BP | –4.58 | –4.74 | –9.50 | 1.1 | 1.49 |
| H–BP | –3.74 | –3.75 | –15.0 | 3.89a | 4.80a (5.60 direct) |
| F–BP | –4.40 | –4.45 | –17.8 | 1.53 | 2.17 |
| BAs | –4.14 | –4.67 | –9.3 | 0.89 | 2.17 |
| H–BAs | –3.54 | –3.82 | –15.3 | 3.50a | 4.43a (5.15 direct) |
| F–BAs | –4.26 | –4.53 | –18.1 | 1.25 | 2.21 |
| HBPF | –4.10 | –17.0 | 4.28 | ||
| FBPH | –4.15 | –16.5 | 3.71 | ||
| HBAsF | –4.14 | –16.6 | 3.82 | ||
| FBAsH | –4.26 | –16.4 | 3.27 |
Indirect gap.
2.3. Dynamical Stability
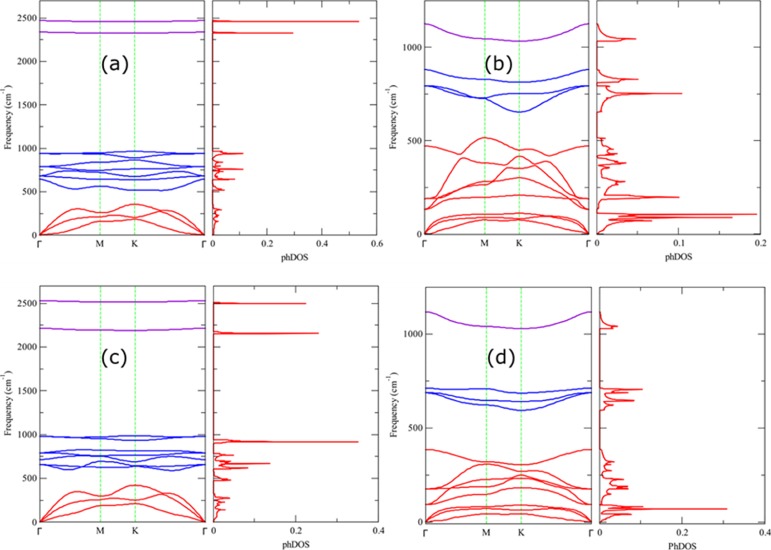
In order to check whether these derivatives are dynamically stable or not, the phonon spectrum is calculated within the density functional perturbation theory36 with 8 × 8 × 1 q-points. The presence of a negative frequency is the sign of instability, and in this regard, all the calculated derivatives are stable as they all lack negative frequencies as can be seen from the phonon band spectrum along with the corresponding phonon density of states (PhDOS). The high-frequency modes in hydrogenated systems are sufficiently higher in frequency as compared to the fluorinated counterparts. The higher-frequency modes in H–BP and H–BAs are in the frequency range of around 2500 cm–1, the latter being a bit higher. This higher-frequency degenerate mode in pristine h-BP/h-BAs appears at a frequency around 1000 cm–1/840 cm–1. Furthermore, this degenerate mode splits into two modes in H–BP, and even more prominently in H–BAs. The phonon spectrum of hydrogenated and fluorinated systems differs from each other, which can be attributed to the different atomic masses of H and F. Additionally, the intensities of hydrogenated systems are higher than those of fluorinated counterparts as can be seen from PhDOS. It is evident from the phonon spectrum/DOS that the phonon can be bifurcated into high-, intermediate-, and low-frequency groups not only for hydrogenated cases but also for fluorinated cases. This characteristic is missing in fluorographene37 where the clear separated groups are absent. Consequently, the H–BX and F–BX systems can be as stable as derivatives just like graphane and fluorographene. The phonon plots can be seen in Figure 2 where these low-, intermediate-, and high-frequency groups are in the range of ∼500, ∼1000, and ∼2500, respectively, for the HBX system. However, these groups span over a (bit) wider range for HBP in comparison with FBAs. For the sack of brevity, the low-, intermediate-, and high-frequency groups are colored as red, blue, and violet, respectively, in phonon bands.
Figure 2.
Phonon band spectrum along with respective PhDOS plots for (a) H–BP, (b) F–BP, (c) H–BAs, and (d) F–BAs. The absence of negative frequencies guarantees the stability of these derivatives.
2.4. Kinetic Stability
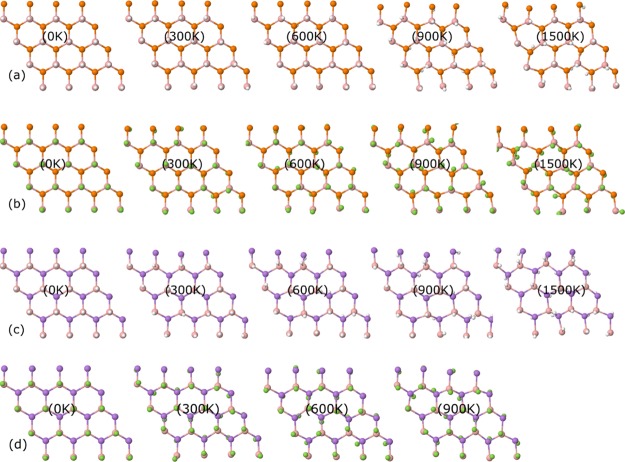
Ab initio molecular dynamic (AIMD) simulations are carried out to assess the thermal stability of these derivatives. We constructed a 4 × 4 unit cell to perform MD at 300, 600, 900, and 1500 K. We use the SIESTA code and the vdW-DF level of theory. The simulations last for 1 fs and are divided into 1000 steps. The NVT ensemble is used with a Nose–Hoover thermostat.41 Snapshots of the final steps at various temperatures are shown in Figure 3. The excellent high-temperature stabilities of these derivatives except the F–BAs at 1500 K guarantee their applications in high-temperature operating devices. Furthermore, the average changes in bonds and angles are depicted in Table S1. Moreover, the stability of some structures was also confirmed by examining them for 2 ps at 1500 K.
Figure 3.
Molecular dynamics snapshots after the end of 1 fs simulations steps treated at various temperatures for (a) H–BP, (b) F–BP, (c) H–BAs, and (d) F–BAs.
2.5Electronic Properties of F–BX and H–BX (X = P, As)
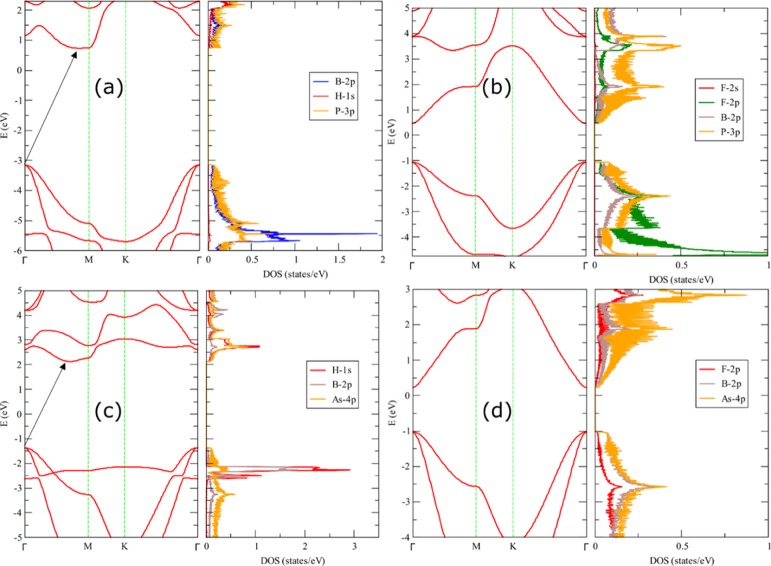
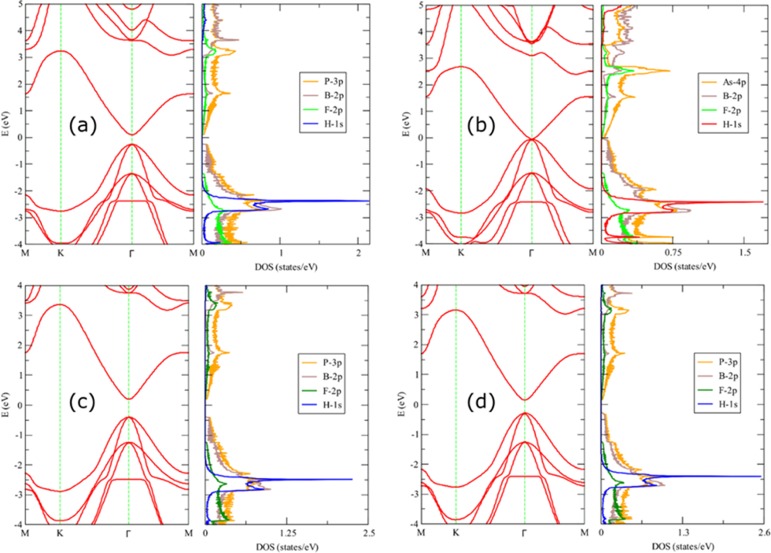
The electronic band structures and projected density of states (PDOS) are calculated, and it is found that these derivatives possess different electronic properties in comparison with each other and also with the pristine case.24 The calculated band gaps of h-BP and h-BAs are found to be 1.10 and 0.89 eV, respectively. These band gaps appear at K and are of direct nature. However, the band gaps of H–BX are of indirect nature, being the valence band maximum (VBM) at Γ and conduction band minimum (CBM) at Γ–M. The computed band gaps of H–BP and H–BAs are 3.89 and 3.50 eV, respectively. Furthermore, PDOS shows that there is a negligible contribution of H to the DOS at VBM or CBM in H–BP. However, in H–BAs, a significant contribution of H to the DOS can be seen, which hybridized mostly with B 2p in valence and with As 4p in the conduction band. F–BP and F–BAs show a band gap opening of 1.53 and 1.25 eV, respectively. Nevertheless, these are direct gaps induced at the Γ point. Moreover, the VBM in both the cases has twofold degeneracy. The P 3p orbitals hybridized with B 2p and F 4p at VBM and CBM, being the P 3p contribution a bit more at CBM. Nearly, the same picture can be seen in the case of F–BAs, where more contribution comes from the As 4p orbitals. Besides, the curvature at CBM and VBM in F–BP and especially in F–BAs is likely to have exceptional mobilities. These show that F–BX systems can be utilized in ultrafast electronic devices. The band structures along with corresponding PDOS are plotted as shown in Figure 4. For the sake of completeness, we also studied the mixed monolayers: HBPF, FBPH, FBAsF, and FBAsH. Interestingly, these systems present band gaps which are bracketed by the ones computed for F–BX and H–BX. Therefore, using Janus-type functionalization, it is possible to obtain a finer tuning of the band gap.
Figure 4.
Electronic band structures determined at the vdW-DF/double zeta plus polarization (DZP) level, along with the respective PDOS plots for (a) H–BP, (b) F–BP, (c) H–BAs, and (d) F–BAs. The Fermi energy is set to zero.
2.6Stability and Electronic Properties of Mixed Bilayers
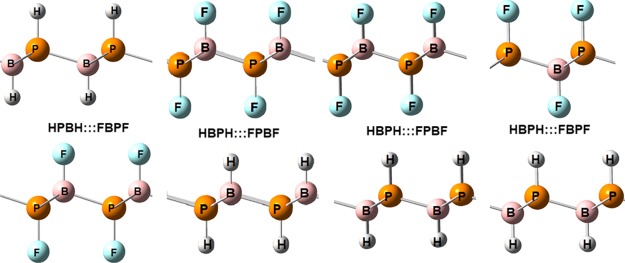
In a recent work, we showed that it is possible to adjust the band gap of functionalized silicene if two layers are stacked.23 In this line, we have considered the case of stacking one layer of H–BP onto F–BP. There are four possible stacking possibilities for these systems which are shown in Figure 5.
Figure 5.
Optimized unit cells for the bilayer systems formed by the stacking of one H–BP layer onto F–BP.
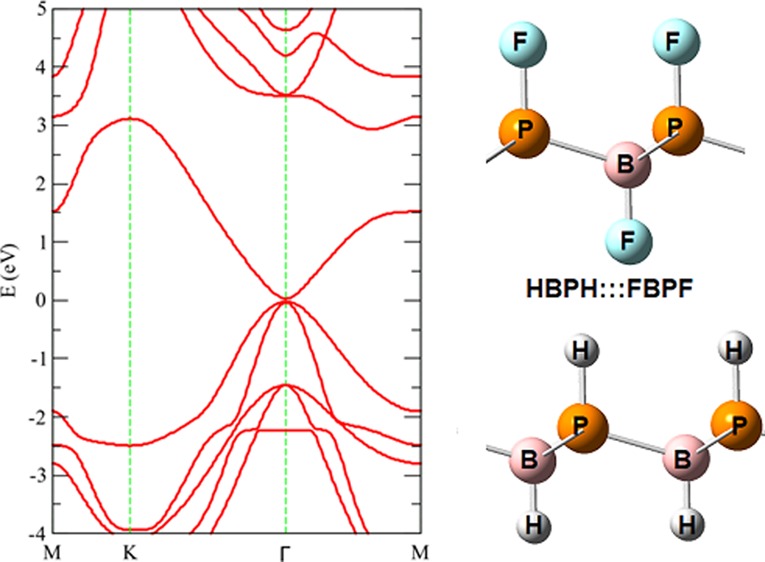
In the case of BP, we found that the four combinations have very similar energy, the most stable one being that which combines HBPH:::FBPF (see Figure 6). This structure is only 0.002 eV/atom more stable than HPBH:::FBPF. The remaining two of structures are in the same range of stability. Interestingly, these systems are expected to be very stable because the fluorine and hydrogen atoms of different layers are expected to interact through F:::H hydrogen bonds because the fluorine atoms are negatively charged while the hydrogen atoms bear a positive charge. For example, in the case of HBPH:::FBPF, according to Mulliken analysis, the H atom bonded to P has a positive charge of +0.1 e while the F atom bonded to B bears a negative charge equal to −0.3 e–, at the M06-L/6-311G* level of theory. Additionally, these outcomes are in accordance with the lower (higher) electronegativity of H (F). Thus, we can expect a strong interaction between monolayers. The interlayer interaction energy (IE) of HBPH:::FBPF is 0.015 eV/atom, at the M06-L/6-31G* level of theory. This value is only 0.06 eV/atom smaller than the stacking interaction computed for bilayer graphene using the same methodology. With regard to the electronic properties, we have found that the band gaps of monolayers were significantly reduced when stacked. For example, HBPH:::FBPF and HBPH:::FPBF are metals, while the HPBH:::FPBF has a band gap of 0.38 eV. Perhaps the most interesting case is HPBH:::FBPF, which is a small band gap semiconductor (0.04 eV) featuring somewhat linear dispersion at the CBM. Furthermore, the VBM is composed of heavy-hole and light-hole bands. To further gain insights, we calculated the effective masses of electrons and holes from the curvature of conduction and valence bands. The calculated value of the effective mass of electrons is 0.027m0. Furthermore, the effective mass of the heavy-hole band is computed to be 0.045m0, while that of the light-hole band is as low as 0.014m0. These exceptional values are the surety of remarkable electronic transport in these bilayers. Consequently, these materials become critically attractive to develop BP-based fast nanoelectronic materials.
Figure 6.
Electronic band structures along with the respective PDOS plots for (a) HPBH:::FPBF, (b) HPBH:::FBPF, (c) HBPH:::FBPF, and (d) HBPH:::FPBF at the vdW-DF/DZP level of theory.
3. Conclusions
The hydrogenation and fluorination of h-BP and h-BAs are studied by means of DFT calculations. The vibrational properties are found to be different from their parent compounds. The hydrogenated and fluorinated BX (X = P, As) systems are likely to have the comparable stabilities as compared to graphane and fluorographene, respectively. The AIMD simulations suggest that these derivatives can be stable at temperatures as high as 1500 K with the sole exception of F–BAs. Just like the vibrational properties, their electronic properties are also different from h-BP/h-BAs and from each other. The H–BX systems show larger and indirect band gaps in comparison with the F–BX counterparts. The former can have applications in hydrogen storage devices, while the latter can be utilized in ultrafast electronic devices. Finally, we investigated the stability and electronic properties of stacked bilayers of functionalized BP. Interestingly, we found that these systems display strong interlayer interactions, which turn them very stable. In contrast with the electronic properties determined for the fluorinated/hydrogenated monolayers, we found that the bilayers have some exciting characteristics, such as nearly linear dispersion of the conduction band and heavy- and light-hole bands. By virtue of these interesting properties, these bilayers can find applications in fast nanoelectronic devices.
4. Methods
All the calculations are performed with quantum espresso (QE),38,39 SIESTA,40,41 and Gaussian42 codes which are based on DFT methods. We use the projector-augmented wave43 method and Perdew–Burke–Ernzerhof (PBE)44 flavor of the generalized gradient approximation to describe the exchange and correlation in QE. The dispersion-corrected PBE-D245 scheme is used. The kinetic energy cutoff for the expansion of wave function is set to 60 Ry and 8 times of this value is set for charge densities. The force-convergence criterion is set to 10–5 Ry/bohr with the energy criteria of 10–12 Ry. We utilized the PBEsol46 and PBE pseudopotentials (PPs) for BP and BAs, respectively, from the Standard Solid-State Pseudopotentials library.47 The vdW-DF48,49 calculations are carried out as implemented in the SIESTA code. The norm-conserving Troullier–Martins PPs were utilized in their complete separable form.50 The basis set selected was the DZP polarization functions. The mesh cutoff is 200 Ry in all the calculations. In the case of the calculations performed with SIESTA, geometry optimization is followed until the forces were less than 0.01 eV/Å. The unit cell is sampled with a 30 × 30 × 1 grid of k-points. The vacuum region along the z-axis is fixed to 20 Å. The M06-L/6-31G*51 and HSEH1PBE/6-31G*52 geometry optimizations are carried out with Gaussian 09 using the default convergence criteria.28 The ultrafine grid was selected, and 3000 k-points were used to sample the unit cell. From now and onward, H–BX and F–BX will be used for monolayer hydrogenated and fluorinated BX, respectively, and X being P and As. Interlayer IEs were calculated as IE = [E(bilayer) – E(monolayer 1) – E(monolayer 2)]/Natoms, where E(bilayer) is the energy of the bilayered system and E(monolayer) corresponds to the energy of the isolated monolayers which form the bilayer. FEs were calculated as53 FE = E(Z–BX–Y) μB – μX – μZ – μY, where E(Z–BX–Y) is the energy of the monolayer and μB, μX, μZ, and μY are the chemical potentials of the atoms involved. In all cases, we selected the energies of the isolated atoms as a reference.
Acknowledgments
S.U. and F.S. are thankful to the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG), Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), and Financiadora de Estudos e Projetos (FINEP) for their financial support. P.A.D. is thankful to PEDECIBA Quimica, CSIC, and ANII Uruguayan institutions for financial support.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b02605.
Average changes in bonds and angles at different temperatures (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Novoselov K. S.; Geim A. K.; Morozov S. V.; Jiang D.; Zhang Y.; Dubonos S. V.; Grigorieva I. V.; Firsov A. A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
- Dikin D. A.; Stankovich S.; Zimney E. J.; Piner R. D.; Dommett G. H. B.; Evmenenko G.; Nguyen S. T.; Ruoff R. S. Preparation and characterization of graphene oxide paper. Nature 2007, 448, 457–460. 10.1038/nature06016. [DOI] [PubMed] [Google Scholar]
- Elias D. C.; Nair R. R.; Mohiuddin T. M. G.; Morozov S. V.; Blake P.; Halsall M. P.; Ferrari A. C.; Boukhvalov D. W.; Katsnelson M. I.; Geim A. K.; Novoselov K. S. Control of graphene’s properties by reversible hydrogenation: evidence for graphane. Science 2009, 323, 610–613. 10.1126/science.1167130. [DOI] [PubMed] [Google Scholar]
- Withers F.; Dubois M.; Savchenko A. K. Electron properties of fluorinated single-layer graphene transistors. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82, 073403. 10.1103/physrevb.82.073403. [DOI] [Google Scholar]
- Nair R. R.; Ren W.; Jalil R.; Riaz I.; Kravets V. G.; Britnell L.; Blake P.; Schedin F.; Mayorov A. S.; Yuan S.; Katsnelson M. I.; Cheng H.-M.; Strupinski W.; Bulusheva L. G.; Okotrub A. V.; Grigorieva I. V.; Grigorenko A. N.; Novoselov K. S.; Geim A. K. Fluorographene: a two-dimensional counterpart of Teflon. Small 2010, 6, 2877–2884. 10.1002/smll.201001555. [DOI] [PubMed] [Google Scholar]
- Sluiter M. H. F.; Kawazoe Y. Cluster expansion method for adsorption: Application to hydrogen chemisorption on graphene. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 68, 085410. 10.1103/physrevb.68.085410. [DOI] [Google Scholar]
- Sofo J. O.; Chaudhari A. S.; Barber G. D. Graphane: A two-dimensional hydrocarbon. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 75, 153401. 10.1103/physrevb.75.153401. [DOI] [Google Scholar]
- Denis P. A.; Iribarne F. On the hydrogen addition to graphene. J. Mol. Struct.: THEOCHEM 2009, 907, 93–103. 10.1016/j.theochem.2009.04.028. [DOI] [Google Scholar]
- Denis P. A. Density functional investigation of thioepoxidated and thiolated graphene. J. Phys. Chem. C 2009, 113, 5612–5619. 10.1021/jp808599w. [DOI] [Google Scholar]
- Charlier J.-C.; Gonze X.; Michenaud J.-P. First-principles study of graphite monofluoride (CF) n. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 16162–16168. 10.1103/physrevb.47.16162. [DOI] [PubMed] [Google Scholar]
- Leenaerts O.; Peelaers H.; Hernández-Nieves A.; Partoens B.; Peeters F.M. First-principles investigation of graphene fluoride and graphane. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82, 195436. 10.1103/physrevb.82.195436. [DOI] [Google Scholar]
- Cheng S.-H.; Zou K.; Okino F.; Gutierrez H. R.; Gupta A.; Shen N.; Eklund P. C.; Sofo J. O.; Zhu J. Reversible fluorination of graphene: Evidence of a two-dimensional wide bandgap semiconductor. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 205435. 10.1103/physrevb.81.205435. [DOI] [Google Scholar]
- Kuklin A. V.; Baryshnikov G. V.; Minaev B. F.; Ignatova N.; Ågren H. Strong Topological States and High Charge Carrier Mobility in Tetraoxa[8]circulene Nanosheets. J. Phys. Chem. C 2018, 122, 22216–22222. 10.1021/acs.jpcc.8b08596. [DOI] [Google Scholar]
- Baryshnikov G. V.; Minaev B. F.; Karaush N. N.; Minaeva V. A. Design of nanoscaled materials based on tetraoxa[8]circulene. Phys. Chem. Chem. Phys. 2014, 16, 6555–6559. 10.1039/c3cp55154g. [DOI] [PubMed] [Google Scholar]
- Baryshnikov G. V.; Minaev B. F.; Karaush N. N.; Minaeva V. A. The art of the possible: computational design of the 1D and 2D materials based on the tetraoxa[8]circulene monomer. RSC Adv. 2014, 4, 25843–25851. 10.1039/c4ra02693d. [DOI] [Google Scholar]
- Karaush N. N.; Baryshnikov G. V.; Minaev B. F. DFT characterization of a new possible graphene allotrope. Chem. Phys. Lett. 2014, 612, 229–233. 10.1016/j.cplett.2014.08.025. [DOI] [Google Scholar]
- Zhang R.-W.; Zhang C.-W.; Ji W.-X.; Li S.-S.; Hu S.-J.; Yan S.-S.; Li P.; Wang P.-J.; Li F. Ethynyl-functionalized stanene film: a promising candidate as large-gap quantum spin Hall insulator. New J. Phys. 2015, 17, 083036. 10.1088/1367-2630/17/8/083036. [DOI] [Google Scholar]
- Zhang M.-h.; Zhang C.-w.; Wang P.-j.; Li S.-s. Prediction of high-temperature Chern insulator with half-metallic edge states in asymmetry-functionalized stanene. Nanoscale 2018, 10, 20226–20233. 10.1039/C8NR07503D. [DOI] [PubMed] [Google Scholar]
- Zhang S.-J.; Zhang C.-W.; Zhang S.-F.; Ji W.-X.; Li P.; Wang P.-J.; Yan S.-S. Intrinsic Dirac half-metal and quantum anomalous Hall phase in a hexagonal metal-oxide lattice. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 205433. 10.1103/physrevb.96.205433. [DOI] [Google Scholar]
- Zhao H.; Zhang C.-w.; Ji W.-x.; Zhang R.-w.; Li S.-s.; Yan S.-s.; Zhang B.-m.; Li P.; Wang P.-j. Unexpected Giant-Gap Quantum Spin Hall Insulator in Chemically Decorated Plumbene Monolayer. Sci. Rep. 2016, 6, 20152. 10.1038/srep20152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y.-p.; Ji W.-x.; Zhang C.-w.; Li P.; Zhang S.-f.; Wang P.-j.; Li S.-s.; Yan S.-s. Two-dimensional arsenene oxide: A realistic large-gap quantum spin Hall insulator. Appl. Phys. Lett. 2017, 110, 213101. 10.1063/1.4983781. [DOI] [Google Scholar]
- Zhang C.-w.; Yan S.-s. First-Principles Study of Ferromagnetism in Two-Dimensional Silicene with Hydrogenation. J. Phys. Chem. C 2012, 116, 4163–4166. 10.1021/jp2104177. [DOI] [Google Scholar]
- Denis P. A. Stacked functionalized silicene: a powerful system to adjust the electronic structure of silicene. Phys. Chem. Chem. Phys. 2015, 17, 5393–5402. 10.1039/c4cp05331a. [DOI] [PubMed] [Google Scholar]
- Şahin H.; Cahangirov S.; Topsakal M.; Bekaroglu E.; Akturk E.; Senger R. T.; Ciraci S. Monolayer honeycomb structures of group-IV elements and III-V binary compounds: First-principles calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 80, 155453. 10.1103/PhysRevB.80.155453. [DOI] [Google Scholar]
- Kim K. K.; Hsu A.; Jia X.; Kim S. M.; Shi Y.; Hofmann M.; Nezich D.; Rodriguez-Nieva J. F.; Dresselhaus M.; Palacios T.; Kong J. Synthesis of monolayer hexagonal boron nitride on Cu foil using chemical vapor deposition. Nano Lett. 2011, 12, 161–166. 10.1021/nl203249a. [DOI] [PubMed] [Google Scholar]
- Watanabe K.; Taniguchi T.; Kanda H. Direct-bandgap properties and evidence for ultraviolet lasing of hexagonal boron nitride single crystal. Nat. Mater. 2004, 3, 404–409. 10.1038/nmat1134. [DOI] [PubMed] [Google Scholar]
- Alem N.; Erni R.; Kisielowski C.; Rossell M. D.; Gannett W.; Zettl A. Atomically thin hexagonal boron nitride probed by ultrahigh-resolution transmission electron microscopy. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 80, 155425. 10.1103/physrevb.80.155425. [DOI] [Google Scholar]
- Denis P. A.; Iribarne F. New Approach to Accomplish the Covalent Functionalization of Boron Nitride Nanosheets: Cycloaddition Reactions. J. Phys. Chem. C 2018, 122, 18583–18587. 10.1021/acs.jpcc.8b05907. [DOI] [Google Scholar]
- Kim K. K.; Hsu A.; Jia X.; Kim S. M.; Shi Y.; Hofmann M.; Nezich D.; Rodriguez-Nieva J. F.; Dresselhaus M.; Palacios T.; Kong J. Synthesis of Monolayer Hexagonal Boron Nitride on Cu Foil Using Chemical Vapor Deposition. Nano Lett. 2012, 12, 161–166. 10.1021/nl203249a. [DOI] [PubMed] [Google Scholar]
- Dean C. R.; Young A. F.; Meric I.; Lee C.; Wang L.; Sorgenfrei S.; Watanabe K.; Taniguchi T.; Kim P.; Shepard K. L.; Hone J. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 2010, 5, 722–726. 10.1038/nnano.2010.172. [DOI] [PubMed] [Google Scholar]
- Liu Z.; Gong Y.; Zhou W.; Ma L.; Yu J.; Idrobo J. C.; Jung J.; MacDonald A. H.; Vajtai R.; Lou J.; Ajayan P. M. Ultrathin high-temperature oxidation-resistant coatings of hexagonal boron nitride. Nat. Commun. 2013, 4, 2541. 10.1038/ncomms3541. [DOI] [PubMed] [Google Scholar]
- Karaush N. N.; Bondarchuk S. V.; Baryshnikov G. V.; Minaeva V. A.; Sun W.-H.; Minaev B. F. Computational study of the structure, UV-vis absorption spectra and conductivity of biphenylene-based polymers and their boron nitride analogues. RSC Adv. 2016, 6, 49505–49516. 10.1039/c6ra06832d. [DOI] [Google Scholar]
- Çakr D.; Kecik D.; Sahin H.; Durgun E.; Peeters F. M. Realization of a p-n junction in a single layer boron-phosphide. Phys. Chem. Chem. Phys. 2015, 17, 13013–13020. 10.1039/c5cp00414d. [DOI] [PubMed] [Google Scholar]
- Zhang R.-w.; Zhang C.-w.; Ji W.-x.; Li S.-s.; Wang P.-j.; Hu S.-j.; Yan S.-s. Hydrogenated boron arsenide nanosheet: a promising candidate for bipolar magnetic semiconductor. Appl. Phys. Express 2015, 8, 113001. 10.7567/apex.8.113001. [DOI] [Google Scholar]
- Li S.-s.; Ji W.-x.; Hu S.-j.; Zhang C.-w.; Yan S.-s. Effect of Amidogen Functionalization on Quantum Spin Hall Effect in Bi/Sb(111) Films. ACS Appl. Mater. Interfaces 2017, 9, 41443–41453. 10.1021/acsami.7b13179. [DOI] [PubMed] [Google Scholar]
- Baroni S.; de Gironcoli S.; Dal Corso A.; Giannozzi P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. 10.1103/revmodphys.73.515. [DOI] [Google Scholar]
- Peelaers H.; Hernández-Nieves A. D.; Leenaerts O.; Partoens B.; Peeters F. M. Vibrational properties of graphene fluoride and graphane. Appl. Phys. Lett. 2011, 98, 051914. 10.1063/1.3551712. [DOI] [Google Scholar]
- Giannozzi P.; Baroni S.; Bonini N.; Calandra M.; Car R.; Cavazzoni C.; Ceresoli D.; Chiarotti G. L.; Cococcioni M.; Dabo I.; Dal Corso A.; de Gironcoli S.; Fabris S.; Fratesi G.; Gebauer R.; Gerstmann U.; Gougoussis C.; Kokalj A.; Lazzeri M.; Martin-Samos L.; Marzari N.; Mauri F.; Mazzarello R.; Paolini S.; Pasquarello A.; Paulatto L.; Sbraccia C.; Scandolo S.; Sclauzero G.; Seitsonen A. P.; Smogunov A.; Umari P.; Wentzcovitch R. M. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter 2009, 21, 395502. 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]
- Giannozzi P.; Andreussi O.; Brumme T.; Bunau O.; Buongiorno Nardelli M.; Calandra M.; Car R.; Cavazzoni C.; Ceresoli D.; Cococcioni M.; Colonna N.; Carnimeo I.; Dal Corso A.; de Gironcoli S.; Delugas P.; DiStasio R. A.; Ferretti A.; Floris A.; Fratesi G.; Fugallo G.; Gebauer R.; Gerstmann U.; Giustino F.; Gorni T.; Jia J.; Kawamura M.; Ko H.-Y.; Kokalj A.; Küçükbenli E.; Lazzeri M.; Marsili M.; Marzari N.; Mauri F.; Nguyen N. L.; Nguyen H.-V.; Otero-de-la-Roza A.; Paulatto L.; Poncé S.; Rocca D.; Sabatini R.; Santra B.; Schlipf M.; Seitsonen A. P.; Smogunov A.; Timrov I.; Thonhauser T.; Umari P.; Vast N.; Wu X.; Baroni S. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys.: Condens. Matter 2017, 29, 465901. 10.1088/1361-648x/aa8f79. [DOI] [PubMed] [Google Scholar]
- Soler J. M.; Artacho E.; Gale J. D.; García A.; Junquera J.; Ordejón P.; Sánchez-Portal D. The SIESTA Method for Ab Initio Order-N Materials Simulation. J. Phys.: Condens. Matter 2002, 14, 2745–2779. 10.1088/0953-8984/14/11/302. [DOI] [Google Scholar]
- Ordejón P.; Artacho E.; Soler J. M. Self-consistent order-N Density-functional Calculations for Very Large Systems. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 53, R10441–R10444. 10.1103/physrevb.53.r10441. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; et al. Gaussian 09, Revision D; Gaussian, Inc.: Wallingford CT, 2009.
- Blöchl P. E. Projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
- Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. 10.1103/physrevlett.100.136406. [DOI] [PubMed] [Google Scholar]
- Prandini G.; Marrazzo A.; Castelli I. E.; Mounet N.; Marzari N.. Precision and efficiency in solid-state pseudopotential calculations. arXiv:1806.05609, 2018. [Google Scholar]
- Dion M.; Rydberg H.; Schröder E.; Langreth D. C.; Lundqvist B. I. Van der Waals density functional for general geometries. Phys. Rev. Lett. 2004, 92, 246401. 10.1103/physrevlett.92.246401. [DOI] [PubMed] [Google Scholar]
- Román-Pérez G.; Soler J. M. Efficient Implementation of a van der Waals Density Functional: Application to Double-Wall Carbon Nanotubes. Phys. Rev. Lett. 2009, 103, 096102. 10.1103/physrevlett.103.096102. [DOI] [PubMed] [Google Scholar]
- Troullier N.; Martins J. L. Efficient Pseudopotentials for Plane-Wave Calculations. Phys. Rev. B: Condens. Matter Mater. Phys. 1991, 43, 1993–2006. 10.1103/physrevb.43.1993. [DOI] [PubMed] [Google Scholar]
- Zhao Y.; Truhlar D. G. A New Local Density Functional for Main-group Thermochemistry, Transition Metal Bonding, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Phys. 2006, 125, 194101. 10.1063/1.2370993. [DOI] [PubMed] [Google Scholar]
- Heyd J.; Scuseria G. E. Assessment and validation of a screened Coulomb hybrid density functional. J. Chem. Phys. 2004, 120, 7274–7280. 10.1063/1.1668634. [DOI] [PubMed] [Google Scholar]
- Ullah S.; Denis P. A.; Sato F. Beryllium doped graphene as an efficient anode material for lithium-ion batteries with significantly huge capacity: A DFT study. Appl. Mater. Today 2017, 9, 333–340. 10.1016/j.apmt.2017.08.013. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.