Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2018 Nov 20;3(11):15821–15828. doi: 10.1021/acsomega.8b02500

Unusual Enhancement of the Adsorption Energies of Sodium and Potassium in Sulfur−Nitrogen and Silicon−Boron Codoped Graphene

Saif Ullah ‡,*, Pablo A Denis †,*, Fernando Sato ‡
PMCID: PMC6643653  PMID: 31458230

Abstract

graphic file with name ao-2018-02500u_0006.jpg

Herein, we have employed first-principles calculations to investigate the interaction between XY dual-doped graphene (DDG) (X = AL, Si, P, S; Y = B, N, O) and sodium/potassium. The introduction of two dopants alters the adsorption energy (AE) of sodium and potassium with respect to perfect graphene by an average of 0.88 and 0.66 eV, respectively. The systems that display the strongest interactions with the two alkalies assayed are SN and SiB DDG. Although the adsorption energy of sodium on graphene is weaker in comparison to that of potassium, the introduction of these dopants significantly reduces this difference. In effect, in some cases, the AE-K and AE-NA differ by less than 0.05 eV. The protrusion of the 3p dopants out of the graphene plane creates a hole where sodium and potassium can easily be intercalated between two layers of dual-doped graphene. The interlayer distances are reduced by less than 0.4 Å after K intercalation, making the process very favorable. Finally, most importantly, this eminent rise in adsorption energies guarantees exceptional storage capacities at the cost of low doping concentration.

1. Introduction

In 2020, the Protocol of Kyoto1 comes to an end and the Paris2 agreement will be implemented to limit the temperature rise of the planet by less than 1.5 °C, with respect to preindustrial levels. The achievement of this goal requires a significant reduction in greenhouse gas emissions. For this reason, major automobile companies are planning to use solely battery-powered engines in their near future, as the famous Rolls Royce Company has recently announced.3 In fact, countries like France are planning to prohibit the commercialization of fossil fuel-based cars by 2040.4 Over the last few decades, lithium has been extensively used to design the best rechargeable batteries. In particular, graphene has been considered to be the most promising material to improve the performance of lithium-based batteries.5−9 A large number of theoretical investigations have been devoted to understanding the interaction between lithium and graphene,10−18 as well as with sulfur,19 fullerenes,20 transition-metal dichalgogenides,21 or two-dimensional boron materials.22 And this task has not been easy because the interaction between carbon materials and alkalies is affected by the self-interaction error when using density functional theory.23−27 For example, it is difficult to obtain a reasonable picture with the most popular density functionals even for the benzene-alkali systems.22,23 Nevertheless, theoretical calculations have been very useful to shed light into the chemistry behind alkali-based secondary batteries.10−18 Recently, we studied the effect of dual doping on the adsorption of lithium onto mono (X) and dual-doped (XY) graphene, where X = B, N, O; Y = Al, Si, P, S.28 Interestingly, we found that for all dual-doped graphene (DDG) systems, the clustering of lithium is inhibited. In the particular case of nitrogen-doped graphene, the adsorption energy (AE) of lithium is lower than that computed for pristine graphene. However, when nitrogen is combined with aluminum, silicon, phosphorus, or sulfur, the AE is tremendously improved. The most paradigmatic case is that of SN DDG, which presents the strongest AE with Li: −2.99 eV, at the van der Waals density functional (vdW-DF)/double-ζ plus polarization (DZP) level. This value is almost three times the AE of Li over pristine graphene. This result is not entirely surprising because, among dual-doped graphene systems, the SN-doped flavor seems to display unique properties.29−38 Although, lithium is the best choice for alkali-based rechargeable batteries, the problem is that it would be impossible to meet the global demand if it is supposed to replace gasoline. Sodium and potassium are much more abundant than lithium in the Earth’s crust. For this reason, they are good candidates to surrogate lithium. However, important challenges must be faced to design useful sodium or potassium rechargeable batteries with reasonable lifetimes.39−43 Bearing in mind the impressive results that we obtained when lithium interacts with DDG,28 we considered that a study that investigates the adsorption of sodium and potassium on these doped graphene systems can help to pave the way toward the development of useful lithium-free rechargeable batteries.

2. Results and Discussion

2.1. Sodium Adsorption on Dual-Doped Graphene

The adsorption energy (AE) of sodium on graphene is −0.67 eV, at the vdW-DF/DZP level. This value is 0.44 eV higher than the one computed for lithium (−1.11 eV), using the same methodology. Also, it is significantly smaller than the cohesive energy of bulk sodium, which is −1.078 eV/atom. Therefore, graphene should be modified to inhibit the agglomeration of sodium atoms. In Table 1, we gathered the AE of sodium on 12 DDG systems when sodium is adsorbed below the 3p dopant. At the vdW-DF/DZP level, for 9 cases, studied the adsorption of sodium is stronger than the cohesive energy of bulk sodium. The three DDG systems for which the AE is higher are PN, SO, and SB DDG, but it is worth mentioning that all dopants decrease the AE with respect to that of graphene. The variation of the AE upon doping strongly depends on the choice of heteroatoms introduced. According to the vdW-DF/DZP results, the lowest AE was determined for SiB DDG (−2.13 eV), being closely followed by SN DDG (−2.00 eV). This trend is different than that observed for the adsorption of lithium on DDG,28 because SN DDG exhibited the lowest AE, and SiB DDG exhibited the second lowest. The net effect of introducing a pair of SiB/SN dopants is a 3.2/3.0 time decrease of the AE of sodium with respect to that of graphene. The results obtained employing the PBE-D2 method and plane waves also point to a significant decrease of the AE when two dopants are introduced. However, SN DDG presents the lowest AE, closely followed by SiB DDG. Thus, it seems to be clear that SN and SiB DDG are the best candidates for increasing the affinity of graphene toward sodium.

Table 1. Sodium Adsorption Energies onto Graphene 5 × 5 and Circumcoronene Dual-Doped.

  vdW-DF/DZP M06-2X/6-311G* PBE-D2/VASP PBE-D2/6-311G*
dopant G5 × 5a circumcoroneneb G5 × 5 circumcoronene
AlB –1.58 –1.81 –2.44 –2.10
AlN –1.55 –1.98 –2.44 –2.05
AlO –1.63 –1.64 –2.43 –1.99
SiB –2.13 –2.90 –2.72 –2.94
SiN –1.63 –2.11 –2.42 –2.09
SiO –1.42 –1.34 –2.21 –1.62
PB –1.47 –1.75 –2.36 –1.91
PN –0.96 –1.15 –1.92 –1.37
PO –1.71 –1.97 –2.51 –2.18
SB –1.10 –1.96 –2.35 –2.03
SN –2.00 –3.35 –2.91 –2.92
SO –0.97 –1.30 –2.13 –1.49
G5 × 5 –0.67 –0.45 –1.08 –0.71
Open in a new tab
a

Calculations were performed using periodic conditions and a 5 × 5 unit cell of graphene.

b

Calculations were performed using a graphene flake (circumcoronene).

Finally, to support the outcome of the vdW-DF and PBE-D2 calculations, we determined the AE onto a hydrogen-terminated graphene cluster. The AE obtained employing the circumcoronene model also indicated a significant increase in the affinity toward sodium adsorption. In line with the PBE-D2 results, SN DDG presents the lowest AE at the M06-2X/6-311G* level of theory, and SiB DDG the second lowest. For SN/SiB DDG, the AE of sodium decreases 7.4/6.4 times with respect to that of graphene. In light of these results, we can confirm that there is a remarkable decrease in the AE of sodium upon doping. Also, this effect is larger than the one observed for lithium. In effect, the AE of Li onto SN DDG is 2.9 times lower than that computed for graphene.28

2.2. Potassium Adsorption on Dual-Doped Graphene

The lower cohesive energy of bulk potassium with respect to that of lithium and sodium is an advantage to develop potassium-anode materials, but its large size is a problem. The cohesive energy of bulk potassium is −0.934 eV/atom, about 0.18 eV higher than that for sodium. Interestingly, the AE of potassium on graphene is lower than the cohesive energy of bulk potassium by 0.144 eV. In Table 2, the AE of potassium onto DDG are presented. In line with the results obtained for sodium, all dopants decrease the AE, but in the case of potassium, all of the AE are lower than the cohesive energy of bulk potassium. In fact, when considering the 12 DDG systems, the average AE for potassium is −1.76 eV whereas that of sodium is −1.55 eV, at the vdW-DF/DZP level. This trend is not surprising because the AE of potassium on graphene is lower by 0.33 eV, with respect to that of sodium. The lowest AE is observed for SN and SiB DDG. At the vdW-DF/DZP level, the AE is −2.43 eV in both cases. This value is 2.2 times lower than the value determined for graphene. This finding is fully supported by the PBE-D2 calculations performed with VASP. Indeed, the AE determined for SN and SiB DDG are −3.03 and −3.06 eV, respectively. In agreement with the vdW-DF results, the AE is 2.2 times lower after co-doping.

Table 2. Potassium Adsorption Energies onto Graphene 5 × 5 and Circumcoronene Dual Doped.

  vdW-DF/DZP M06-2X/6-311G* PBE-D2/VASP PBE-D2/6-311G*
dopant G5 × 5a,c circumcoroneneb,c G5 × 5c circumcoronenec
AlB –1.81 –2.22 –2.55 –2.33
AlN –1.75 –2.35 –2.51 –2.27
AlO –1.78 –1.95 –2.47 –2.18
SiB –2.42 –3.36 –3.06 –3.24
SiN –1.84 –2.47 –2.51 –2.32
SiO –1.64 –1.75 –2.31 –1.88
PB –1.81 –2.20 –2.51 –1.93
PN –1.40 –1.57 –2.05 –1.65
PO –1.95 –2.32 –2.58 –1.39
SB –1.08 –2.36 –2.47 –2.31
SN –2.42 –3.64 –3.03 –3.05
SO –1.20 –1.69 –2.22 –1.73
G5 × 5 –1.1 –0.96 –1.40 –1.10
Open in a new tab
a

Calculations were performed using periodic conditions and a 5 × 5 unit cell of graphene.

b

Calculations were performed using a graphene flake (circumcoronene).

c

Lowest values are in bold.

The variations observed for the AE of potassium on DDG systems were reproduced by the M06-2X calculations carried out for dual-doped circumcoronene. However, again SN DDG is the best system if we are interested in obtaining record-breaking AE. At the M06-2X/6-311G* level, the AE of potassium on SN DDG is 3.8 times lower than that for graphene. This enhancement is almost a half of that observed for sodium at the same level of theory. This result is likely to be linked to the fact that the bonding of sodium on graphene is weaker than for potassium.

2.3. Comparison between Sodium and Potassium

Inspection of the results presented in Tables 1 and 2 clearly indicates that the AE can be finely tuned if the adequate combination of dopants is selected. Also, it is clear that for the 12 cases assayed, the dual doping is an effective method to increase the adhesion of these two alkalies onto graphene. For sodium and potassium, the differences between the largest and lowest AEs are very similar. For example, at the vdW-DF/DZP level, it is 1.17 eV for sodium, whereas the value computed for potassium is 1.34 eV. However, the M06-2X method suggests a value that is twice larger. This deviation is likely to be related to the fact that for the latter functional, we used a circumcoronene model. This statement is supported by the results obtained when the cluster models are studied using the PBE-D2/6-311G* method. For example, in the case of potassium, the difference between the largest and lowest AE is 1.58 eV, significantly larger than the value obtained using the PBE-D2 method and periodic conditions, namely, 1.1 eV.

The four methods employed suggested stronger adsorption for potassium as compared to that of sodium. In the case of pristine graphene, the AEs of potassium are lower than those computed for sodium by 0.43, 0.51, 0.32, and 0.39 eV, at the vdW-DF/DZP, M06-2X/6-311G*, PBE-D2, and PBE-D2/6-311G* levels of theory, respectively. However, after doping, these values become smaller. In effect, the average difference between the AE-K and AE-Na is 0.25, 0.39, 0.14, and 0.23 eV, at the vdW-DF/DZP, M06-2X/6-311G*, PBE-D2, and PBE-D2/6-311G* levels of theory, respectively. Therefore, doping is an effective method to equilibrate the AE of sodium and potassium on graphene. It is difficult to identify a method that can predict when the AE of sodium and potassium are more similar. For example, at the PBE-D2 level, the difference AE-K – AE-Na is 0.04 eV for AlO DDG, about 0.1 eV smaller than the average value. A similar trend is observed if the vdW-DF method is employed. However, discrepancies occur for SB and PO DDG. Inspection of the M06-2X results seems to indicate that AlO DDG is the system for which sodium and potassium display more similar AE. Finally, the PBE-D2/6-311G* results are not in line with those obtained with the same functional and periodic conditions. Indeed, the cluster model calculations performed at the PBE-D2/6-311G* level of theory indicated that for PB DDG, the AE of potassium is only 0.02 eV lower than that computed for sodium.

2.4. Why is Co-Doping So Useful?

In the introduction, we mentioned that the adsorption of Li on N-doped graphene (N in graphitic configuration) is weaker than that on undoped graphene. This is not strange since nitrogen has one more electron than carbon and thus induces an n-type doping. In contrast, boron, which is a p-type dopant, significantly increases the adsorption of Li on graphene. Given that boron has one electron less than carbon, it facilitates the charge transfer from lithium to graphene. The AE of Li on B-doped graphene is −2.41 eV, more than twice the value computed for graphene. On the same lines, Al also improves the interaction since the AE of Li on Al-doped graphene is −2.71 eV. This value is 0.3 eV larger than that computed for B-doped graphene. In the case of Al, there is another fact, besides having one electron less than carbon, which contributes to lowering the AE: the introduction of a 3p dopant induces significant structural modifications, as can be appreciated in Figure 1. In effect, a hole is created around the dopant, which facilitates the interaction of the alkali with the carbon atoms. This finding is not new; it has been documented before that the adsorption on curved π surfaces is stronger than that on planar ones.59 Also, this is the reason why the adsorption below the 3p dopant is much stronger than that above it.28 In the particular base of SiB DDG, the two factors are maximized. On one hand, we have the p-type doping of graphene. On the other hand, silicon creates the structural distortion that creates a hole where sodium or potassium can be adsorbed. Finally, in the case of SN DDG, the peculiar structure of this system is the reason behind the strong affinity toward alkalies. As we have explained in our previous investigation of SN DDG,29−31 the S and N dopants replace a CC bond but are not bonded. Therefore, nitrogen adopts a pyridinic configuration, which facilitates the interaction with alkalies. We note that the interaction between alkalies and pyridinic nitrogen is markedly different than that observed for graphitic nitrogen. This is not surprising since it is well documented that in the Li:::pyridine complex, the Li atom prefers a σ bonding mode, i.e., Li near the nitrogen and in the pyridine plane, instead of a π complexation.60 Thus, to make the N doping of graphene useful, the pyridinic configuration of the nitrogen dopant should be favored during the synthetic procedure.

Figure 1.

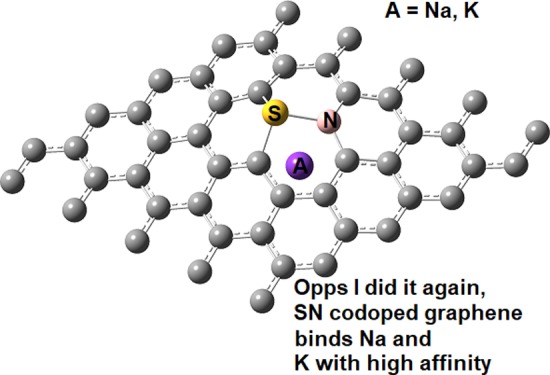
Figure 1

Open in a new tab

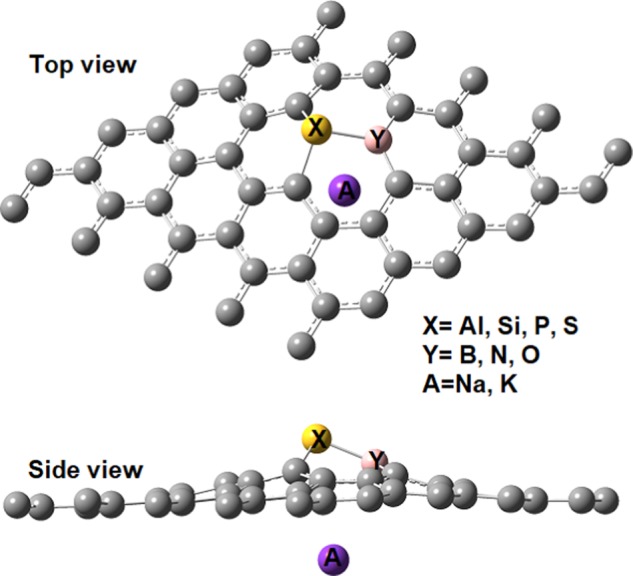
Optimized structure for dual-doped graphene with an ortho disposition of dopants and an alkali atom adsorbed below the 3p dopant.

2.5. Electronic Structure of SN and SiB Dual-Doped Graphene with Adsorbed Alkalies

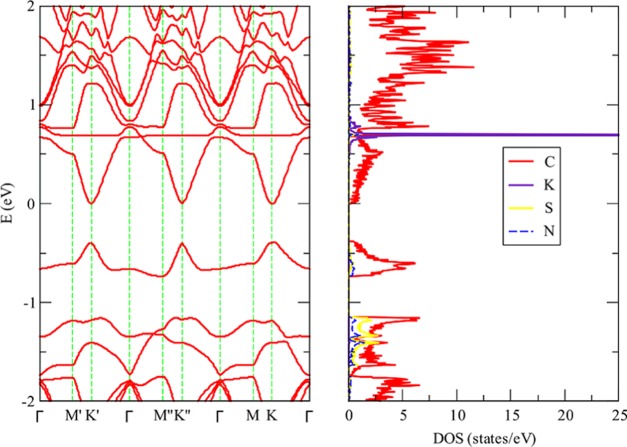
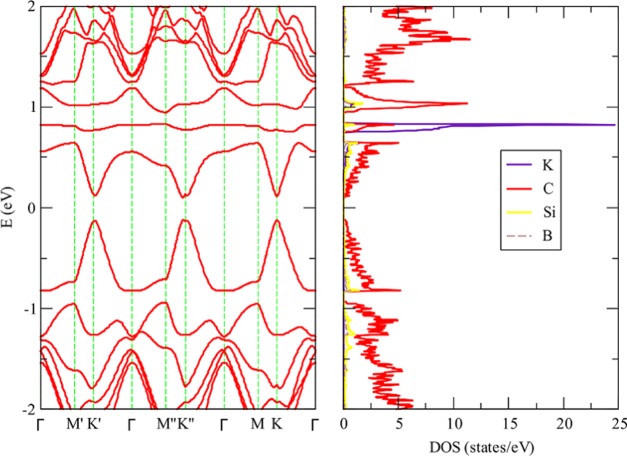
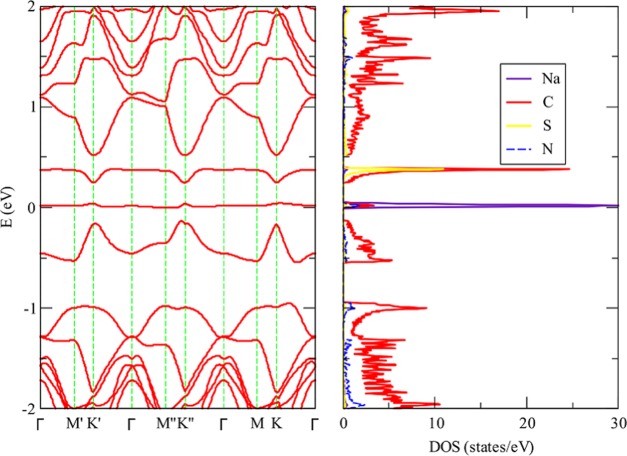
In our previous work about lithium adsorption on DDG, we found that when lithium is adsorbed on SN DDG the system is not a metal but a semiconductor with a gap of 0.2 eV for an 8 × 8 unit cell. This results in a contrast with the electronic structure determined when lithium is adsorbed on pristine graphene since this system has a metallic character. In Figure 2, we present the band structure and density of states determined when potassium is adsorbed on SN DDG. In line with the results obtained for lithium, a gap of 0.42 eV is opened. In the same vein, when potassium is adsorbed on SiB DDG, we can observe in Figure 3 that the system is a semiconductor. In this case, the gap is smaller, that is, 0.21 eV. The partial density of states clearly shows that the empty potassium states are located far from the Fermi level. For the sake of completeness, we plotted the band structure and density of states for SN DDG with a sodium atom adsorbed. As we can appreciate in Figure 4, the system is also a small band gap semiconductor.

Figure 2.

Figure 2

Open in a new tab

Band structure and partial density of states determined for potassium adsorbed onto 5 × 5 SN dual-doped graphene, at the vdW-DF/DZP level of theory. (The Fermi level is located at 0.0 eV.)

Figure 3.

Figure 3

Open in a new tab

Band structure and partial density of states determined for potassium adsorbed onto 5 × 5 SiB dual-doped graphene, at the vdW-DF/DZP level of theory. (The Fermi level is located at 0.0 eV.)

Figure 4.

Figure 4

Open in a new tab

Band structure and partial density of states determined for sodium adsorbed onto 5 × 5 SiN dual-doped graphene, at the vdW-DF/DZP level of theory. (The Fermi level is located at 0.0 eV.)

2.6. Are the Cluster Model Calculations Useful?

The use of polycyclic aromatic hydrocarbon instead of graphene is useful to identify which combination of dopants is more useful if one is interested in increasing the strength of the alkali–graphene interaction. SN and SiB DDG have been indicated by the four methods as the most promising materials to develop alkali-based rechargeable batteries. Also, the four methods point to PN DDG as the system displaying less affinity toward sodium. However, for potassium, the picture is different as the DFT methods suggest three different systems to have the highest AE with K: SB, PN, and PO DDG. Thus, the differences cannot be attributed to the use of a finite graphene model.

In the case of the PBE-D2/6-311G* method, the AEs computed using cluster models are higher (less negative) than those obtained when using that same functional and periodic conditions. On average, they are 0.35 and 0.45 eV higher than those computed for sodium and potassium, respectively. This difference is expected to be increased if the basis set superposition error (BSSE) is included for the PBE-D2/6-311G* calculations (Note: PBE-D2 periodic calculations with VASP are BSSE free). On the contrary, the AEs computed using the M06-2X/6-311G* method are among significantly lower than those computed using the other methods. Although the doping level is very similar, the hydrogen atoms of the cluster induce a different charge distribution. For example, according to the Mulliken analysis at the M06-L/6-311G* level, the 18 carbon atoms of circumcoronene bonded to the hydrogen atoms bear a negative charge of −0.2e. However, in graphene, the carbon atoms located at the same distance from the dopants are not charged. This difference, for sure, will alter the long-range interactions.

2.7. Intercalation in SN Dual-Doped Graphene

Due to their high affinity toward alkalies, we investigated their intercalation between two layers of SN DDG when both sulfur atoms protrude out forming a hole, as shown in Figure 5. At the PBE-D2 level and using VASP, the interaction energy between sodium and the two SN DDG layers is −6.32 eV. This value is larger (in absolute terms) than twice the Eads of sodium on one layer of SN DDG by 0.50 eV. On the contrary, the interaction is weaker than the sum of interlayer interaction energy of two layers of SN DDG plus twice the AE of sodium on SN DDG by 2.03 eV. Thus, some energy is clearly lost during the intercalation process. Yet, it is not too much because of the hole created by the protrusion of the sulfur atoms out of the graphene plane.

Figure 5.

Figure 5

Open in a new tab

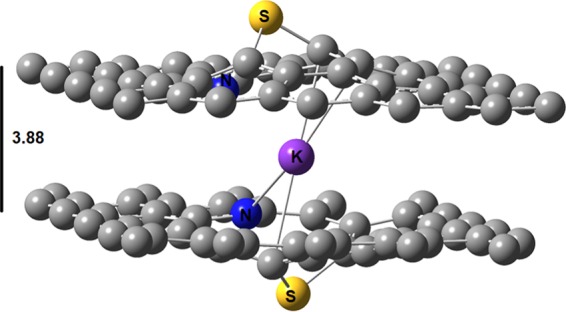
Optimized structure for S, N dual-doped bilayer graphene with a potassium atom intercalated.

Interestingly, the intercalation of potassium does not significantly affect the interlayer distance of bilayer SN DDG. At the vdW-DF/DZP level, the two layers of SN DDG are separated by an average distance of 3.59 Å, when sulfur atoms protrude out. This value is increased to 3.88 Å when one potassium atom is placed in the hole created by the S and N dopants introduced in both layers. The structures are shown in Figure 2. In the same line, for potassium, the interaction with the two SN DDG layers plus the interlayer interaction energy of two layers of SN DDG is −8.59 eV. This value is 2.85 eV lower than the intercalation energy of potassium between two layers of SN DDG. The energy forfeited to intercalate potassium is 0.84 eV larger than that of sodium because potassium has a larger atomic radius. Alkali intercalation is a possible process from a thermodynamic standpoint since energy is gained when these alkalies are inside the hole created by the dopants. For example, when the sulfur atoms protrude out of the interlayer region, the two layers of SN DDG are held by −2.53 eV, but after potassium intercalation, this value decreases to −5.74 eV.

3. Conclusions

We have studied the interaction between XY dual-doped graphene (X = AL, Si, P, S; Y = B, N, O) and sodium/potassium by employing periodic and finite models. The introduction of two dopants decreases the adsorption energy of sodium and potassium with respect to that of perfect graphene by 0.88 and 0.66 eV on average. The systems that display the strongest interactions with the two alkalies assayed are SN and SiB DDG. Although the adsorption energy of sodium on graphene is weaker than that for potassium, the introduction of dopants reduces the difference. In effect, in some cases, the AE-K and AE-NA differed by less than 0.05 eV. The protrusion of the 3p dopants out of the graphene plane creates a hole where sodium and potassium can be easily intercalated between two layers of dual-doped graphene. The interlayer distances are reduced by less than 0.4 Å after K intercalation, making the process very favorable. The monumental rise in AE guarantees the remarkable storage capacities at the cost of lower doping concentration, thus preserving the extraordinary properties of graphene up to a large extent.

4. Methods

We studied the adsorption of sodium and potassium onto dual-doped graphene (DDG) using two approaches. In the first place, we carried out periodic calculations using a 5 × 5 unit cell of graphene. Second, we performed simulations employing a graphene flake terminated with hydrogen atoms. The molecule selected was circumcoronene (C54H18). The disposition of the dopants is the same that employed in our previous studies for the DDG systems.28−32 In general, the 2p and 3p dopants prefer to replace a CC bond, except in the case of SiB, which prefers a para disposition of the dopants, as has been documented by us in ref (25). The structure is shown in Figure 1.

For the periodic calculations, we selected the vdW-DF functional developed by Dion et al.,44 as implemented in SIESTA.45,46 We utilized the double-ζ basis set (DZP) with polarization functions and fixed the orbital confining cutoff to 0.01 Ry. The split norm used was 0.15. For all systems, the calculations were performed with the inclusion of spin polarization. The interaction between ionic cores and valence electrons was described by the Troullier–Martins norm-conserving pseudopotentials.47 Optimizations were carried out using the conjugate gradient algorithm until all residual forces were smaller than 0.01 eV/Å. The unit cells were optimized, and they were sampled using a 40 × 40 × 1 (about 900 k-points γ centered) Monkhorst–Pack sampling.

For comparative purposes, we performed PBE-D248−50 calculations, as implemented in VASP.51−54 The projector-augmented plane wave approach (PAW) was selected, and the plane wave cutoff was 450Ry. The Brillouin zone was sampled with a 7 × 7 × 1 γ centered k-point grid. For sodium and potassium, the PV PAW potentials were utilized, which include 7 valence electrons.

The calculations that involved the circumcoronene model were performed using the M06-2X55,56 and PBE-D2 methods. The basis set selected was the 6-311G*,57 and the ultrafine grid was utilized. All systems were confirmed to be minima by the calculations of vibrational frequencies. These calculations were carried out with Gaussian 2009.58 We determined the adsorption energy as follows: AE = E(graphene + X) – E(X) – E(graphene). The E(graphene + X), E(X), and E(graphene) represent the energy of the total system, energy of Na/K, and the energy of the slab, respectively. Zero-point energy corrections were not considered for computing AE. According to this definition, the negative value is for favorable interaction; a more negative value means stronger the interaction. Hereafter, PBE-D2 refers to the results obtained using VASP and a 5 × 5 unit cell, whereas the notation PBE-D2/6-311G* is utilized to discuss the results obtained using the circumcoronene model.

Acknowledgments

S.U. and F.S. are grateful to the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), Fundação de Amparo à Pesquisa do Estado de Minas Gerais (FAPEMIG), Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), and Financiadora de Estudos e Projetos (FINEP) for their financial support. P.A.D. is grateful to PEDECIBA Quimica, CSIC and ANII Uruguayan institutions for financial support, all authors acknowledge PEDECIBA Quimica, ANII, and CSIC for financial support.

The authors declare no competing financial interest.

References

  1. https://unfccc.int/process/the-kyoto-protocol.
  2. https://unfccc.int/sites/default/files/english_paris_agreement.pdf.
  3. https://driving.ca/auto-news/news/rolls-royce-will-gradually-switch-to-fully-electric-cars-by-2040.
  4. https://www.theguardian.com/business/2017/jul/06/france-ban-petrol-diesel-cars-2040-emmanuel-macron-volvo.
  5. Zhang C.; Mahmood N.; Yin H.; Liu F.; Hou Y. Synthesis of Phosphorus-Doped Graphene and its Multifunctional Applications for Oxygen Reduction Reaction and Lithium Ion Batteries. Adv. Mater. 2013, 25, 4932–4937. 10.1002/adma.201301870. [DOI] [PubMed] [Google Scholar]
  6. Reddy A. L. M.; Srivastava A.; Gowda S. R.; Gullapalli H.; Dubey M.; Ajayan P. M. Synthesis Of Nitrogen-Doped Graphene Films For Lithium Battery Application. ACS Nano 2010, 4, 6337–6342. 10.1021/nn101926g. [DOI] [PubMed] [Google Scholar]
  7. Ning G.; Ma X.; Zhu X.; Cao Y.; Sun Y.; Qi C.; Fan Z.; Li Y.; Zhang X.; Lan X.; Gao J. Enhancing the Li Storage Capacity and Initial Coulombic Efficiency for Porous Carbons by Sulfur Doping. ACS Appl. Mater. Interfaces 2014, 6, 15950–15958. 10.1021/am503716k. [DOI] [PubMed] [Google Scholar]
  8. Zhang M.; Lei D.; Yu X.; Chen L.; Li Q.; Wang Y.; Wang T.; Cao G. Graphene oxide oxidizes stannous ions to synthesize tin sulfide–graphene nanocomposites with small crystal size for high performance lithium ion batteries. J. Mater. Chem. 2012, 22, 23091–23097. 10.1039/c2jm34864k. [DOI] [Google Scholar]
  9. Ma X.; Ning G.; Sun Y.; Pu Y.; Gao J. High Capacity Li Storage in Sulfur and Nitrogen Dual-doped Graphene Networks. Carbon 2014, 79, 310–320. 10.1016/j.carbon.2014.07.072. [DOI] [Google Scholar]
  10. Kamphaus E. P.; Balbuena P. B. Long-Chain Polysulfide Retention at the Cathode of Li–S Batteries. J. Phys. Chem. C 2016, 120, 4296–4305. 10.1021/acs.jpcc.5b12538. [DOI] [Google Scholar]
  11. Denis P. A. Chemical Reactivity of Lithium Doped Monolayer and Bilayer Graphene. J. Phys. Chem. C 2011, 115, 13392–13398. 10.1021/jp203547b. [DOI] [Google Scholar]
  12. Jalbout A. F.; Ortiz Y. P.; Seligman T. H. Spontaneous symmetry breaking and strong deformations in metal adsorbed graphene sheets. Chem. Phys. Lett. 2013, 564, 69–72. 10.1016/j.cplett.2013.01.051. [DOI] [Google Scholar]
  13. Valencia F.; Romero A. H.; Ancilotto F.; Silvestri P. L. Lithium Adsorption on Graphite from Density Functional Theory Calculations. J. Phys. Chem. B 2006, 110, 14832–14841. 10.1021/jp062126+. [DOI] [PubMed] [Google Scholar]
  14. Lu M.; Zhang M.; Liu H. Predicted two-dimensional electrides: Lithium–carbon monolayer sheet. Phys. Lett. A 2015, 379, 2511–2514. 10.1016/j.physleta.2015.07.023. [DOI] [Google Scholar]
  15. Deng X.; Wu Y.; Dai J.; Kang D.; Zhang D. Electronic structure tuning and band gap opening of graphene by hole/electron codoping. Phys. Lett. A 2011, 375, 3890–3894. 10.1016/j.physleta.2011.08.070. [DOI] [Google Scholar]
  16. Rani P.; Bhandari R.; Jindal V. K. Band Gap Modulation of Graphene with Increasing Concentration of Li/B Doping. Adv. Sci. Lett. 2015, 21, 2826–2829. 10.1166/asl.2015.6363. [DOI] [Google Scholar]
  17. Rani B.; Jindal V. K.; Dharamvir K. Energetics of a Li Atom adsorbed on B/N doped graphene with monovacancy. J. Solid. State Chem. 2016, 240, 67–75. 10.1016/j.jssc.2016.05.014. [DOI] [Google Scholar]
  18. Ullah S.; Denis P. A.; Sato F. Beryllium doped graphene as an efficient anode material for lithium-ion batteries with significantly huge capacity: A DFT study. Appl. Mater. Today 2017, 9, 333–340. 10.1016/j.apmt.2017.08.013. [DOI] [Google Scholar]
  19. Chen X.; Hou T.; Persson K. A.; Zhang Q. Combining theory and experiment in lithium–sulfur batteries: Current progress and future perspectives. Mater. Today 2018, 10.1016/j.mattod.2018.04.007. [DOI] [Google Scholar]
  20. Sood P.; Kim K. C.; Jang S. S. Electrochemical and electronic properties of nitrogen doped fullerene and its derivatives for lithium-ion battery applications. J. Energy Chem. 2018, 27, 528–534. 10.1016/j.jechem.2017.11.009. [DOI] [PubMed] [Google Scholar]
  21. Fan S.; Zou X.; Du H.; Gan L.; Xu C.; Lv W.; He Y. B.; Yang Q. H.; Kang F.; Li J. Theoretical Investigation of the Intercalation Chemistry of Lithium/Sodium Ions in Transition Metal Dichalcogenides. J. Phys. Chem. C 2017, 121, 13599–13605. 10.1021/acs.jpcc.7b05303. [DOI] [Google Scholar]
  22. Jiang N.; Li B.; Ning F.; Xia D. All boron-based 2D material as anode material in Li-ion batteries. J. Energy Chem. 2018, 27, 1651–1654. 10.1016/j.jechem.2018.01.026. [DOI] [Google Scholar]
  23. Ferre-Vilaplana A. Storage of Hydrogen Adsorbed on Alkali Metal Doped Single-Layer All-Carbon Materials. J. Phys. Chem. C 2008, 112, 3998–4004. 10.1021/jp0768874. [DOI] [Google Scholar]
  24. Martínez J. I.; Cabria I.; López M. J.; Alonso J. A. Adsorption of Lithium on Finite Graphitic Clusters. J. Phys. Chem. C 2009, 113, 939–941. 10.1021/jp8063195. [DOI] [Google Scholar]
  25. Baker T. A.; Head-Gordon M. Modeling the Charge Transfer between Alkali Metals and Polycyclic Aromatic Hydrocarbons Using Electronic Structure Methods. J. Phys. Chem. A 2010, 114, 10326–10333. 10.1021/jp105864v. [DOI] [PubMed] [Google Scholar]
  26. Denis P. A.; Iribarne F. C2V or C6V: Which is the most stable structure of the benzene–lithium complex?. Chem. Phys. Lett. 2013, 573, 15–18. 10.1016/j.cplett.2013.04.009. [DOI] [Google Scholar]
  27. Ullah S.; Denis P. A.; Sato F. Coupled Cluster and Density Functional Investigation of the Neutral Sodium-Benzene and Potassium-Benzene Complexes. Chem. Phys. Lett. 2018, 706, 343–347. 10.1016/j.cplett.2018.06.028. [DOI] [Google Scholar]
  28. Denis P. A. Lithium adsorption on heteroatom mono and dual doped graphene. Chem. Phys. Lett. 2017, 672, 70–79. 10.1016/j.cplett.2017.01.036. [DOI] [Google Scholar]
  29. Denis P. A.; Pereyra C. P. Structural Characterization and Chemical Reactivity of Dual Doped Graphene. Carbon 2015, 87, 106–115. 10.1016/j.carbon.2015.01.049. [DOI] [Google Scholar]
  30. Denis P. A.; Pereyra Huelmo C.; Martins A. S. Band Gap Opening in Dual-Doped Monolayer Graphene. J. Phys. Chem. C 2016, 120, 7103–7112. 10.1021/acs.jpcc.5b11709. [DOI] [Google Scholar]
  31. Denis P. A.; Pereyra Huelmo C.; Iribarne F. Theoretical Characterization of Sulfur and Nitrogen Dual-doped Graphene. Comput. Theor. Chem. 2014, 1049, 13–19. 10.1016/j.comptc.2014.08.023. [DOI] [Google Scholar]
  32. Denis P. A.; Iribarne F. The effect of the dopant nature on the reactivity, interlayer bonding and electronic properties of dual doped bilayer graphene. Phys. Chem. Chem. Phys. 2016, 18, 24693–24703. 10.1039/C6CP02481E. [DOI] [PubMed] [Google Scholar]
  33. You J. M.; Ahmed M. S.; Han H. S.; Choe J.; Ustundag Z.; Jeon S. New approach of nitrogen and sulfur-doped graphene synthesis using dipyrrolemethane and their electrocatalytic activity for oxygen reduction in alkaline media. J. Power Sources 2015, 275, 73–79. 10.1016/j.jpowsour.2014.10.174. [DOI] [Google Scholar]
  34. Feng B.; Xie J.; Dong C.; Zhang S.; Cao G.; Zhao X. From graphite oxide to nitrogen and sulfur co-doped few-layered graphene by a green reduction route via Chinese medicinal herbs. RSC Adv. 2014, 4, 17902–17907. 10.1039/c4ra01985g. [DOI] [Google Scholar]
  35. Wohlgemuth S.-A.; Vilela F.; Titirici M.-M.; Antonietti M. A One-pot Hydrothermal Synthesis of Tunable Dual Heteroatom-doped Carbon Microspheres. Green Chem. 2012, 14, 741–749. 10.1039/c2gc16415a. [DOI] [Google Scholar]
  36. Wohlgemuth S.-A.; White R. J.; Willinger M.-G.; Titirici M.-M.; Antonietti M. A One-pot Hydrothermal Synthesis of Sulfur and Nitrogen Doped Carbon Aerogels with Enhanced Electrocatalytic Activity in the Oxygen Reduction Reaction. Green Chem. 2012, 14, 1515–1523. 10.1039/c2gc35309a. [DOI] [Google Scholar]
  37. Xu J.; Dong G.; Jin C.; Huan M.; Guan L. Sulfur and Nitrogen Co-Doped, Few-Layered Graphene Oxide as a Highly Efficient Electrocatalyst for the Oxygen-Reduction Reaction. ChemSusChem 2013, 6, 493–499. 10.1002/cssc.201200564. [DOI] [PubMed] [Google Scholar]
  38. Ma X.; Ning G.; Sun Y.; Pu Y.; Gao J. High Ccapacity Li Storage in Sulfur and Nitrogen Dual-doped Graphene Networks. Carbon 2014, 79, 310–320. 10.1016/j.carbon.2014.07.072. [DOI] [Google Scholar]
  39. Ullah S.; Denis P. A.; Sato F. First-principles study of dual-doped graphene: toward promising anode materials for Li/Na-ion batteries. New. J. Chem. 2018, 42, 10842–10851. 10.1039/C8NJ01098F. [DOI] [Google Scholar]
  40. Wang X.; Li G.; Hassan F. M.; Li J.; Fan X.; Batmaz R.; Xiao X.; Chei Z. Sulfur covalently bonded graphene with large capacity and high rate for high-performance sodium-ion batteries anodes. Nano Energy 2015, 15, 746–754. 10.1016/j.nanoen.2015.05.038. [DOI] [Google Scholar]
  41. Yang S.; Li S.; Tang S.; Dong W.; Sun W.; Shen D.; Wang M. Sodium adsorption and intercalation in bilayer graphene from density functional theory calculations. Theor. Chem. Acc. 2016, 135, 164 10.1007/s00214-016-1910-0. [DOI] [Google Scholar]
  42. Luo X. F.; Wang S. Y.; Tseng C. M.; Lee S. W.; Chiang W. H.; Chang J. K. Microplasma-assisted bottom-up synthesis of graphene nanosheets with superior sodium-ion storage performance. J. Mater. Chem. A 2016, 4, 7624–7631. 10.1039/C6TA00743K. [DOI] [Google Scholar]
  43. Zhou Q.; Liu L.; Guo G.; Yan Z.; Tan J.; Huang Z.; Chen X.; Wang X. Sandwich-like cobalt sulfide–graphene composite—an anode material with excellent electrochemical performance for sodium ion batteries. RSC Adv. 2015, 5, 71644–71651. 10.1039/C5RA12478F. [DOI] [Google Scholar]
  44. Dion M.; Rydberg H.; Schroder E.; Langreth D. C.; Lundqvist B. I. Van der Waals density functional for general geometries. Phys. Rev. Lett. 2004, 92, 246401 10.1103/PhysRevLett.92.246401. [DOI] [PubMed] [Google Scholar]
  45. Soler J. M.; Artacho E.; Gale J. D.; Garcia A.; Junquera J.; Ordejon P.; Sanchez-Portal D. The SIESTA Method for Ab Initio Order-N Materials Simulation. J. Phys.: Condens. Matter 2002, 14, 2745–2779. 10.1088/0953-8984/14/11/302. [DOI] [Google Scholar]
  46. Ordejón P.; Artacho E.; Soler J. M. Self-consistent order-N Density-functional Calculations for Very Large Systems. Phys. Rev. B 1996, 53, R10441–R10444. 10.1103/PhysRevB.53.R10441. [DOI] [PubMed] [Google Scholar]
  47. Troullier N.; Martins J. L. Efficient Pseudopotentials for Plane-Wave Calculations. Phys. Rev. B 1991, 43, 1993–2006. 10.1103/PhysRevB.43.1993. [DOI] [PubMed] [Google Scholar]
  48. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  49. Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
  50. Grimme S.; Ehrlich S.; Goerigk L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
  51. Kresse G.; Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  52. Kresse G.; Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. J. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  53. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  54. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  55. Zhao Y.; Truhlar D. G. A New Local Density Functional for Main-group Thermochemistry, Transition Metal Bonding, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Phys. 2006, 125, 194101 10.1063/1.2370993. [DOI] [PubMed] [Google Scholar]
  56. Zhao Y.; Truhlar D. G. Density Functionals with Broad Applicability in Chemistry. Acc. Chem. Res. 2008, 41, 157–167. 10.1021/ar700111a. [DOI] [PubMed] [Google Scholar]
  57. Hehre W.; Radom L.; Schleyer P. v. R.; Pople J. A.. Ab Initio Molecular Orbital Theory; Wiley: NY, 1986. [Google Scholar]
  58. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.. et al. Gaussian 09, revision D.01; Gaussian, Inc.: Wallingford, CT, 2009.
  59. Denis P. A. Methane adsorption inside and outside pristine and N-doped single wall carbon nanotubes. Chem. Phys. 2008, 353, 79–86. 10.1016/j.chemphys.2008.07.024. [DOI] [Google Scholar]
  60. Krasnokutski S. A.; Yang D. S. High-resolution electron spectroscopy and σ/π structures of M(pyridine) and M+(pyridine) (M = Li, Ca, and Sc) complexes. J. Chem. Phys. 2009, 130, 134313 10.1063/1.3109688. [DOI] [PubMed] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES