Abstract

Simple procedures to estimate Hansen solubility parameter (HSP) components from structural formulas are investigated. The best results are obtained using a simple relationship with molar volume and refractivity for the dispersion component, and using additivity models based on tailored fragments specifically designed for the polar and hydrogen bonding components. Despite large errors for some classes of chemicals, including small inorganic molecules, ionic liquids, and high halogen compounds, these models yield average absolute deviations from reference on par with state-of-the-art models and lower than reported using molecular dynamics simulations or nonlinear quantitative structure–property relationship models based on a limited set of quantum chemical descriptors. In contrast to group contribution methods that are either more restricted in scope or heavily parameterized, they are thoroughly validated and very easy to apply. Furthermore, the errors observed are easy to rationalize and may usually be anticipated. This work sheds light on some limitations inherent to pure additivity approaches for HSP prediction and provides a first step toward better models. A Python script implementing the procedure and the fully detailed results are provided as the Supporting Information.
1. Introduction
Hansen solubility parameters (HSPs) have a long history.1,2 Initially developed as a practical guide for the selection of solvents in coating systems,3,4 they are presently used in diverse fields such as pharmaceutical chemistry,5,6 dentistry,7 molecular biology,8 civil engineering,9 vapor sensing10 and optical sensing,11 food science,12 or waste treatment.13 Although new needs for such parameters arise from growing environmental concerns,6 many present applications regarding processes in microelectronics14 and nanotechnology,15,16 as well as systems presently focusing much attention such as organogels17 or ionic liquids.18 Beyond solvent selection,19 HSPs now find widespread applications for a growing number of related problems involving mixing or diffusion phenomena, including swelling behavior,20,21 intestinal drug absorption properties,22 studies of the morphology of polymer films,23 prediction of environmental stress cracking in plastics,24 optimization of polymer additives, including stabilizers, antistatic agents, fire retardants,25,26 or plasticizers aimed at improving the performance of binders for explosives or propellants.27
The HSP approach relies on the partition of the total cohesive energy E into dispersive, polar, and hydrogen bonding contributions, according to E = Ed + Ep + Eh. The three HSP components δd, δp, and δh are defined in terms of these three energetic contributions as δk = (Ek/Vm)1/2, where Vm is the molar volume. The total solubility parameter δ = (E/Vm)1/2 is related to the individual components through δ2 = δd2 + δp + δh2. Unfortunately, although E (and thus δ) may be derived from thermodynamic studies, this is not the case for the individual components δk which are not measurable quantities. Therefore, the experimental derivation of HSP data is especially tedious, requiring extensive measurements associated with the concept of a solubility sphere.2 In this context, predictive models are of much interest. Many procedures have been put forward to derive HSP data without experiments.28−40 However, they all exhibit limitations.
Some of them, including the Hoy additivity scheme34 or procedures based on molecular simulations,28 yield values that are not consistent with the original HSP reference data.41 The derivation of HSP components from simulations based on analytical intermolecular potentials might appear especially attractive as most force fields rely on similar decomposition of E into dispersive, polar, and hydrogen bonding contributions. Unfortunately, this approach is not consistent with the standard HSP data. For instance, it predicts that δh is zero for any aprotic solvent, due to the lack of labile protons to form hydrogen bonds in the pure fluid. Actually, such solvents may exhibit significant values of δh as they can play the role of a proton acceptor and form hydrogen bonds when mixed with another fluid. For example, a value as high as 15.4 MPa1/2 is reported for formaldehyde.2 This discrepancy between HSP predictions based on empirical force fields and accepted experimental values stems from the fact that A–B interactions between two different species A and B are not well represented in this case as an average of A–A and B–B interactions. On the other hand, HSPs being primarily a tool for engineers and experimental researchers, resorting to molecular simulations to estimate their values is not practical.
In fact, current approaches consist either of heavily parameterized group contribution (GC) or quantitative structure–property relationship (QSPR) methods, including models based on state-of-the-art machine learning (ML) techniques.42 A physically consistent GC method should decompose each cohesive energy component Ek into additive contributions associated with specific moieties G (either atoms or groups of atoms) on the molecule
| 1 |
where NG is the number of occurrences of group G in the compound. Unfortunately, available models based on this approach are restricted to the most common chemical moieties owing to the limited amount of data considered for their parameterization.29−33
In recent years, more general relationships have been put forward to estimate HSPs using group contribution (GC) methods.35−38 Stefanis and Panayiotou (SP) introduced a specially popular method,36 implemented in a commercial software named HSPiP.43 Notwithstanding their parameterization against extensive data including many different chemical groups, the SP relationships exhibit distinctive features compared with earlier methods. First, they rely on first and second order group contributions denoted as Cki and Dk, respectively. The former are in fact UNIFAC groups, whereas the latter are defined according to the ABC framework44 in an attempt to capture nonlocal effects associated with conjugation.45 Secondly, every HSP component δk is directly expressed as a linear function of the number of occurrences of the different first and second order groups, denoted as i and j, respectively
| 2 |
In eq 2, k = d, p, h, Ck0 is an empirical constant, Ck and Dkj are the contributions of first and second order groups to δk. Finally, Ni, and Mj are the occurrences of groups i and j in the molecule. Another method introduced by Marrero and Gani introduces third order groups l, with occurrences of Ol and associated parameters Dk.46 This method was recently applied to HSP prediction,35,37 according to
| 3 |
Although they might yield better fits than eq 1 for the training sets considered, eqs 2 and 3 are inconsistent with the definition of the HSP components as size-intensive quantities. This necessarily restricts their predictive value. In recent years, a new approach called Y-MB arising from extensive work on HSPs has been introduced in the HSPiP software.39,40 Unfortunately, the details of this model have not been published. Although the scarcity of the data do not allow to draw definite conclusions, results reported in the literature suggest that HSP components obtained using either the SP or Y-MB models exhibit a similar reliability.47
It must be emphasized that such models rely on extensive parameterizations. Furthermore, for δp and δh, the SP model relies on distinct parameter sets depending on whether their actual value is smaller or larger than 3 MPa1/2. The need for different parameter sets probably reflects an inadequacy of a linear relationship such as eq 2. All in all, the SP scheme requires 113 parameters to fit 344 δd values, and 156 parameters to fit either 350 δh values or 375 δp values. Similarly, the model of Modarresi et al. was fitted against 1050 compounds using slightly less than 300 parameters. They usually fit the training data very well, confirming that the predictive value of such methods would require further validation, at least through cross-validation, as most experimental data at hand is used to fit many parameters involved and it is difficult to find additional data to compile an external test set.
Instead of increasing the number of groups, another possibility to introduce additional flexibility is to consider more general QSPR models like artificial neural networks (ANNs) or other ML techniques. Interesting models are commercially available from COSMOlogic GmbH, especially an approach in which HSP values for any compound are obtained from its simulated activity coefficients (using the COSMO-RS model48) in a predefined set of 29 reference solvents.49 Another attractive QSPR model for HSPs is an ANN taking quantum chemical descriptors as input.38 This method is very interesting as it successfully handles very different compounds, including ionic liquids and organic salts. However, it requires specialized software to compute the descriptors and implement the ANN, in addition to significant computing resources. Moreover, the purely empirical nature of ANNs makes it difficult to derive systematic improvement. Very recently, a systematic study provided deeper insight into the potential of ML techniques for HSP prediction.42 However, in view of their empirical nature and reliance on numerous parameters, GC and QSPR models may hardly be used as a basis for further development.
Therefore, the present paper investigates simpler procedures to estimate the HSP data, based on more straightforward schemes to split molecules into additive fragments, and extensively validated against external data. The following section reports the general strategy adopted in this work and results of a preliminary study aimed at identifying suitable systematic fragmentation levels to represent molecules as collections of additive fragments. The next ones describe more successful models obtained on the basis of tailored fragmentation schemes for the dispersion, polar, and hydrogen bonding HSP components and report the corresponding results. For convenience, units are not explicitly mentioned throughout the sequel. Implicit units are MPa1/2 for HSP components, kJ mol−1 for energy components, and cm3 mol–1 for molar volumes and refractivities.
2. Present Strategy
2.1. Reference Data
2.1.1. Source of Data
Like most recent predictive schemes, the present methods are fitted and validated using the HSP data compiled in the Hansen handbook.2 However, it should be kept in mind that most data reported in this compilation are estimated values. In this work, the procedures introduced were fitted using only experimentally confirmed data (reported in bold characters in the handbook), including 90 entries obtained from the literature in addition to the data gathered from industrial experience.2,3,50,51 After removing mixtures and compounds for which some data is lacking, a data set made of 174 compounds is obtained. In addition, the present predictions are systematically compared to accepted reference estimates compiled in the Hansen handbook for 769 other compounds, hereafter referred to as the test set.
2.1.2. Uncertainties on Reference Data
HSPs are primarily used to obtain qualitative conclusions regarding the compatibility of various species or the ability of solvents to dissolve a given material. It is important to keep in mind that quantitative HSP values exhibit significant uncertainties, especially if the estimated data are considered. For instance, among 1188 compounds for which the HSP data have been compiled on a website,52 16 have multiple sets of components reported, including water, carbon tetrachloride, trinitrotoluene, ethylene glycol, or dimethyl ether. The differences between the maximal and minimal values reported for any HSP component exhibit root mean square values of 1.3, 4.5, and 7.8 for δd, δp, and δh, respectively (or 1.1 and 4.6 for δd and δh if water is excluded). The large uncertainties for δp arise mainly from symmetric compounds, where the dipole moments associated with polar groups mutually cancel, as for carbon tetrachloride (δp values ranging from 0.0 to 8.3), trinitrotoluene (δp values ranging from 3.5 to 10.0), or 1,4-dioxane. In each case, the value derived from the dipole moment (e.g., using the Hansen–Beerbower equation) is much smaller than an alternative value derived from group contributions. Not surprisingly, the large inconsistencies between δh values are observed for compounds with strong hydrogen bonds, like urea (δh values ranging from 16 to 26.4) or methanol clusters (δh values ranging from 10 to 22.3). However, significantly different δh values are also observed for other compounds. For instance, values ranging from 0 to 6 are reported for bromotrichloromethane.
Valuable insight into uncertainties on experimental data may be obtained from a comparison of HSP values derived using either conventional methods or an equation of state model.53 Typical differences between experimental HSP values derived using distinct procedures are 0.7–0.8 for δd and δp, and 0.16 for δh, suggesting that the hydrogen bonding component is more accurately defined than the dispersion and polar components.
2.1.3. Partition into Training and Test Sets
Each model for a given HSP component k = d, p, h is actually fitted against a subset of the 174 compounds for which an experimental value of δk is available. Indeed, some compounds are excluded as lying outside the applicability domain (AD) of the method, owing to under-represented chemical moieties or types of compounds. In practice, for the three HSP components, ionic liquids, inorganic compounds (i.e., those with no C atom), and molecules with less than two H atoms are assumed to lie outside the applicability domain (AD) of the present models. For δp, molecules with under-represented polar groups are also assumed to lie outside the model, including compounds with aromatic C–N, C–S, or C–O bonds, sulfones, isocyanates and isothiocyanates, carbon dioxide, F-, I-, and B-containing molecules, molecules with S–H or Si–H bonds. Finally, although the model for δd appears to be especially general as it does not rely on fragment contributions, especially underestimated values were obtained for the two only fluorinated compounds in the training set, namely 1,1,1,3,3,3-hexafluoro-2-propanol and 1,2,3,4,5,6-hexafluorohexan-1-ol, whereas the results obtained for F-containing compounds from the test set are in good agreement with previous estimates. Therefore, these two compounds are assumed to lie outside the AD of the model for δd. Finally, the exact partition of the data into training set, test set, and outliers depends on the HSP component and model under consideration. The partitions associated with the models eventually retained may be obtained from Table S1 in the Supporting Information (SI).
2.2. Modeling Methodology
In view of the tendency of recent GC models for HSPs to rely on increasingly complex fragmentation schemes, and of the current preference for linear expressions for HSP components like
| 4 |
instead of the more theoretically appealing eq 1, we started this work with a comparison of systematic fragmentation schemes of increasing complexity, using both eqs 1 and 4. The exact fragmentation algorithms and the corresponding results are detailed in Section S1 (SI). For δd and δp, a performance comparable to that of the SP model36 could only be obtained using as many as 62 distinct atom types. However, the models thus obtained are of limited practical interest as they are applicable to only about 30% of the data set. Their applications to the remaining of 70% would require additional parameters that cannot be derived from the presently available data. The use of the Hansen–Beerbower equation for δp was also considered (Section S2). This approach proves to be of similar accuracy to heavily parameterized additivity schemes. However, it is not practical in view of its dependence on the dipole moment.
In view of the experimental uncertainties discussed in Section 2.1.2, there is no point in striving to match the reference data through extensive parameterization. Therefore, this work focuses on simple and practical models whose performance arise from stronger physical grounds compared to the available additivity methods. In particular, a feature shared by all recent HSP prediction methods is the fact that they do not explicitly involve the molar volume Vm. Actually, there appears to be no reason to not take advantage of this property as it is available for most synthesized compounds on the market and may otherwise be easily evaluated to within a few percents from experiment.54−56 On the other hand, additive contributions to Ep/Eh are introduced only for groups with heteroatoms/proton acceptors or donors. For the dispersion component Ed, all atoms must in principle be considered. As a result, Ed scales roughly linearly with Vm and it proves quite challenging to quantitatively predict the difference in δd values within a set of compounds. Therefore, instead of a fragment-based approach for δd, we start from the London equation for the dispersion interaction between two atoms A and B
| 5 |
where αA and αB are the atom polarizabilities and R the interatomic distance.57 By analogy, the dispersion interaction between two molecules within a pure phase may be assumed to be given by the product of their polarizabilities (or equivalently, of their molar refractivities) divided by an effective intermolecular distance Re
| 6 |
where RD is the molar refractivity of the molecule derived from a simple additivity model.58 However, determining a suitable value for Re is difficult for two reasons. First, the interatomic distance between nonspherical molecules is ill-defined. Secondly, Re in eq 6 actually reflects an average distance arising from all surrounding molecules interacting with the central one. Dimensional analysis suggests either
| 7 |
if the molecules are viewed as spherical, or
| 8 |
if Ed is assumed to be determined by close contact interactions between neighboring atoms, with an interatomic distance that does not depend on the overall molecular volume, but rather on the van der Waals radii of the atoms. To accommodate both eqs 7 and 8, the following expression was first assumed
| 9 |
This simple three-parameter model already yields fair performance. However, the fit and cross-validation score turned out to be both further improved by assuming the first term to be independent on RD and to scale linearly with Vm, leading to the following expression for the dispersion HSP component
| 10 |
2.3. Fragmentation Algorithms
The fragmentation scheme is critical to the success of any additivity method. A too crude distinction, e.g., using atomic contributions that do not depend on the atomic environment, is clearly unlikely to provide accurate results. On the other hand, overly cautious distinctions lead to an excessive number of possibly ill-defined parameters. Group contribution methods reported previously use similar sets of standard groups (such as UNIFAC groups) for all three HSP components. This approach is probably not optimal since these components arise from different interactions. For instance, although dispersion forces involve all atoms, Coulomb interactions are insignificant in the lack of heteroatoms, whereas hydrogen bonding requires the presence of labile protons. Therefore, δd, δp, and δh probably require distinct fragmentation schemes. Since eq 10 proves satisfactory for δd, fragmentation schemes are required only for δp and δh.
2.3.1. Contributing Fragments for the Polar Component
Instead of systematically assigning a fixed Ep contribution to every fragment in a molecule, the observation that δp = 0 for alkanes suggests that hydrogen atoms and saturated carbon atoms do not contribute to Ep. Non-zero values for δp require strong Coulomb interactions associated with the presence of heteroatoms and/or polarization interactions that are especially significant for compounds with multiple (polarizable) bonds. Therefore, the present additive contributions are associated with such structural features of the molecules.
In the first step, only saturated heteroatoms are considered. Their contribution to Ep is assumed to depend primarily on their number of hydrogen neighbors. Thus, the contribution of a saturated heteroatom with symbol X and bonded to nH hydrogen atoms is simply denoted as X(HnH).
In the second step, unsaturated functional groups are considered. Specific Ep contributions are introduced for isolated multiple bonds (C=O, C≡N, and P=O) and for clusters of the adjacent multiple bonds (i.e., the nitro group). According to this procedure, specific parameters would be needed for other groups with adjacent multiple bonds, like sulfone or azide. However, they are not introduced in this study due to the lack of experimental data to safely determine their values.
Finally, additional parameters are introduced for specific moieties, i.e., amide groups, whose polarity is enhanced by the electron transfer between the nitrogen and oxygen atoms, carboxylic acids, in which the overall polarity of the group is decreased due to dipoles along O–H directions opposing the C–O dipoles, and ester and carbonate groups which are well-known components of polar solvents for electrolytes.
2.3.2. Contributing Fragments for the Hydrogen Bonding Component
Taking advantage of established knowledge about the hydrogen bonding donor and acceptor moieties, it proves especially straightforward to obtain a satisfactory model for δh. Within the present data set, hydrogen atoms are bound either to C, O, or N, and labeled accordingly as HC, HO, and HN. In fact, special contributions denoted as HN(amide), H2N and HO(COOH) are introduced for hydrogens in amides, primary amines, and carboxylic acids, respectively. This yields a total of six descriptors for H-bond donors. On the other hand, the data set exhibits mainly three potential proton acceptors: nitrogen (except if in nitro group), oxygen, and halogen atoms, denoted as N, O, and X, respectively.
2.4. Validation Procedures
The validation of GC methods and other additivity schemes typically relies on their ability to fit large datasets using a relatively small number of empirical parameters. However, since experimental HSP data are available for only a relatively small number of compounds, it is desirable to use a more stringent validation procedure. In this work, the predictive value of the models is estimated from a leave-one-out (LOO) cross-validation, as done recently for ML models.42
In addition, in the lack of an extensive set of experimentally confirmed HSP data, predictions are made using the present models for the external test set and compared to previous estimates reported in ref (2). Although the latter are deemed to be less reliable than genuine experimental values, it must be stressed that even the latter may exhibit significant uncertainties. For instance, two conflicting values of respectively 0 and 8.3 MPa1/2 are reported for the polar component of tetrachloromethane CCl4, depending on whether this value was estimated from the dipole moment of the molecule (i.e., 0 D) or from group contributions. Despite the even larger uncertainties to be expected for the test set, a comparison between the present and earlier estimates is meaningful as the latter values have been used successfully to draw qualitative conclusions about practical solubility problems.
The present predictions are compared with the results obtained using the state-of-the-art procedures, including a reparametrization of the GC methods of ref (36) against the present training set (the corresponding procedure is hereafter referred to as the GC method) and very recent ML models which were training against a slightly larger trained set of 193 solvents.42
The relative performances of various procedures are compared using the average absolute deviation (AAD) from reference values and the determination coefficient (R2). These statistical indicators are calculated either for the training set (reflecting the quality of fit), for the outcome of a cross-validation against the training set or for the test set (thus reflecting the predictive value of the method).
3. Results
3.1. Dispersion Component
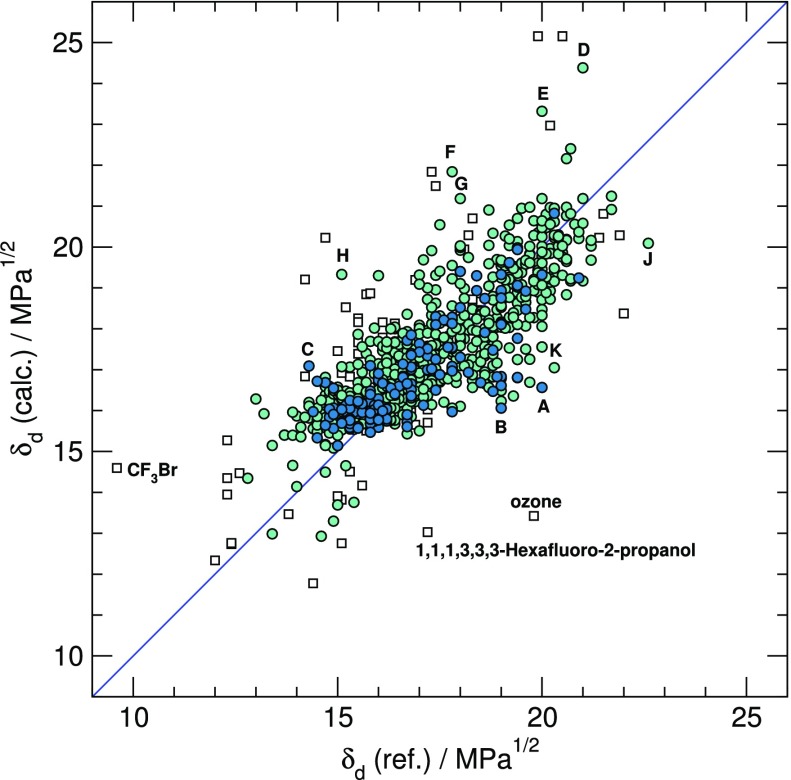
For δd, the fitting parameters involved in eq 10 are reported in Table 1. They prove to be statistically well-defined. Results obtained using this equation are shown in Figure 1. As expected, larger deviations from reference values tend to be observed for compounds lying outside the AD (i.e., those represented using white squares). Propylene carbonate, dimethyl sulfone, and formic acid are the only two compounds from the training set for which significant deviations from experiment are observed. Interestingly, the largest discrepancies between the present and previous estimates tend to arise for compounds with S, Br, and I atoms.
Table 1. Parameters Required to Estimate δd via equation 10 and the Corresponding Standard Deviations (Dev.).
| value | dev. | |
|---|---|---|
| c0 | 93.8 | 13 |
| c1 | 2016 | 184 |
| c2 | 75 044 | 11 350 |
Figure 1.
Presently calculated δd components versus reference (experimental or previously calculated) data for compounds in the training set (dark circles), test set (light circles), and out of the AD (white squares). Main deviations from reference values are for (A) propylene carbonate, (B) dimethyl sulfone, (C) formic acid, (D) tetrathiafulvalene, (E) thiourea, (F) diiodomethane, (G) resorcinol, (H) 1,1-dibromoethene, (J) 1,1,2,2-tetrabromoethane, and (K) tetraiodothiophene.
All in all, the results are remarkably good considering the simplicity of the model. With an AAD of 0.68 derived from the LOO, they are on par with gpHSP, the recent ML model based on Gaussian processes put forward by Sanchez-Lengeling et al. and better than any alternative state-of-the-art ML model considered by these authors.42
In view of their typical magnitude close to 0.8 (Section 2.1.2), the experimental uncertainties on reference δd data might appear as the limiting factor restricting the accuracy of the present and gpHSP predictive models. However, even better results are obtained using the GC method (AAD = 0.49 from LOO). This excellent performance might be a matter of chance. Anyway, according to the literature results, these three procedures are more reliable than any alternative approach, including molecular simulations (AAD = 0.98)28 or the ANN/QSPR model based on quantum calculations (AAD = 1.37),38 although present comparisons with the models reported in refs (28) and (38) must be considered with caution as the latter were respectively applied to polymers and to a significant fraction of compounds beyond the scope of the present model.
Finally, it is encouraging to observe that the AAD between earlier (reported in the Hansen handbook) and present δd estimates for the test set is 0.75, i.e., only slightly larger than the value of 0.68 obtained for the training set on the basis of genuine experimental data.
3.2. Polar Component
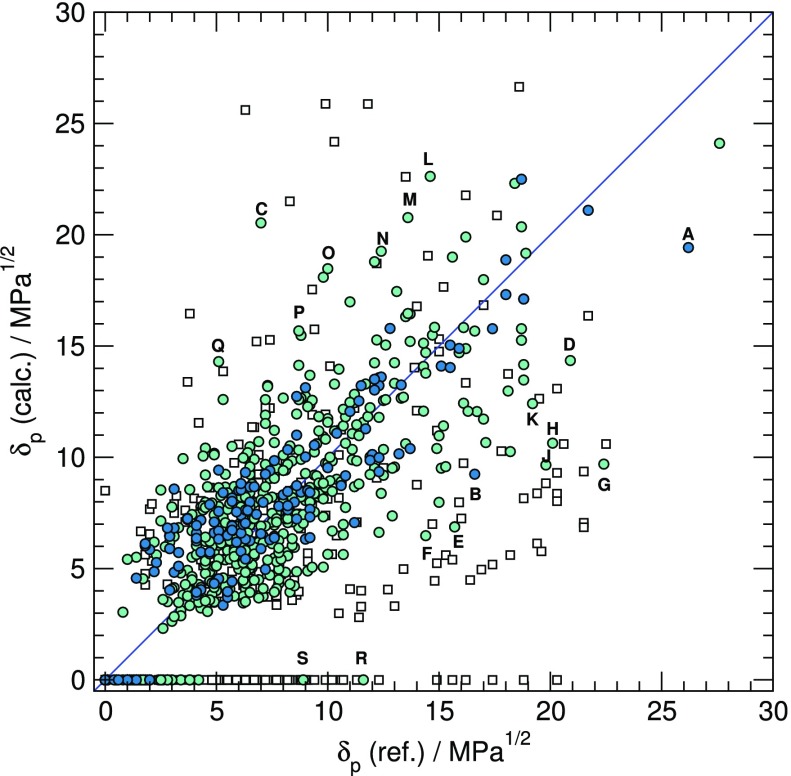
The parameters of the model for δp are compiled in Table 2. HSP data estimated on this basis are compared to reference values in Figure 2. Despite the very small number of parameters, some values appear to be statistically ill-defined, especially N(H1) for N atoms with one H atom attached.
Table 2. Parameters Required to Estimate δp via equation 1 (J mol–1).
| value | dev. | no. | |
|---|---|---|---|
| Saturated Heteroatoms | |||
| N(H1) | 2783 | 2275 | 5 |
| N(H2) | 8235 | 1044 | 6 |
| O(H0) | 1603 | 663 | 95 |
| O(H1) | 4125 | 518 | 49 |
| Cl(H0) | 1637 | 793 | 10 |
| Unsaturated Polar Moieties | |||
| C=O | 7492 | 1322 | 17 |
| COOH | –5494 | 1827 | 5 |
| C=O (amide) | 15 972 | 2799 | 3 |
| carbonate | 19 019 | 3330 | 2 |
| ester | 3653 | 1643 | 37 |
| C≡N | 16 056 | 1451 | 5 |
| nitro | 13 276 | 2215 | 4 |
| P=O | 20 310 | 4506 | 5 |
Figure 2.
Calculated δp components versus reference (experimental or previously calculated) data for compounds in the training set (dark circles), test set (light circles), and out of the AD (white squares). Main deviations from reference values are for formamide (A), butyrolactone (B), picric acid (C), 4-nitrophenol (D), (Z)-1,2,3-trichloro-1-propene (E), butadiene diepoxide (F), triethanolamine (G), phthalic anhydride (H), 2(5H)-furanone (J), succinic anhydride (K), biuret (L), fumaronitrile (M), 2-chloroacetamide and acrylamide (N), TNT and propionamide (O), N-acetylcaprolactam (P), diacetyl (Q), and hexamethylene tetramine (R).
Similar to δd, the AAD derived from the LOO against the training set (2.00) is consistent with the corresponding value for the test set (2.08), which suggests that it correctly reflects the predictive value of the model. Accordingly, the present additivity scheme for δp is slightly less accurate than most alternatives (GC: 1.75, ANN/QSPR: 1.85, gpHSP: 1.93) except molecular simulations, which led to a value of 3.84 for the AAD.28
The present model for δp is clearly hampered by the lack of data to assign all parameters that would be needed for every specific polar group that may be encountered. The value of δp is especially seriously overestimated for picric acid, as the calculated value of 20.3 is dramatically larger than the reference value of 7. A similar overestimation is observed for trinitrotoluene (18.5 instead of 10). Such deviations clearly arise because the contributions of the nitro groups to the overall dipole moment of the molecule cancel each other, a cancellation that is not taken into account by any additivity scheme.
Another interesting case is hexamethylene tetramine, a cage molecule for which the dipole moment is expected to be zero for symmetry reasons, leading to a null value of δp according to the Hansen–Beerbower equation.29 In the present model, the contribution of any tertiary amine to Ep is zero within statistical uncertainty. Therefore, the predicted value of δp is zero as well. However, the reference value reported in the Hansen handbook for this molecule is as high as 11.6.
In fact, taking advantage of quantum chemically derived electrostatic descriptors is an alternative that appears especially attractive for the polar HSP component, as it is in principle fully determined by the charge distribution. The significance of such descriptors for this specific component was empirically confirmed by Sanchez-Lengeling et al.42
3.3. Hydrogen Bonding Component
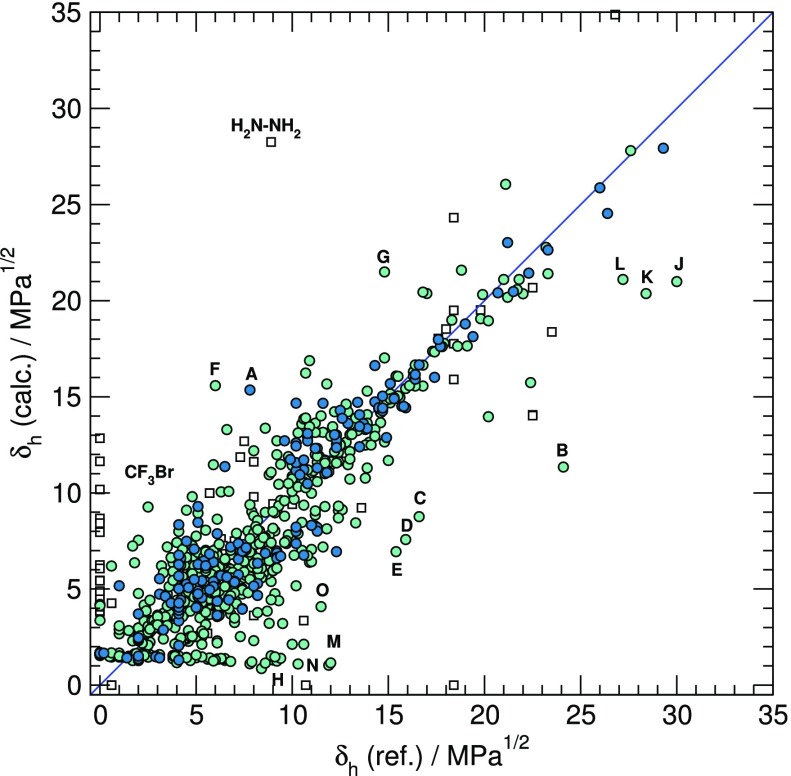
The parameters of the present model for δh based on eq 1 are compiled in Table 3. As expected, the contribution of protons bonded to O atoms is especially large, whereas it is very small for hydrogen atoms bonded to carbon. The latter parameter is in fact ill-defined. However, setting its value to zero would significantly affect the performance of the model in view of the large number of hydrogens bonded to C atoms in organic compounds.
Table 3. Parameters Required to Estimate δh via equation 1 (J mol–1).
| value | dev. | no. | |
|---|---|---|---|
| HC | 24.5 | 63 | 152 |
| HN | –1576 | 2118 | 4 |
| HN (amide) | 5060 | 3140 | 1 |
| H2N | 5484 | 547 | 6 |
| HO | 16 945 | 482 | 48 |
| HO (COOH) | 7094 | 1132 | 5 |
| N | 3252 | 813 | 24 |
| O | 1980 | 337 | 125 |
| X | 412 | 410 | 13 |
The performance of the resulting model is illustrated in Figure 3. Not surprisingly, the fit is not as good as for more extensively parametrized models. However, the AAD values of 1.55 and 1.67 derived, respectively, from the LOO against the training set and from the application of the model to the test set are quite satisfactory compared to alternative methods (gpHSP: 1.57, GC: 1.95, ANN/QSPR: 2.58, molecular simulations: 5.96). Specially large errors are observed for small hydrogen bonded compounds clearly outside the AD of the model, like hydrazine (H2N–NH2) or phosphoric acid (H3PO4).
Figure 3.
Calculated δh components versus reference (experimental or previously calculated) data for compounds in the training set (dark circles), test set (light circles), and out of the AD (white squares). Main deviations from reference values are for 2-butanone oxime (A), 1-phenyl-2-methylamino-1-propanol (B), succinic anhydride (C), N-methylformamide (D), formaldehyde (E), picric acid (F), thiourea (G), tetrahydrothiophene, methyl mercaptan, and tetrathiafulvalene (H), methyl peroxide (J), dl-lactic acid (K), hydroquinone (L), acetylene and vinyl acetylene (M), thiophenol (N), and N-methylaniline (O).
3.4. Discussion
Although the present models might appear to lack reliability considering all presently obtained results, the most significant errors may be anticipated on the basis of simple physical or statistical considerations. Focusing on standard organic compounds that may be described as functionalized hydrocarbon backbones, and excluding other compounds (with no/few H, C atoms, or unusual polar groups), an accuracy on par with the state-of-the-art techniques is obtained on the basis of only a handful of adjustable parameters.
An obvious drawback of the present models, especially for δp and δh, is the fact that they are restricted to the most common functional groups. However, similar restrictions apply to any fragment-based model. The apparent reliability of sophisticated GC methods probably arises to some extent as a consequence of the numerous parameters involved, and their predictive value would probably prove lower than suggested by the good fit reported in the literature, although the present investigation confirms the superiority of the GC model of Stefanis and Panayiotou for the polar component.36
4. Conclusions
The present work reports extremely simple and widely applicable procedures allowing pencil and paper estimation of the dispersion, polar, and hydrogen bonding components of the Hansen solubility parameters, using only 3, 13, and 9 fitting parameters, respectively. The simplicity of the model for the dispersion component, taking advantage of molar refractivity and volume, is especially remarkable.
A close examination of the results shows that the applicability domain of these procedures is fairly broad and well-defined in terms of molecular structural features. With the exception of the polar component for which a previously established group contribution method should prove more reliable in view of its extensive parameterization, other HSP components are predicted with about state-of-the art-reliability from the present models. Reliable results may also be obtained for the dispersion component for standard organic compounds not belonging to the categories presently identified as lying beyond the applicability domain of the method. These results are encouraging in view of future development.
In contrast to previously available additivity methods for HSPs, the present models are based on tailored and physically motivated procedures to split molecules into fragments, fitted against a comprehensive set of experimental data and validated against an extensive test set of previously estimated values. In contrast, other recent models, like SP or Y-MB, involve many empirical parameters whose determination requires that the whole database compiled in the Hansen handbook2 be used. This has two disadvantages. First, most values included in this large training set are estimated rather than measured, which can lead to significant uncertainties in their values. Secondly, as most published HSP data are included in this training set, this only allows the model to be validated on a very limited external test set.
The fact that introducing the molar refractivity leads to better models for the dispersion component demonstrates that the relative scarcity of data for HSP components can be circumvented by the use of related ancillary properties easier to estimate, as a result of greater simplicity or more extensive data at hand. For instance, the fact that Hansen’s original derivations were based around total cohesive energy density (which may be obtained for much larger datasets than available for HSP data), as follows naturally from their founding theory, suggests that it might prove fruitful for improved hand-based methods to take advantage of the database values.
Regarding the polar component, the inability of the present model to provide data consistent with previously established values for compounds with a low polarity arising from polar groups pointing to opposite directions is a limitation inherent to additivity schemes. Using three-dimensional models for every rigid substructure encountered and/or considering explicit charge distributions might provide a road to better predictions.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b02601.
Study of models based on systematic (rather than tailored) fragmentation procedures (Section S1), assessment of the Hansen–Beerbower equation (Section S2), and worked-out examples of application of the present models (Section S3) (PDF)
Full database used in the present study with presently calculated values of the Hansen solubility parameters (XLSX)
Python script implementing the present procedures (ZIP)
The author declares no competing financial interest.
Supplementary Material
References
- Hansen C. M. 50 Years with solubility parameters: past and future. Prog. Org. Coat. 2004, 51, 77–84. 10.1016/j.porgcoat.2004.05.004. [DOI] [Google Scholar]
- Hansen C. M.Hansen Solubility Parameters: A User’s Handbook; CRC Press: Boca Raton, 2007. [Google Scholar]
- Hansen C. M. The Three Dimensional Solubility Parameter—Key to Paint Component Affinities I.–Solvents, Plasticizers, Polymers, and Resins. J. Paint. Technol. 1967, 39, 104–117. [Google Scholar]
- Hansen C. M. The Universality of the Solubility Parameter. Ind. Eng. Chem. Prod. Res. Dev. 1969, 8, 2. 10.1021/i360029a002. [DOI] [Google Scholar]
- Adamska K.; Voelkel A.; Héberger K. Selection of solubility parameters for characterization of pharmaceutical excipients. J. Chromatogr. A 2007, 1171, 90–97. 10.1016/j.chroma.2007.09.034. [DOI] [PubMed] [Google Scholar]
- Bordes C.; Fréville V.; Ruffin E.; Marote P.; Gauvrit J.; Briancon S.; Lantéri P. Determination of poly(ϵ-caprolactone) solubility parameters: Application to solvent substitution in a microencapsulation process. Int. J. Pharm. 2010, 383, 236–243. 10.1016/j.ijpharm.2009.09.023. [DOI] [PubMed] [Google Scholar]
- Castellan C. S.; Pereira P. N. R.; Viana G.; Chen S.-N.; Pauli G. F.; Bedran-Russo A. K. Solubility study of phytochemical cross-linking agents on dentin stiffness. J. Dent. 2010, 38, 431–436. 10.1016/j.jdent.2010.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen C. M. Polymer science applied to biological problems: Prediction of cytotoxic drug interactions with DNA. Eur. Polym. J. 2008, 44, 2741–2748. 10.1016/j.eurpolymj.2008.07.005. [DOI] [Google Scholar]
- Redelius P. G. Solubility parameters and bitumen. Fuel 2000, 79, 27–35. 10.1016/S0016-2361(99)00103-9. [DOI] [Google Scholar]
- Cakar F.; Moroglu M. R.; Cankurtaran H.; Karaman F. Conducting poly(ether imide)-graphite composite for some solvent vapors sensing application. Sens. Actuators, B 2010, 145, 126–132. 10.1016/j.snb.2009.11.045. [DOI] [Google Scholar]
- Medina-Castillo A. L.; Fernandez-Sanchez J. F.; Segura-Carretero A.; Fernandez-Gutierrez A. A semi-empirical model to simplify the synthesis of homogeneous and transparent cross-linked polymers and their application in the preparation of optical sensing films. Biosens. Bioelectron. 2009, 25, 442–449. 10.1016/j.bios.2009.07.034. [DOI] [PubMed] [Google Scholar]
- Srinivas K.; King J. W.; Monrad J. K.; Howard L. R.; Hansen C. M. Optimization of subcritical fluid extraction of bioactive compounds using Hansen solubility parameters. J. Food Sci. 2009, 74, E342–E354. 10.1111/j.1750-3841.2009.01251.x. [DOI] [PubMed] [Google Scholar]
- Durkee J. Cleaners from the farm. Met. Finish. 2008, 106, 40–45. 10.1016/S0026-0576(08)80008-6. [DOI] [Google Scholar]
- Kesters E.; Claes M.; Le Q.; Barthomeuf K.; Lux M.; Vereecke G.; Durkee J. B. Selection of ESH solvents for the wet removal of post-etch photoresists in low-k dielectrics integration. Microelectron. Eng. 2009, 86, 160–164. 10.1016/j.mee.2008.10.002. [DOI] [Google Scholar]
- Detriche S.; Zorzini G.; Colomer J. F.; Fonseca A.; Nagy J. B. Application of the Hansen solubility Parameters theory to carbon nanotubes. J. Nanosci. Nanotechnol. 2008, 8, 6082–6092. 10.1166/jnn.2008.SW16. [DOI] [PubMed] [Google Scholar]
- Hernandez Y.; Lotya M.; Rickard D.; Bergin S. D.; Coleman J. N. Measurement of multicomponent solubility parameters for graphene facilitates solvent discovery. Langmuir 2010, 26, 3208–3213. 10.1021/la903188a. [DOI] [PubMed] [Google Scholar]
- Bonnet J.; Suissa G.; Raynal M.; Bouteiller L. Organogel formation rationalized by Hansen solubility parameters: dos and don’ts. Soft Matter 2014, 10, 3154–3160. 10.1039/c4sm00244j. [DOI] [PubMed] [Google Scholar]
- Bara J. E.; Gabriel C. J.; Carlisle T. K.; Camper D. E.; Finotello A.; Gin D. L.; Noble R. D. Gas separations in fluoroalkyl-functionalized room-temperature ionic liquids using supported liquid membranes. Chem. Eng. J. 2009, 147, 43–50. 10.1016/j.cej.2008.11.021. [DOI] [Google Scholar]
- Mao B.; Guo D.; Qin J.; Meng T.; Wang X.; Cao M. Solubility-Parameter-Guided Solvent Selection to Initiate Ostwald Ripening for Interior Space-Tunable Structures with Architecture-Dependent Electrochemical Performance. Angew. Chem., Int. Ed. 2018, 57, 446–450. 10.1002/anie.201710378. [DOI] [PubMed] [Google Scholar]
- Nielsen T. B.; Hansen C. M. Elastomer swelling and Hansen solubility parameters. Polym. Test. 2005, 24, 1054–1061. 10.1016/j.polymertesting.2005.05.007. [DOI] [Google Scholar]
- Navarro-Lupión F. J.; Bustamante P.; Escalera B. Relationship between swelling of hydroxypropylmethylcellulose and the Hansen and Karger partial solubility parameters. J. Pharm. Sci. 2005, 94, 1608–1616. 10.1002/jps.20370. [DOI] [PubMed] [Google Scholar]
- Breitkreutz J. Prediction of Intestinal Drug Absorption Properties by Three-Dimensional Solubility Parameters. Pharm. Res. 1998, 15, 1370–1375. 10.1023/A:1011941319327. [DOI] [PubMed] [Google Scholar]
- Bubb D.; Papantonakis M.; Collins B.; Brookes E.; Wood J.; Gurudas U. The influence of solvent parameters upon the surface roughness of matrix assisted laser deposited thin polymer films. Chem. Phys. Lett. 2007, 448, 194–197. 10.1016/j.cplett.2007.10.002. [DOI] [Google Scholar]
- Hansen C. M.; Just L. Prediction of Environmental Stress Cracking in Plastics with Hansen Solubility Parameters. Ind. Eng. Chem. Res. 2001, 40, 21–25. 10.1021/ie9904955. [DOI] [Google Scholar]
- Hansen C. M. Polymer additives and solubility parameters. Prog. Org. Coat. 2004, 51, 109–112. 10.1016/j.porgcoat.2004.05.003. [DOI] [Google Scholar]
- Tamizifar M.; Sun G. Control of surface radical graft polymerization on polyester fibers by using Hansen solubility parameters as a measurement of the affinity of chemicals to materials. RSC Adv. 2017, 7, 13299–13303. 10.1039/C6RA27186C. [DOI] [Google Scholar]
- Abou-Rachid H.; Lussier L.-S.; Ringuette S.; Lafleur-Lambert X.; Jaidann M.; Brisson J. On the Correlation between Miscibility and Solubility Properties of Energetic Plasticizers/polymer Blends: Modeling and Simulation Studies. Propellants, Explos., Pyrotech. 2008, 33, 301–310. 10.1002/prep.200700211. [DOI] [Google Scholar]
- Belmares M.; Blanco M.; Goddard W. A. III; Ross R. B.; Caldwell G.; Chou S.-H.; Pham J.; Olofson P. M.; Thomas C. Hildebrand and Hansen Solubility Parameters from Molecular Dynamics with Applications to Electronic Nose Polymer Sensors. J. Comput. Chem. 2004, 25, 1814–1826. 10.1002/jcc.20098. [DOI] [PubMed] [Google Scholar]
- Hansen C. M.; Beerbower A.. Solubility Parameters. In Kirk-Othmer Encyclopedia of Chemical Technology, 2nd ed.; Standen A., Ed.; Interscience: NY, 1971; pp 889–910. [Google Scholar]
- Beerbower A.Interdisciplinary Approach to Liquid Lubricant Technology; NASA Publication SP-318, 1973; pp 365–431. [Google Scholar]
- Fedors R. F. A method for estimating both the solubility parameters and molar volumes of liquids. Polym. Eng. Sci. 1974, 14, 147–154. 10.1002/pen.760140211. [DOI] [Google Scholar]
- Hoftyzer P. J.; van Krevelen D. W.. Properties of Polymers, 2nd ed.; Elsevier: Amsterdam, 1976; Chapter 7, pp 152–155. [Google Scholar]
- Krevelen D. W. V.Properties of Polymers, 3rd ed.; Elsevier: Amsterdam, 1990. [Google Scholar]
- Hoy K. L. Solubility Parameter as a Design Parameter for Water Borne Polymers and Coatings. J. Coated Fabr. 1989, 19, 53–67. 10.1177/152808378901900106. [DOI] [Google Scholar]
- Modarresi H.; Conte E.; Abildskov J.; Gani R.; Crafts P. Model-Based Calculation of Solid Solubility for Solvent Selections—A Review. Ind. Eng. Chem. Res. 2008, 47, 5234–5242. 10.1021/ie0716363. [DOI] [Google Scholar]
- Stefanis E.; Panayiotou C. Prediction of Hansen Solubility Parameters with a New Group-Contribution Method. Int. J. Thermophys. 2008, 29, 568–585. 10.1007/s10765-008-0415-z. [DOI] [Google Scholar]
- Hukkerikar A.; Sarup B.; Kate A. T.; Abildskov J.; Sin G.; Gani R. Group-contribution (GC+) based estimation of properties of pure components: improved property estimation and uncertainty analysis. Fluid Phase Equilib. 2001, 183–184, 183–208. 10.1016/S0378-3812(01)00431-9. [DOI] [Google Scholar]
- Járvás G.; Quellet C.; Dallos A. Estimation of Hansen solubility parameters using multivariate nonlinear QSPR modeling with COSMO screening charge density moments. Fluid Phase Equilib. 2011, 309, 8–14. 10.1016/j.fluid.2011.06.030. [DOI] [Google Scholar]
- https://www.pirika.com/ENG/HSP/E-Book/Chap30.html (accessed November 2018).
- https://www.hansen-solubility.com/conference/papers.php (accessed November 2018).
- Hansen C. M.2010; pp 9–13 and pp 324–328 in ref 2.
- Sanchez-Lengeling B.; Roch L. M.; Perea J. D.; Langner S.; Brabec C. J.; Aspuru-Guzik A. A Bayesian Approach to Predict Solubility Parameters. Adv. Theory Simul. 2018, 17, 1800069 10.1002/adts.201800069. [DOI] [Google Scholar]
- http://www.hansen-solubility.com (accessed November 2018).
- Mavrovouniotis M. L. Estimation of properties from conjugate forms of molecular structures: the ABC approach. Ind. Eng. Chem. Res. 1990, 29, 1943–1953. 10.1021/ie00105a029. [DOI] [Google Scholar]
- Constantinou L.; Prickett S. E.; Mavrovouniotis M. L. Estimation of thermodynamic and physical properties of acyclic hydrocarbons using the ABC approach and conjugation operators. Ind. Eng. Chem. Res. 1993, 32, 1734–1746. 10.1021/ie00020a030. [DOI] [Google Scholar]
- Marrero J.; Gani R. Group Contribution Based Estimation of Pure Component Properties. Fluid Phase Equilib. 2001, 183–184, 183–208. 10.1016/S0378-3812(01)00431-9. [DOI] [Google Scholar]
- Bergin S. D.; Sun Z.; Rickard D.; Streich P. V.; Hamilton J. P.; Coleman J. N. Multicomponent Solubility Parameters for Single-Walled Carbon Nanotube-Solvent Mixtures. ACS Nano 2009, 3, 2340–2350. 10.1021/nn900493u. [DOI] [PubMed] [Google Scholar]
- Klamt A.; Eckert F.; Arlt W. COSMO-RS: An Alternative to Simulation for Calculating Thermodynamic Properties of Liquid Mixtures. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 101–122. 10.1146/annurev-chembioeng-073009-100903. [DOI] [PubMed] [Google Scholar]
- Hansen C. M.COSMOquick User Guide, version 1.4; COSMOlogic GmbH & Co KG: Imbacher Weg 46, 51379, Leverkusen, Germany, http://www.cosmologic.de, 2016.
- Hansen C. M.; Skaarup K. The Three Dimensional Solubility Parameter – Key to Paint Component Affinities III. – Independent Calculation of the Parameter Components. J. Paint Technol. 1967, 39, 511–514. [Google Scholar]
- Hansen C. M.The Three Dimensional Solubility Parameter and Solvent Diffusion Coefficient; Doctoral Dissertation, Danish Technical Press: Copenhagen, 1967. [Google Scholar]
- https://www.stevenabbott.co.uk/practical-solubility/hsp-basics.php (accessed November 2018).
- Stefanis E.; Tsivintzelis I.; Panayiotou C. The partial solubility parameters: An equation-of-state approach. Fluid Phase Equilib. 2006, 240, 144–154. 10.1016/j.fluid.2005.12.020. [DOI] [Google Scholar]
- Beaucamp S.; Mathieu D.; Agafonov V. Optimal partitioning of molecular properties into additive contributions: the case of crystal volumes. Acta Crystallogr., B 2007, 63, 277–284. 10.1107/S0108768106052463. [DOI] [PubMed] [Google Scholar]
- Mathieu D.; Becker J.-P. Improved evaluation of liquid densities using van der Waals molecular models. J. Phys. Chem. B 2006, 110, 17182–17187. 10.1021/jp0574347. [DOI] [PubMed] [Google Scholar]
- Mathieu D.; Bouteloup R. Reliable and Versatile Model for the Density of Liquids Based on Additive Volume Increments. Ind. Eng. Chem. Res. 2016, 55, 12970–12980. 10.1021/acs.iecr.6b03809. [DOI] [Google Scholar]
- Israelachvili J. N.Intermolecular and Surface Forces; Academic Press, Burlington, MA, 2011. [Google Scholar]
- Bouteloup R.; Mathieu D. Improved model for the refractive index: application to potential components of ambient aerosol. Phys. Chem. Chem. Phys. 2018, 20, 22017–22026. 10.1039/C8CP02701C. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.