A Systematist’s Guide to Estimating Bayesian Phylogenies From Morphological Data

Abstract

Phylogenetic trees are crucial to many aspects of taxonomic and comparative biology. Many researchers have adopted Bayesian methods to estimate their phylogenetic trees. In this family of methods, a model of morphological evolution is assumed to have generated the data observed by the researcher. These models make a variety of assumptions about the evolution of morphological characters, and these assumptions are translated into mathematics as parameters. The incorporation of prior distributions further allows researchers to quantify their prior beliefs about the value any one parameter can take. How to translate biological knowledge into mathematical language is difficult, and can be confusing to many biologists. This review aims to help systematics researchers understand the biological meaning of common models and assumptions. Using examples from the insect fossil record, I will demonstrate empirically what assumptions mean in concrete terms, and discuss how researchers can use and understand Bayesian methods for phylogenetic estimation.

Phylogenetic trees are central to the study of evolutionary biology. They establish the historical relationships between lineages, enabling researchers to ask further questions about a wide range of evolutionary dynamics. From trait evolution (Blanchard and Moreau 2017), to species interactions (Majer et al. 2007), to biochemistry (Yek and Mueller 2010), phylogenetic trees are found in all corners of the literature. And yet, phylogenetics itself is an evolving science. Our understanding of how to estimate a tree is tightly coupled to statistical and mathematical advances, as well as to our ever-changing understanding of organismal biology. In this review, I will discuss Bayesian methods for modeling morphological data for phylogenetic inference.

The earliest phylogenetic trees were estimated from morphological characters (Hennig and Davis 1966, Farris et al. 1970). For many years, morphology was the only source of data from which to build a phylogeny, and when molecular data sources (such as allozymes) became popular, the two resources were often compared (Mickevich and Johnson 1976). Workers building these trees predominantly used the maximum parsimony optimality criterion. This criterion is an application of Occam’s Razor. Under maximum parsimony, the tree that implies the fewest changes in the data used to estimate it should be preferred. In the eyes of many fossil researchers, parsimony reflects the vagary of the fossil record: even though phenotypic change over time is commonplace, it may not be frequently observed due to preservation (Gould and Eldredge 1977). Due to its analytical simplicity, researchers working with extant taxa have also used the criterion widely.

As DNA sequence data became more accessible to researchers, method development began to cater more to the needs of molecular systematists, with the initial implementations of parametric models tested on DNA data (Felsenstein 1981). Attempts to model DNA and amino acid evolution first drove the development of mathematical representations of evolutionary processes (Jukes and Cantor 1969, Kimura 1980, Felsenstein 1981, Hasegawa et al. 1985, Tavaré 1986). These methods became very common for analyzing DNA data because parsimony has been documented to provide positively misleading inferences in some cases (Felsenstein 1978). Under parsimony, similarities are interpreted as evidence of common ancestry. In cases where changes are homoplasious or superimposed (i.e., multiple changes at the same character on a branch), parsimony can become inconsistent. In small state-space problems (such as nucleotides, with only four possible character states), this inconsistency can cause what is known as long-branch attraction, in which taxa are grouped together by homoplasious similarity. Parametric methods, such as likelihood and Bayesian estimation, have the ability to account for parallel or convergent evolution.

However, molecular data exhibit properties and expectations that are distinct from morphological datasets (Wright et al. 2016, Goloboff et al. 2019). In 2001, the first likelihood model for estimating phylogeny from discrete morphological data was published (Lewis 2001). Called the Markov K-States (Mk) model, the model made the same assumptions as the simple Jukes-Cantor model for molecular sequence evolution (Jukes and Cantor 1969, see section ‘Bayesian modeling of morphology for phylogenetic estimation’ for details of this model). In the time since the proposal of this model, the role of morphological data in phylogenetic estimation has changed greatly. While estimation of phylogeny from morphological data remained fairly common (see landmark studies using Bayesian methods, such as Nylander et al. 2004 and Clarke and Middleton 2008), it also became common for fossils to be included without any morphological data coded and used as ‘calibration’ points to date phylogenetic trees (Marshall 2008). Even when molecular data are available, morphology and fossils are recognized for being key factors in modeling past evolutionary dynamics (e.g., Moreau and Bell 2013), uncovering historical trends in trait evolution (e.g., Blanchard and Moreau 2017, Branstetter et al. 2017, Mueller et al. 2018), and in phylogeographic inference (e.g., Moreau et al. 2006, Barden et al. 2017). Likewise, methods for time-scaling phylogenetic trees have more thoroughly embraced the use of morphological data, and models now allow for morphology to be modeled jointly with molecular data and stratigraphic data to estimate time since divergence (Heath et al. 2014, Gavryushkina et al. 2017).

There is a new world of methods for working with morphological data. This new world is rich in statistical and computational thinking. In this review, I will discuss some of the fundamentals needed to understand how many of the newer methods and models work, their biological interpretation, and how they correspond to traditional methods, such as parsimony.

What is Bayesian Modeling?

Bayesian methods have become very commonplace in molecular systematics research. These methods seek to apply mathematical models to questions of phylogenetics, phylogeography, divergence time estimation, and comparative methods in order to estimate a distribution of plausible solutions to biological problems. Initially described in the 18th century, Bayesian methods are not unique to systematics, having been applied to nearly every field of study over the past century (McGrayne 2011). Fundamentally, and across all fields, a Bayesian model involves three pieces: a likelihood model describing the process that generated the data, statistical distributions representing prior beliefs about the process that generated the data, and the posterior distribution, representing the knowledge synthesized from the previous two parts. Methods to apply Bayesian analysis to phylogeny were proposed in the late 1990s (Rannala and Yang 1996, Mau and Newton 1997). Analytical software to make Bayesian methods available to systematic biologists became widely available around the turn of the century (Huelsenbeck and Ronquist 2001). Since that time, many models have been implemented for the analysis of biological data in a Bayesian context.

What is a Model?

At the heart of the discussion of Bayesian methodology is a discussion of models. A model is a mathematical construct used to describe the process that generated a set of observed data. Models are defined by their assumptions. Assumptions are statements of what the researcher believes to be true about their data. For example, a common statistical assumption is that observations are independent and identically distributed. If this were true, this would mean that each data point is independent, or that it does not depend on any other data point in the data that have been collected. It would also mean that every data point in the data set is described by the same model. In model-based systematics, the given model makes assumptions about the process of evolution that generated the data that have been collected (also called the observed data). Because a model is a mathematical construct, the assumptions will then be translated into parameters, or quantities describing facets of the process which generated the data.

Let us take a dataset from Barden and Grimaldi (2016). In this dataset, we have 13 ant taxa from the fossil record, five outgroups, and several extant ants. There are 42 characters, some binary (two states, usually 0 and 1) and some multistate (three or more states). One common model, equal-weights parsimony (Hennig and Davis 1966), makes the assumption that any state at a character is equally likely to transition to any other character state, but that each of the 42 characters in the character matrix can have their own length (number of changes) on a shared topology. Another common model, the Mk model (Lewis 2001), makes the same assumptions about character state transitions (called exchangeabilities) but assumes that the 42 characters share a common underlying tree and branch lengths. The difference between these two models may not sound large, but it has implications for the methods by which we infer the tree from the data, as we will discuss below.

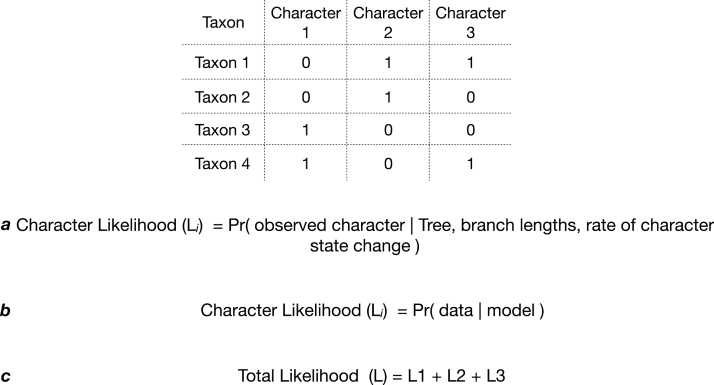
In the case of the Mk model, the model parameters will be a tree, a set of branch lengths on that tree (i.e., the expected number of substitutions between a node and its descendants), and a rate of exchange between different states in the model. Using a model, we can evaluate the likelihood of each character in our dataset given the parameters in the model. These likelihood values are typically on a log scale to avoid problems storing them in the computer’s memory. The individual character likelihoods are summed to compute the total likelihood of the dataset given the model. This is seen in Fig. 1. When we work with a mathematical model, we calculate how likely we are to observe our data, given the assumptions we are making about the underlying process of evolution. In the case of parsimony, the model is similar, except every character can have its own number of steps (character transitions) on a unified tree, potentially expanding to 42 sets of unique branch lengths.

Fig. 1.

This figure displays a character matrix of three binary characters for four taxa. Equation (a) describes the likelihood of a single character. The expression can be read as a character likelihood being equal to the probability of the observed data given the tree, branch lengths, and assumptions (collectively called the model) about the evolutionary process that generated the observed data. Equation (b) demonstrates another way of expressing the same idea—in this case, that the model being represented by the value theta. Equation (c) demonstrates how character likelihoods are summed to give a total likelihood of the dataset.

There are other models that make more complex assumptions, and make assumptions not solely about the exchangeabilities of characters, but about the distribution of speciation events on a tree, or about correlation between characters. We will discuss these methods more in the section ‘Bayesian modeling of morphology for phylogenetic estimation’. Regardless of what precise models are being discussed, the key point for systematists to understand is that every model makes assumptions, and it is crucial to think about how well-aligned a particular model and its assumptions are to the observed data.

Bayesian methods are not the only methods to use models. Parsimony can be considered a model. Maximum likelihood estimation assumes a model of character evolution. Under maximum likelihood, combinations of parameters are scored for their likelihood until a combination of parameters is found that maximizes the likelihood of the data. The key difference between maximum likelihood and Bayesian modeling is described in the next section.

What is a Prior?

Crucial to the Bayesian methodology is the incorporation of uncertainty. In the case of our 42 characters, we may be able to make some statements about that which we believe to be true about the underlying tree, branch lengths, and exchangeabilities. For example, the matrix was scored to uncover the relationship of Cretaceous ants relative to modern lineages (Barden and Grimaldi 2016). Some of these stem ants retain some characteristics of the wasp outgroup (Wilson et al. 1967). Some of these features are subsequently lost in crown-group ants. In these characters, we might expect to see more transitions from a ‘presence’ character state to an ‘absence’ character state. But how strong should this bias be? Are these the only characters in which we expect to see this bias? What do we expect the magnitude of the bias to be? Bayesian modeling enables us to use a prior distribution to describe our beliefs about parameters of our model. This can be seen in Fig. 2.

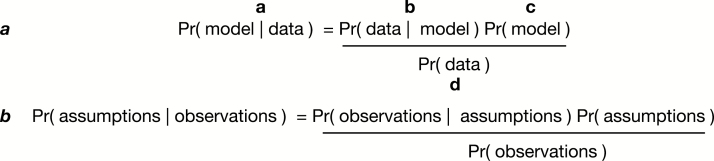
Fig. 2.

Bayes theorem. Panel ‘a’ shows all the terms of Bayes’ theorem. (a) is read ‘the probability of the model given the data’, and refers to the posterior probability. (b) is the likelihood, and is read ‘the probability of the data given the model’. (c) is the prior probability of the model. (d) is the marginal probability of the data. Panel ‘b’ shows the same equation, but with which terms are model assumptions and which terms are observed data annotated.

In Bayesian inference, the value a parameter can take may be fixed, meaning it is given to the analysis by the researcher, and not estimated from the data. Alternatively, the parameter value may be a random variable, meaning different values may be sampled for the parameter over the course of the analysis. The prior allows researchers to place a probability distribution on a parameter, which specifies how likely the random variable is to take on a specific set of values. A probability distribution provides the probabilities of different outcomes or solutions in the estimation.

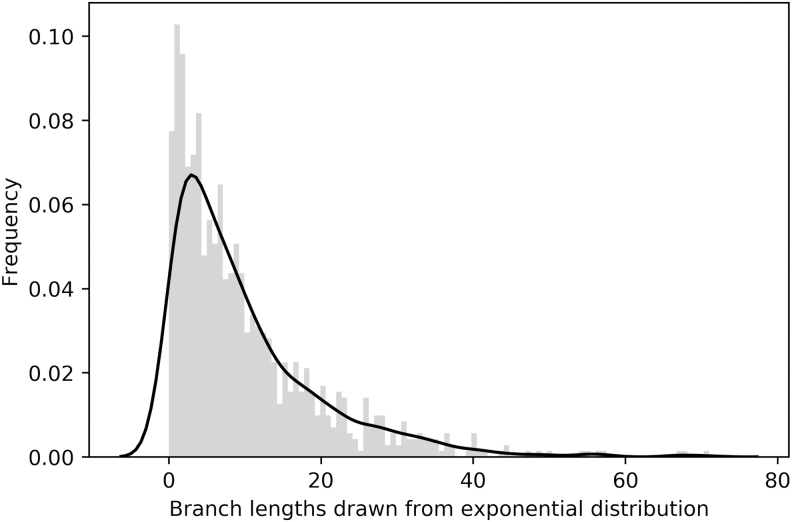
The type of prior a researcher places on a parameter will dictate the types of estimated values one is likely to see in the results of a Bayesian analysis. For example, using an exponential distribution with a rate of 10 on branch lengths is quite common. This distribution can be seen in Fig. 3. The reason for this choice is that most branch lengths are observed to be fairly short. The exponential (10) distribution specifies this, while also allowing for some branches to be longer.

Fig. 3.

Schematic of an exponential (10) distribution. A commonly used distribution in Bayesian phylogenetics, the exponential is often used to place a prior on branch lengths. Under the exponential (10), most branch lengths are expected to be fairly short (to the left-hand side of the distribution), though longer branches are allowed.

As we will discuss below, the prior is not absolute. A prior can be enforced with different weights, according to the researcher’s prior beliefs. For example, a lightly enforced prior can easily be overturned by the weight of evidence. Little evidence will be required to break free of its influence. However, a more strongly enforced prior will need stronger observed data to overturn it. In this case, the values evaluated during the analysis will almost all be drawn from the prior. In practice, it can be difficult to choose a logical prior, and many biologists choose vague and lightly enforced priors.

How do the Prior and the Posterior Fit Together?

Bayesian modeling differs from other types of model-based inference due to the incorporation of the prior. Bayes’ theorem is given in Fig. 2. In Bayes’ theorem, the probability of the observed data (the likelihood) given some hypothesis is multiplied by the prior probability of that hypothesis. This product is divided by the marginal probability of the observed data, meaning the probability of the data with the parameter values integrated out. The end result is the probability of the hypothesis given the observed data. This probability is called the posterior probability, and it is proportional to the product of the prior and the likelihood.

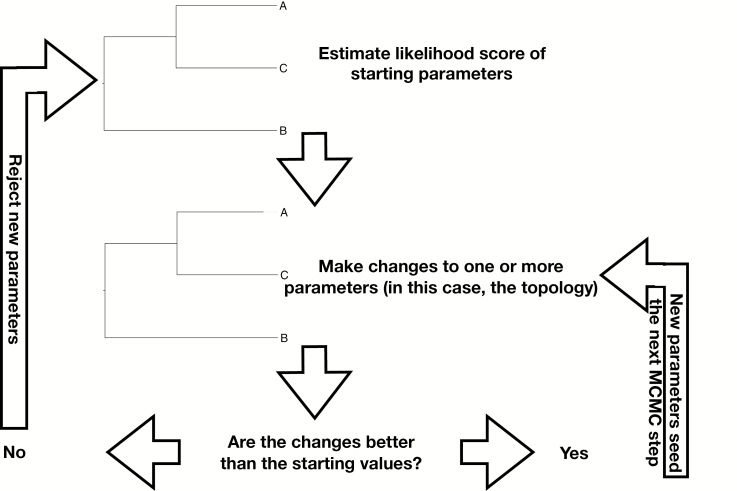
This is a challenging quantity to calculate—what is the marginal likelihood of the data? We evaluate combinations of values for our parameters using Markov Chain Monte Carlo, or MCMC, simulation (Metropolis et al. 1953, Hastings 1970, Mau et al. 1999). MCMC allows new random values for each parameter to be proposed, so that the solutions can be evaluated. In the MCMC algorithm, an initial set of values for the model parameters is proposed. These values are then changed, and new values obtained. This is the ‘Monte Carlo’ aspect of the name: we choose new values at random, though often within some constraining conditions. The act of changing the values for the parameters is often referred to as a ‘move’. These new parameters are then evaluated. The product of the likelihood and the prior is calculated, approximating the posterior probability. Generally, if the posterior probability improves on the old values or is the same, the evaluated parameter values will be kept and used as the basis for the next set of moves. The MCMC algorithm is shown in Fig. 4.

Fig. 4.

Flowchart of the MCMC algorithm. In the MCMC algorithm, initial conditions are proposed and evaluated for likelihood. Then, the tree and/or other model parameters are changed. The likelihood of these new values is then evaluated. If they represent an improvement over the old ones, they are used to seed the next MCMC step. If not, they are rejected.

A move may be large in scale, changing a particular parameter radically, or it may be small in scale, making only minor changes to a parameter. Moves also vary in how often they are performed. More important model parameters may be ‘moved’ more often in order to estimate good solutions for them. Previous states tested by the MCMC algorithm are not considered when making moves. That is why this process is a ‘Markov Chain’, or memoryless process. Previously visited solutions are not removed from the population of possible solutions; therefore, a truly good solution will be revisited many times during MCMC sampling. The goal of MCMC sampling is to visit solutions in proportion to their posterior probability. Regions of parameter space can be included or excluded from MCMC sampling through the use of priors. A well-specified model will eventually converge to the true distribution of each random variable. By sampling many possible combinations of parameters over the course of a phylogenetic estimation, we estimate the posterior without having to explicitly calculate the marginal likelihood. This allows us to complete the equation shown in Fig. 2 in order to calculate the posterior probability.

While MCMC does not consider its previous steps in taking new ones, most phylogenetics software packages do write out the previous combinations of parameters. What is produced is often termed the posterior sample, a log of the trees, branch lengths, and model parameters that were examined during the phylogenetic analysis. Summary trees can then be built from this sample, and the degree of confidence in any particular bipartition on the tree assessed. How often different solutions for any particular parameter were visited can also be assessed. The consideration of a posterior sample of phylogenetic trees is somewhat different than other ways of estimating trees and has implications for how researchers should consider broader macroevolutionary analyses.

What are Morphological Data?

In the section ‘What is a model?’, I outlined Lewis’ Mk model for estimating phylogeny from discrete morphological data. Before we think about coherent models of morphological evolution, we need to think about what morphological data are. What are the properties of morphological data, and how are morphological data collected? Broadly, morphological data often fall into two categories, discrete and continuous. These data types differ greatly, with implications for how they can be analyzed.

Discrete Morphological Data

Discrete data can be found in many fields, not just phylogenetics. Any data that can be broken into distinct and nonoverlapping classes may be considered discrete. In Bayesian phylogenetics, much of the work on morphology has focused on discrete traits (Lewis 2001, Nylander et al. 2004, Ronquist et al. 2012, Heath et al. 2014, Wright and Hillis 2014, Harrison and Larsson 2015, Wright et al. 2016), in part due to the availability of methods to work with molecular data, which is also discrete. In these cases, an individual character is broken down into states, each with diagnostic morphology. Our example matrix from Barden and Grimaldi (2016) is made up of discrete characters (see Supplemental Information to look at the matrix).

Discrete characters can be broken down into categories. Binary data are characters which have two states, typically 0 and 1. These states often correspond to presence (1) and absence (0). Alternatively, they may have more complex diagnoses, such as specific morphological features assigned to the 0 and 1 states. An example of this type of character from the Barden and Grimaldi matrix is ‘Anterior margin of clypeus with row of peg-like denticles’. This character refers to setae on the margin of the clypeus. In this case, we have a trait that is described qualitatively. This character is broken down into present (1) and absent (0). Multistate characters are those characters which are broken down into more than two character states. In these characters, each state corresponds to a specific morphology, though 0 may still correspond to absent. An example of this character type from the Barden and Grimaldi dataset is the ‘Mandibular shape’, which is broken into six states, each with a clear definition of the morphology of each state. More examples of discrete traits can be seen in Fig. 5.

Fig. 5.

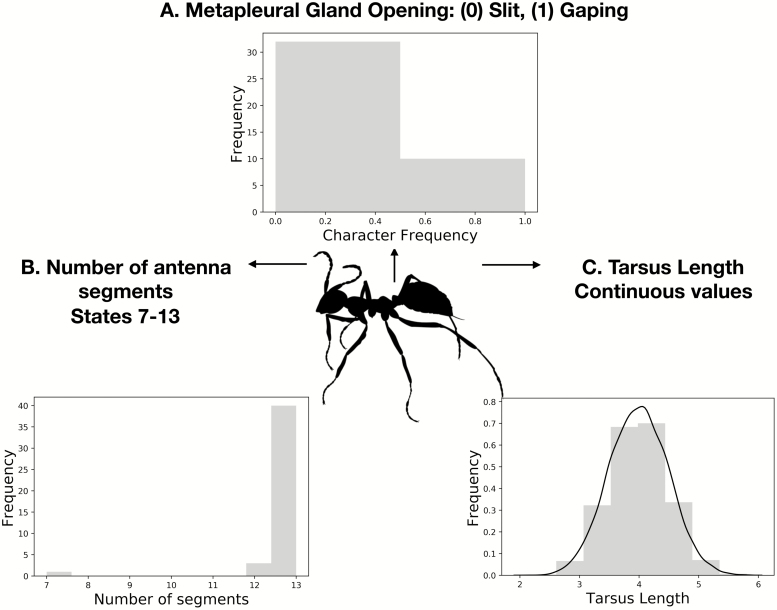
A drawing showing different types of characters. In the center is Sphecomyrma freyi Wilson 1967 (Hymenoptera: Formicidae), a Cretaceous ant (Wilson 1967). Ant silhouette via T. Michael Keesey. (A) shows a binary discrete trait, fusion of the petiole. This trait has two possible states—fused and unfused. The distribution beside it shows how common each of the two character states are in the Barden and Grimaldi (2016) dataset. (B) shows a discrete, multistate trait. The number of antennal segments can take on multiple possible values, though only three are observed in the dataset. (C) shows a hypothetical continuous trait, tarsus length. Continuous traits can take on any real number, not only discrete values.

Characters may be coded with respect to what is called polarity (De Queiroz 1985, Stevens 1991). In these cases, the phylogeny has informed the way in which the character is coded. The result of this is that one character state is designated pleisiomorphic (ancestral), and one is denoted apomorphic (derived) a priori. This is often seen in the form of the 0 state representing the state possessed by outgroup, or the purported ancestral state (Watrous and Wheeler 1981). Researchers may also choose to use ordering, in which they specify that changes must occur in a specific order. For example, if the character states are 0, 1, and 2, an ordered character may be specified such that the 0 → 2 transition is not allowed, but must instead be a 0 → 1 change followed by a 1 → 2 change.

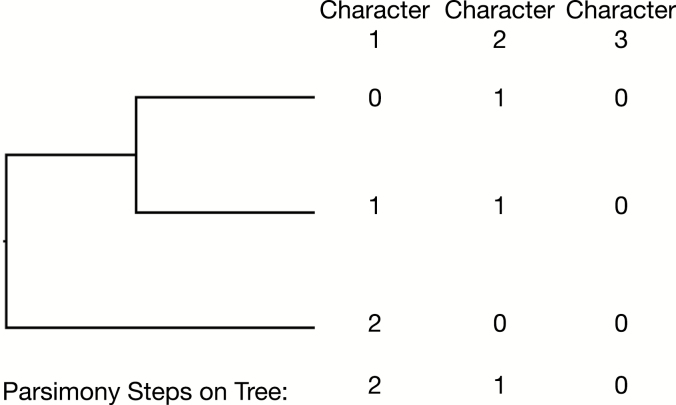
The act of choosing which characters to use, and what the states should be is typically performed by an expert examining populations of samples, and deciding which facets of organismal form vary, and what variation is considered phylogenetically informative. Phylogenetically informative refers to whether or not a character can be used to favor one set of bipartitions on a tree over another under the parsimony criterion. For example, a character which does not vary in the set of taxa on the tree is not considered to be phylogenetically informative because it will have the same parsimony score on any set of bipartitions. These characters are called ‘invariant’. Invariant characters are common in molecular data, but are often not scored in morphological data. Likewise, a character for which every taxon has a different character state is not considered phylogenetically informative because it will also have the same parsimony score on any set of bipartitions. A character which varies among the set of taxa, but is shared by at least two tips on the tree is considered phylogenetically informative. A schematic of this concept is in Fig. 6.

Fig. 6.

The parsimony length of three characters on a single tree. Each character has been scored for how many changes it exhibits on the displayed tree. Character one is not considered parsimony informative, as every tip on the tree has a different state, and therefore, it cannot be used to discriminate among trees. Character three is non-informative because it has no variation. Character two is considered informative because it favors trees containing one grouping over another. Under parsimony, characters one and three would not be collected. Under a Bayesian model, not observing invariant characters must be corrected for in order to avoid overestimating the true rate of evolutionary change (Lewis 2001).

All of the above concepts—character coding, polarity, phylogenetic informativeness—have implications for modeling the data, and will be discussed in the section ‘Bayesian modeling of morphology for phylogenetic estimation’.

Continuous Characters

Continuous characters are those characters that cannot be broken into discrete states as easily (Fig. 5). Examples of these types of characters may include height, weight, or the length of a structure on the body. These traits can take on the value of any real number and may represent a specific morphometric observation from one individual, or another measurement, such as the mean of some trait in a population of individuals. As such, continuous characters are often also referred to as quantitative characters, as they cannot be described qualitatively.

In the case of discrete data, there is typically an expert observer choosing which characters are worth collecting, as outlined in the previous section. Expert observers also play a role in the collection of continuous data. When a specific structure is being measured, this is typically chosen by an expert observer because it varies within the set of taxa that will be placed on the tree. Some researchers choose to then discretize the data into categories of variation (i.e., gap-coding, Mickevich and Johnson 1976, Thorpe 1982, Thiele 1993, Lawing et al. 2008, Randle and Sansom 2017).

In the case of landmark-based morphometrics, the data are the coordinates of the location of distinct anatomical features on the organism. The landmarks are typically decided upon by an expert and are homologous across the sample of organisms. This may be done in 2-D, such as from an image, or in 3-D, such as from a computer-based anatomical scan. While an expert has traditionally been required for this type of analysis, recent work has explored crowd-sourcing this type of data collection (Chang and Alfaro 2016). Landmarks can also be defined automatically, without the use of an expert (Aneja et al. 2015, Li et al. 2017). Automated landmarking typically requires a high-quality 3-D scan of the specimen to be quantified, and some way to normalize the size and view of the scan (Chollet et al. 2014). These methods are promising because they allow the collection of larger datasets with less time investment, but also they avoid observer bias about which facets of the individual are important, and have error sources that are easier to detect and correct (Li et al. 2017).

Lesser-used forms of continuous data may include sonic information (May-Collado et al. 2007, Escalona Sulbarán et al. 2019), and behavioral information (Blomberg et al. 2003, C. R. Turner et al. 2007). Traits of this nature are typically not used in cladistic model-based phylogenetic estimation, but rather for the inference of macroevolutionary patterns.

Bayesian Modeling of Morphology for Phylogenetic Estimation

Discrete Morphological Data

The manner in which discrete morphological data are collected introduces potential biases into phylogenetic estimation. Since many of the modern methods for handling phylogenetic data were described to handle molecular data, it is instructive to contrast molecular and morphological data. Molecular sequence data has a defined number of states (four for nucleotides, 20 for amino acids), and it is generally assumed that an instance of one particular molecule will have the same properties across the sequence. These assumptions do not hold for morphological data. A change between one state and another (say between 0 and 1) at one character might require only a small underlying genetic change. That same change at another character may involve wholly different underlying molecular machinery, and be of a much larger magnitude. For example, Fig. 5 shows two different discrete morphological characters. In panel A, we have the metapleural gland opening. The metapleural gland has chemosensory and communication function. A slit-like metapleural opening can be used in a brush-like manner, implying a role in signaling, and perhaps correlation with behavioral traits (Yek and Meuller 2010). In panel B, we have the number of antennae segments. To change states in this character means to lose or gain a repeat of an already-repetitive structure. To specify one model that adequately describes the probabilities of observing changes in both these characters may not be possible. The lack of ability to specify a single mechanism across the whole dataset has long limited the types of models that can be considered for morphology.

Due to these difficulties, discrete morphology has been analyzed under a very simple model. This model is often referred to as the Mk model of morphological evolution (Lewis 2001). This is a generalization of the Jukes-Cantor model for molecular sequence evolution (Jukes and Cantor 1969). As such, it makes the same set of assumptions. We will now discuss what these assumptions are, what they mean for character evolution, and how priors on these assumptions can be used to enable more flexible models of evolution.

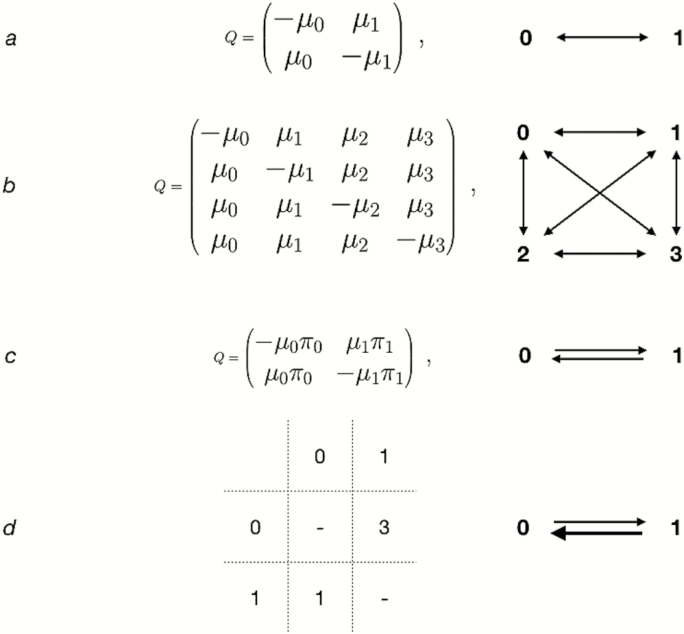
Exchangeabilities define the rate at which we expect a given change between two character states. In the Jukes-Cantor model, the exchangeabilities between any state and any other state are held to be equal. A Q-matrix, the matrix specifying the likelihood of different transitions at a given instant in evolutionary time can be seen in the equation on Fig. 7a. In the case of morphological data, this means that the probability of transitioning between one character state and any other are equal. If we have binary, presence-absence data, these data would be equally likely to show gains as losses. However, in molecular phylogenetics, the probability of observing a change depends on two quantities: the exchangeability, and the equilibrium frequency of the starting state. The Jukes-Cantor model assumes the character states have equal equilibrium frequency. This can be seen in Fig. 7c stationary state frequencies define how many of each state we would expect to see if the process of evolution were allowed to continue infinitely long (allowed to equilibrate). Even if the exchangeability between two states is high, if the starting state is rare, we will observe that change rarely (Felsenstein 1981). The default assumption of the Mk and Jukes-Cantor models is that equilibrium character frequencies are equal. Taken with the assumption of equal exchangeabilities, this disallows differential rates of change between character states.

Fig. 7.

A schematic showing common assumptions about character evolution. (a) shows the Q-matrix under the Mk model for binary data. This corresponds to the assumptions on the right-hand side of the figure, that a character is equally likely to change from a 0 state to a 1 state as the reverse. (b) shows the same assumptions, expanded to a multistate character. (c) shows a Q-matrix with each character state allowed to have a different stationary character frequency, enabling different 0 → 1 and 1 → 0 rates. (d) displays a parsimony step matrix that penalizes 0 → 1 transitions. In (d), the rows represent the starting state, and the columns represent the state to which the character is changing.

This assumption likely strikes many readers as unrealistic. Bayesian methods provide us a solution to escape this problematic assumption. In a Bayesian context, assumptions are translated into mathematics as model parameters. The value of a parameter is usually treated as a random variable, and we can use priors to create distributions of values that the random variable is likely to take. Under parsimony, individual characters having differential probabilities on state transitions is often handled by specifying a transition matrix with the desired weights on different changes. For example, if it is considered more likely to lose a character state (transition from a 1 state to a 0 state) than to gain another state (transition from a 0 state to a 1 state), a step matrix can be specified for that character that penalizes 0 to 1 transitions. This can be seen in Fig. 7d. This is, functionally, an extremely strong prior on certain types of changes. The correspondence between parsimony and Bayesian methods is discussed in ‘Interpretation of Bayesian and parsimony analyses’.

In the example of differential rates of character state changes, in a Bayesian framework, one can place a prior on the state frequencies, biasing the parameter towards taking on values in a specified distribution. In the case of state frequencies, one approach to allow variation has been to use a Beta prior for binary data, or a Dirichlet prior for multistate data (Nylander et al. 2004, Wright et al. 2016). When values are sampled for the parameter, the posterior is proportional to the model likelihood times prior on the parameter. In the case of data that are strongly informative, the prior could be overwhelmed by the data. If the data are weakly informative, the prior will likely dominate the posterior distribution. In practice, this allows us to sample different character state frequencies. If the frequency of a character state is very high, we will observe more transitions from that character state to other character states. Practically, this allows for different rates of change between states to be sampled in the analysis, informed by the data, as opposed to being fixed as they would in a parsimony analysis.

Bayesian methods open the door to using mixture models. Mixture models treat the total dataset as an aggregate of smaller populations, which may have different parameter values. A common example of this is the use of among-character rate variation (ACRV) (Yang 1994). One long-acknowledged issue in phylogenetics is that not all sites in a molecular alignment or characters in a data matrix will evolve at the same rate (Fitch and Margoliash 1967, Yang 1996). Declining to model this variation can lead to incorrect inferences (i.e., Sullivan et al. 1996, Buckley et al. 2001; see also discussion in Sullivan and Joyce 2005). Under this model, the rate of evolution at any one character is assumed to be drawn from a Gamma distribution. Because approximating a continuous Gamma distribution would be too computationally intensive, a discrete Gamma distribution with a user-specified number of categories is used. Four categories have been supported in some empirical studies and is a common default value in phylogenetics software. When this value is chosen, there are four rate categories used to describe the data (i.e., for subpopulations in the mixture model).

This same framework can be applied to other parameters. Relaxing character change symmetry has been accomplished using similar principles (Nylander et al. 2004, Wright et al. 2016). When we place a prior on character frequencies, this is typically done as a mixture model. In this case, the Beta distribution (binary data) or Dirichlet distribution (multistate data) is typically discretized into several categories. The likelihood is then computed according to each category and summed to generate a character likelihood. Treating character rates, or character change asymmetry, as a mixture model allows the dataset to potentially have multiple classes of transition rate symmetry for a given dataset. Each class specifies the same model parameters but allows those parameters to take on different values. In this way, there can be multiple rates of evolution, or multiple 0 to 1 transition rates, in the dataset.

In Bayesian analysis, it can be confusing for researchers to understand what is the model, what is the prior, and how each part affects the analysis. Parameters define what a researcher believes are the key facets of the process by which the data were generated. A prior specifies a range of values for that parameter that the researchers consider reasonable.

Continuous Data

Continuous data have been less commonly used for phylogenetic inference. As discussed in the section ‘What are morphological data?’, continuous data are often discretized before being used in phylogenetic analysis. This, however, introduces an element of user interpretation to the data that does not otherwise need to exist, and is not modeled explicitly when analyzing the data (Wiens 2001). Continuous data have often been used for what is termed comparative phylogenetic analysis or macroevolutionary analysis (see examples and discussions in Felsenstein 1988, Maddison 1991, O’Meara et al. 2006, Felsenstein 2011, Beaulieu et al. 2012, Landis et al. 2013, Cooper et al. 2016). Despite their relatively rare use for Bayesian inference, these data have a longer history of use in parsimony (Goloboff et al. 2006) and been demonstrated to contain phylogenetic signal (Smith and Hendricks 2013).

The rich history of using continuous characters for comparative analysis enables those same models to be used for phylogenetic estimation. Brownian motion has been used to model trait data for phylogenetic estimation (Parins-Fukuchi 2017). Brownian motion is used to model the value of continuously varying data over time (Butler and King 2004, O’Meara et al. 2006). This model is often referred to as the ‘random walk’, due to the fact that in any time interval, the value of a trait can change randomly in both direction (positive or negative) and magnitude (small or large changes). Brownian motion was originally used to describe the movement of particles suspended in fluids. In biology, Brownian motion may be compatible with a number (or combination) of evolutionary forces (see discussion in Harmon 2018 for more context).

In a Brownian motion model, evolution is typically described by two parameters: the mean trait value, X, at the start of a particular time interval, and the evolutionary rate parameter, σ. X will be the value with which the trait can ‘walk’ during the time interval. σ will determine the magnitude with the trait will step away from X. Changes are expected to be distributed according to a normal distribution with mean 0 and variance proportional to the rate and duration of the time interval. At very short time intervals, we expect to see little change. For long intervals, we expect the normal to become wider and wider, indicating that the amount of change has the potential to be larger.

Brownian motion has been used to model the evolution of traits on a tree. Recently, it has been implemented for phylogenetic estimation in both dated and undated trees. Simulation research indicates that estimating phylogenetic trees from continuous characters simulated under Brownian motion can lead to lower topological error than discrete morphological traits (Parins-Fukuchi 2017). In particular, this is true in datasets with multiple rates of evolution. Wright and Hillis (2014) demonstrated that in discrete morphological traits, phylogenetic error is very high for characters with low rates of evolutionary change (due to low signal), and characters with very high rates of evolution (due to homoplasy of changes). Continuous characters do not display this relationship as strongly due to their large state space, though more research is needed to demonstrate this effect empirically.

Use of continuous characters is promising because the Brownian motion model is fairly lightweight, relative to some Bayesian methods for discrete characters. This allows for each character to have its own σ, enabling multiple mechanisms in a dataset without having to calculate a character likelihood according to multiple Beta categories (Parins-Fukuchi 2018). Expectations about the evolution of continuous characters are complex, but Brownian motion can be expanded to accommodate them. For example, characters are expected to covary in a Brownian motion framework. This character correlation can be accounted for by estimating a correlation matrix from individuals in a lineage (Álvarez-Carretero et al. 2019). If within-lineage correlation is not accounted for, morphological evolution rates will be overestimated, possibly leading to branch length and topology error. The correlation matrix can be used to correct within-lineage character correlation. Because the lineages are all connected by an underlying phylogeny, character correlation may also occur among lineages. The correlation matrix can then be used to establish a correlation matrix among lineages, as well.

The use of continuous characters in morphological phylogenetics is an exciting prospect along several lines. Firstly, Brownian motion is one of many comparative models of evolution (for a review of many different models, see Harmon 2018). Others could be substituted, or multiple models used among characters. Even in the case that other models are not explored, the Brownian motion can correspond to different biological interpretations. Brownian motion is typically interpreted to be analogous to traits evolving under drift, having no selective optima. Prior work demonstrates that several models incorporating selection still appear indistinguishable from Brownian motion (Martins and Hansen 1996). In sum, there are a variety of mechanisms that could be described by Brownian motion, such that the researcher does not have to explicitly choose a model corresponding to a given mechanism.

Secondly, these implementations are exciting because they enable the use of a third independent data source (continuous character data), modeled under different assumptions. Modeling traits according to Brownian motion to estimate a phylogeny from continuous trait data allows researchers to work in the same MCMC framework for continuous, discrete, and discrete molecular data. Using all available data will enable researchers to validate the tree among sources, and formulate testable hypotheses of how model assumptions may impact the tree estimated. This also opens the path to perform joint estimation across multiple types of data. Indeed, fossil datasets are often limited in size (Wright et al. 2016). Opening up new paths to collect data, particularly if automation of data collection becomes commonplace, will allow researchers to make complete use of specimens.

How Does Bayesian Modeling Differ From Parsimony?

I have said very little thus far in this review about parsimony. My main purpose has been to lay out how Bayesian modeling of morphology works in a phylogenetic context. Parsimony is still a dominant optimality criterion in morphological phylogenetics. It is informative to look at how the assumptions, mechanisms, and interpretation of Bayesian and parsimony methods are similar, and how they are different. There are two main comparisons I would like to make between the two criteria: assumptions made about the evolutionary process, interpretation of parsimony and Bayesian analysis.

Assumptions About the Evolutionary Process

Parsimony can come in several variations, just as we can relax various assumptions of the Mk model. The most common variation is equal-weight parsimony. This typically refers to an application of parsimony in which it is held that any change between any two character states is weighted equally, and all characters contribute equally to the tree search. In this case, a change from 0 to a 1 state is as likely as a reversal between the two. Superficially, this is quite similar to one of the chief assumptions of the Mk model—that character changes are symmetrical.

However, there are core differences between parsimony and Bayesian approaches which change the results and interpretation of these two ways of estimating trees. In a Bayesian analysis, values are sampled for each of the parameters in the model, including branch lengths. Branch lengths are typically sampled as number of expected character changes per character. In a parsimony analysis, the tree that is favored is the one that minimizes the number of changes in the dataset across that tree. Each character may have its own number of steps on the tree. The final branch lengths represent the number of changes in the dataset along each branch, as a whole number, rather than a rate. This has desirable properties—in a maximum parsimony analysis, character changes can be mapped to specific branches. In Bayesian estimation, either more complex models or post-hoc analyses (Pagel 1999, Nielsen 2002, Bollback 2006, Maddison et al. 2007, FitzJohn et al. 2009, FitzJohn 2012, Revell 2012) are required to do this.

Advocates for parsimony often point to the aforementioned as a positive. Parsimony is often referred to as a ‘No Common Mechanisms model’ (NCM), which allows every character in the character matrix to have its own number of steps on a common tree (Tuffley and Steel 1997). This is intuitively appealing—it is unlikely that every character in a matrix evolves at the same rate. Allowing each character to have its own rate of evolution means that no matter how different the rates actually are, they can be accommodated. However, this same assumption makes it impossible to choose a likelihood implementation of the NCM model via even liberal information criteria due to its parameter richness (Holder et al. 2010). The number of parameters to be estimated grows extremely rapidly as more taxa and characters included in the analysis. Model selection techniques typically attempt to balance parameter richness with how much the fit of the model to the data improves with those additional parameters. Statistical model selection procedures indicate that the NCM model is so complex as to never be statistically justified, meaning that the increase in explanatory power of the model is never justified given the number of parameters added. What a model selection technique cannot tell you is if the added parameters add biological realism. There may very well be reasons why, even in the absence of statistical evidence, researchers consider the assumptions of parsimony to make more sense for their data. The purpose of this review is not to argue for one method over another, but to lay the groundwork for researchers to understand the underlying assumptions of these two different types of phylogenetic estimation.

Bayesian estimation can enable researchers to relax the assumptions of the Mk model (Nylander et al. 2004, Wright et al. 2016). Parsimony also allows users to specify alternatives to equal-weight parsimony. A parsimony step matrix can be specified, which allows researchers to place different weights on various character state transitions. For example, if a researcher believed it would be easy to lose a trait, but hard to regain it, they could weight the loss lightly, and the gain heavily (Hennig and Davis 1966, Moss and Hendrickson 1973, Farris 1977, Ree and Donoghue 1998). Then, when the parsimony tree is estimated, trees that contain gains of the trait will have to compensate by minimizing parsimony steps in other parts of the dataset. This penalizes trees containing the penalized gain. Researchers can specify custom step matrices for every character in the matrix, if desired. This flexibility enables researchers to, in effect, completely control the tree estimated through a priori specifications of the types of changes that can be seen. Specifying a step matrix can be thought of as a type of very strong prior. However, where Bayesian estimation has a variety of well-characterized model selection tools to evaluate the statistical appropriateness of a particular prior, there is a little statistical framework for evaluating the effect and appropriateness of assumptions made in a parsimony context.

There is another type of weighting that has become popular. This type is referred to as character weighting (Farris 1969). In a dataset with character weighting applied, changes in certain characters are held to count more towards the parsimony score than others. This often takes the form of downweighting characters thought to be highly homoplasious (Goloboff 1993, Turner and Zandee 1995, Wiens 1998). This is similar to allowing ACRV: if a character is not penalized for changing frequently, more frequent changes will be observed in that character. When a researcher does this, they specify that certain characters are less reliable indicators of the true phylogeny than others. This may be done by hand, with the researcher specifying that a change in one character (the character thought to hold the least homoplastic signal) must be balanced by multiple (two or more) changes in others. This can also be automated, a process often referred to as implied weighting. Under this approach, the first time a character changes state on a tree, the change is given the weight of one. Subsequent changes are given smaller weights. In effect, this means that the more a character changes, the less it is allowed to influence the estimated tree. First implemented in 1993 by Goloboff, the implied weighting approach allows for the process of weighting to be more reproducible, and less dependent on observer bias about which characters to weight.

Interpretation of Bayesian and Parsimony Analyses

Parsimony aims to estimate the most parsimonious tree, i.e., the tree that minimizes the number of changes in the dataset along that tree. This is fairly straightforward to understand. Multiple ‘most’ parsimonious trees may be estimated from the same dataset if multiple sets of relationships or branch length distributions are equally parsimonious. We can think of parsimony methods as aiming to estimate one tree. This may not be possible due to lack of information content or conflicting signals in a given dataset.

Bayesian methods, however, provide a distribution of trees and parameter values sampled during the tree search. These are the values and trees proposed and evaluated by the MCMC algorithm during estimation. This posterior distribution can be used to test if the estimation has converged, or drawn enough independent samples that the true posterior has been approximated. A Bayesian estimation is not expected to provide one evolutionary history, and set of parameters. Rather, visualizing this uncertainty is considered by many to be integral to Bayesian estimation. For example, in a dated phylogeny node ages are typically shown as distributions of possible ages, rather than point estimates. The shape and spread of the distribution itself is important information—a very wide distribution might indicate little precision in the value, while very peaked distributions indicate very attenuated levels of uncertainty around specific values. For a very useful review on the posterior sample, and its relationship to other distributions of trees, see Alfaro and Holder 2006.

Both parsimony and Bayesian methods often rely on building a consensus tree. There are many ways to estimate a consensus tree (for a review see, O’Reilly and Donoghue 2017), but fundamentally, a consensus tree summarizes the bipartitions on the tree, and turns a sample of trees into a single tree object. In a Bayesian analysis, those trees are normally labeled with the posterior probability of the bifurcations on the tree. In parsimony analyses, further estimations such as bootstrap, must be performed in order to quantify uncertainty in a particular bipartition (Felsenstein 1985). These approaches subsample columns of data in a phylogenetic matrix and re-estimate trees from the generated samples. Whereas Bayesian posterior probability can be thought of as the probability of the phylogenetic hypothesis given the data, the bootstrap can be thought of as a measure of repeatability of the hypothesis given the data (Felsenstein and Kishino 1993, Hillis and Bull 1993). For example, if 1,000 subsampled replicate datasets are used to estimate trees, and 999 of them support the same tree, this is the evidence that the collected data strongly support the estimated topology. However, collection of additional data could change the bootstrap values. For a comparison of the Bayesian posterior with other methods of assessing confidence in a split, see Huelsenbeck and Rannala (2004).

These two approaches have implications for how model fit and adequacy can be addressed. As discussed above, both Bayesian methods and parsimony make assumptions about the data. In a Bayesian method, the fit of the model to the data can be described by calculating the marginal likelihood of the data, the probability of the data with model parameters integrated out. The calculation of this quantity can be complex, and beyond the scope of this paper, but for further theoretical reading see Lartillot and Philippe 2006, Xie et al. 2011, Hug et al. 2015. This quantity allows for the comparison of models using the Bayes Factor, a standardized statistical framework for comparing the weight of evidence for different models (Kass and Raftery 1995, Suchard et al. 2005, Brown and Lemmon 2007). In this way, assumptions about the data either via the model or the prior can be tested. An equivalent framework does not exist for parsimony. Under the maximum parsimony criterion, if a shorter tree is returned, that is considered to be the better tree.

New Worlds of Data-Intensive Morphology

As we’ve seen in the previous sections, estimating phylogenetic trees from morphological information is an evolving science. Between parsimony estimation and Bayesian methods, many combinations of assumptions can be made to suit a given dataset. Researchers have a greater range of choices than at any point in the past to try, and create, new models for understanding the evolution of taxa and traits. Below, I will highlight two advances that are particularly interesting.

Modularity of the Prior and the Model

Historically, many Bayesian estimation software suites have allowed only limited choices of priors on any model parameter, and limited control over the shapes that the prior distribution can take. More modern software allows researchers to experiment more broadly with novel combinations of parameters and priors.

In the section ‘Bayesian modeling of morphological data’, we discuss placing priors on ACRV and character state frequencies. In the previous generation of phylogenetics software (i.e., MrBayes, Huelsenbeck and Ronquist 2001), priors of this nature had to be coded into the software by the developers (see Table 1 for an overview of phylogenetic software). If a user wanted to use a certain prior distribution with a new data type, they may have needed to program it into the actual software. Current generation software (BEAST2, Bouckaert et al. 2014; RevBayes, Höhna et al. 2016, Höhna et al. 2017) allows users to generate new combinations of parameters and priors, and to contribute the scripts to do so back so other users may find them via contributions to their open-access software repositories.

Table 1.

A brief overview of software that can analyze morphological data

Software	Optimality criterion	Modular	Allows relaxation of Mk assumptions
PAUP (Swofford 2003)	Parsimony and Likelihood	No	No
TNT (Goloboff et al. 2008)	Parsimony	No	No*
RAxML (Stamatakis 2014)	Likelihood	No	No
Mr. Bayes (Huelsenbeck and Ronquist 2001)	Bayesian	No	Yes
RevBayes (Höhna et al. 2016, Höhna et al. 2017)	Bayesian	Yes	Yes*
BEAST2 (Bouckaert et al. 2014)	Bayesian	Yes	Yes
MCMCTree (Yang 2007, Álvarez-Carretero et al. 2019)	Bayesian	No	Yes*

The modularity column assesses if the software is modular per the section ‘Modularity of the prior and the model’. The final column specifies if researchers can relax any assumptions of the Mk model in the software. An asterisk indicates that continuous characters and models can be used in the software.

This philosophy of flexibility is important to progress in this field. Firstly, many of the models we use to estimate phylogenies were not generated with morphology in mind (Jukes and Cantor 1969). For example, prior work indicates that using the Gamma distribution to model ACRV may not be optimal for morphological data (Wagner 2011, Harrison and Larsson 2015). On its face, this makes a great deal of sense: traditionally, invariant characters have not been collected by researchers. Nor have characters that change only once on a tree. This means that we typically must correct for this omission, often referred to as correcting for ascertainment bias. But when we use Gamma-distributed rate variation, we assume that there are some extreme low-rate characters in the dataset. For morphology, this is unlikely to be true. A modular framework allows a user to simply substitute a more appropriate prior distribution.

An implicit benefit to this is that researchers can realize models that they believe will fit their data without needing to involve a developer of the software. In previous software generations, when a researcher needed a new model, they would contact the developer, and let them know what they needed. Depending on how much time the developer had to handle user requests, perhaps they would implement it. Modular software allows researchers to be the developer of the model. This enables the expert on the data to create models to describe those data, without having to wait on a software expert. Likewise, the software expert is also freed from needing to constantly balance user requests with their own work. Embracing open source contribution also allows users to contribute back their scripts for analyses, such that other users can find and use them. Modularity and openness enable faster scientific progress as researchers can implement new models quickly, and disseminate those results with an interested community of scientific practice.

Ontogeny-Aware Phylogenetic Models

Dependence between characters has long been an elusive phenomenon in morphological phylogenetics. Gene regulatory networks and developmental cascades deeply impact the morphological characters we collect. And yet, we are unable to observe these dynamics in paleontological data and not every morphologist is an experimental developmental biologist with the training to gather data on underlying regulatory networks. Even in the absence of these data, the effect of these processes can be modeled.

Sewell Wright (1934) proposed a model for discrete characters called the threshold model. Under this model, which character state an organism has at a character is determined by a hidden, underlying character called ‘liability’. Liability is continuous, but when it crosses some threshold in trait space, the discrete character changes states. This trait is a stand-in—there is no explicit mechanism being modeled. Liability could be some unobservable, but real, aspect of the phenotype. One such example could be a simple factor, such as circulating hormone concentrations causing a trait change. It could also be a more complex factor, such as a gene regulatory network. Felsenstein applied this model for inferring correlations between characters (Felsenstein 2005, Felsenstein 2011), and the model has subsequently been applied to ancestral state estimation (Revell 2014). To date, it has not been used to infer phylogenetic trees, though flexibility in new phylogenetics software may allow this, as discussed above.

New methods for modeling similar dynamics for inference of phylogeny rely on Hidden Markov Models (HMM) and Structured Markov Models (SMM) (Tarasov 2019). HMMs make a similar assumption to liability—that there are some underlying variables affecting the observable discrete states. In an HMM, the transitions between states are occurring between the hidden states, as opposed to the observed states, as in a regular Markov Model. Each observed state is typically affected by multiple hidden states. If this is not true, the model collapses to a regular Markov Model. SMMs allow for among-character dependencies, such as if an organism must have antennae in order to have antennae segments. This combination of models allows for phylogenetic inference that integrates underlying genetic and developmental process information.

Integrating hidden state information into phylogenetic analysis is an exciting new direction. It’s also very challenging: in subsequent work, use of ontologies is proposed to assist in annotating characters (Tarasov et al. 2019). Ontologies establish a shared, machine-readable syntax for discussing characters and representing relationships among characters. In approaches that incorporate information about hierarchical relationships among characters, ontologies are used to connect characters to the ontology. This enables higher relationships between characters and suites of characters to be accounted for in estimation. However, this also means an ontology must be assembled, requiring in-depth morphological work with specimens by an expert observer. Due to many homoplasious changes in large, speciose groups, invertebrate systematics has been a leader in adopting the ontology framework, making this particular field well-situated to explore these new methods.

Concluding Remarks

Morphological data have been crucial in phylogenetic estimation from the very first forays into the estimation of evolutionary history from observed data. This scope of this review was to look at models for inferring phylogeny from morphological data. I have covered many exciting advances in how researchers can codify their knowledge of the evolutionary processes that lead to their observed morphological matrices. What is beyond the scope of this review is a discussion of comparative methods, for inferring the evolutionary history of traits on a tree. We have also not discussed divergence time estimation models, such as the fossilized birth-death model, which allow for modeling a discontinuous fossil record to infer divergence times and also further dynamics, such as speciation, extinction, and turnover. The methods allow researchers to fully integrate molecular and morphological data to estimate time-scaled phylogenetic trees.

Morphological systematists are taking advantage of the full richness of statistical methods, such as Bayesian inference, and more classical methods, such as parsimony variations including implied weights. New methods for integrating hierarchical character information promises to help unlock the full richness of systematist’s knowledge. Closer relationships between software, developers, and empiricists facilitated by open science are enabling researchers to participate more fully in the process of model generation and testing. In short, morphology is experiencing a new golden age, facilitated by cross-disciplinary communication and sharing of knowledge.

Glossary

Model: A representation of a process, rendered in mathematics. In Bayesian systematics, a model typically describes the process of evolution leading to the data.

Assumptions: Factors about the model that are assumed to be true. For example, an equal-weight parsimony analysis assumes changes between two character states are equally likely. In a Bayesian model, assumptions are written down into parameters, or mathematical facets of the model.

Observed Data: The data that have been collected by the researcher and will be used to infer the phylogeny. In the case of morphological data, these will be the morphological characters collected, whether from extinct or extant organisms.

Discrete data: Data that can be broken into distinct and non-overlapping classes. A common example of these data type is presence/absence data. Data with two classes are referred to as binary; data with more classes are referred to as multistate.

Random variable: A variable whose value is the result of a random draw. In most Bayesian models, the value of a given parameter is a random variable. For example, the value of a particular branch length on a phylogeny is a random variable, which may be drawn from a distribution.

Continuous data: Data which cannot be broken into distinct and non-overlapping classes, and may take the value of any real number. Examples include geometric morphometric measurements, weights, and lengths.

Exchangeabilities: The rate at which one character state is expected to transition to another. The exchangeabilities may be represented by one model parameter (in the case of the Mk model) or more (in the case of other, more complex phylogenetic models).

Prior distribution: A statistical distribution that describes the researcher’s prior beliefs or other outside information about the distribution of a model parameter. This allows the researcher to specify reasonable values for a parameter to take. A weak prior can be easily overcome by the data. A strong prior will require stronger signal in the data to be overcome.

Equilibrium character state frequencies: The frequencies of the character states in the dataset if the evolutionary process is allowed to run infinitely long. In practice, the expected rate of a particular change between two character states is the product of the equilibrium character frequency and the exchangeability.

Q-matrix: A matrix defining the exchangeabilities and equilibrium character frequencies for a model at a given instant in evolutionary time. The Q-Matrix will have a number of rows and columns equal to the number of character states of the data.

Posterior distribution: The posterior distribution is a distribution of plausible values for a parameter or set of parameters given the data and the prior distribution. The posterior distribution is proportional to the model likelihood times the prior distribution.

Markov Chain Monte Carlo: An algorithm by which new values are proposed for model parameters, and evaluated. In this procedure, initial values are scored under a model, then changed. If the changed parameter values improve on the old ones, they are used to seed the next step of estimation.

Brownian motion: A model of morphological change in which the value of a continuous character, X, is expected to change in proportion to an evolutionary rate, σ. σ is expected to be normally distributed, with a variance that increases with time, such that more evolutionary change may be expected with time.

Model selection: A set of statistical approaches designed to determine whether an increase in the number of parameters of a model is justified given its increased ability to model variation in the data. The addition of a parameter that does not increase the explanatory power of the model will not be supported by model selection. The exact degree of increase in explanatory power required to add a parameter will vary by model selection criteria.