Site-selective CO disproportionation mediated by localized surface plasmon resonance excited by electron beam

Abstract

Recent reports of hot-electron-induced dissociation of small molecules, such as hydrogen, demonstrate the potential application of plasmonic nanostructures for harvesting light to initiate catalytic reactions. Theories have assumed that plasmonic catalysis is mediated by the energy transfer from nanoparticles to adsorbed molecules during the dephasing of localized surface plasmon (LSP) modes optically excited on plasmonic nanoparticles. However, LSP-induced chemical processes have not been resolved at a sub-nanoparticle scale to identify the active sites responsible for the energy transfer. Here, we exploit the LSP resonance excited by electron beam on gold nanoparticles to drive CO disproportionation at room temperature in an environmental scanning transmission electron microscope. Using in situ electron energy-loss spectroscopy with a combination of density functional theory and electromagnetic boundary element method calculations, we show at the subparticle level that the active sites on gold nanoparticles are where preferred gas adsorption sites and the locations of maximum LSP electric field amplitude (resonance antinodes) superimpose. Our findings provide insight into plasmonic catalysis and will be valuable in designing plasmonic antennas for low-temperature catalytic processes.

Recently, light-driven localized surface plasmon (LSP) resonances on Au or Al nanoparticles have been shown to dissociate hydrogen molecules at room temperature ^1,2. Moreover, temperature reduction of dehydrogenation and oxidation reactions has also been achieved by visible light excitation of LSP modes on Ag nanocubes³. It has been proposed that such reactions are enabled by harnessing the energized charge carriers generated by LSP resonances and transferring their energy to gas molecules adsorbed on the metal surfaces ^4-6. The variants of optical spectroscopy employed so far to measure LSP-induced reactions lack the spatial resolution to experimentally map the nanoscale distributions of the gas adsorption sites, the intensity distribution of the LSP modes and the actual catalytic reaction sites.

The excitation of LSP modes by light is polarization-sensitive and diffraction-limited at best, precluding control of the light–plasmon coupling at the subparticle level. However, such control—needed to determine the aforementioned spatial information on a single nanoparticle—can be achieved by using a focused electron beam instead of light to excite the LSP resonances. For example, a nanometre-sized electron beam formed in a scanning transmission electron microscope (STEM) is an effective tool to excite LSP resonances with well-defined energies and distribution of modes on metal nanoparticles of a variety of elements (for example, Au, Ag and Al) with different shapes (for example, spheres, rods and prisms)^7-9. However, the use of electron-beam-excited LSP resonance to induce chemical reactions has not been reported so far. Here, using CO disproportionation (2CO _(g) → C _(s) + CO_2(g); known as the Boudouard reaction) as an example, we show that this reaction, which typically takes place between 400 and 600 °C (refs. ^10,11), can be initiated at room temperature by spatially optimized electron beam excitation of LSP resonances on shape-controlled Au nanoparticles, and the solid product (carbon deposits) can serve as markers for the active sites on the nanoparticle surface.

Preferred CO adsorption sites on Au nanoparticles

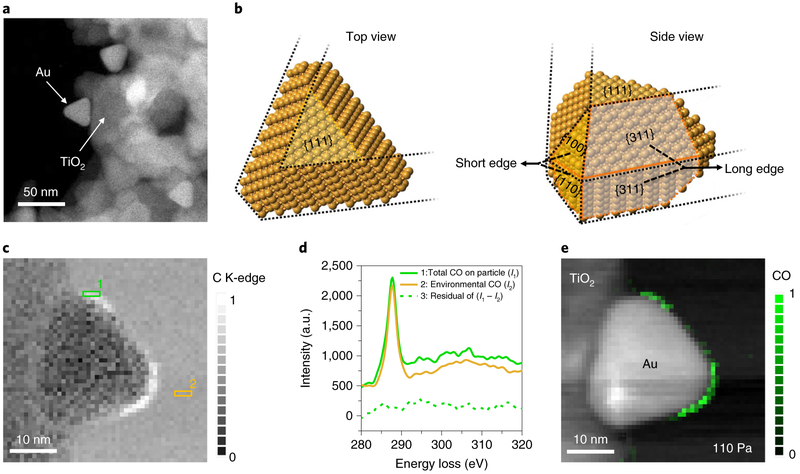
We know that adsorption of gas molecules on a nanoparticle surface results in a reduction in the total free energy of the gas–solid interface, thereby reducing the energy barrier for any given reaction. Therefore, density functional theory (DFT) calculations were used to choose an ideal nanostructure bound by Au surfaces (Supplementary Fig. 1 and Methods) with a variety of thermodynamic favourability for CO adsorption. The calculated reductions in total energy due to CO adsorption on various low-index gold surfaces are provided in Supplementary Table 1. Of the three morphologies of Au nanoparticles commonly synthesized (spheres, rods and triangular prisms), we found that a triangular Au nanoprism is optimal in terms of offering a range of exothermic CO-binding energies, comprising {311} surfaces and {110}/{100} surfaces, which display strong and intermediate adsorption, respectively. We thus synthesized shape-controlled triangular Au nanoprisms (side length ~28 nm) and loaded them onto TiO₂ support particles (~100 nm at the longest dimension). The Au nanoprisms supported on TiO₂ provide a cantilevered configuration, with one side of the triangular outline in close contact with the support and the remainder extending into free space (Fig. 1a and Methods), which allows the Au nanoprisms to be characterized without interference from the substrate. The crystal structure of the Au nanoprisms (Fig. 1b), confirmed by measuring electron diffraction at a series of tilt angles, shows that the plate surface is perpendicular to the Au <111> zone axes (Supplementary Fig. 3). The triangular outlines consist of three short edges and three long edges; the short edges are formed at the junction of the {110}/{100} facets and the long edges are the intersections of the {311}/{311} facets, respectively (Fig. 1b). By choosing particles with the <111> zone axis parallel to the electron beam, the triangular outline including both types of edge can be simultaneously probed.

Fig. 1 ∣. DFT-calculation-based choice of Au nanoprisms supported by TiO₂ particles to realize a variety of local CO adsorption probabilities.

a, STEM annular dark-field (ADF) image of the triangular Au nanoprisms supported on TiO₂. b, Crystal models of a triangular Au nanoprism bound by {111}, {110}, {100} and {311} planes (facets). c, STEM-EELS maps showing increased C K-edge signal at the edge of the Au nanoprism in a CO environment (p_CO = 110 Pa). The contrast, ranging from 0 to 1, represents the normalized C K-edge intensity, integrated from 285 eV to 315 eV. d, EEL spectra from area 1 (green) and area 2 (yellow) in c, corresponding to the total CO at the nanoprism edges (1, green) and the environmental CO (2, yellow), respectively. Both spectra are shifted vertically for clarity and intensity is given in arbitrary units (a.u.). Spectrum 3 (green dashed curve) is the intensity difference between spectra 2 and 1. e, After removing the environmental CO contribution to the C K-edge intensity, the STEM-EELS map is overlaid on an ADF image of the nanoprism showing the location of the adsorbed CO at 110 Pa. The green contrast shows the normalized C K-edge intensity integrated from 285 eV to 315 eV. Note that the particle edge near the lower left corner of the Au nanoprism does not show the CO adsorption because the visibility of the adsorbates at the edges is limited by the line of sight of the electron beam (Supplementary Fig. 4).

The measurements were performed using an environmental STEM (ESTEM), operated at 80 kV, equipped with a monochromated field-emission electron source (0.08 eV energy spread; see Methods) and a sample chamber in which a partial pressure of a gaseous environment such as CO can be achieved¹². In situ core loss (up to atomic-scale spatial resolution) and low-loss (nanometre spatial resolution) electron energy-loss spectroscopy (EELS)¹³ was used to map the CO adsorption sites and the electron-beam-excited LSP mode distribution, respectively. Finally, these two maps were used to detect the reaction product and LSP resonance maxima at specific subparticle locations.

STEM-EELS (core-loss) maps acquired in a CO partial pressure (p_CO) of 110 Pa show that the intensity of the C K-edge at the edges of the Au nanoprism is higher than that of the gas background (Fig. 1c). However, the source of the C K-edge (spectrum 1, Fig. 1d) can also be from the CO in the environment (spectrum 2). Therefore, spectrum 3 (Fig. 1d) was obtained by subtracting the contribution from the environmental CO, and the resultant STEM-EELS map (Fig. 1e) represents the contribution from the adsorbed CO only (see Methods). Interestingly, we found CO adsorption to be confined to the nanoprism edges (Fig. 1e and Supplementary Fig. 4) formed by the junctions of the {311}/{311} and {110}/{100} facets, but not covering either the {311} or {110} planes, which is not entirely surprising as the low coordination numbers for Au atoms at the junctions make them more favourable adsorption sites than the flat surfaces¹⁴.

Electron-beam-excited LSP resonance

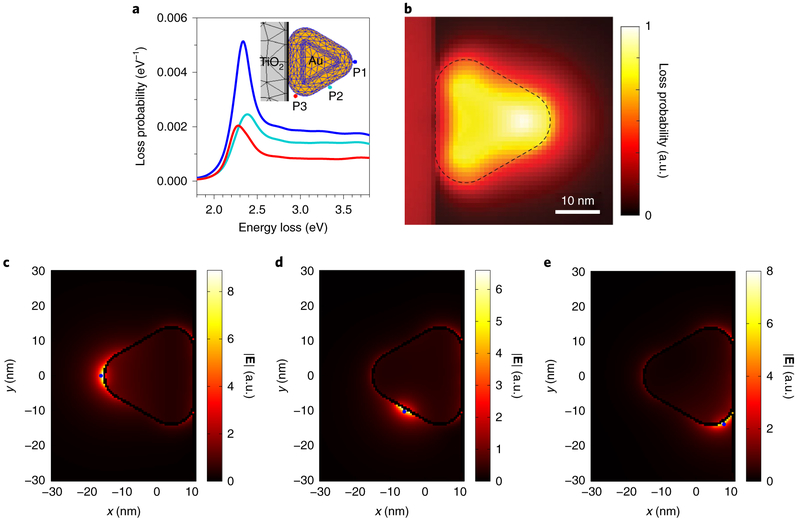
Next, for a given electron beam location, the polarized surface charges on the discretized Au surface were employed to calculate the electron energy-loss probability, induced electric field and photonic local density of states (LDOS) (using the metallic nanoparticle boundary element method, MNPBEM)^15-17 and to determine the possibility of exciting LSP resonances, with an electron beam, on the Au nanoparticle (see Methods and Supplementary Fig. 5). The surface charges oscillate at a range of plasmon resonant frequencies, represented by peaks in the energy-loss spectra, and presumably correlate with the spatial distribution of a specific mode (Supplementary Fig. 5b-d). Therefore, we simulated the electron energy-loss probability spectra (Fig. 2a,b) and induced electric field (Fig. 2c-e and Supplementary Fig. 6) at three characteristic locations with the electron beam offset by 1 nm from the nanoprism surface (mimicking aloof mode excitation¹⁸) and centred on a short edge (P1), a long edge (P2) and short edge near TiO₂ (P3). Similar simulations were also performed by replacing TiO₂ with SiO₂ as the support material (Supplementary Section III). With the electron beam positioned at each location in the case of TiO₂, excitation of the LSP resonance is represented by a distinct electron energy-loss peak located between 1.8 eV and 2.8 eV (Fig. 2a). This resonance mode is most efficiently excited at P1, with a peak energy-loss centred at 2.3371 ± 0.0002 eV (the error represents the single standard deviation of peak fitting). In contrast, excitations at P2 and P3 provide substantially lower coupling efficiencies to this mode, evidenced by energy-loss probabilities reduced by factors of 0.34 and 0.46, respectively, along with peak spectral positions shifted to 2.3872 ± 0.0002 eV and 2.2830 ± 0.0006 eV, respectively—still located within the energy-loss range of the resonance mode measured at P1. The blueshift at P2 may be due to the increased contribution from the hexapole modes¹⁹, whereas the redshift at P3 is caused by the different dielectric property in the vicinity of the TiO₂ support²⁰. The LSP electric field amplitude distributions simulated using the electron beam locations at P1, P2 and P3 as well as the correlated resonance energies (2.3371 eV for P1, 2.3872 eV for P2 and 2.2830 eV for P3) display an enhanced electric field at all three nanoprism corners as well as in the vicinity of each electron beam location (Fig. 2c-e). The spatial relationship between the loss probability (Supplementary Fig. 9) and the LSP electric field (Fig. 2c-e and Supplementary Fig. 6) can be linked through the excited LDOS at the resonance energies near the Au surface (Supplementary Figs. 7 and 8). Overall, the strongest LSP electric field occurs at the cantilevered nanoprism corner (Fig. 2c) when the electron beam excitation is positioned at P1. For Au on TiO₂, the sum of simulated loss probability maps for the energy-loss range from 1.8 eV to 3.8 eV shows that the excitation locations—leading to strong coupling between the electron beam and the Au nanoprism—are at the cantilevered corner and several nanometres beyond in the vacuum (Fig. 2b; see the comparison to SiO₂ in Supplementary Fig. 10). Therefore, the most efficient location for the electron beam to excite the LSP mode (approximately 2.337 eV) and the LSP electric field on the Au nanoprism on TiO₂ is near the cantilevered short edge.

Fig. 2 ∣. Simulated electron-energy loss probability and induced electric field originating from electron-beam-excited LSP resonance on a Au nanoprism on TiO₂ in a cantilevered configuration.

a, Simulated electron energy-loss probability spectra of the LSP resonance of a cantilevered Au nanoprism on a TiO₂ particle associated with the aloof excitation locations marked in the inset. b, Map obtained by summing the simulated loss probability (in the range between 1.8 eV and 3.8 eV, with 0.01 eV resolution), showing the highest loss probability near the cantilevered short edge, either on or off the particle. The contrast represents the normalized loss probability from 0 to 1 (the maximum value observed). The dashed outline indicates the Au nanoprism edges. c–e, The LSP electric field amplitude simulated using the electron beam locations as marked (blue points) at P1 (c), P2 (d) and P3 (e) as well as the correlated resonance energies, indicating that the maximum LSP electric field amplitude (resonance antinode) is located near the cantilevered nanoprism corner when excited by the electron beam at P1.

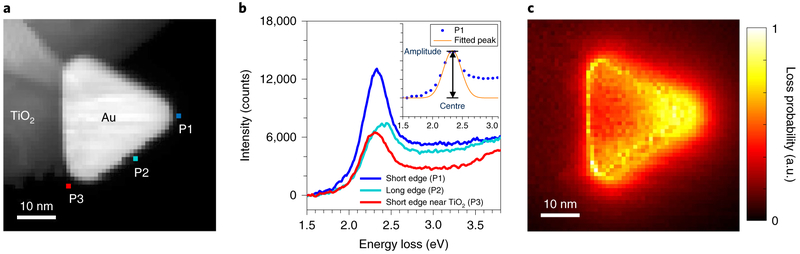
To check the LSP resonance predictions of the simulations, a Au nanoprism was probed in the ESTEM vacuum (~10⁻⁶ Pa) using low-loss EELS at the three characteristic locations (Fig. 3a). We found that the respective spectra (Fig. 3b) and peak centres (P1: 2.332 ± 0.001 eV, P2: 2.412 ± 0.003 eV, P3: 2.308 ± 0.002 eV) match the simulated results closely (Fig. 2a), confirming the excitation of the LSP mode on the particle using an aloof electron beam. The EELS intensity map of the same Au nanoprism for the energy-loss range from 1.8 eV to 3.8 eV (Fig. 3c) shows experimentally that the electron beam can be most efficiently coupled with the LSP modes on the Au nanoprism by placing the electron beam at the cantilevered corner and several nanometres beyond in the vacuum. It is important to note that the spatial resolution of STEM-EELS maps is at the atomic scale for core-loss maps but at the nanometre scale for low-loss maps as the EELS spatial resolution is an inverse function of energy lost by electrons¹³.

Fig. 3 ∣. EELS measurements of electron-beam-excited LSP resonance on a Au nanoprism on TiO₂ in a cantilevered configuration.

a, STEM-ADF image of a triangular Au nanoprism on a TiO₂ particle. b, Experimental EELS spectra acquired using the electron beam locations marked in a: near the short edge (P1), the long edge (P2) and the short edge near TiO₂ (P3). The centre (energy) and amplitude (intensity) of the LSP resonance peak are derived by fitting a Gaussian profile (see inset). c, Experimental EELS intensity map of the same Au nanoprism in a for the energy-loss range from 1.8 eV to 3.8 eV, confirming that the optimal electron beam location to excite LSP modes is at the cantilevered corner and several nanometres beyond in the vacuum. The EELS intensity is normalized to the zero-loss peak intensity to enhance the attenuated signal within the bulk of Au due to scattering and is therefore given in arbitrary units.

Response of LSP resonance to CO adsorption

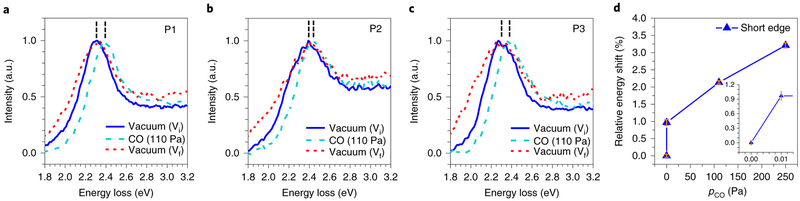
We then explored the effect of CO adsorption at the Au edges on the electron-beam-excited LSP mode. In the CO environment (p_CO = 110 Pa), the typical LSP resonance peaks at P1, P2 and P3 blue-shifted by 0.087 ± 0.002 eV, 0.040 ± 0.002 eV and 0.078 ± 0.002 eV, respectively, but returned to the original energies after CO evacuation (V_f) (Fig. 4a-c), indicating that the electron density of the Au nanoprism was increased by electron transfer from the adsorbed CO molecules (Fig. 1e) to the Au surface²¹, resulting in the observed energy shifts that disappeared upon CO desorption. The energy shifts measured at P1 for a typical Au nanoprism on TiO₂ at various p_CO (0, 0.01, 110 and 250 Pa) changed asymptotically with increasing p_CO (Fig. 4d). The percentage of energy shift with respect to the original LSP energy in vacuum was ~0.97% at 0.01 Pa and increased to ~3.21% with increasing p_CO, suggesting that most of the adsorption sites on Au edges were saturated at a p_CO of 0.01 Pa and further CO adsorption increased at a lower rate with increasing p_CO.

Fig. 4 ∣. Effect of CO adsorption on LSP resonance energy.

a–c, The resonance energy of the same Au nanoprism as shown in Fig. 3a, measured by EELS at P1 (a), P2 (b) and P3 (c) in vacuum (V_i, blue solid line), CO (p_CO = 110 Pa, turquoise dash-dotted line) and after CO evacuation (V_f, red short-dashed line), displaying the blueshifts of LSP resonance in the presence of CO by 0.087±0.002 eV, 0.040±0.002 eV and 0.078±0.002 eV, respectively, and the recovery to the original energies. d, Relative energy shifts of LSP resonance, ΔE (%) = (E_LSP(P_CO)–E_LSP,0)/E_LSP,0×100%, measured by EELS at P1 as a function of p_CO, show ΔE increases with increasing p_CO. Inset, ΔE at V_i and p_CO = 0.01 Pa, respectively. Error bars indicate single standard deviation uncertainties of determining the LSP resonance energy by peak fitting.

CO disproportionation mediated by LSP resonance

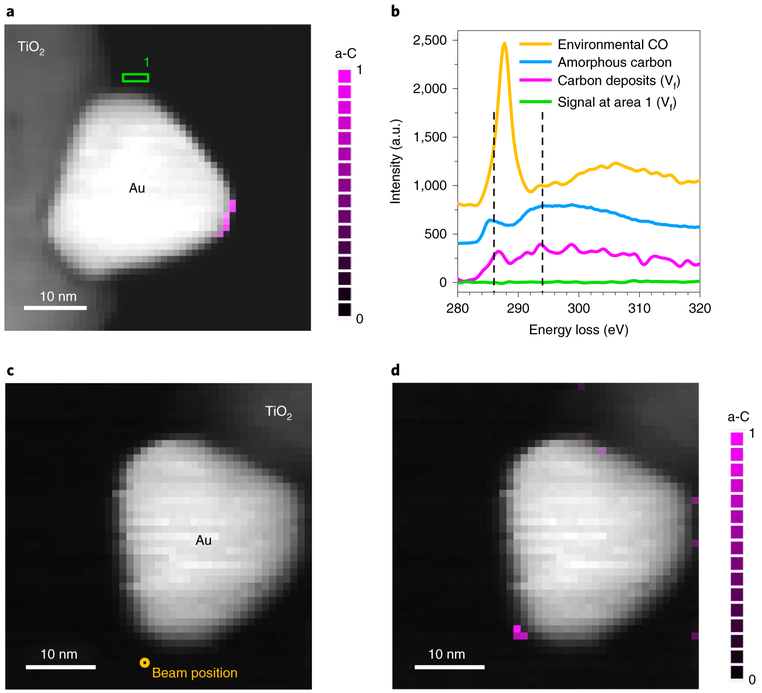
Finally, we scanned the electron beam across the same nanoprism as in Fig. 1e in STEM mode for a total time of ~26 min (0.64 s per pixel; see Methods) in a CO environment (p_CO = 110 Pa). A core-loss STEM-EELS map obtained after CO evacuation (V_f) revealed carbon deposits at the short edge (Fig. 5a), whereas the LSP resonance energies returned to the original values, indicating no adsorbed CO was left. The reported onset of the C K-edge and its near-edge fine structure are different for CO, CO₂, CO₃²⁻, amorphous carbon, graphite and diamond (Supplementary Fig. 11)^22,23. It is clear from Fig. 5b that the detected C K-edge in V_f (magenta) is distinct from that in environmental CO (yellow). We can attribute the observed signal to amorphous carbon by comparing the near-edge fine structure (magenta, Fig. 5b) of the carbon deposits at 286 eV and 294 eV to that of a typical amorphous carbon spectrum (blue). Moreover, the absence of the C K-edge in the spectrum (green, Fig. 5b) acquired from area 1 in Fig. 5a (identical to Fig. 1c) indicates that CO adsorption sites are not the only criteria for LSP-induced CO disproportionation to take place. It is also important to note that carbon deposits did not occur during STEM image and EELS acquisitions in vacuum, eliminating the possibility of contamination from residuals. Next, we deliberately excited the LSP mode in a CO environment (p_CO = 110 Pa) for 52 min by placing the electron beam at an aloof position with respect to a fresh Au nanoprism (near P1), to avoid any direct impact of the electron beam on the nanoparticle (Fig. 5c), instead of raster scans. A core-loss EELS map (Fig. 5d) acquired after CO evacuation (V_f) shows the deposited amorphous carbon exclusively at the edge of the cantilevered particle corner, which provides direct evidence that CO disproportionation (1) is initiated by electron-beam-excited LSP resonance and (2) occurred only where the LSP electric field amplitude maxima overlapped with preferred CO adsorption sites. Additionally, we found that the scanning electron beam, during CO exposure, does not result in carbon deposits at p_CO = 0.01 Pa (Supplementary Fig. 12a). Amorphous carbon deposits occur at the cantilevered particle corner only for p_CO above 40 Pa, and the amount increases with increasing p_CO (Supplementary Fig. 12b,c).

Fig. 5 ∣. CO disproportionation reaction driven by electron-beam-excited LSP resonance.

a, STEM-EELS map of Au/TiO₂ afteracquired after CO evacuation (V_f) showing the C K-edge signal (285-315 eV) (magenta), following raster scans of the electron beam (beam current of ~0.5 nA) across the entire area in the CO environment (p_CO = 110 Pa). b, The detected C K-edge signal (magenta in a) using EELS has the fine structures corresponding to amorphous carbon (a-C) (blue, measured from amorphous carbon film coated on a TEM grid) at 286 and 294 eV, which are distinct from environmental CO (yellow). The spectrum in green, acquired from area 1 in a after CO evacuation (V_f), shows no trace of C K-edge. c, Experiments were also performed by positioning the electron beam ~3 nm away from the cantilevered corner of a different Au nanoprism in CO (p_CO = 110 Pa), marked by the yellow circle. d, Carbon deposits were observed near the cantilevered nanoprism corner in a STEM-EELS map after CO evacuation (V_f). Note that a-C indicates amorphous carbon in a and d.

Determination of reaction location

Researchers so far have reported that CO disproportionation can be catalysed at temperatures above 400 °C (refs. ^10,11), but the size of the Au nanoprisms used here, ~28 nm in length at each side of the triangle, is exceptionally large compared to the commonly used Au catalyst nanoparticles²⁴. While our DFT calculations indicate that the favourable CO binding energy at preferential adsorption sites can potentially lower the reaction energy barrier for CO disproportionation that is comparable to the LSP resonance energy (Supplementary Table 2), the location of amorphous carbon deposits is found to be localized to the cantilevered short edge that represents the maximum LSP electric field amplitude, and not over the entire experimentally observed CO adsorption sites (Fig. 1e). This indicates that the maximum plasmonic field is an important parameter for initiating the CO disproportionation reaction, confirming that the gas adsorption and local field enhancement are both criteria necessary for the LSP-resonance-induced reactions to proceed. Similar conclusions have been reported for charge transfer to adsorbed molecules resulting from the decay of optically excited LSP modes at the macroscale, as characterized by surface-enhanced Raman spectroscopy ^25,26. Pt-coated Ag or Au nanocubes have also been used to characterize charge transfer from plasmonic nanoparticles to the surface to initiate LSP-resonance-induced chemical reactions ^27,28. Although our experimental results cannot reveal the charge-transfer mechanism (hot electron transfer or chemical interface damping) from the Au nanoprism to the adsorbed CO molecules ^29-32, we clearly show that the ideal plasmonic nanostructure design for surface-plasmon-assisted chemical reactions is essential to provide the superimposed locations of local field enhancement and gas adsorption sites to harvest the LSP resonance energy, especially for antenna-based plasmonic catalyst systems³³.

In conclusion, we have engineered plasmonic nanostructures that provide sites for both gas adsorption and local field enhancement of the LSP resonance, enabling the direct transfer of energy to reactants at gas–solid interfaces to initiate chemical reactions at room temperature. Moreover, we provide the methodology to measure both gas adsorption sites and spatial distributions of LSP energy and intensity at the sub-nanoparticle scale. The use of CO disproportionation initiated by electron-beam-excited LSP resonance successfully labels the active sites on Au edges with the carbon product. Our findings will assist in the development of antenna-based plasmonic catalysts that may reduce energy consumption by harnessing solar radiation for large-scale chemical processes.

Online content

Any methods, additional references, Nature Research reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41563-019-0342-3.

Methods

DFT calculations for CO adsorption and disproportionation on Au surfaces.

Our calculations are based on the generalized Kohn–Sham scheme as implemented in Quantum-ESPRESSO³⁴, utilizing the exchange-correlation functional described by the Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA)³⁵ and the interaction between core electrons and valence electrons by the frozen-core projector-augmented wave (PAW) method³⁶. The Au {100}, {110}, {111} and {311} surface calculations were performed with 2 nm spacing in the Z direction (Supplementary Fig. 1) and 24, 20, 16 and 20 atom supercells, respectively. Testing of 2, 3, 4, 5 and 6 nm spacing showed no differences for any of the surface planes. The results are shown in Supplementary Table 1. During relaxation with a plane-wave basis set cutoff of 60 eV and a 10 × 10 × 1 Monkhorst–Pack k-point set, all atoms in the supercells were allowed to move until the force on each atom was less than 0.26 eV nm⁻¹. Based on experimental data and previous theoretical studies³⁷ on Fe, the CO molecules were initially placed on top of Au surface atoms, establishing the optimized structure with an upright orientation (Supplementary Fig. 2, and the delta self-consistent fields were calculated using the energy of CO, C, O and CO₂ in the same unit cell box as the respective surfaces. The results are shown in Supplementary Table 2.

Au nanoparticle synthesis.

Shape-controlled Au nanoparticles were synthesized using Au seeds, cetyltrimethylammonium bromide (CTAB), gold(III) chloride trihydrate (HAuCl₄·3H₂O) and ascorbic acid (AA) in ultrapure de-ionized water, based on a procedure modified from a previously described technique³⁸. Au seeds were prepared by reducing HAuCl₄·3H₂O using sodium borohydride (NaBH₄ in the presence of CTAB solution. The growth of Au nanoparticles was initiated by the addition of Au seeds and AA to a mixture of HAuCl₄ and CTAB solution in a water bath at 30 °C so that the final solution contained Au seeds, CTAB, Au³⁺ and AA in a molar ratio of 1:128,000:1,600:48,000. The mixed solutions of Au seeds, capping ligand (CTAB), Au precursors (Au³⁺) and reducing agent (AA) led to the seeded growth of triangular Au nanoprisms. Following a washing procedure that included centrifugation and redispersing of the nanoparticles, the Au nanoprisms were suspended in ultrapure deionized water. TiO₂ particles were then added and mixed well with the suspension to make the Au/TiO₂ suspension.

Simulations of LSP resonances excited by an electron beam.

LSP resonances of triangular Au nanoprisms with one side anchored to a TiO₂ (or SiO₂) support particle to form a cantilevered configuration were simulated using the MNPBEM toolbox³⁹. The boundary element method (BEM) approach is designed to solve Maxwell’s equations in a dielectric environment where substances with homogeneous and isotropic dielectric functions are divided by discretized interfaces. In this work, we use this approach to simulate (1) electron energy-loss probability and (2) the distribution of surface charges on the discretized interfaces with respect to the electron beam (excitation) locations (Supplementary Fig. 5). The simulated results match the EELS measurement of LSP resonances and shed light on the oscillation of surface charges induced by electron beam.

ESTEM measurements.

The Au nanoprisms on TiO₂ samples were loaded onto a lacey carbon TEM grid and inserted in an ESTEM operated at 80 kV. A monochromated electron beam with energy resolution of 0.08 eV was used to excite LSP resonance, imaging and EELS. The microscope was operated in STEM mode with a beam diameter of ~1 nm and a beam current of ~0.05 nA to excite LSP resonances and to perform EELS in either vacuum or a CO environment by scanning the electron beam across a region of interest or alternatively positioning it at a specific location. A region of interest that included a chosen Au nanoprism supported by a TiO₂ particle was divided into pixels (1 nm × 1 nm) to define the beam location during a raster scan. EELS was acquired using a spectrometer with a spectral dispersion of 0.01 eV per channel for low-loss EELS and 0.25 eV per channel for core-loss EELS, respectively. During EELS acquisition, a convergence semi-angle of ~7.8 mrad was used, while the collection semi-angle was set at 15.2 mrad. Spectrum images acquired in these conditions comprised a three-dimensional data cube that included energy-loss information in the Z direction at each pixel of a STEM-ADF image. A STEM-EELS map of the C K-edge could be obtained by properly choosing a pre-edge window to extrapolate the power-law background underneath the C K-edge and subtracting the background from a signal window that spanned the energy range of the C K-edge at each pixel of the spectrum image. To investigate the spatial distribution of (1) environmental CO, (2) adsorbed CO molecules and (3) amorphous carbon (the product of the CO disproportionation reaction) in a STEM-EELS map of the C K-edge, it was essential to remove the spectral features associated with environmental CO at each pixel as it filled up the volume near the sample area uniformly, and its spectral features were identical from pixel to pixel. An environmental CO spectrum image was extracted from a square area where only environmental CO was present in the original STEM-EELS map (Fig. 1c). The extracted spectrum image was then rescaled into the same dimensions as the original STEM-EELS map to obtain the uniform environmental CO spectrum image. This was then subtracted from the original spectrum image so that the spectral features of the environmental CO at each pixel were removed. The EELS map of the C K-edge (Fig. 1e) were generated from the processed STEM-EELS map using one power-law background window and one signal window.

Data availability

All relevant data are available from the corresponding author upon request.