Quantile regression for survival data in modern cancer research: expanding statistical tools for precision medicine

Abstract

Quantile regression links the whole distribution of an outcome to the covariates of interest and has become an important alternative to commonly used regression models. However, the presence of censored data such as survival time, often the main endpoint in cancer studies, has hampered the use of quantile regression techniques because of the incompleteness of data. With the advent of the precision medicine era and availability of high throughput data, quantile regression with high-dimensional predictors has attracted much attention and provided added insight compared to traditional regression approaches. This paper provides a practical guide for using quantile regression for right censored outcome data with covariates of low- or high-dimensionality. We frame our discussion using a dataset from the Boston Lung Cancer Survivor Cohort, a hospital-based prospective cohort study, with the goals of broadening the scope of cancer research, maximizing the utility of collected data, and offering useful statistical alternatives. We use quantile regression to identify clinical and molecular predictors, for example CpG methylation sites, associated with high-risk lung cancer patients, for example those with short survival.

Introduction

In cancer research, the main objective is often to estimate and infer the relationship between censored outcomes, say, time to cancer death (denoted by T), and various independent variables, for example gender, age, cancer stage, smoking status, and molecular biomarkers. Cox proportional hazards models, which link the hazard (the instantaneous rate of failure) to independent variables, have long been a standard tool for analyzing censored outcome data. However, the proportional hazards assumption may not often hold and, moreover, some practitioners find the concept of hazard difficult to understand. Accelerated failure time (AFT) models, which directly link T (or log(T)) to independent variables, have become a useful alternative because of the straightforward interpretation with survival time. The emergence of precision medicine has realigned our attention to use patients’ demographic, behavioral, and genetic data to identify individuals at the highest risk for disease and to design therapeutic strategies for specific patient subpopulations,^1–3 in which case the focus is typically placed on the relationship between severe cases (e.g. those with shorter survival times) and risk factors.^4,5 For most studies, the analytical tools are either Cox or AFT models, but both models face many challenges. For example, AFT models assume that risk factors possess homogeneous effects on every sample by linking them to the average survival time.⁶ Although Cox models offer more flexibility, they are somewhat restricted because the proportional hazards assumption does not allow the sign of a covariate to vary between the high-risk subpopulation (those with shorter survival time) and the low-risk subpopulation (those with longer survival time). For example, increased radiation dose may prolong survival among men with high-risk prostate cancer, but not those at low risk.⁷ Identifying the heterogeneous effects of a treatment and maximizing its effectiveness on a subgroup has been a focal point of precision medicine. For this purpose, it is necessary to go beyond the realm of traditional methods that may have difficulty modeling the heterogeneous effects of predictors.

Quantile regression, since its inception in 1978, has emerged as a powerful and natural approach to model the heterogeneous effects of predictors for a non-homogeneous population.⁸ In contrast with the mean-based and hazard-based models, quantile regression models the quantile of survival time and links it to the covariates. Compared to the popular Cox models, quantile regression relaxes the proportional hazards assumption and links the whole distribution of an outcome to the covariates of interest. It may offer extra flexibility by more fully using data and thus provide more complete information related to covariate-outcome relationships. Such models will be particularly useful for exploring the heterogeneity in the effects of risk factors in the Boston Lung Cancer Study Cohort (BLCSC) study, a hospital-based cancer epidemiology cohort established in 1992 by Dr. Christiani (author).

The BLCSC collects rich demographic, clinical, and genetic information from lung cancer cases, including smoking and pathology information along with CT images, whole-genome microarray, mRNA expression, DNA genotype, and methylation data. The role of epigenetics in cancer initiation and progression has stimulated much interest and Cox regression models have been the main statistical tool used for analysis.^9–12 As lung cancer is characterized by molecular heterogeneity, recent insights have pinpointed the functional roles of aberrant DNA methylation in the disease progression.^13–15 An intriguing question is whether and how each DNA methylation site might play a different role among the high-risk (e.g. lower quantiles of overall survival) and low-risk (e.g. higher quantiles of overall survival) cancer survivors. In particular, it has been conjectured that the difference in histologic patterns of lung cancer may be associated with the heterogeneity in causal factors for the high- and low-risk populations.^16,17 Addressing this question using lung cancer survivors may lead to improved risk stratifications of lung cancer with epigenetic biomarkers. Quantile regression could be a natural choice as it helps decipher the various roles each methylation site plays on different quantile levels of survival.

Recent years have witnessed a steady increase in use of quantile regression in cancer research. A PubMed search returned 103 publications on applications of quantile regression related to cancer research from 2014 to 2018. For example, Faradmal et al.¹⁸ showed that changes in the age at diagnosis, number of involved lymph nodes, and tumor size could significantly change the median and some other quantiles of overall survival. Meanwhile, Xu et al.¹⁹ developed a G-E interaction identification approach using the quantile regression technique, as most of the existing G-E interaction approaches for prognosis data cannot accommodate long-tailed or contaminated outcomes.

Many methods have been developed for quantile regression for complete data without censoring.^20–22 When data are subject to censoring, statistical estimation and inference for quantile regression have become more involved. Using a dataset from the BLCSC, this paper provides a practical guide to using quantile regression to analyze survival data in cancer research. We are very cognizant of the existence of an overview of quantile regression by Koenker,²³ as well as several excellent tutorial papers with various contexts, such as child health,²⁴ ecology,²⁵ health services research,²⁶ and labor market analysis.²⁷ This paper introduces the use of quantile regression for censored outcome data from the perspective of precision medicine, with the ultimate goal of broadening the scope of research, maximizing the utility of collected data, and offering additional statistical insight. As the most commonly encountered censoring type in cancer studies is right censoring (e.g. in a cancer trial, a patient drops out or survives the whole study period and thus the exact death time is unobserved), this paper focuses mainly on right censoring cases.

Censored quantile regression with low-dimensional features

We begin by introducing the concept of quantiles, followed by censored quantile regression. For any τ that is between 0 and 1, the τ-quantile is a value at or below which a τ-fraction of the data lies. When τ is 0.5, the 0.5 quantile is called the median, which cuts a distribution into two equal areas. When the quantile is defined based on the distribution of T alone, without considering covariates, X, it is called the marginal quantile or unconditional quantile. When we consider the quantile of T [or log(T)] within subgroups defined by X, for example, we refer to the τ-th conditional quantile of T given X, denoted by Q_T|X(τ|X). A quantile regression describes how the covariate or covariate vector of interest impacts the conditional quantiles of the outcome. Often, a linear functional form is assumed with

$$Q_{T|X}(\tau |X)=X^{\text{'}}\mathit{\beta }\left(\tau \right)$$ (1)

where β(τ) refers to the effect of X on the τ-th quantile. Model (1) allows the covariate effect to change with τ, adding more flexibility. Going beyond linear or more broadly, parametric models, one can also non-parametrically estimate the relationship between the conditional quantiles and covariates.²⁸ This approach is computationally intensive, and the estimates typically have large variations when the number of covariates is moderate, or the sample size is not large.²⁹

In reality, T is not always observable because of loss of follow-up or the termination of the study. In a right censoring situation, Y = min (T, C) and ∆ = I (T ≤ C), the censoring indicator, are observed, where C is the potential censoring time. Ignoring censoring and directly fitting Y using quantile regression for complete data will lead to a biased estimate of β(τ). To deal with censoring, several authors have introduced censored quantile regression approaches. For example, Portnoy²⁹ proposed reweighting of the censored observations using a scheme similar to the redistribution-of-mass idea³⁰ for the Kaplan-Meier estimator, and Peng and Huang³¹ proposed a class of martingale-based estimating equations, which involve minimization of a convex objective function.

These two methods have been implemented using various statistical software packages including quantreg in R and PROC QUANTLIFE in SAS. By specifying various values of τ between 0 and 1, we can obtain distinct sets of estimated quantile regression coefficients and also predict the conditional quantiles of outcomes based on the given covariates. For the readers’ convenience, we provide sample commands in R and SAS in the Appendix for analyzing our data.

Taking τ to be close to 0 or 1, quantile regression can address whether the different quantiles of the survival time (lower or upper quantiles of survival time within each group) differ across the male and female groups, giving more insight than an AFT model that stipulates the same gender effect across all quantiles. For example, if we use X to code gender (1 = male and 0 = female) and set τ = 0.2 or 0.5, then β(0.2) and β(0.5) address how much the 0.2 quantile of survival and the median survival time differ across the male and female groups. More specifically, based on the patients (n = 153) from the Boston Lung Cancer Survivor Cohort, β(0.2) and β(0.5) can be estimated to be −0.67 and −0.69. Because we use X = 1 for the male group and 0 for the female group, the negative signs of the coefficient estimates indicate that the male group had shorter 0.2 and 0.5 quantiles of survival than the female group. Indeed, the Kaplan-Meier estimates of the 0.2 and 0.5 quantiles were 1.67 and 6.08 for male, and 2.34 and 6.77 for female, respectively.

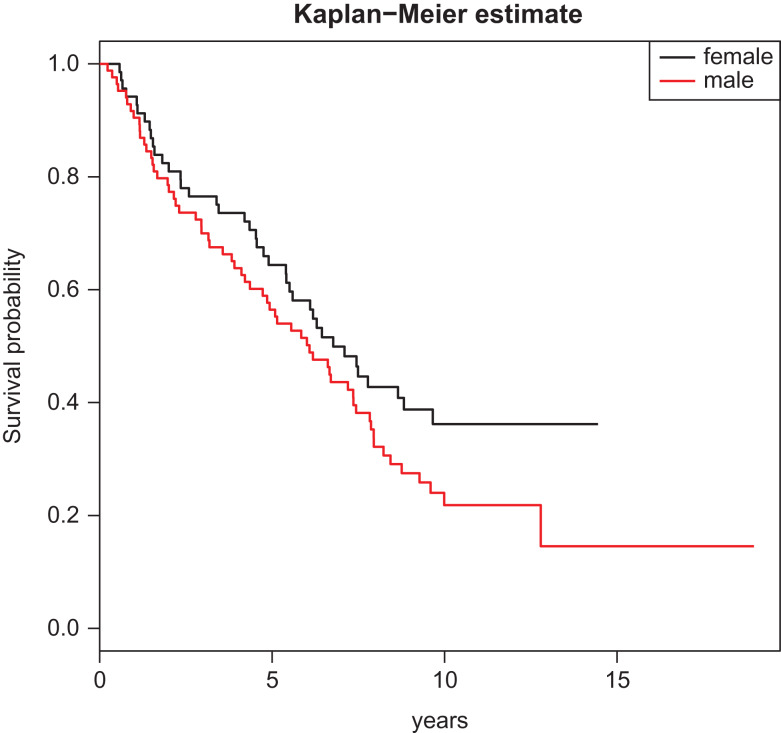
Conceptually, one can consider conditional quantile estimates for any τ between 0 and 1. In the presence of censoring, however, some regression quantiles for censored outcomes may not be estimable and the upper bound of the estimable quantile level is close to the point where the curve becomes a plateau; see Fig. 1 and more detailed discussion later. Standard errors and confidence limits for the quantile regression coefficient estimates can be obtained with bootstrapping methods, which are available in the output of R and SAS.

Figure 1.

Kaplan-Meier estimates for male and female.

We demonstrate the use of quantile regression using the BLCSC study. We considered 153 patients with complete methylation data (which will be modeled in the next section) from BLCSC, of whom 55% were male, 68% had stage 1 cancer, and 32% had stage 2 or above.

Among these patients, the mean age was 68 ± 9.9 years. The average follow-up was 8.15 years, and during the follow-up, 101 deaths were observed and 34% were censored. The majority of the patients were adenocarcinoma patients, as a total of 64% patients were lung adenocarcinoma cases, and the other 36% were squamous cell carcinoma or other subtypes of lung cancer. Smoking intensity was measured for each patient as lifetime pack-years at diagnosis and the average pack-years was 53.4 ± 43.8. Using age (in years), gender (0: female; 1: male), pack-years, cancer type (0: adenocarcinoma; 1: non-adenocarcinoma), and cancer stage (0: stage = 1; 1: stage > 1) as predictors for the lung cancer patients’ overall survival, we considered a quantile regression model that links the conditional quantile of overall survival, often an endpoint of major interest, to these predictors. In Fig. 1, the survival curve levels off around the 0.65 quantile for the female group. This means that the conditional quantile in the female group at any level higher than 0.65 would be estimated to be infinity. Therefore, we focused on the quantile levels of 0.2 and 0.5, where the 0.2 quantile represents the time for early deaths while the 0.5 quantile corresponds to the median survival, although one can choose different levels of interest as long as they do not exceed 0.65.

Table 1 documents the modeling results, which are worth discussing. First, compared with the more advanced stage (stage > 1) patients, the early stage patients’ (stage = 1) 0.2 and 0.5 quantiles of overall survival were 2.56 and 5.64 years longer, both of which were significant. This reveals that cancer stage played an important role in both quantiles. In addition, compared to the adenocarcinoma cases, non-adenocarcinoma cases had 0.73 fewer years in the 0.2 quantile, but 0.86 more years in the median survival. Even though the numbers were not statistically significant, the opposite signs of the coefficients at these two quantiles might hint that the effects of the cancer subtype are heterogeneous. At the quantile level of 0.5, the effect of age was highly significant and a 1 year increase in age was associated with 0.23 years loss in median survival. On the other hand, the effect of age was not significant for the 0.2 quantile, indicating that age may have heterogeneous effects on survival.

Table 1.

Point estimates and CI (in parentheses) for censored quantile regression with demographic and clinical factors from the Boston Lung Cancer Survivor Cohort (BLCSC).

	τ = 0.2		τ =0.5
(Intercept)	12.35	(8.67, 18.15)	32.48	(14.97, 47.72)
age	−0.07	(−0.14, −0.01)	−0.23	(−0.52, −0.07)
sex	−0.32	(−2.47, 1.53)	−1.05	(−3.74, 2.07)
packyrs	−0.00	(−0.02, 0.01)	−0.03	(−0.05, −0.01)
cstage: stage > 1 vs. stage=1	−2.56	(−4.32, −1.13)	−5.64	(−7.57, −3.67)
ctype: non-adeno vs. adeno	−0.73	(−2.60, 0.99)	0.86	(−0.97, 4.90)

Similarly, at the quantile level of 0.5, the effect of smoking intensity was highly significant and a one unit increase in pack-years resulted in 0.03 years loss in the median survival. On the other hand, the effect of smoking intensity was not significant for the 0.2 quantile, indicating that smoking intensity may have heterogeneous effects on survival, which could not be detected by the Cox model.

As the conditional quantiles under a Cox model are not linear in covariates, the coefficients from the Cox model are not directly comparable with their counterparts from a censored quantile regression model.²⁹ Nevertheless, a local quantile measure of the effects of covariates in a Cox model on conditional quantiles was proposed by Koenker and Geling³² and Portnoy,²⁹ which can be compared with the coefficients from censored quantile regression.

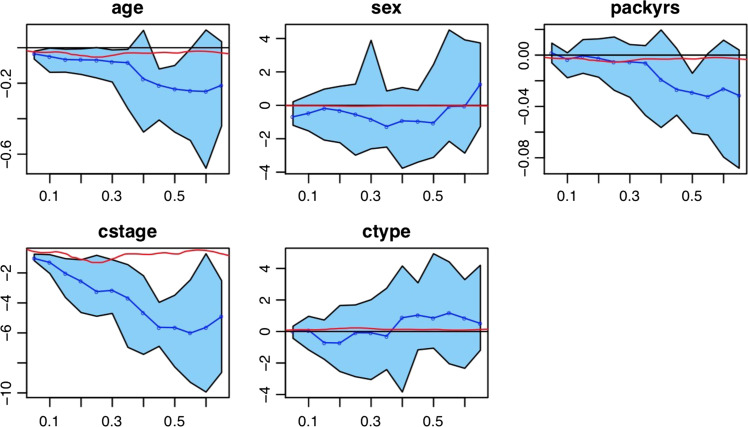
Figure 2 further illustrates the differences in censored quantile regression and Cox models by comparing the estimates of β(τ) (in blue) and the local quantile measure (in red) for τ ∈ (0.05, 0.10, . . . , 0.60, 0.65). Here, the estimated quantile measure for each covariate was computed using Eq. (9) of Portnoy,²⁹ and the light blue shaded regions represented 95% pointwise confidence interval (CI) for the estimated β(τ). For all the covariates, the estimates of β(τ) (in blue) were largely in disagreement with the local quantile measure as suggested by the plots. The flexibility offered by quantile regression may lead to more granular analysis of the data.

Figure 2.

Results of censored quantile regression with point estimates (blue curves) and 95% CI (lighter blue shaded regions); the red lines are the estimated local quantile measures for the Cox proportional hazards model.

Censored quantile regression with high-dimensional features

Modern cancer studies have generated massive data with high-dimensional biomarkers such as gene expressions, SNPs, methylation, and next-generation RNA sequencing. Identifying molecular biomarkers that are associated with survival of cancer patients is key to understanding disease progression processes and designing more effective cancer treatments. Selecting informative biomarkers for cancer survival from high-dimensional molecular data is challenging because quantile regression, along with classical regression such as Cox and AFT, was designed to be applicable only in low-dimensional settings, where the number of predictors is much less than the sample size. Variable screening is often needed to select informative predictors, often 10 or 20, out of thousands or millions of predictors, before feeding the selected variables into a regression model to reach a final predictive model. See Hong and Li³³ for a review of variable screening techniques in the context of high-dimensional censored data analysis.

Although some biomarkers may not be important for the median survival time, they may be highly associated with the lower tail of the survival time distribution, representing the subpopulation with poor survival. In this case, applying the screening approaches that were designed for mean-based regression models would not help identify predictors with the heterogeneous effects. Quantile regression approaches may help detect biomarkers that are associated with the low- or high-risk groups. For this purpose, He et al.³⁴ proposed the quantile adaptive sure independence screening (QA). The algorithm can be implemented in the following simplified steps.

Step 1. For a τ, compute a ranking statistic, such as in He et al.,³⁴ for each biomarker (e.g. methylation site). The magnitude of the statistic represents the level of importance of that biomarker.

Step 2. Rank the biomarkers based on their statistics and choose the top ranked biomarkers, often 10 or 20.

Step 3. Repeat Steps 1 and 2 for all τ of interest.

Many studies demonstrate that methylation can be used as a biomarker to improve risk stratification of cancer patients. For example,³⁵ developed a model to predict survival in clear cell renal cell carcinoma (ccRCC) based on five CpG methylation profiling. The BLCSC, with methylation data available on 442 613 sites, provides a unique opportunity to conduct methylation profiling by applying QA to identify methylation sites that play an important role at different quantiles of the patients’ overall survival.

Although we could directly apply QA screening to the entire 400 000 methylation sites, we used the target gene approach by focusing on those residing within the genes that have been identified by the literature to be associated with development of lung cancer. These genes include ROS1, RET, PIK3CA, NRAS, BRAF, ALK, AKT1, VGLL2, MET, KRAS, EGFR, KDM4, ST3GAL3, and CDH13. We used the array annotations from the Bioconductor package FDb.InfiniumMethylation.hg19 (version 2.2.0) to identify a total of 589 methylation sites that lie within these genes.

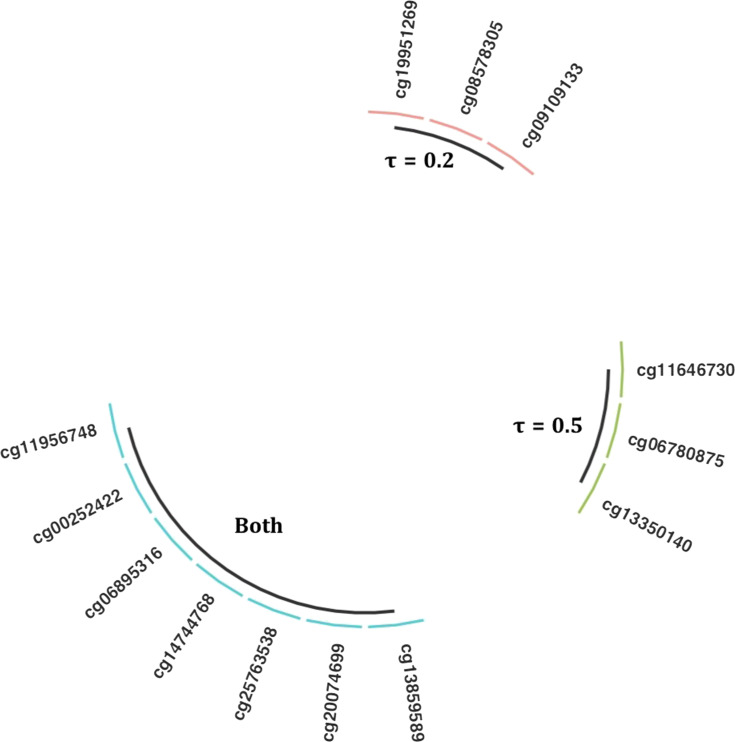
Applying QA, we selected the top 10 methylation sites at τ = 0.2 and 0.5. The selected methylation sites were not identical for these two quantiles. While there were seven overlapping methylations sites selected for both quantiles, three distinctive sites were also selected for each of these quantiles, revealing that the CpG sites might have heterogeneous effects on survival time (see Fig. 3).

Figure 3.

Selected CpG sites related to the 0.2 or 0.5 quantiles of overall survival.

We further built a joint model with all of the selected CpG sites (in percent values), along with age, gender, pack-years, cancer stage, and cancer type, as predictors for the lung cancer patients’ overall survival. We fitted models separately for the two quantiles and estimation results are given in Table 2. Some interesting observations can be made. For example, a unit (or 1%) increase in cg11956748 leads to 0.014 years loss in the 0.2 quantile, but 0.033 years increase in the 0.5 quantile (i.e. median survival), after controlling for all of the other confounders. Moreover, a unit increase in cg00252422 was associated with 0.002 years loss in the 0.2 quantile and 0.003 years increase in the median survival, while a unit increase in cg25763538 was associated with 0.001 years loss in the 0.2 quantile and 0.002 years increase in the median survival. On the other hand, a unit increase in cg06895316 results in 0.003 years increase in the 0.2 quantile, but 0.001 years decrease in the median survival. Varied effects of the other CpG sites were also observed across the 0.2 and 0.5 quantile models. All of these results hint that quantile regression could be a useful tool for discerning predictors with heterogeneous effects.

Table 2.

Point estimates and CI (in parentheses) for censored quantile regression with additional methylation sites from Boston Lung Cancer Survivor Cohort (BLCSC) regression with demographic and clinical factors from BLCSC.

	τ =0.2		τ =0.5
(Intercept)	13.38	(1.93, 20.57)	29.39	(3.16, 55.47)
age	−0.03	(−0.18, 0.19)	−0.22	(−0.55, 0.12)
gender	−0.64	(−2.91, 1.41)	−0.23	(−2.73, 3.01)
packyrs	−0.01	(−0.04, 0.03)	−0.02	(−0.05, 0.02)
cstage: stage> 1 vs. stage=1	−3.75	(−6.32, −0.62)	−4.6	(−6.82, −1.32)
ctype: non-adeno vs. adeno	−0.99	(−4.34, 1.79)	0.36	(−2.14, 3.58)
cg13859589	−0.0079	(−0.0345, 0.0121)	−0.0013	(−0.0216, 0.0235)
cg19951269	0.0032	(−0.0074, 0.0149)	-	-
cg11646730	-	-	0.0033	(−0.0167, 0.0212)
cg08578305	0.0101	(−0.0288, 0.0268)	-	-
cg20074699	−0.0028	(−0.0152, 0.0204)	−0.0078	(−0.0261, 0.0109)
cg25763538	−0.0009	(−0.0103, 0.014)	0.002	(−0.0156, 0.0146)
cg06780875	-	-	0.0022	(−0.0235, 0.0269)
cg14744768	−0.0042	(−0.0248, 0.0167)	−0.0112	(−0.0325, 0.0154)
cg06895316	0.0027	(−0.019, 0.0307)	−0.0011	(−0.0121, 0.014)
cg00252422	−0.0019	(−0.0069, 0.0047)	0.0033	(−0.0215, 0.088)
cg11956748	−0.0135	(−0.0598, 0.0366)	0.0332	(−0.0306, 0.1025)
cg09109133	0.0037	(−0.0173, 0.0248)	-	-
cg13350140	-	-	−0.0114	(−0.0316, 0.0143)

Discussion and future directions

The analysis of censored outcome data in cancer research is predominated by Cox regression models and accelerated failure time models. This paper tries to convey the message that quantile regression methods can be a powerful alternative to these popular approaches. For example, it relaxes the implicit assumption of AFT that the associations between the outcome and the covariates are the same across all levels and the proportional hazards assumption of the Cox model. Using a dataset from the BLCSC, we have illustrated the use of censored quantile regression by identifying clinical and molecular predictors, for example CpG methylation sites, that may have heterogeneous impacts on lung cancer patient survival. The past decade has seen flourishing research in censored quantile regression. We envision that the following areas may attract attention soon.

Model diagnostics

It is an essential task to examine whether the linear assumption (1) holds for all τ, for some τ, or for no τ at all. One may also need to check whether the slopes β(τ) are the same or differ across different quantile levels by examining the interaction terms with observed covariates. Although some tools, such as the conditional Q-Q plot (sometimes called the “worm” plot), have been proposed for the model diagnostics of quantile regression with complete data (see Ref. [36] for a detailed introduction), model diagnostics for censored quantile regression is still greatly underdeveloped. Designing effective model diagnostic tools for censored quantile regression warrants more in-depth research.

Quantile regression for different types of censoring

This paper has concentrated on the outcome data that were right censored, as this was the main feature of our motivating dataset. More broadly speaking, we are aware that the emergence of other censoring types, such as interval censored data, current status data, and left truncated data, has prompted the extension of quantile regression. See, for example, the extended quantile regression work of Zhou et al.,³⁷ Kim et al.,³⁸ and Lin et al.³⁹ for interval censored outcome data, of Ou et al.⁴⁰ for current status data, and of Cheng et al.⁴¹ and Shen⁴² for left truncated data.

Unconditional quantile regression

The quantile regression we have focused on is, more precisely, the conditional quantile regression, which assesses the impact of a covariate on a quantile of the outcome given specific values of other covariates. Some authors, however, argue that interpretation of such effects becomes limited when the effects for different conditional quantiles vary and the estimated effects do not translate to relevant policy questions that are linked to these covariates. Recently, the unconditional quantile regression approach has been proposed to overcome the limitations of the conditional quantile regression.⁴³ As its formulation and inference are less intuitive, its readiness for practical implementation may still need some work.

Non-parametric high-dimensional models

With high-dimensional predictors, quantile regression forests have been proposed as a non-parametric way of estimating conditional quantiles.⁴⁴ Efforts have been made to extend the approach to accommodate censoring,⁴⁵ but its practical implementability remains to be studied.

Finally, as DNA methylation is likely to change during the course of lung cancer development, it is plausible that integrated approaches that combine a variety of molecular biomarkers, such as whole-genome microarray, mRNA expression, DNA genotype, and methylation data, with demographic, environmental, and clinical indicators, will be superior for survival prediction. Our work, nevertheless, represents a proof of principal, providing evidence that quantile regression can be a valuable tool for detecting the heterogeneous effects of clinical variables and molecular biomarkers on lung cancer survival.

Appendix

R and SAS commands for the analysis of the BLCSC data in Section 2

R commands and output

Censored quantile regression can be fitted by the function crq in the quantreg package: The object fit produced by calling crq utilizes, by default, the Portnoy estimator. Other options are ‘Powell’ and ‘PengHuang’. The bootstrap-based standard errors are reported in the output.

The following code was used to draw Fig. 2.

SAS commands

The same model can be fitted using the following SAS commands. The categorical variables are listed in the CLASS statement. The MODEL statement specifies the model, and the option QUANTILE specifies a set of quantiles of interest for comparing quantile-specific covariate effects. The METHOD=KM and METHOD=NA are analogous to the ‘Portnoy’ and ‘PengHuang’ options in R.

R codes for the analysis of the BLCSC data in Section 3

The R function, QaSIS.surv, to perform the QA screening, is available at the author’s website. The following code generates the selected methylation sites with τ = 0.2 in Fig. 3.

Acknowledgement

This study was supported by the National Institute of Health (U01CA209414).

Conflict of interest

None.