Abstract
Suspended micromechanical structures are typically formed by dissolving underlying spacer material. However, capillary force-induced collapse during solvent removal can damage soft structures. If instead capillary forces are directed in the plane, they can drive liquid polymeric bridges to directly transform into suspended fibers. The various capillary force-directed methods for fabricating arrays of suspended fibers have suffered from either low manufacturing rates or an inability to produce arbitrary patterns. Shape transformation photolithography (STP) demonstrated herein is a method of producing arbitrarily patterned arrays of suspended fibers that are potentially capable of high fabrication rates. In STP, holes are prepatterned in a polymer nanofilm supported on a micropillar array, and then the film is heated above its glass transition temperature. First, the holes expand by dewetting and then capillary forces drive thinning of the polymer channels defined by the holes. Prepatterning overcomes the energy barrier for hole nucleation and ensures that all fibers form at the same time and with similar diameters. Arrays of fibers and fiber lattice networks are formed from dyed polystyrene films that are patterned with nanosecond laser pulses at 532 nm. The exposure threshold for forming holes is 10.5 mJ/cm2 for single pulses and 3.3 mJ/cm2 per pulse for repetitive pulsing, which is only about 3× larger than the dose available from current 193 nm wafer-stepping projection printers that are used in device manufacture. With the increased absorption of polystyrene at 193 nm and with additional proposed material modifications to the thin film, it may even be possible to employ STP in production wafer steppers at economically feasible manufacturing rates of over 50 wafers/h.
1. Introduction
There have been several recent studies on the formation of polymers into patterned arrays of suspended fiber air bridges with diameters from microns down to a few nanometers. These methods include point-to-point fiber drawing from melted1 or solvated polymers,2−5 drawing5 or electrospinning6 over a substrate that is rotating and translating in synchronism with the polymer jet, direct-write from an electrospinning jet in close proximity to the substrate,7,8 and brushing on2 or withdrawing9 solvated polymers from an array of micropillars resulting in an array of suspended fibers. These fiber bridges can have very high aspect ratios of 1000:1 or greater, and correspondingly low bending stiffnesses. Because these structures assemble from material that is suspended at some distance above the substrate, capillary forces (rather than inducing collapse, a common failure mechanism for flexible microstructures that are made by undercut and release using liquid solvents) drive threads of polymeric fluids to thin and solidify into suspended structures. Depending on the polymer concentration, molecular weight and extension rate, fiber geometry due to capillary thinning can vary from near constant diameter10 to bead-on-a-string structures of regularly spaced single and multidiameter beads.11 Under conditions of ongoing polymerization and slow enough brushing speeds, arrays of suspended membranes form that resemble trampolines, with each membrane anchored between four pillars.12
These various structures can be used directly as micromechanical elements or serve as templates for fabricating suspended structures from other materials. An example of templated fabrication with these structures is that polymer air bridges filled with nanomaterials have been decomposed to produce suspended bridges of nanowires, nanotubes, and graphene.13 Another example is that overcoating air bridges with various materials followed by decomposition or dissolution has been used to fabricate suspended capillaries out of both organic and inorganic materials,2 and overcoating has even been used to template complete, electrokinetically pumped micronscale flow cells.14 Other more exotic multifunctional microsystems that could be built from these processing steps are considered in ref (15). Therefore, compared to traditional lithographic processes of deposition, patterning, and release by undercutting, these various approaches to forming suspended polymer structures offer ways to self-assemble very flexible and delicate structures, in the third dimension above the substrate, and with fewer steps and less likelihood of capillary force-induced snap-down.
However, all these methods of directly fabricating fiber air bridges1−9 suffer either from low manufacturing throughput, in the case of serial direct-write methods, or from a limited range of geometries (basically, only periodic arrays) that can be patterned by brush-on methods and synchronized electrospinning. In this report, we introduce shape transformation photolithography (STP), a method to form much more general and arbitrary patterns of fiber bridges.
In STP (Figure 1), a micropillar-suspended nanofilm is optically prepatterned, followed by thermal annealing during which the low-resolution patterns transform through capillary thinning into a defined pattern of fiber bridges. Prepatterning of holes overcomes the otherwise uncontrolled nucleation of holes at random times and locations and the undesirable evolution of these holes into fibers of widely varying diameters, orientations, and random breaking times.16−18 Here, we experimentally demonstrate that the prepatterned films can be formed by photolithography, which enables, for the first time, a parallel method of capillary force-directed self-assembly that produces arbitrarily defined patterns of suspended fibers.
Figure 1.
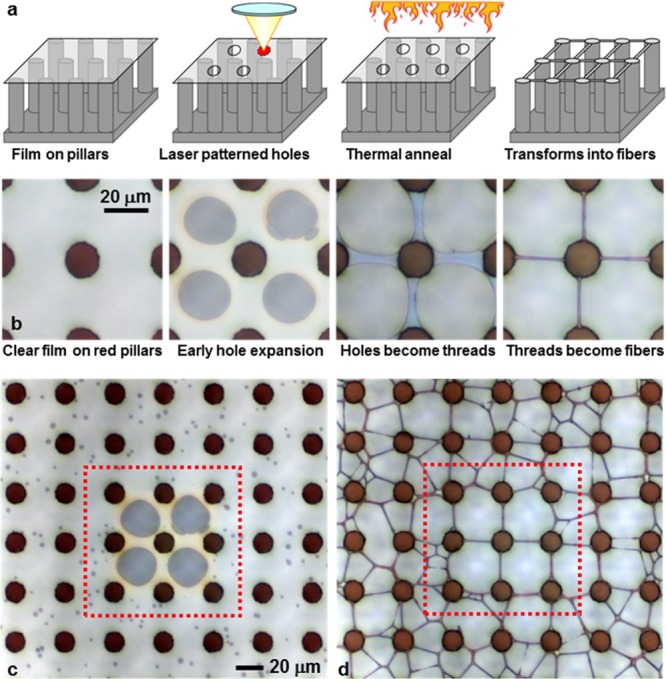
STP: method and demonstration of the transformation of a polymer thin film (the 80 nm thick region of film 6) into patterned arrays of polymer fiber air bridges. (a) Three-dimensional schematic view of the method. (b) Photographs of the film before patterning and at various stages of the thermal anneal as the film transforms from holes into fibers. (c) Wider field of view of the film in (b) during early hole expansion. The unpatterned areas (outside the dotted box) have many randomly nucleated holes. The temperature has just reached 97 °C when the nuclei first appear. In (d) where the temperature has reached 125 °C, the nuclei expand to produce a random pattern of fibers, while the prepatterned areas (inside the dotted box) have transformed into a well-ordered array of fibers in (d).
A perspective on the significance of the method can be gained by considering the degree to which this process is compatible with current tools used in the mass production of integrated circuits, specifically, in terms of available optical energy and exposure throughput rate (which is dictated by economic arguments about return on investment). The rate-limiting step for STP, and photolithography in general, is pattern exposure (because the thermal annealing and membrane attachment steps can be performed on an entire wafer, or even a cartridge of prepatterned wafers all at the same time.)
We specifically consider compatibility of STP with the widely deployed 193 nm wavelength production steppers that use excimer laser light sources (that produce nanosecond pulses at kilohertz rates) which currently dominate the manufacture of computer processors and memory chips. (Only recently have 13.5 nm extreme UV steppers begun to be used in chip manufacture.) The 193 nm wavelength is strongly absorbed by many organic polymers,20−22 many of which have been employed as photoresists, including polystyrene (PS), which is considered in this report.
For STP to be used in production setting, it is necessary that holes be patterned in the polymer films with the fluence available from these steppers (around 0.3–1.1 mJ/cm2, see Table 2 in Section 3). While previous reports and experiments presented herein suggest that the exposure threshold of PS is somewhat higher than the levels available from production steppers, other polymers and modifications to PS are expected to have lower exposure thresholds (which is discussed in Section 3.1).
Table 2. Characteristics of Two Production Steppers.
| |
light
at film surface |
||||||
|---|---|---|---|---|---|---|---|
| light
source |
fluence
per pulse |
||||||
| model | frequency (kHz) | power (W) | pulse energy (mJ) | intensity (W/cm2) | (mJ/cm2) | (mJ/die)c | stepping time (ms) |
| PAS5500/1150Ca | 4 | 20 | 5 | 1.1 | 0.275 | 2.4 | 560f |
| NXT1980Dib | 6 | 120d | 20 | 6.6e | 1.1 | 9.44 | 132g |
Specifications from https://www.asml.com/products/systems/pas-5500/en/s46437?dfp_product_id=1964.
Specifications from https://www.asml.com/products/systems/twinscan-nxt/en/s46772?dfp_product_id=10567.
For a die size of 2.6 cm × 3.3 cm = 8.58 cm2 as stated in the manufacturer’s specifications.
Reference (19) authored by Cymer, a subsidiary of AMSL.
Aerial intensity for NXT is not given by the manufacturer. Instead, losses in the imaging optics are assumed identical to the PAS stepper, giving an aerial intensity 6× larger than the PAS.
Stepping time from specified 135 wafers/h (46 dies/wafer) at an exposure dose of 20 mJ/cm2 (that takes 18 ms).
Stepping time from specified 275 wafers/h (96 dies/wafer) at an exposure dose of 30 mJ/cm2 (that takes 4.5 ms).
2. Results
This section presents several experimental demonstrations of STP. The process (documented in Materials and Methods) is summarized in the schematic (Figure 1a). A polymer thin film mounted on a micropillar array is optically patterned with holes by laser exposure. The holes may be simple round holes or more complex patterns (as shown in Figures 1–4). Upon heating to a point where the polymer can flow, the holes expand and transform to threads that bridge pairs of pillars. These threads thin further into fibers of nearly constant diameter over most of their length.
Figure 4.
Diagonal fibers formed by STP from film 5 (100 nm thick). Prepatterned films (upper row) and films after annealing (lower row) that form diagonal fibers at (a) 45°, (b) both +45° and 45°, and (c) 26.6° from horizontal. The pitch of the (silicon) pillars is 40 μm in (a) and 30 μm in (b,c).
In these experiments, PS films and 532 nm lasers (initially, continuous wave and later, nanosecond pulsed) were used. PS absorbs almost no light at this wavelength, so the films are dyed to a level approaching the absorbance of pure PS at 193 nm. The threshold fluence that we find for forming holes at 532 nm (presented below in Figure 5 and Table 1) is close to the reported ablation threshold for PS at 193 nm.23 The dye not only increases optical absorption, but also lowers the glass transition temperature of PS (see Table 1 and Section 3.1 below). The relevant characteristics of the various films used in experiments are presented in Table 1a,b together with calculated optical transmission characteristics of PS films at 193 nm (Table 1c) derived from measurements in ref (22).
Figure 5.
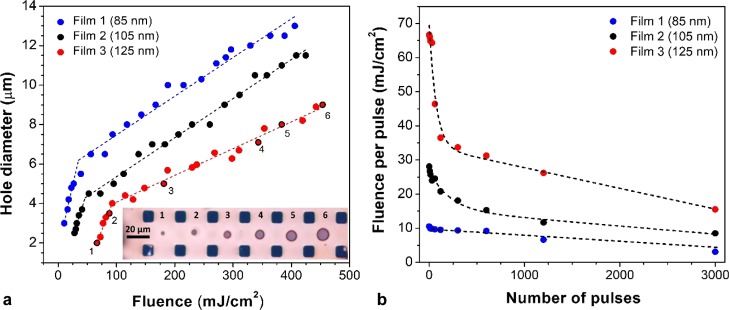
Exposure threshold at 532 nm for dyed PS films 1–3. (a) Resulting hole diameter as a function of fluence for single laser pulses. The inset shows a series of holes in film 3 that increase in diameter with increasing fluence. The numbers identify the corresponding diameter-fluence values on the film 3 graph. (b) Dependence of exposure threshold on the fluence (per pulse) for the given number of pulses that produces the first observed (minimum diameter) hole. Dashed lines in (a,b) are included to guide the eye.
Table 1. Properties of the Pure and Dyed PS Films Studied Herein.
| temperature
at which |
exposure
threshold per pulse |
|||||||
|---|---|---|---|---|---|---|---|---|
| film | starting solutiona (wt % PS) | film thicknessb (nm) | hole expandscT1 (°C) | film disappears T2 (°C) | transmittance 532 nm T | absorbance 532 nm A = 1 – T – R | single pulse (mJ/cm2) | 0.5 s of pulsesd (mJ/cm2) |
| (a) Exposure: Pulsed Laser; Film: Spun on, Dyed; MW PS: 400 000 (Films 1–4), 45 000 (Film 5) | ||||||||
| 1 | 0.25 | 85 (20) | 55 (100) | 65 (110) | 0.44 | 0.45 | 10.5 | 3.3 |
| 2 | 0.75 | 105 (30) | 65 (100) | 75 (110) | 0.36 | 0.55 | 28.1 | 7.4 |
| 3 | 1.25 | 125 (55) | 95 (110) | 105 (120) | 0.27 | 0.66 | 66.7 | 15.5 |
| 4 | 1.75 | 200 | 110 | 120 | 0.18 | 0.77 | ||
| 5 | 0.75 | 100 | 45 | 50 | 0.37 | 0.55 | 11.6 | 9.7/5.6 |
| (b) Exposure: CW Laser; Film: Doctor Blade, Gradient Thickness, Dyed; MW PS: 400 000 | ||||||||
| 6 | 1.25 | 80 | 120 | 125 | 0.52 | 0.37 | 2.6 × 106 | |
| 120 | 0.49 | 0.40 | ||||||
| 170 | 0.40 | 0.50 | ||||||
| (c) calculatede optical properties for pure PS | ||||||||
| thickness (nm) | transmittance 193 nm | absorbance 193 nm | ||||||
| 30 | 0.16 | 0.63 | ||||||
| 55 | 0.04 | 0.82 | ||||||
| 80 | 0.01 | 0.84 | ||||||
| >120 | <10–3 | 0.846 | ||||||
For dyed films 1–6, the starting solutions all have 1.25 wt % SR7B.
Values in parentheses (in this column and the following two) are for spin-coated films made without dye.
For dyed films, the temperature at which holes first begin to expand. For films without dye, the temperature at which holes first become visible.
For films 1–4, the pulse rate is 6 kHz. For film 5, the two listed thresholds are for 6 and 55 kHz, respectively.
2.1. Transformation from Film to Fibers
The location of holes in a micropillar-suspended film determines the pattern of fibers that evolve during the annealing step. The evolution from holes to fibers is shown in Figure 1b. The fibers form by heating the film to between T1 and T2 (Table 1).
For the pure PS samples, these empirical temperatures are within a few degrees of the reported glass transition temperature (Tg). At T1, the patterned holes begin to expand (by viscoelastic dewetting17,25,26). While the fibers thin to a stable diameter above T1, scattered remnants of the membrane may remain at this temperature. However at T2, these last remnants do flow and absorb into the fibers. As shown in Figure 1b, for a pair of holes patterned on each side of an imaginary line connecting two pillars, the hole edges expand toward each other to form a capillary bridge. In Figure 1b, the four holes define two vertical and two horizontal bridges. The bridges continue to thin, but eventually reach a stable diameter that persists for a considerable period of time (on the order of 25 min at 130 °C for pure PS18) before the fibers show necking or beaded features of Rayleigh plateau breakup. This stability provides considerable processing latitude for when the heat can be removed and the fiber is allowed to solidify.
2.2. Need for Prepatterned Holes
Figure 1c,d gives a wider field of view of the same experiment from Figure 1b. Here, the film is slowly heated (at 1 °C/min) to help observe the process. Holes are first observed to randomly nucleate at 97 °C in the unpatterned region (outside the red box in Figure 1c.) At 125 °C (Figure 1d), fibers are fully formed with well-oriented fibers in the prepatterned region and with randomly oriented networks of fibers in the unpatterned regions.
Not only does the prepatterned region have a much lower density of nucleated holes, but the expansion and transformation into fibers of the prepatterned holes appear negligibly affected by the smaller holes. The four fibers that form from the prepatterned holes first reach stable diameters at 125 °C and remain at the same diameter up to the final temperature of 130 °C. In the unpatterned area, individual branches of branched fibers begin to break at 125 °C and most branches are broken at 130 °C, leaving mostly single unbranched fibers spanning pairs of pillars. These unbranched fibers are poorly oriented with respect to rows and columns of the array, and some pairs of pillars are not bridged by any of the fibers. Occasionally, well-oriented fibers form if a prepatterned hole is placed on only one side of the line between a pair of pillars (e.g., in Figure 1d, the horizontal and vertical fiber in the lower right corner of the dashed box). In summary, prepatterning of the film followed by annealing causes fibers both to form at the same time and to persist over the same period of time. This method permits rather general patterning of fiber bridges, as is shown next.
2.3. Defining Arbitrary Patterns of Fibers in x and y
Figure 2a shows a film that has been prepatterned with the logo “UofL”. A film free border has been patterned to cleanly separate the patterned from the unpatterned regions. Rather than patterning circular holes one hole at a time, in this experiment, entire areas were cleared by continuously translating a focused laser spot over the film (this sequential exposure process in obviously slow, and done here for demonstrating STP. However, such exposures can be done rapidly enabling production rate throughputs, as is considered in Section 3.1).
Figure 2.
Evolution of a prepatterned film (film 6, 80 nm region) into suspended fibers. Each photograph (a–h), taken in a chronological order, is annotated with the temperature at the time the photograph was taken. The temperature was either increasing with time or held constant for a specific duration. The hold time at which a photograph is taken is also noted. The dark spot to the right of the “UofL” pattern is residue from the destruction of a pillar by unintentionally illuminating it with the laser while prepatterning the film. The fiber-thinning characteristics do not appear to be affected by proximity to the residue. There are additional periods where film-to-fiber transformation appears unchanging. These are 2.5 min between 25 and 95 °C, 8 min between 114 and 120 °C and 2 min between 120 and 126 °C. The scale bar applies to all panels a–h.
The patterned region of the film only begins to show noticeable signs of thinning into fibers around 120 °C (Figure 2e). The thinning is accelerated at 126 °C, with the fibers reaching a stable diameter after 6 min (Figure 2f). There are a few small regions that have not completely thinned, for example, the bottom of the “U” and the upper right of the “o”. After 20 min at 126 °C (Figure 2g), these remnants of the film have also evolved into the fully formed fibers. The fibers that did form at 6 min appear to have hardly changed in diameter by 20 min. The fibers formed from the patterned film continue to persist even after an additional 5 min at 129 °C (Figure 2h), after which the sample was returned to room temperature. This result demonstrates the long-term persistence of the fibers and the stability of their resulting diameters.
On the other hand, the unpatterned region behaves much less controllably, as can be seen by comparing them with the patterned region of Figure 2f–h. While many fibers have reached stable diameters, there are still many areas where the membrane continues to evolve toward fibers even after 5 min at 129 °C. Also, at least one fiber breaks (fiber upper center, between 6 and 20 min at 126 °C).
2.4. Resulting Fiber Diameter
The midpoint diameters of the four well-oriented fibers measured from Figure 1d are d′ = ∼1 μm, and the diameters are nearly constant in length except where they widen close to their anchor points on the pillars. Approximating one of these fibers as a cylinder of length l = 20 μm and diameter d gives a volume
| 1 |
If the volume of the suspended thin film between four pillars Vs completely transforms into the idealized fiber geometry, then Vf = Vs/2 (assuming that the material is uniformly distributed between four fibers) because the fiber forms from material from two adjacent four-pillar cells. The volume of the suspended thin film between four pillars can be written as
| 2 |
where D = αl is the diameter of each pillar and h is the film thickness. The subtracted term in brackets corresponds to leaving out the portion of the film resting directly on the pillars. An additional term corresponding to the volume ablated by the optical exposure could also be subtracted from eq 2 (and is considered further at the end of this section). However, this term can be ignored if the exposure is close to the threshold, where the hole diameter is minimal. Combining eqs 1 and 2 and rearranging for fiber diameter gives
| 3 |
For the experimental parameters for Figure 1 of h = 80 nm and α = 3/4, the diameter d based on this conservation of volume argument is 1.63 μm, or the volume of the experimental fiber is only ∼38% [that is, (d′/d)2] of the volume in the suspended film. The remainder of the polymer must be wetting the pillar or lost because of thermal decomposition during the hole patterning step. Because the holes in this experiment were made by continuous laser heating (see Table 1), we assume that the holes formed by nucleation rather than by decomposition, and we believe that the thinner than modeled fiber diameter is due to a significant fraction of the film wetting the pillars.
There are approaches, beyond using more closely spaced pillars, to make thinner fibers by STP. A thinner film would reduce fiber diameters, but using a thinner film also increases the probability of random nucleation of holes. An alternative is to ablate large areas of the film to reduce material available for formation of fibers. Another way to reduce the fiber diameter is to prepattern a pair of holes off center and closer to the midline where a fiber is to be formed. Similarly, prepatterning that is designed to produce multiple fibers between pairs of pillars would also result in thinner fibers. An experimental demonstration of producing thinner fibers by hole placement is described in the next section.
2.5. Patterning with Increased Generality
Hole placement strongly affects the suspended structures that develop during the annealing step. Figure 3 shows three different patterns formed for three different hole placement patterns on film 3. A dose (1.3 J/cm2) that is much larger than the threshold was used to produce holes of 16–18 μm (dose selected based on extrapolation of the trend line in Figure 5a). The darker red to purple regions are where the film is resting on the pillars. The image is blue where the film has been removed by the laser pulses. The dark rings around the holes are thickened areas of the film due to dewetting of melted portions of the film. The thickened edges are visible in electron micrographs. In the close up of microscope images, these ridges do not appear black, suggesting that deposition of carbon byproducts (i.e., charring) is not significant. Also, PS is known to cleanly and nearly completely decompose into volatile components,27 though charring does increase at increased heating rates when oxygen is the reactant.
Figure 3.

How varying the location of holes in 125 nm thick film 3 (top row of images) leads to different structures forming during annealing (bottom row of images). (a) Holes centered between four pillars produce fibers in x and y. (b) Holes centered between each pair of pillars in a group of four pillars form lattice-like structures. (c) At the junction between hole patterns centered between four pillars, like (a), and centered between two pillars, like (b), additional fiber forms in y that are thinner than the fibers to the left. The scale bar applies to all six panels of the figure.
In Figure 3a (top row), the holes are centered between each group of four pillars, similar to the patterns in Figure 1, with fibers forming in x and y (Figure 3a, bottom row), as before. However, if the holes are positioned between two pillars (Figure 3b, top row), lattice type structures form, which have the appearance of fused tapered fiber optic couplers (Figure 3b, bottom row).
Figure 3c (top row) shows the boundary between the patterns of holes in Figure 3a,b. Annealing then produces a different pattern at the boundary in the y direction (Figure 3c, bottom row). At first glance, the new structure appears to be a combination of a fiber and a lattice structure. However, the fiber is not identical to the other fibers to the left. Instead, it has a smaller diameter. It is apparent that the holes, as they expanded, isolated a narrow thread of the polymer film, which, because of its smaller area and volume than available when the holes are centered holes (as in Figure 3a), produces a thinner fiber.
The result in Figure 3c shows that patterning additional holes could be used to define multiple channels that transform during annealing into multiple parallel fibers between two pillars, or instead, could form bifurcated and more highly branched fibers originating from one pillar and terminating on one or more pillars. For purposes of design, computational modeling of viscoelastic fluid flow could be used to both identify new types of suspended structures, and to more precisely predict the resulting geometries. Such models also can be used in the development of design rules that compensate for “proximity effects,” that is, possible modifications in the formation of one structure by nearby structures.
Single fibers also can be formed in diagonal directions, as shown in Figure 4. Rather than using well-defined holes, film 5 is patterned so as to leave strips connecting pairs of pillars (Figure 4, upper row). The strips have quite jagged edges because in these experiments (1), the fluence is set high to remove a large area with each pulse, (2) in order to minimize the number of exposures, the laser spot is stepped so as to minimize overlap with the previous exposures, and (3) the stage position is manually adjusted while viewing the sample through a microscope. Despite the rough edges, after annealing, the fibers (Figure 4, bottom row) are much smoother than the original strips, which is a desirable feature of STP. However, if projection printing is used to prepattern the film, as proposed herein, then an entire film can be patterned in a single parallel exposure, and the resulting patterns can have minimal edge roughness. Furthermore, the optical resolution of the image projected on the film does not necessarily need to be at the maximum printer resolution because the annealing process converts thicker structures (e.g., strips of film) into thinner fibers.
2.6. Measured Exposure Thresholds for Forming Holes in the Films
In comparing our results with previous reports on laser etching and thermal decomposition of polymers,23,32,33,34 it should be noted that these were all performed on bulk samples, and therefore the hole formation threshold and etching threshold are not precisely comparable. Nonetheless, we do find that the hole formation is of the same order of magnitude as the reported ablation thresholds.
Figure 5 presents hole diameter as a function of fluence for films 1–3 in Table 1. The films were exposed to single (Figure 5a) and multiple (Figure 5b) 25–30 ns pulses (where pulse width varies with the pulse energy) from a 532 nm Q-switched laser (Spectra-Physics Nd:YAG Explorer One). The laser is focused onto a film to a spot with waist size wo = 1.65 μm (measured by video microscopy and fit to a Gaussian profile). Here, we report fluence, the average intensity across the spot, as
| 4 |
where Ep is the energy of a single pulse. For reference, note that fluence at the peak of a Gaussian profile is 2F.
Figure 5a shows hole diameter as a function of laser dose. It is used to determine the threshold doses reported in Table 1. Each curve has a low slope and a high slope region. The lower slope is related to the interaction of the film with the exponential tails of the Gaussian beam. A flat-top beam would be expected to result in a zero or near zero slope. The higher slope region could be extrapolated to zero hole diameter, though we report the threshold value more conservatively as the lowest dose for which a hole was observed in a light microscope. Also, while not investigated, it is worth noting that exposure at somewhat lower levels could still possibly lead to the controllable formation of holes at the start of the thermal annealing step.
The exposure threshold depends on film thickness and amount of SR7B. The values for film 1 (starting solution 0.25 wt % PS) are close to the previous threshold values of 10 mJ/cm2 for etching of pure PS with 193 nm nanosecond laser pulses.23 However, direct comparison between these previous results and those reported here are not straightforward, given that in the previous experiments, a much shorter wavelength was used, and the threshold was based on seeing a detectable change in the thickness (of a few nanometers) of bulk PS. Furthermore, because our films have a significant fraction of SR7B, the exposure threshold is lower (see Table 1), which correlates with the lowering of the empirically determined temperatures T1 (at which the prepatterned hole begins to expand) and T2 (where the last remnant of membrane disappears).
Figure 5b reports thresholds for exposure with various numbers of laser pulses. Each threshold is derived from a plot of the same form as Figure 5a. The maximum number of pules in Figure 5b is equivalent to a one-half second exposure (corresponding to a throughput of around 60 wph for an NXT stepper, as discussed in Section 3.1). The threshold decreases with the increasing number of pulses to as low as 3.3 mJ/cm2 (85 nm thick film 1). Film 5 (made with a lower molecular weight PS) was characterized at two repetition rates. For a 0.5 s exposure at each rate, the threshold is substantially lower for the 55 kHz rate than for the 6 kHz rate. The lower threshold is likely due to there being less time to cool between each pulse for the higher rate than for the lower rate. However, the threshold is lowered only by around 10% at the higher rate when comparing the thresholds for the same number of pulses.
The results in Table 1 give some insight into ways to vary the exposure threshold, and interrelationships between the threshold and other relevant properties of the film. For films 1–4, the threshold is lower for films that are thinner. Also, the empirical temperatures T1 and T2 decrease for thinner films. The lower temperatures are due to the increased fraction of SR7B in the thinner films (which have a higher ratio of dye to polymer in the starting solution). While ultrathin films are known to have a lower glass transition temperature than bulk polymers,28 the transition temperatures are much lower than the transition temperatures for pure PS films (for the undyed, pure PS films 1–3, listed in parentheses, there is no more than a 10 °C lowering of the empirical temperatures for these 20–55 nm thick films). Instead, the lowering of these temperatures is due to the SR7B dye acting basically as a plasticizer. One film (film 5) was made with lower molecular weight PS. Its thickness (100 nm) and optical absorption are nearly the same as film 2 (105 nm). However, the empirical annealing temperatures are 20–25 °C lower than those for film 2.
3. Conclusions and Discussion
The abovementioned experimental results demonstrate that arbitrary general patterns of high aspect ratio suspended polymer structures can be formed by first photopatterning a suspended polymer film with holes, and then, thermally annealing the patterned film. This method avoids the traditional approach of producing air bridges by removal of an underlying support layer, which has advantages of supporting very flexible, soft, and delicate (even biological) materials that have high likelihood of being damaged by capillary collapse or by harsh solvents that are used for traditional methods of release. The annealing step also tends to smooth out rough features and produces patterns that can be of much higher spatial resolution than the photomask pattern.
Furthermore, the results demonstrate that the method supports mass production of a layer of suspended polymer structures, given that pulsed laser illumination of sufficient fluence (which are available, though not integrated into current production steppers) is used. STP could be custom-integrated into roll-to-roll manufacturing systems or developed for future wafer steppers.
However, for published PS etching properties or the dyed PS films considered in this study, the hole formation threshold exceeds the fluence available from 193 nm production rate steppers, which means that STP does not yet work at economically feasible mass production rates.
3.1. Discussion: Proposed Approaches for Reducing the Exposure Threshold
A stepper throughput of 50 wafers per h (wph), equivalent to 1.33 devices per s (see notes in Table 2), is generally considered the minimum rate for an economically feasible manufacturing process. At the minimum feasible throughput rate, there is up to 190 and 618 ms per exposure for the PAS and NXT steppers (after mechanical stepping time, from Table 2, has been subtracted from the period between pulses.). Therefore, doses up to 0.2 J/cm2 for the PAS and 4 J/cm2 for the NXT steppers would be available for exposure of a single device (though using the maximum available dose could produce undesirable heating of the underlying substrate).
Considering in more detail Lazare and Granier’s report of single pulse fluence for PS,23 which reports an etching threshold of 10 mJ/cm2, the experimental curve of etch depth d as a function of fluence F is well fit (between 10 and 100 mJ/cm2) as
| 5 |
where F is in units of mJ/cm2 and d is in units of nanometers. Thus, to etch or ablate a hole in, for example, a 55 nm film at 27.5 mJ/cm2 requires 5 pulses or 138 mJ/cm2 total dose. Closer to threshold at 15.3 mJ/cm2, it requires 12 pulses and the total dose increases to 183 mJ/cm2. The total dose only increases further as F approaches the threshold. Therefore, direct etching of PS, in practice, requires higher fluence per pulse than the etching threshold. Brygo et al. reported, for an unnamed paint, that the measured threshold was lowered by a factor 8.5× by increasing the number of pulses from 8 to 275 pulses.29 For comparison, in our exposure experiments with repetitive pulses of the dyed PS film (Table 2), the multiple pulse threshold was 3.2 to 4.3× lower than the single pulse threshold for films 1–3. This still exceeds the single pulse fluence from the production steppers in Table 1, and the total dose for the multiple pulses was 10–46 J/cm2. By any measure, a considerable reduction in threshold is required to make STP compatible with production rate steppers.
Ways to lower the threshold are to use different or modified materials that decompose at lower temperatures or to dissolve in the film or surround the film with a vapor that becomes locally reactive underneath the laser. One way to lower the decomposition temperature has already been demonstrated in our experiments. This is mixing the polymer with a second material that lowers the hole formation exposure threshold, as well as hole expansion temperature T1 in Table 1 (and closely related Tg). While the added material SR7B was intended as a dye, it also appears to act as a plasticizer that lowers the hole formation temperature. These results with doped PS suggest a possible route to lowering the threshold for 193 nm exposures.
Specifically, PS could be doped with low molecular weight PS, oligomeric PS, or even styrene monomers. There is already some evidence in Table 1 of lower molecular weight PS affecting the empirical temperature and threshold dose. Compare the results for film 2 and film 5. The thickness and absorbance of the two films is essentially identical. However, film 5, which is made with the lower molecular weight PS, has considerably lower empirical temperatures and threshold dose. Mixing even lower molecular weight PS with high molecular weight PS could produce a film with an even lower exposure threshold.
To the extent that styrene or similar aromatics that absorb strongly at 193 nm can be mixed with PS, it may be possible to increase the concentration of these chromophores, thereby increasing absorbance and decreasing the optical penetration depth. In so doing, the energy density would be further increased, reducing the exposure threshold. In fact, comparing the calculated UV absorbance to the dyed films from Table 1, the penetration depth can be seen to be considerably shorter at UV.
As mentioned above, ablation and hole formation thresholds are not identical, and other factors may favor a lower hole formation threshold. Some possibilities already mentioned above are nanocracks produced by thermal shock, and that holes may spontaneously form with only partial etching through the film. In addition to these factors, one can consider that a film has increased surface area, increased permeability to admitting and releasing of gas species, and increased thermal confinement over bulk samples. Finally, while it was noted that spontaneous hole formation of a melted thin film is of the order of 1 min, the formation time is dramatically reduced with lower molecular weight.30 Given that photolithographic patterning is based on breaking down the molecular weight of the polymeric resist, together with partial etching and thinning of the film, suggests that hole nucleation could also occur at a lower single pulse threshold, especially when there are multiple pulses that exceed the photolithographic exposure dose (e.g., those typical numbers of 20–30 mJ/cm2 that are used in developing the stepper specifications in Table 2 notes f, g.)
3.2. Summary of Findings
While the method of STP is already suitable for custom fabrication and prototyping of devices that include a flexible MEMS layer, the factors discussed above suggest promising materials and process modifications that could enable hole exposure thresholds low enough to perform STP with current production steppers at economically feasible manufacturing rates. It is also worth noting that this method of producing suspended fiber structures is amenable to the various material modifications and device applications2,13−15 mentioned in the Introduction section that have been demonstrated or proposed for the previous methods of producing suspended fibers.1−9
4. Materials and Methods
Figure 1a summarizes the steps used to fabricate suspended structures. The steps are essentially identical to those reported in earlier studies on the dynamic breakup of thin films into fibers,16−18 but with the addition of a step in which holes are optically patterned (Figure 1a, second panel from left). The wafer throughput estimates presented herein also assume a laser is used, but rather than being focused to a single spot, as done in experiments, a photomask would be illuminated by a laser that is imaged onto the membrane. In the experiments, a 532 nm laser is used, while for the throughput estimates, a 193 nm wavelength pulsed excimer laser, as is used in current wafer steppers, is assumed.
4.1. Film Preparation
Films 1–6 are cast from starting solutions (listed in Table 1) of atactic (non-crystallizable) PS (Mn = 400 kDa, Mw/Mn = 1.06, Pressure Chemical Company), dissolved at from 0.25 to 1.25 wt % in toluene, together with 1.25 wt % Sudan Red 7B (SR7B, Sigma-Aldrich). Undissolved SR7B is removed by filtering the solution through a 0.45 μm PTFE filter (VWR). Films are coated onto a polished silicon wafer that has been cleaned by sonication in acetone for 5 min, toluene for 5 min, and then exposed in air to UV-generated ozone for 30 min. Immediately after ozone treatment, the wafer is dipped in deionized water for 1 min and air-dried, which facilitates the separation of the polymer film from Si in the following step.
The wafers were coated either by the doctor blade method with a blade acceleration of 6 mm/s2 to produce gradient thickness film16,31 or by spin-coating at 8000 rpm to form a constant thickness film. The resulting thicknesses (Table 1) are measured by atomic force microscopy (Asylum MFP-3D) for all films, except for the gradient thickness film (film 6) which was measured optically (using a Filmetrics F20 thickness monitor). Table 1 also shows that the films are much thinner with the dye omitted. The experiments that were performed with the 80 nm thick regions of the gradient films are shown in Figures 1 and 2, and the experiments with the spun on films are shown in Figures 3 and 4.
The films are detached from the silicon substrate by immersing them in water. The film floats to the surface of the water and then is brought in contacted from below with a submerged micropillar array. A second identically prepared film is mounted onto a microscope slide for optical absorption measurements in a spectrometer (2000 USB, Ocean Optics). Some pillar arrays were cast from SU8 photoresist (MicroChem Corporation) that are dyed red to help distinguish them in microscope images from the polymer film and fibers. Other micropillar arrays were fabricated by patterned etching of silicon. The suspended films are dried under vacuum (∼20 Torr) for 12–24 h at 50–55 °C (i.e., below the ∼100 °C glass transition temperature of PS), primarily to remove any water trapped between the film and the tips of the micropillars (residual toluene also would be removed by vacuum baking, but we observed for films coated on silicon wafers that the film thicknesses are identical after either 2 h of drying in air or after an additional day of vacuum baking). In passing, we note that the temperature and time of aging of PS films does play a role in hole nucleation and film thickness and therefore should be considered in the use of STP. Reiter et al. found that the spontaneous hole nucleation rates at temperatures close to Tg decreased with increased aging times at 50 °C for 40 nm thick 4.8 MDa PS films.25 Aging above Tg also releases residual stress of spun on films from solvated polymers, which results in thickening of the films32 and spontaneous formation of holes.25,30
The optical absorption (A = 1 – T – R) of the (duplicate glass-mounted) films at 532 nm is determined by spectrometer measurements of T and R, which are the relative amounts of transmitted and reflected energy with respect to the incident energy. Table 1 reports A and T. The dyed films absorb somewhat less energy at 532 nm than suspended films of pure PS at 193 nm (as calculated from the Fresnel equations24 at normal incidence). Also, the films at UV hardly absorb any additional energy at depths greater than about 50 nm.
4.2. Film Prepatterning
Initially, a continuous wave laser was used to prepattern the films. The film was heated to 75 °C to reduce the heat required from the laser. For the CW laser focused to around 6.5 μm spot radius on an 80 nm film, the preferred exposure was 122 mW for 0.025 s (or 3.5 mJ or, using eq 4, ∼2.6 kJ/cm2). This is an unrealistically large fluence for commercial steppers. The reason for such a high dose is thermal diffusion that, over the relatively long exposure time, spreads the heat out and creates a surface area for cooling that is much larger than the area that is irradiated by the laser.
Originally, we had assumed that heating thin films to melting was sufficient to nucleate holes, however, a review of the literature shows that for films of around 20 nm, nucleation is spontaneous, while for films of 60–100 nm, hole nucleation events can take around 1 min or longer.30,33 This amount of time is too long for practical/economical use in commercial wafer steppers. As a result, in the later studies, we used nanosecond laser pulses (and with the film at room temperature). Holes in thin films can then be produced by a combination of thermal decomposition and photodissociation, with photodissociation becoming more significant at 193 nm than at 532 nm.34,35 Laser-induced shock waves, vaporization, and cavitation also can produce holes in thin films, though they are not the dominant contribution in polymer etching for pulse durations greater than 1 ns. Nonetheless, while not investigated here, if nanoscale defects are produced below the hole formation threshold by these thermal effects, these defects may be sufficient to produce expanding holes at the start of thermal anneal.
Repetitive pulses have been observed to reduce the energy threshold (per pulse) over single pulse exposures.29 With a fast enough repetition rate, the polymer does not completely cool between pulses, but instead gradually heats with each pulse.29,36 The longer heating period provides adequate time for the polymer to thermally decompose.36 Extrapolating from the kinetic models of thermal decomposition of PS measured at seconds to minutes timescales27 shows that hundreds of degrees higher decomposition temperatures (assuming that the same oxygen reaction pathway controls decomposition at these elevated temperatures) are required for the nanosecond and microsecond time scales in refs (29) and (36).
An unresolved issue in the preparation of PS thin film is the differences found between the spun on and doctor blade-prepared films. The doctor blade-coated sample (film 6) has somewhat higher empirical temperatures, and the 120 nm thick portion of the gradient thickness film absorbs considerably less light than film 3 (which has nearly the same thickness, 125 nm, and identical starting solution as film 6.)
Acknowledgments
This study was partially supported with funds from National Science Foundation (ECCS 0506941) and the Kentucky Science and Technology Corporation (KSEF-1947-RDE-012).
Author Present Address
§ Nikon Instruments, Inc., 1303 Shelby Ave, Nashville, TN 37206.
The authors declare no competing financial interest.
References
- Nain A.; Sitti M.. 3-D nanoscale manufacturing by nanoprobes based controlled pulling of liquid polymers. IEEE Nanotechnology Conference 2, San Francisco, Aug 2003; pp 60–63.
- Harfenist S. A.; Cambron S. D.; Nelson E. W.; Berry S. M.; Isham A. W.; Crain M. M.; Walsh K. M.; Keynton R. S.; Cohn R. W. Direct Drawing of Suspended Filamentary Micro- and Nanostructures from Liquid Polymers. Nano Lett. 2004, 4, 1931–1937. 10.1021/nl048919u. [DOI] [Google Scholar]
- Nain A. S.; Wong J. C.; Amon C.; Sitti M. Drawing suspended polymer micro-/nanofibers using glass micropipettes. Phys. Lett. 2006, 89, 183105. 10.1063/1.2372694. [DOI] [Google Scholar]
- Liu A.; Zhu H.; Liu G.; Noh Y.-Y.; Fortunato E.; Martins R.; Shan F. Draw spinning of wafer-scale oxide fibers for electronic devices. Adv. Electron. Mater. 2018, 4, 1700644. 10.1002/aelm.201700644. [DOI] [Google Scholar]
- Bai X.; Liao S.; Huang Y.; Song J.; Liu Z.; Fang M.; Xu C.; Cui Y.; Wu H. Continuous draw spinning of extra-long silver submicron fibers with micrometer patterning capability. Nano Lett. 2017, 17, 1883–1891. 10.1021/acs.nanolett.6b05205. [DOI] [PubMed] [Google Scholar]
- Theron A.; Zussman E.; Yarin A. L. Electrostatic field-assisted alignment of electrospun nanofibres. Nanotechnology 2001, 12, 384–390. 10.1088/0957-4484/12/3/329. [DOI] [Google Scholar]
- Bisht G. S.; Canton G.; Mirsepassi A.; Kulinsky L.; Oh S.; Dunn-Rankin D.; Madou M. J. Controlled continuous patterning of polymeric nanofibers on three-dimensional substrates using low-voltage near-field electrospinning. Nano Lett. 2011, 11, 1831–1837. 10.1021/nl2006164. [DOI] [PubMed] [Google Scholar]
- Li X.; Li Z.; Wang L.; Ma G.; Meng F.; Pritchard R. H.; Gill E. L.; Liu Y.; Huang Y. Y. S. Low-voltage continuous electrospinning patterning. ACS Appl. Mater. Interfaces 2016, 8, 32120–32131. 10.1021/acsami.6b07797. [DOI] [PubMed] [Google Scholar]
- Lin C. H.; Guan J. J.; Chau S. W.; Chen S. C.; Lee L. J. Patterning nanowire and micro-/nanoparticle array on micropillar-structured surface: Experiment and modeling. Biomicrofluidics 2010, 4, 034103. 10.1063/1.3474639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKinley G. H.Visco-elasto-capillary thinning and break-up of complex fluids. Rheology Reviews; The British Society of Rheology: Aberystwyth U.K., 2005; pp 1–48. [Google Scholar]
- Bhat P. P.; Appathurai S.; Harris M. T.; Pasquali M.; McKinley G. H.; Basaran O. A. Formation of beads-on-a-string structures during break-up of viscoelastic filaments. Nat. Phys. 2010, 6, 625–631. 10.1038/nphys1682. [DOI] [Google Scholar]
- Pabba S.; Yazdanpanah M. M.; Fasciotto Totten B. H.; Dobrokhotov V. V.; Rathfon J. M.; Tew G. N.; Cohn R. W. Biopolymerization-driven self-assembly of nanofiber air-bridges. Soft Matter 2009, 5, 1378–1385. 10.1039/b817761a. [DOI] [Google Scholar]
- Pabba S.; Sidorov A. N.; Berry S. M.; Yazdanpanah M. M.; Keynton R. S.; Sumanasekera G. U.; Cohn R. W. Oriented Nanomaterial Air Bridges Formed from Suspended Polymer-Composite Nanofibers. ACS Nano 2007, 1, 57–62. 10.1021/nn700047n. [DOI] [PubMed] [Google Scholar]
- Berry S. M.; Roussel T. J.; Cambron S. D.; Cohn R. W.; Keynton R. S. Fabrication of suspended electrokinetic microchannels from directly written sacrificial polymer fibers. Microfluid. Nanofluid. 2012, 13, 451–459. 10.1007/s10404-012-0973-z. [DOI] [Google Scholar]
- Cohn R. W.Freestanding Metal & Polymer Nanostructures: Directed Self-Assembly; Lyshevski E., Ed.; Dekker Encycl. Nanosci. & Nanotech.; CRC, 2014. [Google Scholar]
- Rathfon J. M.; Grolman J. M.; Crosby A. J.; Tew G. N. Formation of oriented, suspended fibers by melting free standing polystyrene thin films. Macromolecules 2009, 42, 6716–6722. 10.1021/ma901121u. [DOI] [Google Scholar]
- Rathfon J. M.; Cohn R. W.; Crosby A. J.; Tew G. N. Hole nucleation and growth in free-standing polystyrene ultrathin films. Macromolecules 2011, 44, 134–139. 10.1021/ma1020227. [DOI] [Google Scholar]
- Rathfon J. M.; Cohn R. W.; Crosby A. J.; Rothstein J. P.; Tew G. N. Confinement effects on chain entanglement in free-standing polystyrene ultrathin films. Macromolecules 2011, 44, 5436–5442. 10.1021/ma1026324. [DOI] [Google Scholar]
- Burdt R.; Duffey T.; Thornes J.; Bibby T.; Rokitski R.; Mason E.; Melchior J.; Aggarwal T.; Haran D.; Wang J.; Rechtsteiner G.; Haviland M.; Brown D.. Flexible power 90W to 120W ArF immersion light source for future semiconductor lithography. Proc. SPIE 9052, Optical Microlithography XXVII, 90522K, March 31, 2014.
- French R. H.; Tran H. V. Immersion lithography: Photomask and wafer-level materials. Ann. Rev. Materials Res. 2009, 39, 93–126. 10.1146/annurev-matsci-082908-145350. [DOI] [Google Scholar]
- Sanders D. P. Advances in patterning materials for 193 nm immersion lithography. Chem. Rev. 2010, 110, 321–360. 10.1021/cr900244n. [DOI] [PubMed] [Google Scholar]
- Inagaki T.; Arakawa E. T.; Hamm R. N.; Williams M. W. Optical properties of polystyrene from the near-infrared to the x-ray region and convergence of optical sum rules. Phys. Rev. B: Solid State 1977, 15, 3243–3253. 10.1103/physrevb.15.3243. [DOI] [Google Scholar]
- Lazare S.; Granier V. Excimer laser light induced ablation and reactions at polymer surfaces as measured with a quartz-crystal microbalance. J. Appl. Phys. 1988, 63, 2110–2115. 10.1063/1.341091. [DOI] [Google Scholar]
- Potter R. F.Basic parameters for measuring optical properties. In Handbook of Optical Constants of Solids; Palik E. D., Ed.; Academic Press: San Diego, CA, 1985; Vol. 1, Chapter 2, pp 11–34. [Google Scholar]
- Reiter G.; Hamieh M.; Damman P.; Sclavons S.; Gabriele S.; Vilmin T.; Raphaël E. Residual stresses in thin polymer films cause rupture and dominate early stages of dewetting. Nat. Mater. 2005, 4, 754–758. 10.1038/nmat1484. [DOI] [PubMed] [Google Scholar]
- Blossey R.Thin Liquid Films: Dewetting and Polymer Flow; Springer: Heidelberg, 2012. [Google Scholar]
- Sánchez-Jiménez P. E.; Pérez-Maqueda L. A.; Perejón A.; Criado J. M. Nanoclay nucleation effect in the thermal stabilization of a polymer nanocomposite: A kinetic mechanism change. J. Phys. Chem. C 2012, 116, 11797–11807. 10.1021/jp302466p. [DOI] [Google Scholar]
- Pye J. E.; Roth C. B. Above, below, and in-between the two glass transitions of ultrathin free-standing polystyrene films: Thermal expansion coefficient and physical aging. J. Polym. Sci., Part B: Polym. Phys. 2014, 53, 64–75. 10.1002/polb.23635. [DOI] [Google Scholar]
- Brygo F.; Semerok A.; Oltra R.; Weulersse J.-M.; Fomichev S. Laser heating and ablation at high repetition rate in thermal confinement regime. Appl. Surf. Sci. 2006, 252, 8314–8318. 10.1016/j.apsusc.2005.11.036. [DOI] [Google Scholar]
- Yu K.; Rasmussen H. K.; Marın J. M. R.; Hassager O. Mechanism of spontaneous hole formation in thin polymeric films. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85, 024201. 10.1103/physrevb.85.024201. [DOI] [Google Scholar]
- Reiter G.; de Gennes P. G. Spin-cast, thin, glassy polymer films: Highly metastable forms of matter. Eur. Phys. J. E 2001, 6, 25–28. 10.1007/s101890170024. [DOI] [Google Scholar]
- Stafford C. M.; Roskov K. E.; Epps T. H.; Fasolka M. J. Generating thickness gradients of thin polymer films via flow coating. Rev. Sci. Instrum. 2006, 77, 023908. 10.1063/1.2173072. [DOI] [Google Scholar]
- Croll A. B.; Dalnoki-Veress K. Hole nucleation in free-standing polymer membranes: The effects of varying molecular architecture. Soft Matter 2010, 6, 5547–5553. 10.1039/c0sm00253d. [DOI] [Google Scholar]
- Steen W. M.; Mazumder J.. Laser Material Processing, 4th ed.; Springer: London, 2010; Chapters 8 and 11. [Google Scholar]
- Niemz M. H.Laser-Tissue Interactions Fundamentals and Applications, 3rd ed.; Springer: Berlin, 2007; Chapter 3. [Google Scholar]
- Kappes R. S.; Schönfeld F.; Li C.; Golriz A. A.; Nagel M.; Lippert T.; Butt H.-J.; Gutmann J. S. A study of photothermal laser ablation of various polymers on microsecond time scales. SpringerPlus 2014, 3, 489. 10.1186/2193-1801-3-489. [DOI] [PMC free article] [PubMed] [Google Scholar]