Octanol–Water Partition Coefficient Measurement by a Simple ¹H NMR Method

Abstract

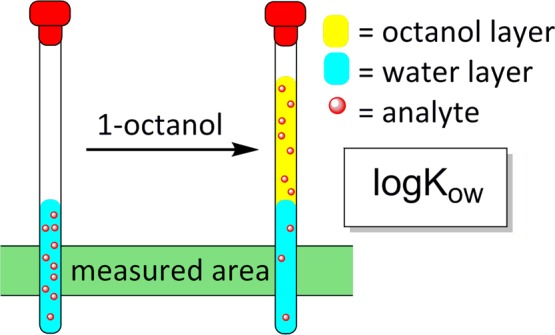
We describe a simple miniature shake-flask method to measure the octanol–water partition coefficient of an organic compound. Partition between water and octanol is performed in an NMR tube; the aqueous phase is analyzed by ¹H NMR spectroscopy using a benchtop low-field NMR instrument. Neither pre-equilibration of solvents nor isolation of the two phases is required. The procedure is fast and easy enough to be used in a students’ laboratory. Scope and limitations as well as possible sources of error are discussed in detail.

Introduction

A compound’s octanol–water partition coefficient (K_OW) is a measure of its hydrophilicity/lipophilicity.¹ Initially, it was considered in drug and pesticide discovery and design, but now it is an important characteristic of any chemical because it determines to a large extent a chemical’s fate both inside a living organism² and in the environment.^3,4 For example, biological properties such as bioaccumulation and toxicity are largely determined by K_OW. Therefore, under the European Union’s chemicals legislation REACH, K_OW has to be determined for every substance manufactured or imported in 1 ton or more per year. K_OW is defined as the equilibrium ratio of the compound’s concentrations in a two-phase system of 1-octanol and water.

1

where c_O^equil = concentration of the compound under consideration (analyte A) in 1-octanol in the equilibrium and c_W^equil = concentration of the analyte in water in the equilibrium.

More exactly, in the partition equilibrium, the octanol phase is a saturated solution of water in octanol, and the aqueous phase is a saturated solution of octanol in water.

The K_OW values of organic compounds span many orders of magnitude, and this is one reason why often the decadic logarithm of K_OW (log K_OW, also called log P) is listed rather than K_OW itself; a more fundamental reason is shown below. Log K_OW values are typically between −3 (very hydrophilic) and +10 (extremely hydrophobic).

Although it is possible to measure K_OW of a compound A indirectly by observing its high-performance liquid chromatography retention time,⁵ measurement according to eq 1 is the most direct and is considered still the most accurate, though it presents several pitfalls as discussed early.^6,7 In the simplest case, it requires preparing a solution of the analyte in either water or 1-octanol, adding the other solvent, achieving equilibration by shaking, allowing phase separation, and quantifying the concentrations by any suitable analytical method (“shake-flask method”). Because compounds differ widely in their solubilities and analytical properties, various analytical methods have been used, such as acid/base titration, ultraviolet (UV) photometry, gas chromatography analysis, and other chromatographic techniques.^2,8−10

By contrast, ¹H NMR spectroscopy, though in principle applicable for most organic compounds, notably for those without UV absorption, was rarely used for K_OW measurements, probably because quantifying ¹H signals of a solute in the presence of a large excess of water or octanol seems difficult. To circumvent this problem, deuterated water (D₂O) and perdeuterated 1-octanol (1-octanol-D₁₈) were used, and the quantification required adding internal standards or using a special double NMR tube.¹¹ Deuterated solvents and internal standards were avoided by using the protons in water and octanol themselves as calibration standards, however, this method requires varying the excitation pulse angle and applying solvent suppression, techniques that are available in present-day high-field NMR instruments.¹² Stein et al. proposed a special “localized” NMR method observing analyte concentrations in slices both above and below the phase boundary in an NMR tube, thus avoiding actual separation of the two phases.¹³

In the present work, it is demonstrated that K_OW can be determined experimentally by ¹H NMR spectroscopy using even a low-field (42.5 MHz) compact (“benchtop”) NMR instrument that may be available in or affordable for a small laboratory.^14,15 There is no need for special hardware or software, for deuterated solvents or internal standards. The method requires low amounts of analyte and 1-octanol (up to 1 and 2.5 mL, respectively, altogether for five parallel runs); it is simple and fast, in that it involves neither pre-equilibration of the solvents nor isolation of the two phases.

Method Basics

According to the K_OW definition, the equilibrium concentrations of analyte A in both the aqueous and octanol phases should be measured. However, when starting with a solution of A in water and then equilibrating with octanol, it suffices to measure the concentrations of A in the aqueous phase before and after equilibration. By mass balance, the equilibrium amount of A in octanol is given as the difference between the initial amount of A in water and its equilibrium amount in water. If the volume of the octanol phase equals that of the aqueous phase, then a corresponding statement holds for the concentrations; the equilibrium concentration of A in octanol is the difference between its initial concentration in water and its equilibrium concentration in the aqueous phase

2

where c_W^init is the initial concentration of A in water.

Because the peak area of an ¹H NMR signal (integration) is proportional to the concentration of the protons causing it (and so to the concentration of the compound of interest), we can replace the concentrations by ¹H signal integrations

3

Absolute integrations, however, are not usually displayed by NMR instruments. Moreover, integrations before and after equilibration may differ because of magnetic-field drift. Such a change in the signal integration, if any, should be the same for both the signal of interest and the water signal. For these reasons, we use relative integrations (RIs), that is, integrations standardized against the integration of the water peak, RI = I/I_water. Of course, I_water is proportional to the water concentration in the aqueous phase which should be nearly constant before and after equilibration, as long as the concentrations of the analyte and 1-octanol in the water phase are low. This means that water is used as the internal standard.

Equation 3 thus transforms into eq 4

4

where RI_W^init = relative NMR signal integration of compound A in water before equilibration with 1-octanol and RI_W = relative NMR signal integration of compound A in the aqueous phase after equilibration.

The experiment thus consists of dissolving an amount of compound A in water in an NMR tube, taking an ¹H NMR spectrum, adding an equal volume of 1-octanol, mixing the phases intensely in the NMR tube, allowing for phase separation, and again taking an NMR spectrum of the aqueous (lower) phase (Figure 1). A characteristic peak of compound A is integrated against the water peak in both spectra (Figure 2). Thus, the first spectrum provides RI_W^init, the second provides RI_W, and K_OW as a first approximation is calculated according to eq 4.

Figure 1.

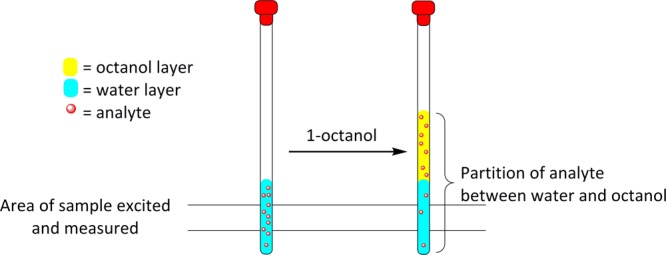
Schematic diagram of the analyte partition between the water and 1-octanol layers upon equilibration.

Figure 2.

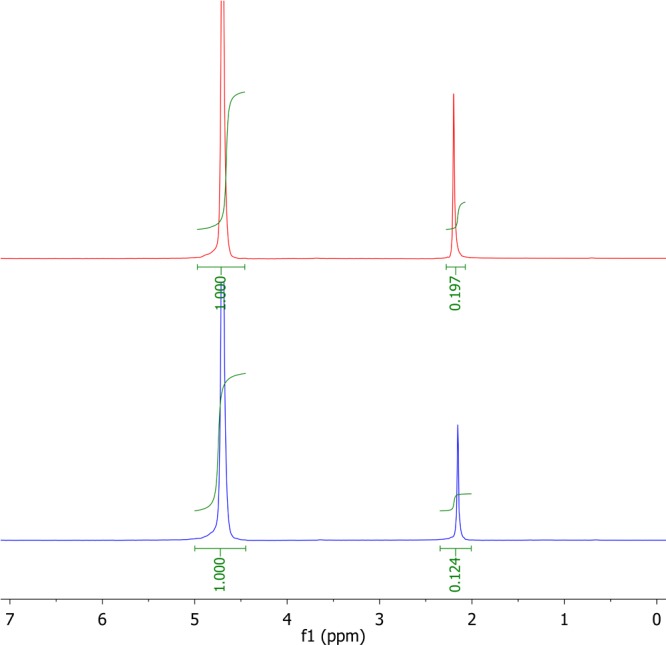
¹H NMR spectrum of acetone in water (top) and in water after equilibration with 1-octanol (bottom).

Representative Procedure

A total of 200 μL (micropipette) of a water-miscible organic compound such as acetone and 500 μL of water are mixed in an NMR tube, and an ¹H NMR spectrum is recorded. 1-Octanol (500 μL) is added, the NMR tube is inverted at least 40 times for equilibration (shaking should be avoided to prevent emulsification), the phases are allowed to separate (approximately 5 min), and again an ¹H NMR spectrum (of the aqueous phase) is taken. In both spectra, the acetone singlet at δ = 2.2 ppm is integrated against the water peak at δ = 4.8 ppm, whose relative intensity is set to 1.000 in each spectrum. In a measurement of acetone, RI_W^init and RI_W were found to be 0.197 and 0.124, respectively (Figure 2), resulting in K_OW = 0.589 and log K_OW = −0.23.

It is advisable to repeat the steps of phase mixing, phase separation, and spectrum recording to ensure that partition equilibrium was achieved. Figure 3 shows that in an experiment with methanol 10 inversions were not enough to approach the partition equilibrium, while 20 inversions were sufficient. As in this experiment, we usually performed five parallel side-by-side runs.

Figure 3.

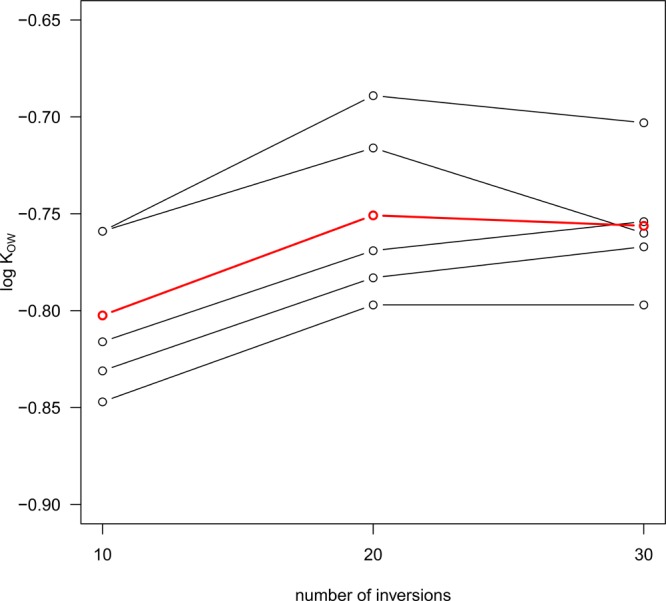
log K_OW of methanol, five parallel runs (black) and mean (red) after 10, 20, and 30 inversions of the NMR tube.

Results

The results obtained by this method are shown in Table 1, columns 1–4.

Table 1. log K_OW Values Obtained by the Present Method at 20–21 °C.

compound name and CAS-RN	amounta	log KOW (ref (14))	log KOW ± SD (eq 4, this work)	volume ratio vO/vW	log(vol ratio)	log KOW (eq 5b)	literature log KOW (ref (9))
dimethyl sulfoxide (DMSO), 67-68-5	200 μL		–1.98 ± 0.070 (n = 5)	0.78	–0.11	–1.87	–1.35
							−2.03 (ref (1))
acetamide, 60-35-5	117–131 mg		–1.48b ± 0.051 (n = 5)	0.89	–0.05	–1.43	–1.26
dimethylformamide (DMF), 68-12-2	200 μL		–1.10 ± 0.026 (n = 5)	0.85	–0.07	–1.03	–1.01 (ref (8))
							−1.04 (ref (16))
methanol, 67-56-1	200 μL		–0.76 ± 0.014 (n = 5)	0.97	–0.013	–0.75	–0.77
			–0.72c ± 0.016 (n = 5)	0.97	−0.013	−0.71c
1,4-dioxane, 123-91-1	200 μL		–0.27 ± 0.008 (n = 5)	1.11	0.05	–0.31	–0.27
acetonitrile, 75-05-8	200 μL	–0.51	–0.22 ± 0.006 (n = 5)	1.14	0.06	–0.28	–0.34
ethanol, 64-17-5	200 μL	–0.29	–0.24 ± 0.018 (n = 5)	1.21	0.08	–0.32	–0.31
			–0.22c ± 0.018 (n = 5)	1.21	0.08	−0.30c
acetone, 67-64-1	200 μL	–0.23	–0.22 ± 0.005 (n = 5)	1.06	0.025	–0.24	–0.24
acetic acid, 64-19-7	30 μL		–0.25d ± 0.034 (n = 5)	1.12	0.05	–0.30	–0.17
			(log D, pH ≈ 2.5)				−0.31 (ref 1)
2-propanol, 67-63-0	200 μL	0.11	0.12 ± 0.012 (n = 5)	1.26	0.10	0.02	0.05
			0.14c± 0.012 (n = 5)	1.26	0.10	0.04c
methyl acetate, 79-20-9	120 μL		0.25 ± 0.027 (n = 5)	1.15	0.06	0.19	0.18
1-propanol, 71-23-8	200 μL		0.42 ± 0.035 (n = 5)	1.39	0.14	0.28	0.25
butanone, 78-93-3	150 μL		0.44 ± 0.013 (n = 5)	1.28	0.11	0.33	0.29
t-butanol, 75-65-0	200 μL	0.36	0.43 ± 0.004 (n = 5)	1.40	0.146	0.28	0.35
			0.44c± 0.004 (n = 5)	1.40	0.146	0.29c
tetrahydrofuran, (THF), 109-99-9	200 μL	0.43	0.57 ± 0.005 (n = 5)	1.35	0.13	0.44	0.46
pyridine, 110-86-1	200 μL		0.57 ± 0.003 (n = 5),	1.38	0.14	0.43	0.60
			(log D, pH ≈ 7.5)				0.65
2-butanol, 78-92-2	80 μL		0.75 ± 0.016 (n = 5)	1.25	0.10	0.65	0.61
ethyl acetate, 141-78-6	40 μL		0.93 ± 0.018 (n = 5)	1.12	0.049	0.88	0.73
2-methylpropanol-1 (isobutanol), 78-83-1	50 μL		0.96 ± 0.043 (n = 5)	1.17	0.068	0.89	0.76
1-butanol, 71-36-3	43 μL		0.96 ± 0.145 (n = 5)	1.19	0.074	0.89	0.88

^aAmounts of nonwater-miscible compounds were chosen so as to result in a nearly saturated solution in 500 μL H₂O.

^bCorrected for NH₂, see text.

^cCorrected for OH, see text.

^dCorrected for COOH, see text.

In most cases, after equilibration, the volume of the octanol phase does not equal that of the aqueous phase, and therefore, the assumption of equal volumes (used in derivation of eqs 2–4) is not justified. This is due to the following two effects:

• (i)The mutual solubility of water and 1-octanol: while the solubility of octanol in water is very low, the equilibrium solubility of water in octanol at room temperature is reported to be about 5 mass percent.^17,18 In fact, mixing equal volumes of water and 1-octanol without any compound A results in a 5% higher volume of the octanol than that of the aqueous phase after equilibration, corresponding to a factor of 1.05 in K_OW or an additive term of log 1.05 = 0.02 in log K_OW.
• (ii)The volume of the analyte is considerable (up to 200 μL vs 500 μL of water and 500 μL of octanol), and its near complete stay in the water phase or near complete migration into the octanol phase may change the volume ratio extensively. In the worst case, 200 μL of the analyte migrates almost completely into the octanol phase, leading to a volume ratio of 0.7 mL/0.5 mL, that is, a factor of 1.4 in K_OW or an additive term of log 1.4 = 0.146 in log K_OW (neglecting any possible volume contraction or expansion on mixing the analyte with solvents).

Both effects are corrected for by taking the phase volume ratio into account as a factor in K_OW determination or its logarithm as an additive term for log K_OW, eqs 5a and 5b. The phase volume ratio is easily measured using a ruler as the ratio of the final phase column heights in the NMR tube.

5a

5b

The results obtained according to eq 5b are shown in Table 1, column 7.

As any equilibrium constant, a compound’s octanol–water partition coefficient is described by a Boltzmann-type equation, it is governed by the corresponding free enthalpy difference, that is, by its free enthalpy of transfer from water to octanol, ΔG_transfer

6a

or

6b

According to eq 6, K_OW depends exponentially on ΔG_transfer, or log K_OW depends linearly on ΔG_transfer. The fundamental reason for preferring log K_OW over K_OW itself is the linear dependence of log K_OW on an energy variable (eq 6b) that in turn is the sum of energy contributions from structural motifs present in a molecular structure. Thus, log K_OW increases linearly with the number of hydrophobic structural elements such as methylene groups, benzene rings, and chlorine atoms in a molecule.

Discussion

Method Basics

Instead of first postulating equal phase volumes and later introducing the actual phase volume ratio as a correcting factor, we may retain the volume ratio inherent in the definition of K_OW from the beginning

7

where n stands for the analyte’s quantity (measured, e.g., in mmol) and v for a phase volume.

Then, replacing n_O^equil by n_W – n_W^equil and replacing each n by RI as above directly lead to eq 5a.

Because the phase volume ratio in an NMR tube is easily measured using a ruler and is explicitly taken into account in this method, it is not critical to set the phase volume ratio to a predetermined value, for example, 1:1. This obviates the need to mutually pre-equilibrate water and octanol and renders the exact amounts of water and octanol used uncritical, while the exact amount of analyte A (within its limit of solubility) does not matter either.

Scope and Limitations

The method requires the analyte to be sufficiently soluble in water. An NMR signal has to be obtained that can be integrated against the strong water peak with sufficient accuracy. A general lower limit of water solubility cannot be given because the required solubility depends on an analyte’s molecular mass; number of H atoms in the molecule; and number, chemical shift, and multiplicity of ¹H NMR signals, as well as its log K_OW. Moreover, even after equilibration with 1-octanol, the analyte’s remaining concentration in the aqueous phase has to be high enough for an integrable peak to be observed. A related limitation is the instrument’s sensitivity: at the low K_OW limit, the difference RI_W^init – RI_W becomes very small, whereas at the high K_OW limit, RI_W^equil is close to zero. Therefore, in the Magritek Laboratory manual,¹⁴ only water-miscible liquids of log K_OW between −0.51 and +0.43 (measured) or between −0.34 and +0.46 (literature values) appeared as examples (column 3 in Table 1). In our experiments, also methyl acetate, n-propanol, and butanone, compounds fitting in this log K_OW range, provided good results.

To extend the amenable log K_OW range to the lower side, we subjected 1,4-dioxane, methanol, DMF, acetamide (a solid), and DMSO to the procedure; the results were close to the respective literature values for the former three compounds, whereas acetamide and DMSO showed some deviations. By contrast, log K_OW of the amino acids glycine, alanine, and proline (zwitterions) could not be measured, as these did not migrate to any detectable extent from water to octanol, in concordance with their literature log K_OW values of between −3 and −2.^19,20

In the direction to higher log K_OW, we tried pyridine, 2-butanol, ethyl acetate, isobutanol, 1-butanol, methyl t-butyl ether (MTBE), diethyl ether, and 2-methyl-THF. While the first five compounds gave reasonable results, the K_OW values of MTBE, diethyl ether, and 2-methyl-THF were unreproducible because of low solubility combined with high volatility (the two ethers) or overlapping of the NMR signal with the water peak (2-methyl-THF).

Larger deviations from the literature were observed for an acid (acetic acid) and a base (pyridine). In such cases of partially ionized compounds, the quantity measured is called log D, describing the overall distribution of the neutral and the ionized species, in contrast to log P that describes the partition of a single species. Ionization depends on both pH and concentration. For these exploratory experiments, we used unbuffered solutions. Moreover, in the present method, concentrations are far higher than recommended for precision measurements (final concentration of acetic acid here ∼0.7 M in the aqueous phase and ∼0.3 M in the octanol phase versus no more than 0.01 M in either phase, according to the relevant US Environmental Protection Agency and Organization for Economic Cooperation and Development guidelines).^21,22 While for single-species compounds K_OW is independent of the concentration, a high concentration favors the well-known association of acetic acid in nonpolar solvents to hydrogen-bonded dimers. A corresponding association may also play a role for acetamide.²³

In all previous variations of the shake-flask method that analyze one phase only, mutually pre-equilibrated samples of water and 1-octanol are used to avoid uncontrolled volume changes. Initially, in our experiment, we waived this precaution for experimental ease, which was justified by this effect being small compared to the volume effect of the analyte in most cases. Theoretically, the analyte effect on the phase volume ratio could be minimized by using a far lower amount of the analyte. However, in practice, the concentration of the analyte cannot easily be reduced owing to limited sensitivity of the NMR instrument because even with the amounts used here the analyte’s NMR signals are of rather low intensity compared to that of the water peak. Therefore, in our final procedure, we adjust for both effects by explicitly taking into account the phase volume ratio (eq 5), easily measured in an NMR tube. For a thorough discussion of the role of the phase volume ratio in K_OW measurement, see ref (10).

In the case of an alcohol, the signal of all OH protons coincides with the water peak in the initial spectrum, whereas in the equilibrium spectrum, some OH protons escape measurement by the alcohol partially evading into the octanol. This can be corrected for by diminishing, in the evaluation of both spectra, the water peak by the contribution of alcohol OH protons, as taken from the observed characteristic NMR signal of the analyte. For methanol, this correction increased log K_OW by 0.04; for ethanol, n-propanol, and isopropanol, the correction amounted to 0.02; and for t-butanol, it was 0.01. For these alcohols, their corresponding corrections are included in Table 1, whereas for the other butanols, the corrections were less than 0.01 and are therefore not included in Table 1. The corresponding correction for NH₂ protons in acetamide was +0.03, and for the COOH protons of acetic acid, it was less than +0.01.

Sources of Error

Being a variation of the shake-flask method, our procedure is in principle subject to potential errors as described for the shake-flask method in ref (6).

A problem specific to the present NMR method is the use of the water peak as the internal standard. After all, we know that the water concentration in the aqueous phase is not constant. Before equilibration, the aqueous phase contains up to 29 vol % of the analyte, whereas after equilibration, part of the analyte and some water are removed in exchange for 1-octanol, with its OH protons adding intensity to the water signal.

Another source of error and a severe limitation of the method is the uncertainty in the NMR peak integration, particularly for peaks of very different intensities, such as the water peak and the analyte peak in cases of higher K_OW. In addition, unfortunately eqs 4, 5a, and 5b by their very form are highly sensitive to measurement errors because of RI_W^equil, a number often close to zero, appearing as the denominator. This follows immediately from the definition of K_OW and is therefore a problem in all K_OW determinations for compounds of very high K_OW. Similarly, for compounds of very low K_OW, the numerator becomes close to zero.

Furthermore, coarseness of the integration display results in coarseness of log K_OW. For example, a measurement of isobutanol gave RI_W^init = 0.052 and RI_W = 0.005, resulting in log K_OW = 0.97. Had RI_W^equil been found as 0.004 or 0.006 (the nearest possibilities with a three-decimal digit display), log K_OW would have been found as 1.08 or 0.88, respectively.

Possible Improvements

For compounds with more than one ¹H NMR peak, each peak may be considered separately, or an average log K_OW may be calculated. However, in many such cases, one peak is more suitable than others. For example, in 2-propanol, the CH₃ doublet is integrated more reliably than the CH septet; therefore, the log K_OW given in Table 1 for 2-propanol is derived from the methyl signal only.

Of course, the method is not restricted to using a low-field instrument. On the contrary, we expect the method to become even more useful when profiting from a high-field instrument’s better resolution and higher sensitivity, which will alleviate some of the limitations and errors mentioned above. However, even with a compact NMR instrument as used here, improvement may be achieved if absolute intensities rather than relative (to water) intensities were displayed. This would liberate us from using H₂O as the internal standard, allowing treatment of less water-soluble compounds or allowing measurement in D₂O rather than in H₂O, both with the effect to broaden the range of amenable log K_OW to higher values.

Conclusion

Within its limitations (compounds of log K_OW roughly between −1 and +1 and sufficient water solubility), this miniature shake-flask method is well-suited for fast and easy experimental log K_OW measurement, in particular, in an educational setting.

Experimental Section

All compounds were commercial samples of >99% purity except acetamide (98%) and were used as received. Water was Millipore water of resistivity 18.2 MΩ·cm and 1-octanol was the ACS reagent of ≥99% purity, purchased from Sigma-Aldrich. The NMR instrument used was a Magritek Spinsolve carbon benchtop of 42.5 MHz ¹H frequency, and the NMR tubes were standard thin-wall tubes of size 5 mm × 178 mm. For integration, the Mnova software (which comes with the instrument) was used with integrals displayed to three decimal places. All operations were done in an air-conditioned laboratory at 20–21 °C. The temperature inside the NMR probe, according to Magritek, is ∼27.5 °C, but the corresponding error can be neglected because the measurement is fast (≤10 min) and the mass exchange across the phase boundary in the NMR tube is slow. For the effect of temperature on log K_OW, see the literature.^1,6,8,24,25

Author Present Address

^§ Plant & Food Research, 293-297 Akersten Street, Nelson 7010, New Zealand (H.C.).

The authors declare no competing financial interest.