Ab Initio Calculations of the Redox Potentials of Additives for Lithium-Ion Batteries and Their Prediction through Machine Learning

Abstract

Ab initio molecular orbital calculations were carried out to examine the redox potentials of 149 electrolyte additives for lithium-ion batteries. These potentials were employed to construct regression models using a machine learning approach. We chose simple descriptors based on the chemical structure of the additive molecules. The descriptors predicted the redox potentials well, in particular, the oxidation potentials. We found that the redox potentials can be explained by a small number of features, which improve the interpretability of the results and seem to be related to the amplitude of the eigenstate of the frontier orbitals.

Introduction

In the almost 30-year history of lithium-ion batteries (LIBs), the cathode and anode active materials have captured the spotlight in the development of LIBs because their combination sets the upper limits of the voltage and capacity of the cell.¹⁻⁴ Electrolytes probably rank second in importance to the cathode and anode active materials. It is worth noting that, in recent years, ultrahigh salt concentration electrolytes⁵ and solid-state electrolytes⁶ have become hot topics in the study of LIBs. In comparison with these major components, the electrolyte additives have a modest supporting role. However, after the significant development history of LIBs, we are now reaching the performance limits of the leading types of LIBs. Silicon anodes, high nickel cathodes, and lithium-rich cathodes are considered to be promising next-generation active materials because their theoretical capacities are higher than those of currently used materials, and, thus, they have been intensively studied.⁷⁻⁹ However, they still have some unresolved issues such as poor cyclability and low-rate performance. Therefore, it will take some time to put these materials into practical use. It is expected that the use of additives may change this situation without greatly changing the cell design; thus, they have gradually attracted attention as a low-cost way to improve cell performance.

In a recent review, Haregewoin et al. discussed in detail the state-of-the-art research into electrolyte additives for LIBs,¹⁰ and that paper constitutes the most thorough report on the current state of additive research in the field of LIBs. They classified electrolyte additives into four categories: (i) anode additives, (ii) cathode additives, (iii) redox shuttles that prevent the cell from overcharging, and (iv) flame retardants; they made a detailed exposition of these four categories. For example, in the case of the cathode additives, various cathodes such as lithium cobalt oxide (LiCoO₂), lithium nickel manganese cobalt oxide [LiNi_xMn_yCo_zO₂ (x + y + z = 1)], Li-rich lithium manganite (Li₂MnO₃), manganese spinel (LiMn₂O₄), and olivine (LiFePO₄) were discussed. Some figures in their paper show that the improvement in the performance indicators, such as the Coulombic efficiency, achieved by additives has stagnated for years. This fact suggests the difficulty in designing suitable additives by conventional chemical intuition and experimental trial-and-error approaches. Thus, in addition to the steady efforts based on the existing methods of materials science, an alternative approach is required to accelerate the development of these additives. Thus, it is interesting that the number of studies categorized into materials informatics (MI) has increased.¹¹⁻¹⁵ MI takes advantage of the sophisticated machine learning techniques developed in data science to reveal useful and sometimes hidden relationships between various properties of materials. MI is a data-driven approach to materials science, and it is expected to become the fourth approach in material research after experimentation, theory, and computer simulation.

We believe that it would be useful to identify the relationships between the structures of the additives developed so far and the properties that allow their use as additives. Among the various properties of additives, redox potentials are suitable for such a purpose. The potential at which a molecule is electrochemically decomposed in the positive or negative electrode is one of the fundamental values in the design of additives. This is because the mechanism by which additives work is electrochemical decomposition, followed by the formation of a film on the electrode surface. Besides the practical importance of the redox potentials in designing additives, they are computationally tractable and comparably reliable, using current quantum chemistry methodologies.

In this study, ab initio molecular orbital methods were used to calculate the redox potentials of additives discussed elsewhere.^10,16,17 The calculated potentials were used as the explained variables of a regression model. We designed features, that is, explanatory variables of the regression model, on the basis of the chemical structures. In spite of the simplicity of the designed features, they reproduced the redox potentials considerably well, in particular, the oxidation potentials. As will be explained later, the discrepancies in the reduction potentials between the ab initio calculations and the predictions by the regression models seem to be due to the decomposition of the additives in the reduced state.

Results and Discussion

Redox Potentials of the Additives

First, we examined the redox potentials of 149 electrolyte additives for LIBs. The calculated results are shown in Figure 1 and are classified into four groups according to their intended use: anode additives, cathode additives, redox shuttles, and flame retardants. Note that the molecular formula, chemical structure, CAS registry number, CAS name, oxidation potential, and reduction potential of all additives calculated in this paper are listed in spreadsheet S1, which is attached as the Supporting Information. The sources of these additives are refs^10,16 and (17). The classification of Figure 1 conforms mainly to ref (10). Note that this classification is somewhat expedient because the additives are not uniquely classified into the four types. In fact, some molecules, such as those containing sulfur, work as additives for both the cathode and the anode because the reduction potential of sulfur-containing additives is usually high, and they are easily decomposed on the anode surface, whereas a part of the decomposition product reaches the cathode to form a film on its surface.

Figure 1.

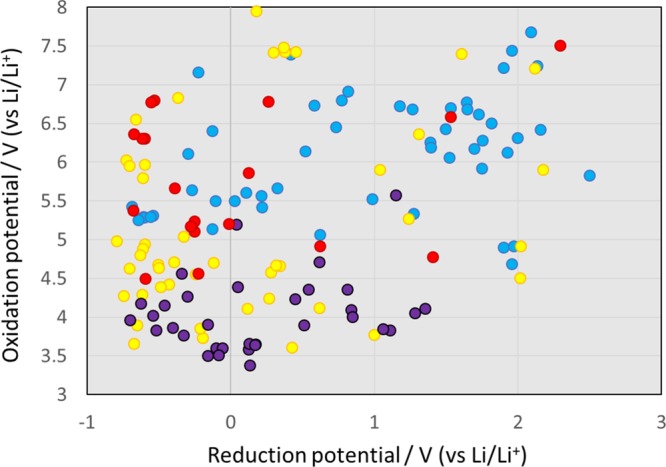
Calculated results of the oxidation vs reduction potential of 149 additives (electronvolts). Blue, yellow, purple, and red circles represent the potentials of the anode additives, cathode additives, redox shuttles, and flame retardants, respectively.

We found that there was no clear relationship between the oxidation and reduction potentials. However, the anode additives seem to be divided into two groups by taking 1 V (vs Li/Li⁺) as a threshold: 49% of the total anode additives have reduction potentials of 1 V (vs Li/Li⁺) or less, whereas 51% of the anode additives have reduction potentials of more than 1 V (vs Li/Li⁺). Anode additives that have a high reduction potential of 1.5 V (vs Li/Li⁺) or more are more easily reduced than carbonate solvent molecules. Conversely, there are quite a few anode additives for which reduction is difficult because of their low reduction potential of around 0 V (vs Li/Li⁺). In addition, most anode additives (94%) have oxidation potentials of 5 V (vs Li/Li⁺) or more, and their oxidation at the cathode is challenging.

Figure 1 also shows that a large number of cathode additives (61%) have oxidation potentials of 5 V (vs Li/Li⁺) or less. They are easily oxidized at the cathode, but their reduction at the anode is difficult because of their low reduction potential. We also found a group of cathode additives that are not easily oxidized at the cathode because of their very high oxidation potential of 7 V (vs Li/Li⁺) or more. It is noteworthy that the oxidation potentials of the redox shuttles are concentrated around 4 V (vs Li/Li⁺) and are close to the operating potential of the cathodes. This is consistent with one of the design requirements for redox shuttles and represents an indirect confirmation of the calculation accuracy. The redox potentials of flame retardant additives are scattered in Figure 1. The presence of phosphorus, which is usually present in these additives, does not seem to provide a clear relationship between the oxidation and reduction potentials.

Feature Design of the Additives

To establish a regression model between the structures of the additives and their redox potentials, it is necessary to determine the features that correctly describe the structures of the additives. Although molecular fingerprints such as MACCS and FP4 are standard methods for describing the partial structures of molecules in the fields of cheminformatics and bioinformatics,¹⁸ such a general-purpose method requires a large data set to obtain the regression model; therefore, it may not be suitable for a relatively small-scale study such as ours. Thus, we determined features to describe the structure of the additives simply, as described in the following paragraph.

(i) For each element, other than hydrogen, in an additive molecule, we counted the number of atoms having the same coordination number. For example, in the case of the left-hand molecule in Figure 2, there are two bidentate oxygen atoms, one monodentate oxygen atom, and three tricoordinate carbon atoms and are counted as O2 → 2, O1 → 1, and C3 → 3, respectively. Similarly, in the case of the right-hand molecule in Figure 2, there are two tetracoordinate carbon atoms, two bidentate oxygen atoms, four monodentate oxygen atoms, and two tetracoordinate sulfur atoms and are counted as C4 → 2, O2 → 2, O1 → 4, and S4 → 2, respectively.

Figure 2.

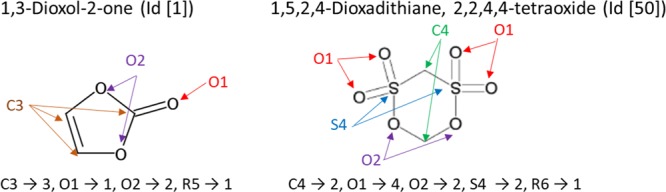
Examples of designed molecular features: 1,3-dioxol-2-one (left) and 1,5,2,4-dioxadithiane 2,2,4,4-tetraoxide (right).

(ii) Count the number of five-membered (R5) and six-membered rings (R6) included in the additive. They are R5 → 1 and R6 → 1 in the left- and right-hand molecules in Figure 2, respectively.

(iii) If the neutral state is a radical, set a flag such as rad → 1 and rad → 0 for radical and nonradical, respectively.

In this way, the structure of the additive molecule is distinguished by a total of 22 features. We are aware that the above feature design has some limitations, for example, geometric isomers cannot be distinguished (e.g., Id [3–5] in spreadsheet S1, Supporting Information). Nonetheless, as will be seen later, the difference in the molecular structures and the nature of redox potentials are fairly well-captured by these features. These features and the redox potentials correspond to the explanatory and explained variables of a regression model, respectively. These values are listed in spreadsheet S1, Supporting Information, together with the total energy of the additives and the total energy of their oxidized and reduced states.

Prediction of Redox Potentials by Machine Learning Approaches

By using the above defined structural features and combining the Gaussian kernel ridge regression (GKRR) and gradient boosting regression (GBR) methods, we predicted the oxidation and reduction potentials of the additives. First, an explanation of the detailed settings of the GKRR method is given. The data (features and redox potentials) were standardized because, if the variance of a certain feature is significantly larger than that of the other features, there is a possibility of it dominating the objective function; in addition, it is possible that the estimator might not correctly learn from other features as expected. Note that although the standardization of data is not necessary for the GBR method because of its scale-invariance character, we also standardized its data to facilitate comparison with the results of the GKRR method. A total of 149 data were randomly divided into two: three-quarters of the data were grouped as the training data and the remaining one-quarter as the test data. This division was also applied to the GBR model. We used k-fold cross-validation, where the training data set is divided into k-subsets, and the holdout method is repeated k times. In each case, one of the k-subsets is used as the test set and the other (k – 1)-subsets are grouped together to form the training set. The mean score over k trials is then calculated. We set k = 5 and used the coefficient of determination, R², to score the model fitness. Two hyperparameters (α and γ) in GKRR were optimized in exponential grids of 50 points between 10^–2 and 1 and 50 points between 10^–3 and 10^–1, for α and γ, respectively.

We now discuss the detailed settings of the GBR method. We used the least-squares regression as the loss function (loss = “ls”). The learning rate at which the contribution of each decision tree shrinks and the number of boosting stages to perform were set in a very conservative way to avoid overfitting (learning rate = 0.0001 and n_estimators = 100 000). In addition, the maximum depth, minimum sample split, and maximum feature parameters of the scikit-learn gradient-boosting regression module (ensemble.GradientBoostingRegressor) were set as 6, 3, and 2, respectively.

Figure 3 shows the results of the learning and prediction of the oxidation potentials by the GKRR and GBR methods. As a visual aid, we also show the 45° line that represents the perfect fitting of the regression model. We found that although both methods fit fairly well with the training data (the R² scores for GKRR and GBR are 0.868 and 0.992, respectively), the predictions with respect to the test data by GKRR are somewhat scattered, and the fitness is not as high as that observed in the GBR model. This can also be recognized from the fact that the R² score of GBR with respect to the test data is 0.851, whereas that of GKRR is 0.801.

Figure 3.

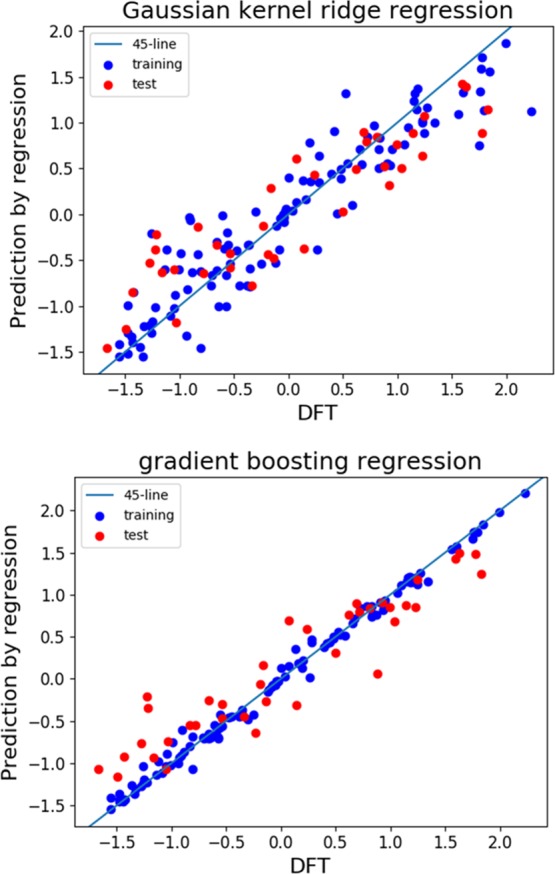
Machine learning and prediction of oxidation potentials by two regression models with standardized data: GKRR with optimized hyperparameters, α = 0.0954 and γ = 0.0222 (top), and GBR (bottom). Blue and red circles correspond to the training data and test data, respectively. Note that the axes are standardized.

Figure 4 shows the results of the learning and prediction of the reduction potentials by the GKRR and GBR methods. We found that GKRR is not so well-adapted, even to the training data. The R² score of GBR is 0.985, whereas that of GKRR is 0.804. Moreover, in comparison with the oxidation potentials, both GKRR and GBR models predict the reduction potentials poorly with respect to the test data. This is indicated by the R² scores of 0.512 and 0.643 for GKRR and GBR, respectively. In fact, it seems that the two outliers designated by arrows 1 and 2 in Figure 4 reduce the accuracy of the predictions with respect to the test data in the GBR method.

Figure 4.

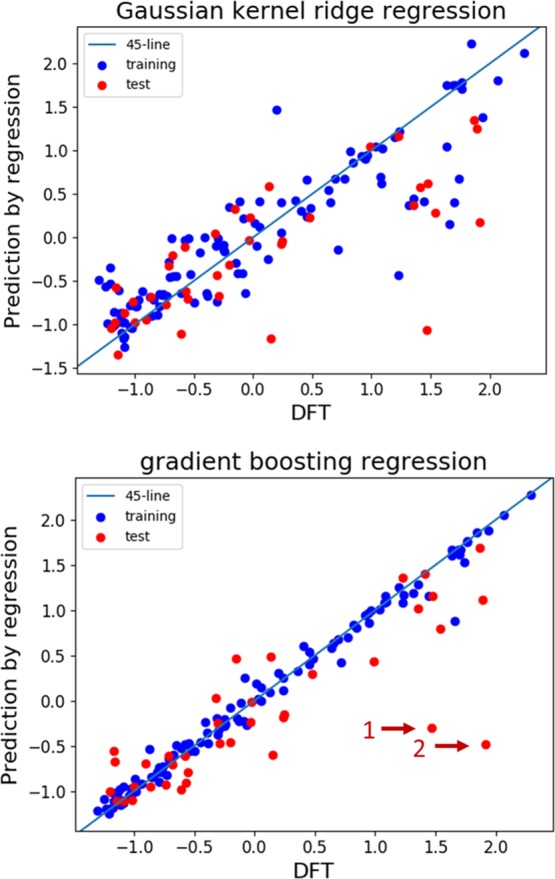
Machine learning and prediction of reduction potentials by two regression models with standardized data: GKRR with optimized hyperparameters, α = 0.0868 and γ = 0.0152 (top), and GBR with two outliers, designated by arrows (bottom). Blue and red circles correspond to the training data and test data, respectively. Note that the axes are standardized.

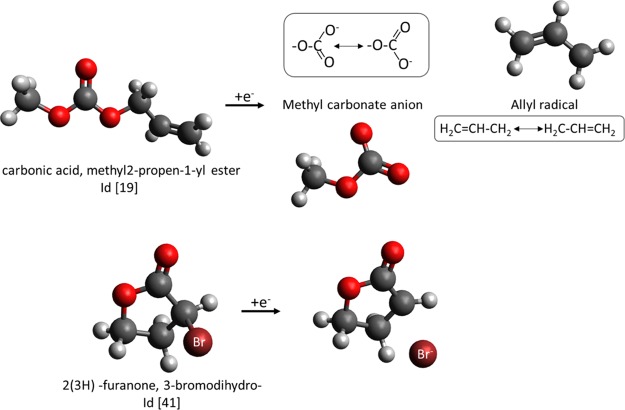
We then examined the two outliers in detail. The top part of Figure 5 shows the optimized geometries of the neutral and reduced states of carbonic acid, methyl-2-propen-1-yl ester (Id [19] in spreadsheet S1, Supporting Information) and the bottom part shows those of 2(3H)-furanone, 3-bromodihydro- (Id [41]). The former and the latter correspond to arrows 1 and 2 in Figure 4, respectively. It is noteworthy that one chemical bond is broken in the reduced state of both molecules. The reduced state of Id [19] contains the allyl radical and the methyl carbonate anion. They are significantly stabilized through resonance, as shown by the contributing structures of these species in the figure. In addition, the reduced state of Id [41] shows that the C–Br bond is broken and a bromide ion is formed in solution. The structures of these reduced states are not consistent with the original feature design based on coordination numbers; this inconsistency resulted in relatively poor prediction of reduction potentials. Note that, in general, chemical bonds are more easily broken in the reduced state than in the oxidized state because, in the reduced state, an excess electron is present in an antibonding orbital, which causes the bond to be elongated or cleaved to mitigate the enhanced electron repulsion arising from the excess electrons. In addition, the aprotic polar solvents used in LIBs sometimes make the formation of anion species energetically favorable by suitable bond cleavage.

Figure 5.

Ball-and-stick models of spontaneous bond breaking caused by reduction corresponding to the two outliers designated by arrows in Figure 4: carbonic acid, methyl-2-propen-1-yl ester (top) and 2(3H)-furanone, 3-bromodihydro (bottom). White, gray, red, and dark red balls represent H, C, O, and Br, respectively.

Thus, in the present calculations, it is somewhat difficult to interpret the results of the reduction potential because there are cases where a chemical bond is spontaneously broken in the reduced state, as shown in Figure 5. When the bond is cleaved, the polarization of the molecular system increases. In a polar solvent, this leads to a stabilization of the reduced state, which in turn leads to an increase in the reduction potential. It seems that there are additive molecules that are thermodynamically more stable in the cleaved state, even if their bonds are not spontaneously broken in the present calculation. For this reason, there is a possibility that the computationally predicted reduction potentials shown in Figure 1 are lower than those in the real systems.

Another cause for the underestimation of the reduction potentials is that there is some ambiguity regarding the value of V_abs employed to scale the redox potentials. Although we used the International Union of Pure and Applied Chemistry (IUPAC) recommended value of 4.44 V, a somewhat smaller value (4.28 V) has been reported.¹⁹ The adoption of the latter increases the reduction potentials by 0.16 V.

Importance of Features in Potential Prediction

The number of features in a regression model is sometimes reduced to improve its fitting accuracy as well as to facilitate the interpretation of the results. Although the least absolute shrinkage and selection operator (LASSO) is often used for that purpose in a linear regression model, LASSO cannot be used for nonlinear regression models, such as the GKRR, because it results in data selection instead of feature selection. By contrast, it is possible to calculate the importance of each feature in the GBR method. Figure 6 shows the relative feature importance in the prediction of oxidation and reduction potentials by the GBR method. We found that features C3, C4, O1, O2, and R6 rank high in both potentials. In addition to these features, the features related to halogens (F1 and Cl1) are also important in the reduction potential, whereas miscellaneous features (F1, N3, and Si4) are important in the oxidation potential.

Figure 6.

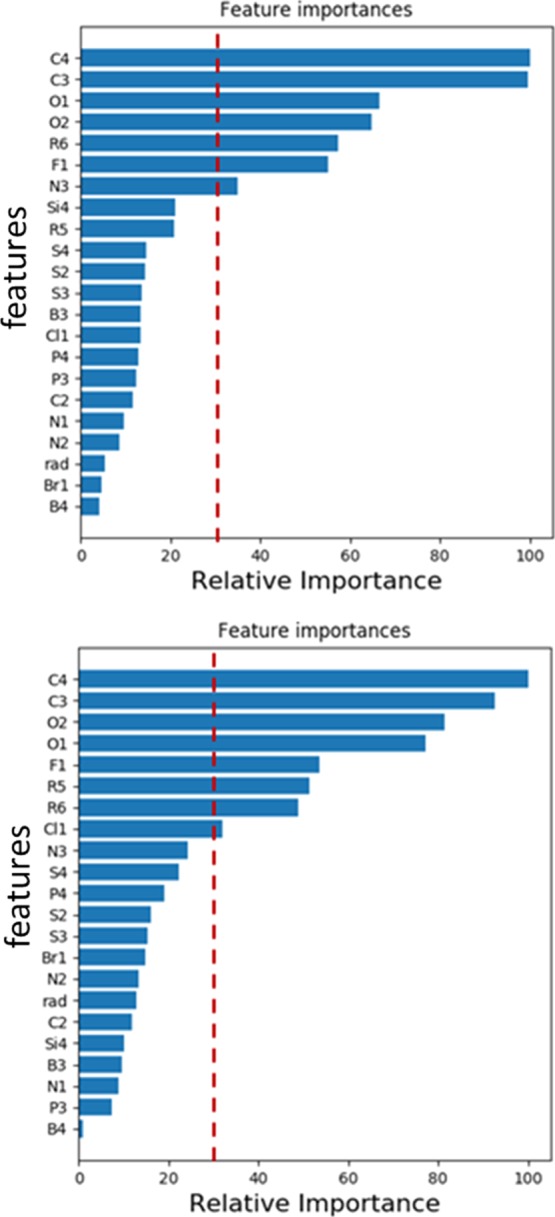
Relative feature importance in GBR models. Oxidation potential (top) and reduction potential (bottom). Dotted vertical lines represent a relative importance of 30%.

We next examined how well the feature selection predicts both potentials. As an example, we used the top eight or nine features that have over 30% relative importance in Figure 6. Figure 7 shows that the degree of fitness to training data is not reduced by the selection. In addition, the R² scores for both potentials did not change much, as shown in Table 1. By contrast, the fitness to the test data by the trimmed model is somewhat worse than that resulting from the full-feature model (Table 1). However, by comparing Figures 3, 4, and 7, we found that the essential behavior of the prediction versus the density functional theory (DFT) calculations can still be reproduced by the trimmed model.

Figure 7.

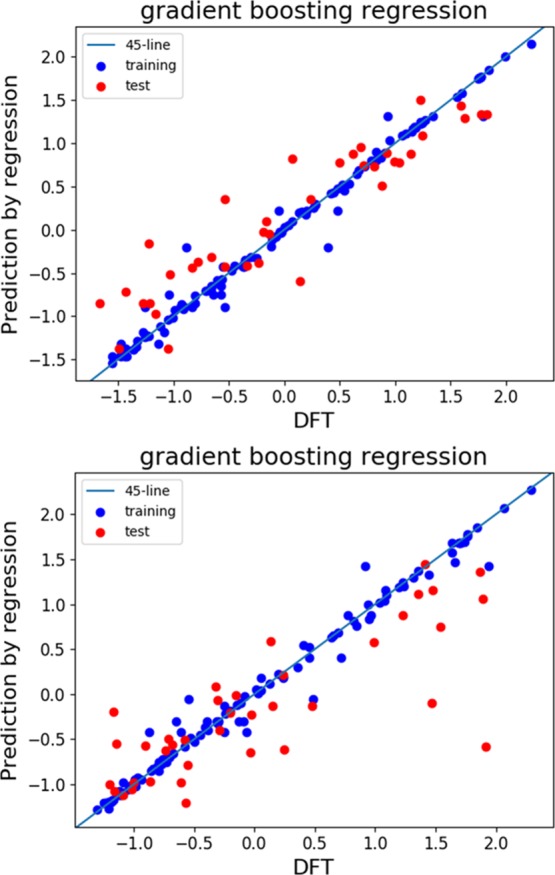
GBR models with a reduced number of features: oxidation potential using eight key features in Figure 6 (top) and reduction potential using nine key features in Figure 6 (bottom). Blue and red circles correspond to the training data and test data, respectively. Note that the axes are standardized.

Table 1. R² Scores of the GBR Method with Full and Reduced Features.

		full-feature	reduced featuresa
oxidation potential	training	0.992	0.982
	test	0.851	0.830
reduction potential	training	0.985	0.982
	test	0.643	0.603

^aThe top eight and nine features were used for the oxidation and reduction potentials, respectively.

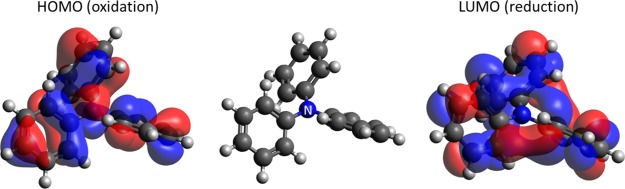
Finally, we considered the reasons why the trimmed model predicted the redox potentials reasonably well, and to a similar extent, to that of the full-feature model. In the oxidized state, an electron is extracted from the highest occupied molecular orbital (HOMO), whereas in the reduced state, it is added to the lowest unoccupied molecular orbital (LUMO). Therefore, these frontier orbitals should be investigated. We focused on N,N-diphenyl-benzenamine (Id [82] in the Supporting Information). This molecule has a three-coordinate nitrogen atom in the center. According to Figure 6, N3 is more important for the oxidation potential than for the reduction potential. This is consistent with the fact that the amplitude of the eigenstate function is observed on nitrogen in the HOMO but not in the LUMO, as shown in Figure 8. Quantitatively, the orbital-by-orbital population analysis shows that the contributions of N3 to the HOMO and LUMO are 0.2778 and 0.0797, respectively. Thus, a correlation was found between the results of machine learning and the electronic structure calculations. Moreover, these results support the exclusion of hydrogen atoms from the feature design because they form σ bonds, whose energy levels are significantly far from those of the frontier orbitals (HOMO and LUMO).

Figure 8.

HOMO and LUMO eigenstates of N,N-diphenyl-benzenamine.

Conclusions

We performed ab initio molecular orbital calculations to examine the redox potentials of 149 representative molecules used as additives for the electrolytes of LIBs. We observed that most of the anode additives have oxidation potentials of 5 V (vs Li/Li⁺) or more, whereas the majority of the cathode additives have oxidation potentials of 5 V (vs Li/Li⁺) or less. We constructed features of the additive molecules based on their constituent elements and their coordination numbers to predict the redox potentials by two regression methods, GKRR and GBR. Although both methods predicted the oxidation potentials fairly well, GBR was somewhat superior to GKRR in the prediction of the reduction potentials. We also found that the essential character of the redox potentials can be described by a smaller number of features derived from the analysis of the important features in GBR. The importance of these features seems to be related to the amplitude of the eigenstate of the frontier orbitals.

Computational Details

All ab initio molecular orbital calculations reported in this paper were carried out with the Gaussian 16 Revision A.03 program.²⁰ Hybrid DFT calculations were carried out using the B3LYP hybrid exchange–correlation functional, which comprises Becke’s three-parameter exchange functional and Lee–Yang–Parr correlation functional.²¹⁻²³ The 6-31++G(d,p) split-valence double-zeta basis set augmented with polarization and diffuse functions was used in this study. For all charge states, the molecular/ionic geometries were fully optimized until the magnitude of the residual forces became less than 4.5 × 10^–4 hartree/bohr. Solvent effects were treated by using the integral equation formalism (IEF)-polarizable continuum model (PCM), which performs a reaction field calculation using the IEF model.²⁴ Dimethyl sulfoxide (DMSO, ε = 46.826) was used as a continuum dielectric material in the IEF-PCM calculations with a default cavity. Note that a mixed solvent composed of carbonates with high and low dielectric constants is commonly used as an electrolyte solvent in LIBs. For example, the dielectric constant of a 1:1 mixed solvent of ethylene carbonate (ε = 90) and diethyl carbonate (ε = 2.8) will be ε = 46, assuming additivity for the dielectric constant with respect to volume. This value is close to the dielectric constant of DMSO. We expect that using DMSO as the solvent will not cause a large error because most of the solvent effect is determined by the dielectric constant, although the solvent effect calculated by PCM includes nonelectrostatic interactions, which reflect the shape of the solvent molecule.

The oxidation (V_ox) and reduction (V_red) potentials of additive A on a voltage (vs Li/Li⁺) scale were calculated as follows

where E_tot(A) is a total energy of A in electronvolts. E_tot(A⁺) and E_tot(A^–) are the total energies of the oxidized and reduced states of A, respectively. V_shift corresponds to the difference between the absolute potential (V_abs) and the magnitude of the redox potential of the Li metal (|V_Li|). The values of V_abs and |V_Li| are 4.44²⁵ and 3.04 V,²⁶ respectively. The value used for V_abs is that estimated by Trasatti and recommended by the IUPAC The use of these values results in a V_shift of 1.4 V. Note that the total energy output from the self-consistent reaction field calculation in Gaussian 16 includes all computed corrections in solution, unlike the Gaussian 03 output.

To find the relationship between the structure of the additives and their redox potentials, we considered two regression models: GKRR and GBR. GKRR is a combination of the Gaussian kernel method and ridge regression with L2-norm regularization term. Because of the flexibility afforded by the nonlinear character of the Gaussian kernel and the ingenious kernel trick, GKRR efficiently finds relationships that ordinary linear regression fails to find.¹⁵ GKRR contains two hyperparameters (σ and λ), which were optimized by using grid search. GBR produces a regression model in the form of ensemble decision trees.²⁷ It evolves the model in a stepwise manner by optimizing the loss function via its gradient. All machine learning calculations in this study were based on the scikit-learn package, which is a collection of APIs for machine learning in Python.²⁸

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b00576.

• Molecular formula, chemical structure, CAS registry number, CAS name, total energy of the additive, total energy of the additive in the oxidized state, total energy of the additive in the reduced state, oxidation potential, reduction potential, and molecular features used in this study (XLSX)

Author Contributions

Y.O. performed the calculations and the analysis of the results. All authors discussed and interpreted the results and contributed to the preparation and writing of the manuscript.

The authors declare no competing financial interest.