One-Step Synthesis, Structure, and Band Gap Properties of SnO₂ Nanoparticles Made by a Low Temperature Nonaqueous Sol–Gel Technique

Abstract

Because of its electrically conducting properties combined with excellent thermal stability and transparency throughout the visible spectrum, tin oxide (SnO₂) is extremely attractive as a transparent conducting material for applications in low-emission window coatings and solar cells, as well as in lithium-ion batteries and gas sensors. It is also an important catalyst and catalyst support for oxidation reactions. Here, we describe a novel nonaqueous sol–gel synthesis approach to produce tin oxide nanoparticles (NPs) with a low NP size dispersion. The success of this method lies in the nonhydrolytic pathway that involves the reaction between tin chloride and an oxygen donor, 1-hexanol, without the need for a surfactant or subsequent thermal treatment. This one-pot procedure is carried out at relatively low temperatures in the 160–260 °C range, compatible with coating processes on flexible plastic supports. The NP size distribution, shape, and dislocation density were studied by powder X-ray powder diffraction analyzed using the method of whole powder pattern modeling, as well as high-resolution transmission electron microscopy. The SnO₂ NPs were determined to have particle sizes between 3.4 and 7.7 nm. The reaction products were characterized using liquid-state ¹³C and ¹H nuclear magnetic resonance (NMR) that confirmed the formation of dihexyl ether and 1-chlorohexane. The NPs were studied by a combination of ¹³C, ¹H, and ¹¹⁹Sn solid-state NMR as well as Fourier transform infrared (FTIR) and Raman spectroscopy. The ¹³C SSNMR, FTIR, and Raman data showed the presence of organic species derived from the 1-hexanol reactant remaining within the samples. The optical absorption, studied using UV–visible spectroscopy, indicated that the band gap (E_g) shifted systematically to lower energy with decreasing NP sizes. This unusual result could be due to mechanical strains present within the smallest NPs perhaps associated with the organic ligands decorating the NP surface. As the size increased, we observed a correlation with an increased density of screw dislocations present within the NPs that could indicate relaxation of the stress. We suggest that this could provide a useful method for band gap control within SnO₂ NPs in the absence of chemical dopants.

1. Introduction

As one of the most important members of the transparent conducting oxide (TCO) class of materials, the electronic and optical properties of pure and doped SnO₂ have been investigated extensively.^1,2 Tin oxide (SnO₂) nanoparticles (NPs) are being developed for applications ranging from their incorporation as an opacifier in ceramic glazes to advanced technologies including gas sensors, lithium-ion batteries, low emission window coatings, touch screens, sensitized solar cells, field emission flat displays, and other optoelectronic devices.³ For each of these applications, it is important to have a simple, low cost and scalable synthesis approach that will produce NPs within a narrow distribution of particle sizes.² Various synthesis strategies have been developed to produce SnO₂ NPs with different size ranges and distributions.⁴⁻¹¹ These processes usually require use of high temperatures, high boiling point or mixed solvents, and expensive organic tin precursors that are often toxic and require a complicated synthesis procedure. The experimental parameters required for such reactions run counter to the ability to produce highly crystalline nanosized structures with controllable properties. To avoid the problems associated with several of the proposed routes, synthetic routes that avoid the use of water and toxic solvents or surfactants and/or toxic solvents have been investigated.^12,13 It is now important to develop one-pot synthesis methods that can produce crystalline SnO₂ NPs with tuneable particle sizes and band gap properties. Nonaqueous sol–gel processing is a flexible and powerful approach to obtain functionally active NPs.¹⁴⁻¹⁸ Here, we present a facile, one-pot, nonhydrolytic synthesis of SnO₂ NPs with controllable average size and with a narrow size distribution at low temperature.

Bulk crystalline SnO₂ with a tetragonal rutile structure (cassiterite phase) is an n-type direct gap semiconductor with the band gap (E_g) equal to 3.6 eV (344 nm). It provides an archetypal TCO, having up to 97% transparency across the visible spectrum.¹⁹ This large value is comparable with that required for complete transparency throughout the visible range (i.e., E_g > 3.1 eV). A large amount of research has been devoted to modifying the SnO₂ conduction band minimum and consequently modifying its optical absorption properties. These can be tuned by substituting elements such as such as F, Sb, or Pb on the anion or cation sites, by controlling NP size and morphology,^1,2 or by causing internal strain within materials prepared as thin-film samples.²⁰ Nearly all of the studies to date have reported that E_g typically increases for smaller NP sizes.²¹⁻²⁶

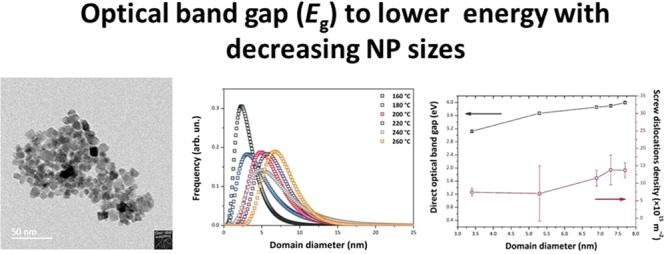
The nonaqueous sol–gel process is based on the reaction between tin(IV) tetrachloride Sn(Cl)₄ and 1-hexanol, leading to the formation of SnO₂ NPs with a narrow dispersion and average sizes between 3.4 and 7.7 nm by varying the synthesis temperature between 160 and 260 °C. Both reagents are readily available, and the potentially scalable process yields NP materials that can be used without further processing. Unusually, we observed that E_g for our materials increased as the NPs became larger, with values determined to lie between 2.22 (indirect) and 3.12 (direct) eV for 3.4 nm NP sizes, to 3.53–3.99 eV for 7.7 nm particles. In order to investigate the origin of these unusual electronic structure changes, we carried out detailed structural and spectroscopic investigations of our SnO₂ NPs using a combination of X-ray powder diffraction (XRPD), high-resolution transmission electron microscopy (HRTEM), UV–visible, IR and Raman, and ¹¹⁹Sn, ¹³C, and ¹H nuclear magnetic resonance (NMR) spectroscopy techniques. Analysis of the XRPD data using the whole powder pattern modeling (WPPM) technique²⁷⁻³³ revealed the presence of axial strains and screw dislocations within the NPs. These strains are correlated with the presence of organic ligands detected by NMR, IR, and Raman spectroscopy and likely determine the unexpected band gap behavior, as well as providing possibilities for further modification and functionalization of the NP surfaces.

2. Results and Discussion

2.1. X-ray Diffraction and HRTEM

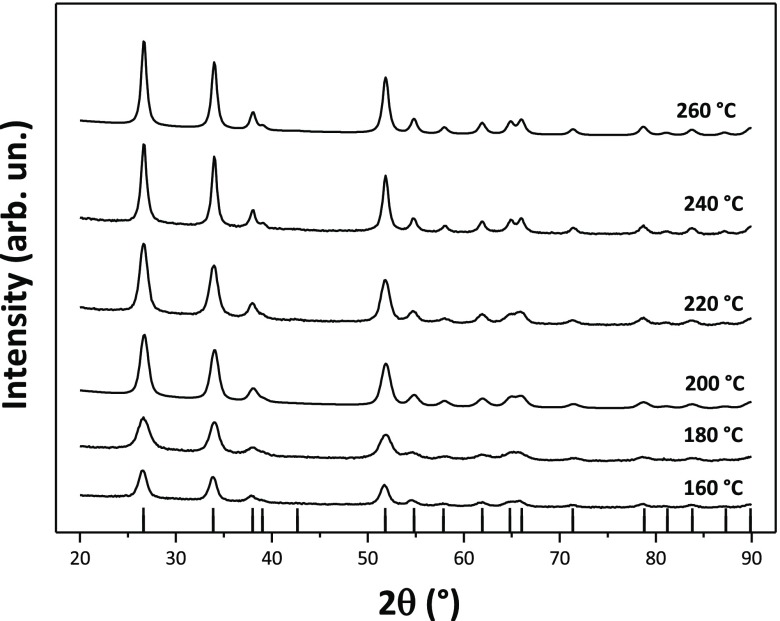
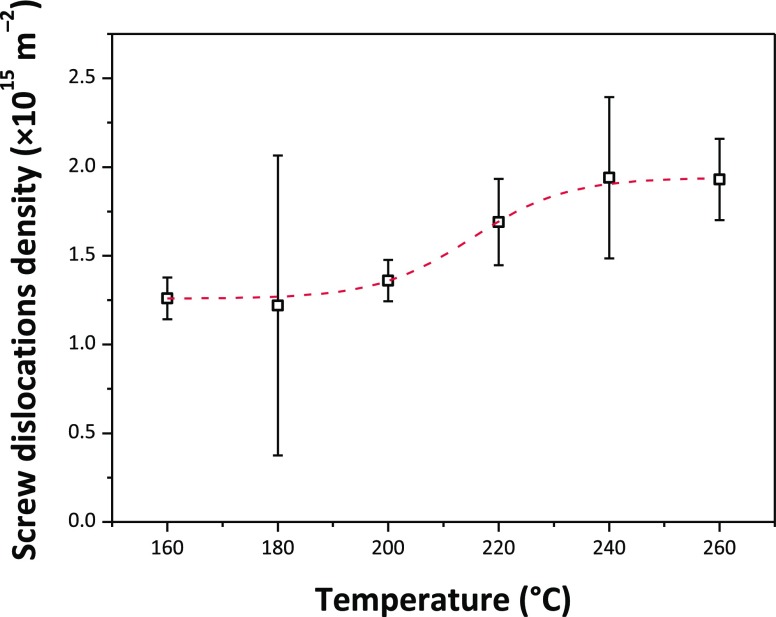
The SnO₂ NPs crystallized with the rutile structure (space group P4₂/mnm), with no additional impurity phases detected by X-ray examination (Figure 1). Initial examination of the XRPD patterns indicates that the peaks became sharper and better resolved with increasing NP size at higher synthesis temperature. We then applied WPPM analysis to the observed XRPD profiles.^27,34 This approach provides information on the average crystalline domain size of the SnO₂ NPs and edge and screw dislocation densities (Table 1 and Figure 2); it has also been applied recently to solve both size and defect concentration in the SnO₂ system.^33,35,36 The almost flat nature of the residual line, displayed in Figure 2, indicates an excellent agreement between the experimental data and the model; this also suggests that the assumption of spherical shape for the investigated SnO₂ nanodomains is likely appropriate. The log-normal size distributions of the SnO₂ NPs synthesized at different temperatures shown in Figure 3 agree generally with the particle size distributions obtained from the HRTEM images described below. However, we note that the X-ray diffraction data and modeling provide more statistically representative sampling for the overall specimens than analysis of the TEM images. The unit cell volumes did not vary significantly as a function of synthesis temperature, but small changes in the tetragonal distortion of the SnO₂ unit cell were observed, primarily that the c/a ratio increased slightly with the increasing synthesis temperature (Table 1). The average crystalline domain diameter of SnO₂ at 160 °C found by WPPM analysis was 3.4 nm with a tail in the log-normal size distribution function extending to ∼10 nm (Table 1, Figure 3). Increasing the synthesis temperature led to a gradual increase in the average crystalline domain diameter—this became 6.9 nm at 220 °C and 7.7 nm by 260 °C. As shown in Table 1 and Figure 3, all the probability distributions have a positive skewness, with some dispersion around the tails to larger NP sizes. The number of screw dislocations “ρ_e” was determined to be greater than that of edge dislocations in all of the samples investigated (Table 1). The number of the edge dislocations did not change, whereas the density of screw dislocations “ρ_s” increased slightly as a function of the synthesis temperature.³³ The population of screw dislocations also exhibited a wider distribution about the mean for syntheses carried out at 180 °C (Figure 4).

Figure 1.

Powder X-ray diffraction patterns (Cu Kα radiation) of the SnO₂ specimens prepared at different temperatures. The vertical lines below indicate the expected reflections for the rutile structured cassiterite phase.

Table 1. Results of WPPM Modeling and Refinement from the X-ray Powder Diffraction Data, Including Unit Cell Parameters, Tetragonality (c/a), Crystalline Domain Diameters (Average, Mode, and Skewness of the log-Normal Size Distribution), and Dislocation Densities (Edge and Screw, ρ_e and ρ_s, Respectively) of Synthesized SnO₂ NPs.

	agreement factors			unit cell parameters (nm)				crystalline domain diameter (nm)			dislocation density (×1015 m–2)
synthesis temperature (°C)	Rwp (%)	Rexp (%)	χ2	a = b (nm)	c (nm)	volume (nm3)	c/a	average	mode	skewness	ρe	ρs
160	2.25	1.38	1.64	0.4751(1)	0.3185(1)	0.072(1)	0.6703	3.4(1)	2.3(1)	1.7(1)	1.0(7)	1.3(1)
180	1.85	1.34	1.38	0.4749(1)	0.3186(1)	0.072(1)	0.6709	5.3(2)	3.1(1)	2.2(1)	1.0(5)	1.2(8)
200	2.20	1.68	1.31	0.4750(1)	0.3189(1)	0.072(1)	0.6713	6.2(4)	4.9(3)	1.3(1)	1.0(7)	1.4(1)
220	1.94	1.33	1.46	0.4748(1)	0.3190(1)	0.072(1)	0.6719	6.9(2)	5.7(2)	1.1(1)	1.0(1)	1.7(2)
240	2.03	1.34	1.51	0.4748(1)	0.3188(1)	0.072(1)	0.6714	7.2(3)	5.0(2)	1.7(1)	1.0(3)	1.9(5)
260	2.04	1.31	1.56	0.4749(1)	0.3189(1)	0.072(2)	0.6714	7.7(1)	6.7(1)	0.9(1)	1.0(5)	1.9(2)

Figure 2.

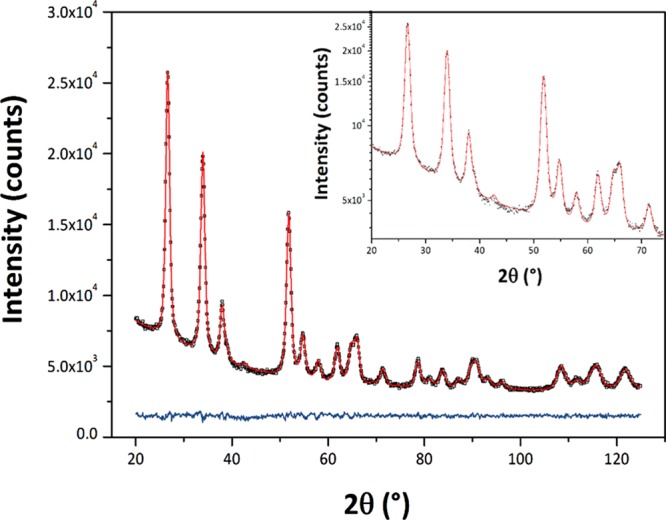
Typical output of the WPPM modeling protocol applied to the observed X-ray diffraction pattern of a specimen synthesized at 220 °C. The black open squares represent the observed data, and the red continuous line represents the refined fit. The blue continuous line below shows the difference between observed and calculated profile. The log-scale plot (up to 75° 2θ) shown in the inset highlights details in the peak tail and background region.

Figure 3.

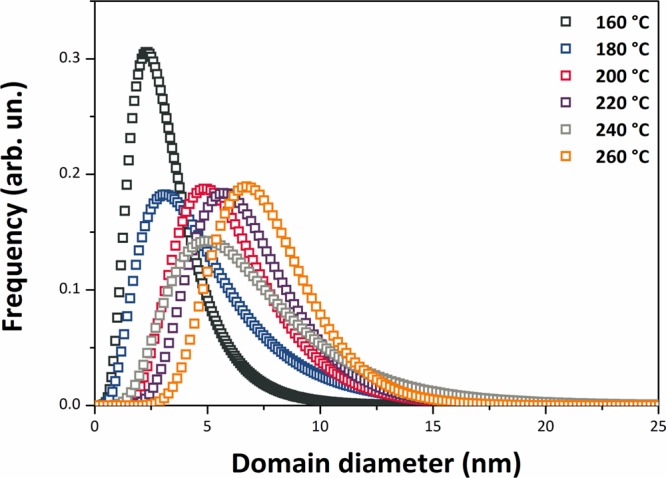
SnO₂ NP size distributions obtained from WPPM modeling.

Figure 4.

Evolution of screw dislocation densities with the synthesis temperature. The red dashed line represents a sigmoidal fit obtained using a sigmoidal Boltzmann function (R² = 0.997).

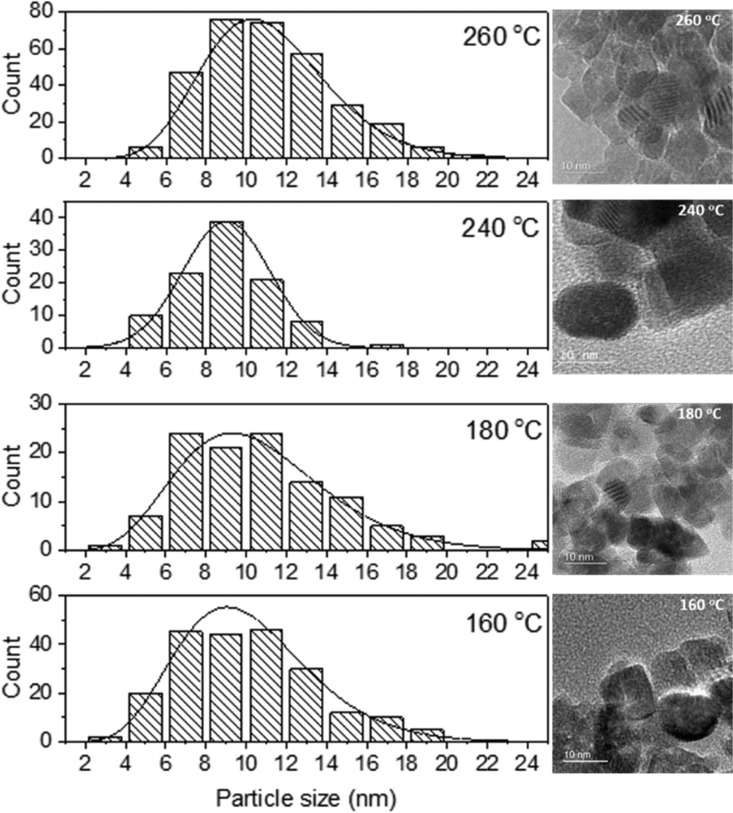
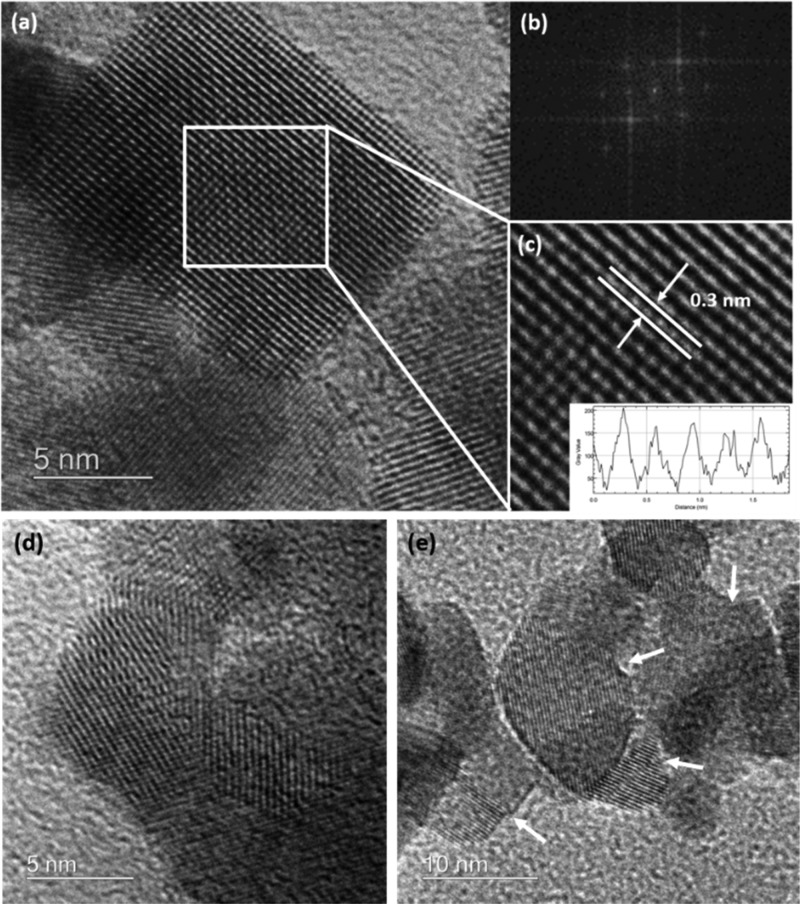
The effects of synthesis temperature on the size, morphology, and development of defects within the SnO₂ NPs were further investigated using HRTEM (Figure 5 and Table 2). All of the NPs exhibited a high degree of crystallinity, with lattice fringes matching the cell parameters of rutile-structured SnO₂ (Figure 6). Our HRTEM images provided direct evidence for the existence of screw as well as edge dislocations within the SnO₂ NP samples deduced from the WPPM XRPD analysis (Figure 6). The SnO₂ crystallite sizes estimated from the recorded images ranged between 2 and 11 nm, generally consistent with our WPPM analysis of the XRPD data, although that analysis provides a more complete average over the entire sample.

Figure 5.

Particle size distribution (left) of SnO₂ NPs prepared at 160, 180, 240, and 260 °C from the analysis of HRTEM images (right).

Table 2. HRTEM Particle Size Distributions Obtained by Analysis of Images for Samples Prepared at 160, 180, 240, and 260 °C.

temperature (°C)	average size (nm)	minimum size (nm)	maximum size (nm)	standard deviation
160	10.2	4.0	19.5	3.4
180	10.6	4.0	24.7	3.9
240	9.0	4.50	17.3	2.2
260	11.2	4.7	21.2	3.1

Figure 6.

(a) HRTEM image of a SnO₂ sample prepared at 180 °C along with (b) its Fourier transform; (c) detail of the image showing lattice fringes with spacing ∼0.3 nm corresponding to the c axis dimension of rutile structured SnO₂. Inset: Atomic density plot profile highlighting the spacing between lattice fringes; (d,e) HRTEM images showing the presence of screw and edge dislocations within NPs from this sample.

2.2. Liquid Phase NMR Spectroscopy

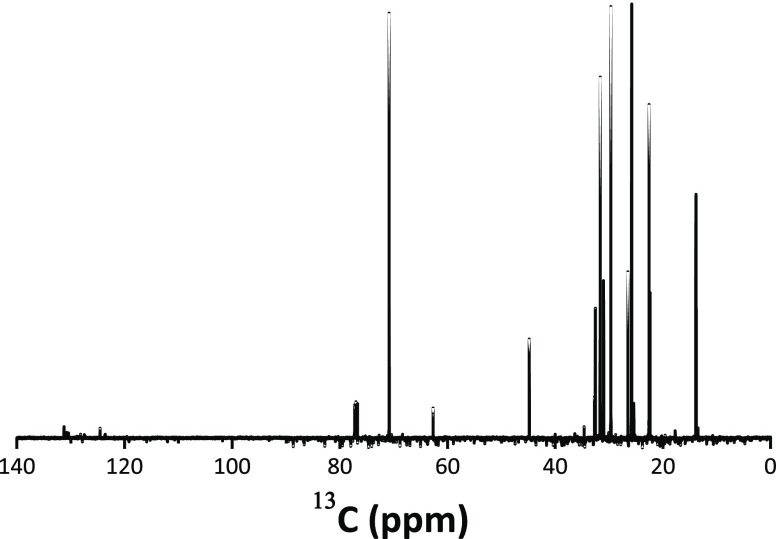
In order to study the reaction of 1-hexanol with SnCl₄ during the synthesis, the supernatant liquid was filtered to remove the SnO₂ solid precipitate, and analyzed using liquid ¹H and ¹³C NMR spectroscopy. The ¹³C NMR spectrum is shown in Figure 7 (the ¹H NMR spectrum is included in the Supporting Information file, Figure S1). From the analysis of this spectrum, the presence of 1-hexanol (with the C1 carbon at 62.8 ppm), dihexyl ether (with the C1 carbon at 71.1 ppm), and 1-chlorohexane (with the C1 carbon at 45.1 ppm) was determined (Table S1). All other peaks from these three hydrocarbons corresponding to hexane carbons C2–C6 appear in the same region at 14–33 ppm. The formation of the dihexyl ether component was deduced from the analysis of the solid-state ¹³C MAS NMR spectra, described in the following section.

Figure 7.

¹³C NMR spectrum of the reaction solution after removal of the NPs.

2.3. Solid-State NMR of SnO₂ NPs

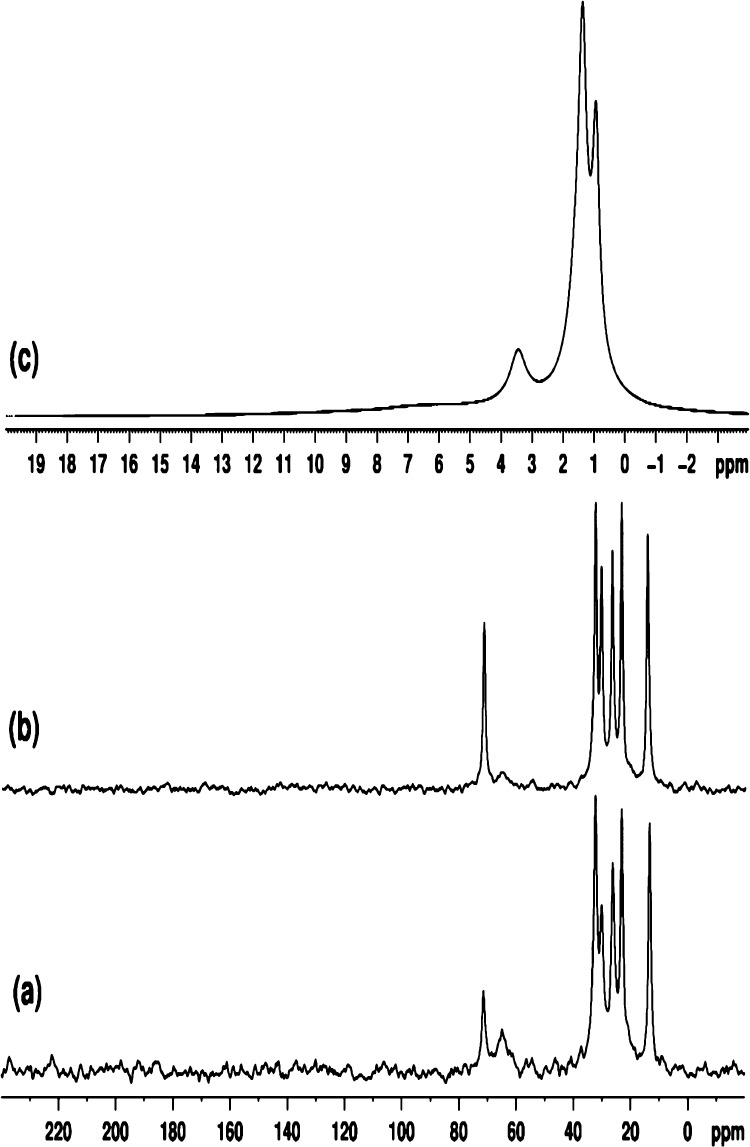
The ¹³C MAS NMR spectra of our samples are consistent with the production of 1-hexanol (C₆H₁₃OH), and also dihexyl ether (C₆H₁₃–O–C₆H₁₃) species during the SnO₂ NP synthesis reaction, that remain associated with the solid SnO₂ NP samples to the highest temperatures studied here. The spectrum of the sample prepared at 160 °C (Figure 8a) shows a broad signal at 64.9 ppm that can be assigned to the C1 atom of 1-hexanol. This is typically expected to occur at ∼62 ppm, and the ∼3 ppm increase in chemical shift can be attributed to strong H-bonding interactions with the SnO₂ NP surface. The 6 narrow signals observed at 72.5, 32.3, 30.1, 26.2, 23.1, and 13.3 ppm, along with analogous signals at 71.4, 32.5, 30.4, 26.6, 23.3, and 14.3 ppm for the 200 °C sample, can be attributed to the 6 inequivalent carbon environments (C1–C6) of the hexyl (C₆H₁₃−) fragments (Figure 8b). The observed shift at ∼72 ppm can suggest dihexyl ether formation due to the change from −CH₂–O–H to −CH₂–O–CH₂C₅H₁₁ environments. An additional β-effect of about +10 ppm of the CH₂C₅H₁₁ substituent (by analogy with the β-effect of the methyl group)³⁷⁻⁴⁰ acting on the chemical shift of the C1 carbon would be consistent with this assignment. The reported ¹³C shifts for dihexyl ether in CDCl₃ solution at 71.05, 31.85, 29.90, 26.01, 22.71, and 14.02 ppm^37,38 agree with those observed here for samples prepared at 160 and 200 °C. Such high frequency shifts are well known from previous ¹³C NMR studies. The signals from C2–C6 atoms of dihexyl ether and 1-hexanol are expected to overlap.³⁷⁻⁴⁰ From Figure 8, increasing the synthesis temperature (T_syn) from 160 to 200 °C leads to significant decrease of the signal intensity at ∼65 ppm, reflecting a decrease in the amount of adsorbed 1-hexanol at higher temperature. From the integral intensities of signals at 72 and 65 ppm, the mole-to-mole ratio of dihexyl ether to 1-hexanol changes from 0.6 at 160 °C to 2.7 at 200 °C. Note that unlike the liquid-state ¹³C NMR spectrum (Figure 7), no signal was observed at ∼45 ppm, indicating the absence of 1-chlorohexane in the ¹³C MAS SSNMR spectra of the SnO₂ NP samples analyzed (Figure 8).

Figure 8.

Proton-decoupled ¹³C MAS (8 kHz) SSNMR spectra of samples prepared at (a) 160 and (b) 200 °C; (c) ¹H MAS (12 kHz) NMR spectrum of the sample prepared at 200 °C.

The ¹H MAS spectrum of the sample prepared at 200 °C shows three well-resolved peaks at 3.4, 1.4, and 0.9 ppm (Figure 8c). The signals at 3.4 and 0.9 ppm are assigned to methylene and methyl protons of dihexyl ether. Signals from the remaining methylene protons of dihexyl ether (in positions 2, 3, 4, and 5) overlap, giving rise to the signal with highest intensity at 1.4 ppm. A very broad peak at ∼6 ppm can also be observed, that we assign to hydroxyl protons of water and 1-hexanol. The ¹H MAS spectrum of the sample prepared at 160 °C was similar to that shown in Figure 8c, with slightly broader lines. The results definitely indicated the presence of dihexyl ether in the sample prepared at 260 °C. However, no 3.4 ppm signal was observed in the ¹H MAS spectrum of one sample prepared at 180 °C, that was subsequently annealed at 240 °C.

In order to gain insight into the structural differences between SnO₂ NPs synthesized at different temperatures, ¹¹⁹Sn SSNMR measurements were undertaken using 300 MHz (Figure 9) and 600 MHz NMR instruments. The half-height linewidths of the isotropic peaks in ¹¹⁹Sn MAS NMR spectra measured on a 600 MHz NMR instrument were as follows: 1.2 ± 0.1 kHz (T_syn = 180 °C, annealed at 240 °C for 72 h) and 8 ± 0.5 kHz (T_syn = 200 °C). Previously, Tunstall et al. measured ¹¹⁹Sn NMR parameters of a series of SnO₂ samples with powder sizes varying between 4 and 32 nm in comparison with data for standard bulk cassiterite SnO₂ powder (∼10 μm) using a 500 MHz NMR spectrometer.⁴¹ In their case, the observed linewidths were between 0.6 and 1.7 kHz, which is significantly less than that measured in this work for our sample prepared at 200 °C.

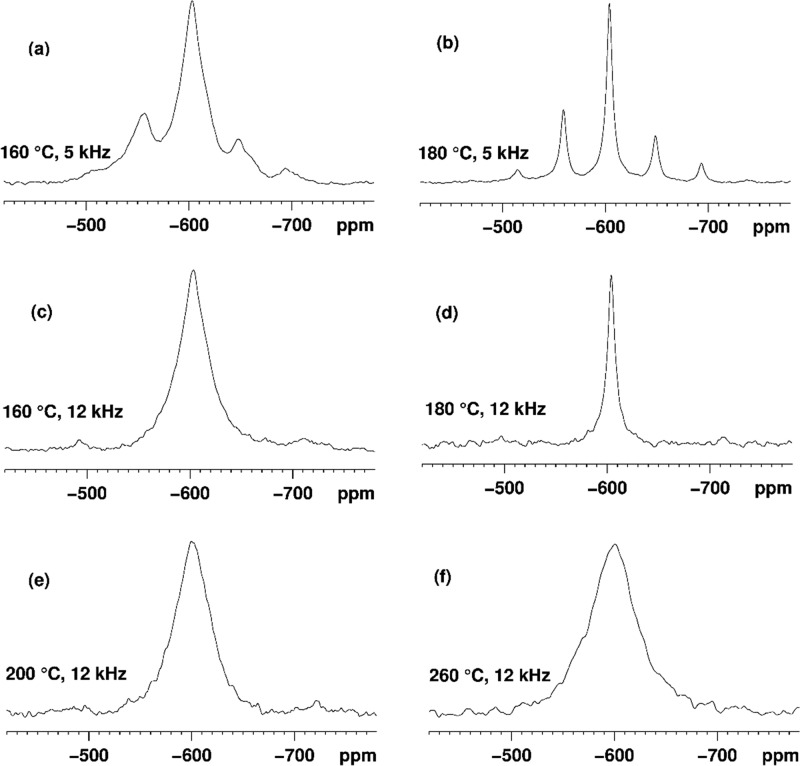
Figure 9.

¹¹⁹Sn MAS SSNMR spectra of SnO₂ samples prepared at (a) 160 °C (MAS 5 kHz); (b) 180 °C (MAS 5 kHz); (c) 160 °C (MAS 12 kHz); (d) 180 °C (MAS 12 kHz); (e) 200 °C (MAS 12 kHz); and (f) 260 °C (MAS 12 kHz). Unlike other samples, the sample prepared at 180 °C was subsequently annealed at 240 °C for 72 h.

We attribute such unusually large signal widths to the small average particle sizes achieved in our studies (<8 nm, where the sample properties are dominated by surface rather than bulk effects),⁴¹ combined with an increase in defect densities noted for the NPs from WPPM and HRTEM analysis. The linewidths of the isotropic peaks in ¹¹⁹Sn MAS NMR spectra measured on a 300 MHz NMR instrument were as follows: 3.5 ± 0.2 kHz (T_syn = 160 °C), 0.68 ± 0.05 kHz (T_syn = 180 °C, then annealed at 240 °C for 72 h), 4.4 ± 0.2 kHz (T_syn = 200 °C), and 5.2 ± 0.5 kHz (T_syn = 260 °C). In previous work, the ¹¹⁹Sn NMR linewidths were found to increase with decreasing particle size. However, our results suggest the opposite behavior. This could be partly due to the increase in dislocation densities determined by WPPM analysis of our XRPD data. The observation of broad lines and their field dependence are also similar to those described by Alla and Lippmaa,⁴² which they attribute to the anisotropy of the magnetic susceptibility, Δχ_υ. They showed that adamantane mixed at a 1:10 ratio with p-dibromobenzene shows severely broadened ¹³C lines due to the magnetic field produced by crystallites of p-dibromobenzene surrounding the adamantane particles. Similar arguments could apply in the case of SnO₂ NPs, where each ¹¹⁹Sn environment experiences the magnetic field produced by large numbers of smaller SnO₂ NPs, leading to broadened lines. Only the sample prepared at 180 °C and annealed at 240 °C shows narrow lines in the ¹¹⁹Sn NMR spectrum, and this is likely due to sintering of the NPs causing agglomeration into larger crystallites.⁴¹ There is a noticeable line narrowing on proton decoupling, giving rise to the following isotropic linewidths measured on a 300 MHz NMR instrument: 3.2 ± 0.2 kHz (160 °C), 0.67 ± 0.05 kHz (180 °C, annealed at 240 °C for 72 h), 4.1 ± 0.2 kHz (200 °C), and 4.9 ± 0.5 kHz (260 °C). This agrees with the ¹H and ¹³C NMR results that indicate that organic species and water are adsorbed on the surface of the SnO₂ NPs. The close proximity of protons to the tin atoms of SnO₂ leads to additional broadening due to ¹H–¹¹⁹Sn dipolar interactions in ¹¹⁹Sn MAS spectra without proton decoupling.

We estimated the ¹¹⁹Sn chemical shift anisotropy (CSA, Δδ) and the asymmetry parameter (η) for our samples.⁴³ As a reference, we used values for crystalline SnO₂, although we note that there is some disagreement in previously reported ¹¹⁹Sn CSA parameters for the cassiterite phase. Clayden et al.⁴⁴ reported Δδ/η values of −125 ppm/0, while Cossement et al.⁴³ found −125 ppm/0.27. From iterative Herzfeld–Berger analysis of the spinning sideband intensities using the HBA program^43,44 in the ¹¹⁹Sn NMR spectrum recorded at a magic-angle spinning (MAS) frequency of 5 kHz at 7.05 T for the sample prepared at 180 °C, our best-fit Δδ/η values are −134 ppm/0.55, with δ₁₁ = −535 ppm, δ₂₂ = −584 ppm, δ₃₃ = −693 ppm, and δ_iso = −604 ppm. These are in agreement with the best-fit Δδ/η values of −136 ppm/0.50 (δ₁₁ = −536 ppm, δ₂₂ = −581 ppm, δ₃₃ = −695 ppm, and δ_iso = −604 ppm) determined from analysis of the ¹¹⁹Sn NMR spectrum recorded at a MAS frequency of 10 kHz at 14.1 T for the same sample. Our best-fit CSA parameters determined from the analysis of spinning sideband intensities at a MAS frequency of 5 kHz were Δδ = −131 ppm and η = 0.37 (δ₁₁ = −542 ppm, δ₂₂ = −575 ppm, δ₃₃ = −690 ppm, and δ_iso = −603 ppm) for the 160 °C sample and Δδ = −134 ppm and η = 0.50 (δ₁₁ = −535 ppm, δ₂₂ = −580 ppm, δ₃₃ = −691 ppm, and δ_iso = −602 ppm) for that prepared at 200 °C. Because of the very large linewidths, these can be only considered as approximate estimates, although they demonstrate an increase in values compared to those for bulk cassiterite^43,44 with an average particle size ≈ 10 μm.⁴¹ Such changes in the ¹¹⁹Sn CSA parameters are commensurate with the increased number of Sn sites near the SnO₂ NP surface compared to bulk atoms in nanometer-sized NPs.

2.4. IR and Raman Spectroscopy

Fourier transform infrared (FTIR) spectra of the samples showed strong absorption occurring between 400 and 750 cm^–1 with two main maxima observed near 650 and 545 cm^–1 (Figure 10). These features are typical of SnO₂ NPs and are related to asymmetric and symmetric Sn–O stretching vibrations of the bulk phase.⁴⁵ The lower wavenumber component is slightly enhanced for samples prepared at lower temperature that have a smaller NP size, whereas an additional structure begins to be observed on the higher frequency band of the 260 °C sample, approaching the IR spectra of bulk SnO₂ powders.⁴⁶ The strong asymmetric band with its maximum near 3450 cm^–1 indicates the presence of adsorbed molecular H₂O on the surface of the NP samples. This also gives rise to the feature near 1630 cm^–1 due to H–O–H bending. The SnO₂ NPs readily adsorb molecular H₂O from the atmosphere, as demonstrated by our thermogravimetric (TGA) analyses of samples that had been exposed to air (Figure S2).

Figure 10.

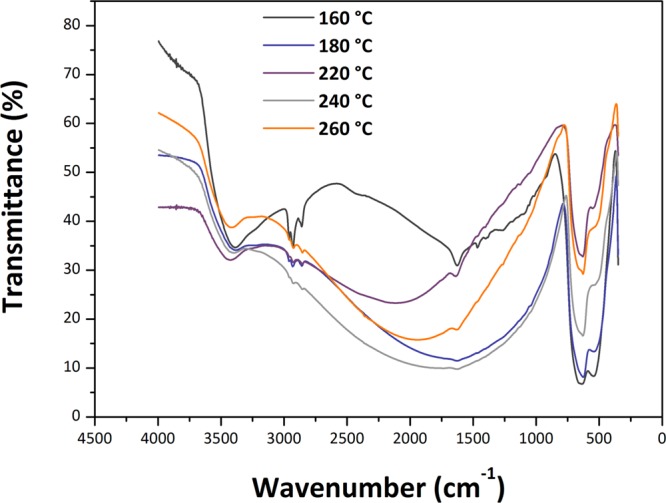
FTIR spectra of the samples containing SnO₂ NPs produced by the reaction between SnCl₄ and 1-hexanol at different temperatures.

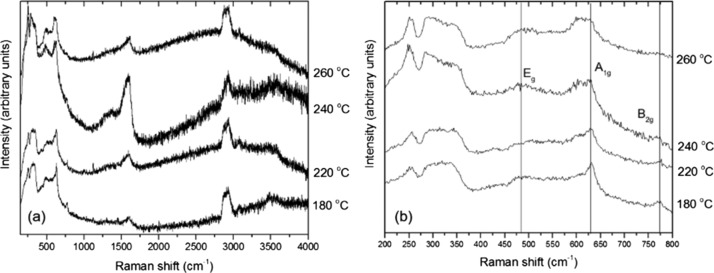
The aliphatic C–H stretching peaks between 2850 and 2950 cm^–1 confirm our NMR results that organic species derived from the 1-hexanol reactant remain present within the solid samples. These features are particularly strong for the sample synthesized at 160 °C, but they remain present to the highest synthesis temperatures studied here, suggesting that the organic species remain strongly bound to the external surfaces of the NPs. We do not yet have a good interpretation for the broad absorption feature observed between approximately 1000 and 3000 cm^–1, that has a maximum that moves to different wavelengths as a function of synthesis temperature, although it could be related to a light scattering effect associated with the dielectric SnO₂ NPs. Raman spectra were obtained for several series of SnO₂ NPs prepared in this study, using different instruments and excitation wavelengths. Representative data obtained with 514.5 nm laser excitation are shown in Figure 11. The spectra in the 400–700 cm^–1 range are similar to observations by Diéguez et al.,⁴⁷ with broad bands dominated by surface rather than bulk modes (Figure 11b). Bulk crystalline SnO₂ with a tetragonal rutile structure (P4₂/mnm space group) exhibits four Raman active peaks due to zone center vibrations: A_1g (634 cm^–1), B_2g (773 cm^–1), E_g (473 cm^–1), and a low frequency (123 cm^–1) B_1g mode that is not reported in all studies. For highly crystalline materials including NPs with sizes above 75–100 nm, the spectra are dominated by the strong A_1g mode that becomes broadened and shift to a lower wavenumber as the particle size decreases.⁴⁸ The B_2g and E_g peaks become less visible, and broad features appear between 450–600 and 750–800 cm^–1, corresponding to vibrational excitations in the density of states function (g(ω)) that become activated as the particle size is reduced. In addition, a weak peak due to a normally IR-active A_2u LO mode can be observed as a surface mode in larger NPs, while a further surface mode is reported to occur at 543 cm^–1.⁴⁸ As the NPs develop sizes below ∼15 nm, a broad feature near 572 cm^–1 begins to dominate the spectrum.^47,49 This mode along with other weak features has also been associated with surface vibrations. Our spectra provide new information on features in the low wavenumber (200–400 cm^–1) region, which correspond roughly with the (g(ω)) profile for the bulk crystalline phase.⁵⁰ Additional Raman features can also become activated because of the presence of defects, including screw dislocations, as shown by our X-ray WPPM analysis and HRTEM observations.⁵¹ Consistent with Diéguez et al,⁴⁷ the A_1g mode broadens and shifts to a lower wavenumber as the NP size decreases, while the frequencies of B_2g and E_g modes approach that of the A_1g vibration. Our samples show broad bands in the 1350–1600 cm^–1 range and near 3000 cm^–1 because of the presence of 1-hexanol and dihexyl ether attached to the NP surface as detected by NMR spectroscopy.⁴⁷

Figure 11.

Raman spectra of SnO₂ samples prepared at 180, 220, 240, and 260 °C recorded using 514.5 nm excitation. (a) 200–4000 cm^–1 wavenumber range; (b) 200–800 cm^–1 wavenumber range.

2.5. UV–Visible Optical Spectroscopy and Band Gap Determination

UV–visible spectra were obtained for the SnO₂ NP samples using diffuse reflectance spectroscopy (DRS) (Figure 12). The UV–vis data were transformed into an absorbance scale by Kubelka–Munk analysis and optical E_g values determined using the Tauc method (Figure 13). The direct E_g for bulk SnO₂ occurs at 3.60 eV.^51,52 For SnO₂ NPs, there is on-going discussion about the direct versus indirect nature of the interband transition.⁵³⁻⁵⁶ For this reason, we examined both (αhν)² and (αhν)^1/2 versus photon energy plots to determine E_g (Figure 13a,b). We note that the direct gap model yields E_g values that are systematically larger than with the indirect gap analysis, and it leads to values that exceed that of bulk SnO₂ for our NPs prepared at the highest temperatures. However, if the transition is indirect, it is found to approach the bulk value for the largest samples (Table 3). In both models, the E_g values increase with NP size and synthesis temperature. This observation contrasts with previous studies that have typically found an increase in the band gap of undoped SnO₂ NPs for smaller particle sizes.^23,24,26,57 Here, we suggest an interpretation of our result based on the observed changes in structural parameters with NP size and preparation temperature, along with the presence of organic ligands derived from the synthesis decorating the NP surface.

Figure 12.

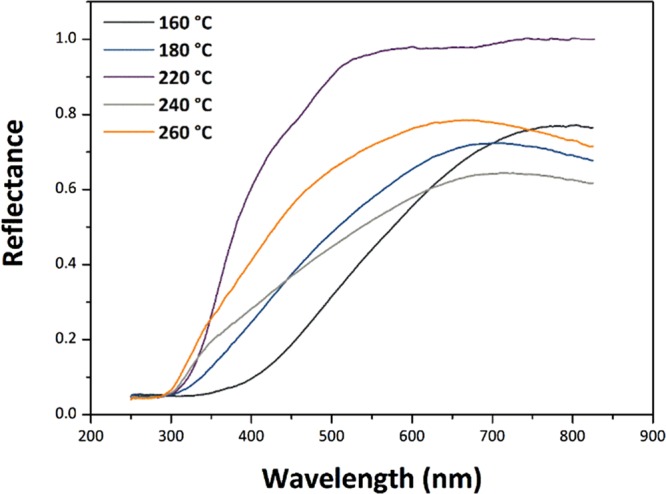
UV–vis diffuse reflectance spectra of SnO₂ NP specimens prepared at different temperatures.

Figure 13.

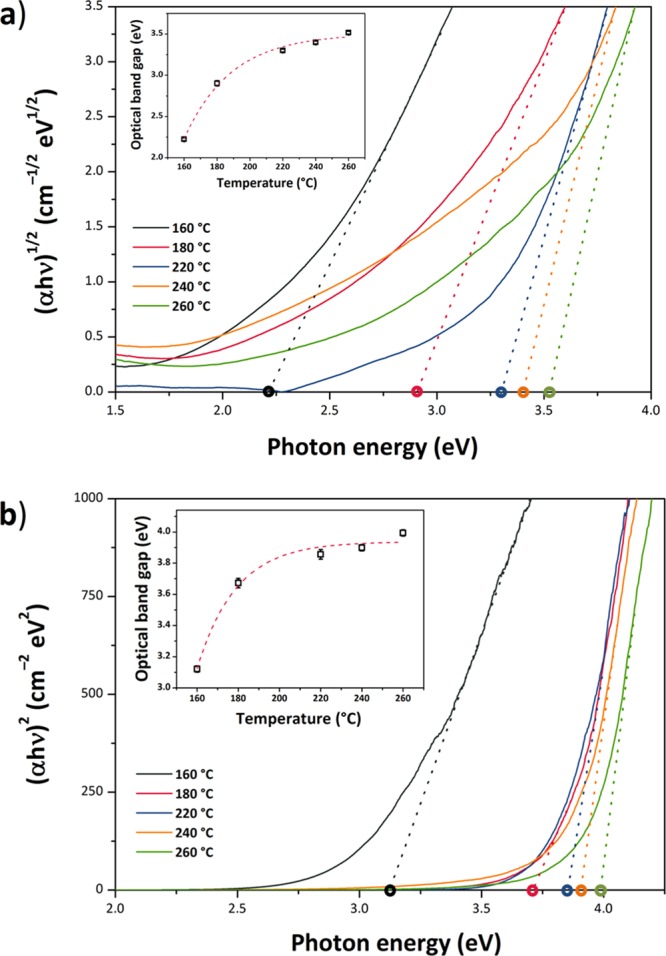
Plots of the Kubelka–Munk function vs photon energy of the specimens synthesized at different temperatures showing the optical E_g estimated using the Tauc procedure. The dashed lines represent the x-axis intercept of the line tangent to the inflection point for each dataset. (a) Indirect E_g model, [F(R_∞)hν]^1/2, γ = 2. The insets show the systematic changes in E_g with increasing synthesis temperature and resulting NP size. (b) Directly allowed E_g model—[F(R_∞)hν]², γ = 1/2; the red dashed lines are drawn as a guide for the eye, showing an approximately exponential trend for the evolution of the optical E_g with the increase in the synthesis temperature.

Table 3. Optical Band Gap (E_g) of the SnO₂ NP Specimens, as Calculated from the UV–Vis Data Using the Tauc Procedure.

	optical Eg (eV)
synthesis temperature (°C)	direct, γ = 1/2	indirect, γ = 2
160	3.12 ± 0.02	2.22 ± 0.02
180	3.67 ± 0.03	2.90 ± 0.03
220	3.86 ± 0.03	3.30 ± 0.02
240	3.90 ± 0.02	3.40 ± 0.02
260	3.99 ± 0.02	3.53 ± 0.02

Our analyses of the XRPD data show that the NPs all have the same unit cell volume (0.072 nm³). This is approximately 6–7% smaller than the bulk value (0.7687 nm³), indicating that our SnO₂ NPs are in a state of lattice compression compared with the bulk material. There is also a slight change in the a_o and c_o lattice parameters, with the smallest NPs prepared at lowest T_syn having the smallest c/a ratio (0.6703) rising to 0.6714 for the larger NPs (Table 1). Both values are larger than the value for bulk SnO₂ (0.6680), indicating a systematic increase in the degree of axial strain. Both tensile and compressive strains are known to modify E_g in SnO₂ and other semiconductors, as well as the direct versus indirect nature of the interband transition.^20,58 We suggest that these lattice strains could be linked to the presence of organic ligands derived from the synthesis procedure decorating the growing NP surfaces. The smallest NPs prepared at lowest temperature show the smallest axial strain values and both their direct and indirect E_g values are smaller than the bulk material. We can relate this effect to the overall state of compression of the NPs, along with the c/a ratio that is 0.3% greater than the bulk material. As the NPs grow in size with higher synthesis temperature, we observe an increase in the c/a ratio along with an increased screw dislocation density (Figure 4, Table 1). The band gap shows a regular increase with the axial distortion, while the NPs remain in a similar compressed state, to either approach or exceed the bulk value depending on whether the transition is direct or indirect (Figure 14). The increased concentration of screw dislocations determined by WPPM modeling of the XRPD data testifies to the presence of mechanical strains within the SnO₂ NPs synthesized by our low temperature nonaqueous sol–gel method (cf. Figure 14, top panel).

Figure 14.

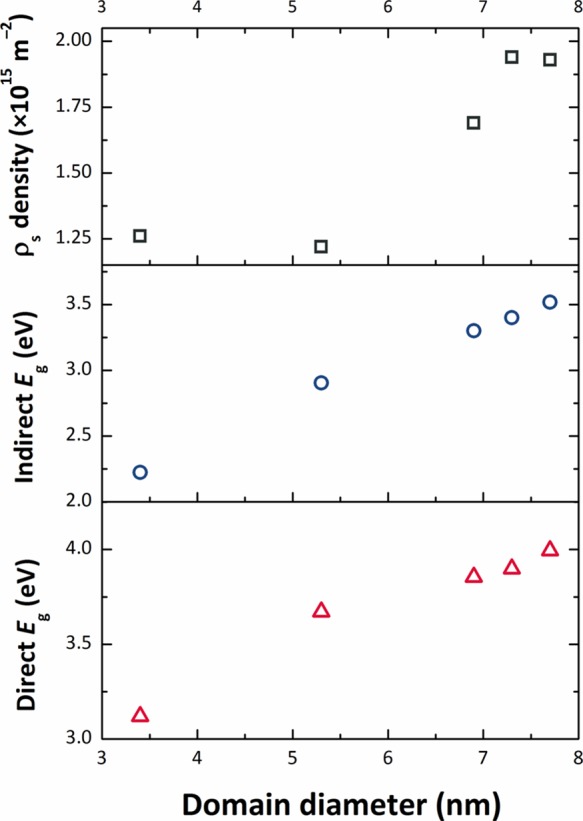
Evolution of the optical gap E_g (bottom panel: direct E_g vs domain diameter; middle panel: indirect E_g vs domain diameter) and the screw dislocation density with the average domain diameter (top panel).

We also note that our UV–visible spectra show significant tailing effects at longer wavelengths, especially for the samples prepared at lowest T. This effect could be partly due to organic ligands attached to the NP surface inducing ligand-to-metal charge transfer transitions⁵⁹ (Figure 12). Similar effects were noted by Wang et al. for carbon-coated SnO₂ NPs,⁶⁰ where the authors suggested that the outer carbonaceous layer could photosensitize SnO₂, extending the light absorption into the visible range. The absorption tails could also be associated with interband defect states associated with mechanical strains or O^2– vacancies within or at the surface of the NPs. We modeled the Urbach energies (E_u) associated with such possible defect states as ∼278 meV.⁵¹

3. Conclusions

We have demonstrated a novel low-temperature (160–260 °C) solvothermal route to achieve crystalline SnO₂ NPs using a one-pot nonhydrolytic sol–gel synthesis method. The use of a readily available short chain alcohol (1-hexanol) as the reaction medium and as one of the reagents provides a potentially scalable process, leading to SnO₂ NPs with very small and controllable NP sizes within a narrow dispersion range. The reaction between SnCl₄ and 1-hexanol avoids the use of expensive and toxic precursors and thus offers an environmentally benign, inexpensive, and size-selected process for production of SnO₂ NPs with tunable optoelectronic properties. The nonaqueous sol–gel method, together with the WPPM analysis of XRPD data—combined with HRTEM imaging—allowed us to engineer functionally active NPs, determine the NP sizes, and identify screw dislocations present within the SnO₂ NPs in detail. This was further confirmed by HRTEM imaging.

We studied changes in the optical band gap E_g by analysis of UV–visible spectroscopic data. Our results indicated that E_g was smaller than that for bulk SnO₂ for the smallest particles but increased with NP size, contrary to previous findings. If we assumed a direct gap model for interband transitions, our value estimated for >3.5 nm particles exceeded that of the bulk solid, whereas indirect gap analysis showed values approaching the bulk for larger NPs prepared at higher temperature. We suggest that the unexpected variation in E_g with a NP size is due to internal strain parameters developed within the NPs that also lead to an increase in screw dislocation densities observed at higher temperatures, as the particles become larger. The internal strains may be associated with the presence of organic ligands attached to the growing NP surfaces derived from the synthesis reaction. Our simple, low-cost synthetic method leads to new possibilities for tailoring the E_g of SnO₂ nanomaterials as a function of NP size, surface decoration, and the presence or relaxation of internal mechanical strains. Such an approach can allow further tuning of the electronic properties and visible light transparency of SnO₂ NPs for optoelectronic devices.

4. Experimental Section

4.1. Synthesis of SnO₂ NPs

Tin(IV) chloride (99.995%) and anhydrous 1-hexanol (99%) were used as obtained from Aldrich. The syntheses were carried out in a glovebox under controlled environmental conditions (O₂ and H₂O < 1 ppm). In a typical procedure, 1 mmol (0.2603 g) of tin(IV) chloride was added to 20 mL of 1-hexanol, and the mixture was transferred into a stainless-steel autoclave and sealed. The autoclave was taken out of the glovebox and heated in a furnace at between 160 and 260 °C for 3 days. The resulting milky suspensions were centrifuged, and the precipitates were washed with ethanol and dichloromethane and dried in air at 60 °C.

4.2. Sample Characterization

The SnO₂ NPs were studied by XRPD using a θ/θ diffractometer (PANanalytical X’Pert Pro, NL) equipped with a fast RTMS detector, using Cu Kα radiation (45 kV, 40 mA), in the 20–125° 2θ range, with a virtual step scan of 0.1° 2θ, and a virtual time per step of 500 s. The diffraction profiles were analyzed via the WPPM approach,²⁷⁻³³ using the PM2K software suite.³⁴ This powerful new technique allows extraction of microstructural information from a powder diffraction pattern, by refining model parameters via a nonlinear least squares fitting routine, fit to the experimental data profile. Within the WPPM method, there is no need for modeling the data using arbitrary peak shape functions (e.g., Gaussian, Lorentzian, and Voigt), as the experimental scattering profile is fit as a convolution of instrumental and sample-related physical effects. In this way, the structural analysis is developed by taking into account physical models of not only the lattice parameters but details of the microstructure and lattice defects including planar and screw dislocations.²⁷⁻³⁴ The WPPM method provides an assessment of all aspects of the microstructure including the crystallite domain shape, size, and distribution, with effects due to dislocations modeled through the description of a dislocation contrast factor in terms of a crystallographic invariant.^29,32 It provides considerably more detailed information compared with other integral methods for line profile analysis of XRPD data, such as the routinely used Scherrer formula,⁶¹ or the Williamson–Hall approach.⁶² In these methods, instrumental profile components, background and peak profile overlap can play an unwanted role in correctly extracting integral breadths.^61,62 Furthermore, additional sources of line broadening and peak asymmetry, including domain size, lattice strain, and the presence of lattice defects, cannot be investigated in detail.⁶³ Here, the instrumental contribution to the XRPD profile was calibrated by modeling 14 hkl reflections from the NIST SRM 660b standard (LaB₆), according to the Caglioti et al. relationship.⁶⁴ Then, SnO₂ described within space group P4₂/mnm for the tetragonal rutile structure was introduced in the WPPM modeling of the data, and the following parameters were refined: background (modeled using a 4th-order shifted Chebyshev polynomial function), peak intensities, specimen displacement, mean and variance of the NP size distributions, and lattice parameters. For simplicity, the crystalline diffracting domains were assumed to be spherical and that their diameter was distributed according to a log-normal size distribution. Both edge and screw dislocations having densities of ρ_e and ρ_s, respectively, were initially assumed to be present in the 101̅ {101} slip system, as was shown by Koffyberg [Burgers vector equal to (a₀² + c₀²)^1/2, with a₀ and c₀ being the lattice parameters],⁶⁵ and validated recently by Scardi’s group by means of the WPPM method.^33,35 Our HRTEM images (see below) showed that screw dislocations constituted the main defect observed in the NPs, and hence, these were considered to be the only source of anisotropy in the XRPD line profile broadening.

Transmission electron microscopy (TEM) was performed using a Jeol-2000 FXII microscope, with point-to-point and line-to-line resolutions of 0.28 and 0.14 nm, respectively. Additional high-resolution TEM (HRTEM) images were obtained using a JEOL 2200FS microscope with a field-emission gun, operated at 200 kV. Samples for TEM/HRTEM observations were prepared by dispersing the NPs in ethanol and methanol, respectively, and evaporating the suspension drops on carbon-coated Cu grids.

FTIR spectra were obtained using a Bruker Tensor 27 spectrometer. The IR measurements were carried out over the wavenumber range 4000–350 cm^–1. Sample powders (2 mg) were mixed with KBr (200 mg, to give ∼1 wt % of powder in the KBr disks) and pressed into thin pellets. Raman spectra were measured using a Renishaw micro-Raman instrument with excitation wavelengths of 325 and 514.5 nm. DRS was used to evaluate the optical properties of SnO₂ in the UV–visible range. Spectra were acquired using a Shimadzu UV 3100 (JP) spectrometer equipped with a BaSO₄ integrating sphere in the 825–250 nm range, with 0.2 nm in step size, and using BaSO₄ as white reference material. The diffuse reflectance data (R_∞) were converted into an absorption coefficient α using the Kubelka–Munk transformation⁶⁶

Here, k is the wavelength-dependent absorption coefficient (k = 4πκ/λ) and S is a scattering coefficient, assumed to be constant over the wavelength range. The optical band gap E_g of the SnO₂ NPs was assessed by the Tauc procedure that assumes the absorption coefficient α of a semiconductor can be expressed as

where A is a material-dependent constant, h is Planck’s constant, and ν is the light frequency. The power coefficient γ is characteristic of the type of transition considered, with a value of 1/2 or 2 depending on whether the transition is directly or indirectly allowed.⁶⁷ There is still not agreement on whether the band-to-band transition in SnO₂ NPs is direct or indirect.^7,53,54 We tested both solutions to estimate E_g values in our study. We fitted the plots given by the transformed Kubelka–Munk equation [F(R_∞)hν]^γ versus hν using a sigmoidal Boltzmann function (Origin ProLab, version 8.5.0). The x-axis intercept of the line tangent to the inflection point of the appropriate curve provided direct versus indirect gap model estimates for each of our SnO₂ NP samples.

Liquid-state ¹H and ¹³C NMR spectroscopies were used to investigate the organic species formed during the reaction and remaining in the supernatant liquid after centrifugation. Spectra were measured in CDCl₃ solutions using a 300 MHz Bruker AVANCE NMR spectrometer. Solid-state NMR experiments to study the SnO₂ NPs were carried out at ambient probe temperature on a Bruker AVANCE 300 spectrometer with a 7.05 T wide-bore magnet. High-resolution solid-state ¹H, ¹³C, and ¹¹⁹Sn NMR spectra were recorded at 300.1, 75.5, and 111.9 MHz, respectively, using a standard Bruker 4 mm double-resonance MAS probe. Powdered solid materials were packed into zirconia rotors of 4 mm external diameter and spun at MAS frequencies of 3–12 kHz with stability better than ±3 Hz. High-resolution solid-state ¹³C NMR spectra were recorded using MAS, with high-power proton decoupling and the pulse sequence of Cory and Ritchey⁶⁸ with the suppression of extraneous signals originating from materials outside the NMR coil. Typical acquisition conditions for ¹³C NMR experiments were as follows: ¹³C 90° pulse duration = 3.0 μs; recycle delay = 10 s; number of transients 6000–17 200. Solid-state ¹³C MAS spectra with high-power proton decoupling and cross-polarization (CP) from protons were also acquired for the sample prepared at 200 °C, with the following acquisition conditions: ¹H 90° pulse duration = 4.0 μs; recycle delay = 5 s; and number of transients 3400. However, the ¹³C CPMAS spectrum showed a poorer signal-to-noise ratio compared to that acquired using the sequence of Cory and Ritchey⁶⁹ with the direct detection of ¹³C nuclei. Solid-state ¹¹⁹Sn MAS spectra at 111.9 MHz with and without high-power proton decoupling were recorded using the following acquisition conditions: ¹¹⁹Sn 60° pulse duration = 1.5 μs; recycle delay = 10–30 s; number of transients 2000–30 000, and MAS frequency = 3–12 kHz. Additionally, ¹¹⁹Sn SSNMR spectra were recorded on a Bruker AVANCE 600 MHz spectrometer at the resonance frequency of 223.8 MHz using the following acquisition conditions: ¹¹⁹Sn 45° pulse duration = 2.0 μs; recycle delay = 5 s; number of transients 1500–12 300, and MAS frequency = 10–12 kHz. The sequence used to collect ¹H MAS NMR spectra at 300.1 MHz comprised a single-pulse excitation with a 2.4 μs long pulse (recycle delay = 5 s; number of transients 8–32, and MAS frequency = 8–12 kHz). The ¹³C and ¹H chemical shifts are given relative to tetramethylsilane (TMS), which were calibrated using glycine (176.46 ppm) and tetrakis(trimethylstannyl)methane doped with TMS (0 ppm), respectively. The ¹¹⁹Sn chemical shifts are given relative to tetramethyltin SnMe₄, calibrated using tetrakis(trimethylstannyl)methane C(SnMe₃)₄ (48.2 ppm).⁶⁹ In the case of the ¹¹⁹Sn CSA (Δδ) for SnO₂ with δ < 0, parameters are defined as follows

Here, the principal components of the chemical shift tensor, δ₁₁, δ₂₂, and δ₃₃, are defined such that the highest frequency (the least shielded) component is labeled as δ₁₁, while δ₃₃ corresponds to the lowest frequency (the most shielded) component.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b02122.

• ¹H NMR spectrum of the filtered reaction solution measured in CDCl₃ of the SnO₂ NPs; TGA of the SnO₂ NP samples synthesized at different temperatures; and ¹³C NMR chemical shift values for key organic species discussed in the text (PDF)

The authors declare no competing financial interest.

Dedication

We dedicate this work to the memory of our colleague and friend, Dr Russell Binions, who passed away unexpectedly during the preparation of this manuscript.