Abstract

Single-chain polymer nanoparticles (SCNPs) obtained through chain collapse via intramolecular cross-linking are attracting significant interest for nanomedicine and biomimetic catalysis applications, among other fields. This interest arises from the possibility to bind active species (e.g., drugs and catalysts)—either temporally or permanently—to the SCNP local pockets formed upon chain collapse. However, direct quantification of the size and number of such local domains in solution—even if highly desirable—is currently highly demanding from an experimental point of view because of the small size involved (<5 nm). On the basis of a scaling analysis, we establish herein a connection between the global compaction degree (R/R0) and the size (ξ) and number (n) of the “collapsed domains” generated upon SCNP formation at high dilution from a linear semiflexible precursor polymer. Results from molecular dynamics simulations and experimental data are used to validate this scaling analysis and to estimate the size and number of local domains in polystyrene SCNPs synthesized through a “click” chemistry procedure, as a representative system, as well as for relevant catalytic SCNPs containing Cu, Pt, and Ni atoms. Remarkably, the present work is a first step toward tuning the local domain size of the next generation of SCNPs for nanomedicine and bioinspired catalysis applications.
1. Introduction
Intramolecular cross-linking of individual polymer chains in a good solvent at high dilution produces single-chain polymer nanoparticles (SCNPs) via intrachain collapse.1−5 The compaction of a single chain to a SCNP resembles—in some way—the conformational rearrangement needed by some biomacromolecules to reach its functional state.6−8 Depending on the specific nature of the intramolecular cross-links formed, dynamic or permanent SCNPs result by involving reversible or irreversible intrachain interactions, respectively.9,10 These soft nano-objects have attracted significant interest for a variety of applications, including nanomedicine and biomimetic catalysis uses.3 The possibility to bind active species (e.g., drugs and catalysts)—either temporally or permanently—to the SCNP local pockets formed upon intrachain chain collapse remains as a driving force toward bioinspired applications.6,8 To understand the possibilities that SCNPs offer for nanomedicine and biomimetic catalysis, the reader is referred to several illustrative works11−25 and a recent book.26
Significant theoretical effort27−32 has been recently devoted to understand how the nature of the intramolecular cross-links (both reversible and irreversible interactions), the amount of functional reactive groups, x, and the precursor molecular weight, Mw, determine the global collapse degree upon intramolecular cross-linking, R/R0, where R0 and R are the linear precursor polymer size and the SCNP size, respectively. However, to our best knowledge, no attempt has been yet carried out to establish a connection between the global compaction degree (R/R0) and the size (ξ) and number (n) of local pockets (domains) generated upon SCNP formation at high dilution. It is worthy of mention that a direct visualization/quantification of such local domains in solution—even if highly desirable—is currently highly demanding from an experimental point of view.26
We use herein the analogy of chain confinement into a spherical cavity33 to the collapse of a linear chain to a SCNP to perform a scaling analysis34,35 allowing to establish a connection between the global compaction degree (R/R0) and the size (ξ) and number (n) of “collapsed domains” generated upon SCNP formation at high dilution. It is worthy of mention that the case of confinement of a linear semiflexible polymer chain into a cavity under good solvent conditions has recently attracted significant theoretical and computer simulations efforts.36−39 Remarkably, the present work provides a solid basis to understand the effect of (i) the strength of the intramolecular interactions, (ii) the amount of functional groups, (iii) the precursor molecular weight, and (iv) the precursor chain stiffness on the size and number of local domains of SCNPs in solution.
The article is organized as follows. In Section 2, we first introduce two expressions for the change in free energy upon collapse based, respectively, on the analogy of SCNP formation to the case of chain confinement into a spherical cavity under good solvent conditions and on the number of new intramolecular bonds formed and the change in free energy per each new bond formed. Next, useful scaling expressions for the global compaction degree and the size and number of local domains are derived. Validation of the scaling analysis with results from molecular dynamics (MD) simulations and reliable experimental data, as well as an estimation of the size and number of local domains for relevant catalytic SCNPs in solution containing Cu, Pt, and Ni atoms, is provided in Section 3 and, finally, the conclusions of the work are given in Section 4.
2. Scaling Analysis
2.1. Free Energy of Collapse
Let us assume that the change in free energy, ΔFc, upon collapse of a linear precursor polymer of size R0 to a SCNP of size R in a good solvent under high dilution conditions follows an expression similar to that corresponding to chain confinement into a spherical cavity under good solvent conditions35−39
| 1 |
where kB is the Boltzmann’s constant, T the absolute temperature, and α is the scaling exponent of the resulting collapsed domains upon SCNP formation (see below). It is reasonable to assume that SCNPs with different chain stiffness will show different values of the exponent in eq 1, as observed in computer simulations of semiflexible chains confined in a spherical cavity.36
Because the free energy of collapse comes from all of the new intramolecular bonds formed, we can additionally write
| 2 |
where xN/2 is the number of new intramolecular bonds formed, x is the fraction of reactive groups in the linear precursor polymer of total number of monomers N, and |Δfc| is the absolute value of the change in free energy per each new bond formed. Implicit in eq 2 is the assumption that by means of dimerization of the corresponding reactive monomers the maximum number of intrachain bonds (xN/2) is obtained. Experimentally, this is expected to be the case for SCNPs prepared through highly reactive cross-linking procedures (e.g., “click” chemistry reactions10) but not for SCNPs prepared by means of weak, dynamic interactions9 (e.g., hydrogen bonds). For real systems, Δfc is expected to contain a favorable enthalpic contribution, Δhc < 0, because of (exothermic) bond formation and an unfavorable entropic contribution, Δsc < 0, because of severe configurational restriction upon chain collapse.
2.2. Global Compaction Degree
By combining eqs 1 and 2, we obtain an analytical expression for the compaction degree (R/R0) as a function of x and N such as
| 3a |
| 3b |
Taking into account that the size of a semiflexible linear chain in a good solvent is given37 (to a first approximation) by R0 ≃ bC∞1/5Nν0, where b is the monomer size, C∞ is the characteristic ratio,34 and ν0 is the Flory exponent (ν0 ≈ 3/5), eq 3a can be rewritten as
| 4a |
| 4b |
Consequently, according to the present scaling analysis, the exponents of the dependence of SCNP size R on x and N are actually connected through eq 4b.
2.3. Local Domain Size
Similar to the case of a linear chain confined in a spherical cavity,35−39 we introduce herein the concept of“cross-linked blobs” or collapsed domains upon SCNP formation via chain collapse. The average number of such domains (n) each one having associated a free energy around kBT and a size ξ can be estimated from the free energy of collapse such as37,39
| 5 |
Therefore, by using eqs 1 and 2, we obtain the following expressions for the domain size
| 6a |
| 6b |
whereas the number of monomers in each collapsed blob (g) is just given by37,39
| 7 |
It is worthy of mention that α in eq 6a is related to the scaling exponent of the cross-linked blobs, so its value gives an idea of compaction at local level (i.e., at domain size ξ). Conversely, the value of ν in eq 4a gives an indication of chain compaction at global scale (i.e., at SCNP size R). In general, one expects 1/3 ≤ (α, ν) ≤ 1 where the lower value is expected for globule-like compaction, whereas the upper value corresponds to rod-like compaction.34
It is instructive to rewrite eqs 5 and 7 by using eq 6b, such as
| 8 |
and
| 9 |
Hence, according to the present scaling analysis n depends linearly on x, N, and |Δfc|, whereas g depends inversely on x and |Δfc| but it is independent on N.
3. Results and Discussion
3.1. Scaling Analysis Validation with Data from MD Simulations
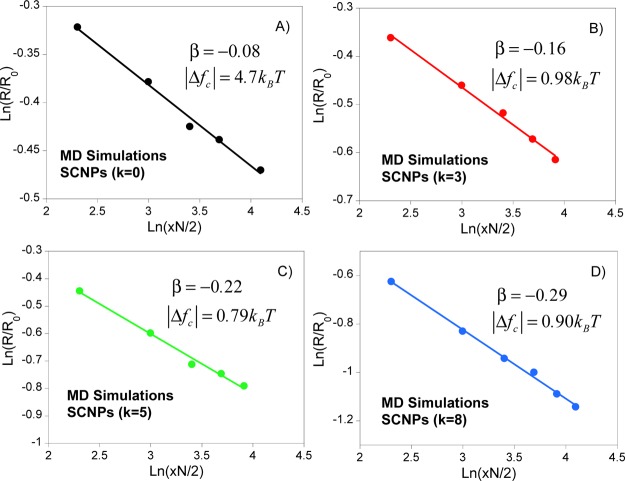
Analysis of R/R0 and xN/2 data from MD simulations of
semiflexible SCNPs in terms of eq 3a allows one to determine the scaling exponent β
(and hence α from eq 3b) as well as the absolute value of the change in free energy
per each new bond formed, |Δfc|. Figure 1 shows such an analysis
for SCNPs having different chain stiffness, as characterized by the
value of the bending constant k employed in the coarse-grained
MD simulations.40 Note that k is related to the well-known characteristic ratio, C∞, and it was previously reported that C∞ ≈ 1.7, 5, 9, and 15 for k = 0 (fully flexible case), 3, 5, and 8, respectively.40 The dependences of β, the exponent of
the free energy of collapse 3/(3α – 1), and |Δfc| on chain stiffness are illustrated in Figure 2 for semiflexible
SCNPs. Upon increasing the SCNP characteristic ratio, the value of
β was found to decrease nearly linearly with C∞ (see Figure 2A). Concerning the exponent of the free energy of collapse,
it decreases abruptly on increasing C∞ toward a plateau value for the stiffer SCNPs (Figure 2B). This behavior is in agreement with that
reported by Cifra and Bleha36 in computer
simulations of the confinement of a semiflexible linear chain in a
closed spherical cavity reaching a limiting value of 2.6 upon increasing
chain stiffness. Interestingly, |Δfc| also reaches a plateau value upon increasing SCNP stiffness (Figure 2C). As noted by Cifra
and Bleha,36 for semiflexible linear chains,
the free-energy penalty on chain compaction is maximum for the fully
flexible case when compared with the case of stiffer systems. According
to the data in Figure 2C, there is a difference in |Δfc| between the fully flexible and stiffer SCNPs around 3.7 kBT. An estimation of the free
energy of collapse as a function of SCNP stiffness at identical compaction
degree can be obtained from eq 1. As an example, at a compaction degree R/R0 = 0.65, we obtain  =
218.0, 14.8, 7.1, and 4.4 for SCNPs with C∞ = 1.7, 5, 9, and 15, respectively.
=
218.0, 14.8, 7.1, and 4.4 for SCNPs with C∞ = 1.7, 5, 9, and 15, respectively.
Figure 1.
MD simulations data of compaction degree (R/R0) as a function of new intramolecular bonds formed (xN/2) for SCNPs having different chain stiffness:40 (A) C∞ = 1.7, (B) C∞ = 5, (C) C∞ = 9, and (D) C∞ = 15 (see text for details).
Figure 2.
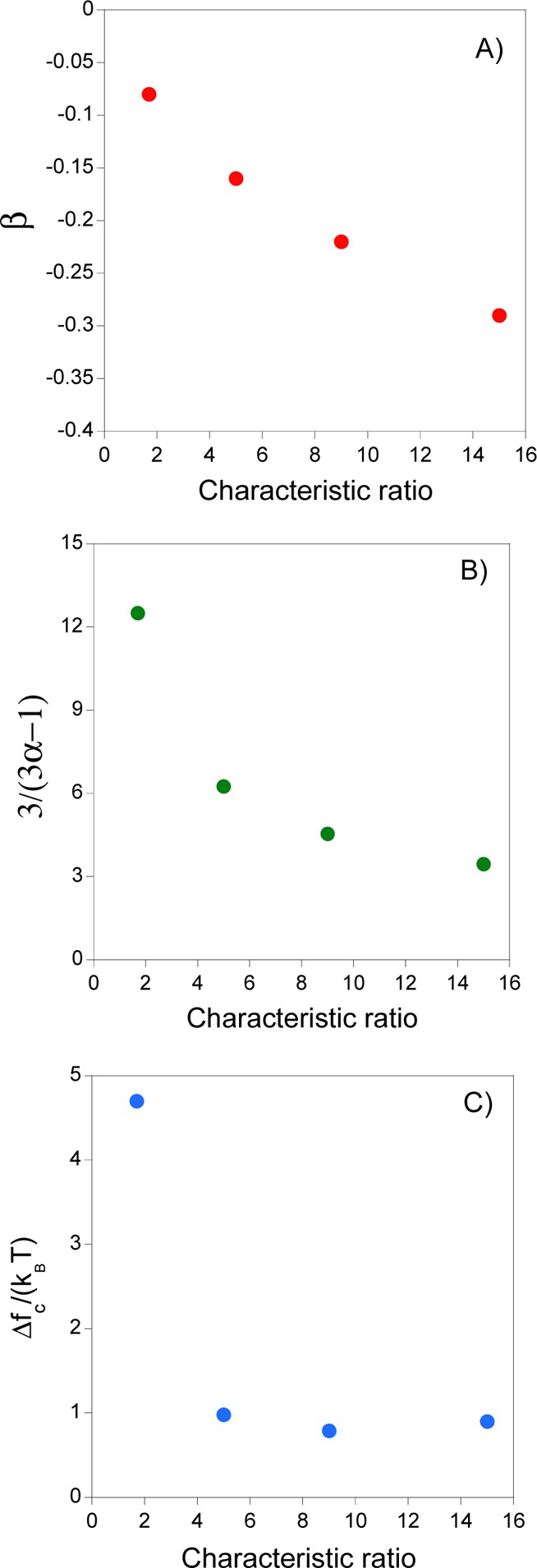
Dependence of (A) scaling exponent β, (B) scaling exponent 3/(3α – 1), and (C) change in free energy per new bond formed, |Δfc|, on chain stiffness for semiflexible SCNPs with different values of characteristic ratio, C∞, according to MD simulations (see eqs 1–3a and text for details).
Table 1 shows
a
comparison of the values of ν = ν0 + β
and 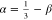 , as derived from the present scaling
analysis,
to those previously reported for semiflexible SCNPs with different C∞ values as estimated directly from MD
simulations data.40 As stated previously
in Section 2, ν
gives an indication of chain compaction at global scale (i.e., at SCNP size R) whereas the value
of α is indicative of chain compaction at local level (i.e., at domain size ξ). In general, a good agreement
is observed between the values of ν from the present scaling
analysis and MD simulations. Concerning the values of α, the
MD simulations provide values that are systematically larger than
those derived from the scaling analysis, although both data sets follow
the general trend of a higher value of α on increasing C∞.
, as derived from the present scaling
analysis,
to those previously reported for semiflexible SCNPs with different C∞ values as estimated directly from MD
simulations data.40 As stated previously
in Section 2, ν
gives an indication of chain compaction at global scale (i.e., at SCNP size R) whereas the value
of α is indicative of chain compaction at local level (i.e., at domain size ξ). In general, a good agreement
is observed between the values of ν from the present scaling
analysis and MD simulations. Concerning the values of α, the
MD simulations provide values that are systematically larger than
those derived from the scaling analysis, although both data sets follow
the general trend of a higher value of α on increasing C∞.
Table 1. Comparison of ν and α Values from the Scaling Analysis of This Work to Estimations from MD Simulations of SCNPs with Different C∞ Values40.
| C∞ | β | ν | α | νMDsim. | αMDsim. |
|---|---|---|---|---|---|
| 1.7 | –0.08 | 0.52 | 0.41 | 0.50 | 0.63 |
| 5 | –0.16 | 0.44 | 0.49 | 0.47 | 0.74 |
| 9 | –0.22 | 0.38 | 0.55 | 0.42 | 0.81 |
| 15 | –0.29 | 0.31 | 0.62 | 0.30 | 0.84 |
Figure 3 shows the evolution of the collapsed domain size, ξ (in σ units, where σ is the bead size) and the number of beads in a domain, g, as a function of SCNP stiffness, for SCNPs with a fraction of reacting monomers of x = 0.2 and N = 400, as calculated from eqs 4a–5 with data from Figure 1 and Table 1. Inspection of Figure 3 reveals that a minimum SCNP stiffness is required for the scaling analysis to provide consistent values of ξ and g. As a matter of fact, the domain size of fully flexible SCNPs in Figure 3A approaches the bead size which invalidates the scaling analysis for this case. Inasmuch C∞ ≥ 5, consistent values of ξ, n, and g are obtained showing a collapsed domain size around 3.7σ, about 33 collapsed blobs per SCNP and ∼12 beads per blob for semiflexible SCNPs (x = 0.2, N = 400) with C∞ = 5, 9, and 15 because of the similar values of |Δfc| (refer to eqs 6bb, 8, and 9).
Figure 3.
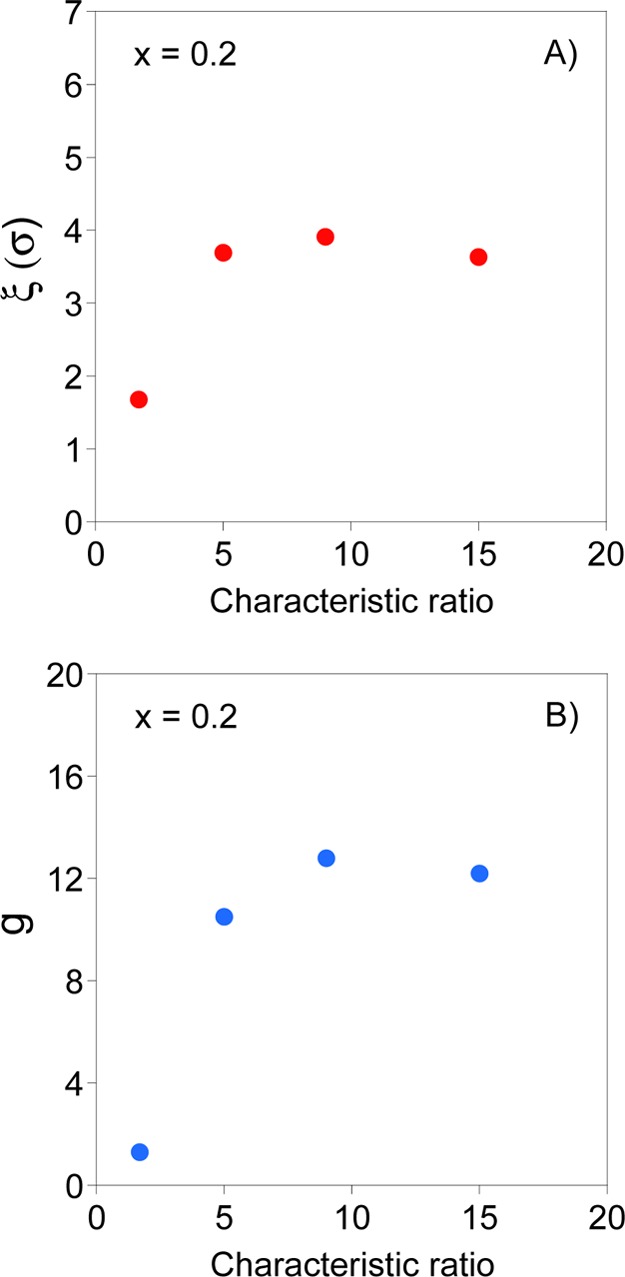
Dependence of (A) collapsed domain size, ξ (in σ units, where σ is the bead size) and (B) number of beads per collapsed domain, g, on chain stiffness for semiflexible SCNPs (x = 0.2, N = 400) as calculated from eqs 6bb and 9 with data from Figure 1 and Table 1.
Figure 4 illustrates the dependence of ξ and g on the fraction of reacting monomers, x, for SCNPs with N = 400 and C∞ = 9. Chain collapse from a linear precursor with low amount of reacting monomers (e.g., x = 0.05) produces a few collapsed domains (∼8) of relatively large size (∼8.4σ) containing a large amount of beads per blob (∼51). Upon increasing x, both collapsed domain size and number of beads per blob reduce notably (refer to eqs 6bb and 9), whereas the number of blobs is found to increase linearly with x (refer to eq 8).
Figure 4.

Dependence of (A) collapsed domain size, ξ, and (B) number of beads in a collapsed domain, g, on the fraction of reacting monomers x for SCNPs with N = 400 and C∞ = 9, as calculated from eqs 6bb and 9 with data from Figure 1 and Table 1.
3.2. Scaling Analysis Validation with Experimental Data
Complementary to the analysis based on MD simulations data, we have also analyzed data for real SCNPs in terms of eq 3a. In this sense, compaction data from well-defined polystyrene (PS)-SCNPs synthesized via “click” chemistry,41 covering from x = 0.025 to x = 0.3 and three different values of weight-average molecular weight (Mw ≈ 44, 111, and 232 kDa) were found to merge into a single master curve with β ≈ −0.20 and |Δfc| ≈ 0.16, when plotted according to eq 3a (see Figure 5).
Figure 5.

Compaction degree (R/R0) as a function of new intramolecular bonds formed (xN/2) for PS-SCNPs (C∞ ≈ 9.5 for PS34) of different molecular weight:41Mw = 44 kDa (solid blue points), Mw = 111 kDa (solid red points), and Mw = 232 kDa (solid green points).
Apparently, the experimental data
best follow the scaling behavior
at large values of N. From ν = ν0 + β and 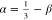 , we obtain
ν = 0.4 and α =
0.53 based on the value of β ≈ −0.20. Note that
the values of β and ν for PS-SCNPs (C∞ ≈ 9.5 for PS34) are in excellent agreement with those predicted by a model of elastic
SCNPs recently developed by our group27 (β = −1/5, ν = 2/5).
, we obtain
ν = 0.4 and α =
0.53 based on the value of β ≈ −0.20. Note that
the values of β and ν for PS-SCNPs (C∞ ≈ 9.5 for PS34) are in excellent agreement with those predicted by a model of elastic
SCNPs recently developed by our group27 (β = −1/5, ν = 2/5).
When compared with MD simulations of SCNPs prepared from a precursor polymer of C∞ = 9, the value of |Δfc| was found to be about fivefold lower for real PS-SCNPs. However, it is worth stressing that similar values should not be expected even at a qualitative level. Thus, though one finds similar scaling properties for the molecular size and may expect similar entropy loss per monomer because of network formation in the coarse-grained and in the real SCNPs, this is not the case for the associated enthalpy change, Δhc, because the bonded and nonbonded interactions in the simplified bead-spring model of the simulations40 are of different nature than that in the real polymers.10
Figure 6 illustrates the dependence of ξ and g on the fraction of reacting monomers, x, for PS-SCNPs of Mw ≈ 44, 111, and 232 kDa, as calculated form eqs 6bb and 9 with data from Figure 5. On increasing the amount of functional monomers from x = 0.1 to x = 0.3, a decrease in the domain size is observed from ξ ≈ 4 nm to ξ ≈ 2 nm. According to the results displayed in Figure 6A, the domain size in PS-SCNPs shows a weak dependence on Mw. Remarkably, on the basis of the present scaling analysis, the number of monomers in each local domain is expected to be independent of Mw, as illustrated in Figure 6B. By taking into account that for real systems σ ≈ 0.64 nm and each bead in the MD simulations comprises ∼5 monomers, the results shown in Figure 6 are in good agreement with those displayed in Figure 4.
Figure 6.
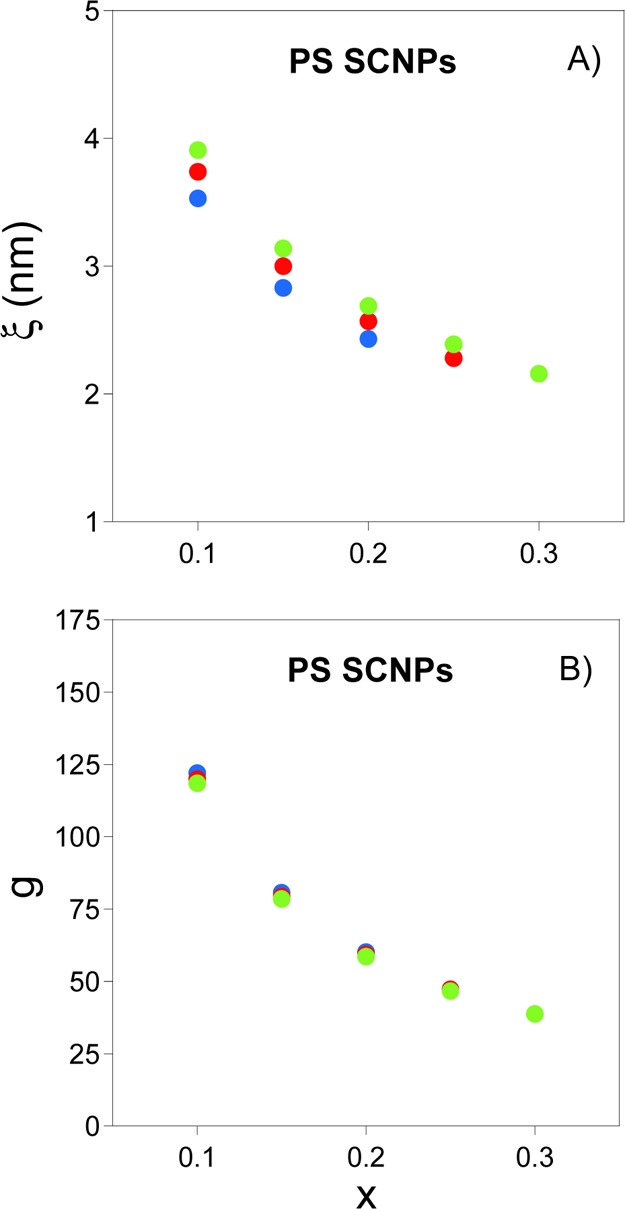
Dependence of (A) collapsed domain size, ξ, and (B) number of monomers in a collapsed domain, g, on the fraction of reacting monomers, x, for PS-SCNPs (C∞≈ 9.5 for PS34) of Mw = 44 kDa (solid blue points), Mw = 111 kDa (solid red points) and Mw = 232 kDa (solid green points) as calculated from eqs 6bb and 9 with data from Figure 5.
3.3. Estimation of Local Domain Size in Pt-, Cu- and Ni-Containing Catalytic SCNPs in Solution
Data about the local domain size, number of domains, and number of monomers per domain for relevant metal-containing catalytic SCNPs20,22,42 in solution are given in Table 2. The precursor polymers were based on either PS or poly(methyl methacrylate) (PMMA), both having a similar value of chain stiffness34 (C∞(PS) = 9.5, C∞(PMMA) = 9.0). Estimations were carried out based on experimental R/R0 data by assuming α ≈ 0.53 in eq 6aa, for PtII-, CuII-, and NiII-containing SCNPs employed with success in amination of allyl alcohol,20 selective alkyne homo-coupling reactions,22 and photoreduction of carbon dioxide,42 respectively.
Table 2. Local Domain Size (ξ), Number of Domains (n), and Number of Monomers per Domain (g) in Relevant Metal-Containing Catalytic SCNPs (See Text).
As stated previously, direct quantification of the size and number of SCNP local domains in solution is currently highly demanding from an experimental point of view, so there are no experimental data available. Nevertheless, experimental evidence of the presence of local compact domains in isolated SCNPs is provided in Figure 7, as revealed by transmission electron microscopy (TEM) measurements performed to Cu-containing SCNPs upon solvent removal and deposition onto a carbon grid.22 Obviously, upon solvent removal the dimensions of the SCNPs change and often a pancake morphology is observed for isolated SCNPs deposited onto solid substrates. Moreover, the SCNP size is found to depend to a large extent on the surface energy of the substrate.27
Figure 7.

TEM image showing the presence of local compact domains in a Cu-containing SCNP in the dry state.22
4. Conclusions
Quantification of the size and number of local domains of SCNPs in solution is currently of great interest because of the possibilities that offer such local pockets to bind—either temporally or permanently—active species to them (e.g., drugs and catalysts) rendering the resulting SCNPs highly attractive for applications in nanomedicine and catalysis, among other fields. A scaling analysis was performed to establish a connection between the global compaction degree (R/R0) and the size (ξ) and number (n) of collapsed domains generated upon SCNP formation at high dilution from a linear semiflexible precursor polymer. The scaling analysis was validated with results from MD simulations and reliable experimental data. On the basis of the scaling equations here proposed, we have estimated—as an example of application—the size and number of local domains for relevant catalytic SCNPs in solution containing Cu, Pt, and Ni atoms. Remarkably, this work is a first step toward tuning the local domain size of the next generation of SCNPs for nanomedicine and bioinspired catalysis applications.
Acknowledgments
The financial support by the Spanish Ministry “Ministerio de Economia y Competitividad”, MAT2015-63704-P (MINECO/FEDER, UE), the Basque Government, IT-654-13, and the Gipuzkoako Foru Aldundia, RED 101/17, is acknowledged.
The authors declare no competing financial interest.
References
- Mavila S.; Eivgi O.; Berkovich I.; Lemcoff N. G. Intramolecular Cross-Linking Methodologies for the Synthesis of Polymer Nanoparticles. Chem. Rev. 2016, 116, 878–961. 10.1021/acs.chemrev.5b00290. [DOI] [PubMed] [Google Scholar]
- Altintas O.; Barner-Kowollik C. Single-Chain Folding of Synthetic Polymers: A Critical Update. Macromol. Rapid Commun. 2016, 37, 29–46. 10.1002/marc.201500547. [DOI] [PubMed] [Google Scholar]
- Lyon C. K.; Prasher A.; Hanlon A. M.; Tuten B. T.; Tooley C. A.; Frank P. G.; Berda E. B. A Brief User’s Guide to Single-Chain Nanoparticles. Polym. Chem. 2015, 6, 181–197. 10.1039/c4py01217h. [DOI] [Google Scholar]
- Müge A.; Elisa H.; Meijer E. W.; Anja R. A. P.. Dynamic Single Chain Polymeric Nanoparticles: From Structure to Function. In Sequence-Controlled Polymers: Synthesis, Self-Assembly, and Properties; American Chemical Society, 2014; Vol. 1170, pp 313–325. [Google Scholar]
- Gonzalez-Burgos M.; Latorre-Sanchez A.; Pomposo J. A. Advances in Single Chain Technology. Chem. Soc. Rev. 2015, 44, 6122–6142. 10.1039/c5cs00209e. [DOI] [PubMed] [Google Scholar]
- Latorre-Sánchez A.; Pomposo J. A. Recent bioinspired applications of single-chain nanoparticles. Polym. Int. 2016, 65, 855–860. 10.1002/pi.5078. [DOI] [Google Scholar]
- Huo M.; Wang N.; Fang T.; Sun M.; Wei Y.; Yuan J. Single-chain polymer nanoparticles: Mimic the proteins. Polymer 2015, 66, A11–A21. 10.1016/j.polymer.2015.04.011. [DOI] [Google Scholar]
- Pomposo J. A. Bioinspired single-chain polymer nanoparticles. Polym. Int. 2014, 63, 589–592. 10.1002/pi.4671. [DOI] [Google Scholar]
- Sanchez-Sanchez A.; Pomposo J. A. Single-Chain Polymer Nanoparticles via Non-Covalent and Dynamic Covalent Bonds. Part. Part. Syst. Charact. 2014, 31, 11–23. 10.1002/ppsc.201300245. [DOI] [Google Scholar]
- Sanchez-Sanchez A.; Pérez-Baena I.; Pomposo J. A. Advances in Click Chemistry for Single-Chain Nanoparticle Construction. Molecules 2013, 18, 3339–3355. 10.3390/molecules18033339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen T.-K.; Lam S. J.; Ho K. K. K.; Kumar N.; Qiao G. G.; Egan S.; Boyer C.; Wong E. H. H. Rational Design of Single-Chain Polymeric Nanoparticles That Kill Planktonic and Biofilm Bacteria. ACS Infect. Dis. 2017, 3, 237–248. 10.1021/acsinfecdis.6b00203. [DOI] [PubMed] [Google Scholar]
- De-La-Cuesta J.; González E.; Pomposo J. A. Advances in Fluorescent Single-Chain Nanoparticles. Molecules 2017, 22, 1819. 10.3390/molecules22111819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez-Sanchez A.; Akbari S.; Moreno A. J.; Lo Verso F.; Arbe A.; Colmenero J.; Pomposo J. A. Design and Preparation of Single-Chain Nanocarriers Mimicking Disordered Proteins for Combined Delivery of Dermal Bioactive Cargos. Macromol. Rapid Commun. 2013, 34, 1681–1686. 10.1002/marc.201300562. [DOI] [PubMed] [Google Scholar]
- Perez-Baena I.; Loinaz I.; Padro D.; García I.; Grande H. J.; Odriozola I. Single-chain Polyacrylic Nanoparticles with Multiple Gd(III) Centres as Potential MRI Contrast Agents. J. Mater. Chem. 2010, 20, 6916–6922. 10.1039/c0jm01025a. [DOI] [Google Scholar]
- Hamilton S. K.; Harth E. Molecular Dendritic Transporter Nanoparticle Vectors Provide Efficient Intracellular Delivery of Peptides. ACS Nano 2009, 3, 402–410. 10.1021/nn800679z. [DOI] [PubMed] [Google Scholar]
- Latorre-Sanchez A.; Pomposo J. A. A simple, fast and highly sensitive colorimetric detection of zein in aqueous ethanol via zein–pyridine–gold interactions. Chem. Commun. 2015, 51, 15736–15738. 10.1039/c5cc06083d. [DOI] [PubMed] [Google Scholar]
- Gillissen M. A. J.; Voets I. K.; Meijer E. W.; Palmans A. R. A. Single Chain Polymeric Nanoparticles as Compartmentalised Sensors for Metal Ions. Polym. Chem. 2012, 3, 3166–3174. 10.1039/c2py20350b. [DOI] [Google Scholar]
- Rothfuss H.; Knöfel N. D.; Roesky P. W.; Barner-Kowollik C. Single-Chain Nanoparticles as Catalytic Nanoreactors. J. Am. Chem. Soc. 2018, 140, 5875–5881. 10.1021/jacs.8b02135. [DOI] [PubMed] [Google Scholar]
- Rubio-Cervilla J.; González E.; Pomposo J. A. Advances in Single-Chain Nanoparticles for Catalysis Applications. Nanomaterials 2017, 7, 341. 10.3390/nano7100341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knöfel N. D.; Rothfuss H.; Willenbacher J.; Barner-Kowollik C.; Roesky P. W. Platinum(II)-Crosslinked Single-Chain Nanoparticles: An Approach towards Recyclable Homogeneous Catalysts. Angew. Chem., Int. Ed. 2017, 56, 4950–4954. 10.1002/anie.201700718. [DOI] [PubMed] [Google Scholar]
- Tooley C. A.; Pazicni S.; Berda E. B. Toward a Tunable Synthetic [FeFe] Hydrogenase Mimic: Single-Chain Nanoparticles Functionalized with a Single Diiron Cluster. Polym. Chem. 2015, 6, 7646–7651. 10.1039/c5py01196e. [DOI] [Google Scholar]
- Sanchez-Sanchez A.; Arbe A.; Colmenero J.; Pomposo J. A. Metallo-Folded Single-Chain Nanoparticles with Catalytic Selectivity. ACS Macro Lett. 2014, 3, 439–443. 10.1021/mz5001477. [DOI] [PubMed] [Google Scholar]
- Perez-Baena I.; Barroso-Bujans F.; Gasser U.; Arbe A.; Moreno A. J.; Colmenero J.; Pomposo J. A. Endowing Single-Chain Polymer Nanoparticles with Enzyme-Mimetic Activity. ACS Macro Lett. 2013, 2, 775–779. 10.1021/mz4003744. [DOI] [PubMed] [Google Scholar]
- Huerta E.; Stals P. J. M.; Meijer E. W.; Palmans A. R. A. Consequences of Folding a Water-Soluble Polymer around an Organocatalyst. Angew. Chem., Int. Ed. 2013, 52, 2906–2910. 10.1002/anie.201207123. [DOI] [PubMed] [Google Scholar]
- Terashima T.; Mes T.; De Greef T. F. A.; Gillissen M. A. J.; Besenius P.; Palmans A. R. A.; Meijer E. W. Single-Chain Folding of Polymers for Catalytic Systems in Water. J. Am. Chem. Soc. 2011, 133, 4742–4745. 10.1021/ja2004494. [DOI] [PubMed] [Google Scholar]
- Single-Chain Polymer Nanoparticles: Synthesis, Characterization, Simulations and Applications; Pomposo J. A., Ed.; Wiley-VCH: Weinheim, 2017. [Google Scholar]
- De-La-Cuesta J.; González E.; Moreno A. J.; Arbe A.; Colmenero J.; Pomposo J. A. Size of Elastic Single-Chain Nanoparticles in Solution and on Surfaces. Macromolecules 2017, 50, 6323–6331. 10.1021/acs.macromol.7b01199. [DOI] [Google Scholar]
- Rabbel H.; Breier P.; Sommer J.-U. Swelling Behavior of Single-Chain Polymer Nanoparticles: Theory and Simulation. Macromolecules 2017, 50, 7410–7418. 10.1021/acs.macromol.7b01379. [DOI] [Google Scholar]
- Pomposo J. A.; Rubio-Cervilla J.; Moreno A. J.; Lo Verso F.; Bacova P.; Arbe A.; Colmenero J. Folding Single Chains to Single-Chain Nanoparticles via Reversible Interactions: What Size Reduction Can One Expect?. Macromolecules 2017, 50, 1732–1739. 10.1021/acs.macromol.6b02427. [DOI] [Google Scholar]
- Latorre-Sánchez A.; Alegría A.; Lo Verso F.; Moreno A. J.; Arbe A.; Colmenero J.; Pomposo J. A. A Useful Methodology for Determining the Compaction Degree of Single-Chain Nanoparticles by Conventional SEC. Part. Part. Syst. Charact. 2016, 33, 373–381. 10.1002/ppsc.201500210. [DOI] [Google Scholar]
- Pomposo J. A.; Perez-Baena I.; Buruaga L.; Alegría A.; Moreno A. J.; Colmenero J. On the Apparent SEC Molecular Weight and Polydispersity Reduction upon Intramolecular Collapse of Polydisperse Chains to Unimolecular Nanoparticles. Macromolecules 2011, 44, 8644–8649. 10.1021/ma201070b. [DOI] [Google Scholar]
- Pomposo J. A.; Rubio-Cervilla J.; González E.; Moreno A. J.; Arbe A.; Colmenero J. Ultrafiltration of single-chain polymer nanoparticles through nanopores and nanoslits. Polymer 2018, 148, 61–67. 10.1016/j.polymer.2018.06.030. [DOI] [Google Scholar]
- de Gennes P.-G.Scaling Concepts in Polymer Physics; Cornell University Press: London, U.K., 1979. [Google Scholar]
- Rubinstein M.; Colby R. H.. Polymer Physics; Oxford University Press, Inc.: New York, 2003. [Google Scholar]
- Grosberg A. Y.; Khokhlov A. R.. Statistical Physics of Macromolecules; American Institute of Physics: New York, 1994. [Google Scholar]
- Cifra P.; Bleha T. Free Energy of Polymers Confined in Open and Closed Cavities. Macromol. Theory Simul. 2012, 21, 15–23. 10.1002/mats.201100061. [DOI] [Google Scholar]
- Sakaue T. Semiflexible Polymer Confined in Closed Spaces. Macromolecules 2007, 40, 5206–5211. 10.1021/ma070594r. [DOI] [Google Scholar]
- Cacciuto A.; Luijten E. Self-Avoiding Flexible Polymers under Spherical Confinement. Nano Lett. 2006, 6, 901–905. 10.1021/nl052351n. [DOI] [PubMed] [Google Scholar]
- Sakaue T.; Raphaël E. Polymer Chains in Confined Spaces and Flow-Injection Problems: Some Remarks. Macromolecules 2006, 39, 2621–2628. 10.1021/ma0514424. [DOI] [Google Scholar]
- Moreno A. J.; Bacova P.; Lo Verso F.; Arbe A.; Colmenero J.; Pomposo J. A. Effect of chain stiffness on the structure of single-chain polymer nanoparticles. J. Phys.: Condens. Matter 2018, 30, 034001. 10.1088/1361-648x/aa9f5c. [DOI] [PubMed] [Google Scholar]
- Harth E.; Van Horn B.; Lee V. Y.; Germack D. S.; Gonzales C. P.; Miller R. D.; Hawker C. J. A Facile Approach to Architecturally Defined Nanoparticles via Intramolecular Chain Collapse. J. Am. Chem. Soc. 2002, 124, 8653–8660. 10.1021/ja026208x. [DOI] [PubMed] [Google Scholar]
- Thanneeru S.; Nganga J. K.; Amin A. S.; Liu B.; Jin L.; Angeles-Boza A. M.; He J. “Enzymatic” Photoreduction of Carbon Dioxide using Polymeric Metallofoldamers Containing Nickel-Thiolate Cofactors. ChemCatChem 2017, 9, 1157–1162. 10.1002/cctc.201601661. [DOI] [Google Scholar]