Abstract
Periodic trends in relativistic effects are investigated from 1H through 103Lr using Dirac–Hartree–Fock and nonrelativistic Hartree–Fock calculations. Except for 46Pd (4d10) (5s0), all atoms have as outermost shell the ns or n’p spinors/orbitals. We have compared the relativistic spinor energies with the corresponding nonrelativistic orbital energies. Apart from 24Cr (3d5) (4s1), 41Nb (4d4) (5s1), and 42Mo (4d5) (5s1), the ns+ spinor energies are lower than the corresponding ns orbital energies for all atoms having ns spinor (ns+) as the outermost shell, as some preceding works suggested. This indicates that kinematical effects are larger than indirect relativistic effects (the shielding effects of the ionic core plus those due to electron–electron interactions among the valence electrons). For all atoms having np+ spinors as their outermost shell, in contrast, the np+ spinor energies are higher than the corresponding np orbital energies as again the preceding workers suggested. This implies that indirect relativistic effects are greater than kinematical effects. In the neutral light atoms, the np– spinor energies are close to the np+ spinor energies, but for the neutral heavy atoms, the np– spinor energies are considerably lower than the np+ spinor energies (similarly, the np– spinors are considerably tighter than the np+ spinors), indicating the importance of the direct relativistic effects in np–. In the valence nd and nf shells, the spinor energies are always higher than the corresponding orbital energies, except for 46Pd (4d10) (5s0). Correspondingly, the nd and nf spinors are more diffuse than the nd and nf orbitals, except for 46Pd.
1. Introduction
In this work, periodic trends are investigated in the relativistic effects occurring in 1H through 103Lr, using Dirac–Hartree–Fock and nonrelativistic Hartree–Fock calculations. Application of the Dirac theory to many-electron atomic systems began with the work of Swirles,1 who used the Hartree–Fock formalism in conjunction with the Dirac equation. The equations of the relativistic self-consistent field have been discussed using the algebra of tensor operators by Grant.2 Compared to numerical methods, expansion methods are more effective because of their wide applicability to molecular electronic structure and solid-state structure. Kim3 set out the relativistic Hartree–Fock equation using the expansion method. Desclaux4 calculated numerical Dirac–Fock spinor energies, total energies, and other properties, such as ⟨r⟩ for neutral atoms from Z = 1 to 120 (Z: nuclear charge). Many papers have since been written on relativistic atomic and molecular theories. Work published up to January 2016 has been summarized by Pyykkö in the database “RTAM”.5
Many reviews exist of relativistic effects in atomic and molecular electronic structures. Desclaux4 compared spinor energies and other properties with nonrelativistic values, but gave very little discussion. Rose, Grant, and Pyper (RGP)6 discussed the relativistic effects on the 71Lu (4f14) (5d1) (6s2), 79Au (5d10) (6s1), and 81Tl (5d10) (6s2) (6p1) states, which involve a single d, s, or p electron. Here, we cite their statement, “the relativistic orbital is normally more tightly bound than corresponding one for s and p– electrons, while for p+ electrons the effect of relativity is normally small. ... For d– and d+ electrons, the relativistic orbital is more loosely bound than the nonrelativistic orbital”. To give a clear explanation, RGP introduced the terms “direct and indirect relativistic effects”, which would be also used in the present article. Pyykkö and Desclaux7 stressed the importance of relativistic effects in heavy atoms, especially in giving rise to the color of 79Au, gold yellow. Pyykkö8,9 also discussed relativistic effects involving s, p, d, and f electrons and pointed out the importance of these effects in heavy atoms. Reiher and Hess10 and Ilias, Kellö, and Urban11 summarized the four-component relativistic theory, as well as approximations, such as the Douglas–Kroll12 transformation. Finally, Dyall and Faegri (DF)13 summarized relativistic effects in atoms and closely discussed 71Lu (4f14) (5d1) (6s2), 79Au (5d10) (6s1), and 81Tl (5d10) (6s2) (6p1) states using the results of RGP, and they further discussed relativistic effects on the 6s orbital energies.
In the present study, we call the one-electron orbital wave function a spinor in the relativistic domain and an orbital in the nonrelativistic domain. We discuss relativistic effects in atoms from 1H to 103Lr by comparing the spinor energies with the orbital energies and by comparing the relativistically calculated radial expectation values (⟨r⟩) with the nonrelativistic values. All of the neutral atoms have ns or np spinors/orbitals as their outermost shell except for 46Pd, which has the electronic configuration (5s0) (4d10). Below, it will be shown that almost all of the outermost s spinors given by the Dirac–Fock calculations are contracted compared to those predicted by nonrelativistic Hartree–Fock calculations and that the spinor energies are more deeply negative than the corresponding orbital energies. In atoms in which np is the outermost shell, in contrast, the outermost np+ spinors are more diffuse than the corresponding np orbitals, and all have higher spinor energies than the corresponding orbital energies, as suggested by RGP6 and DF.13 The outermost d± and f± spinors behave in the same manner as the outermost p+ spinors.
In Section 3.1 the relativistic and nonrelativistic solutions of the hydrogenic ions are discussed. In this case, the solutions are exact. Sections 3.2–3.7 are devoted to relativistic effects arising in the atomic electronic structure of neutral atoms. The spinors and orbitals involved are all calculated by expansion methods with Gaussian-type functions (GTFs).
2. Method of Calculations
To discuss the nonrelativistic total energy (TE) and the orbital energies, we used the nonrelativistic Hartree–Fock–Roothaan (HFR) method.14 The relativistic TE and spinor energies are given by the Dirac–Fock–Roothaan (DFR) method.15 The Hamiltonian for the relativistic calculation is composed of a one-electron Dirac term + a nuclear attraction term + an electron–electron interaction term. This is called the Dirac–Coulomb Hamiltonian. In HFR and DFR, the spinors and orbitals are expanded with GTFs. The nonrelativistic calculations were performed by Koga, Tatewaki, and Shimazaki,16 and the relativistic calculations by Koga, Tatewaki, and Matsuoka,17−19 in which the average-of-configuration (AOC) approximation,4 the uniform nuclear charge distribution model,4 and strict kinetic balance20,21 were used.
3. Results and Discussion
3.1. Relativistic Effects in the Hydrogenic Ions
Exact relativistic solutions for the hydrogen atom were given analytically by Gordon22 and Darwin23 in 1928. Exact nonrelativistic solutions for the hydrogenic wave functions are also known analytically and are summarized by, for example, Pauling and Wilson.24 The present authors have given tables25 of the angular part of the exact Dirac equation of the hydrogenic atom and provided three-dimensional (3D) density plots running from 1s1/2,1/2 (1s+) to 4f7/2,7/2 (4f+).
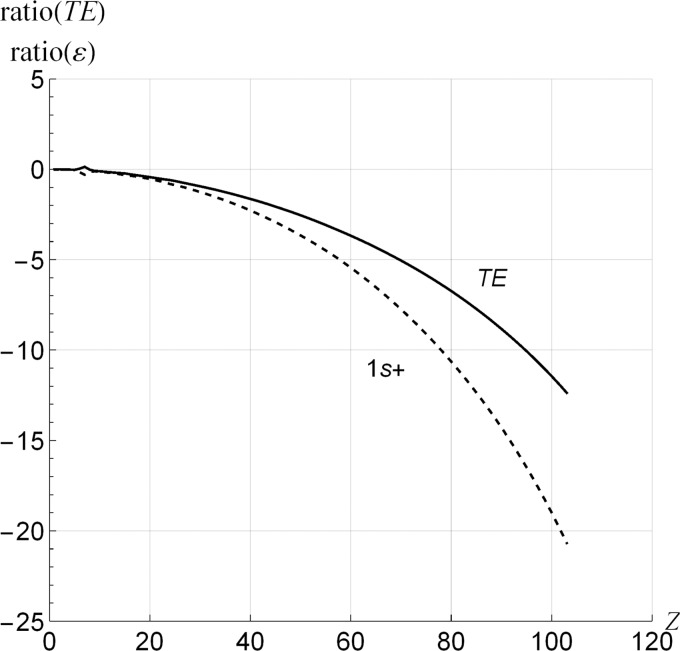
In Figure 1, we show the relativistic correction as a proportion of the nonrelativistic value of the total energy (TE) for hydrogenic ions from 1H to 103Lr102+; in Figure 2, we do the same for the expectation value of r (defined below). Because the hydrogenic ions are composed of a single electron, these results act as a reference for judging the magnitude of electron–electron interaction effects in relativistic effects.
| 1 |
| 2 |
If ratio(TEexact) is negative, the TE value given by the exact solution of the Dirac equation is lower than that given by the exact solution of the Schrödinger equation. We use henceforth symbols j and n to denote the electronic total angular momentum quantum number and the principal quantum number, respectively.
Figure 1.
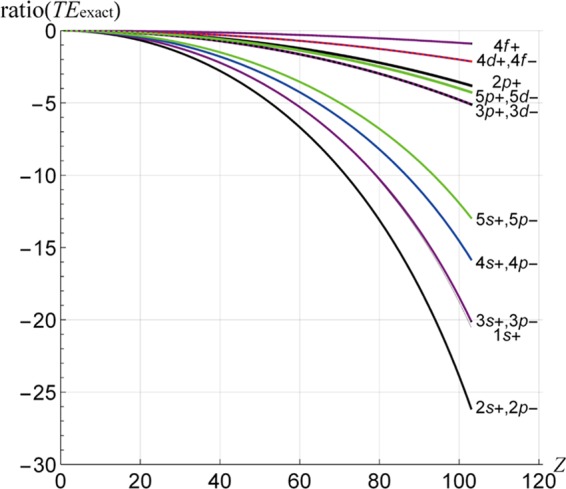
Ratio(TEexact) (=TE(exact Schrödinger) – TE(exact Dirac) × 100/TE(exact Schrödinger)) for the s, p, d, and f shells of the hydrogenic ions.
Figure 2.
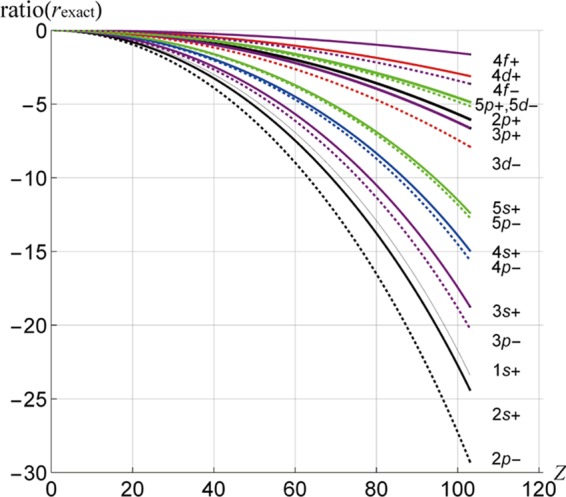
Ratio(rexact) (=⟨r (exact Dirac)⟩ – ⟨r (exact Schrödinger)⟩ × 100/⟨r (exact Schrödinger)⟩) for the s, p, d, and f shells of the hydrogenic ions.
From Figure 1, we observe that (1) the energies given by the Dirac equation are lower than the corresponding energies given by the Schrödinger equation; (2) states with the same values of j and n from the Dirac equation are degenerate; (3) ratio(TEexact) decreases monotonically as the nuclear charge (Z) increases, indicating that relativistic effects increase as Z increases; and (4) relativistic effects decrease as j increases. In Figure 2, we see a trend in ratio(rexact) similar to that in ratio(TEexact). The degeneracy in ratio(TEexact) disappears; however, in ratio(rexact), the difference in ratio(r) between 2s+ and 2p– is large. We shall see that, in the ionic core of the neutral atoms, ratio(r) defined by eq 6 for (2s+, 2p–), ..., (5s+, 5p–) behaves like (2s+, 2p–), ..., (5s+, 5p–) in Figure 2.
3.2. Relativistic Effects in 1s and TEs of Neutral Atoms
We now discuss the values of TE and the 1s spinor/orbital energies for the neutral atoms obtained using the expansion methods. In Figure 3, we show the total energy (TE) ratios and the 1s orbital energy ratios for neutral atoms from 1H to 103Lr.
| 3 |
| 4 |
From Figure 3, we see that the ratios for 1s+ of the neutral atoms are close to those of hydrogenic ions in Figure 1, indicating that the behavior of ratio(ε) for 1s+ in the neutral atoms is similar to that for the hydrogenic ions. No anomalies in the ratio(ε) for 1s+ are observed. It is safe to say that in the 1s spinor direct relativistic effects (see below) overcome shielding effects from the outer electrons and the other 1s electron. The value of ratio(TE) also decreases monotonically from 1H to 103Lr as does ratio(ε) of 1s+. Finally, we used the electron configuration (6d1) (7s2) for 103Lr instead of (7p1) (7s2)26,27 because we used the HFR and DFR results given by refs (16−19), where (6d1) (7s2) was employed.
Figure 3.
Ratio(TE) (=(TE(HFR) – TE(DFR)) × 100/TE(HFR)) and ratio(ε) (=(ε(HFR) – ε(DFR) × 100/ε(HFR)) for 1s (from 1H to 103Lr).
3.3. Relativistic Effects in the Outermost s and p Shells of Neutral Atoms
Except for 46Pd (4d10)(5s0), all atoms have ns or n’p orbitals/spinors as their outermost shell so far as the diffuseness is concerned. In this study, we classify atoms into three categories by the diffuseness of their spinors. The group 13–18 atoms except for 2He (1s2) have the electron configuration (ns2) (npm; m = 1–6), where np+ is the outermost spinor. The remaining atoms have an ns+ spinor as their outermost shell except for 46Pd. We may call the group 13–18 atoms p atoms, and the remaining atoms s atoms except for 46Pd, which we refer to as a d atom. The values of ratio(ε) given by eq 4 for the outermost ns’s and np’s are plotted in Figure 4. The 46Pd atom has 4d+ as its outermost shell, and we mark the ratio(ε) for 46Pd with a closed blue square. The value of ratio(ε) for the outermost ns is negative for all s atoms except for 24Cr (3d5) (4s1), 41Nb (4d4) (5s1), and 42Mo (4d5) (5s1). Relativistic effects lower the ns spinor energy in comparison to the corresponding ns orbital energy.
Figure 4.
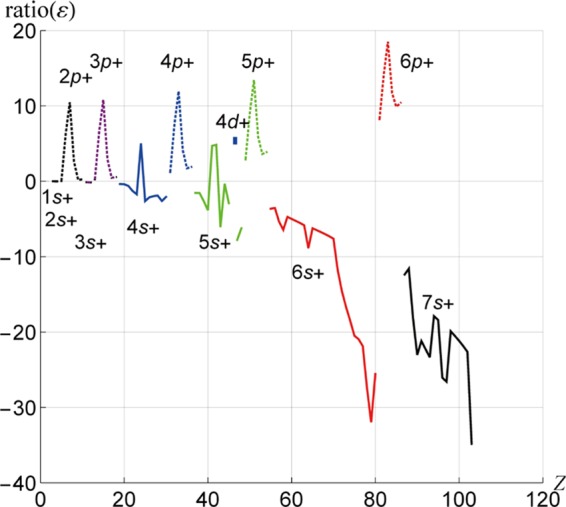
Ratio(ε) (=(ε(HFR) – ε(DFR)) × 100/ε(HFR)) for the outermost shells (from 1H to 103Lr).
According to RGP6 and DF,13 relativistic effects in the Dirac–Coulomb Hamiltonian are divided into two parts, direct relativistic effects and indirect relativistic effects. Direct relativistic effects arise from the Dirac term plus nuclear attraction term, which is roughly divided into the spin–orbit interaction term and the so-called kinematical term.10 The kinematical term is expressed approximately as the sum of the mass–velocity term and the Darwin term, and it is due to electrons moving at high velocity in the vicinity of the nucleus.
For the valence electrons, indirect relativistic effects appear as differences between relativistic and nonrelativistic electron–electron interactions among the valence–core and valence–valence shells. (Likewise, for the core electrons, indirect effects appear as differences between relativistic and nonrelativistic electron–electron interactions among the core–core and core–valence shells.) Indirect relativistic effects can be interpreted also as differences between relativistic and nonrelativistic shielding effects due to electron–electron interactions among the core–valence and valence–valence shell electrons. Kinematical effects cause the spinor energy to be lower than the orbital energy, whereas indirect relativistic effects cause the spinor energy to be lower or higher than the orbital energy, depending on the electronic structure. If the shielding effects in the relativistic calculation are larger than those in the nonrelativistic one, the indirect relativistic effects make the spinor energy higher. Conversely, if the shielding effects in the relativistic calculation are smaller than those in the nonrelativistic calculation, indirect relativistic effects reinforce the kinematical effects; the spinor energy becomes deeper.
The negative value of ratio(ε) for the s atoms shows that the effects of the kinematical term surpass the indirect relativistic effects, even if the indirect relativistic effects are oppositely oriented. The role of indirect effects in the s atoms will be discussed below. In the p atoms, ratio(ε) is positive for all of the outermost np+. This tells us that indirect relativistic effects, which cause the spinor energy to be shallow, surpass the direct relativistic effects; the inner closed shells and valence shells shield the nuclear charge more efficiently when relativity is taken into account. We also expect that relativistic effects cause p+ to be more diffuse than the nonrelativistic p. This tendency illustrated in Figure 5 is seen parallelly in ref (6).
Figure 5.
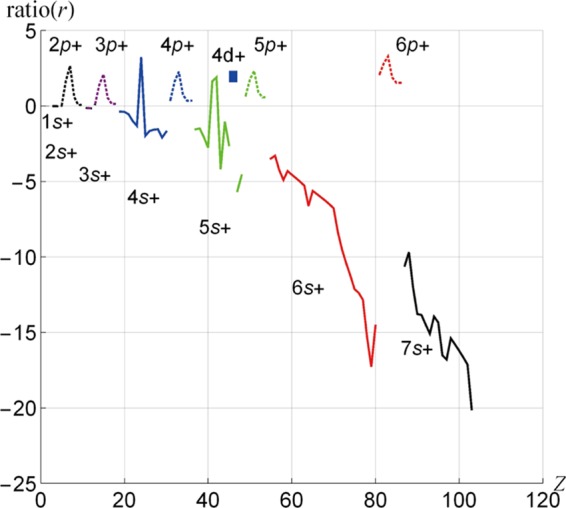
Ratio(r) (=(⟨r(DFR)⟩ – ⟨r(HFR)⟩) × 100/⟨r(HFR)⟩) for the outermost shells (from 1H to 103Lr).
We now discuss relativistic effects in the valence ns shells in more detail. Relativistic effects are negligibly small for 1H, 2He, 3Li, 4Be, 11Na, 12Mg; then, they increase gradually for the series 19K, 20Ca, the first transition-metal atoms (21Sc–29Cu), 30Zn, 37Rb, 38Sr, the second transition-metal atoms (39Y–47Ag), 48Cd, 55Cs, 56Ba, the lanthanoid atoms (57La–71Lu), the third transition-metal atoms (72Hf–79Au), 80Hg, 87Fr, 88Ra, and the actinoid atoms (89Ac–103Lr). We, however, note that between the alkali-metal atoms and alkaline-earth metal atoms (between 19K and 20Ca, 37Rb and 38Sr, 55Cs and 56Ba, 87Fr and 88Ra), ratio(ε) is almost constant, indicating that shielding effects from the inner core of the alkali-metal atoms and alkaline-earth metal atoms are similar and the shielding effects from another ns electron are quite small. Because ratio(ε) for 4s+ and 5s+ is negative (the ns spinor energy is lower than the ns orbital energy), and decreases as the number of d electrons increases, we infer that the shielding effects of the relativistic nd shell decreases faster than those of the nonrelativistic nd shell. Indirect relativistic effects in the first and second transition-metal atoms enhance the relativistic effects. In Figure 5, we see anomalies at 24Cr (3d5) (4s1), 41Nb (4d4) (5s1), and 42Mo (4d5) (5s1), which are high-spin states in the LS-coupling scheme. These anomalies are presumably due to the use of AOC in DFR.
The shielding effects of the relativistic nf shell on the 6s shell are further decreased compared to the nonrelativistic nf shell. For these atoms, we observe two dips (see Figure 5). The first is at 58Ce (4f1) (5d1) (6s2), and the second at 64Gd (4f7) (5d1) (6s2). The shielding effect of the 5d spinor/orbital is expected to be smaller than that of the 4f spinor/orbital. This lowers the 6s spinor/orbital energies of 58Ce and 64Gd compared to the other atoms, which are not associated with a 5d electron. The example is an excited state of 64Gd, (4f8) (6s2). If we write the spinor/orbital energy of 6s of the 64Gd (4f8) (6s2) excited state as ε′(DFR)6s and ε′(HFR)6s+, respectively, the value of ratio(ε) for 6s+ of 64Gd (4f7) (5d1) (6s2) is given by
| 5 |
where the two δ terms are due to the change of occupation (4f → 5d). These δ terms are negative, as suggested above. For this ratio to be smaller than (ε′(HFR)6s – ε′(DFR)6s+) × 100/ε′(HFR)6s, it is necessary that (δε′nonrel,6s – δε′rel,6s+) ≫ 0. From the spinor/orbital energies of 63Eu (4f7) (6s2) and 65Tb (4f9) (6s2), we have estimated the spinor/orbital energies and δ’s for 64Gd (4f8) (6s2) as ε′(DFR)6s+ = −0.183 au and ε′(HFR)6s = −0.173 au. The spinor/orbital energies (ε’s) of 64Gd (4f7) (5d1) (6s2) are −0.1996 and −0.1833 au, respectively. We then have δε′rel,6s+ = −0.016 au and δε′nonrel,6s = −0.011 au. The absolute value of δε′rel,6s+ is 150% times that of δε′nonrel,6s. Thus, 6s+ is far more stabilized than 6s by the change of occupation (4f → 5d). That is the origin of the dip at 64Gd. Actually, eq 5 gives ratio(ε) of −8.9%, whereas (ε′(HFR)6s – ε′(DFR)6s+) × 100/ε′(HFR)6s gives ratio(ε) of −5.6%.
For 71Lu, and for the third transition-metal atoms (72Hf–79Au) and 80Hg, the indirect relativistic effects increase as suggested by ratio(ε) for 6s+. Ratio(ε) decreases sharply and has a minimum at 79Au (5d10) (6s1). RGP6 calculated that ε6s = −0.221 au and ε6s+ = −0.292 au. Replacing the relativistic core with nonrelativistic core and by similar replacement, RGP6 gave an approximate value of the direct relativistic and indirect relativistic contributions. The given values are −0.072 au for the direct relativistic contribution and −0.006 au for the indirect contribution. Following RGP, the direct relativistic contribution governs the lowering in the spinor energy relative to orbital energy at 79Au. The sharp decrease in the ε(DFR) given in Figure 4 is thus mainly brought by the direct effects supported with indirect relativistic effects. Finally, Dyall and Faegri13 showed the anomalies of 6s+ spinor energies at 74W, 78Pt, and 79Au. These are due to the electron configuration (5dn+1) (6s1). We have anomalies at 78Pt and 79Au, but not at 74W. In the present work, 78Pt and 79Au have (5dn+1) (6s1), but 74W does (5dn; n = 4) (6s2).
We summarize the relativistic corrections for the s atoms as follows: (1) the kinematical effect10 mainly lowers the outermost ns+ energies compared to the ns orbital energies and (2) the smaller shielding effects of the electrons in the d and f orbitals (part of the indirect relativistic effects10) than those of electrons in the d and f orbitals further support the lowering in energy of ns+.
We next discuss about the p atoms. Their electronic structures are fairly simple. The np electrons always move in the electric field generated by the closed-shell ion core, which gives a similar shape for the np+ ratio(ε) regardless of n. The repulsive potential generated from the closed-shell ion core plus the two-electron interaction terms among the np electrons in the DFR is greater than that in the HFR. The indirect relativistic effects6,10,13 cause the np+ spinor energies to be shallow, the opposite situation to the ns+ cases discussed above. Indirect relativistic effects are stronger than the direct relativistic effects so that the np+ spinor energies are higher than the orbital energies. The value of ratio(ε) has a peak at (np3). We believe that this peak is exaggerated as a result of the use of AOC in the DFR calculations. Finally, RGP6 estimated the magnitude of the direct and indirect relativistic effects for 81Tl 6p– and 6p+. For 6p–, the direct relativistic effect is −0.057 au and the indirect one is 0.028 au. For 6p+, they are −0.014 and 0.028 au, respectively. Totally, the relativistic effects decrease the 6p– spinor energy and increase the 6p+ spinor energy. Ratio(ε)’s for 81Tl by the use of their estimated values are −7 and 17% for the 6p– and 6p+ spinors, respectively, which are consistent with the present values of −9.5% for 6p–, which would be shown later, and 8.3%, given in Figure 4, for 6p+.
| 6 |
is shown for the outermost ns+ for the s atoms, and np+ for the p atoms. The results for ratio(r) are similar to those for ε in Figure 4, although the absolute values of ratio(r) are smaller than ratio(ε). The explanation given for Figure 4 holds also for Figure 5. It is well known that for heavy atoms, such as the lanthanoid atoms, the size of ⟨r⟩ of 6s contracts as Z increases. In fact, in both the relativistic and nonrelativistic calculations, the 6s ⟨r⟩ value decreases as Z increases. As shown in Figure 5, the lanthanoid contraction (57Ce–70Yb) and the actinoid contraction (89Ac–102No) are strengthened by relativistic effects. In 71Lu, the third transition-metal atoms (72Hf–79Au), and 80Hg, the relativistic effects are fairly large.
Spinor/orbital energies of the outermost shells and inner shells and the mean distances of r for spinors/orbitals are given in the Supporting Information.
3.4. Relativistic Effects in the Inner s and p Shells of Neutral Atoms
In the case of the hydrogenic ions described in Section 2, the spinors specified by j with the same principal quantum number n are energetically degenerate, and their values of ratio(ε) take the same value. As shown in Figure 6, even for the neutral atoms, these ratios for the (ns+, np–) pair of j = 0 in the ion cores behave like those of the hydrogenic ions. In this figure, solid lines show ratio(ε) for ns+ or np+ and dotted lines show ratio(ε) for np–. We discuss these pairs in detail.
Figure 6.
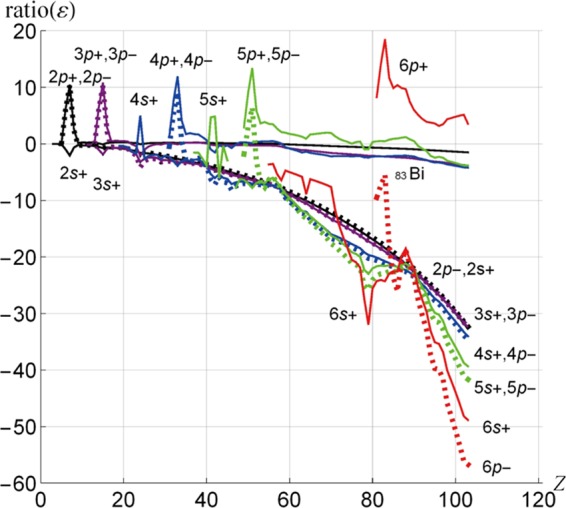
Ratio(ε) (=(ε(HFR) – ε(DFR)) × 100/ε(HFR)) for the valence and inner s and p shells. (1) Black solid lines denote 2p+ and 2s+, and the black dotted line denotes 2p–. (2) Purple solid lines denote 3p+ and 3s+, and the purple dotted line denotes 3p–. (3) Blue solid lines denote 4p+ and 4s+, and the blue dotted line denotes 4p–. (4) Green solid lines denote 5p+ and 5s+, and the green dotted line denotes 5p–. (5) Red solid lines denote 6p+ and 6s+, and the red dotted line denotes 6p–.
The value of ratio(ε) for 2p– (black dotted line) is close to that (upper black solid line) for 2p+ of the neutral atoms from 5B to 8O, but for those from 9F (2s+: −0.22%, 2p–: −0.18%) to 103Lr (2s+: −32.66%, 2p–: −32.31%), its value is close to that (lower black solid line) of 2s+. Values of ratio(ε) for 2p+ of 9F and 103Lr are +0.19 and −1.50%, respectively. Values of ratio(ε) for 2p+ of 9F and 103Lr are far from the corresponding ratio(ε) for 2p–. Values of ratio(ε) for 2s+, 2p–, and 2p+ of atoms beyond 8O decrease monotonically as Z increases. The valence shell electronic structure is not reflected in the value of ratio(ε) after 9F; the influence of the valence shell structure is observed in, for instance, the rapid decrease of ratio(ε) for 4s+, 4p–, 5s+, and 5p– and the local minimum at 79Au. It can be stated with reasonable confidence that after 11Na, the 2s and 2p spinor/orbital energies are stable, meaning that they are not influenced by the electronic structures of the outer shells.
A similar discussion to that given above holds for the 3s–3p and 4s–4p shells. The value of ratio(ε) for 3p– (purple dotted line in Figure 6) is near to that of 3p+ (upper purple solid line) in the case of the neutral atoms from 13Al to 16S, but it is close to that of 3s+ (lower purple solid line) from 17Cl (3s+: −0.62%, 3p–: −0.56%) to 103Lr (3s+: −32.42%, 3p–: −32.43%). The values of ratio(ε) for 3p+ of 17Cl and 103Lr are +0.47 and −3.83%, respectively. Relativistic effects are large for the (3s+, 3p–) pair compared to 3p+, especially for the heavy atoms. The difference in the outer-shell electronic structure is not reflected in the values of ratio(ε) for the inner 3s and 3p shells after 17Cl. Beyond 19K, the spinor/orbital energies appear to be stable, meaning that they are not influenced by the electronic structures of the outer shells. The value of ratio(ε) for 4p– (blue dotted line) is close to that for 4p+ (upper blue solid line) of the neutral atoms from 31Ga to 34Se, but close to that for 4s+ (lower blue solid line) from 35Br (4s+: −2.84%, 4p–: −2.79%) to 103Lr (4s+: −34.02%, 4p–: −34.66%). The values of ratio(ε) for 4p+ of 35Br and 103Lr are +1.72 and −4.21%, respectively. Kinematical effects are large for the (4s+, 4p–) pair compared to 4p+, especially for the heavy atoms, as also for the (3s+, 3p–) pair compared to 3p+. The outer-shell electronic structures have some influence on the (4s+, 4p–) pair as far as roughly 86Rn; they have scarcely any influence on the (4s+, 4p–) pair beyond 87Fr.
Values of ratio(ε) for 5s+–5p– and 6s+–6p– inner shells are quite different from the 3s+–3p– and 4s+–4p– inner shells referred to above. Ratio(ε) for 5s+ (lower green solid) begins at 37Rb and that for 5p– (green dotted) begins at 49In. However, ratio(ε) for 5p– is different from that for 5p+ (upper green solid) at 49In (5p–: −1.83%, 5p+: 2.91%). The value of ratio(ε) for 5p– is the same as for 5s+ at 53I (−6.76%). Beyond 53I, ratio(ε) is similar for 5s+ and 5p–, but does not decrease monotonically as Z increases; see the local minimum at 79Au. The solid red line shows ratio(ε) for 6s+, beginning at 55Cs; the red dotted line showing 6p– begins at 81Tl. From 55Cs to 80Hg, the outermost shell is 6s+. As shown in Figures 4 and 6, the value of ratio(ε) for the 6s shell changes dramatically as Z decreases. Ratio(ε) for 6p– begins at 81Tl and takes a very different value from that for 6p+ (6p–: −9.49%, 6p+: 8.26%); the 6p– spinor energy is considerably lower than the 6p orbital energy, and the 6p+ spinor energy is considerably higher than the 6p orbital energy; ε(6p–) = −0.2105 au, ε(6p) = −0.1923 au, and ε(6p+) = −0.1764 au at 81Tl. The values of ratio(ε) for 6s+ and 6p– of 85At are comparable (6s+: −22.52%, 6p–: −23.67%), but are different at 86Rn (6s+: −22.54%, 6p–: −26.09%). For 6p+ of 85At, ratio(ε) is +9.88%. After 87Fr, for which ratio(ε) is 6s+: −19.82% and 6p–: −20.82%, values for 6s+ and 6p– behave similarly. Although beyond 87Fr 6s+, 6p– and 6p+ are inner shells, the values of ratio(ε) for these shells vary considerably. Kinematical effects and indirect relativistic effects are both important for 6s+ and 6p–. For 6p+, on the other hand, the indirect relativistic effects are important.
Figure 7 shows ratio(r) for the inner ns and np spinors together with the valence spinors. The results for 2s+, ..., 5p– of the heavy atoms run parallel to ratio(r) in Figure 2; this indicates the importance of the kinematical effects for these spinors.
Figure 7.
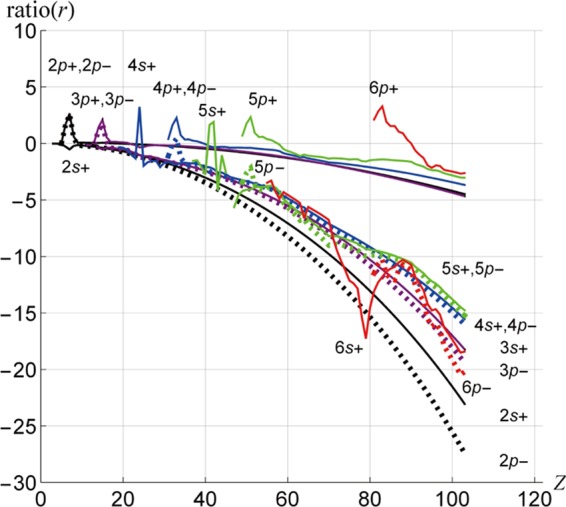
Ratio(r) (=(⟨r(DFR)⟩ – ⟨r(HFR)⟩) × 100/⟨r(HFR)⟩) for the valence and inner s and p shells. (1) Black solid lines denote 2p+ and 2s+, and the black dotted line denotes 2p–. (2) Purple solid lines denote 3p+ and 3s+, and a purple dotted line denotes 3p–. (3) Blue solid lines denote 4p+ and 4s+, and a blue dotted line denotes 4p–. (4) Green solid lines denote 5p+ and 5s+, and a green dotted line denotes 5p–. (5) Red solid lines denote 6p+ and 6s+, and a red dotted line denotes 6p–.
3.5. Relativistic Effects in the Outermost d Shells of the Neutral Atoms
We now discuss relativistic effects in the outermost d shell. The 3d shell is a valence shell, together with 4s from 21Sc to 30Zn. Figure 8 shows ratio(ε) for the d and f shells. We observe that 3d+ and 3d– are more unstable than 3d from 21Sc to 30Zn. Ratio(ε) for 3d+ takes a maximum value of +15.7% at 24Cr (3d5) (4s1), although this may be an overestimate because of the AOC used in the relativistic calculations; the 3d+ spinor energy and the 3d orbital energy of 24Cr are −0.3148 and −0.3734 au, respectively. Because ratio(ε) begins at 2.5% of 21Sc and ends at 3.6% of 30Zn, we are in no doubt that the indirect relativistic effects cause the 3d spinor energies to be more unstable than the corresponding orbital energies. Figure 9 shows ratio(r) for the d and f shells. The Z-dependence of ratio(r) is similar to that of ratio(ε) for the atoms 21Sc–30Zn. The relativistic calculation gives larger ⟨r⟩ values for 3d than the nonrelativistic. This is consistent with the fact that ε is shallower for the former than for the latter.
Figure 8.
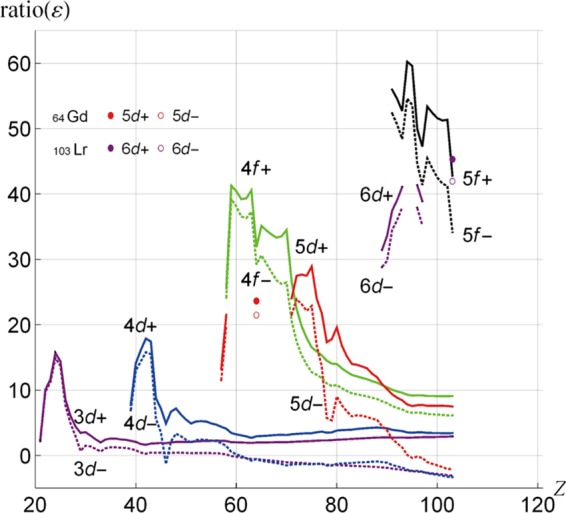
Ratio(ε) (=(ε(HFR) – ε(DFR)) × 100/ε(HFR)) for all d and f shells.
Figure 9.
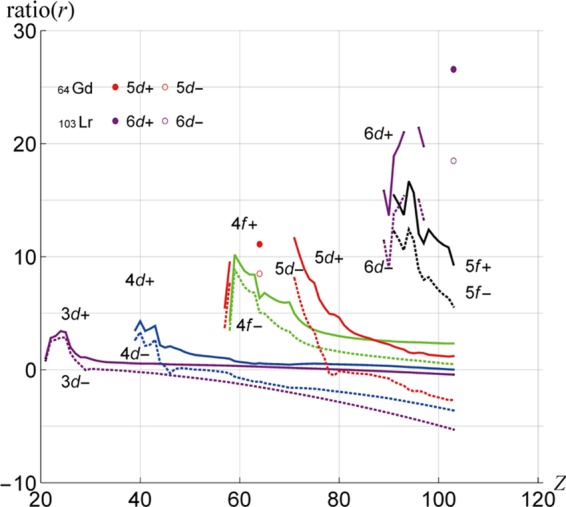
Ratio(r) (=(⟨r(DFR)⟩ – ⟨r(HFR)⟩) × 100/⟨r(HFR)⟩) for all d and f shells.
The second transition-metal atoms run from 39Y to 47Ag. All 4d+ and 4d– have positive ratio(ε) except for 4d– of 46Pd, for which the electronic configuration is (4d10) (5s0). Ratio(ε) for 4d+ has a maximum value of +17.9% at 42Mo (4d5) (5s1); again, this value may be an overestimate because of the AOC used in the relativistic calculations; the 4d+ spinor and 4d orbital energies of 42Mo are −0.2937 and −0.3577 au, respectively. Because high-spin and low-spin states are included in AOC, the resulting TE is higher than the lowest state with the proper symmetry. Again, we are in no doubt that indirect relativistic effects help to make the 4d spinors to be more unstable than those of the corresponding 4d orbitals. The Z-dependence of ratio(r) in Figure 9 runs parallel to that of ratio(ε) in Figure 8 for the atoms 39Y–48Cd. For the d atom (46Pd), ratio(ε) is positive for the outermost 4d+ but negative for the outermost 4d–.
In 71Lu, in the third transition-metal atoms (72Hf–79Au) and in 80Hg, the 5d+ and 5d– all have positive ratio(ε)’s; these ratios are twice as large as the corresponding ratios in the first and second transition-metal atoms. This implies larger indirect relativistic effects in 71Lu and the third transition-metal atoms (72Hf–79Au) and 80Hg. For 5d+, ratio(ε) reaches a maximum value of +28.9% at 75Re (5d5) (6s2). The 5d+ spinor energy and the 5d orbital energy of 75Re are −0.3655 and −0.5141 au, respectively. The difference between ratio(ε)’s for 5d+ and 5d– is the largest among nd+ and nd– (n = 3, 4, and 5), suggesting that the effect of the spin–orbit interaction is greatest for atoms having 5d shells. As we say above, the indirect relativistic effects cause the 5d spinors to be more unstable than the corresponding 5d orbitals. RGP6 gave approximate values for the indirect and direct relativistic effects in 71Lu (5d1) (6s2); for 5d–, the indirect and direct relativistic effects are 0.069 and −0.025 au, respectively, whereas for 5d+, the corresponding values are 0.067 and −0.010 au. Using these values given by RGP, we obtained ratio(ε)’s of 18 and 23% for 5d– and 5d+, which are consistent with the present values of 22 and 24% for 5d– and 5d+, respectively, shown in Figure 8.
Ratio(ε) has minima at 78Pt and 79Au. The electronic configuration of 79Au is (5d10) (6s1), and the 5d+ spinor and the 5d orbital energies are, respectively, −0.4281 and −0.5207 au. The large instability in 5d and the strong stability exhibited by 6s (6s+ ε: −0.2912 au; 6s ε: −0.2206 au) of 79Au due to relativistic effects are responsible for the gold yellow color, as discussed by Pyykkö and Desclaux.6
3.6. Relativistic Effects in the Outermost f Shells of Neutral Atoms
Consider now the lanthanoid atoms from 57La to 70Yb, excluding 71Lu. The electronic configuration of 57La is (4f0) (5d1) (6s2) and that of 58Ce is (4f1) (5d1) (6s2). The others have configurations (4fn; n = 3–14) (5d0) (6s2), except for 64Gd (4f7) (5d1) (6s2). The relativistic 4f shells without a 5d electron are more destabilized than shells with a 5d electron. For 4f+, ratio(ε) takes a maximum value of +41.3% at 59Pr (4f3) (5d0) (6s2). The 4f+ spinor energy and the 4f orbital energy of 59Pr are −0.3224 and −0.5491 au, respectively. For 4f±, ratio(ε) has a local minimum at 64Gd (4f7) (5d1) (6s2). Because 5d in the relativistic and nonrelativistic wave functions is more diffuse than 4f’s, the shielding effects are smaller for 4f’s in 64Gd (4f7) (5d1) (6s2) than in 64Gd (4f8) (6s2). Consequently, the effective nuclear charge for 4f’s in 64Gd (4f7) (5d1) (6s2) is larger than in 64Gd (4f8) (6s2). In the relativistic and nonrelativistic calculations, therefore, states with 5d have deeper 4f spinor/orbital energies than states without 5d. We write the 4f spinor and orbital energies of 64Gd (4f8) (6s2) as ε′(DFR)4f and ε′(HFR)4f and write the corresponding energy lowering in the 4f’s in 64Gd (4f7) (5d1) (6s2) as δε′rel,4f± and δε′nonrel,4f. The value of ratio(ε) for 4f+ of (4f7) (5d1) (6s2) may be expressed as
| 7 |
The 10% drop in ratio(ε) at 64Gd can be explained by assuming that δε′nonrel,4f is near to δε′rel,4f+ and that the magnitude of δε′nonrel,4f is not less than about 30% of ε′(HFR)4f. From the spinor/orbital energies of 63Eu (4f7) (6s2) and 65Tb (4f9) (6s2), we have estimated the spinor/orbital energies and values of δ for 64Gd (4f8) (6s2); in particular, ε′(DFR)4f+ = −0.437 au and ε′(HFR)4f = −0.703 au. The values of ε for 4f+ and 4f of 64Gd (4f7) (5d1) (6s2) are −0.7106 and −1.0433 au, respectively. We then find that δε′rel,4f+ = −0.274 au and δε′nonrel,4f = −0.340 au. The two δ’s in the numerator largely cancel each other, and the absolute value of the denominator is 50% greater than the value without δε′nonrel,4f. From these values, we find that ratio(ε) = 31.8%, which is much lower than the value of 37.8% for (4f8) (6s2). The large orbital energy lowering in the 4f orbital of 64Gd (4f7) (5d1) (6s2) compared to that of (4f8) (6s2) might be responsible for the local minimum ratio(ε) of 64Gd. In the lanthanoid and actinoid atoms, the 4f and 5f spinors are significantly destabilized by the indirect relativistic effects.
Figure 9 shows that the shape of ratio(r) plotted versus Z is similar to that for ratio(ε). The value of ratio(r) for 4f is considerably lower compared to the ratio(ε) in Figure 8. Let us consider why ratio(r) for 4f is low, taking 64Gd as an example. The 4f electron cloud is in the narrow space sandwiched between the (4s, 4p, 4d) shell and the (5s, 5p) shell, whereas the 5d electron cloud is in the extensive space between the (5s, 5p) shell and the 6s shell. Because of this narrow space, the difference (⟨r(DFR)⟩ – ⟨r(HFR)⟩) = 0.8389 – 0.7890 au = 0.0499 au for the 4f+ shell is 5 times smaller than that for (⟨r(DFR)⟩ – ⟨r(HFR)⟩) = 2.7330 −2.4600 au = 0.2730 au for 5d+ shell. Consequently, ratio(r)’s for 4f+ and 5d+ are 6.32 and 11.10%, respectively, as shown in Figure 9. The restriction on the space causes the differences (⟨r(DFR)⟩ – ⟨r(HFR)⟩) in 4f± to be smaller than for 5d±.
Let us discuss the actinoid atoms from 89Ac to 103Lr. The 5f and 6d shells are both occupied in the ground-state configurations of the following six atoms: 91Pa (5f2) (6d1) (7s2), 92U (5f3) (6d1) (7s2), 93Np (5f4) (6d1) (7s2), 96Cm (5f7) (6d1) (7s2), 97Bk (5f8) (6d1) (7s2), and 103Lr (5f14) (6d1) (7s2). Ratio(ε) has local minima at 93Np and 97Bk, as shown in Figure 8. These local minima would be explicable in the same manner as that for 64Gd (4f7) (5d1) (6s2). The values of ε for 5f–, 5f+, and 5f of 97Bk, for instance, are −0.5795, −0.5214, and −0.9884 au, respectively. Figure 9 shows that the shape of ratio(r) for 5f versus Z resembles the shape of ratio(ε) for the relativistic 5f. However, ratio(r) for 5f examined in relation to that for 6d is unusually low compared to ratio(ε) for 5f examined in relation to that for 6d. The 5f electron cloud is located in the narrow space sandwiched between the (5s, 5p, 5d) shell and the (6s, 6p) shell, whereas the 6d electron cloud is in the extensive space between the (6s, 6p) shell and the 7s shell. This restriction in volume causes the variation of ⟨r(DFR)⟩ – ⟨r(HFR)⟩ of 5f± to be smaller than that of 6d±. Accordingly, the ratio(r) for 5f± is smaller than that for 6d±.
3.7. Relativistic Effects in the Inner d and f Shells of Neutral Atoms
The 3d, 4d, and 5d shells begin to form an ion core at 31Ga, 49In, and 81Tl, respectively, and the 4f shell, at 71Lu. For 31Ga–58Ce 3d–, 49In–60Nd 4d–, and 81Tl–94Pu 5d–, the value of ratio(ε) is positive, indicating that the 3d, 4d, and 5d spinors are less stable than the corresponding nonrelativistic orbitals; indirect relativistic effects strongly influence the characteristics of the spinor energies. Although ratio(ε) for 4f± is positive after 71Lu, it decreases sharply. This suggests that the importance of the direct relativistic effects increases.
For 59Pr–103Lr 3d–, 61Pm–103Lr 4d–, and 95Am–103Lr 5d–, the value of ratio(ε) is negative and kinematical effects are important, as in the hydrogenic ions. Values of ratio(ε) for 3p+, 3d–, and 3d+ at 59Pr are, respectively, −0.69, −0.08, and 2.05%. Ratio(ε) for 3d– is closer to ratio(ε) for 3p+ than ratio(ε) for 3d+. The values of ratio(ε) for these spinors change slowly as Z increases (see Figures 6 and 8). At 103Lr, the values for 3p+, 3d–, and 3d+ are, respectively, −3.83, −3.07, and 2.92%. We can say that beyond 59Pr, 3p+ and 3d– tend to pair. The values of ratio(ε) for 4p+, 4d–, and 4d+ at 61Pm are −1.03, −0.10, and 3.09%, respectively. Beyond 61Pm, shells having the same value of j tend to pair. Values of ratio(ε) for 5p+, 5d–, and 5d+ at 95Am are, respectively, −2.44, −0.37, and 7.57%. Beyond 95Am, shells having the same value of j tend to pair.
The plot in Figure 9 has a similar shape to that in Figure 8, but differences emerge upon closer examination. Figure 9 reveals that ratio(r) for 3d– becomes negative (−0.01%) at 33As, suggesting that kinematical effects surpass the indirect effects for 33As. Figure 8 indicates that the kinematical effects surpass the indirect relativistic effects for 59Pr, however. We believe that ratio(ε) reflects the characteristics of the atomic shell structure more realistically than ratio(r) because ratio(ε) is derived directly from comparison of the eigenvalues of the DFR and HFR equations.
4. Conclusions
We have discussed relativistic effects in atoms from 1H to 103Lr. Except for 46Pd (4d10) (5s0), all atoms have, as their outermost shall, their ns or n’p spinors/orbitals. It is the case that for all of the atoms having the ns spinor (ns+) as their outermost shell, the ns+ spinor energies are lower than the corresponding ns orbital energies. This result indicates that kinematical effects are more important than indirect relativistic effects for the ns shell. In contrast, in all atoms having np+ spinors as the outermost shell, the np+ spinor energies are higher than the corresponding np orbital energies (similarly, the np+ spinors are more diffuse than the np orbitals). This indicates that the indirect relativistic effects are stronger than the kinematical effects. Specifically, in the valence p+ spinors, the shielding effects provided by the ionic core and the valence electrons surpass the kinematical effects. The same is true for p– of light atoms, but for heavy atoms, the importance of the kinematical effects increases. The p– spinors take considerably lower spinor energies than the corresponding p orbitals. This is especially remarkable for the 5th group 13–18 atoms. In the nd and nf shells, the indirect relativistic effects are strengthened, and the instability of the spinor energies compared to the corresponding orbital energies increases further. The enhancement of contractions of the outermost s orbitals by the relativistic effects in the lanthanoid atoms, the third transition-metal atoms, and the actinoid atoms have also been discussed. Diffuseness of the nd and nf spinors compared to the corresponding nonrelativistic orbitals was also investigated.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.7b00802.
The authors declare no competing financial interest.
Supplementary Material
References
- Swirles B. The Relativistic Self-Consistent Field. Proc. R. Soc. London, Ser. A 1935, 152, 625–649. 10.1098/rspa.1935.0211. [DOI] [Google Scholar]
- Grant I. P. Relativistic Self-Consistent Fields. Proc. R. Soc. London, Ser. A 1961, 262, 555–576. 10.1098/rspa.1961.0139. [DOI] [Google Scholar]
- Kim Y.-K. Relativistic Self-Consistent-Field Theory for Closed-Shell Atoms. Phys. Rev. 1967, 154, 17–39. 10.1103/PhysRev.154.17. [DOI] [Google Scholar]
- Desclaux J. P. Relativistic Dirac-Fock expectation values for atoms with Z = 1 to Z = 120. At. Data Nucl. Data Tables 1973, 12, 311–406. 10.1016/0092-640X(73)90020-X. [DOI] [Google Scholar]
- a Pyykkö P. The RTAM electronic bibliography, version 17.0, on relativistic theory of atoms and molecules. J. Comput. Chem. 2013, 34, 2667. 10.1002/jcc.23454. [DOI] [PubMed] [Google Scholar]; b See http://rtam.csc.fi/ Database ‘RTAM’ version 20.0 (January 4, 2017).
- Rose S. J.; Grant I. P.; Pyper N. C. The direct and indirect effects in the relativistic modification of atomic valence orbitals. J. Phys. B: At. Mol. Phys. 1978, 11, 1171–1176. 10.1088/0022-3700/11/7/016. [DOI] [Google Scholar]
- Pyykkö P.; Desclaux J.-P. Relativity and the Periodic System of Elements. Acc. Chem. Res. 1979, 12, 276–281. 10.1021/ar50140a002. [DOI] [Google Scholar]
- Pyykkö P. Relativistic Effects in Structural Chemistry. Chem. Rev. 1988, 88, 563–594. 10.1021/cr00085a006. [DOI] [Google Scholar]
- Pyykkö P. Relativistic Effects in Chemistry: More Common Than You Thought. Annu. Rev. Phys. Chem. 2012, 63, 45–64. 10.1146/annurev-physchem-032511-143755. [DOI] [PubMed] [Google Scholar]
- Reiher M.; Hess B. In Modern Methods and Algorithms of Quantum Chemistry. Proceedings, 2nd ed.; Grotendorst J., Ed.; John von Neumann Institute for Computing: Jülich, 2000; Vol. 3, pp 479–505.
- Ilias M.; Kellö V.; Urban M. Relativistic effects in atomic and molecular properties. Acta Phys. Slovaca 2010, 60, 259–391. 10.2478/v10155-010-0003-1. [DOI] [Google Scholar]
- Douglas M.; Kroll N. M. Quantum electrodynamical corrections to the fine structure of helium. Ann. Phys. 1974, 82, 89–155. 10.1016/0003-4916(74)90333-9. [DOI] [Google Scholar]
- Dyall K. G.; Faegri K. Jr.. Introduction to Relativistic Quantum Chemistry; Oxford University Press: New York, 2007; pp 453–456. [Google Scholar]
- Roothaan C. C. J.; Bagus P. S.. Methods in Computational Physics; Academic Press Inc.: New York, 1963; Vol. 2, pp 47–94. [Google Scholar]
- Matsuoka O.; Watanabe Y. An atomic Dirac-Fock-Roothaan program. Comput. Phys. Commun. 2001, 139, 218–234. 10.1016/S0010-4655(01)00198-9. [DOI] [Google Scholar]
- Koga T.; Tatewaki H.; Shimazaki T. Chemically reliable uncontracted Gaussian-type basis sets for atoms H to Lr. Chem. Phys. Lett. 2000, 328, 473–482. 10.1016/S0009-2614(00)00948-9. [DOI] [Google Scholar]
- Koga T.; Tatewaki H.; Matsuoka O. Relativistic Gaussian basis sets for molecular calculations: H–Xe. J. Chem. Phys. 2001, 115, 3561–3565. 10.1063/1.1373426. [DOI] [Google Scholar]
- Koga T.; Tatewaki H.; Matsuoka O. Relativistic Gaussian basis sets for molecular calculations: Cs–Hg. J. Chem. Phys. 2002, 117, 7813–7814. 10.1063/1.1508772. [DOI] [Google Scholar]
- Koga T.; Tatewaki H.; Matsuoka O. Relativistic Gaussian basis sets for molecular calculations: Tl–Lr. J. Chem. Phys. 2003, 119, 1279–1280. 10.1063/1.1570814. [DOI] [Google Scholar]
- Lee Y. S.; McLean A. D. Relativistic effects on Re and De in AgH and AuH from all-electron Dirac-Hartree-Fock calculations. J. Chem. Phys. 1982, 76, 735–736. 10.1063/1.442680. [DOI] [Google Scholar]
- Stanton R. E.; Havrilliak S. Kinetic balance: A partial solution to the problem of variational safety in Dirac calculations. J. Chem. Phys. 1984, 81, 1910–1918. 10.1063/1.447865. [DOI] [Google Scholar]
- Gordon W. Die Energieniveaus des Wasserstoffatoms nach der Diracschen Quantentheorie des Elektrons. Z. Phys. 1928, 48, 11–14. 10.1007/BF01351570. [DOI] [Google Scholar]
- Darwin C. G. The Wave Equations of the Electron. Proc. R. Soc. London, Ser. A 1928, 118, 654–680. 10.1098/rspa.1928.0076. [DOI] [Google Scholar]
- Pauling L.; Wilson E. B.. Introduction to Quantum Mechanics; Dover Publ. Inc.: Mineola, NY, 1985; pp 113–150. [Google Scholar]
- Hatano Y.; Yamamoto S.; Tatewaki H. Visualization of the Exact Solution of Dirac Equation. J. Comput. Chem. Jpn. 2016, 15, 105–117. (mainly in Japanese) 10.2477/jccj.2016-0014. [DOI] [Google Scholar]
- WebElements: the periodic table on the WWW. http://www.webelements.com/ (July 24, 2017).
- Sato T. K.; Asai M.; Borschevsky A.; Stora T.; Sato N.; Kaneya Y.; Tsukada K.; Düllmann Ch. E.; Eberhardt K.; Eliav E.; Ichikawa S.; Kaldor U.; Kratz J. V.; Miyashita S.; Nagame Y.; Ooe K.; Osa A.; Renisch D.; Runke J.; Schädel M.; Thörle-Pospiech P.; Toyoshima A.; Trautmann N. Measurement of the first ionization potential of lawrencium, element 103. Nature 2015, 520, 209–212. 10.1038/nature14342. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.