Nature and Hierarchy of Hydrogen-Bonding Interactions in Binary Complexes of Azoles with Water and Hydrogen Peroxide

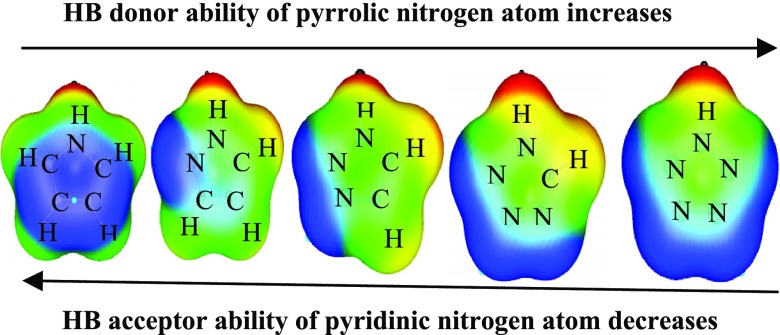
Abstract

In the present study, the hydrogen-bonded complexes of azole with water and hydrogen peroxide are systematically investigated by second-order Møller–Plesset perturbation theory and density functional theory with dispersion function calculations. This study suggests that the ability of pyrrolic nitrogen (NH) atom to function as hydrogen-bond donor increases with the introduction of nitrogen atoms in the ring, whereas the ability of pyridinic nitrogen (N) atom to act as hydrogen-bond acceptor reduces with successive aza substitution in the ring. With introduction of nitrogen atoms in the ring, the vibrational frequency, stabilization energy, and electron density in the σ antibonding orbitals of the X–H (X = N, C of azole) bond of the complexes all increase or decrease systematically. Decomposition analysis of total stabilization energy showed that the electrostatic energy term is a dominant attractive contribution in comparison to induction and dispersion terms in all of the complexes under study.

1. Introduction

Noncovalent interactions such as hydrogen bonding dictate the important role in regulating the structure and function of all biological molecules.^1,2 These hydrogen-bonding interactions are essential in many biologically relevant processes, such as biological information transfer mechanism by nucleic acids, recognition between DNA base pairs, ligand-binding to receptor sites, enzyme catalysis, and α-helix or β-sheet formation.³⁻⁸ Strong conventional hydrogen bonds (HBs) of the type N–H···O play a dominant role in controlling the conformational preferences of small molecules as well as complex heterostructures due to their strength and directionality. On the other hand, weak unconventional C–H···O interactions become considerable when their collective effect is taken into account.

Among various biological active compounds, azoles are an important class of nitrogen-containing five-membered heterocyclic compounds that are gaining much more attention in the field of medicinal chemistry. These molecules possess conventional N–H and unconventional C–H hydrogen bond (HB) donor. Pyrrole (PYR) unit appears in a large number of pharmaceutical agents and natural products.⁹ Furthermore, they fabricate the structure of porphyrin rings, which serve as a key moiety in chlorophyll, heme, vitamin B12, or bile pigments. Imidazole nucleus constructs the main structure of some renowned components of human organisms, that is, amino acid histidine, a component of DNA base structure, and purines, histamine, and biotin. Imidazole plays an important role in the purification of histidine-tagged proteins.¹⁰ Pyrazoles exhibit a wide spectrum of biological activities and can surely serve the purpose to be used as efficient chemotherapeutics.¹¹⁻¹⁷ Triazole (TAZ) and its derivatives possess a variety of biological properties, including antimicrobial,¹⁸ antifungal,¹⁹⁻²¹ antileishmanial,²² antiviral,²³ antitubercular,²⁴ anticancer,^25,26 antioxidant,²⁷ anticholinesterase,²⁸ anti-inflammatory,^29,30 antidepressant, antianxiety, and anticonvulsant activities.³¹

Theoretical studies revealed information about the structure of hydrogen-bonded complexes and strength of binding interactions. Due to the significant role of water in biosystem and biological effects of hydrogen peroxide (HP), hydrogen-bonded complexes of azoles with water and HP have been extensively studied with computational techniques in the present manuscript. These complexes convey information about the hydrogen-bonding interaction in biological systems, in which azoles act as biologically active scaffold. The capability of azoles to form hydrogen bond is due to the existence of hydration sites: a pyrrolic nitrogen (NH) that performs the role of hydrogen-bond donor and a pyridinic nitrogen (N) that acts as acceptor group. When azoles are exposed to water in a large number of biological systems, these hydration sites give high solubility to these compounds.³² The attractiveness of azoles originates from their application in both supramolecular and coordination chemistry. The nitrogen-rich azole offers several N-coordination modes that allow complexation with water and hydrogen peroxide (HP) through hydrogen bonding. Recent findings suggest that the biological effects of hydrogen peroxide (HP) are actually mediated by hydrogen-bonded complexes of HP and molecules of biological interest. In the last decade, several studies³³⁻³⁷ had been conducted to describe the energetic and structural properties of hydrogen-bonded complexes of azoles.

This manuscript has focused attention on the influence of sequential addition of nitrogen atoms on the hydrogen-bonding ability of azoles with water and HP. Gas-phase quantum studies reflect that coordination of water/HP molecules around azoles through N–H···O and/or N···H–O hydrogen bonds, urging significant changes in the geometrical and electronic structures of the azole. It is also intriguing to investigate how both of the intermolecular interactions affect each other through the aromatic ring.

2. Results and Discussion

2.1. Stability and Structural Parameters of Azole–Water/HP Complexes

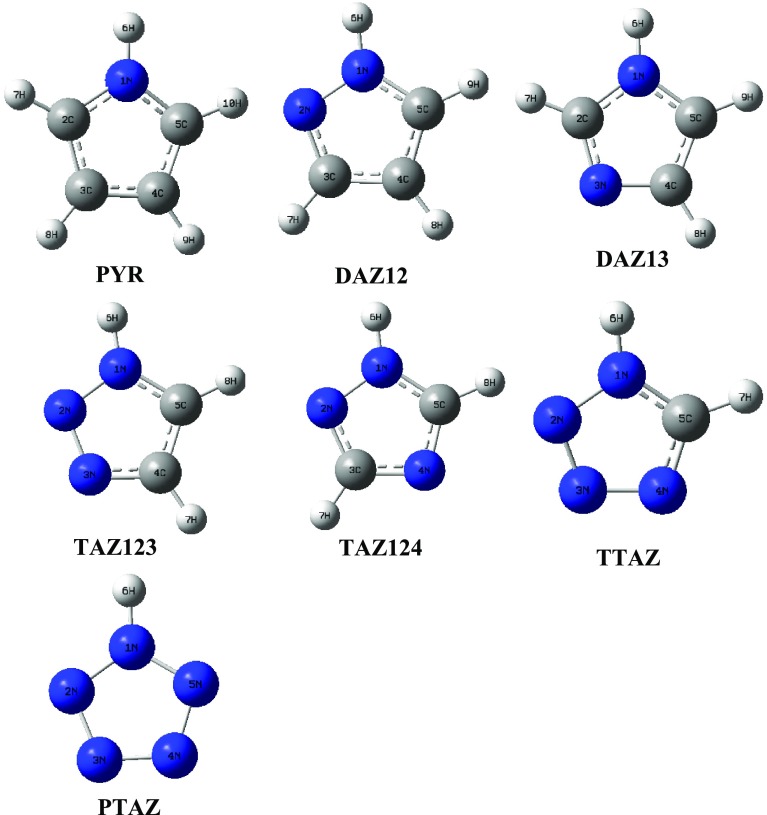
Pyrrole (PYR), diazole (DAZ), triazole (TAZ), tetrazole (TTAZ), and pentazole (PTAZ) have been optimized at wB97XD/aug-cc-pVDZ (L1), MP2/aug-cc-pVDZ (L2), and MP2/aug-cc-pVTZ (L3) theoretical levels (Table 1). As can be seen from Figure 1, DAZ12 and DAZ13 are two isomeric forms of DAZ with 1,2 and 1,3 positioning of two N atoms, the DAZ13 being 10.18 kcal/mol more stable than DAZ12 at L3 level. Similarly, TAZ123 and TAZ124 are isomeric forms of TAZ, with TAZ124 being more stable with respect to TAZ123 and relative energy difference between the two is 15.94 kcal/mol. Thus, it is observed that DAZ13 and TAZ124 are more stable relative to their isomeric forms DAZ12 and TAZ123 that have nitrogen atoms adjacent to each other, which is reasonable. The hydrogen-bonded complexes of different azoles with water and with HP in 1:1 ratio have been optimized at all of the three levels mentioned above and the stabilization energies of all of the studied complexes are presented in Table 2. The stabilization energies of the complexes were estimated as the differences in energy between the complex and the sum of the monomers in their optimized geometries, corrected for basis set superposition error (BSSE) using the counterpoise (CP) method. Jeffrey proposed that for weak HBs, stabilization energies lie in the range of 1–4 kcal/mol; for moderate HBs, these energies are 4–15 and 15–40 kcal/mol is for strong HBs.³⁸ Thus, it is concluded that the HBs in the present study generally fall in “weak” to almost “moderate” categories. The hydrogen-bonded complex is more stable in the case of complex having more negative stabilization energy. In general, all O···H and N···H HB contact distances are shorter than the sum of van der Waals radii of two relevant atoms (2.60 Å for the former and 2.74 Å for the latter). The HB angle X–H···Y usually tends toward linearity (180°), and closer the angle to 180°, stronger is the HB. Azole offers two hydration sites toward water/HP:pyrrolic nitrogen (NH) atom, which can act as HB donor and pyridinic nitrogen (N), which can act as HB acceptor. Depending on HB donor and acceptor sites, the hydrogen-bonded complexes of azoles with water/HP have been placed into five categories (Figure 2).

Table 1. Intermolecular Hydrogen-Bond Distance (r, Å) and Angles (θ, deg) for 1:1 Hydrogen-Bonded Complexes of Azole–Water and Azole–HP at MP2/aug-cc-pVTZ Level.

	azole–water					azole–HP
categories	complexes	hydrogen-bond distances (r, Å)		hydrogen-bond angles (θ, deg)		complexes	hydrogen-bond distances (r, Å)		hydrogen-bond angles (θ, deg)
(N–H···O)	PYR-WI	H6···O11	1.962	N1–H6···O11	179.98	PYR-HPI	H6···O11	2.050	N1–H6···O11	173.31
	DAZ12-WI	H6···O10	1.926	N1–H6···O10	179.51	DAZ12-HPI	H6···O10	1.984	N1–H6···O10	169.70
	DAZ13-WI	H6···O10	1.935	N1–H6···O10	179.64	DAZ13-HPI	H6···O10	2.010	N1–H6···O10	165.49
	TAZ123-WI	H6···O9	1.886	N1–H6···O9	175.88	TAZ123-HPI	H6···O9	1.949	N1–H6···O9	167.28
	TAZ124-WI	H6···O9	1.881	N1–H6···O9	173.23	TAZ124-HPI	H6···O11	1.963	N1–H6···O11	164.30
	TTAZ-WI	H6···O8	1.831	N1–H6···O8	175.94	TTAZ-HPI	H6···O8	1.911	N1–H6···O8	165.11
	PTAZ-WI	H6···O7	1.765	N1–H6···O7	179.29
II (N···H–O)	DAZ13-WII	H10···N3	1.921	O11–H10···N3	160.24
	TAZ123-WII	H10···N3	1.997	O9–H10···N3	145.25
	TAZ124-WII	H9···N4	2.014	O10–H9···N4	154.67
	TTAZ-WII	H8···N3	2.164	O9–H8···N3	177.63	TTAZ-HPII	H8···N3	1.937	O9–H8···N3	161.29
	PTAZ-WII	H7···N3	2.082	O8–H7···N3	174.38	PTAZ-HPII	H7···N3	1.989	O8–H7···N3	163.70
	PTAZ-WII′	H7···N5	2.132	O8–H7···N5	178.26
III (N–H···O and N···H–O)	DAZ12-WIII	H11···N2	2.011	O10–H11···N2	136.12	DAZ12-HPIII	H10···N2	1.850	O11–H10···N2	158.98
		H6···O10	2.149	N1–H6···O10	120.91		H6···O12	2.042	N1–H6···O12	133.97
	TAZ123-WIII	H9···N2	2.138	O10–H9···N2	127.35	TAZ123-HPIII	H9···N2	1.887	O10–H9···N2	154.90
		H6···O10	2.021	N1–H6···O10	125.99		H6···O11	2.013	N1–H6···O11	134.38
	TAZ124-WIII	H10···N2	2.146	O9–H10···N2	128.90	TAZ124-HPIII	H11···N2	1.892	O10–H11···N2	157.00
		H6···O9	2.036	N1–H6···O9	125.61		H6···O9	2.012	N1–H6···O9	134.65
	TTAZ-WIII	H10···N2	2.381	O8–H10···N2	116.06	TTAZ-HPIII	H11···N2	1.958	O10–H11···N2	151.52
		H6···O8	1.933	N1–H6···O8	132.15		H6···O8	1.957	N1–H6···O8	136.00
						PTAZ-HPIII	H10···N5	2.050	O9–H10···N5	148.23
							H6···O7	1.917	N1–H6···O7	136.42
IV (N–H···O and C–H···O)						DAZ13-HPIV	H10···N3	1.825	O11–H10···N3	165.56
							H7···O12	2.575	C2–H7···O12	113.67
						TAZ123-HPIV	H9···N3	1.864	O10–H9···N3	162.12
							H7···O1I	1.074	C4–H7···O11	114.86
						TAZ124-HPIV	H9···N4	1.864	O10–H9···N4	162.87
							H8···O11	2.528	C5–H8···O11	113.85
	TTAZ-WIV	H8···N4	2.092	O9–H8···N4	133.75	TTAZ-HPIV	H8···N4	1.905	O9–H8···N4	157.01
		H7···O9	2.432	C5–H7···O9	106.86		H7···O10	2.464	C5–H7···O10	113.68
V (C–H···O)	PYR-WV	H9···O11	2.423	C4–H9···O11	169.62
	DAZ13-WV	H8···O10	2.356	C4–H8···O10	169.89
	TAZ123-WV	H7···O9	2.171	C4–H7···O9	169.32

Figure 1.

Optimized geometries of azoles along with their isomeric forms at MP2/aug-cc-pVTZ level.

Table 2. Stabilization Energies (ΔE_BSSE in kcal/mol) of Azole–Water and Azole–HP Complexes at wB97XD/aug-cc-pVDZ (L1), MP2/aug-cc-pVDZ (L2), and MP2/aug-cc-pVTZ (L3) Levels.

azole–water					azole–HP
		ΔEBSSE (−ve)				ΔEBSSE (−ve)
categories	complexes	L1	L2	L3	complexes	L1	L2	L3
I	PYR-WI	5.31	5.04	5.36	PYR-HPI	4.86	4.61	4.80
	DAZ12-WI	5.34	5.44	5.65	DAZ12-HP1	5.36	5.18	5.38
	DAZ13-WI	6.16	5.83	5.98	DAZ13-HPI	5.29	5.37	5.58
	TAZ123-WI	7.48	6.68	7.46	TAZ123-HPI	6.17	6.39	6.41
	TAZ124-WI	7.21	6.74	7.13	TAZ124-HPI	6.04	6.20	6.17
	TTAZ-WI	8.62	8.20	8.63	TTAZ-HPI	7.60	7.37	7.61
	PTAZ-WI	9.88	9.42	9.93
II	DAZ13-WII	7.86	7.05	7.78
	TAZ123-WII	6.69	6.14	6.65
	TAZ124-WII	7.00	6.17	6.69
	TTAZ-WII	5.18	4.73	4.89	TTAZ-HPII	6.50	6.17	6.56
	PTAZ-WII	3.96	3.50	3.83	PTAZ-HPII	5.12	4.66	4.86
	PTAZ-WII′	2.83	3.03	3.34
III	DAZ12-WIII	8.50	8.16	8.81	DAZ12-HPIII	11.83	11.16	12.06
	TAZ123-WIII	8.43	8.38	8.99	TAZ123-HPIII	11.24	10.86	11.71
	TAZ124-WIII	8.22	7.92	8.54	TAZ124-HPIII	11.13	10.69	11.09
	TTAZ-WIII	8.49	8.42	8.97	TTAZ-HPIII	10.40	9.99	10.79
					PTAZ-HPIII	9.33	9.06	9.80
IV					DAZ13-HPIV	10.77	10.42	10.54
					TAZ123-HPIV	9.26	8.66	9.35
					TAZ124-HPIV	9.37	8.74	9.45
	TTAZ-WIV	5.22	6.08	6.58	TTAZ-HPIV	9.08	8.23	8.89
V	PYR-WV′	0.78	0.58	0.69
	DAZ13-WV	1.73	1.48	1.64
	TAZ123-WV	1.78	1.69	1.95

Figure 2.

Optimized geometries of 1:1 hydrogen-bonded complexes of azole–water and azole–HP at MP2/aug-cc-pVTZ level (categories I–V).

In category I, water and HP are positioned with its lone pair on oxygen pointing directly toward pyrrolic nitrogen (NH) of azole in azole–water and azole–HP complexes respectively. These complexes involve monodentate HB formation with N–H···O interaction. The azole–water complexes exhibit shorter O···H bonds and more linear N–H···O bond angles compared to their counterpart azole–HP complexes, which indicate the formation of stronger HB in azole–water complexes. The stabilization energies of azole–water complexes are 0.27–1.05 kcal/mol higher than those of azole–HP complexes owing to the fact that the proton acceptor ability of water is marginally higher in comparison to HP. Experimentally, it was determined that the gas-phase proton affinity of water (697 kJ/mol) is higher than that of HP (678 kJ/mol), which clearly shows that water is better proton acceptor than HP.³⁹ The stabilization energies of these complexes depend on the number and type of additional ring nitrogen atoms. The order of stabilization energies in these complexes is PYR < DAZ12 < DAZ13 < TAZ124 < TAZ123 < TTAZ < PTAZ; thus, ΔE_BSSE systematically enhances with continuous inclusion of nitrogen atoms in the ring. This supports the fact that successive aza substitution expedites the tendency of pyrrolic ring nitrogen (NH) atom to serve as better HB donor. Table 1 reflects that the consecutive addition of nitrogen atoms in the ring allows the azoles to form progressively stronger interactions with water/HP molecule. The intermolecular N–H···O HB distances get shorter with addition of nitrogen atoms and consistently the stabilization energies get higher. There exists a strong correlation between stabilization energy and r (N–H···O) HB distance, as shown in Figure 3.

Figure 3.

Correlation between hydrogen bond length r (N–H···O) and stabilization energy (ΔE_BSSE) at MP2/aug-cc-pVTZ level. Series 1 implies the complexes of azole with water. Series 2 implies the complexes of azole with HP.

In category II, pyridinic nitrogen (N) of azole is placed with its lone pair facing directly toward hydrogen atom of water in azole–water and hydrogen of HP in azole–HP complexes. These complexes involve single HB formation with N···H–O interaction. The attempts to optimize complexes of HP with azoles corresponding to category II complexes of azole–water resulted in complexes of category IV, where in addition to N···H–O HB, the C–H···O_HP HB also forms simultaneously. Hence, only TTAZ-HPII and PTAZ-HPII could only be optimized. The N···H–O HB distances in azole–HP complexes are comparatively shorter in comparison to the corresponding azole–water complexes, resulting in higher stabilization energies of HPII complexes of TTAZ and PTAZ relative to their counterpart WII complexes. This is due to the fact that HP is far better proton donor in comparison to water, illustrated from the difference in acid dissociation constant (pK_a) values of HP (11.6) and water (15.7), which clearly indicates higher acidity of HP in comparison to water. The results of stabilization energy reflect that azole–water complexes are ordered in terms of stability as DAZ13 > TAZ124 > TAZ123 > TTAZ > PTAZ; thus, sequential addition of nitrogen atoms in the ring leads to significant decrease in ΔE_BSSE values. This supports the fact that the tendency of ring nitrogen atom to function as HB acceptor reduces with the introduction of nitrogen atoms in the ring. As displayed by structural parameters, the N···H–O HB length increases with increase in the number of nitrogen atoms in the ring, which indicates the fact that as the aza substitution increases, the aforementioned HB becomes more longer and thus gets more weaker. The stabilization energy linearly decreases with increase in r (N···H–O) distance shown in Figure 4. The WII complexes (N···H–O bonded) are 0.44–6.10 kcal/mol less stable in comparison to their corresponding WI complexes (N–H···O bonded) except DAZ13, which reflect that proton donor ability of pyrrolic nitrogen (NH) of azole toward water is higher than that of proton acceptor ability of pyridinic nitrogen. The complex PTAZ-WII is 0.49 kcal/mol more stabilized than PTAZ-WII′, signifying that less stability is gained when pyrrole-type nitrogen (NH) is placed in an adjacent position to pyridinic-type nitrogen (N) as in the case of PTAZ-WII′.

Figure 4.

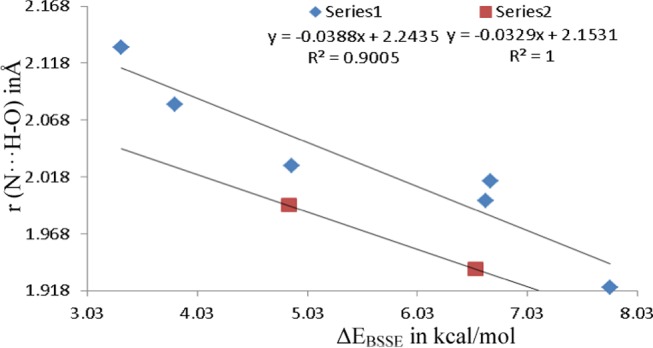
Correlation between hydrogen-bond length r (N···H–O) and stabilization energy (ΔE_BSSE) at MP2/aug-cc-pVTZ level. Series 1 implies the complexes of azole with water. Series 2 implies the complexes of azole with HP.

In category III, water/HP molecules are oriented to interact simultaneously with two hydration sites, leading to the formation of five- and six-membered hydrogen-bonding ring in azole–water and azole–HP complexes, respectively. In these complexes, water/HP acts as bridge between pyrrolic (NH) and pyridinic (N) hydration sites that result in the formation of two HBs N···H–O and N–H···O. The participation of these two interactions in the complexes leads to significant deviation from linearity of both HBs. The stabilization energy of azole–HP complexes is 1.82–3.25 kcal/mol higher than that of the corresponding azole–water complexes. The N···H–O interaction is the major contributing interaction toward ΔE_BSSE of azole–HP complexes. It is observed that r (N···H–O) values are 0.161–0.423 Å shorter in azole–HP complexes in relation to azole–water complexes consistent with the fact that HP is a far better HB donor than water. The complexes of category III are more stable in comparison to their corresponding complexes of categories I and II since the interaction with two hydration sites (pyrrolic and pyridinic) forms stronger hydrogen-bond network and gain more stability in terms of stabilization energy in complexes of category III.

In category IV complexes, azoles form strong binary hydrogen-bonded complexes, in which water/HP acts not only as HB donor toward pyridinic nitrogen (N) but also as HB acceptor toward C–H bond of heterocyclic ring, resulting in the formation of pseudo-five- and six-membered hydrogen-bonding ring in azole–water and azole–HP complexes, respectively. The deviation from linearity of C–H···O and N···H–O HB angles is due to strain introduced by the hydrogen-bonded ring structure, as shown in Figure 2. The stabilization energies of these complexes are ordered in terms of stability as DAZ > TAZ > TTAZ, which further authenticates the fact that increase of aza substitution in the ring decreases the hydrogen-bond acceptor ability of ring nitrogen atom. In these complexes, the N···H–O is the major contributing interaction in ΔE_BSSE in comparison to C–H···O as proposed by geometrical parameters. The C–H···O interaction only cooperatively strengthens the hydrogen-bonded system as a source of secondary stabilization. The complexes of category IV are less stabilized than category III complexes, as there is one unconventional C–H···O HB present in the former complexes.

In category V, water acts as HB acceptor toward C–H bond of azoles. These complexes involve single C–H···O HB interaction. The order of stabilization energies in these complexes is TAZ > DAZ > PYR, consistent with the fact that the hydrogen-bond donor capability of C–H bond toward oxygen of water increases with increase in the aza substitution. In these complexes, as the number of nitrogen atoms in the ring increases, the C–H···O HB length decreases, which shows that the above-mentioned HB becomes shorter and thus stronger with increase in the aza substitution. The C–H···O HB angles in these complexes lie in the range 169.32–169.89°. The HB angles in complexes of categories I, II, and V that are stabilized by single HB are more linear, while the presence of secondary HB in the complexes of categories III and IV complexes leads to cause sizable deviation from linearity. The W–V complexes are 4.34–5.51 kcal/mol are less stabilized than those of their corresponding W–I complexes as it is obvious that strong conventional N–H HB present in the latter complexes is better proton donor in comparison to the unconventional C–H bond in the former.

2.2. Vibrational Properties of Hydrogen-Bond Donor Group

In the case of HBs N···H–O and N–H···O, the X–H (proton donor fragment) frequency decreases upon HB formation and is called red shift, whereas in the case of C–H···O HB, the frequency increases and this phenomenon is called blue shift. Red shifting in the vibrational frequencies is expressed as negative values of Δυ, whereas blue shifting is expressed as positive Δυ values. The shift in stretching frequency is related to the elongation and contraction of the X–H bond length in the cases of red and blue shifts, respectively. A negative value of Δd refers to a bond contraction upon HB formation, and a positive value refers to a bond elongation. The blue and red shifting associated with hydrogen bonds have been offered several explanations in the literature. Alabugin et al. proposed that the competition between the n_Y → σ*_X–H hyperconjugation (elongates the X–H bond) and polarization of X–H bond due to rehybridization (shortens the X–H bond) is the origin of both red- and blue-shifted HBs.⁴⁰ Hyperconjugation and rehybridization have opposite effects on X–H bond, and their balance will determine red shift or blue shift of the formed HB. Table 3 displays the change in HB donor distance (Δd in Å) and shifts of stretching frequencies (Δυ in cm^–1) of the HB donor group upon complex formation relative to monomers at L2 level. As anticipated for conventional HBs, the HB donor O–H bond of water/HP and N–H bond of azole consistently undergo red shifting upon hydrogen bonding. In contrast, HB donor C–H bond of azole undergoes shortening and its stretching frequency shifts to the blue region. In fact, larger red shifts have been noted in O–H stretching frequencies of HP (−89.62 to −407.61 cm^–1) in azole–HP complexes relative to that of water (−63.92 to −231.22 cm^–1) in azole–water complexes, which can be explained on the basis of the fact that HP is a remarkable proton donor in comparison to water. In the present study, the higher acidity of O–H bond of HP relative to that of water is also demonstrated by larger elongation of O–H bond in azole–HP in comparison to azole–water complexes. The values of Δd and Δυ for O–H bond decline systematically upon progressive aza substitution. Excellent correlation is found to exist between Δd and Δυ for O–H bond of azole–water and azole–HP complexes shown in Figure 5. Larger red shifts have appeared in N–H stretching frequencies of azole in azole–water (−81.96 to −321.65 cm^–1) complexes relative to that of azole–HP (−55.93 to −160.67 cm^–1) because water is a better proton acceptor in comparison to HP. The higher acidity of N–H bond of azole toward water relative to HP is also demonstrated by larger elongation of N–H bond in azole–water in comparison to azole–HP complexes. The values of Δd and Δυ for N–H bond increase systematically with enhancement of aza substitution in the ring.

Table 3. Change in Bond Length (Δd, Å) and Shifts of Stretching Frequencies Δυ (in cm^–1) of the HB Donor Group upon Complex Formation for 1:1 Hydrogen-Bonded Complexes of Azole–Water and Azole–HP Evaluated at MP2/aug-cc-pVDZ (L2) Level.

	azole–water				azole–HP
categories	complexes	HB donor	Δυ	Δd	complexes	HB donor	Δυ	Δd
(N–-H···O)	PYR-WI	N1–H6	–97.41	0.006	PYR-HPI	N1–H6	–55.93	0.004
	DAZ12-WI	N1–H6	–128.49	0.008	DAZ12-HPI	N1–H6	–85.04	0.005
	DAZ13-WI	N1–H6	–124.99	0.007	DAZ13-HPI	N1–H6	–72.44	0.004
	TAZ123-WI	N1–H6	–195.88	0.011	TAZ123-HPI	N1–H6	–115.79	0.006
	TAZ124-WI	N1–H6	–198.74	0.011	TAZ124-HPI	N1–H6	–105.34	0.006
	TTAZ-WI	N1–H6	–252.81	0.014	TTAZ-HPI	N1–H6	–149.49	0.011
	PTAZ-WI	N1–H6	–321.65	0.018
II (N···H–O)	DAZ13-WII	O11–H10	–231.22	0.013
	TAZ123-WII	O9–H10	–161.78	0.010
	TAZ124-WII	O10–H9	–154.18	0.010
	TTAZ-WII	O9–H8	–106.76	0.007	TTAZ-HPII	O9–H8	–206.34	0.010
	PTAZ-WII	O8–H7	–63.92	0.005	PTAZ-HPII	O11–H12	–89.62	0.005
	PTAZ-WII′	O8–H7	–133.21	0.010
III (N–H···O and N···H–O)	DAZ12-WIII	O10–H11	–161.21	0.011	DAZ12-HPIII	O11–H10	–375.48	0.019
		N1–H6	–81.96	0.006		N1–H6	–96.45	0.007
	TAZ123-WIII	O10–H9	–144.91	0.008	TAZ123-HPIII	O10–H9	–307.80	0.016
		N1–H6	–95.49	0.007		N1–H6	–112.63	0.008
	TAZ124-WIII	O9–H10	–143.26	0.011	TAZ124-HPIII	O10–H11	–300.81	0.015
		N1–H6	–93.35	0.006		N1–H6	–107.59	0.007
	TTAZ-WIII	O8–H10	–137.96	0.008	TTAZ-HPIII	O10–H11	–251.93	0.018
		N1–H6	–125.50	0.005		N1–H6	–144.84	0.009
					PTAZ-HPIII	O9–H10	–150.31	0.008
						N1–H6	–160.67	0.010
IV (N–H···O and C–H···O)					DAZ13-HPIV	O11–H10	–407.61	0.020
						C5–H8	5.42	–0.000
					TAZ123-HPIV	O10–H9	–320.74	0.016
						C5–H8	5.35	0.000
					TAZ124-HPIV	O10–H9	–320.61	0.016
						C5–H8	5.42	0.000
	TTAZ-WIV	O9–H8	–103.96	0.007	TTAZ-HPIV	O9–H8	–251.72	0.012
		C5–H7	–3.13	0.000		C5–H7	3.68	0.000
V (C–H···O)	PYR-WV	C4–H9	1.50	0.000
	DAZ13-WV	C4–H8	7.86	0.000
	TAZ123-WV	C4–H7	9.35	0.000

Figure 5.

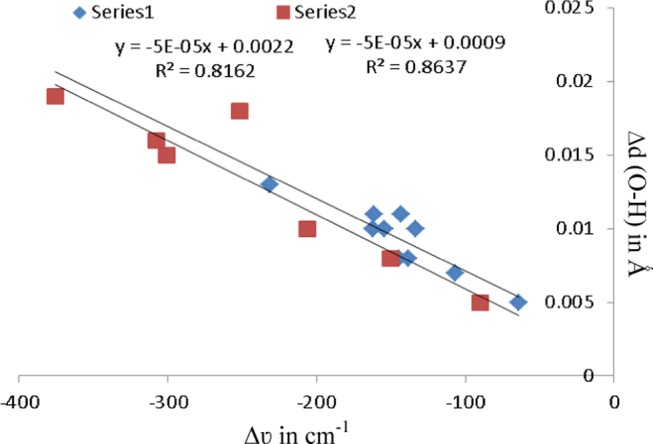
Correlation between O–H stretching frequency (Δυ in cm^–1) and change in O–H bond length (Δd in Å). Series 1 implies the azole–water complexes. Series 2 implies the azole–HP complexes.

A strong correlation is found to exist between Δd and Δυ for N–H bond of azole–water and azole–HP complexes shown in Figure 6. In the complexes of category III, larger red shifts have been observed in the O–H stretching frequency of water/HP and smaller red shifts appear in the stretching frequency of N–H bond of azole except PTAZ-HPIII, which reflect that O–H bond of water/HP acts as a better proton donor in comparison to N–H bond of azole.

Figure 6.

Correlation between N–H stretching frequency (Δυ in cm^–1) and change in N–H bond length (Δd in Å). Series 1 implies the azole–water complexes. Series 2 implies the azole–HP complexes.

2.3. Natural Bond Orbital (NBO) Analysis

2.3.1. Atomic Charges

The values of atomic charges of atoms forming HB evaluated at L3 level utilizing NBO analysis are presented in Table 4. In the complexes of categories II, III, and IV, the contiguous nitrogen atoms of DAZ12, TAZ123, and TTAZ influence the atomic charge on pyridinic nitrogen atom directly involved in hydrogen bonding and atomic charge reduces with sequential addition of nitrogen atoms in the ring. In contrast, DAZ13 and TAZ124 complexes of the above-mentioned category in which nitrogen involved in hydrogen bonding is adjacent to carbon atom favor a strong electrostatic component in comparison to complexes of DAZ12, TAZ123, and TTAZ. In the complexes of both I and III categories, the atomic charge on oxygen of water lies in the range −0.940 to −0.972 au, while this value on oxygen atom of HP is nearly half, i.e., −0.470 to −0.519 au. This suggests that the electrostatic component is more favored in interactions, where water is involved as HB acceptor relative to that of HP. The sequential addition of nitrogen atom in the ring boosts the atomic charge on hydrogen atom attached to pyrrolic nitrogen (NH) in category I and III complexes but reduces the atomic charge on hydrogen atom attached to water/HP in category II and III complexes. The atomic charge on hydrogen is quite low in W–V complexes involving only one unconventional C–H···O_w HB interaction, but high electron density present at oxygen atom of water reflects that electrostatic interaction still plays significant role.

Table 4. Atomic Charges, the Amount of Charge Transfer (CT in e), and Second-Order Delocalization Energies (E⁽²⁾ in kcal/mol) Associated with Orbital Interactions Obtained from NBO Analysis for 1:1 Hydrogen-Bonded Complexes of Aazole–Water and Azole–HP at MP2/aug-cc-pVTZ Level.

	azole–water					azole–HP
complexes	atomic charges		CT	orbital interactions	E(2)	complexes	atomic charges		CT	orbital interactions	E(2)
PYR-WI	qO11(qH6)	–0.943(0.441)	–0.012	nO11 → σ*N1–H6	7.79	PYR-HPI	qO11(qH6)	–0.474(0.426)	–0.016	nO11 → σ*N1–H6	5.65
DAZ12-WI	qO11(qH6)	–0.945(0.446)	–0.016	nO11 → σ*N1–H6	12.72	DAZ12-HPI	qO10(qH6)	–0.470(0.427)	–0.018	nO10 → σ*N1–H6	7.70
DAZ13-WI	qO10(qH6)	–0.944(0.449)	–0.014	nO10 → σ*N1–H6	11.72	DAZ13-HPI	qO10(qH6)	–0.476(0.434)	–0.017	nO10 → σ*N1–H6	6.67
TAZ123-WI	qO9(qH6)	–0.946(0.454)	–0.020	nO9 → σ*N1–H6	13.62	TAZ123-HPI	qO9(qH6)	–0.474(0.438)	–0.026	nO9 → σ*N1–H6	9.56
TAZ124-WI	qO9(qH6)	–0.940(0.451)	–0.020	nO9 → σ*N1–H6	13.88	TAZ124-HPI	qO11(qH6)	–0.475(0.435)	–0.028	nO11 → σ*N1–H6	8.22
TTAZ-WI	qO8(qH6)	–0.943(0.463)	–0.024	nO8 → σ*N1–H6	17.18	TTAZ-HPI	qO8(qH6)	–0.476(0.448)	–0.033	nO8 → σ*N1–H6	11.47
PTAZ-WI	qO7(qH6)	–0.946(0.468)	–0.030	nO7 → σ*N1–H6	21.97
DAZ13-WII	qN3(qH10)	–0.590(0.506)	0.015	nN3 → σ*O11–H10	10.27
TAZ123-WII	qN3(qH10)	0.312(0.498)	0.010	nN3 → σ*O9–H10	6.91
TAZ124-WII	qN4(qH9)	–0.623(0.500)	0.010	nN4 → σ*O10–H9	6.13
TTAZ-WII	qN3(qH8)	–0.097(0.494)	0.009	nN3 → σ*O9–H8	5.51	TTAZ-HPII	qN3(qH8)	–0.106(0.491)	0.018	nN3 → σ*O9–H8	12.60
PTAZ-WII	qN3(qH7)	–0.128(0.488)	0.006	nN3 → σ*O8–H7	3.97	PTAZ-HPII	qN3(qH7)	–0.139(0.488)	0.008	nN3 → σ*O8–H7	7.33
PTAZ-WII′	qN5(qH7)	–0.071(0.484)	0.005	nN5 → σ*O8–H7	3.41
DAZ12-WIII	qN2(qH11)	–0.360(0.503)	0.004	nN2 → σ*O10–H11	4.74	DAZ12-HPIII	qN2(qH10)	–0.377(0.508)	0.016	nN2 → σ*O11–H10	18.57
	qO10(qH6)	–0.972(0.438)		nO10 → σ*N1–H6	2.40		qO12(qH6)	–0.517(0.440)		nO12 → σ*N1–H6	4.96
TAZ123-WIII	qN2(qH9)	–0.108(0.498)	0.003	nN2 → σ*O10–H9	2.12	TAZ123-HPIII	qN2(qH9)	–0.372(0.502)	0.008	nN2 → σ*O10–H9	14.12
	qO10(qH6)	–0.968(0.453)		nO10 → σ*N1–H6	3.58		qO11(qH6)	–0.519(0.452)		nO11 → σ*N1–H6	6.01
TAZ124-WIII	qN2(qH10)	–0.399(0.500)	0.002	nN2 → σ*O9–H10	2.33	TAZ124-HPIII	qN2(qH11)	–0.399(0.506)	0.007	nN2 → σ*O10–H11	11.70
	qO9(qH6)	–0.970(0.477)		nO9 → σ*N1–H6	3.24		qO9(qH6)	–0.518(0.447)		nO9 → σ*N1–H6	4.73
TTAZ-WIII	qN2(qH10)	–0.101(0.493)	0.001	nN2 → σ*O8–H10	0.33	TTAZ-HPIII	qN2(qH11)	–0.134(0.497)	0.002	nN2 → σ*O10–H11	9.33
	qO8(qH6)	–0.963(0.464)		nO8 → σ*N1–H6	6.15		qO8(qH6)	–0.518(0.461)		nO9 → σ*N1–H6	7.43
						PTAZ-HPIII	qN5(qH10)	–0.100(0.489)	–0.010	nN5 → σ*O9–H10	5.43
							qO7(qH6)	–0.515(0.465)		nO7 → σ*N1–H6	9.15
						DAZ13-HPIV	qN3(qH10)	–0.598(0.508)	0.027	nN3 → σ*O11–H10	19.23
							qO12(qH7)	–0.502(0.204)		nO12 → σ*C2–H7	0.24
						TAZ123-HPIV	qN3(qH9)	–0.324(0.500)	0.023	nN3 → σ*O10–H9	17.53
							qO12(qH7)	–0.496(0.228)		nO12 → σ*C2–H7	0.25
						TAZ124-HPIV	qN4(qH9)	–0.635(0.502)	0.023	nN4 → σ*O10–H9	17.69
							qO11(qH8)	–0.502(0.219)		nO11 → σ*C5–H8	0.33
TTAZ-WIV	qN4(qH8)	–0.394(0.496)	0.005	nN4 → σ*O9–H8	3.53	TTAZ-HPIV	qN4(qH8)	–0.408(0.503)	0.015	nN4 → σ*O9–H8	13.39
	qO9(qH7)	–0.966(0.231)		nO9 → σ*C5–H7	0.16		qO10(qH7)	–0.505(0.233)		nO10 → σ*C5–H7	0.42
PYR-WV	qO11(qH9)	–0.930(0.230)	–0.005	nO11 → σ*C4–H8	2.15
DAZ13-WV	qO10(qH8)	–0.928(0.242)	–0.006	nO10 → σ*C4–H8	2.18
TAZ123-WV	qO9(qH7)	–0.935(0.237)	–0.007	nO9 → σ*C4–H7	4.12

2.3.2. Charge Transfer and Second-Order Delocalization Energy [E⁽²⁾]

NBO analysis depicted that during the formation of HB, certain amount of electron density is transferred from proton acceptor to proton donor and electron density is rearranged. In accordance with Wang et al., the charge transfer and electrostatic interactions are responsible for variation in frequency, which also affects the strength of HB.⁴¹Table 4 illustrates the values of charge transfer (CT) from azole to water/HP for the complexes under study at MP2/aug-cc-pVTZ level. Positive CT values represent that electron density is transferred from azole to water/HP, and the reverse happens in the case of negative CT values. The magnitude of CT values in azole–HP complexes is higher than their respective azole–water complexes. The CT occurs from water/HP to azole in complexes of category I and V complexes, as indicated by their negative CT values. Upon progressive aza substitution in the ring, the azole molecule becomes more acidic and it becomes a better proton donor and electron acceptor; hence, the magnitude of charge transfer increases in the above-mentioned categories, as we move from PYR to PTAZ. The CT occurs from azole to water/HP in category II and III complexes as CT values come out to be positive. The magnitude of CT in the above-mentioned categories reduces with subsequent inclusion of nitrogen atoms in the ring, since with reduction of nitrogen atoms in the ring, pyridinic nitrogen (N) atom of azole becomes more basic and hence it becomes better proton acceptor. The CT values of complexes of categories III and IV involve HBs, with both azole and water/HP acting as HB donor as well as acceptor; therefore, charge transfer occurs from azole to water/HP and vice versa. The CT values of complexes of category III being positive except PTAZ-HPIII indicate that charge transfer from the azole to water/HP is higher than that from water/HP to azole, so the direction of net charge transfer is from azole to water/HP. The relatively lower CT values in complexes of categories III and IV in comparison to their counterpart complexes in categories I and II are understandable since charge transfer arising in two HBs is in the opposite direction in former categories. The magnitude of CT in category IV complexes is higher in comparison to that in category III, since in the former category, one of the interactions involved is unconventional C–H···O, expected to be weak in nature, hence negligible to small charge transfer occurring through this interaction and other interaction is mainly responsible for charge transfer. The variation in charge transfer in category II, III, and IV complexes suggests that it is favored by reduction in the number of nitrogen atoms in the ring, whereas in categories I and V, it is favored by inclusion of nitrogen atoms in the ring.

The information about electron delocalization is reflected by the E⁽²⁾ values, the second-order perturbation energies associated with the orbital interactions important for HB formation. The E⁽²⁾ values for n_O(water) → σ*_N–H orbital interaction are higher in comparison to n_O(HP) → σ*_N–H, as observed in category I complexes due to the fact that water acts as a better proton acceptor compared to HP. The enhancement in E⁽²⁾ values for n_O(water/HP) → σ*_N–H orbital interactions with continuous addition of nitrogen atoms in the ring as seen in complexes of category I and III concludes that additional nitrogen atom in the ring increases the electron density in the σ* antibonding N–H orbitals that leads to weakening and elongation of N–H bond and is also in line with concomitant increase in the red shift of stretching vibration. This statement is also supported by a good linear correlation between E⁽²⁾ values and red shift in the N–H stretching vibration of azole–water and azole–HP complexes shown in Figure 7. The E⁽²⁾ values for n_N → σ*_O–H(HP) orbital interaction are higher relative to n_N → σ*_O–H(water) orbital interactions as seen in category II, III, and IV complexes, which is in accordance with the fact that HP is a far better hydrogen bond donor than water. The decline in E⁽²⁾ values for n_N → σ*_{O–H(water/HP)} orbital interactions with consecutive aza substitution in the ring as seen in the complexes of categories II, III, and IV reflects that additional nitrogen atom in the ring decreases the electron density shift from lone pair of pyridinic nitrogen (N) to the σ* antibonding O–H orbital of water/HP and is also in line with concomitant decrease of red shift in O–H stretching vibration upon progressive aza substitution in the ring. The n_N → σ*_O–H orbital interactions in category WII complexes are 18.07–87.63% lower than n_O → σ*_N–H orbital interaction in the corresponding complexes of category WI, and this percentage stability progressively reduces with sequential introduction of nitrogen atoms in the ring. The higher magnitude of n_O → σ*_N–H orbital interaction compared to that of n_N → σ*_O–H orbital interaction in WIII complexes except DAZ12-WIII reflects that the proton donor ability of pyrrolic nitrogen (NH) of azoles toward water is higher than that of proton acceptor ability of pyridinic nitrogen (N). The n_N → σ*_O–H orbital interaction is stronger than that of n_O → σ*_N–H orbital interaction in category HPIII complexes, except PTAZ-HPIII, which reflects that the proton acceptor ability of pyridinic nitrogen (N) of azoles toward HP is higher than that of the proton donor ability of pyrrolic nitrogen (NH). The E⁽²⁾ values for both n_O → σ*_N–H and n_N → σ*_O–H orbital interactions are reduced to a larger extent in complexes of category III in comparison to their counterpart complexes in categories I and II, which possess sole n_O → σ*_N–H and n_N → σ*_O–H charge-transfer interactions, respectively, indicating the role of alignment of orbitals in orbital interactions.

Figure 7.

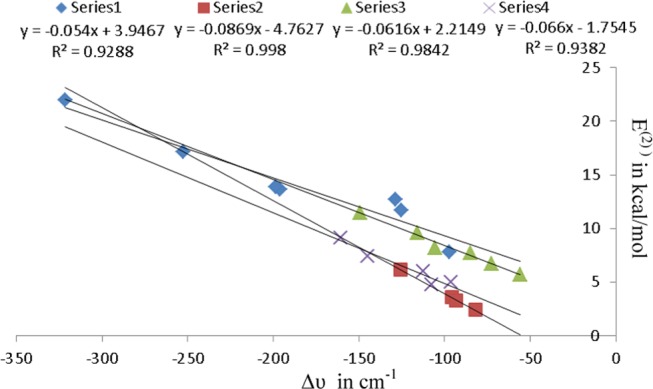
Correlation between N–H stretching frequency (Δυ in cm^–1) and second-order stabilization energy [E⁽²⁾]. Series 1 implies the azole–water complexes for category I. Series 2 implies the azole–water complexes for category III. Series 3 implies the azole–HP complexes for category I. Series 4 implies the azole–HP complexes for category III.

2.4. Topological Parameters

The atoms in molecules (AIM) theory provides an additional tool for detection and characterization of hydrogen-bonding interactions. The analysis of critical points appears to be most crucial for studies on interatomic interactions. Two types of topologically stable critical points are present in the complexes under study, which are assigned as (3, −1) called bond critical points (BCPs) and (3, +1) called ring critical points (RCPs) present in the interior of the ring. AIM analysis has been used to investigate the properties of HBs in the sense of electron density properties estimated in the BCPs, while that of π-electron system, in terms of electron density properties in RCPs. Figure 8 shows the molecular graphs of complexes of azoles with water/HP. The main topological properties at the (3, −1) and (3, +1) critical points, such as electron density (ρ_c), its Laplacian (∇²ρ_c), the total electron energy density (H_c), and its two components potential electron energy density (V_c) and kinetic electron energy density (G_c) are summarized in Table S21. Several reports in the literature reflect that ρ is a good index of HB strength; larger ρ_c at the BCP indicates stronger HB. According to the criteria of HBs proposed by Koch and Popelier,⁴² the electron density ρ_c at the BCPs lies in the range of 0.002–0.040 au and Laplacian ∇²ρ_c of the electron density at the BCPs falls in the range of 0.024–0.139 au. The positive values of ∇²ρ_c imply that interactions are closed-shell such as ionic interactions, van der Waals interactions, or HBs, whereas negative value of ∇²ρ_c indicates that there is a shared interaction such as covalent bonds. The positive ∇²ρ_c and the negative H_c mean that the interaction is partly covalent in nature. The ratio −G_c/V_c has also been used to classify the bonding interaction. If −G_c/V_c > 1, then the interaction is noncovalent; if 0.5 < G_c/V_c < 1, then the interaction is partly covalent in nature.

Figure 8.

Molecular graphs of complexes of azoles with water and HP at MP2/aug-cc-pVTZ level. The small red balls indicate bond critical points, and the small yellow balls indicate ring critical points.

In the present work, the wave functions of hydrogen-bonded molecular geometries obtained from MP2/aug-cc-pVTZ have been employed to characterize the topological properties. As seen in Table S21, all of the HBs in complexes under study satisfy Koch and Popelier’s criteria with ρ_c and ∇²ρ_c of (3, −1) values well in the respective ranges of 0.010–0.036 and 0.047–0.121 au, respectively. The ∇²ρ and H_c values are greater than zero for all of the interactions; therefore all of the complexes display the characteristics of closed-shell interaction. This is also supported by the ratio -G_c/V_c, which is more than 1 for all of the interactions.

In category WI and WIII complexes, ρ_c and ∇²ρ_c of (3, −1) values for the HBs involving N–H···O_w interaction lie in the ranges of 0.016–0.036 and 0.077–0.113 au, respectively. In category HPI and HPIII complexes, ρ_c and ∇²ρ_c of (3, −1) values for the HBs involving N–H···O_HP interaction lie in the ranges of 0.017–0.026 and 0.078–0.107 au, respectively. The higher ρ_c and ∇²ρ_c values for N–H···O_w interaction compared to N–H···O_HP in these complexes can be rationalized on the basis of better HB acceptor ability of water than HP. The uptrend in ρ_c and ∇²ρ_c values for the HBs involving N–H···O interaction with incorporation of nitrogen atoms in the ring in these complexes is consistent with the fact that successive aza substitution in the ring boosts the tendency of ring nitrogen atom to play the role of HB donor.

In category WII, WIII, and WIV complexes, ρ_c and ∇²ρ_c of (3, −1) values for the HBs involving N···H–O_w interaction lie in ranges of 0.010–0.028 and 0.047–0.109 au, respectively. In category HPII, HPIII, and HPIV complexes, ρ_c and ∇²ρ_c of (3, −1) values for the HBs involving N···H–O_HP interaction lie in the ranges of 0.020–0.035 and 0.072–0.121 au, respectively. The ρ_c and ∇²ρ_c values for N···H–O_HP interaction are higher compared to N···H–O_w in these complexes, which can be justified in terms of significantly better proton donor ability of HP compared to that of water. The downtrend in ρ_c and ∇²ρ_c values for HBs involving N···H–O interaction upon progressive aza substitution in the ring ensures the fact that the tendency of ring nitrogen atom to play the role of HB acceptor reduces with increase in the aza substitution.

In all of these complexes, the (3, +1) values of ρ_c and ∇²ρ_c follow the order PTAZ > TTAZ > TAZ > DAZ > PYR, which clearly shows that as the aza substitution increases, the value of ring critical point (RCP) increases.

2.5. Molecular Electrostatic Potential (MEP)

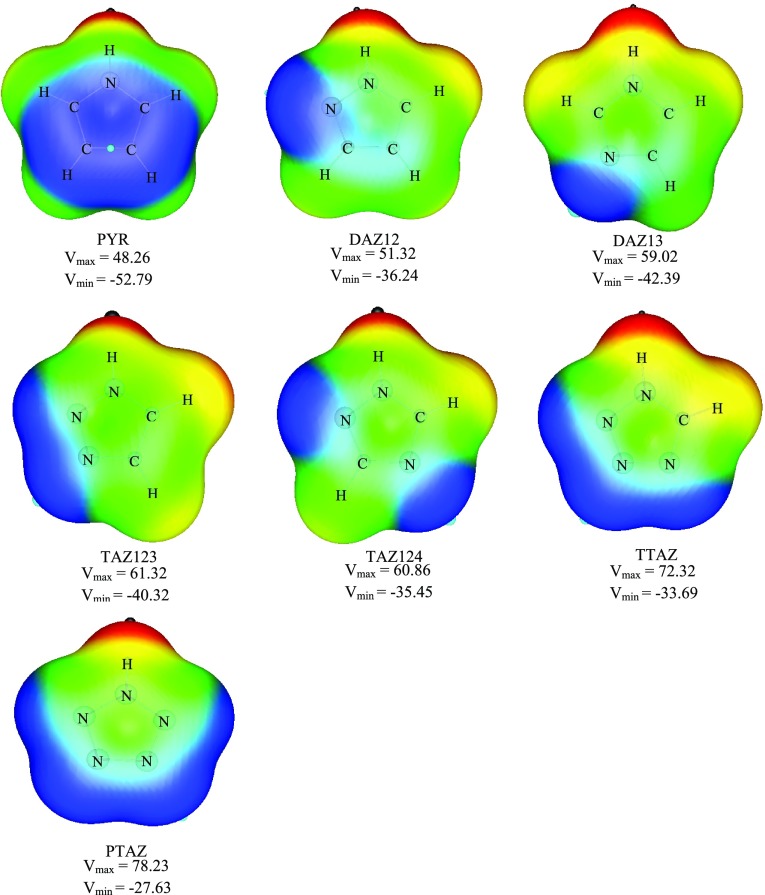
Molecular electrostatic potential (MEP) is helpful in understanding the electrophilic and nucleophilic regions present in the molecule. Figure 9 depicts the contour maps of MEP of azoles, where the red and blue regions indicate positive and negative MEP regions, respectively. The most negative-valued points in the MEP topography, usually recognized with the notation V_min, is widely used to gauze the electron-rich site of the molecule, while the most positive-valued points denoted by V_max is used to indicate the electron-deficient site of the molecule.

Figure 9.

Molecular electrostatic potential of azoles. The black circles represent the position of V_max (in kcal/mol), and the blue circles represent the position of V_min (in kcal/mol) at MP2/aug-cc-pVTZ level.

As evident from the MEP of azoles, the strong negative electrostatic potentials associated with ring pyridinic nitrogen atom make these sites attractive for electrophiles. The magnitude of these negative potentials V_min reduces with addition of nitrogen atoms in the ring, which reflects the fact that more nitrogens compete for polarizable electronic charge and each receives a small share of it. The strong positive electrostatic potentials V_max along the N–H bond vector of azole make these sites attractive for nucleophiles. The very electronegative heteroatom nitrogen withdraws electron density from the aromatic heterocycle. With increasing number of nitrogen atoms in the ring, the π electron density in the ring decreases and molecular electrostatic potential (MEP) becomes more positive. The magnitude of these positive electrostatic potentials expedites with introduction of nitrogens in the ring.

The electronic changes during the HB formation can be clearly understood by comparing V_min values of isolated azoles with V_min values of azoles in the complex (designated as V′_min). Hence, the electronic reorganization during the HB formation can be gauzed as ΔV_min = V′_min – V_min, and these MEP parameters are summarized in Table 5. It is to be anticipated from V_min values that upon coordination of azole with water/HP, there is large decrease in negative lone pair potentials of pyridinic nitrogen atom in the case of complexes involving single N···H–O interaction, whereas increase is observed in the negative lone pair potential of ring nitrogens in the case of complexes involving single N–H···O interaction. The category II, III, and IV complexes have a positive value of ΔV_min, which indicates that the amount of negative lone pair is transferred from azole ring to water/HP during the formation of complex. The category I and IV complexes have a negative value of ΔV_min, which indicates the gain in negative lone pair potential by azole at the expense of water molecule during the formation of complex.

Table 5. MEP Parameters V_max, V′_min, and ΔV_min (in kcal/mol) in Azole–Water and Azole–HP at MP2/aug-cc-pVTZ Level.

	azole–water				azole–HP
categories	complexes	Vmax	V′min	ΔVmin	complexes	Vmax	V′min	ΔVmin
I	PYR-WI	7.89	–54.80	–2.01	PYR-HPI	7.09	–54.18	–1.39
	DAZ12-WI	8.96	–40.22	–3.98	DAZ12-HP1	8.15	–40.60	–4.36
	DAZ13-WI	16.03	–47.40	–5.01	DAZ13-HPI	15.82	–48.31	–5.92
	TAZ123-WI	19.52	–46.60	–6.28	TAZ123-HPI	18.73	–47.30	–6.98
	TAZ124-WI	17.63	–40.48	–5.03	TAZ124-HPI	16.32	–41.56	–6.11
	TTAZ-WI	26.32	–40.79	–7.10	TTAZ-HPI	25.89	–41.97	–8.28
	PTAZ-WI	35.66	–33.99	–6.36
II	DAZ13-WII	64.28	–20.77	+21.62
	TAZ123-WII	69.56	–22.73	+17.59
	TAZ124-WII	68.03	–17.06	+18.39
	TTAZ-WII	77.63	–14.90	+18.79	TTAZ-HPII	78.92	–11.29	+22.40
	PTAZ-WII	82.16	–19.35	+8.28	PTAZ-HPII	84.15	–24.26	+3.37
	PTAZ-WII′	80.15	–25.43	+2.20
III	DAZ12-WIII	37.63	–25.63	+10.61	DAZ12-HPIII	39.54	–19.39	+16.85
	TAZ123-WIII	43.69	–39.84	+0.48	TAZ123-HPIII	47.62	–38.24	+2.08
	TAZ124-WIII	44.17	–34.42	+1.03	TAZ124-HPIII	46.86	–34.95	+0.50
	TTAZ-WIII	49.18	–32.68	+1.01	TTAZ-HPIII	56.12	–32.92	+0.77
					PTAZ-HPIII	59.32	–26.95	+0.68
IV					DAZ13-HPIV	63.54	–20.40	+21.99
					TAZ123-HPIV	67.20	–12.39	+27.93
					TAZ124-HPIV	64.29	–13.98	+21.47
	TTAZ-WIV	72.89	–31.82	+1.87	TTAZ-HPIV	76.28	–32.63	+1.06
V	PYR-WV	63.05	–49.63	–3.16
	DAZ13-WV	66.89	–43.82	–1.43
	TAZ123-WV	67.21	–41.92	–1.60

2.6. Symmetry-Adapted Perturbation Theory (SAPT) Analysis

To get more insight into the nature of intermolecular interactions, symmetry-adapted perturbation theory (SAPT) offers the advantage to decompose the stabilization energy into components like electrostatic (E_els), induced (E_ind), dispersion (E_disp), exchange (E_exch) interactions, etc. The E_els, E_ind, and E_disp components are attractive energy terms stabilizing the complexes, whereas the E_exch component is repulsive. When all energy terms are put together, we obtain the total SAPT energy. Table 6 shows that the order of SAPT energies in each category is the same as that of BSSE-corrected stabilization energy at MP2/aug-cc-pVTZ basis set. The major attractive force in all of these complexes is the electrostatic interaction, with its contribution being large compared to the corresponding contribution from induction and dispersion. The absolute value of the electrostatic term increases with increasing number of nitrogen atoms in all of the complexes under study. A larger value of this term correlates with more positive molecular electrostatic potential of heterocyclic compound with more nitrogen atoms. Generally, all energy components increase with increasing number of nitrogen atoms in the heterocycle. In category I, a larger value of electrostatic term in azole–water complexes in comparison to azole–HP is in agreement with more positive molecular electrostatic potential associated with former complexes while in category II, III and IV, the situation is opposite and is also in accordance with more positive electrostatic potential associated with azole–HP in comparison to azole–water complexes. A larger value of electrostatic term is associated with the complexes where both pyrrolic and pyridinic hydration sites are involved in hydrogen bonding as in category III in comparison to the complexes, where only pyrrolic hydration site is involved as in category I. This is also consistent with more positive electrostatic potential associated with category III complexes in comparison to category I. The larger role of induction term relative to dispersion term is observed in red-shifted hydrogen-bonded complexes as in categories I, II, and III, while the reverse happens in blue-shifted hydrogen-bonded complexes as in category V.

Table 6. SAPT Components (in kcal/mol) of the Stabilization Energy for Azole–Water and Azole–HP Complexes Evaluated at MP2/aug-cc-pVTZ Level.

	azole–water						azole–HP
complexes	Eels	Eind	Edisp	Eexc	δEint,rHF	Eint	complexes	Eels	Eind	Edisp	Eexc	δEint,rHF	Eint
PYR-WI	–12.94	–3.96	–2.98	16.38	–1.89	–5.39	PYR-HPI	–9.18	–3.50	–2.08	12.08	–1.83	–4.51
DAZ12-WI	–13.62	–4.17	–3.24	17.08	–1.84	–5.72	DAZ12-HPI	–9.38	–3.86	–2.27	12.22	–1.72	–5.01
DAZ13-WI	–13.89	–4.28	–3.52	17.62	–1.78	–5.85	DAZ13-HPI	–9.46	–4.01	–2.43	12.35	–1.75	–5.30
TAZ123-WI	–14.62	–4.58	–3.84	18.23	–1.89	–6.70	TAZ123-HPI	–10.76	–4.12	–2.94	13.65	–1.84	–6.01
TAZ124-WI	–14.18	–4.53	–3.76	17.83	–1.89	–6.53	TAZ124-HPI	–10.89	–4.44	–3.02	13.89	–1.80	–6.26
TTAZ-WI	–15.68	–5.16	–4.14	18.54	–1.92	–8.36	TTAZ-HPI	–11.32	–5.01	–3.09	14.28	–1.97	–7.11
PTAZ-WI	–16.24	–5.89	–4.85	18.84	–1.76	–9.90
DAZ13-WII	–12.01	–4.23	–3.46	13.61	–1.53	–7.62
TAZ123-WII	–12.92	–4.36	–3.62	15.29	–1.39	–7.02
TAZ124-WII	–13.48	–4.68	–3.54	15.46	–1.38	–7.62
TTAZ-WII	–13.69	–4.73	–3.68	17.82	–1.49	–5.77	TTAZ-HPII	–14.26	–4.43	–3.91	16.48	–1.62	–7.74
PTAZ-WII	–14.01	–4.89	–3.82	19.15	–1.58	–5.15	PTAZ-HPII	–14.92	–4.54	–4.02	19.27	–1.32	–5.53
PTAZ-WII′	–13.89	–4.78	–3.92	19.03	–1.52	–5.08
DAZ12-WIII	–14.32	–4.65	–3.15	15.16	–1.63	–8.59	DAZ12-HPIII	–14.96	–4.92	–3.25	13.26	–1.70	–11.57
TAZ123-WIII	–14.75	–4.92	–3.32	15.62	–1.69	–9.06	TAZ123-HPIII	–15.13	–5.12	–3.64	14.54	–1.88	–11.27
TAZ124-WIII	–14.13	–5.23	–3.46	16.72	–1.72	–8.62	TAZ124-HPIII	–15.58	–5.21	–3.69	15.04	–1.85	–11.29
TTAZ-WIII	–15.01	–5.34	–3.58	16.84	–1.75	–8.84	TTAZ-HPIII	–15.82	–5.34	–3.81	17.05	–1.76	–9.68
							PTAZ-HPIII	–16.10	–5.48	–3.94	17.85	–1.82	–9.19
							DAZ13-HPIV	–14.49	–4.64	–3.42	13.12	–1.55	–10.98
							TAZ123-HPIV	–15.25	–4.88	–3.85	15.29	–1.48	–10.20
							TAZ124-HPIV	–15.48	–5.04	–3.92	15.33	–1.43	–10.34
TTAZ-WIV	–14.59	–5.27	–3.82	17.15	–1.53	–8.06	TTAZ-HPIV	–15.62	–5.18	–4.01	17.21	–1.42	–9.02
PYR-WV	–12.95	–3.01	–3.52	18.85	–0.39	–1.02
DAZ13-WV	–13.52	–3.12	–3.38	18.58	–0.42	–1.86
TAZ123-WV	–13.89	–3.16	–3.18	18.89	–0.55	–1.89

In the complexes of category I, the electrostatic potential contributes 60.19–65.09% in azole–water complexes, while it accounts for 58.29–62.19% of total attractive interaction in azole–HP complexes and thus the percentage stability due to electrostatic interaction is higher in azole–water complexes in comparison to their counterpart azole–HP complexes. It is worth noting that the percentage contribution of the electrostatic component reduces with introduction of nitrogen atoms in the ring. In the above-mentioned category, the percentage contribution of the E_disp component is higher in azole–water complexes compared to azole–HP complexes, and it is observed that the dispersion component seems to increase the red shift of N–H bond in azole–water complexes compared to azole–HP complexes. It is our opinion that this is due to the intensified orbital overlap and consequently more efficient antibonding donation to σ* orbitals of N–H bond in azole–water complexes.

3. Conclusions

A comparative study on azole–water and azole–HP hydrogen-bonded complexes has been performed with the aid of MP2 and density functional theory with dispersion function (DFT-D) calculations. The ΔE_BSSE values for azole–water complexes fall in the range of −0.69 to −9.93 kcal/mol, while for azole–HP complexes, the range is −4.80 to −12.06 kcal/mol at MP2/aug-cc-pVTZ level. By analyzing the geometries, vibrational frequency, natural bond orbitals, stabilization energies, and MEP and SAPT calculations, we conclude the following remarks:

• 1.The HB interactions N···H–O_HP are found to be more stronger compared to N···H–O_water interactions, while N–H···O_HP are weaker in magnitude than N–H···O_water. This is due to the fact that HP is a better proton donor and water a better proton acceptor.
• 2.The HB donor ability of pyrrolic nitrogen (NH) atom of azole increases in the order as PYR < DAZ < TAZ < TTAZ < PTAZ, which reflects that successive aza substitution expedites the tendency of pyrrolic nitrogen (NH) to serve as better HB donor.
• 3.The HB acceptor ability of pyridinic nitrogen (N) atom of azole increases in the order PTAZ < TTAZ < TAZ < DAZ, which supports that the tendency of pyridinic nitrogen to function as HB acceptor reduces with successive addition of nitrogen atoms.
• 4.The complexes where both hydration sites (pyrrolic and pyridinic) are involved in hydrogen bonding gain more stability in comparison to the complexes, in which only single hydration site is involved.
• 5.Vibration analysis reflects that the magnitude of red shift in the stretching frequency of N–H bond of azole upon complexation with water (−81.96 to −321.65 cm^–1) is magnificently higher compared to that of complexation with HP (−55.93 to −149.49 cm^–1), since water is better HB acceptor compared to HP and has been explained on the basis of difference in acidity of water and HP. The increment in the red shift of N–H stretching vibration of azole in the complexes involving n_O(water/HP) → σ*_N–H orbital interactions with continuous addition of nitrogen atoms in the ring concludes that additional nitrogen atom enhances the orbital overlap and thus more efficient antibonding donation to σ* orbitals of N–H that leads to elongation of N–H bond.
• 6.A significantly higher magnitude of red shift in the stretching frequency of O–H_HP bond (−89.62 to −407.61 cm^–1) in azole–HP complexes compared to that of O–H_water bond (−47.96 to −231.22 cm^–1) in azole–water complexes has been observed, which is due to the fact that HP is better HB donor than water. The decrement in the red shift of O–H stretching vibration of water/HP in the complexes involving n_N → σ*_{O–H(water/HP)} orbital interactions with introduction of nitrogen atoms in the ring reflects that additional nitrogen atoms decrease the orbital overlap and thus inefficient antibonding donation to σ* orbitals of O–H upon progressive aza substitution in the ring.
• 7.SAPT analysis reflects that the electrostatic energy term is a dominant attractive contribution in comparison to induction and dispersion terms in all of the hydrogen-bonded complexes under study. Generally, all energy components increase with the introduction of nitrogen atoms in the ring. This study also reflects that the induction term is larger than the dispersion term in red-shifted hydrogen-bonded complexes as in categories I, II, and III, while the reverse situation happens in blue-shifted complexes as in category V.

4. Computational Methods

The geometries of azoles and their corresponding hydrogen-bonded complexes with water and HP were optimized by employing second-order Møller–Plesset perturbation (MP2) level in combination with aug-cc-pVDZ and aug-cc-pVTZ basis sets. For comparison purpose, the DFT-D method utilizing wB97XD level was also used in conjunction with aug-cc-pVDZ basis set.⁴³⁻⁴⁵ All of the calculations of azole–water and azole–HP complexes were carried out using Gaussian 09 software.⁴⁶ During the optimization, no constraints were imposed on the molecular geometries of the complexes of azole with water/HP. Frequency calculations were performed at the same level to corroborate that the obtained structures correspond to energy minima. In complex, one monomer may compensate for the incompleteness of the basis set using the basis function of another monomer, thus lowering its energy, and the strength of the HB is overestimated. This is known as basis set superposition error (BSSE). The stabilization energies of azole complexes included basis set superposition error (BSSE) corrections, which were employed by the counterpoise (CP) method of Boys and Bernardi.⁴⁷ The BSSE can be measured as the difference between monomer energies with the regular basis set and the full basis functions for the complex. The stabilization energy (ΔE_BSSE) is given by

where E_X(Y) is the energy of the subscript fragment X calculated in the basis of unit Y (X = Y or X ⊂ Y); E_A⁰ and E_B⁰ are the energies of the fragments A and B, respectively, in their actual geometries within the complex; and E_A(A) and E_B(B) are the energies of the free fragments in their equilibrium geometries. The natural bond orbital (NBO) analysis has been performed to obtain charge-transfer interactions, atomic charges, and E⁽²⁾ values at MP2/aug-cc-pVTZ within the Gaussian 09 package.⁴⁸ The lone pair on hydrogen-bond acceptor interacts with the antibonding orbital of hydrogen-bond donor to give rise to the second-order delocalization [E⁽²⁾], which is given by

where ΔE_ij is the energy difference between interacting orbitals and F_ij is the Fock matrix elements. The electron density properties at bond critical points (BCPs) and ring critical points (RCPs) of azole–water and azole–HP complexes have been analyzed by employing the AIMALL program.^49,50 The molecular electrostatic potential (MEP) was calculated using WFA surface analysis suite.^51,52 The total stabilization energy was decomposed by using symmetry-adapted perturbation theory (SAPT) at MP2/aug-cc-pVTZ level with the use of GAMESS package linked to the SAPT 2012.2 code.⁵³⁻⁵⁵

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b01523.

• Optimized parameters for azole–water and azole–HP complexes at wB9X7D/aug-cc-pVDZ (L1), MP2/aug-cc-pVDZ (L2), and MP2/aug-cc-pVTZ (L3) level (Tables S1–S20); topological and energetic properties at the bond critical points (BCPs) and the ring critical points (RCPs) for the complexes of azoles with water/HP evaluated at MP2/aug-cc-pVTZ theoretical level using QTAIM analysis (Table S21) (PDF)

The authors declare no competing financial interest.