Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2018 Aug 14;3(8):9086–9095. doi: 10.1021/acsomega.8b01493

Thermodynamics of the Binding of Lysozyme to a Dendritic Polyelectrolyte: Electrostatics Versus Hydration

Qidi Ran †,‡,§, Xiao Xu ∥, Joachim Dzubiella ⊥,‡,§, Rainer Haag †,§,*, Matthias Ballauff ‡,§,#,*
PMCID: PMC6644519  PMID: 31459043

Abstract

graphic file with name ao-2018-01493k_0009.jpg

The interaction between dendritic polyglycerol sulfate (dPGS) of the second generation and lysozyme was studied by isothermal titration calorimetry (ITC) at different temperatures and salt concentrations. Analysis by ITC showed that 2–3 lysozyme molecules were bound to each dPGS. The resulting binding constant Kb and the Gibbs free energy ΔGo decreased markedly with increasing salt concentration but were nearly independent of temperature. The salt dependence of Kb led to the conclusion that ca. 3 counterions bound to dPGS were released upon complex formation. The gain in entropy ΔGci by this counterion-release scales logarithmically with salt concentration and is the main driving force for binding. The temperature dependence of ΔGo was analyzed by the nonlinear van’t Hoff plot, taking into account a finite heat capacity change ΔCp,vH. This evaluation led to the binding enthalpy ΔHvH and the binding entropy ΔSvH. Both quantities varied strongly with temperature and even changed sign, but they compensated each other throughout the entire range of temperature. Coarse-grained computer simulations with explicit salt and implicit water were used to obtain the binding free energies that agreed with ITC results. Thus, electrostatic factors were the driving forces for binding whereas all hydration contributions leading to the strongly varying ΔHvH and ΔSvH canceled out. The calorimetric enthalpy ΔHITC measured directly by ITC differed largely from ΔHvH. ITC measurements done in two buffer systems with different ionization enthalpies revealed that binding was linked to buffer ionization and a partial protonation of the protein.

Introduction

The interaction of proteins with polyelectrolytes is a long-standing subject in biochemistry, drug design, and materials science.1−5 Many biopolymers, for example DNA, are highly charged and interact with proteins via electrostatic forces.6 Proteins may form complexes with natural or synthetic polyelectrolytes of opposite charge (”complex coacervates” cf. refs (2) and (3)) that have applications as food colloids.5 Central to this field is the investigation of the equilibrium binding constant between a given protein and a polyelectrolyte in order to explore the various thermodynamic factors that lead to binding. Isothermal titration calorimetry (ITC) has become a pivotal technique to explore the thermodynamics of ligands binding with proteins.7−9 The heat signal measured directly by ITC can be converted to the binding constant Kb, the temperature dependence of which may then yield the enthalpy and entropy of binding ΔHb and ΔSb, respectively.10−12 The total heat ΔHITC also furnished by ITC need not agree with ΔHb because linked equilibria may also contribute to the heat signal.13,14 It is thus evident that ITC can be used to explore the full thermodynamics of binding between polyelectrolytes and proteins. However, the use of these data for the design of drugs may be difficult and in parts questionable.15 Additional information furnished by computer simulations using coarse-grained (CG) and molecular models would clearly be helpful to clarify the details of binding in order to use these data for drug design and for predicting the binding constants of polyelectrolytes to a given protein.

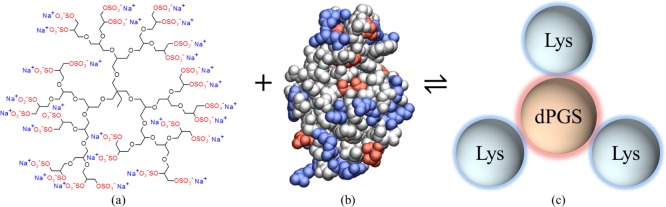
We have recently shown that ITC data can directly be combined with molecular dynamics (MD) simulations.16 As a model polyelectrolyte, we used the dendritic polyglycerol sulfate (dPGS). The scaffold of these dPGS dendrimers is made up from a hyperbranched polyglycerol core. Sulfate groups attached to all terminals render these molecules very hydrophilic and highly charged. dPGS has been shown to be promising drug and carrier recently.17−23 It has also been the subject of a comprehensive study by computer simulation24 and can be considered a well-controlled model polyelectrolyte. Figure 1 displays the chemical structure of a dPGS. The synthesized dPGS with a hyperbranched structure25 comes close to the perfect dPGS dendrimer of generation 2 (see the discussion in ref (24)).

Figure 1.

Figure 1

Open in a new tab

(a) Chemical representative of the dPGS. (b) Molecular structure of lysozyme (PDB: 2LZT).26 The blue, red, and white beads represent positive, negative, and neutral amino acids, respectively. (c) Idealized sketch of the dPGS–Lys complex taking all molecules as spheres. The overall positive lysozymes and negative dPGS are characterized with blue and red surfaces, respectively. The stoichiometry of complexation is ∼3 at 310 K and 10 mM salt purely driven by electrostatic interaction.16

In our recent study, ITC and computer simulations with implicit water were used to study the binding of lysozyme to dPGS of different generations.16 This investigation demonstrated that the interaction of the dPGS dendrimers with proteins can be traced back mainly to electrostatic effects. The main part of the electrostatic interaction was shown to be counterion-release: a part of the counterions condensed to the polyelectrolyte dPGS24 is released upon binding of the protein. Counterion condensation and release influence the thermodynamics of a polyelectrolyte and its complex formation with other molecules.27 The released counterions increase the entropy of the system. The decrease of Gibbs free energy ΔGo scales therefore with ln cs, where cs denotes the salt concentration in the solution.6,28 In addition to this, the screened electrostatic attraction on the Debye–Hückel (DH) level between the negatively charged dPGS and the positively charged lysozyme plays a role at low concentration of added salt.16 We found that the binding constant derived from MD-simulations with explicit ions but implicit water fully agreed with the experimental values derived by ITC. The same result was obtained in a recent study of the binding of poly(acrylic acid) to human serum albumin (HSA) by both ITC and computer simulations.29 These findings led to the conclusion that electrostatic terms dominate the binding of charged polymers to proteins to a large extend.

To elucidate this point further, we have recently performed a comprehensive thermodynamic investigation of the binding of HSA to dPGS by ITC.30 The binding constant Kb was measured at different temperatures at low salt concentration. In addition to this, the dependence of the binding constant on salt concentration was determined. Then, the analysis on the binding constant Kb of the 1:1 complex of HSA and dPGS-G2 demonstrated that the binding free energy depended hardly on temperature. However, both the binding enthalpy and entropy were found to vary strongly with temperature but compensated each other. This enthalpy–entropy compensation (EEC) has been observed in many systems by now15,31−35 and is related to a high value of the heat capacity change ΔCp. It is clearly seen also in systems of biological relevance.10−12

Here, we extend these investigations to the binding of dPGS-G2 to lysozyme using again a systematic variation of both the salt concentration and the temperature. In this way, the electrostatic factors contributing to binding can be separated from hydrophilic/hydrophobic hydration/dehydration. The EEC can hence be studied in detail for this system, which will allow us to discuss the role of thermodynamic quantities for predicting the interaction of proteins with highly charged macromolecules. In addition to these experimental studies, we extend our previous MD simulations of the system dPGS/lysozyme.16 Special effort is laid to the direct comparison of the data obtained by experiments and simulations. In this context, it is revealing to consider the various contributions to the enthalpy ΔHITC measured directly by ITC. The entire set of data will allow us a comprehensive discussion of the use of thermodynamic data when discussing and predicting thermodynamic equilibria between proteins and highly charged macromolecules.

Results and Discussion

The complex formation of lysozyme with dPGS of different generations was studied recently by ITC and computer simulations at 310 K and 10 mM salt concentration.16 Lysozyme has a net charge of +8 e at physiological pH. The synthetic dPGS-G2 bears −28 e total charges while its effective charge is −11 e in solution because of counterion condensation.24Figure 1 sketches the adsorption process for dPGS-G2. We found that approximately 3 lysozyme molecules and 1 dPGS form a complex with Kb ≈ 108 M–1 at 10 mM salt.16 The sulfate terminal groups bind with positive patch on the protein, thereby releasing ca. 3 counterions bound to dPGS. In the present work, all binding experiments are done in phosphate buffer whereas the experiments in ref (16) were done in 3-(N-morpholino)propanesulfonic acid (MOPS) buffer. Here, we chose the phosphate buffer because the adjusted pH hardly changes with temperature.36 In addition, the use of different buffers will allow us to discern possible heat contributions from the buffer aside from binding.13,14

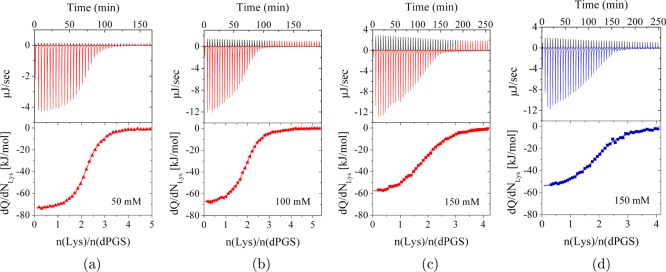
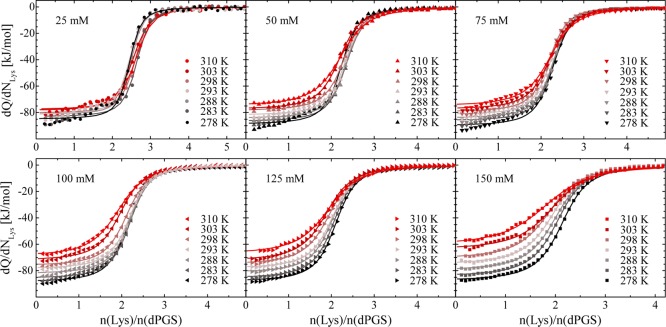
The raw data of the titration peaks and the respective isotherms at 310 K and cs = 50, 100, 150 mM are shown in Figure 2. The interaction is exothermic under all conditions. All the parameters including binding number N, binding constant Kb, and ITC enthalpy ΔHITC could be obtained very well by fitting the data with the single set of identical sites (SSIS) model.37Figure 3 gives a survey of all ITC isotherms together with the respective fits referring to all salt concentrations and temperatures under consideration here. Table 1 summarizes all fit parameters obtained from ITC experiments. The number N of bound lysozyme molecules decreases slightly with salt concentration but stays approximately constant with temperature. In the present salt concentration of 25 mM, it is found slightly smaller than previously observed 3–4 in 10 mM MOPS buffer.16 The binding affinity of lysozyme with dPGS decreases with salt concentration as expected. Table 1 furthermore shows that the binding free energy ΔGo hardly changes with temperature but decreases significantly with increasing ionic strength.

Figure 2.

Figure 2

Open in a new tab

ITC isotherms in phosphate buffer pH 7.4 at ionic strengths: (a) 50, (b) 100, and (c) 150 mM at 310 K. (d) Isotherm in MOPS buffer at 150 mM and 310 K done in ref (16). The black peaks in the upper panels represent the dilution heat of lysozyme into respective buffer which will be subtracted from the adsorption heat. The signal gets stronger at higher ionic strength because of higher sample concentration. The red and blue peaks are the adsorption heat into dPGS solutions. The symbols in the lower panel are the integrated molar heat for each titration related to the added protein. The solid curves are fitted by the SSIS model.

Figure 3.

Figure 3

Open in a new tab

ITC isotherms for dPGS-G2 binding with lysozyme in phosphate buffer pH 7.4 with ionic strengths: 25, 50, 75, 100, 125, and 150 mM at different temperatures. The solid lines present the fits by the SSIS model.

Table 1. Thermodynamic Properties of Lysozyme Binding to dPGS-G2 in Phosphate Buffer pH 7.4 under Different Conditionsa.

cs [mM] T [K] N Kb [105 M–1] ΔGo [kJ/mol] (kBT) ΔHITC [kJ/mol] ΔHvH [kJ/mol] TΔSvH [kJ/mol] ΔCp,ITC [kJ/(mol K)] ΔCp,vH [kJ/(mol K)]
25 278 2.4 ± 0.02 384 ± 99 –40.4 ± 0.7(−17.5) –84.9 ± 0.8 3.5 ± 12.3 43.9 ± 12.0 0.22 ± 0.02 –1.20 ± 0.75
  283 2.6 ± 0.03 362 ± 110 –41.0 ± 0.7(−17.4) –83.1 ± 0.9 –2.5 ± 8.7 38.6 ± 8.7    
  288 2.4 ± 0.02 433 ± 100 –42.1 ± 0.6(−17.6) –81.3 ± 0.7 –8.5 ± 5.5 33.3 ± 5.6    
  293 2.4 ± 0.01 345 ± 48 –42.3 ± 0.3(−17.4) –81.3 ± 0.7 –14.4 ± 3.6 27.8 ± 3.6    
  298 2.5 ± 0.02 325 ± 65 –42.9 ± 0.5(−17.3) –80.4 ± 0.6 –20.4 ± 4.9 22.3 ± 4.9    
  303 2.5 ± 0.01 216 ± 20 –42.5 ± 0.3(−16.9) –78.6 ± 0.5 –26.4 ± 8.0 16.6 ± 8.0    
  310 2.5 ± 0.01 217 ± 20 –43.5 ± 0.2(−16.9) –77.7 ± 0.5 –34.8 ± 12.9 8.6 ± 13.1    
50 278 2.2 ± 0.02 55.1 ± 9.3 –35.9 ± 0.4(−15.5) –88.9 ± 0.7 11.7 ± 4.8 47.4 ± 4.7 0.43 ± 0.03 –1.99 ± 0.29
  283 2.3 ± 0.01 51.7 ± 3.9 –36.4 ± 0.2(−15.5) –86.8 ± 0.5 1.7 ± 3.4 38.2 ± 3.4    
  288 2.3 ± 0.01 53.7 ± 4.1 –37.1 ± 0.2(−15.5) –84.4 ± 0.5 –8.3 ± 2.2 28.8 ± 2.2    
  293 2.3 ± 0.01 47.5 ± 3.7 –37.5 ± 0.2(−15.4) –82.1 ± 0.5 –18.2 ± 1.4 19.3 ± 1.4    
  298 2.3 ± 0.01 43.8 ± 1.9 –37.9 ± 0.1(−15.3) –78.6 ± 0.3 –28.2 ± 1.9 9.6 ± 1.9    
  303 2.2 ± 0.01 34.7 ± 1.7 –37.9 ± 0.1(−15.1) –77.5 ± 0.4 –38.2 ± 3.1 –0.3 ± 3.1    
  310 2.2 ± 0.01 21.7 ± 1.1 –37.6 ± 0.1(−14.6) –74.9 ± 0.2 –52.2 ± 5.0 –14.4 ± 5.1    
75 278 2.3 ± 0.02 22.8 ± 3.1 –33.8 ± 0.3(−14.6) –90.1 ± 0.5 16.4 ± 3.8 50.2 ± 3.8 0.46 ± 0.02 –2.06 ± 0.24
  283 2.2 ± 0.01 25.2 ± 2.2 –34.7 ± 0.2(−14.7) –86.2 ± 0.6 6.1 ± 2.7 40.7 ± 2.7    
  288 2.2 ± 0.01 23.9 ± 1.9 –35.2 ± 0.2(−14.7) –84.3 ± 0.5 –4.2 ± 1.7 31.1 ± 1.7    
  293 2.2 ± 0.01 23.3 ± 1.7 –35.7 ± 0.2(−14.7) –81.7 ± 0.5 –14.5 ± 1.1 21.2 ± 1.1    
  298 2.2 ± 0.01 21.7 ± 1.5 –36.1 ± 0.2(−14.6) –79.5 ± 0.4 –24.8 ± 1.5 11.2 ± 1.5    
  303 2.2 ± 0.01 16.1 ± 0.9 –36.0 ± 0.1(−14.3) –77.6 ± 0.4 –35.1 ± 2.5 1.0 ± 2.5    
  310 2.2 ± 0.01 11.5 ± 0.6 –36.0 ± 0.1(−14.0) –75.1 ± 0.4 –49.5 ± 4.0 –13.6 ± 4.1    
100 278 2.1 ± 0.01 11.4 ± 1.0 –32.2 ± 0.2(−13.9) –88.5 ± 0.4 11.0 ± 3.0 43.2 ± 3.0 0.63 ± 0.02 –1.89 ± 0.19
  283 2.2 ± 0.01 12.2 ± 0.7 –33.0 ± 0.1(−14.0) –85.8 ± 0.4 1.6 ± 2.2 34.5 ± 2.1    
  288 2.2 ± 0.01 11.0 ± 0.6 –33.3 ± 0.1(−13.9) –82.4 ± 0.4 –7.9 ± 1.4 25.6 ± 1.4    
  293 2.2 ± 0.01 10.9 ± 0.5 –33.9 ± 0.1(−13.9) –78.6 ± 0.4 –17.3 ± 0.9 16.5 ± 0.9    
  298 2.1 ± 0.01 9.2 ± 0.4 –34.0 ± 0.1(−13.7) –76.3 ± 0.3 –26.7 ± 1.2 7.3 ± 1.2    
  303 2.0 ± 0.01 7.6 ± 0.4 –34.1 ± 0.1(−13.5) –72.2 ± 0.4 –36.2 ± 2.0 –2.1 ± 2.0    
  310 1.9 ± 0.01 5.0 ± 0.2 –33.8 ± 0.1(−13.1) –69.1 ± 0.4 –49.4 ± 3.2 –15.5 ± 3.2    
125 278 2.1 ± 0.01 6.2 ± 0.4 –30.8 ± 0.2(−13.3) –88.0 ± 0.3 –3.4 ± 2.0 27.4 ± 1.9 0.65 ± 0.02 –1.11 ± 0.12
  283 2.1 ± 0.01 5.9 ± 0.2 –31.3 ± 0.1(−13.3) –85.6 ± 0.2 –9.0 ± 1.4 22.3 ± 1.4    
  288 2.0 ± 0.01 5.5 ± 0.1 –31.6 ± 0.1(−13.2) –81.4 ± 0.2 –14.6 ± 0.9 17.1 ± 0.9    
  293 2.0 ± 0.01 4.9 ± 0.1 –31.9 ± 0.1(−13.1) –78.3 ± 0.2 –20.1 ± 0.6 11.7 ± 0.6    
  298 2.0 ± 0.01 4.0 ± 0.2 –31.9 ± 0.1(−12.9) –75.2 ± 0.3 –26.7 ± 0.8 6.3 ± 0.8    
  303 1.9 ± 0.01 3.4 ± 0.2 –32.1 ± 0.1(−12.7) –72.5 ± 0.4 –31.3 ± 1.3 0.8 ± 1.3    
  310 2.0 ± 0.02 2.5 ± 0.3 –32.0 ± 0.3(−12.4) –67.2 ± 0.6 –39.1 ± 2.1 –7.0 ± 2.1    
150 278 2.1 ± 0.01 4.4 ± 0.02 –30.1 ± 0.1(−13.0) –87.6 ± 0.2 –3.2 ± 4.3 26.8 ± 4.2 0.88 ± 0.04 –1.47 ± 0.27
  283 2.1 ± 0.01 4.0 ± 0.09 –30.3 ± 0.1(−12.9) –84.2 ± 0.2 –10.5 ± 3.1 19.8 ± 3.1    
  288 2.0 ± 0.01 3.4 ± 0.08 –30.5 ± 0.1(−12.7) –79.9 ± 0.2 –17.9 ± 1.9 12.8 ± 2.0    
  293 2.0 ± 0.01 3.2 ± 0.1 –30.9 ± 0.1(−12.7) –75.2 ± 0.3 –25.2 ± 1.3 5.6 ± 1.3    
  298 1.9 ± 0.01 2.6 ± 0.1 –30.9 ± 0.1(−12.5) –71.0 ± 0.4 –32.3 ± 1.7 –1.7 ± 1.7    
  303 2.0 ± 0.01 2.1 ± 0.1 –30.9 ± 0.1(−12.3) –64.0 ± 0.4 –39.9 ± 2.8 –9.1 ± 2.8    
  310 1.9 ± 0.01 1.3 ± 0.07 –30.4 ± 0.1(−11.8) –60.9 ± 0.5 –50.2 ± 4.5 –19.9 ± 4.6    
Open in a new tab
a

N, Kb, and ΔHITC are fitting parameters by ITC. ΔGo is calculated according to eq 6. ΔCp,ITC is the linear dependence of ΔHITC on temperature obtained from Figure 8. ΔHvH, ΔSvH, and ΔCp,vH are the binding enthalpy, entropy, and heat capacity change fitted by eq 6, respectively.

Electrostatic and Steric Contributions to the Binding Affinity

The electrostatic interaction between oppositely charged polyelectrolytes has been used for many decades in areas such as multilayer film formation.38,39 In our previous study, we discussed the electrostatic contributions to the binding between dPGS and lysozyme. On the basis of a comparison of ITC data with MD simulations, we found that the binding was mainly driven by counterion-release.16 Simulations of the highly charged dPGS dendrimers24 demonstrated that there was a thin shell or Stern layer of condensed counterions on the surface of the dendrimers. From this, a surface concentration of condensed counterions cci can be estimated (see Table S3 of ref (16)). In the case of G2, cci = 0.96 M is much higher than the salt concentrations in bulk used here in the ITC-runs. When lysozyme is bound to dPGS, the positive patch on the surface of the protein becomes a multivalent counterion to the dendrimer. A concomitant number of the condensed counterions of dPGS are thereby released into the bulk solution. The corresponding gain of entropy follows as

graphic file with name ao-2018-01493k_m001.jpg 1

where cci and cs are the concentrations of local condensed counterions and bulk salt, respectively, and ΔNci is the number of released counterions.16,40 From this, it follows that the binding constant is related to ΔNci if counterion-release is a dominant driving force6,28

graphic file with name ao-2018-01493k_m002.jpg 2

Figure 4 presents the dependence of the binding constant on salt concentration. The number of released counterions ranges between 2.5 and 2.7 (data referring to other temperatures are shown in the Supporting Information), which is in accord with our previous result where ΔNci = 3.1 in MOPS buffer at 310 K.16 The released counterions from the dPGS surface upon binding can also be monitored by computer simulations,16 and the results agree with experiments (see Supporting Information). Because cci equals to 0.96 M at 310 K for dPGS-G2,24eq 1 predicts ΔGci at 25 mM salt concentration to be −9.8 kBT. It hence presents a major contribution in the total binding free energy. The solid lines in Figure 4 referring to different temperatures are approximately parallel so the number of released counterions does not depend on temperature within the limits of error. It thus demonstrates that counterion-release does not contribute to the heat capacity ΔCp on this level of approximation.

Figure 4.

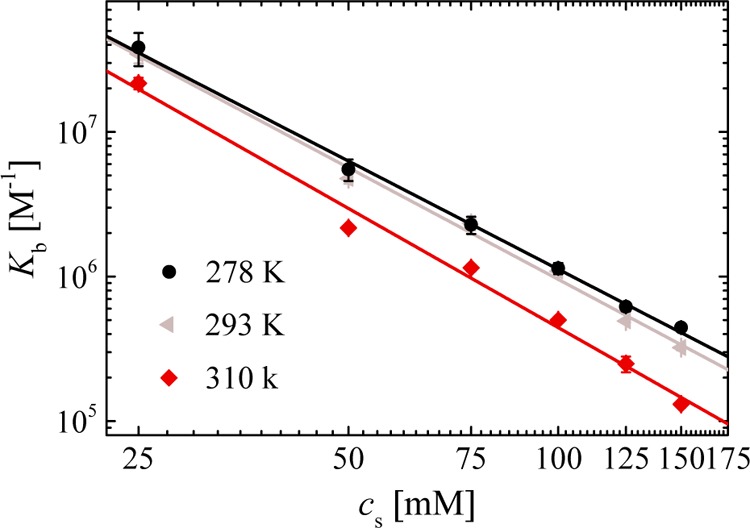
Figure 4

Open in a new tab

Dependence of binding constant on salt concentration for three different temperatures. The number of released counterions ΔNci from the slope of these lines fitted according to eq 2 is 2.5 ± 0.1 at 278 K, 2.6 ± 0.1 at 293 K, and 2.7 ± 0.1 at 310 K in phosphate buffer. ΔNci measured in MOPS buffer at 310 K is 3.1 ± 0.1.16

In addition to counterion-release, there is a DH attraction ΔGele between dPGS and the bound lysozyme. Moreover, there is an electrostatic repulsion between bound proteins. Considering all the charged beads individually, the pairwise charge–charge interaction on the DH level was summarized by computer simulation.16 The resultant overall electrostatic interaction between lysozyme and dPGS-G2 was attractive and decreased slightly with the uptake of bound proteins. For the first three bound proteins at cs = 10 mM, the attraction was found similar to be −26 kJ/mol (−10 kBT) (see Figure 2D in ref (16)).

Steric repulsion between the bound lysozymes enters as a third term. This packing penalty is non-existent for the first uptake and positive for the subsequent proteins. It becomes a limiting factor when the packing of the proteins leads to a more or less full coverage of the surface. For the situation encountered for G2 where 4 lysozymes are bound, simulations showed this term to be of minor importance.16

The findings above lead to the conclusion that the binding free energy of subsequent lysozymes is not a constant but decreases with the number of bound proteins. The Langmuir model which is the basis of the SSIS fitting, on the other hand, assumes that each bound protein is attached independently and the free energy of binding is equivalent for all bound proteins.

To elucidate the cooperativity in a multivalent binding, we measured the complexation of lysozyme with dPGS-G2 for different coordination numbers i by MD simulations. Figure 5 shows the potential of mean force (PMF) profile at 293 K and two salt concentrations. The respective local minimum reveals the binding distance rb and binding free energy ΔGbsim at the given coordination number. The complexation between dPGS and the first bound lysozyme is purely driven by electrostatic effects with a binding free energy −27 kBT at 10 mM salt (see the discussion of Figure 2C in ref (16)). The magnitude of ΔGb decreases with i, which indicates a negative cooperativity caused by electrostatic repulsion and steric hindrance.

Figure 5.

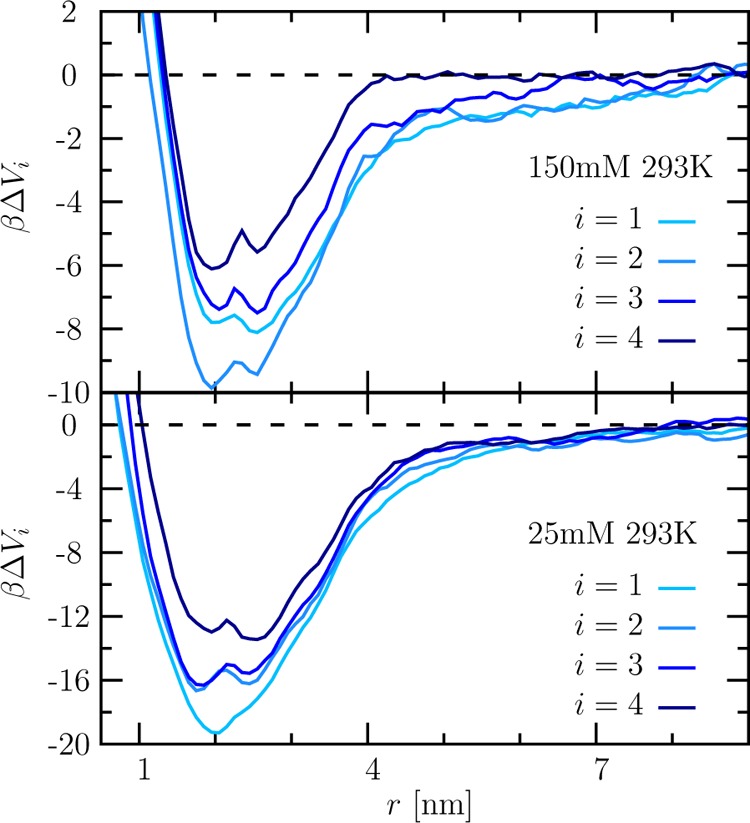
Figure 5

Open in a new tab

PMF curves βΔVi for the complexation between dPGS-G2 and lysozyme vs the dPGS–lysozyme center of mass distance r. ΔVi is in the unit of kBT (β = 1/kBT). The binding coordination number i ranges from 1 to 4 as indicated in the graph. The simulation was done at T = 293 K and salt concentration cs = 25 mM (lower panel) and 150 mM (upper panel).

To account for this negative cooperativity, we recently developed a new way of comparing ΔGb between the simulation and ITC experiments:16 in canonical simulations, the concentration cbound of bound and non-interacting ligands follows as16

graphic file with name ao-2018-01493k_m003.jpg 3

where cfree is the concentration of free (unbound) ligands and Vb refers to the effective volume in which the bound ligands are confined. ΔGb defines the transfer free energy from bulk to the bound state, which can be taken directly from the minimum of the PMF profile.16 We now assume that the binding complex consists of i lysozyme ligands bound in a shell on the surface of dPGS which are idealized as spheres. Hence, the binding volume Vb = 4π(rb)2δb. We take the binding distance rb = 2.5 nm at saturation together with the thickness of the spherical binding shell δb = 1 nm.

In the Langmuir model used for the evaluation of the experiments, the protein coverage θ is defined as

graphic file with name ao-2018-01493k_m004.jpg 4

with Kb = v0 exp(−βΔGo) the binding constant related to the Langmuir binding free energy ΔGo in Table 1. Here, the volume prefactor v0 is defined to be 1 L/mol. Combination of eq 3 with 4 leads to the “simulation-referenced” Langmuir free energy by

graphic file with name ao-2018-01493k_m005.jpg 5

which leads to a direct comparison between the experimental ITC curves and the simulations discussed previously.16 The degree of coverage θ* is obtained from the inflection point of the ITC isotherms, where n(Lys)/n(dPGS) = N and is smaller than unity.16

We apply this method to the present data and find θ* at four different conditions (see Supporting Information). ΔGbITC at the inflection point can then be calculated with eq 5 and compared to ΔGb in Figure 6. We find a full agreement between simulation and ITC for all conditions. Thus, the experimental results can be rationalized very well in terms of the simulations.

Figure 6.

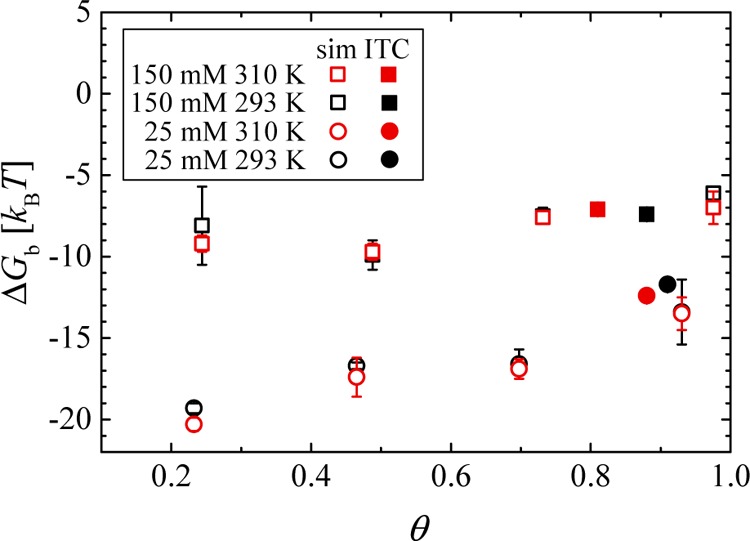
Figure 6

Open in a new tab

Binding free energy ΔGbsim vs the protein coverage θ = i/Nsim, where i is the binding coordination number and Nsim is the binding stoichiometry from simulations. ΔGb values by simulations at different conditions are depicted by the empty symbols. These results are compared with the “simulation-referenced” Langmuir free energy ΔGbITC according to eq 5 at θ*, denoted by the filled points.

It is interesting to note that the data taken at higher salt concentration exhibit a much weaker dependence on θ (squares in Figure 6) than the ones obtained for lower salt concentrations (circles). This means that the binding affinity at cs = 150 mM shows much lower negative cooperativity, which can be traced back to the weaker DH interaction in the presence of more salt. At the same time, the simulations confirm a weak dependence of ΔGb on temperature consistent with the experimental data.

A meaningful comparison of ΔGo measured at different conditions requires that θ* remains constant under all conditions. Table 1 shows that the number N of bound lysozymes measured for a given salt concentration does not depend on temperature. Therefore, the present set of data can be used to discuss the dependence on temperature without restrictions. There are small changes of N for a given temperature when going from low salt concentrations to higher ones. However, this change can be disregarded in good approximation. Hence, the data gathered in Table 1 allow us to discuss the dependence of ΔGo on both salt concentration and temperature which is done in the following.

Enthalpy–Entropy Compensation

As discussed above, the accuracy of the obtained ΔGo is fully sufficient for a meaningful analysis of the dependence on T. Previous work on complex formation of proteins with nucleic acids has clearly revealed that the binding enthalpy depends markedly on temperature,11,12 which shows that the heat capacity change ΔCp is of appreciable magnitude. Therefore, the binding free energy must be rendered in terms of the nonlinear van’t Hoff relation11,41

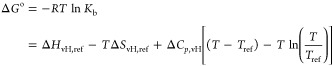graphic file with name ao-2018-01493k_m006.jpg 6

where ΔHvH,ref and ΔSvH,ref are the binding enthalpy and entropy, respectively, at a given reference temperature Tref.

The analysis of the data shown in Figure 7 according to eq 6 is done as follows: the given temperature is chosen as reference temperature Tref, and the corresponding binding enthalpy ΔHvH,ref, entropy ΔSvH,ref, and heat capacity change ΔCp,vH are obtained as fit parameters. This procedure is done for all temperatures under consideration here. The values ΔHvH, ΔSvH, and ΔCp,vH obtained for all temperatures by this fit are listed in Table 1. Here, ΔCp,vH has been treated as a freely floating parameter but the fit results are constant for each salt concentration.

Figure 7.

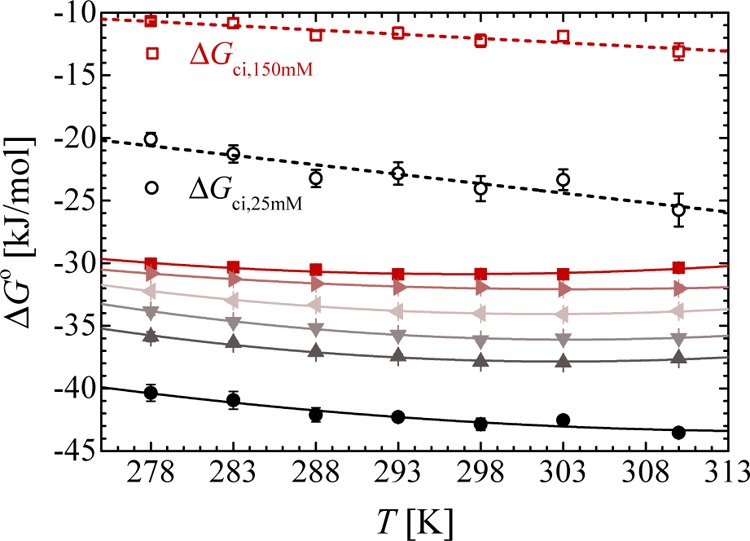
Figure 7

Open in a new tab

Nonlinear van’t Hoff analysis for dPGS–Lys complexation at different ionic strengths according to eq 6: 25 mM (•), 50 mM (▲), 75 mM (▼), 100 mM (◀), 125 mM (▶), and 150 mM (■). The counterion-release entropy gain ΔGci is calculated with ΔNci according to eq 1.

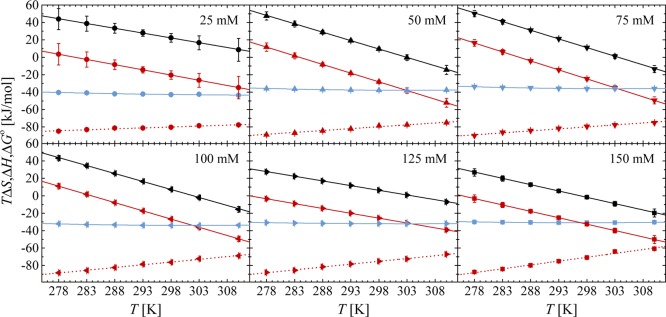
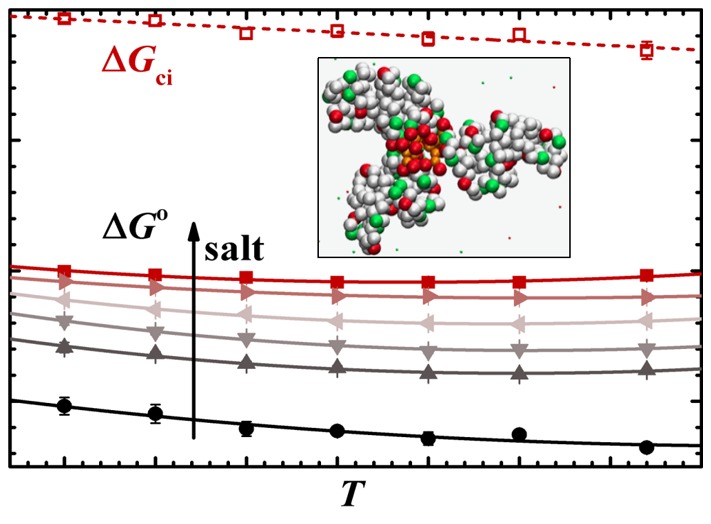
The curvature in Figure 7 which is due to the heat capacity ΔCp,vH is similar and the data are of sufficient precision to determine this quantity. ΔCp,vH is constant in this range of temperature and approximately −2 kJ/(mol K) for all the ionic strengths. Both ΔHvH and ΔSvH change strongly with temperature, whereas ΔGo is nearly a constant. This insensitivity of ΔGo to T necessarily leads to a marked EEC considering a large ΔCp,vH.

Figure 7 also contains the part ΔGci calculated for 25 and 150 mM salt by eq 1. The magnitude of ΔGci varies linearly with temperature, which is obvious from eq 1: ΔSci = ΔNcikB ln(cci/cs) does not depend on T if one disregards small change of cci with temperature. The difference between ΔGci and ΔGo is mainly due to the electrostatic interaction ΔGele as discussed above and in ref (16). At constant temperature, for example 293 K, this electrostatic part can be read off to be −19 kJ/mol at both 25 and 150 mM salt from Figure 7. It does not vanish with added salt as expected for a simple DH-interaction. Thus, the analytical modeling of the electrostatic interaction between the protein adhering directly to the dendritic polyelectrolyte requires a more detailed description containing higher order multipole terms. It should be noted, however, that the simulation carries along all necessary contributions because it fully agrees with the experimental data.

Figure 8 depicts the entropic and enthalpic contributions in the total free energy at all ionic strengths. It demonstrates directly the EEC. ΔHvH and ΔSvH even change sign in most cases in Figure 8, whereas ΔGo is almost constant. It is thus evident that the EEC is leading to a nearly constant free energy of binding because ΔHvH and TΔSvH run strictly parallel within the present window of temperature. Hence, for our system, the enthalpic and entropic changes with temperature due to hydration effects seem to cancel out each other nearly completely. In general, EEC is a commonly observed phenomenon for binding of polyelectrolytes with proteins.32,33,42 This effect has widely frustrated the use of thermodynamic data for drug design.15 The present discussion underscores this problem and accentuates that one should strive to calculate binding free energy rather than enthalpic or entropic contributions individually.

Figure 8.

Figure 8

Open in a new tab

Entropic (TΔSvH, black) and enthalpic (ΔHvH, red) contributions in total free energy (ΔGo, blue) at different ionic strengths. The calorimetric enthalpy ΔHITC (dashed red) is plotted as a comparison to ΔHvH.

Figure 8 shows clearly that ΔHvH deviates markedly from the directly measured ΔHITC, which is different from the dPGS–HSA binding system in our previous study.30 It is well-known that ΔHITC measured directly in the calorimetry experiment need not agree with the binding enthalpy ΔHvH.15,41,43−45 Explanations for this finding are based on the fact that ΔHITC may also contain contributions of linked equilibria such as ionization or conformational changes of the protein or ligand. The next section will discuss the measured enthalpy in more detail.

Binding Enthalpy Versus Calorimetric Enthalpy

The directly measured ΔHITC rises with both temperature and salt concentration (see Table 1). In general, the linear dependence of enthalpy ΔHITC on temperature corresponds to a heat capacity change ΔCp,ITC. Figure 8 includes the linear fitting at different salt concentrations. The exothermic process is accompanied by a positive heat capacity change (see Table 1). Notably, ΔCp,ITC increases with salt concentration similar to findings made for a protein–DNA binding system.46 The value increases with ionic strength thus suggesting an exothermic process that is repressed by ions (see the discussion of this point in ref (46)). Compared to ΔCp,ITC, the intrinsic part ΔCp,vH has opposite sign and does not depend on ionic strength within the limits of error. This is indicative of linked equilibria that compensate ΔCp,vH and gives overall positive ΔCp,ITC.

According to Kozlov and Lohman, the observed enthalpy change by calorimetry can be split up into several contributions as13

graphic file with name ao-2018-01493k_m007.jpg 7

Thus, the calorimetric enthalpy contains the binding enthalpy ΔHvH, the protonation enthalpy of free or bound protein/ligand ΔHprot, and the ionization (deprotonation) enthalpy of the buffer ΔHion = ΔnH+ΔHiono with positive ΔnH+ being the number of protons supplied by the buffer. ΔHion is the molar enthalpy of buffer deprotonation. Similarly, the temperature dependence gives the observed ΔCp,ITC as13

graphic file with name ao-2018-01493k_m008.jpg 8

Here, ΔCp,vH is due to binding. The electrostatic contribution to ΔCp is relatively small.47 The hydration or dehydration of nonpolar and polar solute gives large heat capacity change with different signs.48

Binding experiments done in two different buffer solutions with distinguishable ΔHiono allow us to calculate the caloric effect of buffer ionization because the first two terms at the right side of eq 7 remain unchanged. Here, we compare the measured ΔHITC in MOPS obtained previously at 310 K and different ionic strengths16 and phosphate buffer done here. From these data, the number of released protons at 310 K can be derived as

graphic file with name ao-2018-01493k_m009.jpg 9

The buffer ionization enthalpies for dPGS–Lys interaction at 310 K in phosphate buffer are summarized in Table 2 taking the data obtained with the MOPS buffer as ref (16) ΔnH+ protons are released from the buffer and it decreases with salt concentration. The positive ionization enthalpy thus decreases with salt and is relatively small. Then, the large discrepancy between ΔHITC and ΔHvH must be traced back to a negative ΔHprot. The protonation enthalpy can also be estimated with ΔnH+ and given ΔHproto; however, it depends on the species of amino acid.49 Here, we roughly estimate the protonation enthalpy with ΔHprot of lysine and arginine from the literature.49 The values in Table 2 are in a comparable range with the calculation according to eq 7, which indicates that positive residues at the binding site may be protonated and the protonation brings a large negative contribution to the measured enthalpy.

Table 2. Enthalpy Contributions of Linked Equilibria for dPGS–Lys Complexation in Phosphate Buffer at 310 Ka.

cs [mM] ΔHITCphos [kJ/mol] ΔHITCMOPS* [kJ/mol] ΔnH+ ΔHion [kJ/mol] ΔHprot [kJ/mol] ΔHprot* [kJ/mol]
25 –77.7 ± 0.5 –65.4 ± 0.4 0.62 ± 0.03 1.8 ± 0.1 –44.7 ± 12.5 –29
50 –74.9 ± 0.2 –65.2 ± 0.2 0.49 ± 0.02 1.4 ± 0.1 –24.1 ± 4.9 –23
75 –75.1 ± 0.4 –66.4 ± 0.3 0.44 ± 0.03 1.3 ± 0.1 –26.9 ± 3.7 –20
100 –69.1 ± 0.4 –64.6 ± 0.3 0.22 ± 0.02 0.6 ± 0.1 –20.3 ± 2.9 –10
125 –67.2 ± 0.6 –60.0 ± 0.2 0.36 ± 0.03 1.0 ± 0.1 –29.1 ± 1.6 –17
150 –60.9 ± 0.5 –56.7 ± 0.5 0.21 ± 0.04 0.6 ± 0.1 –11.3 ± 4.1 –10
Open in a new tab
a

ΔHITCMOPS* is taken from previous measurements.16 According to ref (36), the ionization enthalpy ΔHion,MOPS and ΔHion,phoso are 22.67 and 2.88 kJ/mol, respectively, at 310 K neglecting the salt dependence. ΔnH+ can then be obtained according to eq 9 and ΔHion = ΔnH+ΔHion,phos in phosphate buffer. ΔHprot is calculated with eq 7. The protonation enthalpy ΔHproto for arginine and lysine is −46 kJ/mol according to the literature.49 Thus, the protonation enthalpy in this system can be calculated according to ΔHprot = ΔnH+ΔHproto.

It should be kept in mind that the binding of several lysozyme molecules to a single dPGS is accompanied by a notable negative cooperativity. This could be seen directly in Figure 6. ΔGo refers to the situation where θ = θ*, that is, at the inflection point of the ITC titration curve and so does ΔHvH derived from eq 7. The measured enthalpy ΔHITC, on the other hand, is fitted by the starting points of an ITC isotherm at low θ. ΔHITC may differ at higher θ in cases where negative cooperativity comes into play. Hence, eq 7 and the estimates given in Table 2 can only work on a qualitative level.

Conclusions

We present a systematic thermodynamic study on complexation of dPGS-G2 with lysozyme. In particular, we measured the dependence of the binding constant on temperature and ionic strength. The dependence on salt concentration clearly revealed counterion-release as the driving force while the dependence on temperature demonstrated strong enthalpy–entropy compensation. Together with the simulations on the dPGS–lysozyme binding, the present thermodynamic analysis shows that the enthalpic and the entropic contributions compensate each other over the entire range of temperature to give a nearly constant free energy driven solely by electrostatic factors. Hence, in case of the present hydrophilic dendritic system, the driving force, namely counterion-release with electrostatic attraction, is responsible for binding while all contributions due to hydration cancel out in good approximation.

Experimental Section

Materials

The protein lysozyme from chicken egg-white with molecular weight 14.3 kDa was purchased from Alfa Aesar (J60701) and used directly. dPGS of second generation (dPGS-G2) was synthesized according to the literature.25,50 The properties of dPGS-G2 are collected in Table 3. More details are given in our previous work.16,24

Table 3. Chemical Properties of dPGS24a.

label Mn,dPGS [kD] PDI DS [%] Nter
dPGS 4.9 1.7 ≥98 28
Open in a new tab
a

Mn,dPGS: number-averaged molecular weight of dPGS; PDI: polydispersity index; DS: degree of sulfation of the terminal groups; and Nter: total number of terminal sulfate groups.

Isothermal Titration Calorimetry

Sodium phosphate dibasic (10 mM; Na2HPO4) and 1.8 mM potassium phosphate monobasic (KH2PO4) were dissolved into solution, and the pH was adjusted to 7.4 at RT by adding 1 M NaOH. To prepare buffers with different ionic strengths, additional NaCl was added into the buffer individually.

ITC was used to evaluate the thermodynamics of dPGS–protein binding. The measurements were performed by a MicroCal VP-ITC instrument (GE Healthcare, Freiburg, Germany) with a syringe volume of 280 μL and a cell volume of 1.43 mL. The interaction was measured at six ionic strengths each with seven temperatures. A solution of lysozyme was located in the syringe and titrated stepwise into the cell filled with dPGS solution. The dilution heat was obtained by titrating a lysozyme solution of the same concentration into pure buffer. Figure 2 displays typical examples of experimental ITC curves. At higher salt concentration, the binding affinity became smaller and the sample concentration had to be increased to obtain a sigmoidal isotherm.37,51 Our previous analysis showed that an increase of the sample concentration did not change the resulting binding constant (see Table S1 of ref (16)). Table 4 gathers the sample concentrations used for the respective concentration of salt.

Table 4. Protein Concentration cLys and dPGS Concentration cdPGS in ITC Measurements at Different Ionic Strength csa.

cs [mM] 25 50 75 100 125 150
cLys [mM] 0.11 0.24 0.56 0.87 1.31 1.36
cdPGS [μM] 2.4 10.3 22.5 35.1 57.8 69.9
Open in a new tab
a

The sample concentrations are the same for different temperatures at one ionic strength.

The raw data were analyzed with the Origin 7.0 (MicroCal) software, and the SSIS model was used to fit the isotherm.37 The SSIS model assumes that all the binding sites are equivalent and independent. The thermodynamic data here are compared with previous ITC measurements at 310 K in a different buffer (MOPS).16

Molecular Dynamics Simulation

CG simulations with implicit water and explicit salt were performed as described in our previous work.16,29 The simulation used the stochastic dynamics integrator in GROMACS 4.5.4 software package.52 The CG model of dPGS-G2 dendrimer was established by us before and used directly here.24 The CG model of Lysozyme (PDB: 2LZT) was constructed taking each amino acid residue as a single CG bead maintained by a structure-based Go-model force field.53 At physiological pH, dPGS-G2 and lysozyme had net charge of −24 e and +8 e, respectively.16 The binding between lysozyme and dPGS-G2 was conducted at 293 and 310 K each with two salt concentrations of 25 mM and 150 mM. The PMF was obtained using steered Langevin dynamics52 with steering velocity vp= 0.2 nm/ns and harmonic force constant K = 2500 kJ mol–1 nm–2. All parameters were the same as in our previous work.16

Acknowledgments

The author X.X. was funded by the China Scholarship Council. The Helmholtz Virtual Institute for Multifunctional Biomaterials for Medicine and the International Research Training Group IRTG 124 funded by the German Science Foundation are gratefully acknowledged for financial support.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b01493.

  • Analysis of counterion-release and determination of θ* (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao8b01493_si_001.pdf (271.4KB, pdf)

References

  1. Miura N.; Dubin P. L.; Moorefield C. N.; Newkome G. R. Complex Formation by Electrostatic Interaction between Carboxyl-Terminated Dendrimers and Oppositely Charged Polyelectrolytes. Langmuir 1999, 15, 4245–4250. 10.1021/la990125l. [DOI] [Google Scholar]
  2. Cooper C. L.; Dubin P. L.; Kayitmazer A. B.; Turksen S. Polyelectrolyte-protein complexes. Curr. Opin. Colloid Interface Sci. 2005, 10, 52–78. 10.1016/j.cocis.2005.05.007. [DOI] [Google Scholar]
  3. Kayitmazer A. B.; Seeman D.; Minsky B. B.; Dubin P. L.; Xu Y. Protein-polyelectrolyte interactions. Soft Matter 2013, 9, 2553–2583. 10.1039/c2sm27002a. [DOI] [Google Scholar]
  4. Wei Q.; Becherer T.; Angioletti-Uberti S.; Dzubiella J.; Wischke C.; Neffe A. T.; Lendlein A.; Ballauff M.; Haag R. Protein interactions with polymer coatings and biomaterials. Angew. Chem., Int. Ed. 2014, 53, 8004–8031. 10.1002/anie.201400546. [DOI] [PubMed] [Google Scholar]
  5. Xiong W.; Ren C.; Tian M.; Yang X.; Li J.; Li B. Complex coacervation of ovalbumin-carboxymethylcellulose assessed by isothermal titration calorimeter and rheology: Effect of ionic strength and charge density of polysaccharide. Food Hydrocolloids 2017, 73, 41–50. 10.1016/j.foodhyd.2017.06.031. [DOI] [Google Scholar]
  6. Record M. T.; Anderson C. F.; Lohman T. M. Thermodynamic analysis of ion effects on the binding and conformational equilibria of proteins and nucleic acids: the roles of ion association or release, screening, and ion effects on water activity. Q. Rev. Biophys. 1978, 11, 103–178. 10.1017/s003358350000202x. [DOI] [PubMed] [Google Scholar]
  7. Velazquez-Campoy A.; Freire E. Isothermal titration calorimetry to determine association constants for high-affinity ligands. Nat. Protoc. 2006, 1, 186–191. 10.1038/nprot.2006.28. [DOI] [PubMed] [Google Scholar]
  8. Lindman S.; Lynch I.; Thulin E.; Nilsson H.; Dawson K. A.; Linse S. Systematic Investigation of the Thermodynamics of HSA Adsorption toN-iso-Propylacrylamide/N-tert-Butylacrylamide Copolymer Nanoparticles. Effects of Particle Size and Hydrophobicity. Nano Lett. 2007, 7, 914–920. 10.1021/nl062743+. [DOI] [PubMed] [Google Scholar]
  9. Kayitmazer A. B. Thermodynamics of complex coacervation. Adv. Colloid Interface Sci. 2017, 239, 169–177. 10.1016/j.cis.2016.07.006. [DOI] [PubMed] [Google Scholar]
  10. Niedzwiecka A.; Stepinski J.; Darzynkiewicz E.; Sonenberg N.; Stolarski R. Positive Heat Capacity Change upon Specific Binding of Translation Initiation Factor eIF4E to mRNA 5’ Cap. Biochemistry 2002, 41, 12140–12148. 10.1021/bi0258142. [DOI] [PubMed] [Google Scholar]
  11. Datta K.; LiCata V. J. Thermodynamics of the binding of Thermus aquaticus DNA polymerase to primed-template DNA. Nucleic Acids Res. 2003, 31, 5590–5597. 10.1093/nar/gkg774. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Datta K.; Wowor A. J.; Richard A. J.; LiCata V. J. Temperature dependence and thermodynamics of Klenow polymerase binding to primed-template DNA. Biophys. J. 2006, 90, 1739–1751. 10.1529/biophysj.105.071837. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kozlov A. G.; Lohman T. M. Large contributions of coupled protonation equilibria to the observed enthalpy and heat capacity changes for ssDNA binding toEscherichia coli SSB protein. Proteins 2000, 41, 8–22. . [DOI] [PubMed] [Google Scholar]
  14. Welsch N.; Becker A. L.; Dzubiella J.; Ballauff M. Core-shell microgels as smart carriers for enzymes. Soft Matter 2012, 8, 1428–1436. 10.1039/c1sm06894f. [DOI] [Google Scholar]
  15. Geschwindner S.; Ulander J.; Johansson P. Ligand binding thermodynamics in drug discovery: still a hot tip?. J. Med. Chem. 2015, 58, 6321–6335. 10.1021/jm501511f. [DOI] [PubMed] [Google Scholar]
  16. Xu X.; Ran Q.; Dey P.; Nikam R.; Haag R.; Ballauff M.; Dzubiella J. Counterion-release entropy governs the inhibition of serum proteins by polyelectrolyte drugs. Biomacromolecules 2018, 19, 409–416. 10.1021/acs.biomac.7b01499. [DOI] [PubMed] [Google Scholar]
  17. Dernedde J.; Rausch A.; Weinhart M.; Enders S.; Tauber R.; Licha K.; Schirner M.; Zugel U.; von Bonin A.; Haag R. Dendritic polyglycerol sulfates as multivalent inhibitors of inflammation. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 19679–19684. 10.1073/pnas.1003103107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Khandare J.; Mohr A.; Calderón M.; Welker P.; Licha K.; Haag R. Structure-biocompatibility relationship of dendritic polyglycerol derivatives. Biomaterials 2010, 31, 4268–4277. 10.1016/j.biomaterials.2010.02.001. [DOI] [PubMed] [Google Scholar]
  19. Weinhart M.; Gröger D.; Enders S.; Riese S. B.; Dernedde J.; Kainthan R. K.; Brooks D. E.; Haag R. The Role of Dimension in Multivalent Binding Events: Structure-Activity Relationship of Dendritic Polyglycerol Sulfate Binding to L-Selectin in Correlation with Size and Surface Charge Density. Macromol. Biosci. 2011, 11, 1088–1098. 10.1002/mabi.201100051. [DOI] [PubMed] [Google Scholar]
  20. Schneider T.; Welker P.; Licha K.; Haag R.; Schulze-Tanzil G. Influence of dendritic polyglycerol sulfates on knee osteoarthritis: an experimental study in the rat osteoarthritis model. BMC Musculoskeletal Disord. 2015, 16, 387. 10.1186/s12891-015-0844-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Boreham A.; Pikkemaat J.; Volz P.; Brodwolf R.; Kuehne C.; Licha K.; Haag R.; Dernedde J.; Alexiev U. Detecting and quantifying biomolecular interactions of a dendritic polyglycerol sulfate nanoparticle using fluorescence lifetime measurements. Molecules 2015, 21, 22. 10.3390/molecules21010022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Maysinger D.; Gröger D.; Lake A.; Licha K.; Weinhart M.; Chang P. K.-Y.; Mulvey R.; Haag R.; McKinney R. A. Dendritic polyglycerol sulfate inhibits microglial activation and reduces hippocampal CA1 dendritic spine morphology deficits. Biomacromolecules 2015, 16, 3073–3082. 10.1021/acs.biomac.5b00999. [DOI] [PubMed] [Google Scholar]
  23. Sousa-Herves A.; Würfel P.; Wegner N.; Khandare J.; Licha K.; Haag R.; Welker P.; Calderón M. Dendritic polyglycerol sulfate as a novel platform for paclitaxel delivery: pitfalls of ester linkage. Nanoscale 2015, 7, 3923–3932. 10.1039/c4nr04428b. [DOI] [PubMed] [Google Scholar]
  24. Xu X.; Ran Q.; Haag R.; Ballauff M.; Dzubiella J. Charged dendrimers revisited: Effective charge and surface potential of dendritic polyglycerol sulfate. Macromolecules 2017, 50, 4759–4769. 10.1021/acs.macromol.7b00742. [DOI] [Google Scholar]
  25. Haag R.; Sunder A.; Stumbé J.-F. An approach to glycerol dendrimers and pseudo-dendritic polyglycerols. J. Am. Chem. Soc. 2000, 122, 2954–2955. 10.1021/ja994363e. [DOI] [Google Scholar]
  26. Ramanadham M.; Sieker L. C.; Jensen L. H. Refinement of triclinic lysozyme: II. The method of stereochemically restrained least squares. Acta Crystallogr., Sect. B: Struct. Sci. 1990, 46, 63–69. 10.1107/s0108768189009195. [DOI] [PubMed] [Google Scholar]
  27. Visakh P. M.; Bayraktar O.; Picó G. A.. Polyelectrolytes: Thermodynamics and Rheology; Springer, 2014; pp 19–86. [Google Scholar]
  28. Record M. T.; Lohman T. M.; de Haseth P. Ion effects on ligand-nucleic acid interactions. J. Mol. Biol. 1976, 107, 145–158. 10.1016/s0022-2836(76)80023-x. [DOI] [PubMed] [Google Scholar]
  29. Yu S.; Xu X.; Yigit C.; van der Giet M.; Zidek W.; Jankowski J.; Dzubiella J.; Ballauff M. Interaction of human serum albumin with short polyelectrolytes: a study by calorimetry and computer simulations. Soft Matter 2015, 11, 4630–4639. 10.1039/c5sm00687b. [DOI] [PubMed] [Google Scholar]
  30. Ran Q.; Xu X.; Dey P.; Yu S.; Lu Y.; Dzubiella J.; Haag R.; Ballauff M. Interaction of human serum albumin with dendritic polyglycerol sulfate: Rationalizing the thermodynamics of binding. J. Chem. Phys. 2018, 149, 163324. 10.1063/1.5030601. [DOI] [PubMed] [Google Scholar]
  31. Lumry R.; Rajender S. Enthalpy-entropy compensation phenomena in water solutions of proteins and small molecules: A ubiquitous properly of water. Biopolymers 1970, 9, 1125–1227. 10.1002/bip.1970.360091002. [DOI] [PubMed] [Google Scholar]
  32. Eftink M. R.; Anusiem A. C.; Biltonen R. L. Enthalpy-entropy compensation and heat capacity changes for protein-ligand interactions: general thermodynamic models and data for the binding of nucleotides to ribonuclease A. Biochemistry 1983, 22, 3884–3896. 10.1021/bi00285a025. [DOI] [PubMed] [Google Scholar]
  33. Cooper A.; Johnson C. M.; Lakey J. H.; Nöllmann M. Heat does not come in different colours: entropy-enthalpy compensation, free energy windows, quantum confinement, pressure perturbation calorimetry, solvation and the multiple causes of heat capacity effects in biomolecular interactions. Biophys. Chem. 2001, 93, 215–230. 10.1016/s0301-4622(01)00222-8. [DOI] [PubMed] [Google Scholar]
  34. Sedlmeier F.; Horinek D.; Netz R. R. Entropy and enthalpy convergence of hydrophobic solvation beyond the hard-sphere limit. J. Chem. Phys. 2011, 134, 055105. 10.1063/1.3530585. [DOI] [PubMed] [Google Scholar]
  35. Chodera J. D.; Mobley D. L. Entropy-enthalpy compensation: role and ramifications in biomolecular ligand recognition and design. Annu. Rev. Biophys. 2013, 42, 121–142. 10.1146/annurev-biophys-083012-130318. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Fukada H.; Takahashi K. Enthalpy and heat capacity changes for the proton dissociation of various buffer components in 0.1 M potassium chloride. Proteins 1998, 33, 159–166. . [DOI] [PubMed] [Google Scholar]
  37. MicroCal . ITC Data Analysis in Origin: Tutorial Guide, 2004. [Google Scholar]
  38. Decher G. Fuzzy Nanoassemblies: Toward Layered Polymeric Multicomposites. Science 1997, 277, 1232–1237. 10.1126/science.277.5330.1232. [DOI] [Google Scholar]
  39. Decher G.; Schlenoff J. B.. Multilayer Thin Films: Sequential Assembly of Nanocomposite Materials, Second Edition; Wiley, 2012. [Google Scholar]
  40. Henzler K.; Haupt B.; Lauterbach K.; Wittemann A.; Borisov O.; Ballauff M. Adsorption of β-Lactoglobulin on Spherical Polyelectrolyte Brushes: Direct Proof of Counterion Release by Isothermal Titration Calorimetry. J. Am. Chem. Soc. 2010, 132, 3159–3163. 10.1021/ja909938c. [DOI] [PubMed] [Google Scholar]
  41. Horn J. R.; Russell D.; Lewis E. A.; Murphy K. P. van’t Hoff and Calorimetric Enthalpies from Isothermal Titration Calorimetry: Are There Significant Discrepancies?. Biochemistry 2001, 40, 1774–1778. 10.1021/bi002408e. [DOI] [PubMed] [Google Scholar]
  42. Klebe G. Applying thermodynamic profiling in lead finding and optimization. Nat. Rev. Drug Discovery 2015, 14, 95–110. 10.1038/nrd4486. [DOI] [PubMed] [Google Scholar]
  43. Naghibi H.; Tamura A.; Sturtevant J. M. Significant discrepancies between van’t Hoff and calorimetric enthalpies. Proc. Natl. Acad. Sci. U.S.A. 1995, 92, 5597–5599. 10.1073/pnas.92.12.5597. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Haidacher D.; Vailaya A.; Horvath C. Temperature effects in hydrophobic interaction chromatography. Proc. Natl. Acad. Sci. U.S.A. 1996, 93, 2290–2295. 10.1073/pnas.93.6.2290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Becker A. L.; Welsch N.; Schneider C.; Ballauff M. Adsorption of RNase A on cationic polyelectrolyte brushes: a study by isothermal titration calorimetry. Biomacromolecules 2011, 12, 3936–3944. 10.1021/bm200954j. [DOI] [PubMed] [Google Scholar]
  46. Kozlov A. G.; Lohman T. M. Calorimetric studies of E. coli SSB protein-single-stranded DNA interactions. Effects of monovalent salts on binding enthalpy 1 1Edited by D. Draper. J. Mol. Biol. 1998, 278, 999–1014. 10.1006/jmbi.1998.1738. [DOI] [PubMed] [Google Scholar]
  47. Gallagher K.; Sharp K. Electrostatic contributions to heat capacity changes of DNA-ligand binding. Biophys. J. 1998, 75, 769–776. 10.1016/s0006-3495(98)77566-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Loladze V. V.; Ermolenko D. N.; Makhatadze G. I. Heat capacity changes upon burial of polar and nonpolar groups in proteins. Protein Sci. 2008, 10, 1343–1352. 10.1110/ps.370101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Marini M. A.; Berger R. L.; Lam D. P.; Martin C. J. Thermal titrimetric evaluation of the heats of ionization of the commonly occurring amino acids and their derivatives. Anal. Biochem. 1971, 43, 188–198. 10.1016/0003-2697(71)90124-2. [DOI] [PubMed] [Google Scholar]
  50. Türk H.; Haag R.; Alban S. Dendritic polyglycerol sulfates as new heparin analogues and potent inhibitors of the complement system. Bioconjugate Chem. 2004, 15, 162–167. 10.1021/bc034044j. [DOI] [PubMed] [Google Scholar]
  51. Wiseman T.; Williston S.; Brandts J. F.; Lin L.-N. Rapid measurement of binding constants and heats of binding using a new titration calorimeter. Anal. Biochem. 1989, 179, 131–137. 10.1016/0003-2697(89)90213-3. [DOI] [PubMed] [Google Scholar]
  52. Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
  53. Noel J. K.; Whitford P. C.; Sanbonmatsu K. Y.; Onuchic J. N. SMOG@ctbp: simplified deployment of structure-based models in GROMACS. Nucleic Acids Res. 2010, 38, W657–W661. 10.1093/nar/gkq498. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao8b01493_si_001.pdf (271.4KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES