Abstract

1H NMR pulsed gradient spin echo attenuation and water density profile analysis by magnetic resonance imaging are both used to determine the mobility of water molecules confined within a porous network of compacted kaolinite clay sample (total porosity of ∼50%). These two complementary experimental procedures efficiently probe molecular diffusion within time scales varying between milliseconds and few hours, filling the gap between the time scale of diffusion dynamics measured by traditional quasi elastic neutron scattering and through-diffusion methods. Furthermore, magnetic resonance imaging is a nondestructive investigation tool that is able to assess the effect of the local structure on the macroscopic mobility of the diffusing probe.
I. Introduction
Clay minerals are ubiquitous at the surface of the earth and play important roles in a large variety of environmental applications, including pollutant retention1−5 and nuclear waste storing,6,7 by exploiting their physicochemical properties (low hydraulic conductivity,6 large anisotropy,8 high specific surface9 and adsorbing power,1,2,4,10 ionic exchange capacity9). In this context, numerous studies have been performed to determine the mobility of water molecules9,11−22 and ions16,22−29 confined within the complex porous network of dense clay samples. For this purpose, quasi elastic neutron scattering13,18,19 (QENS) and through-diffusion17,21,28,30,31 measurements are the two complementary approaches generally used to quantify the mobility of water molecules confined within the clay porous network. While QENS is an ideal probe of local water motions performed during a limited diffusion period (less than 1 ns), through-diffusion experiment probes macroscopic displacements of confined fluids at a time scale larger than a few minutes. Because of the multi-scale organization of clay aggregates within the dense samples, it appears useful to investigate fluid mobility at intermediate time scales. Such investigations are necessary to efficiently relate the apparent macroscopic mobility of the confined fluid to the organization of the clay sample. For this purpose, we investigate the potentialities of the two applications of NMR, i.e., measurement of the water self-diffusion tensor by using pulsed gradient spin echo (PGSE) attenuation11,12,16,24,32−37 and analysis of time evolution of water density profiles by exploiting magnetic resonance imaging33,38 (MRI). This approach contributes significantly to characterize the multi-scale mobility of confined water molecules because PGSE-NMR adequately probes diffusion times larger than 1 ms, whereas diffusion times larger than a few seconds are easily investigated by MRI, thus filling the above-mentioned gap between the time scales investigated by QENS and through-diffusion experiments. Previous studies have demonstrated the applicability of PGSE-NMR11,12 and MRI39,40 to investigate the mobility of water molecules within aqueous dispersions and dense pastes of synthetic minerals. The application of the same NMR experiments for dense clay samples is never obvious because of the presence of iron within natural clay particles, strongly enhancing the NMR relaxation14 of the nuclear magnetization pertaining to the protons of the confined water molecules. To settle this question, we selected natural clay (kaolinite) whose composition17 (0.039 iron per unit cell) and size distribution8 were already characterized. Furthermore, by contrast with other natural clays (like montmorillonite), kaolinite (like illite) is a nonswelling clay mineral, thus avoiding the occurrence of some interlayer porosity after saturation of the clay sample by water molecules. As a consequence, the porous network accessible to water molecules is limited to interparticle porosity.
In this study, 1H PGSE-NMR attenuation measurement is first used to determine the components of the tensor describing the water self-diffusion within the water-saturated sample of kaolinite. MRI is then used to determine the water concentration profiles after the addition of a controlled amount of heavy water on the top of the water-saturated clay sample. The exchange between the added heavy water and initially confined water molecules is quantified by integrating the water concentration profiles whose asymptotic limit may be used to determine the porosity of the clay sample. Numerical modeling performed by Brownian dynamics (BD)41 is finally used to interpret the observed exchange kinetics on the basis of the clay sample porosity and the longitudinal component of the water self-diffusion tensor previously measured by PGSE-NMR, thus demonstrating the agreement between both experimental procedures.
II. Materials and Methods
II.1. Sample Preparation
The kaolinite clay sample (i.e., KGa-2 kaolinite reference from the Source Clay Repository of The Clay Minerals Society) was used to prepare a cylindrical compacted clay sample (diameter 6.5 mm, height 12.3 mm) for NMR measurements. For this purpose, the original kaolinite sample was Na saturated using three saturation cycles in a 1 mol/L NaCl solution, washed in distilled water, and dried at room conditions. The obtained powder was then placed within a poly(tetrafluoroethylene) (Teflon) cylinder fitting the size of the NMR detection coil and underwent a uniaxial compression to reach a porosity ϕ value close to ∼0.5. Information on the chemical composition and properties of the kaolinite sample are available in the literature.8 Transmission electron microscopy (TEM) images (see Figure 1a,b) are recorded after the dispersion of the sample into ethanol to illustrate the size distribution of the stacks composed of individual clay platelets. The porosity of the dry clay sample (ϕ = 0.52) is determined by helium pycnometry, corresponding to an average grain density of 2.75 g/cm3. The PGSE-NMR experiments are first performed with the water-saturated clay sample. The kinetics of the water/heavy water exchange is determined by 1H MRI profile analysis after the addition of 0.23 mL of D2O on the top of the hydrated clay sample. The compactness of the clay sample was obtained by uniaxial compression to reach the same porosity (ϕ ∼ 0.5). The clay sediment is carefully saturated by water and equilibrated during 2–3 days before performing PGSE measurements. However, no boundary condition is applied to the sediment after compression. As a consequence, the porosity of the clay sample must be determined independently by helium pycnometry for the dry sample and after hydration by MRI. Some difference is expected to occur because no boundary is applied to restrict the swelling of the clay sample.
Figure 1.
(a, b) TEM images of the dispersed kaolinite sample at two different magnifications.
II.2. 1H NMR Measurements
NMR measurements were performed using a Bruker DSX100 Bruker spectrometer with a static field of 2.35 T and equipped with a saddle detection coil. A typical pulse duration of 5 μs is required for transferring the equilibrium longitudinal magnetization into the detection plane perpendicular to the static magnetic field B0 (also called π/2 pulse). Figure 2 illustrates the pulse sequence used to perform the PGSE-NMR attenuation measurements.32,33 The encoding of transverse magnetization is performed by a pulse sequence composed of an initial π/2 pulse used to create transverse magnetization, a set of bipolar field gradients (duration δ, strength G) applied along any desired direction, and a final π/2 pulse to transfer back magnetization in the longitudinal direction. After the evolution period (Δ), transverse magnetization is refocused by using a pulse sequence similar to the encoding one, but with opposite field gradients. NMR relaxation times are critical parameters limiting the feasibility of this PGSE-NMR experiment. Because of the paramagnetic impurities17 (iron) present in the atomic network of kaolinite, the NMR relaxation time of the longitudinal magnetization of the confined water molecules (T1 = 0.053 s) is fifty times smaller14 than that of bulk water (T1 = T2 ≈ 3 s). Furthermore, the transverse relaxation time of the same confined water molecules (T2 = 1.2 × 10–3 s) is again reduced by more than 1 order of magnitude because confinement42−45 is responsible for large differences between the NMR relaxation rates of liquids (T2 < T1). The purpose of the stimulated echo32,33 used in our PGSE-NMR experiment is to transfer the transverse magnetization encoded by the first set of pulsed gradient into the longitudinal direction parallel to the static magnetic field B0. As illustrated in Figure 2, the stimulated echo allows them to probe the mobility of the confined water molecules during roughly 150 ms since the longitudinal magnetization becomes negligible after the diffusion time Δmax ∼ 3T1. Another limitation arises from the time required to build the field gradients (typically 60 μs). As a consequence, the duration (4τ = 3.04 ms) of the coding and refocusing pulse sequences (see Figure 2) reaches milliseconds (i.e., the order of magnitude of the transverse relaxation rate T2), leading to important attenuation of the NMR magnetization according to the exponential law exp(−4τ/T2) = 0.08. Finally, the intensity of the NMR signal varies according to the relationship32,33
| 1 |
where, q = γδG/π, γ is the gyromagnetic ratio (2.6752 × 108 rad/s for 1H), G is the strength of the field gradient (see Figure 2) and e⃗G its director, D is the self-diffusion tensor, and δ, Δ, and τ are time delays illustrated in Figure 2. Since our PGSE-NMR echo attenuations are recorded for a unique set of time delays (δ = 500 μs, Δ = 20 ms, and τ = 760 μs), the components of the self-diffusion tensor are obtained by fitting the attenuation of the NMR signal measured for a set of strengths of the field gradient G according to a Gaussian propagator33
| 2 |
This Gaussian propagator of self-diffusion33 is equivalent to the intermediate scattering function46 probed by neutron scattering experiments (QENS). The maximum resolution of spatial domains probed by these PGSE-NMR measurements is given by the maximum strength of the magnetic field gradient33 (Gmax = 1.6 T/m)
| 3 |
where, q is equivalent to the wave vectors probed by QENS.
Figure 2.
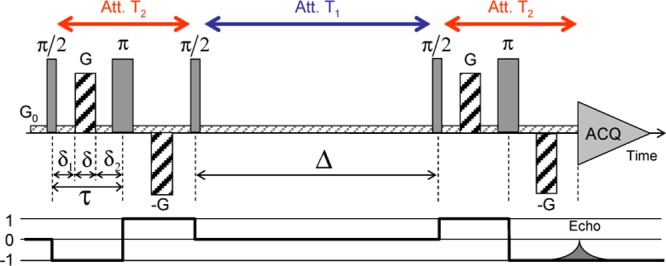
Schematic view of the pulse sequence used to perform pulsed gradient spin echo (PGSE-NMR) attenuation measurements. Details on the time delays, pulse durations, and strength of the magnetic field gradients are given in the text (see Section II.2).
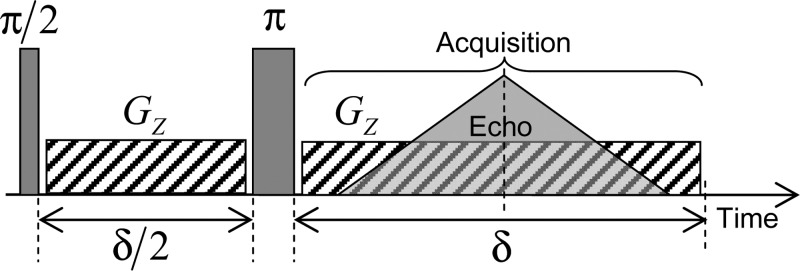
1H magnetic resonance imaging is also used to study the exchange between the initially confined water molecules and excess bulk heavy water added to the saturated clay samples. Figure 3 illustrates the pulse sequence used for these MRI experiments.33 After an initial π/2 excitation pulse, a magnetic field gradient (noted GZ) is applied during the time period δ/2 along the vertical direction (Oz) corresponding to the cylindrical axis of the clay sample. Inversion pulse (noted π) is then applied and the same field gradient GZ is applied during the evolution time δ = 2.56 ms with a simultaneous acquisition of the NMR signal. This sequence is selected to generate an echo of the NMR signal after the evolution period δ/2, leading again to a noticeable attenuation (exp(−δ/(2T2)) ≈ 0.34) of the NMR signal pertaining to the confined water molecules without significantly altering the NMR intensity of free water (see T2 values reported above). Our MRI measurements were performed for an evolution period δ composed of 256 elementary time steps of 10 μs. As the time domain is used to sample the NMR signal, the corresponding frequency domain obtained by Fourier transform is also composed of 256 elementary frequency steps. As a consequence, the resulting longitudinal MRI profiles are digitalized into 256 superposed sheets. To easily investigate the water molecules located in the hydrated clay sample (length L1 = 12.3 mm) and the amount of added heavy water (length L2 = 7 mm), we want to probe a total sample length of 25 mm, leading to a spatial resolution of 97.7 μm (since resolution = 25/256 mm). This spatial resolution corresponds to a wave vector q of 1.024 × 104 m–1 obtained by applying a magnetic field gradient of 0.094 T/m (see eq 3).
Figure 3.
Schematic view of the pulse sequence used to perform magnetic resonance imaging (MRI) of the water concentration profiles inside the compacted kaolinite clay sample (see text Section II.2).
II.3. Numerical Simulations
Numerical simulations of Brownian dynamics41 (BD) are used to analyze the macroscopic exchange between the water molecules initially confined within the clay sample and the added heavy water as investigated by profile analysis obtained by 1H MRI. To our knowledge, determination of water diffusivity by direct analysis of the time evolution of the water concentration profiles is not possible. For this reason, we proceeded to numerical simulations of BD to perform a quantitative comparison between the experimental and numerical data, thus extending to hours the time-scale initially probed by PGSE-NMR spectroscopy (typically a few milliseconds). For this purpose, N1 H2O molecular probes (N1 = 386 571) are uniformly distributed within an ideal parallelepiped (longitudinal length L1 = 12.3 mm, section S1 = 13.75 mm2) in contact through its upper surface with another parallelepiped (longitudinal length L2 = 7 mm, section S1 = 25 mm2) containing N2 D2O molecular probes (N2 = 400 000). These dimensions and water contents have been selected to reproduce the volumetric ratios between the diffusing spaces inside the clay sample (labeled 1) and the added bulk water (labeled 2). The self-diffusion coefficients of both water and heavy water molecules are set equal to the value determined by 1H PGSE-NMR attenuation measurements, whereas their values in bulk water are set equal to 2.1 × 10–9 m2/s, in agreement with the available experimental data. Simple reflecting conditions are applied when a molecular probe hits any wall of the simulation cell except for the surface connecting the two independent sub-volumes: when a probe, initially diffusing in the cell corresponding to the clay sample (labeled 1), hits the separating surface, its transfer to the cell labeled 2 is always considered. By contrast, a molecular probe initially diffusing in the cell corresponding to bulk water (labeled 2) and hitting the separating surface will be considered to potentially transfer to the clay sample with a probability equal to the porosity of the clay sample. Adequately formulating the condition for accepting these potential transfers between the two sub-cells is the only difficulty for modeling such water exchange between the two sub-cells with different sizes, water concentrations, and mobilities. An interesting suggestion was the use of detailed balance conditions.47 Unfortunately, such a procedure is valid only for describing stationary states.47 By contrast, our problem is typically a transient dynamical process for which detailed balance condition becomes inadequate. For this purpose, we selected to use a systematic control, at each step of the BD iteration, of the water flux across the separating interface between the two sub-cells. We simply impose that the total number of H2O and D2O molecules leaving a given sub-cell must be perfectly compensated by the same number of H2O and D2O molecules leaving the other sub-cell. Such condition corresponds to some extension, at the microscopic scale, of the macroscopic incompressibility of liquid water. An equivalent procedure was already used to describe by Brownian dynamics the ionic exchange28 between ions confined within clay interlayers and freely diffusing in aqueous solution.
The displacement of the molecular probes (labeled i) is described by the Langevin equation41
| 4 |
where, mi and ξi are respectively the molecular mass and friction coefficient, and R⃗i(t) is a random force resulting from thermal collisions within the liquid. This random force must satisfy statistical requirements: it must be Markovian and time independent (see eq 5a), with zero mean (eq 5b), without correlation with the velocities (eq 5c), and distributed along a Gaussian law (eq 5d)
| 5a |
| 5b |
| 5c |
| 5d |
where, P(|R⃗i|) is the distribution law of the modulus of the random displacements, k is the Boltzmann constant, and T is the temperature. Equation 5a results from the fluctuation–dissipation theorem ensuring the balance between the increase of the velocities induced by the random force and its decrease resulting from the intermolecular friction. Various algorithms have been proposed to solve the set of eqs 4 and 5a–5d, depending on the ratio between the friction coefficient (ξi) and the time step (Δt) selected to simulate the molecular trajectories. If the time step is much larger than the velocity correlation time (i.e., ξiΔt ≫ 1), the solution of eqs 4 and 5a–5d becomes41
| 6a |
the new random force R⃗i also satisfies Gaussian distribution law with zero mean and standard deviation given by
| 6b |
where, Di is the local self-diffusion coefficient of the molecular probes. We can use this simplified equation since the time step (Δt) used to integrate eq 6a is equal to 1 s, while the friction coefficients (ξi) are equal to 15 × 1013 and 6.55 × 1013 s–1 for confined and bulk water, respectively. The average molecular displacements (see eq 6b) of the confined water molecules reach 45 μm, i.e., are compatible with the spatial resolution probed by our MRI analysis of the water density profiles.
III. Results and Discussion
Figure 4 illustrates the results obtained by the measurements of the PGSE-NMR attenuation of the 1H NMR signal for the water saturated sample of kaolinite. As detailed in eq 2, the decrease in the relative intensity of the NMR signal as a function of the strength of the magnetic field gradient Gi is perfectly described by a Gaussian relationship,33 leading to the apparent water self-diffusion coefficient along any direction Oxi of the applied gradient Gi. This field gradient is constructed along six non-collinear directors48−51 noted e⃗1 = (1,0,0), e⃗2 = (0,1,0), e⃗3 = (0,0,1), e⃗4 = (1,1,0), e⃗5 = (1,0,1), and e⃗6 = (1,1,0), where the longitudinal director e⃗3 is parallel to the cylindrical axis of the clay sample (i.e., Oz). The six corresponding components of the water self-diffusion tensor are easily determined (see Figure 4) and the principal axes describing the water mobility are identified by tensor diagonalization.48 A small difference is then detected between the water self-diffusion coefficient in the direction parallel {Dlong = 0.92 ± 0.02 × 10–9 m2/s} and perpendicular {Dtrans = 1.05 ± 0.02 × 10–9 m2/s} to the cylinder axis which coincides with the compression axis of the dense clay sample (see Section II.2). By dividing the self-diffusion coefficient of bulk water (D0 = 2.1 × 10–9 m2/s) by its value measured within the dense sample, we obtain an evaluation of the tortuosity52,53 of the clay, noted θ, i.e., θ = 2.28 ± 0.05 in the longitudinal direction and θ = 2.00 ± 0.05 in the direction perpendicular to the cylinder axis.
Figure 4.
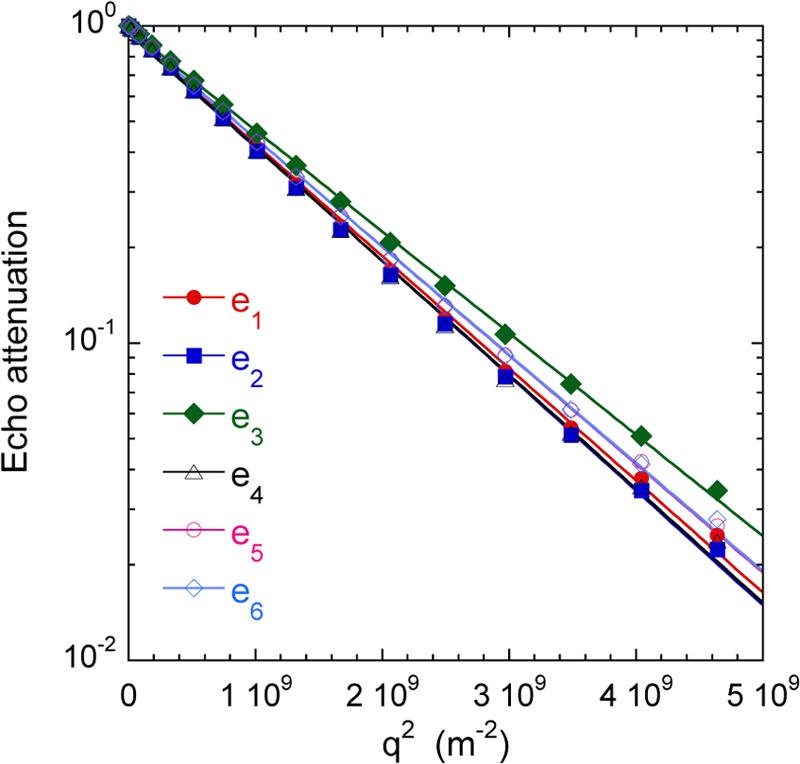
Water self-diffusion propagators measured within the saturated clay sample. More details on the selected diffusion directors e⃗i are given in Section III, leading to the components of the self-diffusion tensor D1 = 1.041 × 10–9 m2/s, D2 = 1.062 × 10–9 m2/s, D3 = 0.918 × 10–9 m2/s, D4 = 1.067 × 10–9 m2/s, D5 = 0.991 × 10–9 m2/s, and D6 = 0.992 × 10–9 m2/s.
It should be interesting to perform diffusion measurements at various time delay Δ to probe the structural properties of the porous network.33 As displayed in Figure 5, the measured self-diffusion coefficient is independent of the time delay Δ in the range of accessible values (i.e., between 2 and 150 ms). As a consequence, the water self-diffusion coefficient measured by PGSE-NMR describes the macroscopic mobility of the water molecules diffusing within the porous network of the dense clay sediment.
Figure 5.
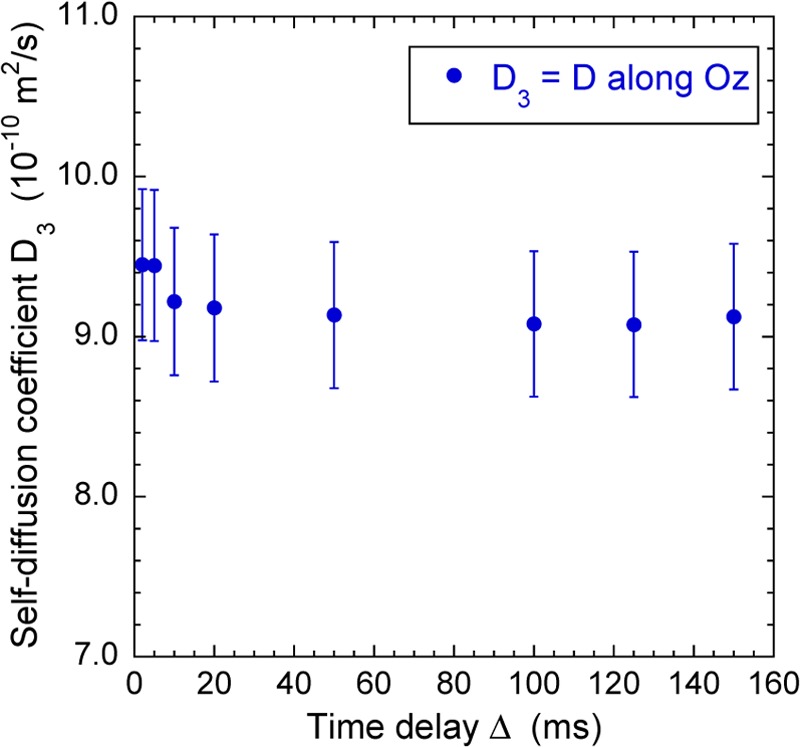
Variations of the water self-diffusion coefficient D3 (diffusion along the direction Oz) measured within the saturated clay sample as a function of the time delay Δ (see the text).
The water concentration profiles are measured by 1H MRI after the addition of bulk heavy water on the top of the water saturated clay sample (see Section II.2). Typical time evolution of the water profiles is illustrated in Figure 6a. As for PGSE-NMR spectroscopy, the intensity of the NMR signals is attenuated by the longitudinal and transverse relaxation times of the NMR probes. Firstly, as explained in Section II.2, because of the large difference between their transverse relaxation times, the concentration profiles of bulk (T2 = T1 = 3 s) and confined (T2 = 1.2 × 10–3 s) water molecules cannot be directly compared. Secondly, the MRI signal results from the averaging of 16 scans with a recycling delay of 0.5 s to efficiently probe the kinetics of the water exchange between the two media. Since the longitudinal relaxation time of the confined water molecule is short enough (T1 = 0.053 s), each scan records 100% of magnetization pertaining to the protons from the confined water molecules. This condition is not fulfilled by the protons from the bulk water (T1 = 3 s) whose magnetization is then saturated by this short recycling delay. As a consequence, quantitative analysis must focus on the relative intensity of the water concentration profiles within the clay sample. Next problem occurs because the total size of the sample slightly exceeds the spatial domain of complete excitation and detection probed by the NMR coil. For this purpose, we must discard magnetization pertaining to water molecules located at distances smaller than 8 mm from the bottom of the detection window whose magnetization is not fully detected. Finally, artifacts also occur at the boundary between the two media, further excluding from the profile analysis the contribution from water molecules located at distances smaller than 2 mm from the interface between the clay sample and the bulk liquid. We are not totally sure about the physical origin of the reported artifact, already detected within dilute clay dispersions.39 We expect that water molecules located in the bulk phase near the upper surface of the clay sediment exhibit some increase in their longitudinal NMR relaxation rate because of the proximity of the paramagnetic impurities (iron) of kaolinite. As a consequence, saturation of their magnetization is reduced with reference to that of “free” bulk water. Another explanation could be the contrast of the magnetic susceptibility between bulk water and the hydrated clay sediment. Obviously, all these artifacts affecting the experimental data are totally excluded from the numerical data, restricting the sample area used for a direct comparison between the data obtained by MRI NMR measurements and BD numerical simulations.
Figure 6.
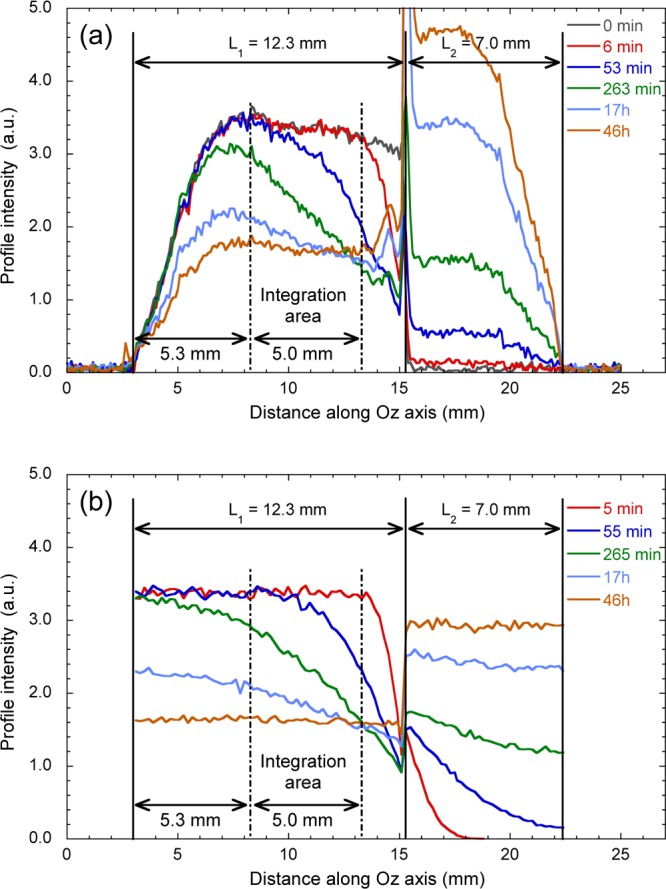
Time evolution of the water concentration profiles: (a) measured by magnetic resonance imaging after the addition of bulk heavy water on the top of the water saturated sample and (b) obtained by numerical simulations of Brownian dynamics (see the text).
Figure 7 illustrates the evolution of the fraction of confined water molecules obtained by integrating the water concentration profiles between 8.3 and 13.3 mm from the bottom of the detection window. As displayed in Figure 7, the experimental data are fitted by an empirical biexponential law, giving two characteristic times {(7800 ± 200) and (39000 ± 2000) s} quantifying the time evolution of the integrated water concentration profiles (see Figure 7). These two time scales have no physical meaning since the biexponential fit is simply used for allowing quantitative comparison between the experimental and numerical data. Figure 7 also displays a long-time asymptotic limit (0.49 ± 0.01) which may be used to evaluate the porosity (noted ϕ) of the clay sample since it must satisfy the relationship
| 7 |
where, L1 (12.3 mm) and L2 (7 mm) are the lengths occupied within the poly(tetrafluoroethylene) (Teflon) cylinder (see Section II.3 and Figure 6a) by the clay sample and the added heavy water. The corresponding porosity (ϕ = 0.55 ± 0.01) is compatible with the value measured by helium pycnometry on the dry clay (ϕ = 0.52). This limited increase in the sample porosity results from the swelling of the dry clay sediment since hydration is performed without applying any boundary condition (see Section II.1).
Figure 7.
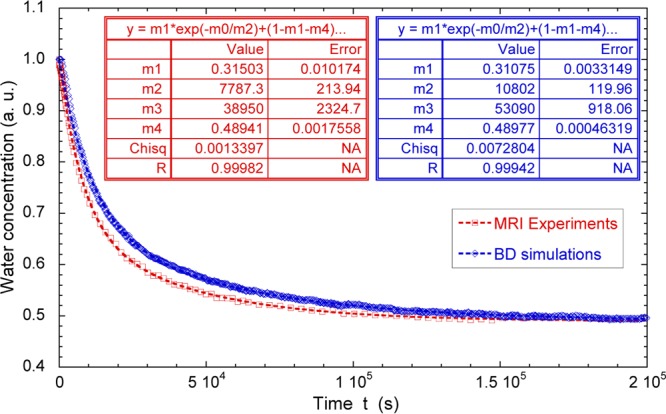
Direct comparison of the time evolutions of the measured and simulated numbers of confined water molecules. Experimental and numerical data are fitted by a biexponential law: f(t) = m1 exp(−t/m2) + (1 – m1 – m4) exp(−t/m3) + m4.
The initial water concentration profile displayed in Figure 6a clearly exhibits a gradual decrease in the signal intensity in the range of complete detection of the 1H magnetization by the NMR probe, i.e., at positions above 8.3 mm from the bottom of the detection window. Such behavior results from a gradient of clay concentration within the compacted sample, leading to some heterogeneity of its porosity. This heterogeneity is the fingerprint of the sample preparation performed by uniaxial compression of the clay powder (see Section II.1). To probe its impact on the water exchange process, we performed numerical simulations of Brownian dynamics to describe the exchange between bulk heavy water and the water molecules confined within the perfectly homogeneous sample (see Section II.3). The corresponding concentration profiles are plotted in Figure 6b, in good agreement with the experimental data (see Figure 6a). More quantitative comparison is given by the concentration profiles integrated over the same spatial range than the experimental data. As displayed in Figure 7, experimental and simulated data exhibit fair agreement without using any fitted parameters. Brownian dynamics simulations slightly underestimate the kinetics of water exchange between the clay sample and the excess heavy water, indicating a limited effect of the sample heterogeneity on the water exchange process. That agreement also illustrates the compatibility between 1H PGSE-NMR attenuation and MRI concentration profile analysis to probe water mobility within dense samples of natural clays. This agreement a posteriori validates our experimental procedure: by carefully selecting the integration domain of the water concentration profiles (see above), the clay sample does not necessarily need to fit the spatial domain of complete excitation of the NMR detection coil.
Although this study concerns only experimental NMR measurements performed for a single clay sample, we feel justified to compare the water mobility measured by 1H PGSE-NMR within kaolinite clay and that evaluated by HDO through diffusion17,21,31 and PGSE-NMR37 within porous networks of various granular materials. While PGSE-NMR experiments directly quantify the intrinsic self-diffusion coefficient33D of the fluid confined within various porous networks,12,16,24,37,39,40,54,55 through-diffusion measurements are sensitive to the fluid permeability of the macroscopic porous media, leading to an effective diffusion coefficient17,21,31De. The corresponding intrinsic mobility of the fluid inside the porous network may be evaluated by the simple relationship
| 8 |
where, ϕ is the porosity of the porous network. This approximation neglects the topological and morphological properties of the porous media.52,53 As a consequence, its validity is restricted to homogeneous and isotropic porous network. Figure 8 nevertheless exhibits clear equivalence between the intrinsic mobility measured by both experimental procedures, validating the use of 1H PGSE-NMR to directly determine the intrinsic self-diffusion tensor of confined fluids. Finally, as displayed in Figure 8, a simple straight line roughly reproduces the variation of the intrinsic mobility of the fluid as a function of the porosity of the confining network. The scaling curve displayed in Figure 8 totally validates the use of 1H PGSE-NMR to directly measure the water self-diffusion within such porous materials saturated by water molecules.
Figure 8.
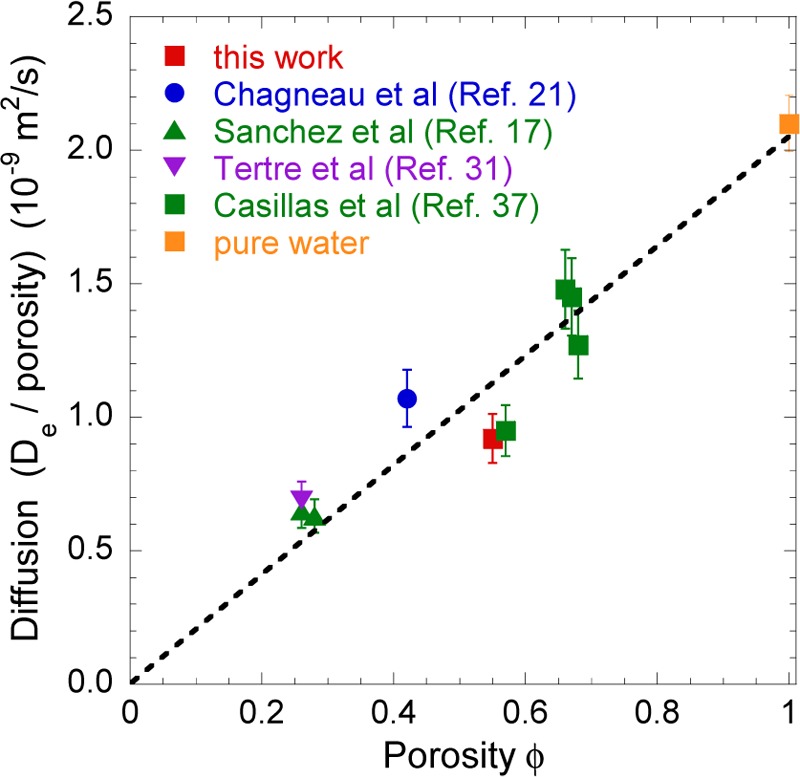
Variation of the apparent water self-diffusion D within samples made of granular materials as a function of the sample porosity ϕ.
1H pulsed gradient spin echo attenuation and magnetic resonance imaging of water density profiles were shown to adequately probe the water mobility within natural compacted clay samples. These experimental procedures give additional information on the water mobility within porous networks. On one hand, PGSE-NMR is able to directly measure the various components of the tensor describing the macroscopic equilibrium self-diffusion of water molecules within the hydrated clay sample, by the direct determination of the corresponding self-diffusion propagators. On the other hand, the time evolution of water concentration profiles detected by MRI allows to investigate the kinetics of water exchange between the water saturated clay and added heavy water. In addition, MRI is a powerful tool to determine the impact of sample heterogeneity on the mobility of the confined water molecules. However, in contrast with PGSE-NMR attenuation measurements, the extraction of quantitative data on the water self-diffusion requires a modeling of the H2O/D2O exchange in relation to the time evolution of the water concentration profiles within the clay samples. Since these two complementary NMR measurements are able to investigate dynamical processes over a broad time scale (typically between milliseconds and hours), they lead to additional information on dynamical process investigated by QENS or through-diffusion experiments. Although this study concerns only water and kaolinite clay, it could be easily extended to other molecular and ionic NMR probes diffusing within a large variety of porous networks. Kaolinite, a nonswelling clay, was selected in this study to probe its feasibility because the water molecules are then localized between the clay aggregates and are easily detected by NMR spectroscopy. The same behavior is expected to occur for other nonswelling clays like illite. By contrast, in the case of swelling clays like montmorillonite, the water molecules localized within the interlamellar space between the individual clay platelets cannot be detected by PGSE or MRI NMR spectroscopy. A strong confinement within such interlamellar space42,45 is indeed expected to enhance the transverse NMR relaxation rate of the water molecules,9,43 prohibiting their detection by PGSE and MRI. By contrast, we are quite sure to easily measure, by the same NMR procedure, the mobility of the water molecules located between the aggregates of montmorillonite platelets. In the near future we plan to measure, by the same NMR procedure, the mobility of water molecules and added ions (cations and anions) diffusing within the porous network of dense sediments resulting from the compression of such swelling clays.
Acknowledgments
The DSX100 spectrometer Bruker used for the PGSE-NMR and MRI studies was purchased, thanks to the funding allocated by the Région Centre (France). The CNRS interdisciplinary “Défi NEEDS” through its “MiPor” program (Project TransReac) is acknowledged for providing financial support for this study.
The authors declare no competing financial interest.
References
- Haderlein S. B.; Weissmahr K. W.; Schwarzenbach R. P. Specific adsorption of nitroaromatic explosives and pesticides to clay minerals. Environ. Sci. Technol. 1996, 30, 612–622. 10.1021/es9503701. [DOI] [Google Scholar]
- Li H.; Teppen B. J.; Johnston C. T.; Boyd S. A. Thermodynamics of nitroaromatic compound adsorption from water by smectite clay. Environ. Sci. Technol. 2004, 38, 5433–5442. 10.1021/es035054y. [DOI] [PubMed] [Google Scholar]
- Li H.; Teppen B. J.; Laird D. A.; Johnston C. T.; Boyd S. A. Geochemical modulation of pesticide sorption on smectite clay. Environ. Sci. Technol. 2004, 38, 5393–5399. 10.1021/es0494555. [DOI] [PubMed] [Google Scholar]
- Gao J.; Pedersen J. A. Adsorption of sulfonamide antimicrobial agents to clay minerals. Environ. Sci. Technol. 2005, 39, 9509–9516. 10.1021/es050644c. [DOI] [PubMed] [Google Scholar]
- Polubesova T.; Nir S.; Zadaka D.; Rabinovitz O.; Serban C.; Groisman L.; Rubin B. Water purification from organic pollutants by optimized micelle-clay systems. Environ. Sci. Technol. 2005, 38, 2343–2348. 10.1021/es049251o. [DOI] [PubMed] [Google Scholar]
- Pusch R. Highly compacted sodium Bentonite for isolating rock-deposited radioactive waste products. Nucl. Technol. 1979, 45, 153–157. 10.13182/NT79-A32305. [DOI] [Google Scholar]
- Charlet L.; Alt-Epping P.; Wersin P.; Gilbert B. Diffusive transport and reaction in clay rocks: A storage (nuclear waste, CO2, H2), energy (shale gas) and water quality issue. Adv. Water Resour. 2017, 106, 39–59. 10.1016/j.advwatres.2017.03.019. [DOI] [Google Scholar]
- Hassan M. S.; Villieras F.; Gaboriaud F.; Razafitianamaharavo A. AFM and low-pressure argon adsorption analysis of geometrical properties of phyllosilicates. J. Colloid Interface Sci. 2006, 296, 614–623. 10.1016/j.jcis.2005.09.028. [DOI] [PubMed] [Google Scholar]
- Fripiat J.; Cases J.; François M.; Letellier M. Thermodynamic and microdynamic behavior of water in clay suspensions and gels. J. Colloid Interface Sci. 1982, 89, 378–400. 10.1016/0021-9797(82)90191-6. [DOI] [Google Scholar]
- Ferrage E.; Sakharov B. A.; Michot L. J.; Delville A.; Bauer A.; Lanson B.; Grangeon S.; Frapper G.; Jiménez-Ruiz M.; Cuello G. J. Hydration properties and interlayer organization of water and ions in synthetic Na-smectite with tetrahedral layer charge. Part 2. Toward a precise coupling between molecular simulations and diffraction data. J. Phys. Chem. C 2011, 115, 1867–1881. 10.1021/jp105128r. [DOI] [Google Scholar]
- Porion P.; Rodts S.; Al-Mukhtar M.; Faugère A. M.; Delville A. Anisotropy of the solvent self-diffusion tensor as a probe of nematic ordering within dispersion of nano-composite. Phys. Rev. Lett. 2001, 87, 208302 10.1103/PhysRevLett.87.208302. [DOI] [PubMed] [Google Scholar]
- Porion P.; Al-Mukhtar M.; Faugère A. M.; Pellenq R. J. M.; Meyer S.; Delville A. Water self-diffusion within nematic dispersion of nanocomposites: a multiscale analysis of 1H pulsed gradient spin-echo NMR measurements. J. Phys. Chem. B 2003, 107, 4012–4023. 10.1021/jp022161q. [DOI] [Google Scholar]
- Michot L. J.; Delville A.; Humbert B.; Plazanet M.; Levitz P. Diffusion of water in a synthetic clay with tetrahedral charges by combined neutron time-of-flight measurements and molecular dynamics simulations. J. Phys. Chem. C 2007, 111, 9818–9831. 10.1021/jp0690446. [DOI] [Google Scholar]
- Porion P.; Michot L. J.; Faugère A. M.; Delville A. Structural and dynamical properties of the water molecules confined in dense clay sediments: a study combining 2H NMR spectroscopy and multiscale numerical modeling. J. Phys. Chem. C 2007, 111, 5441–5453. 10.1021/jp067907p. [DOI] [Google Scholar]
- Porion P.; Michot L. J.; Faugère A. M.; Delville A. Influence of confinement on the long-range mobility of water molecules within clay aggregates: a 2H NMR analysis using spin-locking relaxation rates. J. Phys. Chem. C 2007, 111, 13117–13128. 10.1021/jp073393y. [DOI] [Google Scholar]
- Porion P.; Faugère A. M.; Delville A. 1H and 7Li NMR pulsed gradient spin echo measurements and multiscale modeling of the water and ionic mobility within aqueous dispersions of charged anisotropic nanoparticles. J. Phys. Chem. C 2008, 112, 11893–11900. 10.1021/jp802928n. [DOI] [Google Scholar]
- Sánchez F. G.; Van Loon L. R.; Gimmi T.; Jakob A.; Glaus M. A.; Diamond L. W. Self-diffusion of water and its dependence on temperature and ionic strength in highly compacted montmorillonite, illite and kaolinite. Appl. Geochem. 2008, 23, 3840–3851. 10.1016/j.apgeochem.2008.08.008. [DOI] [Google Scholar]
- Marry V.; Dubois E.; Malikova N.; Durand-Vidal S.; Longeville S.; Breu J. Water dynamics in Hectorite clays: influence of temperature studied by coupling neutron spin echo and molecular dynamics. Environ. Sci. Technol. 2011, 45, 2850–2855. 10.1021/es1031932. [DOI] [PubMed] [Google Scholar]
- Michot L. J.; Ferrage E.; Jiménez-Ruiz M.; Boehm M.; Delville A. Anisotropic features of water and ion dynamics in synthetic Na- and Ca-smectites with tetrahedral layer charge. A combined Quasi-Elastic Neutron-Scattering and Molecular Dynamics simulations study. J. Phys. Chem. C 2012, 116, 16619–16633. 10.1021/jp304715m. [DOI] [Google Scholar]
- Porion P.; Faugère A. M.; Delville A. Multiscale water dynamics within dense clay sediments probed by 2H multiquanta NMR relaxometry and two-time stimulated echo NMR spectroscopy. J. Phys. Chem. C 2013, 117, 26119–26134. 10.1021/jp4093354. [DOI] [Google Scholar]
- Chagneau A.; Claret F.; Enzmann F.; Kersten M.; Heck S.; Madé B.; Schäfer T. Mineral precipitation-induced porosity reduction and its effect on transport parameters in diffusion-controlled porous media. Geochem. Trans. 2015, 16, 13 10.1186/s12932-015-0027-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porion P.; Delville A. Multi-Quanta spin-locking Nuclear Magnetic Resonance relaxation measurements: An analysis of the long-time dynamical properties of ions and water molecules confined within dense clay sediments. Magnetochemistry 2017, 3, 35 10.3390/magnetochemistry3040035. [DOI] [Google Scholar]
- Bostick B. C.; Vairavamurthy M. A.; Karthikeyan K. G.; Chorover J. Cesium adsorption on clay minerals: An EXAFS spectroscopic investigation. Environ. Sci. Technol. 2002, 36, 2670–2676. 10.1021/es0156892. [DOI] [PubMed] [Google Scholar]
- Porion P.; Al-Mukhtar M.; Faugère A. M.; Delville A. 23Na Nuclear Magnetic Resonance and 1H Pulsed Gradient Spin-Echo detection of the critical concentration corresponding to the Isotrope/Nematic transition within aqueous dispersions of charged anisotropic nanoparticles. J. Phys. Chem. B 2004, 108, 10825–10831. 10.1021/jp049617j. [DOI] [Google Scholar]
- Liu C. An ion diffusion model in semi-permeable clay materials. Environ. Sci. Technol. 2007, 41, 5403–5409. 10.1021/es0624117. [DOI] [PubMed] [Google Scholar]
- Porion P.; Faugère A. M.; Delville A. Long-time scale ionic dynamics in dense clay sediments measured by the frequency variation of the 7Li multiple-quantum NMR relaxation rates in relation with a multiscale modeling. J. Phys. Chem. C 2009, 113, 10580–10597. 10.1021/jp9007625. [DOI] [Google Scholar]
- Porion P.; Warmont F.; Faugère A. M.; Rollet A.-L.; Dubois E.; Marry V.; Michot L. J.; Delville A. 133Cs Nuclear Magnetic Resonance relaxometry as a probe of the mobility of cesium cations confined within dense clay sediments. J. Phys. Chem. C 2015, 119, 15360–15372. 10.1021/acs.jpcc.5b03880. [DOI] [Google Scholar]
- Tertre E.; Delville A.; Prêt D.; Hubert F.; Ferrage E. Cation diffusion in the interlayer space of swelling clay minerals—A combined macroscopic and microscopic study. Geochim. Cosmochim. Acta 2015, 149, 251–267. 10.1016/j.gca.2014.10.011. [DOI] [Google Scholar]
- Wigger C.; Van Loon L. R. Importance of interlayer equivalent pores for anion diffusion in clay-rich sedimentary rocks. Environ. Sci. Technol. 2017, 51, 1998–2006. 10.1021/acs.est.6b03781. [DOI] [PubMed] [Google Scholar]
- Chagneau A.; Tournassat C.; Steefel C. I.; Bourg I. C.; Gaboreau S.; Esteve I.; Kupcik T.; Claret F.; Schäfer T. Complete restriction of 36Cl– diffusion by celestite precipitation in densely compacted illite. Environ. Sci. Technol. Lett. 2015, 2, 139–143. 10.1021/acs.estlett.5b00080. [DOI] [Google Scholar]
- Tertre E.; Savoye S.; Hubert F.; Prêt D.; Dabat T.; Ferrage E. Diffusion of water through the dual-porosity swelling clay mineral vermiculite. Environ. Sci. Technol. 2018, 52, 1899–1907. 10.1021/acs.est.7b05343. [DOI] [PubMed] [Google Scholar]
- Cotts R. M.; Hoch M. J. R.; Sun T.; Markert J. T. Pulsed field gradient stimulated echo methods for improved NMR diffusion measurements in heterogeneous systems. J. Magn. Reson. 1989, 83, 252–266. 10.1016/0022-2364(89)90189-3. [DOI] [Google Scholar]
- Callaghan P. T.Principles of Nuclear Magnetic Resonance Microscopy; Clarendon Press: Oxford, 1991. [Google Scholar]
- Nakashima Y. Pulsed field gradient proton NMR study of the self-diffusion of H2O in montmorillonite gel: Effects of temperature and water fraction. Am. Mineral. 2001, 86, 132–138. 10.2138/am-2001-0114. [DOI] [Google Scholar]
- Nakashima Y.; Mitsumori F. H2O self-diffusion restricted by clay platelets with immobilized bound H2O layers: PGSE NMR study of water-rich saponite gels. Appl. Clay Sci. 2005, 28, 209–221. 10.1016/j.clay.2004.01.017. [DOI] [Google Scholar]
- Takahashi T.; Ohkubo T.; Ikeda Y. Montmorillonite alignment induced by magnetic field: evidence based on the diffusion anisotropy of water molecules. J. Colloid Interface Sci. 2006, 299, 198–203. 10.1016/j.jcis.2006.01.049. [DOI] [PubMed] [Google Scholar]
- Martinez Casillas D. C.; Longinotti M. P.; Bruno M. M.; Chavez F. V.; Acosta R. H.; Corti H. R. Diffusion of water and electrolytes in mesoporous silica with a wide range of pore sizes. J. Phys. Chem. C 2018, 122, 3638–3647. 10.1021/acs.jpcc.7b11555. [DOI] [Google Scholar]
- Kimmich R.NMR: Tomography, Diffusometry, Relaxometry; Springer Verlag: Berlin, 1997. [Google Scholar]
- Duval F. P.; Porion P.; Van Damme H. Microscale and macroscale diffusion of water in colloidal gels. A pulsed field gradient and NMR imaging investigation. J. Phys. Chem. B 1999, 103, 5730–5735. 10.1021/jp9909210. [DOI] [Google Scholar]
- Patural L.; Porion P.; Van Damme H.; Govin A.; Grosseau P.; Ruot B.; Devès O. A pulsed field gradient and NMR imaging investigations of the water retention mechanism by cellulose ethers in mortars. Cem. Concr. Res. 2010, 40, 1378–1385. 10.1016/j.cemconres.2010.04.001. [DOI] [Google Scholar]
- van Gunsteren W. F.; Berendsen H. J. C.; Rullmann J. A. C. Stochastic dynamics for molecules with constraints Brownian dynamics of n-alkanes. Mol. Phys. 1981, 44, 69–95. 10.1080/00268978100102291. [DOI] [Google Scholar]
- Korb J. P.; Delville A.; Xu S.; Demeulenaere G.; Costa P.; Jonas J. Relative role of surface interactions and topological effects in nuclear magnetic resonance of confined liquids. J. Chem. Phys. 1994, 101, 7074–7081. 10.1063/1.468333. [DOI] [Google Scholar]
- Delville A.; Letellier M. Structure and dynamics of simple liquids in heterogeneous condition: An NMR study of the clay-water interface. Langmuir 1995, 11, 1361–1367. 10.1021/la00004a050. [DOI] [Google Scholar]
- Porion P.; Delville A. Multinuclear NMR study of the structure and micro-dynamics of counterions and water molecules within clay colloids. Curr. Opin. Colloid Interface Sci. 2009, 14, 216–222. 10.1016/j.cocis.2008.08.002. [DOI] [Google Scholar]
- Korb J.-P. Multiscale nuclear magnetic relaxation dispersion of complex liquids in bulk and confinement. Prog. Nucl. Magn. Reson. Spectrosc. 2018, 104, 12–55. 10.1016/j.pnmrs.2017.11.001. [DOI] [PubMed] [Google Scholar]
- Hansen J. P.; McDonald I. R.. Theory of Simple Liquids; Academic Press: London, 1986. [Google Scholar]
- Bacle P.; Dufrêche J.-F.; Rotenberg B.; Bourg I. C.; Marry V. Modeling the transport of water and ionic tracers in a micrometric clay sample. Appl. Clay Sci. 2016, 123, 18–28. 10.1016/j.clay.2015.12.014. [DOI] [Google Scholar]
- Basser P. J.; Mattiello J.; LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin-echo. J. Magn. Reson., Ser. B 1994, 103, 247–254. 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- Li T. Q.; Häggkvist M.; Ödberg L. Porous structure of cellulose fibers studied by Q-space NMR imaging. Langmuir 1997, 13, 3570–3574. 10.1021/la970045m. [DOI] [Google Scholar]
- Li T.-Q.; Häggkvist M.; Ödberg L. The porous structure of paper coatings studied by water diffusion measurements. Colloids Surf., A 1999, 159, 57–63. 10.1016/S0927-7757(99)00162-4. [DOI] [Google Scholar]
- Skare S.; Hedehus M.; Moseley M. E.; Li T. Q. Condition number as a measure of noise performance of diffusion tensor data acquisition schemes with MRI. J. Magn. Reson. 2000, 147, 340–352. 10.1006/jmre.2000.2209. [DOI] [PubMed] [Google Scholar]
- Latour L. L.; Mitra P. P.; Kleinberg R. L.; Sotak C. H. Time-dependent diffusion coefficient of fluids in porous media as a probe of surface-to-volume ratio. J. Magn. Reson., Ser. A 1993, 101, 342–346. 10.1006/jmra.1993.1056. [DOI] [Google Scholar]
- Latour L. L.; Kleinberg R. L.; Mitra P. P.; Sotak C. H. Pore-size distributions and tortuosity in heterogeneous porous media. J. Magn. Reson., Ser. A 1995, 112, 83–91. 10.1006/jmra.1995.1012. [DOI] [Google Scholar]
- Duval F. P.; Porion P.; Faugère A. M.; Van Damme H. An NMR investigation of water self-diffusion and relaxation rates in controlled ionic strength Laponite sols and gels. J. Colloid Interface Sci. 2001, 242, 319–326. 10.1006/jcis.2001.7806. [DOI] [Google Scholar]
- Busignies V.; Porion P.; Leclerc B.; Evesque P.; Tchoreloff P. Application of PGSTE-NMR technique to characterize the porous structure of pharmaceutical tablets. Eur. J. Pharm. Biopharm. 2008, 69, 1160–1170. 10.1016/j.ejpb.2008.02.008. [DOI] [PubMed] [Google Scholar]