Reinforcement Learning for Dynamic Microfluidic Control

Abstract

Recent years have witnessed an explosion in the application of microfluidic techniques to a wide variety of problems in the chemical and biological sciences. Despite the many considerable advantages that microfluidic systems bring to experimental science, microfluidic platforms often exhibit inconsistent system performance when operated over extended timescales. Such variations in performance are because of a multiplicity of factors, including microchannel fouling, substrate deformation, temperature and pressure fluctuations, and inherent manufacturing irregularities. The introduction and integration of advanced control algorithms in microfluidic platforms can help mitigate such inconsistencies, paving the way for robust and repeatable long-term experiments. Herein, two state-of-the-art reinforcement learning algorithms, based on Deep Q-Networks and model-free episodic controllers, are applied to two experimental “challenges,” involving both continuous-flow and segmented-flow microfluidic systems. The algorithms are able to attain superhuman performance in controlling and processing each experiment, highlighting the utility of novel control algorithms for automated high-throughput microfluidic experimentation.

1. Introduction

Microfluidics has emerged as a formidable tool in high-throughput and high-content experimentation, because the miniaturization of functional operations and analytical processes almost always yields advantages when compared to the corresponding macroscale process.^1,2 Such benefits are many, and include the ability to process ultra-small sample volumes, enhanced analytical performance, reduced instrumental footprints, ultra-high analytical throughput, and the facile integration of functional components within monolithic substrates.³ At a fundamental level, the high surface area-to-volume ratios typical of microfluidic environments guarantee that both heat and mass transfer rates are enhanced, providing for unrivalled control over the chemical or biological environment. That said, at a more pragmatic level, microfluidic experiments performed over extended timescales almost always require extensive manual intervention to maintain operational stability.⁴ Accordingly, there is a significant and currently untapped opportunity for purpose-built algorithms that enable real-time control over microfluidic environments. Recent advances in machine learning, specifically in artificial neural networks (ANNs)⁵ and reinforcement learning (RL) algorithms,⁶ provide an exciting opportunity in this regard, with the control of high-throughput experiments being realized through efficient manipulation of the microfluidic environment, based on real-time observations.

The implementation of advanced control algorithms can help mitigate some key drawbacks of traditional microfluidic experiments.⁴ For example, inherent variations in both conventional and soft lithographic fabrication methods introduce discrepancies and variations between microfluidic device sets.^7,8 The use of machine learning can help achieve consistent operation between different devices, reducing manual intervention and ensuring consistency in information quality. More importantly, by their very nature microfluidic systems have characteristics that vary with time. For instance, in continuous-flow microfluidic systems, surface fouling and substrate swelling are recognized problems that almost always degrade long-term performance if left unchecked.^8,9 This is particularly problematic when using polydimethylsiloxane (PDMS) chips because of the adsorption of hydrophobic molecules from biological samples,¹⁰⁻¹² or when performing small-molecule/nanomaterial synthesis in continuous-flow formats.¹³ In such situations, machine learning can help maintain stable flow conditions over extended time periods, by automatically adjusting flow conditions using control infrastructure. Finally, over the past decade, microfluidic platforms with integrated real-time detection systems and control algorithms have also been used to extract vital information from a range of chemical and biological environments. Of particular note has been the use of such systems to control the size, shape, and chemical composition of nanomaterials. The combination of microfluidic reactors, prompt assessment of product characteristics, and algorithms able to effectively map the experimental parameter space of a reaction system has allowed the rapid reaction optimization and synthesis of a diversity of high-quality nanomaterials possessing bespoke physiochemical characteristics.¹⁴⁻¹⁸

ANN algorithms are inspired by biological neural networks and are well-suited to a range of machine learning applications.^5,19 ANNs have been used for diverse data transformation tasks, including image pattern recognition,²⁰ speech synthesis,²¹ and machine translation.²² ANNs are a key tool in RL,²³ where supervised machine learning algorithms inspired by behavioral psychology can be developed. Here, the control algorithm (or agent) repeatedly interacts with an environment and iteratively maximizes a reward signal obtained from the environment.⁶ The agent observes the environment and performs an action based on the observation. The environment is updated based on the action, and a scalar reward signal (“score”), representing the quality of the action, is returned. The general formulation of the problem allows application to a variety of environments, including robot control,²⁴ visual navigation,²⁵ network routing,²⁶ and playing computer games.²⁷

Deep Q-Networks (DQNs) combine ANNs and RL to interpret high-dimensionality data and deduce optimal actions to be performed in the observed environment.^27,28 Significantly, it has recently been shown that DQNs can surpass human performance when applied to a variety of computer and board games, including Atari video games²⁹ and Go.³⁰ However, to date there have been few, if any, applications of RL in non-simulated environments, primarily due to difficulties in obtaining input data and exerting tight control over the environment. Examples of RL in non-simulated environments include the control of robotic arms³¹ as well as the control of building air conditioning systems.³²

Recently, a more data-efficient RL algorithm called the model-free episodic controller (MFEC) has been proposed.³³ Analogous to hippocampal learning,³⁴ the algorithm stores a table of observations and associated reward values. The optimal action for a novel observation is then deduced by estimating a reward from previous but closely related observations. MFEC can thus repeat high-reward sequences of actions, even if a sequence has been visited only once. In general, training times for the MFEC are reduced compared to those for DQN, but at the cost of peak performance.

Herein, we present the application of RL algorithms to the control of real-world experiments performed within microfluidic environments. Specifically, we use RL to navigate two microfluidic control problems, namely, the efficient positioning of an interface between two miscible flows within a microchannel under laminar flow conditions and the dynamic control of the size of water-in-oil droplets within a segmented flow. To achieve this, two RL algorithms, based on DQNs and MFEC, are used. In practical terms, the algorithms are tasked with controlling the volumetric flow rates of precision pumps that deliver fluids into microfluidic devices. Significantly, all decisions are based solely on visual observations using a standard optical microscope, with the control algorithms maximizing a scalar reward that is calculated independently for each frame via classical image processing. To the best of our knowledge, this study is the first example of reinforcement in a microfluidic environment. Moreover, we believe that such intelligent control in microfluidic devices will enable improved reproducibility in microfluidic experimentation.

2. Results and Discussion

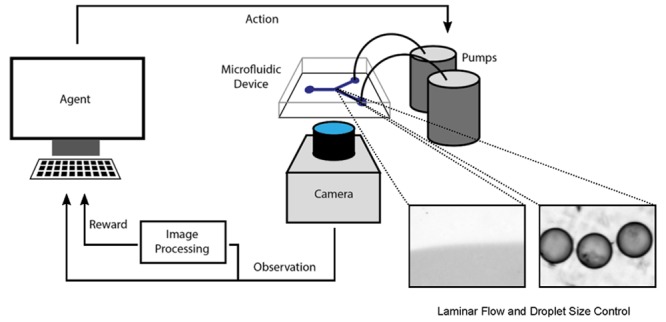
A generalized setup of the microfluidic system is illustrated in Figure 1. Here, an agent interacts with an environment and continuously improves its “performance.” An observation of the environment is made (using a camera connected to a microscope), and a reward is calculated using classical image processing. A higher reward tells the agent that the previous action was a “good choice,” which it then uses to influence its next action. The agent improves performance by choosing better actions for a certain observation, which results in an overall higher reward signal.

Figure 1.

A generalized illustration of the RL-enabled microfluidic experimental setup.

2.1. Laminar Flow Control

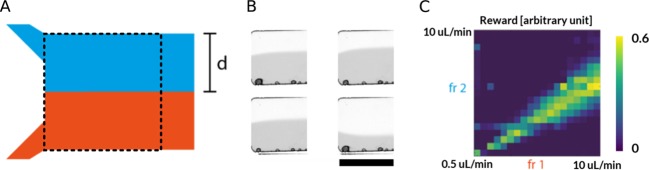
Low Reynolds numbers (Re) are typical for fluids flowing through microfluidic channels, with viscous forces dominating over inertial (or turbulent) forces.³ This almost always yields a laminar flow, with no disruption between fluid layers. The ability to control and align the interface between two co-flowing streams within a microfluidic channel is critical in many applications (Figure 2A), for example, the controlled synthesis of vesicles³⁵ or droplet trapping and transport systems.³⁶ In the current experiments, a simple converging flow environment was used to investigate automatic control over the laminar flow interface position (see Figure S1A for device architecture). This involved the confluence of two aqueous streams under low Re, where the fluid interface was made visible by adding ink to one of the input solutions (Figure 2B). The controller repeatedly altered the flow rates of the two fluid phases, resulting in various laminar flow interface positions. After a fixed number of interactions (set at 250, corresponding to one episode), the environment was reset to random flow rates, and the controller restarted its task. The volumetric flow rates of each flow stream were limited to values between 0.5 and 10 μL/min (resulting in total flow rates between 1 and 20 μL/min), representing typical flow rates used in microfluidic experiments over extended time periods. As previously stated, volumetric flow rates were set to random values within this acceptable range at the start of every episode. The challenge then involved adjusting the flow rates such that the fluid interface moved to an (arbitrary) optimal position (defined as 30% of the channel width) within one episode. The scalar reward for the previous action was defined as the proximity of the laminar flow interface to the optimal position, which was extracted from the captured frame via classical image-processing methods. The control algorithm adjusted the volumetric flow rates by performing one of five discrete actions: increasing or decreasing the flow rate of the continuous phase, increasing or decreasing the flow rate of the dispersed phase, or maintaining the flow rates unchanged. An optimal fixed step size of 0.5 μL/min was determined empirically to limit any strain on the pumps and ensure that an optimum was found within one episode. Additionally, control algorithms were limited in interaction frequency (1.5 Hz for the DQN and 2.5 Hz for the MFEC) to prevent equipment damage and enhance coupling between the performance of an action and the observation of the resulting conditions within the microfluidic system. Inspection of Figure 2B highlights a small number of trapped air bubbles along the lower channel wall. These bubbles occur because of fluidic defects (aspiration of air in the piston-based pumps) and posed an additional challenge to the control algorithm by increasing the amount of noise in both the reward calculation and the observed frame.

Figure 2.

Laminar flow control. (A) Schematic of a standard laminar flow environment established within a simple microfluidic device. The dashed black box indicates the experimental observation window. (B) Example image frames captured during the training phase (scale bar 150 μm). (C) Results of a complete environmental characterization of a single microfluidic device. Rewards are shown for various flow rates between 0.5 and 10 μL/min.

2.1.1. Environment Characterization

Figure 2C shows a complete characterization of a reward surface for the laminar flow challenge. Intuitively, it was expected that the position of the laminar flow interface should correlate with the ratio between the flow rates of the two fluid phases. Indeed, the reward surface presented clearly identified an optimal region, where the flow rates produced the desired interface position, and thus achieved high rewards. However, as previously noted, the data graphically shown in Figure 2C are valid only for a specific microfluidic device, with replicate devices (having the same putative dimensions) exhibiting significantly different behavior because of small variations intrinsic to the fabrication process.

2.1.2. Laminar Flow Control Using DQN

Figure 3 reports algorithmic performance in the laminar flow environment (see Figure S2 for raw data plots). DQN performance during the first 5500 frames (ca. 1 h) was comparable to the random agent. This was because of the initial exploration phase of the DQN, where the share of predicted actions was slowly increased from 100% random actions to 95% controller-based actions (see Figure 3A, where the exploration phase ends after 27 h). Over the course of the next 36 h of training (which equates to ca. 195 000 image frames) the algorithm managed to perform at a level comparable to a human tester, and at times surpassing it (e.g., between 27 and 37 h during the blue line experiment in Figure 3A). It was observed that, although separate experiments indicated the same general trends in performance, short-term performance variations differed markedly between experiments. It is hypothesized that performance would be improved further by employing longer training phases, noting that typical benchmarks for Atari environments involve training for up to 200 million frames.³⁷ This was impractical in the current study, as 200 million frames corresponds to over 4 years of training time at the investigated frame rates. During the initial exploration phase, as the share of random actions was slowly reduced and DQN improved its accuracy, a gradual increase in performance was expected. Even though such a trend was apparent, some experimental runs required longer than the initial exploration phase to realize peak performance. It is hypothesized that the control algorithm gets captured within the vicinity of local minima during poorer performance runs. We suggest that such effects could be mitigated by using multiple asynchronous experimental setups, such as A3C,³⁸ allowing the controller to interact with multiple but similar environments at the same time, thus greatly reducing the chances of being captured in such a local minimum. However, although using multiple environments is trivial in simulated environments, it is often impractical in real-world scenarios. It is also noted that all experiment repeats eventually surpassed the performance of human testers. Performance generally fluctuated around human level after 48 h (ca. 260 000 frames) of training, with longer run times not significantly improving performance. In the current study, DQN was retrained from scratch for each new experiment. In future experiments, algorithm training from pooled experimental data (collected using multiple devices over multiple experiments) could improve the stability of the control algorithm across a wider variety of situations.

Figure 3.

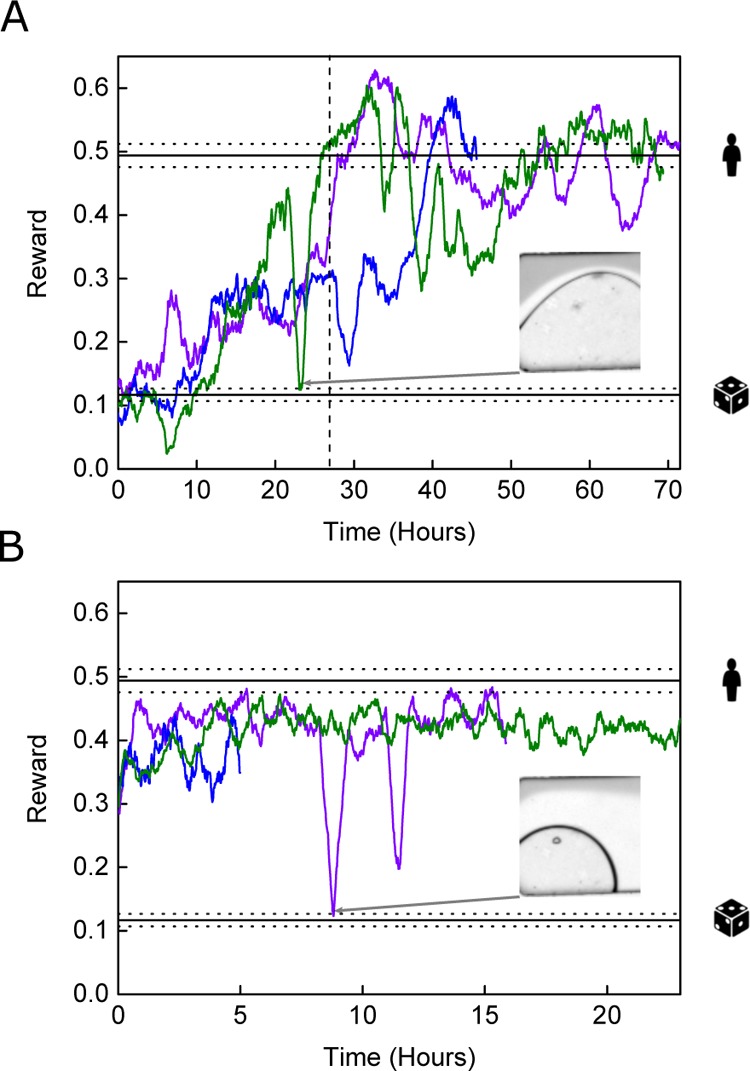
Variation of the reward as a function of time for (A) DQN and (B) MFEC controllers within the laminar flow environment (N = 3). Inset widths are 150 μm. Benchmark performance ranges are displayed with dotted horizontal lines using mean performance and 95% confidence intervals. Human performance level is indicated with a human figure, and random performance level is indicated with a die. Data plotted with a 35 point moving average for clarity.

On a practical level, the deposition of debris within microfluidic channels often leads to blockage, with gas bubble accumulation leading to flow instability. It is therefore notable that the presented control algorithm could successfully maintain performance and adjust to changing conditions over extended periods of time. Indeed, the presence of a gas bubble has only a short-term effect (see inset highlighting the performance dip shown in Figure 3A), with the algorithm recovering quickly after bubble dissipation. It should be noted that there was no evidence of the algorithm learning to get rid of the bubbles actively within the observed time frame, but such a feat would not be trivial even for a human operator. Consequently, we conclude that the DQN was able to achieve human-level performance for the laminar flow challenge, albeit requiring considerable training time to achieve peak performance.

Overall, it was found that the DQN was well suited to the automated handling of the real-world complications arising because of the extended experimental time frames, which should enable automation of a variety of long-term experiments. Our results highlight, for the first time, the capabilities of DQN for maintaining complex control situations in microfluidic devices based on visual inputs over extended time periods.

2.1.3. Laminar Flow Control Using MFEC

The MFEC exhibited a rapid learning capability and showed peak performance within the first 11 000 frames, ca. 2 h, of training. This compares favorably to the 130 000 frames (or 24 h) needed by DQN (Figure 3B). Such a situation is to be expected, as every rewarding situation can be exploited by the algorithm. However, the maximum performance achieved by the model-free controller did not consistently reach human-level performance (unlike DQN), albeit showing only a marginal reduction in performance (typically 90% of human-level performance in terms of achieved scores). In a typical experiment, this might pose an acceptable trade-off, given the significant reductions in initial training time. Similar to the disturbances observed during DQN experiments, sharp performance drops were detected when a bubble entered the microfluidic channel (see inset highlighting the performance dip shown in Figure 3B). However, the model-free controller exhibited a substantially faster recovery, once the bubble was dislodged and the environment reverted to the default state, when compared to the DQN controller. It is hypothesized that such behavior was because of the model-free nature of the MFEC algorithm, which does not update an internal model when encountering flawed observations caused by short-term fluctuations. Therefore, the MFEC could quickly recover performance as soon as the bubble was dislodged, and normal observations were resumed. Furthermore, the model-free controller empirically showed less performance fluctuations than the DQN, especially over long time frames. Indeed, because of its consistent performance, the MFEC is well suited to the control of relatively simple experimental environments, where slight reductions in peak performance are acceptable. In practical terms, the short training time requirements heavily favor MFEC over DQN, because training a controller in a few minutes is simply not feasible using DQN.

2.2. Droplet Size Control

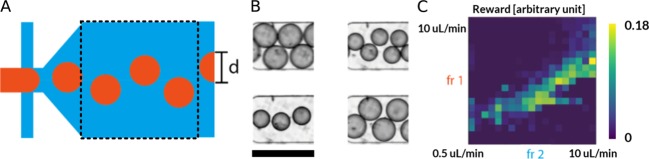
Under certain circumstances, co-flowing two immiscible fluids through a narrow orifice (a flow-focusing geometry) within a microfluidic channel results in the formation of monodisperse droplets of one of the fluids within the other.³ Importantly, these droplets represent separate reaction containers and can be produced at rates exceeding 10 000 Hz. Such segmented-flow formats have attracted enormous attention from the biological research community and are now an essential part of high-throughput experimental platforms for single-cell genomic sequencing,³⁹ early-stage kinetic studies,⁴⁰ or high-throughput screening.⁴¹ The goal of the droplet size challenge was to adjust the flow rates of the two droplet-forming phases to produce droplets of a predetermined size (Figure 4A, and see Figure S1B for device architecture). As in the laminar flow challenge, volumetric flow rates were limited to values between 0.5 and 10 μL/min, with the step size being fixed to 0.5 μL/min, and the interaction frequency to 1.5 Hz for the DQN and 2.5 Hz for the MFEC. Furthermore, the control algorithms interacted with the environment using the same set of actions used in the laminar flow challenge, that is, increasing or decreasing the flow rates of the two droplet-forming phases, as well keeping the flow rates constant. Example droplets are shown in Figure 4B.

Figure 4.

Droplet size control. (A) Schematic illustration of the droplet size challenge, with droplets being formed at a flow-focusing geometry. The dashed black box indicates the experimental observation window. (B) Example frames captured during an experimental run (scale bar 150 μm). (C) An example reward surface for a complete scan of the environment for various flow rates of the dispersed phase (fr1) and the continuous phase (fr2) both within a range of 0.5–10 μL/min.

2.2.1. Environment Characterization

Figure 4C shows an example reward surface for the droplet size challenge. Similar to the laminar flow reward surface (Figure 2C), results indicated optimal flow rate ratios, which frequently produced droplets of the correct size (e.g., continuous phase flow rate (fr1) = 5 μL/min and dispersed phase flow rate (fr2) = 3.2 μL/min, resulting in a diameter of 54 μm). However, the boundaries of this optimal region were much less defined than those observed in the laminar flow challenge. Furthermore, larger variations were found between reward surfaces originating from separate microfluidic devices. It is believed that this increased uncertainty stems from the sensitivity of the droplet formation process to surface-wetting effects,⁴² as well as the circle Hough transform used in the reward calculation, which in turn results in a noisier reward signal. On the basis of the direct comparison between reward surfaces, it is expected that the droplet size environment requires a more sophisticated control solution, providing additional challenges for the applied control algorithms.

2.2.2. Droplet Size Control Using DQN

Figure 5 reports algorithmic performance in the droplet environment (see Figure S3 for raw data plots). Starting from random performance, the DQN controller typically managed to surpass human-level performance prior to the end of the exploration phase (Figure 5A), and superhuman-level performance was achieved in all experiments. Again, short-term and absolute performance variations were seen between experiments, largely because of the separate experiments being performed with different microfluidic devices, with different reagent solutions, and at different times. Given that similar differences in maximal performance were observed with the MFEC, it is likely that such differences originated partially from differences in the fabrication and surface treatment. Further, inconsistencies can arise while setting up the microfluidic platform, for example when connecting the tubing and aligning the optics. However, because RL in non-simulated environments constitutes a stochastic process, performance variations stemming from the algorithm (because of capture in local optima) are also expected, especially given the limited training times involved.

Figure 5.

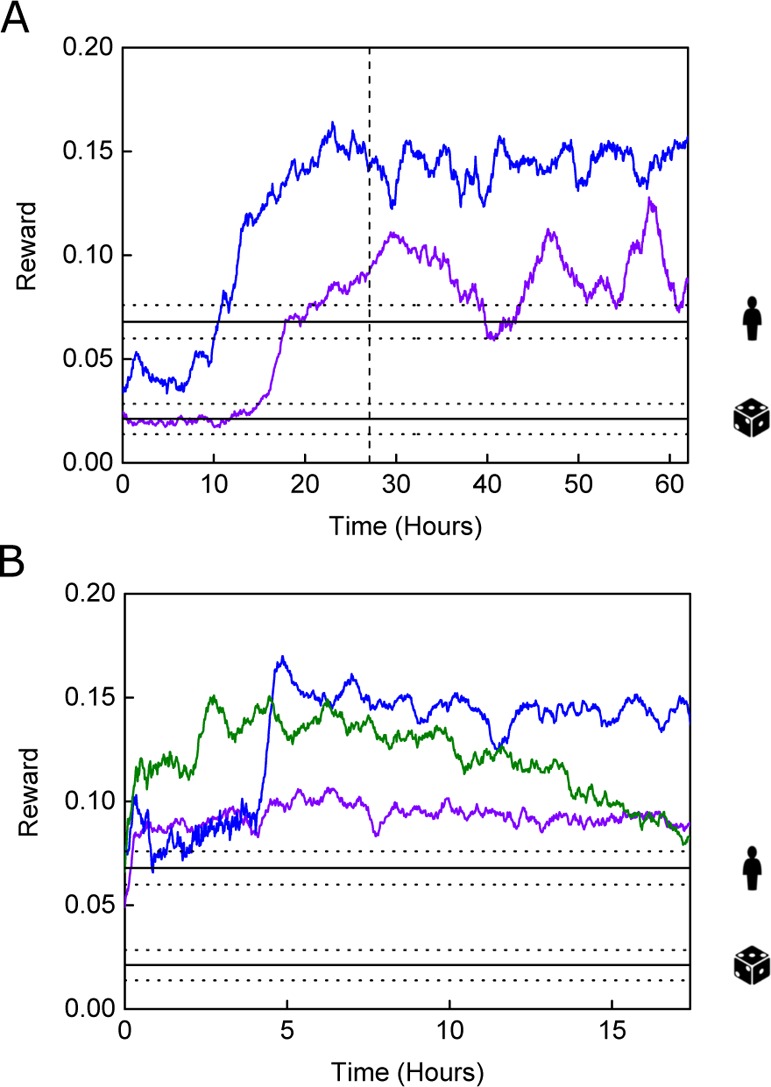
Variation of the reward as a function of time for (A) DQN (N = 2) and (B) MFEC controllers (N = 3) in the droplet environment. Benchmark performances are displayed using mean performance and 95% confidence intervals. Human performance level is indicated with a human figure, and random performance level is indicated with a die. Data plotted with a 35-point moving average for clarity.

In a similar manner to the laminar flow challenge, large-scale performance fluctuations over extended time periods were observed. This could be explained by the increased sensitivity of droplet formation to surface-wetting effects, when compared to the single-phase system of the laminar flow challenge. For example, Xu et al. have shown that altering wetting properties by changing the surfactant concentration results in different co-flow regimes, varying between laminar flow and droplet flow because of surface aging effects in PDMS microfluidic devices.⁴² Therefore, reaction conditions in the flow-focusing geometry are expected to vary greatly, as surface conditions change over long timescales. Further, long-term drift can also be caused by small-scale fluid leakage, as fluidic connectors can loosen over time. However, despite these phenomena, DQN performance was observed to remain close to or exceed human-level performance. Such results clearly indicate that DQN is a viable option for maintenance of reaction conditions during long-term microfluidic experiments, even in complex environments.

2.2.3. Droplet Size Control Using MFEC

The performance of the MFEC in the current task was outstanding and on par with the DQN performance (Figure 5B). Typically, the model-free controller achieved human-level performance very soon after the start of the experiment and surpassed it for most of the time. Interestingly, after quickly surpassing human-level performance, one experiment (green line in Figure 5B) showed a slow but steady decline toward human-level performance over the final 10 h. A similar decline was not observed in any experimental repeats; therefore, this decline was believed to be device specific and related to variable factors between devices (e.g., sub-optimal channel surface treatment⁴³).

In general, the MFEC was well suited to the droplet size challenge. The absolute performance of the MFEC was comparable to the DQN and almost always superior to human-level performance. Even though significant attention was focused on ensuring a level playing field for the human testers (see Experimental Methods: Benchmarking Learning Performance), it is believed that the superhuman performance observed in this task was largely because of the rapid decision-making of the algorithm. Droplet formation occurred at ca. 1000 Hz, and the interaction frequency of the algorithm was set at 2.5 Hz. The interaction frequency of the human testers was variable and difficult to quantify, but was certainly less than 2.5 Hz.

3. Conclusions

Numerous microfluidic tasks can be performed in a previously unachievable manner using machine learning methods. This is especially true for operations that are currently performed using fixed or manually tuned parameters. Herein, we have demonstrated for the first time that state-of-the-art machine learning algorithms can surpass human-level performance in microfluidic experiments, solely based on visual observations. Moreover, we have confirmed this through the use of two different RL algorithms, based on neural networks (DQN) and episodic memory (MFEC).

In our experiments, algorithms surpassed human-level performance over variable timescales. For example, the DQN in the laminar flow challenge took ca. 27 h, whereas the MFEC in the droplet challenge rapidly (within minutes) achieved sustained superhuman performance. It will be important in future applications to minimize this time, and we anticipate that further development of RL algorithms will make this possible in a wide variety of scenarios. Further, we hypothesize that a combination of algorithms could provide a solution that leverages the advantages of each method. For example, MFEC could provide initial guesses, via rapid policy improvement, that could then be used to improve DQN training. This would almost certainly decrease the overall time required for DQN to reach peak performance (which as shown herein is superhuman in all studied environments).

Bright-field microscopy is one of the most commonly used experimental techniques in chemical and biological analysis because of its simplicity and high information content. Since visual observations are exclusively used in the current study, the proposed control algorithms could be easily integrated into existing experimental setups. Moreover, we found that the computational requirements for learning were much lower than anticipated, presumably because the rate-limiting step was typically the interaction with the physical environment and not controller evaluation. This further highlights the applicability of RL to various microfluidic environments.

It is important to note that this study purposely used proof-of-concept-level challenges, which simpler control algorithms (e.g., PID controllers) could also perform. However, it is anticipated that the ultimate capability of such algorithms is much higher and applicable to a large variety of visual tasks. Indeed, a novel environment is simply established by defining a reward function and then re-training the same algorithm. Accordingly, further research will extend the presented findings by investigating more complex environments using the same algorithms. Finally, it is believed that this study highlights the benefits of combining experimental platforms with “smart” decision-making algorithms. To date, there have been few applications of RL in non-simulated environments. Nevertheless, it is expected that a large variety of microfluidic-based experiments could be used to generate state-of-the-art results through the use of advanced interpretation or control algorithms. Examples of such experiments include the manipulation of organisms on chip, cell sorting, and reaction monitoring.

To conclude, and based on the results presented herein, it is believed that RL and machine learning in general have the potential to disrupt and innovate not only microfluidic research, but many related experimental challenges in the biological and life sciences.

4. Materials and Methods

4.1. Microfluidic Device Fabrication

Microfluidic devices were fabricated using conventional soft lithographic methods in PDMS.¹⁰ Microfluidic geometries were designed using AutoCAD 2014 (Autodesk GmbH, Munich, Germany) and printed on high-resolution film masks (Micro Lithography Services Ltd, Chelmsford, UK). In a class 100 cleanroom, a silicon wafer (Si-Mat, Kaufering, Germany) was spin-coated with a layer of SU-8 2050 photoresist (MicroChem, Westborough, USA) and exposed to a collimated UV source. After application of SU-8 developer (MicroChem, Westborough, USA), the fabricated master mold was characterized using a laser scanning microscope (VK-X, Keyence, Neu-Isenburg, Germany). Sylgard 184 PDMS base and curing agent (Dow Corning, Midland, USA) were mixed in a ratio of 10:1 wt/wt, degassed, and decanted onto the master. The entire structure was oven-cured (70 °C for at least 8 h), then separated by peeling. Inlet and outlet ports were punched through the structured PDMS layer; then it was bonded to a flat PDMS substrate using an oxygen plasma and incubated on a hot plate at 95 °C for at least 2 h. Finally, a hydrophobic surface treatment, 5 v/v % 1H-1H-2H-2H-perfluorooctyltrichlorosilane (PFOS; abcr GmbH, Karlsruhe, Germany) in isopropyl alcohol (Sigma-Aldrich, Buchs, Switzerland), was applied for 1 min to ensure hydrophobicity of the channel surface. Channel depths of 50 μm were used in all experiments. Device architectures are shown in Figure S1.

4.2. Experimental Setup

Deionized water and deionized water containing 1 v/v % ink were used as the two phases for the laminar flow experiments. For droplet-based experiments, the same ink solution was used as the dispersed phase, and HFE7500 (3M, Rüschlikon, Switzerland) containing 0.1 wt/wt % EA-surfactant (Pico-Surf 1; Sphere Fluidics, Cambridge, UK) was used as the continuous phase. Two piston-based pumps (milliGAT; Global FIA, Fox Island, USA) were used to deliver fluids and control volumetric flow rates. A high-speed fluorescence camera (pco.edge 5.5; PCO AG, Kelheim, Germany) was used to observe fluids through an inverted microscope (Ti-E; Nikon GmbH, Egg, Switzerland), with a 4× objective (Nikon GmbH, Egg, Switzerland). In both environments (laminar flow and droplet generation), attainable flow rates were limited to between 0.5 and 10 μL/min, in 0.5 μL/min steps. The interaction frequency was limited (1.5 Hz for the DQN and 2.5 Hz for the MFEC), and the environments were reset to random flow rates after a set number of interactions (250 for the DQN, 150 for the MFEC), thereby splitting the challenge into separate episodes. Because of extensive training times, separate experiments were terminated after a performance plateau was reached, which occurred at different times in different experiments. Experimental repeats (N) were conducted at separate times using different devices.

4.3. Data Pre-Processing

Observations from the high-speed camera were minimally pre-processed before being fed as an input into the controller. The raw camera frame was converted to a floating-point representation (black pixel value 0.0, white pixel value 1.0), then resized to 84 × 84 pixels, following a published protocol.²⁷

4.4. Reward Calculation

The reward estimator for the laminar flow environment evaluated the position of the laminar flow interface across the microfluidic channel by performing a thresholding operation on the raw frame. The dye solution yielded black pixels, whereas the clear solution produced white pixels. The interface position was then estimated using the average intensity of pixels across the complete image. Finally, the reward was calculated as an error between the current position and the desired position. The desired position was chosen to be one-third of the channel width to prevent the “simple solution” of using the maximum flow rate on both pumps. The reward in the droplet-based experiments was calculated by detecting the radii of droplets in the observed frame. Initially, both Gaussian blur (5 × 5 kernel) and Otsu thresholding⁴⁴ operations were applied to achieve proper separation of the black (dye) droplets from the background. A dilation operation (with a 3 × 3 kernel) was used to additionally discriminate the droplets from the channel walls. Subsequently, circles were detected in each processed frame using a Hough circle transform⁴⁵ and the radii of all detected droplets extracted. The final reward was calculated from the mean error between the droplet radii and a desired radius of 27 pixels (corresponding to 54 μm). All reward calculations were performed using classical image processing employing the OpenCV Python module.⁴⁶

4.5. Environment Characterization

Because of the limited complexity of the model environments, a complete characterization of the reward space was performed. Using an automated scheme, observations for every possible flow rate combination were made and post-processed offline, using the respective reward estimators. The obtained reward surface was specific to a single microfluidic device, because variations in the manufacturing and treatment process of identical devices result in altered reward surfaces.

4.6. DQN Algorithm

Our DQN architecture is similar to the dueling network architecture reported by Wang and co-workers.²⁹ Raw camera frames were used as inputs to the neural network–based Q-function. An initial random phase of 10 000 frames and an annealing phase of 135 000 frames (number of frames to change from 100% random actions to 0.05% random actions) were used. Furthermore, the target network parameters were updated every 5000 frames, storing and learning from only the most recent 50 000 frames. A custom DQN version was used, implemented in Python 2.7 using Keras⁴⁷ and the Theano⁴⁸ backend running on Windows 7 (Microsoft Corporation, Redmond, USA). For training and inference of the ANN, a GPU (Quadro K2000; Nvidia, Santa Clara, USA) was used. Finally, custom Python scripts were used to post-process and visualize results.

4.7. MFEC Algorithm

A custom version of MFEC was used, implemented using Python 2.7 according to the published architecture outline.³³ An approximate nearest neighbor search was used to determine related observations with 10 estimators (LSHForest,⁴⁹ implemented by the sklearn Python module⁵⁰). This method was chosen as it allowed for a partial fit (addition) of new data, without needing to recalculate the entire tree for each new observation. Such a complete re-balancing of the tree is performed only in 10% (randomly sampled) of data additions. Observations were pre-processed using the same pre-processing pipeline as DQN. Subsequently, input frames were encoded using a random projection into a vector with 64 components.

Random encoding was used as it showed similar performance compared to a more complex encoding scheme using a variational auto-encoder.³³ The MFEC algorithm required the environment interaction to be split up into episodes (regular intervals at which the complete environment was reset, and performance evaluated).

4.8. Benchmarking Learning Performance

Controller performance in the fluidic environments was benchmarked using scores obtained by both a human tester and a random agent. Random performance benchmarks were obtained by choosing a random action from the available action set every frame and recording the obtained rewards. The random agent represented a lower boundary on performance and served to check initial DQN performance, as it was expected to be random. Human-level performance results were obtained by having two separate trained human agents solve an identical task (observation at the identical position, with identical resolution and an identical action set) for ca. 20 min while recording rewards. Prior to benchmarking, each human tester was given an explanation of the underlying physics and allowed to practice the task for at least 10 min. All benchmarks shown represent the mean reward obtained as well as a 95% confidence interval.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b01485.

• Device architectures, laminar flow challenge raw data, and droplet size challenge raw data (PDF)

The authors declare no competing financial interest.