Adsorption of CO₂ on Heterostructures of Bi₂O₃ Nanocluster-Modified TiO₂ and the Role of Reduction in Promoting CO₂ Activation

Abstract

The capture and conversion of CO₂ are of significant importance in enabling the production of sustainable fuels, contributing to alleviating greenhouse gas emissions. While there are a number of key steps required to convert CO₂, the initial step of adsorption and activation by the catalyst is critical. Well-known metal oxides such as oxidized TiO₂ or CeO₂ are unable to promote this step. In addressing this difficult problem, a recent experimental work shows the potential for bismuth-containing materials to adsorb and convert CO₂, the origin of which is attributed to the role of the bismuth lone pair. In this paper, we present density functional theory (DFT) simulations of enhanced CO₂ adsorption on heterostructures composed of extended TiO₂ rutile (110) and anatase (101) surfaces modified with Bi₂O₃ nanoclusters, highlighting in particular the role of heterostructure reduction in activating CO₂. These heterostructures show low coordinated Bi sites in the nanoclusters and a valence band edge that is dominated by Bi–O states, typical of the Bi³⁺ lone pair. The reduction of Bi₂O₃–TiO₂ heterostructures can be facile and produces reduced Bi²⁺ and Ti³⁺ species. The interaction of CO₂ with this electron-rich, reduced system can produce CO directly, reoxidizing the heterostructure, or form an activated carboxyl species (CO₂^–) through electron transfer from the reduced heterostructure to CO₂. The oxidized Bi₂O₃–TiO₂ heterostructures can adsorb CO₂ in carbonate-like adsorption modes, with moderately strong adsorption energies. The hydrogenation of the nanocluster and migration to adsorbed CO₂ is feasible with H-migration barriers less than 0.7 eV, but this forms a stable COOH intermediate rather than breaking C–O bonds or producing formate. These results highlight that a reducible metal oxide heterostructure composed of a semiconducting metal oxide modified with suitable metal oxide nanoclusters can activate CO₂, potentially overcoming the difficulties associated with the difficult first step in CO₂ conversion.

1. Introduction

Increasing energy demand is leading to fossil fuel supply issues, and the use of fossil fuels has pushed the atmospheric CO₂ concentration to 410 ppm. Continuing CO₂ emissions are projected to result in a higher than 2 °C rise in average global temperatures. Given these severe societal problems, there is an urgent need to find materials that can convert the CO₂ produced by the combustion of fossil fuels back to the fuels or to the precursors for the production of more useful chemicals. This will reduce our reliance on nonsustainable fossil fuels and contribute to curbing anthropogenic CO₂ emissions. The solar-driven photoreduction or thermal reduction of CO₂ to CO or directly to liquid fuels will enable a sustainable approach to producing fuels and storing solar energy in high-energy chemical bonds.¹⁻¹¹

Using solar energy, for example, through solar concentrators, coupled with catalysts that can promote activation of CO₂ to drive the CO₂ reduction process, is an attractive strategy to meet this ambitious aim. However, to date, there are no practical catalysts that can exploit solar energy to efficiently reduce CO₂ to useful chemical species. A range of different catalysts for CO₂ conversion using electrocatalysis, thermochemical catalysis, and photocatalysis has been investigated in recent years, and an example of such a photocatalyst is Pt-modified TiO₂ nanotubes.^8,12,13 However, the efficiencies for methane production are extremely low, and Pt will never be an economically viable catalyst for large-scale CO₂ conversion.

Irrespective of how electrons are provided to reduce CO₂, the key step in any CO₂ capture and use/conversion process is the initial adsorption of CO₂, which should promote the “activation” of the molecule. This activation can be a charge transfer to CO₂, distortions to the molecular structure such as bending of O–C–O away from the linear elongations in the molecular C–O distances, or hydrogenation. CO₂ should either dissociate to a CO molecule or undergo hydrogenation to produce methane or methanol, via formate or carboxyl pathways. The activation should also avoid the production of overstabilized inactive surface-bound carbonates which would poison the catalyst.

In recent years, catalysts based on metallic Cu, oxide-derived Cu, or Cu with mixed oxidation states have gained great interest and have been demonstrated to reduce CO₂ to useful molecules such as methane, methanol, or ethanol.¹⁴⁻²² Recent experimental work indicates the ability of nanocatalysts containing a mix of Cu⁺ and Cu²⁺ oxidation states and in oxide-like structures to promote CO₂ reduction^{1,2,10,14−16,18,19,21−29} and this includes Cu metal, oxide-derived Cu, and mixed oxidation state Cu. Modeling the interaction of CO₂ with copper oxides using density functional theory (DFT) has provided useful results for further development of catalysts for CO₂ conversion. Wu et al. studied the adsorption of CO₂ at the Cu₂O(111) surface in which excess electrons were produced through the formation of oxygen vacancies¹⁸ and found that dissociative adsorption of CO₂ was thermodynamically unfeasible, and although a CO₂^δ− anion could be formed, this was not favorable, and hence excess electrons are not necessarily sufficient to promote CO₂ capture and conversion. Wu et al. also studied the adsorption of CO₂ and its derivatives at Cu₂O(111) using hybrid DFT²¹ and found that only the adsorption of linear CO₂ was favorable. This is supported by the work of Benavid and Carter who showed that physisorption of linear CO₂ is favored over adsorption of bent anionic CO₂.¹⁹ Mishra and colleagues reported strong CO₂ chemisorption at the high-energy Cu–O-terminated (110) surface of Cu₂O¹⁵ and exothermic adsorption of CO₂ at the high-energy (011) surface of CuO.² Uzunova et al. studied the conversion of CO₂ to methanol on Cu₂O nanolayers and clusters¹⁶ using hybrid DFT. The authors considered water as the source of H atoms for the hydrogenation of CO₂ and described a reaction pathway from a carboxyl group (*COOH) to formic acid, which was the rate-limiting step, and then onto formaldehyde and finally methanol. This work would suggest other pathways for CO₂ conversion beyond the dissociation into CO. In the work of Favaro et al.,²⁴ a model of Cu with subsurface oxygen was required for copper to adsorb CO₂ in the first place and understand the experimental findings. However, despite these advances, there still remains an urgent need from both a fundamental and a technoeconomic perspective to discover new materials that can activate and reduce CO₂, in particular to produce sustainable fuels, particularly if renewable energy can be used, either for electroreduction or to produce renewable hydrogen from water.

Another popular metal oxide is titanium dioxide, and the adsorption of CO₂ at different titania surfaces and nanostructures has been widely studied. The roles of excess electrons introduced by oxygen vacancies, low coordinated atomic sites, and the surface structure in CO₂ adsorption and activation have been discussed.³⁰⁻³² The presence of excess electrons and holes was shown to influence the adsorption and activation of CO₂ at rutile (110), and both bent CO₂^– anion and CO₂⁺ cation configurations were identified from the DFT calculations.³³ Lee and Kanai³² used DFT to explore the difference between anatase (101) and a nanostructured TiO₂ quantum dot for CO₂ activation and hydrogenation. They found that the TiO₂ quantum dot promoted CO₂ activation and hydrogenation when compared to the extended anatase (101) surface. Yang and colleagues showed that subnanometer Pt clusters supported on the anatase (101) surface enhanced CO₂ activation through the provision of additional adsorption sites and the transfer of electron density to the TiO₂ substrate.³⁴

Various other metal oxides have been investigated for CO₂ conversion, and several theoretical studies have been conducted into the reaction pathways involving the hydrogenation of CO and CO₂ at a variety of catalytic surfaces, including Cu/CeO₂ and Cu/CeO₂/TiO₂¹⁷ or Cu/ZnO/Al₂O₃.³⁵ An enhanced photoreduction of CO₂ with H₂O vapor has been reported for dispersed CeO₂/TiO₂.³⁶ Here, the ceria is modeled as a small cluster supported on rutile TiO₂, similar to the work on water gas shift,³⁷⁻³⁹ and the role of Ce³⁺ in visible light absorption, photogenerated charge separation, and strengthening of the CO₂–surface bonding was highlighted.

Recent experimental works from Rosenthal and co-workers⁴⁰⁻⁴³ and Walker et al.⁴⁴ strongly suggest that non-transition-metal based catalysts, in particular those containing bismuth or tin, are able to activate CO₂ or convert it to other molecules with good efficiency. The catalysts in refs^40,43 are composed of Bi–glassy carbon and use ionic liquids or Bi nanoparticles, which have large amounts of Bi³⁺. The former materials can convert CO₂ to alcohols with high efficiency, and even though ionic liquids are used, the role of Bi in the catalyst remains crucial to promote the conversion of CO₂.

The bismuth pyrochlore oxide Bi₂Ti₂O₇ was studied in ref (44) and was shown to have high CO₂ chemisorption capacity. In this system, low-energy ion scattering (LEIS) shows clearly that the surface layer is terminated by a bismuth oxide layer. This surface structure arises from the well-known stereochemical lone pair in Bi³⁺.^45,46 By contrast, in the pyrochlore Y₂Ti₂O₇, there is no surface enrichment with Y³⁺ (lacking the lone pair). This Bi-oxide-terminated pyrochlore was examined for its capacity to adsorb and activate CO₂ using infrared spectroscopy. The features in the infrared spectrum corresponding to the adsorbed CO₂ were clearly present upon heating to 308 K. Y₂Ti₂O₇, by contrast, does not strongly adsorb CO₂. This suggests that the adsorption of CO₂ arises from the presence of Bi³⁺ and a bismuth oxide surface layer in the pyrochlore surface.

From the studies in refs,^40,44 it is reasonable to propose that the presence of the Bi³⁺ cation, with its stereochemically active lone pair, in a Bi-oxide structure will be active in promoting the interaction of Bi-containing oxides with CO₂. However, the mechanism of CO₂ adsorption and conversion on Bi³⁺-containing materials, as a good exemplar of the p-block metal oxides, needs to be further investigated, and this is one of the aims of this study.

Previously, we have used first-principles DFT simulations to design heterostructured materials which are composed of TiO₂ (rutile or anatase) surfaces modified with metal oxide nanoclusters. In our earlier work, the emphasis has been on new heterostructured materials with predicted visible light absorption⁴⁷⁻⁵⁹ and reduced charge recombination.^{48−52,60−62} We have recently studied the interaction of molecules, such as CO₂, with tin(II) oxide,⁴⁷ zirconia,⁴⁷ manganese oxide,⁶³ alkaline earth oxide,⁶⁴ and ceria⁶⁵ nanocluster-modified TiO₂ heterostructures. We have found that such nanocluster-modified TiO₂ heterostructures can adsorb CO₂,⁴⁷ but that some heterostructures, such as reduced MnO_x–TiO₂, do not show favorable CO₂ adsorption, even though reduced cations are present.⁶³ There is still much work to be done to understand the factors that drive CO₂ activation on metal oxides.

In the present paper, we take the ideas from the experimental work on CO₂ activation on Bi-containing materials, the ability of nanostructures to activate CO₂, and the activity of nanocluster-modified TiO₂ and use first-principles DFT to examine in detail the interaction and adsorption of CO₂ at Bi₂O₃ nanocluster-modified rutile and anatase TiO₂. We explore the role of the Bi-oxide^, the low coordinated sites in nanoclusters and reduction of the Bi₂O₃–TiO₂ heterostructures in CO₂ adsorption and activation. In some examples, we examine further interaction with hydrogen for the first steps in hydrogenation and formation of intermediates such as COOH or HCOO. The role of heterostructure reduction in CO₂ activation is crucial, wherein the charge transfer from the reduced oxide heterostructure can result in the formation of a carboxylate or direct formation of CO.

2. Methods

In the DFT computations, we follow our approach from previous work⁶¹ and prepare heterostructures of Bi₂O₃ nanoclusters supported on the extended low-energy rutile (110) and anatase (101) surfaces; although other rutile and anatase surfaces can be present in, for example, typical TiO₂ nanoparticles, these are the dominant surface facets and are well-studied.

All DFT computations use a three-dimensional periodic surface slab within the VASP code⁶⁶⁻⁶⁹ and a plane-wave basis set to describe the valence electrons. Projector-augmented wave potentials,^70,71 with 4, 5, 6, 4, and 1 valence electrons for Ti, Bi, O, C, and H, respectively, describe the core–valence electron interactions, and this setup was extensively tested in our earlier work on Bi₂O₃-modified TiO₂.⁶¹ The cutoff for the kinetic energy is 396 eV, and the exchange–correlation functional is the Perdew–Wang 91⁷² approximation. A Monkhorst–Pack (2 × 1 × 1) k-point sampling grid is used. For consistency with our previous work, we apply the DFT + U approach^73,74 to describe the Ti 3d states, with a value of U = 4.5 eV. The convergence criteria for the electronic and ionic relaxations are 0.0001 eV and 0.02 eV/Å. Methfessel–Paxton smearing is used with σ = 0.1 eV (also for the broadening of the peaks in the projected density of states). We use the Newton–Raphson relaxation algorithm, and all calculations are spin-polarized throughout, with no constraints on the spin.

The rutile (110) surface is terminated by twofold coordinated bridging O atoms, with threefold coordinated in-plane oxygen atoms in the surface layer. In the same layer, the Ti atoms take fivefold and sixfold coordinations. The anatase (101) surface is characterized by twofold coordinated oxygen atoms terminating the surface layer, and the outermost Ti atoms are fivefold coordinated. Surface supercell expansions of (2 × 4) and (4 × 2) are employed for rutile and anatase, respectively, and the vacuum gap in all cases is 12 Å.

In forming these composite structures, we first relax the gas-phase metal oxide nanoclusters and the unmodified rutile and anatase surfaces using the same computational setup described above. The oxide nanocluster modifier is adsorbed at the TiO₂ surfaces in different configurations, and each of these are relaxed, as described in refs.^48,57,61,75 We selected the most stable Bi₂O₃–TiO₂ composites for the study of CO₂ activation in the present paper. We will use the term Bi₂O₃–TiO₂ throughout this paper to indicate the general Bi₂O₃ nanocluster-modified TiO₂ heterostructure, using the precise nanocluster composition and TiO₂ surface when necessary.

The stability of the heterostructure is characterized by the computed nanocluster adsorption energy, E^ads

1

where E[(Bi₂O₃)_n–TiO₂] is the computed total energy of the Bi₂O₃ nanocluster-modified TiO₂ surface (in which n is the number of Bi₂O₃ units in the nanocluster, so that in this paper n = 2 or 3), E[(Bi₂O₃)_n] is the computed total energy of the free (Bi₂O₃)_n nanocluster, and E[(TiO₂)] is the computed total energy of the unmodified TiO₂ (rutile/anatase) surface.

The reduction of the Bi₂O₃–TiO₂ heterostructures is studied by removing oxygen from the nanocluster modifier (which is always more stable than removing oxygen from the TiO₂ support) and computing the formation energy of the oxygen vacancy as follows

2

where E{((Bi₂O_3–x)–TiO₂) is the total energy of the Bi₂O₃–TiO₂ composite with one oxygen removed and 1/2E(O₂) is the reference energy for oxygen, namely half the total energy of the O₂ molecule. We correct the oxygen vacancy formation energy for entropy, which, at 298 K, is 0.60 eV. Despite the known errors in the DFT energy of the reference O₂ molecule, the trends in oxygen vacancy formation are independent of this error. We also use ab initio thermodynamics to determine the stability of the reduced Bi₂O₃–TiO₂ heterostructures formed by removing oxygen over a range of temperatures.

To analyze the stability of the reduced heterostructured models when exposed to an environment of oxygen, we use the DFT-derived total energies as an input into an atomistic thermodynamics framework, which considers the effect of the surrounding gas phase as a reservoir that is in thermodynamic equilibrium with the heterostructure. If we assume that the oxygen reservoir exchanges particles with the system without affecting its chemical potential, the oxygen vacancy formation energy is calculated as follows

3

where E(Bi₂O_3−δ–TiO₂) and E(Bi₂O₃–TiO₂) are the total DFT energies of the Bi₂O₃–TiO₂ heterostructures with and without the oxygen vacancy, N_O is the number of oxygen atoms removed, and μ_O(p,T) is the chemical potential of oxygen. Approximating oxygen as an ideal gas, we explicitly introduce pressure and temperature in our model through the analytic relation between the chemical potentials and the temperature and pressure of the two gas reservoirs as follows

4

Here, T and p represent the temperature and partial pressure of oxygen, p⁰ denotes atmospheric pressure, and k_B is the Boltzmann constant. μ′ is the energetic term that includes contributions from the rotations and vibrations of the molecule, as well as the ideal-gas entropy at 1 atm, which can be calculated or taken from the experimental values listed in the thermodynamic tables. Thus, for a given pressure, the stability of oxygen vacancies can be determined over a range of temperatures.

The CO₂ adsorption energy at Bi₂O₃-modified TiO₂ heterostructures is defined in eq 5

5

where E(CO₂@(Bi₂O₃)_n–TiO₂) is the computed total energy of the relaxed adsorption structure of CO₂ at Bi₂O₃-modified TiO₂ composites, whether stoichiometric or reduced. We examined many CO₂ adsorption structures, and those shown in the following text are the most stable that we have found. Although van der Waals corrections can be added to these computations, we have tested and found that the change in the adsorption energies is ca. 0.15 eV, which is not significant compared to the magnitude of the computed CO₂ adsorption energies, and furthermore, there is no effect of the inclusion of vdW corrections on the relative stability of different CO₂ adsorption structures.

3. Results and Discussion

3.1. Bi₂O₃-Modified Rutile and Anatase TiO₂ Heterostructures

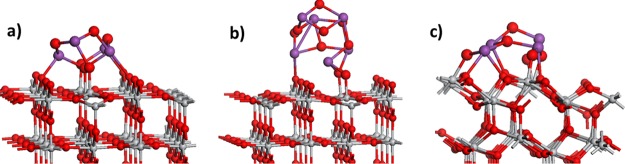
Figure 1 shows the atomic structures of the nanocluster-modified anatase (101) and rutile (110) surfaces of Bi₄O₆ and Bi₆O₉. We have described these heterostructured systems in detail in previous work,⁶¹ and we briefly summarize the key features required for this paper. The adsorption energies can be computed relative to the corresponding gas-phase stoichiometric Bi₂O₃ nanoclusters, and these are −5.18, −5.18, and −5.72 eV for Bi₄O₆-rutile, Bi₆O₉-rutile, and Bi₄O₆-anatase, respectively. If we consider these energies in terms of the deposition of the nanoclusters at very low loading/coverage through atomic layer deposition, chemisorption–calcination, or incipient wetness impregnation, then the above energies can be related to the desorption of the Bi₂O₃ nanoclusters from the TiO₂ supports. The magnitude of the computed energies indicates a strong binding of the nanocluster modifiers at both TiO₂ surfaces and suggests they would only desorb at very high temperatures.

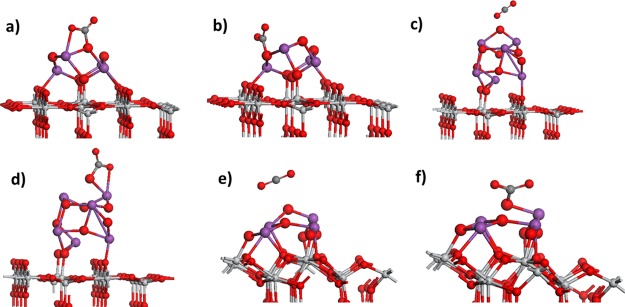
Figure 1.

Relaxed atomic structure for Bi₂O₃ nanocluster-modified rutile (110) and anatase (101). (a) Bi₄O₆-rutile (110), (b) Bi₆O₉-rutile (110), and (c) Bi₄O₆-anatase (101). The color coding in this and subsequent figures is Ti = light gray sphere, O = red sphere, and Bi = purple sphere. Bi and O atoms in the adsorbed nanoclusters are depicted by larger radius spheres.

We can also consider the stability against sintering into larger nanoclusters. In the gas phase, the gain in energy when two nanoclusters of composition Bi₂O₃ coalesce into a larger Bi₄O₆ nanocluster is −6.1 eV, and the coalescence of a gas-phase Bi₂O₃ and a gas-phase Bi₄O₆ nanocluster results in a gain of 3.1 eV. On the surface, we use the total energies of the bismuth oxide nanocluster-modified rutile heterostructures to assess the nanocluster stability against coalescence into larger nanoclusters.⁷⁵ For the example of Bi₂O₃ and Bi₄O₆ coalescing to a Bi₆O₉ nanocluster

The computed energy is +2.69 eV against coalescence of the two smaller nanoclusters supported on rutile (110). Thus, when the Bi₂O₃ nanoclusters are supported on rutile or anatase, they will be stable against desorption or aggregation. The high stability of the supported Bi₂O₃ nanoclusters is primarily driven by the formation of new interfacial bonds between the nanocluster and the surface. We also note that the extensive work of Graciani et al. on ceria–TiO₂ used small Ce₂O₃ species supported on rutile (110),^38,39 which were also shown to be highly stable.

On Bi₄O₆-rutile, two Bi cations bind to the bridging surface oxygen, with typical Bi–O distances of 2.17 Å. These Bi cations are threefold coordinated, whereas the remaining Bi cations are twofold coordinated. Three oxygen atoms from the nanocluster bind to the fivefold coordinated Ti surface atoms, with the Ti–O distances in the range of 1.83–2.05 Å. In the Bi₆O₉-rutile nanocluster, one Bi cation binds to a bridging oxygen, with a Bi–O distance of 2.37 Å. Two oxygen atoms from the nanocluster bind to the surface Ti atoms, with the Ti–O distances of 1.94 and 1.86 Å. Here, the terminal Bi cations, furthest away from the cluster–surface interface, are threefold coordinated, and there are twofold coordinated oxygen sites in the nanocluster.

In Bi₄O₆-anatase, three Bi cations bind to the surface oxygen, with the Bi–O distances of 2.14, 2.14, 2.24, and 2.17 Å. The two Bi cations furthest away from the cluster–surface interface are threefold coordinated and the remaining Bi cations are fourfold coordinated. Four oxygen atoms in the nanocluster bind to the surface Ti, with the distances Ti–O in the range of 1.87–2.06 Å. There are three twofold coordinated oxygen sites: one is the terminal oxygen in the nanocluster and the remaining two sites bridge the nanocluster and the anatase (101) surface.

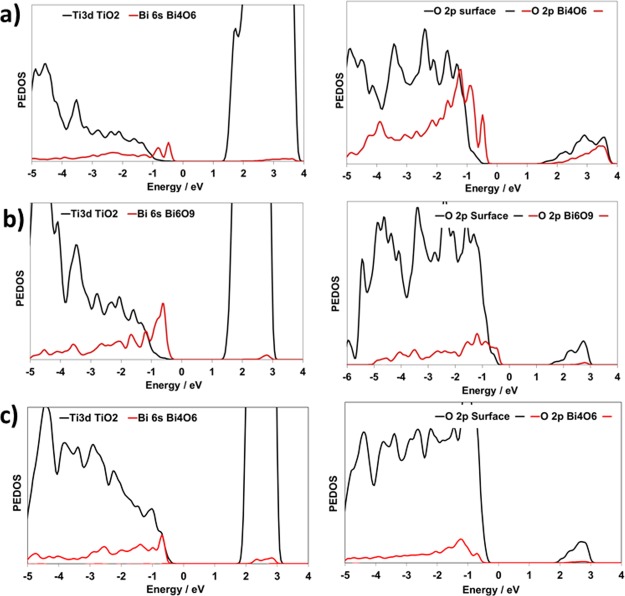
The other important aspect of the Bi₂O₃–TiO₂ composites for the interaction with CO₂ is their electronic properties, and in Figure 2 we show the projected electronic density of states (PEDOS) for the Bi₂O₃-rutile and Bi₂O₃-anatase systems. Bi³⁺ is an interesting species as it has a stereochemically active lone pair, which results in the presence of Bi-derived electronic states at the top of the valence band. This gives rise to the distorted structure of bulk Bi₂O₃⁴⁶ and the Bi-rich surface region in the pyrochlore Bi₂Ti₂O₇.⁴⁴ The other metal oxides with +3 cations do not show these structural distortions.

Figure 2.

PEDOS projected onto the Bi 6s, Ti 3d, and O 2p states (nanocluster and surface) for (a) Bi₄O₆ rutile (110), (b) Bi₆O₉-rutile (110), and (c) Bi₄O₆-anatase (101). The zero of energy in all cases is the Fermi level. The left panels show the cation PEDOS and the right panels show the oxygen 2p PEDOS.

In the PEDOS of the Bi₂O₃–TiO₂ heterostructures, the Bi electronic states are present at the valence band edge of all the composite systems studied. For modified rutile (110), we see Bi (6s + 6p) and O 2p states originating from the nanoclusters lying at a higher energy than the corresponding TiO₂ valence and conduction band edges, which should result in a small red shift in light absorption. For anatase, the Bi₂O₃-derived states lie just below the anatase valence band edge, which results in no predicted red shift. The key finding is that the Bi states lie at the top of the valence band edge, and this can be important in the reduction or CO₂ adsorption on the Bi₂O₃–TiO₂ heterostructures.

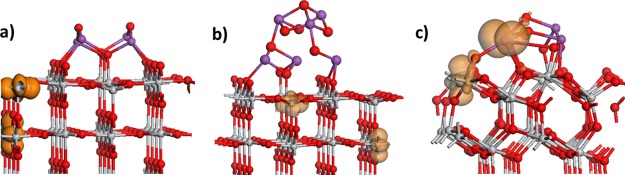
Finally, we present the results for the reduction of the Bi₂O₃–TiO₂ heterostructures. The reduced heterostructures are prepared by removing oxygen atoms from the Bi₂O₃ nanoclusters and computing the oxygen vacancy formation energy. From a practical perspective, reduction can be facilitated by a thermochemical process using concentrated solar radiation or by the introduction of hydrogen in a redox process. Relaxing the structure after the removal of oxygen, the most stable reduced heterostructures are shown in Figure 3. The computed formation energies for the most stable oxygen vacancy sites are 1.75 eV (1.12 eV) for Bi₄O₆-rutile (110), 1.64 eV (1.01 eV) for Bi₆O₉-rutile (110), and 3.0 eV (2.37 eV) for Bi₄O₆-anatase (101), where the formation energies corrected for TΔS at 298 K are given in parentheses. These formation energies that show a moderate cost for oxygen vacancy formation in the supported Bi₂O₃ nanoclusters are notably smaller than that on the corresponding bare TiO₂ surfaces (3.5 eV for rutile (110) and 3.6–4.1 eV for anatase (101)⁷⁶), so that reduction should be possible under moderate conditions. The other oxygen sites have formation energies larger than 2 eV on Bi₄O₆-rutile and between 3.4 and 3.7 eV on Bi₄O₆-anatase. Figure 4 shows the stability of the most stable oxygen vacancy sites in each heterostructure as a function of temperature at a pressure of 1 atm. From this plot, we can see that reduction should take place at 500–600 K, which is certainly feasible in the context of CO₂ reduction/conversion processes. For the rutile-supported Bi₆O₉ nanocluster, the larger formation energy of the vacancy clearly results in a higher temperature for vacancy formation, although this is still notably lower than that on bare rutile (110).

Figure 3.

Atomic structure and spin density isosurfaces of the most stable reduced Bi₂O₃–TiO₂ heterostructures: (a) Bi₄O₆-rutile (110), (b) Bi₆O₉-rutile (110), and (c) Bi₄O₆-anatase (101). Spin density isosurfaces enclose spin densities up to 0.02 electrons/ų. The color coding of the atoms is the same as in Figure 1.

Figure 4.

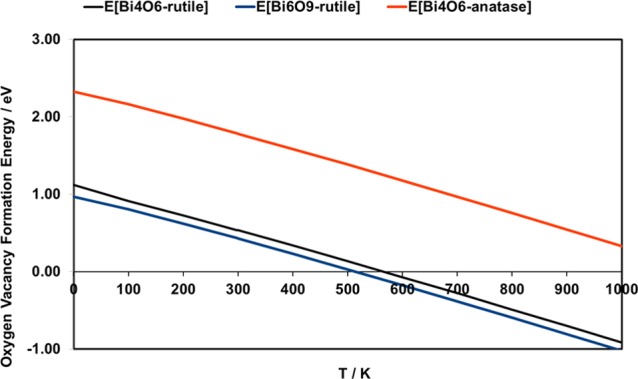
Computed oxygen vacancy formation energy for Bi₂O₃-modified TiO₂ as a function of temperature at a pressure of 1 atm.

After the reduction of the Bi₂O₃ nanoclusters, the local atomic structure shows some changes. On Bi₄O₆-rutile (110), the removal of oxygen results in the formation of a structure that shows symmetry, with two twofold coordinated oxygen atoms terminating the nanocluster. The Bi cations are threefold coordinated, and each Bi atom binds to a bridging oxygen atom from the rutile (110) surface, with the Bi–O distances in the range of 2.17–2.18 Å. Furthermore, each Bi atom also coordinates to one oxygen from the nanocluster, which itself binds to a surface Ti atom, with the Bi–O distances of 2.07–2.15 Å and Ti–O distances of 2.03 Å.

On Bi₆O₉-rutile, the formation of the most stable oxygen vacancy results in small changes to the nanocluster structure. Two Bi cations are coordinated to the surface-bridging oxygen sites, with the Bi–O distances of 2.20–2.23 Å. Two nanocluster oxygen bind to the surface fivefold coordinated Ti, with the Ti–O distances of 1.89 and 2.02 Å, whereas after relaxation, four oxygen atoms take a twofold coordination environment by breaking the bonds with Bi cations (giving long Bi–O distances of 2.51 and 2.56 Å).

On Bi₄O₆-anatase, two Bi cations are threefold coordinated and the remaining cations are fourfold coordinated. The typical Bi–O distances range from 1.86 to 2.15 Å, and the Bi–O distances to the surface range from 2.12 to 2.16 Å. One oxygen atom from the surface migrates outward to bind to a Bi cation in the nanocluster, with three oxygen atoms in the nanocluster binding to the surface Ti sites; the Bi–O distances are in the range 1.86–1.90 Å.

The localization of the two electrons released upon removal of the neutral oxygen atom is shown by the spin density isosurfaces in Figure 3. For both Bi₂O₃ nanocluster-modified rutile (110) composites, the electrons preferentially localize on the Ti sites in the rutile (110) surface, with the computed Ti Bader charges of +1.65/1.71 electrons in Bi₄O₆-rutile and +1.65/1.69 electrons in Bi₆O₉-rutile and spin magnetization in the range 0.92–0.94 μ_B. For reference, Ti⁴⁺ cations have computed Bader charges of +1.30 electrons and zero spin magnetization. The first electron localizes on a subsurface Ti site and the second electron localizes onto a surface fivefold coordinated Ti site that has no interaction with the supported nanocluster. These values are typical of the reduced Ti³⁺ species in rutile (110).

In contrast, on Bi₄O₆-anatase (101), the two electrons localize on a surface fivefold coordinated Ti³⁺ site and on a Bi site in the nanocluster, which results in the formation of a reduced Bi²⁺ species. The computed Bader charges are +1.74 electrons on Ti and +2.99 electrons on Bi; the latter is comparable to a computed Bi Bader charge of +2.1 electrons for Bi³⁺ cations, indicating the reduction of the Bi species. The computed spin magnetizations on Ti and Bi are 0.96 and 0.7 μ_B. This Bi site binds to the oxygen that migrated out of the surface, and this particular oxygen bridges the two reduced Ti³⁺ and Bi²⁺ sites.

3.2. Adsorption of CO₂ at Reduced Bi₂O₃–TiO₂ Heterostructures

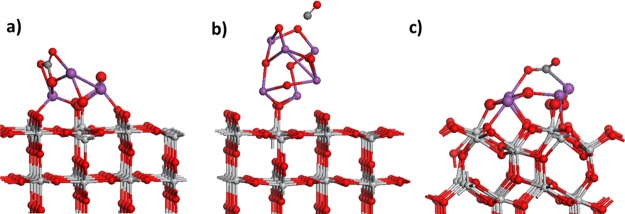
We now discuss the adsorption of CO₂ at the Bi₂O₃ nanocluster-modified TiO₂ heterostructures, and in this section we focus on the reduced heterostructures. We examined the interaction of the reduced Bi₂O₃–TiO₂ heterostructures with CO₂ in a number of adsorption configurations. Figure 5 shows the most stable relaxed structures after the relaxation of adsorbed CO₂ on each reduced Bi₂O₃–TiO₂ heterostructure. The computed interaction energies for CO₂ are −0.45 eV on reduced Bi₄O₆-rutile (110), −0.53 eV on reduced Bi₆O₉-rutile (110), and −0.93 eV on reduced Bi₄O₆-anatase (101). These energies indicate a moderately strong interaction between the initially reduced metal oxide heterostructure and the CO₂ molecule.

Figure 5.

Atomic structure of the most stable CO₂ adsorption structures on reduced Bi₂O₃–TiO₂ composites: (a) Bi₄O₆-rutile (110), (b) Bi₆O₉-rutile (110), and (c) Bi₄O₆-anatase (101). The color coding is the same as in Figure 1, with an additional inclusion of a gray sphere for carbon. The Bi and O atoms in the supported Bi₂O₃ nanoclusters are depicted with larger diameter spheres.

CO₂ binds to reduced Bi₄O₆-rutile (110) with the formation of two Bi–O bonds, with the Bi–O distances of 2.45 and 2.52 Å. The carbon of CO₂ binds to the oxygen in the nanocluster, with a C–O distance of 1.38 Å. The C–O distances in the adsorbed CO₂ are elongated to 1.27 Å, and the O–C–O angle is 130°. Thus, the CO₂ molecule adsorbs moderately exothermically on the reduced supported Bi₄O₆ nanocluster in a manner that can be considered carbonate-like with a tridentate adsorption configuration, although one of the C–O bonds is significantly longer than the typical C–O carbonate distance.

Examining the electronic structure in the CO₂–Bi₄O₆-rutile system, the computed Bader charges on the previously reduced Ti atoms are now +1.3 electrons, signifying the presence of oxidized Ti⁴⁺ species. Interestingly, we find that the charge on two Bi cations in the nanocluster changes to 2.8 and 3.2 electrons, indicating that these Bi cations are partially reduced. One of these Bi cations binds to the oxygen of CO₂, suggesting a rearrangement of charge upon CO₂ adsorption.

On Bi₆O₉-rutile (110), the relaxation of initially adsorbed CO₂ leads to spontaneous breaking of a C–O bond in the molecule, which results in the release of a free CO molecule, with no energy barrier to this process. Although one might expect a significant energy gain in breaking a C–O bond, we have to consider that this process heals the vacancy site on the Bi₂O₃ nanocluster, which has a high stability, and there would also be an energy cost to break the C–O bond in the molecule. In any case, the key point is the exothermic release of CO.

When CO is released, the previous supported Bi₆O₈ nanocluster is reoxidized, with the Bi₆O₉ composition. Examining the atomic structure, we see that the free CO has a C–O distance of 1.14 Å, which is typical of the gas-phase CO, and the Bi–O distances are similar to those in the stoichiometric Bi₆O₉-rutile system. In the Bi₆O₉-rutile system, the computed Bader charges of Ti and Bi are +1.3 and +2.2 electrons, consistent with the presence of only oxidized Ti⁴⁺ and Bi³⁺ species. The electrons on the TiO₂ surface after reduction are therefore transferred to CO₂ to allow the formation of new Bi–O bonds and a free CO molecule.

To examine this in more detail and complete a redox cycle, we adsorb H₂ at the site of the oxygen species that results from CO₂ dissociation, that is, oxygen that reoxidized reduced Bi₆O₈-rutile. Upon relaxation, a water molecule spontaneously forms, with an exothermic energy gain of 1.13 eV which reduces the Bi₆O₉ nanocluster; removal of water from the supercell requires 0.43 eV, and the reduced supported nanocluster is available for reaction with another CO₂. Thus, the Bi₆O₉ nanocluster supported on rutile TiO₂ appears to show a pathway for CO₂ dissociation through a redox process involving water formation in a reverse water gas shift-like process.

Finally, on Bi₄O₆-anatase (101), the computed Bader charges on the CO₂ molecule indicate a charge transfer of ca. 1.5 electrons to the molecule from the reduced composite. The computed Bader charges of 1.3 and 2.1 electrons on previously reduced Ti and Bi further support this electron transfer, which reoxidises Ti and Bi. This process then results in the formation and stabilization of a carboxyl, CO₂^– species. This is one of the activated CO₂ species that is important in CO₂ conversion. In the gas phase, the potential required for the formation of CO₂^– is prohibitively high, but in the reduced Bi₂O₃-modified anatase system, the presence of both low coordinated active sites and excess electrons after reduction appears to facilitate electron transfer to the adsorbed CO₂ molecule. In adsorbed carboxyl, the C–O distances are 1.25 and 1.27 Å, again showing a significant elongation over the free molecule. The bending of CO₂ upon interaction with the nanocluster is also apparent, with an O–C–O angle of 130°. CO₂ binds to the nanocluster through a Bi–O bond, which has a distance of 2.42 Å and a Bi–C bond of 2.37 Å involving a second Bi atom in the nanocluster.

The computed vibrational frequencies for CO₂ adsorbed on reduced heterostructures are shown in Table 1. The computed gas-phase vibrational modes of CO₂ are 2354, 1325, and 632 cm^–1, with the latter being degenerate. These correspond to the asymmetric C=O stretch, the symmetric C=O stretch, and the O–C–O bending mode. The large red shift in the C=O stretching mode of 760 and 767 cm^–1 on Bi₄O₆-rutile and Bi₄O₆-anatase is consistent with the strong adsorption of CO₂, as is the breaking of the degeneracy in the CO₂ bending mode upon adsorption. We note that on Bi₄O₆-anatase the splitting of the degeneracy in the CO₂ bending mode is larger, the origin of which is likely due to one oxygen of CO₂ not binding with the Bi₂O₃ nanocluster. By contrast, the two oxygen atoms in CO₂ bind with the nanocluster in Bi₄O₆-rutile, so that the split in the degeneracy of the two modes is smaller.

Table 1. Computed CO₂ Vibrational Frequencies for Activated CO₂ at Reduced Bi₂O₃–TiO₂^a.

reduced Bi2O3–TiO2 heterostructure	CO2 vibrational frequencies/cm–1
Rutile (110)
Bi4O6-rutile (110)	1594, 1254, 941, 774
Bi6O9-rutile (110)	gas-phase CO
Anatase (101)
Bi4O6-anatase (101)	1587, 1203, 700, 531

^aOur computed vibrational frequencies of free CO₂ are 2354, 1325, and 632 cm^–1, which can be compared with the experimental data: 2349 cm^–1 (C=O asymmetric stretch), 1388 cm^–1 (C=O symmetric stretch), and 667 cm^–1 (C=O bonding, degenerate).

In addition to the excess electrons introduced by reduction and the presence of Bi–O electronic states at the top of the valence band, the atomic structure of the supported Bi₂O₃ nanoclusters can facilitate CO₂ adsorption because of the presence of low coordinated atomic sites and the flexibility in these supported nanoclusters that allows strong relaxations after the adsorption of molecules. We can also relate these findings to the work of Walker et al.⁴⁴ on the Bi-containing pyrochlore. In this system, the surface is terminated by a Bi–O layer, similar to our Bi₂O₃ nanocluster-modified TiO₂, and the Bi 6s/6p electronic states are mixed with O 2p states at the top of the valence band. Thus, the pyrochlore has a suitable electronic structure to permit interaction with CO₂ and an atomic structure that also facilitates the interaction with CO₂.

Given that the adsorption of CO₂ is the crucial first step in the catalytic conversion of CO₂, which is generally not favorable or could form highly stable carbonates on metal oxides, our finding that CO₂ interacts moderately strongly with the reducible Bi₂O₃-modified TiO₂ and can form CO or a carboxyl intermediate is a key result of this work.

3.3. CO₂ Adsorption at Oxidized Bi₂O₃–TiO₂ Heterostructures

Table 2 presents the computed adsorption energies of the two most stable adsorption configurations of CO₂ at each oxidized Bi₂O₃–TiO₂ heterostructure, and Figure 6 shows the relaxed atomic structures for these CO₂ adsorption configurations. From Table 2, we can see that there is at least one moderately strong interacting CO₂ adsorption configuration at each Bi₂O₃– TiO₂ heterostructure, with the computed adsorption energies of −0.54, −1.01, and −0.82 eV on Bi₄O₆-rutile, Bi₆O₉-rutile, and Bi₄O₆-anatase, respectively. Compared to the computed adsorption energies of CO₂ on other oxidized metal oxide-modified TiO₂ systems, for example, in ref (47) or on polymorphs of TiO₂ itself,^10,30,31 the adsorption energies of CO₂ on Bi₂O₃-modified TiO₂ are notably stronger, indicating that these heterostructures are more favorable toward CO₂ adsorption, although we note that there is no direct formation of CO or carboxylate, suggesting that the oxidized Bi₂O₃–TiO₂ heterostructures may facilitate CO₂ capture.

Table 2. Computed Adsorption Energies, in eV, of CO₂ at Bi₂O₃-Modified Rutile (110) and Anatase (101) Heterostructures.

adsorption configuration	Eads/eV
On Rutile (110)
Bi4O6-rutile (110) + CO2	–0.37
Bi4O6-rutile (110) + CO2	–0.54
Bi6O9-rutile (110) + CO2 (linear)	–0.28
Bi6O9-rutile (110) + CO2	–1.01
On Anatase (101)
Bi4O6-anatase (101) + CO2 (linear)	–0.51
Bi4O6-anatase (101) + CO2	–0.82

Figure 6.

Relaxed adsorption structures of CO₂ at Bi₂O₃-modified rutile (110) and anatase (101) composites; the composition is indicated in each case. (a,b) CO₂ adsorption at Bi₄O₆-rutile (110) (c,d) CO₂ adsorption at Bi₆O₉-rutile (110), and (e,f) CO₂ adsorption at Bi₄O₆-anatase (101). The color coding is the same as in Figure 3.

Examining the atomic structures for the adsorbed CO₂, we see that there are adsorption configurations on Bi₆O₉-rutile and Bi₄O₆-anatase, namely the configurations in Figure 6c,e, which have the weakest interactions and show a linear CO₂ that is unchanged from the gas phase. This is a CO₂ physisorption mode, which we do not expect to be important.

The other adsorption modes in Figure 6 are of more interest, and these show new C–O interactions with the supported nanoclusters, and the adsorption structure is consistent with a carbonate-like adsorption mode, albeit without the strong stabilization usually found for carbonate adsorption,^64,65 and consistent with the CO₂ adsorption on the Bi-oxide-terminated pyrochlore.⁴⁴

Table 3 presents the important C–O distances, O–C–O bending angles, and the computed CO₂ vibrational modes. The common feature of these adsorption modes of CO₂ is that the molecule is clearly bent (gas-phase CO₂ is linear, with an O–C–O angle of 180°). The O–C–O angles in the adsorbed CO₂ are 131°, 127°, and 130° on Bi₄O₆-rutile, Bi₆O₉-rutile, and Bi₄O₆-anatase. This is consistent with the bending of activated CO₂ observed on other materials, including transition-metal carbides, or on ceria-modified rutile (110).^4,77,78

Table 3. Computed C–O and Bi–O Distances and CO₂ Vibrational Frequencies for CO₂ Adsorbed at Bi₂O₃-Modified Rutile (110) and Anatase (101)^a.

structure	C–O/Å	O–C–O angle/°	CO2 vibrational frequencies/cm–1
Rutile (110)
Bi4O6-rutile (110) + CO2	1.27, 1.26, 1.39	131	1617, 1250, 924, 774
Bi6O9-rutile (110) + CO2	1.26, 1.29, 1.39	127	1531, 1304, 1028, 774
Anatase (101)
Bi4O6-anatase (101) + CO2	1.26, 1.27, 1.39	130	1593, 1243, 917, 790

^aThe first two C–O distances in column 2 are in the adsorbed molecule and the third C–O distance is to oxygen in the Bi₂O₃ nanocluster. Our computed vibrational frequencies of free CO₂ are 2354, 1325, and 632 cm^–1, with the latter being degenerate.

On Bi₄O₆-rutile, the C–O distances in the adsorbed CO₂ elongate to 1.26 and 1.27 Å, whereas the C–O distance to nanocluster oxygen is 1.39 Å. This is a notable elongation in the C–O distances over those in the gas-phase molecule (which is 1.16 Å). Similarly, on Bi₆O₉-rutile, the resulting bidentate adsorption configuration has elongated C–O distances of 1.26 and 1.29 Å in the molecule, whereas the C–O distance to the nanocluster is 1.39 Å. On Bi₄O₆-anatase, the carbon atom binds in a monodentate fashion to one oxygen in the nanocluster, with a C–O distance of 1.39 Å, whereas the C–O distances in the molecule are 1.26 and 1.27 Å.

Clearly, on Bi₂O₃-modified TiO₂, although the CO₂ molecule does not adsorb in a typical carbonate adsorption mode in which the three C–O distances are equal (∼1.29 Å) and the O–C–O angles are 120°, we can nonetheless describe the adsorption as carbonate-like. Although a new C–O interaction with a C–O distance of 1.39 Å is present, we can propose that this interaction participates in helping to stabilize the adsorbed CO₂, so that it can further interact with hydrogen (see Section 3.3).

We have also computed the vibrational modes of adsorbed CO₂ on Bi₂O₃-modified TiO₂. Upon the adsorption of CO₂ at the oxidized Bi₂O₃–TiO₂ heterostructures, there are significant red shifts in the asymmetric C=O stretch of 737, 823, and 761 cm^–1 on Bi₄O₆-rutile, Bi₆O₉-rutile, and Bi₄O₆-anatase, respectively. The degeneracy of the O–C–O bending mode is lifted upon adsorption at Bi₂O₃–TiO₂. CO₂ adsorbed on Bi₆O₉-rutile shows the largest red shift of the C=O stretch, which is consistent with its larger adsorption energy and distortions away from the gas-phase CO₂ geometry. This shift in the C=O stretching mode correlates with the strength of the CO₂–Bi₂O₃–TiO₂ interaction, and it has been observed in the experimental studies of CO₂ adsorption on a range of materials.⁷⁹⁻⁸¹

Finally, we briefly examine the electronic structure. Figure 7 shows the PEDOS for C and O atoms in CO₂, and Ti and Bi atoms, as the examples of CO₂ adsorbed on Bi₆O₉-rutile and Bi₄O₆-anatase. In both cases, the CO₂-derived C 2p and O 2p electronic states lie at the top of the valence band. Furthermore, there is a strong interaction between the Bi 6s/6p states and the carbon and oxygen 2p states of CO₂. This is consistent with the strong interaction and distortion of CO₂ when adsorbed at the supported Bi₂O₃ nanoclusters. We have also computed the Bader atomic charges upon CO₂ adsorption. These do not show a significant charge transfer between Bi₂O₃–TiO₂ and CO₂, indicating that there is no charge transfer upon the adsorption of CO₂.

Figure 7.

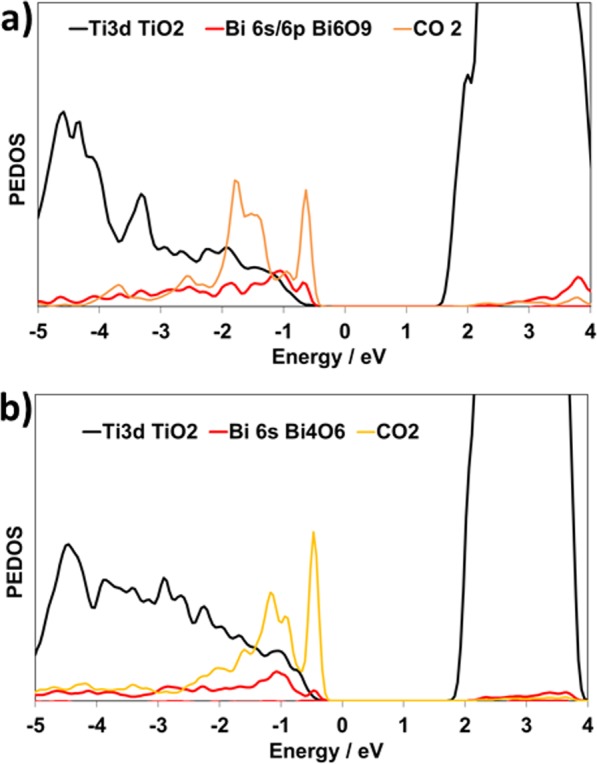
PEDOS projected onto the Ti 3d, Bi 6s/6p, and CO₂ 2p states after the adsorption of CO₂ onto (a) Bi₆O₉-rutile and (b) Bi₄O₆-anatase.

In understanding the strong CO₂ adsorption without any significant charge transfer, we consider the atomic and electronic structures of Bi₂O₃ nanocluster-modified TiO₂. The nature of the valence band of Bi₂O₃–TiO₂, with high-lying Bi₂O₃-derived electronic states, permits the interaction of these Bi–O electronic states with the C and O atoms of CO₂. This can be considered similar to the case of the alkaline earth oxides, which show increased basicity and higher energy valence band states on going from Mg to Ca to Ba, and the interaction with CO₂ is stronger with the increased basic character along this series.

3.4. Hydrogenation of Adsorbed CO₂

Starting from the CO₂ adsorption structures in Section 3.3, which show moderate adsorption energies and distortions to CO₂ but no direct CO formation, we first examined the dissociation and formation of CO and adsorbed oxygen. However, such starting structures relax back to those already described, and if we remove CO, this is endothermic by up to 3 eV.

We have therefore examined the first steps in hydrogenation to explore if the adsorbed CO₂ species can be hydrogenated. We focus on Bi₄O₆-rutile and Bi₄O₆-anatase, with the most favorable CO₂ adsorption modes discussed above. We adsorb a hydrogen atom at the Bi₂O₃–TiO₂ heterostructure to simulate the dissociation of H₂ and the formation of a hydroxyl on the nanocluster. We then use the climbing image NEB method with three images to determine the activation barrier for H migration, from which either a formate or carboxyl species can be produced.

Figure 8a,b shows the structure of the H atom adsorbed as a hydroxyl on Bi₄O₆-rutile and Bi₄O₆-anatase. The energy gain relative to 1/2 H₂ (in gas phase) is 1.42 eV on Bi₄O₆-rutile and 0.63 eV on Bi₄O₆-anatase. These are moderate energy gains for hydrogen adsorption. Upon H adsorption at Bi₄O₆-rutile, the O–H distance is 0.98 Å, and the Bi–O distances involving this oxygen are 2.25 and 2.44 Å. On Bi₄O₆-anatase, the O–H distance is 1.01 Å, and the Bi–O distances for this oxygen are 2.31 and 2.18 Å.

Figure 8.

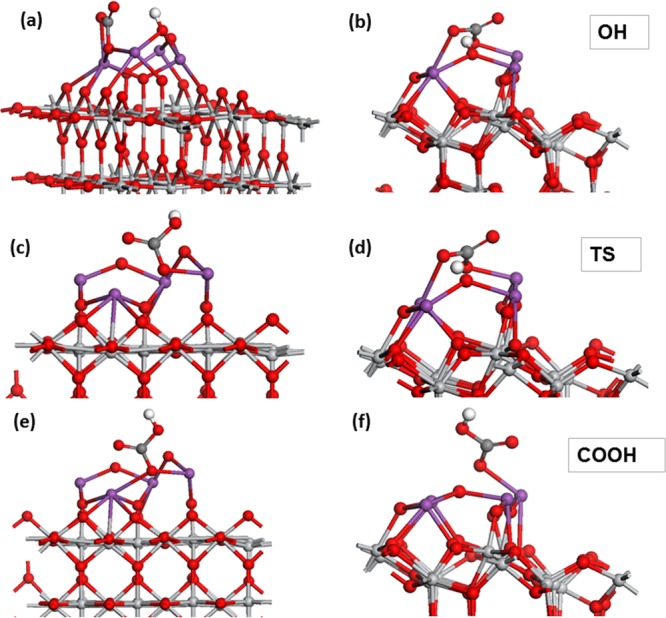
(a) Atomic structure of a hydroxyl species on Bi₄O₆-rutile with adsorbed CO₂. Hydrogen is denoted by the white sphere. (b) Atomic structure of a hydroxyl species on Bi₄₆O₆-anatase with adsorbed CO₂. (c) Atomic structure of the transition state for H migration to adsorbed CO₂ on Bi₄O₆-rutile. (d) Atomic structure of the transition state for H migration to adsorbed CO₂ on Bi₄O₆-anatase. (e) Atomic structure of a COOH intermediate on Bi₄O₆-rutile. (f) Atomic structure of a COOH intermediate on Bi₄O₆-anatase.

The computed barrier for H migration from the hydroxyl to oxygen in CO₂ to form a carboxyl intermediate is 0.77 eV on Bi₄O₆-rutile (110) and 0.68 eV on Bi₄O₆-anatase (101). These are moderate barriers for the H transfer to the adsorbed CO₂. The atomic structure of the transition state is shown in Figure 8c,d. In the transition state on Bi₄O₆-rutile, the H atom has migrated away from the nanocluster toward the oxygen of the adsorbed CO₂. On Bi₄O₆-anatase, the transition state involves the H atom migrating away from the oxygen of the nanocluster by 0.25 Å toward CO₂.

The atomic structure of the carboxyl intermediate on Bi₄O₆-rutile and Bi₄O₆-anatase is shown in Figure 8e,f. For the COOH intermediates, the C=O, C–O(H), OH, and C–O(Bi) distances are presented in Table 4. We also examined the formation of a formate intermediate. However, formate either lies higher by ca. 3 eV, on Bi₄O₆-rutile, or is not stable, relaxing to COOH on Bi₄O₆-anatase, and thus the COOH intermediate is preferred. If we introduce a second hydrogen atom to make COOH₂, this always relaxes to water and CO₂, removing oxygen from the Bi₂O₃ nanocluster, and thus we conclude that although CO₂ can adsorb at the oxidized Bi₂O₃–TiO₂ nanoclusters, it is difficult to hydrogenate to useful products.

Table 4. Computed C=O, C–O(H), OH, and C–O(Bi) Distances in COOH Intermediates on Bi₄O₆-Rutile and Bi₄O₆-Anatase in Å.

Bi4O6-rutile (110)		Bi4O6-anatase (101)
C=O	1.24	C=O	1.24
C–O(H)	1.35	C–O(H)	1.37
OH	0.98	OH	0.98
C–O(Bi)	1.31	C–O(Bi)	1.31

4. Conclusions

We have studied the interaction and activation of CO₂ at the novel heterostructure of Bi₂O₃ nanoclusters supported on rutile and anatase TiO₂ surfaces. Previous experimental work has demonstrated that Bi-containing materials can activate and convert CO₂ to more useful molecules, but the origin of this is not yet clear.

The Bi₂O₃–TiO₂ heterostructures can be reduced, with moderate energy costs, which should be possible through a thermochemical process or by the addition of hydrogen. This results in the reduction of Ti sites, and Bi sites in the nanocluster can also be reduced. The interaction of the reduced heterostructures with CO₂ can result in direct exothermic CO formation, or charge transfer to CO₂ (reoxidizing Bi and Ti cations), to give an activated carboxylate species. The CO can be removed, and the addition of hydrogen is an exothermic process that forms water and reduces the nanocluster. This suggests a promising approach for CO₂ conversion via CO.

We find that CO₂ adsorbs moderately strongly at the oxidized Bi₂O₃–TiO₂ heterostructures, with the computed adsorption energies ranging from −0.54 to 1.01 eV; van der Waals interactions simply shift these energies by ca. 0.15 eV, but do not change the overall trends. CO₂ adsorbs in a carbonate-like adsorption mode (but is not overstabilized), with no charge transfer to the molecule. Finally, the computed vibrational modes of the adsorbed CO₂ show a significant red shift of over 750 cm^–1 in the C=O stretching mode and a breaking of the degeneracy in the O–C–O bending mode. The magnitude of the red shift in the C=O stretching mode correlates with the strength of the adsorption of CO₂. The position of the high-lying valence band states derived from Bi³⁺–O interactions appear to drive the activation of CO₂.

We find that the CO₂ adsorbed in this fashion can be hydrogenated to a COOH intermediate, with the migration barriers from the nanocluster to the adsorbed CO₂ of less than 0.8 eV, whereas CO₂ dissociation is not favorable. However, further hydrogenation of COOH does not result in any useful products, and we conclude that reduction is the key to the activation and subsequent conversion of CO₂ on Bi₂O₃-modified TiO₂ heterostructures.

These results show that the unique properties of bismuth-containing oxides can be exploited to adsorb and activate carbon dioxide, which is the key first step in the reductive conversion of CO₂ to useful molecules. The combination of a non-bulk-like nanocluster-containing Bi³⁺ species, which is reducible, provides an interesting material that can activate CO₂, whether that be by strong adsorption and distortion, electron transfer to form a carboxylate, or by direct breaking of a C–O bond, and we propose that these heterostructures can be synthesized and tested for CO₂ activation.

The author declares no competing financial interest.