Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2017 Oct 13;2(10):6708–6714. doi: 10.1021/acsomega.7b01004

Energetics of Saddling versus Ruffling in Metalloporphyrins: Unusual Ruffled Dodecasubstituted Porphyrins

Jeanet Conradie †,‡,*, Abhik Ghosh †,*
PMCID: PMC6644939  PMID: 31457262

Abstract

graphic file with name ao-2017-01004m_0006.jpg

Presented herein is a first major density functional theory (BP86/D3/STO-TZ2P) survey of the energetics of saddling versus ruffling for a wide range of dodecasubstituted metalloporphyrins with M = Ni, Cu, Zn, Pd, and Pt. For the majority of X8TPP (i.e., β-octasubstituted-meso-tetraphenylporphyrin), the calculations indicated a clear preference for the saddled conformation, consistent with a large body of experimental data. The preference for the saddled conformation relative to the ruffled conformation was found to vary from about ∼0.3–0.4 eV for Me8TPP derivatives up to 1 eV for I8TPP and (CF3)8TPP derivatives. For X = Ph, that is, dodecaphenylporphyrins, the saddled and the ruffled conformation are almost equienergetic, with even a slight preference for the ruffled conformation in some cases. This finding provides a satisfactory explanation for the X-ray crystallographic observation of both saddled and ruffled conformations for dodecaphenylporphyrin complexes as well as for spectroscopic evidence for conformational mobility of these complexes in solution. The calculations also indicate near-equienergetic saddled and ruffled conformations for meso-tetraacetylenyltetrabenzoporphyrins, again consonant with key crystallographic findings. By and large, both the energetics and nonplanar distortions of the metalloporphyrin derivatives correlated well with the Charton and Sterimol B1 steric parameters of the peripheral substituents.

Introduction

Despite their aromatic character, metalloporphyrins adopt a variety of nonplanar conformations such as the ruffled, saddled, domed, waved, and various intermediate conformations.1−3 These deformations result from such factors as a sterically hindered set of substituents, a coordinated atom that is too small or too large, and specific metal–porphyrin orbital interactions. Of the various deformations, ruffling and saddling are the most common. Ruffling, where the meso carbons are alternately displaced above and below the mean porphyrin plane, commonly occurs for a coordinated atom/ion that is too small for a planar porphyrin; a common example is the Ni(II) ion.4−8 Certain sterically hindered substitution patterns, such as four bulky meso substituents, also result in ruffling. meso-Tetraisopropyl-9−11 and meso-tetrakis(t-butyl)porphyrin12 derivatives provide good examples of such ruffled porphyrins. Saddling, where the pyrrole rings are alternately tilted above and below the mean porphyrin plane, is most commonly associated with dodecasubstituted porphyrin derivatives, where it provides relief from peripheral steric overcrowding. Interestingly, the ruffled conformation has been observed for a handful of dodecasubstituted porphyrin derivatives. Thus, Smith and co-workers reported X-ray structures for both the ruffled (CCDC: XAWRUI) and saddled (CCDC: TEZXEB) conformations of Ni dodecaphenylporphyrin13,14 and underscored the flexibility of the system. There is also significant spectroscopic evidence that Ni dodecaphenylporphyrin is conformationally mobile in solution.15 A ruffled conformation has been found for a Pt β-octaalkyl-meso-tetraacetylenyl-porphyrin (CCDC: LUTYOO, Figure 1).16 Unlike for ruffled porphyrins17−19 and hydroporphyrins,20−23 few major quantum chemical studies have addressed the question of energetics associated with saddling in porphyrins,24,25 which has left us relatively in the dark about the relative energies of the saddled versus ruffled conformations of various dodecasubstituted metalloporphyrins. Detailed information on this subject should not only allow for a better appreciation of metalloporphyrin structural chemistry and spectroscopy1,2,15,25−27 but also stimulate the use of nonplanar porphyrins to create novel supramolecular and nanoscale structures.28,29

Figure 1.

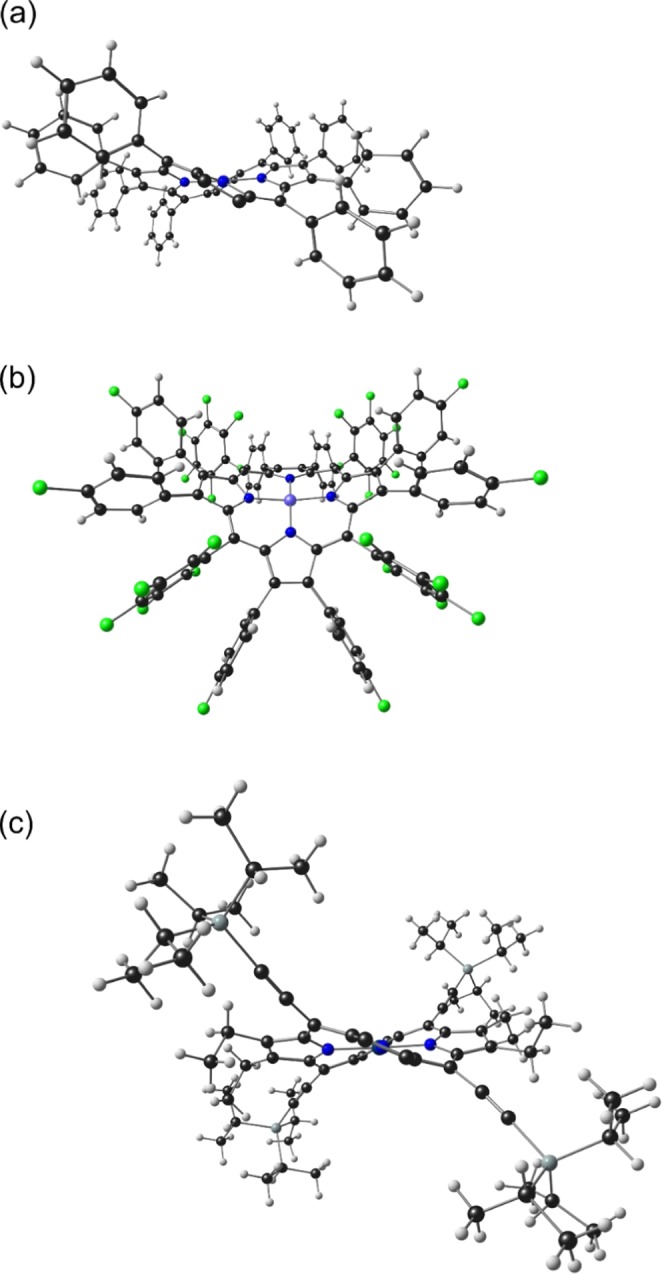
Figure 1

Open in a new tab

Representative diagrams of a (a) ruffled and (b) saddled NiDPP and (c) ruffled Pt acetylenyl porphyrins. In (a) and (c), the substituents at C2, C3, C12, and C13 have been removed for clarity.

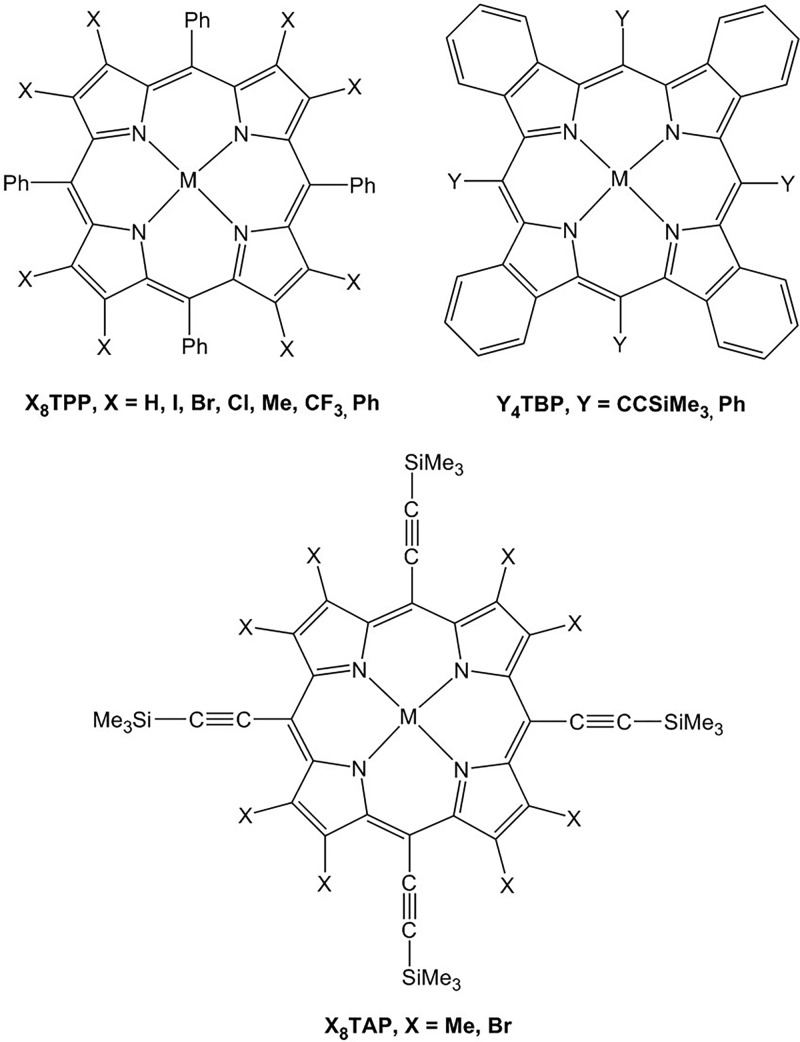
Prompted by the above considerations, we undertook a dispersion-corrected density functional theory (DFT) study (BP86-D3/STO-TZ2P) of a wide range of dodecasubstituted metalloporphyrins. As shown in Figure 2, three broad classes of complexes were examined (a) X8TPP (TPP = tetraphenylporphyrin), where the meso substituent is phenyl and the β substituent X = Me,30−32 Cl,33−36 Br,37−39 Ph,13,14,40,41 I,42 and CF3;43 (b) Y4TBP (TBP = tetrabenzoporphyrin), where the meso substituent Y = C≡C-SiMe3 (hereafter abbreviated as A) and Ph,44−47 and (c) X8TAP (TAP = meso-tetrakis(trimethylsilylacetylenyl)porphyrin), where X = Me16 and Br. For each porphyrin ligand, five different divalent metals were examined, namely, Ni,13,14,16,35,36,38,39,42,43,45,46 Cu,33,38,40,42,44 Zn,13,34,37,41 Pd, and Pt.16,47 For each metalloporphyrin, the ruffled and saddled conformations were optimized. Table 1 lists various geometry parameters and the energy difference between the saddled and ruffled conformations (Esadd – Eruff). The key geometry parameters of interest are the ruffling (ψ) and saddling dihedrals (χ), defined in Figure 3, and the out-of-plane displacements of meso (zmeso), α (zα), and β (zβ) carbons.

Figure 2.

Figure 2

Open in a new tab

Molecules studied in this work.

Table 1. Electronic Energy Differences (eV) between the Saddled and Ruffled Optimized Geometries, M–N Distances (Å), Ruffling (Ψ) and Saddling (χ) Angles (deg), and α, β and meso Carbon Displacements (Å) above the Mean N4 Plane.

    ruffled
 saddled
  
complex M (M–N)av Ψ zmeso (M–N)av χ zα zβ Esadd – Eruff
TPP Cu 2.008 1.1 0.019 2.012 15.7 0.075 0.244 –0.05
Ni 1.933 31.3 0.514 1.945 14.7 0.239 0.573 –0.03
Pd 2.025 1.0 0.017 2.027 13.6 0.083 0.248 –0.03
Pt 2.024 0.7 0.013 2.026 11.3 0.070 0.208 –0.03
Zn 2.043 0.3 0.005 2.048 16.3 0.033 0.163 –0.06
Me8TPP Ni 1.890 56.0 0.890 1.903 36.0 0.507 1.223 –0.32
Cu 1.979 43.0 0.695 1.987 44.9 0.429 1.106 –0.40
Zn 2.040 31.5 0.517 2.033 45.4 0.384 1.018 –0.38
Pd 2.014 37.5 0.608 2.012 43.5 0.407 1.056 –0.38
Pt 2.015 36.9 0.602 2.010 39.0 0.401 1.020 –0.36
Cl8TPP Ni 1.894 56.0 0.893 1.912 35.5 0.492 1.193 –0.42
Cu 1.990 40.6 0.656 1.996 44.0 0.412 1.069 –0.47
Zn 2.060 22.1 0.362 2.037 38.3 0.365 0.944 –0.37
Pd 2.027 32.1 0.520 2.018 41.7 0.388 1.009 –0.43
Pt 2.028 30.8 0.501 2.015 35.7 0.381 0.965 –0.39
Br8TPP Ni 1.888 59.1 0.932 1.906 38.2 0.521 1.261 –0.57
Cu 1.979 46.2 0.740 1.992 48.4 0.446 1.154 –0.65
Zn 2.045 33.4 0.541 2.034 44.2 0.407 1.055 –0.58
Pd 2.019 39.2 0.629 2.016 46.5 0.424 1.102 –0.62
Pt 2.020 38.2 0.614 2.011 40.6 0.420 1.065 –0.58
I8TPP Ni 1.873 64.7 1.010 1.897 44.3 0.557 1.357 –0.81
Cu 1.955 55.3 0.874 1.987 56.8 0.490 1.274 –0.92
Zn 2.017 46.3 0.740 2.028 54.2 0.457 1.196 –0.93
Pd 1.999 49.4 0.785 2.011 54.7 0.470 1.225 –0.95
Pt 2.002 48.3 0.770 2.005 48.5 0.468 1.193 –0.90
(CF3)8TPP Ni 1.842 73.8 1.167 1.880 67.9 0.652 1.615 –0.56
Cu 1.919 67.0 1.071 1.984 88.1 0.599 1.586 –0.88
Zn 1.977 60.8 0.981 2.026 87.7 0.575 1.541 –1.00
Pd 1.966 62.2 1.003 2.000 80.1 0.580 1.522 –0.91
Pt 1.973 61.0 0.986 1.993 62.7 0.547 1.398 –0.85
DPP Ni 1.860 64.9 1.048 1.933 25.9 0.423 1.011 0.15
Cu 1.946 53.4 0.887 1.995 30.3 0.336 0.850 0.02
Zn 2.013 41.2 0.710 2.048 22.9 0.240 0.615 0.01
Pd 1.990 46.5 0.786 2.024 26.6 0.536 0.768 0.00
Pt 1.994 45.3 0.770 2.023 22.0 0.283 0.700 0.05
Ph4TBP Ni 1.889 60.2 0.946 1.928 25.2 0.485 1.132 –0.15
Cu 1.983 47.3 0.753 1.998 28.6 0.415 1.003 –0.25
Zn 2.049 34.9 0.563 2.045 26.5 0.368 0.894 –0.26
Pd 2.018 41.6 0.665 2.024 31.0 0.385 0.954 –0.24
Pt 2.018 40.8 0.654 2.022 28.3 0.379 0.927 –0.24
A4TBP Ni 1.890 60.9 1.005 1.893 13.5 0.356 0.808 0.02
Cu 1.987 46.9 0.805 1.987 20.0 0.417 0.960 –0.03
Zn 2.059 31.5 0.576 2.039 21.0 0.412 0.949 –0.10
Pd 2.021 40.8 0.716 2.020 24.3 0.399 0.944 –0.02
Pt 2.021 40.4 0.711 2.019 22.6 0.391 0.918 –0.01
Me8TAP Ni 1.890 55.7 0.931 1.903 21.5 0.522 1.184 0.18
Cu 1.981 41.8 0.731 1.982 26.1 0.442 1.038 0.05
Zn 2.047 27.1 0.506 2.031 25.9 0.390 0.929 0.00
Pd 2.016 35.6 0.636 2.014 28.7 0.404 0.974 0.07
Pt 2.016 35.4 0.636 2.015 26.4 0.395 0.943 0.08
Br8TAP Ni 1.885 59.8 1.019 1.900 28.0 0.568 1.306 0.25
Cu 1.975 47.4 0.845 1.979 29.3 0.431 1.036 0.03
Zn 2.040 35.0 0.661 2.027 31.9 0.455 1.085 –0.01
Pd 2.013 41.1 0.752 2.015 35.7 0.457 1.110 0.06
Pt 2.013 40.5 0.745 2.013 31.5 0.448 1.073 0.10
Open in a new tab

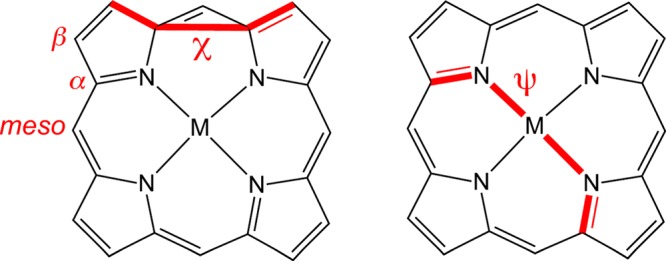
Figure 3.

Figure 3

Open in a new tab

Definition of ruffling (χ) and saddling (ψ) dihedrals.

Results and Discussion

Table 1 shows that the majority of the complexes prefer a saddled conformation by a clear margin of energy, consistent with the large body of available crystallographic data.1 Also, as shown in Figure 4, with the possible exception of Ni(II), the smallest metal ion considered, Esadd – Eruff is essentially independent of the metal, for the metal ions considered.

Figure 4.

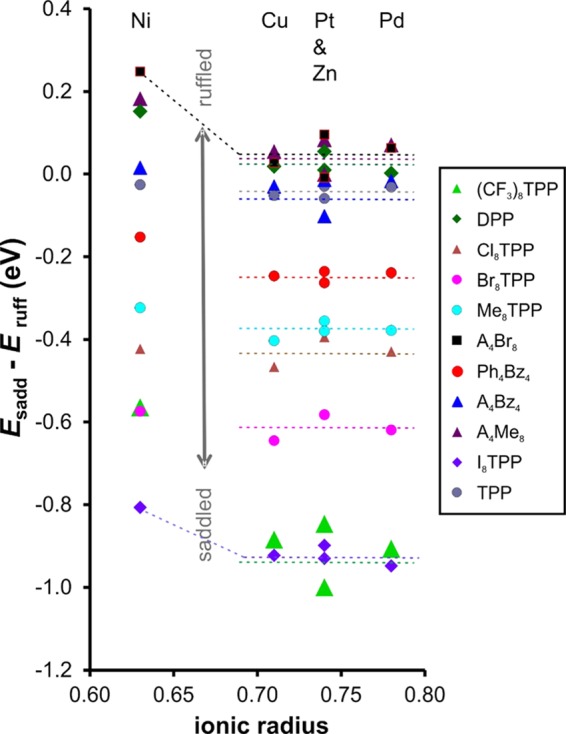
Figure 4

Open in a new tab

Energy difference (eV) between saddled and ruffled conformations as a function of metal ion ionic radius. Ionic radii (Å): Cu 0.71, Ni 0.63, Pd 0.78, Pt 0.74, and Zn 0.74. The horizontal dotted lines represent the average value off Esadd – Eruff for Cu, Pt, Zn, and Pd, underscoring that only Ni deviates significantly from this value.

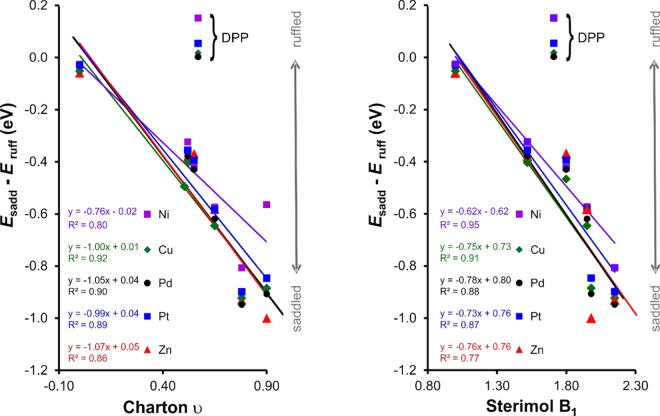
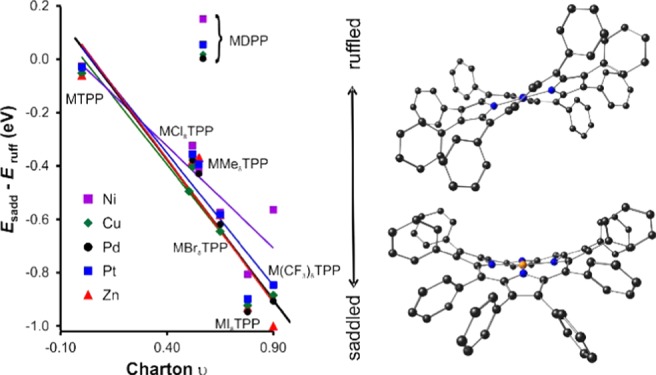
For the X8TPP complexes and for a given metal ion, Esadd – Eruff exhibits a strong, linear dependence on the steric bulk of the β substituent X, as measured by either the Charton48−51 or the Sterimol B152−57 parameters (Figure 5), with one key exception, X = Ph. Thus, the preference for the saddled conformation relative to the ruffled conformation ranges from about ∼0.3–0.4 eV for Me8TPP derivatives up to 1 eV for I8TPP and (CF3)8TPP derivatives. Interestingly, for X = Ph, that is, dodecaphenylporphyrins, the saddled and the ruffled conformations are almost equienergetic, with even a slight preference for the ruffled conformation in some cases. In other words, the phenyl groups in dodecaphenylporphyrins exert a much lower steric effect than that implied by their Charton and Sterimol B1 parameters. The anomalously low steric effects of the phenyl groups are most reasonably ascribed to the manner in which they stack in a circular arrangement around the porphyrin periphery. These results explain the experimental observation of both the saddled and ruffled conformations of nickel dodecaphenylporphyrin.15

Figure 5.

Figure 5

Open in a new tab

Energy difference (eV) between saddled and ruffled conformations of X8TPP (X Me, Cl, Br, I, CF3, or Ph) complexes of different metal ions as a function of the Charton (H 0.00, Cl 0.55, Br 0.65, I 0.78, Me 0.52, CF3 0.90, and Ph 0.57) and Sterimol B1 (H 1.00, Me 1.52, Cl 1.80, Br 1.95, I 2.15, CF3 1.98, and Ph 1.71) steric parameters.

The acetylenyl-substituted metalloporphyrins considered here, Y4TBP complexes with Y = C≡C-SiMe3 and X8TAP complexes, behave similar to dodecaphenylporphyrins in that they too exhibit essentially equienergetic saddled and ruffled conformations. We view this finding to be quite reasonable because acetylenyl and phenyl substituents are expected to exhibit similar minimum widths and similar Sterimol B1 parameters. Energetics considerations thus provide a rationale for the experimental observation of a ruffled platinum β-octaalkyl-meso-tetraacetylenylporphyrin.16

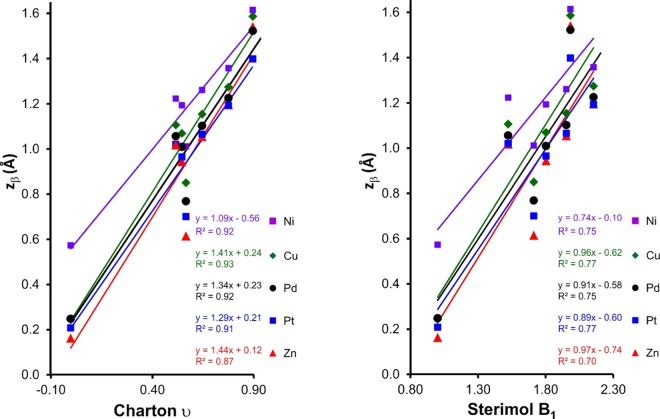
Table S1, Supporting Information shows key experimental structural data for selected saddled porphyrins relevant to this study. The reader may verify that the present calculations generally do an excellent job of reproducing the experimentally observed saddling distortions. For the full set of complexes studied, the degree of saddling (as measured by either zβ or χ, Figure 6) or ruffling (as measured by either zmeso or ψ, Figure 7) also shows an excellent correlation with the Charton parameter and a somewhat worse correlation with Sterimol B1.

Figure 6.

Figure 6

Open in a new tab

Degree of saddling (zβ) of X8TPP (X Me, Cl, Br, I, CF3, or Ph) complexes of different metal ions as a function of the Charton (H 0.00, Me 0.52, Cl 0.55, Ph 0.57, Br 0.65, I 0.78, and CF3 0.90) and Sterimol B1 (H 1.00, Me 1.52, Ph 1.71, Cl 1.80, Br 1.95, I 2.15, and CF3 1.98) steric parameters of X.

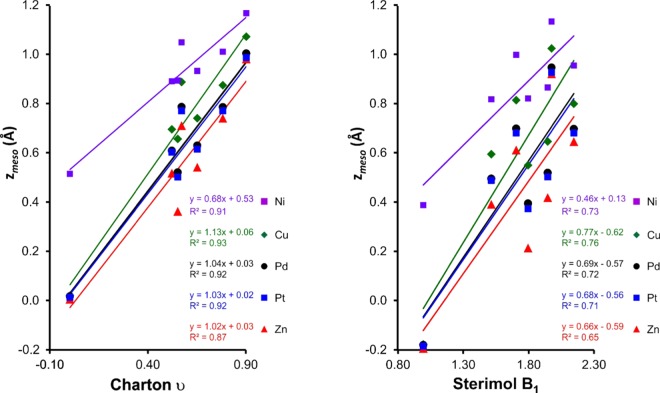
Figure 7.

Figure 7

Open in a new tab

Degree of ruffling (zmeso) of X8TPP (X Me, Cl, Br, I, CF3, or Ph) complexes of different metal ions as a function of the Charton (H 0.00, Me 0.52, Cl 0.55, Ph 0.57, Br 0.65, I 0.78, and CF3 0.90) and Sterimol B1 (H 1.00, Me 1.52, Ph 1.71, Cl 1.80, Br 1.95, I 2.15, and CF3 1.98) steric parameters of X.

Conclusions

Dispersion-corrected DFT calculations indicate a clear preference for the saddled conformation for the majority of X8TPP complexes, consistent with a large body of experimental data. For X8TPP complexes, where X = Ph (i.e., dodecaphenylporphyrins), or Y4TBP complexes, where Y = C≡C-SiMe3, as well as for X8TAP complexes, however, the saddled and ruffled conformations are found to be nearly equienergetic, which explains the experimental observation of the ruffled conformation for a few dodecasubstituted metalloporphyrins. In general, the degree of saddling or ruffling exhibits a clear correlation with the Charton or Sterimol B1 steric parameters of the substituents in question, except for dodecaphenylporphyrins and acetylenyl-substituted porphyrins. For these compounds, both the Charton and Sterimol B1 parameters appear to greatly overestimate the actual steric effects exerted by phenyl and acetylenyl substituents.

Experimental Section

All DFT calculations were carried out with the ADF (Amsterdam Density Functional) 2013 program system,58 the BP86 functional in conjunction with Grimme’s D359 dispersion corrections, Slater-type TZ2P basis sets, a fine mesh for numerical integration, and full geometry optimizations with tight convergence criteria. D2d or D2 symmetry constraints were used to derive the saddled and ruffled optimized conformations for each metalloporphryin. Free energy differences between the two conformations were calculated for several selected complexes and were found to be very similar (to well within 0.1 eV) to the electronic energy differences, and accordingly only the latter have been reported in Table 1.

Acknowledgments

This work was supported by grants 231086 and 262229 of the Research Council of Norway (AG) and by the National Research Fund of the Republic of South Africa (JC).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.7b01004.

  • DFT-optimized coordinates (232 pages) (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao7b01004_si_001.pdf (994.3KB, pdf)

References

  1. Shelnutt J. A.; Song X.-Z.; Ma J.-G.; Jia S.-L.; Jentzen W.; Medforth C. J.; Medforth C. J. Nonplanar Porphyrins and Their Significance in Proteins. Chem. Soc. Rev. 1998, 27, 31–42. 10.1039/A827031Z. [DOI] [Google Scholar]
  2. Golubchikov O. A.; Pukhovskaya S. G.; Kuvshinova E. M. Structures and Properties of Spatially Distorted Porphyrins. Russ. Chem. Rev. 2005, 74, 249–264. 10.1070/RC2005v074n03ABEH000925. [DOI] [Google Scholar]
  3. Kleingardner J. G.; Bren K. L. Acc. Chem. Res. 2015, 48, 1845–1852. 10.1021/acs.accounts.5b00106. [DOI] [PubMed] [Google Scholar]
  4. Brennan T. D.; Scheidt W. R.; Shelnutt J. A. J. Am. Chem. Soc. 1988, 110, 3919. 10.1021/ja00220a033. [DOI] [Google Scholar]
  5. Meyer E. F. Jr. Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem. 1972, 28, 2162. 10.1107/S0567740872005722. [DOI] [Google Scholar]
  6. Jia S.-L.; Jentzen W.; Shang M.; Song X.-Z.; Ma J.-G.; Scheidt W. R.; Shelnutt J. A. Axial Coordination and Conformational Heterogeneity of Nickel(II) Tetraphenylporphyrin Complexes with Nitrogenous Bases. Inorg. Chem. 1998, 37, 4402–4412. 10.1021/ic980289+. [DOI] [PubMed] [Google Scholar]
  7. Kozlowski P. M.; Rush T. S. III; Jarzecki A. A.; Zgierski M.; Chase B.; Piffat C. A.; Ye B.-H.; Li Z.-Y.; Pulay P.; Spiro T. G. DFT-SQM Force Field for Nickel Porphine: Intrinsic Ruffling. J. Phys. Chem. A 1999, 103, 1357–1366. 10.1021/jp9819700. [DOI] [Google Scholar]
  8. Rush T. S. III; Kozlowski P. M.; Piffat C. A.; Kumble R.; Zgierski M.; Spiro T. G. Computational Modeling of Metalloporphyrin Structure and Vibrational Spectra: Porphyrin Ruffling in NiTPP. J. Phys. Chem. B 2000, 104, 5020–5034. 10.1021/jp000266s. [DOI] [Google Scholar]
  9. Nakamura M. Electronic Structures of Highly Deformed Iron(III) Porphyrin Complexes. Coord. Chem. Rev. 2006, 250, 2271–2294. 10.1016/j.ccr.2006.03.001. [DOI] [Google Scholar]
  10. Senge M. O.; Bischoff I.; Nelson N. Y.; Smith K. M. Synthesis, reactivity and structural chemistry of 5,10,15,20-tetraalkylporphyrins. J. Porphyrins Phthalocyanines 1999, 3, 99–116. . [DOI] [Google Scholar]
  11. Ema T.; Senge M. O.; Nelson N. Y.; Ogoshi H.; Smith K. M. 5,10,15,20-Tetra-tert-butylporphyrin and Its Remarkable Reactivity in the 5- and 15-Positions. Angew. Chem., Int. Ed. 1994, 33, 1879–1881. (CSD reference code HETDAL) 10.1002/anie.199418791. [DOI] [Google Scholar]
  12. Senge M. O.; Ema T.; Smith K. M. Crystal structure of a remarkably ruffled nonplanar porphyrin (pyridine)[5,10,15,20-tetra(tert-butyl)porphyrinato]zinc(II). J. Chem. Soc., Chem. Commun. 1995, 733–734. (CSD reference code ZIJDAX) 10.1039/c39950000733. [DOI] [Google Scholar]
  13. Barkigia K. M.; Nurco D. J.; Renner M. W.; Melamed D.; Smith K. M.; Fajer J. Multiconformational Surfaces in Porphyrins: Previews into Excited-State Landscapes. J. Phys. Chem. B 1998, 102, 322–326. 10.1021/jp973013g. [DOI] [Google Scholar]
  14. Nurco D. J.; Medforth C. J.; Forsyth T. P.; Olmstead M. M.; Smith K. M. Conformational Flexibility in Dodecasubstituted Porphyrins. J. Am. Chem. Soc. 1996, 118, 10918–10919. (CSD reference code TEZXEB, TEZXIF) 10.1021/ja962164e. [DOI] [Google Scholar]
  15. Drain C. M.; Kirmaier C.; Medforth C. J.; Nurco D. J.; Smith K. M.; Holten D. Dynamic Photophysical Properties of Conformationally Distorted Nickel Porphyrins. 1. Nickel(II) Dodecaphenylporphyrin. J. Phys. Chem. 1996, 100, 11984–11993. 10.1021/jp960735j. [DOI] [Google Scholar]
  16. Krivokapic A.; Cowley A. R.; Anderson H. L. Contracted and Expanded meso-Alkynyl Porphyrinoids: from Triphyrin to Hexaphyrin. J. Org. Chem. 2003, 68, 1089–1096. (CSD reference code LUTYOO, LUTYII) 10.1021/jo026748c. [DOI] [PubMed] [Google Scholar]
  17. Vangberg T.; Ghosh A. A First-Principles Quantum Chemical Analysis of the Factors Controlling Ruffling Deformations of Porphyrins: Insights from the Molecular Structures and Potential Energy Surfaces of Silicon, Phosphorus, Germanium, and Arsenic Porphyrins and of a Peroxidase Compound I Model. J. Am. Chem. Soc. 1999, 121, 12154–12160. 10.1021/ja992457i. [DOI] [Google Scholar]
  18. Conradie J.; Wondimagegn T.; Ghosh A. Spin States at a Tipping Point: What Determines the dz21 Ground State of Nickel(III) Tetra(tbutyl)porphyrin Dicyanide?. J. Phys. Chem. B 2008, 112, 1053–1056. 10.1021/jp709980y. [DOI] [PubMed] [Google Scholar]
  19. Ghosh A.; Halvorsen I.; Nilsen H. J.; Steene E.; Wondimagegn T.; Lie R.; Van caemelbecke E.; Guo N.; Ou Z.; Kadish K. M. Electrochemistry of Nickel and Copper β-Octahalogeno-meso-tetraarylporphyrins. Evidence for Important Role Played by Saddling-Induced Metal(dx2-y2)–Porphyrin(“a2u”) Orbital Interactions. J. Phys. Chem. B 2001, 105, 8120–8124. 10.1021/jp011984x. [DOI] [Google Scholar]
  20. Wondimagegn T.; Ghosh A. Ruffling Deformations of Nickel(II) and Zinc(II) Hydroporphyrin and Chlorophin Complexes: Implications for F430, the Nickel Tetrapyrrole Cofactor of Methylcoenzyme M Reductase. J. Phys. Chem. B 2000, 104, 10858–10862. 10.1021/jp000081l. [DOI] [Google Scholar]
  21. Ryeng H.; Gonzalez E.; Ghosh A. DFT at Its Best: Metal- versus Ligand-Centered Reduction in Nickel Hydroporphyrins. J. Phys. Chem. B 2008, 112, 15158–15173. 10.1021/jp805486b. [DOI] [PubMed] [Google Scholar]
  22. Sharma M.; Ticho A. L.; Samankumara L.; Zeller M.; Brückner C. Conformational Landscapes of Metal(II) Porphyrinato, Chlorinato, and Morpholinochlorinato Complexes. Inorg. Chem. 2017, 56, 11490–11502. 10.1021/acs.inorgchem.7b00799. [DOI] [PubMed] [Google Scholar]
  23. Guberman-Pfeffer M. J.; Greco J. A.; Samankumara L. P.; Zeller M.; Birge R. R.; Gascón J. A.; Brückner C. Bacteriochlorins with a Twist: Discovery of a Unique Mechanism to Red-Shift the Optical Spectra of Bacteriochlorins. J. Am. Chem. Soc. 2017, 139, 548–560. 10.1021/jacs.6b12419. [DOI] [PubMed] [Google Scholar]
  24. Wondimagegn T.; Ghosh A. Conformational Flexibility of meso-Tetrakis(perfluoroalkyl)porphyrins: Energetics of Ruffling versus Saddling. J. Phys. Chem. A 2000, 104, 4606–4608. 10.1021/jp0000376. [DOI] [Google Scholar]
  25. Ryeng H.; Ghosh A. Do Nonplanar Distortions of Porphyrins Bring about Strongly Red-Shifted Electronic Spectra? Controversy, Consensus, New Developments, and Relevance to Chelatases. J. Am. Chem. Soc. 2002, 124, 8099–8103. 10.1021/ja0202659. [DOI] [PubMed] [Google Scholar]
  26. Wasbotten I. H.; Conradie J. H.; Ghosh A. Electronic Absorption and Resonance Raman Signatures of Hyperporphyrins and Nonplanar Porphyrins. J. Phys. Chem. B 2003, 107, 3613–3623. 10.1021/jp014417i. [DOI] [Google Scholar]
  27. Lebedev A. Y.; Filatov M. A.; Cheprakov A. V.; Vinogradov S. A. Effects of Structural Deformations on Optical Properties of Tetrabenzoporphyrins: Free-Bases and Pd Complexes. J. Phys. Chem. A 2008, 112, 7723–7733. 10.1021/jp8043626. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Fukuzumi S.; Kojima T.. Nanostructures and Electron-Transfer Functions of Nonplanar Porphyrins. In Organic Nanomaterials: Synthesis, Characterization, and Device Applications; Torres T.; Bottari G., Eds.; Wiley: Hoboken, NJ, 2013; Ch. 6. [Google Scholar]
  29. Shahroosvand H.; Zakavi S.; Sousaraeia A.; Eskandaria M. Saddle-Shaped Porphyrins for Dye-Densitized Solar Cells: New Insight into the Relationship Between Nonplanarity and Photovoltaic Properties. Phys. Chem. Chem. Phys. 2015, 17, 6347–6358. 10.1039/C4CP04722B. [DOI] [PubMed] [Google Scholar]
  30. Barkigia K. M.; Berber M. D.; Fajer J.; Medforth C. J.; Renner M. W.; Smith K. M. Nonplanar porphyrins. X-ray Structures of (2,3,7,8,12,13,17,18-Octaethyl- and -octamethyl-5,10,15,20-tetraphenylporphinato)zinc(II). J. Am. Chem. Soc. 1990, 112, 8851–8857. 10.1021/ja00180a029. [DOI] [Google Scholar]
  31. Sparks L. D.; Medforth C. J.; Park M.-S.; Chamberlain J. R.; Ondrias M. R.; Senge M. O.; Smith K. M.; Shelnutt J. A. Metal Dependence of the Nonplanar Distortion of Octaalkyltetraphenylporphyrins. J. Am. Chem. Soc. 1993, 115, 581–592. 10.1021/ja00055a030. [DOI] [Google Scholar]
  32. Senge M. O.; Medforth C. J.; Sparks L. D.; Shelnutt J. A.; Smith K. M. A Planar Dodecasubstituted Porphyrin. Inorg. Chem. 1993, 32, 1716–1723. 10.1021/ic00061a030. [DOI] [Google Scholar]
  33. Schaefer W. P.; Hodge J. A.; Hughes M. E.; Gray H. B.; Lyons J. E.; Ellis P. E. Jr.; Wagner R. W. Copper(II) tetrakis(pentafluorophenyl)-β-octachloroporphyrin. Acta Crystallogr., Sect. C: Cryst. Struct. Commun. 1993, 49, 1342–1345. 10.1107/S0108270193000587. [DOI] [Google Scholar]
  34. Birnbaum E. R.; Hodge J. A.; Grinstaff M. W.; Schaefer W. P.; Henling L.; Labinger J. A.; Bercaw J. E.; Gray H. B. 19F NMR Spectra and Structures of Halogenated Porphyrins. Inorg. Chem. 1995, 34, 3625–3632. 10.1021/ic00118a010. [DOI] [Google Scholar]
  35. Spyroulias G. A.; Despotopoulos A. P.; Raptopoulou C. P.; Terzis A.; de Montauzon D.; Poilblanc R.; Coutsolelos A. G. Comparative Study of Structure–Properties Relationship for Novel β-Halogenated Lanthanide Porphyrins and Their Nickel and Free Bases Precursors, as a Function of Number and Nature of Halogens Atoms. Inorg. Chem. 2002, 41, 2648–2659. 10.1021/ic000738h. [DOI] [PubMed] [Google Scholar]
  36. Kumar R.; Chaudhria N.; Sankar M. Ratiometric and Colorimetric “Naked Eye” Selective Detection of CN– Ions by Electron Deficient Ni(II) Porphyrins and Their Reversibility Studies. Dalton Trans. 2015, 44, 9149–9157. 10.1039/C5DT00937E. [DOI] [PubMed] [Google Scholar]
  37. Marsh R. E.; Schaefer W. P.; Hodge J. A.; Hughes M. E.; Gray H. B.; Lyons J. E.; Ellis Jnr P. E. A highly solvated zinc(II) tetrakis(pentafluorophenyl)-β-octabromoporphyrin. Acta Crystallogr., Sect. C: Cryst. Struct. Commun. 1993, 49, 1339–1342. (CSD reference code LALRIZ) 10.1107/S0108270193000642. [DOI] [Google Scholar]
  38. Henling L. M.; Schaefer W. P.; Hodge J. A.; Hughes M. E.; Gray H. B.; Lyons J. E.; Ellis Jnr P. E. Copper(II) and nickel(II) octabromo-tetrakis(pentafluorophenyl)porphyrin complexes. Acta Crystallogr., Sect. C: Cryst. Struct. Commun. 1993, 49, 1743–1747. (CSD reference code LATSEE, PAHKOY01) 10.1107/S0108270193003051. [DOI] [Google Scholar]
  39. Mandon D.; Ochenbein P.; Fischer J.; Weiss R.; Jayaraj K.; Austin R. N.; Gold A.; White P. S.; Brigaud O. β-Halogenated-pyrrole porphyrins. Molecular structures of 2,3,7,8,12,13,17,18-octabromo-5,10,15,20-tetramesitylporphyrin, nickel(II) 2,3,7,8,12,13,17,18-octabromo-5,10,15,20-tetramesitylporphyrin, and nickel(II) 2,3,7,8,12,13,17,18-octabromo-5,10,15,20-tetrakis(pentafluorophenyl)porphyrin. Inorg. Chem. 1992, 31, 2044–2049. (CSD reference code PAHKIS, PAHKOY) 10.1021/ic00037a012. [DOI] [Google Scholar]
  40. Medforth C. J.; Senge M. O.; Smith K. M.; Sparks L. D.; Shelnutt J. A. Nonplanar distortion modes for highly substituted porphyrins. J. Am. Chem. Soc. 1992, 114, 9859–9869. (CSD reference code LADGIG) 10.1021/ja00051a019. [DOI] [Google Scholar]
  41. Ishizuka T.; Sankara M.; Kojima T. Control of the spatial arrangements of supramolecular networks based on saddle-distorted porphyrins by intermolecular hydrogen bonding. Dalton Trans. 2013, 42, 16073–16079. (CSD reference code ODIPIC) 10.1039/c3dt51467f. [DOI] [PubMed] [Google Scholar]
  42. Thomassen I. K.; Vazquez-Lima H.; Gagnon K. J.; Ghosh A. Octaiodoporphyrin. Inorg. Chem. 2015, 54, 11493–11497. (CSD reference code JUZQIG, JUZQEC) 10.1021/acs.inorgchem.5b02127. [DOI] [PubMed] [Google Scholar]
  43. Liu C.; Chen Q-Y. Fluoroalkylation of Porphyrins: A Facile Synthesis of Trifluoromethylated Porphyrins by a Palladium-Catalyzed Cross-Coupling Reaction. Eur. J. Org. Chem. 2005, 2005, 3680–3686. (CSD reference code TAWVOD) 10.1002/ejoc.200500027. [DOI] [Google Scholar]
  44. Sugawara S.; Hirata Y.; Kojima S.; Yamamoto Y.; Miyazaki E.; Takimiya K.; Matsukawa S.; Hashizume D.; Mack J.; Kobayashi N.; Fu Z.; Kadish K. M.; Sung Y. M.; Kim K. S.; Kim D. Synthesis, Characterization, and Spectroscopic Analysis of Antiaromatic Benzofused Metalloporphyrins. Chem. – Eur. J. 2012, 18, 3566–3581. 10.1002/chem.201101846. [DOI] [PubMed] [Google Scholar]
  45. Ongayi O.; Fronczek F. R.; Vicente M. G. H. Benzoylbiliverdins from Chemical Oxidation of Dodecasubstituted Porphyrins. Chem. Commun. 2003, 2298–2299. 10.1039/B306586C. [DOI] [PubMed] [Google Scholar]
  46. Barkigia K. M.; Renner M. W.; Furenlid L. R.; Medforth C. J.; Smith K. M.; Fajer J. Crystallographic and EXAFS studies of conformationally designed nonplanar nickel(II) porphyrins. J. Am. Chem. Soc. 1993, 115, 3627–3635. (CSD reference code SULDEI) 10.1021/ja00062a029. [DOI] [Google Scholar]
  47. Borek C.; Hanson K.; Djurovich P. I.; Thompson M. E.; Aznavour K.; Bau R.; Sun Y.; Forrest S. R.; Brooks J.; Michalski L.; Brown J. Highly Efficient, Near-Infrared Electrophosphorescence from a Pt–Metalloporphyrin Complex. Angew. Chem., Int. Ed. 2007, 46, 1109–1112. (CSD reference code SEWCUT) 10.1002/anie.200604240. [DOI] [PubMed] [Google Scholar]
  48. Charton M. Steric effects. I. Esterification and acid-catalyzed hydrolysis of esters. J. Am. Chem. Soc. 1975, 97, 1552–1556. 10.1021/ja00839a047. [DOI] [Google Scholar]
  49. Charton M. Steric effects. 7. Additional V constants. J. Org. Chem. 1976, 41, 2217–2220. 10.1021/jo00874a035. [DOI] [Google Scholar]
  50. Charton M. The Upsilon Steric Parameter – Definition and Determination. Top. Curr. Chem. 1983, 114, 57–91. [Google Scholar]
  51. Charton’s steric parameters υX are derived from van der Waals radii (Å) of a substituent X via the equation υX = rX – rH = rX – 1.20, where rX and rH are the van der Waals radii of X and hydrogen, respectively. For an unsymmetrical substituent X, rX is chosen as the minimum van der Waals radius.
  52. Verloop A.The Use of Linear Free Energy Parameters and Other Experimental Constants in Structure–Activity Studies. In Drug Design; Ariens E. J., Ed.; Academic: New York, 1972; Vol. 3, pp 133–187. [Google Scholar]
  53. Verloop A.; Hoogenstraaten W.; Tipker J.. Development and Application of New Steric Substituent Parameters. In Drug Design; Ariens E. J., Ed.; Academic: New York, 1976; Vol. 7, pp 165–207. [Google Scholar]
  54. Verloop A.; Tipker J. Use of Linear Free Energy Related and Other Parameters in the Study of Fungicidal Selectivity. Pestic. Sci. 1976, 7, 379–390. 10.1002/ps.2780070410. [DOI] [Google Scholar]
  55. Verloop A.; Tipker J.. A Comparative Study of New parameters in Drug Design. In Biological Activity and Chemical Structure; Buisman J. A. K., Ed.; Elsevier: Amsterdam, 1977; pp 63–81. [Google Scholar]
  56. For a review, see:Harper K. C.; Bess E. N.; Sigman M. S. Multidimensional steric parameters in the analysis of asymmetric catalytic reactions. Nat. Chem. 2012, 4, 366–374. 10.1038/nchem.1297. [DOI] [PubMed] [Google Scholar]
  57. Verloop’s current steric parameters contain three subparameters, two width parameters B1 and B5 and a length parameter L. The B1 parameter describes the minimum profile width of the substituent from the primary bond axis and the B5 parameter describes the maximum width from the same axis.
  58. The ADF program system uses methods described in:Velde G. t.; Bickelhaupt F. M.; Baerends E. J.; Guerra C. F.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. J. Comput. Chem. 2001, 22, 931–967. 10.1002/jcc.1056. [DOI] [Google Scholar]; For additional details, including the procedure for calculation of Gibbs free energies, see the ADF program manual: http://www.scm.com/ADF/.
  59. Grimme S.; Anthony J.; Ehrlich S.; Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao7b01004_si_001.pdf (994.3KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES