Structural Characteristics, Population Analysis, and Binding Energies of [An(NO₃)]²⁺ (with An = Ac to Lr)

Abstract

Efficient predictive capabilities are essential for the actinide series since regulatory constraints for radioactive work, associated costs needed for specialized facilities, and the short half-lives of many actinides present great challenges in laboratory settings. Improved predictive accuracy is advantageous for numerous applications including the optimization and design of separation agents for nuclear fuel and waste. One limitation of calculations in support of these applications is that the large variations observed from predictions obtained with currently available methods can make comparisons across studies uncertain. Benchmarking currently available computational methodologies is essential to establish reliable practices across the community to guarantee an accurate physical description of the systems studied. To understand the performance of a variety of common theoretical methods, a systematic analysis of differences observed in the prediction of structural characteristics, electron withdrawing effects, and binding energies of [An(NO₃)]²⁺ (with An = Ac to Lr) in gas and aqueous phases is reported. Population analysis obtained with Mulliken and Löwdin reflect a large dependence on the level of theory of choice, whereas those obtained with natural bond orbital show larger consistency across methodologies. Predicted stability across the actinide series calculated with coupled cluster with perturbative doubles and triples at the triple ζ level is equivalent to the one obtained when extrapolated to the complete basis set limit. The ground state of [Fm(NO₃)]²⁺ and [Md(NO₃)]²⁺ is predicted to have an electronic structure corresponding to An III state in gas and An IV in aqueous phase, whereas the ground state of [An(NO₃)]²⁺ (with An = Ac to Es, Lr) presents an electronic structure corresponding to An IV in the gas and aqueous phase. The compounds studied with No in gas and aqueous phase present a preferred No III state, and the Lr compounds did not follow trends predicted for the rest of the actinide series, as previously observed in studies regarding its unusual electronic structure relative to its position in the periodic table.

Introduction

All of the actinides are radioactive, with a broad range of half-lives ranging from seconds to millions of years.¹ Yet despite their radioactivity, these elements are of considerable importance in a number of disparate areas, including military nuclear applications,² civilian nuclear power,³⁻⁵ neutron radiography,⁶⁻⁸ and radiothermal generators for space missions.⁹ Furthermore, they are also employed in cancer treatments and neutron therapy,¹⁰⁻¹⁴ in geological analysis in marine sediment modeling,¹⁵ and in astronomy.¹⁶ Due to their radioactivity and often short half-lives, they present challenges for experimental science, which intimates that effective theory could aide many applications without the need for specialized radiation laboratories.¹⁷⁻²³ Unfortunately, electronic structure calculations performed with traditional approaches become increasingly more difficult as the number of electrons and relativistic effects increase, which leads to a higher computational cost to achieve accuracy.²⁴ Theoretical considerations, including electronic correlation, multireference character, the interaction of core and valence electrons, and relativistic effects, intensify challenges and contribute to limitations in investigations involving the actinide series.²⁵

One research area where improved, reliable calculations would have immediate impact is on selective binding of ligands to actinides, which is critical for a range of applications, but in particular, the civilian nuclear fuel cycle.³⁻⁵ Optimization and design of extracting agents with high binding selectivity depend largely on computational feedback to reduce the processing cost.²⁶⁻²⁸ In 2012, Glatz cataloged all of the industrial processes for handling spent nuclear fuel²⁹ and he noted that nitric acid was essential in the first step of this process. In the initial phases of nuclear fuel treatment, all of the actinide elements, such as Ac, Th, Pa, U, Np, Pu, Am, Cm, and Bk, are present in the nuclear fuel depending on the reactor type. The URanium EXtraction (UREX) and Plutonium URanium EXtraction (PUREX) methods of removing weapons usable U or Pu from the fuel cycle both employ nitrates, whereby the spent fuel is divided into small pieces and dissolved into nitric acid in molarities of 0.5–4 M depending on the process.³⁰ Therefore, we chose the [An(NO₃)]²⁺ (with An = Ac to Lr) as a model system for calculations due to the importance of nitric acid binding in actinide separation processes.

Understanding structural characteristics, electron withdrawing effects, and binding energies is essential for optimization of separations, and computational tools can greatly aid in the prediction of these properties.^31,32 Yet, to our knowledge, in-depth evaluations of level of theory dependence on structural and population predictions for actinide-containing compounds with nitrates for the entire series have not been performed. Three metrics have been advanced across the actinide series for understanding ligand–actinide interactions: population analysis, structural characteristics, and binding energies. Population analysis is a useful aid for the analysis of electron withdrawing effects and their effect on selective binding to actinides.^33,34 Mulliken population analysis has been extensively used with uranium compounds,³⁵⁻⁴² but this type of analysis is largely dependent on the level of theory of choice, which makes comparisons across different studies uncertain. Structural characteristics include careful comparisons on bond distances and angles between the ligand and actinide. Finally, Dolg and co-workers evaluated the hydration energy across the actinide series through electronic structure calculations, showing an accuracy of the methodologies employed to be within 1% of experimental values; however, there was only experimental data for two actinides (uranium and plutonium).²³ In some cases, all of these aspects were evaluated for a ligand (cyclic imide dioximes) but only with a small subset of the actinides.³³ Last, we note that the extent of variations in the prediction of these properties for actinide-containing compounds from utilizing different methodologies or levels of theory is often problematic as few methods have been used in systematic studies across the entire actinide series.

One of the most challenging aspects when applying electronic structure calculations to actinides is assuring the calculation is reaching the true ground state for the actinide. In many instances, the user needs to manually alter orbitals to ensure correct orbital occupancies. However, as the number of atoms increases in compounds, the orbital mixing is often challenging to fix due to the closely degenerate f orbitals. Moreover, without a computational protocol that ensures the compound is in the true ground state, various results can be obtained, as illustrated in the Results and Discussion section.

In this manuscript, we showcase an exhaustive comparison of different methodologies and levels of theory to generate an in-depth understanding of the performance of electronic structure methods illustrated through nitrate binding across the entire series of actinides. We address the dependence of population analysis (part I), structural characteristics (part II), and binding energies (part III) on the level of theory of choice through a systematic study of [An(NO₃)]²⁺ structures (with An = Ac to Lr). To this end, gas-phase structures are optimized with local density approximation (LDA), TPSS, B3LYP, PBE0, B972, M06, and M11, the Stuttgart RSC 1997 ECP and associated basis set for the actinide atoms including and excluding the most diffuse basis functions, with the 6-31G*, cc-pVDZ, 6-311++G**, cc-pVTZ, and cc-pVQZ basis sets for the nitrogen and oxygen atoms. Single-point energy calculations are obtained with coupled cluster with perturbative doubles and triples (CCSD(T)) and all-electron correlation-consistent basis sets. Additionally, [An(NO₃)]²⁺ (with An = Ac to Lr) structures are optimized with an implicit solvation model and a subset of functionals and basis sets. Evaluation of methodologies in the prediction of differences amongst contiguous actinides is included to aid in targeted selective separations across the series.

Results and Discussion

Unless otherwise indicated, the results discussed in this section correspond to An IV configuration and gas-phase calculations. The An IV and An III notation follows the NIST Atomic Spectra Database spectra name classifications, which correspond to a defined electronic structure associated with each state, as shown in Table 1.⁴³

Table 1. Electronic Configuration for An IV and An III⁴³.

An	An IV	An III
Ac	[Hg]6p6	[Rn]7s
Th	[Rn]5f	[Rn]5f6d
Pa	[Rn]5f2	[Rn]5f26d
U	[Rn]5f3	[Rn]5f4
Np	[Rn]5f4	[Rn]5f5
Pu	[Rn]5f5	[Rn]5f6
Am	[Rn]5f6	[Rn]5f7
Cm	[Rn]5f7	[Rn]5f8
Bk	[Rn]5f8	[Rn]5f9
Cf	[Rn]5f9	[Rn]5f10
Es	[Rn]5f10	[Rn]5f11
Fm	[Rn]5f11	[Rn]5f12
Md	[Rn]5f12	[Rn]5f13
No	[Rn]5f13	[Rn]5f14
Lr	[Rn]5f14	[Rn]5f147s

Proper considerations were given to include the ground state for all compounds. Several combinations of methods and basis sets initially converged to an An III configuration. After altering the orbital occupancies to reflect an An IV configuration, a lower energy was obtained for [Bk(NO₃)]²⁺ and [Es(NO₃)]²⁺. Calculations with CCSD(T) indicate a preferred An III state for [Fm(NO₃)]²⁺, [Md(NO₃)]²⁺, and [No(NO₃)]²⁺ in the gas phase, with Fm and No having energies at least 100 kcal mol^–1 lower than in the An IV state, and Fm and Md in an An IV state in solution. It has been previously observed that No is found in a divalent state (An III) configuration in solution,⁴⁴ due to stabilization of the 5f shell, which corroborates the correctness in the evaluated lowest energy configuration state in this study. Differences in predicted ΔG_rxn calculated between some compounds with the actinide in An IV and An III states are shown in Table 2.

Table 2. Predicted Difference in ΔG_rxn for An-Containing Compounds with an An III to An IV Configuration Change^a.

An	method	An basis set	N and O basis set	Δ(ΔG)rxn (kcal mol–1)	configuration change
Bk	M11	ad	cc-pVDZ	–49.08	An III to An IV
			6-311++G**	–62.45	An III to An IV
			cc-pVQZ	–70.38	An III to An IV
		nd	6-311++G**	–44.01	An III to An IV
Es	PBE0	ad	6-311++G**	–19.66	An III to An IV
			cc-pVQZ	–18.88	An III to An IV
		nd	6-311++G**	–16.14	An III to An IV
	B972	ad	cc-pVTZ	–13.04	An III to An IV
	M11	ad	6-31G*	–16.36	An III to An IV
			cc-pVDZ	–14.70	An III to An IV
			6-311++G**	–13.49	An III to An IV
			cc-pVTZ	–24.16	An III to An IV
		nd	cc-pVTZ	–11.87	An III to An IV
			cc-pVQZ	–21.42	An III to An IV
Fm	CCSD(T)	cc-pVTZ-X2C	cc-pVTZ-DK	–106.70	An IV to An III
		V∞Z	V∞Z	–111.23	An IV to An III
No	CCSD(T)	cc-pVTZ-X2C	cc-pVTZ-DK	–138.50	An IV to An III
		V∞Z	V∞Z	–141.88	An IV to An III

^aThe “method” column indicates CCSD(T) or the functional of choice when utilizing DFT. The “An basis set” column indicates ad or nd for DFT, and cc-pVTZ-X2C or CBS (V∞Z) for CCSD(T). (An III to An IV is calculated as ΔG_rxn in An IV state – ΔG_rxn in An III state.)

Spin–orbit corrections are not included in the thermochemical data and discussion throughout this study. The calculated spin–orbit contribution to [Ac(NO₃)]²⁺ and [Lr(NO₃)]²⁺ following the proposed reaction in eq 3a is −0.92 and −3.24 kcal mol^–1, respectively (calculated with the DIRAC16 software, using the eXact-2-Component (X2C)–Dirac–Hartree–Fock and a triple ζ level basis set⁴⁵ developed by Dyall).

Figure 1 shows the identifying atom labels in the proposed [An(NO₃)]²⁺ complex.

Figure 1.

Identifying labels in [An(NO₃)]²⁺ (An = Ac to Lr).

Part I: Population Analysis

Level of Theory Dependence

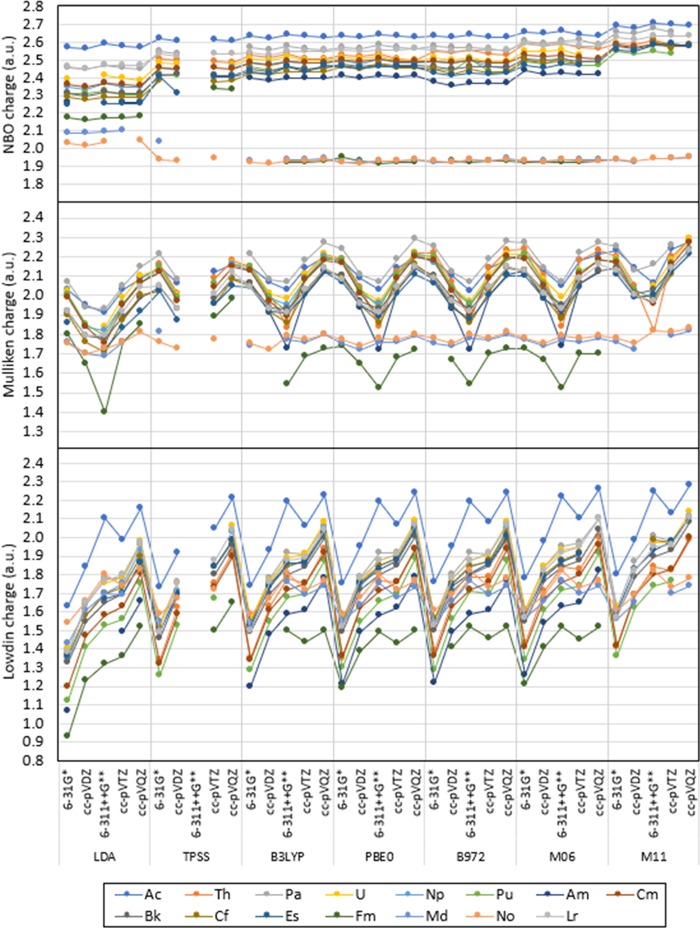
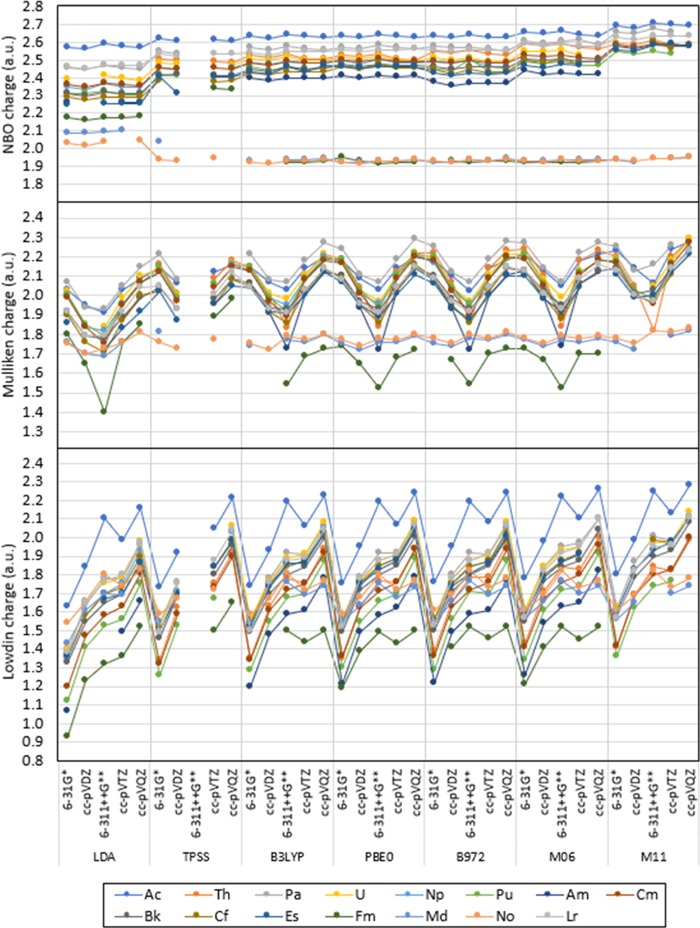
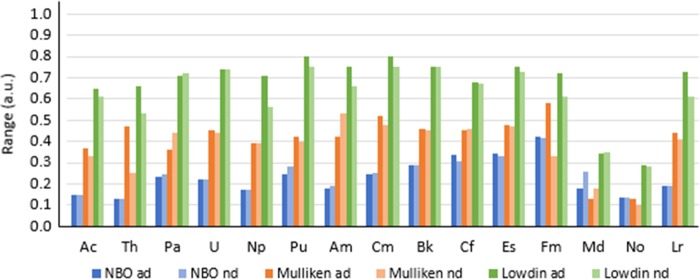
Overall, it is observed that the partial atomic charges calculated with natural bond orbital (NBO) are largely independent from the level of theory of choice, whereas partial charges calculated with Mulliken and Löwdin showed larger ranges of predicted populations and a strong dependence on the level of theory of choice. Figures 2 and 3 show the predicted charge of An in [An(NO₃)]²⁺ calculated with NBO, Mulliken, and Löwdin, where is it apparent that predicted charges with Mulliken and Löwdin show fluctuations when utilizing different combinations of functionals and basis sets, whereas partial charges calculated with NBO seem largely independent of the level of theory of choice for all functionals tested. Variations in predicted partial charge of An in the compounds evaluated with the levels of theory proposed show a range calculated with NBO, Mulliken, and Löwdin (indicated order as NBO/Mulliken/Löwdin) for Ac (0.15/0.37/0.65), Th (0.13/0.47/0.66), Pa (0.24/0.44/0.72), U (0.22/0.45/0.74), Np (0.17/0.39/0.71), Pu (0.28/0/42/0.80), Am (0.19/0.53/0.75), Cm (0.25/0.52/0.80), Bk (0.29/0.46/0.75), Cf (0.34/0.46/0.68), Es (0.34/0.48/0.75), Fm (0.42/0.58/0.72), Md (0.26/0.18/0.35), No (0.14/0.13/0.29), and Lr (0.19/0.44/0.73), as shown in Figures 2 and 3. Including and excluding the most diffuse basis functions in the An basis set give negligible differences in the predicted partial charge of An in the compounds tested with NBO and the levels of theory previously specified, as shown in Figures 4 and S.1 in the Supporting Information (SI). Significant differences including and excluding the most diffuse functions with Mulliken are observed for Ac (up to 0.17), Th (up to 0.32), Fm (up to 0.28), and Lr (up to 0.11), and with Löwdin for Ac (up to 0.14), Th (up to 0.38), Pu (up to 0.13), Am (up to 0.22), Cm (up to 0.14), Fm and Lr (up to 0.31) (also shown in Figures 4 and S.1 in the SI). Partial charges calculated with Löwdin show larger overall differences than those with NBO and Mulliken for Th, Pu, Am, Cm, Fm, and Lr. All calculated differences in partial charges with NBO, Mulliken, and Löwdin ad and nd are included in Tables S.1–S.3 in the SI.

Figure 2.

NBO, Mulliken, and Löwdin charge calculated for An³⁺ in [An(NO₃)]²⁺ with LDA, TPSS, B3LYP, PBE0, B972, M06, and M11 with the Stuttgart RSC 1997 ECP and associated basis set, including all diffuse basis functions on the An basis set. The lines are included as a visual aid and do not represent function continuity.

Figure 3.

NBO, Mulliken, and Löwdin charge calculated for An³⁺ in [An(NO₃)]²⁺ with LDA, TPSS, B3LYP, PBE0, B972, M06, and M11 with the Stuttgart RSC 1997 ECP and associated basis set, excluding the most diffuse basis functions on the An basis set. The lines are included as a visual aid and do not represent function continuity.

Figure 4.

NBO, Mulliken, and Löwdin ranges calculated for An³⁺ in [An(NO₃)]²⁺ with LDA, TPSS, B3LYP, PBE0, B972, and M06, with the Stuttgart 1997 ECP including all diffuse functions (ad) and without most diffuse functions (nd). (Range = largest predicted charge – smallest predicted charge, as indicated in eq 7a.)

Electron Withdrawing Effects and Orbital Occupancies in [An(NO₃)]²⁺

An An IV configuration is predicted for all [An(NO₃)]²⁺ structures in the gas phases for Ac, Th, Pa, U, Np, Pu, Am, Cm, Bk, Cf, Es, and Lr, whereas an An III is obtained in the gas phase for Fm, Md, and No. The orbital occupancies of optimized [An(NO₃)]²⁺ structures (for An = Ac, Th, Pa, U, Np, Cm, Bk, Es, Fm, Md, No, and Lr) in solution calculated with NBO show the 5f occupancy is less than 0.12 from the values calculated in the gas phase for Ac, Pa, U, Np, Cm, Bk, Es, and Lr for all options tested. The calculated 5f occupancy is approximately 0.4, 0.9, and 0.7 lower in aqueous phase than in gas phase in [Th(NO₃)]²⁺, [Fm(NO₃)]²⁺, and [Md(NO₃)]²⁺, respectively, for all functional/basis set options tested, suggesting an An III in the gas phase and an An IV in solution for Fm and Md.

Overall, the occupancy of the 5f orbital for the actinides predicted in the optimized structures in the gas phase is within 0.1 units of those obtained when applying a solvation model for an aqueous environment for Ac, Pa, U, Np, Cm, Bk, and Es, predicting an An IV state with all the options tested. For [Fm(NO₃)]²⁺, optimized structures in gas phase predict an Fm III state, whereas optimized structures in an aqueous environment predict an Fm IV configuration. Similarly, optimized [Md(NO₃)]²⁺ structures in the gas phase predict an Md III state and aqueous structures predict an Md IV configuration. For [No(NO₃)]²⁺, the aqueous environment reduces the 5f occupancy by approximately 0.4 units but it is not fully changed to an An IV state, which suggests an No III preference in gas and solution. The change in 5f occupancy in gas and aqueous phase for [Th(NO₃)]²⁺, [Fm(NO₃)]²⁺, [Md(NO₃)]²⁺, and [No(NO₃)]²⁺ is included in Table 3.

Table 3. Predicted Electronic Occupancy of the 5f Orbital of Th, Fm, Md, and No in [An(NO₃)]²⁺ in Gas (g) and Aqueous (aq) Environments Calculated with NBO.

			5f
An	functional	N and O basis set	(g)	(aq)
Th	B3LYP	6-31G*	0.7	0.4
		6-311++G**	0.7	0.4
	PBE0	6-31G*	0.7	0.3
		6-311++G**	0.7
Fm	B3LYP	6-31G*
		6-311++G**	12.0	11.1
	PBE0	6-31G*	12.0	11.1
		6-311++G**	12.0	11.1
Md	B3LYP	6-31G*	13.0
		6-311++G**	13.0	12.3
	PBE0	6-31G*	13.0
		6-311++G**	13.0	12.3
No	B3LYP	6-31G*	14.0	13.6
		6-311++G**	14.0	13.7
	PBE0	6-31G*	14.0	13.7
		6-311++G**	14.0	13.7

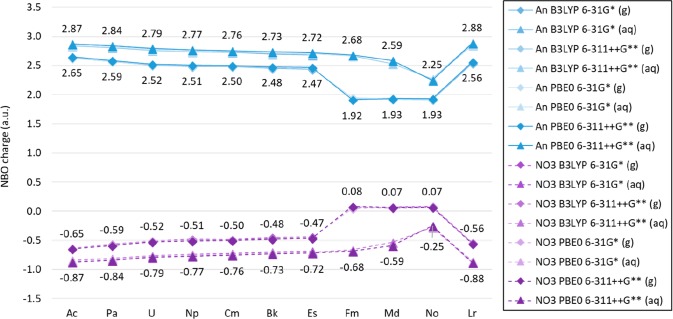
The partial charge of the actinides in [An(NO₃)]²⁺ in the gas phase calculated with NBO reveals a charge approximately between 2.4 and 2.6 for Ac to Es and Lr and approximately 1.9 for Fm, Md, and No. The 5f orbitals show an occupancy of approximately 1 for Th, 2 for Pa, 3 for U, 4 for Np, 5 for Pu, 6 for Am, 7 for Cm, 8 for Bk, 9 for Cf, 10 for Es, 12 for Fm, 13 for Md, and 14 for No and Lr. No significant differences are observed in the predicted 5f orbital occupancies, including and excluding the most diffuse basis functions in the An basis set. It is possible that these occupancies suggest an An IV configuration for Ac to Es and Lr and An III for Fm, Md, and No when bound to only one nitrate in the gas phase, as proposed in this study. The partial charge calculated with NBO for An and NO₃ in [An(NO₃)]²⁺ is shown in Figure 5. Predicted orbital occupancies for all actinides are shown in Tables S.4 and S.5 in the SI.

Figure 5.

An and NO₃ partial charges calculated with NBO in [An(NO₃)]²⁺ in gas and aqueous phases with the Stuttgart RSC 1997 ECP and basis set, including all diffuse basis functions for the actinides, with the 6-31G* and 6-311++G** basis sets for oxygen and nitrogen, and the B3LYP and PBE0 functional. (Numerical labels shown correspond to values obtained with PBE0 and 6-311++G**. Lines are included as a visual aid, and do not represent function continuity.)

Part II: Structural Analysis

Level of Theory Dependence

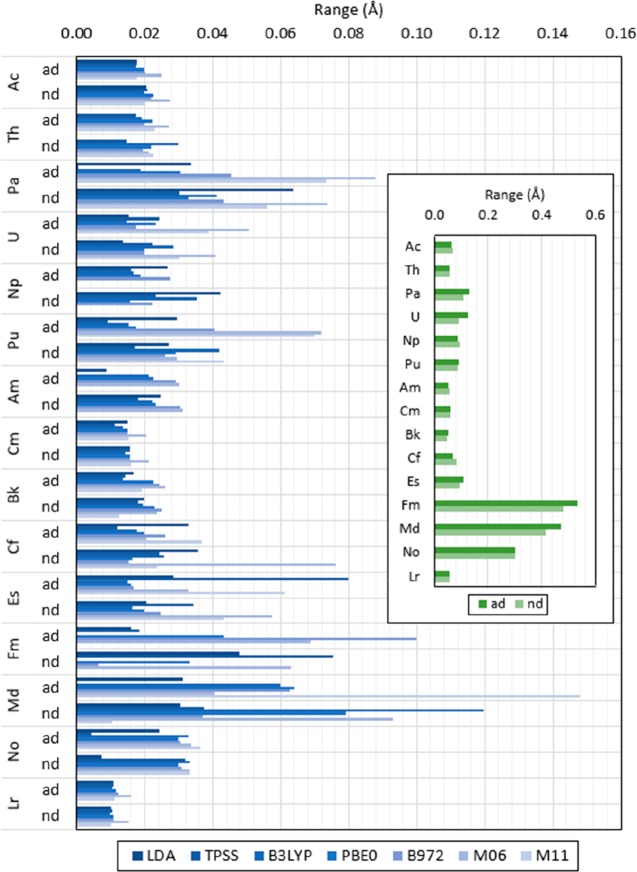
Optimized structures with the levels of theory previously indicated predict structures with an An–O1 distance with variations between 0.05 and 0.53 Å and between 0.05 and 0.48 Å when including and excluding the most diffuse basis functions in the An basis set, respectively, as shown in Figure 6. Overall, the largest ranges (as defined in eq 7b) when including all the basis functions in the An basis set are predicted when utilizing the M06 and M11 functionals, with differences in predicted An–O1 distance larger than 0.05 Å for Md with B3LYP, PBE0, B972, and M11, Fm with B972, and Es with TPSS. When excluding the most diffuse basis functions, predicted ranges larger than 0.05 Å are found with LDA for Pa, TPSS for Fm, B3LYP for Md, M06 for Md, Fm, Es, and Cf, and M11 for Pa. All An–O1 predicted distances are shown in Tables S.6 and S.7 in the SI.

Figure 6.

Predicted An–O1 distance range in [An(NO₃)]²⁺ calculated with LDA, TPSS, B3LYP, PBE0, B972, M06, and M11, the 6-31G*, 6-311++G**, cc-pVDZ, cc-pVTZ, and cc-pVQZ basis set for N and O, and the Stuttgart RSC 1997 ECP for An including (ad) and excluding (nd) the most diffuse basis functions in the basis set. Inset shows the overall range per actinide for all predicted values with all functional and basis set combinations. (Values shown are in angstrom. Ranges are calculated as indicated in eq 7b.)

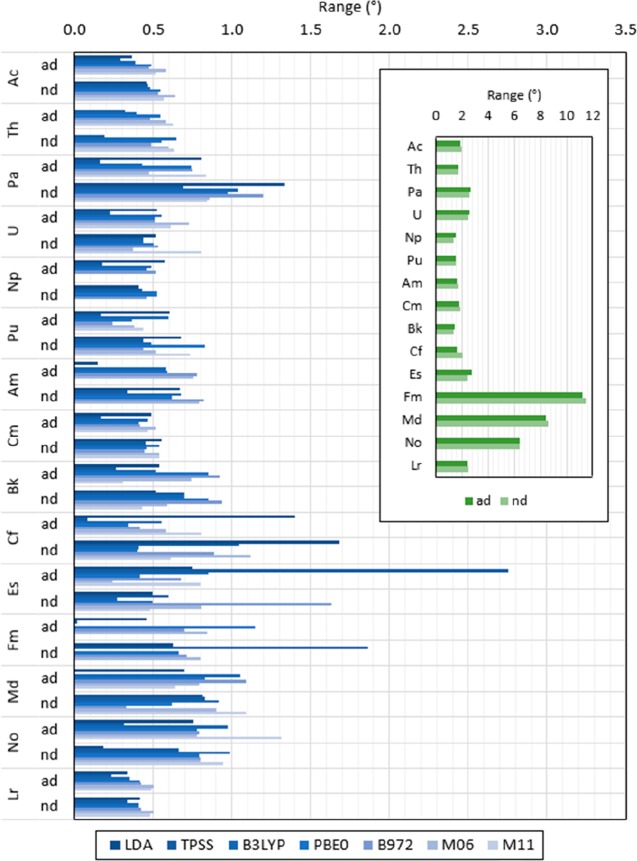
The O1–An–O2 angle in predicted structures shows a range between 1.45 and 11.24° when including all basis functions and between 1.32 and 11.46° when excluding the most diffuse basis functions in the An basis set, as shown in Figure 7. Ranges larger than 1° are predicted for structures optimized with M11 for Pa, B972 for Md, PBE0 for Fm, B3LYP for Md, TPSS for Es, and LDA for Cf when including all the basis functions in the An basis set. When excluding the most diffuse basis functions in the An basis set, a range larger than 1° is predicted with M11 for Md, M06 for Cf, B972 for Es and Pa, B3LYP for Pa, TPSS for Fm and Cf, and LDA for Cf and Pa.

Figure 7.

Predicted O1–An–O2 angle range in [An(NO₃)]²⁺ calculated with LDA, TPSS, B3LYP, PBE0, B972, M06, and M11, the 6-31G*, 6-311++G**, cc-pVDZ, cc-pVTZ, and cc-pVQZ basis set for N and O, and the Stuttgart RSC 1997 ECP for An including (ad) and excluding (nd) the most diffuse basis functions in the basis set. Inset shows the overall range per actinide for all predicted values with all functional and basis set combinations. (Values shown are in degrees. Ranges are calculated for angles, as indicated in eq 7b for interatomic distances.)

Structural Changes in [An(NO₃)]²⁺

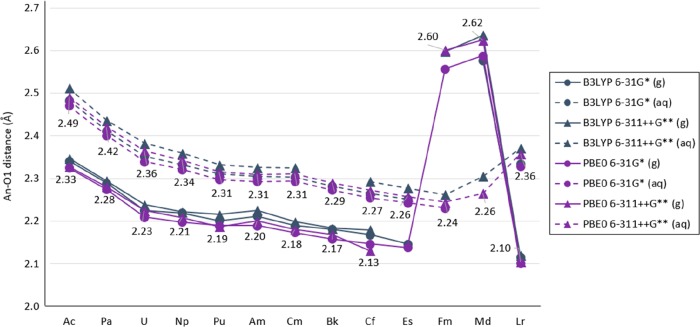
The predicted An–O1 distance has an overall gradual decrease from Ac to Lr from 2.3 to 2.1 Å; however, structures with Fm, Md, and No showed an An–O1 distance of approximately 2.6 Å (Figure 8). It is likely that this difference of almost 0.5 Å is due to Fm, Md, and No presenting an An III configuration (instead of the An IV from the rest of the actinide series). Figure S.2 in the SI shows the An–O1 trend for Ac to Es/Lr calculated with PBE0 including all basis functions. Moreover, Fm, Md, and No presented variations in An–O1 distance when calculated with the proposed methodologies, giving an Fm–O1 distance between 2.1 and 2.6 Å, an Md–O1 distance between 2.2 and 2.6 Å, and No–O1 between 2.3 and 2.6 Å (shown in Figure S.3 in the SI).

Figure 8.

Calculated An–O1 distance in [An(NO₃)]²⁺ in gas and aqueous phase with the B3LYP and PBE0 functional, the 6-31G* and 6-311++G** basis set for N and O atoms, and the Stuttgart RSC 1997 ECP and basis set including all diffuse basis functions in the basis set (in angstrom). Labels shown correspond to results obtained with PBE0 and 6-311++G**. Th and No are shown in Figures 10 and 11. (Lines are included as a visual aid and do not represent function continuity.)

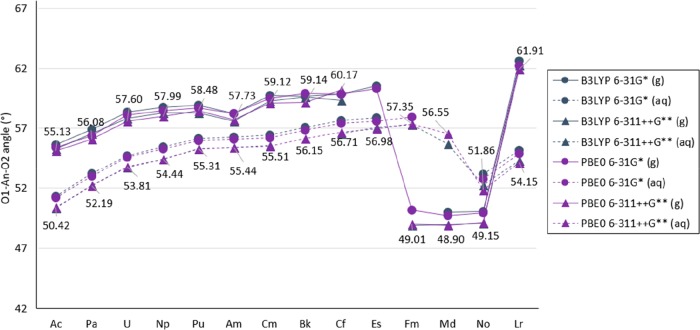
The predicted O1–An–O2 angle has an overall gradual increase from 55.6 to 62.3° from Ac–Es to Lr (Figure 9). Similar to the analysis in the An–O1 distance, the O1–An–O2 angle for Fm, Md, and No shows a large difference in which the O1–An–O2 angle is approximately 10° more narrow than the contiguous actinides (Es and Lr). Furthermore, a variation in predicted O1–An–O2 angles is observed for Fm, Md, and No structures optimized with the levels of theory listed in which the O1–Fm–O2 angle ranges from 49 to 60°, O1–Md–O2 ranges from 49 to 57°, and O1–No–O2 ranges from 49 to 55°. All values discussed in this paragraph are included in Figures S.4 and S.5 in the SI (with S.5 showing ‘ad’ in grey, and ‘nd’ in black).

Figure 9.

Calculated O1–An–O2 angle in [An(NO₃)]²⁺ in gas and aqueous phase with the B3LYP and PBE0 functional, the 6-31G* and 6-311++G** basis set for N and O atoms, and the Stuttgart RSC 1997 ECP and basis set, including all diffuse basis functions in the basis set (in degrees). Labels shown correspond to results obtained with PBE0 and 6-311++G**. Th is shown in Figure 1. (Lines are included as a visual aid and do not represent function continuity.)

The An–O1 distance in solvated [An(NO₃)]²⁺ compounds is longer than in gas-phase structures for Ac, Pa, U, Np, Pu, Am, Cm, Bk, Cf, Es, No, and Lr (less than 0.16 Å for Ac, Pa, U, Np, Pu, Am, Cm, Bk, Cf, and Er). It is shorter for Md and Fm (between 0.33 and 0.36 Å). Similarly, the O1–An–O2 angle is smaller in solvated compounds than in the gas phase for Ac, Pa, U, Np, Pu, Am, Cm, Bk, Cf, Es, and Lr and larger for Th, Fm, Md, and No. (The An–O1 distances are shown in Figure 8, and the O1–An–O2 angles in Figure 9.) The O1 and O2 are predicted to be equidistant to the An in [Th(NO₃)]²⁺ and [No(NO₃)]²⁺ in the gas phase. However, the solvated [Th(NO₃)]²⁺ structures have a difference of up to 1 Å between the An–O1 and An–O2 distance for structures optimized with B3LYP and 0.5 Å for [No(NO₃)]²⁺ compounds optimized with B3LYP and PBE0, as shown in Figures 10, 11 and S.9, S.10 in the SI.

Figure 10.

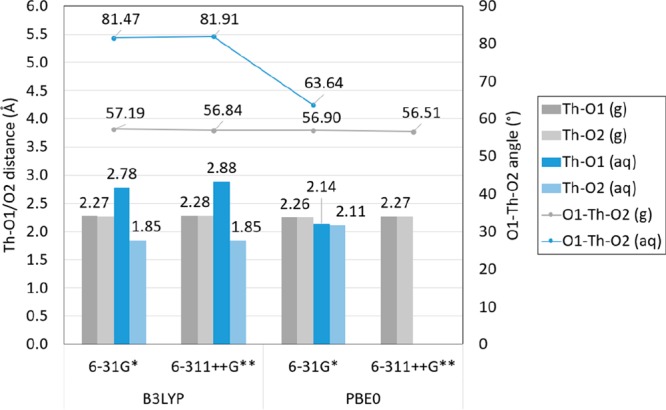
Calculated Th–O1 and Th–O2 distance in [Th(NO₃)]²⁺ in gas and aqueous phase with the B3LYP and PBE0 functional, the 6-31G* and 6-311++G** basis set for N and O atoms, and the Stuttgart RSC 1997 ECP and basis set including all diffuse basis functions in the basis set (in angstrom). Labels shown correspond to results obtained with PBE0 and 6-311++G**. (Lines are included as a visual aid and do not represent function continuity.)

Figure 11.

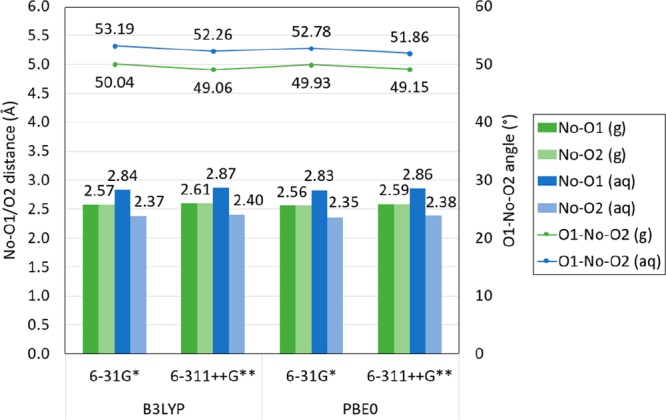
Calculated No–O1 and No–O2 distance in [No(NO₃)]²⁺ in gas and aqueous phase with the B3LYP and PBE0 functional, the 6-31G* and 6-311++G** basis set for N and O atoms, and the Stuttgart RSC 1997 ECP and basis set including all diffuse basis functions in the basis set (in angstrom). Labels shown correspond to results obtained with PBE0 and 6-311++G**. (Lines are included as a visual aid and do not represent function continuity.)

The structural characteristics of [Lr(NO₃)]²⁺ illustrated in Figures 8 and 9 do not follow the trend that would have otherwise been expected from extrapolation of An–O1 distances and O1–An–O2 angles calculated for other actinides in the series, which is likely due to the electronic rearrangement occurring due to relativistic effects⁴⁶⁻⁴⁸ that prevents inference of chemical characteristics for transactinides. This break in the trendline along the periodic table was similarly observed by Toyoshima.⁴⁹ A decrease in ionic radii from Cf to Md has been previously discussed within changes of actinide contractions across the series,⁵⁰⁻⁵³ which is likely affecting the bond length predicted in our study. The second break to Lr is consistent with recent experimental and theoretical results that treat it as similar to Lu but distinct from other later transactinides.⁵⁴⁻⁵⁷

The An–O1 distance (for An = Fm, Md, and No) in [An(NO₃)]²⁺ compounds is approximately 0.3 Å longer than in [An(NO₃)]⁺. The O1–An–O2 angle is approximately 8° wider in [An(NO₃)]⁺ than in [An(NO₃)]²⁺, and the O1–N–O2 angle is approximately 10° wider in [An(NO₃)]²⁺ than in [An(NO₃)]⁺. All values are shown in Table S.8 in the SI.

Part III: Gibbs Free Energies of Reaction

Level of Theory Dependence

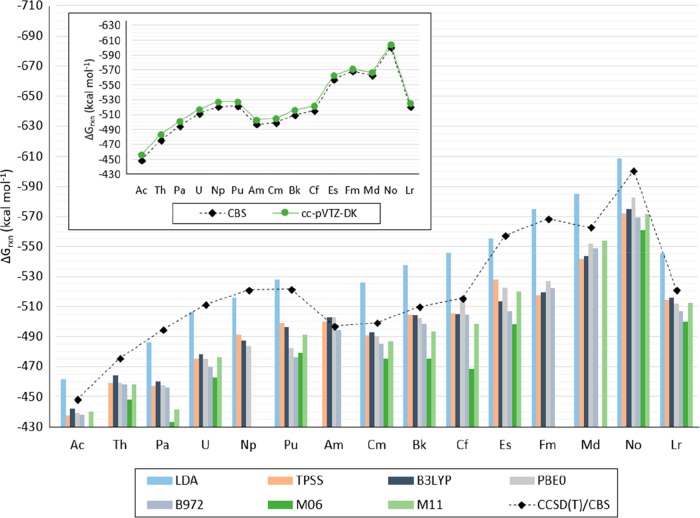
Calculated Gibbs free energies of reaction of the [An(NO₃)]²⁺ compounds (from Ac to Lr), as shown in eq 4a with CCSD(T), the cc-pVTZ-DK and cc-pVQZ-DK basis set for N and O atoms, and the cc-pVTZ-X2C and cc-pVQZ-X2C basis set for the actinides show the same stability trend as when calculated at the CBS limit, as indicated in eqs 1 and 2. The predicted Gibbs free energies of reaction calculated with cc-pVQZ-X2C/cc-pVQZ-DK are within 2 kcal mol^–1 from those calculated at the CBS limit. The predicted Gibbs free energies of reaction with cc-pVTZ-X2C/cc-pVTZ-DK are within 3 and 8 kcal mol^–1 of those calculated at the CBS limit (with a difference of 8 kcal mol^–1 for Ac and Th; 7 for Pa; 6.0 for U, Np, Pu, Am, Cm, Bk, Cf; 5 for Es and Lr; 4 for Md and No; and 3 for Fm). Predicted Gibbs free energies of reaction calculated with CCSD(T) are shown in Figures 12, 13, and Table S.11 in the SI.

Figure 12.

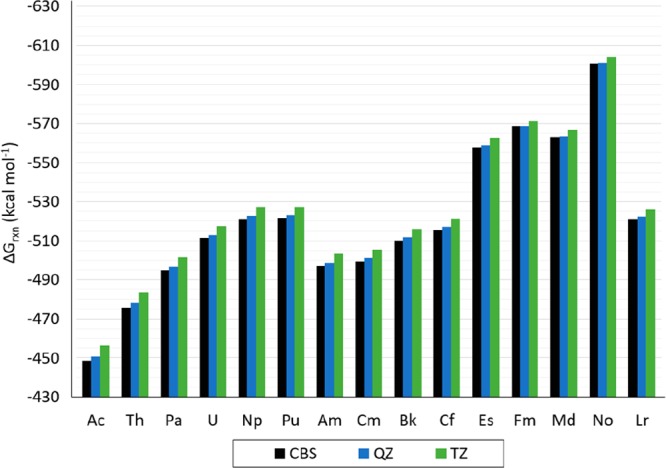
Calculated ΔG_rxn for [An(NO₃)]²⁺ (with An = Ac to Lr) with CCSD(T)/cc-pVTZ-X2C:cc-pVTZ-DK (indicated as TZ), CCSD(T)/cc-pVQZ-X2C:cc-pVQZ-DK (indicated as QZ), and CCSD(T)/cc-pV∞Z-X2C:cc-pV∞Z-DK (indicated as CBS).

Figure 13.

Calculated ΔG_rxn for [An(NO₃)]²⁺, with An = Ac to Lr, with CCSD(T)/cc-pVTZ-X2C:cc-pVTZ-DK, CCSD(T)/cc-pV∞Z-X2C:cc-pV∞Z-DK, and LDA, TPSS, B3LYP, PBE0, B972, M06, and M11 with the Stuttgart RSC 1997 ECP and associated basis set for An, and the 6-311++G** basis set for N and O. Values are reported in kcal mol^–1. LDA is indicated in blue, the meta-GGA functional (TPSS) in orange, the hybrid GGA (B3LYP, PBE0, and B972) functionals in gray, and the meta-hybrid GGA functionals (M06 and M11) in green. (Lines for CCSD(T) are included as a visual aid and do not represent function continuity.)

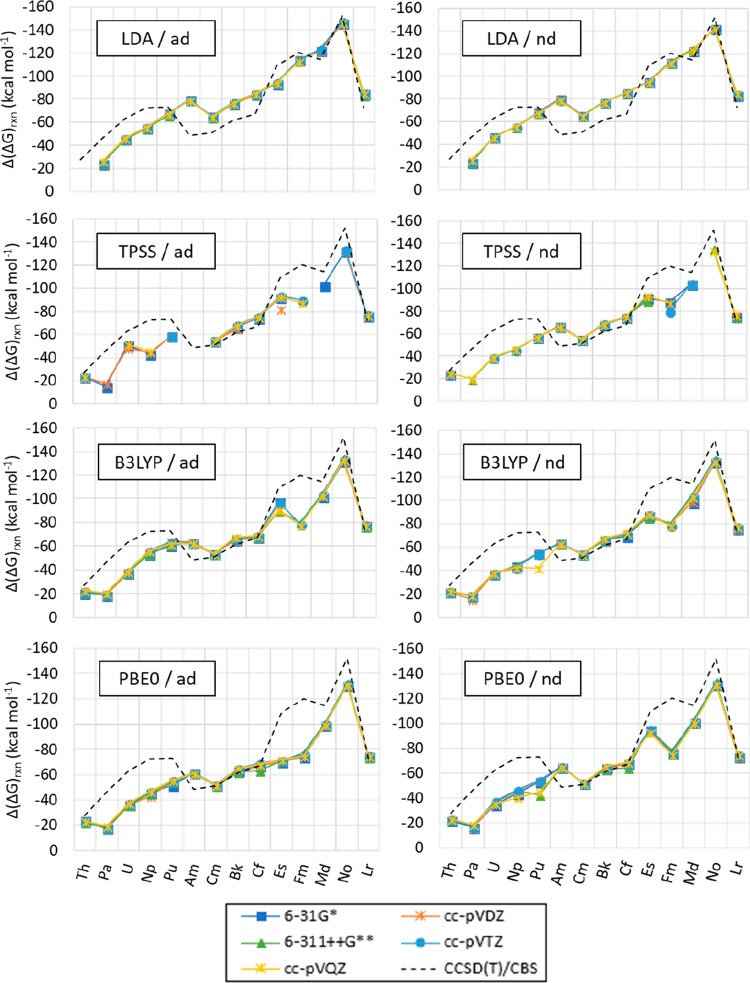
Including and excluding the most diffuse basis functions in the basis set of the actinide in the calculated Gibbs free energies of reaction give a difference of less than 6 kcal mol^–1 with most levels of theory tested. Exceptions are predicted (listed in this paragraph specifying the basis set used for the N and O atoms, in kcal mol^–1) when utilizing TPSS for U with cc-pVQZ (13.20) and Fm with cc-pVTZ (9.98); for B3LYP with Np with 6-31G* (10.49), cc-pVDZ (13.52), 6-311++g** (10.70), cc-pVTZ (13.64), and cc-pVQZ (13.35); for Pu with 6-31G* (6.73), cc-pVDZ (10.59), 6-311++G** (8.02), cc-pVTZ (9.10), and cc-pVQZ (20.31); and for Es with 6-31G* (11.24), cc-pVDZ (9.46), and cc-pVTZ (9.25); for PBE0 with Np and cc-pVQZ (6.39), Pu with 6-311++G** (12.90) and cc-pVQZ (10.57), and Es with 6-31G* (23.40), cc-pVDZ (21,65), 6-311++G** (22.90), cc-pVTZ (23.50), and cc-pVQZ (20.30); with B972 for Pu, Cf, and Es with 6-311++G** (10.13, 7.78, 6.28), and for Md with 6-31G* (16.77); with M06 for Pu with 6-311++G** (12.50), Md with cc-pVTZ (17.27) and cc-pVQZ (17.54), and No with cc-pVQZ (17.12); and with M11 for U with cc-pVTZ (24.51), Pu with 6-311++G** (10.99), and cc-pVTZ (8.59), Cf with 6-311++G** (12.26), Es with cc-pVTZ (19.77), Md with cc-pVDZ (7.69), and No with 6-3G* (12.33) and cc-pVDZ (12.24). All predicted differences between including and excluding the most diffuse basis functions in the basis set of the actinide are shown in Figures 14, S.6, and Tables S.12–S.16 in the SI.

Figure 14.

Δ(ΔG)_rxn for [An(NO₃)]²⁺ normalized to Ac calculated with LDA, TPSS, B3LYP, and PBE0 with the Stuttgart RSC 1997 ECP and basis set including (ad) and excluding (nd) the most diffuse basis functions for An, and the 6-31G*, cc-pVDZ, 6-311++G**, cc-pVTZ, and cc-pVQZ for N and O. Δ(ΔG)_rxn calculated with CCSD(T), the cc-pV∞Z-X2C (CBS) basis set for An, and the cc-pV∞Z-DK (CBS) basis set for N and O is included as reference (indicated as CCSD(T)/CBS in labels). Values are reported in kcal mol^–1. [Δ(ΔG)_rxn = ΔG_rxn,An – ΔG_rxn,Ac, as indicated in eq 5a, with An = Th to Lr.] The lines are included as a visual aid, and do not represent function continuity.

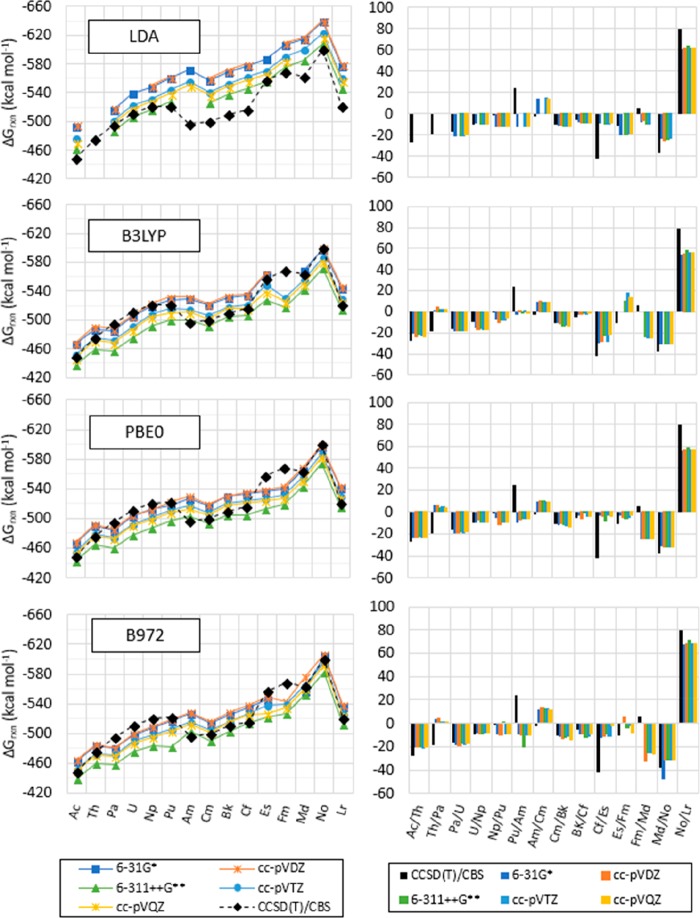
The difference between the predicted Gibbs free energies of reaction with LDA, TPSS, B3LYP, PBE0, B972, M06, and M11 with the Stuttgart RSC 1997 ECP and basis set including all basis functions and varying the basis set of N and O amongst contiguous actinides show that the Δ(ΔG)_rxn for Ac/Th is within 12 from those predicted by CCSD(T)/CBS for all options tested.

Differences between Pa and Th (Th/Pa) are between 19 and 36 kcal mol^–1 from those predicted with CCSD(T)/CBS. The Δ(ΔG)_rxn difference is between −19 and 7 kcal mol^–1 for Pa/U, between −8 and 17 kcal mol^–1 for U/Np, between −15 and 4 kcal mol^–1 for Np/Pu, between −47 and −24 kcal mol^–1 for Pu/Am, and between 11 and 17 kcal mol^–1 for Am/Cm. The predicted Δ(ΔG)_rxn with all options tested is between −4 and 10 kcal mol^–1 for Cm/Bk, between −6 and 12 kcal mol^–1 for Bk/Cf, between 11 and 46 for Cf/Es, between −10 and 30 kcal mol^–1 for Es/Fm, between −38 and −6 kcal mol^–1 for Fm/Md, between −10 and 37 kcal mol^–1 for Md/No, and between −36 and −8 kcal mol^–1 for No/Lr (as shown in Figures 15, S.7–S.9, and Tables S.17–S.21 in the SI).

Figure 15.

Calculated ΔG_rxn (left) and difference between contiguous actinides (right) for [An(NO₃)]²⁺ (with An = Ac to Lr) with LDA, TPSS, B3LYP, and PBE0, the Stuttgart RSC 1997 ECP and associated basis set, including all diffuse functions for An, and the 6-31G*, cc-pVDZ, 6-311++G**, cc-pVTZ, and cc-pVQZ for N and O, and CCSD(T)-FC1/cc-pV∞Z-X2C:cc-pV∞Z-DK (indicated as CCSD(T)/CBS in labels). Values are reported in kcal mol^–1. (Δ(ΔG)_rxn An1/An2 = ΔG_rxn,An2 – ΔG_rxn,An1, as indicated in eq 5a, with An = Ac to Lr. The lines are included as a visual aid and do not represent function continuity.)

Binding Energies in [An(NO₃)]²⁺

Overall, it is calculated that the [An(NO₃)]²⁺ compounds increase in stability as the atomic number increases (i.e., the Gibbs free energies of reaction, as proposed in eqs 3a and 4a, decrease) from Ac to Pu and from Cm to No. The stability from Pu to Am is predicted to decrease with CCSD(T)/CBS and increase with other methods tested (as shown in Figure 15). There is a slight decrease in predicted stability (less than 6 kcal mol^–1) from Fm to Md and a decrease from No to Lr (approx. 80 kcal mol^–1). For [An(NO₃)]²⁺ compounds with solvation, the difference in predicted ΔG_rxn amongst contiguous actinides was within 20 kcal mol^–1 from those predicted in the gas phase in most cases, with larger differences when calculated with B3LYP/6-31G* and B3LYP/6-311++G** of approximately 40 and 50 kcal mol^–1 for Ac/Th and Th/Pa, respectively, with B3LYP/6-31G* for Cf/Es, and 30 kcal mol^–1 for Md/No with B3LYP and PBE0 with 6-311++G** (shown in Figures S.10–S.11 in the SI).

The contribution of the enthalpy (ΔH_rxn) to the Gibbs free energy of reaction (ΔG_rxn) of [An(NO₃)]_(g)²⁺ is approximately 99%, and the contribution from the entropy term (TΔS_rxn) is approximately 1% (shown in Tables S.22–S.27 in the SI). When applying the implicit solvation model, the enthalpy contribution to the Gibbs free energy of reaction to [An(NO₃)]_(aq)²⁺ is between 84 and 96% and the entropy term contribution is between 4 and 16% (shown in Table S.28 in the SI).

T₁/D₁ Diagnostics

The T₁ and D₁ diagnostic values for [An(NO₃)]²⁺ are between 0.018 and 0.029 for T₁ and between 0.065 and 0.136 for D₁ for all actinides except for Pa. The T₁ and D₁ values for [Pa(NO₃)]²⁺ are 0.075 and 0.358, respectively. T₁/D₁ diagnostic limits are 0.02/0.10,^58,59 0.05/0.15,⁶⁰ and 0.045/0.12⁶¹ for main group, 3d, and 4d metals, respectively. To our knowledge, there is no such set limit to determine multireference characters for actinides. The known guidelines for main group, 3d, and 4d metals are applied to the T₁ and D₁ values obtained for the [An(NO₃)]²⁺ compounds in this study (shown in Figure 16). The only compound with both T₁ and D₁ values higher than limits set for 3d and 4d is [Pa(NO₃)]²⁺. It is possible that a limit set for actinides in the future could also find [Th(NO₃)]²⁺, [Es(NO₃)]²⁺, [Fm(NO₃)]²⁺, [Md(NO₃)]²⁺, and [No(NO₃)]²⁺ to have a T₁/D₁ diagnostic indicative of multireference character. This suggests that [Pa(NO₃)]²⁺, and likely [Th(NO₃)]²⁺, [Es(NO₃)]²⁺, [Fm(NO₃)]²⁺, [Md(NO₃)]²⁺, and [No(NO₃)]²⁺ should be studied with multireference methods (which is the focus of future work). All T₁ and D₁ values are included in Table S.29 in the SI.

Figure 16.

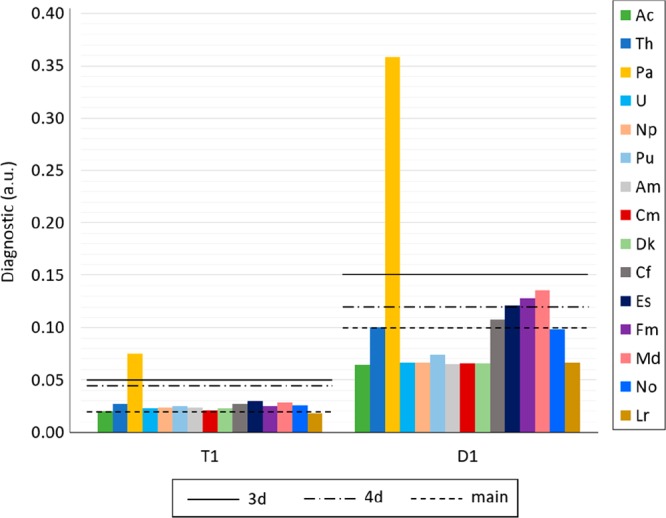
T₁/D₁ diagnostics for [An(NO₃)]²⁺ (with An = Ac to Lr). Lines represent limits for main group elements (T₁ = 0.02, D₁ = 0.1), 3d metals (T₁ = 0.05, D₁ = 0.15), and 4d metals (T₁ = 0.045, D₁ = 0.12).

B₁ Diagnostics

The B₁ diagnostic for [An(NO₃)]²⁺ (with An = Ac to Es) calculated as indicated in eq 9 is between 6 and 21 for n₁, between 3 and 11 for n₂, between 2 and 7 for n₃, and between 1 and 5 for n₄ (as shown in Figure 17). As explained in the methods, the B₁ diagnostics was designed for dissociation energies and establishes that the system for which the B₁ is greater than 10 kcal mol^–1 presents multireference character.⁶² Although there is no bond dissociation in the proposed reaction, there are two An–O bonds, which would likely infer an n₂ for the B₁ diagnostic. For n₂, only [Es(NO₃)]²⁺ is slightly above 10 kcal mol^–1 (10.68 kcal mol^–1), whereas all remaining [An(NO₃)]²⁺ (with An = Ac to Cf) had n₂B₁ values below 10 kcal mol^–1. All compounds tested have B₁ diagnostic values below 10 kcal mol^–1 for n₃ and n₄. The B₁ diagnostic for n₁ was above 10 kcal mol^–1 for [An(NO₃)]²⁺ (with An = U to Es), but n₁ is an nonphysical representation for bonding in the binding reaction proposed. Nonetheless, it is provided as reference. All B₁ diagnostic values are included in Table S.30 in the SI.

Figure 17.

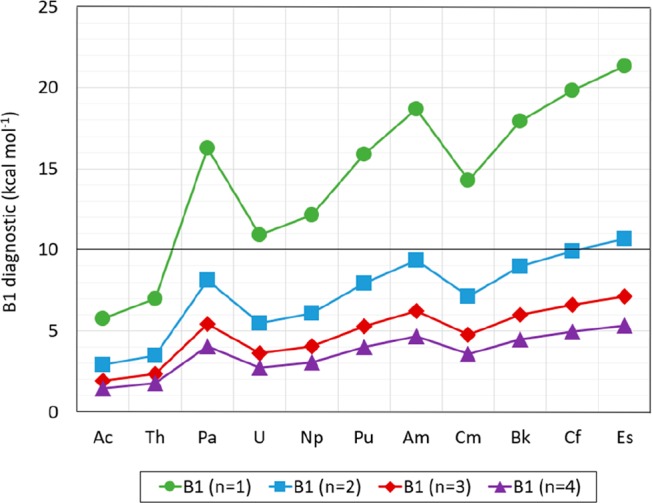
B₁ diagnostics for [An(NO₃)]²⁺ (with An = Ac to Lr). (Lines are included as visual aid, but do not constitute function continuity.)

Conclusions

Computational predictions are essential for understanding binding selectivity preferences for actinide separations. Establishing differences in predictive capabilities from available electronic structure methodologies and their effect on optimization of structures containing actinide atoms is essential for the design of selective extracting agents. This study analyzes the effects various methodologies have in the prediction of population analysis, structural characteristics, and Gibbs free energies of reaction in a systematic study of [An(NO₃)]²⁺ structures (with An = Ac to Lr). An An IV electronic configuration is predicted for [An(NO₃)]²⁺ structures in the gas phase across the series except for Fm, Md, and No that have an An III configuration; whereas in solution, all structures except for No present an An IV configuration.

The predicted Gibbs free energies of reaction calculated with coupled cluster with perturbative doubles and triples (CCSD(T)) with the eXact-2-Component (X2C) Hamiltonian, the all-electron, correlation-consistent basis sets (cc-pVnZ-X2C) for the actinide atoms and the cc-pVnZ-DK basis sets for N and O shows the same trend as that when calculated at the CBS limit, with the triple ζ level providing a ΔG_rxn between 2 and 8 kcal mol^–1 lower than those predicted at the CBS limit. Predicted Gibbs free energies of reaction amongst contiguous actinides seem largely independent from the basis set of the nonactinide atoms with most functionals and show a larger dependence on the functional of choice.

Understanding electron withdrawing effects is essential to design selective binding agents for actinide separations, and population analysis can greatly aid in this analysis. On the basis of the findings in this study, utilizing NBO would minimize having to choose amongst functional and basis set combinations, as large dependence on level of theory of choice is observed when utilizing Mulliken and Löwdin. Excluding and including the most diffuse basis functions in the basis set of the actinide shows negligible variations with NBO and larger differences with Mulliken and Löwdin. Although Mulliken population analysis has been largely the method of choice for various population analyses in the field, this research suggests a shift to NBO is advantageous for improved comparisons between studies.

The An–O1 bond length shows larger variations with respect to the functional than with respect to the basis set of choice for the N and O atoms. Moreover, the An–O1-predicted distances show differences of less than 0.09 Å when including and excluding the most diffuse basis functions for the actinide atoms. The decrease in the An–O1 bond length and increase in O1–An–O2 angle in [An(NO₃)]²⁺ across the actinide presents discontinuities in An–O1 distance for [Fm(NO₃)]²⁺, [Md(NO₃)]²⁺, and [No(NO₃)]²⁺, which showed a longer bond length and smaller angle in the gas phase due to being in an An III state instead of An IV. However, for solvated structures, an overall trend is followed from Ac to Md but not for No, which has an An III configuration in [No(NO₃)]²⁺ both in gas and solution when calculated with the methods included in this study. Calculations for compounds with Lr show an An IV preferred state, but structural characteristics including interatomic distances and angles do not follow the trend including Ac to Md, as expected given their electronic configuration.

Finally, T₁/D₁ and B₁ diagnostics are performed to provide insight into the multireference character of the [An(NO₃)]²⁺ complexes studied. Future determination of limits for the B₁, T₁, and D₁ values for actinide systems and multireference calculations on the same or similar complexes can be aided by the B₁, T₁, and D₁ coefficients included in this study. This study provides in-depth and systematic findings that can be used as an initial assessment for future work involving multireference and spin–orbit effects on physicochemical and thermochemical characteristics across the actinide series (including other single-reference ab initio methods, as well as basis sets including all-electron descriptions for the actinides). The results obtained in this study will provide a strong baseline for future studies evaluating functionals to provide recommendations for actinide-containing compounds. Future in-depth studies for NBO predictions will encompass a more exhaustive set of levels of theory in gas and liquid phases.

Methods

Partial charges, structural characteristics, and Gibbs free energies of reaction are calculated with various levels of theory for [An(NO₃)]²⁺ structures (with An = Ac to Lr) in the gas phase optimized with local density approximation (LDA),⁶³ the meta-GGA TPSS⁶⁴ functional, the hybrid-GGA B3LYP,⁶⁵ PBE0,⁶⁶ and B972⁶⁷ functionals, the meta-hybrid-GGA M06⁶⁸ and M11⁶⁹ functionals, the Stuttgart RSC 1997 ECP and associated basis set for actinide atoms (including and excluding the most diffuse s, p, d, and f basis functions) for the actinide atoms, and the 6-31G*,⁷⁰ cc-pVDZ,⁷¹ 6-311++G**,⁷⁰ cc-pVTZ,⁷¹ and cc-pVQZ⁷¹ basis sets for nitrogen and oxygen atoms. The ECP on the actinide atom accounts for scalar relativistic effects by replacing 60 electrons with a relativistic pseudopotential. Partial charges, electron withdrawing effects, and orbital occupancies are calculated with Mulliken, Löwdin, and natural bond orbital (NBO). Aqueous-phase calculations are included with the B3LYP and PBE0 functional and the 6-31G* and 6-311++G** basis set for the nitrogen and oxygen atoms. The COSMO⁷² solvation model is utilized for accounting for implicit solvation effects.

Additionally, Gibbs free energies of reaction as single-point calculations are obtained with coupled cluster with single-double, and perturbative triple (CCSD(T)) method with all-electron, correlation-consistent basis sets (cc-pVnZ-X2C)¹⁹ (where n = ζ level) for the actinide atoms to account for scalar relativistic effects. The cc-pVnZ-X2C basis sets are used for the actinide atoms, and the cc-pVnZ-DK basis sets are used for N and O. The CCSD(T) calculations include the eXact-2-Component (X2C) Hamiltonian⁷³ to account for scalar relativistic effects. The spin unrestricted CCSD(T) method [UCCSD(T)] is used for open-shell CCSD(T) calculations.^74,75 Complete Basis Set (CBS) energies are included following a two-point extrapolation using energies from cc-pVTZ-X2C and cc-pVQZ-X2C calculations. Values obtained at the CBS limit are referred to as cc-pV∞Z-X2C. The Hartree–Fock energy is extrapolated using a formula from Karton and Martin⁷⁶ showed in eq 1.

1

The correlation energy is extrapolated as described by eq 2.⁷⁷

2

The CCSD(T) calculations correlate the 6s6p5f electrons of the actinide atom and the 2s2p electrons of the oxygen and nitrogen atoms in the correlation space. The T₁(58)D₁(59) diagnostics for multireference analysis is obtained with CCSD/cc-pVQZ-X2C.

The model reaction proposed for this study is shown in eq 3a, with eq 3a describing binding in the gas phase and eq 3b binding in an aqueous environment.

3a

3b

The Gibbs free energy of reaction for eq 3a and 3bis calculated as shown in eqs 4a and 4b, respectively.

4a

4b

Relative Gibbs free energies of reaction, Δ(ΔG)_rxn, between two compounds with contiguous actinides are calculated as indicated in eqs 5a and 5b.

5a

5b

with An.1 and An.2 representing the An of the compounds being compared.

The equation representing the difference between including (denoted “ad”) and excluding (denoted “nd”) the most diffuse basis functions in the calculation of Gibbs free energy of reaction is indicated (eq 6).

6

Ranges are defined as the difference between the largest and smallest data points in the calculation of partial charges (C), bond lengths (r_e), and Gibbs free energies (ΔG_rxn), as indicated in eqs 7a, 7b, and 7c, respectively.

7a

7b

7c

Effects of including (ad) and excluding (nd) the most diffuse basis functions in population analysis to calculate particle charges (C), bond lengths (r_e), and Gibbs free energies (ΔG_rxn) are calculated as indicated in eqs 8a, 8b, and 8c, respectively.

8a

8b

8c

The B1LYP-diagnostic (B₁)⁶² developed by Schultz and co-workers is utilized to provide insight into possible multireference character of [An(NO₃)]²⁺ structures (with An = Ac to Es). This diagnostic is defined as indicated in eq 9

9

where n corresponds to the number of bonds being broken.⁶²

The proposed binding reaction in this study (shown in eq 3a) does not provide bond dissociations. Since the B₁ diagnostic was developed for dissociations,⁶² there is no equivalent n for the proposed reaction. Therefore, n is evaluated from 1 to 4 to illustrate the dependence of the B₁ diagnostic on n for the proposed reaction. The n variable evaluated at 1, 2, 3, and 4 is indicated as n₁, n₂, n₃, and n₄, respectively.

Additional calculations for [An(NO₃)]⁺ structures are included when needed for discussion purposes, given findings obtained for structural characteristics.

Geometry optimization calculations are obtained with tight tolerances and extra fine grid. The optimizations are performed without symmetry constraints to avoid enforcing a preconceived symmetry. Harmonic vibrational frequencies are included for thermochemical corrections and to verify that no complex frequencies are obtained. Thermochemical corrections are calculated for each structure at each level of theory at 298.15 K, except for CCSD(T) calculations that include thermochemical corrections and geometries obtained with the B3LYP functional, the Stuttgart RSC 1997 ECP including all diffuse basis functions for the actinide atoms, and the 6-311++G** basis set for nitrogen and oxygen atoms. Harmonic vibrational frequency calculations reveal that the optimized structures have all real frequencies (i.e., no complex frequencies are observed). CCSD(T) single-point calculations utilize MOLPRO2015 defaults.

The NWChem 6.6 package⁷⁸ is used to obtain DFT geometry optimizations, harmonic vibrational frequency calculations, as well as Mulliken and Löwdin population analysis. The NBO⁷⁹ population analysis is obtained with the Natural Bond Orbital 6.0 (NBO6) program.⁸⁰ Molpro2015⁸¹ is used for CCSD(T) calculations. The DIRAC16⁸² package is used for Dirac–Hartree–Fock calculations. Basis sets and effective core potentials are obtained from EMSL^83,84

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b01800.

• Bond lengths and angles from structural analysis, partial charges and orbital occupancies from population analysis, and thermochemical data from Gibbs free-energy calculations (PDF)

The authors declare no competing financial interest.