How Precise Are Our Quantitative Structure–Activity Relationship Derived Predictions for New Query Chemicals?

Abstract

Quantitative structure–activity relationship (QSAR) models have long been used for making predictions and data gap filling in diverse fields including medicinal chemistry, predictive toxicology, environmental fate modeling, materials science, agricultural science, nanoscience, food science, and so forth. Usually a QSAR model is developed based on chemical information of a properly designed training set and corresponding experimental response data while the model is validated using one or more test set(s) for which the experimental response data are available. However, it is interesting to estimate the reliability of predictions when the model is applied to a completely new data set (true external set) even when the new data points are within applicability domain (AD) of the developed model. In the present study, we have categorized the quality of predictions for the test set or true external set into three groups (good, moderate, and bad) based on absolute prediction errors. Then, we have used three criteria [(a) mean absolute error of leave-one-out predictions for 10 most close training compounds for each query molecule; (b) AD in terms of similarity based on the standardization approach; and (c) proximity of the predicted value of the query compound to the mean training response] in different weighting schemes for making a composite score of predictions. It was found that using the most frequently appearing weighting scheme 0.5–0–0.5, the composite score-based categorization showed concordance with absolute prediction error-based categorization for more than 80% test data points while working with 5 different datasets with 15 models for each set derived in three different splitting techniques. These observations were also confirmed with true external sets for another four endpoints suggesting applicability of the scheme to judge the reliability of predictions for new datasets. The scheme has been implemented in a tool “Prediction Reliability Indicator” available at http://dtclab.webs.com/software-tools and http://teqip.jdvu.ac.in/QSAR_Tools/DTCLab/, and the tool is presently valid for multiple linear regression models only.

1. Introduction

Quantitative structure–activity relationship (QSAR) models are now used as popular tools for prediction of response data of chemicals to bridge data gaps.¹ They have varied applications in medicinal chemistry, agricultural chemistry, environmental chemistry, nanosciences, food sciences, materials science, and so forth.² The statistical quality of QSAR models is typically judged by a series of quality metrics while the quality of predictions is examined by methods such as cross-validation, test set validation, Y-randomization, and so forth, and the results are expressed in terms of different validation metrics, for which different threshold values have been reported in the literature.^3,4 However, it is not always obvious how well a QSAR model will perform for truly new, unknown data points in spite of having different quality measures related to internal and external validation tests. A model with respectable values of different correlation coefficients (R², Q_LOO², Q_Ext-F1², Q_Ext-F2², Q_Ext-F3², r_m², etc.) and/or error measures [mean absolute prediction error (MAE), RMSEP, etc.]⁵ is not necessarily expected to perform well while predicting the response for a new query chemical. This is because usually QSAR models are developed using rather limited datasets. While they exhibit good performance for closely related chemicals, the prediction error may increase heavily when the new query chemical is far from the training set.⁶ In other words, the QSAR model performance is not consistent across molecules, as it is typically better for compounds whose molecular structures were adequately represented by training compounds. It is very important to establish the credibility of the computational models to the experimental community who do the actual laboratory tests to find out the response values experimentally. A prediction with a good reliability measure or confidence can only be used as a replacement of experimentally derived data. At the same time, it is true that it is not possible to experimentally derive response values of all possible compounds in the large chemical space for numerous chemical/biological/toxicological endpoints. We must have some computational tools to derive prediction data for the real or hypothetical compounds for possible screening purposes, and we should have some measures to estimate the reliability of predictions. This will help us in prioritizing potential compounds for costly experiments. Although the concept of confidence of predictions was originally introduced^7,8 through applicability domain (AD) of QSAR models,⁹ the reliability of predictions is certainly not dependent only on chemical similarity, as from QSAR modeling experiences one can see that different compounds within the AD (those which are sufficiently similar to training compounds) might also show bad predictions.¹⁰

Recently, different attempts have been made to provide measures of confidence estimates of QSAR predictions. Some of these reports include methods based on the number of neighbors in the training dataset,⁷ average Euclidean distance to the training dataset,^11,12 local sensitivity of a regression model,¹³ leave-one-out (LOO) cross-validation of nearest neighbors,¹⁴ bagging (variance of the predicted responses),^15,16 and so forth. The first three among these do not consider the prediction model and, hence, might be less sensitive to model specific prediction behavior. Additionally, none of these approaches take actual prediction errors into account. Briesemeister and others⁶ have proposed two confidence estimators CONFINE and CONFIVE. The first one determines the error rates of the nearest members of a test compound in the training set, whereas the second one examines the variance in the surrounding local environment. Sazonovas et al.¹⁷ proposed a property-based similarity index using a bootstrapping technique to define a reliability index for predictions. Huang and Fan used prediction confidence in terms of probability for checking reliability of predictions in case of a tree-based classification problem.¹⁰ Sahlin et al. discussed AD-dependent predictive uncertainty in QSAR regressions based on Euclidean distances and standard deviation in perturbed predictions, combined with variance estimated by nearest-neighbor averaging.¹⁸ Toplak et al. suggested methods to quantify prediction confidence through estimation of the prediction error at the point of interest and showed that these methods can outperform standard reliability scores relying only on similarity-based approaches.¹⁹ However, recently, a probability oriented distance-based approach (which is essentially an AD-based approach) was proposed by another group as a robust and automatic method for defining the interpolation space where true and reliable predictions can be expected.²⁰ In the conformal prediction approach, the prediction values are complemented with measures of their confidence, in the form of prediction intervals, which are determined by some measures of dissimilarity of the new chemical compound to the training compounds.²¹ Very recently, Liu and others have proposed a new AD metric that considers the contributions of every training compound, each weighted by its distance to the molecule for which a QSAR prediction is made. They show that their proposed metric correlates strongly with prediction error.²²

In the literature, several attempts have been made to increase the quality of predictions and to ensure the reliability of the developed models. The model performance is usually tested by employing the hold-out method. However, because the composition of the training set remains the same in this method, it is not certain that the resultant model is optimal, as there may be a bias in descriptor selection. As compared to a single test set, double cross-validation (in which, the training set is further divided into “n” calibration and validation sets resulting in diverse compositions) provides a more realistic picture of model quality and should be preferred over a single test set.^23,24 Double cross-validation reliably and unbiased estimates prediction errors under model uncertainty for regression models. In another approach, consensus modeling has been applied by several researchers to improve the quality of predictions.^25,26 In this method, the final result takes into account the different assumptions characterizing each model, encompassing chemical structure to partitioning and cut-off criteria allowing for a more reliable judgment in a complex situation. Hewitt et al. have discussed a scheme for the peer verification of in silico models that enables end users and modelers to assess the scientific validity of the models.²⁷ Patel et al. have recently emphasized on the assessment of model reproducibility, particularly by users who might be nonexperts.²⁸ However, to ascertain the quality of predictions for a new query chemical is a challenge for QSAR model developers and a key concept central to the applicability of computational predictive models by the experimental scientists. Many of the reliability estimates developed so far are in some way related to similarity measures of the query compounds to the training compounds. However, the current similarity-based reliability scoring approaches should be complemented with alternative estimation techniques, as AD solely cannot justify the reliability of predictions.¹⁹ On the basis of our previous QSAR modeling exercises and observations made in those studies,²⁹⁻³¹ we have developed here a scheme to define reliability of predictions from QSAR models for new query compounds and implemented the method in an online tool freely available from http://dtclab.webs.com/software-tools and http://teqip.jdvu.ac.in/QSAR_Tools/DTCLab/. Presently, the tool is applicable for predictions of multiple linear regression (MLR) models, but the suggested method may potentially be applied to other chemometric models as well.

2. Materials and Methods

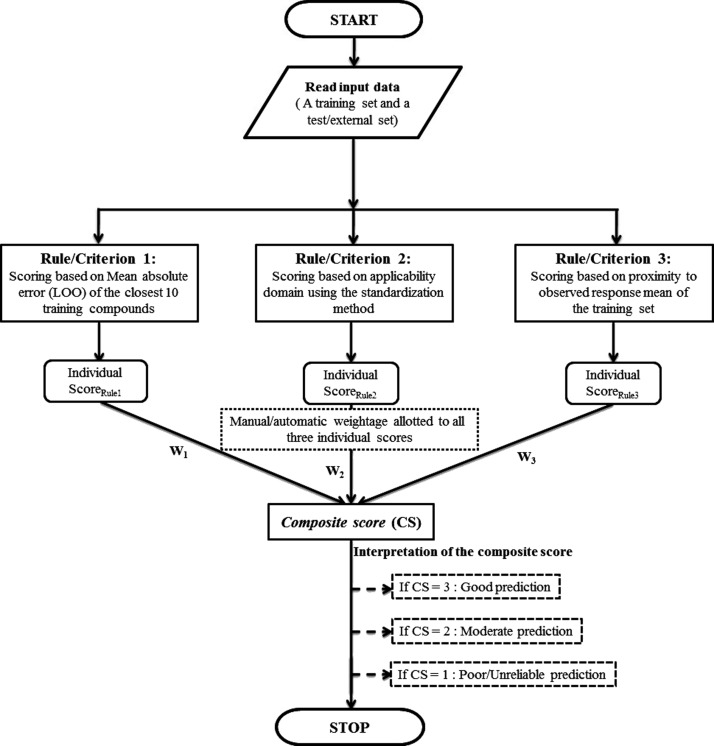
The aim of the present work has been to formulate a set of rules/criteria that will eventually enable the user to forecast the quality of predictions for individual test (external) compounds. Please note that usually test set compounds are derived from the original whole data set after application of a rational division strategy while external compounds are derived from a completely different source not reporting the original data set. In general, in our QSAR modeling exercises, we always observe that while predicting a set of test/external compounds, the quality of predictions of every external compound might not always be very good; for some query compounds, the quality of predictions is good, for some other compounds it is moderate, while some predictions can be poor or outside the reliability zone (unreliable). Keeping this in mind, in this work, we have proposed a set of three rules/criteria which might help in categorizing the quality of predictions for individual test/external set compounds into good, moderate, and poor/unreliable ones. The rules suggested here are based on the results of some of our previous studies and hypotheses proposed in those reports.^26,29−31 For analyzing the results, we have used a scoring system (1, 2, and 3) in this work. After applying each rule/criterion, the compounds whose quality of predictions are categorized as “good” are given the highest score, that is, 3, and the compounds with moderate quality predictions are given a moderate score equal to 2 and compounds with poor/unreliable predictions are given the lowest score of 1. The final categorization of each test/external compound is performed based on a composite score (described later), which is computed using the three individual scores (with different weighting schemes) obtained from each rule/criterion. We have also implemented the proposed scheme in a software tool “Prediction Reliability Indicator” that is made freely available for download from http://dtclab.webs.com/software-tools and http://teqip.jdvu.ac.in/QSAR_Tools/DTCLab/ (see a snapshot shown in Figure 1). This tool can presently deal with the MLR model-derived predictions only. Now, we will discuss all three rules/criteria and the categorization/scoring techniques in detail.

Figure 1.

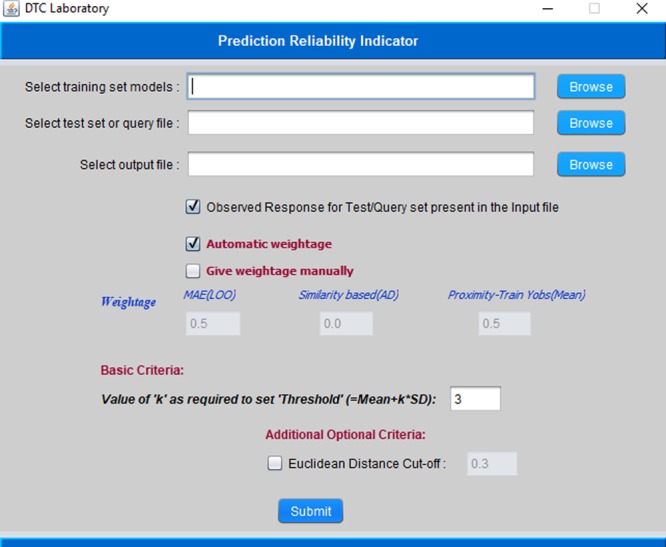
Snapshot of the developed software Prediction Reliability Indicator.

2.1. Rule/Criterion 1: Scoring Based on the Quality of LOO Predictions of Closest 10 Training Compounds to a Test/External Compound^26,28

According to this rule, 10 training set compounds are initially identified that are most similar to a particular test/external compound in the descriptor space, where similarity is determined based on a distance metric (in our case, we have used Euclidean distance). Next, the mean of absolute LOO prediction error (MAE_LOO) is calculated for the selected closest 10 compounds. Further, we have considered that the test/external set compounds whose corresponding closest training compounds have the lowest MAE_LOO value will be predicted well and thus should get the highest score (equal to 3), while those test compounds with corresponding close training compounds have medium MAE_LOO values should get a moderate score (equal to 2), and those test compounds with corresponding close training compounds having high MAE_LOO values should get the least score (equal to 1). Here, the scoring/categorization is performed based on the MAE-based criteria²⁸ (proposed by us earlier) which considers both MAE_LOO and standard deviation (σ_LOO) of the absolute prediction error values and is defined as follows:

2.1.1. Good Predictions

Here, the MAE_LOO denotes mean absolute LOO error for the selected closest training compounds to a test compound and σ_LOO value denotes the standard deviation of the absolute error values for the same observations.

Thus, the test/external compounds obeying the above conditions get score 3.

2.1.2. Bad Predictions

The test/external compounds obeying this condition get score 1.

2.1.3. Moderate Predictions

The predictions which do not fall under either of the above two conditions may be considered as of moderate quality. Thus, the rest of the test/external compounds get scores 2.

Now, to make sure that the selected set of 10 closest training compounds do not have any outlier in terms of chemical structural similarity, we have employed one additional criterion, that is, if the Euclidean distance of a test set compound to a particular training set compound out of those 10 selected ones is higher than the set threshold value, then discard that training set compound. Here, the threshold value is equal to the mean_ED + k × σ_ED (in our case, k = 3), where both mean_ED and standard deviation (σ_ED) are calculated using the Euclidean distance scores computed among all the training set compounds using the descriptor matrix appearing in the input training model. Notably this criterion is based on the assumption that the computed Euclidean distance scores between a test set compound and the training set compounds hypothetically follows a normal distribution pattern, and according to this distribution, most (99.7%) of the population remains inside the mean + 3 × σ_range. Thus, any distance score that is outside the threshold value can be considered dissimilar to the most of the training set compounds and is considered as an outlier. Further, in the developed software, a user can optionally set a Euclidean distance cutoff value (between 0 and 1) to limit the selection of only those training set compounds with Euclidean distance score less than or equal to the user-defined cut-off value. Here, the Euclidean distance score calculated between a test set compound and a training set compound “i” is scaled using the maximum and minimum distance scores computed for that training set compound “i” from all the remaining training set compounds. In a similarity scale, the Euclidean distance score “0” means exactly similar compounds, whereas, as the distance score value increases, the similarity decreases. Moreover, after applying these criteria, if the number of selected similar training compounds becomes less than 3, then we have set the lowest score to that particular test set compound. In this case, there are only limited or no similar compounds present in the training set, and thus the chemical features of the particular test chemical are less likely to be dealt with by the training model which is not trained for the features present in the particular test chemical. In case, the number of similar training compounds is equal or greater than 3, the model is considered as “qualified” for prediction of respective test set compound and the scoring is then performed based on the MAE-based criteria.

2.2. Rule/Criterion 2: Scoring Based on the Similarity-Based AD Using Standardization Method³⁰

The AD of a QSAR model plays an important role for identifying the uncertainty in the prediction of a specific chemical by that model, which is based on the similarity of that chemical to the training set chemicals that were employed to develop the model.³⁰ If a test set compound is similar to none or a very small fraction of the training set compounds, then its prediction is expected not to be reliable, as the model has not captured the features of that test set compound which is different from all or majority of the training set compounds. Such test set compounds are expected to be outside the AD of the model and their predictions are not reliable. Thus, the prediction is valid only if the compound being predicted falls within the AD of the model. We have considered the abovementioned fact to derive our rule/criterion 2. Here, we have employed a simple AD method, that is, AD using the standardization approach³⁰ (previously proposed by us) for scoring or categorizing the quality of test/external set predictions. Further, the methodology of scoring based on the similarity-based AD using standardization method is discussed here.

First, the modeled descriptors columns are standardized based on the corresponding mean and standard deviation (for the training set compounds only) of respective descriptors. The logic behind standardization of descriptors is that if the corresponding standardized value for descriptor i of compound k (S_ki) is more than 3, then the compound should be outside AD based on the descriptor i.

The scoring performed for each test set compound is defined as follows:

• (i)If the maximum S_i value of a test compound k is lower than 3, then the test compound is quite similar to a good number of compounds in the training set with respect to all descriptors (the compound is within AD). Therefore, such test compounds are assigned with the highest score, that is, 3.
• (ii)If the minimum S_i value of a test compound k is higher than 3, then the test compound is quite dissimilar to most of the compounds in the training set with respect to all descriptors (the compound is not within AD). Therefore these test compounds get the lowest score, that is, 1.

If the compound has a maximum S_i value above 3 but the minimum S_i value below 3, then the compound is similar to some of the training set compounds with respect to some descriptors and at the same time dissimilar to some of the training set compounds with respect to other descriptors. Thus, in such cases:

• (iii)If mean of the S_i values of a test compound for all descriptors in a model plus 1.28 times corresponding standard deviation (denoted as S_new) is lower than 3, there is 90% probability that the S_i values of that test compound are lower than 3. Thus, when S_new value of a test compound is lower than 3, then the test compound can be considered to be within the AD. For such test compounds, we have assigned a moderate score, that is, 2.
• (iv)If S_new value of a test compound is higher than 3, then the test compound can be considered as outside the AD. As these test compounds are outside AD, they get the lowest score, that is, 1.

2.3. Rule/Criterion 3: Scoring Based on the Proximity of Predictions to the Training Set Observed/Experimental Response Mean³¹

We have previously observed³¹ that the quality of fit or predictions of MLR models is better for compounds having the experimental response values (training and test compounds) close to the training set observed response mean. Thus, in rule/criterion 3, we have proposed to judge the prediction quality of a test compound based on the proximity of predicted response value to the training set observed/experimental response mean. Note that here the predicted response of test compounds is taken as a measure of their experimental response as an approximation, as for new query compounds, experimental response values might be unavailable. First, the predicted response value (Y_pred^Test) of each test compound is calculated using the training set model, and then this Y_pred value is compared with the training set experimental response mean (Y_mean^Train) and the corresponding standard deviation (σ^Train) in the following manner:

• (i)A test compound with Y_pred^Test value falling within the range inside Y_mean ± 2σ^Train, that is, (Y_mean^Train + 2σ^Train) ≥ Y_pred ≥ (Y_mean^Train – 2σ^Train) can be presumed to be predicted well by the model and thus gets score 3.
• (ii)A test compound with Y_pred^Test value falling within the range (Y_mean + 3σ^Train) ≥ Y_pred^Test ≥ (Y_mean – 3σ^Train) and (Y_mean^Train + 2σ^Train) < Y_pred < (Y_mean^Train – 2σ^Train) can be presumed to be predicted moderately by the model and thus gets score 2.
• (iii)A test set compound with Y_pred^Test value falling within the range (Y_mean + 3σ^Train) < Y_pred^Test < (Y_mean – 3σ^Train) can be presumed to be predicted poorly by the model and thus gets score 1.

2.4. Computation of a Composite Score

Further, we have employed a weighting scheme to compute a composite score for judging the prediction quality of each test compound using all the three individual scores that are obtained after applying above three rules. The composite score is defined as follows:

where score_rule1, score_rule2, and score_rule3 represent individual scores obtained after applying respective rules, whereas W₁, W₂, W₃ indicate user-defined or automatic weighting given to each of the three individual scores.

The derived composite score is then converted to the nearest whole number and interpreted as follows: Score 3 (good confidence); Score 2 (moderate confidence) and Score 1 (poor/unreliable confidence).

For testing our scheme, we have performed a few case studies using five datasets comprising corresponding training and test sets with known observed/experimental responses. The first dataset represents 224 cyclin-dependant kinase 5/p25 (CDK5/p25) inhibitors,³² the second set represents acetylcholinesterase (AChE) inhibitory activity of 426 functionalized organic chemicals,³³ the third set deals with solubility of C₆₀ in 156 organic solvents,³⁴ the fourth set represents 104 chemicals with bioluminescent repression of the bacterium genus Pseudomonas,³⁵ and the final set comprises persistent, bioaccumulative, and toxic (PBT) index values of 180 chemicals.³⁶ All five datasets were first rationally divided into respective training and test sets using three different techniques, namely, sorted response, Kennard–Stone algorithm,³⁷ and modified-k-medoids clustering³⁸ using two software tools, namely, Dataset Division version 1.2 (for sorted response and Kennard–Stone algorithm based divisions) and Modified k-medoid version 1.2 developed by us.³⁹ The Kennard–Stone algorithm and modified-k-medoids clustering-based division are widely known techniques that are well described in the literature,^37,38 whereas the sorted response-based division involves sorting of all of the chemicals based on the response values, and then a predetermined number of chemicals are selected from the list at a constant interval as the test set chemicals while the remaining chemicals are utilized as the training set chemicals. Here, all of the divisions were performed such that in each case the entire dataset was divided into a training set and a test set of about 70:30 ratio with respect to the number of compounds. Followed by this, five individual models were developed for each division employing any one or more of the diverse statistical approaches like stepwise MLR, genetic function algorithm, and so forth. All developed models were validated based on the internal validation metrics such as R², Q_LOO², MAE_Train and external validation metrics such as Q_F1², MAE_Test. Note that the training and test sets information for all of the developed models in this study are provided in the Supporting Information.

As experimental responses are available for the test set compounds, one can easily compute absolute prediction errors of all of the test compounds using the experimental and predicted response values. Further, based on the actual absolute prediction errors, we have classified the prediction quality of each test set compound into three groups: good, moderate, and poor or unreliable predictions. The criteria for this classification based on the absolute prediction errors of test compounds are defined as follows:

• (i)A test compound with absolute prediction error ≤(0.15 × training set range) gets score equal to 3 (good predictions).
• (ii)A test compound with absolute prediction error >(0.25 × training set range) gets score equal to 1 (bad predictions).
• (iii)A test compound with absolute prediction error >(0.15 × training set range), but ≤(0.25 × training set range), gets score equal to 2 (moderate predictions)

Now, for each test set, we have two sets of rank, that is, one based on the composite score (predicted scores) and other based on the absolute prediction error (reference scores). Therefore, now we have computed percent (%) correct predictions by comparing the scores derived directly from the absolute residual errors and the composite score obtained by giving different weighting to each of the individual scores and iteratively changing the weighting values from 1:0:0 to 0:0:1 with an increment of 0.1 at each step. Here, our objective was to find out the correct weighting combination (to all three individual scores), which will give the maximum percent correct predictions. The workflow of the whole process is shown in Figure 2.

Figure 2.

Schematic diagram of workflow of the analysis.

2.5. Validation of Our Scheme

For validation of our scheme, we have employed four additional datasets, each comprising a training set, a test set, and a true external set. In this case, the true external datasets are not part of the original modeling sets, but they are collected separately and with experimental response values. The first dataset represents refractive index of 319 (including 98 true external data points)polymers,⁴⁰ the second set represents BACE1 activity of 90 (including 17 true external data points) chemicals,⁴¹ the third set deals with glass transition temperature of 244 (including 38 true external data points) polymers,⁴² and the fourth set comprises sweetness potency of 300 (including 60 true external data points) organic molecules.⁴³ All four datasets were rationally divided into respective training and test sets using Kennard–Stone (first and second datasets) and sorted response (third and fourth datasets) techniques, respectively, as reported in the original studies. Here, five models were developed for each dataset. The model development and validation tests were performed in the similar way as mentioned in the previous section. Note that the training, test, and external set information for all of the models are provided in the Supporting Information. Further, for each model, at first the best weighting combination (to all three individual scores) was selected based on the optimal % correct prediction (test set) value, which are calculated and compared for all possible weighting combinations (using test set data). Then the % correct predictions for the true external set were computed using the selected weighting combination to confirm whether the selected combination (using the test set) also works aptly for judging the prediction quality of the true external set compounds. In the present work, the external sets have never been used to tune the weighting scheme, and these have only been used only once for the final calculations shown.

2.6. Retrospective Analysis

In the present study, we have also performed the retrospective analysis for the test or true external set compounds which do not show concordance between the reference score (based on the actual absolute prediction error) and the predicted composite score. For such compounds, we have analyzed the following:

• 1.Whether such test or true external compounds are outside the AD?
• 2.Whether their observed responses are close to the training set mean, that is, within ±1σ^Train or distant at different levels, that is, between ±1σ^Train and ±2σ^Train or between ±2σ^Train and ±3σ^Train or beyond ±3σ^Train?
• 3.The minimum Euclidean distance between the test/external compound and the closest member in the training set.
• 4.The generalized Jaccard similarity coefficient (similarity index based on the modeled descriptors)⁴⁴ between the test/external compound and the close member in the training set. Here, before calculating the generalized Jaccard coefficient, the descriptor matrix is first normalized by scaling between 0 and 1, and then the Jaccard similarity coefficient is computed using the following formula:

where x = (x₁, x₂, ..., x_n) and y = (y₁, y₂, ..., y_n) are two vectors; x vector represents modeled normalized descriptor values for a test/external compound; y vector represents modeled normalized descriptor values for the closest training set compound to the test/external compound; min(x_i,y_i) denotes minimum value between x_i and y_i; max(x_i,y_i) denotes maximum value between x_i and y_i; and n represent number of modeled descriptors.

The above analysis was made to get an insight into the factors responsible for imprecise predictions from otherwise predictive MLR models for some specific query compounds.

3. Results and Discussion

The present communication has defined a composite score which can be used as a marker of prediction quality of each individual compound of a true external test set. The success of any QSAR model lies in precisely predicting a true external test set which has not been used during model development as well as in validation stage. Thus, we have employed three criteria which use information about experimental response values as well as structural and physicochemical properties of training compounds to provide us with a final composite score based on which we can categorize the prediction quality in terms of “good”, “moderate”, and “bad”. The details about the scoring system have already been discussed in the Materials and Methods section.

To judge the composite scoring system, we have used nine diverse datasets previously used by us for developing predictive QSAR/QSPR/QSTR models against different activity, physicochemical property, and toxicity endpoints. The first five datasets (modeling datasets) had training and test set divisions derived using different methods and these were used to find out the optimum weighting of different criteria (as discussed before) to obtain the best possible quality of predictions. For each of these cases, each dataset was divided into training and test sets using three different approaches, namely, sorted response-based method, Kennard–Stone method, and modified-k-medoids methods. Thereafter, models were developed employing the GA-MLR approach from each training set and in each case five models were recorded. Thus, 15 models were developed for each dataset. Followed by this, an automatic weighting checking of three criteria was performed employing the training and respective test set by selecting “automatic weightage” tab of the developed software tool. For each dataset, we have checked which weighting combination is emerging for maximum number of times for the 15 models developed giving best % correct predictions for the test set(s). Followed by this, automated weighting selection-based analysis of the results was performed and the outcomes are illustrated in Tables S1–S5 in the Supporting Information. The obtained optimum weighting was then used to check the correct percentage prediction of test set compounds for all developed models by selecting “give weightage manually” in the developed software tool along with additional validation metrics and AD information for each model. The obtained results are reported in Tables 1–5.

Table 1. Results for CDK Dataset (Model Dataset 1) with Best Weighting (0.5–0–0.5) Combination as Obtained from the Retrospective Study.

model	division method	R2	Q2	MAE95%Train	QExt-F12	MAE95%Test	correct prediction in %	training set range	number of compounds outside ADa
1	sorted responseb	0.74	0.71	0.15	0.73	0.14	87.84	2.396	0
2		0.71	0.69	0.14	0.69	0.13	86.49		0
3		0.68	0.66	0.14	0.68	0.13	85.14		1 (122)
4		0.70	0.67	0.14	0.67	0.13	85.14		4 (118, 119, 122, 123)
5		0.63	0.61	0.17	0.65	0.17	77.02		0
6	Kennard–Stonec	0.78	0.75	0.14	0.63	0.13	85.29	2.342	0
7		0.77	0.75	0.14	0.59	0.14	79.41		1 (195)
8		0.74	0.71	0.14	0.54	0.13	89.71		0
9		0.72	0.70	0.14	0.56	0.12	83.82		0
10		0.71	0.68	0.14	0.54	0.13	86.76		0
11	modified-k-medoidsd	0.74	0.71	0.13	0.70	0.17	86.67	2.397	0
12		0.69	0.66	0.13	0.65	0.14	89.33		3 (30, 38, 39)
13		0.69	0.66	0.13	0.65	0.14	88		0
14		0.70	0.68	0.14	0.68	0.13	92		0
15		0.64	0.61	0.16	0.65	0.14	88		0

^aAD using standardization technique is used and compound ID mentioned under parenthesis.

^bN_Training = 154, N_Test = 74.

^cN_Training = 156, N_Test = 68.

^dN_Training = 149, N_Test = 75.

Table 5. Results for PBT Index of Chemicals (Model Dataset 5) with Best Weighting (0.5–0–0.5) Combination as Obtained from the Retrospective Study.

model	division method	R2	Q2	MAE95%Train	QExt-F12	MAE95%Test	correct prediction in %	training set range	number of compounds outside ADa
1	sorted responseb	0.88	0.87	0.36	0.92	0.37	91.67	8.1	1 (189)
2		0.90	0.89	0.33	0.95	0.27	100		2 (41, 189)
3		0.89	0.88	0.35	0.94	0.30	100		2 (14, 189)
4		0.89	0.88	0.34	0.93	0.34	91.67		1 (14)
5		0.89	0.88	0.34	0.94	0.32	88.89		4 (14, 41, 189, 206)
6	Kennard–Stonec	0.91	0.90	0.35	0.87	0.34	95.56	8.1	2 (211, 212)
7		0.90	0.89	0.34	0.88	0.29	95.56		0
8		0.91	0.90	0.34	0.88	0.34	95.56		0
9		0.91	0.90	0.34	0.88	0.31	95.56		0
10		0.92	0.91	0.33	0.88	0.31	95.56		0
11	modified-k-medoidsd	0.91	0.90	0.32	0.84	0.45	88.64	7.24	3 (11, 25, 189)
12		0.90	0.89	0.32	0.87	0.40	86.36		2 (11, 25)
13		0.92	0.91	0.31	0.86	0.43	93.18		2 (11, 25)
14		0.90	0.89	0.32	0.88	0.39	93.18		0
15		0.92	0.91	0.31	0.86	0.43	93.18		2 (11, 25)

^aAD using standardization technique is used and compound ID mentioned under parenthesis.

^bN_Training = 144, N_Test = 36.

^cN_Training = 135, N_Test = 45.

^dN_Training = 136, N_Test = 44.

Each of the remaining four datasets had a true external set each along with training and test set divisions. Each of these datasets consists of one training, one test and one true external test sets on which five models are applied. Employing the methodology previously described, an “automatic weightage” scheme was selected in the developed software tool using the training and test set compounds to find out the optimum weighting. We have checked for occurrence of a specific weighting for maximum number of times, and then we have used each selected weighting to predict the true external test set by selecting “give weightage manually” option in the developed software. Interestingly, in many circumstances, we got a different percentage of correct predictions for the true external set employing the weighting combinations obtained from the automatic weighting selection scheme, although these weightages showed same percentage correct predictions for the respective test sets. After automated weighting selection based analysis (Tables S6–S9 in the Supporting Information), we have used the optimum weighting to predict the response for the respective test and true external test sets for each model along with different validation metrics and information on AD (Tables 6–9). The results from different datasets are described in detail below.

Table 6. Results for Refractive Index of Polymers Dataset (True External Dataset 1) with Best Weighting (0.5–0–0.5) Combination as Obtained from the Retrospective Study.

	training set			test set				true external test set
model	R2	Q2	MAE95%Train	QExt-F12	MAE95%Test	correct prediction in %	number of compounds outside ADa	QExt-F12	MAE95%Test	correct prediction in %	number of compounds outside ADa
1	0.90	0.88	0.01	0.88	0.01	98.51	1 (143)	0.87	0.01	94.90	0
2	0.91	0.90	0.01	0.89	0.01	97.01	1 (1)	0.87	0.01	91.84	5 (319, 333, 334, 339, 340)
3	0.90	0.89	0.01	0.89	0.01	97.01	2 (1, 143)	0.87	0.01	94.90	6 (319, 331, 333, 334, 339, 340)
4	0.90	0.88	0.01	0.90	0.01	97.01	2 (1, 185)	0.88	0.01	94.90	7 (319, 331, 333, 334, 339, 341)
5	0.90	0.89	0.01	0.90	0.01	98.51	2 (1, 143)	0.88	0.01	93.88	0

^aAD using standardization technique is used and compound ID mentioned under parenthesis; division method: Kennard–Stone; N_Training = 154, N_Test = 67, N_{True-External-Test} = 98.

Table 9. Results forf Sweetness Potency of Organic Molecules (True External Dataset 4) with Best Weighting (0.5–0–0.5) Combination as Obtained from the Retrospective Study.

	training set			test set				true external test set
model	R2	Q2	MAE95%Train	QExt-F12	MAE95%Test	correct prediction in %	number of compounds outside ADa	QExt-F12	MAE95%Test	correct prediction in %	number of compounds outside ADa
1	0.84	0.82	0.40	0.87	0.40	93.75	1 (228)	0.74	0.59	80	0
2	0.85	0.83	0.43	0.87	0.42	95	2 (137, 228)	0.75	0.63	83.33	0
3	0.71	0.69	0.59	0.75	0.57	73.75	2 (137, 228)	0.64	0.79	75	0
4	0.86	0.85	0.39	0.83	0.48	93.75	1 (228)	0.69	0.66	73.33	0
5	0.85	0.83	0.39	0.85	0.40	92.5	1 (228)	0.79	0.56	86.67	0

^aAD using standardization technique is used and compound ID mentioned under parenthesis; division method: activity sorted; N_Training = 160, N_Test = 80, N_{True-External-Test} = 60.

3.1. Results for Modeling Datasets

3.1.1. Model Dataset 1: Cyclin-Dependant Kinase 5/p25 (CDK5/p25) Inhibitors

Among 15 models (5 models obtained from each of three different division strategies), 9 models showed highest percentage of correct predictions (for the respective test sets) with the weighting combinations of 0.5–0–0.5 [weighting – score(MAE-LOO)/weighting – score(AD)/weighting – score(train-mean)] along with other combinations. For the remaining models, the combination 0.5–0–0.5 stays at second or third position with a very low difference in % correct predictions from the winner combination. The % correct prediction ranges from 83.78 to 92% for all 15 models (Table S1). In case of the six models where the weighting combination of 0.5–0–0.5 does not evolve as the winner, we checked those specific models with 0.5–0–0.5 manual weighting selection (correct % prediction for model 5: 78%, model 6: 85.29%, model 7: 79.41%, model 8: 89.71%, model 9: 83.82%, model 11: 86.67%), and in each case reduction in % correction for a specific model is within 5% in comparison to the value when the model is predicted with the obtained optimum weighting combination, which is different from 0.5–0–0.5 (Table S1). Thus, employing the weighting combination of 0.5–0–0.5, we got the % correct prediction ranging around 78–92%. Model qualities were checked through classical QSAR metrics followed by AD studies. The values of R² metric range from 0.63 to 0.78, Q² range from 0.61 to 0.75, and Q_Ext-F1² or R_pred² range from 0.54 to 0.73, considering all developed 15 models. The AD study suggested that no compounds remain outside the AD for 11 models and 1, 4, 1, and 3 compounds remain outside the AD for models 3, 4, 7, and 12, respectively. Considering 74, 74, 68, and 75 compounds in the test sets for models 3, 4, 7, and 12, respectively, the obtained results are highly acceptable and reliable ones. The details about the number of training and test compounds in different divisions along with training set range followed by results of statistical parameters and AD are enlisted in Table 1 and in Supporting Information excel files.

3.1.2. Model Dataset 2: AChE Inhibitory Activity

In case of AChE inhibitory activity dataset, 13 models showed best weighting combinations of 0.5–0–0.5 out of developed 15 models along with other weighting combinations for the highest % of correct predictions. More interestingly, the weighting combinations of 0.5–0–0.5 evolved as the sole winner for 6 models. Considering all 15 models, the % correct prediction ranges from 84.38 to 91.41% (Table S2). Two models where 0.5–0–0.5 weighting does not evolve as the winner, we checked them with 0.5–0–0.5 manual weighting combination (% correct predictions for model 4: 85.21%, model 9: 85.93%) and the % correct prediction change is around 1–2.5% for the specific models (Table S2). This result supports that all 15 models can be successfully predicted with the obtained best weighting combination of 0.5–0–0.5 for this specific dataset and the % correct prediction range for the test set remain within the range of 84.38–91.41%. The developed models showed R² metric values ranging from 0.52 to 0.74, Q² ranging from 0.50 to 0.71, and Q_Ext-F1² or R_pred² ranging from 0.50 to 0.63, which support that all models are valid and acceptable, considering a large number of data points of 426 where the training and test sets in each case consist of 284 compounds and 142 compounds, respectively. The AD study is also performed concurrently suggesting that the number of compounds stay outside the AD for all models reported in Table 2. The details about the number of training and test compounds in different divisions along with the training set response range followed by results of statistical parameters and AD information are enlisted in Table 2 and in Supporting Information excel files.

Table 2. Results for AChE Dataset (Model Dataset 2) with Best Weighting (0.5–0–0.5) Combination as Obtained from the Retrospective Study.

model	division method	R2	Q2	MAE95%Train	QExt-F12	MAE95%Test	correct prediction in %	training set range	number of compounds outside ADa
1	sorted responseb	0.68	0.65	0.49	0.58	0.55	87.32	7.82	10 (13, 336–338, 340, 342–344, 347, 360)
2		0.67	0.64	0.49	0.61	0.52	85.92		5 (242–244, 323, 360)
3		0.64	0.60	0.46	0.52	0.53	86.62		11 (32, 33, 35, 336–338, 340, 342–344, 347)
4		0.52	0.47	0.48	0.56	0.52	85.21		15 (32, 33, 242–244, 323, 336–338, 340, 342–344, 347, 368)
5		0.64	0.60	0.46	0.53	0.55	86.62		14 (32, 33, 35, 174, 218, 323, 336–338, 340, 342–344, 347)
6	Kennard–Stonec	0.71	0.69	0.49	0.48	0.58	84.38	7.82	1 (201)
7		0.69	0.67	0.51	0.48	0.58	91.41		1 (201)
8		0.74	0.71	0.47	0.53	0.56	91.41		1 (1)
9		0.69	0.67	0.51	0.50	0.59	85.94		1 (1)
10		0.70	0.68	0.48	0.53	0.57	88.26		0
11	modified-k-medoidsd	0.68	0.65	0.48	0.63	0.51	86.62	7.76	8 (177–179, 203, 219, 246, 310, 311)
12		0.68	0.65	0.49	0.61	0.52	87.32		8 (177–179, 203, 219, 246, 310, 311)
13		0.66	0.63	0.49	0.60	0.53	85.92		7 (177–179, 203, 219, 310, 311)
14		0.67	0.65	0.50	0.55	0.58	85.21		8 (177–179, 203, 219, 246, 310, 311)
15		0.65	0.62	0.50	0.58	0.56	87.32		1 (246)

^aAD using standardization technique is used and compound ID mentioned under parenthesis.

^bN_Training = 284, N_Test = 142.

^cN_Training = 284, N_Test = 142.

^dN_Training = 284, N_Test = 142.

3.1.3. Model Dataset 3: C₆₀ Solubility in Organic Solvents

Like previous datasets, for this specific dataset also we have checked which weighting combination emerges for maximum number of times among 15 models. Interestingly, 11 models showed best weighting combinations of 0.5–0–0.5 with other combinations for this dataset. Among the 11 models, for 2 models, the weighting combination of 0.5–0–0.5 evolved as the sole winner. With the automated weighting screening, the % correct prediction ranges from 91.49 to 100%, taking into consideration all 15 models (Table S3). Four models, where 0.5–0–0.5 weighting combination does not evolve as the winner, we checked them with 0.5–0–0.5 manual weighting (correct % prediction for model 3: 91.5%, model 11: 93.62%, model 13: 89.36%, model 15: 89.36% for the best weighting combinations) and the % correct prediction range reduces by about 2% in case of the manually selected combination of 0.5–0–0.5 compared with automated weighting (Table S3). Therefore, taking the 0.5–0–0.5 weighting combination for all 15 models, the % correct predictions range (89.36–100%) remain almost similar and highly acceptable and reliable ones for checking external data points. The values of R² metric range from 0.79 to 0.89, Q² range from 0.77 to 0.88, and Q_Ext-F1² or R_pred² range from 0.78 to 0.88, taking into consideration all 15 models. Although the dataset consists of 156 data points (all divisions consist of 109 compounds in the training set and 47 compounds in the test set), still the obtained values of statistical parameters are highly acceptable. The AD study suggested that no compounds remain outside the AD for seven models and one compound each remains outside the AD for six models. For remaining two models, two compounds each remain outside the AD. The training set response ranges along with the statistical metric values and the details of AD analysis are enlisted in Table 3. The values of model descriptors and division pattern for each model are illustrated in Supporting Information excel files.

Table 3. Results for C₆₀ Solubility in Organic Solvents Dataset (Model Dataset 3) with Best Weighting (0.5–0–0.5) Combination as Obtained from the Retrospective Study.

model	division method	R2	Q2	MAE95%Train	QExt-F12	MAE95%Test	correct prediction in %	training set range	number of compounds outside ADa
1	sorted responseb	0.87	0.85	0.34	0.85	0.33	97.87	6.97	1 (128)
2		0.88	0.85	0.33	0.84	0.34	95.74		1 (128)
3		0.88	0.87	0.33	0.81	0.33	91.49		1 (85)
4		0.88	0.86	0.34	0.85	0.32	95.74		1 (21)
5		0.87	0.86	0.33	0.81	0.36	95.74		1 (128)
6	Kennard–Stonec	0.85	0.84	0.33	0.88	0.35	100	6.97	0
7		0.86	0.85	0.33	0.87	0.35	97.87		0
8		0.86	0.85	0.32	0.86	0.34	95.74		2 (87, 148)
9		0.79	0.77	0.37	0.84	0.39	95.74		0
10		0.86	0.85	0.33	0.87	0.34	95.74		0
11	modified-k-medoidsd	0.84	0.83	0.36	0.82	0.32	93.62	6.97	0
12		0.84	0.83	0.37	0.80	0.34	93.62		2 (64, 144)
13		0.89	0.88	0.34	0.78	0.34	89.36		0
14		0.88	0.85	0.33	0.82	0.33	95.74		1 (128)
15		0.89	0.88	0.34	0.79	0.33	89.36		0

^aAD using standardization technique is used and compound ID mentioned under parenthesis.

^bN_Training = 109, N_Test = 47.

^cN_Training = 109, N_Test = 47.

^dN_Training = 109, N_Test = 47.

3.1.4. Model Dataset 4: Bioluminescent Repression of the Bacterium Genus Pseudomonas

A similar trend as in case of the previous datasets is observed in case of this dataset also. Among the developed 15 models, 13 models showed 0.5–0–0.5 as the best weighting combination out of 15 models along with other combinations. Now, taking the obtained automated weighting for all models, the % correct prediction ranges from 78.13 to 87.10% (Table S4). For the two models, where the 0.5–0–0.5 weighting combination does not emerge as the winner, we checked them with the 0.5–0–0.5 manual weighting (correct % prediction for model 5: 83.87%, model 13: 77.42%) and the % correct prediction reduces for about less than 1% compared with that in case of automatically selected weighting combination (Table S4). The values of R² metric range from 0.67 to 0.80, Q² range from 0.60 to 0.74, and Q_Ext-F1² or R_pred² range from 0.42 to 0.66, taking all 15 models into consideration. It is interesting to point out that two models failed based on external predictive parameter Q_Ext-F1² and this is why the values of this specific parameter are below the acceptable limit for these two models although both models possessed acceptable internal validation parameter values. On the contrary, the % correct prediction for both these models is 80.65% which is an acceptable value for our present study. The AD study suggested that no compounds remain outside the AD for nine models and one compound each remain outside the AD for five models. For the remaining one model, two compounds remain outside the AD. The information about training set response ranges along with the values of statistical parameters values of individual models, and the details of AD are reported in Table 4. The values of individual descriptors appearing in the models and the division pattern of each model are illustrated in Supporting Information excel files.

Table 4. Results for Bioluminescent Repression of the Bacterium Genus Pseudomonas Dataset (Model Dataset 4) with Best Weighting (0.5–0–0.5) Combination as Obtained from the Retrospective Study.

model	division method	R2	Q2	MAE95%Train	QExt-F12	MAE95%Test	correct prediction in %	training set range	number of compounds outside ADa
1	sorted responseb	0.78	0.73	0.32	0.42	0.32	80.65	4.06	0
2		0.73	0.69	0.35	0.45	0.31	80.65		2 (45, 47)
3		0.80	0.74	0.28	0.64	0.30	87.10		1 (47)
4		0.78	0.73	0.29	0.55	0.30	83.87		1 (47)
5		0.80	0.74	0.29	0.66	0.31	83.87		1 (47)
6	Kennard–Stonec	0.67	0.61	0.32	0.62	0.40	81.25	4.06	0
7		0.72	0.60	0.32	0.66	0.39	84.38		0
8		0.68	0.65	0.32	0.62	0.39	78.13		0
9		0.67	0.60	0.33	0.62	0.40	81.25		0
10		0.69	0.63	0.32	0.63	0.39	78.13		0
11	modified-k-medoidsd	0.75	0.70	0.30	0.63	0.32	80.65	4.06	0
12		0.72	0.68	0.31	0.65	0.34	83.87		0
13		0.72	0.68	0.32	0.62	0.32	77.42		0
14		0.71	0.67	0.31	0.63	0.31	80.65		1 (64)
15		0.69	0.65	0.32	0.62	0.29	87.10		1 (64)

^aAD using standardization technique is used and compound ID mentioned under parenthesis.

^bN_Training = 73, N_Test = 31.

^cN_Training = 72, N_Test = 32.

^dN_Training = 73, N_Test = 31.

3.1.5. Model Dataset 5: PBT Index of Chemicals

This dataset also followed the same trend as described above, and 11 out of 15 models showed the occurrence of the weighting combination of 0.5–0–0.5 along with other weighting in case of automated weighting selection setting to obtain the best % correct prediction for the respective test sets. Considering the automatically obtained weighting combinations for all models, the % correct predictions range from 86.36 to 100%. In case of the four models, for which the 0.5–0–0.5 weighting combination does not emerge as the winner with the automated weighting selection, we checked them with the 0.5–0–0.5 manual weighting setting (model 1: 91.67%, model 4: 91.67%, model 11: 88.64%, model 14: 93.18%) and the % correct predictions for these models reduce around 2–5% compared with that in case of the best automated weighting setting results (Table S5). The values of R² metric range from 0.88 to 0.92, Q² range from 0.87 to 0.91, and Q_Ext-F1² or R_pred² range from 0.84 to 0.95 taking into consideration all 15 models which support that all models are highly reliable and acceptable, considering the large number of data points. The concurrent AD study suggested that no compounds remain outside the AD for five models, and 1 and 2 compounds remain outside the AD for models 2 and 6, respectively. For the remaining two models, 3 and 4 compounds remain outside the AD. Information about training set response ranges along with the values of statistical parameters of the individual models and the details of AD are reported in Table 5. The values of the individual descriptors appearing in the models and the division pattern of each model are illustrated in Supporting Information excel files.

3.2. Results for True External Datasets

The idea for using a true external test set is to check the % correct prediction for them using the obtained optimum weighting from the modeling set (training and test sets). The real success of predictions and their reliability depend on the performance of a model on a true external test set. As discussed earlier, four datasets are studied, and each dataset was divided into different sets of training and test sets. Additionally, a true external test set was also available for each data set which was not a part of the original data set and obtained separately. Thus, the true external set was not used during model development and validation process.

3.2.1. True External Dataset 1: Refractive Index of Polymers

To find the optimum weighting employing training and test sets, five models were subjected to automated weighting combination selection. The obtained results for all five models suggested that 0.5–0–0.5 combination evolved as the real winner, as this weighting emerged singly for four models and jointly along with other combinations for the best % correct prediction in case of model 2. The % correct predictions for the test sets in case of all models range from 97.01 to 98.51%, which is no doubt a highly respectable number range (Table S6). As for this dataset, 0.5–0–0.5 is a distinct winner as the optimum weighting combination, we have employed our true external test set to check the % correct predictions using the mentioned weighting combination employing the manual weighting tab in the software tool. The true external test set also showed highly acceptable % correct prediction range of 91.84–94.90%. The values of R² metric range from 0.90 to 0.91, Q² range from 0.88 to 0.90, and Q_Ext-F1² or R_pred² range from 0.88 to 0.90 for the test sets, while those for Q_Ext-F1² range from 0.87 to 0.88 for the true external test set taking into account all five models, and this supports the robustness, quality, and high predictive ability of the developed models. Out of 67 test set data points, one compound each for models 1 and 2 and two compounds each for models 3 to 5 remained outside the AD zone defined by the respective training data. On the contrary, out of 98 true external test set data points, 0, 5, 6, 7, and 0 molecules remained outside the domain of applicability for models 1, 2, 3, 4, and 5, respectively. Considering the large number of compounds in both test and true external test sets, the number of compounds remaining outside the AD is quite low, and the developed models can reliably perform predictions for majority of the molecules. Different statistical qualities and outcome from the AD study are illustrated in Table 6. The values of the descriptors appearing in the models and distribution pattern of the data set into training and test sets are reported in Supporting Information excel files.

3.2.2. True External Dataset 2: BACE1 Activity of Chemicals

A similar scheme as discussed above is applied to find the optimum weighting for this dataset using the automatic weighting tab in the developed software tool. Like the other datasets, for all five models, the 0.5–0–0.5 combination evolved as the common weighting combination in case of all five models for with the highest % correct predictions for the test set compounds. In the automated weighting selection based analysis, we have employed each weighting combination to check the % correct predictions for the true external test sets. Interestingly, in case of models 2, 3, and 4, we got same % correct predictions of 91.30, 88.24, and 85.35%, respectively, employing all available weighting combinations from automated weighting selection scheme (Table S7). In case of models 1 and 4, we got two values 82.35%/76.47% and 82.35%/88.24%, respectively, employing all obtained weighting combinations for the true external test set (Table S7). Most importantly, we got the best % correct prediction values (82.35 and 88.24%) for models 1 and 4 when we have used the 0.5–0–0.5 combination. Here, it is important to mention that two combinations of weighting 0–0.1–0.9 and 0–0.2–0.8 also showed similar % correct predictions like that of the 0.5–0–0.5 combination, not only based on test sets but also using the true external test set. However, just on the basis of the outcome of modeled datasets and the true external dataset, we can consider the 0.5–0–0.5 combination among the best three combinations for this dataset. Once the optimum weighting is established for this dataset for five models, all models were used to check the final % correct predictions for the test and true external sets along with other statistical parameters and AD information (Table 7). The values appearing in the models and the composition of training and test sets are reported in Supporting Information excel files. The ranges of % correct predictions for five models for the test set and the true external test set are 86.6–95.65 and 82.35–88.24%, respectively. The values of R² range from 0.76 to 0.83, Q² range from 0.71 to 0.76, and Q_Ext-F1² or R_pred² range from 0.75 to 0.91 for the test set, while Q_Ext-F1² values range from 0.72 to 0.90 for the true external test set considering all 5 models; this supports the robustness, quality, and high predictability of the developed models. Out of 23 test set compounds, not a single compound remained outside the AD zone defined by the respective training data. On the contrary, out of 17 true external test set data points, 2, 2, 1, 2, and 1 molecules remained outside the domain of applicability for models 1, 2, 3, 4, and 5, respectively.

Table 7. Results for BACE1 Dataset (True External Dataset 2) with Best Weighting (0.5–0–0.5) Combination as Obtained from the Retrospective Study.

	training set			test set				true external test set
model	R2	Q2	MAE95%Train	QExt-F12	MAE95%Test	correct prediction in %	number of compounds outside ADa	QExt-F12	MAE95%Test	correct prediction in %	number of compounds outside ADa
1	0.83	0.76	0.37	0.75	0.32	86.36	0	0.90	0.31	82.35	2 (81, 91)
2	0.80	0.75	0.37	0.79	0.32	91.30	0	0.72	0.37	88.24	2 (81, 89)
3	0.80	0.76	0.35	0.91	0.24	95.65	0	0.83	0.34	88.24	1 (81)
4	0.76	0.71	0.38	0.77	0.27	91.30	0	0.75	0.37	88.24	2 (81, 89)
5	0.79	0.75	0.38	0.79	0.28	91.30	0	0.86	0.33	82.35	1 (81)

^aAD using standardization technique is used and compound ID mentioned under parenthesis; division method: Kennard–Stone; N_Training = 51, N_Test = 23, N_{True-External-Test} = 17.

3.2.3. True External Dataset 3: Glass Transition Temperature of Polymers

For this specific dataset, out of five models, the 0.5–0–0.5 weighting combination emerged as the best combination for two models (models 1 and 2) only. On the contrary, combinations like 0–0.1–0.9, 0–0.2–0.8, 0.1–0–0.9, 0.1–0.1–0.8, and 0.2–0–0.8 are the winners using automated weighting selection for the test set predictions. In the automated weighting selection-based analysis, the % correct predictions for five models for the test set are 86.54, 88.46, 92.31, 94.23, and 86.54%. Now, considering the winner weighting combinations used manually for the true external test set, the % correct predictions are 68.42, 84.21, 86.84, 78.95, and 78.95% (Table S8). Although 0.5–0–0.5 weighting is not the winner for the test set predictions, still we have employed this combination to check the % corrected predictions for the true external test set, and we found the obtained % values (68.42, 84.21, 84.21, 84.21, and 81.58%) very similar to or even better in few cases than those obtained in case of the best combination derived from the automated weighting selection based analysis. It is important to note that we have checked the models 3−5 for the test set predictions where 0.5–0–0.5 combination is not the winner with this specific combination to know how the % correct predictions are changing compared with the predictions when the best weighting combination has been employed. We found the % correct predictions are 84.21, 84.21 and 81.58% for models 3, 4, and 5, respectively, which are lower values compared with the best ones, but still acceptable considering more than 80% correct predictions. Therefore, for the final analysis of five models for the test set and the true external test set, we have employed 0.5–0–0.5 combination as the optimum weighting for this dataset considering automated weighting selection based analysis and taking into account the outcome from other datasets. The final % correct predictions along with values of statistical parameters and the AD information for this dataset are provided in Table 8. The values of different descriptors and the composition of training and test sets are reported in Supporting Information excel files. The values of R² range from 0.76 to 0.74, Q² range from 0.66 to 0.72, and Q_Ext-F1² or R_pred² range from 0.70 to 0.80 for the test sets, while the values of Q_Ext-F1² range from 0.75 to 0.85 for the true external test set considering all five models; this supports the robustness, quality, and high predictability of the developed models. Out of 52 test set compounds, 3 compounds each for models 1–4 and 4 compounds for model 5 remained outside the AD defined by the respective training data (Table 8). On the contrary, out of the 38 true external set data points, 1 compound each for models 2–5 and 2 compounds for model 1 reside outside the domain of applicability (Table 8).

Table 8. Results for Glass Transition Temperature of Polymers Dataset (True External Dataset 3) with Best Weighting (0.5–0–0.5) Combination as Obtained from the Retrospective Study.

	training set			test set				true external test set
model	R2	Q2	MAE95%Train	QExt-F12	MAE95%Test	correct prediction in %	number of compounds outside ADa	QExt-F12	MAE95%Test	correct prediction in %	number of compounds outside ADa
1	0.74	0.68	0.04	0.74	0.04	86.54	3 (2, 16, 37)	0.75	0.06	68.42	2 (14, 39)
2	0.75	0.71	0.04	0.73	0.05	88.46	3 (2, 16, 324)	0.77	0.05	84.21	1 (39)
3	0.76	0.72	0.04	0.80	0.04	88.46	3 (2, 16, 37)	0.85	0.04	84.21	1 (39)
4	0.71	0.66	0.04	0.70	0.04	90.38	3 (2, 16, 37)	0.80	0.04	84.21	1 (14)
5	0.76	0.70	0.05	0.72	0.04	82.69	4 (2, 16, 37, 324)	0.81	0.04	81.58	1 (39)

^aAD using standardization technique is used and compound ID mentioned under parenthesis; division method: activity sorted; N_Training = 154, N_Test = 52, N_{True-External-Test} = 38.

3.2.4. True External Dataset 4: Sweetness Potency of Organic Molecules

Out of five models, only one combination, that is, 0.1–0.5–0.4 emerged for all five test sets with the automated weighting selection scheme. In the automated weighting selection-based analysis, with the winner combination from automated weighting, the % correct predictions for five test sets are 95, 95, 80, 93.75, and 92.5%. Now, considering the specific combinations manually for true external test sets, the % correct predictions are 80, 83.33, 75, 73.33, and 86.67% (Table S8). For this dataset, 0.5–0–0.5 weighting combination occurred in three models (models 2, 4, and 5). Although, 0.5–0–0.5 weighting is not the winner for test set predictions, still we have employed this combination to check the % correct predictions for the true external test set and we found the % correct prediction values (93.75, 95, 73.75, 93.75, and 92.5%) are almost similar for four models and this is a little bit lower for model 3 compared with the performance observed with the best weighting combination as found from the automated weighting selection-based analysis. It is important to note that we found the % correct predictions for five true external sets with the 0.5–0–0.5 combination are 80, 83.33, 75, 73.33, and 86.67% which are completely same with those obtained with the winner combination weighting 0.1–0.5–0.4 for this dataset. Therefore, for the final analysis of the test set and the true external set for the five models, we have employed 0.5–0–0.5 combination as the optimum weighting for this dataset considering automated weighting selection-based analysis and taking into account outcome from other datasets. The final % correct predictions along with values of statistical parameters and AD information for this dataset are provided in Table 9. The values of different descriptors and composition of training and test sets are reported in Supporting Information excel files. The values of R² range from 0.71 to 0.86, Q² range from 0.69 to 0.85, and Q_Ext-F1² or R_pred² range from 0.75 to 0.87 for the test sets, while the values of Q_Ext-F1² range from 0.64 to 0.79 for the true external test set considering all 5 models, which supports the robustness, quality, and high predictability of the developed models. Out of 80 test set data points, 1, 2, 2, 1, and 1 molecules were outside the domain of applicability for models 1, 2, 3, 4, and 5, respectively. On the contrary, out of 60 true external test set compounds, not a single compound remained outside the AD zone defined by the respective training data. On the basis of the number of data points and considering the AD study and % correct predictions, the statistical quality and predictability of the developed models are highly reliable and confident ones.

3.3. Results of Retrospective Analysis

In the retrospective analysis, we have closely checked the effects of each weighting combination on the composite score for predictions from a specific model of an explicit dataset taking into account different aspects such as closeness of the response of a particular test set compound to the training set response mean, ED distance, and Jaccard similarity coefficient between a test compound and its close congeners in the training set along with AD of each test set compound. We have identified the cases showing nonconcordance between the composite score (based on our defined criteria) and the prediction score (based on absolute predicted residual). From several examples, we have come to the following generalized consensus that nonconcordance between the two scores occur mostly in the following cases:

• 1.Euclidean distance value is high (>0.025) (a higher Euclidean distance means lower similarity of a test compound to training compounds, thus the model may not be able to efficiently predict such compounds); or
• 2.The Jaccard coefficient between a test compound and its closest congener in the training set is lower (signifying lower degree similarity); or
• 3.The test compound’s (actual) response value is away from training response mean (in the range of 1 SD to 2 SD or more than 2 SD from training response mean). The model performs the best when a particular data point has a response close to training response mean.

While determining the quality of predictions, we have not apparently found any significant role of the AD test. Majority of compounds which are showing nonconcordance between two scores (because of any one of the abovementioned three criteria) are inside the AD. This observation is also supported by the obtained optimum weighting combination of 0.5–0–0.5 for all modeled datasets. In this particular weighting combination, the obtained results are most acceptable and maximum number of compounds show concordance between the two scoring system (all CSV files are provided in the Supporting Information). Considering the score derived from absolute predicted residual as a reflection of the true prediction quality, a high degree of concordance between the two scoring system actually indicates the reliability of the suggested criteria in evaluating the quality of predictions for new compounds. However, this does not mean that AD is not important. All QSAR models are developed based on a similarity principle, and in AD we usually measure chemical similarity. Within the acceptable AD zone of a model, there may be different clusters of compounds for which prediction quality of the model might be different. This aspect is taken into account by the criterion 1 of the scoring system which also account for chemical similarity to some extent.

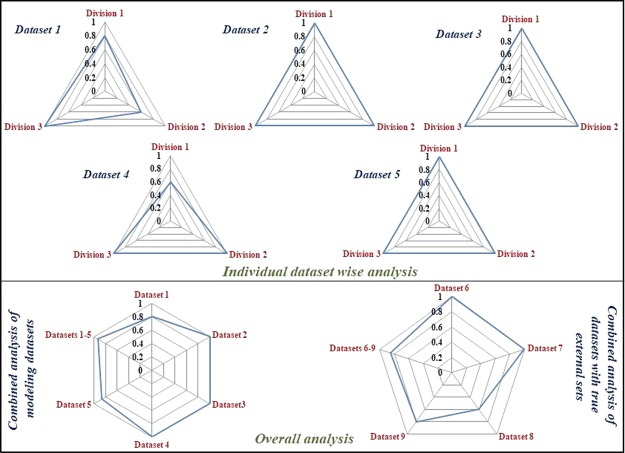
Considering the results of retrospective analysis, we have proposed that the weighting combination 0.5–0–0.5 is the optimum one among the studied combinations for the studied datasets. In the similar way, we have performed a retrospective analysis for true external datasets (vide infra) and a similar trend was observed where 0.5–0–0.5 weighting evolved as the winner for those datasets for reliable and confident predictions in terms of % correct predictions (degree of concordance between two scoring systems). The occurrences of weighting 0.5–0–0.5 as the winner combination for maximum % correct predictions for the developed models are shown in radar plots for individual datasets and all datasets in Figure 3. Although the AD feature might appear useless due to the occurrence of its 0 weighting in most of the cases, it may be noted that the other two studied aspects (LOO performance and closeness to the training set response mean) are other forms to define a sort of “applicability potential” or “AD”. In other words, the concept of AD might still be necessary, while the method to evaluate or represent it properly may be a challenging task to explore.

Figure 3.

Radar plots showing occurrence (in fractions of all cases) of weighting 0.5–0–0.5 for maximum % correct predictions for individual datasets and combined datasets.

4. Overview and Conclusion

The real challenge of a QSAR model is to estimate the reliability of predictions when the model is applied to a completely new data set (true external set) even when the new data points are within AD of the developed model. Thus, in the present study, we have classified the quality of predictions for the test set or true external set into three groups “good”, “moderate”, and “bad” based on absolute prediction errors. Then, we have used three criteria as suggested earlier in different weighting schemes for making a composite score of predictions. The observations are summarized as following:

It was found that using the most frequently appearing weighting scheme 0.5–0–0.5, the composite score-based categorization showed concordance with absolute prediction error-based categorization for more than 80% test data points while working with five different datasets with 15 models for each set derived in three different splitting techniques. These observations were also confirmed with four true external sets suggesting the applicability of the scheme to judge the reliability of predictions for new datasets.

For QSAR modelers’ and beginners’ ease, we have developed an user friendly tool named Prediction Reliability Indicator to check the prediction reliability score, followed by classification of predictions in term of “good”, “moderate”, “bad” along with details about AD information and QSAR statistical parameters. The tool is presently valid for MLR models only.

The studied datasets in the present study showed 0.5–0–0.5 weighting combination as one of the optimum ones. For almost 80% of models, we got the optimum weighting 0.5–0–0.5 as the best combination considering the three criteria. On the basis of this, we can find that there is no apparent contribution from the similarity-based AD weighting. There are many evidences where a compound within AD may have bad predictions and a compound outside AD might have good predictions.¹⁹ Therefore, the quality of predictions might not be completely related to AD. However, the first criterion of LOO-based MAE based on close 10 training compounds capture the behavior of similar 10 training compounds. Therefore, it appears that it is not only closeness or similarity that is important, but behavior of the similar compounds for being predicted by a particular model is also important, and this actually varies for different clusters of compounds because of a fixed composition of the model with respect to descriptors. Thus, we can conclude that chemical AD may only grossly show reliability of predictions but the criteria proposed here can reflect both reliability and prediction quality. The employed datasets in this present study showed 0.5–0–0.5 weighting combination as one of the optimum ones. However, users should check the optimum weighting for their respective dataset employing their own training and test sets. Once they are sure with their optimum weighting for their respective dataset, they should use the obtained weighting manually for the true external set for classifying the quality of predictions for individual compounds.

Users can set different options like Euclidean cutoff distance and threshold value based on their requirement under the tool GUI. Along with the mentioned outcomes, users can get information like closest training compound, Euclidean distance, and generalized Jaccard coefficient for individual test set and true external test set compounds denoting their similarity to their close congeners in the training set.

We can finally conclude that the reliability of predictions for a new compound can be confidently judged using the developed tool Prediction Reliability Indicator.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b01647.

• Automated weighting analysis results for nine datasets (PDF)

• Excel files of original datasets and analysis (ZIP)

The authors declare no competing financial interest.