Abstract

After carefully analyzing the Kamlet–Jacobs (K–J) equations and the structural traits of well-known explosives, hexahydro-1,3,5-trinitro-1,3,5-triazin (RDX), octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine (HMX), and hexanitrohexaazaisowurtizitane (CL-20), diverse nitramine explosives including linear (Models IAn, IBn, and ICn), cyclic (Model IIn), and caged (Models IIIAn and IIIBn) molecules were designed by incorporating various number (n) of −CH2NNO2– structural unit and studied using the B3LYP/6-31G* and B3PW91/6-31G** methods of the density functional theory. Computational results show that all of the energetic parameters, that is, density (ρ), detonation velocity (D), and detonation pressure (P), follow the order of IIIBn > IIIAn > IIn > IAn > IBn > ICn. With the increasing n, the D and P of linear nitramines eventually keep stable. This clearly indicates that elongating the chain length (e.g., polymerization) brings little or even negative benefit in boosting the explosive properties. The oxygen balance and the K–J equation parameter ϕ both have a significant influence on the detonation properties. Caged compound IIIA2 has not only comparable energetic properties but also better sensitivity and thermal stability than CL-20.
1. Introduction
High-energy materials are generally organic compounds containing functional groups such as nitro (−NO2), nitrate ester (−ONO2), azido (−N3), nitramino (−NNO2), and so on. To construct or synthesize a new ideal explosive, some specific issues need to be paid attentions to: (a) as high as possible detonation velocity, detonation pressure, and density and acceptable level of stability in comparison with the benchmark explosives and (b) environmentally compatible detonation or combustion end products.1,2 Searching for the promising high-energy materials during the last one decade has discovered a large number of energetic oxidizers, fuels, and explosives.3−6
One of which is the so-called energetic nitro compounds, the high-energy materials with −NO2 groups, such as 2,4,6-trinitrotoluene (TNT),7 hexanitrobenzene,8 1,3,5-triamino-2,4,6-trinitrobenzene,9 2,2′,4,4′,6,6′-hexanitrostilbene,10 heptanitrocubane,11 octanitrocubane,11 and so on. The well-known explosive TNT has been widely used in military, industrial, and mining applications. Energetic nitrate esters with −ONO2 groups, such as nitroglycerine (NG)12 and penerythritol tetranitrate,13 have been widely used in the military applications too. Combining NG with nitrocellulose, hundreds of composites are produced and used by rifle, pistol, and shotgun reloaders. Energetic azides with −N3 groups, such as 1,3-diazido-2-nitrazapropane, 1,5-diazido-2,4-dinitrazapentane, 1,7-diazido-2,4,6-trinitrazaheptane, and so on, are another kind of energetic compounds which possess high density, positive heat of formation, good thermal and hydrolytic stability, low impact sensitivity, high burning rate, and reduced flash.15−17 Potential high-energy azides include trinitroazetidine,19 hexahydro-1,3,5-trinitro-1,3,5-triazine (RDX),20 octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine (HMX),21 and hexanitrohexaazaisowurtizitane (CL-20).22 The structures of the above-mentioned famous explosives are shown in Figure S1 of the Supporting Information.
By observing the molecular structures of the traditional famous explosives, we noted that the geometries are ranging from linear to cyclic to caged structures. Besides, energetic nitramines, RDX and HMX, have similar molecular structures which are made up with the identical basic structural unit (−CH2NNO2−). Many research studies23−26 are devoted to investigate the derivatives of HMX and RDX. It is known that HMX has one additional −CH2NNO2– unit, and it possesses higher energetic performance than RDX. However, the specific contributions of the −CH2NNO2– unit on the energetic properties are not very clear. In this work, various nitramines, including linear (Model I), cyclic (Model II), and caged (Model III) structures, were constructed and studied using the density functional theory (DFT) method. The molecular skeletons of all models are depicted in Figure 1. It aims to explore the effect of −CH2NNO2– unit on the energetic properties and screen the promising nitramines with better performance than the benchmarks RDX, HMX, and CL-20.
Figure 1.

Molecular skeletons of Models IAn, IBn, ICn, IIn, IIIAn, and IIIBn.
This work is instructive to explore the relationships between the structures and properties of energetic nitramines. In addition to the inherent interest in searching for potential new nitramine explosives, the study on the linear nitramines can serve as precursors to understand the effect of unit on the performance of the whole energetic polymers, which has a certain significance in the field of developing energetic binders.
2. Design Strategy and Theoretical Methods
Linear nitramines (Model IAn, Model IBn, and Model ICn, n = 0–8) were constructed by connecting −CH2NNO2– units one by one. For Model IAn, both sides use H as the terminal. For Model IBn, one side uses H as the terminal and the other side uses −CH3 as the terminal. For Model ICn, both sides use −CH3 as the terminal. Its destination was to determine how the basic unit affects the performance of energetic polymers.
Cyclic nitramines (Model IIn, n = 1–8) were built by connecting −CH2NNO2– units into a loop. Its destination was to examine how different it can be between the linear and cyclic structures.
Caged nitramines (Model IIIAn, n = 1–8) were formed by connecting two identical cyclic molecules into a two-layered cage. By the full consideration of the Kamlet–Jacobs (K–J) eqs 1–3,27 Model IIIBn (n = 1–8) was constructed by inserting O atoms into the C–C links of Model IIIAn to evaluate how oxygen balance affects the energetic properties. It needs to mention that Models IIIAn and IIIBn are our designed compounds, which have not been synthesized yet.
| 1 |
| 2 |
| 3 |
where D is the detonation velocity (km/s); P is the detonation pressure (GPa); ρ is the packed density of explosive (g/cm3); N is the moles of gas produced by per gram of explosive (mol); Ma is the average molar weight of detonation gas products (g/mol), and Q is the energy of detonation (cal/g). N, Ma, and Q were determined according to the largest exothermicity principle.27 The detonation products of Models IAn, IBn, ICn, IIn, and IIIAn are N2, CO2, H2O, and C. The detonation products of Model IIIBn are N2, CO2, and H2O. The specific calculated formulas of N, Ma, and Q are presented in Table 1.
Table 1. Formulas of N, Ma, and Q for CaHbOcNd Explosivesa.
| N | ||||||
| Ma | ||||||
| N·Ma | 1 | |||||
| Q × 10–3 |
N, mol; M, g/mol; Ma, g/mol; ΔHf°, kJ/mol; and Q, cal/g.
All designed molecules were fully optimized at the B3LYP/6-31G* and B3PW91/6-31G** levels, and the molecular electrostatic potential was calculated at the B3PW91/6-31G** level. Their initial structures are constructed by consideration of the molecular symmetry and steric-hindrance effect to try to make their relaxed structures with the minimum energy. The optimized structures were characterized to be the energy minima on the potential energy surface by vibrational analysis. These calculations were carried out using the Gaussian program package28 and Multiwfn software.29 The density was predicted by ρ1 = M/Vm first and then corrected by eq 4(30)
| 4 |
where M is the molecular weight (g/mol); Vm is the average molar volume within the 0.001 a.u. electron density contour (cm3/mol); ν is the degree of balance between positive and negative potential on the molecular surface; σtot2 is a measure of variability of the electrostatic potential (kcal/mol)2; and the coefficients α1, β1, and γ1 are 0.9183, 0.0028, and 0.0443, respectively.30
The gas-phase heat of formation [ΔHf°(g)] was estimated by designing isodesmic reactions, which has been proved to be an effective way to predict the ΔHf(g) and has been widely used in previous studies.31−33 The designed isodemic reactions for all models are as follows
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
The reaction enthalpy (ΔHr) of the above isodemic reactions at 298 K was calculated using the following equation
| 11 |
where ΔHf,P° and ΔHf,R are the heats of formation of the products and the reactants at 298 K, respectively. ΔE0 is the difference between the total energy of the reactants and the products at 0 K. ΔEZPV is the difference between the zero-point vibrational energies of the reactants and the products, and ΔHT is the thermal enthalpy correction from 0 to 298 K. The experimental ΔHf°(g)s of CH4 (−74.6 kJ/mol34), CH3CH3 (−84.0 kJ/mol34), and CH3OCH3 (−184.1 kJ/mol34) are available. For CH3NNO2CH3, CH3NHNO2, CH3NNO2CH2CH2NNO2CH3, and CH3NNO2CH2OCH2NNO2CH3 which lack experimental ΔHf(g)s, additional calculations were performed with the G3 method which can predict the ΔHf° from the atomization reaction accurately. The predicted ΔHf(g)s of CH3NNO2CH3, CH3NHNO2, CH3NNO2CH2CH2NNO2CH3, and CH3NNO2CH2OCH2NNO2CH3 are −5.053, 2.329, 11.006, and −115.703 kJ/mol, respectively.
The heat of formation in solid state [ΔHf°(s)] and sublimation enthalpy (ΔHsub) were then estimated using the following equations35
| 12 |
| 13 |
where AS is the area of the isosurface of 0.001 e/Bohr3 electron density of the molecule (Å2); the coefficients α2, β2, and γ2 at the B3PW91/6-31G** level are 4.43 × 10–4, 2.0599, and −2.4825, respectively.35
The sensitivity plays a key role in determining the potential application and handing safety of explosives. There are many ways to predict the sensitivity, such as molecular surface electrostatic potentials, crystal lattice free space (ΔV), and maximum heat of detonation per unit volume (ρQmax).36−38 In this work, we used ΔV (Å3), ρQmax (kcal/cm3), and h50 (cm), the height from where 50% probability of the “drops” results in reaction of the sample, to measure the impact sensitivity of all designed molecules. ΔV and h50 were predicted by formulas 14(39,40) and 15,41 respectively. Generally, the sensitivity tends to increase as ΔV and ρQmax becomes large.
| 14 |
where Veff is the effective volume of the molecule that would correspond to 100% packing of the unit cell, which is usually quite similar to the 0.001 a.u. contour of the molecule’s electronic density. Vint is the space encompassed by the 0.003 a.u. contour of the molecule’s electronic density.
| 15 |
The coefficients α3, β3, and γ3 at the B3PW91/6-31G** level are −0.0064, 241.42, and −3.43, respectively.41
Thermal stability was examined by calculating the bond dissociation energy (EBD) of all possible pyrolysis processes. The formula is as follows
| 16 |
where A–B stands for the neutral molecule and A• and B• stand for the corresponding radical products after the dissociation of A–B bond; EA•, EB•, and EA–B are their corresponding total energies after the correction of the zero-point energy.
3. Results and Discussion
The optimized molecular coordinates
of all models at the B3LYP/6-31G*
level are supplied in the Supporting Information. The calculated values of ρ1, ρ, ΔHf°(g), ΔHf(s), D, P, and h50 for all models are tabulated
in Table 2. It is worth
noting that the predicted D and P using K–J equations are similar to those obtained using EXPLO5,
given in Table S1 of the Supporting Information. The variations of ρ, D, and P with n are plotted in Figure 2. Clearly, the rigid and highly compact caged
structures result in a highly dense and more powerful explosives,
and the orders of ρ, D, and P are Model IIIBn > Model IIIAn >
Model IIn > Model IAn > Model
IBn > Model ICn. The only exception
is that D and P of IIIB1 are a little
bit lower
than those of IIIA1. The order of ρ, D, and P is almost consistent with that of oxygen balance parameter
(POB). For the compounds with the formula
CaHbOcNd, POB equals to  , as seen in 17−22. Obviously, POB follows
the order of Model IIIBn > Model IIIAn > Model IIn > Model IAn >
Model
IBn > Model ICn. However, POB is not the only factor, ϕ also has
a big influence on the D and P.
The higher ϕ of IIIA1 (7.4030) than that of IIIB1 (7.0056) makes
IIIA1 have higher D and P, even
though the POB of IIIA1 is lower than
that of IIIB1. That is to say, to improve the energetic properties,
both POB and ϕ should be taken into
consideration. The data of N, Ma, POB, and ϕ are listed
in Table S2 of the Supporting Information.
, as seen in 17−22. Obviously, POB follows
the order of Model IIIBn > Model IIIAn > Model IIn > Model IAn >
Model
IBn > Model ICn. However, POB is not the only factor, ϕ also has
a big influence on the D and P.
The higher ϕ of IIIA1 (7.4030) than that of IIIB1 (7.0056) makes
IIIA1 have higher D and P, even
though the POB of IIIA1 is lower than
that of IIIB1. That is to say, to improve the energetic properties,
both POB and ϕ should be taken into
consideration. The data of N, Ma, POB, and ϕ are listed
in Table S2 of the Supporting Information.
| 17 |
| 18 |
| 19 |
| 20 |
| 21 |
| 22 |
Table 2. ρ [g/cm3], ΔHf°(g) [kJ/mol], ΔHf(s) [kJ/mol], D [km/s], P [GPa], ΔV [Å3], h50 [cm], and ρQmax [kcal/cm3] of All Modelsa.
| model | n = 0 | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Ian | ρ1 | 1.624 | 1.729 | 1.776 | 1.803 | 1.819 | 1.820 | 1.828 | 1.834 | 1.838 |
| ρ | 1.694 | 1.727 | 1.757 | 1.783 | 1.794 | 1.791 | 1.797 | 1.800 | 1.803 | |
| ΔHf°(g) | 9.121 | 235.021 | 279.765 | 328.762 | 377.617 | 426.291 | 475.285 | 524.271 | 573.441 | |
| ΔHf°(s) | –57.952 | 156.695 | 170.119 | 173.386 | 167.590 | 147.866 | 118.732 | 79.061 | 28.147 | |
| D | 7.475 | 9.364 | 9.174 | 9.108 | 9.042 | 8.952 | 8.909 | 8.865 | 8.827 | |
| P | 23.892 | 37.940 | 36.810 | 36.610 | 36.208 | 35.458 | 35.190 | 34.876 | 34.614 | |
| ΔV | 17.726 | 31.244 | 44.476 | 57.238 | 69.643 | 82.817 | 93.620 | 108.192 | 120.901 | |
| h50 | 35 | 35 | 36 | 38 | 39 | 38 | 39 | 38 | 38 | |
| ρQmax | 1.20 | 3.14 | 2.97 | 2.89 | 2.83 | 2.75 | 2.71 | 2.66 | 2.62 | |
| Ibn | ρ1 | 1.457 | 1.627 | 1.701 | 1.740 | 1.765 | 1.783 | 1.795 | 1.804 | 1.812 |
| ρ | 1.520 | 1.630 | 1.691 | 1.728 | 1.747 | 1.761 | 1.771 | 1.778 | 1.784 | |
| ΔHf°(g) | 2.329 | 137.227 | 185.163 | 234.323 | 283.175 | 332.154 | 381.043 | 429.817 | 478.908 | |
| ΔHf°(s) | –67.93 | 49.799 | 62.284 | 61.66 | 51.854 | 30.759 | –1.831 | –44.843 | –98.956 | |
| D | 7.713 | 8.371 | 8.515 | 8.595 | 8.620 | 8.630 | 8.631 | 8.621 | 8.610 | |
| P | 23.713 | 29.244 | 30.964 | 31.984 | 32.383 | 32.613 | 32.734 | 32.739 | 32.720 | |
| ΔV | 22.805 | 37.053 | 48.729 | 58.074 | 73.820 | 89.770 | 102.483 | 114.149 | 125.296 | |
| h50 | 55 | 54 | 51 | 51 | 50 | 49 | 48 | 47 | 47 | |
| ρQmax | 1.99 | 2.52 | 2.57 | 2.58 | 2.57 | 2.55 | 2.53 | 2.51 | 2.48 | |
| ICn | ρ1 | 1.372 | 1.553 | 1.646 | 1.695 | 1.726 | 1.749 | 1.765 | 1.778 | 1.788 |
| ρ | 1.385 | 1.583 | 1.630 | 1.681 | 1.707 | 1.725 | 1.742 | 1.752 | 1.761 | |
| ΔHf°(g) | –5.053 | 62.852 | 91.037 | 140.519 | 188.965 | 260.746 | 286.827 | 335.627 | 384.642 | |
| ΔHf°(s) | –69.181 | –40.646 | –42.379 | –46.653 | –60.595 | –61.760 | –121.453 | –167.419 | –225.748 | |
| D | 6.917 | 7.690 | 7.931 | 8.141 | 8.242 | 8.322 | 8.353 | 8.376 | 8.389 | |
| P | 17.880 | 24.215 | 26.253 | 28.204 | 29.186 | 29.951 | 30.354 | 30.635 | 30.826 | |
| ΔV | 28.817 | 42.556 | 55.261 | 66.766 | 80.232 | 91.893 | 104.791 | 117.005 | 129.564 | |
| h50 | 45 | 56 | 57 | 57 | 56 | 53 | 55 | 54 | 53 | |
| ρQmax | 1.52 | 2.14 | 2.23 | 2.31 | 2.35 | 2.38 | 2.37 | 2.36 | 2.35 | |
| IIn | ρ1 | 1.728 | 1.810 | 1.852 | 1.857 | 1.848 | 1.865 | 1.875 | 1.870 | |
| ρ | 1.705 | 1.784 | 1.850 | 1.875 | 1.878 | 1.868 | 1.852 | 1.854 | ||
| ΔHf°(g) | 217.903 | 209.165 | 278.948 | 355.804 | 502.813 | 520.903 | 547.743 | 627.408 | ||
| ΔHf°(s) | 140.485 | 100.502 | 128.945 | 160.866 | 244.544 | 214.992 | 190.155 | 208.456 | ||
| D | 8.676 | 8.789 | 9.008 | 9.096 | 9.145 | 9.063 | 8.974 | 8.980 | ||
| P | 32.317 | 34.099 | 36.601 | 37.615 | 38.056 | 37.255 | 36.342 | 36.420 | ||
| ΔV | 33.775 | 45.570 | 56.499 | 67.328 | 79.617 | 91.534 | 97.830 | 109.956 | ||
| h50 | 41 | 41 | 48 | 41 | 29 | 29 | 28 | 20 | ||
| ρQmax | 2.80 | 2.72 | 2.81 | 2.85 | 2.91 | 2.83 | 2.76 | 2.76 | ||
| IIIAn | ρ1 | 1.944 | 2.040 | 2.075 | 2.105 | 2.128 | 2.122 | 2.122 | 2.119 | |
| ρ | 1.887 | 1.954 | 1.979 | 2.009 | 2.031 | 2.025 | 2.035 | 2.044 | ||
| ΔHf°(g) | 735.199 | 579.092 | 790.871 | 1094.159 | 1330.736 | 1714.584 | 1988.724 | 2333.670 | ||
| ΔHf°(s) | 601.269 | 373.759 | 493.874 | 705.770 | 862.111 | 1123.901 | 1280.021 | 1450.196 | ||
| D | 9.483 | 9.322 | 9.404 | 9.550 | 9.632 | 9.651 | 9.685 | 9.719 | ||
| P | 41.029 | 40.464 | 41.470 | 43.123 | 44.128 | 44.234 | 44.670 | 45.088 | ||
| ΔV | 53.466 | 69.766 | 89.202 | 103.141 | 116.856 | 131.218 | 151.586 | 163.066 | ||
| h50 | 13 | 13 | 6 | 3 | 3 | 2 | 4 | 6 | ||
| ρQmax | 3.50 | 3.06 | 3.09 | 3.20 | 3.24 | 3.29 | 3.30 | 3.32 | ||
| IIIBn | ρ1 | 1.999 | 2.091 | 2.131 | 2.150 | 2.175 | 2.159 | 2.172 | 2.156 | |
| ρ | 1.923 | 1.997 | 2.034 | 2.051 | 2.078 | 2.071 | 2.081 | 2.078 | ||
| ΔHf°(g) | 247.437 | 163.530 | 412.497 | 681.056 | 947.737 | 1006.187 | 1035.389 | 1348.192 | ||
| ΔHf°(s) | 97.925 | –68.7 | 108.555 | 239.018 | 419.699 | 316.055 | 165.498 | 210.264 | ||
| D | 9.350 | 9.443 | 9.687 | 9.793 | 9.936 | 9.857 | 9.833 | 9.831 | ||
| P | 40.329 | 42.016 | 44.674 | 45.867 | 47.548 | 46.706 | 46.603 | 46.549 | ||
| ΔV | 57.835 | 76.252 | 92.880 | 111.282 | 124.233 | 144.062 | 162.392 | 193.002 | ||
| h50 | 15 | 9 | 15 | 5 | 10 | 6 | 7 | 6 | ||
| ρQmax | 3.06 | 2.96 | 3.17 | 3.26 | 3.37 | 3.28 | 3.22 | 3.22 | ||
II2 is RDX and II3 is HMX. IIIA2 is a structural isomer of CL-20. ρ1 is the uncorrected density calculated by M/Vm. ρ is the corrected density evaluated by ρ = αρ1 + β(νσtot2) + γ.
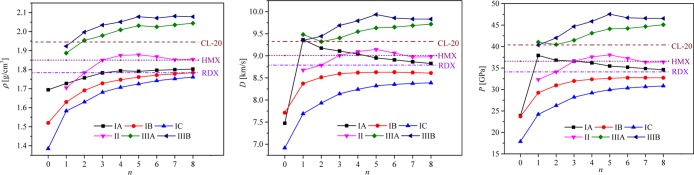
Figure 2.
Variations of ρ, D, and P with n for all models.
In linear models (Models IAn, IBn, and ICn), increasing n is equivalent to polymerizing the molecular structure. The underlying purpose of studying this model is to address a potential issue, that is, understanding the contribution of the unit on the performance of the whole polymer. The order of ρ, D, and P of linear models is Model IAn > Model IBn > Model ICn, which tells us that the −CH3 group has a negative influence on the energetic properties. D and P of Models IBn and ICn both increase until reaching flat, whereas those of IAn increase first with n = 1 reaching the maximum and then decrease until keeping stable. Generally, the higher density implies better performance. Why does this situation in IAn happen? From IA0–IA1, ρ increases, whereas POB and ϕ decrease. The tiny increase in ρ cannot defend the decrease in POB and ϕ, thus, the energetic properties have a trend to decrease. The best energetic properties of IA1 suggest that for the analogues, the compounds with zero oxygen balance (POB = 1) have better performance than the ones with positive oxygen balance (POB > 1) and negative oxygen balance (POB < 1). In addition, when n → ∞, POB(IAn), POB(IBn), and POB(ICn) are infinitely closed to a definite value (2/3); that is why ρ, D, and P of Models IAn, IBn, and ICn all eventually keep stable, which tells us that to increase energetic properties of energetic polymers, elongating the chain length infinitely is not an effective way, and sometimes it may decrease performance.
In cyclic Model II, it can be seen that ρ, D, and P increase first and then decrease with II5 possessing the maximum value (ρ = 1.878 g/cm3, D = 9.145 km/s, and P = 38.056 GPa). Model IIn is formed by connecting Model IBn end to end, clearly; Model IIn has better energetic properties than Model IBn, which implies that one way to improve the energetic performance is making linear compounds into a loop to construct the multicyclic compounds. Here, it should be mentioned that II2 is RDX and II3 is HMX. Obviously, II4 and II5 have better energetic properties. To verify the reliability of our adopted methods, the calculated and experimental data of RDX, HMX, and CL-20 are summarized in Table S3 of the Supporting Information. The predicted ρs are slightly lower than the experimental data. The calculated ρs of RDX, HMX, and CL-20 are 1.784, 1.850, and 1.945 g/cm3, respectively, and their corresponding experimental data are 1.820,1 1.910,1 and 2.0401 g/cm3, respectively. The predicted ΔHf°(g)s are quite similar with their reported data. The calculated ΔHf(g)s are 209.165 kJ/mol for RDX and 278.948 kJ/mol for HMX, and their reported data are 191.87835 and 263.700 kJ/mol,42 respectively. For RDX, the predicted D and P are similar to their experimental ones, whereas for HMX and CL-20, the data are slightly underestimated. These results suggest that D and P evaluated in this work may be slightly lower that their true values.
In caged models (Models IIIAn and IIIBn), a remarkable increase in energy content is achieved. That is why much more attentions have been focused upon applications of caged molecules in recent years. All of the compounds in Models IIIAn and IIIBn possess higher (or comparable) D (9.322–9.936 km/s) and P (40.329–47.548 GPa) than CL-20 (9.40 km/s, 42.00 GPa1). The better performance of Model IIIBn than Model IIIAn can be attributed to the additional O atoms. The additional O atoms make ρ and POB increase. Besides, it needs to mention that IIIA2 and CL-20 have the same chemical formula (C6H6O12N12).
Observing the values of ΔV, h50, and ρQmax, it can be found that ΔV, h50, and ρQmax values do not obtain absolutely consistent results. However, it can be concluded that the overall trend of sensitivity decreases with the increasing number of n and the caged molecules have higher impact sensitivities than the linear and cyclic compounds, as stated in ref (36): “generally, sensitivity increases as ΔV and ρQmax become more larger and h50 becomes more smaller, but there are not correlations but rather overall trends”. The high impact sensitivity (h50 = 5–15 cm) makes caged compounds hard to synthesize and utilize. However, the predicted h50s of IIIA1 (13 cm), IIIA2 (13 cm), IIIB1 (15 cm), and IIIB3 (15 cm) are slightly higher than that of CL-20 (12 cm41), which means IIIA1, IIIA2, IIIB1, and IIIB3 have relatively lower sensitivity than CL-20. Thermal stability is another important parameter to evaluate the performance of energetic materials. Thus, thermal stabilities of IIIA1, IIIA2, IIIB1, and IIIB3 were examined by consideration of three possible decomposition reactions, that is, homolysis of N–NO2; breakage of C–C or C–O between two layers; and rupture of C–N in one layer. The required energies are marked as EBD(N–NO2), EBD(C–C), EBD(C–O), and EBD(C–N), respectively (Table 3). Generally, the bond that requires the minimum energy to break is the weakest and is most likely to be the trigger bond. Obviously, the pyrolysis of IIIA1 is from the breakage of C–N bond. The small energy barrier (18.42 kJ/mol) can be attributed to its considerable tension of the molecular skeleton, which means IIIA1 is extremely thermally instable. The pyrolysis of IIIA2, IIIB1, and IIIB3 are all initiated from the rupture of N–NO2 bond. Comparing with the EBD(N–NO2) of CL-20 (141.16 kJ/mol), it can be found that the N–NO2 bonds in IIIA2 and IIIB2 have higher strengths, which suggests that IIIA2 and IIIB2 have higher thermal stability than CL-20. On the overall consideration of the energetic properties, sensitivity, and thermal stability, it can be concluded that IIIA2 (Figure 3) possesses better performance than CL-20. IIIA2 and CL-20 have the same chemical formula (C6H6O12N12), whereas the good skeleton and better performance make IIIA2 meaningful and valuable to find proper experimental method to synthesize it.
Table 3. Bond Dissociation Energy (EBD, kJ/mol) of All Possible Initial Bonds.
| IIIA1 | IIIA2 | IIIB1 | IIIB3 | |
|---|---|---|---|---|
| EBD(N–NO2) | 99.08 | 149.90 | 132.02 | 117.02 |
| EBD(C–C) | 72.05 | 230.83 | ||
| EBD(C–O) | 276.52 | 211.85 | ||
| EBD(C–N) | 18.42 | 269.31 | 189.90 | 248.52 |
Figure 3.

Optimized structure of IIIA2.
4. Conclusions
A series of nitramines, including linear, cyclic, and caged molecules, were constructed and investigated using the DFT method at the B3LYP/6-31G* and B3PW91/6-31G** levels. It gives a preliminary comparison on the energetic properties of different kinds of nitramines. More results will be reported in due course. The conclusions are as follows:
-
(1)
To improve the performance of explosives, the improvement of ρ is crucial. One way to improve the density is by changing the molecular geometries from linear to cyclic to caged structures.
-
(2)
The trends of ρ, D, and P in linear nitramines suggest that infinite extension of the chain length is not an advisable way to improve the energetic properties of the energetic binders.
-
(3)
POB and ϕ both have big influences on the detonation properties. Generally, the compounds with zero oxygen balance have better performance than the ones with positive or negative oxygen balance.
-
(4)
The order of ρ, D, and P (IIIBn > IIIAn > IIn > IAn > IBn > ICn) suggests that the caged nitramines are much more appealing in seeking high-energy materials. IIIA2 possesses not only comparable energetic properties but also better sensitivity and thermal stability than CL-20.
Acknowledgments
We gratefully thank the 111 project (G2017001) in China, State Key Laboratory of Explosion Science and Technology (ZDKT18-02 and KFJJ18-10M), for the financial support. J.Y. would like to thank the financial support from the China Scholarship Council and Natural Sciences and Engineering Research Council (NSERC) of Canada.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b00614.
Structures of selected well-known explosives; detonation velocity (D) and detonation pressure (P) predicted using the K–J equation (D1 and P1) and EXPLO5 (D2 and P2); K–J equation parameters for all models; chemical formulas, oxygen balance parameter POB, density, gas-phase molar enthalpy of formation ΔHf°(g), solid-phase molar enthalpy of formation ΔHf(s), enthalpy of sublimation ΔHsub, detonation velocity D, and detonation pressure P for benchmark molecules RDX, HMX, and CL-20; and Cartesian coordinates of optimized molecular structures of all models (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Talawar M. B.; Sivabalan R.; Mukundan T.; Muthurajan H.; Sikder A. K.; Gandhe B. R.; Rao A. S. Environmentally Compatible Next Generation Green Energetic Materials (GEMs). J. Hazard. Mater. 2009, 161, 589–607. 10.1016/j.jhazmat.2008.04.011. [DOI] [PubMed] [Google Scholar]
- Wang C.; Li P.; Gao Z.; Don W.-S. Three-Dimensional Detonation Simulations with the Mapped Weno-Z Finite Difference Scheme. Comput. Fluids 2016, 139, 105–111. 10.1016/j.compfluid.2016.04.016. [DOI] [Google Scholar]
- Badgujar D. M.; Talawar M. B.; Asthana S. N.; Mahulikar P. P. Advances in Science and Technology of Modern Energetic Materials: An Overview. J. Hazard. Mater. 2008, 151, 289–305. 10.1016/j.jhazmat.2007.10.039. [DOI] [PubMed] [Google Scholar]
- Klapötke T. M.; Krumm B.; Widera A. Synthesis and Properties of Tetranitro-Substituted Adamantane Derivatives. ChemPlusChem 2018, 83, 61–69. 10.1002/cplu.201700542. [DOI] [PubMed] [Google Scholar]
- Gaur P.; Dev S.; Kumar S.; Kumar M.; Vargeese A. A.; Soni P.; Siril P. F.; Ghosh S. Dendritic Polynitrato Energetic Motifs: Development and Exploration of Physicochemical Behavior through Theoretical and Experimental Approach. ACS Omega 2017, 2, 8227–8233. 10.1021/acsomega.7b00880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar D.; Imler G. H.; Parrish D. A.; Shreeve J. M. Resolving synthetic challenges faced in the syntheses of asymmetric N,N′-ethylene-bridged energetic compounds. New J. Chem. 2017, 41, 4040–4047. 10.1039/c7nj00327g. [DOI] [Google Scholar]
- Wilbrand J. Notiz über Trinitrotoluol. Justus Liebigs Ann. Chem. 1863, 128, 178–179. 10.1002/jlac.18631280206. [DOI] [Google Scholar]
- Akopyan Z. A.; Struchkov Y. T.; Dashevskii V. G. Crystal and Molecular Structure of Hexanitrobenzene. J. Struct. Chem. 1966, 7, 385–392. 10.1007/bf00744430. [DOI] [Google Scholar]
- Kolb J. R.; Rizzo H. F. Growth of 1,3,5-Triamino-2,4,6-trinitrobenzene (TATB) I. Anisotropic thermal expansion. Propellants, Explos., Pyrotech. 1979, 4, 10–16. 10.1002/prep.19790040104. [DOI] [Google Scholar]
- Bellamy A. J. Synthesis of Hexanitrostilbene (Hns) Using a Kenics Static Mixer. Org. Process Res. Dev. 2010, 14, 632–639. 10.1021/op1000644. [DOI] [Google Scholar]
- Zhang M.-X.; Eaton P. E.; Gilardi R. Hepta- and Octanitrocubanes. Angew. Chem., Int. Ed. 2000, 39, 401–404. . [DOI] [PubMed] [Google Scholar]
- Townend D. J.; Warren R. C. Relaxations in Double Base Propellants. Polymer 1985, 26, 79–83. 10.1016/0032-3861(85)90059-x. [DOI] [Google Scholar]
- Yoo C. S.; Holmes N. C.; Souers P. C.; Wu C. J.; Ree F. H.; Dick J. J. Anisotropic Shock Sensitivity and Detonation Temperature of Pentaerythritol Tetranitrate Single Crystal. J. Appl. Phys. 2000, 88, 70–75. 10.1063/1.373626. [DOI] [Google Scholar]
- Flanagan J. E.; Frankel M. B.. 1,3-Diazido-2-Nitrazapropane. U.S. Patent 4,085,123 A, April 18, 1978.
- Flanagan J. E.; Frankel M. B.; Witucki E. F.. Azido Compounds. U.S. Patent 4,141,910 A, Feb 27, 1979.
- Nagayama K.; Oyumi Y. Combustion Characteristics of High Burn Rate Azide Polymer Propellant. Propellants, Explos., Pyrotech. 1996, 21, 74–78. 10.1002/prep.19960210205. [DOI] [Google Scholar]
- Pagoria P. F.; Lee G. S.; Mitchell A. R.; Schmidt R. D. A Review of Energetic Materials Synthesis. Thermochim. Acta 2002, 384, 187–204. 10.1016/s0040-6031(01)00805-x. [DOI] [Google Scholar]
- Chakraborty D.; Muller R. P.; Dasgupta S.; Goddard W. A. The Mechanism for Unimolecular Decomposition of Rdx (1,3,5-Trinitro-1,3,5-Triazine), an Ab Initio Study. J. Phys. Chem. A 2000, 104, 2261–2272. 10.1021/jp9936953. [DOI] [Google Scholar]
- Sewell T. D.; Menikoff R.; Bedrov D.; Smith G. D. A Molecular Dynamics Simulation Study of Elastic Properties of HMX. J. Chem. Phys. 2003, 119, 7417–7426. 10.1063/1.1599273. [DOI] [Google Scholar]
- Nielsen A. T.; Chafin A. P.; Christian S. L.; Moore D. W.; Nadler M. P.; Nissan R. A.; Vanderah D. J.; Gilardi R. D.; George C. F.; Flippen-Anderson J. L. Synthesis of Polyazapolycyclic Caged Polynitramines. Tetrahedron 1998, 54, 11793–11812. 10.1016/s0040-4020(98)00711-x. [DOI] [Google Scholar]
- Shen C.; Wang P.; Lu M. Molecular Design and Property Prediction for a Series of Novel Dicyclic Cyclotrimethylene Trinitramines (RDX) Derivatized as High Energy Density Materials. J. Phys. Chem. A 2015, 119, 8250–8255. 10.1021/acs.jpca.5b04969. [DOI] [PubMed] [Google Scholar]
- Pan Y.; Zhu W. Designing and Looking for Novel Cage Compounds Based on Bicyclo-HMX as High Energy Density Compounds. RSC Adv. 2018, 8, 44–52. 10.1039/c7ra11584a. [DOI] [Google Scholar]
- Türker L.; Varis S. Structurally Modified RDX - a DFT Study. Def. Technol. 2017, 13, 385–391. 10.1016/j.dt.2017.02.002. [DOI] [Google Scholar]
- Pouretedal H. R.; Damiri S.; Shahsavan A. Modification of RDX and HMX Crystals in Procedure of Solvent/Anti-Solvent by Statistical Methods of Taguchi Analysis Design and Mlr Technique. Def. Technol. 2018, 14, 59–63. 10.1016/j.dt.2017.08.003. [DOI] [Google Scholar]
- Kamlet M. J.; Jacobs S. J. Chemistry of Detonations. I. A Simple Method for Calculating Detonation Properties of C-H-N-O Explosives. J. Chem. Phys. 1968, 48, 23–35. 10.1063/1.1667908. [DOI] [Google Scholar]
- Frisch M. J.; et al. Gaussian 03, Revision B.05: Wallingford, 2004.
- Lu T.; Chen F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- Politzer P.; Martinez J.; Murray J. S.; Concha M. C.; Toro-Labbé A. An Electrostatic Interaction Correction for Improved Crystal Density Prediction. Mol. Phys. 2009, 107, 2095–2101. 10.1080/00268970903156306. [DOI] [Google Scholar]
- Liu Y.; Gong X.; Wang L.; Wang G.; Xiao H. Substituent Effects on the Properties Related to Detonation Performance and Sensitivity for 2,2′,4,4′,6,6′-Hexanitroazobenzene Derivatives. J. Phys. Chem. A 2011, 115, 1754–1762. 10.1021/jp200512j. [DOI] [PubMed] [Google Scholar]
- Wang F.; Du H.; Zhang J.; Gong X. Computational Studies on the Crystal Structure, Thermodynamic Properties, Detonation Performance, and Pyrolysis Mechanism of 2,4,6,8-Tetranitro-1,3,5,7-tetraazacubane as a Novel High Energy Density Material. J. Phys. Chem. A 2011, 115, 11788–11795. 10.1021/jp2049469. [DOI] [PubMed] [Google Scholar]
- Yang J.; Zhang X.; Gao P.; Gong X.; Wang G. Exploring Highly Energetic Aliphatic Azido Nitramines for Plasticizers. RSC Adv. 2014, 4, 53172–53179. 10.1039/c4ra04240a. [DOI] [Google Scholar]
- Lide D. R.CRC Handbook of Chemistry and Physics; CRC press, 2004. [Google Scholar]
- Rice B. M.; Pai S. V.; Hare J. Predicting Heats of Formation of Energetic Materials Using Quantum Mechanical Calculations. Combust. Flame 1999, 118, 445–458. 10.1016/s0010-2180(99)00008-5. [DOI] [Google Scholar]
- Politzer P.; Murray J. S. Some Molecular/Crystalline Factors That Affect the Sensitivities of Energetic Materials: Molecular Surface Electrostatic Potentials, Lattice Free Space and Maximum Heat of Detonation Per Unit Volume. J. Mol. Model. 2015, 21, 25. 10.1007/s00894-015-2578-4. [DOI] [PubMed] [Google Scholar]
- Politzer P.; Murray J. S. Impact Sensitivity and the Maximum Heat of Detonation. J. Mol. Model. 2015, 21, 262. 10.1007/s00894-015-2793-z. [DOI] [PubMed] [Google Scholar]
- Politzer P.; Murray J. S. High Performance, Low Sensitivity: Conflicting or Compatible?. Propellants, Explos., Pyrotech. 2016, 41, 414–425. 10.1002/prep.201500349. [DOI] [Google Scholar]
- Pospíšil M.; Vávra P.; Concha M. C.; Murray J. S.; Politzer P. Sensitivity and the Available Free Space Per Molecule in the Unit Cell. J. Mol. Model. 2011, 17, 2569. 10.1007/s00894-010-0953-8. [DOI] [PubMed] [Google Scholar]
- Politzer P.; Murray J. S. Impact Sensitivity and Crystal Lattice Compressibility/Free Space. J. Mol. Model. 2014, 20, 2223. 10.1007/s00894-014-2223-7. [DOI] [PubMed] [Google Scholar]
- Pospíšil M.; Vávra P.; Concha M. C.; Murray J. S.; Politzer P. A Possible Crystal Volume Factor in the Impact Sensitivities of Some Energetic Compounds. J. Mol. Model. 2010, 16, 895–901. 10.1007/s00894-009-0587-x. [DOI] [PubMed] [Google Scholar]
- Wang F.; Wang G.; Du H.; Zhang J.; Gong X. Theoretical Studies on the Heats of Formation, Detonation Properties, and Pyrolysis Mechanisms of Energetic Cyclic Nitramines. J. Phys. Chem. A 2011, 115, 13858–13864. 10.1021/jp2047536. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.