Gas-Phase Stereoinversion in Aspartic Acid: Reaction Pathways, Computational Spectroscopic Analysis, and Its Astrophysical Relevance

Abstract

Noncatalytic reaction pathways for the gas-phase stereoinversion in aspartic acid are mapped employing a global reaction route mapping strategy using quantum mechanical computations. The species including the transition states (TSs) traced along the stereoinversion pathways are characterized using rotational and vibrational computational spectroscopic analysis while accounting for the vibrational corrections to rotational constants and anharmonic effects. Notably, the TS structures traced along the stereochemical pathways resemble the achiral ammonium ylide and imine intermediates as observed in the Strecker synthesis of chiral amino acids. A few of the probable stereoinversion pathways proposed proceed through the proton or hydrogen atom transfer. The feasibility of the pathways under conditions akin to interstellar medium (ISM) is further discussed in terms of natural bond orbital analysis. The stereoinversion pathways proposed in this work may proceed via photoirradiation in the ISM, which though can be revealed by exploring the excited-state potential energy surface. In this context, the spectroscopic data generated in this work can provide valuable assistance toward the astrophysical detection of chiral molecules in outer space.

1. Introduction

Despite decades of human efforts, the origin of biohomochirality (the favorability toward only one kind of handedness) in molecules, for example, which is exhibited by the amino acids still remained unanswered.¹⁻⁵ Although amino acids are one of the most essential elements of life on the earth, the proposed mechanisms,² for their synthesis on the prebiotic earth, do not provide enough evidence about their preference toward only L-enantiomeric form.⁶ Besides the existing terrestrial proposals,² according to one of the astrochemical hypotheses, which is being looked quite actively now-a-days,⁷⁻⁹ it is believed that the amino acids synthesized in the interstellar medium (ISM) were delivered in sufficient enantiomeric excess to the earth via astrophysical objects such as meteoroids, asteroids or comets. This in fact is based on several reports on the detection of significant enantiomeric excess of L-amino acids in meteoritic samples,¹⁰⁻¹² suggesting their presence in the outer space bodies. The recent discovery of propylene oxide in molecular cloud Sagittarius B2(N),¹³ the first chiral molecule ever to be confirmed in any star-forming region, is revolutionary in this field because it opens up the door to search for other chiral molecules such as amino acids and sugars, to be present in the ISM. However, there are several studies, but mainly speculative ones, on the probable presence of important chiral molecules in the ISM.¹⁴⁻¹⁸

Several experimental studies^5,15,18,19 had suggested the synthesis of proteinogenic as well as nonproteinogenic amino acids in ISM by simulating the interstellar or circumstellar ice analogues. The latter are a gaseous mixture of basic molecules such as CO, CO₂, CH₄, CH₃OH, NH₃, and H₂O, which when irradiated with the photons of suitable energy, for example, UV,²⁰⁻²² gamma,^23,24 or even highly energetic protons,²⁵ result into the precursors of amino acids and subsequent acid hydrolysis of which leads to the amino acids. The amino acid of interest in the present work is aspartic acid, which is also proposed to be formed in several investigations focusing on the synthesis of astrochemical molecules. For example, a study by Meinert et al.¹⁹ reported aspartic acid among a total of 26 amino acids synthesized using a mixture of H₂O, CH₃OH, and NH₃ in the presence of UV light. Besides this, Takano et al.²⁵ synthesized aspartic acid by bombarding a mixture of H₂O, CO, and NH₃ with energetic protons. Moreover, further irradiation of the amino acid precursors by circularly polarized UV light results in asymmetric synthesis of amino acids.²⁵ The mechanism for the synthesis of amino acids can be ascertained using the one suggested by Miller,²⁶ via Strecker synthesis,²⁷ as illustrated in Figure 1. Aspartic acid can result from the conversion of β-hydrogen of alanine to carboxylic acid,²⁸ where alanine is expected to be formed from the hydrolysis of 2-amminopropionitrile (2-APN). The latter’s presence in the ISM is only speculated till date, but it is being intensively searched there, though in the lab it can be readily prepared from the condensation of methanal and ammonia through an achiral imine intermediate. Note that aspartic acid itself has yet not been detected in the ISM. However, an alternate mechanism for the synthesis of aspartic acid, from the elementary molecular species (NH₃, CO₂, HCN, CH₂, and H₂O) already detected in the ISM, can be proposed based on the study of Maeda and Ohno,²⁹ on the formation of glycine, as summarized in Figure 1. The addition of methylene to glycine followed by carboxylation and isomerization can result in aspartic acid through achiral ammonium ylide intermediates.

Figure 1.

Plausible mechanistic routes toward the synthesis of aspartic acid from the elementary molecular species detected in the ISM.

Aspartic acid has one unique property that it is susceptible to chiral inversion in living organisms.³⁰ This property of aspartic acid has been used to determine the age of living and nonliving things through carbon dating.³¹ However, the asymmetry in amino acids synthesized in the ISM is believed to be due to irradiation by circularly polarized UV light.^5,25 Therefore, it is quite fascinating to reveal its mechanism for stereoinversion under conditions akin to ISM. For past many decades, the researchers have paid considerable attention to the isomerization reactions occurring in the ISM.³²⁻³⁵ For example, in nitrile/isonitrile (HCN/HNC) isomerization, HCN is considerably stable than HNC (by ca. 55 kJ/mol), with an isomerization barrier of 124 kJ/mol, but both the isomers are found to be equally abundant in the ISM particularly at low temperatures.³² In one of our previous quantum mechanical computational study,³⁶ we proposed the gas-phase pathways for stereoinversion in one of the probable candidates for extraterrestrial chiral molecule, namely, 2-APN, which is supposed to be an important intermediate in the amino acid synthesis in the ISM as depicted in Figure 1. Such investigations had also been carried out for the amino acids alanine³⁷ and serine³⁸ and very recently by our research group on threonine, an amino acid with two stereocenters.³⁹

In the present work, through advanced quantum mechanical computations, we perform a systematic search for the mechanistic pathways of the gas-phase stereoinversion in aspartic acid while revealing the intermediate and transition-state (TS) species connecting its enantiomers. Notably, the prediction of intermediates along the stereoinversion pathways of molecules can aid in the detection of molecules in ISM, for which computational quantum mechanical spectroscopic investigations play an integral role.⁴⁰⁻⁴³ It can be used to identify the ISM molecules by creating a computational spectroscopic database for the intermediates explored along the reaction routes of molecule of interest and then matching the computed spectral pattern with those observed through the spectrometers on space probes and space observatories. In this aspect, the rotational spectroscopy has become an inevitable tool in the field of astronomy because of the fact that the low temperature in the ISM’s molecular clouds maintains the molecules in their electronic and vibrational ground state, thereby limiting the infrared emissions from this part of the outer space. For example, the spectrum of the giant molecular cloud, Orion nebula, consists of many sharp lines but only corresponding to the rotational transitions.⁴⁰ The vibrational transitions may be observed at the periphery of the dense molecular clouds as well as in the diffuse interstellar clouds, where molecular excitations may not be a rare phenomenon as the high-energy photons emitted by the hot stars may excite them.^41,42 Keeping this in the view, computational rotational and vibrational spectroscopic studies of aspartic acid and important intermediates along the proposed stereoisomerization pathways have been performed in this work, in particular, accounting for the vibrational corrections to the rotational constants and anharmonic effects in the vibrational transitions. However, note that the present work explores the stereoinversion pathways that require the swapping of groups around the chiral center, which may be facilitated by photoirradiation. However, a search over the excited-state potential energy surface (PES) will be necessary to establish the mechanism of such photoreactions, whereas the present study is restricted only to the exploration of ground-state PES as described in the next section.

2. Computational Methodology

Although aspartic acid is abundant in nature in its L-form, energetically both l- and d-aspartic acids are the same except for their optical rotation. Therefore, in the present work, only the L-form, the enantiomer with (S)-configuration, has been considered for investigation. Note that in the present work, we are mainly interested in locating an appropriate achiral intermediate along the pathways that may facilitate stereoinversion. The stereoinversion pathways connecting various equilibrium structures (EQs) through TSs were explored using a global reaction route mapping (GRRM) strategy of Ohno and co-workers,⁴⁴⁻⁴⁹ employing appropriate quantum mechanical methods. Note that to trace the reaction pathways, the exploration of the PES of a molecular system of even a few atoms is computationally quite challenging. Therefore, the initial computations for the search of various EQs and TSs were performed at a lower level of quantum mechanical method, namely, the DFT/B3LYP/6-31G level of the density functional theory (DFT), using a hybrid Becke-three-parameter-Lee–Yang–Parr (B3LYP)^50,51 exchange–correlation functional of DFT and 6-31G Gaussian basis set. The geometries of the located EQs and TSs at the B3LYP/6-31G level were further refined using a meta-hybrid Minnesota exchange correlation functional,⁵² M06-2X of the DFT, while employing Dunning-style correlation-consistent triple zeta basis set, aug-cc-pVTZ, (aug)mented by the diffuse functions. The geometry optimization was followed by the harmonic vibrational frequency calculations to check the nature of each stationary point, that is, minima or TS depending on the number of imaginary frequencies and to obtain the zero-point energy (ZPE) correction. Any species with one and only one imaginary frequency is designated as TS, whereas minima should have all real frequencies. The final refinement for energy of the species along the proposed pathways was carried out using coupled-cluster (CC) calculations⁵³ at the CCSD(T)/cc-pVDZ//DFT/M06-2X/aug-cc-pVTZ level of the theory as well as using a density fitting (DF) DF-CCSD(T)/cc-pVTZ//DFT/M06-2X/aug-cc-pVTZ method.⁵⁴ Note that we had tried to choose the best quantum mechanical method that can be afforded using the computational resources available with us. All computations using the GRRM were performed in assistance with the Gaussian 09 quantum mechanical software package,⁵⁵ except for the computations at the DF-CCSD(T)/cc-pVTZ//DFT/M06-2X/aug-cc-pVTZ level, for which PSI-code quantum mechanical software package⁵⁶ was utilized employing an energy convergence criterion of 10^–8.

The aforementioned DFT methods are generally believed to be not much accurate in determining the centrifugal distortion constants, and therefore, at the first sight, the DFT-computed force field may seem to be inappropriate for the investigations being carried out in the present work. In particular, the rotational spectra being computed in the present work are likely affected by the internal motion, which may not be accounted by the DFT. However, in spite of these shortcomings of the DFT method employed here, we were able to successfully trace the achiral intermediates, which are responsible for the stereoinversion of aspartic acid. To further compare the results predicted using the DFT method and check their reliability, the computations were also carried out using ab initio Møller–Plesset second-order perturbation theory (MP2)⁵⁷ at the level of MP2/6-31+G(d,p) method employing a 6-31+G(d,p) Gaussian basis set. However, the vibrationally corrected rotational constants calculated using the DFT/M06-2X/aug-cc-pVDZ method are observed to be more accurate (see later).

Initially, an attempt was made to find the stereoinversion pathways with low energy barrier (as in our previous studies),³⁶⁻³⁹ employing a “first only” restrictive option of GRRM, but it resulted in only various conformers (12 to be exact) of aspartic acid, as provided in the Supporting Information (Figure S1). To trace the low energy barrier pathways, the PES was also searched by following the five largest anharmonic downward distortions employing LAAD = 5 option during the GRRM search, but even using this, an achiral stationary point relevant to stereoinversion could not be located. This indicates a high energy barrier for stereoinversion in aspartic acid, but our further attempt to locate a TS along the stereoinversion pathways was complicated by the hydrogen bonding interactions among −NH₂, −COOH, and −CH₂COOH groups in aspartic acid. These H-bonding interactions in the amino acids can be categorized into three types, being designated as I: {(NH₂)N–H···O=C (α-COOH in cis-confirmation)}, II: {(NH₂)N···H–O (α-COOH in trans-confirmation)}, and III: {(NH₂)N–H···O–H (α-COOH in cis-confirmation)}.^58,59 In the present work, the global minimum (as located in the GRRM search) at the DFT/B3LYP/6-31G level of the theory was found to be EQ0^# as depicted in Figure 2a, which has also been reported to be the most stable (conformer Ib-1) in a previous study by Sanz et al. at the MP2/6-311++G(d,p) level of the theory,⁵⁹ in which type-I H-bonding interactions were predicted. However, its another lowest-energy rotational conformer EQ0 depicted in Figure 2b and reported as conformer Ia-1 by Sanz et al. at the MP2/6-311++G(d,p) level of theory is predicted to be 129 kcal/mol more stable at the more appropriate M06-2X/aug-cc-pVTZ level of the quantum mechanical method than that predicted by the B3LYP/6-31G method. Note that although EQ0 is not the global conformer, different groups attached to the chiral carbon are so oriented as to facilitate their suitable migrations, resulting in stereoinversion as traced by the GRRM (see next section). Subsequently, all the results and discussion are presented with respect to EQ0.

Figure 2.

(a) Global minimum EQ0^# (with symmetry point group C₁) obtained through the GRRM search at the DFT/B3LYP/6-31G level of the theory, in which type-I H-bonding interactions are shown, (b) optimized geometry of conformer EQ0 (with symmetry point group C₁) at the DFT/M06-2X/aug-cc-pVTZ level of the theory, depicting the bond angles (in degrees) in (S)-EQ0, (c) depicting the bond lengths (in Å) in (R)-EQ0, and (d) depicting the dihedral angles (in degrees) in (S)-EQ0. Note that all the geometrical parameters coincide in both the enantiomers; these are depicted in different isomers only for the sake of clarity. The nomenclature in square brackets is adapted from the study of Sanz et al (ref (59)).

Coming to our primary motive of tracing stereoinversion routes, after failing to locate a low-lying TS in the initial GRRM search using first-only and LAAD = 5 options, further computations using two-point scaled hypersphere search and intrinsic reaction coordinates were carried out through the GRRM to intuitively trace the required TSs and intermediates, particularly the achiral intermediate species and to establish the right connectivity among them. However, note that the stereoinversion pathways traced in this work depend on the assumption that the GRRM has sufficiently sampled the chemical space of the reaction system being investigated. Further, the energy values (including the ZPE correction) for all the species located along the proposed stereoinversion pathways, depicted in Figures 3 and 4, are provided in Table 1. The relative energy profiles along the pathways are further depicted in Figures 5 and 6, whereas the Gibbs free-energy change and its temperature dependence are analyzed in Table 4. Besides these, the natural bond orbital (NBO)⁶⁰ charge analysis for the relevant stereoinversion pathways is presented in Table 3, which was utilized in deciding whether the [−H] migrates as an atom or a proton (see later).

Figure 3.

Stereoinversion pathways in aspartic acid, arising through the shift of [−H] (i) to the −NH₂ group (Path 1), (ii) to the −COOH group (Path 2), and (iii) to the −CH₂COOH group (Path 3). The values depicted are the relative energies (in kcal/mol) including the ZPE correction at the DF-CCSD(T)/cc-pVTZ//DFT/M06-2X/aug-cc-pVTZ level of the theory.

Figure 4.

Same as Figure 3 but for the pathways arising through the shift of the −CH₂COOH group (i) to the −NH₂ group (Path 4) and (ii) to the −COOH group (Path 5).

Table 1. Relative Energies (in kcal/mol)^b of the Intermediates (EQs) and TSs Traced along the Stereoinversion Pathways and DCs of Aspartic Acid Depicted in Figures 3 and 4 Wrt the Lowest Energy Conformer of Aspartic Acid (EQ0) at the Specified Levels of the Theory Including the Relative ZPE Correction (Indicated in the Parentheses)^a.

	species	symmetry point group	MP2/6-31+G(d,p) + (ZPE)	DF-CCSD(T)/cc-pVTZ//M06-2X/aug-cc-pVTZ + (ZPE)
Stereoinversion Pathways
Path 1	TS0/1	C1	62.83 (−3.65)	63.32 (−3.71)
	EQ1	C1	31.63 (0.19)	31.26 (0.12)
	TS1	Cs	35.86 (−0.04)	34.59 (−0.27)
Path 2	TS0/2	C1	53.62 (−3.17)	52.90 (−3.18)
	EQ2	C1	20.55 (−0.74)	19.69 (−0.56)
	TS2	Cs	24.11 (−0.59)	22.81 (−0.44)
Path 3	TS0/3	C1	106.73 (−3.85)	97.92 (−3.75)
	EQ3	C1	41.56 (−0.29)	41.58 (−0.13)
	TS3/3′	C1	96.88 (−4.57)	96.04 (−4.26)
	EQ3′	C1	22.17 (0.70)	21.57 (−0.22)
	TS3	Cs	28.10 (−1.13)	27.08 (−0.72)
Path 4	TS0/4	C1	102.80 (−3.18)	102.22 (−2.87)
	EQ4	C1	42.58 (−0.37)	41.86 (−0.22)
	TS4c	Cs	48.14 (−0.06)	47.12 (−0.29)
Path 5	TS0/5	C1	54.45 (−2.34)	55.50 (−2.10)
	EQ5	C1	19.77 (−1.25)	19.39 (−0.92)
DCs
EQ0 →DC1P1 [CH3COOH + C2H3O2N]
DC1	DC1TS1	C1	62.74 (−5.09)	66.99 (−4.78)
	DC1P1	C1	42.67 (−2.50)	42.58 (−2.68)
EQ0 →DC2P2 [CO + H2O + C3H5O2N]
DC2	DC2TS2	C1	69.24 (−4.49)	74.72 (−4.25)
	DC2P2	C1	6.94 (−5.39)	13.54 (−5.12)
EQ0 →DC3P3 [H2O + C4H5O3N]
DC3	DC3TS3	C1	67.64 (−5.64)	75.68 (−5.24)
	DC3P3	C1	28.11 (−4.41)	31.66 (−4.11)
EQ1 →DC4P4 [NH3+ C4H4O4]
DC4	DC4TS4	C1	80.87 (−5.41)	80.27 (−5.51)
	DC4P4	C1	43.91 (−2.95)	42.95 (−2.79)

^aNote that the TSs are represented as TSm/n for stereoinversion pathways connecting nth EQ with mth EQ.

^bThe total energies including ZPE of EQ0 at the MP2/6-31+G(d,p) and DF-CCSD(T)/cc-pVDZ//DFT/M06-2X/aug-cc-pVTZ levels of the theory are −510.8387 (0.1254) and −511.5796 (0.1249) a.u., respectively (1 a.u. = 627.5095 kcal/mol). [For results using other quantum mechanical methods employed, see the Supporting Information (Table S5).]

^cNote that the point group of TS2 and TS4 is observed to be C_s at all the DFT and CCSD//DFT levels of theory employed except at the MP2/-6-31+G(d,p) level of theory where it was determined to be C₁.

Figure 5.

Potential energy profiles (relative to EQ0) obtained using the MP2/6-31+G(d,p) method for the stereoinversion pathways (Paths 1–4) depicted in Figures 3 and 4 for aspartic acid (EQ: equilibrium structure and TS: transition state).

Figure 6.

Same as Figure 5 but at the DF-CCSD(T)/cc-pVTZ//DFT/M06-2X/aug-cc-pVTZ level of the theory. [For profile using other quantum mechanical methods employed, see the Supporting Information (Figure S4).]

Table 4. Temperature Dependence of the Relative Gibbs Free-Energy Change (ΔG) Wrt EQ0, in kcal/mol, for the Stereoinversion Pathways between (R)- and (S)-Enantiomers of Aspartic Acid Depicted in Figures 3 and 4 at DFT/M06-2X/aug-cc-pVTZ of the Theory^a.

	T (K)
pathway	10		50		100		298.15		500		1000
EQ0 → TS0/1	59.67	62.83	59.66	62.81	59.68	62.81	59.69 (59.67)	62.76 (62.83)	59.64	62.69	59.61	62.60
TS0/1 → EQ1	–31.04	–31.20	–31.04	–31.20	–31.04	–31.19	–30.98 (−31.04)	–31.13 (−31.20)	–30.89	–31.05	–30.62	–30.86
EQ1 → TS1(Cs)	2.85	4.23	2.85	4.27	2.86	7.48	2.98 (2.85)	4.88 (4.23)	3.32	5.63	4.73	8.11
ΔGPath1	31.48	35.86	31.48	35.88	31.50	39.09	31.69 (31.48)	36.50 (35.86)	32.08	37.27	33.72	39.85
EQ0 → TS0/2	49.33	53.61	49.32	53.61	49.35	53.65	49.63 (49.33)	53.90 (53.62)	50.03	54.28	51.24	55.40
TS0/2 → EQ2	–29.89	–33.07	–29.94	–33.09	–30.06	–33.19	–30.78 (−29.86)	–33.75 (−33.07)	–31.69	–34.49	–34.29	–36.67
EQ2 → TS2(Cs)	3.50	3.56	3.48	3.56	3.51	3.61	4.01 (3.50)	4.22 (3.55)	4.85	5.16	7.57	8.11
ΔGPath2	22.94	24.10	22.87	24.08	22.80	24.08	22.87 (22.93)	24.37 (24.11)	23.19	24.94	24.52	26.84
EQ0 → TS0/3	103.69	106.73	103.70	106.75	103.76	106.81	104.06 (103.69)	107.13 (106.73)	104.37	107.45	105.16	108.28
TS0/3 → EQ3	–64.73	–65.17	–64.73	–65.17	–64.73	–65.18	–64.82 (−64.73)	–65.30 (−65.17)	–64.89	–65.43	–65.13	–65.88
EQ3 → TS3/3′	54.57	55.32	54.57	55.32	54.60	55.34	54.73 (54.57)	55.39 (55.32)	54.80	55.38	54.99	55.38
TS3/3′ → EQ3′	–71.77	–74.71	–71.79	–74.73	–71.83	–74.79	–72.00 (−71.77)	–74.99 (−74.71)	–72.13	–75.16	–72.52	–75.68
EQ3′ → TS3(Cs)	5.68	5.92	5.67	5.90	5.67	5.89	5.68 (5.68)	5.94 (5.92)	5.85	6.17	6.80	7.28
ΔGPath3	27.44	28.09	27.43	28.07	27.46	28.07	27.66 (27.44)	28.16 (28.10)	28.00	28.41	29.29	29.39
EQ0 → TS0/4	99.00	102.80	98.99	102.79	98.98	102.80	99.00 (99.00)	102.80 (102.80)	98.98	102.80	98.93	102.72
TS0/4 → EQ4	–59.63	–60.23	–59.66	–60.24	–59.73	–60.31	–60.19 (−59.63)	–60.72 (−60.22)	–60.64	–61.13	–61.67	–62.08
EQ4 → TS4(Cs)	4.39	5.57	4.41	5.58	4.49	5.68	4.97 (4.39)	6.40 (5.56)	5.68	7.44	8.04	10.64
ΔGPath4	43.76	48.14	43.74	48.14	43.74	48.17	43.77 (43.76)	48.49 (48.14)	44.02	49.10	45.31	51.28

^aThe temperature range, in kelvin (K), corresponds to different regions of the ISM. The point group symmetry of achiral TSs is specified in parenthesis. The values depicted in bold are calculated using the MP2/6-31+G(d,p) method. The values in parenthesis are the corresponding ZPE-corrected relative energies (note that these are temperature-independent).

Table 3. Atomic Charges (in the Units of Electronic Charge e) Estimated Using the NBO Analysis at Reactive Atomic Centers in the EQs and the TSs Explored along the Stereoinversion Pathways of Aspartic Acid at the DFT/M06-2X/aug-cc-pVTZ Level of the Theory^a.

species	N(1)	C(2)	H(3)	C(4)	C(5)	H(6)	H(7)	C(8)	O(9)
EQ0	–0.856	–0.135	0.213	0.821	–0.504	0.250	0.244	0.831	–0.621
TS0/1	–0.847	–0.297	0.495	0.739	–0.522	0.267	0.225	0.837	–0.639
EQ1	–0.695	–0.226	0.470	0.685	–0.531	0.274	0.221	0.840	–0.659
TS1	–0.672	–0.231	0.468	0.685	–0.524	0.245	0.245	0.841	–0.659
TS0/2	–0.711	0.302	0.120	0.469	–0.566	0.281	0.274	0.833	–0.622
EQ2	–0.638	0.288	0.138	0.367	–0.592	0.252	0.282	0.833	–0.611
TS2	–0.654	0.278	0.153	0.367	–0.590	0.262	0.262	0.832	–0.606
TS0/3	–0.825	–0.246	0.263	0.831	0.135	0.215	0.180	0.332	–0.639
EQ3	–0.834	–0.161	0.227	0.804	0.037	0.198	0.189	0.375	–0.542
TS3/3′	–0.770	0.050	0.284	0.791	–0.121	0.262	0.104	0.380	–0.807
EQ3′	–0.600	0.205	0.242	0.758	–0.493	0.248	0.124	0.431	–0.764
TS3	–0.568	0.195	0.250	0.759	–0.488	0.250	0.157	0.759	–0.588

^aThe significant values are depicted in bold.

Further, the species explored along the proposed stereoinversion pathways were characterized using computational rotational and vibrational spectroscopy. The most relevant spectroscopic parameters, provided in Table 2 and Tables S2–S4 (Supporting Information), were computed using different quantum mechanical methods. To accurately determine these parameters, the quartic and cubic force fields are required for calculating the vibrational corrections to rotational constants as well as anharmonic effects, which are obtained using second-order vibrational perturbation theory (VPT2),⁶¹ as implemented in Gaussian 09⁵⁵ (see the input file provided in the Supporting Information). In the present work, for the experimentally known conformers EQ0^# (Ib-1) and EQ0 (Ia-1), these calculations were attempted at different levels of theory, namely, MP2/6-31+G(d,p), M06-2X/cc-pVDZ, M06-2X/aug-cc-pVDZ, and M06-2X/cc-pVTZ as well as using the B3LYP/SNSD method. The latter has recently been forwarded as a computationally less-expensive approach for such calculations.⁶¹

Table 2. Vibrationally Corrected Ground-State Rotational Constants A₀, B₀, and C₀ along with Vibrational Corrections ΔA₀, ΔB₀, and ΔC₀ (All in MHz), Ray’s Asymmetry Parameter κ = (2B – A – C)/(A – C), ¹⁴N Nuclear Quadrupole Coupling Tensors χ_aa, χ_bb, and χ_cc (All in MHz), Electric Dipole Moment Components μ_a, μ_b, and μ_c (All in Debye), Quartic Centrifugal Distortion Constants Δ_J, Δ_K, Δ_JK, δ_J, and δ_K (in kHz)^b for the Aspartic Acid Conformers EQ0^# and EQ0, and the Important Intermediates EQ1–EQ4 Depicted in Figures 3 and 4^a.

	EQ0# (Ib-1)	EQ0 (1a-1)	EQ1	EQ2	EQ3	EQ3′	EQ4
A0	2564, 2504	3363, 3327	2955, 2849	3644, 3496	3295, 3233	3485, 3459	5050, 4690
	2534, (2553.85523)	3389, (3378.20873)
B0	1204, 1208	903, 900	998, 1015	872, 864	977, 980	882, 882	637, 651
	1219, (1205.08478)	909, (907.373507)
C0	1070, 1069	780, 776	823, 841	735, 752	862, 864	733, 732	630, 647
	1092, (1069.14318)	785, (780.042139)
ΔA0	11.982, 27.324	56.803, 47.385	78.39, –52.173	–24.467, 5.586	69.737, 29.335	44.716, 37.699	–219.264, 120.039
ΔB0	18.687, 9.028	10.153, 7.699	–10.442, 31.722	3.329, 6.277	8.278, 7.177	8.759, 7.578	16.766, –3.876
ΔC0	10.642, 8.606	–1.711, 4.715	–3.809, 23.273	3.593, 12.761	–0.644, 6.652	8.416, 5.046	22.074, –4.364
κ	–0.820, –0.806	–0.905, –0.903	–0.836, –0.826	–0.906, –0.918	–0.906, –0.902	–0.890, –0.890	–0.997, –0.998
	–0.811, (−0.812)
χaa	–0.13, –0.27	1.28, 1.04	–0.60, –0.56	–2.49, –1.88	–2.27, –2.65	–3.11, –2.83	0.32, 0.40
	–0.33, (−0.2774)	1.08, (0.9560)
χbb	–0.64, –0.28	2.62, 2.46	0.16, 0.31	–0.62, –0.48	2.15, 2.32	–0.27, 0.08	–0.56, –0.42
	–0.27, (−0.2640)	2.78, (2.7296)
χcc	0.77, 0.55	–3.89, –3.50	0.44, 0.26	3.11, 2.36	1.42, 0.33	3.38, 2.75	–0.88, 0.01
	0.60, (0.5414)	–3.85, (−3.6856)
μa	1.22, 0.95	–0.63, –0.40	3.45, 3.37	1.99, 1.97	–1.14, –1.55	–1.54, –2.01	5.19, 5.43
	–0.9	0.3
μb	–1.14, –1.25	–1.97, –1.75	2.16, 2.77	–2.35, –2.22	–1.94, –1.85	–1.02, –0.82	–1.22, –1.45
	1.3	1.7
μc	–1.80, –1.53	0.75, 0.91	1.73, 1.49	0.73, 0.57	–1.38, –1.54	–0.75, –0.83	–1.37, –0.88
	1.5	–0.9
ΔJ	0.2708, 0.2940	0.0482, 0.0550	0.2493, 0.5148	0.0424, 0.0965	0.1024, 0.1072	0.0321, 0.0339	0.1171, 0.0869
ΔK	0.2028, 0.2890	0.5440, 0.4929	5.2825, 7.7767	0.4347, 1.8885	1.9999, 1.6726	0.5572, 0.4996	18.2927, 12.8568
ΔJK	0.5876, 0.7480	0.3232, 0.4067	–0.0016, –3.0455	0.2862, 0.3573	–0.0299, 0.1020	0.0949, 0.1308	–1.4928, –0.8943
δJ	0.0492, 0.0550	0.0008, –0.0013	0.0164, 0.0748	0.0058, –0.0153	0.0004, –0.0003	0.0043, 0.0038	–0.0136, –0.0053
δK	0.4208, 0.5722	0.7480, 0.9955	0.2901, 0.2651	0.7735, 2.0816	0.3156, 0.4475	0.1893, 0.2188	14.8875, 12.1534

^aThe values listed in normal fonts are at the DFT/M06-2X/aug-cc-pVDZ level of the theory, whereas the values in bold are calculated using the MP2/6-31+G(d,p) method. The values compared in italics are from ref (59) calculated at the MP2/6-311++G(d,p) level of theory, whereas the corresponding experimental values for EQ0^# and EQ0 are indicated in parenthesis.

^bUsing A-reduced Hamiltonian.

The experimental and calculated values of vibrationally corrected ground-state rotational constants for conformers EQ0^# and EQ0 are compared in Table 2 and Table S3 (Supporting Information). Clearly, those computed with the M06-2X/aug-cc-pVDZ method exhibit greater accuracy than any other theory/basis set attempted here, in fact better than those obtained using the cc-pVTZ basis set, clearly indicating the role of long-range diffuse functions as had also been highlighted in the approach of Puzzarini et al.⁶¹ However, our computations using aug-cc-pVTZ could not be completed mainly because of the limited computational resources. Nevertheless, it is reasonable to accept the M06-2X/aug-cc-pVDZ level for rotational spectroscopic analysis presented in this work. For a more accurate prediction of rotational spectroscopic parameters, the state-of-the-art composite schemes employing CC methods through the CFOUR program package⁶² may be followed as suggested by Puzzarini et al.,^61,63,64 although our attempt to employ this scheme failed at CCSD(T) and MP2 levels of the theory as recommended in these studies. The relevant spectroscopic parameters for simulating the rotational spectra of different intermediates explored along the stereoinversion pathways are further provided in Table 2, whereas those for the TSs along the pathways are provided in Table S4 (Supporting Information).

However, for the computations of anharmonic vibrational frequencies, the meta-hybrid DFT functional M06-2X is known to give inaccurate results.⁶⁵ Hence, for the vibrational spectra, calculations using MP2/6-31+G(d,p) are utilized. Note that all these computations are quite expensive for the size of the molecular species being considered in the present work. The harmonic and anharmonic frequency values along with the potential energy distribution (PED) analysis of all the fundamental modes of vibration of the two important conformers of aspartic acid (EQ0^# and EQ0) and other EQs located along the feasible pathways in this study are listed in Table S1 (Supporting Information). The PED is performed using the Vibrational Energy Distribution Analysis (VEDA4) program of Jamroz.⁶⁶ The calculated anharmonic frequency values for the global minimum conformer EQ0^# are further compared with the experimental values⁶⁷ in Table 5.

Table 5. Anharmonic Vibrational Frequencies (ν) and Intensities (I) of Relevant Vibrational Modes along with Their Vibrational Assignments and PED of Conformer EQ0^# of Aspartic Acid at the MP2/6-31+G(d,p) Level of the Theory^a.

		present work (gas phase)
vibrational mode	experimental (solid phase) ν (cm-1) ref (66)	ν (cm-1)	I (km mol–1)	vibrational assignment (PED ≥ 10%)
2	3022	3592	71.7	ν[O14H15] (98)
3	3140	3490	10.6	νaNH2 (99)
4	3077	3414	3.6	νsNH2 (99)
5	3016	3069	0.5	νaCH2 (−99)
6	2958	3033	4.1	νsCH2 (98)
7	2999	2983	10.4	νa[C3–H4] (98)
8	1691	1787	121.1	ν[C10=O16] (79)
10	1644	1628	40.0	β(sciss)[H2–N1–H8] (73) + τa[{H8–N1–C3–C5} + {H2–N1–C3–C5}] (22)
11	1459	1450	16.2	β(sciss)[H7–C5–H6] (77) + τa[{H6–C5–C9–O12} + {H7–C5–C9–O12}] (16)
12	1408	1412	39.9	νa[{C3–C5} + {C5–C9}] (−17) + τa[{H6–C5–C9–O12} + {H7–C5–C9–O12}] (35)
14	1336	1345	8.6	νa[{C3–C10} + {C10–O14}] (23) + β[H15–O14–C10] (−11) + τ[{H4–C3–C10–C14}] (10)
15	1307	1309	27.9	β[H13–O12–C9] (33) + τ[{H4–C3–C10–C14}] (−11)
17	1259	1263	0.7	νs[{N1–C3} + {O12–C9}] (−11) + β[H6–C5–C9] (−11) + τa[{H6–C5–C9–O12} + {H7–C5–C9–O12}] (11)
19	1152	1148	31.6	νs[{N1–C3} + {O12–C9}] (31) + β[H13–O12–C9] (−19) + τ[{H4–C3–C10–C14}] (−10)
24	899	892	106.0	νs[{N1–C3} + {O12–C9}] (−10) + τa[{H8–N1–C3–C5} + {H2–N1–C3–C5}] (30) + τs[{H6–C5–C9–C12} + {H7–C5–C9–O12}] (26)
27	753	754	21.6	νa[{C3–C10} + {C9–O12}] (35) + β[{C3–C10–O14} + {C10–C3–N1} + {C5–C9–O12} + {O16–C10–O14}] (16) + γ[O16–C3–O14–C10] (−10)
28	656	651	11.7	βs[{O16–C10–O14} + {O11–C9–O12}] (25) + τ[H15–O14–C10–C3] (26) + γ[O16–C3–O14–C10] (−14)
30	599	605	66.2	βs[{O16–C10–O14} (−28) + {O11–C9–O12}] (−31) + τ[H15–O14–C10–C3] (44)
35	368	367	9.5	β[C5–C3–N1] (58)

^aThe experimental values compared are for the solid-phase l-aspartic acid (ref (67)). For harmonic and anharmonic vibrational frequencies of all the modes and of other EQs, see the Supporting Information (Table S1) (ν: stretching, β: bending, τ: torsional, γ: out-of-plane vibrations, a: asymmetric, s: symmetric, sciss: scissoring).

3. Results and Discussion

3.1. Stereoinversion Pathways

It is well-established³⁷⁻³⁹ that for stereoinversion to occur in chiral molecules with one stereocenter, the molecular structure (which can be a TS or an intermediate along the stereoinversion route) should possess an achiral geometry. This can happen provided one of the groups around the stereocenter migrates to any one of the remaining three groups (depending on whether the group can accept the incoming moiety). However, all the intuitively inferred shifts are unlikely to occur; only the chemically possible shifts can take place such that any subsequent dissociation is less feasible than the prospective isomerization. For instance, in the present case, the four groups around stereocentric carbon (C*) are as follows: −H, −NH₂, −COOH, and −CH₂COOH. The shift of [−H] to −NH₂ is chemically possible because the lone pair of nitrogen atom can accept proton, but this may lead to dissociation, resulting in NH₃ (see later), though there may be exceptions such as in the formation of ammonium ylides (R₁)R₂C^––⁺NH₃. However, the reverse (shift of −NH₂ to −H) is improbable because the H atom is unlikely to accept the incoming group. Similarly, the amino group (−NH₂) cannot shift to the carboxylic group because the resulting intermediate will have the negative charge on the carbonyl oxygen and positive charge on the central carbon, which is likely to drive the system back into the original form (see Supporting Information, Figure S2). Therefore, depending upon the possible migrations, only five pathways (depicted in Figures 3 and 4) could be located in the present work, which can be further categorized in two ways: one is the shift of −H to the other groups and the other is the shift of −CH₂COOH. One of these five routes seems to be infeasible wrt stereoinversion of aspartic acid because no achiral stationary point could be located along this pathway (see later). It should be noted that out of the various possible rotational conformers of aspartic acid (depicted in Supporting Information, Figure S1), the conformer EQ0 serves as the starting EQ for all the five possible shifts as discussed in detail below.

3.1.1. Shift of [−H]

3.1.1.1. Shift to the [−NH₂] Group

For the stereoinversion of aspartic acid through the shift of [−H] from central asymmetric carbon (C*) to the amino group, as depicted along Path 1 in Figure 3, the conformer (S)-EQ0 must change into conformer (S)-EQ1 via TS0/1 with a barrier height of 63.32 kcal/mol. In TS0/1, note that the C*–H distance is 1.328 Å and the N–H distance is 1.193 Å. This transformation is endergonic as analyzed in Table 1. Note that EQ1 is a zwitterion ammonium ylide species with a negative charge on central carbon (a stereogenic carbanion) and a positive charge on the nitrogen atom, that is, ⁺NH₃^–C(R)COOH, but this intermediate is relatively unstable than the conformer EQ0. In the subsequent step, (S)-EQ1 may go back either to (S)-EQ0 with a barrier height of 32.06 kcal/mol or invert into (R)-EQ1 with a stereoinversion energy barrier of 3.33 kcal/mol via the achiral TS1 of C_s symmetry, which is again ammonium ylide species as also depicted in Figure 1. The former conversion is thermodynamically quite feasible because EQ0 is highly stabilized wrt EQ1, but the latter is kinetically more probable because the barrier height for stereoinversion is quite low along which quantum tunneling may occur because of transfer of hydrogen atom or proton along this path.

Further, (R)-EQ1 has the same fate as that of (S)-EQ1; therefore, there is a possibility that it may finally invert into (R)-EQ0 via (R)-TS0/1, resulting into the enantiomer of opposite chirality. However, this is only possible if there is any probability of forming EQ1 intermediate from EQ0, which in fact seems less likely to occur thermally as evident from ΔG values in Table 4. In fact, in living systems, stereoinversion in aspartic acid occurs through catalytic pathways.⁶⁸ Further, to check whether [−H] migrates to [−NH₂] as a proton or as the H atom, the NBO analysis was carried out. From the NBO atomic charge on relevant atomic sites as given in Table 3, it can be inferred that it is migrating as a proton because the natural atomic charge on H(3) changes to +0.495e in TS0/1 from +0.213e in EQ0, whereas at stereocenter (C*), it increases from −0.135e in EQ0 to −0.297e in TS0/1.

3.1.1.2. Shift to the [−COOH] Group

The second pathway Path 2 presented in Figure 3 involves the migration of [−H] from chiral carbon to the carboxyl group carbon atom in (S)-EQ0. This results into an intermediate (S)-EQ2 via TS0/2 in which the distance between the stereocentric carbon and the proton to be shifted is 1.669 Å compared to a distance of 1.252 Å for the C–H bond to be formed between carboxyl carbon and the migrating proton. The NBO charge analysis in this case suggests the shift of the hydrogen atom instead of proton as the natural atomic charge on the migrating hydrogen in this case is +0.120e (see Table 3). Similar to the previous pathway (Path 1), here also, the first step is endergonic in nature with a Gibbs free-energy barrier height of 52.90 kcal/mol, which is ∼10 kcal/mol less than that along Path 1 and hence, stereoinversion along Path 2 is more probable than Path 1. Further transformation of (S)-EQ2 into (R)-EQ2 is feasible through the achiral TS2 (C_s), which resembles an imine R₁(C=NH)R₂ as in Strecker synthesis illustrated in Figure 1. The energy barrier for stereoinversion in this case is also quite low, although the possibility of retention of configuration does exist as discussed previously for Path 1. Note that the MP2/6-31+G(d,p) method predicts the symmetry of TS2 to be C₁. However, the geometries predicted by the DFT methods are known to be more reliable than MP2; therefore, the achiral TS2 can be trusted.

3.1.1.3. Shift to the [−CH₂COOH] Group

This pathway though improbable is unusual in the sense that unlike the first two pathways, it involves double migration instead of one as depicted in Figure 3. The first step is the formation of (S)-EQ3, which is an epoxide, via TS0/3 involving a concerted movement of methylenic H and carboxylic O atoms (note that EQ3 is similar to propylene oxide, which is first ever chiral species to be detected in the ISM). However, the activation energy for the formation of EQ3 is found to be quite high (97.92 kcal/mol). This is followed by the conversion of (S)-EQ3 into (S)-EQ3′ (a dihydroxy amino acid) via another high barrier (S)-TS3/3′, involving again a concerted shift of H and O atoms but this time at different locations. Finally, (S)-EQ3′ isomerizes to (R)-EQ3′ via the achiral TS3 (C_s) which in fact is an achiral imine. The NBO charge analysis reveals that in this case as well, the hydrogen travels as an atom, in the first step, either H(6) or H(7) with charge +0.2e shifts to C(8), and in the second step, H(3) with charge +0.284e goes to C(5). Further, this path is also specific because it is found to be possible only for the migration of proton from central carbon to the −CH₂COOH group because one of the methylenic protons is shifted to the carbonyl carbon. However, the migration of −NH₂ or −COOH to −CH₂COOH could not be traced, which may be due to the steric effects and the requirement of a perfect orientation. Nonetheless, this pathway seems to be least probable because of the presence of two high energy barriers (see later).

3.1.2. Shift of [−CH₂COOH]

3.1.2.1. Shift to the Amino Group [−NH₂]

The migration of the −CH₂COOH group to the amino group leads to the conversion of EQ0 into EQ4 via TS0/4 but with a barrier height of 102.22 kcal/mol as depicted in Figure 4. (S)-EQ4 changes into (R)-EQ4 via the achiral TS4 (C_s), which is actually an ammonium ylide. In TS4, one of the N–H protons is shared by the carboxylic group (C=O) of the −COOH group, similar to that observed along Paths 2 and 3. However, here also, MP2/6-31+G(d,p) disagrees with the prediction of DFT that the symmetry of TS4 is C_s.

3.1.2.2. Shift to the Carboxylic Group [−COOH]

Contrary to the −NH₂ shift, an attempt to locate the pathway involving migration of the −CH₂COOH group to the −COOH group failed. Through this shift, the conformer (S)-EQ0 does convert into an intermediate (S)-EQ5 through TS0/5 as depicted in Figure 4, but its subsequent conversion to an achiral intermediate/TS could not be traced despite several attempts because of the requirement of C_s symmetry at two consecutive carbon atoms, that is, −CH₂–C(OH)₂–, as can be seen from EQ5 in Figure 4. During the optimization of planar TS in this case, the system tends to go out of plane at one of these carbon positions, resulting into the geometry with point chirality.

3.1.3. Relative Feasibility of Proposed Stereoinversion Pathways

The potential energy profiles of the aforementioned stereoinversion pathways in aspartic acid at MP2/6-31+G(d,p) and at the CC levels of the theory are given in Figures 5 and 6, respectively, whereas Table 4 compares the Gibbs free-energy change along these pathways. Comparing the feasibility trend of the possible chiral inversion pathways when analyzed using the DFT and CCSD//DFT methods, it can be seen that the second pathway (Path 2), which involves the shift of proton to the carboxylic group is the most favorable pathway (both in terms of relative energy and Gibbs free-energy change). The transition state species TS0/2 and TS2 (C_s), as well as the intermediate EQ2 along this route lay much lower in energy than the respective stationary points of other pathways. However, note that the MP2 method differs from the DFT methods on the possibility of Path 2.

Besides Path 2, another pathway (Path 1) involving the migration of proton to the amino group also seems to be probable because the intermediates and TSs are relatively lower lying in energy than those along Paths 3 and 4. The results using the MP2/6-31+G(d,p) method reveal that TS0/4 along Path 4 is lower in energy than the first transtion state species TS0/3 along Path 3, whereas both the CCSD(T) methods indicate that TS0/4 is the highest energy barrier. However, along Path 3, although the system has to go through two high energy barriers: TS0/3 and TS3/3′, before attaining the achiral planar TS3 (C_s), but the intermediates EQ3 and EQ3′ are relatively more stable than those along Path 4, making the overall pathway more probable than Path 4. Therefore, it may be predicted from the CCSD(T)//DFT energy profiles that the pathways follow the feasibility trend as Path 2 > Path 1 ≫> Path 3 > Path 4, with Path 2 being the most feasible though the MP2 method excludes the possibility of Path 2 and Path 4.

The stereoinversion pathways proposed were further analyzed for their relative feasibility under different temperature conditions of ISM, in particular, ranging from 10 to 1000 K. As this study explored only the ground-state PES of the aspartic acid, the higher temperature regions of the ISM are excluded in which case the excited electronic states become more important. The region of interstellar molecular clouds ranges from 10 K in cold dense medium to 100 K in diffuse molecular clouds, where in fact much of the exotic gas-phase interstellar chemistry has been discovered,⁶⁹ whereas the temperature region above 100 K corresponds to the dense “hot cores” of ISM where the star formation process occurs.^70,71 From the analysis presented in Table 4, it can be seen that within the temperature ranges considered here, the overall change in Gibbs free energy is positive along all the pathways. The initial step as well as the stereoinversion step is found to be endergonic, though in the latter’s case it is <10 kcal/mol. Comparing the overall change in free energy for the pathways, it is analyzed that stereoinversion is more likely to occur in the temperature range of 100–500 K. It is to be noted that this temperature region is already observed to be a source of complex organic molecules detected in the ISM,^70,71 and the present study also found that the temperature region of 100–500 K is more suitable for stereoinversion in aspartic acid to occur. However, a vast part of the ISM is not under thermal equilibrium; therefore, the aforementioned usage of the free energy may not even be valid. Nevertheless, even though the analysis in terms of Gibbs free energies may not be appropriate here, but as evident in Table 4 and in Figure 6, the free energies follow the same trend as the ZPE-corrected energies, which in fact need not be dependent on the thermal equilibrium conditions.

Further, to compare the probability of stereoinversion to occur over that of the dissociation of aspartic acid, a few dissociation channels (DCs) were also traced intuitively, which are listed in Table 1 and depicted in Figure S3 (Supporting Information). Note that the DCs (1–3) were searched from the same conformer of aspartic acid from which the stereoinversion pathways were located. Overall, three dissociation pathways (from EQ0) and one dissociation path (from intermediate isomer EQ1 along the stereoinversion Path 1), all endothermic, were traced, similar to that of DCs recently reported for glycine.⁷² Comparing the energy barrier along DCs with that along the most probable stereoinversion pathways (Paths 1 and 2) in Table 1, it is clearly evident that stereoinversion is more likely to occur than dissociation, even though the latter is entropically more favored. For example, the dissociation leading to the formation of H₂O and CO requires ca. 20 kcal/mol more than the highest barrier for stereoinversion along Path 2. However, in glycine, a low-lying DC leading to ammonia and acetylactone has been revealed by another study.⁷² The barrier of ca. 46 kcal/mol along this DC is found to be much lower than the most preferable stereoinversion pathways proposed for aspartic acid. However, an analogue’s DC could not be traced in aspartic acid conformer (EQ0) from which the proposed stereoinversion pathways actually initiate. This may be due to different groups and their orientation around the stereocenter in EQ0 than that in glycine. Nevertheless, it is highly likely that other conformers of aspartic acid and intermediate isomers along the proposed stereoinversion pathways may dissociate through such channels. One such DC (DC4) but with a quite high barrier of ca. 80 kcal/mol (wrt EQ0), listed in Table 1 and depicted in Figure S4 (Supporting Information), was intuitively traced for intermediate isomer EQ1 along stereoinversion Path 1. However, as evident in Table 1, the conversion of EQ1 to its counterpart of opposite chirality is associated with much lower energy barrier than the barrier along DC4. Hence, the dissociation is unlikely to proceed over stereoinversion even along Path 1.

Furthermore, from the data discussed in the aforementioned analysis, there may be apprehensions that the proposed stereoinversion pathways are too slow to proceed and may not even occur on the time scale of our universe. However, note that it is mainly the initial step which involves quite high energy barrier, leading to the key intermediate and TS species. The subsequent steps from these leading finally to the stereoinversion are in fact quite fast. This is supported by the conventional TS theory (TST)-computed rate constants provided in the Supporting Information (Table S6), which are calculated taking into account quantum mechanical tunneling estimated using an unsymmetrical Eckart’s potential.⁷³ As evident from the computed rate constants, the overall stereoinversion pathway proposed are kinetically unfavorable despite involving significant quantum mechanical tunneling. Though the unimolecular rate constant for the initial step along Path 2, for example, at 298.15 K, is ca. 10^–24 s^–1 leading to a key intermediate (EQ2), the subsequent inversion step occurs quite fast with a rate constant of ca. 10⁹ s^–1. Note that the intermediate and TS species traced along the proposed pathways resemble those commonly observed during the synthesis of amino acids, for example, an imine intermediate R′(C=NH)R″ in the Strecker synthesis. If the synthesis of amino acids in the ISM occurs via such intermediates, then the stereoinversion proceeding through these becomes highly probable, in fact during the synthesis of amino acids itself. However, once the amino acid is formed, it may not be possible to invert it because of a very high initial barrier.

3.2. Spectroscopic Analysis

3.2.1. Rotational Spectral Analysis

The spectroscopic details of the intermediate isomers along the proposed gas-phase stereoinversion pathways of aspartic acid can be of utmost importance, particularly for the investigations related to the detection of interstellar amino acids. In view of this, vibrationally corrected rotational and anharmonic vibrational spectral analysis of relevant species explored along the feasible stereoinversion pathways has been performed computationally. To quantitatively analyze the nature of rotational spectra of all the species of interest, “R” branch transitions have been simulated in ∼1–20 GHz range using PGOPHER program⁷⁴ for rotational, vibrational, and electronic spectra employing the parameters provided in Table 2 at the M06-2X/aug-cc-pVDZ level of the theory (for the detailed computational procedure, see the Supporting Information). Note that the vibrationally corrected ground-state rotational constants computed at the M06-2X/aug-cc-pVDZ level provided the best estimate (to be reported in the literature) for rotational constants when compared with the experimental results available for the global conformer of aspartic acid. For the latter, the agreement with experimental data for rotational constants, B and C, is found to be within 1 MHz, and for constant A, it is within 10 MHz, which is even better than those predicted by the MP2/6-311++G(d,p) method, the best known in the existing literature.⁵⁹ Therefore, this level of theory can be taken to be quite reliable, though in no way, it is comparable with the state-of-the-art composite scheme forwarded by the groups of Barone and Puzzarini (see ref (64) and references therein).

Aspartic acid and related intermediates along the pathways are analyzed to be near asymmetric top molecules, with EQ4 being the most symmetrical according to the Ray’s asymmetry value that depends on the rotational constants and determines the position of any transition. The simplified rotational spectra (without including ¹⁴N nuclear hyperfine splitting) of isomers EQ0^#, EQ0, EQ1, EQ2, EQ3, EQ3′, and EQ4 are depicted in Figure 7. These spectra depict the transitions with a rotational quantum number J = 2 ← 1 (as in Figure 7a for isomers EQ1, EQ3′, and EQ4) and J ≤ 6 (as in Figure 7b for isomers EQ1, EQ3′, and EQ4), whereas the characteristic transitions for other isomers (EQ0^#, EQ0, EQ2, and EQ3) are exemplified in Figure 7c.

Figure 7.

Computed rotational spectra in the frequency range of 1–20 GHz at T = 10 K for isomers EQ1, EQ3′, and EQ4 (a) with J = 2 ← 1; (b) with J ≤ 6; and (c) for isomers EQ0^#, EQ0, EQ2, and EQ3 but with J = 2 ← 1. The marked transitions are labeled as 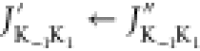, where J and K are conventional rotational quantum numbers for near-prolate asymmetric tops. a-type, b-type, and c-type transitions are specified in red, blue, and green text, respectively (note that these are depicted only for illustration purpose to reveal the type of spectra). The spectra depicted are generated using parameters of Table 2 calculated with the M06-2X/aug-cc-pVDZ method. Note that the normalized intensity has been specified, for the absolute intensity (in nm² MHz molecule^–1), use the conversion 4.16 × 10^–5 × freq (MHz) × normalized intensity.

Note that the strength of any particular type of transition depends on the electric dipole moment (μ) components along the (a, b, c) axis and on the distribution of energy states, which in turn depends on the temperature, hence all the spectra are compared at a fixed temperature of 10 K akin to the cold region of ISM. Therefore, as μ_a values of EQ1, EQ3′, and EQ4 are greater than the μ_b and μ_c values, these species exhibit the a-type transitions, as depicted for EQ1, EQ3′, and EQ4 in Figure 7a, with the most intense transitions following the selection rule: ΔK_a = 0 and ΔK_c = 1, −1, in terms of the second rotational quantum number K. In fact, a-type transitions are easier to locate in a spectrum because such transitions occur in a band. The most intense transition in the band, J_0J′^′ ← J_0J″ (where prime refers to the upper state and double prime to the lower state), is the characteristic of the a-type spectra that repeats periodically after (B₀ + C₀) MHz. This rule, however, is found to be strictly followed only in the case of EQ4 as evident in Figure 7b. It is observed that the greater the deviation in Ray’s asymmetry value from −1 (as in prolate symmetric top), the more the variation is in the predicted frequency values of transitions as per this rule.

Further, because μ_a ≫> μ_b and μ_c for EQ4, the spectra are predicted to be comparatively less complex than those of EQ1 and EQ3′, with a-type transitions dominating the entire spectrum. However, weak μ_b- and μ_c-type transitions are also present in the spectra of EQ1 and EQ3′, which seem to complicate the spectra. For other isomers: EQ0, EQ2, and EQ3, μ_b is the largest value; therefore, b-type transitions, following the selection rule: ΔK_a = 1, −1 and ΔK_c = 1, −1, are predicted to be the most intense. The difference between μ_b and μ_a increases in the order EQ2 < EQ3 < EQ0; therefore, extremely weak a-type transitions are predicted for EQ0 than the b-type as depicted in Figure 7c. Similarly, extremely weak c-type transitions are predicted for EQ0 and EQ2, though these are predicted to be relatively more intense in EQ3. These species can be identified by the position of a characteristic doublet in b-type transitions, J_2J′-1^′ ← J_1J″-1 and J_2J′-2^′ ← J_1J″, centered at (3A₀ + C₀ + (B₀ – C₀)/2) + (B₀ + C₀)(J″ – 1) and separated by (B₀ – C₀)/2J′J″. The location of J_1J′^′ ← J_0J″ transition is predicted at (A₀ + C₀ + 2C₀J″) as specified in Figure 7c for EQ0, EQ2, and EQ3.

The global minimum EQ0^# can be characterized by c-type transitions because of μ_c being the largest of all the three dipole moments. However, as μ_a and μ_b are of comparable magnitude with that of μ_c, weak b- and c-type transitions are also present. To identify this species, one can locate J_1J′-1^′ ← J_0J″ transition that occurs at (A₀ + B₀ + 2B₀J″). Note that while predicting the location of transitions using the aforementioned conventional relations, it is necessary to consider the effect of magnitude of Ray’s asymmetric parameter as well as higher J values.⁷⁵ For EQ0^# and EQ0, the most intense transitions in the range of 1–20 GHz have been calculated with the rotational quantum numbers J ≤ 6 and K ≤ 2 following the selection rules: ΔK_a = 0, 1, −1 and ΔK_c = 0, 1, −1 and are provided in the Supporting Information (Table S2), which also compares these with the available experimental data.⁵⁹ Notably, the agreement between computed and experimental data, for the most intense transitions in EQ0^# and EQ0, is found to be within <100 MHz. Therefore, the rotational spectra for other isomers predicted here could be reliable in resolving the experimental transitions for the specified frequency region in cold interstellar clouds.

3.2.2. Vibrational Spectral Analysis

Further, for the vibrational spectra, harmonic and anharmonic vibrational frequency analysis at the MP2/6-31+G(d,p) level of theory was carried out to characterize all the normal modes of gas-phase aspartic acid and important intermediates relevant to its stereoisomerization pathways. Each fundamental mode is analyzed using potential-energy distribution (PED) through VEDA4 program.⁶⁶ Aspartic acid and all the related intermediates are nonlinear with 16 atoms; hence, a total of 42 active fundamental modes are associated with them as listed in the Supporting Information (Table S1). The PED analysis of the lowest energy conformer EQ0^# along with anharmonic vibrational frequencies and the corresponding intensities is provided in Table 5. The experimental values but available for the solid sample of l-aspartic acid⁶⁷ are also compared. It is quite evident from Table 5 that except for the vibrations at high frequencies (due to hydrogen bonding interactions), most of the gas-phase anharmonic frequencies are in good agreement with the experimental (solid sample) values than the harmonic vibrational frequencies (provided in Table S1). For example, an intense anharmonic O–H stretch associated with the two −COOH groups of gas-phase EQ0^# is predicted to appear at 3595 and 3592 cm^–1, whereas in the solid sample, it is shifted to a much lower value of 3022 cm^–1, mainly due to the intramolecular hydrogen bonding interactions. Similarly, weak asymmetric and symmetric stretch for NH₂ and CH₂ is observed to be at a lower frequency in the solid sample than those predicted in the gas phase. The two most intense −C=O stretch is predicted to appear at 1787 and 1775 cm^–1 compared to 1691 cm^–1 observed in the solid sample. Except for these high-frequency vibrations, there exists a close agreement (within 10 cm^–1) between other gas-phase anharmonic frequencies and the corresponding experimental solid sample values, particularly those observed at low frequencies as evident in Table 5. For example, anharmonic C–H stretch predicted at 2983 cm^–1 is observed at an experimental solid sample value of 2999 cm^–1. Similarly, scissoring-type bending vibrations for NH₂ and CH₂ predicted at 1644 and 1459 cm^–1 are experimentally observed at 1628 and 1450 cm^–1, respectively. In fact, most of the fundamental vibrations at medium and low frequencies match well with the experimental values, keeping in view of the fact that the present predictions are for the isolated gas-phase aspartic acid molecule in the neutral state as may be envisaged in the ISM, compared to the solid sample experimental data. The latter though may well correspond to a zwitterionic form accompanied by intermolecular and intramolecular hydrogen bonding interactions. Also note that the anharmonic frequencies predicted here can be directly employed to characterize the fundamental vibrational modes without using any ad-hoc scaling factor often required in the case of harmonic frequencies. Moreover, the PED analysis provided along with corresponding intensity values can be utilized while detecting aspartic acid or its intermediates proposed along the stereoinversion pathways in the ISM.

4. Conclusions

In this work, using quantum mechanical computations, four gas-phase pathways for stereoinversion in aspartic acid were traced, either involving proton and hydrogen atom transfer or migration of CH₂COOH around the stereogenic carbon atom. The stereoinversion pathways, Path 1 and Path 2, proceeding through the shift of a proton to NH₂ and COOH groups, respectively, were found to be more probable than the dissociation pathways searched for aspartic acid. Stereoinversion is proposed to be more feasible via Path 2 and may be observed in the “hot cores” of the protostars rather than the cold denser region of molecular clouds. Besides this, the TS species along the proposed stereochemical pathways are of types, R₁(R₂)C^––⁺NH₃ and R′(C=NH)R″, which resembles, respectively, the achiral zwitterionic ammonium ylide and imine intermediates, the latter being a key intermediate in the Strecker synthesis of chiral amino acids. The quantum mechanically computed vibrationally corrected rotational and anharmonic vibrational spectral data provided in this work for the aspartic acid, its intermediates, and TS species along the proposed stereoinversion pathways will be quite helpful for the detection of chiral amino acids in the ISM.

Note that the present work has explored truly unimolecular gas-phase isomerization pathways leading to stereoinversion in molecules. This is most likely to happen where the molecular density is too low for a collisional event to occur. The molecular density in ISM ranges from ∼10³ to 10⁶ molecules per cm³ in the cold molecular clouds to only a few molecules per cm³ in the hot regions. Therefore, ISM is a likely place where such gas-phase unimolecular stereoinversion could be observed. Such an isomerization reaction, however, may be induced by photoirradiation. However, to trace the pathways of photoreactions, a computational exploration of the excited-state PES will be necessary, which is likely to be complicated by conical intersections.⁷²

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b01721.

• Rotational conformers of aspartic acid; probable shifts leading to EQ0 from the intermediate in which NH₂ goes to COOH; DCs for aspartic acid conformer EQ0 and an intermediate EQ1 along stereoinversion Path 1; potential energy profiles; all the fundamental (normal mode) harmonic and anharmonic vibrational frequency values and their corresponding intensity for the aspartic acid conformers EQ0^# and EQ0 and important intermediates EQ1–EQ4; calculated rotational frequencies (in MHz) and normalized intensities at the M06-2X/aug-cc-pVDZ level of the theory for isomers EQO^#, EQ0-EQ4; vibrationally corrected ground-state rotational constants A₀, B₀, and C₀ (in MHz) for the aspartic acid conformers EQ0^# and EQ0; rotational spectroscopic parameters for TSs along the feasible pathways; energy values (including the ZPE correction) for all the species located along the proposed stereoinversion pathways by using other quantum mechanical methods employed; TST rate constants (k) in s^–1, and tunneling transmission coefficient (χ) for each elementary step along the feasible stereoinversion pathways; Cartesian coordinates of important stationary points traced along the proposed stereoinversion pathways; input file for carrying out the anharmonic frequency analysis; and stepwise procedure to simulate rotational spectra (PDF)

The authors declare no competing financial interest.