Abstract

In the present work, predictive quantitative structure–property relationship models have been developed to predict refractive indices (RIs) of a set of 221 diverse organic polymers using theoretical two-dimensional descriptors generated on the basis of the structures of polymers’ monomer units. Four models have been developed by applying partial least squares (PLS) regression with a different combination of six descriptors obtained via double cross-validation approaches. The predictive ability and robustness of the proposed models were checked using multiple validation strategies. Subsequently, the validated models were used for the generation of “intelligent” consensus models (http://teqip.jdvu.ac.in/QSAR_Tools/DTCLab/) to improve the quality of predictions for the external data set. The selected consensus models were used for the prediction of refractive index values of various classes of polymers. The final selected model was used to predict the refractive index of four small virtual libraries of monomers recently reported. We also used a true external data set of 98 diverse monomer units with the experimental RI values of the corresponding polymers. The obtained models showed a good predictive ability as evidenced from a very good external predicted variance.
Introduction
Polymers are macromolecules made up of multiple repeating units or monomers.1 Due to the presence of multiple repeating units, polymer molecules possess high relative molecular mass and various associated properties. Over the past few decades, polymers have been intensively studied due to their broad applications in multiple fields such as petrochemical industries, oil and gas storage,2−5 and plastic industries that involve bags, boxes, etc. They are used in packaging of food items, agricultural products, etc. and are also used in the synthesis of catalysts and sensor substrates,6−9 in drug delivery,10 and in chromatographic separation.11
Among several physical properties, the refractive index (RI) is an important one. The refractive index of a polymer is defined as the velocity of light in a vacuum relative to the velocity of light in the polymeric material.12 It is an important optical property as it is directly associated with additional fundamental properties such as other optical, electrical, and magnetic properties.13 For example, specific refractive index increment in light scattering is an essential factor that can be used for the determination of molecular weight, size, and shape of a polymeric molecule.14 The knowledge of refractive indices of polymers is needed for understanding the behavior of polymers in the optical wavelength range and is extensively used to design optical devices in the industry. Over the last decades, high-refractive-index polymers have grabbed a considerable attention of scientific research community due to their wide range of applications, including advanced optoelectronic fabrications such as high-performance substrates for advanced display devices,15 optical adhesives or encapsulants for organic light-emitting diode devices,16 antireflective coatings for advanced optical applications,17−19 immersion lithography,20 microlens components for charge-coupled devices, complementary metal oxide semiconductor image sensors,21 optical data storage,22 lenses,23 ophthalmic applications,24 image sensors,25 optical fibers,26 integrated optics, and optoelectronics.27,28
Moreover, nanocomposites are related to a multiphase solid material made up of high-refractive-index organic polymer matrices and inorganic nanoparticles. They can easily attain a higher refractive index value above 1.80. These polymer nanocomposites have some demerits such as storage instability, high optical loss, and poor processability.29,30 The nanoparticle content and size inversely affect the shelf life and processability of nanocomposites, rendering them unstable and hence unsuitable for various applications.29 Therefore, researchers are synthesizing new organic polymers with higher refractive index values as these polymers would have various advantages such as easy storage, transport, tunability, and processability. In the present work, we have used an in silico method called quantitative structure–property relationship (QSPR) to predict the refractive indices of a diverse set of polymers.
QSPR31,32 is a quantitative method providing a mathematical relationship between different properties such as physical, chemical, and physicochemical properties with the information encoded in the chemical structure of molecules. A QSPR model is composed of dependent and independent variables. In the QSPR model, the dependent variable is estimated from the independent variables. Independent variables are molecular descriptors computed from the chemical structure of compounds, and the dependent variable is the endpoint of the study. A statistically significant and robust QSPR model can be obtained by the selection of relevant molecular descriptors and using a suitable statistical modeling technique.
In the past, several studies were reported to predict the refractive indices of polymers from their respective chemical structure using different statistical methods. Several efforts have been made using QSPR modeling to predict the refractive indices of polymers. For example, Bicerano33 reported a ten-descriptor model with a good determination coefficient of R2 = 0.954 using a set of 183 polymers. Katritzky et al.12 predicted the refractive index of a set of 95 polymers using software called Comprehensive Descriptors for Structural and Statistical Analysis; they developed a five-descriptor model with a correlation of R2 = 0.940. Xu et al.34 obtained a four-descriptor QSPR model using a set of 121 linear polymers with a correlation coefficient of R2 = 0.929 and mean relative error (MRE) of 0.87%. Astray et al.35 generated a model for prediction of refractive indices of diverse polymers using density functional theory (DFT) and obtained a model with a correlation coefficient of R2 = 0.92. Yu et al.36 also used DFT to compute quantum-chemical descriptors from repeating units of polymers and obtained a QSPR model with R2 of 0.926 and mean relative error (MRE) of 1.048%. Linear and nonlinear QSPR models with R2 = 0.94 and 0.97, respectively, were built by Xu et al.37 using a diverse set of 120 polymers, by employing the multilinear regression analysis and artificial neural network statistical techniques, respectively. Duchowicz et al.38 developed a single-descriptor model using the conformation-independent approach with a correlation coefficient of R2 = 0.96 from a set 234 polymers to predict refractive indices of polymers. Tong et al.39 developed a model using the multiple linear regression (MLR) approach from a 121 unconjugated polymer data set to predict the refractive indices and obtained a good correlation coefficient of R2 = 0.91. García-Domenech et al.40 developed a ten-descriptor model using the topological indices with correlation coefficient of R2 = 0.962.
Most of the previously reported models were developed using quantum-chemical descriptors, which are computationally demanding, requiring time-consuming and extensive computations. To overcome this problem, a two-dimensional (2D) QSPR approach based on constitutional and topological molecular descriptors of molecules can be applied.41,42 The developed model’s predictive ability can be improved by excluding three-dimensional-structural feature aspects, by avoiding the problems associated with ambiguities, resulting from an incorrect computational geometry optimization due to the existence of molecules in more than one conformational state. Small data sets of polymers or homologous series of polymers were involved in model development in many of the previous studies, leading to a small applicability domain (AD) of the developed models. Most importantly, none of the reported studies considers mixtures/copolymers for modeling of refractivity of polymers.
The purpose of the present work was to develop novel QSPR models to predict the refractive index from a set of diverse polymers including mixtures. In this work, we have developed models using only 2D descriptors that are effective, avoiding the computational complexity of energy minimization, conformational analysis, and alignment problems. We have used experimental refractive index values for a set of 221 diverse organic polymers including mixtures43 for model development. Subsequently, the validated individual models (IMs) were used for the generation of consensus models to improve the quality of external predictions. Finally, the selected consensus model was used to predict the refractive indices of various classes of virtual polymers. In this study, we have screened four small virtual libraries of monomers previously designed by Jabeen et al.44 and one small library of monomers designed by current authors. The refractive indices of novel monomers were predicted using the newly developed consensus QSPR models.
Result and Discussion
QSPR Modeling of the Refractive Index
The data set used for the present QSPR modeling of the refractive index of a diverse set of polymers comprises 221 data points obtained from the Scientific Polymer Products, Inc.43 These polymers consist of repeating units (monomers); due to the presence of a number of repeating units, polymers have a large size and complex nature as well as a higher molecular weight. Because of the large overall structure of polymers, it is quite difficult to calculate the molecular descriptors directly from the polymer molecules. Hence, only single monomeric units end-capped with hydrogen were used to drive the descriptors.45
The data set of 221 diverse polymers was split into a training set and a test set by the Kennard–Stone method46 using the software tool Dataset Division version 1.2 (http://teqip.jdvu.ac.in/QSAR_Tools/DTCLab/). The training set consisting of 154 polymeric compounds (ntraining = 154) was used to develop the model, and the test set comprising 67 compounds (ntest = 67) was used for external validation of the model. In the current studies, the final statistically most convincing and robust models for a set of diverse polymers were obtained by double cross-validation (DCV)47 followed by partial least squares (PLS).48 We have four best models developed using the same training set with a different combination of descriptors to predict the refractive indices of polymers. These four PLS48 models were developed using three, four, three, and three latent variables (LVs), respectively, which contained the extracted information from the descriptors appearing in the individual models. Each of the final four models with a different combination of descriptors to predict refractive indices of diverse polymers contains six descriptors, obtained from Dragon49 and PaDEL-Descriptor50 software, as depicted in Table 1. However, Figure S1 in the Supporting Information provides scatter plots of four individual models obtained from observed and predicted values of the training and test sets. The finally selected models were satisfactory in terms of all of the internal as well as external validation metrics including mean absolute error (MAE)-based criteria51 and Golbraikh and Tropsha’s criteria,52 proving the significance of the models. Table S1 in the Supporting Information lists the diverse organic polymers and their experimental refractive values, transformed logarithmic values, and predicted refractivity obtained from four individual models.
Table 1. Detailed Results of Various QSPR Modeling Studies of the Refractive Indices for Diverse Polymers (221 Data Points, Ntraining = 154, Ntest = 67).
The obtained models possess acceptable values for internal as well as external validation metrics.32 The complete list of values of validation parameters of all of the four DCV-PLS models is depicted in Table 1, which proves reliability and statistical significance of all of the four QSPR models.
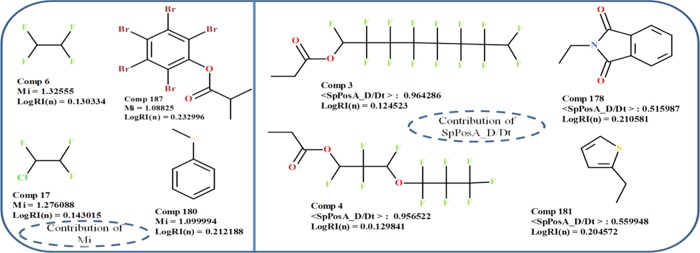
Mi stands for a mean first ionization potential (scaled on a carbon atom), and it belongs to the category of constitutional descriptors. The first ionization potential is defined as the amount of energy required to remove one valence electron from a neutral atom, and it is an atomic property that reflects the outermost electronic configuration and provides information on the binding energy of valence electrons and therefore also on the degree of relativistic stabilization.53 This descriptor negatively contributes to the refractive index of polymers in all of the obtained QSPR models, which means that the higher the value of the descriptor, the lower the refractive index and, in contrast, the lower the value of the Mi descriptor, the higher the refractive index. We can see from the data set that the compounds with higher values of descriptor (#6, 3, 17, 7, and 4) showed low refractive index (Figure 1). Molecule 6 (poly(tetrafluoroethylene)) has a high value of descriptor due to the presence of fluorine atoms; fluorine has a dense electron cloud in its valence shell since the outer shell electrons in fluorine are closer to the nucleus, and it takes more energy to remove the electrons from the fluorine atom, which ultimately results in the high first ionization potential. This consequently contributed to a low refractive index value of the corresponding polymer. On the other hand, molecules with low values of the descriptor (#187, 225, 222, 180, and 227) showed a high refractive index.
Figure 1.
Contributions of Mi and SpPosA_D/Dt descriptors to the refractive index of diverse polymers.
SpPosA_D/Dt represents the normalized spectral positive sum from the distance/detour matrix; it is estimated by the ratio of the sum of the positive eigenvalues obtained from the distance/detour matrix to the number of non-H atoms in the molecule.54 This descriptor showed a negative contribution to the refractive index of polymers, and it occurs in three obtained QSPR models (1, 3, and 4). The negative coefficients of the SpPosA_D/Dt descriptor suggest that an increase in the value of descriptor would lead to a decrease in the refractive indices of compounds and vice versa. The polymers with a comparatively high value of descriptor (#3, 4, 7, 29, and 67) showed low refractive indices (Figure 1). In comparison, the polymers with low values of descriptors (#186, 73, 207, 176, and 181) show high refractive index values.
MLFER_E is a molecular linear free energy relation (MLFER) descriptor, which refers to the excessive molar refraction that characterizes the solute’s polarizability as well as providing information about the ability of a solute to interact with a solvent through n- and π-electron pairs.55−57 In simple words, the excess molar refraction can be defined as the difference between the solute molar refraction and the molar refraction of an alkane with the same characteristic volume. Equations 1–4 indicate that the MLFER_E descriptor shows a positive contribution to the refractive index of polymers, which means that a polymer molecule having higher values for the MLFER_E descriptor tend to have a higher refractive index value. This is actually observed in the data set that the molecules with high values of MLFER_E descriptors (#224, 225, 222, 187, and 186) show high refractive index values and the polymers with low values of the descriptor (#3, 4, 7, 5, and 8) exhibit low refractive values (Figure 2). The low values of the descriptor occur in the case of, for example, the presence of fluorine atoms in the monomeric unit. Compound 3 (poly(pentadecafluorooctyl acrylate)) having a low value of the descriptor due to the presence of fluorine atoms into its structure shows a low refractive index value because of low electronic polarizability of the carbon–fluorine bond and the presence of greater fractional free volume in polymer chain packing.58,59
Figure 2.
Contributions of MLFER_E and B01[O–Si] descriptors to the refractive index of diverse organic polymers.
B01[O–Si] (presence/absence of O–Si at topological distance 1) belongs to the class of 2D atom pair (ap) descriptors, and it is calculated based on the distance between the pair of atoms.60 In the original atom pair (ap), “atom type” includes element, number of neighbors, and number of π electrons and the distance is measured in bonds along the shortest path. The descriptor B01[O–Si] indicates a topological distance between the pair of oxygen–silicon atoms of one edge, which provides information on the distribution of atomic properties along the topological structure. This descriptor is found in all obtained QSPR models with negative contributions to the refractive index of polymers, suggesting that the presence of the O–Si atom pair at topological distance 1 (as in #19, 20, 29, 30, and 31) leads to lower refractive index values (Figure 2). On the other hand, high refractive index is observed in the absence of the O–Si atom pair at a distance of one edge (#187, 186, 184, 227, and 182).
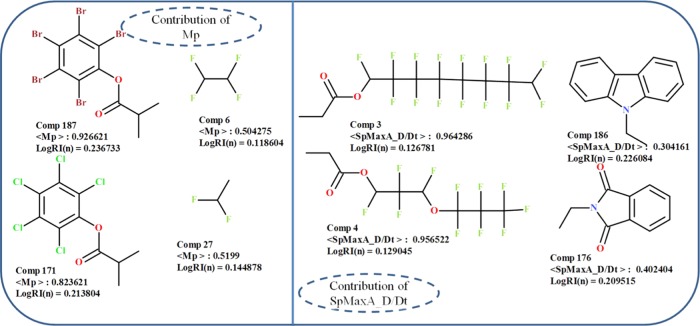
Mp is a constitutional descriptor, which stands for mean atomic polarizability, calculated as the mean of all atomic polarizabilities scaled over the carbon atoms. It describes the response of electron cloud to an external field of atom or molecules.61 The atoms with least electronegativity and a wider covalent radius have the maximum average atomic polarizabilities and vice versa. The average atomic polarizabilities of atoms decrease in the following manner: I, Br, S, P, Cl, C, N, O, F, and H.62 In the obtained QSPR models 1 and 3, the occurrence of Mp suggests that an increase in the polarizability of the molecules resulted in enhanced refractive index values of polymers and a decrease in the polarizability of polymers leads to low-refractive-index polymers. The compounds with high Mp values (#187, 171, 180, 19, and 121) showed a high refractive index, whereas the compounds with low Mp values (#73, 6, 42, 27, and 56) showed low refractive index of polymers (Figure 3). Molecule 187 (poly(pentabromophenyl methacrylate)) showed a high polarizability value due to the presence of a less electronegative atom, i.e., bromine, in the chemical structure. In contrast, molecule 6 (poly(tetrafluoroethylene)) showed low polarization because of the presence of a highly electronegative atom, i.e., fluorine in its chemical structure.
Figure 3.
Contributions of Mp and SpMaxA_D/Dt descriptors to the refractive index of diverse organic polymers.
B01[C–F] also belongs to the class of 2D atom pair descriptors; it represents presence/absence of C–F at topological distance 1.60 According to the QSPR eq 1, the absence of pair of carbon and fluorine at topological distance one would lead to an increase in the refractive index of polymers, and the presence of C–F atom pair at topological distance one result into the low value of refractive indices because of low electronic polarizability of carbon–fluorine bond and presence of greater fractional free volume in polymer chain packing. The compounds with the absence of a pair of these atoms at the stated distance 1 (#180, 225, 224, 186, and 222) are found to be with high refractive index values than the compounds with the presence of C–F atom pair at a distance 1 (#45, 26, 23, 24, and 28). From this observation, we can conclude that a decrease in the polarizability leads to a decrease in the refractive index of a polymer.
SpMaxA_D/Dt belonging to the class of 2D matrix-based descriptors accounts for normalized leading eigenvalue from the distance/detour matrix.63 The distance/detour matrix is derived from detour and distance matrices. It is a square symmetric matrix, whose off-diagonal entries are the ratios of the lengths of the shortest over the longest path between any pair of vertices. These descriptors convey the information about the molecular branching and cyclicity of the molecules. In the current QSPR eq 2, this descriptor was found to be negatively correlated with the refractive index of polymers, suggesting that for lower values of the descriptor the refractive index will be high and vice versa. For example, polymers with low values of this descriptor (#186, 176, 73, 100, and 225) showed a high refractive index (Figure 3). The repeat unit of polymer molecule 186 (poly(N-vinyl carbazole)) contained an aromatic heterocyclic ring (carbazole), which shows a low value of the descriptor due to the greater longest path between the pair of vertices. On the other hand, the polymers with high values of SpMaxA_D/Dt descriptor (#3, 4, 67, 7, and 29) showed low refractive index values. For example, the monomeric unit of polymer molecule 3 (poly(pentadecafluorooctyl acrylate)) shows a high value of the descriptor, which corresponds to a low refractive index due to the presence of too many numbers of branching vertex in the molecule, leading to the shorter longest path between a pair of vertices.
nCIC stands for the number of rings (cyclomatic number), and it belongs to a category of ring descriptors.60 It provides a numerical value about the presence of the ring in a molecule and is derived using the Euler formula
In the above equation, μ is a cyclomatic number and B and A are the total numbers of bonds and atoms, respectively. Equation 2 shows that nCIC has a negative contribution to the refractive index, suggesting that a higher value of the descriptor leads to a higher refractive index and vice versa. The molecules with higher descriptor values include 163, 217, 127, and 216 due to the presence of a number of rings in the molecular structure, and they showed low refractive index values. On the other hand, molecules with low values of the descriptor (#170, 220, 130, 129, and 128) due to the absence of ring in the molecular structure showed high refractive index values.
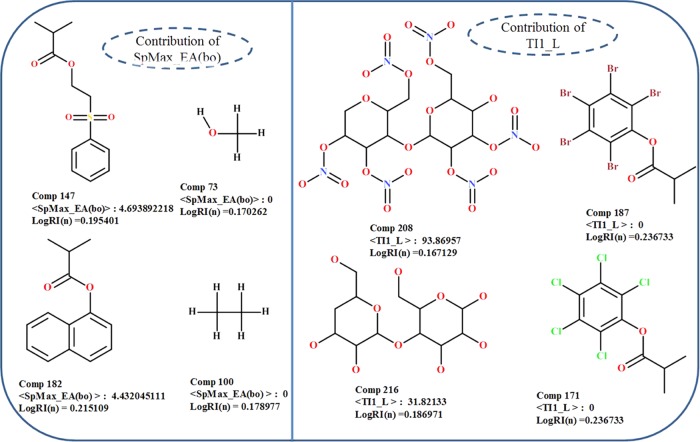
The SpMax_EA(bo) descriptor, an edge adjacency indices descriptor,64 accounts for the leading eigenvalue from the edge adjacency matrix weighted by bond order, and it encodes the connectivity between graph edges. SpMax_EA(bo) reflects the molecular shape, and it implies the substituent position in the phenyl ring of the polymer material; the substitution at the p- or α-position of the phenyl or naphthalene ring has a larger value of SpMax_EA(bo), and substituents at the o- or β-position lead to a lower value of the descriptor. This means that substitution at the o- or β-position of the phenyl or naphthalene ring, respectively, leads to a decrease in refractive index values. In QSPR eq 2, this descriptor contributes positively to the refractive index, as can be found from the data set that polymers with high values of the SpMax_EA(bo) descriptor (#147, 182, 171, 187, and 179) have high refractive index values, in contrast to the molecules with low descriptor values (#73, 100, 19, 35, and 125) having low refractive index values (Figure 4).
Figure 4.
Contributions of SpMax_EA(bo) and TI1_L descriptors to the refractive index of diverse organic polymers.
TI1_L, described as the first Mohar index from the Laplace matrix, belongs to the class of 2D matrix-based descriptors.65,66 The Laplace matrix (L) is a symmetrical matrix estimated from the difference between the adjacency matrix and the vertex degree matrix; therefore, the diagonal entries of the matrix are vertex degrees of atoms in a molecule and off-diagonal entries representing the pairs of bonded atoms are set at −1, otherwise at 0. The first Mohar index (TI1_L) is calculated from the eigenvalues of the Laplacian matrix as follows
In the above equation, QW_L is the quasi-Wiener index and nBO and nSK are the numbers of non-H bonds and non-H atoms in the molecules. In the currently studied QSPR model (3), the TI1_L descriptor is inversely correlated with refractive indices of polymers, showing that a greater value of the descriptor (#208, 216, 157, and 14) leads to a lower-refractive-index polymer (Figure 4). Compounds with lower values of the TI1_L descriptor (#187, 171, 180, 181, and 178) showed high refractive index values.
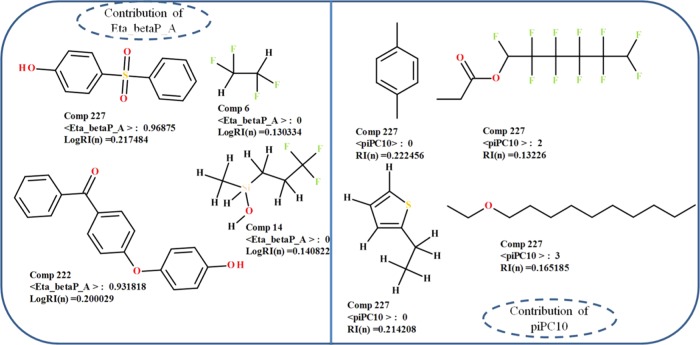
Eta_betaP_A is defined as the sum of β values of all nonhydrogen bonds including a lone pair of electrons involved in the resonance of a structure relative to a number of vertices in the molecule.67 It describes the electron-richness of molecules relative to the molecular size and the presence of multiple bonded electronegative atoms like O, S, etc.68 In the present QSPR eq 4, Eta_betaP_A has a positive coefficient. This reflects that the Eta_betaP_A descriptor is directly proportional to refractive indices of diverse polymers. The compounds with high values of this descriptor (#186, 222, 224, 225, and 227) showed a high refractive index (Figure 5) due to the presence of lone pairs of electrons involved in the resonance of the aromatic ring system in their chemical structure in comparison with the compounds with low values of descriptors (#7, 14, 17, 19, and 20).
Figure 5.
Contributions of Eta_beta_A and piPC10 descriptors to the refractive index of diverse organic polymers.
piPC10, a topological descriptor, stands for molecular multiple path count of order 10. It describes size, shape, symmetry, and atom distribution in a molecule.69 In our QSPR eq 4, the appearance of the piPC10 descriptor might indicate the size of polymers, and it correlates negatively with the refractive indices of polymers. This suggests that the polymers with high values of the descriptor (#7, 47, 37, 63, and 29) due to the larger size of monomers lead to low refractive indices in comparison of the compounds with lower values of the descriptor (#184, 181, 180, 178, and 172) (Figure 5)
Importance and Ranking of Variables in Different QSPR Models
In the present study, we have reported four individual QSPR models for prediction of refractive index with a different combination of descriptors. A repetition of some molecular descriptors in different models simply describes their importance in terms of their contribution to the response. Each final model has at least one or two different descriptors not present in other models; in this way, all four models covered all of the necessary features for QSPR model generation for refractive index prediction. Some variables are consistently repeating in all of the models, showing that these descriptors have impact on the response modeled and are vital for the model development.
To rank the variables based upon their importance in the obtained QSPR models, we derived the variable importance plot (VIP) by considering various parameters such as the classical PLS regression coefficient, weight vector, and t-statistic cutoff threshold.70 The VIPs of four individual models are depicted in Figure S2 in the Supporting Information. The VIP summarizes the importance of each descriptor presented in the obtained QSPR equations based on the score and loading plot observations. The VIP reflects the importance of descriptors in the model with respect to the Y variable (correlation with property) and X variable (projection). A variable with a score more than 1 shows more significance than the variables with low VIP scores. In the present work, we developed four individual QSPR models; we can see that the variable MLFER_E has the highest impact on the response in model 1 and Mi has the highest relative importance to the response in models 2, 3, and 4. The least important descriptor in all of the generated models is B01[O–Si].
Next, we have derived loading plots to find out the most influential variables in the obtained QSPR equations. The loading plots of four individual models are shown in Figure S3 in the Supporting Information. The variable MLFER_E is highly influential with a positive correlation toward the Y variable in model 1; at the same time, the variable Mi has been found to be the most influential variable in models 2, 3, and 4 with a negative contribution to the refractivity of polymers. In contrast, the variable B01[O–Si] with the least influence and with a negative correlation with the property is found in all of the obtained models.
In addition, it was shown that the final models were not obtained by chance (random) as evidenced from randomization plots (Figure S4 in the Supporting Information). A number of models are generated by shuffling the values of Y variables keeping the X variables intact. The new (random) models were generated using the permuted data, and the quality of such models was compared to that of the nonrandom models. Here, we have used 100 permutations. The value of the r2Y intercept should not exceed 0.3, and the value of the q2Y intercept should not exceed 0.05. The obtained models in the current study show the intercept at r2Y = −0.0157, q2Y = −0.173, r2Y = −0.0205, q2Y = −0.211, r2Y = −0.0171, q2Y = −0.174, and r2Y = −0.0245, q2Y = −0.187 (Figure 4), signifying the validity of the models. This proves that the finally selected models were nonrandom and robust.
AD Studies of All Individual QSPR Models for Refractive Index Prediction
The final assessments of the developed models were done by defining the applicability domain (AD) of obtained models using the distance to model in the X-space (DModX) approach using SIMCA-P57 software. The compounds in the training set outside this domain were considered as outliers, and the compounds in the test set having DModX values greater than the threshold value are called outside AD. The list of compounds that are outliers and outside of AD in different models is depicted in Table 2.
Table 2. List of Compounds That Are Outliers and Outside AD in Different QSPR Models.
| model no. | training set (outlier) | test set (outside AD) |
|---|---|---|
| model 1 | poly(oxymethylene), polyethylene, poly(N-vinyl carbazole), poly(pentabromophenyl methacrylate), polysulfone resin. | |
| model 2 | polysulfone resin | |
| model 3 | poly(tetrafluoroethylene), poly(methyl 3,3,3-trifluoropropyl siloxane), poly(chlorotrifluoroethylene), poly(vinylidene fluoride), poly(2-bromo-4-trifluoromethyl styrene), poly(N-vinyl carbazole), cellulose nitrate, cellulose, polysulfone resin. | poly(hexafluoropropylene oxide), poly(2-vinylnaphthalene) |
| model 4 | poly(methyl hydrosiloxane), poly(dimethylsiloxane), poly(methyl octadecylsiloxane), poly(methyl hexylsiloxane), poly(methyl octylsiloxane), poly(methyl hexadecylsiloxane), poly(methyl tetradecylsiloxane), poly(acryloxypropyl methylsiloxane), poly(dicyanopropylsiloxane), poly(mercaptopropyl methylsiloxane), poly(methyl phenylsiloxane), poly(methyl m-chlorophenylethylsiloxane), poly(dimethylsiloxane-co-diphenylsiloxane) | poly(methyl m-chlorophenylsiloxane) |
After analysis of AD of the QSPR models, the coverage of models 1 and 2 was 100% in the case of the test set (Figure S5 in the Supporting Information), but the training set (Figure S6 in the Supporting Information) has five and one structural outliers, respectively, although their prediction quality is good. In the case of model 3, the training set has nine outliers and two compounds outside the AD in the test set while it is found that the prediction quality of the compounds outside AD is good. Model 4 shows that 13 compounds are outliers in the training set (all of them belong to the class of polysilylenes, and the descriptors obtained in the model do not cover the chemical features of this class of compounds) and one compound is outside the AD in the test set; however, all of these compounds have excellent prediction quality.
Intelligent Consensus Prediction (ICP) for Refractive Indices of Polymers
In this study, the data set of 221 diverse polymers was divided into a training set (154 compounds) and a test set (67 compounds). Then, we have used the derived four models for application of the Intelligent Consensus Predictor (http://teqip.jdvu.ac.in/QSAR_Tools/DTCLab/) with an objective to improve the quality of predictions. We have compared the results of predictions from individual models (IMs) with those four consensus models (CM0–CM3). The analysis shows that values of external validation metrics are better in consensus models, particularly CM0, than in IM models. In addition, based upon the MAE95% metric, three consensus models (CM0, CM1, and CM2) possess significantly lower error values than the IM.
True External Set Predictions
For QSPR modeling, in general, the whole data set is divided into training and test sets prior to model building; during this step, it is ensured that each compound of the test set has a few similar structural analogues in the training set and the test set is used to determine the predictive capability of the developed model. However, the compounds in the true external set are not designed to be similar to the training set compounds and they are used as an unseen data set (not employed while modeling) to determine the external predictive quality of the model. To validate the predictive ability of generated individual models, we also used a true external data set of 98 diverse monomer units with the experimental RI values of the corresponding polymers.38Table S2 in the Supporting Information lists the true external set polymers and their experimental refractive values, transformed logarithmic values, and predicted refractivity obtained from four CM3 models. The derived models showed good predictive ability, as evidenced from the very good external predicted variance. Also, the corresponding values of rm2 metrics imply the accuracy of predictions of all of the individual models. Furthermore, we have applied consensus models obtained from the individual models using the Intelligent Consensus Predictor tool (http://teqip.jdvu.ac.in/QSAR_Tools/DTCLab/) with an objective to improve the quality of predictions. Finally, we have compared the results of predictions from individual models (IMs) with those from four consensus models (CM0–CM3). The values of external validation metrics of the individual as well as consensus models are depicted in Table 3.
Table 3. Summary of External Prediction Quality (Based on MAE100%) of Individual and Consensus Models for the True External Data Seta.
| model no. | Rpred2 | Rpred(95%)2 | rm2 | Δrm2 | MAE100% | MAE95% |
|---|---|---|---|---|---|---|
| IM1 | 0.867 | 0.918 | 0.819 | 0.044 | 0.006 | 0.005 |
| IM2 | 0.884 | 0.936 | 0.831 | 0.022 | 0.006 | 0.005 |
| IM3 | 0.878 | 0.929 | 0.826 | 0.003 | 0.006 | 0.005 |
| IM4 | 0.878 | 0.931 | 0.827 | 0.011 | 0.006 | 0.005 |
| CM0 | 0.887 | 0.931 | 0.839 | 0.001 | 0.006 | 0.005 |
| CM1 | 0.887 | 0.931 | 0.839 | 0.001 | 0.006 | 0.005 |
| CM2 | 0.889 | 0.933 | 0.841 | 0.006 | 0.006 | 0.005 |
| CM3 | 0.895 | 0.940 | 0.847 | 0.017 | 0.005 | 0.005 |
The best model based on the MAE100% is shown in bold.
After analysis of the results from four IMs (IM1–IM4) and the corresponding four generated consensus models (CM0–CM3), it was evident that the results of external validation metrics of consensus models were better than those of the individual models. Considering the external predicted variance (Rpred2) and MAE100% metrics, consensus model 3 was found to have considerably higher predictive ability and lower error values than those of the other ones.
After the complete analysis of the results obtained from the true external data set, we can conclude that prediction errors for the external set compounds can be dropped significantly using the “intelligent” consensus prediction models, and, particularly, CM3 appears to be most useful and reliable among all of the developed consensus models.
Additionally, the quality of predictions for external compounds from the finally selected individual QSPR models has been checked using the “Prediction Reliability Indicator” software tool.76 This tool generates the prediction quality composite score, and on the basis of the obtained score, it categorizes the quality of predictions into three different classes, that is, good (score 3), moderate (score 2), and bad predictions (score 1) (Table S3 in the Supporting Information). The results show that most of the predictions are of good quality.
Virtual Screening of the Obtained Library of New Monomeric Units of Polymers
Four sets of small virtual libraries of monomers designed by Jabeen et al.44 were screened using the generated consensus model CM0 to predict the refractive index of designed monomers. We have then compared the predicted refractive indices obtained from consensus model CM0 with the predictions reported in the previous work. The monomers of four different libraries were sorted out on the basis of predicted refractive index values (high to low), and top 25% compounds (24 compounds) from individual libraries with the higher predicted refractive indices were selected for comparison with the top 25% predicted values from the model reported by Jabeen et al. It was found that 21 compounds (out of 24 compounds from each set) were common in the sorted lists from both models.
Virtual Screening of the Designed Library of New Monomeric Units of Polymers
We have also designed a virtual monomer library of 91 compounds using the basic chemistry knowledge. The two basic scaffolds selected for the design of library are (poly(2-vinylthiophene) (n = 1.6376) and poly(phenyl α-bromoacrylate) (n = 1.612). The selected core was substituted by various functional groups (halogen, nitro, carboxy, etc.) to form a library of novel monomers. The structure of monomers was drawn and optimized using Marvin Sketch (version 14.10.27) (https://www.chemaxon.com) software, and, finally, the refractive index values of the designed monomer library were predicted using the generated models.
Comparison with a Previously Developed RI Model
Next, we compared our results with those of the previous study carried out by Jabeen et al.,44 where authors have reported a QSPR model for the prediction of refractive indices (n) in a diverse set of organic polymers. They developed models by the genetic algorithm (GA)–MLR statistical technique, which gave reliable predictions of the refractive index. To obtain the model, they have used the data set of 133 diverse polymers and the data set was divided randomly into a training set and a test set. During the initial step of model development, they have marked six molecules as outliers, which were removed. The final statistically reliable model was developed using the set of 98 training compounds and validated by 29 test compounds. The final model for prediction of refractive indices had four variables obtained from Dragon software, and the model quality was as follows: R2 = 0.932, QLOO2 = 0.914, and the Rext2 for the test set was found to be 0.882. Also, the final selected model is used to predict the refractive index of four small virtual libraries. Several structures from each set of virtual libraries were reported to have high values of predicted refractive indices.
In the present study, we have collected a larger data set and developed several models for refractive index using the double cross-validation approach followed by PLS,48 from an extended list of diverse polymers offering a broader applicability domain. The extended data set comprised 221 diverse polymers. The data set was split into a training set and a test set using the Kennard–Stone method. The training set (Ntrain = 154) was used to develop the models, and the test set (Ntest = 67) was used for external validation. The final statistically most convincing and robust model for prediction of refractive indices was obtained by double cross-validation (DCV) followed by PLS.48 The final model for diverse polymers including some mixtures had six 2D descriptors, obtained from Dragon and PaDEL-Descriptor software, and the model quality was as follows: R2 = 0.911, QLOO2 = 0.902, and Rpred2 for the test set was found to be 0.893. We have used the final selected model for the prediction of the refractive index of four small virtual libraries of monomers designed by Jabeen et al.44 and finally compared the predictions of refractive indices from our model with previously reported model predictions. The monomers were sorted out on the basis of higher refractive index predictions, and 25% of compounds (24 compounds) with the higher predicted refractive indices (in either set) were selected for comparison. It was found that 21 compounds (out of 24 compounds from each set) were common in the sorted lists from both models. Furthermore, when multiple models were used for application of the Intelligent Consensus Predictor (http://teqip.jdvu.ac.in/QSAR_Tools/DTCLab/), the quality of external predictions was further improved.
Conclusions
We developed four individual QSPR models with six different combinations of variables using a diverse set of polymers with significant predictive power. All of the internal as well as external validation parameters were examined to confirm the quality, significance, robustness, and high predictive ability. To determine the predictive ability, we have used a true external set that shows the good predictive ability of models. Furthermore, to improve the quality of prediction of the external set, we have generated consensus models from the obtained multiple models. Finally, the selected consensus model was used for screening of a small set of virtual design libraries.
From the presented work, we have found out that a number of different variables play an essential role to predict the refractive index of diverse polymers. These variables encode information to predict the refractivity of polymers. The descriptors SpMaxA_D/Dt and Eta_betaP_A suggest that the presence of the aromatic ring in monomers increases refractivity. The descriptor SpMax_EA(bo) implies the substituent position in the phenyl ring of the polymer material; the substitution at the p- or α-position of the phenyl or naphthalene ring has a larger value of SpMax_EA(bo), and substituents at the o- or β-position lead to a lower value of the descriptor. The Mi descriptor shows that a higher mean ionization potential caused an increase in the refractivity of polymers. The MLFER_E and Mp descriptors, which are polarizability-weighted, show that the increase in the polarizability value increases the refractivity index. Furthermore, the F01[C–F] and B01[O–Si] descriptors confirm that the number of C–F groups and the number of O–Si groups, respectively, would lead to a decrease in the refractivity index of the investigated polymers. Finally, the presence of piPC10 descriptor confirms the importance of the size of monomeric units.
Also, we have screened five small virtual libraries of monomers encompassing one small library of monomers designed by us and four designed by Jabeen et al.44 and then predicted their respective refractive indices by utilizing the developed models. Various monomers from each set of small libraries predicted higher refractive index values as compared to those from polymers used in the original data set. By using the approaches used in this study, a suitable number of polymers with higher refractive index values can be developed and transformed into the new, stable, easy-to-handle, and processable novel polymers for different applications in materials or optical science such as new optical devices, lenses, etc.
Materials and Methods
The data set of 221 diverse polymers was employed for the development of QSPR models for prediction of refractive index values. The data set includes nine mixtures/copolymers in a particular ratio of monomers (%). The experimental refractive index (n) values of polymers were obtained from the Scientific Polymer Products, Inc.43Figure 6 depicts the summary of the applied methodology in the present work.
Figure 6.
Work flow diagram of the used methodology.
After gathering experimental data and selection of the data set, the data were further carefully checked to remove duplicate compounds. For ease of estimation and interpretation, the experimental refractive index values were converted into the logarithmic scale, i.e., log(n). A lower value of log(n) represents a lower refractive index and vice versa. The data set used is diverse, which comprises various classes of organic polymers such as polyolefins, polysilylenes, polyimides, polyamides, polyacrylates, and polyesters.
Chemical Structures and Molecular Descriptors
The chemical structures of monomers or repeating units, end-capped with hydrogen, were drawn using Marvin Sketch (version 14.10.27) (https://www.chemaxon.com) software. The structures were saved as .sdf format, which is the recommended input format for PaDEL-Descriptor50 and Dragon49 Descriptor software. We may mention here that QSPR modeling was done in this work using 2D descriptors that are estimated from the monomeric unit of polymers. The calculated descriptors contained the information related to the topology of the monomer unit. Although the monomeric unit is not capable of accounting the overall molecular topology of polymers, it provides important information for model building. On the other hand, use of the whole polymer structure is difficult and a challenging job because of the large size of polymer molecules, complex structure, and high molecular weight; it is difficult to estimate molecular descriptors from the entire polymer structure.
Calculation of Descriptors for Mixtures/Copolymers
To calculate the descriptors from copolymers/mixtures, we have used both monomer units of copolymers individually for the estimation of descriptors, and then the obtained descriptor values from individual monomers were multiplied by their percentage ratio present in the copolymers and finally added together to get the final descriptor values for copolymers/mixtures. For example, in the case of the ethylene/vinyl acetate copolymer (28% vinyl acetate), we have calculated the descriptors from ethylene and vinyl acetate monomers individually; then, descriptor values of ethylene were multiplied by 0.72 and those of vinyl acetate with 0.28 and finally both values were added to obtain the descriptors for the ethylene/vinyl acetate copolymer.
In the present study, to obtain the QSPR models, a wide range of molecular descriptors (2D) were used that included 2D matrix-based descriptors, 2D atom pairs, constitutional indices, ring descriptors, connectivity indices, functional group count, atom-centered fragments, atom type, CATS2D descriptor, E-state indices calculated from Dragon49 software version 7, and also the extended topochemical atom and the MLFER descriptor calculated by the PaDEL-Descriptor50 (version 2.21).
Tuning of the generated initial pool of descriptors was carefully done by removing the descriptors with constant and near-constant values or zero values, descriptors with at least one missing value, descriptors with all missing values, and descriptors with (absolute) pair correlation larger than or equal to 0.90.
QSPR Modeling
Division of the Data set
The data set of 221 diverse polymers was divided into a training set (∼70% of compounds) and a test set (∼30% of compounds) using the Kennard–Stone method46 using the software tool Dataset Division version 1.2 available at http://teqip.jdvu.ac.in/QSAR_Tools/DTCLab/. The training set was used for model development and the test set for external validation. The test set compounds were not included at all in the model development stage to select the descriptors.68
Variable Selection and Model Development
Further descriptor selection has been done by employing a genetic algorithm (GA)71 method. GA71 is based on a genetic evolution principle where at the first step a random population of models is generated, and parents are selected for mating based upon the fitness score of the individual models. In later generations, the parents are replaced by daughter models and the fitness of the new model is checked; the process continues until it gets the best set of descriptors in that run. In our work, the process was repeated several times to find the best correlating descriptors. Finally, the selected descriptors (35 descriptors out of an initial pool of 1730 descriptors) were subjected to the double cross-validation (DCV) tool47,51 followed by partial least squares (PLS) regression48 to obtain the optimum models for the prediction of the refractive index of polymers. The DCV tool algorithm is based on two nested loops that are internal and external cross-validation loops. In the outer loop, the data set is divided into training and test sets. In the inner loop, the training set compounds used for model development and model selection were repeatedly split into calibration (used for model development) and validation (to estimate the error) data sets. Finally, the model with the least prediction error was selected from the inner loop. Then, the test set that was present in the outer loop was used for assessing the predictive performance of the selected models.47,51 Finally, four statistically most convincing and robust models with different sets of descriptor combinations were derived.
Model Validation
Validation of the obtained QSPR models was performed by analyzing the various statistical parameters of internal stability and the external prediction, according to the OECD principles for QSAR validation.72 The values of determination coefficients indicate the goodness of fit; other internal validation parameters of models were determined on the basis of leave-one-out (LOO) cross-validation. The external predictive power of models was estimated using the test set. The reported validation metrics included Rtrain2, LOO-Q2 for the training set, and Rpred2 for the test set predictions. However, these parameters were primarily based on the sum of squared differences between observed values of the training/test set compounds and the mean observed value of the training set compounds. Thus, to avoid bias in the predictive potential of models, we have additionally reported rm2 metrics73 such as rmLOO, ΔrmLOO2, rmtest, and Δrmtest2 proposed by Roy et al. Finally, the mean absolute error (MAE)-based criteria proposed by Roy et al.51 and Golbraikh and Tropsha52 criteria were examined to justify the robustness of reported models.
Applicability Domain (AD) Studies
To define the AD of the generated models, we used the distance to model in the X-space (DModX) approach using SIMCA-P74 software. In this case, the quality of the model has been judged on the basis of the X residual values.48 In general, X residual values are high in numbers, so the X residual was abstracted by SD of the X-residuals of the corresponding row of the residual matrix. The SD of X-residuals is directly linked to the distance between each data point and the model plane in X-space, often called DModX (distance to the model in X-space). Molecules having the DModX values higher than the critical value are outliers (training set)/outside of AD (test set) of the model.48
Intelligent Consensus Refractive Indices’ QSPR Modeling of Polymers
Consensus models were generated by integrating all validated individual models by application of the Intelligent Consensus Predictor tool (http://teqip.jdvu.ac.in/QSAR_Tools/DTCLab/) to improve the quality of external predictions.75 A consensus model covers different issues such as all features of the chemical structure of training set compounds in large descriptor space from all of the individual models as well as a vast applicability domain (the consensus method can also afford greater chemical space coverage) in comparison of individual models (IMs). Consensus models can improve the prediction quality for test set compounds in contrast to IM. The approach of Intelligent Consensus Predictor (ICP) is based on a similarity principle to identify the best model for the prediction of test compounds. In this method, at the first step, 10 most similar training compounds are selected for each test set compound. In this way, every generated model contained 10 similar compounds for each test set compound. Note that the selected 10 compounds should not to be outliers in terms of chemical structure similarity. The selection of 10 training set compounds is made on the basis of the criteria that the Euclidean distance of the test set compound to a particular training set compound out of those 10 selected ones is not higher than the set threshold value. The threshold value is obtained from the mean Euclidean distance plus 3 times standard deviation (SD) (threshold = mean + 3 × SD), which is estimated from the Euclidean distance scores of the entire training set compounds using descriptor values present in the particular model. The threshold value for each test compound might be different for different models. Finally, “n” number of qualified models were obtained with acceptable specified criteria and can be further compared with the predictive performance of IM. In ICP, three different ways of consensus predictions were integrated including (1) consensus model 0 (original consensus): average of predictions from all individual input models, (2) consensus model 1 (CM1): average of predictions from all qualified individual models, (3) consensus model 2 (CM2): weighted average prediction from all qualified individual models, and (4) consensus model 3 (CM3): best selection of predictions (compoundwise) from individual models.75 The finally selected consensus models were used for the screening of the external set (and designed libraries of monomers).
Virtual Screening of a Designed Library of New Monomeric Units of Polymers
Four sets of small virtual libraries of monomers were introduced by Jabeen et al.44 by selecting a scaffold of two polymers poly(N-vinyl carbazole) (n = 1.683) and poly(pentabromophenyl methacrylate) (n = 1.71). The library was obtained by substitution of different functional groups to the two primary selected cores. The designed libraries were screened in the present work using the generated models to predict the refractive index of designed monomers, and predictions obtained from our models were compared to those of Jabeen et al. In this work, we have also designed a virtual monomer library of 91 compounds by substituting the various functional groups on the selected fundamental core of two polymers from the data set, i.e., (poly(2-vinylthiophene) (n = 1.6376) and poly(phenyl α-bromoacrylate) (n = 1.612). The refractive indices of the designed monomer library were predicted using the generated models.
Acknowledgments
P.M.K. would like to thank the Ministry of Chemicals & Fertilizers, Department of Pharmaceuticals, Government of India, and the National Institute of Pharmaceutical Education and Research-Kolkata (NIPER-Kolkata) for providing financial assistance in the form of a fellowship during this work. B.R. thanks National Science Foundation for the support under NSF ND EPSCoR Award No. IIA-1355466 and the State of North Dakota.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b01834.
(PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Coleman M. M.; Painter P. C.. Fundamentals of Polymer Science: An Introductory Text; Technomic Publishing Company Inc.: Pennsylvania, 1997; pp 412–413. [Google Scholar]
- Budd P. M.; Butler A.; Selbie J.; Mahmood K.; McKeown N. B.; Ghanem B.; Msayib K.; Book D.; Walton A. The potential of organic polymer-based hydrogen storage materials. Phys. Chem. Chem. Phys. 2007, 9, 1802–1808. 10.1039/b618053a. [DOI] [PubMed] [Google Scholar]
- McKeown N. B.; Budd P. M.; Book D. Microporous polymers as potential hydrogen storage materials. Macromol. Rapid Commun. 2007, 28, 995–1002. 10.1002/marc.200700054. [DOI] [Google Scholar]
- Germain J.; Fréchet J. M.; Svec F. Nanoporous polymers for hydrogen storage. Small 2009, 5, 1098–1111. 10.1002/smll.200801762. [DOI] [PubMed] [Google Scholar]
- McKeown N. B.; Budd P. M. Polymers of intrinsic microporosity (PIMs): organic materials for membrane separations, heterogeneous catalysis and hydrogen storage. Chem. Soc. Rev. 2006, 35, 675–683. 10.1039/b600349d. [DOI] [PubMed] [Google Scholar]
- Rose M. Nanoporous polymers: Bridging the gap between molecular and solid catalysts?. ChemCatChem 2014, 6, 1166–1182. 10.1002/cctc.201301071. [DOI] [Google Scholar]
- Du X.; Sun Y.; Tan B.; Teng Q.; Yao X.; Su C.; Wang W. Tröger’s base-functionalised organic nanoporous polymer for heterogeneous catalysis. Chem. Commun. 2010, 46, 970–972. 10.1039/b920113k. [DOI] [PubMed] [Google Scholar]
- Jiang K.; Fei T.; Zhang T. Humidity sensing properties of LiCl-loaded porous polymers with good stability and rapid response and recovery. Sens. Actuators, B 2014, 199, 1–6. 10.1016/j.snb.2014.03.047. [DOI] [Google Scholar]
- Jiang K.; Kuang D.; Fei T.; Zhang T. Preparation of lithium-modified porous polymer for enhanced humidity sensitive properties. Sens. Actuators, B 2014, 203, 752–758. 10.1016/j.snb.2014.07.020. [DOI] [Google Scholar]
- Li B.; Yang X.; Xia L.; Majeed M. I.; Tan B. Hollow microporous organic capsules. Sci. Rep. 2013, 3, 2128 10.1038/srep02128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davankov V.; Tsyurupa M. P.. Hypercrosslinked Polymeric Networks and Adsorbing Materials: Synthesis, Properties, Structure, and Applications; Elsevier, 2010; Vol. 56, pp 445–497. [Google Scholar]
- Katritzky A. R.; Sild S.; Karelson M. General quantitative structure–property relationship treatment of the refractive index of organic compounds. J. Chem. Inf. Model. 1998, 38, 840–844. 10.1021/ci980028i. [DOI] [Google Scholar]
- Knoll W. Interfaces and thin films as seen by bound electromagnetic waves. Annu. Rev. Phys. Chem. 1998, 49, 569–638. 10.1146/annurev.physchem.49.1.569. [DOI] [PubMed] [Google Scholar]
- Van Krevelen D. W.; Te Nijenhuis K.. Properties of Polymers: Their Correlation with Chemical Structure; Their Numerical Estimation and Prediction from Additive Group Contributions; Elsevier, 2009; pp 21–24. [Google Scholar]
- Nakamura T.; Fujii H.; Juni N.; Tsutsumi N. Enhanced coupling of light from organic electroluminescent device using diffusive particle dispersed high refractive index resin substrate. Opt. Rev. 2006, 13, 104–110. 10.1007/s10043-006-0104-8. [DOI] [Google Scholar]
- Liang J.; Li L.; Niu X.; Yu Z.; Pei Q. Elastomeric polymer light-emitting devices and displays. Nat. Photonics 2013, 7, 817. 10.1038/nphoton.2013.242. [DOI] [Google Scholar]
- Wang Y.-W.; Chen W.-C. Synthesis, properties, and anti-reflective applications of new colorless polyimide-inorganic hybrid optical materials. Compos. Sci. Technol. 2010, 70, 769–775. 10.1016/j.compscitech.2010.01.008. [DOI] [Google Scholar]
- Li X.; Yu X.; Han Y. Polymer thin films for antireflection coatings. J. Mater. Chem. C 2013, 1, 2266–2285. 10.1039/c2tc00529h. [DOI] [Google Scholar]
- Krogman K. C.; Druffel T.; Sunkara M. K. Anti-reflective optical coatings incorporating nanoparticles. Nanotechnology 2005, 16, S338. 10.1088/0957-4484/16/7/005. [DOI] [PubMed] [Google Scholar]
- Dammel R.; Houlihan F. M.; Sakamuri R.; Rentkiewicz D.; Romano A. 193 nm immersion lithography-Taking the plunge. J. Photopolym. Sci. Technol. 2004, 17, 587–601. 10.2494/photopolymer.17.587. [DOI] [Google Scholar]
- Chen Q.; Das D.; Chitnis D.; Walls K.; Drysdale T.; Collins S.; Cumming D. A CMOS image sensor integrated with plasmonic colour filters. Plasmonics 2012, 7, 695–699. 10.1007/s11468-012-9360-6. [DOI] [Google Scholar]
- Yetisen A. K.; Montelongo Y.; Butt H. Rewritable three-dimensional holographic data storage via optical forces. Appl. Phys. Lett. 2016, 109, 061106 10.1063/1.4960710. [DOI] [Google Scholar]
- Simmrock H. U.; Mathy A.; Dominguez L.; Meyer W. H.; Wegner G. Polymers with a high refractive index and low optical dispersion. Angew. Chem., Int. Ed. 1989, 28, 1122–1123. 10.1002/anie.198911221. [DOI] [Google Scholar]
- Mentak K.High Refractive Index Polymers for Ophthalmic Applications. US7,354,9802008.
- Yu G.; Srdanov G.; Wang J.; Wang H.; Cao Y.; Heeger A. J. Large area, full-color, digital image sensors made with semiconducting polymers. Synth. Met. 2000, 111–112, 133–137. 10.1016/S0379-6779(99)00327-6. [DOI] [Google Scholar]
- Zhou M. Low-loss polymeric materials for passive waveguide components in fiber optical telecommunication. Opt. Eng. 2002, 41, 1631–1644. 10.1117/1.1481895. [DOI] [Google Scholar]
- Liu J.-g.; Ueda M. High refractive index polymers: fundamental research and practical applications. J. Mater. Chem. 2009, 19, 8907–8919. 10.1039/b909690f. [DOI] [Google Scholar]
- Macdonald E. K.; Shaver M. P. Intrinsic high refractive index polymers. Polym. Int. 2015, 64, 6–14. 10.1002/pi.4821. [DOI] [Google Scholar]
- Jeon I.-Y.; Baek J.-B. Nanocomposites derived from polymers and inorganic nanoparticles. Materials 2010, 3, 3654–3674. 10.3390/ma3063654. [DOI] [Google Scholar]
- Li S.; Lin M. M.; Toprak M. S.; Kim D. K.; Muhammed M. Nanocomposites of polymer and inorganic nanoparticles for optical and magnetic applications. Nano Rev. 2010, 1, 5214. 10.3402/nano.v1i0.5214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dearden J. C. The history and development of quantitative structure-activity relationships (QSARs). Int. J. Quant. Struct.–Prop. Relat. 2016, 1–44. 10.4018/IJQSPR.2016010101. [DOI] [Google Scholar]
- Roy K.; Kar S.; Das R. N.. A Primer on QSAR/QSPR Modeling: Fundamental Concepts; Springer, 2015; pp 24–25. [Google Scholar]
- Bicerano J.Prediction of Polymer Properties; CRC Press, 2002; pp 321–340. [Google Scholar]
- Xu J.; Chen B.; Zhang Q.; Guo B. Prediction of refractive indices of linear polymers by a four-descriptor QSPR model. Polymer 2004, 45, 8651–8659. 10.1016/j.polymer.2004.10.057. [DOI] [Google Scholar]
- Astray G.; Cid A.; Moldes O.; Ferreiro-Lage J.; Gálvez J.; Mejuto J. Prediction of refractive index of polymers using artificial neural networks. J. Chem. Eng. Data 2010, 55, 5388–5393. 10.1021/je100885f. [DOI] [Google Scholar]
- Yu X.; Yi B.; Wang X. Prediction of refractive index of vinyl polymers by using density functional theory. J. Comput. Chem. 2007, 28, 2336–2341. 10.1002/jcc.20752. [DOI] [PubMed] [Google Scholar]
- Xu J.; Liang H.; Chen B.; Xu W.; Shen X.; Liu H. Linear and nonlinear QSPR models to predict refractive indices of polymers from cyclic dimer structures. Chemom. Intell. Lab. Syst. 2008, 92, 152–156. 10.1016/j.chemolab.2008.02.006. [DOI] [Google Scholar]
- Duchowicz P. R.; Fioressi S. E.; Bacelo D. E.; Saavedra L. M.; Toropova A. P.; Toropov A. A. QSPR studies on refractive indices of structurally heterogeneous polymers. Chemom. Intell. Lab. Syst. 2015, 140, 86–91. 10.1016/j.chemolab.2014.11.008. [DOI] [Google Scholar]
- Tong J.-b.; Xu X.-m.; Chen Y.; Cheng F.-l.; Du J.-w. QSPR Study on Part of the Refractive Index of the Polymer. J. Shaanxi Univ. Sci. Technol. (Nat. Sci. Ed.) 2012, 5, 014. [Google Scholar]
- García-Domenech R.; de Julián-Ortiz J. Prediction of indices of refraction and glass transition temperatures of linear polymers by using graph theoretical indices. J. Phys. Chem. B 2002, 106, 1501–1507. 10.1021/jp012360u. [DOI] [Google Scholar]
- Duchowicz P. R.; Comelli N. C.; Ortiz E. V.; Castro E. A. QSAR study for carcinogenicity in a large set of organic compounds. Curr. Drug Saf. 2012, 7, 282–288. 10.2174/157488612804096623. [DOI] [PubMed] [Google Scholar]
- Talevi A.; Bellera C. L.; Di Ianni M.; Duchowicz P. R.; Bruno-Blanch L. E.; Castro E. A. An integrated drug development approach applying topological descriptors. Curr. Comput. Aided Drug Des. 2012, 8, 172–181. 10.2174/157340912801619076. [DOI] [PubMed] [Google Scholar]
- Scientific Polymer Products, Inc. 2018. http://scientificpolymer.com/technical-library/refractive-index-of-polymers-by-index/ (accessed on April 2018).
- Jabeen F.; Chen M.; Rasulev B.; Ossowski M.; Boudjouk P. Refractive indices of diverse data set of polymers: A computational QSPR based study. Comput. Mater. Sci. 2017, 137, 215–224. 10.1016/j.commatsci.2017.05.022. [DOI] [Google Scholar]
- Katritzky A. R.; Kuanar M.; Slavov S.; Hall C. D.; Karelson M.; Kahn I.; Dobchev D. A. Quantitative correlation of physical and chemical properties with chemical structure: utility for prediction. Chem. Rev. 2010, 110, 5714–5789. 10.1021/cr900238d. [DOI] [PubMed] [Google Scholar]
- Kennard R. W.; Stone L. A. Computer aided design of experiments. Technometrics 1969, 11, 137–148. 10.1080/00401706.1969.10490666. [DOI] [Google Scholar]
- Baumann D.; Baumann K. Reliable estimation of prediction errors for QSAR models under model uncertainty using double cross-validation. J. Cheminf. 2014, 6, 47. 10.1186/s13321-014-0047-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wold S.; Sjöström M.; Eriksson L. PLS-regression: a basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. 10.1016/S0169-7439(01)00155-1. [DOI] [Google Scholar]
- Mauri A.; Consonni V.; Pavan M.; Todeschini R. Dragon software: An easy approach to molecular descriptor calculations. MATCH Commun. Math. Comput. Chem. 2006, 56, 237–248. [Google Scholar]
- Yap C. W. PaDEL-descriptor: An open source software to calculate molecular descriptors and fingerprints. J. Comput. Chem. 2011, 32, 1466–1474. 10.1002/jcc.21707. [DOI] [PubMed] [Google Scholar]
- Roy K.; Das R. N.; Ambure P.; Aher R. B. Be aware of error measures. Further studies on validation of predictive QSAR models. Chemom. Intell. Lab. Syst. 2016, 152, 18–33. 10.1016/j.chemolab.2016.01.008. [DOI] [Google Scholar]
- Golbraikh A.; Tropsha A. Beware of q2!. J. Mol. Graphics Modell. 2002, 20, 269–276. 10.1016/S1093-3263(01)00123-1. [DOI] [PubMed] [Google Scholar]
- Sato T. K.; Asai M.; Borschevsky A.; Stora T.; Sato N.; Kaneya Y.; Tsukada K.; Düllmann C. E.; Eberhardt K.; Eliav E.; et al. Measurement of the first ionization potential of lawrencium, element 103. Nature 2015, 520, 209. 10.1038/nature14342. [DOI] [PubMed] [Google Scholar]
- Liu H.; Yang X.; Yin C.; Wei M.; He X. Development of predictive models for predicting binding affinity of endocrine disrupting chemicals to fish sex hormone-binding globulin. Ecotoxicol. Environ. Saf. 2017, 136, 46–54. 10.1016/j.ecoenv.2016.10.032. [DOI] [PubMed] [Google Scholar]
- Platts J. A.; Butina D.; Abraham M. H.; Hersey A. Estimation of molecular linear free energy relation descriptors using a group contribution approach. J. Chem. Inf. Model. 1999, 39, 835–845. 10.1021/ci980339t. [DOI] [PubMed] [Google Scholar]
- Antanasijević J.; Antanasijević D.; Pocajt V.; Trišović N.; Fodor-Csorba K. A QSPR study on the liquid crystallinity of five-ring bent-core molecules using decision trees, MARS and artificial neural networks. RSC Adv. 2016, 6, 18452–18464. 10.1039/C5RA20775D. [DOI] [Google Scholar]
- Basant N.; Gupta S. Modeling uptake of nanoparticles in multiple human cells using structure–activity relationships and intercellular uptake correlations. Nanotoxicology 2017, 11, 20–30. 10.1080/17435390.2016.1257075. [DOI] [PubMed] [Google Scholar]
- Hougham G.; Tesoro G.; Viehbeck A. Influence of free volume change on the relative permittivity and refractive index in fluoropolyimides. Macromolecules 1996, 29, 3453–3456. 10.1021/ma9503423. [DOI] [Google Scholar]
- Hougham G.; Tesoro G.; Viehbeck A.; Chapple-Sokol J. Polarization effects of fluorine on the relative permittivity in polyimides. Macromolecules 1994, 27, 5964–5971. 10.1021/ma00099a006. [DOI] [Google Scholar]
- Todeschini R.; Consonni V.. Handbook of Molecular Descriptors; John Wiley & Sons, 2008; Vol. 11, p 91. [Google Scholar]
- Wang J.; Xie X.-Q.; Hou T.; Xu X. Fast approaches for molecular polarizability calculations. J. Phys. Chem. A 2007, 111, 4443–4448. 10.1021/jp068423w. [DOI] [PubMed] [Google Scholar]
- Bosque R.; Sales J. Polarizabilities of solvents from the chemical composition. J. Chem. Inf. Model. 2002, 42, 1154–1163. 10.1021/ci025528x. [DOI] [PubMed] [Google Scholar]
- Randić M. On characterization of cyclic structures. J. Chem. Inf. Model. 1997, 37, 1063–1071. 10.1021/ci9702407. [DOI] [Google Scholar]
- Yu X.; Huang X. A quantitative relationship between Tgs and chain segment structures of polystyrenes. Polímeros 2017, 27, 68–74. 10.1590/0104-1428.00916. [DOI] [Google Scholar]
- Mohar B.; Babic D.; Trinajstic N. A novel definition of the Wiener index for trees. J. Chem. Inf. Model. 1993, 33, 153–154. 10.1021/ci00011a023. [DOI] [Google Scholar]
- Trinajstic N.; Babic D.; Nikolic S.; Plavsic D.; Amic D.; Mihalic Z. The Laplacian matrix in chemistry. J. Chem. Inf. Model. 1994, 34, 368–376. 10.1021/ci00018a023. [DOI] [Google Scholar]
- Roy K.Quantitative Structure-Activity Relationships in Drug Design, Predictive Toxicology, and Risk Assessment; IGI Global, 2015. [Google Scholar]
- Das R. N.; Roy K. Predictive modeling studies for the ecotoxicity of ionic liquids towards the green algae Scenedesmus vacuolatus. Chemosphere 2014, 104, 170–176. 10.1016/j.chemosphere.2013.11.002. [DOI] [PubMed] [Google Scholar]
- Farkas O.; Zenkevich I. G.; Stout F.; Kalivas J. H.; Héberger K. Prediction of retention indices for identification of fatty acid methyl esters. J. Chromatogr. A 2008, 1198–1199, 188–195. 10.1016/j.chroma.2008.05.019. [DOI] [PubMed] [Google Scholar]
- Akarachantachote N.; Chadcham S.; Saithanu K. Cutoff threshold of variable importance in projection for variable selection. Int. J. Pure Appl. Math. 2014, 94, 307–322. 10.12732/ijpam.v94i3.2. [DOI] [Google Scholar]
- Ambure P.; Aher R. B.; Gajewicz A.; Puzyn T.; Roy K. “NanoBRIDGES” software: Open access tools to perform QSAR and nano-QSAR modeling. Chemom. Intell. Lab. Syst. 2015, 147, 1–13. 10.1016/j.chemolab.2015.07.007. [DOI] [Google Scholar]
- OECD . OECD Principles for the Validation, for Regulatory Purposes, of (Quantitative) Structure–Activity Relationship Models; Organisation for Economic-Operation and Development: Paris, 2004. [Google Scholar]
- Roy K.; Mitra I.; Ojha P. K.; Kar S.; Das R. N.; Kabir H. Introduction of rm2 (rank) metric incorporating rank-order predictions as an additional tool for validation of QSAR/QSPR models. Chemom. Intell. Lab. Syst. 2012, 118, 200–210. 10.1016/j.chemolab.2012.06.004. [DOI] [Google Scholar]
- SIMCA-P, version 10.0; Umetrics: Umea, Sweden, 2002. info@umetrics.com, www.umetrics.com.
- Roy K.; Ambure P.; Kar S.; Ojha P. K. Is it possible to improve the quality of predictions from an “intelligent” use of multiple QSAR/QSPR/QSTR models?. J. Chemom. 2018, e2992 10.1002/cem.2992. [DOI] [Google Scholar]
- Roy K.; Ambure P.; Kar S. How Precise Are Our Quantitative Structure–Activity Relationship Derived Predictions for New Query Chemicals?. ACS Omega 2018, 3, 11392–11406. 10.1021/acsomega.8b01647. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.