Abstract

With the retention of many of the unrivaled properties of bulk diamond but in thin-film form, nanocrystalline diamond (NCD) has applications ranging from micro-/nano-electromechanical systems to tribological coatings. However, with Young’s modulus, transparency, and thermal conductivity of films all dependent on the grain size and nondiamond content, compositional and structural analysis of the initial stages of diamond growth is required to optimize growth. Spectroscopic ellipsometry (SE) has therefore been applied to the characterization of 25–75 nm thick NCD samples atop nanodiamond-seeded silicon with a clear distinction between the nucleation and bulk growth regimes discernable. The resulting presence of an interfacial carbide and peak in nondiamond carbon content upon coalescence is correlated with Raman spectroscopy, whereas the surface roughness and microstructure are in accordance with values provided by atomic force microscopy. As such, SE is demonstrated to be a powerful technique for the characterization of the initial stages of growth and hence the optimization of seeding and nucleation within films to yield high-quality NCD.
1. Introduction
Through the advent of nanocrystalline diamond (NCD), many of the superlative properties of diamond are available in a large-area, heteroepitaxial thin-film form at a fraction of the cost of bulk diamond.1 As such, NCD has been touted for use in applications typically unsuited to bulk diamond, such as micro- and nano-electromechanical systems (MEMS/NEMS),2 tribology,3 and thermal management coatings.4 However, the quality of NCD films is heavily dependent on the nucleation density, and hence seeding, and the initial stages of growth.4
The large free surface energy of diamond relative to the substrate (6 vs 1.5 J m–2 for the (100) face of silicon) and the low sticking coefficient of methyl precursors ensure that attempts at heteroepitaxial growth typically follow the Volmer–Weber (VW) mechanism.5 Surface diffusion will then ensure that any impinging adatoms preferentially bond to existing nuclei, resulting in the formation of three-dimensional isolated islands capable of growing both laterally and vertically.5,6 With the densities of these islands typically 104–105 on bare silicon, pretreatment with diamond particles or alteration of the substrate surface is therefore required to increase the nucleation density as required to realize coalesced thin films (1011 cm–2).1 When growing atop silicon, any native oxide not covered by diamond growth will be etched by the predominantly hydrogen plasma, allowing the formation of an amorphous/β-SiC layer from carbon (CH4)-derived radicals or reaction with the diamond seeds.7−10 The thickness of this layer is then kinetically limited by silicon diffusion through the existing carbide, with studies of bias-enhanced nucleation (BEN)-produced samples placing an upper limit on the thickness of 9 nm.11 After sufficient lateral growth, the diamond islands will then coalesce to form columnar crystals in accordance with the van der Drift growth model, trapping a variety of dangling bonds and hydrogenated sp3, sp2, and sp1 hybridized impurities within the grain boundaries between individual crystallites.12,13 Finally, as growth continues, the differing growth rates as a result of the anisotropy in surface diffusivities of the diamond facets will result in the overgrowth of slower-growing crystallite facets and a roughness that evolves with film thickness.6 With Young’s modulus,14 transparency,15 and thermal conductivity16 all correlated to the sp2 fraction and grain size within the film, and surface roughness shown to have a detrimental effect on NEMS performance,17,18 characterization and subsequent optimization of the initial stages of NCD film growth are therefore paramount.
While Raman spectroscopy is commonly used for characterization of diamond films, the relative strengths of the spectral features are sensitive to the distribution of nondiamond carbon19 and unaltered by changes in the void content. Techniques utilizing electrons, such as Auger electron spectroscopy, reflection high-energy electron diffraction, and X-ray photoelectron spectroscopy (XPS), are limited in their sensitivity to different carbon environments,20 while the short mean free path of the probing electrons prevents all but characterization of the surface. Through measuring the change in the polarization state of light reflected off a sample, the technique of spectroscopic ellipsometry (SE) is thus able to nondestructively probe the variation in optical properties with depth of thin films. Comparing the measured spectra to those of a modeled sample structure and minimizing the difference between the two then allows determination of the microstructure and composition of the sample. Having previously demonstrated nearly equal sensitivity to diamond, sp2, and void fractions for polycrystalline diamond samples as thin as 4 nm,21 SE is thus a powerful tool for the characterization of the initial stages of diamond film growth.
Previous attempts at SE characterization of bulk nanocrystalline and microcrystalline diamond films have predominantly focused on the use of a Bruggeman effective medium approximation (EMA) to mix reference optical indices of the expected constituents and represent the film by a single homogenous medium,22−25 successfully showing incremental improvements in fit upon the addition of components to represent grain boundary sp2 carbon and void content between the nuclei, and surface roughness.19,20,26−28 Although “seed” layers of 15–41 nm adjacent to the substrate rich in sp2, void, and occasionally SiC content have been observed with such an approach,20,24,25 parameter correlation with the impurity fractions within the bulk prevents determination of the microstructure of this layer with any confidence.26 More comprehensively, in situ characterization of the initial stages of diamond growth atop diamond grit-abraded silicon substrates modeled the transition from isolated islands to coalesced film.21,29−31 During these studies, the authors noted an initial parabolic reduction in the void content, indicative of lateral VW-type growth, followed by coalescence and a sharp peak in the sp2 fraction indicative of the trapping of nondiamond material within the grain boundaries,21,29 accentuated by the large surface/volume ratio of crystallites. However, as a result of the significant damage imparted after mechanical abrasion with diamond grit, a rough amorphous silicon layer with a conformal oxide best modeled the high defect density surface.29 With the surface undergoing recrystallization upon subjecting to growth conditions, the similarities in the optical properties between amorphous silicon and the carbon allotropes, and the comparatively low seeding density (1010 cm–2), the detection of diamond and other carbon-containing species were ruled out and the volume fractions were fixed during the initial stages of growth.29 The aim of this work is to therefore use SE to characterize the initial stages of growth on Si seeded with nano diamonds, with the order of magnitude enhanced nucleation densities and without the damage inherent to mechanical abrasion. The trends in fitting parameters are then corroborated with Raman spectroscopy, atomic force microscopy (AFM), scanning electron microscopy (SEM), and X-ray diffraction (XRD), demonstrating the applicability of SE to the initial stages of nanocrystalline diamond film growth.
2. Results and Discussion
2.1. Morphology
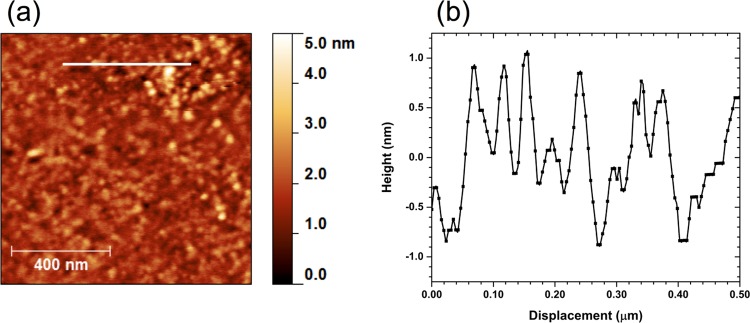
A typical AFM scan of a nanodiamond-seeded silicon wafer and a 500 nm long height profile are shown in Figure 1a,b, respectively. Due to the large ζ potential difference between the hydrogen-terminated seeds and the native oxide at pH 7, the strong electrostatic attraction results in the complete coverage of the Si substrate, reminiscent of the nucleation densities of the order of 1011 cm–2 observed by Hees et al. upon the use of similar purification and dispersion methods.32 The height profile reiterates this close packing while showing a maximum variation of ∼2 nm, less than the 4–8 nm particle size, and suggesting that the surface and the seeding solution are free of agglomerated particles.33 The large ∼40 nm lateral size of individual nanodiamonds is meanwhile believed to be due to convolution of the surface topography and the shape of the tip.34
Figure 1.
(a) AFM image and (b) 500 nm line trace of seeded silicon. The ∼2 nm maximum deviation in height suggests a high seeding density of the 4–8 nm monodispersed seeds, whereas the large ∼40 nm lateral size is attributable to the convolution of the tip shape and topography of the sample.
AFM images of seeded wafers subjected to 4–123 min of growth are then shown in Figure 2a–h, whereas Figure 3 details the averaged root-mean-square (RMS) roughness for the varying growth duration samples with the error bars representing ±0.5 of the range of values obtained across multiple scans. After 4 min of growth, a large increase in height variation appears with the formation of clusters of crystallites ∼20 nm above the surrounding grains along with a corresponding increase in the roughness from 0.5 to 3.3 nm RMS. Meanwhile, little reduction in the density of crystallites is observed, indicative of a large number of seeds withstanding the predominantly H+ plasma, with previously estimated etch rates of nanodiamond under a hydrogen plasma of the order of nanometers per hour.7 As growth proceeds, the lateral size increases, whereas the maximum height variation changes little in accordance with the VW-type growth model. The roughness then locally peaks at a value of 4.6 nm RMS after 8 min of growth as a result of the islands reaching a maximum size while still remaining isolated. As the voids between crystallites are filled upon coalescence, the roughness subsequently relaxes to 3.7 nm RMS, before finally rising linearly from 8.9 to 34.3 nm RMS after 40 and 123 min of growth due to the continued overgrowth of competing crystals in accordance with the van der Drift and Structure Zone models.35 Particle size analysis performed on the SEM images of Figure 4a–h reiterates this increasing particle size with average diameter values increasing from 20 to 42 and 178 nm for the 4, 40, and 123 min growth duration samples, respectively. Also visible in Figure 3 is the increase in the range of roughness values upon longer growth periods: as the average crystallite size increases, the number of grains within the scan area decreases and the difference in growth rate between the different diamond facets becomes more pronounced, increasing the range in the roughness values observed.
Figure 2.
AFM images of the (a) 4 min to (h) 123 min growth duration samples. Steady lateral growth with minor changes in the maximum displacement occurs for the first 20 min of growth, before continued growth leads to the significant increase in the height of protruding facets.
Figure 3.
AFM-obtained roughness for the seeded silicon and 4–123 min growth duration samples. Little change in the roughness during the initial 6 min of growth is observed up to the local peak at 8 min of 4.6 nm RMS as a result of coalescence. The roughness then relaxes and subsequently increases for the 13 min growth duration sample onward.
Figure 4.
SEM images of the (a) 4 min to (h) 123 min growth duration samples. A steady increase in particle size is observable, indicating constant lateral growth, with the clear crystallinity suggesting the samples are free from significant amounts of non-sp3-bonded material.
2.2. Raman Spectroscopy
Raman spectroscopy was performed to characterize the forms of carbon present during the initial stages of growth, with an excitation wavelength of 488 nm chosen to ensure the resonance of both sp2 and sp3 sites.36 Resulting spectra of the 6–40 min growth duration samples normalized to the second-order TO peak of silicon at 980 cm–1 and the unadjusted spectra of the thicker 123 min growth duration sample are plotted in Figure 5a. The scattering from the 4 min growth duration sample was deemed too weak to allow inferences to be made on its composition. As expected for such short-duration growth samples, the most prominent peaks are the first- and second-order TO peaks of silicon at 520 and 980 cm–1, respectively.37 The features visible on the tail of the first-order silicon peak are ascribed to the boron within the heavily doped (∼1019 cm–3) substrate, with doping concentrations exceeding 1018 cm–3 previously shown to lead to the superposition of two local modes onto the optical phonon of diamond at 620 and 644 cm–1 for the B11 and B10 isotopes, respectively.38,39 The relatively constant intensity feature at 830 cm–1 is meanwhile attributed to amorphous SiC, with a similar broad peak positioned between 800 and 830 cm–1 observed in sputtered,40 pulsed laser,41 and chemical vapor deposition (CVD)42,43-produced SiC films.
Figure 5.
(a) Raman spectra of the 6–123 min growth duration samples and (b) magnified spectra of the carbon-associated spectral features. The relatively constant broad peak present at 830 cm–1 is attributed to the amorphous SiC, whereas an increase in the ordered carbon and trans-polyacetylene (TPA) is visible after 13 min of growth, which subsequently decreases with growth duration.
Figure 5b shows a magnified view of the spectra between 1050 and 1800 cm–1 normalized to the first-order diamond line at 1332 cm–1. As typical for NCD films, the diamond phonon line (Di) exhibits peak broadening due to the reduced crystallite size and thickness of the samples. Heavily convoluted with the diamond line is the disordered carbon D peak at 1360 cm–1 arising from the breathing mode of graphitic rings, whereas the G band peak due to the in-plane stretching of pairs of sp2 sites, typically present at 1560 cm–1 upon visible excitation,44 can be seen at approximately 1500–1510 cm–1. Such a decrease in the G band position to 1450–1510 cm–1 is indicative of the introduction of disorder within carbon sheets and the transition from nanocrystalline graphite to amorphous carbon, with weaker bonds softening the sp2 vibrational modes.44 Combined with the low I(D)/I(G) ratio, which has been shown to be linearly related to the particle size due to the loss of aromatic rings,44 it is therefore believed that the sp2 sites within the samples are largely amorphous in nature. Finally, the peak at 1150 cm–1 is attributable to trans-polyacetylene (TPA) present at the grain boundaries.45 Always accompanied by a peak at 1450 cm–1 due to the pair representing the sum and difference of C=C and C–H modes within the TPA chain,45 this additional peak is shrouded by the relatively large G band peak.45
From the magnified spectra, it then can be seen that after 13 min of growth, an increase in the G band peak with respect to the diamond phonon line occurs. The intensity of the G band then peaks at 20 min, before decreasing for the longer growth duration films and reaching a minimum after 123 min of growth. The TPA content meanwhile, believed to lie predominantly within grain boundaries, only becomes apparent after 13 min of growth, peaks at 20–30 min, and then decreases for the longer growth duration samples.
While the composite nature of the samples ensures that the spectral features are also dependent on the distribution of sp2-bonded carbon within the film in addition to amount,19 through using a scattering efficiency ratio of 75 to account for the enhanced resonance of the sp2 inclusions, the diamond and nondiamond peak areas within a series of films can be compared.46−49 Deconvolution of the 123 min growth duration spectra within the 800–2000 cm–1 range to the peaks assigned previously yields an sp2 fraction of 13%. Deconvolution of the 40 and 20 min growth duration samples meanwhile suggests sp2 fractions of 27 and 23%, respectively, quantitatively showing the reduction in impurity content with increasing growth duration past 40 min of growth. The fit process did not converge for the remaining samples due to the weak signal emanating from the films.
2.3. X-ray Diffraction
Grazing incidence X-ray diffraction (GIXRD) scans for the seeded silicon to 123 min growth duration sample are plotted in Figure 6. As visible from the plot, the silicon substrate shows broad peaks, wider than those expected from Bragg peaks and characteristic of thermal diffuse scattering, at 2θ values of 42 and 71°. To prevent the location of these peaks from coinciding with the expected positions of the Bragg peaks of diamond, the ⟨110⟩ direction of the substrate was placed approximately parallel to the propagation direction of the beam. Upon drop-seeding the substrate with the nanodiamond colloid, the (111) Bragg peak of diamond becomes visible at 27.8°, suggesting a lattice parameter of 3.576 Å, 0.26% larger than that of bulk diamond at 3.5667 Å. Such an increase is in accordance with previous XRD studies of diamond nanoparticles, where strain on the surface, which constitutes a large fraction of the atoms within the particle, leads to the shifting of the apparent lattice parameter.50
Figure 6.

XRD of Si substrate, seeded Si, and 4–123 min growth duration samples. After drop seeding of the substrate, the (111) Bragg peak of diamond becomes apparent, rising in intensity and reducing in full width at half-maximum (FWHM) upon growth.
After subjecting the seeded substrates to growth conditions, the (111) peak then rises in intensity while steadily increasing in 2θ for the first 8 min of growth, suggestive of a decrease in the lattice constant closer to that of natural diamond. In addition, the (220) and (113) peaks of diamond appear and steadily rise in intensity. Further growth then leads to a reduction in the FWHM of the (111) peak, suggesting an increase in domain size, and the plateauing off of the lattice constant before reaching a value of 3.5639 Å for the 123 min growth duration sample, 0.07% lower than that of natural diamond.
2.4. Spectroscopic Ellipsometry
To prevent problems with parameter correlation occurring upon direct modeling of the nanocrystalline diamond films and the fitting of multiple layer thicknesses, the optical properties of the substrate and native oxide were first determined. On top of the silicon substrate, thick enough to prevent incoherent back-side reflection affecting the acquired spectra, a 1.64 nm thick native oxide layer was identified with refractive index between that of Si and bulk SiO2 due to incomplete oxidation.51 An additional two layers were then added to model the NCD samples, creating a stack consisting of a Bruggeman EMA surface roughness layer of 50% void and 50% bulk; a bulk layer composed of two oscillators matched to the optical constants of type I and II natural diamond;52 a native oxide layer; and finally the silicon substrate.51 While the incorporation of nitrogen in the transition from type IIa to Ia natural diamond is known to cause a shift in the UV absorption edge of diamond,52 use of optical constants from a Tauc–Lorentz oscillator fitted to thicker polished films had little effect on the trends in composition and absolute values, permitting the use of the natural diamond as a reference dielectric function. Column 1 of Figure 7a plots the composition of the model upon fitting to the 13 min growth duration sample along with the mean square error (MSE) between the measured and modeled spectra, whereas Figure 7b plots the 70° incidence angle spectra. As a result of the thin nanocrystalline nature of the samples and the associated inclusions however, fitting with the model and the optical constants of natural diamond was poor with a large MSE of 40.8 for the 13 min growth duration sample and an average value of 78 across the entire 4–40 min growth duration sample set, signaling a large difference between the measured and modeled spectra.
Figure 7.
(a) Evolution of models fitted to the 13 min growth duration sample detailing composition and thickness of layers within the stack and associated MSE, (b) model 1 fitted to the measured spectra of the 13 min growth duration sample, and (c) model 6 fitted to the measured spectra of the 13 min growth duration sample. After the incorporation of a g-C and void content to represent the intergranular regions and more accurate modeling of the interface, an improvement in fit is gained with a reduction in the MSE from 40.8 to 12.4.
Accounting for the void content arising from the transition from VW- to van der Drift-type growth and nondiamond carbon hybridizations present, the optical constants of void, glassy carbon (g-C),53 or tetrahedral amorphous carbon (ta-C)54 were then mixed with those of diamond through the use of the Bruggeman EMA.22 Although the addition of void content alone did little to improve the fit as visible in column 2 of Figure 7a, upon combination with g-C, a reduction in MSE to 24.3 was observed for the 13 min growth duration sample and 52 across the entire sample set. The use of the optical constants of ta-C to account for the nondiamond inclusions however was deemed unreasonable with an indicated fraction of 68% for the 40 min growth duration film, contradicting the crystallinity observed in the SEM images in Figure 4 and highlighting the need for validation of SE-obtained results with non-model-dependent characterization methods.
Further reductions in MSE were attained through more accurately modeling the interface between NCD and substrate; as discussed, XPS studies of growth at temperatures exceeding 800 °C have indicated the presence of a <10 nm amorphous SiC layer due to combined carburization from CH4-derived radicals within the plasma and direct reaction with nanodiamond particles.7,11 Meanwhile, hydrogen plasmas have been shown to result in the etching of the native oxide of silicon,8,55 with etch rates of SiO2 of 0.3 nm min–1 demonstrated.56 Therefore, a β-SiC layer was then placed atop the native oxide, with the linear regression procedure indicating a layer thickness of 5–9 nm decreasing with growth duration,57 reducing the MSE to 14.8 for the 13 min growth duration sample, and an average of 39 for the 4–40 min growth duration samples. Finally, upon allowing the thickness of the native oxide to vary from the 1.64 nm obtained during modeling of the substrate, the fitting procedure suggests a thickness of less than one, indicating that it does not improve the fit and thus unlikely to be present within the samples. As a result, the MSE is further reduced to 12.5 for the individual sample and to 37 across the 4–40 min growth duration samples.
Finally, as the samples were cooled in a purely H2-fed plasma, it is to be expected that the surface will be free from any adventitious carbon, reiterated by the clear homogenous faceted features in the SEM images of Figure 4. Replacing the bulk component of the surface roughness EMA layer with that of the optical constants of diamond then further reduces the MSE to 12.4 for the 13 min growth duration sample, reiterated by the closer fitting of the modeled and measured spectra in Figure 7c, and to 34 for the 4–40 min growth duration sample set. Upon this removal of the g-C content from the surface roughness layer, a correlated increase in the fraction within the bulk is observed to maintain a constant absolute content, following the behavior observed in previous studies.21 To investigate this correlation further, the correlation matrix of model 6 fitted to the 13 min growth duration sample in Figure 7a is shown in Table 1, with values equal to ±1 indicating that the two parameters achieve the same result and are not unique. Of note is the relatively low correlation of the bulk g-C contents with the other fit parameters suggesting that the indicated fraction is unique, whereas the surface roughness layer thickness is highly correlated to the thickness of the bulk and SiC layers and the void fraction within the bulk, warranting validation with AFM.
Table 1. Fitting Parameter Correlation Matrix for the 13 min Growth Duration Samplea.
| S.R. thickness | bulk thickness | bulk g-C % | bulk void % | SiC thickness | |
|---|---|---|---|---|---|
| S.R. thickness | 1 | –0.91 | 0.54 | –0.95 | –0.94 |
| bulk thickness | –0.91 | 1 | –0.28 | 0.88 | 0.74 |
| bulk g-C % | 0.54 | –0.28 | 1 | –0.53 | 0.58 |
| bulk void % | 0.95 | 0.88 | –0.53 | 1 | 0.94 |
| SiC thickness | –0.94 | 0.74 | 0.58 | 0.94 | 1 |
With values close to ±1 signifying that the two parameters produce the same result and are not unique, high correlation can be observed between the S.R. thickness and the volume fractions and thicknesses of other layers within the stack, warranting validation with AFM.
Once settled on the optimal structure, the optical constants of the nondiamond content and carbide layer were varied using reference dielectric functions of ta-C, graphite, DLC produced under various conditions, amorphous SiC,58 and α-SiC from the Woollam database and the literature. In a similar result to Cella et al., changing the optical constant of the nondiamond carbon content results in a varying concentration of the said impurity within the samples,23 whereas the trend with growth duration remains the same. Meanwhile, minor changes are observed in the MSE and the remaining fit parameters due to the relatively low correlation with the g-C fraction. Previous characterization by Hong et al. demonstrate that while the dielectric function of g-C does not follow the shape of the sp2 inclusions within a ∼200 nm thick NCD film, particularly the presence of a fundamental band gap of 0.77 eV, the average magnitudes are similar.29 In combination with trends observed with Raman spectroscopy, the optical constants modeled by g-C were therefore retained. Upon changing the optical constants of the carbide interface however, large deviation in the surface roughness and bulk void content occurs; all but the β-SiC optical constants demonstrate relatively consistent roughness values for the 4–30 min growth duration films in the range of 10–20 nm before increasing for the final 40 min growth duration sample, contradicting the roughness values obtained with AFM plotted in Figure 3. The use of the optical constants of β-SiC meanwhile rejects the surface roughness layer for the 4–8 min growth samples, which then increases linearly with growth duration, with the point of inclusion of this surface roughness layer coinciding with the peak in the roughness plot of Figure 3. As described earlier, such a local maximum would be expected at the point of coalescence with the height of the islands reaching their peak while still being isolated crystals. As such, β-SiC was chosen to model the optical constants of the interfacial region.
The resulting trends in the fitting parameters with growth duration are plotted in Figure 8. For the results reported, further depolarization was fitted manually to account for thickness nonuniformity, leading to minor improvements in MSE with little modification to the structural parameters reported previously. As is visible in the plot, before growth, the spectra of the seeds are best modeled by a 4.38 nm thick Bruggeman EMA layer with 54.9 and 4.5% void and g-C content, respectively, sitting on top of a 1.64 nm thick native oxide layer. Upon being subjected to CVD, the thickness of the porous layer then increases to ∼30 nm for the first 8 min of growth, whereas the decreasing void content to 28.8% for the 8 min growth duration sample suggests steady lateral growth. During this time, the g-C-to-diamond ratio remains the same, whereas the thickness of the newly formed SiC layer peaks at 8.9 nm. After 13 min of growth, a surface roughness layer is required to accurately model the spectra, correlating with the peak in roughness observed with AFM and the point at which the thickness of the bulk begins to rapidly rise from ∼30 to 79.3 nm for the 40 min growth duration sample. Meanwhile, plotting the RMS roughness obtained through AFM with a multiplication factor of 2/3 shows a course correlation with the thickness of this surface roughness layer. Along with the increase in thickness also comes an increase in the indicated g-C content, rising to 22.7% for the 40 min growth duration sample, whereas the void content falls parabolically before plateauing at 7.4%. Finally, the SiC layer thickness decreases and remains relatively constant at 5–6 nm. For the thicker and rougher 123 min growth duration sample, the surface roughness is no longer homogenous within the wavelength range used, resulting in the breakdown of the EMA and an overestimation of the void content within the bulk at 22.1%, should it be allowed to vary; therefore, the value was fixed at 7.5%. Meanwhile, the thickness of the film prevents fitting of the buried SiC layer, which was set to 5.03 nm as for the films of shorter growth duration. Should the parameters be allowed to vary, the low correlation results in minor changes to all but the bulk thickness, with values of 43.8 nm, 6.7%, 22.1%, and 12.46 nm for the surface roughness layer thickness, g-C and void contents within the bulk, and SiC layer thickness, respectively, validating the trends observed in the g-C content and surface roughness.
Figure 8.
Fitting parameter trends for the seeded substrate and 4–123 min growth duration samples. The point at which a second EMA is required to model the surface roughness corresponds to the local maximum in AFM roughness and marks the onset of the increase in bulk thickness. Before this point of coalescence, the g-C content remains constant before increasing to 22.7% and subsequently dropping with growth duration, whereas the void content parabolically decreases with increasing thickness, suggesting the occurrence of a significant fraction of the content adjacent to the substrate.
2.5. Applicability of SE Model
As a result of the high nucleation densities achievable and the lack of substrate damage with the use of electrostatically attracted diamond nanoparticles, a clear seed layer is visible with SE. Best modeled by a 4.38 nm thick EMA composed of 54.9% and 4.5% void and g-C contents, respectively, atop a native oxide, as shown in the schematic of Figure 9, the porous layer suggests that the 4–8 nm particles are monodispersed.33 Upon subjecting such seeded substrates to growth, a clear distinction can then be observed between the nucleation period and bulk growth regime in Figure 8, not requiring composition fixing due to the visibility of the diamond seeds. For the 4–8 min growth duration films, the fitting procedure rejects the presence of a surface roughness layer composed of 50% void and 50% diamond, instead being best modeled by a single EMA composed of diamond, void, and g-C, as highlighted in Figure 9. During this time, minor increases in sample thickness occur, whereas the void content decreases parabolically, indicative of growth occurring faster within the plane of the substrate rather than normal to the surface. Reiterating this VW-type growth, the AFM images in Figure 2a–c show agglomerated islands with the displacement in height larger than the thickness determined with SE. Meanwhile, the average particle diameter deduced from the SEM images indicates a 20% increase in the particle diameter from 20 to 24 nm for the 4 and 8 min growth duration samples accompanied by a reducing FWHM of the (111) diamond Bragg peak in Figure 6. After the AFM-indicated roughness, shown in Figure 3, locally peaks at an SE-indicated thickness of 31 nm, a second layer is then required to model the surface roughness, indicative of the formation of a coalesced film. A peak in SE-deduced roughness, indicating the requirement of a second EMA layer, has been observed during in situ studies of the growth of nanocrystalline diamond atop microscratched silicon and attributed to the size of the isolated crystallites reaching a maximum before making contact and forming a coalesced film.21,29−31 Through assuming growth atop hemispherical nuclei arranged on a square grid, a void fraction of 48% indicates coalescence of the individual grains and the formation of a complete film.21 Modeling the initial nuclei as a surface roughness and adding a bulk layer upon the void fraction dropping below 50%, previous in situ studies achieved relatively constant seed layer thicknesses of 20–40 nm for nucleation densities of the order of 1010 cm–2.29 In the present study, however, SE estimates an initial seed layer composed of 55% void dropping to 33% upon 4 min of growth and the formation of aggregated less ordered nuclei. Therefore, with the high packing density of the 4–8 nm DND seeds demonstrated by the low vertical displacement in Figure 1b reminiscent of that demonstrated by Hees et al. and the previously reported stability of seeds under H2 plasma conditions, it is likely that the nucleation density is of the order of 1011 cm–2.32,7 For thicker NCD films modeled with a seed layer to account for the inferior diamond present at the interface with the substrate, similar thicknesses of 15–41 nm are reported.24,26
Figure 9.

Schematic detailing the growth of nanocrystalline diamond from monodispersed nanodiamond seeds to coalesced film, along with SE-indicated layer constituents. After subjecting to CVD conditions, the nanodiamond seeds act as nucleation sites for Volmer–Weber-type growth, whereas the native oxide is stripped by the predominantly atomic hydrogen plasma and replaced with an amorphous SiC layer. Continued growth leads to coalescence of the individual islands and the distinct requirement of a second EMA to model the surface roughness, whereas non-sp3-bonded carbon is trapped within newly formed grain boundaries.
The fitted surface roughness EMA thickness and the AFM RMS roughness obtained through the averaging of 1 and 25 μm2 scans for the 4–40 and 123 min growth duration samples, respectively, are plotted in the second panel of Figure 8. Due to the nature of the effective medium approximation, SE is most sensitive to roughness between the atomic scale and a tenth of the wavelength of the probing light,27 with finite element method simulations showing the breakdown of the approximation as the roughness increases.27,59 In comparison, AFM offers greater sensitivity to larger undulations of the order of a micron and reduces the surface texture down to a single parameter.27,60 Correlating the two characterization methods, SE and AFM studies on hydrogenated amorphous Si produced with plasma-enhanced CVD have demonstrated a relationship between the thickness of the roughness layer deduced with SE (tSE) and the RMS roughness obtained with AFM (RRMS) of the form tSE ≈ 1.5RRMS + 0.4 nm for 1 ≤ tSE < 10 nm.61 Similarly, SE characterization of polycrystalline silicon has meanwhile observed tSE/RRMS values of 0.89–1.46 dependent on the AFM scan size, demonstrating the effect of sample inhomogeneity when comparing AFM-obtained roughness to the light-based technique with a spot size of the order of mm2.60 As previous SE studies on NCD films have demonstrated a similar relationship, a factor of 1.5 was incorporated into the SE-deduced roughness plot in Figure 8,24 with the modified trend matching the AFM-measured roughness values well for the 13–30 min growth duration samples. After 30 min of growth, the considerable surface roughness, exceeding λ/10, results in nonhomogenous mixing of the constituents at scales close to the probing wavelength and the breakdown of the EMA. This difference is then believed to be exacerbated by the underestimation of the roughness by AFM as the grain size approaches the 1 μm2 area scanned for the 40 min growth duration sample.
Of particular interest is the trend in g-C content observed upon the formation of a coalesced film as plotted in the third panel of Figure 8. During the seed and nucleation phase of growth, the ratio of the g-C to diamond absolute content remains constant at approximately 0.09, before increasing to a peak of 0.25 for the 40 min growth duration sample upon the transition to a coalesced film and subsequently reducing to 0.1 for the 123 min growth duration sample. With the low correlation observed in the matrix of Table 1 between this g-C content and the other parameters, it is unlikely that this peculiar increase is an artifact of the fitting procedure, with such a low correlation also being reported during in situ SE NCD studies.21 This trend is supported by the increase in the Raman G band at 1500–1560 cm–1 with the D band at 1360 cm–1 remaining constant after 20 min of growth, indicative of an increase in the amorphous sp2 content within the film. The intensity of the G peak then begins to decrease for the 30 min growth duration sample before reaching a minimum for the 123 min growth duration sample. Meanwhile, deconvolution of the Raman diamond peak and D and G bands of the 20, 40, and 123 min growth duration samples and accounting for the larger resonance of sp2 sites for visible wavelengths suggest nondiamond contents of 23, 27, and 13%, reiterating this decrease in nondiamond content after 40 min of growth. This discrepancy in the trends of values upon comparing Raman spectroscopy and SE is believed to be due to the nonuniformity of the samples over the spot size of the ellipsometer. A clear color change was visible by eye over the 1 × 1 cm2-sized 40 min growth duration sample, which when coupled with the sharp increase in the SE-indicated g-C content from 13.8 to 22.7% within the 26 nm thickness difference between 30 and 40 min of growth could lead to an apparent shift in the point at which the peak in g-C content occurs.
During NCD film growth, the competing, randomly orientated crystals will prevent the formation of sp3 bonds between neighboring crystallites, allowing the formation of hydrogenated amorphous sp3, sp2, and sp1 sites.12,46 With the rise of isolated islands during the initial VW-type growth, it is therefore to be expected that the nondiamond content will be at a minimum due to the lack of trapping of material between coalescing crystallites. Such a supposition is supported in the current study, as the increased methane admixture of 3.86% for the first 3 min of growth before reducing to 0.6% appears to have little effect on the g-C content during the nucleation phase of growth, with the content remaining constant between 4.5 and 6%. Should the increased methane admixture solely be responsible for the inclusion of nondiamond carbon within the sample, a reduction in the content would be observed for the 4 min growth duration sample onward. Supporting this, previous in situ SE studies have shown that upon varying the oxygen content within the feed gas from O2/(O2 + H2) concentrations of 0–10% the sp2 content within the nuclei remains near the detection limit of 1%, whereas the content within the bulk linearly decreases from 15 to 2% due to the reduction in the lifetime of sp2 sites with preferential etching by oxygen ions.29 Upon coalescence, the formation of grain boundaries then leads to an increase in the g-C content, which peaks when the surface/volume ratio of the grains is at a maximum before reducing with increasing crystallite size. Furthermore, shadowing of crystallite facets from preferential etching by atomic hydrogen within the plasma is expected to cause the peak to increase further, with SEM studies demonstrating the formation of sp2 sites on the facets of micron-sized diamond particles.29 The rise in the peak assigned to grain boundary TPA at 1150 cm–1 after 13 min of growth and the indication of the formation of a coalesced film then support such an argument.
Finally, previous in situ SE studies performed during the subjection of an unseeded silicon wafer to CVD growth conditions have revealed the formation of a 4–7 nm thick porous SiC layer, with longer growth durations increasing the density of the layer while leaving the thickness unchanged.62 However, such studies did not extend to include a variable-thickness interlayer upon diamond growth on seeded wafers, due to the difficulty in distinguishing such a thin layer from scratching-induced damage and recrystallization at elevated temperatures, or near substrate diamond.19,21,63 In situ XPS studies on BEN and mechanically scratched seeded films have shown the removal of signal arising from silicon suboxides atop the substrate during the first 15 min and domination by a signal attributable to SiC, with overlayer calculations placing thicknesses at 2–9 nm.9−11 The source of such carbon can be either from CH4-derived radicals within the plasma or through etching/direct interaction with diamond crystallites, with XPS studies on nanodiamond-seeded silicon revealing the formation of SiC upon subjection to either H2 or H2/CH4 plasmas.7 While the thickness of this amorphous SiC layer is kinetically limited by silicon diffusion through the existing carbide, for thicker interfaces, EELS has shown spectra identical to those of single-crystal β-SiC.11 After the formation of a diffusion layer, preferential evaporation of Si and/or etching of SiC then occur, hastened by the transition to a hydrogen-rich plasma after the termination of bias-enhanced seeding and the beginning of conventional growth.11,64 It is therefore believed that during the 3 min period of increased methane admixture the growth of the SiC layer is enhanced, leading to the peak thickness of 8.85 nm, less than the diffusion-limited thickness of 9 nm indicated during in situ XPS.11 This layer begins to reduce in thickness after 8 min, with the believed nonuniformity in growth of the samples allowing this reduction to continue past 13 min when the entirety of the film sampled by ellipsometry has coalesced. Stable thicknesses of ∼5.5 nm are then observed for the 20–40 min growth duration samples and fixed for the thicker 123 min sample. Raman spectroscopy tentatively supports the presence of such a SiC layer with the constant appearance of a broad peak at 830 cm–1 for all but the thicker 123 min growth duration sample, indicative of the presence of amorphous SiC.
3. Conclusions
SE has been applied to the initial stages of nanocrystalline diamond growth atop nanodiamond-seeded silicon substrates, with the resulting trends validated with AFM, SEM, Raman spectroscopy, and XRD. Through the use of a Bruggeman EMA and reference optical constants of diamond, glassy-C, and void, a porous seed layer was visible atop the native oxide. Upon growth, the transition from isolated islands to coalesced film atop a SiC interlayer is then discernable, with the transition coinciding with a peak in the AFM roughness and the introduction of a Raman peak attributable to the formation of TPA within the grain boundaries. The subsequent SE-indicated peak in nondiamond content after coalescence is supported by Raman spectroscopy, whereas the thickness of the newly formed surface roughness layer is observed to correlate with AFM-derived roughness values. Thus, with its ease of measurement and the ability to characterize the void, nondiamond, and SiC contents present within newly formed films, SE is a powerful method for the characterization of the early stages of nanocrystalline diamond film growth.
4. Experimental Methods
Silicon (100) p-type wafers (2 in.) of <0.005 Ω cm resistivity and 500 μm thickness were used as substrates throughout. To reach the nucleation densities required to produce coalesced films, the substrates were first immersed in a hydrogen-terminated monodispersed nanodiamond/DI H2O colloid and placed in an ultrasonic bath for 10 min, known to result in seeding densities >1011 cm–2.32 The seeded substrates were then rinsed, spun dry, and placed inside an Astex AX6500 series microwave plasma chemical vapor deposition reactor in preparation for growth.
During CVD, a methane fraction of 3.86% diluted in hydrogen was used to stabilize and prevent etching of the ∼5 nm seeds for the first 3 min, before being reduced to 0.6% for the remainder of growth to realize high-quality NCD films. The pressure and microwave power were meanwhile maintained at 40 Torr and 3.5 kW, respectively, with heating of the substrate from the plasma resulting in growth temperatures of ∼860 °C, as determined by dual-wavelength pyrometry. After 4–123 min of growth, the samples were cooled in a purely H2-fed plasma to prevent the formation of non-sp3-bonded carbon. The films were then diced with a diamond scribe, and a ∼1 × 1 cm2 piece was taken from the center of each for all subsequent characterizations.
Spectroscopic ellipsometry was performed with a J.A. Woollam M-2000D rotating compensator-type ellipsometer and CompleteEASE software between the wavelength range of 1.2–6.2 eV (200–1000 nm), with an acquisition period of 1 s, and at incidence angles of 65, 70, and 75°. The samples were then modeled within the CompleteEASE program while iterating the sample structure to minimize the difference between the measured and modeled spectra, as detailed in Section 2.2. To account for the significant depolarization observed, an instrument bandwidth of 5 nm was incorporated into the fitting procedure.
GIXRD was carried out on beamline I07 at Diamond Light Source (Didcot, U.K.) with a monochromatic energy of 12.5 keV. The samples were held within a helium-flushed chamber to minimize background scatter. The angle of incidence was set at 0.4°, and a Pilatus 100 K area detector was used to collect the scattered intensity for an exit angle of 0.1°, below the critical angle of diamond to reduce the penetration depth and enhance the thin-film contribution to the scattered signal.
Raman scattering was performed using a WITec Alpha scanning near-field optical microscope equipped with a 488 nm laser with a power of 0.5 mW at an acquisition time of 30 s. SEM images were taken using the Inlens detector of a Raith eLine system operating at 15 kV and 10 mm working distance, with particle size analysis performed using ImageJ. AFM was performed using a Park Systems XE-100 AFM operating in noncontact mode and equipped with TESPA silicon tips (320 kHz resonant frequency, 42 N m–1 spring constant, and 8–12 nm tip radius). Multiple areas of 1 and 25 μm2 were scanned for the seeded silicon to 40 min growth duration sample and 123 min growth duration samples, respectively, with analysis carried out through the use of WSxM and Gwyddion SPM analysis software. During scanning of the seeded silicon, the oscillation amplitude and tip–sample interaction were kept as small as possible to minimize tip wear and the associated imaging artifacts.
Acknowledgments
The authors acknowledge the financial support of EPSRC under the grant “New routes to diamond nucleation, epitaxy and growth at low temperatures” reference number EP/K007459/1 and the willing assistance of the beamline team at I07. CLC appreciates the financial support by the Ministry of Science and Technology (MOST) of Taiwan for research grant: MOST-103-2112-M-259-001-MY3 and MOST-RS International Exchange Scheme under Grant No. MOST-103-2911-I-259-501. OAW gratefully acknowledges the Royal Society International Exchanges Scheme. Information on the data underpinning the results presented here, including how to access them, can be found in the Cardiff University data catalog at http://doi.org/10.17035/d.2017.0040949318.
The authors declare no competing financial interest.
References
- Williams O. A. Nanocrystalline diamond. Diamond Relat. Mater. 2011, 20, 621–640. 10.1016/j.diamond.2011.02.015. [DOI] [Google Scholar]
- Gaidarzhy A.; Imboden M.; Mohanty P.; Rankin J.; Sheldon B. W. High quality factor gigahertz frequencies in nanomechanical diamond resonators. Appl. Phys. Lett. 2007, 91, 203503 10.1063/1.2804573. [DOI] [Google Scholar]
- Kumar N.; Panda K.; Dash S.; Popov C.; Reithmaier J. P.; Panigrahi B. K.; Tyagi A. K.; Raj B. Tribological properties of nanocrystalline diamond films deposited by hot filament chemical vapor deposition. AIP Adv. 2012, 2, 032164 10.1063/1.4751272. [DOI] [Google Scholar]
- Philip J.; Hess P.; Feygelson T.; Butler J. E.; Chattopadhyay S.; Chen K. H.; Chen L. C. Elastic, mechanical, and thermal properties of nanocrystalline diamond films. J. Appl. Phys. 2003, 93, 2164–2171. 10.1063/1.1537465. [DOI] [Google Scholar]
- Jiang X.; Schiffmann K.; Klages C. P. Nucleation and initial growth phase of diamond thin films on (100) silicon. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 8402–8410. 10.1103/PhysRevB.50.8402. [DOI] [PubMed] [Google Scholar]
- Petrov I.; Barna P. B.; Hultman L.; Greene J. E. Microstructural evolution during film growth. J. Vac. Sci. Technol., A 2003, 21, S117–S128. 10.1116/1.1601610. [DOI] [Google Scholar]
- Arnault J. C.; Saada S.; Nesladek M.; Williams O. A.; Haenen K.; Bergonzo P.; Osawa E. Diamond nanoseeding on silicon: Stability under H2 MPCVD exposures and early stages of growth. Diamond Relat. Mater. 2008, 17, 1143–1149. 10.1016/j.diamond.2008.01.008. [DOI] [Google Scholar]
- Belton D. N.; Harris S. J.; Schmieg S. J.; Weiner A. M.; Perry T. A. In situ characterization of diamond nucleation and growth. Appl. Phys. Lett. 1989, 54, 416–417. 10.1063/1.100938. [DOI] [Google Scholar]
- Saada S.; Arnault J. C.; Tranchant N.; Bonnauron M.; Bergonzo P. Study of the CVD process sequences for an improved control of the Bias Enhanced Nucleation step on silicon. Phys. Status Solidi A 2007, 204, 2854–2859. 10.1002/pssa.200776339. [DOI] [Google Scholar]
- Stöckel R.; Janischowsky K.; Rohmfeld S.; Ristein J.; Hundhausen M.; Ley L. Growth of diamond on silicon during the bias pretreatment in chemical vapor deposition of polycrystalline diamond films. J. Appl. Phys. 1996, 79, 768–775. 10.1063/1.360823. [DOI] [Google Scholar]
- Stoner B. R.; Ma G. H. M.; Wolter S. D.; Glass J. T. Characterization of bias-enhanced nucleation of diamond on silicon by /textit{invacuo} surface analysis and transmission electron microscopy. Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 45, 11067–11084. 10.1103/PhysRevB.45.11067. [DOI] [PubMed] [Google Scholar]
- Michaelson S.; Ternyak O.; Hoffman A.; Lifshitz Y. Correlation between diamond grain size and hydrogen retention in diamond films studied by scanning electron microscopy and secondary ion mass spectroscopy. Appl. Phys. Lett. 2007, 90, 031914 10.1063/1.2432996. [DOI] [Google Scholar]
- Tsigkourakos M.; Hantschel T.; Simon D. K.; Nuytten T.; Verhulst A. S.; Douhard B.; Vandervorst W. On the local conductivity of individual diamond seeds and their impact on the interfacial resistance of boron-doped diamond films. Carbon 2014, 79, 103–112. 10.1016/j.carbon.2014.07.048. [DOI] [Google Scholar]
- Williams O. A.; Kriele A.; Hees J.; Wolfer M.; Müller-Sebert W.; Nebel C. E. High Young’s modulus in ultra thin nanocrystalline diamond. Chem. Phys. Lett. 2010, 495, 84–89. 10.1016/j.cplett.2010.06.054. [DOI] [Google Scholar]
- Nesládek M.; Meykens K.; Stals L. M.; Vaněček M.; Rosa J. Origin of characteristic subgap optical absorption in CVD diamond films. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 5552–5561. 10.1103/PhysRevB.54.5552. [DOI] [PubMed] [Google Scholar]
- Angadi M. A.; Watanabe T.; Bodapati A.; Xiao X.; Auciello O.; Carlisle J. A.; Eastman J. A.; Keblinski P.; Schelling P. K.; Phillpot S. R. Thermal transport and grain boundary conductance in ultrananocrystalline diamond thin films. J. Appl. Phys. 2006, 99, 114301 10.1063/1.2199974. [DOI] [Google Scholar]
- Huang X. M. H.; Feng X. L.; Zorman C. A.; Mehregany M.; Roukes M. L. VHF, UHF and microwave frequency nanomechanical resonator. New J. Phys. 2005, 7, 247. 10.1088/1367-2630/7/1/247. [DOI] [Google Scholar]
- Ergincan O.; Palasantzas G.; Kooi B. J. Influence of surface modification on the quality factor of microresonators. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85, 205420 10.1103/PhysRevB.85.205420. [DOI] [Google Scholar]
- Cong Y.; Collins R. W.; Epps G. F.; Windischmann H. Spectroellipsometry characterization of optical quality vapor-deposited diamond thin films. Appl. Phys. Lett. 1991, 58, 819–821. 10.1063/1.104499. [DOI] [Google Scholar]
- Pintér I.; Petrik P.; Szilágyi E.; Kátai S.; Deák P. Characterization of nucleation and growth of MW-CVD diamond films by spectroscopic ellipsometry and ion beam analysis methods. Diamond Relat. Mater. 1997, 6, 1633–1637. 10.1016/S0925-9635(97)00029-0. [DOI] [Google Scholar]
- Hong B.; Wakagi M.; Collins R. W.; An I.; Engdahl N. C.; Drawl W.; Messier R. Real-time spectroscopic ellipsometry studies of diamond film growth by microwave plasma-enhanced chemical vapour deposition. Diamond Relat. Mater. 1994, 3, 431–437. 10.1016/0925-9635(94)90198-8. [DOI] [Google Scholar]
- Aspnes D. E.; Theeten J. B.; Hottier F. Investigation of effective-medium models of microscopic surface roughness by spectroscopic ellipsometry. Phys. Rev. B: Condens. Matter Mater. Phys. 1979, 20, 3292–3302. 10.1103/PhysRevB.20.3292. [DOI] [Google Scholar]
- Cella N.; El Rhaleb H.; Roger J. P.; Fournier D.; Anger E.; Gicquel A. Ex-situ spectroscopic ellipsometry studies of micron thick CVD diamond films. Diamond Relat. Mater. 1996, 5, 1424–1432. 10.1016/S0925-9635(96)00578-X. [DOI] [Google Scholar]
- Lohner T.; Csíkvári P.; Khánh N. Q.; Dávid S.; Horváth Z. E.; Petrik P.; Hárs G. Spectroellipsometric and ion beam analytical investigation of nanocrystalline diamond layers. Thin Solid Films 2011, 519, 2806–2810. 10.1016/j.tsf.2010.12.061. [DOI] [Google Scholar]
- Cifre J.; Campmany J.; Bertran E.; Esteve J. Spectroscopic Ellipsometry Measurements of the Diamond Crystalline Si Interface in Chemically Vapor-Deposited Polycrystalline Diamond Films. Diamond Relat. Mater. 1993, 2, 728–731. 10.1016/0925-9635(93)90212-K. [DOI] [Google Scholar]
- Mistrik J.; Janicek P.; Taylor A.; Fendrych F.; Fekete L.; Jager A.; Nesladek M. Spectroscopic ellipsometry characterization of nano-crystalline diamond films prepared at various substrate temperatures and pulsed plasma frequencies using microwave plasma enhanced chemical vapor deposition apparatus with linear antenna delivery. Thin Solid Films 2014, 571, 230–237. 10.1016/j.tsf.2014.10.071. [DOI] [Google Scholar]
- Gupta S.; Dudipala A.; Williams O. A.; Haenen K.; Bohannan E. Ex situ variable angle spectroscopic ellipsometry studies on chemical vapor deposited boron-doped diamond films: Layered structure and modeling aspects. J. Appl. Phys. 2008, 104, 073514 10.1063/1.2990058. [DOI] [Google Scholar]
- Wang L.; Xia Y.; Zhang M.; Shen H.; Su Q.; Gu B.; Lou Y. Spectroscopic ellipsometric study of CVD diamond films: modelling and optical properties in the energy range of 0.1–0.4 eV. J. Phys. D: Appl. Phys. 2004, 37, 1976–1979. 10.1088/0022-3727/37/14/013. [DOI] [Google Scholar]
- Hong B.; Lee J.; Collins R. W.; Kuang Y.; Drawl W.; Messier R.; Tsong T. T.; Strausser Y. E. Effects of processing conditions on the growth of nanocrystalline diamond thin films: real time spectroscopic ellipsometry studies. Diamond Relat. Mater. 1997, 6, 55–80. 10.1016/S0925-9635(96)00591-2. [DOI] [Google Scholar]
- Lee J.; Hong B.; Messier R.; Collins R. W. Application of real-time spectroscopic ellipsometry for the development of low-temperature diamond film growth processes. Thin Solid Films 1998, 313–314, 506–510. 10.1016/S0040-6090(97)00874-2. [DOI] [Google Scholar]
- Lee J.; Hong B.; Messier R.; Collins R. W. Real time spectroellipsometry for optimization of diamond film growth by microwave plasma-enhanced chemical vapor deposition from CO/H2 mixtures. J. Appl. Phys. 1996, 80, 6489–6495. 10.1063/1.363668. [DOI] [Google Scholar]
- Hees J.; Kriele A.; Williams O. A. Electrostatic self-assembly of diamond nanoparticles. Chem. Phys. Lett. 2011, 509, 12–15. 10.1016/j.cplett.2011.04.083. [DOI] [Google Scholar]
- Williams O. A.; Hees J.; Dieker C.; Jäger W.; Kirste L.; Nebel C. E. Size-Dependent Reactivity of Diamond Nanoparticles. ACS Nano 2010, 4, 4824–4830. 10.1021/nn100748k. [DOI] [PubMed] [Google Scholar]
- Williams O. A.; Douhéret O.; Daenen M.; Haenen K.; O̅sawa E.; Takahashi M. Enhanced diamond nucleation on monodispersed nanocrystalline diamond. Chem. Phys. Lett. 2007, 445, 255–258. 10.1016/j.cplett.2007.07.091. [DOI] [Google Scholar]
- Barna P. B.; Adamik M. Fundamental structure forming phenomena of polycrystalline films and the structure zone models. Thin Solid Films 1998, 317, 27–33. 10.1016/S0040-6090(97)00503-8. [DOI] [Google Scholar]
- Leeds S. M.; Davis T. J.; May P. W.; Pickard C. D. O.; Ashfold M. N. R. Use of different excitation wavelengths for the analysis of CVD diamond by laser Raman spectroscopy. Diamond Relat. Mater. 1998, 7, 233–237. 10.1016/S0925-9635(97)00261-6. [DOI] [Google Scholar]
- Parker J. H.; Feldman D. W.; Ashkin M. Raman Scattering by Silicon and Germanium. Phys. Rev. 1967, 155, 712–714. 10.1103/PhysRev.155.712. [DOI] [Google Scholar]
- Cerdeira F.; Fjeldly T. A.; Cardona M. Raman study of the interaction between localized vibrations and electronic excitations in boron-doped silicon. Phys. Rev. B: Condens. Matter Mater. Phys. 1974, 9, 4344–4350. 10.1103/PhysRevB.9.4344. [DOI] [Google Scholar]
- Chandrasekhar M.; Chandrasekhar H. R.; Grimsditch M.; Cardona M. Study of the localized vibrations of boron in heavily doped Si. Phys. Rev. B: Condens. Matter Mater. Phys. 1980, 22, 4825–4833. 10.1103/PhysRevB.22.4825. [DOI] [Google Scholar]
- Fraga M. A.; Massi M.; Oliveira I. C.; Maciel H. S.; dos Santos Filho S. G.; Mansano R. D. Nitrogen doping of SiC thin films deposited by RF magnetron sputtering. J. Mater. Sci.: Mater. Electron. 2008, 19, 835–840. 10.1007/s10854-007-9487-y. [DOI] [Google Scholar]
- Neri F.; Trusso S.; Vasi C.; Barreca F.; Valisa P. Raman microscopy study of pulsed laser ablation deposited silicon carbide films. Thin Solid Films 1998, 332, 290–294. 10.1016/S0040-6090(98)00994-8. [DOI] [Google Scholar]
- Lattemann M.; Nold E.; Ulrich S.; Leiste H.; Holleck H. Investigation and characterisation of silicon nitride and silicon carbide thin films. Surf. Coat. Technol. 2003, 174–175, 365–369. 10.1016/S0257-8972(03)00695-9. [DOI] [Google Scholar]
- Pascual E.; Andújar J. L.; Fernández J. L.; Bertran E. Optical and structural characterization of hydrogenated amorphous silicon carbide thin films prepared by r.f. plasma chemical vapour deposition. Diamond Relat. Mater. 1995, 4, 1205–1209. 10.1016/0925-9635(95)00296-0. [DOI] [Google Scholar]
- Ferrari A. C.; Robertson J. Raman spectroscopy of amorphous, nanostructured, diamond–like carbon, and nanodiamond. Philos. Trans. R. Soc. London, Ser. A 2004, 362, 2477–2512. 10.1098/rsta.2004.1452. [DOI] [PubMed] [Google Scholar]
- Ferrari A. C.; Robertson J. Origin of the 1150 cm–1 Raman mode in nanocrystalline diamond. Phys. Rev. B: Condens. Matter Mater. Phys. 2001, 63, 121405 10.1103/PhysRevB.63.121405. [DOI] [Google Scholar]
- Ballutaud D.; Jomard F.; Kociniewski T.; Rzepka E.; Girard H.; Saada S. Sp3/sp2 character of the carbon and hydrogen configuration in micro- and nanocrystalline diamond. Diamond Relat. Mater. 2008, 17, 451–456. 10.1016/j.diamond.2007.10.004. [DOI] [Google Scholar]
- Taylor A.; Fendrych F.; Fekete L.; Vlček J.; Řezáčová V.; Petrák V.; Krucký J.; Nesládek M.; Liehr M. Novel high frequency pulsed MW-linear antenna plasma-chemistry: Routes towards large area, low pressure nanodiamond growth. Diamond Relat. Mater. 2011, 20, 613–615. 10.1016/j.diamond.2011.01.003. [DOI] [Google Scholar]
- Fortunato W.; Chiquito A. J.; Galzerani J. C.; Moro J. R. Crystalline quality and phase purity of CVD diamond films studied by Raman spectroscopy. J. Mater. Sci. 2007, 42, 7331–7336. 10.1007/s10853-007-1575-0. [DOI] [Google Scholar]
- Silva F.; Gicquel A.; Tardieu A.; Cledat P.; Chauveau T. Control of an MPACVD reactor for polycrystalline textured diamond films synthesis: role of microwave power density. Diamond Relat. Mater. 1996, 5, 338–344. 10.1016/0925-9635(95)00428-9. [DOI] [Google Scholar]
- Palosz B.; Grzanka E.; Gierlotka S.; Steĺmakh S.; Pielaszek R.; Bismayer U.; Neuefeind J.; Weber H. P.; Proffen T.; Von Dreele R.; Palosz W. Analysis of short and long range atomic order in nanocrystalline diamonds with application of powder diffractometry. Z. Kristallogr. - Cryst. Mater. 2002, 217, 497. 10.1524/zkri.217.10.497.20795. [DOI] [Google Scholar]
- Herzinger C. M.; Johs B.; McGahan W. A.; Woollam J. A.; Paulson W. Ellipsometric determination of optical constants for silicon and thermally grown silicon dioxide via a multi-sample, multi-wavelength, multi-angle investigation. J. Appl. Phys. 1998, 83, 3323–3336. 10.1063/1.367101. [DOI] [Google Scholar]
- Edwards D. F.; Philipp H. R.. Cubic Carbon (Diamond). In Handbook of Optical Constants of Solids; Palik E. D., Ed.; Academic Press: Boston, 1985; pp 665–673. [Google Scholar]
- Williams M. W.; Arakawa E. T. Optical properties of glassy carbon from 0 to 82 eV. J. Appl. Phys. 1972, 43, 3460–3463. 10.1063/1.1661738. [DOI] [Google Scholar]
- Larruquert J. I.; Rodríguez-de Marcos L. V.; Méndez J. A.; Martin P. J.; Bendavid A. High reflectance Ta-C coatings in the extreme ultraviolet. Opt. Express 2013, 21, 27537–27549. 10.1364/OE.21.027537. [DOI] [PubMed] [Google Scholar]
- Ishii M.; Nakashima K.; Tajima I.; Yamamoto M. Properties of silicon surface cleaned by hydrogen plasma. Appl. Phys. Lett. 1991, 58, 1378–1380. 10.1063/1.105211. [DOI] [Google Scholar]
- Qin S.; Bernstein J. D.; Chan C. Hydrogen etching for semiconductor materials in plasma doping experiments. J. Electron. Mater. 1996, 25, 507–511. 10.1007/BF02666628. [DOI] [Google Scholar]
- Alterovitz S. A.; Woollam J. A.. Cubic Silicon Carbide (β-SiC) A2. In Handbook of Optical Constants of Solids; Palik E. D., Ed.; Academic Press: Burlington, 1997; pp 705–707. [Google Scholar]
- Larruquert J. I.; Pérez-Marín A. P.; García-Cortés S.; Rodríguez-de Marcos L.; Aznárez J. A.; Méndez J. A. Self-consistent optical constants of SiC thin films. J. Opt. Soc. Am. A 2011, 28, 2340–2345. 10.1364/JOSAA.28.002340. [DOI] [PubMed] [Google Scholar]
- Fodor B.; Kozma P.; Burger S.; Fried M.; Petrik P. Effective medium approximation of ellipsometric response from random surface roughness simulated by finite-element method. Thin Solid Films 2016, 617, 20–24. 10.1016/j.tsf.2016.01.054. [DOI] [Google Scholar]
- Petrik P.; Biró L. P.; Fried M.; Lohner T.; Berger R.; Schneider C.; Gyulai J.; Ryssel H. Comparative study of surface roughness measured on polysilicon using spectroscopic ellipsometry and atomic force microscopy. Thin Solid Films 1998, 315, 186–191. 10.1016/S0040-6090(97)00349-0. [DOI] [Google Scholar]
- Koh J.; Lu Y.; Wronski C. R.; Kuang Y.; Collins R. W.; Tsong T. T.; Strausser Y. E. Correlation of real time spectroellipsometry and atomic force microscopy measurements of surface roughness on amorphous semiconductor thin films. Appl. Phys. Lett. 1996, 69, 1297–1299. 10.1063/1.117397. [DOI] [Google Scholar]
- Collins R. W.; Cong Y.; Kim Y. T.; Vedam K.; Liou Y.; Inspektor A.; Messier R. Real-time and spectroscopic ellipsometry characterization of diamond and diamond-like carbon. Thin Solid Films 1989, 181, 565–578. 10.1016/0040-6090(89)90525-7. [DOI] [Google Scholar]
- Collins R. W.; Cong Y.; Nguyen H. V.; An I.; Vedam K.; Badzian T.; Messier R. Real time spectroscopic ellipsometry characterization of the nucleation of diamond by filament-assisted chemical vapor deposition. J. Appl. Phys. 1992, 71, 5287–5289. 10.1063/1.350544. [DOI] [Google Scholar]
- Li X.; Hayashi Y.; Nishino S. In-situ ellipsometry study of initial stage of bias-enhanced nucleation and heteroepitaxy of diamond on silicon(100) by hot filament chemical vapor deposition. Diamond Relat. Mater. 1997, 6, 1117–1123. 10.1016/S0925-9635(97)00125-8. [DOI] [Google Scholar]