Abstract
We have determined the time-dependent displacement fields in molecular sub-micrometer thin films as response to femtosecond and picosecond laser pulse heating by time-resolved X-ray diffraction. This method allows a direct absolute determination of the molecular displacements induced by electron–phonon interactions, which are crucial for, for example, charge transport in organic electronic devices. We demonstrate that two different modes of coherent shear motion can be photoexcited in a thin film of organic molecules by careful tuning of the laser penetration depth relative to the thickness of the film. The measured response of the organic film to impulse heating is explained by a thermoelastic model and reveals the spatially resolved displacement in the film. Thereby, information about the profile of the energy deposition in the film as well as about the mechanical interaction with the substrate material is obtained.
1. Introduction
When short laser pulses interact with a molecular solid, the energy is transferred to the electronic structure within 1 fs.1 The dynamical aspects of this process are key in, for example, charge transport in organic electronic devices.2,3 Subsequent to excitation, the energy is transferred to crystal lattice vibrations via electron–phonon coupling on the time scale up to 10 ps. A sudden release of thermal stress can create high-frequency coherent acoustic phonons traveling inside the film as either longitudinal4,5 or transverse6 displacement waves. The shape of the energy distribution throughout the film determines the pattern of atomic displacements. Two extreme cases can be distinguished: (i) if the thickness of the film is significantly larger than the penetration length of the excitation laser pulse, the thermal stress is localized near the thin-film surface. The stress field releases a strain pulse twice as wide as the penetration depth and moving at the speed of sound from the surface to the substrate interface. In the opposite regime (ii), the film thickness is small compared to the penetration depth of the exciting laser pulse, and the film will experience a nearly uniform thermal stress after excitation. Then, the traveling pulse is wider than the film thickness. Hence, it is represented by a strain step moving at the speed of sound through the film, dividing two regions with uniform, but different strains. In both cases, (i) and (ii), the moving strain field bounces back and forth within the thin film by reflection at the interfaces of the thin film. While it experiences a phase shift of π and no significant damping at the interface to air, reflection at the film–substrate interface contains information about the substrate material and possible interfacial layers.7,8 If the film is strongly bound to a harder substrate, the strain wave is reflected without a phase shift. In this case, the phase of the wave is restored after two reflections at each interface, that is, after traveling a distance of four times the film thickness.4 Strain waves in thin films have previously been studied by the change of reflectivity of optical light,5 probed indirectly by the first-order perturbation of the material permittivity.9−12 Quantitative measurements of the displacement are therefore only possible with prior knowledge of the photoelastic constants of the investigated material. Time-resolved X-ray scattering techniques have been successfully used to obtain the exact atomic displacements and thus the shape of the light-induced strain waves.13−17 Their nanometer-sized shape is not discernible by optical wavelengths. We demonstrate that time-resolved grazing incidence X-ray diffraction (GIXD) directly measures the displacement waves in molecular organic films to a detail that allows us to distinguish between different excitation mechanisms. There have been a number of recent time-resolved X-ray studies of phonon dynamics in inorganic materials,18 but herein the focus is on how the organic matter is impacted by light. The light–solid matter interactions of the organic material are central and have been addressed in previous studies involving femtosecond lasers19 but rarely with time-resolved diffraction.
2. Results and Discussion
Thin films of perylene were chosen as a model system. The films consist of micrometer-sized crystallites of the monoclinic α-perylene polymorph20 (space group P21/a) with the a- and b-axis in the plane of the glass substrate and the c-axis thus inclined with respect to the surface plane by β = 100:55°, as determined by GIXD21 (Figure 1a). This geometry gives rise to anisotropic thermoelastic properties including a thermally induced shear movement in the monoclinic angle β.22 After optical excitation to the S1 state (above 2.6 eV), α-perylene quickly undergoes structural relaxation to a trapped dimer state.23 The excess vibrational energy is released within less than 1 ps,24 making coherent excitation of acoustic waves possible. Time-resolved optical reflectivity measurements showed two different strain waves propagating at different speeds, 955 and 4460 m/s (see the Supporting Information). The observed values match the speed of sound of the corresponding transverse acoustic (TA) and longitudinal acoustic (LA) modes in single crystals.25
Figure 1.
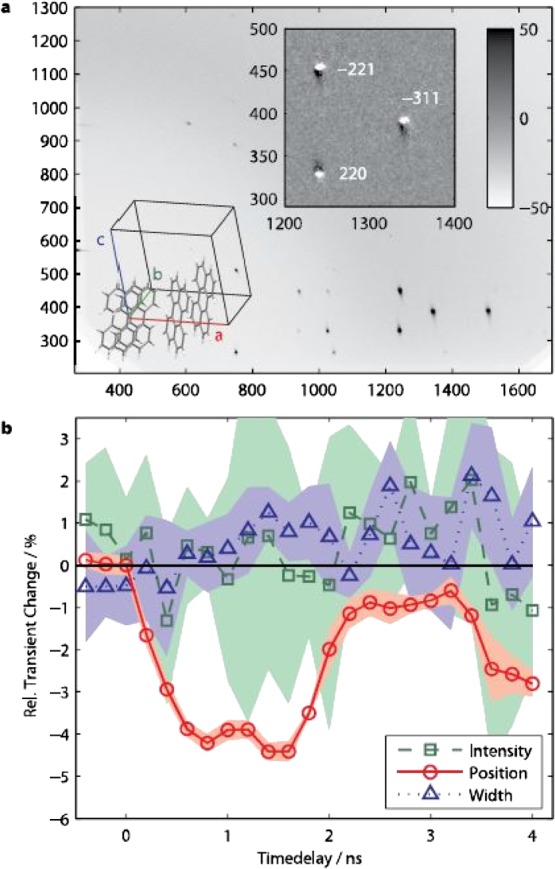
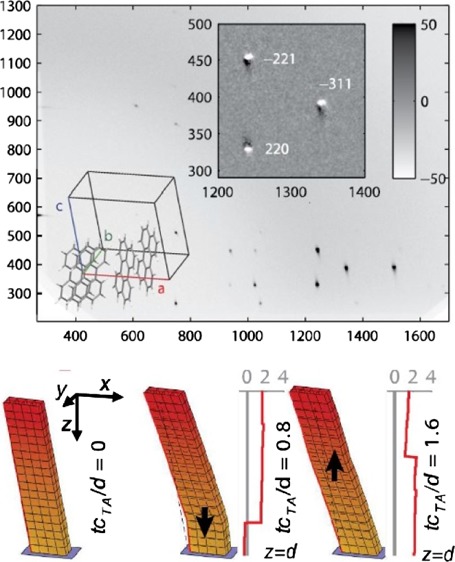
(a) GIXD pattern from a thin polycrystalline film of perylene in detector pixel units (to remain as close to the raw data as possible). The beam center is at (266, 201), and the (horizontal) sample horizon can be discerned near the horizontal axis. Upper inset: Difference of diffraction patterns taken at positive (+600 ps) and negative X-ray probe pulse time delay, showing a small shift of peak positions. Lower inset: Monocline α-perylene unit cell with parameters a = 11:277 Å, b = 10:826 Å, c = 10:263 Å, and β = 100:55°. (b) Transient changes of the peak area, position, and width of the reflection in the Qz-direction, relative to the unexcited state. The shaded areas represent 90% Student’s t-distribution certainty intervals from five repeated measurements.
Time-resolved GIXD measurements were carried out at the optical pump/X-ray probe setup beamline ID09b at the European Synchrotron Radiation Facility (ESRF).26 Thin-film samples of 3 × 3 mm2 size were excited by Ti:sapphire laser pulses of 390 nm wavelength and approximately 100 fs pulse length with angles of incidence of 10° [case (i)] as well as 90° [case (ii)] with respect to the film surface. The thin-film structure after laser excitation was probed by 100 ps short X-ray pulses of 15 and 18 keV at an incidence angle of 0.3°. The time-resolved GIXD signal shows lattice distortions through individual shifts ΔQz of all Bragg reflections along the surface normal of the film (Figure 1a, inset). These shifts are relatively long-lived with a lifetime of 1–2 μs (data not shown), superposed by smaller amplitude oscillations until about 10 ns after excitation (Figures 1b and 3).
Figure 3.
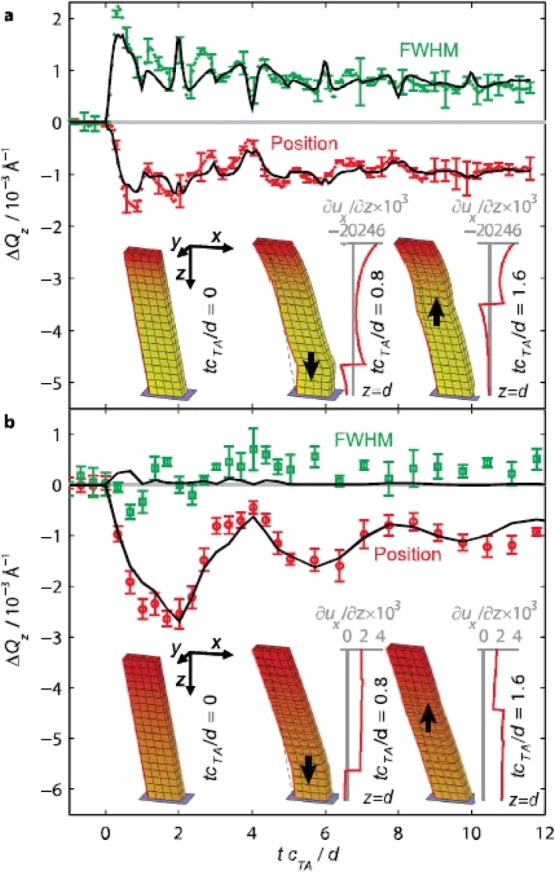
Data: Transient changes of the reflection width and position in the Qz-direction, measured from two different α-perylene films at different experimental conditions: (a) film thickness 700 nm/d = 0.17 and (b) film thickness 300 nm/d = 2.16. Error bars represent 90% Student’s t-distribution certainty intervals of the parameter mean determined from two and six repeated measurements in cases (a,b), respectively. Solid lines: Fit of modeled X-ray diffraction data from an α-perylene crystal, distorted by a strain wave as described by a classical mechanic model. The peak profiles were parameterized by split Pearson VII functions29 (the curves of remaining parameters are shown in the Supporting Information). The transient time delay is expressed in units of the propagation time of a TA wave from the film surface to the substrate interface d/cTA. Both datasets were acquired with polychromatic X-radiation (3% BW). Insets: Schematic α-perylene crystallite column distorted by the displacement fields fitted to either measured films at different points of time (displacement exaggerated by a factor of 200). Dashed lines: at times tcTA/d > 0 indicate the crystal position in the ground state. The red contrast represents the thermal energy dissipated at time zero by light excitation (color version online; animated movie in the Supporting Information). The fitted shear strain component is shown to the right of the columns with tcTA/d > 0.
The integrated Bragg peak intensity, governed by the unit cell structure factor, remains unchanged, suggesting that no structural relaxations occur within the unit cell. This excludes the trapped dimer state as the origin of the lattice distortions. The transient positions of 16 most intense Bragg reflections were used for refining the average changes of the unit cell parameters in the entire probed film volume. Knowing the transient unit cell changes gives access to the average transient strain in the film (Figure 2), which exhibits an expansion in direction perpendicular to the surface (z-direction) superposed by a coherently oscillating shear motion in direction of the unit cell’s a-axis (x-direction). The oscillation period T is related to the speed of sound cTA of the corresponding shear mode by T = 4d/cTA,4 in agreement with the speed of sound found by optical reflectivity and the measured film thickness of d = 700 nm as measured by atomic force microscopy (AFM). Coherent oscillations of the faster longitudinal mode could not be resolved. The average transient strain within the observed time range, 0–4 ns, shows similar relative values as the static thermal strain (Figure 2).
Figure 2.
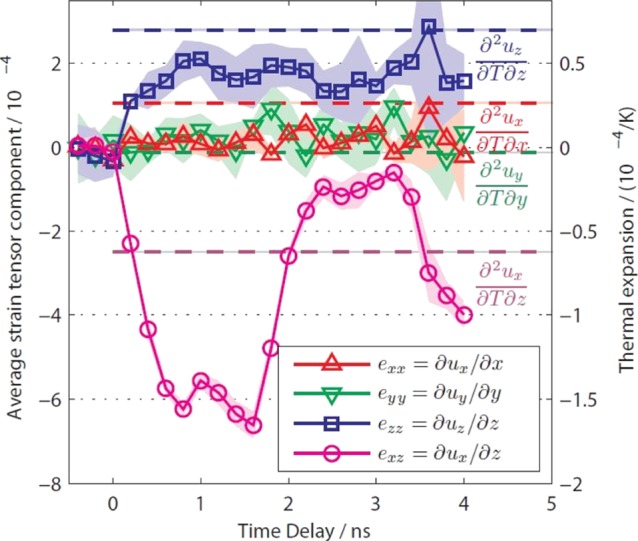
Transient changes of strain components εij = δui/δxj (left scale) averaged over the entire measured perylene film of 700 nm thickness. The transient strain was obtained from a unit cell refinement to Bragg peak positions recorded with monochromatic X-rays. The shaded areas represent 90% Student’s t-distribution certainty intervals of the mean strain determined from five repeated measurements. The dashed horizontal lines represent the corresponding components of the static thermal displacement gradient tensor as labeled on the right side (scale to the right; data measured from the same sample at beamline BW2, HASYLAB).
Together with the long lifetime of the strain and the time-independent structure factor, this emphasizes the thermal origin of the transient observations.
The X-ray diffraction signal from a distorted crystal, in the kinematical approximation, is given by the sum of phase factors of all diffracting unit cells in the scattering material.27 Small distortions from the periodic structure lead to changes in the vicinity of Bragg reflections.28 As the main strain components, δux = δz and δuz = δz (where ux and uz are components of the three-dimensional displacement u), do not change the distances in the ab-plane of the crystal, the Bragg peak profiles only change in Qz. Figure 3 shows the transient changes of the peak shape of the 2̅21-reflection that is the reflection with the most significant chance in the Qz-direction, obtained from two experiments with different excitation light penetration depths relative to the film thickness (see the Supporting Information). In case (i), where μ < d (Figure 3a), the peak shape exhibits a complex temporal behavior, whereas in case (ii), where μ > d, only the positions of the Bragg peaks show significant transient changes (Figure 3b). While the latter case can be approximately described by oscillatory changes in the lattice parameters of the entire X-ray probed sample volume, a more complex distortion model is needed to describe the former case. To that end, the detailed peak profile was simulated (cf. Supporting Information). Both nonzero strain components are time-dependent functions of the depth z and were calculated in a mechanical model using the formalism established by Thomsen et al.,12 assuming a thermal stress field exponentially decaying with z. The transient changes of the simulated and measured peak profiles were both parameterized using an asymmetric peak profile (“split Pearson VII”29) and could thus be directly compared (cf. Figure 3 for global fits) (see the Supporting Information).
Considering the simplicity of the model, the fits produce a remarkably good agreement with the observed feature-rich peak shape changes. The fit results show coherent strain pulses up to an amplitude of 3 × 10–3 and a bandwidth of 1 GHz, making up a displacement of the order of 5 Å for the crystal surface. The wave packet spectrum of the strain pulse in case (i) (Figure 3, inset) is rather broad and accordingly affects the shape of the Bragg peak as seen in the rise of peak width. The strain profile in case (ii) is more uniform and hence does not lead to a similar increase in peak width but still shifts the Bragg peak. In both measurements shown in Figure 3, the refined reflection coefficient of the transverse wave at the film–substrate interface is 0.7, in good agreement with the expected value of 0.64 for a perfectly coupled α-perylene–glass interface as calculated from the acoustic impedances of both materials. The acoustic impedance Z = ρcs was calculated from the speed of sound cTA measured by optical reflectivity and the density ρ. The tabulated values were used for glass.
The refined values of the penetration depth of the excitation light, 140 and 610 nm, differ from the expected values assuming linear light absorption, 570 and 750 nm, for the cases (i) and (ii), respectively.
This supports the presence of nonlinear and two-photon absorption. Further evidence for this interpretation is given by the fact that the excitation pulse fluence used in the time-resolved GIXD experiment (approx. 3.5 and 15.3 mJ/cm2) was above the threshold reported for the linear increase of fluorescence with increasing excitation fluence (1.5 mJ/cm2).30 In future more detailed models, one could consider including stress profiles of a more complex nature than the exponential decay.
3. Conclusions
We have determined the detailed transverse atomic displacement wave profile in perylene thin films and demonstrated that the form of the strain wave can be controlled via the ratio between the excitation depth and the film thickness. The accurate atomic displacements of the TA waves were measured by time-resolved GIXD and fitted by a thermoelastic model including the absorption depth of the excitation light with the focus being on the organic layer. The reflection of the TA wave at the film–substrate interface was shown to be determined by the mechanical properties of most likely both materials, suggesting a direct mechanic contact without an interfacial layer. This time-resolved X-ray approach to light-induced distortion in materials does reach far beyond perylene and will certainly prove very valuable for charge transport mechanisms that are key in, for example, perovskites and other optoelectronic materials.
4. Experimental Section
4.1. Sample Preparation
Thin films of perylene were grown by vapor deposition on microscope glass slides at deposition rates of 0.2–0.4 mm/s to thicknesses ranging from 100 to 1000 nm.
The linear light absorption coefficients of the films were measured using an optical microscope equipped with a fiber spectrometer. The effective penetration depths in the linear absorption regime were calculated from the absorption coefficients, also including refraction at the film surface.
4.2. Static Strain Measurements
The thermal expansion coefficients in the temperature range 20–60 °C were determined by temperature-dependent GIXD measurements at beamline BW2, HASYLAB.
4.3. Time-Resolved GIXD
Time-resolved GIXD measurements were carried out at the optical pump/X-ray probe setup beamline ID09b at the European Synchrotron Radiation Facility (ESRF).26 Thin-film samples of 3 il3 mm2 size were excited by Ti:sapphire laser pulses of 390 nm wavelength and ∼100 fs pulse length with angles of incidence of 10° [case (i)] as well as 90° [case (ii)] with respect to the film surface.
The thin-film structure after laser excitation was probed by 100 ps short X-ray pulses of 15 and 18 keV at an incidence angle of 0.3°, sufficiently above the critical angle of SiO2 to prevent additional diffraction from X-rays which are totally reflected from the film substrate. The diffraction signal from the stroboscopically repeated pump–probe experiment was integrated on a charge-coupled device area detector while rotating the thin-film sample around the surface normal (10°/s) during exposure in order to average the signal from a large number of crystallites in the X-radiated footprint.
4.4. Mechanical Modeling
The transient displacement model described by Thomsen et al.12 was applied independently for both longitudinal and transversal displacements in the c*-direction of the α-perylene unit cell. The amplitudes of the waves reflected from the film–substrate interface were reduced according to the reflection coefficients calculated from the acoustic impedances of the materials at the interface, characteristic for a direct mechanical coupling. Changes of the thermal stress field due to thermal diffusion were ignored, as they occur on much longer timescales. The ratio of the time-averaged strain after excitation was fixed to the measured ratio of (∂ux/∂z)/(∂uz/∂z) = −2.0 (as seen in Figure 2).
The transient changes of the X-ray diffraction peaks were modeled by applying the spatial displacements ux and uz to the lattice sum of phase factors from unperturbed ab lattice planes. The resulting profile, a function of the z-component Qz of the wave vector transfer Q, was convoluted with a broad peak profile, accounting for the alignment distribution of crystallites in the film and for the instrumental resolution function. The resulting profile was analyzed by a split Pearson VII profile29 and compared to the measured profile in the Qz-direction.
The experimental data shown in Figure 3 were χ2-fitted by the modeled data, taking into account the peak shape parameters by a split Pearson VII while refining the penetration depth of the excitation light, the reflection coefficient rTA of the TA wave at the film–substrate interface, the strain amplitude, and the fraction of the excited sample volume. The speeds of sound of the LA and TA waves were fixed at the values determined by transient optical reflectivity. The film thickness was fixed at the values determined by the observed oscillatory features in the GIXD data, giving a value inside the uncertainty limits of the thickness measurements by AFM. The reflection coefficient rLA was set to the expected value of a perfectly coupled α-perylene–glass interface (0.34), calculated from the acoustic impedance and using tabulated values for the mass density of both materials.
Acknowledgments
The help provided by E. Pontecorvo at the ID09B beamline as well as S. Nozawa, K. Ichiyanagi, T. Sato, M. Chollet, and L. Guerin at beamline NW14 is very much appreciated. This work was made possible through the support from the Danish National Science Foundation’s Centre for Molecular Movies. Financial support from DAN-SCATT is gratefully acknowledged.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b01400.
Transient optical reflectivity measurements and solution of strain field refinement (PDF)
Author Present Address
∇ SwissFEL Bernina, Paul Scherrer Institute, WBBA/022, 5232 Villigen PSI, Switzerland (H.T.L.).
Author Present Address
○ Ferrosan Medical, Sydmarken 5, 2860 Søborg, Danmark (P.H.).
Author Present Address
⧫ European XFEL GmbH, Holzkoppel 4, 22869 Schenefeld, Germany (D.K.).
Author Present Address
†† Photon Factory, Institute of Materials Structure Science, High Energy Accelerator Research Organization (KEK) 1-1 Oho, Tsukuba, Ibaraki, 305-0801, Japan (S.-I.A.).
Author Present Address
‡‡ Novozymes, Krogshøjvej 36, 2880 Bagsværd (T.S.K.).
The authors declare no competing financial interest.
Supplementary Material
References
- Cavalieri A. L.; Müller N.; Uphues T.; Yakovlev V. S.; Baltuška A.; Horvath B.; Schmidt B.; Blümel L.; Holzwarth R.; Hendel S.; Drescher M.; Kleineberg U.; Echenique P. M.; Kienberger R.; Krausz F.; Heinzmann U. Attosecond Spectroscopy in Condensed Matter. Nature 2007, 449, 1029–1032. 10.1038/nature06229. [DOI] [PubMed] [Google Scholar]
- Giuggioli L.; Andersen J. D.; Kenkre V. M. Mobility Theory of Intermediate-Bandwidth Carriers in Organic Crystals: Scattering by Acoustic and Optical Phonons. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 67, 045110. 10.1103/physrevb.67.045110. [DOI] [Google Scholar]
- Bredas J.-L.; Silbey R. CHEMISTRY: Excitons Surf Along Conjugated Polymer Chains. Science 2009, 323, 348–349. 10.1126/science.1168821. [DOI] [PubMed] [Google Scholar]
- Thomsen C.; Strait J.; Vardeny Z.; Maris H. J.; Tauc J.; Hauser J. J. Coherent Phonon Generation and Detection by Picosecond Light Pulses. Phys. Rev. Lett. 1984, 53, 989–992. 10.1103/physrevlett.53.989. [DOI] [Google Scholar]
- Kanner G. S.; Vardeny Z. V.; Hess B. C. Picosecond acoustics in polythiophene thin films. Phys. Rev. B: Condens. Matter Mater. Phys. 1990, 42, 5403–5406. 10.1103/physrevb.42.5403. [DOI] [PubMed] [Google Scholar]
- Matsuda O.; Wright O. B.; Hurley D. H.; Gusev V. E.; Shimizu K. Coherent shear phonon generation and detection with ultrashort optical pulses. Phys. Rev. Lett. 2004, 93, 095501. 10.1103/physrevlett.93.095501. [DOI] [PubMed] [Google Scholar]
- Pezeril T.; Leon F.; Chateigner D.; Kooi S.; Nelson K. A. Picosecond Photoexcitation of Acoustic Waves in Locally Canted Gold Films. Appl. Phys. Lett. 2008, 92, 061908. 10.1063/1.2841823. [DOI] [Google Scholar]
- Pezeril T.; Klieber C.; Andrieu S.; Nelson K. A. Optical Generation of Gigahertz-Frequency Shear Acoustic Waves in Liquid Glycerol. Phys. Rev. Lett. 2009, 102, 107402. 10.1103/physrevlett.102.107402. [DOI] [PubMed] [Google Scholar]
- Lin H.-N.; Stoner R. J.; Maris H. J.; Tauc J. Phonon attenuation and velocity measurements in transparent materials by picosecond acoustic interferometry. J. Appl. Phys. 1991, 69, 3816–3822. 10.1063/1.348958. [DOI] [Google Scholar]
- Matsuda O.; Wright O. B.; Hurley D. H.; Gusev V.; Shimizu K. Coherent Shear Phonon Generation and Detection with Picosecond Laser Acoustics. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77, 224110. 10.1103/physrevb.77.224110. [DOI] [Google Scholar]
- Pezeril T.; Ruello P.; Gougeon S.; Chigarev N.; Mounier D.; Breteau J.-M.; Picart P.; Gusev V. Generation and Detection of Plane Coherent Shear Picosecond Acoustic Pulses by Lasers: Experiment and Theory. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 75, 174307. 10.1103/physrevb.75.174307. [DOI] [Google Scholar]
- Thomsen C.; Grahn H. T.; Maris H. J.; Tauc J. Surface Generation and Detection of Phonons by Picosecond Light Pulses. Phys. Rev. B: Condens. Matter Mater. Phys. 1986, 34, 4129–4138. 10.1103/physrevb.34.4129. [DOI] [PubMed] [Google Scholar]
- Bargheer M.; Zhavoronkov N.; Gritsai Y.; Woo J. C.; Kim D. S.; Woerner M.; Elsaesser T. Coherent Atomic Motions in a Nanostructure Studied by Femtosecond X-ray Diffraction. Science 2004, 306, 1771–1773. 10.1126/science.1104739. [DOI] [PubMed] [Google Scholar]
- Larsson J.; Allen A.; Bucksbaum P. H.; Falcone R. W.; Lindenberg A.; Naylor G.; Missalla T.; Reis D. A.; Scheidt K.; Sjogren A.; Sondhauss P.; Wulff M.; Wark J. S. Picosecond X-ray Diffraction Studies of Laser-Excited Acoustic Phonons in InSb. Appl. Phys. A: Mater. Sci. Process. 2002, 75, 467–478. 10.1007/s003390201421. [DOI] [Google Scholar]
- Lindenberg A. M.; Kang I.; Johnson S. L.; Missalla T.; Heimann P. A.; Chang Z.; Larsson J.; Bucksbaum P. H.; Kapteyn H. C.; Padmore H. A.; Lee R. W.; Wark J. S.; Falcone R. W. Time-Resolved X-ray Diffraction from Coherent Phonons During a Laser-Induced Phase Transition. Phys. Rev. Lett. 2000, 84, 111–114. 10.1103/physrevlett.84.111. [DOI] [PubMed] [Google Scholar]
- Sokolowski-Tinten K.; Blome C.; Blums J.; Cavalleri A.; Dietrich C.; Tarasevitch A.; Uschmann I.; Förster E.; Kammler M.; Horn-von-Hoegen M.; von der Linde D. Femtosecond X-ray Measurement of Coherent Lattice Vibrations Near the Lindemann Stability Limit. Nature 2003, 422, 287–289. 10.1038/nature01490. [DOI] [PubMed] [Google Scholar]
- Sondhauss P.; Wark J. S. Extension of the time-dependent dynamical diffraction theory to ‘optical phonon’-type distortions: application to diffraction from coherent acoustic and optical phonons. Acta Crystallogr., Sect. A: Found. Crystallogr. 2003, 59, 7–13. 10.1107/s010876730201704x. [DOI] [PubMed] [Google Scholar]
- Höfer S.; Kämpfer T.; Förster E.; Stöhlker T.; Uschmann I. Communication: The formation of rarefaction waves in semiconductors after ultrashort excitation probed by grazing incidence ultrafast time-resolved x-ray diffraction. Struct. Dynam. 2016, 3, 051101. 10.1063/1.4963011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purdum G. E.; Yao N.; Woll A.; Gessner T.; Weitz R. T.; Loo Y.-L. Understanding Polymorph Transformations in Core-Chlorinated Naphthalene Diimides and their Impact on Thin-Film Transistor Performance. Adv. Funct. Mater. 2016, 26, 2357–2364. 10.1002/adfm.201502412. [DOI] [Google Scholar]
- Camerman A.; Trotter J. The Crystal and Molecular Structure of Perylene. Proc. R. Soc. London, Ser. A 1964, 279, 129–146. 10.1098/rspa.1964.0094. [DOI] [Google Scholar]
- Breiby D. W.; Bunk O.; Andreasen J. W.; Lemke H. T.; Nielsen M. M. Simulating X-ray Diffraction of Textured Films. J. Appl. Crystallogr. 2008, 41, 262–271. 10.1107/s0021889808001064. [DOI] [Google Scholar]
- Botoshansky M.; Herbstein F. H.; Kapon M. Towards a Complete Description of a Polymorphic Crystal: The Example of Perylene. Helv. Chim. Acta 2003, 86, 1113–1128. 10.1002/hlca.200390097. [DOI] [Google Scholar]
- Tanaka J. The Electronic Spectra of Aromatic Molecular Crystals. II. The Crystal Structure and Spectra of Perylene. Bull. Chem. Soc. Jpn. 1963, 36, 1237–1249. 10.1246/bcsj.36.1237. [DOI] [Google Scholar]
- Furube A.; Murai M.; Tamaki Y.; Watanabe S.; Katoh R. Effect of Aggregation on the Excited-State Electronic Structure of Perylene Studied by Transient Absorption Spectroscopy. J. Phys. Chem. A 2006, 110, 6465–6471. 10.1021/jp060649b. [DOI] [PubMed] [Google Scholar]
- Schleifer J.; Kalus J.; Schmelzer U.; Eckold G. Phonon Dispersion in an α-Perylene d12-Crystal at 10 K. Phys. Status Solidi B 1989, 154, 153–166. 10.1002/pssb.2221540114. [DOI] [Google Scholar]
- Wulff M.; Plech A.; Eybert L.; Randler R.; Schotte F.; Anfinrud P. The Realization of Sub-Nanosecond Pump and Probe Experiments at the ESRF. Faraday Discuss. 2003, 122, 13–26. 10.1039/b202740m. [DOI] [PubMed] [Google Scholar]
- Als-Nielsen J.; McMorrow D.. Elements of Modern X-ray Physics; Wiley: New York, 2001. [Google Scholar]
- Warren B.X-Ray Diffraction; Dover Publications, 1990. [Google Scholar]
- Toraya H. Array-Type Universal Profile Function for Powder Pattern Fitting. J. Appl. Crystallogr. 1990, 23, 485–491. 10.1107/s002188989000704x. [DOI] [Google Scholar]
- Tamai N.; Porter C. F.; Masuhara H. Femtosecond transient absorption spectroscopy of a single perylene microcrystal under a microscope. Chem. Phys. Lett. 1993, 211, 364–370. 10.1016/0009-2614(93)87074-d. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


