Natural Indices for the Chemical Hardness/Softness of Metal Cations and Ligands

Abstract

Quantitative understanding of reactivity and stability for a chemical species is fundamental to chemistry. The concept has undergone many changes and additions throughout the history of chemistry, stemming from the ideas such as Lewis acids and bases. For a given complexing ligand (Lewis base) and a group of isovalent metal cations (Lewis acids), the stability constants of metal–ligand (ML) complexes can simply correlate to the known properties of metal ions [ionic radii (r_Mⁿ⁺), Gibbs free energy of formation (ΔG°_f,Mⁿ⁺), and solvation energy (ΔG°_s,Mⁿ⁺)] by 2.303RT log K_ML = (α*_MLΔG°_f,Mⁿ⁺ – β*_MLr_Mⁿ⁺ + γ*_MLΔG°_s,Mⁿ⁺ – δ*_ML), where the coefficients (α*_ML, β*_ML, γ*_ML, and intercept δ*_ML) are determined by fitting the equation to the existing experimental data. Coefficients β*_ML and γ*_ML have the same sign and are in a linear relationship through the origin. Gibbs free energies of formation of cations (ΔG°_f,Mⁿ⁺) are found to be natural indices for the softness or hardness of metal cations, with positive values corresponding to soft acids and negative values to hard acids. The coefficient α*_ML is an index for the softness or hardness of a complexing ligand. Proton (H⁺) with the softness index of zero is a unique acid that has strong interactions with both soft and hard bases. The stability energy resulting from the acid–base interactions is determined by the term α*_MLΔG°_f,Mⁿ⁺; a positive product of α*_ML and ΔG°_f,Mⁿ⁺ indicates that the acid–base interaction between the metal cation and the complexing ligand stabilizes the complex. The terms β*_MLr_Mⁿ⁺ and γ*_MLΔG°_s,Mⁿ⁺, which are related to ionic radii of metal cations, represent the steric and solvation effects of the cations. The new softness indices proposed here will help to understand the interactions of ligands (Lewis bases) with metal cations (Lewis acids) and provide guidelines for engineering materials with desired chemical reactivity and selectivity. The new correlation can also enhance our ability for predicting the speciation, mobility, and toxicity of heavy metals in the earth environments and biological systems.

Introduction

Many chemical reactions can be generalized as Lewis acid–base reactions in which the Lewis acid is an electron acceptor and the Lewis base is an electron donor.^1,2 If Lewis acids are metal cations, the Lewis bases are called ligands. A metal–ligand complex formation can be generalized as

1

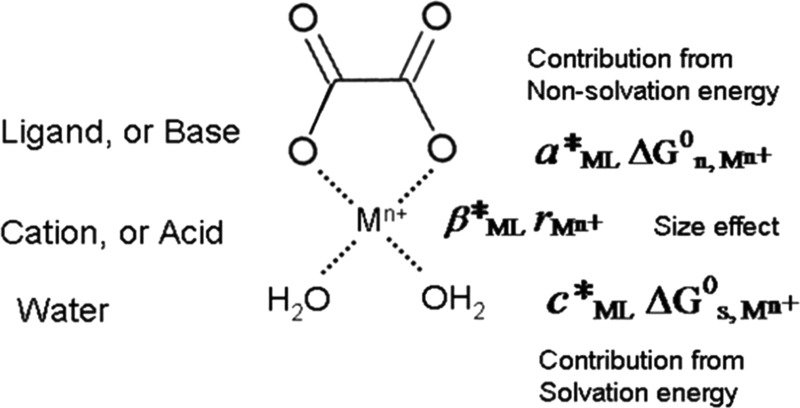
where M is a Lewis acid that can accept electrons and L is a Lewis base that can donate electrons (Figure 1). Stability of the Lewis acid–base complex was tackled by pioneers such as Williams and Irving, who proposed that stability of transition metal–ligand complexes were related to ionic radii and the second ionization potentials of the metals concerned (the Irving–Williams order).³ Much progress was made with the development of hard/soft acids/bases (HSABs) principle by Pearson^1,2 and its explanation for observed stabilities in Lewis acid/base reactions. Later, Klopman tried to quantify the HSAB principle by using terms from ionic interaction (contribution from charge-controlled reaction) and covalent interaction (contribution from frontier molecular orbital) through a generalization of Fukuis frontier orbital’s density.⁴ Hancock and Martell⁵ summarized empirical parameters for estimating stability constants of some acid–base compound ligands based on HSAB principle by considering contributions from ionic interactions (E_A·E_B), covalent bonding (C_A·C_B), and size effects (D_A·D_B) using an equation

2

Parameters E and C are the tendency of acid A and base B to undergo ionic and covalent bonding, respectively. The method is very limited in predicting stabilities of metal complexes.

Figure 1.

Diagram schematically showing metal–ligand (ML) complex in water and different energy contributions to the formation of an aqueous metal complex.

Parr and Pearson used the density functional theory (DFT) to calculate the absolute hardness of Lewis acids and bases.⁶ The absolute hardness (η) is the second derivative of the energy with respect to the number of electrons with a fixed external potential analogous to the absolute electronegativity. The absolute softness is reciprocal value of hardness (1/η).⁷ The hardness/softness concept was supported by the DFT calculations.⁸⁻¹⁰ However, the absolute hardness of acids and bases cannot be directly used to calculate the stability constants of acid–base complexes. Furthermore, there are still some exceptions to the definition for acids such as H⁺ and Be²⁺.

Results and Discussion

We here report a linear free energy relationship that correlates the stability constants of metal–ligand (ML) complexes to the known properties of metal ions including ionic radius (r_Mⁿ⁺), Gibbs free energy of formation (ΔG°_f,Mⁿ⁺), and solvation energy (ΔG°_s,Mⁿ⁺). In this correlation, Gibbs free energy of formation (ΔG°_f,Mⁿ⁺) of a cation is broken into two parts—the solvation energy (ΔG°_s,Mⁿ⁺) and the nonsolvation energy (ΔG°_n,Mⁿ⁺) (see the list of Symbols Used for details)

3

The solvation energy of a cation can be calculated with Born equation

4

where ε is the dielectric constant of water (78.47 at 25 °C). ΔG°_s,Mⁿ⁺ is negative. The parameter ω_Mⁿ⁺ is the Born solvation coefficient of the cation, which can be further related to the radius of the cation (r_Mⁿ⁺).¹¹⁻¹³ The parameter ω_Mⁿ⁺ is the Born solvation coefficients for aqueous cations and can be calculated by

4a

In eq 4a, ω^abs_H⁺ is the absolute Born solvation coefficient of H⁺ (53.87 kcal/mol) and ω^abs_Mⁿ⁺ is the absolute Born solvation coefficient of the cations with the effective electrostatic radii of aqueous ions (r_e,Mⁿ⁺). They can be calculated by

4b

4c

The solvation energies of divalent and trivalent cations have been calculated and tabulated (Table 1)^12,13 using ionic radii provided in refs (14−16).

Table 1. Ionic Radii, Solvation Energies, Gibbs Free Energy of Formation of Divalent Cations (or, Natural Indices for Lewis Acid Softness), and Stability Constants for Some Metal–Ligand Complexes Families^a,b,c.

				log KML
M2+	rM2+ (Å)	ΔGs,M2+ (aq)	ΔGf,M2+ (aq)	acetate (exp.)	acetate (calcd ±0.25)	oxalate (exp.)	oxalate (calcd ±0.32)	ADP (exp.)	ADP (calcd ±0.19)	H-ADP (exp.)	H-ADP (calcd ±0.18)	sulfuric acid (exp.)	sulfuric acid (calcd ±0.16)
Pt	0.80	–141.87	54.80		2.08		9.34		5.80		3.39		2.02
Pd	0.80	–141.87	42.49		1.97		8.97		5.57		3.54		2.04
Hg	1.02	–119.71	39.36		2.60		8.48		5.84		3.13		2.11
Cu	0.73	–144.83	15.55	2.22	1.91	6.23	6.00	5.90	5.28	3.16	3.57	2.36	2.31
Pb	1.18	–107.89	–5.79	2.68	2.30		9.26		4.92		3.78	2.75	2.01
Sn	1.11	–112.91	–6.63		2.27		8.22		4.96		3.72		2.11
Ni	0.70	–147.75	–10.90	1.43	1.60	5.16	5.21	4.50	4.75	4.24	3.93	2.32	2.36
Co	0.74	–144.35	–13.00	1.46	1.68	4.72	5.16	4.20	4.76	4.25	3.90	2.36	2.37
Cd	0.95	–125.31	–18.57	1.93	2.04		6.07		4.78		3.80	2.46	2.29
Fe	0.77	–141.04	–21.87	1.40	1.69		4.95		4.63		3.95	2.20	2.38
Zn	0.75	–143.30	–35.17	1.57	1.52	4.87	4.45	4.28	4.37	4.20	4.13	2.38	2.42
Mn	0.82	–136.46	–55.20	1.40	1.51	3.95	4.12	4.05	4.06	4.17	4.29	2.26	2.44
Be	0.45	–175.02	–89.80		–0.01	(4.08)	4.49		2.77		5.58	1.95	2.33
Mg	0.72	–145.80	–108.83	1.27	0.82		2.30	3.17	2.98	4.91	5.05	2.23	2.56
Eu	1.17	–108.59	–129.10		1.25		5.43		2.66		5.21		2.28
Ca	1.00	–121.28	–132.12	1.18	1.13	3.19	3.16		2.69	5.16	5.13	2.31	2.49
Ba	1.36	–95.99	–132.73	1.07	1.19		8.65	2.36	2.38	5.52	5.55	2.70	1.97
Sr	1.16	–109.30	–133.72	1.14	1.21		5.15	2.54	2.58	5.43	5.26	2.55	2.30
Ra	1.39	–94.14	–134.20		1.16		9.21		2.31		5.63		1.91
UO2	0.75	–142.54	–227.70		–0.10		–1.21		0.83		6.39		2.81

^aADP = adenosine-5′-diphosphate; H-ADP = protonated ADP that forms metal complexes in M–HL form.

^bRadii of the cations are from ref (15). The values of log K metal complexes are from ref (17). All of the values were determined at standard state, except for ADP and H-ADP in ionic strength of 0.1. The stability constant (log K = 4.08) for Be²⁺–oxalate was determined in ionic strength of 0.1 at 20 °C. The predicted value should be very close to its real value in ionic strength of 0.

^cThe values of ΔG_f of the cations are from refs (12, 16, 18), except for Pt²⁺, Pd²⁺ from ref (19).

For a given complexing ligand (Lewis base) and a group of isovalent metal cations (Lewis acids), our correlation assumes that the total free energy of a metal–ligand complex can be written as a linear combination of three main contributors (Figure 1): (1) the interaction between the cation and the ligand, which is characterized by the nonsolvation energy (ΔG°_n,Mⁿ⁺), (2) the interaction between the cation and the surrounding water, which is characterized by the solvation energy (ΔG°_s,Mⁿ⁺), and (3) the size (r_Mⁿ⁺) effect of the cation on coordination environments (the steric effect)

5

The intercept b_ML is related to the strength of the complexing ligand L. Because ΔG°_f,ML dominates other terms, direct use of eq 5 for correlation may falsely lead to a high correlation coefficient between the quantities on the two sides of the equation. Therefore, it is preferable to use stability constants of metal complexes (log K_ML) for correlation. The log K_ML can be expressed in terms of the free energy of reactants (Mⁿ⁺ and L) and products (ML)

6

where ΔG°_f,L is Gibbs free energy of formation of a ligand L. Substituting eq 5 into eq 6, we obtain

7

where δ*_ML = b_ML – ΔG°_f,L. Finally, we have

8

where α*_ML = (1 – a_ML) and γ*_ML = (a_ML – c_ML).

The coefficients (α*_ML, β*_ML, γ*_ML) and intercept δ*_ML can be calculated by fitting eq 8 to existing experimental data for each ligand.

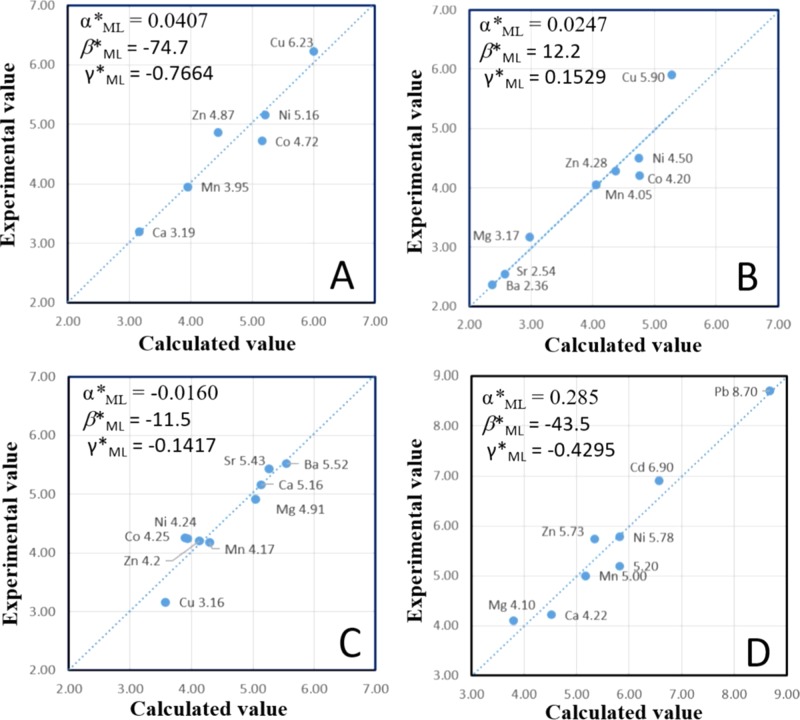
A large body of stability constants and Gibbs free energies of formation for metal–ligand complexes have been documented.¹⁶⁻¹⁸Equation 8 closely fits the existing experimental data for all of the metal complex families, even very complicated M–humate complexes (Figure 2D) (detail values for M–humate and M–fulvic acid complexes are listed in Supporting Information). Some selected metal-complex families are listed in Table 1. Figure 2 illustrates the differences between the experimental and the calculated values using eq 8. The discrepancies between the calculated and experimental data are within ±0.7 kcal/mol (or ∼0.5 log unit) for the majority of the data, especially for well-studied ligands. Previously proposed linear free energy relationship based on metals binding to one ligand (e.g., OH^–) and metals binding to other ligand.²⁰ The difference between the experimentally measured value and predicted value is also large (∼1–2 log units).²⁰

Figure 2.

Diagrams showing the differences between experimental (vertical axis) and calculated log K values (horizontal axis) for four M²⁺–ligand families: M²⁺–oxalate (A), M²⁺–ADP (B), protonated ADP, or M²⁺–H-ADP (C), and complicated M²⁺–humate complexes (D), respectively.

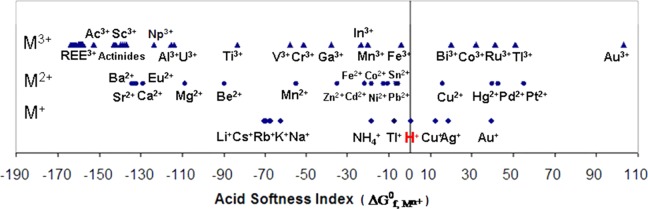
Interestingly, as shown in Figure 3, Gibbs free energies of formation of cations (ΔG°_f,Mⁿ⁺) are natural indices for the hardness/softness of metal cations (Lewis acids). Cations with positive ΔG°_f,Mⁿ⁺ values are soft acids, and those with negative ΔG°_f,Mⁿ⁺ values are hard acids (Figure 3). Cations with a high positive ΔG°_f,Mⁿ⁺ values tend not to lose electrons but to share them: softness is coincidentally related to the tendency of a complex to form covalent bonds. The new index is better than the empirical parameter Δβ (=log β⁰_MF – log β⁰_MCl) used for defining cation types like (a)-type, (b)-type, and borderline cations.²¹ Previously proposed criteria can qualitatively categorize metal cations into three groups, hard acids (or type A metal cations), borderline (or intermediate cations), and hard acids (or B type metal cations).^1,21 The product of the term α*_MLΔG°_f,Mⁿ⁺ is related to the stability of a metal–ligand complex. Both positive and both negative values of α*_ML and ΔG°_f,Mⁿ⁺ will result in a positive product and hence stabilize the metal–ligand complex. It is then logical to postulate that the coefficient α*_ML is an index for the hardness/softness of ligands (Lewis bases). Positive α*_ML values indicate soft bases, and the negative α*_ML values indicate hard bases.

Figure 3.

Gibbs free energy of formations (G°_f,Mⁿ⁺) as natural indices for the softness of Lewis acids. The values of ΔG_f of the cations are taken from refs (12, 16, 18), except for Bi³⁺ from ref (22), Ti³⁺ from ref (23), Pu³⁺, Np³⁺, and Am³⁺ from refs (13, 24), and Pt²⁺, Pd²⁺ from ref (19). See Table 1 for detail values of divalent cations.

Table 2 lists the softness of some bases according to their α*_ML values. Hard bases (e.g., F^– with α*_ML = −0.0101) have lower α*_ML values than that of soft bases (e.g., ethylenediaminetetraacetate (EDTA) with α*_ML = 0.0931) in divalent metal-complex families. For a ligand with coefficient α*_ML close to 0 (e.g., Cl^– with α*_ML = 0.0036), the relative selectivity for metal cations is mainly determined by the ionic radii of the cations. If both coefficients α*_ML and γ*_ML are close to 0 (e.g., formic acid, and SO₄²), the ligand will have no selectivity for metal cations. In general, the overall stability constants are determined by both the ionic radii of metal cations and the softness of cations (acids) and ligands (bases). The new relationship can quantitatively explain the Irving–Williams order. The coefficient δ*_ML relates to the complexing strength of a ligand with metals. A large negative δ*_ML value indicates a strong chelating ability of the ligand if other coefficients are same. Both coefficients β*_ML and γ*_ML have the same sign (Table 2). Positive β*_ML or γ*_ML values indicate that increasing cation size will lower the stability of complex in a ML family (e.g., M²⁺–EDTA family, see Table 2), whereas negative β*_ML or γ*_ML values indicate that increasing cation size will increase the stability of metal complex in a ML family (e.g., Pb²⁺ in M²⁺–humate family with α*_ML = 0.0285, see Figure 2D, Table S1, and Table 2). Some bases (like phosphoric acids) and diazoles have very low or zero values of β*_ML and γ*_ML (Table 2). This indicates that the size effect from the cations is diminished for such kinds of bases. It is proposed that the lesser hydrophilic (or more hydrophobic) nature of the bases causes this phenomenon.

Table 2. Summary of Regression Coefficients^a,c,d.

bases, L	α*ML	β*ML	γ*ML	δ*ML or dML	Ib
hydrogen cyanide, ML	0.5876	343.4	3.277	–772.5	0
sulfide, ML	0.4390	195.56	2.3997	–528.08	0
ethylenediamine, ML	0.1458	24.7	0.2246	–62.39	0.1
protein of hTFf, ML	0.1368	95.5	0.8632	−209.46	0
histidine, ML2	0.1337	–22.5	–0.4334	58.62	0.1
cysteine, ML	0.1193	–74.7	–0.8502	163.26	0.1
methylenephosphonic acid, ML	0.1172	0	0	–23.29	0.1
glycine, ML	0.1072	55	0.6116	–138.5	0.1
EDTA, ML	0.0931	33.5	0.4074	–107.54	0.1
1,3-diazole, ML2	0.0794	0	0	–8.45	0.16
O2–, ML	0.0789	–163.3	–1.9486	368.91e	0
ammonia, ML2	0.0758	295.8	3.2876	–700.64	0.1
methionine, ML2	0.0712	–29.9	–0.4147	73.81	0.1
histidine, ML	0.0694	–22.3	–0.3368	53.97	0.1
pyrindine, ML	0.0652	15.7	0.206	–52.02	0.1
ammonia, ML	0.0547	130	1.4563	–310.45	0.1
aspartic acid, ML	0.0466	–25.1	–0.3329	57.93	0.1
OH–, ML	0.0440	–73.6	–0.8944	138.75	0
oxalic acid, ML	0.0407	–74.7	–0.7664	157.96	0
glutamic acid, ML	0.0315	–52.33	–0.7216	135.07	0.1
methionine, ML	0.0291	–102.8	–1.2322	252.87	0.1
humic acid, ML	0.0285	–43.5	–0.4295	85.66	0
citric acid, ML	0.0257	–14.9	–0.2632	41.57	0.1
ADP, ML	0.0247	12.2	0.1529	–37.78	0.1
glycylglycine, ML	0.0221	–36.1	–0.4663	88.25	0
phthalic acid, ML	0.0196	–30.8	–0.39	75.24	0.1
dimethylmalonic acid, ML	0.0190	5.3	0.0781	–19.07	0.1
malonic acid	0.0180	–15	–0.2059	34.89	0.1
1,3-diazole, ML	0.0180	0	0	–4.65	0.16
ATP, ML	0.0173	11.4	0.1374	–35.47	0.1
lactic acid, ML	0.0145	3.2	0.0392	–11.27	0.1
fulvic acid, ML	0.0132	9.8	0.1115	–28.91	0
adenosine 5′-monophosphate (AMP-5′), ML	0.0119	0.9	0.0114	–6.29	0.1
acetic acid, ML	0.0115	8.6	0.1261	–26.95	0.1
adenosine 2′-monophosphate (AMP-2′), ML	0.0111	2.5	0.0318	–10.26	0.1
salicyclic acid, ML	0.0110	26.6	0.2106	–59.41	0.1
Cl, ML2	0.0105	56	0.7511	–213.83e	0
adenosine 3′-monophosphate (AMP-3′), ML	0.0100	0.9	0.0105	–5.9	0.1
Cl, ML	0.0036	49.5	0.6505	–161.63e	0
formic acid, ML	0.0018	0	0	–2.15	0.1
sulfuric acid, ML	–0.0028	7.4	0.0774	–19.81	0
ATP, MHL	–0.0090	–8.7	–0.1025	15.79	0.1
F, ML	–0.0101	14.3	0.1615	–102.72e	0
ADP, MHL	–0.0160	–11.5	–0.1417	23.8	0.1
methylenephosphonic acid, MHL	–0.0235	0	0	–11.57	0.1
F, ML2	–0.0517	–69.1	–0.7212	20.38e	0
CO3, ML	–0.0808	–16.2	–0.2219	–77.08	0
inosine-5′-dihydrogenphosphase	–0.1198	0	0	–6.03	0.1
iodic acid, ML	–0.1198	–79.1	–1.1107	228.99	0.1

^aThe coefficient α*_ML is the natural indices for the chemical softness of the ligands or Lewis bases.

^bI: ionic strength.

^cThe values of log K metal complexes are from ref (17), except for M–Cl, M–Cl₂, M–F, M–F₂, and M–O^2– complexes from refs (16, 18). M–OH complexes are from reference¹⁷ except for Hg because of large discrepancy and no Hg values were suggested in references.^16,18

^dM–humates data are from refs (21) and (25). A Cu(II)–humate value is not used because it is pH dependent and related to the formation of polynuclear complexes (i.e., both ML and ML₂ complexes).²⁶ The data for M–fulvic acid complexes are from Schnitzer and colleagues.²⁷⁻²⁹

^eThe value is d_ML for the Gibbs free energy of formation.

^fProtein of human serum transferrin.

According to Table 2, EDTA is one of the strongest chelating agents for divalent metals. The softness of bases follows the order of cyanide > sulfide (S^2–) > ethylenediamine > cysteine > glycine > EDTA > O^2– > histidine > ammonia > OH^– > carboxylic acids > Cl^– > sulfuric acid > F^– > CO₃^2– > iodic acid. Based on the obtained softness indices (Table 2), increasing the number of soft bases (like Cl, histidine, or ammonia) bonded to metal cations generally results in an even softer ligand, that is, Cl₂ in M–L₂ is softer than Cl in M–L. Increasing the number of hard bases (like F) bonded to metal cations generally results in an even harder ligand, that is, F₂ in M–L₂ is harder than F in M–L (Table 2). Softness also changes based on the arrangement of atoms in isomers. For instance, andenosine monophosphate (AMP-5′) is the precursor to ADP, and the biologically important AMP has two other isomers: AMP-2′ (α*_ML = 0.0111) and AMP-3′ (α*_ML = 0.0100). AMP-5′ is the softest (α*_ML = 0.0119) among the three isomers (Table 2). The new softness indices for Lewis bases can serve as a guideline for designing new functional materials or even engineered proteins with chemical selectivity because each individual functional group (like amine, carboxylic group, carbonate, and phosphate) has its own softness value.

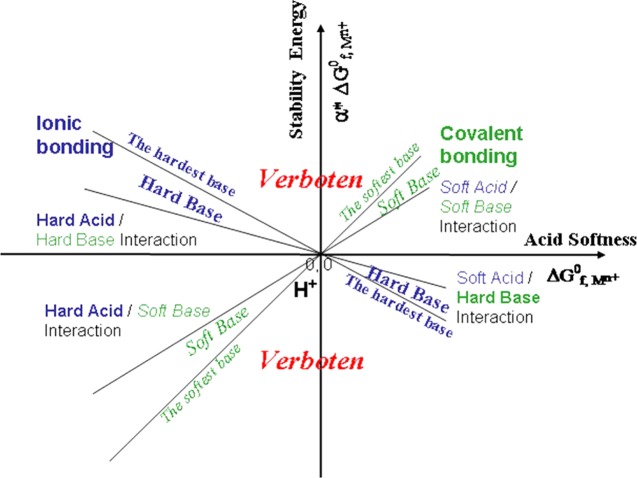
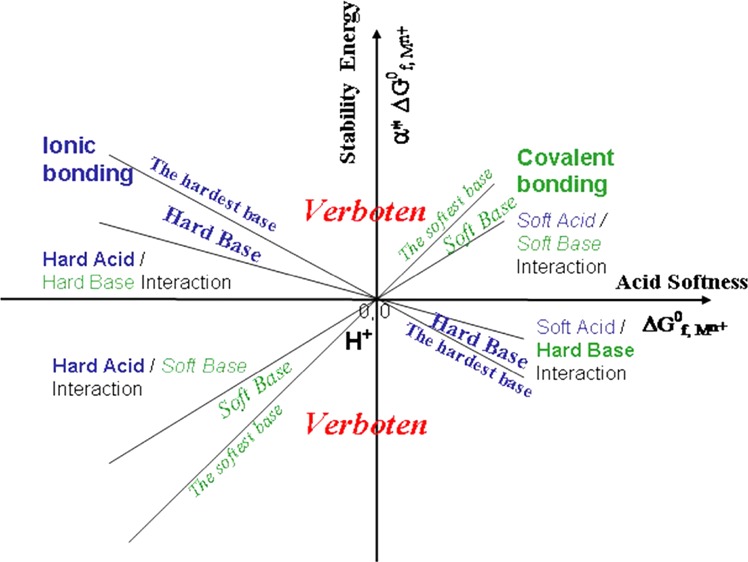
Unlike the hardness parameters (η) proposed by Parr and Pearson,⁶ the new softness (or hardness) indices have positive and negative signs, which clearly indicate the reaction tendencies between Lewis acids and Lewis bases. The product of the acid softness (ΔG°_f,Mⁿ⁺) and base softness (α*_ML) or the term of α*_MLΔG°_f,Mⁿ⁺ corresponds to the acid–base interaction energy. By plotting the α*_MLΔG°_f,Mⁿ⁺ term against the Lewis acid softness ΔG°_f,Mⁿ⁺, we can clearly see that the stability energies due to the acid–base interactions follow lines with different slopes (α*_ML) (Figure 4). Soft bases follow lines with positive slopes, and hard bases follow lines with negative slopes. The areas labeled “verboten” are beyond the softness of the softest base and the hardness of the hardest base. The four quadrants in the plot correspond to soft acid–soft base interaction (quadrant I), hard acid–hard base interaction (quadrant II), hard acid–soft base interaction (quadrant III), and soft acid–hard base interaction (quadrant IV). The acid–base interaction energy not only quantitatively explains Pearson’s statement of “hard acids prefer to associate with hard bases, and soft acids prefer to associate with soft bases”,^2,30 but also accounts for all other reactions of varying hardness/softness.

Figure 4.

A diagram illustrating Lewis acid–base interaction, or acid–base stability energies in term of α*ΔG°_f,Mⁿ⁺ vs ΔG°_f,Mⁿ⁺ plot. The proton (H⁺) is at the unique position of the origin. The softness of a base (ligand) is gauged with the slope of α*ΔG°_f,Mⁿ⁺ vs ΔG°_f,Mⁿ⁺ with a positive slope for a soft base. A positive α*ΔG°_f,Mⁿ⁺ value indicates a preferential complexation between the acid and the base.

Hydrogen has puzzled scientists in the past in their explanations of both its role as a hard or a soft cation, and its effect on bases/ligands. Previous HSAB models were not able to qualitatively explain its behavior, much less quantify it. To briefly illustrate, H⁺ can bond to F^–, which is very hard. H⁺ is also known to bond to S^2–, a soft base, forming HS^– or H₂S. So, hydrogen as a cation exhibits both hard and soft behaviors depending on the ligand. On an arbitrary scale, such a quantification is quite impossible, as H⁺ would have to appear twice—two contradicting facts. Our equation and new softness indices appropriately explain hydrogen’s behavior by positioning its softness at 0. This point is equally positive as it is negative, which allows it to react with both hard and soft bases, and forms stable bonds.

The second unique feature of hydrogen is its effect on ligands, or more specifically, what happens when a ligand is protonated. It is observed that protonated ligands become less soft with the addition of protons, such as ML complexes and MHL complexes for ATP, ADP, and methylenephosphonic acid (Table 2). In the M–ADP family, the Cu–ADP complex is the strongest. The order of binding strength is reversed in the M–H-ADP family (Figure 2) because protonated ADP (H-ADP) becomes a hard base (Table 2), and its coefficients β*_ML and γ*_ML become negative. OH^– may be considered as protonated O^2– in this regard. This phenomenon is difficult to explain, but is nevertheless observable. We currently believe that hydrogen changes the covalency of a bond between cation and ligand. For instance, in an ideal covalent metal–ligand complex, the electrons in a neutral position receive equal forces from both nuclei. If a proton with a high electron affinity is added to a ligand, the electron in the neutral position moves toward the protonated side, “pinching off” the bond. The compound is now less covalent, which implies that it is less soft than its deprotonated base.

Previous models also had trouble explaining the behavior of beryllium (Be²⁺). Its family exhibits ionic properties (a general indicator of a hardness) when it reacts with Cl^–. According to the previous charge over radius rule, Be²⁺, which is both small and highly charged, should be more ionic and thus harder than other divalent cations in the alkali earth group. BeCl₂, however, is more covalent than others in its family, as it is observed to be soluble in organic solvents, and the molten material is a poor conductor.³¹ The reason as explained is that because Be²⁺ is so small and also highly charged, it is capable of pulling enough electrons toward it to form a quasi-covalent structure. Charge over radius could not be extended to calculate the hardness of Be²⁺, and likewise rules devised around the Be²⁺ case could not be used to define other Lewis acids. Based on Pearson–Klopman HSAB model, Be²⁺ is considered an anomaly and exception. As we have found, the key to softness or hardness is not solely charge over radius, but the Gibbs free energy of formation, ΔG°_f,Mⁿ⁺. Be²⁺ has the highest ΔG°_f,Mⁿ⁺ value among the alkali earth elements (Table 1); therefore, it is softer than all of the other divalent cations in the alkali earth group. However, the charge/radius cannot be ignored. In our equation, the terms of β*_MLr_Mⁿ⁺ (steric effect) and γ*_MLΔG°_s,Mⁿ⁺ (solvation effect) still account for this. Ignoring the size effect terms can cause major discrepancies when cations are very small (e.g., Be²⁺) because the solvation energy is proportional to the reciprocal value of ionic radius.¹¹ Our equation produces the results for Be²⁺–ligand complexes that are difficult to be measured, consistent with the experimental data (Tables 1 and S1, Figure S1).

If we plot the values of β*_ML against γ*_ML, then a linear relationship between β*_ML and γ*_ML values is displayed (Figure 5)

9

The straight line passes through the origin (Figure 5), which indicates that β*_ML and γ*_ML are not independent. The value of slope is about 81.5 kcal/Å. The slope applies to all of the divalent metal–ligand complexes in a given solvent, water in this case. The slope (or “charge-solvent parameter”) corresponds to the strength of the coordination field around the cation in a given solvent. Equation 9 for divalent cations may be modified as

10a

or

10b

The new equation will help us better understand the hardness/softness of Lewis acids and bases. It can also predict the unknown thermodynamic data based on a limited number of the existing measurements, and this equation can also be used to check the internal consistency of the thermodynamic databases. It is essential to have reliable data for metal–ligand complexes to evaluate the impact of pollutants on water, soils, and biological systems, as metal complexation with various inorganic or organic ligands in aqueous solutions directly controls the solubility, sorption, and toxicity of metals including radionuclides in natural environments. The effectiveness of these calculations heavily depends on the completeness and quality of the thermodynamic databases on which the calculations are based.^32,33 The equation can also be used to predict M³⁺–ligand bindings and metal–protein bindings, which, in turn, can be used in the future for designing metal-based anticancer drugs like Ru³⁺ compounds^34,35 and microbe–mineral interactions in natural environments.^36,37

Figure 5.

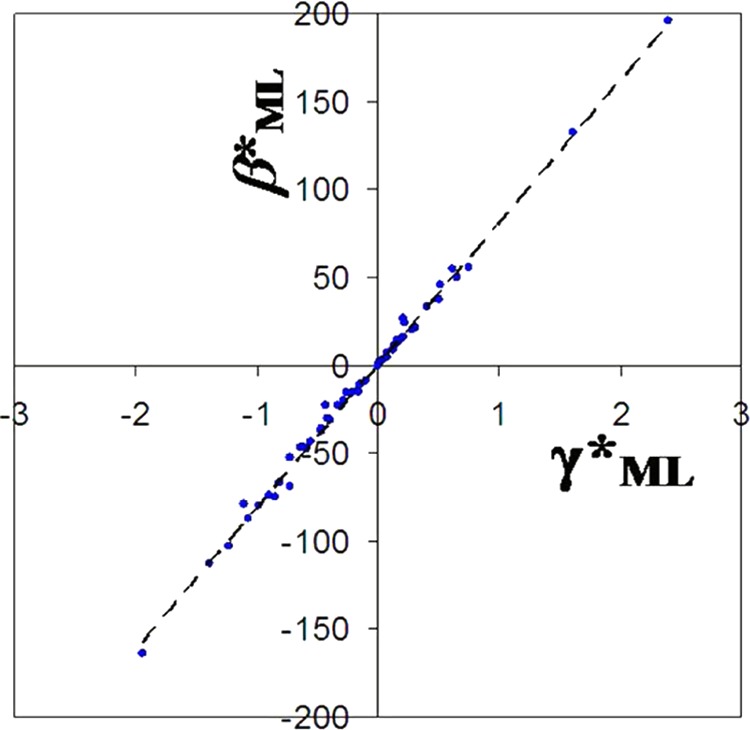
Diagram showing a linear relationship between the fitting parameters β*_ML and γ*_M based on 80 metal–ligand complex families with β*_ML < 200 kcal/Å. A slope of 81.5 kcal/Å is a charge-solvent parameter for solvent water.

Glossary

Symbols Used

r_Mⁿ⁺

Ionic radii of metal cations with charge +n, experimental quantity

ΔG°_f,Mⁿ⁺

Gibbs free energy of formation (softness) of cations, experimental quantity

ΔG°_s,Mⁿ⁺

Solvation energy of cations, calculated using Born solvation theory eq 4

ΔG°_n,Mⁿ⁺

Non-solvation energy of cations, a quantity defined by eqs 3 and 4 in term of experimental quantity of ΔG°_f,Mⁿ⁺

α*_ML

Softness of ligand or Lewis base, a fitting coefficient obtained by fitting eq 8

β*_ML

A fitting coefficient obtained by fitting eq 8

γ*_ML

A fitting coefficient obtained by fitting eq 8

δ*_ML

A fitting coefficient obtained by fitting eq 8

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.7b01039.

• Ionic radii, solvation energies, Gibbs free energy of formation of divalent cations, and stability constants for M²⁺–humic acid, M²⁺–fulvic acid, M²⁺–ATP, and M²⁺–H-ATP complexes (Table S1); plots showing experimental values versus calculated values for M–ATP and M–H-ATP complexes (Figure S1) (PDF)

The authors declare no competing financial interest.