A Quantitative and Predictive Model for RNA Binding by Human Pumilio Proteins

Inga Jarmoskaite; Sarah K Denny; Pavanapuresan P Vaidyanathan; Winston R Becker; Johan OL Andreasson; Curtis J Layton; Kalli Kappel; Varun Shivashankar; Raashi Sreenivasan; Rhiju Das; William J Greenleaf; Daniel Herschlag

doi:10.1016/j.molcel.2019.04.012

. Author manuscript; available in PMC: 2020 Jun 6.

Published in final edited form as: Mol Cell. 2019 May 8;74(5):966–981.e18. doi: 10.1016/j.molcel.2019.04.012

A Quantitative and Predictive Model for RNA Binding by Human Pumilio Proteins

Inga Jarmoskaite ^1,¹⁴, Sarah K Denny ^2,^10,¹⁴, Pavanapuresan P Vaidyanathan ^1,^11,¹⁴, Winston R Becker ^2,¹⁴, Johan OL Andreasson ^3,¹², Curtis J Layton ³, Kalli Kappel ², Varun Shivashankar ⁴, Raashi Sreenivasan ^1,¹³, Rhiju Das ¹, William J Greenleaf ^3,^5,^6,^*, Daniel Herschlag ^1,^7,^8,^9,^15,^*

PMCID: PMC6645366 NIHMSID: NIHMS1034674 PMID: 31078383

SUMMARY

High-throughput methodologies have enabled routine generation of RNA target sets and sequence motifs for RNA-binding proteins (RBPs). Nevertheless, quantitative approaches are needed to capture the landscape of RNA-RBP interactions responsible for cellular regulation. We have used the RNA-MaP platform to directly measure equilibrium binding for thousands of designed RNAs and to construct a predictive model for RNA recognition by the human Pumilio proteins PUM1 and PUM2. Despite prior findings of linear sequence motifs, our measurements revealed widespread residue flipping and instances of positional coupling. Application of our thermodynamic model to published in vivo crosslinking data reveals quantitative agreement between predicted affinities and in vivo occupancies. Our analyses suggest a thermodynamically driven, continuous Pumilio binding landscape that is negligibly affected by RNA structure or kinetic factors, such as displacement by ribosomes. This work provides a quantitative foundation for dissecting the cellular behavior of RBPs and cellular features that impact their occupancies.

Graphical Abstract

graphic file with name nihms-1034674-f0001.jpg

In Brief

As RNA-binding proteins play key roles in cellular regulation, quantitative approaches are needed to capture RNA-protein interaction landscapes. Jarmoskaite et al. establish a quantitative model that predicts human PUM1/2 protein-RNA affinities and cellular PUM2-RNA occupancies, suggesting a continuous binding landscape negligibly affected by RNA structure and kinetic factors.

INTRODUCTION

A grand challenge in biology is to understand, predict, and ultimately control gene expression programs that allow cells to function. RNA processing is central to regulation of gene expression, and each processing step, from splicing and end-processing to translation and decay, is regulated by a suite of RNA-binding proteins (RBPs), which constitute >5% of the eukaryotic proteome (Mitchell and Parker, 2014; Müller-McNicoll and Neugebauer, 2013; Singh et al., 2015). By binding specific sequence or structure elements, RBPs can provide coordinated regulation of sets of functionally related RNAs, as shown, for example, for iron regulatory proteins, PUF (Pumilio and FBF) proteins, and the Nova RBP (Gerber et al., 2004; Keene and Tenenbaum, 2002; Rouault, 2006; Ule et al., 2003).

Given the central importance of RBPs, defining and predicting RBP interactions has been a major research focus, and transcriptome-wide RNA target sets have been identified for hundreds of RBPs, facilitating elucidation of RBP roles in regulatory processes (e.g., Darnell, 2010; Dominguez et al., 2018; Gerber et al., 2004; Hogan et al., 2008; Ray et al., 2013; Ule et al., 2003; Wheeler et al., 2018; Xue et al., 2009). While the RNA target databases provide immense value, several critical limitations to our current knowledge remain.

First, RBP targets are commonly defined in a binary manner, with RNA molecules considered either “targets” or “non-targets” of a given RBP. However, binding is a continuum, determined by RBP affinities, RBP and target concentrations, and other cellular factors. Therefore, quantitative affinity measurements are needed to define and predict RBP binding occupancies across the RNA sequences present in a cell—i.e., the RBP binding landscape—and the subsequent regulation. A second limitation is that most current approaches are optimized for identifying RBP targets rather than for quantitative determination of RBP affinities or occupancies. Third, current models of RBP specificity are limited to short, linear sequence logos and motifs, which assume energetic additivity (Schneider and Stephens, 1990; Stormo, 2000). Yet, the accuracy of such models remains to be quantitatively and comprehensively tested.

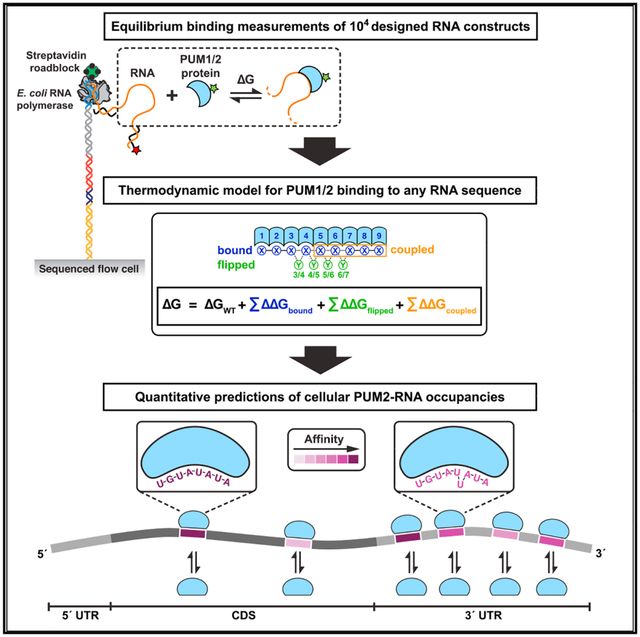
The above limitations and the importance of regulation by RBPs have sparked a growing interest in developing quantitative genomic-scale approaches for measuring RBP-RNA interactions and affinities. Methods such as MITOMI (mechanically induced trapping of molecular interactions), HiTS-EQ (high-throughput sequencing equilibrium), HiTS-RAP (high-throughput sequencing–RNA affinity profiling), RNA Bind-n-Seq, and RNA-MaP (RNA on a massively parallel array) can provide equilibrium binding constants or apparent affinities (Buenrostro et al., 2014; Jain et al., 2017; Jankowsky and Harris, 2017; Lambert et al., 2014; Martin et al., 2012; Tome et al., 2014). Of these, RNA-MaP and HiTS-RAP, two related techniques that utilize a modified sequencing platform and an array of ~10⁵ unique immobilized RNA species, eliminate an intermediate capture step that can alter binding occupancies, thereby allowing highly accurate direct thermodynamic and kinetic binding measurements via fluorescence readout (Buenrostro et al., 2014; Tome et al., 2014 and vide infra). Recent studies have demonstrated the utility of RNA-MaP for systematic investigation of RNA-protein and RNA-RNA interactions and for generation of quantitative thermodynamic models (Buenrostro et al., 2014; Denny et al., 2018; She et al., 2017).

We used the RNA-MaP platform to interrogate the sequence preferences of the human PUF family proteins PUM1 and PUM2 across a diverse designed RNA library. PUF family proteins (Figure 1A) are universal in eukaryotes and have been implicated in regulation of mRNA turnover, transport, translation, and localization; in mammals, PUF proteins play important roles in brain and germline development, regulation of innate immunity, and other processes (Goldstrohm et al., 2018; Miller and Olivas, 2011). Extensive prior biochemical, structural, evolutionary, and in vivo studies of PUF proteins provide a powerful starting point for our quantitative and systematic dissection of specificity (Figure S1A and references therein) and allow us to pose specific biological, engineering, and biophysical questions.

PUF proteins have a modular structure of eight conserved tandem repeats that recognize RNA in a sequence-specific manner (Figure 1A), and this modularity provides a best-case scenario for building a simple predictive thermodynamic binding model (Wang et al., 2002). However, we show that the simplest, energetically additive model breaks down and that tight-binding RNA sequences exist that are not represented by previously defined motifs. Our large, quantitative RNA-MaP dataset enabled the generation of a predictive model for PUM1 and PUM2 binding that includes residue flipping and coupling terms. The model can also be applied to an engineered PUM1 variant, after changing a single parameter to account for the local specificity change. Remarkably, our in-vitro-derived binding model quantitatively explains median in vivo occupancies in prior PUM2 crosslinking data, demonstrating that RNA binding sites in vivo exhibit, on average, thermodynamically driven occupancies (Van Nostrand et al., 2016). Further analysis indicates that predicted RNA secondary structures do not lead to decreased PUM2 occupancy in vivo, suggesting that these structures are strongly disfavored in cells. Our thermodynamic model provides a quantitative foundation for dissecting the cellular behavior of RBPs and represents a step toward a quantitative and predictive understanding of the complex networks of RBP-RNA interactions and their regulatory consequences.

RESULTS

Library Design

Starting with the PUM2 consensus motif, which has been determined by pull-down, cross-linking, and in vitro selection experiments (Figures 1A and S1A), we designed an oligonucleotide library to systematically address the factors that determine binding specificity (Figure S1B). A designed (versus randomized) library allowed us to maximize the information content by leveraging prior specificity information. We introduced single and multiple mutations into the PUM2 consensus site, focusing on sequence variants outside the UGUA core to avoid preponderance of non-binders (Figure S1B). We also varied the flanking sequences and included insertions to test the potential for noncontiguous binding sites; finally, we included variants of sequence motifs of related PUF proteins to provide additional sequence variation for testing PUM2 binding models (Figure S1B). To control for structural and context effects, each sequence variant was embedded in two to four scaffolds (Figure 1B).

Massively Parallel Measurements of PUM2-Binding Affinities

Using RNA-MaP, we determined PUM2 protein binding affinities for >20,000 distinct RNAs, and we report on >5,000 herein; sequences designed to address distinct questions will be reported separately. The DNA library was sequenced on an Illumina MiSeq flow cell, followed by in situ transcription in a custom-built imaging and fluidics setup (Figure 1C; Buenrostro et al., 2014; She et al., 2017). RNA transcripts were immobilized by stalling the RNA polymerase at the end of the DNA template, and RNA-protein association was measured by equilibrating the RNA with increasing concentrations of fluorescently labeled protein and by imaging binding to each cluster (comprising ~1,000 copies of an RNA variant) (Buenrostro et al., 2014) (Figure 1C). The resulting binding curves were used to obtain the dissociation constant (K_D) and the corresponding ΔG value (= RTlnK_D) of the protein for each RNA variant.

Figure 1D shows representative binding curves for a consensus sequence (UGUAUAUA, “WT”) and a mutated sequence (UGUAGCGC, “mut”) that exhibit divergent affinities (K_D =0.17 nM and >340 nM, respectively). For most protein concentrations, protein binding to the consensus sequence followed a canonical binding curve (Figure 1D, WT). At the highest protein concentrations, modest additional increase in fluorescence was observed only for sequences that significantly bound PUM2. This signal was well fit by a model in which a second PUM2 weakly binds to the RNA/PUM2 complex (Figure 1D, WT versus mut), and was accounted for by including a nonspecific binding term (STAR Methods), which led to somewhat greater uncertainty in K_D values for weakly bound RNAs (Figure S1C).

Because our RNA array contained multiple clusters for each sequence variant, numerous binding curves were determined in parallel for each construct. The median number of independent clusters per sequence variant was 23 and 42 in experiment replicate 1 and 2, respectively. Molecular variants were included in downstream analysis when measured in at least five clusters per experiment (Figure S1C), with additional quality filters described in STAR Methods. Independent binding experiments using distinct RNA chips indicated quantitative agreement (R² = 0.95; Figure 1E), with average reproducibility within less than 2-fold (RMSE = 0.26 kcal/mol) after accounting for a small systematic shift.

Dissecting and Defining PUM2 Specificity

PUM2 and related Puf3-type PUF proteins appear to recognize RNA in a modular fashion, with each base contacted by one of the eight PUF repeats (Figure 1A; Wang et al., 2002). Thus, independent energetic contributions might be expected from consecutive RNA bases bound at each of the eight PUF repeats, as assumed in motif descriptions (Schneider and Stephens, 1990; Stormo, 2000). In this section, we test this and other thermodynamic models.

Comprehensive Analysis of Single-Mutant Variants

We first assessed the binding of all single mutants of the 8-mer consensus UGUAUAUA in two to four scaffolds (Figure 2A). At all positions, we see the strongest binding for the consensus residue (circled), with very low discrimination at position 5, consistent with prior results (Dominguez et al., 2018; Galgano et al., 2008; Hafner et al., 2010; Lu and Hall, 2011).

Surprisingly, while the effects of single mutations generally agreed across scaffolds, the spread of deviations was considerably greater than expected from error (Figure 2B; 25°C, “Observed” versus dashed line; Figure S2A). Significant deviations between scaffolds occurred in 13 of the 25 sequence variants, at a 10% false discovery rate (FDR; Figure 2A, “^*”). We considered several potential origins for how scaffolds might influence single mutant effects.

First, we assessed if RNA secondary structure might limit PUM2 access to its site (Figure 2C) to differing extents among scaffolds. If structure affected binding, the differences between scaffolds should decrease at 37°C. Indeed, smaller differences were observed at this higher temperature (Figures 2B and S2A), with only 2 of the 25 sequence variants exhibiting significant deviations between scaffolds (Figure S2C). Accounting for structure effects with stabilities predicted by Vienna RNAfold (Lorenz et al., 2011) also considerably reduced the between-scaffold deviations (Figures 2B and 2D), with only 5 of the initial 13 variants exhibiting significant inter-scaffold deviations at 25°C and none at 37°C (asterisks in Figure 2A versus Figures 2D and S2C). Thus, RNA secondary structure can account for most inter-scaffold variation.

We next investigated whether scaffold differences were associated with alternative binding registers, which would diminish the observed mutational penalty (Figure S2D). We calculated predicted binding affinities in all possible binding registers (scaffold + designed binding site) using a model that assumes independent effects of individual mutations. 18 of the 61 variants in Figures 2A and 2D had an alternative register with a predicted K_D within 5-fold of the measured value (Table S1). For the 2C mutant, three of the four scaffolds have alternative registers with affinities matching the observed values (Figure S2E). Thus, in this case the seeming outlier (scaffold S1b) gives the most accurate mutant penalty, underscoring the value of multiple scaffolds and the importance of accounting for alternative binding sites.

Finally, we assessed whether scaffold variation was caused by sequence preferences outside the canonical PUM2 8-mer site. The library included a set of constructs that varied the flanking sequence two bases upstream (−2,−1) and downstream (+1, +2) of the common consensus sequence (n = 209 across four scaffolds; Figure S2F). We found modest effects at position +1, with G(+1) bound most tightly (Figure S2F), with no significant effects at other flanking positions. The G(+1) effect was confirmed in gel shift experiments (Figure S2G). However, since none of our scaffolds contained a G at this position, flanking effects did not impact the observed differences of single mutant measurements between scaffolds.

The above insights enabled us to determine high-confidence single mutant effects for all positions, using values corrected for secondary structure stability (Figure S2D) and using only sequence variants without alternative binding registers. We additionally took advantage of the observation that substituting the uridine at position 5 with A or C residues did not affect the binding affinity (Figure 2D (Lu and Hall, 2011)) and that none of the single mutants in the 5A or 5C backgrounds had stable predicted alternative registers (Figure S3A). Figure 2E summarizes the median single mutant effects across scaffolds and across 5A/C/U backgrounds. We observed excellent agreement between the effects derived from 25°C and 37°C data, with a constant destabilization of binding by (20 ± 10)-fold at the higher temperature (Figures S3A–S3E). RNA array measurements also agreed with gel-shift measurements of 14 single mutants (Figures 2F and S3F).

Testing an Additive Model for PUM2 Specificity

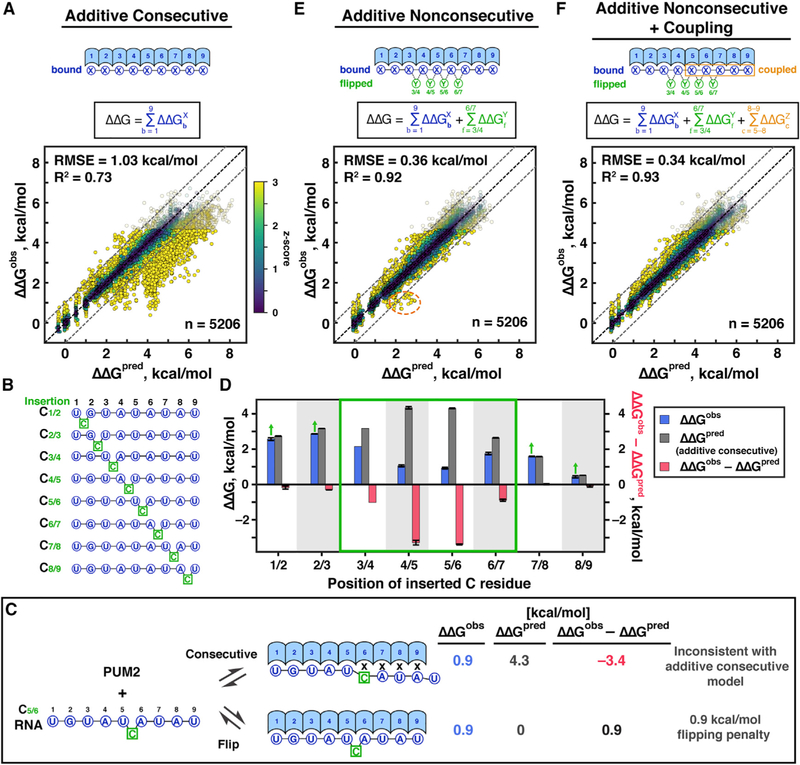
If binding of RNA residues by consecutive PUF repeats contributed independently to PUM2 affinity, then the affinities for any RNA sequence ought to be predicted from adding the measured single mutant penalties (“additive consecutive model”; Figure 3A, top). To test this model, we calculated the predicted affinities for our entire library using 36 terms, one for each residue at each of the 9 recognition sites (8 canonical PUF repeats and the additional G9 site), determined from our single mutant data (Figure 2E; Table S2). In the predictions, we accounted for all possible binding registers by calculating the ensemble affinity across all possible 9mers (STAR Methods). We then compared the predicted and measured affinities for RNAs predicted to contain little or no structure (ΔΔG_fold > −0.5 kcal/mol; n = 5,206). This set included RNAs with mutations or insertions throughout the PUM2 consensus sequence, variation in flanking sequence, and variations of consensus motifs of other PUF proteins (Figure S1B).

Figure 3. — (A) Top: schematic representation and test of the additive consecutive model. b is the position of bound base, and X is the base at position b. $Δ Δ G_{b}^{x}$ values correspond to the measured single mutation penalties at 25°C (Figure 2E; Table S2). Bottom: predicted versus observed ΔΔG values relative to the UGUAUAUAU consensus sequence for all unstructured variants in the library. Predicted ΔΔG values account for the ensemble of all possible registers along the RNA sequence (STAR Methods). Transparent symbols indicate variants bound more weakly than the threshold for high-confidence affinity determination; these variants were excluded from determining the R² and RMSE values and from global fitting in parts E and F. Points are colored based on the deviation from predicted affinity, divided by the uncertainty of the measurement ( $z = | Δ G_{obs} - Δ G_{pred} | / σ_{Δ G}$ ; capped at z = 3 for visualization). The black dashed line is the unity line and the dashed gray lines denote 1 kcal/mol deviation from the predicted value.

(B) C-insertion library for base-flipping analysis.

(C) Example of an insertion that gives binding tighter than predicted by the additive consecutive binding model and provides evidence for base flipping. X indicates a mismatch. ΔΔG^pred corresponds to the prediction from additive consecutive model (Figure 3A). With flipping, ΔΔG^pred indicates the prediction accounting for bound positions only, which is 0 as the consensus residues are in each site.

(D) Summary of observed and predicted ΔΔG values for each of the C insertions in part B. Green box indicates positions at which the observed ΔΔG values are smaller than predicted, suggesting base flipping. Arrows indicate that the observed affinities are lower limits for base flipping penalties. Averages and standard errors for library variants containing the consensus sequence with the indicated insertion and lacking stable alternative registers are shown (Table S3).

(E) Additive nonconsecutive model. Y indicates the residue(s) flipped at position f. Numbering of flipped residues is based on the flanking bound residues; 3/4–6/7. The dashed orange outline indicates a cluster of outliers with residue coupling.

(F) Final model including binding, flipping, and coupling terms. c indicates the positions of coupled residues, and Z is the identity of coupled residues. Final model parameters are provided in Table 1.

See also Figures S4–S6 and Tables S2, S3, S4, and S5.

While the predicted and observed binding energies strongly correlated (R² = 0.73), 27% of the observed values deviated from predictions by >1.0 kcal/mol, well beyond our experimental error of 0.14 kcal/mol (Figure 3A). Furthermore, the vast majority of outliers bound tighter than predicted (Figure S4A). We therefore explored additional features that might lead to tighter-than-predicted PUM2 binding.

Residue Flipping Accounts for Most Deviations from the Additive Consecutive Model

Several PUF proteins bind RNAs with residues “flipped out” to yield longer, nonconsecutive binding motifs (Gupta et al., 2008; Miller et al., 2008; Valley et al., 2012; Wang et al., 2009; Wilinski et al., 2015). Human PUM1 protein, which has >90% sequence identity to PUM2 in its RNA-binding domain, has two X-ray structures with bound RNA sequences each with one residue flipped out (Gupta et al., 2008). To assess whether base flipping significantly contributes to RNA binding to PUM2, we had included in our library a set of RNAs with C insertions throughout the UGUAUAUA consensus sequence (Figure 3B), with C insertions chosen, because none of the PUM2 repeats preferentially bind C. In the absence of base flipping, a C insertion would cause one or more mismatches in the PUM2 binding site, leading to a large penalty (Figure 3C). Instead, at four positions within the PUM2 motif, insertion of the C residue had a much smaller effect than predicted by the additive consecutive model, consistent with base flipping (Figures 3C and 3D). For example, the insertion between residues 5 and 6 leads to binding that is 3.4 kcal/mol stronger than predicted (Figure 3C), and the 0.9 kcal/mol observed destabilization relative to the consensus sequence suggests an energetic penalty for flipping a C residue at this position of 0.9 kcal/mol. Thus, our data suggest that PUM2 can bind RNAs with flipped out residues in certain positions, and we modeled this behavior in an extended “additive nonconsecutive model.”

The additive nonconsecutive model combines independent energetic contributions from each of the 9 bound residues with the ability to flip up to two residues (Figure 3E, top). To determine the associated energetic penalties, this model was fit to our 5206 measured binding affinities, accounting for all possible binding modes and registers (STAR Methods; see Figure 4A). The additive nonconsecutive model gave improved agreement with the data, with the root mean square error (RMSE) reduced from 1.03 to 0.36 kcal/mol and R² increased from 0.73 to 0.92 (Figure 3E versus Figure 3A). This large improvement is not a consequence of allowing the single-mutant values to vary in global fit, as a global fit to the additive consecutive model with variable single-mutant values gave considerably poorer predictions (Figures S4B and S4C). Despite the overall improvement observed with the additive nonconsecutive model, there remained a subset of significant outliers (Figure 3E) that led us to carry out additional analyses for energetic coupling.

Figure 4. — (A) An RNA sequence of length n can be bound in a series of 9- to 11-mer registers (r), within which the RNA residues are variably distributed between bound and flipped positions. Representative subsets of binding registers and base arrangements are shown for each of the four binding modes included in the model: consecutive, 1-nt, and 2-nt flips (at a single position) and two flips at different positions. The equations indicate integration of predicted ΔΔG values for all possible binding sites to obtain the final affinity. The ΔΔG values for predicting individual binding site configurations are given in Table 1. ΔG_WT is the affinity for the consensus sequence.

(B) Schematic representation of a predictive model of PUM2 occupancies on an mRNA target (see STAR Methods).

Energetic Coupling between Neighboring Residues

Inspection of the cluster of variants that bound tighter than predicted even after accounting for flipping (Figure 3E, dashed outline) revealed an enrichment for variants with a G mutation at position 7 accompanied by mutations at position 8, suggesting potential coupling between these neighboring mutations. For an unbiased assessment of coupling at all positions, we considered all double mutants of the PUM2 consensus site, which revealed that coupling between positions 7 and 8 was the strongest, and deviations from additive predictions at all other positions were <0.5 kcal/mol (Figure S4D). Further analysis revealed that (1) coupling between positions 7 and 8 occurred with G or C at position 7; (2) for 7G, coupling occurred only when position 6 was the consensus residue (A) and a pyrimidine was present at position 5 (Figure S4E), and these variants fully explained the cluster of outliers observed in Figure 3E (Figure S4E, top); and (3) for 7C, the deviations from additivity were greatest when position 6 was mutated (not A) (Figure S4F).

We also observed small deviations from additivity at positions 8 and 9 (Figure S4D). Physically, an absence of stable binding in the PUM2 site “8” would be expected to increase the entropic penalty for forming the site “9” interaction and thus might weaken or eliminate this interaction. Indeed, we found that the modest stabilizing effect of 9G relative to other residues was only present with the consensus A at position 8 (Figure S4G).

Figure 3F shows the global fit to our final model that includes additive terms for bound and flipped residues and the coupling terms described above (Table 1). For 99% of the data, this final model predicted our observations to within 1 kcal/mol and it gave a slight overall improvement relative to the additive nonconsecutive model (Figure 3E versus Figure 3F).

Table 1.

Thermodynamic Parameter Values for the Additive Nonconsecutive Coupling Model

Term I	$Δ Δ G_{b}^{X}$ (kcal/mol)
	X =
Bound Residue Position b =	A	C	G	U
1	3.08	2.91	3.04	0.00
2	1.93	3.14	0.00	3.14
3	2.39	2.49	2.92	0.00
4	0.00	1.92	1.71	1.46
5	−0.03	0.17	0.79	0.00
6	0.00	1.83	1.82	1.49
7	1.55	1.78	1.59	0.00
8	0.00	1.57	1.52	1.01
9	0.30	0.29	−0.07	0.00

Term II	$Δ Δ G_{f}^{Y}$ (kcal/mol)
	Y =
Flipped Residue Position f =	A	C	G	U	NN^a	Ø
3/4	>2^b	1.79	>1.5	1.41	>2.5	0
4/5	>2	>3	>2.5	>2.5	>2.5	0
5/6	1.22	1.05	1.57	0.81	2.18	0
6/7	>2	1.77	>2	2.02	2.04	0

Term III	$Δ Δ G_{c}^{Z}$ (kcal/mol)^c
	Z =
	5	6	7	8	6	7	8	8	9
Coupled Residue Positions c =	C/U	A	G	C/G/U	C/G/U	C	C/G/U	C/G/U	X	all other
5–8	−1.53				-			-		0
6–8	-				−0.91			-		0
8–9	-				-			$Δ Δ G_{9}^{X}$ ^d		0

Open in a new tab

2-nt flip of any sequence.

“>” indicates a lower limit (see Figure S6A).

Coupling terms are defined as combinations of residues that meet all of the indicated conditions at the indicated sets of positions. For example, the coupling term $Δ Δ G_{c}^{6 - 8}$ has the value of −0.91 kcal/mol if position 7 residue is a C and position 6 and 8 residues are not A (C/G/U); for all other combinations of sequences, the value of the coupling term is 0.

Coupling term indicates that the position 9 binding term ( $(Δ Δ G_{9}^{X}$ ; “term I”) is only implemented when position 8 is the consensus residue A.

Evaluating the Final PUM2-Binding Model

Control fits and analyses demonstrated that the fit model parameters were stable to variation in initial parameter values, data resampling, and the use of different fitting methods (STAR Methods). Training and testing sets gave essentially identical R² and RMSE values, suggesting that the model was not overfit. Assessment of RMSE sensitivity to individually varying each model parameter revealed that, as expected, the free energy terms for the consensus residues were most highly constrained, as these residues were present in the majority of the RNAs, while penalties for mismatched bound residues were less well constrained (Figure S5A). Approximately half of the flipping terms in the model were well constrained, while the other half provided lower limits for the free energy penalties, generally because the penalties were sufficiently high that either no binding or binding in an alternative register was observed (Figure S6A). In addition, the lack of specificity for the “bound” base at position 5 limited our ability to distinguish flipping at position “4/5” versus position “5/6” (numbering of flipped residues is based on the flanking bound residues; Figure 3E).

Implementation of the Predictive Model of RNA Binding by PUM2

The thermodynamic model for PUM2 binding can be applied to any RNA by calculating the ensemble free energy across each of the possible binding modes (consecutive, one or two residues flipped) and binding registers, as illustrated for a 15-nt RNA example in Figure 4A. The model can be further extended to predict PUM2 occupancies along larger, physiological RNAs, as illustrated schematically for an mRNA target in Figure 4B, and we provide an algorithm for occupancy predictions (see STAR Methods).

Evaluating Specificity across Human Pumilio Proteins

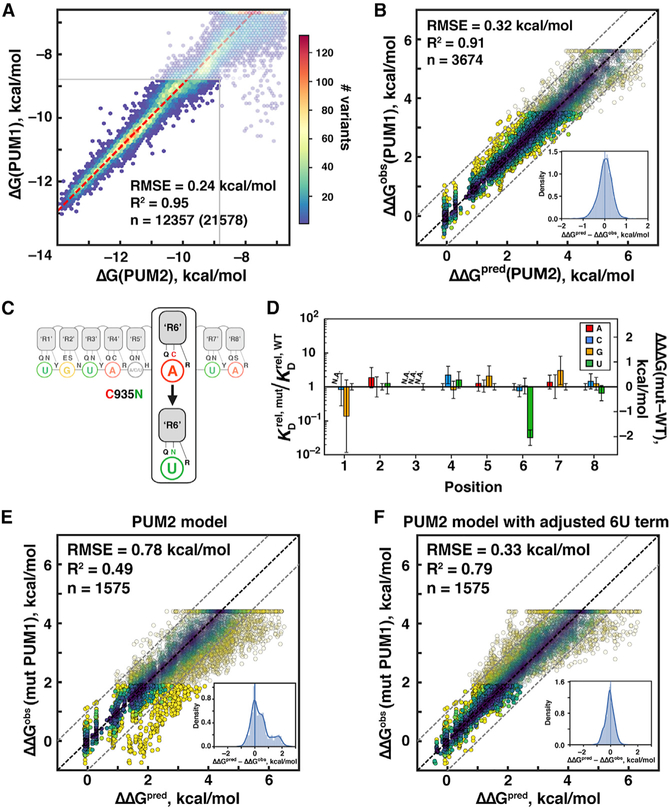
Human PUM1 shares 91% sequence identity and 97% sequence similarity in its RNA-binding domain (RBD) with PUM2, and all of the RNA-interacting amino acids are identical between the two proteins. Prior studies revealed nearly identical RNA sequence motifs and considerable overlap in apparent targets, highlighting the question of why humans retain two seemingly redundant proteins (Figure S1A) (Goldstrohm et al., 2018). To test potential quantitative differences in PUM1 and PUM2 sequence specificity and to assess if our PUM2-derived binding model could be extended to predict PUM1 binding, we compared PUM1 and PUM2 binding across our RNA sequence library.

PUM1 and PUM2 binding showed high agreement, indistinguishable from the concordance between PUM2 replicates (Figure 5A versus Figure 1E). Therefore, our model derived from PUM2 data can also be used to predict PUM1 binding (Figure 5B). The identical RNA sequence specificities suggest that any functional differences between PUM1 and PUM2 are fully determined by other factors, such as differences in modification patterns, protein interaction partners, or subcellular localization (Goldstrohm et al., 2018; Kedde et al., 2010; Thul et al., 2017).

Evaluating the Precision of Pumilio Engineering

The modular structure of PUF proteins has made them attractive platforms for engineering new RNA specificities (Chen and Varani, 2013; Lu et al., 2009). Given our observation of complexity of the PUF protein specificity landscape that is not captured by a simple linear motif, we aimed to comprehensively evaluate the precision of PUF protein engineering using a previously designed PUM1 mutant, in which specificity for position 6 in the RNA was altered from A to U through a single amino-acid substitution in repeat “R6” (Cheong and Hall, 2006) (Figure 5C).

Analysis of single-mutant penalties relative to wild-type PUM1 confirmed a change in mutant PUM1 specificity at position 6, with no significant differences observed for other residues and positions, supporting a local effect from the PUM1 mutation (Figure 5D).

We next asked if our thermodynamic model could be applied to the engineered PUM1 protein. Changing a single term in our binding model to account for the altered 6U penalty for mutant PUM1 (−0.32 kcal/mol instead of +1.49 kcal/mol) gave accurate predictions across our library, with 99% of variant affinities predicted to within 1 kcal/mol (Figures 5E and 5F). Thus, our quantitative model can be readily modified and applied to new PUF proteins.

Assessing the Thermodynamic Model for PUM2-RNA Occupancies In Vivo

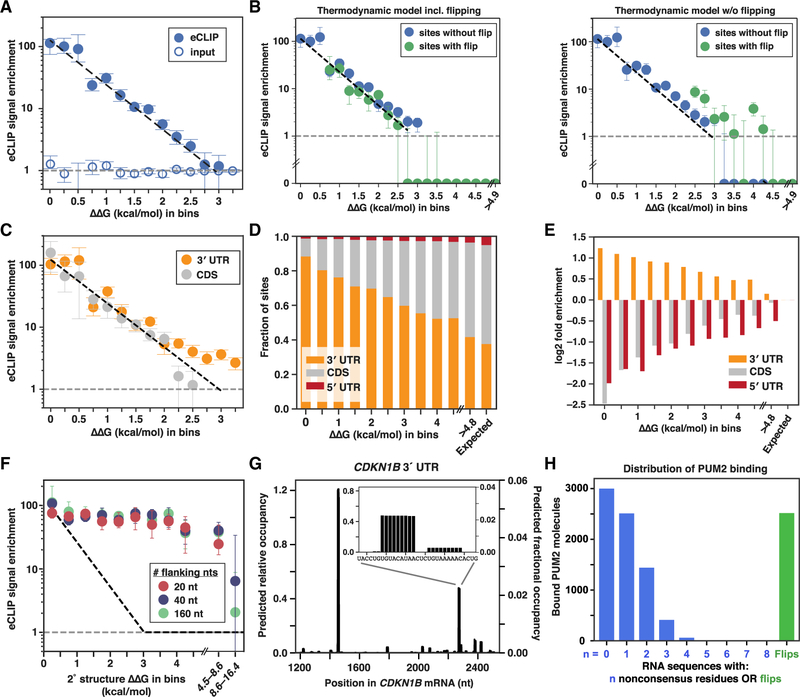
To assess the extent to which in vivo binding is driven thermodynamically, we compared predictions from our thermodynamic binding model to published in vivo enhanced UV crosslinking and immunoprecipitation (eCLIP) measurements for PUM2 from the ENCODE project (Consortium, 2012; Van Nostrand et al., 2016). Putative PUM2 binding sites within expressed mRNAs were identified as sites with predicted binding affinities within 4.0 kcal/mol (~1,000-fold) of the consensus sequence. eCLIP signal was divided by the relative expression of its transcript and evaluated in bins of predicted affinity, because quantification of individual RNA sites is currently limited by low sequencing depths and may be further subject to experimental biases (Darnell, 2010; Sugimoto et al., 2012; Wheeler et al., 2018). Strikingly, we observed quantitative agreement between relative affinities predicted by our thermodynamic model and the median eCLIP enrichment signal across the predicted affinity bins (Figure 6A, points versus dashed line). Close agreement was observed for predicted sites both with and without flipped residues (Figure 6B). Thus, in vivo binding data are consistent with thermodynamically driven occupancy, and the binding sequences and modes identified by RNA-MaP are bound, on average, at the levels expected based on their affinities.

Figure 6. — (A) Thermodynamic affinity predictions compared to eCLIP enrichment in K562 cells (Van Nostrand et al., 2016). Median eCLIP enrichments across sites within bins of predicted relative affinities are shown, and error bars indicate 95% CIs on the median. Only sites lacking adjacent UGUA-containing sites (within 100 nt) are shown due to inflation of eCLIP signal observed in the presence of nearby sites (Figure S7A). Black dashed line indicates the predicted change in eCLIP signal with increasing predicted ΔΔG values, relative to the eCLIP signal in the lowest ΔΔG bin. eCLIP (closed circles) and input (open circles) correspond to crosslinked samples that were or were not treated with anti-PUM2 antibody, respectively (Van Nostrand et al., 2016). The gray dashed line indicates the eCLIP enrichment for sites with predicted ΔΔG values greater than 4.5 kcal/mol (expressed transcripts); since eCLIP signal and input were each normalized to this value, this expected enrichment is equal to 1. Numbers of sites per bin range from 97 to 14,787 and are provided in Table S6.

(B) Median eCLIP enrichment and 95% CIs across bins of predicted ΔΔG, using either the full thermodynamic model (left) or a model that does not take into account flipped residues (right). Only bins with at least 25 sites are shown.

(C) Comparison of eCLIP enrichment for sites within 3′ UTR (orange) or CDS (gray) regions of expressed genes in K562 cells. Medians and 95% CIs are shown. Black and gray lines are as in A.

(D) Fractions of sites annotated as 3′ UTR, CDS, or 5′ UTR within bins of predicted ΔΔG values.

(E) Fold difference (log2) of the observed fraction of sites with the given annotation (5′ UTR, CDS, and 3′ UTR) versus the expected fraction (based on randomly selected sites).

(F) Median eCLIP enrichment of consensus sites across bins of predicted secondary structure stabilities for structures blocking the PUM2 consensus site (Figure 2C; STAR Methods). Colors indicate the number of flanking nucleotides (nt) included in the stability calculations. Dashed line indicates the predicted change in eCLIP signal for increasing secondary structure stability at 37°C. Medians and 95% CIs for bins with at least 20 sites are shown.

(G) Example of thermodynamic occupancy predictions for the 3′ UTR region of the human cyclin-dependent kinase inhibitor 1b *CDKN1B* mRNA, a known target of human Pumilio proteins (Kedde et al., 2010). The left axis indicates predicted relative occupancies with respect to the UGUAUAUAU consensus; the right axis indicates predicted fractional occupancies (i.e., fraction of bound versus total *CDKN1B* mRNA) after accounting for cellular PUM2 and RNA abundances (see STAR Methods).

(H) PUM2-binding landscape across the human transcriptome, predicted by our thermodynamic model using *in vivo* PUM2 and mRNA levels (see STAR Methods). Bars indicate the number of bound PUM2 molecules across RNA binding sites with zero to eight nonconsensus residues without flipped residues (blue) or with up to two flipped residues (green). The consensus was defined as UGUA[ACU]AUAN. See Table S6 for numbers of sites of each type.

See also Figure S7 and Table S6.

Because Pumilio proteins have generally been identified to act via 3′ UTRs (Goldstrohm et al., 2018), we wondered whether there might be lower average occupancy in coding sequences (CDSs) and in 5′ UTRs (e.g., due to displacement of PUM2 from CDS sites by translating ribosomes). Comparison of the occupancy around PUM2 sites in 3′ UTRs and CDSs showed indistinguishable eCLIP enrichments (Figure 6C; 5′ UTR sites were not included because of the small number of predicted sites in this region), suggesting that inherent thermodynamic stability of a site is the overarching driver of in vivo occupancy rather than the location of the site within the mRNA.

We observed a strong enrichment of PUM2 consensus sites in 3′ UTR sequences relative to CDS and 5′ UTR regions, with ~90% of consensus sites located in 3′ UTRs, despite 3′ UTRs constituting on average only 38% of the mRNA length (Figures 6D and 6E; Consortium, 2012). 3′ UTR enrichment was evident, though diminished, for sites with weaker predicted affinities, suggesting that these sites may also play functional roles via 3′ UTR binding.

In vitro measurements indicated that RNA secondary structure formation can strongly limit the accessibility of PUM2 binding sites and thus decrease PUM2 binding (Figures 2C and 2D) (Becker et al., 2019a). In contrast to the pronounced structure effects observed in vitro, comparisons of in vivo eCLIP signal around consensus sites with varying predicted structure content revealed no change in median occupancy for predicted structural stability of up to ~4 kcal/mol (Figure 6F; 37°C). A rare subset (<2%) of sites had very high predicted structure stability (ΔΔG_fold > 8.6 kcal/mol) and showed slightly diminished eCLIP signal, suggesting that highly stable structures may lead to decreased binding. However, RNA structure effects on the vast majority of PUM2 sites appear to be negligible in vivo.

DISCUSSION

RNA-protein interactions are integral to regulation of gene expression (Singh et al., 2015). To define and predict the complex networks of RNA-protein interactions, quantitative descriptions of RNA-RBP thermodynamics are needed. Toward this goal, we have built a predictive model for RNA binding by the human PUM1 and PUM2 proteins. This model, along with direct thermodynamic binding measurements for thousands of RNAs, provides testable predictions of in vivo RNA interactions and yields biological and biophysical insights.

Applications to Cellular Interactions and RNA Properties

Comparison of predictions from the thermodynamic binding model to published in vivo cross-linking data (Van Nostrand et al., 2016) supports the simple notion that thermodynamics is a prime driver in determining RNA occupancy for PUM2 (Figures 6A and S7B). While it would be surprising if thermodynamic affinities did not influence RNA binding in vivo, other models are possible. For example, rapid Pumilio protein dissociation by the action of RNA helicases would level occupancies for all sites above a certain threshold affinity (Figure S7C), and translation by ribosomes that displaces PUM2 proteins faster than equilibration of PUM2 binding would yield CDS occupancies lower than 3′ UTR occupancies. However, a close correspondence between thermodynamic predictions and in vivo crosslinking provides evidence against these alternate models (Figures 6A and 6C). Ribosomes traverse CDS sites, and presumably displace bound factors, approximately once every 10 s (~0.1 s⁻¹; Halstead et al., 2015; Schwanhäusser et al., 2013). This rate sets an upper limit for the equilibration time for PUM2 binding—it must occur faster than ribosomal displacement for us to observe no difference in occupancy in CDSs compared to 3′ UTRs. This rough lower limit estimate is similar to the rate constant for dissociation of PUM2 from the consensus sequence in vitro (~0.1 s⁻¹;37°C; unpublished data), suggesting that indeed PUM2 dissociates from consensus sites on the timescale of translation, and faster for nonconsensus sites.

Recent studies have suggested that RNA structure is destabilized in the cellular milieu (Ding et al., 2014; Guo and Bartel, 2016; Rouskin et al., 2014; Spitale et al., 2015). Using published in vivo eCLIP data (Van Nostrand et al., 2016), we observed that binding sites predicted to be minimally accessible (<0.1%; ΔΔG_fold ≳ 4 kcal/mol) gave PUM2 enrichments essentially indistinguishable from sites predicted to lack structure (Figure 6F). These results provide independent support for structure disruption in vivo, which could result from a high density of bound RBPs that outcompete RNA structure formation and/or the action of RNA chaperones. Moving forward, coupling in vitro thermodynamic measurements with quantitative in vivo analysis will aid in determination of cellular factors responsible for destabilizing RNA structure.

Generalizability of the Thermodynamic Model and Potential Improvements

The rational design of our RNA-MaP library ensured high coverage of predicted binding sites; for example, despite measuring only 4.2% of all possible 9mers, the fraction of predicted “binders” (9mers with ΔΔG^pred < 4.5 kcal/mol) in this library was 35%. Comparisons to published RNA Bind-n-Seq (RBNS) data for human PUM1 (Consortium, 2012; Dominguez et al., 2018) confirmed that the model performed indistinguishably for sequences that were or were not represented in the RNA-MaP library (R²: 0.74 versus 0.75; Figure S7D), supporting generalizability. In the future, the model may be further improved through more comprehensive measurements of neighboring double and triple mutations, which may identify additional weak coupling terms; additionally, greater sequence coverage of insertions longer than 1 nt would allow full assessment of the sequence dependence of flipping penalties. While we do not expect these improvements to have major effects on the overall accuracy, they may lead to identification of additional stable binders.

An Algorithm for Predicting PUM1 and PUM2 Occupancies

The thermodynamic binding model, along with estimated in vivo PUM1, PUM2, and RNA levels, allows prediction of PUM1 and PUM2 occupancy across the entire transcriptome. We supply a computational algorithm to carry out these predictions, and depict the output of this tool for one transcript in Figure 6G. The algorithm can be used to predict occupancies for individual sites and RNAs and to design future tests for cellular factors that might affect PUM1 and PUM2 binding.

Implications for Other RBPs

Despite the simple, modular structure of the PUM RNA-binding domain, our data revealed considerable complexity in PUM1 and PUM2 interactions with RNA, due to base flipping, coupling, and binding in multiple modes and registers. These features are likely even more important for RBPs that lack a well-defined modular architecture. In fact, the requirement for more sophisticated models may explain the difficulty in obtaining sequence motifs for many RBPs, and the apparent degeneracy and redundancy of many of the hundreds of motifs that have been determined (e.g., Dominguez et al., 2018; Ray et al., 2013). Building on these motifs as starting points for rational library design and carrying out quantitative equilibrium measurements will be essential for developing predictive models of RBP interactions across all levels of RBP complexity.

Functional Implications

The connection between PUM2 occupancy and its functional effects on mRNA abundance remains to be fully explored. Recent analysis of transcriptome-wide effects of PUM1 and PUM2 depletion showed that consensus sites located in 3′ UTRs were more likely to give significant regulation than CDS sites (Bohn et al., 2018). Using our thermodynamic model to account for all sites (including nonconsensus sites) within each mRNA region supports this conclusion: PUM2 occupancy across 3′ UTR sites was moderately predictive of mRNA upregulation in response to PUM1 and PUM2 knockdown (Figure S7E; area under the curve [AUC], 0.63), whereas PUM2 occupancy across the CDS or 5′ UTR regions was less predictive (AUC = 0.57). As a point of comparison, the eCLIP signal in the 3′ UTR was similarly predictive of regulation as thermodynamically predicted PUM2 occupancy (AUC = 0.63; Figure S7F). The difference between functional outcomes from binding to 3′ UTR versus non-3′ UTR sites, despite indistinguishable PUM2 binding occupancies (Figure 6C), indicates the importance of additional cellular factors in determining the extent of PUM1- and PUM2-mediated repression.

The model further allows certain mRNAs to be confidently ruled out as direct PUM1 and PUM2 targets. In their study of global effects of PUM1 and PUM2 depletion on mRNA abundance, Bohn et al. observed a set of 300 mRNAs that were significantly downregulated, indicating a noncanonical role of Pumilio proteins in activating rather than repressing these targets (Bohn et al., 2018). Our thermodynamic model predicts that these mRNAs do not bind PUM1 and PUM2 significantly more than unregulated RNAs, suggesting that their expression is not controlled through direct interactions with Pumilio proteins. These genes may instead be regulated by factors that are themselves repressed by PUM1 and PUM2 (Figure S7G).

Specificity and Cellular RNA-Protein-Binding Landscapes

Determining quantitative RBP binding landscapes and how these landscapes change with changes in RBP and RNA expression levels is critical for a complete description of the RBP-RNA networks. The shape of the binding landscape—i.e., RBP occupancies across RNA sequences present in a cell—has implications for regulation, evolution, and engineering. We illustrate some of these implications for PUM2.

The thermodynamic model predicts that less than a third of cellular PUM2 is bound to consensus sites and that the majority of the protein is distributed across nonconsensus sequences (Figure 6H; STAR Methods)—a consequence of the large excess of nonconsensus sites (Table S6) and the moderate binding penalties associated with many mutations and insertions (Table 1).

The varied, moderate nonconsensus residue penalties allow for a smooth gradient of PUM2 binding occupancies (Figure 6A; see also Figure 3F), and we speculate that this continuum of occupancies can be used to finely tune regulatory effects that occur through PUM2 binding.

A less obvious influence of RBP specificity on regulation arises because the binding to nonconsensus RNA sites reduces the pool of protein available to bind to consensus sites. Because of this titration effect and because of the much greater number of potential binding sites than the number of PUM2 molecules in cells, only a small fraction of each consensus site (UGUA [ACU]AUAN) is predicted to be occupied by protein (<10%, based on known amounts of cellular PUM2 and mRNA; STAR Methods). Thus, even in the presence of total protein concentration in excess of the consensus affinity ([PUM2] = 10 nM versus K_D = 3 nM at 37°C), binding is decidedly subsaturating. This subsaturating binding renders per-site occupancies highly sensitive to changes in PUM2 levels or affinity, much as observed for enzymes that operate in a subsaturating regime ([substrate] ~K_M) to enable greater sensitivity to cellular changes in substrate concentration (Berg and Stryer, 2002).

The near-continuous nature of PUM2 occupancies across mRNA sequences would be expected to render the PUM2-binding landscape highly evolvable. The presence of a large number of sites bound with moderate affinities, and the often-subtle effects of individual substitutions should allow evolution to both tune regulation of existing sites as well as co-opt binding sites for new regulation. Indeed, PUM2 orthologs throughout Eukarya recognize distinct sets of RNAs, and these transitions that occurred multiple times in evolution may have been facilitated by the moderate specificity of PUF proteins (Gerber et al., 2006; Hogan et al., 2015; Jiang et al., 2010).

Given the diversity of RBP properties and abundances (Singh et al., 2015), we expect considerable variation between occupancy landscapes of individual RBPs. For example, in contrast to the PUM2 example above, highly expressed RBPs ([RBP] ≫ K_{D, consensus} and [RBP] ≫ [RNA]_consensus) will saturate their consensus sites, rendering binding insensitive to concentration changes and less discriminatory to nonconsensus sites. Quantitatively defining cellular RBP occupancy landscapes across diverse specificity and concentration regimes, their dynamic changes, and the biological consequences of these changes represents an intriguing challenge for future studies.

Biophysical Insights into Pumilio-RNA Interactions

Our data revealed that the A-recognition modules (“R4”, “R6”, and “R8”; Figure 1A) give highly similar specificities, whereas the U-recognition modules (“R1”, “R3”, “R5”, and “R7”) vary dramatically in their specificities, from no discrimination against A and C at position 5 to~10²-fold specificity at positions 1 and 3 (Figures 2E and S7H–S7J). The differential specificity across the U-recognition modules could arise, at least in part, from differences in orientations and constraints imposed by the different neighboring positions, which can allow more or less optimal positioning at each U-recognition module. Similarly, the slightly weaker discrimination by the “R8” module, at the end of the PUM domain, relative to the internal A-recognition modules, may arise because there are fewer RNA conformational restraints 3′ of this position, allowing noncognate bases to more readily find alternative bound conformations.

The absence of measurable coupling between most neighboring residues suggests that the orientation of entry of the RNA into a site is not generally affected by the identity of the neighboring residue. This observation suggests that cognate and noncognate residues are bound with similar backbone configurations (or ranges of backbone conformations), consistent with crystallographic observations that backbone trajectories leading into and out of Pumilio repeat sites are similar with cognate and noncognate bases (Gupta et al., 2008; Lu and Hall, 2011; Wang et al., 2009). More generally, the observed energetic independence between most adjacent RNA residues suggests sufficient room in the binding sites and/or sufficient degrees of freedom in the RNA backbone to allow the backbone to “forget” its specific interactions at the adjacent sites. Nevertheless, a subset of positions do exhibit coupling, and coupling is likely more prevalent for at least a subset of other RBPs.

Larger energetic effects are observed in cases of inserted residues that can flip away from the recognition sites (Figure 3D; Table 1). A residue that follows a flipped residue will experience a larger loss in conformational entropy upon docking than a residue that is positionally restricted by a preceding docked residue. Nevertheless, the specificity for neighbors is the same whether or not there is an intervening flipped residue—i.e., the same free energy terms can be used for each bound residue whether or not there is a flipped residue and associated flipping penalty. This constancy suggests that flipped residues do not significantly alter the docked states for neighboring cognate and noncognate residues and that there are no alternative bound states for the neighboring residues that are more favorable energetically than the standard docked state.

These observations are of practical importance for engineering PUF proteins and of broader importance for understanding and modeling RNA recognition by RBPs. Relative to DNA/protein interactions, more diverse conformational broader ensembles are expected for ssRNA, both bound and unbound to RBPs, highlighting the enormous challenge faced in modeling RNA-RBP binding affinities and specificities. Developing models that ultimately predict thermodynamics and binding landscapes for all RBPs we believe will require guidance and testing with large accurate thermodynamic datasets, such as those obtained herein.

STAR★METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Daniel Herschlag (herschla@stanford.edu).

METHOD DETAILS

Library design

Summary of library designs and complete sequence information is provided in Table S5.

Library preparation and sequencing

Ordering

DNA constructs consisting of the PUF library and short constant regions for subsequent PCR assembly (Figure S1D & Table S7; 5′–TGTATGGAAGACGTTCCTGGATCC–[Variable region]–AGATCGGAAGAGCGGTTCAG–3′) were ordered from CustomArray, Inc. as part of a 90,000 oligo pool of 130 nt sequences. Each of the 34,927 unique sequences in the library (including variants not discussed herein) was included at least in duplicate to increase the probability of error-free generation. In cases where the designed sequence was shorter than 130 nt, the construct was “padded” at the 3′ end with a random sequence that was eliminated during PCR assembly. Primers and DNA oligonucleotides used in the RNA-MaP protocol were ordered from Integrated DNA Technologies (IDT).

Emulsion PCR

The oligonucleotide pool was amplified using emulsion PCR (ePCR) (Williams et al., 2006), allowing us to decrease length and other biases during PCR amplification of our highly diverse library (lengths of 64–130 nt, variable structure content). We closely followed a MYcroarray adaptation of the ePCR protocol from (Williams et al., 2006), as detailed below. Flat-bottom glass vials (1 mL) were cleaned with sterile water, dried, covered with parafilm, and frozen in a Petri dish filled with sterile water. The oil phase was prepared from 4% (v/v) ABIL EM-90, 0.05% (v/v) Triton X-100 and 96% (v/v) mineral oil. The 50 μL aqueous phase consisted of 1.45 ng/μL of the CustomArray oligo pool, 0.2 mM dNTPs, 1 μL of Phire Hot Start II DNA Polymerase (Thermo Fisher Scientific), 1x Phire II buffer, 0.5 mg/mL bovine serum albumin (BSA), and 2 μM of each of RNAPstall and Read2 primers (Table S7 and Figure S1D). A 300 μL aliquot of the vortexed, pre-chilled oil phase was added to the glass vial embedded in the ice-filled Petri dish and stirred on a stir plate with a sterile magnetic bar at 1000 rpm for 5 min. The aqueous phase was then added in five 10 μL aliquots and stirred for another 10 min. The emulsion was divided between seven PCR tubes and amplified for 40 cycles of 98°C for 10 s, 65° C for 10 s, and 72° C for 30 s. Completed PCR reactions were pooled in a 1.7 mL Eppendorf tube, and 1 μL of gel loading dye was added to visualize the aqueous phase. Mineral oil (100 μL) was added and the mix was vortexed for 30 s, followed by centrifugation for 10 min at 13,000 g. The oil was discarded and 1 mL diethyl ether was added, the mixture was vortexed in a fume hood for 3 min and centrifuged for 1 min at 13,000 g. Diethyl ether was discarded, 1 mL ethyl acetate was added, and the mixture was vortexed in a fume hood for 3 min and centrifuged for 1 min at 13,000 g. Ethyl acetate was removed and the diethyl ether extraction step was repeated, followed by discarding the diethyl ether. The tube was incubated for 5 min at 37°C with an open cap to allow residual diethyl ether to evaporate. Water (40 μL) and Agencourt AMPure XP beads (Beckman Coulter; 72 μL) were added and incubated for 15 min at room temperature; the supernatant was removed, the beads were washed with 70% ethanol (2 × 100 μL), dried, and the DNA was eluted in 10.5 μL water.

Size fractionation

To further prevent bias toward short oligonucleotides during the subsequent PCR assembly steps, the ePCR-amplified library was fractionated by length on an 8% polyacrylamide gel. Following SYBR Green staining (1x; Lonza), the library-containing lane was covered with aluminum foil to prevent UV-induced damage (Gründemann and Schömig, 1996; Sinha and Häder, 2002), and divided into 6 fractions based on UV visualization of marker lanes. The cut-out bands were frozen on dry ice and eluted overnight in TE buffer (10 mM Tris,HCl, pH 8.0, 1 mM Na₂EDTA) on a rotating platform at 8°C. The DNA was purified using the QIAGEN Gel Extraction Kit (using a protocol adapted for PAGE purification: http://www.qiagen.com/kr/resources/resourcedetail?id=1426dbb4-da09-487c-ae01-c587c2be14c3&lang=en, with QIAGEN MinElute columns). To remove residual co-purified short fragments, each fraction was re-purified on an 8% denaturing gel (8 M urea). For denaturing PAGE, the samples and a Low-MW DNA ladder (New England Biolabs; NEB) were heated in loading buffer (84% (v/v) formamide, 50 mM Na₂EDTA, 0.04% Xylene cyanol, 0.04% Bromophenol blue (BPB); 2.8 μL loading buffer per 5 μL sample) at 90°C for 3 min immediately before loading. The gel was stained with SYBR Gold, the library-containing lanes were covered with aluminum foil and fractions were cut out based on UV visualization of marker lanes. (Additional lanes with 83 nt and 129 nt DNA oligonucleotides were used to facilitate alignment of the NEB low-MW marker with desired lengths.) The DNA was extracted from the gel as above and eluted in QIAGEN EB buffer with 0.1% Tween-20. Purified fractions were re-amplified using the Read2 and RNAPstall_adapt primers (Table S7). The PCR reactions (25 μL) consisted of 2.5 μL of the purified library fractions, 0.5 μM of each primer, 0.2 mM dNTPs, 3% DMSO, 0.02 U/μL Phusion HF Polymerase (Thermo Fisher Scientific), and 1x Phusion HF buffer. The reactions proceeded for 15–23 cycles of 98°C for 10 s, 63°C for 20 s, and 72 °C for 20 s and were purified using QIAGEN MinElute PCR Purification Kit. In all cases here and below, the number of PCR cycles was determined by quantitative PCR (qPCR), using the same primer and template concentrations as in preparative PCR, but in the presence of 0.2–0.5x SYBR Green. To prevent accumulation of by-products, cycle numbers corresponding to about one-third saturation (C_t value) were used in preparative PCR reactions. Each library fraction was amplified for two to three different numbers of cycles around the C_t value, and only reactions lacking high-molecular weight byproducts were propagated to the next step.

PCR assembly

Each purified length fraction was assembled into the final RNA array construct with the C_read1_bc_RNAP, D_read2, OligoC and OligoD primers, as illustrated in Figure S1D (see Table S7 for primer sequences). The C_read1_bc_RNAP primer contained a randomized 15 nt ‘barcode’ region that served as a unique molecular identifier (UMI) and allowed high-confidence sequence mapping during subsequent steps (Buenrostro et al., 2014). The PCR reactions consisted of 0.5 nM of the amplified library fractions, 1.5 nM of C_read1_bc_RNAP primer, 1.5 nM of D_read2 primer, 0.5 μM of Oligo C and Oligo D primers, 0.2 mM dNTPs, 3% DMSO, 1x Phusion HF buffer, and 0.01 U/μL Phusion HF Polymerase. The reactions proceeded for 18 cycles of 98 °C for 10 s, 63° C for 30 s, and 72° C for 30 s, and the PCR products were purified using QIAquick PCR purification kit (QIAGEN).

Bottlenecking

To ensure that multiple copies of each UMI were present on the RNA array, the library was bottlenecked to ~700,000 total molecules (Buenrostro et al., 2014; Denny et al., 2018; Kivioja et al., 2011). UMI redundancy allows distinguishing between sequencing errors and real sequence differences, as errors are unlikely to co-occur in both the UMI and the variable region (see Computational analyses below). To bottleneck, the PCR products were quantified by qPCR relative to the PhiX standard (Illumina). As noted above, the six ‘sublibraries’, corresponding to the different oligonucleotide lengths in our library, were kept separate during all pre-sequencing PCR steps to minimize bias in the final library assayed by RNA-MaP. Dilutions of 1000-fold and 10,000-fold for each fraction were prepared in 0.1% Tween-20. The PhiX standard (Illumina) was diluted to 200 pM and seven serial dilutions were prepared in 0.1% Tween-20. The DNA was then added to a PCR master mix containing 500 nM OligoC and OligoD primers, 200 μM dNTP mix, 0.5x SYBR Green, 3% DMSO, 0.02 U/μL Phusion DNA Polymerase, and 1x Phusion buffer. The PCR reactions proceeded for 35 cycles of 98° C for 10 s, 63° C for 30° s, and 72° C for 30 s. The library concentrations were determined based on the PhiX standard curve of C_t values over concentration (determined in duplicate). The volumes corresponding to a total of 700,000 molecules across all sublibraries were calculated, and each sublibrary was amplified with OligoC and OligoD primers. The PCR reactions contained1.1–5.3 fM of individual sublibraries (in 0.1% Tween-20), 500 nM OligoC and OligoD primers, 200 μM dNTP mix, 3% DMSO, 1x Phusion buffer, and 0.01 U/μL Phusion DNA Polymerase. The reactions proceeded for 23 cycles of 98° C for 10 s, 63° C for 30 s, and 72° C for 30 s, and the PCR products were purified with QIAquick PCR cleanup kit (QIAGEN). Concentrations of 1000-fold dilutions were quantified by qPCR, and the different sublibraries were combined for sequencing. Due to a short OligoD byproduct detected as dominant species in the initial sequencing of our library, the bottlenecked library fractions were re-purified on a denaturing 8% acrylamide gel and amplified using Phusion Hot Start II DNA Polymerase (Thermo Fisher Scientific) instead of regular Phusion, which eliminated the primer byproduct. This library was sequenced and used in all RNA-MaP experiments reported herein.

Fiduciary marker preparation

To facilitate RNA array image alignment and quantification, we included a fiduciary marker oligonucleotide in our RNA array library sample prior to sequencing (see below). This oligonucleotide resembled the library constructs, except for lacking the barcode, RNAP promoter and RNAP start/stall regions and was PCR-assembled separately using an analogous series of steps. The final sequence of the fiduciary oligo consisted of [C_adapter][Read1] CTT GGG TCC ACA GGA CAC TCG TTG CTT TCC [Read2′][D′_adapter] (Fiducial_chip, Table S7).

Sequencing

The bottlenecked, qPCR–quantified library fractions were combined and sequenced using MiSeq Reagent Kit v3 (150-cycle; 56 nt in Read 1, 96 nt in Read 2). To ensure appropriate density of RNA clusters in the RNA-MaP experiments, our library constituted 9%–15% of the total 6–9.6 fmol DNA. The remaining DNA consisted of 84%–90% PhiX DNA and 1% of the fiduciary marker oligonucleotide (Fiducial_chip, Table S7). The final numbers of transcribable clusters were 3.6 × 10⁵−6.5 × 10⁵ on the sequencing chips used in this study.

Protein expression and purification

The RNA-binding domains of H. sapiens PUM1 (828–1176; isoform 2), PUM2 (706–1059; isoform 1), and mutant PUM1 (MUT3–1 in (Cheong and Hall, 2006)) (828–1176) were cloned into a custom pET28a-based expression vector in frame with an N-terminal Histag and a SNAP tag (New England Biolabs) at either the N- (PUM2) or C terminus (hPUM1 and hPUM1 MUT3–1; primers and plasmid sequences available upon request). Constructs were sequenced and transformed into E. coli protein expression strains BL21 (DE3) or RIPL BL21 CodonPlus (Agilent). Protein expression was induced at an OD600 of between 0.6–0.8 with 0.5–1 mM IPTG at 18–20°C for 18–20 h. Cell pellets were lysed four times using an Emulsiflex (Avestin) in Buffer A containing 20 mM Na-HEPES, pH 7.4, 500 mM potassium acetate (KOAc), 5% glycerol, 0.2% Tween-20, 10 mM imidazole, 2 mM dithiothreitol (DTT), 1 mM phenylmethylsulfonyl fluoride (PMSF) and 2X Complete Mini protease inhibitor cocktail (Roche). The lysate was centrifuged at 20,000 g for 20 min to remove membranes and unlysed cells. Nucleic acids in the lysate were precipitated with dropwise addition of Polyethylene Imine (Sigma) to a final concentration of 0.21% (v:v) with constant stirring at 4° C and pelleted by centrifugation at 20,000 g for 20 min. Cleared lysates were then loaded on a Nickel-chelating HisTrap HP column (GE), washed extensively, and His-tagged proteins were eluted over a 10–500 mM imidazole gradient. Protein fractions were pooled and desalted into Buffer B (20 mM Na-HEPES, pH 7.4, 50 mM KOAc, 5% glycerol, 0.1% Tween-20, 2 mM DTT) using a HiPrep 26/10 desalting column. The His-tag was removed by incubation with TEV protease for 13–16 h at 4°C, and the protein solution was loaded for a second time on the HisTrap HP column. The flow-through containing cleaved protein was collected and subsequently desalted into Buffer B. The protein was then loaded on a Heparin or HiQ column and eluted over a linear gradient of KOAc from 50 to 1000 mM. Fractions were pooled and desalted into Buffer C containing 20 mM Na-HEPES, pH 7.4, 100 mM KOAc, 5% glycerol, 0.1% Tween-20 and 2 mM DTT, concentrated using Amicon Ultra–0.5 10KDa filters and diluted two-fold with Buffer C containing 80% glycerol for final storage at −20°C. SDS-PAGE gels of final purified protein constructs are shown in Figure S7K.

Cy3B-labeling of SNAP-tagged proteins

Cy3B-labeled SNAP tag substrate was prepared by coupling Cy3B NHS ester (GE Healthcare, 0.75 μmol) with 1.5-fold excess(1.13 μmol) of amine-terminated benzylguanine (NH2-BG; New England BioLabs) in the presence of 1.13 μmol triethylamine in dimethylformamide. The reaction (103 μL) was incubated overnight on a rotating platform at 30°C. The Cy3B-BG product was purified by reverse phase HPLC on an Agilent ZORBAX Eclipse Plus 95Å column and dried by speed-vac evaporation (46% yield).

SNAP-tagged PUF proteins were labeled by incubating 5–10 μM of purified protein with 20 μM of Cy3B-BG in Buffer C. The tube was covered with aluminum foil and rotated at 4°C for 12–14 h. Unincorporated dye was removed with Zeba Spin Desalting Columns (Thermo Fisher Scientific) equilibrated with Buffer C; the protein was concentrated using Amicon Ultra 10KDa filters and diluted two-fold with Buffer C containing 80% glycerol for final storage at −20°C. The labeling efficiencies (based on total protein concentration and Cy3B absorbance at 559 nm; Cy3B extinction coefficient: 130,000 M⁻¹cm⁻¹) were 60% (PUM2-SNAP), 53% (SNAP-PUM1) and 36% (mutant SNAP-PUM1).

RNA-MaP measurements

Imaging station setup

The RNA-MaP imaging platform was built out of a repurposed Illumina GAIIx instrument with custom-designed additions as described in (Buenrostro et al., 2014; Denny et al., 2018; She et al., 2017). Briefly, the custom additions included a fluidics adaptor interface to pump reagents to the MiSeq flow cell, a Peltier-based temperature-controlled platform to house the flow cell, an autosampler with 96-well cooling block for RNA-MaP reagents, and a dual–color laser excitation system. Two lasers were employed: a 660 nm ‘red’ laser with a 664 nm long pass filter and a 530 nm ‘green’ laser with a 590 nm band pass filter. MATLAB scripts developed in-house were used to control the fluidics, temperature, position, and imaging of the flow cell. Flow cell images were acquired with 400 ms exposures at 200 mW laser power. Camera focal distances were determined through iterative rounds of imaging of the flow cell and adjustment of the camera’s z-position.

RNA transcription in the flow cell

Using the imaging station fluidics system, the flow cell was washed with 5 mM Na₂EDTA in formamide to remove hybridized DNA (250 μL flowed at 100 μL/min, 55°C), followed by Reducing buffer (100 mM Tris·HCl, 125 mM NaCl, 0.05% Tween-20, 100 mM Tris[2-Carboxyethyl]phosphine-HCl (TCEP), pH 7.4) to remove any residual fluorescence from the sequencing reaction (390 μL, 10 min at 60°C). A fluorescent probe complementary to the RNA Polymerase stall sequence (Fluorescent_stall’; sequences of oligonucleotides used in the RNA-MaP protocol are indicated in Table S7) was then annealed to the library and imaged to determine the efficiency of the cleaning steps (500 nM Fluorescent_stall’ in Annealing buffer: 1x SSC buffer, 7 mM MgCl₂, 0.01% Tween-20; 11 min at 37°C). After imaging, the fluorescent probe was removed by washing with 250 μL of 100% formamide (55° C). The flow cell was washed with Wash buffer between steps (290 μL; 10 mM Tris·HCl, pH 8.0, 5 mM Na₂EDTA, pH 8.0, 0.05% Tween-20). Henceforth, wash steps were performed with a 250 μL volume of the specified buffer, unless otherwise noted.

To prepare double-stranded DNA (dsDNA), 5′–biotinylated primer (Biotin_D_Read2, 500 nM) was annealed to the library in Hybridization buffer (5x SSC buffer, 5 mM Na₂EDTA, 0.05% Tween-20) for 15 min at 60°C followed by a 10 min incubation at 40°C. The fluorescent oligonucleotide complementary to the fiducial marker (Fiducial_flow) was also included in the hybridization mixture at 250 nM. After washing the flow cell with Annealing buffer, an additional 500 nM of Biotin_D_Read2 (and 250 nM Fiducial_flow) was annealed to the library in Annealing buffer at 37°C for 8 min. The flow cell was then washed with Klenow buffer (1x NEB buffer 2 (NEB B7002S), 250 μM each dNTP, 0.01% Tween-20). Double-stranded DNA was generated by pumping 130 μL of 0.1 U/μl Klenow fragment (3′−5′ exo(−); NEB M0212L) into the flow cell in three stages separated by 10 min intervals each. The flow cell was maintained at 37°C for this period. Unextended single-stranded DNA templates were subsequently blocked by annealing a non-fluorescent version of the stall probe (Dark_stall′) in a process identical to the one described above.

After dsDNA generation, 1 μM streptavidin in Annealing buffer was pumped into the flow cell and allowed to bind to the biotinylated primer for 5 min at 37°C. Excess streptavidin was then washed out of the flow cell with Annealing buffer. Unbound biotin binding sites in the streptavidin tetramer were saturated by incubating the flow cell for 5 min with 5 μM free biotin in Annealing buffer. Excess unbound biotin was washed out with Annealing buffer.

RNA transcription proceeded in two stages, initiation/stall and extension. In the initiation/stall phase, 130 μL of 0.06 U/μL E. coli RNA polymerase holoenzyme (RNAP; NEB M0551S) was allowed to initiate transcription for 20 min at 37°C on the dsDNA templates in Initiation buffer, which lacked CTP (20 mM Tris·HCl pH 8.0, 7 mM MgCl₂, 20 mM NaCl, 0.1% 2-Mercaptoethanol (BME), 0.1 mM Na₂EDTA, 1.5% glycerol, 0.02 mg/mL BSA, 0.01% Tween-20, and 2.5 μM each of ATP, GTP, and UTP). Upon encountering the first cytosine (C27), the polymerase stalls, thereby sterically preventing the loading of additional enzymes on the same template (Buenrostro et al., 2014). Excess RNAP was washed out of the flow cell with Initiation buffer. Subsequently, Extension buffer was added, which contained all 4 ribonucleotides (20 mM Tris·HCl pH 8.0, 7 mM MgCl₂, 20 mM NaCl, 0.1% BME, 0.1 mM Na₂EDTA, 1.5% glycerol, 0.02 mg/mL BSA, 0.01% Tween-20, and 1 mM each of ATP, GTP, UTP and CTP). The Extension buffer also contained 500 nM each of Fluorescent_stall′ and Dark_read2 oligonucleotides, which were intended to block the regions flanking the variable region in the nascent RNA transcript (Figure 1C) and to prevent undesired intramolecular interactions, as well as to allow visualization of the transcript. Transcription was allowed to proceed for 10 min at 37°C. RNA polymerase eventually is stalled at the streptavidin roadblock at the end of the DNA template, exposing the nascent RNA molecules for binding experiments (Figure 1C).

To ensure complete blocking of RNA regions flanking the variable sequence, transcription was followed by further hybridization of Fluorescent_stall′ and Dark_read2 oligonucleotides (500 nM) for 10 min at 37°C in Annealing buffer. Finally, the flow cell was washed with Binding buffer (20 mM Na-HEPES, pH 7.4, 100 mM KOAc, 0.1% Tween-20, 5% glycerol, 0.1 mg/ml BSA, 2 mM MgCl₂ and 2 mM DTT), the temperature was lowered to 25°C (except for 37°C experiments), and the flow cell was imaged to quantify the fluorescence from the RNA-annealed Fluorescent_stall′ probe.

RNA-MaP equilibrium binding experiments

To determine PUM1 and PUM2 binding affinities, the RNA library was sequentially equilibrated with increasing concentrations of Cy3B-labeled PUM proteins, and the amount of Cy3B fluorescence colocalized with each RNA cluster was determined at each concentration. Two-fold serial protein dilutions (15–17) were prepared in 1x Binding buffer and were stored in light-protected tubes on ice or in the 4°C autosampler chilling block until the incubation. Protein solution (460 μL) was pumped into the flow cell at each concentration and incubated for times ranging from 33 min for the lowest concentrations to 19 min for the highest protein concentrations (25°C; 15–23 min at 37°C). These incubation times were established to be sufficient for equilibration by association and dissociation time courses (halftime ≤ 5.3 min; see also (Vaidyanathan et al., 2017)). The incubation temperature was 25 or 37°C, as indicated for the individual experiments.

HPLC purification of RNA oligonucleotides for competition binding measurements

Desalted RNA oligonucleotides were ordered from IDT and purified by reverse-phase HPLC (XBridge Oligonucleotide BEH C18 Prep column or Agilent ZORBAX Eclipse Plus C18 column), using an acetonitrile gradient in the presence of 0.1 M triethylamine acetate. Following purification, the solvent was exchanged into MilliQ water with Amicon Ultra 3KDa concentrators.

[γ- ³²P]-labeling of RNA oligonucleotides

RNA oligonucleotides for direct binding measurements were ordered from IDT and 5′ labeled with [γ- ³²P] ATP (Perkin Elmer) using T4 polynucleotide kinase (T4 PNK, Thermo Fisher Scientific). The 5 μL reactions contained 1x PNK buffer (Thermo Fisher Scientific), 5 μM oligonucleotide, 5 μM [γ- ³²P] ATP and 1 μL of T4 PNK. The reactions were incubated at 37°C for 30 min and purified by non-denaturing gel electrophoresis (20% acrylamide).

Gel-shift binding measurements

Competition binding measurements

To obtain PUM2 binding affinities in the absence of potential structure formation and alternative sites, and to compare the affinities determined by different approaches, we performed competition gel shift binding measurements with 8-mer oligonucleotides carrying a subset of single mutations in the UGUAUAUA background. PUM2 (0.68 nM) was combined with trace labeled “S1a” RNA (UCUCUUUGUAUAUAUCUCUU, <0.08 nM) in binding buffer (2 mM DTT, 100 mM KOAc, 0.2% Tween-20, 20 mM sodium HEPES, pH 7.4, 5% glycerol, 0.1 mg/mL BSA, 2 mM MgCl₂), and diluted two-fold into solutions containing varying concentrations of unlabeled competitor RNAs (3-fold serial dilution series; 7–8 concentrations per oligonucleotide; final concentrations were 0.34 nM PUM2, < 0.04 nM labeled S1a RNA, 0.17––3330 nM competitor RNA, depending on the oligonucleotide). Binding reactions were incubated at 25°C for at least 1 h; equilibration was established by measuring binding after 1 h and 4.5 h incubations, which gave consistent results. We also performed controls for titration effects, by incubating the most tightly bound oligonucleotides (consensus, 5G and 7G variants) with 0.16 or 0.32 nM PUM2 (final concentration), giving consistent affinities. Following equilibration, 7.5 μL aliquots were transferred to 7.5 μL ice-cold loading buffer (5% Ficoll PM 400 (Sigma), 0.03% BPB, and 2 μM unlabeled S1a RNA in binding buffer). The low temperature and unlabeled consensus RNA in the loading buffer prevented changes due to potential re-equilibration during sample loading (Vaidyanathan et al., 2017)). The samples were carefully and immediately loaded on a continuously running 20% native acrylamide gel (5°C, 750 V, 0.5x Tris/Borate/EDTA (TBE) running buffer: 44.5 mM Trisborate, 1 mM Na₂EDTA, pH 8.3; DANGER: extreme caution is required in this step due to high voltage; https://ehs.stanford.edu/reference/electrophoresis-safety). Gels were dried, exposed to phosphorimager screens and scanned with a Typhoon 9400 Imager.

Binding affinity for the labeled S1a oligonucleotide was measured in parallel by incubating 0.0038–81 nM PUM2 (3-fold serial dilutions) with trace labeled S1a RNA (<0.04 nM) in binding buffer for at least 1 h at 25°C. Samples were analyzed by gel electrophoresis as above. Measurements with three labeled RNA concentrations across a 9-fold range (upper limits of 13–120 pM) gave consistent results, indicating no titration effects. Sufficient equilibration time was established by measuring the dissociation rate (0.011 s⁻¹, corresponding to 5.25 min upper limit of equilibration time—i.e., five half-lives; see below (Vaidyanathan et al., 2017)).

The gels were quantified with TotalLab Quant and fitting was performed with KaleidaGraph 4.1 (Synergy). The affinity for the labeled S1a RNA was determined by fitting to a single-site binding equation:

θ = A \times \frac{[P]}{K_{D} + [P]} + b

(Eq. 1)

where θ is fraction bound RNA, A is amplitude, [P] is PUM2 concentration, K_D is the equilibrium dissociation constant and b is background. Competitor affinities (K_D,comp) were determined using the equation by Lin & Riggs (Lin and Riggs, 1972):

K_{D, comp} = \frac{2 \times K_{D}^{*} \times {[R_{comp}]}_{1 / 2}}{2 \times {[P]}_{total} - {[R *]}_{total} - 2 \times K_{D}^{*}}

(Eq. 2)

where K_D* is the dissociation constant of the labeled S1a RNA; [R_comp]_1/2, the competitor concentration at which half of the labeled RNA is bound; [P]_total, the protein concentration; and [R*]_total the labeled RNA concentration. To determine the fraction of competitor RNA at which half of labeled RNA was bound, the competition binding curves were normalized by the fraction of labeled S1a RNA bound at saturation with no competitor (0.94). [R*]_total was the upper limit of the labeled RNA concentration based on the total input and elution volume in the labeling reaction (<0.04 nM). Using the lower limit based on scintillation measurements of the ³²P label (~0.004 nM) did not affect relative affinity calculations and affected absolute affinities by <10%. The values shown in Figure 2F, S3F are averages and 95% CIs from two replicate measurements.

For determination of flanking sequence effects, CUUGUAUAUAN oligonucleotides (N = A/C/G/U) were ordered from IDT, 5′ end labeled with [γ - ³²P] ATP, and binding was measured as described for the S1a RNA above.

To compare single mutant effects determined by gel-shift to those determined by RNA-MaP, ΔΔG values for the 8-mer oligonucleotides were calculated relative to the UGUAUAUA consensus. For position 9 variants, ΔΔG values were determined relative to the most tightly bound residue (‘G’; Figure S2D).

Dissociation rate constant measurements

PUM2 dissociation rate constant from S1a RNA was measured by incubating 3.8 nM PUM2 with labeled S1a RNA (<0.5 nM) in binding buffer at 25°C for 50 min, followed by addition of 2.5-fold volume excess of unlabeled RNA chase in binding buffer (final concentrations: 1 nM PUM2, <0.14 nM labeled S1a RNA, 1 μM unlabeled S1a RNA). At various time points, 7.5 μL aliquots were moved to 7.5 μL ice-cold loading buffer (5% Ficoll PM 400 (Sigma), 0.03% BPB in binding buffer) and immediately loaded on continuously running 20% native acrylamide gel. The dissociation curve was fit to a single exponential in Kaleidagraph:

θ = (A - b) \times e^{- k_{off} t} + b

(Eq. 3)

where θ is fraction bound RNA, A is the fraction bound before adding the chase (A = 0.90), b is the fraction bound at the completion of the dissociation reaction (b = 0.02), k_off is the dissociation constant, and t is time after adding chase.

Determination of active protein fraction by titration

Saturating concentration of unlabeled consensus RNA (10–200 nM; S1a or UCUUGUAUAUAUA for wild-type PUM1 and PUM2, UCUUGUAUUUAUA for mutant PUM1) was mixed with trace ³²P-labeled RNA of the same sequence (<0.15 nM) and incubated with protein concentrations at least 4-fold below and above the RNA concentration for 45 min – 1 h (25°C). Following native gel electrophoresis, active protein fraction was determined from the intersection of lines fit through protein concentrations below and above the breakpoint. Throughout, the protein concentrations and absolute affinities reflect active protein concentrations (SNAP-Cy3B-PUM2: 57%, PUM1-SNAP-Cy3B: 61%, mutPUM1-SNAP-Cy3B: 20%, unlabeled SNAP-PUM2 used for gel-shift experiments: 38%–45%).

QUANTIFICATION AND STATISTICAL ANALYSIS

Computational analyses

Processing sequencing data

Illumina MiSeq sequencing data were computationally processed to extract the tile identifier and the x- and y-locations of each sequenced cluster from the fastq file output (Denny et al., 2018; She et al., 2017). Sequence clusters were divided into three categories: (1) clusters encoding our RNA library, (2) clusters containing the fiducial sequence, and (3) inert “background” sequence clusters lacking the RNAP initiation site or the fiducial sequence. This assessment was based on alignment of the read1 sequence to (1) the RNA polymerase initiation site and stall sequence “TTTATGCTATAATTATTTCATGTAGTAAGGAGGTTGTATGGAAGACGTTCCTGGATCC,” or to (2) the fiducial sequence “CTTGGGTCCACAGGACACTCGTTGCTTTCC,” or (3) neither, respectively.

While every cluster was fit during the 2D Gaussian fitting (described below), only clusters containing the fiducial sequence were used during the cross-correlation of the images to the sequencing data. K_D fitting was only performed on RNA-encoding clusters (described below).

Fitting images

To attribute fluorescent binding events to individual sequence variants, the images taken during the RNA array experiment were mapped to the sequencing data output from the Illumina MiSeq. Each image had a set of fiducial clusters, which were visualized with a fluorescently labeled complementary oligo (see RNA transcription in the flow cell above). The x- and y-locations of each fiducial cluster were cross-correlated with each fluorescent image in an iterative fashion to determine a smooth function of x and y that represents the location-dependent offset between the image and the sequencing data locations. This “registration offset map” enabled correlation between image and sequencing locations at sub-pixel resolution, as described in (She et al., 2017). Once this map was determined, each image was fit to the sum of 2D Gaussians, with each Gaussian centered at each of the cluster locations from the registered sequencing data output. The quantified fluorescence of each cluster was thus the integrated fluorescence within the fit 2D Gaussian (f = 2πaσ² where f is the integrated fluorescence and a and σ are the fit amplitude and standard deviation, respectively).

Identifying library variants from sequencing data

Incorporation of a 15-nt unique molecular identifier (UMI) in our library allowed us to minimize the effect of sequencing errors when associating each sequenced cluster with its underlying sequence variant, as described in (Buenrostro et al., 2014). Prior to sequencing, the library was bottlenecked and reamplified (see Library preparation above), resulting in increased representation of each UMI that survived the bottlenecking. We assumed that all sequences associated with the same UMI came from the same molecular variant, so that any variation between these sequences was the result of sequencing error. To resolve sequencing errors, a consensus sequence of the associated library variant was determined for each UMI with a per-base voting strategy. Only UMIs with a significant fraction of variants matching the consensus sequence were used, as evaluated by a binomial null model. For each UMI, a p value was calculated based on the number of associated sequences that matched the consensus sequence and the total number of sequences, assuming a rate of success under the null model of 25%. UMIs with a higher rate of matching than expected by chance under the null model (i.e., with p value <0.01) were defined as successfully associating with a consensus sequence. Clusters were then associated to a designed library variant based on the cluster’s UMI.

Fluorescence normalization

To account for inter-cluster variation in maximum fluorescence, we normalized the amount of protein bound at a given cluster by the total amount of transcribed RNA in that cluster. This normalization was performed by dividing the integrated fluorescence of the cluster in the green channel (i.e., the channel imaging the bound protein) by the integrated fluorescence of the same cluster in the red channel (i.e., the channel imaging the fluorescent oligo annealed to the transcribed RNA). To prevent dividing by small numbers and inflating the normalized signal toward infinity, values of the red channel fluorescence below the threshold of the first percentile of the distribution of the red channel fluorescence across clusters were set to the value of the threshold.

Determining the free energy of binding

The normalized fluorescence values of bound protein across different solution protein concentrations were used to determine the equilibrium dissociation constant (K_D) between the protein and each RNA variant. The fitting procedure was split into several steps to allow robust fitting across a range of affinities, and the binding model accounted for observed non-specific binding events. In brief, the normalized fluorescence values for each individual cluster were fit to a binding curve to obtain best-fit values for K_D and other fit parameters (see Single cluster fitting below). These best-fit values for individual clusters were used to determine distributions for fit parameters that we expect to be variant-independent –i.e., K_D,NS, f_min, and f_max, which are each defined below. The distributions of these common values across library variants were used to refine the K_D value for each RNA variant.

Single cluster fitting

Initially, fluorescent values for each cluster were fit to a binding curve. This binding model incorporated a nonspecific binding term, as follows:

R + P \overset{K_{D}}{⇌} R \cdot P \overset{\begin{array}{l} K_{D, NS} \\ + P \end{array}}{⇌} R \cdot P \cdot P

(Eq. 4)

where R is RNA, P is protein, K_D is the dissociation constant (K_D = e^ΔG/RT) and K_D,NS is the non-specific dissociation constant for a second protein monomer that binds to the RNA-protein complex $(K_{D, NS} = e^{Δ G_{NS} / RT})$ .

The normalized fluorescence of a cluster at protein concentration [P] can be defined as:

f = f_{m i n} + f_{m a x} \frac{[P]}{[P] + K_{D}} (1 + \frac{[P]}{[P] + K_{D, NS}})

(Eq. 5)

where f_min is the background fluorescence in the absence of bound protein, f_max is the fluorescence signal at saturation, and [P] is the concentration of the protein in solution (here, [P] ≈ [P]_total). This model was used to account for an observed increase in fluorescence at high concentrations of protein after apparent saturation (Figure 1D). We did not observe a corresponding increase in fluorescence for non-binding variants, and the extent of ‘non-specific’ binding increased with greater specific binding affinity. Together, these observations support the model that a second protein monomer binds to the RNA-protein complex on chip (as opposed to non-specific binding to the DNA or unbound RNA, which would be independent of bound protein).

Least-squares fitting was performed using the Python package lmfit (v0.8.3). The initial estimates and constraints are as follows: f_min was initialized to the median fluorescence across clusters in the images with no protein applied, and was constrained to be not less than zero during the fitting; f_max was initialized at the maximum fluorescence observed at any concentration of protein for that cluster, and was similarly constrained to not be less than zero; K_D was initialized at the highest concentration of the protein; and K_D,NS value was initialized at five-fold the highest concentration of the protein.

Finding common values for K_D,NS, f_min, and f_max across variants

Allowing all four free parameters (f_min, f_max, K_D, and K_D,NS) to float during the fitting process led to some spurious effects. In particular, variants with low affinity that do not achieve saturation within the probed protein concentration range can be fit approximately equally well with different values for f_max and K_D,NS, ultimately leading to uncertainty in the fit value for K_D. For example, a variant that does not achieve saturation may be fit equally well with lower values for K_D and f_max, higher values for K_D and f_max, or a higher value for the K_D,NS and lower value for K_D. On the other hand, the library contains numerous tightly bound variants which have achieved saturation and from which we can extract most likely values for the sequence-independent parameters f_min, f_max, and K_D,NS. These values are largely constant across different molecular variants that did achieve near-saturation (Figure S1E,F), allowing us to reasonably assume that the same values are applicable to all molecular variants, i.e., even those that did not achieve saturation, and applying these well-defined estimates for f_min, f_max, and K_D,NS allows more confident fitting of the K_D values. To limit noise, the estimates for f_min, f_max, and K_D,NS were determined based on the per-variant values of each fit parameter, where per-variant values are the median of the single-cluster values associated with the same molecular variant.

Estimating f_min

The value for f_min was largely consistent across variants (Figure S1E); thus, the estimate for this fit parameter was simply the median value across variants.

Estimating the distribution of f_max

To define the distribution of f_max values across molecular variants, a subset of variants with low and precisely measured K_D values was used, based on the single cluster fits. Variants used to define this distribution had K_D values less than 5% of the highest concentration of protein. In addition, the precision of the per-variant values of K_D was evaluated based on the proportion of the variant’s single cluster fits having a goodness-of-fit (R²) greater than 0.5, the standard error on ΔG (ΔG = RTln(K_D)) less than 1 kcal/mol, and the standard error on the fit f_max less than f_max. If a significant fraction of the clusters associated with this variant passed these filters, then the variant was considered to have a “precise” measurement of K_D. Significance was assessed based on rejecting the null hypothesis that 25% of clusters would pass all these filters by chance alone (binomial p value < 0.01). For variants that did not achieve saturation the f_max was undefined, so the distribution of f_max values across the tightly bound molecular variants was used to find error estimates on the K_D values that reflect this uncertainty.

The f_max distribution across these variants was fit to a gamma distribution with fixed mean for the entire experiment, but whose standardp deviation was dependent on the number of clusters per molecular variant (i.e., standard deviation should be proportional to $1 / \sqrt{n}$ , where n is the number of clusters per variant). This distribution reflects the fact that as the number of clusters increases, we can obtain more precise estimates of f_max and thus K_D. The mean f_max value was obtained by fitting the per-variant f_max values to a gamma distribution, and obtaining the mean of the distribution, μ_global. To obtain the standard deviation of the f_max distribution at each value of n (where n is the number of clusters per variant), the distribution of per-variant f_max values of variants with n clusters was fit to the gamma function f(x), for every normalized fluorescence value x:

f (x - k_{n}, a_{n}, θ_{n}) = {(\frac{x - k_{n}}{θ_{n}})}^{a_{n} - 1} e x p (- \frac{x - k_{n}}{θ_{n}}) / Γ (a_{n})

(Eq. 6)

where k_n is a free parameter, a_n·θ_n≡ μ_global, and the resulting standard deviation is $σ_{n} = \sqrt{a_{n} θ_{n}^{2}}$ . Allowing k to float resulted in better estimates of the standard deviation when distributions were more asymmetric, as often occurred for variants with small n. The value of k_n was initialized at 0, and σ_n was initialized at the standard deviation of the f_max values.

The values for σ_n may be subject to noise, given that some values of n had many more variants associated with that number of clusters than others did. To smooth these values, the σ_n values were used to fit the expected analytical function that defines the relationship between number of measurements and standard error, $σ (n) = (σ_{1} / \sqrt{n}) + σ_{0}$ , where σ₀ and σ₁ are free parameters. σ₁ is the standard deviation on the estimate of f_max with only one measurement, and σ₀ represents the standard deviation of f_max among different molecular variants if all variants were measured an infinite number of times. We expect this term to be nonzero in the case that the f_max depends on the molecular variant: e.g., if certain variants are trapped in stable secondary structures that do not unfold on the timescale of the binding experiment.

The estimator for f_max for each molecular variant with n clusters per variant is then the gamma distribution:

f (x, a_{n}, θ_{n}) = {(\frac{x}{θ_{n}})}^{a_{n} - 1} e x p (- \frac{x}{θ_{n}}) / Γ (a_{n})

(Eq. 7)

where $a_{n} = {(μ_{g l o b a l} / σ (n))}^{2}$ and $θ_{n} = σ {(n)}^{2} / μ_{g l o b a l}$ , which depends only on μ_global and σ(n), and the number of clusters per variant n.

Estimating K_D,NS

The value for K_D,NS was determined by taking the median value across the subset of variants with low and precisely measured K_D values, based on the single cluster fits, as described above for determining the distribution of f_max values. The ΔG_NS terms ( = RTlog(K_D,NS)) for each protein were similar, with the following values: PUM2: −8.98 and −8.87 kcal/mol for replicates 1 and 2, respectively (25°C), −8.65 kcal/mol (37°C); WT PUM1: −8.46 kcal/mol; mutant PUM1: −8.19 kcal/mol.

Applying common values forK_D,NS, f_min, and f_max to refine estimates for K_D

Binding isotherms were refined for all variants using the variant-independent values for f_min, K_D,NS, and, for the cases in which the variant did not achieve near-saturation, f_max. To perform this refinement, clusters associated with each variant were resampled to obtain median fluorescence values across resampled clusters. This vector of median fluorescence values was fit to a binding isotherm with the values for f_min and K_D,NS fixed to the variant-independent values obtained above. For the cases where the variant did not reach near-saturation the value for f_max was also fixed. Not achieving near-saturation was defined as the median fluorescence value at the highest concentration of protein being less than the lower bound of the 95% confidence interval on f_max. In this case, the value for f_max was sampled from the variant-independent distribution of f_max,n (with n equal to the number of clusters associated with this variant) (Equation 7). To obtain uncertainty estimates on the fit f_max and K_D values, this resampling procedure was repeated 100 times. In the case that the variant did not achieve saturation, a different value for f_max was sampled for each iteration.

The 95% confidence intervals on K_D were obtained using these 100 values. The median fit K_D obtained from the initial single cluster fits was used as the initial value in the least-squares fitting of each fitting iteration. For variants where f_max was allowed to float, the median fit f_max was used as the initial value.

Fitting background clusters to determine maximum measurable ΔG

To obtain a reasonable estimation of the highest K_D that can be measured by this method, we applied this fitting procedure to a set of “background” variants—i.e., variants on the chip lacking an RNAP initiation site. To normalize the bound fluorescence in the green channel to a similar scale as those clusters that do transcribe RNA, the fluorescence values were divided by the median fluorescence value in the red channel across clusters that do have RNAP initiation sites. Background clusters were randomly assigned to a “variant ID,” such that the set of “background variants” had a similar number of associated clusters as our library members. Finally, fitting was carried out as described in “Applying common values for K_D,NS, f_min, and f_max to refine estimates for K_D,” with the variant-independent values for f_min, f_max, and K_D,NS applied. The reliable ΔG threshold determined by this analysis for PUM2 was approximately −8.5 kcal/mol (Figure S1F), and only variants with ΔG values less than this threshold (corrected for active protein fraction) were included in the high-confidence affinity data reported herein.

Data filtering

Variants were included in our analyses if they met the following criteria (unless otherwise indicated): (1) observed ΔG values lower than −8.5 kcal/mol; this range was established as clearly distinguishable from background of non-transcribed clusters (see Fitting background clusters to determine maximum measurable ΔG in the Computational analyses section above); (2) five or more clusters in at least one replicate experiment, to allow robust cluster statistics; in cases where one of the replicates contained fewer than five clusters, only the ΔG value from the replicate with five or more clusters was used; (3) 95% bootstrap confidence interval of the ΔG value (or the weighted error of replicate ΔG values for PUM2 measurements at 25°C) less than 1 kcal/mol; all 95% CI values were corrected to account for inter-experimental error, as described in (Denny et al., 2018). The numbers of variants passing each filter are indicated in Table S5.

Given the overall weaker binding of mutant PUM1 and to allow more comprehensive comparisons of single-mutant binding by wild-type and mutant protein (Figure 5D), we relaxed the affinity filter for mutant PUM1 data. Rather than applying a ΔG < −8.5 threshold, we included variants with at least 15% of RNA bound by PUM1 mutant at the highest probed protein concentration.

In comparisons of PUM2 replicate experiments (Figure 1D), and of PUM1 versus PUM2 affinities (Figure 5A), the entire oligonucleotide library was used, including sublibraries that will be fully addressed in future manuscripts. In these comparisons, an additional filter was applied to exclude any oligonucleotides with more than one binding site, defined as two UGUA sites separated by at least four bases.

Assessing reproducibility and combining experimental replicates

Two replicate experiments of PUM2 binding were combined by calculating the error-weighted mean:

Δ G_{comb} = (\frac{Δ G_{1}}{σ_{1}^{2}} + \frac{Δ G_{2}}{σ_{2}^{2}}) {(\frac{1}{σ_{1}^{2}} + \frac{1}{σ_{2}^{2}})}^{- 1}

(Eq. 8)

where the ΔG₁ and ΔG₂ are DG values from each replicate and σ₁ and σ₂ are 95% confidence intervals of the respective ΔG values. Weighted propagated error was calculated as:

σ_{comb} = {(\sqrt{\frac{1}{σ_{1}^{2}} + \frac{1}{σ_{2}^{2}}})}^{- 1}

(Eq. 9)

The observed small systematic offset (Figure 1E) was subtracted from Replicate 2 values before averaging to prevent distortions in cases where a variant was only present in one replicate. The offset (0.28 kcal/mol) was derived from mean replicate difference between highest affinity variants (ΔG < −9.8 kcal/mol).

Assessing the significance of scaffold differences

The significance of single mutant scaffold differences before and after accounting for structure was assessed via a false discovery rate (FDR) approach. For each single mutant and consensus sequence, the deviation of the ΔG value (weighted replicate average, Equation 8) from the scaffold average (ΔG_avg) was determined and converted into a z-score:

z = \frac{Δ G - Δ G_{avg}}{σ_{Δ G}}

(Eq. 10)

where σ is the weighted replicate error (Equation 9). The distribution of resulting z-scores was then compared to a null distribution, where the z-scores are normally distributed around a zero mean with a standard deviation of 1. For each z-score, the number of false discoveries was determined from the probability of obtaining a value more extreme than this z-score given the null distribution (two tailed; value = 2*CDF(−|z|)), multiplied by the total number of variants. The total number of discoveries corresponded to the sum of the number of false discoveries (above) and the number of actual z-scores whose absolute values were greater than or equal to that z-score threshold. Scaffold differences were considered significant if the respective z-score had FDR ≤10%. Asterisks in Figures 2A, D and in Figure S2C indicate mutants where at least one scaffold showed a significant deviation from the scaffold mean.

To assess the contributions of RNA secondary structure to the scaffold variance, the above analysis was repeated using structure-corrected affinities (see Accounting for RNA structure below; ‘Structure-corrected’ in Figures 2B, S2A), as well as affinities of variants that lacked significant predicted structure (ΔG_fold > −0.5 kcal/mol; 44 of 65 total variants, including the UGUAUAUA consensus).

Accounting for RNA structure

We used Vienna RNAfold (v. 2.1.9) (Lorenz et al., 2011) to predict ensemble stabilities for RNA structures in which the protein binding site is accessible versus occluded due to base pairing (Figure 2C). The effect of accessibility on protein binding was defined as follows (see model in Figure S3B):

K_{D}^{obs} = K_{D} \times \frac{1 + K_{fold}}{1 + K_{fold, acessible}}

(Eq. 11)

where $K_{D}^{obs}$ is the measured dissociation constant, K_D is the intrinsic dissociation constant (for accessible RNA), K_fold is the folding equilibrium constant that represents the ensemble of RNAs that are structured (accessible + occluded) and K_{fold,accessible} is the folding equilibrium constant representing RNA structures in which the protein binding site is accessible. Accessible binding sites were defined as lacking base-pairing in the 8-mer core binding site (for the purpose of structure predictions) (Figure 2C). Folding equilibrium constants were based on ensemble stabilities predicted by RNAfold (RNAfold -p0 -T 25 C or RNAfold -p0 -T 37 C); stabilities of accessible RNA structures were predicted by including the constraint flag (RNAfold -p0 -T 25 C -C) and constraining the 8-mer binding site to a single-stranded state, e.g.:UCUCUUUGUAUAUAUCUCUU

……xxxxxxxx……,

where ‘x’ indicates unpaired residues. Structure effects were considered if they exceeded 0.5 kcal/mol, except as noted.

Assessing alternative binding registers in single mutant variants

To determine potential alternative binding registers in our single mutant constructs, we computationally scanned the full RNA sequence (including scaffold and variable region) with the additive consecutive model, wherein the predicted relative affinity (expressed as ΔΔG) at each 8-mer site corresponds to the sum of effects of each individual residue:

Δ Δ G^{pred} = \sum_{b = 1}^{8} Δ Δ G_{b}^{X}

(Eq. 12)

b is the position in the 8-mer RNA binding sequence and X is the identity of the residue at position b. The $Δ Δ G_{b}^{X}$ values were derived from weighted scaffold averages for each single mutant relative to the weighted average of consensus affinities, after accounting for structure effects as described in Accounting for RNA structure. In calculating the predicted affinities for each register, structure effects were estimated by individually constraining the respective 8-mer site to the single-stranded state.

Figure S2D,E and Table S1 show the results of the initial assessment of register shifting, based on scaffold averages of mutant effects in the 5U background. No additional variants with shifted registers within less than 1 kcal/mol from the designed register were identified when the analysis was repeated for single mutants across 5A/C/U backgrounds, using mutant effects averaged across scaffolds and 5A/C/U backgrounds in Equation 12 (Figure S3A,B).

Development, testing and evaluation of thermodynamic binding models

To ensure the highest accuracy of model testing and global fitting, the library was filtered to only include variants without significant predicted secondary structure (ΔG_fold > −0.5 kcal/mol). For variants in the S1a and S1b scaffolds, we considered the ensemble structure of the entire RNA construct; for S2a and S2b scaffolds, only the stability of structures within the hairpin loop was considered, due to the high stability of the stem. The ensemble stability of structures involving the loop region was determined as the difference between RNAfold-predicted stabilities with and without the loop region constrained to the single-stranded state (ΔG_fold,loop = ΔG_fold − ΔG_fold,ss). Only the loop sequences were used for binding predictions in global fitting.

To reduce potential systematic bias in the ΔΔG values (ΔΔG = ΔG − ΔG_WT) that may affect the fit, we did the following. The ΔΔG values (observed and predicted) were defined relative to the UGUAUAUAU reference sequence rather than the slightly more stable UGUAUAUAG sequence (Figures 2E, S2F), because UGUAUAUAU was more highly represented in our library and was predicted to have less residual structure (n = 183 for ΔG_fold > −0.2 kcal/mol). To determine the median consensus affinity, we applied the more stringent structure cutoff of −0.2 kcal/mol (versus −0.5 kcal/mol) due to the greater, asymmetric spread of values observed when the −0.5 kcal/mol threshold was used, consistent with residual structure effects. The variants used for global fitting and their affinities and ΔΔG values measured for PUM2, PUM1 and mutant PUM1 are indicated in Table S5.

Importantly, in testing and globally fitting the models below, we accounted for all possible binding modes and registers, because the strongest binding can arise from a site downstream of or partially overlapping with the original designed site, and these altered registers become more probable the larger the destabilization from mutations within the original consensus site (see Figure 4A). The presence of multiple binding modes of similar affinity will also increase the overall observed affinity.

Testing the additive consecutive model. Additive consecutive model predictions were calculated using the equation in Figure 3A for every 9-mer register in each oligonucleotide in the library, based on measured single mutant penalties (Table S2). The ensemble affinity for a given oligonucleotide was determined as illustrated in Figure 4A (‘Consecutive’; top left):

Δ Δ G_{ensemble} = - RT ln (\sum_{r = 1}^{n - 8} e^{\frac{- Δ Δ G_{r}}{RT}})

(Eq. 13)

where n is the length of the oligonucleotide variant, r is the index of an individual 9-mer register, ΔΔG_r is the predicted penalty for binding in register r, R is the gas constant and T is temperature (25°C).

For direct comparison of the performance of the additive consecutive and additive nonconsecutive models (with and without coupling), data for all unstructured variants (n = 5206) were plotted in Figure 3A, including the single mutants (n = 113 across the four scaffolds and 5A/C/U backgrounds); excluding the single mutants did not significantly alter the fit values (RMSE = 1.04 kcal/mol; R² = 0.73).

Global fitting to the additive consecutive model (Figure S4B,C) was performed as described in the Global fitting section below, using terms for bound residues only.

Base flipping analysis

For the initial assessment of the additive nonconsecutive model that permits base-flipping, we focused on oligonucleotides in our library that contained C-insertions at various positions of the consensus sequence (UGUAUAUAU). For comparisons to the additive consecutive model predictions in Figure 3C,D, we used variants without predicted register shifts to favorable sites involving flanking sequences, as this allowed for the most accurate estimation of the lower limit of the flipping penalty at the indicated site. The construct sequences used are indicated in Table S3.

Global fitting

To fit the final model (additive nonconsecutive with coupling; Figure 3F), the ΔΔG values for all registers with no flips, all registers with single flips, all registers with double flips, and all registers with two single nucleotide flips were included when computing the partition function for binding (see Figure 4A). Registers with more than two flipped residues were not included in the partition function calculation because their predicted affinity was low enough that it minimally affected the overall binding affinity of the ensemble of bound states. The ΔΔG values for individual registers were used to compute the partition function and the overall ΔΔG for the ensemble of bound states for each RNA variant( $Δ Δ G (ensemble) = - RT ln (\sum e^{- Δ Δ G_{i} / RT})$ , where i is the register number (Figure 4A)). This ensemble ΔΔG was compared to the experimentally observed ΔΔG values during fitting. The model assumed a single protein bound to each RNA variant, which was supported by the tight distribution of f_max values and our ability to detect binding of multiple bound protein monomers based on proportional increase in fluorescence (Figure S1E; Becker et al., 2019b, in preparation). The additive consecutive and additive nonconsecutive models (Figure 3A,E) were fit analogously, but with the flipping and coupling terms (additive consecutive model) or coupling terms (additive nonconsecutive) excluded from the model.

During fitting, the only values that were not allowed to vary were the bound parameters for the consensus ‘UGUAUAUAU’ residues, which were set to a penalty of 0 kcal/mol. The other bound parameters for non-consensus residues were allowed to vary within the higher of the 95% confidence interval determined from the individual single mutant measurements or ± 0.4 kcal/mol from the median ΔΔG values from the individual single mutant measurements (Figure 2E, Table S2). Single and double flip parameters were essentially unconstrained during fitting and were allowed to vary between 0 and 7 kcal/mol. The coupling terms were constrained to between −4 and 0 kcal/mol. The coupling terms were included in both consecutive and flipped registers, with the condition that no flips interrupted the series of flipped residues. The script used for global fitting can be found on https://github.com/pufmodel.

All models were initially trained on a randomly selected subset of half the data and tested on the remainder of the data to prevent overfitting. In all cases, the model performed nearly identically on the training and test sets. To compute the final parameters, the model was fit with all sequences meeting the structure cutoff. All models described in the text were fit by minimizing the sum of the squared error between the predicted and measured ΔΔG values for each sequence. To help ensure that the fit was finding a global minimum, both the BFGS and differential evolution algorithms implemented in the lmfit module in Python were used for fitting. Additionally, fits with flipping parameters were initialized to different values between 1 and 4 kcal/mol and led to the same fit parameters, providing additional support for convergence to a global minimum.

We assessed the stability of the final fit parameters (additive nonconsecutive including coupling model; Table 1, Figure 3F) by performing multiple fits with bootstrapping and a parameter sensitivity analysis. Bootstrapping was performed as follows: the 5206 sequences were sampled with replacement and the model parameters were fit to each resampled dataset. The 95% confidence intervals from the bootstrapping analysis are reported in Table S4. To examine how well bounded the model parameters were, we computed the sensitivity of the RMSE of predicted versus observed affinities to variations in each individual parameter while holding all others constant at their fit values (Figures S5, S6). Each value varied within the constraints that were applied during fitting. For some flipping parameters, the same RMSE value resulted from all parameter values greater than a given value, implying that for these parameters the penalty must be larger than a certain value so that it will not occur in the most stable register in any of our constructs, but because the parameter is so destabilizing we can only say that it must be at least as perturbative as the minimum value resulting in a constant RMSE. As a result, we reported the lower bound for these parameters (Table 1, ‘Term II’).

Coupling analysis

To assess positional coupling, we tested double mutants of the UGUA[A/C/U]AUAU reference sequence for systematic deviations from predictions by the additive consecutive model. To obtain the library variants for this analysis, we filtered our mutant library for all sequences that featured a single dominant consecutive register (i.e., with less than twofold, or 0.4 kcal/mol, further stabilization provided by other consecutive or flipped registers, as predicted by the additive nonconsecutive model in Figure 3E). Variants deviating from the consensus sequence at two positions were identified and their predicted affinities were calculated by adding the respective experimentally determined single mutation penalties (ΔΔG^pred = ΔΔG₁ + ΔΔG₂; Figure 2E, Table S2). We used the experimentally derived instead of globally fit single mutant penalties in this analysis, as coupling may affect the fit values. Qualitatively, the conclusions were not affected by the fit parameters, as in both cases the strongest coupling was observed between positions 7 and 8, with negligible deviations at other positions. Only double mutant combinations represented by more than one variant in our library were considered. Deviations between the observed and predicted ΔΔG value were determined and averaged across all mutants with mutations at a given pair of positions (Figure S4D).

The double mutant analysis indicated coupling between mutated positions 7 and 8, with negligible deviations from additivity at other positions for which data were available. Because of the highly destabilizing effects of mutations in the 5′ half of the binding site, these mutations were strongly underrepresented among double mutants, as they generally lead to alternative registers being preferred or fall outside the reliably measurable affinity range. For the same reasons, any couplings involving 5′ mutations are unlikely to be biologically relevant.

To determine the sequence dependence of position 7 and 8 couplings, including potential longer-range couplings, we next extended the analysis to varying combinations of residues flanking each position 7 and 8 residue. Specifically, and recognizing that coupling is most likely to occur between neighboring residues, we assessed the following combinations for systematic deviations from predicted values: 1) residue of interest flanked by two consensus residues; 2) only the 5′ neighboring base mutated; 3) only the 3′ neighboring base mutated; 4) both neighboring residues mutated. In this analysis, we included all variants that contained the indicated combination in the best predicted consecutive register (as predicted by additive nonconsecutive model; Figure 3E); any sequence was permitted outside the indicated combination.

Only 7G and 7C showed strong systematic deviations from predicted affinity for the indicated neighbor combinations (Figure S4E,F), and to a lesser extent—the 9G residue, which showed systematically tighter binding when preceded by the consensus residue 8A as opposed to residue 8 mutations (Figure S4G). Further inspection of 7G coupling indicated an additional bifurcation based on position 5 identity, indicating longer-range coupling (Figure S4E). The previously observed structural differences in purine and pyrimidine recognition at position 5, with dramatic effects on backbone configuration and in some structures—on position 6 recognition provide a potential structural rationale for this longer-range coupling (Lu and Hall, 2011).

Analysis of in vivo crosslinking data

Determining a set of position weight matrices to find putative binding sites

The analysis of in vivo crosslinking data was carried out in two stages: first, we identified the transcriptome sites predicted to be bound by PUM2 (ΔΔG^pred ≤ 4 kcal/mol) by using a set of position weight matrices (PWMs) that approximate our thermodynamic model to efficiently identify binding sites. Second, we applied the full thermodynamic model, as described in Figure 3F and Figure 4A, to this set of putative binding sites. Using PWMs for genome-wide searches is supported with currently available software and can computationally obtain matches to the whole transcriptome within a reasonable amount of time. In contrast, genome-wide application of the full thermodynamic model was prohibitively computationally expensive.

Each PWM is a matrix with rows representing different positions within the binding sequence and columns representing the four bases that could be at that position. The value of the PWM for each position and base is the probability of observing that base at that position in a set of binding sequences, wherein the probability is proportional to the ΔΔG terms from our thermodynamic model, as detailed below: $p_{i, j} = \sum_{j} exp (Δ Δ G_{i, j} / RT) / exp (Δ Δ G_{i, j} / RT)$ for position i and base j. For the simplest binding configuration (i.e., 9 bound positions with no flipped residues), ΔΔG_i,j values corresponded to the binding terms in Table 1 ( $Δ Δ G_{b}^{x}$ ; ‘Term I’). Each genomic sequence was compared with the PWM to determine a log-odds score: $s = \sum_{i} l_{i, j} log (p_{i, j} / 0.25)$ , where I_i,j = 1 if the sequence at position i has base equal to j, otherwise I_i,j = 0. A log-odds score of ≥2 was found to capture the large majority of variants with ΔΔG < 4 kcal/mol, and so this value was applied as the threshold above which a sequence was considered as a putative binding site.

To account for binding registers with a single flipped residue, a row was inserted at the flipped position, with values derived from the base flipping penalties ( $Δ Δ G_{f}^{Y}$ , Table 1, ‘Term II’). Our thermodynamic model found that flipping is accommodated only in four positions; thus, a PWM was determined for each of these four binding registers. In practice, for a given sequence, flips between positions 4/5 and 5/6 had very similar PWMs, and so a single PWM was derived to search for both of these binding configurations, using the average values. On average, an inserted residue penalized the overall affinity by ~1.5 kcal/mol. To account for this overall destabilization, the threshold log-odds score for these three flipped PWMs was increased to 4 (i.e., a sequence had to have log odds score ≥4 for the sequence to be considered as a putative binding site).

A set of four additional PWMs were derived to account for having two flipped residues at each of the four flipped positions. Once again positions 4/5 and 5/6 produced very similar PWMs and were averaged, resulting in three distinct PWMs. For these PWMs, the threshold for log-odds score was increased to 5 to account for the additional destabilization of having two flipped residues.

The PWM for no flipped residues and with one flipped residue had two or one fewer positions to account for, respectively, than the PWM for two flipped residues. Thus, all PWMs were brought to the same length of 11 rows (corresponding to 11 bound or flipped positions) by padding at the 3′ end with rows that do not contribute to the log odds score of any sequence (values were set equal to 0.25 for all bases).

Finally, these seven PWMs and their respective threshold values were saved in a single file, with format defined by the program HOMER, as described: http://homer.ucsd.edu/homer/motif/creatingCustomMotifs.html.

Determining binding sites within the transcriptome

The seven PWMs described above were used to determine putative binding sites across the transcriptome for subsequent quantitative analysis with our full thermodynamic model. Initially, a set of genome locations was determined from the Gencode v24 annotation file, obtained from the ENCODE project:

wget https://www.encodeproject.org/files/gencode.v24.primary_assembly.annotation/@@download/gencode.v24.primary_assembly.annotation.gtf.gz.

These genome annotations were converted to a bed file format, and any overlapping regions were merged, using the program bed-tools merge (v2.25.0). The package HOMER (v4.8.3) was used to search for matches to the PWMs within these genome locations, with the command:

annotatePeaks.pl ${genome_locations} hg38 -m ${pwm_file} -mbed {output_motif_locations} -noann -nogene.

The set of output motif locations, corresponding to putative binding sites, was subsequently filtered to remove any overlapping regions (bedtools merge), and if two regions overlapped, only the site with the lowest log odds score was kept. This set of motif sites was annotated again using HOMER to map each site to a gene, mRNA location (i.e., 5′ UTR, CDS, 3′ UTR), and gene type (i.e., protein-coding, noncoding RNA, etc.), each of which come from the default Refseq annotations for human genome assembly GRCh38 (hg38) (O’Leary et al., 2016).

annotatePeaks.pl ${motif_locations} hg38 > ${output_annotations}

These annotations were used to filter motif locations based on: (1) Being part of a protein-coding gene in the 5′ UTR, CDS, 3′ UTR; (2) Being on the same strand as its annotated gene. This filtering resulted in a final set of 640,675 binding motif locations around which PUM2 binding was assessed.

In addition to this set of filtered motif locations, a set of “random” sites were determined, which served as controls throughout. These sites were obtained by choosing 5,000,000 random start sites within the original set of genome locations. These random sites spanned the same number of nucleotides as the putative binding sites (11 nt). These 5 million sites were subsequently annotated and filtered exactly as the putative binding sites were, resulting in 76,137 “random” locations.

Using the thermodynamic model to predict ΔΔG values of each putative binding site

The 11-nt sequence of all motif locations (“binding” or “random”) were each assessed for their predicted ΔΔG using the full thermodynamic model (Figure 4A; 37°C). The sequence within each motif location was determined using the bedtools getfasta command and the hg38 genome build in fasta format.

This 11-nt window has three possible binding registers if no residues are flipped (ΔΔG_{consecutive,1}, ΔΔG_{consecutive,2}, ΔΔG_{consecutive,3}), in addition to other binding registers with one or two residues flipped (see Figure 4A). Each sequence was also assessed for the ΔΔG_noflip, which represents the ensemble energy of the three ΔΔG_consecutive values, with no contribution from any of the flipped binding registers.

Determining expression of putative PUM2 binding sites

RNA-seq expression data for K562 cell lines was obtained from the ENCODE project (Consortium, 2012). These data consisted of transcript-per-million (TPM) values for each ENSEMBL transcript across two replicates (https://www.encodeproject.org/files/ENCFF272HJP/@@download/ENCFF272HJP.tsv and https://www.encodeproject.org/files/ENCFF471SEN/@@download/ENCFF471SEN.tsv). The TPM values for each transcript were averaged across the two replicates, and the value for each Refseq transcript identifier was then determined using Ensembl Biomart for hg38. The TPM value for each Refseq transcript gave the relative expression of motif sites within that transcript, as assessed using the annotations from HOMER described above.

Only motif sites on transcribed genes (TPM > 0 in K562) were included in certain subsequent analyses, resulting in further filtering of the number of motif sites examined to 396,578 total sites.

Obtaining eCLIP signal around putative PUM2 binding sites

Enhanced UV crosslinking and immunoprecipitation (eCLIP) data for PUM2 protein in human K562 cells was obtained from ENCODE (Van Nostrand et al., 2016). Sequencing read alignments (in the form of a BAM file) were obtained for two replicate pulldown samples and one input sample which did not undergo antibody pulldown for PUM2 but was otherwise experimentally processed identically (https://www.encodeproject.org/files/ENCFF786ZZB/@@download/ENCFF786ZZB.bam, https://www.encodeproject.org/files/ENCFF732EQX/@@download/ENCFF732EQX.bam, https://www.encodeproject.org/files/ENCFF231WHF/@@download/ENCFF231WHF.bam). The published eCLIP data had already been processed to exclude PCR duplicates by collapsing sequencing reads with identical barcodes (Van Nostrand et al., 2016). Only alignments corresponding to the second sequencing read (read2) were kept, as the 5′ end of this read corresponds to the nucleotide immediately following the putative crosslinking site (Van Nostrand et al., 2016). The alignments were obtained using the package samtools (version 0.1.19–96b5f2294a):

samtools view -bh -f 128 ${input_bam} > ${output_R2_bam}

This set of filtered alignments was used to determine the number of observed crosslinks (i.e., read2 start sites) on each strand at any position within the genome, using the package bedtools:

bedtools genomecov -ibam {R2_bam} -strand + -bg −5 > {output_bedgraph_plus}

bedtools genomecov -ibam {R2_bam} -strand − -bg −5 > {output_bedgraph_minus}

The number of crosslink sites (from eCLIP data) at each nucleotide position within each motif location was determined using the package pyatac ins (https://nucleoatac.readthedocs.io/en/latest/pyatac/). Only crosslink sites on the same strand as the motif were included in the total count. The number of reads starting 55 nt upstream and extending to 25 nt downstream of the motif location center (80 nt total; Figure S7L) were summed for each sample, corresponding to the motif site’s eCLIP read count; this window accounted for the asymmetrical observed distribution of crosslink sites around PUM2 consensus motifs. eCLIP signal for each motif site was determined as the sum of eCLIP read count for the two replicates, divided by the relative expression of that motif site. Similarly, eCLIP input for each motif site was the eCLIP read count for the input sample, divided by the relative expression of that motif site.

The median eCLIP signal and input around sites identified as ‘background’ sites was determined from sites with predicted ΔΔG > 4.5 kcal/mol, regardless of whether the site originated from the “binding” or “random” motif locations. The eCLIP signal (or input) values were divided by the ‘background’ signal (or input) value to obtain the eCLIP signal (or input) enrichment above the background expectation.

To assess the eCLIP occupancies of sites with and without flipped residues (Figure 6B), sites were defined as containing flipped residues if their predicted ΔΔG value using the full thermodynamic model (Figure 3F) was lower than the ΔΔG value predicted by the additive consecutive model by more than 0.5 kcal/mol.

While the eCLIP data (Van Nostrand et al., 2016) enabled us to perform initial tests of thermodynamic predictions for PUM2 in vivo, future tests will be needed to assess factors that lead to occupancy variation at the level of individual RNAs and to confidently distinguish variation caused by biological factors versus technical artifacts (Wheeler et al., 2018). Whereas median eCLIP occupancies are well predicted by thermodynamics, there is wide variation in eCLIP read coverage between sites of identical sequence or predicted affinity (Figure S7M), either because of crosslinking bias or yet-to-be-identified biological and methodological factors. Improvements in individual-RNA signal intensity and quantitative controls will allow dissection of these factors.

Assessing secondary structure around motif sites

Consensus motif sites (ΔΔG^pred < 0.5 kcal/mol), comprising 4,816 non-overlapping sites, were assessed for local secondary structure occluding the binding site. The sequence around each motif site was determined using bedtools getfasta. Multiple different lengths of flanking regions were included in this assessment (10 nt, 20 nt, or 80 nt on either side of the motif site). An additional line within the sequence fasta file gives the constraint that the binding site (i.e., the first 8 nt of the motif site, given the weak interaction at position 9) remains unpaired. Using the program RNAfold (v2.1.8 (Lorenz et al., 2011)), the ensemble energy was determined for each sequence:

cat ${input_fasta} | RNAfold–noPS -p0 -C -T37 > ${output_values_wconstraint}

cat ${input_fasta} | RNAfold–noPS -p0 -T37 > ${output_values_noconstraint}

The difference in ensemble free energy with and without the constraint gives the accessibility of that site: ΔΔG_ss = ΔG_{no_constraint} – ΔG_constraint (see also Accounting for RNA structure above). Note that the thermodynamic linkage between RNA folding and RBP binding, depicted in Figure 2C, applies fundamentally to any RBP, as the effects of RNA structure on binding only depend on the relative free energies of the accessible and occluded RNA states (see, e.g., (Hackermüller et al., 2005; Li et al., 2010; Taliaferro et al., 2016) for examples of structure effects on other RBPs). Thus, the weaker than predicted structure effects on PUM2 binding in vivo must reflect cellular factors that destabilize RNA structure, rather than properties specific to PUM2. Current limitations of eCLIP-based structure analysis include that, in the presented case, the analysis only provides insight into local structural context around PUM2 sites (i.e., cytosolic and primarily located in 3′ UTRs), under the conditions of an eCLIP experiment; further, the analysis relies on structural predictions by nearest-neighbor algorithms, which have limited accuracy (Becker et al., 2019a).

Enrichment of PUM2 sites within 3′UTRs

Sites derived from the PUM2 PWMs (described in Analysis of in vivo crosslinking data above; not filtered for being expressed in K562 cells) were divided into bins based on the predicted ΔΔG, and the fraction of motifs within each bin that were annotated as 5′ UTR, CDS, or 3′ UTR was determined as described above (i.e., using HOMER), and are shown in Figure 6D. Enrichment for transcript annotations of motif sites (Figure 6E) was determined relative to the annotation frequencies of “random” locations.

Modeling the cellular PUM2 binding landscape

To assess the distribution of PUM2 across cellular RNA sites, we determined the numbers of each 9-mer, 10-mer and 11-mer sequence in the human transcriptome (representing consecutive sites and sites containing one or two flipped residues). For simplicity, here we assumed equal expression of all protein-coding transcripts, with sequences obtained from GENCODE (genome release GRCh38.p12; ‘Protein-coding transcript sequences’ fasta file) (Harrow et al., 2012). Absolute numbers of each binding site were determined by normalizing the nucleotide count in the above transcriptome file to match the estimated mRNA nucleotide count in a single human cell (8.9 × 10⁸ nucleotides, corresponding to ~0.5 pg mRNA per cell) (Livesey, 2003; Marinov et al., 2014; Tang et al., 2011). These numbers can be adjusted to account for cell-specific variation in total mRNA levels and differential expression based on publicly available RNaseq data (Consortium, 2012).

The number of PUM2 molecules per cell was estimated at 10,000, based on published numbers of 2,000 and 18,000 in HCT116 and HeLa cells, respectively (Lee et al., 2016; Nagaraj et al., 2011).

To calculate the distribution of cellular protein bound across the different mRNA sequences, we first calculated PUM2 relative affinities for each 9–11-mer site using our thermodynamic model. The affinities for consecutive 9-mer sites were calculated using the binding and coupling terms in Table 1; to determine affinities for sites containing flipped residues, we calculated the ensemble affinities of the four possible registers with one single-nucleotide flip (Figure 4A; 10-mer sites); and the ensemble of the four possible registers with a two-nucleotide flip and six possible registers of two single-nucleotide flips (11-mer sites), using the terms in Table 1.

PUM2 occupancies for each RNA species were calculated using an equilibrium competition model, where the occupancy of a given RNA species (P·R_i) is a function of protein abundance (P), and the affinities and abundances of all RNA (R) sites:

P + R_{1} \overset{K_{1}}{⇌} P \cdot R_{1} P + R_{2} \overset{K_{2}}{⇌} P \cdot R_{2} \dots P + R_{n} \overset{K_{n}}{⇌} P \cdot R_{n} .

The fraction of total protein bound to RNA sequence R₁ equals:

\frac{[P \cdot R_{1}]}{{[P]}_{total}} = \frac{K_{1} [P] [R_{1}]}{[P] + K_{1} [P] [R_{1}] + K_{2} [P] [R_{2}] + \dots + K_{n} [P] [R_{n}]} = \frac{K_{1} [R_{1}]}{1 + K_{1} [R_{1}] + K_{2} [R_{2}] + \dots + K_{n} [R_{n}]} = \frac{K_{1} [R_{1}]}{1 + \sum_{i = 1}^{n} K_{i} [R_{i}]}

(Eq. 14)

We used affinities predicted for each RNA by our thermodynamic model:

K_{i} = e^{- Δ G_{i} / RT}

(Eq. 15)

where ΔG_i = ΔG_WT + ΔΔG_i; ΔG_WT is the measured affinity for the UGUAUAUAU reference sequence at 37°C (−12.1 kcal/mol), and ΔΔG_i is the relative free energy for binding to sequence R_i (ΔΔG_i) predicted by our thermodynamic model.

To convert the sequence counts into concentrations, we used the cell volume of 10⁻¹² L (Fujioka et al., 2006). Given the much greater number of RNA sites than the number of cellular PUM2 molecules (78,000 consensus UGUA[ACU]AUAN sites alone versus 10,000 PUM2 molecules), we assume that most RNA sites are unbound, i.e., that $[R_{i}] \approx {[R_{i}]}_{total}$ . [This assumption will not hold at very high protein concentrations or for certain RBPs with very high specificity; these alternate regimes can be readily simulated using KinTek Explorer or similar software (Johnson et al., 2009).]

The occupancies plotted in Figure 6H correspond to the amount of PUM2 bound to each RNA species (i.e., fractional protein occupancy from Equation 14 multiplied by the total amount of protein):

[P \cdot R_{1}] = {[P]}_{total} \times \frac{K_{1} [R_{1}]}{1 + \sum_{i = 1}^{n} K_{i} [R_{i}]}

(Eq. 16)

Concentrations of occupied sites were converted into the number of protein-bound sequences as follows: [P·R₁] × N_A × V_cell, where N_A is Avogadro’s number and V_cell is the cell volume.

The bars in Figure 6H denote the sum of occupancies for all 9-mer RNA species containing the indicated numbers of nonconsensus residues (blue) and 10–11-mer species with flipped residues (green).

Fractional occupancies of each RNA sequence were determined (using the definition of the amount of bound RNA from Equation 14), as follows:

\frac{[P \cdot R_{1}]}{{[R_{1}]}_{total}} = \frac{{[P]}_{total} \times K_{1} [R_{1}]}{{[R_{1}]}_{total} \times (1 + \sum_{i = 1}^{n} K_{i} [R_{i}])} \approx \frac{{[P]}_{total} \times K_{1}}{1 + \sum_{i = 1}^{n} K_{i} [R_{i}]}

(Eq. 17)

The fractional occupancy of consensus sequences calculated using Equation 17 and the published cellular amounts of PUM2 and mRNA (see above) was 3.4%. We emphasize that these binding predictions are based on ‘typical’ expression levels, which suggest a large excess of consensus RNA sites over the cellular PUM2 level and over the K_D. As a result, none of the RNA sites are predicted to be saturated with PUM2 and the occupancies should linearly scale with predicted affinity; this concentration regime is supported by the linear relationship between predicted affinities and eCLIP occupancies (Figure 6A). Nonetheless, given the changes in PUM1 and PUM2 expression across tissues and during development (reviewed in (Goldstrohm et al., 2018)), as well as cellular changes in expression and accessibility of RNA, PUM1 and PUM2 expression may in some cell types reach saturating levels. This saturating binding to consensus sites would lead to poorer discrimination between consensus and nonconsensus sites and an even greater fraction of PUM2 being bound to nonconsensus sites (not shown).

Occupancy prediction algorithm

A script for predicting PUM2 occupancy on any RNA sequence (see Figure 6G) can be found on https://github.com/pufmodel. The script accepts any RNA sequence in fasta format and predicts PUM2 occupancies relative to the UGUAUAUAU consensus at each site along the sequence based on our thermodynamic model. The algorithm currently assumes a linear relationship between affinity and occupancy, as explained above in Modeling the cellular PUM2 binding landscape, as we do not expect saturating binding in vivo in the presence of the large excess of tight RNA binding sites over cellular protein. Currently the script provides normalized occupancies relative to the consensus sequence; to determine fractional RNA occupancies within the cell, experimental PUM2 and RNA concentrations will need to be considered. The fractional occupancies in the example shown in Figure 6G have been calculated based on our landscape model and the estimated amounts of PUM2 and mRNA in a typical cell (see Modeling the cellular PUM2 binding landscape).

Predicting PUM1 and PUM2-mediated regulation

To assess how predicted PUM1 and PUM2 occupancies related to regulation of mRNA abundance, we analyzed a previously published dataset that measured gene expression changes in response to simultaneous siRNA knockdown of PUM1 and PUM2 in human HEK293 cells (Bohn et al., 2018). This study labeled each gene as significantly upregulated, downregulated, or unchanged (Table S4 of (Bohn et al., 2018); 19219 genes total). Different entries with the same gene name were aggregated by only keeping the first entry with that gene name (19135 genes). Predicted relative occupancies were determined by identifying all putative PUM2 binding sites within the 3′ UTR, CDS and 5′ UTR regions of each mRNA (using labels from Determining binding sites within the transcriptome in the Analysis of in vivo crosslinking data section) and integrating the occupancies across all sites in a given region:

Relative occupancy = \sum_{i}^{N} e^{- Δ Δ G_{i} / RT}

(18)

Here, occupancy is calculated relative to the UGUAUAUAU consensus, and assumes subsaturating binding (see Modeling the cellular PUM2 binding landscape). Genes with no putative PUM2 binding sites in any part of the mRNA were not included in the analysis (n = 3886).

To assess if PUM1 and PUM2 binding to different mRNA regions contributed differently to the regulation of mRNA expression, Receiver Operating Characteristic (ROC) plots were generated (Figure S7E). The true positive and false positive rates were assessed for each predicted occupancy value; predicted positives were those genes with occupancy greater than or equal to that occupancy value within the indicated region (3′ UTR versus CDS/5′ UTR), and true positives were those that were significantly upregulated with PUM1 and PUM2 depletion (i.e., repressed by PUM1 and PUM2).

To compare the thermodynamics-based predictions to those based on eCLIP data in K562 cells, two additional ROC plots were generated, in which predicted positives are those genes with 1) at least a certain number of eCLIP peaks, or 2) at least a certain number of eCLIP reads, normalized for expression in K562 cells. Each is described in more detail below.

To determine if the number of eCLIP peaks in the 3′ UTR region was predictive of regulation, the two replicate datasets of PUM2 eCLIP peak locations were downloaded from ENCODE, concatenated and sorted Van Nostrand et al., 2016. HOMER was used to identify the gene and region associated with each peak (i.e., intron, exon, 3′ UTR, etc.). Genes with no peaks were included in the analysis.

To determine if the number of eCLIP reads per 3′ UTR was predictive of regulation, eCLIP reads were summed within any putative binding site of a gene’s 3′ UTR, as described in the Analysis of in vivo crosslinking data section (Obtaining eCLIP signal around putative PUM2 binding sites). The reads in each of the two eCLIP replicates were summed, and the number of eCLIP reads per 3′UTR was divided by the expression of that gene in K562 cells (in TPM, as described in Analysis of in vivo crosslinking data (Determining expression of putative PUM2 binding sites). Genes with no associated putative PUM2 binding site were not included in the analysis. The number of normalized CLIP reads per gene was shown to be a moderate predictor of the gene expression change with PUM1 and PUM2 knockdown, comparable to thermodynamics-based predictions (Figure S7F). Note that eCLIP and PUM1 and PUM2 knock-down experiments were performed in different cell types (K562 and HEK293, respectively), which may affect these comparisons.

RNA Bind-n-Seq analysis

To independently test the thermodynamic model using a large dataset of sequences not present in our library, we analyzed enrichments of all 11-mer sequences in the publicly available RNA Bind-n-Seq (RBNS) dataset for human PUM1 (Consortium, 2012; Dominguez et al., 2018). We focused on the data for the lowest PUM1 concentration, 5 nM, which provided the greatest dynamic range of enrichments over the no–protein input. Analysis of data obtained at higher PUM1 concentrations (20–1300 nM) indicated declining enrichments for representative single mutants, suggesting saturating PUM1 binding at the low RBNS experimental temperature of 4°C. Enrichments of 11-mer sequences were calculated over the no-PUM1 input as follows:

{Enrichment}_{i} = \frac{frequency of 11 {mer}_{i} (5 nM PUM 1)}{frequency of 11 {mer}_{i} (input)}

(Eq. 19)

where frequency indicates the number of occurrences of each 11-mer in the dataset divided by the total number of 11mers in the dataset. 99.98% of all possible 11mers (n = 4,193,377) were represented in both input and PUM1 samples.

The log10 enrichments were compared to the relative affinities predicted for each 11-mer sequence by our thermodynamic model at 4°C (Figure 4A). Analysis of median enrichments across 0.5 kcal/mol bins revealed above-background enrichments for 11-mer sequences with predicted ΔΔG values of up to 3.5 kcal/mol. Thus, further quantitative comparisons were based on 11mers within this range (Figure S7D).

To compare the performance of the thermodynamic model for 11mers that were versus were not present in our RNA-MaP library, we calculated the coefficients of determination (R²) between predicted ΔΔG values and log10 RBNS enrichments for each set. The RNA-MaP variants were defined as those 11mers that were present in the set of the 5206 unstructured library variants used for global fitting of the thermodynamic model. Given the non-uniform distribution of 11mers across the affinity bins (e.g., 50.3% of the RBNS 11mers with ΔΔG^pred ≤ 3.5 kcal/mol were in the 3.0–3.5 kcal/mol bin, while the RNA-MaP variants were distributed more evenly; Table S6), we randomly subsampled the data to have the same number of 11mers in each ΔΔG^pred bin (bin size: 0.5 kcal/mol). The sample size (n = 101) corresponded to the number of variants in the bin with the fewest variants. 100 rounds of random subsampling were performed using the pandas DataFrame.sample() function. The median and bootstrapped 95% confidence intervals of the resulting R² values were determined using the Python modules scipy.stats and scikits.bootstrap. The bootstrapped 95% confidence intervals were [0.737, 0.743] and [0.747, 0.754] for 11mers that were or were not present in our RNA-MaP library, respectively.

While the RBNS analysis allowed us to assess the performance of the thermodynamic model beyond the library tested by RNA-MaP, there are critical experimental differences that contribute to the observed significant spread between predicted affinities and observed RBNS enrichments. For example, RBNS was performed at 4°C, using long, 65 nt oligonucleotides that are predicted by Vienna RNAfold to form stable structures, and enrichment is expected to be biased against highly structured sequences. Inspection of variants that were systematically less enriched than predicted by thermodynamics revealed that these were dominated by 11mers containing multiple G residues.

In addition to stabilizing RNA structure, the low temperature (4°C) may preclude equilibration in the course of the 2 h experiment, by slowing PUM1 dissociation. (E.g., measurements of PUM2 dissociation from the consensus sequence at 0°C indicate a dissociation half-life of 20 h (Vaidyanathan et al., 2017).) Another key limitation is that RBNS is a disruptive technique, and the washing steps that follow the PUM1-RNA incubation may perturb binding equilibria.

11mers that displayed high enrichment values despite low predicted affinities could be explained by partially overlapping consensus sites present in the same RBNS oligonucleotide. This was supported by a strong enrichment for partial consensus sites among these highly enriched 11mers. E.g., comparison of sequences of 11mers that had predicted ΔΔG values greater than 2.5 kcal/mol, and that were versus were not enriched >10-fold over input (Figure S7D) revealed that 13.7% of variants with >10-fold enrichment contained the NNNNUGUA[ACU]AU sequence and 20.4% contained the NNNNNUGUA[ACU]A sequence. In contrast, only 0.0030% and 0.050% of sequences with enrichment of <10-fold contained these partial consensus sites. While alternative binding sites within the same RNA oligonucleotide are straightforward to account for in RNA-MaP analysis, accounting for neighboring sites in RBNS data is time- and computationally intensive Lambert et al., 2014. Given the above limitations of available RBNS data for PUM1, this analysis was omitted herein.

DATA AND SOFTWARE AVAILABILITY

Thermodynamic binding data generated in this study are available for download (Table S5).

Key scripts for analyses reported herein have been deposited to github, as indicated in the Key Resources Table.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and Virus Strains
BL21(DE3) competent cells	Agilent	Cat#200131
BL21-CodonPlus (DE3)-RIPL competent cells	Agilent	Cat#230280
Chemicals, Peptides and Recombinant Proteins
SNAP-hPUM2	This paper	N/A
hPUM1-SNAP	This paper	N/A
hPUM1 MUT3–1-SNAP	This paper	N/A
His-TEV Protease	This paper	N/A
cOmplete, Mini, EDTA-free Protease Inhibitor Cocktail	Sigma-Aldrich	Cat#11836153001
Cy3B NHS ester	GE Healthcare	Cat#PA63100
BG-NH2	New England Biolabs (NEB)	Cat#S9148S
Agencourt AMPure XP beads	Beckman Coulter	Cat#A63881
SYBR Green I Nucleic Acid Stain	Lonza	Cat#50513
SYBR Gold Nucleic Acid Gel Stain	Invitrogen	Cat#S11494
Phusion High-Fidelity DNA Polymerase	Thermo Fisher Scientific	Cat#F530S
Phusion Hot Start II DNA Polymerase	Thermo Fisher Scientific	Cat#F549
Klenow fragment (3’−5’ exo(−))	NEB	Cat#M0212L
Streptavidin	PROzyme	Cat#SA10
D-Biotin	Thermo Fisher Scientific	Cat#B20656
E. coli RNA polymerase holoenzyme	NEB	Cat#M0551S
Low Molecular Weight DNA Ladder	NEB	Cat#N3233S
T4 Polynucleotide Kinase	Thermo Fisher Scientific	Cat#EK0031
Gamma-32P ATP	Perkin Elmer	Cat#NEG035C
Bovine Serum Albumin	NEB	Cat#B9000S
Critical Commercial Assays
MiSeq Reagent Kit v3 (150-cycle)	Illumina	Cat#MS-102–3001
PhiX Control V3	Illumina	Cat#FC-110–3001
QIAquick Gel Extraction Kit	QIAGEN	Cat#28704
MinElute PCR Purification Kit	QIAGEN	Cat#28004
QIAquick PCR Purification Kit	QIAGEN	Cat#28106
Zeba Spin Desalting Columns 7K MWCO, 5 mL	Thermo Fisher Scientific	Cat#89892
Amicon Ultra-4 Centrifugal Filter Unit, 3KDa	Millipore Sigma	Cat#UFC800324
Amicon Ultra-0.5 Centrifugal Filter Unit, 10KDa	Millipore Sigma	Cat#UFC501024
Oligonucleotides
DNA oligonucleotide library, see Table S5	CustomArray, this Study	N/A
DNA oligonucleotides used for library assembly and RNA array preparation, see Table S7	IDT	N/A
RNA oligonucleotides used in gel-shift measurements, see STAR Methods	IDT	N/A
Deposited data
RNA-seq expression data for K562 cell lines	ENCODE project (Consortium, 2012)	https://www.encodeproject.org/files/ENCFF272HJP/@@download/ENCFF272HJP.tsv,https://www.encodeproject.org/files/ENCFF471SEN/@@download/ENCFF471SEN.tsv
eCLIP data for PUM2 protein in human K562 cells	(Consortium, 2012; Van Nostrand et al., 2016)	https://www.encodeproject.org/files/ENCFF786ZZB/@@download/ENCFF786ZZB.bam,https://www.encodeproject.org/files/ENCFF732EQX/@@download/ENCFF732EQX.bam,https://www.encodeproject.org/files/ENCFF231WHF/@@download/ENCFF231WHF.bamhttps://www.encodeproject.org/files/ENCFF141SVY/@@download/ENCFF141SVY.bed.gzhttps://www.encodeproject.org/files/ENCFF141SVY/@@download/ENCFF141SVY.bed.gz
Refseq annotations for human genome assembly GRCh38 (hg38)	(O’Leary et al., 2016)	https://www.ncbi.nlm.nih.gov/refseq/
Protein-coding transcript sequences, genome release GRCh38.p12	(Harrow et al., 2012)	https://www.gencodegenes.org/human/release_28.html
RNA Bind-N-Seq data for PUM1	(Consortium, 2012; Dominguez et al., 2018)	https://www.encodeproject.org/files/ENCFF894MLG/ https://www.encodeproject.org/files/ENCFF761JAF/ (input)
Software and Algorithms
RNAfold, v2.1.8, v2.1.9	(Lorenz et al., 2011)	https://www.tbi.univie.ac.at/RNA/RNAfold.1.html
Bedtools		https://bedtools.readthedocs.io/en/latest/
HOMER (v4.8.3)	(Heinz et al., 2010)	http://homer.ucsd.edu/homer/
Ensembl Biomart	(Zerbino et al., 2018)	http://ensembl.org
Samtools (v0.1.19–96b5f2294a)		http://www.htslib.org/
pyatac ins		https://nucleoatac.readthedocs.io/en/latest/pyatac/
Global fitting scripts to determine PUM2 thermodynamic model parameters	This paper	https://github.com/pufmodel/PUM2_global_fitting
Pipeline for comparing in vivo to in vitro occupancy across genomic sites	This paper	https://github.com/GreenleafLab/puflibs/blob/master/analyze_clip_data.py
Pipeline for fitting thermodynamic constants from fluorescence data	This paper	https://github.com/GreenleafLab/array_fitting_tools/

Open in a new tab

Supplementary Material

Supplemental Figures and Tables

NIHMS1034674-supplement-Supplemental_Figures_and_Tables.pdf^{(2.3MB, pdf)}

Highlights.

A thermodynamic model quantitatively predicts PUM1/2 binding to any RNA sequence
Factors beyond simple recognition of consecutive residues influence binding
Comparison to X-linking data reveals thermodynamic control of PUM2 binding in cells
Analysis of RNA structure effects suggests disruption of RNA structure in cells

ACKNOWLEDGMENTS

We thank Wipapat Kladwang for outstanding technical assistance with emulsion PCR; Andre Gerber for PUM1 and PUM2 plasmids; Traci Hall for engineered PUM1 plasmid; Namita Bisaria, Greg Hogan, Julia Salzman, Erik Van Nostrand, and members of the Herschlag lab for helpful discussions and comments on the manuscript. This work was funded by NIH grants P01 GM066275 (D.H., R.D., and W.J.G.), R35 GM122579 (R.D.), and R01 GM121487 and R01 GM111990 (W.J.G.) and by the Beckman Center. W.J.G. acknowledges support as a Chan-Zuckerberg Investigator.

Footnotes

SUPPLEMENTAL INFORMATION

Supplemental Information can be found online at https://doi.org/10.1016/j.molcel.2019.04.012.

DECLARATION OF INTERESTS

The authors declare no competing interests.

SUPPORTING CITATIONS

The following references appear in the Supplemental Information: Campbell et al. (2012), Elemento et al. (2007), Gasch et al. (2000), Kershaw et al. (2015), Lapointe et al. (2015), Morris et al. (2008), Riordan et al. (2011), and Wilinski et al. (2017).

REFERENCES

Becker WR, Jarmoskaite I, Kappel K, Vaidyanathan PP, Denny SK, Das R, Greenleaf WJ, and Herschlag D (2019a). Quantitative high-throughput tests of ubiquitous RNA secondary structure prediction algorithms via RNA/protein binding. bioRxiv. 10.1101/571588. [DOI] [Google Scholar]
Becker WR, Jarmoskaite I, Vaidyanathan PP, Greenleaf WJ, and Herschlag D (2019b). Demonstration of Protein Cooperativity Mediated by RNA Structure Using the Human Protein PUM2. RNA 118, 10.1261/rna.068585.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
Berg JM, and Stryer L (2002). Biochemistry, 5th edition (W H Freeman; ). [Google Scholar]
Bohn JA, Van Etten JL, Schagat TL, Bowman BM, McEachin RC,Freddolino PL, and Goldstrohm AC (2018). Identification of diverse target RNAs that are functionally regulated by human Pumilio proteins. Nucleic Acids Res. 46, 362–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
Buenrostro JD, Araya CL, Chircus LM, Layton CJ, Chang HY, Snyder MP, and Greenleaf WJ (2014). Quantitative analysis of RNA-protein interactions on a massively parallel array reveals biophysical and evolutionary landscapes. Nat. Biotechnol 32, 562–568. [DOI] [PMC free article] [PubMed] [Google Scholar]
Campbell ZT, Bhimsaria D, Valley CT, Rodriguez-Martinez JA, Menichelli E, Williamson JR, Ansari AZ, and Wickens M (2012). Cooperativity in RNA-protein interactions: global analysis of RNA binding specificity. Cell Rep. 1, 570–581. [DOI] [PMC free article] [PubMed] [Google Scholar]
Chen Y, and Varani G (2013). Engineering RNA-binding proteins for biology. FEBS J. 280, 3734–3754. [DOI] [PMC free article] [PubMed] [Google Scholar]
Cheong CG, and Hall TM (2006). Engineering RNA sequence specificity of Pumilio repeats. Proc. Natl. Acad. Sci. USA 103, 13635–13639. [DOI] [PMC free article] [PubMed] [Google Scholar]
Consortium EP; ENCODE Project Consortium (2012). An integrated encyclopedia of DNA elements in the human genome. Nature 489, 57–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
Darnell RB (2010). HITS-CLIP: panoramic views of protein-RNA regulation in living cells. Wiley Interdiscip. Rev. RNA 1, 266–286. [DOI] [PMC free article] [PubMed] [Google Scholar]
Denny SK, Bisaria N, Yesselman JD, Das R, Herschlag D, and Greenleaf WJ (2018). High-throughput investigation of diverse junction elements in RNA tertiary folding. Cell 174, 377–390.e20. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ding Y, Tang Y, Kwok CK, Zhang Y, Bevilacqua PC, and Assmann SM (2014). In vivo genome-wide profiling of RNA secondary structure reveals novel regulatory features. Nature 505, 696–700. [DOI] [PubMed] [Google Scholar]
Dominguez D, Freese P, Alexis MS, Su A, Hochman M, Palden T, Bazile C, Lambert NJ, Van Nostrand EL, Pratt GA, et al. (2018). Sequence, structure, and context preferences of human RNA binding proteins. Mol. Cell 70, 854–867.e859. [DOI] [PMC free article] [PubMed] [Google Scholar]
Elemento O, Slonim N, and Tavazoie S (2007). A universal framework for regulatory element discovery across all genomes and data types. Mol. Cell 28, 337–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fujioka A, Terai K, Itoh RE, Aoki K, Nakamura T, Kuroda S, Nishida E, and Matsuda M (2006). Dynamics of the Ras/ERK MAPK cascade as monitored by fluorescent probes. J. Biol. Chem 281, 8917–8926. [DOI] [PubMed] [Google Scholar]
Galgano A, Forrer M, Jaskiewicz L, Kanitz A, Zavolan M, and Gerber AP (2008). Comparative analysis of mRNA targets for human PUF-family proteins suggests extensive interaction with the miRNA regulatory system. PLoS ONE 3, e3164. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gasch AP, Spellman PT, Kao CM, Carmel-Harel O, Eisen MB, Storz G, Botstein D, and Brown PO (2000). Genomic expression programs in the response of yeast cells to environmental changes. Mol. Biol. Cell 11, 4241–4257. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gerber AP, Herschlag D, and Brown PO (2004). Extensive association of functionally and cytotopically related mRNAs with Puf family RNA-binding proteins in yeast. PLoS Biol. 2, E79. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gerber AP, Luschnig S, Krasnow MA, Brown PO, and Herschlag D (2006). Genome-wide identification of mRNAs associated with the translational regulator PUMILIO in Drosophila melanogaster. Proc. Natl. Acad. Sci. USA 103, 4487–4492. [DOI] [PMC free article] [PubMed] [Google Scholar]
Goldstrohm AC, Hall TMT, and McKenney KM (2018). Post-transcriptional regulatory functions of mammalian Pumilio proteins. Trends Genet. 34, 972–990. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gründemann D, and Schömig E (1996). Protection of DNA during preparative agarose gel electrophoresis against damage induced by ultraviolet light. Biotechniques 21, 898–903. [DOI] [PubMed] [Google Scholar]
Guo JU, and Bartel DP (2016). RNA G-quadruplexes are globally unfolded in eukaryotic cells and depleted in bacteria. Science 353, aaf5371. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gupta YK, Nair DT, Wharton RP, and Aggarwal AK (2008). Structures of human Pumilio with noncognate RNAs reveal molecular mechanisms for binding promiscuity. Structure 16, 549–557. [DOI] [PubMed] [Google Scholar]
Hackermüller J, Meisner NC, Auer M, Jaritz M, and Stadler PF (2005). The effect of RNA secondary structures on RNA-ligand binding and the modifier RNA mechanism: a quantitative model. Gene 345, 3–12. [DOI] [PubMed] [Google Scholar]
Hafner M, Landthaler M, Burger L, Khorshid M, Hausser J, Berninger P, Rothballer A, Ascano M Jr., Jungkamp AC, Munschauer M, et al. (2010). Transcriptome-wide identification of RNA-binding protein and microRNA target sites by PAR-CLIP. Cell 141, 129–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
Halstead JM, Lionnet T, Wilbertz JH, Wippich F, Ephrussi A, Singer RH, and Chao JA (2015). Translation. An RNA biosensor for imaging the first round of translation from single cells to living animals. Science 347, 1367–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]
Harrow J, Frankish A, Gonzalez JM, Tapanari E, Diekhans M, Kokocinski F, Aken BL, Barrell D, Zadissa A, Searle S, et al. (2012). GENCODE: the reference human genome annotation for The ENCODE Project. Genome Res. 22, 1760–1774. [DOI] [PMC free article] [PubMed] [Google Scholar]
Heinz S, Benner C, Spann N, Bertolino E, Lin YC, Laslo P, Cheng JX, Murre C, Singh H, and Glass CK (2010). Simple combinations of lineage-determining transcription factors prime cis-regulatory elements required for macrophage and B cell identities. Mol. Cell 38, 576–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hogan DJ, Riordan DP, Gerber AP, Herschlag D, and Brown PO (2008). Diverse RNA-binding proteins interact with functionally related sets of RNAs, suggesting an extensive regulatory system. PLoS Biol. 6, e255. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hogan GJ, Brown PO, and Herschlag D (2015). Evolutionary conservation and diversification of Puf RNA binding proteins and their mRNA targets. PLoS Biol. 13, e1002307. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jain N, Lin HC, Morgan CE, Harris ME, and Tolbert BS (2017). Rules of RNA specificity of hnRNP A1 revealed by global and quantitative analysis of its affinity distribution. Proc. Natl. Acad. Sci. USA 114, 2206–2211. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jankowsky E, and Harris ME (2017). Mapping specificity landscapes of RNA-protein interactions by high throughput sequencing. Methods 118–119, 111–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
Jiang H, Guan W, and Gu Z (2010). Tinkering evolution of post-transcriptional RNA regulons: puf3p in fungi as an example. PLoS Genet. 6, e1001030. [DOI] [PMC free article] [PubMed] [Google Scholar]
Johnson KA, Simpson ZB, and Blom T (2009). Global kinetic explorer: a new computer program for dynamic simulation and fitting of kinetic data. Anal. Biochem 387, 20–29. [DOI] [PubMed] [Google Scholar]
Kedde M, van Kouwenhove M, Zwart W, Oude Vrielink JA, Elkon R, and Agami R (2010). A Pumilio-induced RNA structure switch in p27–3^′ UTR controls miR-221 and miR-222 accessibility. Nat. Cell Biol. 12, 1014–1020. [DOI] [PubMed] [Google Scholar]
Keene JD, and Tenenbaum SA (2002). Eukaryotic mRNPs may represent posttranscriptional operons. Mol. Cell 9, 1161–1167. [DOI] [PubMed] [Google Scholar]
Kershaw CJ, Costello JL, Talavera D, Rowe W, Castelli LM, Sims PF, Grant CM, Ashe MP, Hubbard SJ, and Pavitt GD (2015). Integrated multi-omics analyses reveal the pleiotropic nature of the control of gene expression by Puf3p. Sci. Rep 5, 15518. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kivioja T, Vähärautio A, Karlsson K, Bonke M, Enge M, Linnarsson S, and Taipale J (2011). Counting absolute numbers of molecules using unique molecular identifiers. Nat. Methods 9, 72–74. [DOI] [PubMed] [Google Scholar]
Lambert N, Robertson A, Jangi M, McGeary S, Sharp PA, and Burge CB (2014). RNA Bind-n-Seq: quantitative assessment of the sequence and structural binding specificity of RNA binding proteins. Mol. Cell 54, 887–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lapointe CP, Wilinski D, Saunders HA, and Wickens M (2015). Protein-RNA networks revealed through covalent RNA marks. Nat. Methods 12, 1163–1170. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lee S, Kopp F, Chang TC, Sataluri A, Chen B, Sivakumar S, Yu H, Xie Y, and Mendell JT (2016). Noncoding RNA NORAD regulates genomic stability by sequestering PUMILIO proteins. Cell 164, 69–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
Li X, Quon G, Lipshitz HD, and Morris Q (2010). Predicting in vivo binding sites of RNA-binding proteins using mRNA secondary structure. RNA 16, 1096–1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lin SY, and Riggs AD (1972). Lac repressor binding to non-operator DNA: detailed studies and a comparison of eequilibrium and rate competition methods. J. Mol. Biol 72, 671–690. [DOI] [PubMed] [Google Scholar]
Livesey FJ (2003). Strategies for microarray analysis of limiting amounts of RNA. Brief. Funct. Genomics Proteomics 2, 31–36. [DOI] [PubMed] [Google Scholar]
Lorenz R, Bernhart SH, Höner Zu Siederdissen C, Tafer H, Flamm C, Stadler PF, and Hofacker IL (2011). ViennaRNA Package 2.0. Algorithms Mol. Biol 6, 26. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lu G, and Hall TM (2011). Alternate modes of cognate RNA recognition by human PUMILIO proteins. Structure 19, 361–367. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lu G, Dolgner SJ, and Hall TM (2009). Understanding and engineering RNA sequence specificity of PUF proteins. Curr. Opin. Struct. Biol 19, 110–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
Marinov GK, Williams BA, McCue K, Schroth GP, Gertz J, Myers RM, and Wold BJ (2014). From single-cell to cell-pool transcriptomes: stochasticity in gene expression and RNA splicing. Genome Res. 24, 496–510. [DOI] [PMC free article] [PubMed] [Google Scholar]
Martin L, Meier M, Lyons SM, Sit RV, Marzluff WF, Quake SR, and Chang HY (2012). Systematic reconstruction of RNA functional motifs with high-throughput microfluidics. Nat. Methods 9, 1192–1194. [DOI] [PMC free article] [PubMed] [Google Scholar]
Miller MA, and Olivas WM (2011). Roles of Puf proteins in mRNA degradation and translation. Wiley Interdiscip. Rev. RNA 2, 471–492. [DOI] [PubMed] [Google Scholar]
Miller MT, Higgin JJ, and Hall TM (2008). Basis of altered RNA-binding specificity by PUF proteins revealed by crystal structures of yeast Puf4p. Nat. Struct. Mol. Biol 15, 397–402. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mitchell SF, and Parker R (2014). Principles and properties of eukaryotic mRNPs. Mol. Cell 54, 547–558. [DOI] [PubMed] [Google Scholar]
Morris AR, Mukherjee N, and Keene JD (2008). Ribonomic analysis of human Pum1 reveals cis-trans conservation across species despite evolution of diverse mRNA target sets. Mol. Cell. Biol 28, 4093–4103. [DOI] [PMC free article] [PubMed] [Google Scholar]
Müller-McNicoll M, and Neugebauer KM (2013). How cells get the message: dynamic assembly and function of mRNA-protein complexes. Nat. Rev. Genet 14, 275–287. [DOI] [PubMed] [Google Scholar]
Nagaraj N, Wisniewski JR, Geiger T, Cox J, Kircher M, Kelso J, Pääbo S, and Mann M (2011). Deep proteome and transcriptome mapping of a human cancer cell line. Mol. Syst. Biol 7, 548. [DOI] [PMC free article] [PubMed] [Google Scholar]
O’Leary NA, Wright MW, Brister JR, Ciufo S, Haddad D, McVeigh R, Rajput B, Robbertse B, Smith-White B, Ako-Adjei D, et al. (2016). Reference sequence (RefSeq) database at NCBI: current status, taxonomic expansion, and functional annotation. Nucleic Acids Res. 44 (D1), D733–D745. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ray D, Kazan H, Cook KB, Weirauch MT, Najafabadi HS, Li X, Gueroussov S, Albu M, Zheng H, Yang A, et al. (2013). A compendium of RNA-binding motifs for decoding gene regulation. Nature 499, 172–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
Riordan DP, Herschlag D, and Brown PO (2011). Identification of RNA recognition elements in the Saccharomyces cerevisiae transcriptome. Nucleic Acids Res. 39, 1501–1509. [DOI] [PMC free article] [PubMed] [Google Scholar]
Rouault TA (2006). The role of iron regulatory proteins in mammalian iron homeostasis and disease. Nat. Chem. Biol 2, 406–414. [DOI] [PubMed] [Google Scholar]
Rouskin S, Zubradt M, Washietl S, Kellis M, and Weissman JS (2014). Genome-wide probing of RNA structure reveals active unfolding of mRNA structures in vivo. Nature 505, 701–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schneider TD, and Stephens RM (1990). Sequence logos: a new way to display consensus sequences. Nucleic Acids Res. 18, 6097–6100. [DOI] [PMC free article] [PubMed] [Google Scholar]
Schwanhäusser B, Busse D, Li N, Dittmar G, Schuchhardt J, Wolf J, Chen W, and Selbach M (2013). Corrigendum: Global quantification of mammalian gene expression control. Nature 495, 126–127. [DOI] [PubMed] [Google Scholar]
She R, Chakravarty AK, Layton CJ, Chircus LM, Andreasson JO, Damaraju N, McMahon PL, Buenrostro JD, Jarosz DF, and Greenleaf WJ (2017). Comprehensive and quantitative mapping of RNA-protein interactions across a transcribed eukaryotic genome. Proc. Natl. Acad. Sci. USA 114, 3619–3624. [DOI] [PMC free article] [PubMed] [Google Scholar]
Singh G, Pratt G, Yeo GW, and Moore MJ (2015). The clothes make the mRNA: past and present trends in mRNP fashion. Annu. Rev. Biochem 84, 325–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
Sinha RP, and Häder DP (2002). UV-induced DNA damage and repair: a review. Photochem. Photobiol. Sci 1, 225–236. [DOI] [PubMed] [Google Scholar]
Spitale RC, Flynn RA, Zhang QC, Crisalli P, Lee B, Jung JW, Kuchelmeister HY, Batista PJ, Torre EA, Kool ET, and Chang HY (2015). Structural imprints in vivo decode RNA regulatory mechanisms. Nature 519, 486–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
Stormo GD (2000). DNA binding sites: representation and discovery. Bioinformatics 16, 16–23. [DOI] [PubMed] [Google Scholar]
Sugimoto Y, König J, Hussain S, Zupan B, Curk T, Frye M, and Ule J (2012). Analysis of CLIP and iCLIP methods for nucleotide-resolution studies of protein-RNA interactions. Genome Biol. 13, R67. [DOI] [PMC free article] [PubMed] [Google Scholar]
Taliaferro JM, Lambert NJ, Sudmant PH, Dominguez D, Merkin JJ, Alexis MS, Bazile C, and Burge CB (2016). RNA sequence context effects measured in vitro predict in vivo protein binding and regulation. Mol. Cell 64, 294–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
Tang F, Lao K, and Surani MA (2011). Development and applications of single-cell transcriptome analysis. Nat. Methods 8, S6–S11. [DOI] [PMC free article] [PubMed] [Google Scholar]
Thul PJ,Åkesson L, Wiking M, Mahdessian D, Geladaki A, Ait Blal H, Alm T, Asplund A, Björk L, Breckels LM, et al. (2017). A subcellular map of the human proteome. Science 356, eaal3321. [DOI] [PubMed] [Google Scholar]
Tome JM, Ozer A, Pagano JM, Gheba D, Schroth GP, and Lis JT (2014). Comprehensive analysis of RNA-protein interactions by high-throughput sequencing-RNA affinity profiling. Nat. Methods 11, 683–688. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ule J, Jensen KB, Ruggiu M, Mele A, Ule A, and Darnell RB (2003). CLIP identifies Nova-regulated RNA networks in the brain. Science 302, 1212–1215. [DOI] [PubMed] [Google Scholar]
Vaidyanathan PP, AlSadhan I, Merriman DK, Al-Hashimi HM, and Herschlag D (2017). Pseudouridine and N⁶-methyladenosine modifications weaken PUF protein/RNA interactions. RNA 23, 611–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
Valley CT, Porter DF, Qiu C, Campbell ZT, Hall TM, and Wickens M (2012). Patterns and plasticity in RNA-protein interactions enable recruitment of multiple proteins through a single site. Proc. Natl. Acad. Sci. USA 109, 6054–6059. [DOI] [PMC free article] [PubMed] [Google Scholar]
Van Nostrand EL, Pratt GA, Shishkin AA, Gelboin-Burkhart C, Fang MY, Sundararaman B, Blue SM, Nguyen TB, Surka C, Elkins K, et al. (2016). Robust transcriptome-wide discovery of RNA-binding protein binding sites with enhanced CLIP (eCLIP). Nat. Methods 13, 508–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang X, McLachlan J, Zamore PD, and Hall TM (2002). Modular recognition of RNA by a human pumilio-homology domain. Cell 110, 501–512. [DOI] [PubMed] [Google Scholar]
Wang Y, Opperman L, Wickens M, and Hall TM (2009). Structural basis for specific recognition of multiple mRNA targets by a PUF regulatory protein. Proc. Natl. Acad. Sci. USA 106, 20186–20191. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wheeler EC, Van Nostrand EL, and Yeo GW (2018). Advances and challenges in the detection of transcriptome-wide protein-RNA interactions. Wiley Interdiscip. Rev. RNA 9, e1436. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wilinski D, Qiu C, Lapointe CP, Nevil M, Campbell ZT, Tanaka Hall TM, and Wickens M (2015). RNA regulatory networks diversified through curvature of the PUF protein scaffold. Nat. Commun 6, 8213. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wilinski D, Buter N, Klocko AD, Lapointe CP, Selker EU, Gasch AP, and Wickens M (2017). Recurrent rewiring and emergence of RNA regulatory networks. Proc. Natl. Acad. Sci. USA 114, E2816–E2825. [DOI] [PMC free article] [PubMed] [Google Scholar]
Williams R, Peisajovich SG, Miller OJ, Magdassi S, Tawfik DS, and Griffiths AD (2006). Amplification of complex gene libraries by emulsion PCR. Nat. Methods 3, 545–550. [DOI] [PubMed] [Google Scholar]
Xue Y, Zhou Y, Wu T, Zhu T, Ji X, Kwon YS, Zhang C, Yeo G, Black DL, Sun H, et al. (2009). Genome-wide analysis of PTB-RNA interactions reveals a strategy used by the general splicing repressor to modulate exon inclusion or skipping. Mol. Cell 36, 996–1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
Zerbino DR, Achuthan P, Akanni W, Amode MR, Barrell D, Bhai J, Billis K, Cummins C, Gall A, Girón CG, et al. (2018). Ensembl 2018. Nucleic Acids Res. 46 (D1), D754–D761. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Figures and Tables

NIHMS1034674-supplement-Supplemental_Figures_and_Tables.pdf^{(2.3MB, pdf)}

Data Availability Statement

Thermodynamic binding data generated in this study are available for download (Table S5).

Key scripts for analyses reported herein have been deposited to github, as indicated in the Key Resources Table.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and Virus Strains
BL21(DE3) competent cells	Agilent	Cat#200131
BL21-CodonPlus (DE3)-RIPL competent cells	Agilent	Cat#230280
Chemicals, Peptides and Recombinant Proteins
SNAP-hPUM2	This paper	N/A
hPUM1-SNAP	This paper	N/A
hPUM1 MUT3–1-SNAP	This paper	N/A
His-TEV Protease	This paper	N/A
cOmplete, Mini, EDTA-free Protease Inhibitor Cocktail	Sigma-Aldrich	Cat#11836153001
Cy3B NHS ester	GE Healthcare	Cat#PA63100
BG-NH2	New England Biolabs (NEB)	Cat#S9148S
Agencourt AMPure XP beads	Beckman Coulter	Cat#A63881
SYBR Green I Nucleic Acid Stain	Lonza	Cat#50513
SYBR Gold Nucleic Acid Gel Stain	Invitrogen	Cat#S11494
Phusion High-Fidelity DNA Polymerase	Thermo Fisher Scientific	Cat#F530S
Phusion Hot Start II DNA Polymerase	Thermo Fisher Scientific	Cat#F549
Klenow fragment (3’−5’ exo(−))	NEB	Cat#M0212L
Streptavidin	PROzyme	Cat#SA10
D-Biotin	Thermo Fisher Scientific	Cat#B20656
E. coli RNA polymerase holoenzyme	NEB	Cat#M0551S
Low Molecular Weight DNA Ladder	NEB	Cat#N3233S
T4 Polynucleotide Kinase	Thermo Fisher Scientific	Cat#EK0031
Gamma-32P ATP	Perkin Elmer	Cat#NEG035C
Bovine Serum Albumin	NEB	Cat#B9000S
Critical Commercial Assays
MiSeq Reagent Kit v3 (150-cycle)	Illumina	Cat#MS-102–3001
PhiX Control V3	Illumina	Cat#FC-110–3001
QIAquick Gel Extraction Kit	QIAGEN	Cat#28704
MinElute PCR Purification Kit	QIAGEN	Cat#28004
QIAquick PCR Purification Kit	QIAGEN	Cat#28106
Zeba Spin Desalting Columns 7K MWCO, 5 mL	Thermo Fisher Scientific	Cat#89892
Amicon Ultra-4 Centrifugal Filter Unit, 3KDa	Millipore Sigma	Cat#UFC800324
Amicon Ultra-0.5 Centrifugal Filter Unit, 10KDa	Millipore Sigma	Cat#UFC501024
Oligonucleotides
DNA oligonucleotide library, see Table S5	CustomArray, this Study	N/A
DNA oligonucleotides used for library assembly and RNA array preparation, see Table S7	IDT	N/A
RNA oligonucleotides used in gel-shift measurements, see STAR Methods	IDT	N/A
Deposited data
RNA-seq expression data for K562 cell lines	ENCODE project (Consortium, 2012)	https://www.encodeproject.org/files/ENCFF272HJP/@@download/ENCFF272HJP.tsv,https://www.encodeproject.org/files/ENCFF471SEN/@@download/ENCFF471SEN.tsv
eCLIP data for PUM2 protein in human K562 cells	(Consortium, 2012; Van Nostrand et al., 2016)	https://www.encodeproject.org/files/ENCFF786ZZB/@@download/ENCFF786ZZB.bam,https://www.encodeproject.org/files/ENCFF732EQX/@@download/ENCFF732EQX.bam,https://www.encodeproject.org/files/ENCFF231WHF/@@download/ENCFF231WHF.bamhttps://www.encodeproject.org/files/ENCFF141SVY/@@download/ENCFF141SVY.bed.gzhttps://www.encodeproject.org/files/ENCFF141SVY/@@download/ENCFF141SVY.bed.gz
Refseq annotations for human genome assembly GRCh38 (hg38)	(O’Leary et al., 2016)	https://www.ncbi.nlm.nih.gov/refseq/
Protein-coding transcript sequences, genome release GRCh38.p12	(Harrow et al., 2012)	https://www.gencodegenes.org/human/release_28.html
RNA Bind-N-Seq data for PUM1	(Consortium, 2012; Dominguez et al., 2018)	https://www.encodeproject.org/files/ENCFF894MLG/ https://www.encodeproject.org/files/ENCFF761JAF/ (input)
Software and Algorithms
RNAfold, v2.1.8, v2.1.9	(Lorenz et al., 2011)	https://www.tbi.univie.ac.at/RNA/RNAfold.1.html
Bedtools		https://bedtools.readthedocs.io/en/latest/
HOMER (v4.8.3)	(Heinz et al., 2010)	http://homer.ucsd.edu/homer/
Ensembl Biomart	(Zerbino et al., 2018)	http://ensembl.org
Samtools (v0.1.19–96b5f2294a)		http://www.htslib.org/
pyatac ins		https://nucleoatac.readthedocs.io/en/latest/pyatac/
Global fitting scripts to determine PUM2 thermodynamic model parameters	This paper	https://github.com/pufmodel/PUM2_global_fitting
Pipeline for comparing in vivo to in vitro occupancy across genomic sites	This paper	https://github.com/GreenleafLab/puflibs/blob/master/analyze_clip_data.py
Pipeline for fitting thermodynamic constants from fluorescence data	This paper	https://github.com/GreenleafLab/array_fitting_tools/

Open in a new tab

[R1] Becker WR, Jarmoskaite I, Kappel K, Vaidyanathan PP, Denny SK, Das R, Greenleaf WJ, and Herschlag D (2019a). Quantitative high-throughput tests of ubiquitous RNA secondary structure prediction algorithms via RNA/protein binding. bioRxiv. 10.1101/571588. [DOI] [Google Scholar]

[R2] Becker WR, Jarmoskaite I, Vaidyanathan PP, Greenleaf WJ, and Herschlag D (2019b). Demonstration of Protein Cooperativity Mediated by RNA Structure Using the Human Protein PUM2. RNA 118, 10.1261/rna.068585.118. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R3] Berg JM, and Stryer L (2002). Biochemistry, 5th edition (W H Freeman; ). [Google Scholar]

[R4] Bohn JA, Van Etten JL, Schagat TL, Bowman BM, McEachin RC,Freddolino PL, and Goldstrohm AC (2018). Identification of diverse target RNAs that are functionally regulated by human Pumilio proteins. Nucleic Acids Res. 46, 362–386. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] Buenrostro JD, Araya CL, Chircus LM, Layton CJ, Chang HY, Snyder MP, and Greenleaf WJ (2014). Quantitative analysis of RNA-protein interactions on a massively parallel array reveals biophysical and evolutionary landscapes. Nat. Biotechnol 32, 562–568. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R6] Campbell ZT, Bhimsaria D, Valley CT, Rodriguez-Martinez JA, Menichelli E, Williamson JR, Ansari AZ, and Wickens M (2012). Cooperativity in RNA-protein interactions: global analysis of RNA binding specificity. Cell Rep. 1, 570–581. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R7] Chen Y, and Varani G (2013). Engineering RNA-binding proteins for biology. FEBS J. 280, 3734–3754. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] Cheong CG, and Hall TM (2006). Engineering RNA sequence specificity of Pumilio repeats. Proc. Natl. Acad. Sci. USA 103, 13635–13639. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R9] Consortium EP; ENCODE Project Consortium (2012). An integrated encyclopedia of DNA elements in the human genome. Nature 489, 57–74. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] Darnell RB (2010). HITS-CLIP: panoramic views of protein-RNA regulation in living cells. Wiley Interdiscip. Rev. RNA 1, 266–286. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R11] Denny SK, Bisaria N, Yesselman JD, Das R, Herschlag D, and Greenleaf WJ (2018). High-throughput investigation of diverse junction elements in RNA tertiary folding. Cell 174, 377–390.e20. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R12] Ding Y, Tang Y, Kwok CK, Zhang Y, Bevilacqua PC, and Assmann SM (2014). In vivo genome-wide profiling of RNA secondary structure reveals novel regulatory features. Nature 505, 696–700. [DOI] [PubMed] [Google Scholar]

[R13] Dominguez D, Freese P, Alexis MS, Su A, Hochman M, Palden T, Bazile C, Lambert NJ, Van Nostrand EL, Pratt GA, et al. (2018). Sequence, structure, and context preferences of human RNA binding proteins. Mol. Cell 70, 854–867.e859. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R14] Elemento O, Slonim N, and Tavazoie S (2007). A universal framework for regulatory element discovery across all genomes and data types. Mol. Cell 28, 337–350. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R15] Fujioka A, Terai K, Itoh RE, Aoki K, Nakamura T, Kuroda S, Nishida E, and Matsuda M (2006). Dynamics of the Ras/ERK MAPK cascade as monitored by fluorescent probes. J. Biol. Chem 281, 8917–8926. [DOI] [PubMed] [Google Scholar]

[R16] Galgano A, Forrer M, Jaskiewicz L, Kanitz A, Zavolan M, and Gerber AP (2008). Comparative analysis of mRNA targets for human PUF-family proteins suggests extensive interaction with the miRNA regulatory system. PLoS ONE 3, e3164. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R17] Gasch AP, Spellman PT, Kao CM, Carmel-Harel O, Eisen MB, Storz G, Botstein D, and Brown PO (2000). Genomic expression programs in the response of yeast cells to environmental changes. Mol. Biol. Cell 11, 4241–4257. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R18] Gerber AP, Herschlag D, and Brown PO (2004). Extensive association of functionally and cytotopically related mRNAs with Puf family RNA-binding proteins in yeast. PLoS Biol. 2, E79. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R19] Gerber AP, Luschnig S, Krasnow MA, Brown PO, and Herschlag D (2006). Genome-wide identification of mRNAs associated with the translational regulator PUMILIO in Drosophila melanogaster. Proc. Natl. Acad. Sci. USA 103, 4487–4492. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] Goldstrohm AC, Hall TMT, and McKenney KM (2018). Post-transcriptional regulatory functions of mammalian Pumilio proteins. Trends Genet. 34, 972–990. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R21] Gründemann D, and Schömig E (1996). Protection of DNA during preparative agarose gel electrophoresis against damage induced by ultraviolet light. Biotechniques 21, 898–903. [DOI] [PubMed] [Google Scholar]

[R22] Guo JU, and Bartel DP (2016). RNA G-quadruplexes are globally unfolded in eukaryotic cells and depleted in bacteria. Science 353, aaf5371. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R23] Gupta YK, Nair DT, Wharton RP, and Aggarwal AK (2008). Structures of human Pumilio with noncognate RNAs reveal molecular mechanisms for binding promiscuity. Structure 16, 549–557. [DOI] [PubMed] [Google Scholar]

[R24] Hackermüller J, Meisner NC, Auer M, Jaritz M, and Stadler PF (2005). The effect of RNA secondary structures on RNA-ligand binding and the modifier RNA mechanism: a quantitative model. Gene 345, 3–12. [DOI] [PubMed] [Google Scholar]

[R25] Hafner M, Landthaler M, Burger L, Khorshid M, Hausser J, Berninger P, Rothballer A, Ascano M Jr., Jungkamp AC, Munschauer M, et al. (2010). Transcriptome-wide identification of RNA-binding protein and microRNA target sites by PAR-CLIP. Cell 141, 129–141. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R26] Halstead JM, Lionnet T, Wilbertz JH, Wippich F, Ephrussi A, Singer RH, and Chao JA (2015). Translation. An RNA biosensor for imaging the first round of translation from single cells to living animals. Science 347, 1367–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R27] Harrow J, Frankish A, Gonzalez JM, Tapanari E, Diekhans M, Kokocinski F, Aken BL, Barrell D, Zadissa A, Searle S, et al. (2012). GENCODE: the reference human genome annotation for The ENCODE Project. Genome Res. 22, 1760–1774. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] Heinz S, Benner C, Spann N, Bertolino E, Lin YC, Laslo P, Cheng JX, Murre C, Singh H, and Glass CK (2010). Simple combinations of lineage-determining transcription factors prime cis-regulatory elements required for macrophage and B cell identities. Mol. Cell 38, 576–589. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R29] Hogan DJ, Riordan DP, Gerber AP, Herschlag D, and Brown PO (2008). Diverse RNA-binding proteins interact with functionally related sets of RNAs, suggesting an extensive regulatory system. PLoS Biol. 6, e255. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R30] Hogan GJ, Brown PO, and Herschlag D (2015). Evolutionary conservation and diversification of Puf RNA binding proteins and their mRNA targets. PLoS Biol. 13, e1002307. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R31] Jain N, Lin HC, Morgan CE, Harris ME, and Tolbert BS (2017). Rules of RNA specificity of hnRNP A1 revealed by global and quantitative analysis of its affinity distribution. Proc. Natl. Acad. Sci. USA 114, 2206–2211. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R32] Jankowsky E, and Harris ME (2017). Mapping specificity landscapes of RNA-protein interactions by high throughput sequencing. Methods 118–119, 111–118. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] Jiang H, Guan W, and Gu Z (2010). Tinkering evolution of post-transcriptional RNA regulons: puf3p in fungi as an example. PLoS Genet. 6, e1001030. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R34] Johnson KA, Simpson ZB, and Blom T (2009). Global kinetic explorer: a new computer program for dynamic simulation and fitting of kinetic data. Anal. Biochem 387, 20–29. [DOI] [PubMed] [Google Scholar]

[R35] Kedde M, van Kouwenhove M, Zwart W, Oude Vrielink JA, Elkon R, and Agami R (2010). A Pumilio-induced RNA structure switch in p27–3^′ UTR controls miR-221 and miR-222 accessibility. Nat. Cell Biol. 12, 1014–1020. [DOI] [PubMed] [Google Scholar]

[R36] Keene JD, and Tenenbaum SA (2002). Eukaryotic mRNPs may represent posttranscriptional operons. Mol. Cell 9, 1161–1167. [DOI] [PubMed] [Google Scholar]

[R37] Kershaw CJ, Costello JL, Talavera D, Rowe W, Castelli LM, Sims PF, Grant CM, Ashe MP, Hubbard SJ, and Pavitt GD (2015). Integrated multi-omics analyses reveal the pleiotropic nature of the control of gene expression by Puf3p. Sci. Rep 5, 15518. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R38] Kivioja T, Vähärautio A, Karlsson K, Bonke M, Enge M, Linnarsson S, and Taipale J (2011). Counting absolute numbers of molecules using unique molecular identifiers. Nat. Methods 9, 72–74. [DOI] [PubMed] [Google Scholar]

[R39] Lambert N, Robertson A, Jangi M, McGeary S, Sharp PA, and Burge CB (2014). RNA Bind-n-Seq: quantitative assessment of the sequence and structural binding specificity of RNA binding proteins. Mol. Cell 54, 887–900. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R40] Lapointe CP, Wilinski D, Saunders HA, and Wickens M (2015). Protein-RNA networks revealed through covalent RNA marks. Nat. Methods 12, 1163–1170. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R41] Lee S, Kopp F, Chang TC, Sataluri A, Chen B, Sivakumar S, Yu H, Xie Y, and Mendell JT (2016). Noncoding RNA NORAD regulates genomic stability by sequestering PUMILIO proteins. Cell 164, 69–80. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R42] Li X, Quon G, Lipshitz HD, and Morris Q (2010). Predicting in vivo binding sites of RNA-binding proteins using mRNA secondary structure. RNA 16, 1096–1107. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R43] Lin SY, and Riggs AD (1972). Lac repressor binding to non-operator DNA: detailed studies and a comparison of eequilibrium and rate competition methods. J. Mol. Biol 72, 671–690. [DOI] [PubMed] [Google Scholar]

[R44] Livesey FJ (2003). Strategies for microarray analysis of limiting amounts of RNA. Brief. Funct. Genomics Proteomics 2, 31–36. [DOI] [PubMed] [Google Scholar]

[R45] Lorenz R, Bernhart SH, Höner Zu Siederdissen C, Tafer H, Flamm C, Stadler PF, and Hofacker IL (2011). ViennaRNA Package 2.0. Algorithms Mol. Biol 6, 26. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R46] Lu G, and Hall TM (2011). Alternate modes of cognate RNA recognition by human PUMILIO proteins. Structure 19, 361–367. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R47] Lu G, Dolgner SJ, and Hall TM (2009). Understanding and engineering RNA sequence specificity of PUF proteins. Curr. Opin. Struct. Biol 19, 110–115. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R48] Marinov GK, Williams BA, McCue K, Schroth GP, Gertz J, Myers RM, and Wold BJ (2014). From single-cell to cell-pool transcriptomes: stochasticity in gene expression and RNA splicing. Genome Res. 24, 496–510. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R49] Martin L, Meier M, Lyons SM, Sit RV, Marzluff WF, Quake SR, and Chang HY (2012). Systematic reconstruction of RNA functional motifs with high-throughput microfluidics. Nat. Methods 9, 1192–1194. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R50] Miller MA, and Olivas WM (2011). Roles of Puf proteins in mRNA degradation and translation. Wiley Interdiscip. Rev. RNA 2, 471–492. [DOI] [PubMed] [Google Scholar]

[R51] Miller MT, Higgin JJ, and Hall TM (2008). Basis of altered RNA-binding specificity by PUF proteins revealed by crystal structures of yeast Puf4p. Nat. Struct. Mol. Biol 15, 397–402. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R52] Mitchell SF, and Parker R (2014). Principles and properties of eukaryotic mRNPs. Mol. Cell 54, 547–558. [DOI] [PubMed] [Google Scholar]

[R53] Morris AR, Mukherjee N, and Keene JD (2008). Ribonomic analysis of human Pum1 reveals cis-trans conservation across species despite evolution of diverse mRNA target sets. Mol. Cell. Biol 28, 4093–4103. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R54] Müller-McNicoll M, and Neugebauer KM (2013). How cells get the message: dynamic assembly and function of mRNA-protein complexes. Nat. Rev. Genet 14, 275–287. [DOI] [PubMed] [Google Scholar]

[R55] Nagaraj N, Wisniewski JR, Geiger T, Cox J, Kircher M, Kelso J, Pääbo S, and Mann M (2011). Deep proteome and transcriptome mapping of a human cancer cell line. Mol. Syst. Biol 7, 548. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R56] O’Leary NA, Wright MW, Brister JR, Ciufo S, Haddad D, McVeigh R, Rajput B, Robbertse B, Smith-White B, Ako-Adjei D, et al. (2016). Reference sequence (RefSeq) database at NCBI: current status, taxonomic expansion, and functional annotation. Nucleic Acids Res. 44 (D1), D733–D745. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R57] Ray D, Kazan H, Cook KB, Weirauch MT, Najafabadi HS, Li X, Gueroussov S, Albu M, Zheng H, Yang A, et al. (2013). A compendium of RNA-binding motifs for decoding gene regulation. Nature 499, 172–177. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R58] Riordan DP, Herschlag D, and Brown PO (2011). Identification of RNA recognition elements in the Saccharomyces cerevisiae transcriptome. Nucleic Acids Res. 39, 1501–1509. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R59] Rouault TA (2006). The role of iron regulatory proteins in mammalian iron homeostasis and disease. Nat. Chem. Biol 2, 406–414. [DOI] [PubMed] [Google Scholar]

[R60] Rouskin S, Zubradt M, Washietl S, Kellis M, and Weissman JS (2014). Genome-wide probing of RNA structure reveals active unfolding of mRNA structures in vivo. Nature 505, 701–705. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R61] Schneider TD, and Stephens RM (1990). Sequence logos: a new way to display consensus sequences. Nucleic Acids Res. 18, 6097–6100. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R62] Schwanhäusser B, Busse D, Li N, Dittmar G, Schuchhardt J, Wolf J, Chen W, and Selbach M (2013). Corrigendum: Global quantification of mammalian gene expression control. Nature 495, 126–127. [DOI] [PubMed] [Google Scholar]

[R63] She R, Chakravarty AK, Layton CJ, Chircus LM, Andreasson JO, Damaraju N, McMahon PL, Buenrostro JD, Jarosz DF, and Greenleaf WJ (2017). Comprehensive and quantitative mapping of RNA-protein interactions across a transcribed eukaryotic genome. Proc. Natl. Acad. Sci. USA 114, 3619–3624. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R64] Singh G, Pratt G, Yeo GW, and Moore MJ (2015). The clothes make the mRNA: past and present trends in mRNP fashion. Annu. Rev. Biochem 84, 325–354. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R65] Sinha RP, and Häder DP (2002). UV-induced DNA damage and repair: a review. Photochem. Photobiol. Sci 1, 225–236. [DOI] [PubMed] [Google Scholar]

[R66] Spitale RC, Flynn RA, Zhang QC, Crisalli P, Lee B, Jung JW, Kuchelmeister HY, Batista PJ, Torre EA, Kool ET, and Chang HY (2015). Structural imprints in vivo decode RNA regulatory mechanisms. Nature 519, 486–490. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R67] Stormo GD (2000). DNA binding sites: representation and discovery. Bioinformatics 16, 16–23. [DOI] [PubMed] [Google Scholar]

[R68] Sugimoto Y, König J, Hussain S, Zupan B, Curk T, Frye M, and Ule J (2012). Analysis of CLIP and iCLIP methods for nucleotide-resolution studies of protein-RNA interactions. Genome Biol. 13, R67. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R69] Taliaferro JM, Lambert NJ, Sudmant PH, Dominguez D, Merkin JJ, Alexis MS, Bazile C, and Burge CB (2016). RNA sequence context effects measured in vitro predict in vivo protein binding and regulation. Mol. Cell 64, 294–306. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R70] Tang F, Lao K, and Surani MA (2011). Development and applications of single-cell transcriptome analysis. Nat. Methods 8, S6–S11. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R71] Thul PJ,Åkesson L, Wiking M, Mahdessian D, Geladaki A, Ait Blal H, Alm T, Asplund A, Björk L, Breckels LM, et al. (2017). A subcellular map of the human proteome. Science 356, eaal3321. [DOI] [PubMed] [Google Scholar]

[R72] Tome JM, Ozer A, Pagano JM, Gheba D, Schroth GP, and Lis JT (2014). Comprehensive analysis of RNA-protein interactions by high-throughput sequencing-RNA affinity profiling. Nat. Methods 11, 683–688. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R73] Ule J, Jensen KB, Ruggiu M, Mele A, Ule A, and Darnell RB (2003). CLIP identifies Nova-regulated RNA networks in the brain. Science 302, 1212–1215. [DOI] [PubMed] [Google Scholar]

[R74] Vaidyanathan PP, AlSadhan I, Merriman DK, Al-Hashimi HM, and Herschlag D (2017). Pseudouridine and N⁶-methyladenosine modifications weaken PUF protein/RNA interactions. RNA 23, 611–618. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R75] Valley CT, Porter DF, Qiu C, Campbell ZT, Hall TM, and Wickens M (2012). Patterns and plasticity in RNA-protein interactions enable recruitment of multiple proteins through a single site. Proc. Natl. Acad. Sci. USA 109, 6054–6059. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R76] Van Nostrand EL, Pratt GA, Shishkin AA, Gelboin-Burkhart C, Fang MY, Sundararaman B, Blue SM, Nguyen TB, Surka C, Elkins K, et al. (2016). Robust transcriptome-wide discovery of RNA-binding protein binding sites with enhanced CLIP (eCLIP). Nat. Methods 13, 508–514. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R77] Wang X, McLachlan J, Zamore PD, and Hall TM (2002). Modular recognition of RNA by a human pumilio-homology domain. Cell 110, 501–512. [DOI] [PubMed] [Google Scholar]

[R78] Wang Y, Opperman L, Wickens M, and Hall TM (2009). Structural basis for specific recognition of multiple mRNA targets by a PUF regulatory protein. Proc. Natl. Acad. Sci. USA 106, 20186–20191. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R79] Wheeler EC, Van Nostrand EL, and Yeo GW (2018). Advances and challenges in the detection of transcriptome-wide protein-RNA interactions. Wiley Interdiscip. Rev. RNA 9, e1436. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R80] Wilinski D, Qiu C, Lapointe CP, Nevil M, Campbell ZT, Tanaka Hall TM, and Wickens M (2015). RNA regulatory networks diversified through curvature of the PUF protein scaffold. Nat. Commun 6, 8213. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R81] Wilinski D, Buter N, Klocko AD, Lapointe CP, Selker EU, Gasch AP, and Wickens M (2017). Recurrent rewiring and emergence of RNA regulatory networks. Proc. Natl. Acad. Sci. USA 114, E2816–E2825. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R82] Williams R, Peisajovich SG, Miller OJ, Magdassi S, Tawfik DS, and Griffiths AD (2006). Amplification of complex gene libraries by emulsion PCR. Nat. Methods 3, 545–550. [DOI] [PubMed] [Google Scholar]

[R83] Xue Y, Zhou Y, Wu T, Zhu T, Ji X, Kwon YS, Zhang C, Yeo G, Black DL, Sun H, et al. (2009). Genome-wide analysis of PTB-RNA interactions reveals a strategy used by the general splicing repressor to modulate exon inclusion or skipping. Mol. Cell 36, 996–1006. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R84] Zerbino DR, Achuthan P, Akanni W, Amode MR, Barrell D, Bhai J, Billis K, Cummins C, Gall A, Girón CG, et al. (2018). Ensembl 2018. Nucleic Acids Res. 46 (D1), D754–D761. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

A Quantitative and Predictive Model for RNA Binding by Human Pumilio Proteins

Inga Jarmoskaite

Sarah K Denny

Pavanapuresan P Vaidyanathan

Winston R Becker

Johan OL Andreasson

Curtis J Layton

Kalli Kappel

Varun Shivashankar

Raashi Sreenivasan

Rhiju Das

William J Greenleaf

Daniel Herschlag

SUMMARY

Graphical Abstract

In Brief

INTRODUCTION

Figure 1. Quantitative High-Throughput Measurements of RNA Binding to PUM2.

RESULTS

Library Design

Massively Parallel Measurements of PUM2-Binding Affinities

Dissecting and Defining PUM2 Specificity

Comprehensive Analysis of Single-Mutant Variants

Figure 2. Analysis of Single-Mutant Variant Binding to PUM2.

Testing an Additive Model for PUM2 Specificity

Figure 3. Development of a Predictive Model for PUM2 Specificity.

Residue Flipping Accounts for Most Deviations from the Additive Consecutive Model

Figure 4. Thermodynamic Model for PUM2 Binding Integrating Binding Modes and Registers.

Energetic Coupling between Neighboring Residues

Table 1.

Evaluating the Final PUM2-Binding Model

Implementation of the Predictive Model of RNA Binding by PUM2

Evaluating Specificity across Human Pumilio Proteins

Figure 5. Comparison of RNA-Binding Specificities of PUM2 and Wild-Type and Engineered PUM1 Proteins.

Evaluating the Precision of Pumilio Engineering

Assessing the Thermodynamic Model for PUM2-RNA Occupancies In Vivo

Figure 6. Testing the Thermodynamic Model in Vivo.

DISCUSSION

Applications to Cellular Interactions and RNA Properties

Generalizability of the Thermodynamic Model and Potential Improvements

An Algorithm for Predicting PUM1 and PUM2 Occupancies

Implications for Other RBPs

Functional Implications

Specificity and Cellular RNA-Protein-Binding Landscapes

Biophysical Insights into Pumilio-RNA Interactions

STAR★METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

METHOD DETAILS

Library design

Library preparation and sequencing

Ordering

Emulsion PCR

Size fractionation

PCR assembly

Bottlenecking

Fiduciary marker preparation

Sequencing

Protein expression and purification

Cy3B-labeling of SNAP-tagged proteins

RNA-MaP measurements

Imaging station setup

RNA transcription in the flow cell

RNA-MaP equilibrium binding experiments

HPLC purification of RNA oligonucleotides for competition binding measurements

[γ- 32P]-labeling of RNA oligonucleotides

Gel-shift binding measurements

Competition binding measurements

Dissociation rate constant measurements

Determination of active protein fraction by titration

QUANTIFICATION AND STATISTICAL ANALYSIS

Computational analyses

Processing sequencing data

Fitting images

Identifying library variants from sequencing data

Fluorescence normalization

Determining the free energy of binding

Single cluster fitting

Finding common values for KD,NS, fmin, and fmax across variants

Estimating fmin

[γ- ³²P]-labeling of RNA oligonucleotides

Finding common values for K_D,NS, f_min, and f_max across variants

Estimating f_min

Estimating the distribution of f_max

Estimating K_D,NS

Applying common values forK_D,NS, f_min, and f_max to refine estimates for K_D