Abstract
Protein L (PpL) is a bacterial protein which is used in the affinity chromatography stage of the production of monoclonal antibodies because of its ability to form high affinity complexes with the light chains of immunoglobulins. In the present work, the binding interfaces between one domain of PpL and antigen-binding fragments (Fab) have been investigated adopting molecular dynamics with the aim of determining the binding contribution of the residues located at the Fab–PpL interface. Because it is known that PpL binds antibodies through two distinct binding sites with different affinities, simulations were performed for both sites to determine interaction free energies to assess the relative binding contribution of the two sites. Mutational studies were then performed only on the dominant binding site. The binding free energy was evaluated with the molecular mechanics Poisson–Boltzmann surface area (MMPBSA) and umbrella sampling/weighted histogram analysis methods. Key residues for the formation of the dominant binding site complex were identified by means of alanine scanning performed both for the Fab and PpL domains. Residues of the light chain of the antibody that contribute most to binding were found to be located between SER7 and VAL13. Four residues from PpL are important for the stability of the complex: PHE839, LYS840, GLU849, and TYR853. Three residues of PpL that do not contribute to the interaction were mutated to histidine (HIS), which changes its protonation state as a function of pH, to find whether this could allow us to control the binding interaction energy. This can be useful in the elution stage of the affinity chromatography purification of antibodies if PpL is used as a ligand. These residues are GLN835, THR836, and ALA837. Molecular dynamics simulations with both protonated and unprotonated HIS were performed to mimic how changing pH may reflect on protein–ligand interaction energies. The MMPBSA approach was used to evaluate the variation of the affinity of the mutated systems with reference to the wild type. Our results show that these mutations could help in disrupting the complex under acidic conditions without impairing the affinity of PpL for the light chains at higher pHs.
1. Introduction
Monoclonal antibodies (mAbs) are one of the most promising classes of biological drugs, both for therapeutic and diagnostic purposes, with a constantly growing significance in the pharmaceutical industry for the last 30 years. The mAb market value in 2010 was of about $40 billion,1 and it is expected to be of nearly $125 billion by 2020.2 Many formats of mAbs are commercially available. Complete antibodies are formed by fragment crystallizable (Fc) and antigen-binding fragments (Fab) domains, whereas the antibody fragments are constituted only by the regions that bind the antigens, such as Fabs and single-chain variable fragments (scFvs). ScFvs consist of variable domains of heavy and light chains, joined together by a flexible peptide linker. Both Fabs and scFvs penetrate tumors much more rapidly than whole antibodies and have a very short serum half-life because of their limited dimensions (50 and 25 kDa, respectively).3 Because of the complexity of these macromolecules and the presence of many different compounds in the production media, the purification step of the production of mAbs and antibody fragments is crucial. The first recovery step in the downstream processing of mAbs is affinity chromatography, a purification methodology that is based on the selective interaction between the solute in the mobile phase to be purified and the affinity ligand in the stationary phase. The most common ligand for mAb purification is staphylococcal protein A,4 which shows a strong affinity for the Fc region of immunoglobulin G (IgG) and has been largely studied in the last 30 years both experimentally and in silico.5−15 Antibody fragments do not have the Fc domain, thus protein L (PpL) is used in the purification step, instead of protein A or protein G.16 PpL is a cell wall protein of the bacterium Peptostreptococcus magnus(17) that contains four or five homologous domains, depending on the bacterial strain,18 capable of binding the VL regions of κ1, κ3, and κ4 light chains with strong affinity (Kd ≈ 10–9 M), but not κ2 and λ subgroups,19 with no restriction on the class of the Ig. The Ig binding domains of PpL contain a four-stranded β-sheet with a single α-helix, similarly to IgG binding domains of protein G from group C and G Streptococci.20 PpL interacts with antibodies through two independent binding sites, denoted here as binding site 1 and binding site 2. The first interface involves the second β-strand and the α-helix, whereas the other involves the third β-strand and the α-helix.21 Both binding sites interact with the second β-strand of the Vκ domain of Igs. VL chains that do not bind PpL have been successfully engineered to add the capability of binding PpL, by substituting the N-terminal sequence corresponding to Vκ FR1 into the sequence of the VL chain of the antibodies.22,23 In this paper, we investigate the interaction between one domain of PpL and Fab fragments using molecular dynamics (MD) simulations with the aim of determining free interaction energies between the protein and the ligand for both binding sites and then evaluate the contributions to the binding affinity of the residues of both PpL and Fab fragments for the dominant binding site. Then, the effect of mutations to histidine and of its protonation state on the dominant binding site affinity has been investigated. In principle, this allows us to find mutations of PpL that could make the use of milder conditions possible during the elution process of an affinity chromatography purification cycle because the low pH used to recover the product, between 2 and about 3.5,24 can induce aggregation and conformational changes in the antibodies.25,26 The rational is that the mutation of residues that do not contribute to binding into histidines may help to tune the interaction energy between the protein and the ligand. In fact at pHs higher than about 5, histidine residues are usually not protonated and are uncharged, and thus the mutation of a nonbinding residue to histidine is not likely to impact significantly the strength of the protein–protein interaction. As the pH decreases, histidines will eventually get protonated and thus, most likely, lead to the establishment of repulsive electrostatic interactions that will decrease the system interaction energy.
2. Results and Discussion
PpL interacts with the variable chain of antibodies through two distinct binding sites. Interaction free energies for the PpL–Fab complexes via both interfaces were evaluated using two approaches. Crystal 1MHH was used to evaluate the free energy of interaction of binding site 1 by means of the molecular mechanics Poisson–Boltzmann surface area (MMPBSA) approach, whereas crystal 1HEZ was used to calculate the free energy of interaction of both binding interfaces, using the MMPBSA and weighted histogram analysis (WHAM) methodologies. In this section, the results of MD simulations are discussed and compared with experimental values available in the literature. In section 2.1, the results of models of binding site 1 are reported, whereas the results of the modeling of binding site 2 are presented in section 2.2. Finally, in section 2.3, a mutational study has been conducted to evaluate possible mutants of PpL that may allow milder elution conditions during the elution phase of the purification process.
2.1. Modeling of the Binding Site 1 Interaction
The binding site 1 interaction between Fab fragments and a PpL domain was investigated to evaluate the free energy of binding and to identify the residues, from both PpL and the Fab fragment, which contribute most to the strength of the affinity interaction. Two molecular models have been used to study the first binding interface. The starting structures were obtained from the crystal structures deposited in the Protein Data Bank as 1HEZ(21) and 1MHH.27 The structure of the 1MHH complex is shown in Figure 1.
Figure 1.
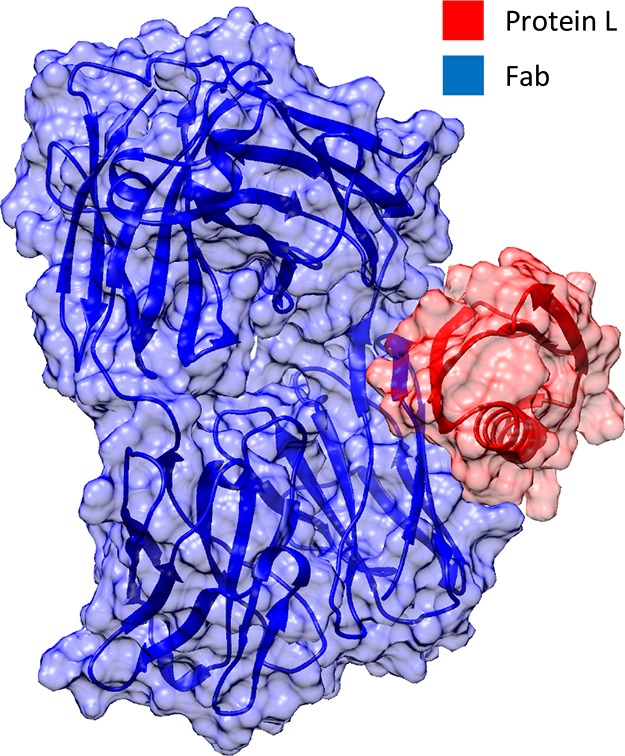
Structure of the PpL–Fab complex obtained from crystal structure 1MHH used as the starting configuration for the simulations.
MD simulations of 20–25 ns in explicit water were carried out to study the conformational evolution of the Fab–PpL complexes for the 1MHH and 1HEZ models, respectively. Configurations from each simulation were saved every 10 ps for further analysis.
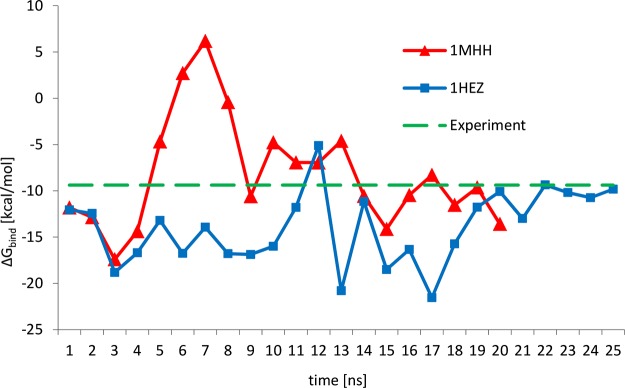
The free energy of binding as a function of simulation time was calculated using the MMPBSA approach. The results are summarized and compared with the experimental value reported by Beckingham et al.28 in Figure 2. The calculated free binding energies averaged over the last 5 ns of each simulation are reported in Table 1.
Figure 2.
Binding free energy for the first interface of PpL–Fab complexes (binding site 1) calculated with the MMPBSA approach as a function of simulation time for the 1MHH and 1HEZ binding complexes and comparison with the experimental data.21
Table 1. Binding Free Energies of Binding Site 1 for Two PpL–Fab Complexes Averaged Over the Entire Simulation and Compared with the Value Averaged Over the Last 5 ns of Simulation Calculated with the MMPBSA Approach.
| ΔGbind [kcal/mol], entire simulation | ΔGbind [kcal/mol], last 5 ns | |
|---|---|---|
| 1HEZ | –13.95 | –10.53 |
| 1MHH | –8.30 | –10.77 |
| exp21 | –9.38 |
Polar and nonpolar contributions to the interaction free energy are reported separately in Figure 3. The polar contribution was evaluated as the sum of the polar terms of ΔEMM and ΔGsol, which are the electrostatic energy calculated with the Coulomb’s law using an infinite cutoff (ΔEcoul) and the solvation free energy obtained solving the Poisson–Boltzmann equation (ΔGPB). The nonpolar contribution was estimated as the sum of van der Waals energy (ΔEvdW) and the free energy associated with the solvent accessible surface area (ΔGSASA). The data analysis shows that the interaction between PpL and the antibody fragment is driven by nonpolar interactions, whereas the polar contribution is unfavorable to the formation of the complex. Formation of protein–ligand complexes is often driven by nonpolar interactions because of the presence of hydrophobic patches on the surface of the proteins involved in the interaction. Although, in the case of the interaction between Fab and PpL, the polar contribution is not favorable to the formation of the binding, it is an important contribution to the formation of other protein–ligand interactions involving antibodies, like in the case of the IgG–protein A complex,7 which has been mentioned above. Fluctuations of the calculated interaction energy shown in Figure 2 can be reasonably attributed to the relaxation of the complexes from the initial conformation obtained from the crystallographic structures. This is the reason why the final 5 ns of both simulations have been used to evaluate binding free energies.
Figure 3.
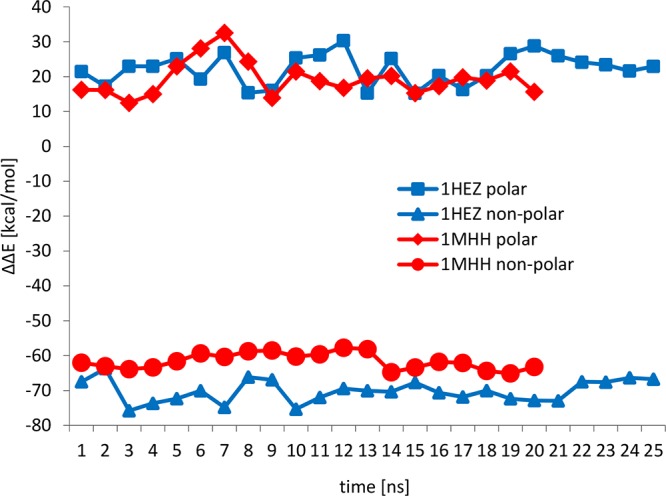
Polar and nonpolar contributions to the binding free energies for the PpL–Fab complexes calculated with the MMPBSA approach.
Curves for both models reported in Figure 2 show the presence of peaks of few kcal/mol. The 1MHH model has a peak at 7 ns, whereas the 1HEZ model shows a rapid variation of the value of the binding free energy between 12 and 17 ns. Comparing Figure 2 with Figure 3, it is possible to note that these variations are due to fluctuations of the polar contribution to the overall binding free energy, given by the relaxation of the proteins from the initial configuration obtained from the crystallographic structures. It is important to highlight that both models converge to the same value of binding free energy, averaged over the last 5 ns of each simulation, of about −10.50 kcal/mol. This value differs from the average values calculated over the entire simulation of −13.95 kcal/mol for the 1HEZ model and −8.30 kcal/mol for the 1MHH model.
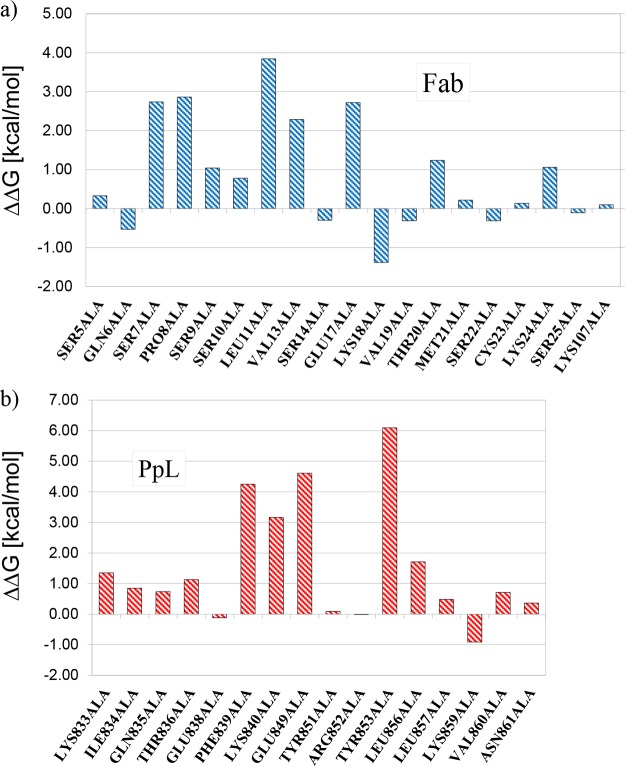
An alanine scanning analysis was performed on the residues in the first interface from both Fab and PpL to determine the contribution of each residue to the affinity binding. The results of the analysis are shown in Figure 4.
Figure 4.
Variation of the binding free energy for the first binding interface calculated substituting the amino acids of (a) Fab and (b) PpL with alanine.
The substitutions to alanine of five residues from the variable chain of the Fab fragment cause an increase of ΔGbind between 2 and 4 kcal/mol. These residues are SER7, PRO8, LEU11, VAL13, and GLU17. This is in agreement with what was shown by Graille and co-workers,21 who compared the amino acidic sequence of κ and λ subgroups of human VL chains, highlighting that the PpL binding ability is concentrated between THR5 and ALA12. In fact, three of them (SER7, PRO8, and LEU11) are inside that interval, and one (VAL13) is just one residue over. The relatively low contribution (less than 4 kcal/mol) of these amino acids to the overall binding energy is consistent with the fact that the interaction between PpL and Fab fragments is dependent on the conformation of the main chain.21
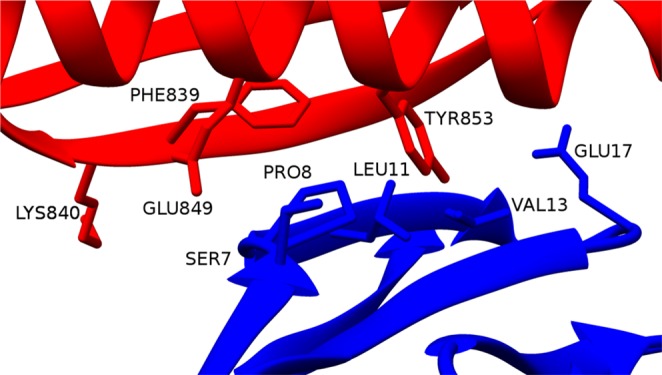
Four residues from PpL contribute significantly to the strength of the first binding interface. These residues are PHE839, LYS840, GLU849, and TYR853. PHE839 and LYS840 are in the second β-strand, whereas GLU849 and TYR853 are in the α-helix. The aromatic ring of PHE839 is known to interact with the ring of PRO8 from the VL chain, and this interaction has been used to perform fluorometric measurements substituting the phenylalanine with a tryptophan.29 GLU849 is involved in a salt bridge with LYS24 from the VL chain, whereas LYS840 is involved in a hydrogen bond with SER9. The greatest contribution to the affinity between PpL and the Fab is given by TYR853. This residue is well known in the literature for its importance in the stability of the interaction. Beckingham et al.28 have shown that the substitution of TYR853 with a phenylalanine leads to a 23-fold drop in affinity. Roque et al.30 proposed an artificial ligand, named ligand 8/7, that may resemble the pocket formed by TYR853, PHE839, and GLU838. Svensson et al.31 estimated the equilibrium dissociation constant with kinetic titration experiments on some PpL mutations and found that the greatest contributions to binding site 1 affinity are from PHE839 and TYR853, which is in good agreement with our predictions. Our calculations also correctly show that TYR851, which is an important residue for the strength of the affinity interaction of binding site 2,31 does not contribute to the interaction of the first interface. This is because TYR851, though located in the α-helix of PpL like its homologous TYR853, faces away from the binding site 1.
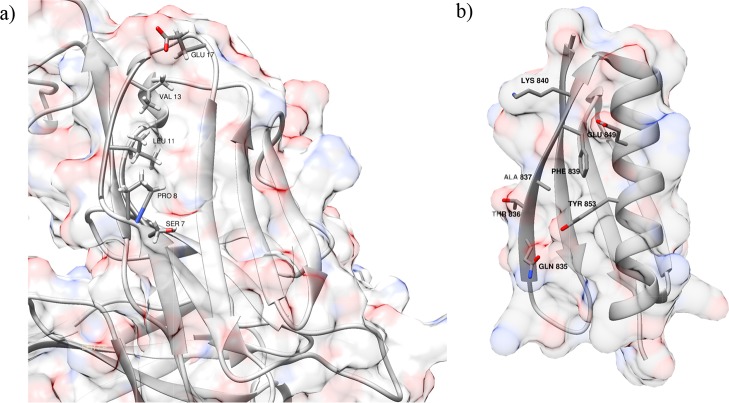
The key residues of PpL and the Fab fragment are shown in Figure 5.
Figure 5.
Key residues of binding site 1 identified with alanine scanning analysis for (a) Fab and (b) PpL.
2.2. Modeling of Binding Site 2
The second binding interface was investigated through 25 ns of MD simulation in explicit water starting from the 1HEZ crystal structure. The MMPBSA has been used to estimate the free energy of interaction. In Figure 6, the result of the MMPBSA calculation is reported. In this case, the model is unable to reproduce the experimental value of 7 kcal/mol reported by Graille et al.,21 and a drift toward lower values of the calculated binding free energy is present. This seems to suggest that the system is reaching a state that is more stable than the initial configuration, but important configurational modifications in the structure of both Fab and PpL have not been observed during the simulation time. A possible reason is that conformational changes during the formation of the complex determine an error in the energy estimation through the MMPBSA protocol. One of the hypotheses underlying the one-trajectory approach for the MMPBSA is that no conformational change occurs during the formation of the complex. This is because to compute the binding free energy with this approach, only one MD simulation of the complex is required, and the sampling of the conformations of the protein and the ligand is obtained from the sampling of the complex. Alternatively, it might be that the modification of the protein structure done by Graille et al. to investigate separately the contributions of the two binding sites to the complex modifies the protein binding properties. This complicates our interpretation of the experimental results as it makes the identification of the dominant binding site unclear, which is necessary to focus our in silico mutational study properly. To further investigate this aspect, we decided to determine the protein binding energy at a higher level of theory.
Figure 6.
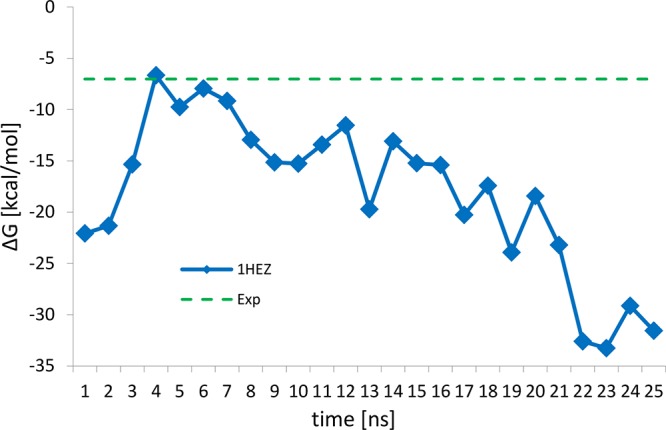
Binding free energy of binding site 2 for the PpL–Fab complex calculated using the MMPBSA approach and reported as a function of simulation time.
A first possibility to improve the quality of the MMPBSA free energy predictions would be to run additional MD simulations of the protein and the ligand, so that conformations of the unbound state may be properly sampled. Unfortunately, this three-trajectory approach, though slightly more computationally demanding, suffers from the problem that intermolecular terms in the calculation of the molecular mechanics energy do not cancel out, thus adding a significant numerical noise to the computational results. For this reason, we chose to use the computationally much more demanding, but more accurate, WHAM approach. The distance between the centers of mass (COMs) of PpL and Fab was used as reaction coordinate. This is motivated by the fact that both Fab and PpL do not undergo large conformational variations, keeping their native fold. 58 windows were used for the umbrella sampling (US) simulations, with a constant spacing of 0.5 Å, from 25.5 to 54.0 Å. A harmonic constant of 19 kcal mol–1 Å–2 was used to force the system in the center of the windows. The calculated potential of mean force (PMF) is shown in Figure 7. The calculated interaction free energy for the second interface is 7.25 kcal/mol, thus in excellent agreement with the value reported by Graille et al.21 mentioned above and supporting our interpretation of the probable cause of the discrepancy between MMPBSA and experimental data. The absolute minimum of the PMF is at a distance between the COMs of 28 Å. After that, a first steep rise of 3 kcal/mol of the potential is found at 35 Å, where the system reaches an intermediate state, whereas a second rise takes place at 45 Å, where a plateau is reached and the two molecules get unbound. Analyzing the MD trajectories it could be observed that the first steep rise of the PMF at 35 Å is due to the disruption of the hydrogen bond formed by TYR851 and the backbone of the VL chain of the Fab. The plateau between 35 and 45 Å is correlated to the rotation of PpL around the bonding interaction of PHE843 and ASN873 with ARG18. This interaction is then broken at 45 Å, which determines the second steep rise of the PMF.
Figure 7.
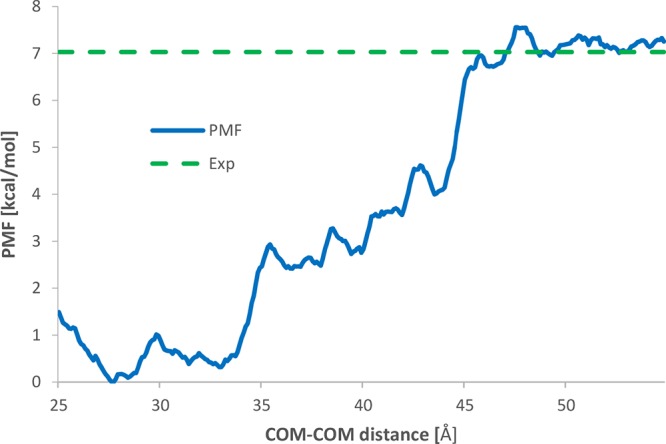
PMF for the second binding interface evaluated as a function of the distance between the COMs of PpL and Fab.
The present computational results support the experimental results, indicating the affinity by PpL and that the antibody is dominated by binding site 1. In the following, therefore, we focused our study on the possibility to tune the energy of this interaction on the modification of residues that were found to be located in the proximity of binding site 1.
2.3. Mutational Study
A typical affinity chromatography cycle is formed by an application phase, where the protein–ligand complex is established, and an elution phase, where the interaction is disrupted by means of a variation in ionic strength or buffer pH. To allow the release of the antibody from the ligand, a pH lower than 4 is often required, but a low pH can damage the product leading to denaturation and/or aggregation,32 and thus milder conditions are preferable. One way to make the use of milder conditions possible is making the interaction between the protein and the ligand weaker during the elution phase, possibly without making the interaction weaker during the application phase. To do so, we tested three mutations to histidine of PpL residues located in the protein–ligand interface of binding site 1, the dominant binding site among the two studied here, that have a low contribution to the stability of the complex. The residues from PpL that we chose to mutate are GLN835, THR836, and ALA837 from the 1MHH model. All the mutated residues are located in the second β-strand of the PpL domain. For each mutation, we performed two MD simulations, testing both the protonated and the deprotonated state of the imidazole ring, with the aim of mimicking a change in pH. Free energies of interaction have been calculated with the MMPBSA approach and have been compared with the reference value. The results are reported in Figure 8.
Figure 8.
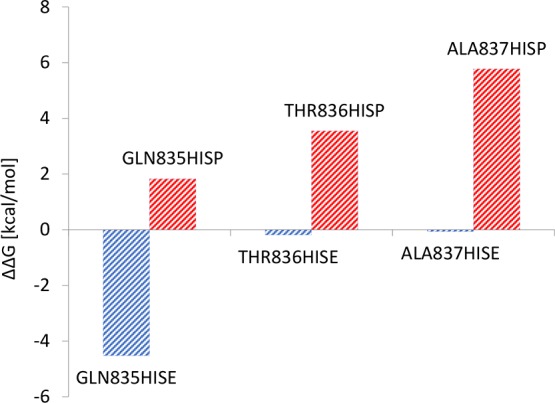
Variation of binding free energy for single-point mutations to protonated (HISP) and not protonated (HISE) histidines using the 1MHH model as the reference evaluated using the MMPBSA approach.
It can be noted that, for the residues mutated to deprotonated histidine (HISE), no weakening of the interaction should occur during the application phase of the chromatographic cycle, but in the case of GLN835, the affinity can increase by about 4 kcal/mol. For all the mutations to protonated histidine (HISP), a weakening of the interaction could occur during the elution phase, allowing milder conditions during the process. The weakening of the interaction may be due to the proximity of these residues with positively charged residue of the VL chain or with polar residues of the PpL domain that interact with the VL chain. In particular, ALA837 is close to TYR853, which is one of the most important residues to the affinity interaction. TYR853 interacts with THR20 in the VL chain by means of a hydrogen bond between the hydroxyl group of tyrosine and the backbone of the VL chain. This hydrogen bond may be weakened by the presence of the positive charge of the protonated HIS837. Svensson et al.31 report that the mutation of the same residue to arginine disrupts binding site 1.
3. Conclusions
The interaction between Fab fragments and PpL has been investigated using MD simulations. PpL binds antibodies via two distinct binding sites. Molecular models of both interactions have been built from crystal structures available in the Protein Data Bank. These molecular models have been used to estimate the binding free energy of both the interactions, by means of two different approaches, MMPBSA and WHAM. Values of the free energy of interaction have been compared with those available in the literature. The properties of the first binding interface have been investigated through an alanine scanning analysis that allowed us to identify the residues that contribute most to the affinity binding. This analysis confirms that the affinity of PpL for the antibodies is dependent on the conformation of the light chain. The key residues of κ light chains are mostly located in the second β strand. Four residues of PpL establish strong interactions with the light chains. These residues, namely PHE839, LYS840, GLU849, and TYR853, have been often mutated to study and disrupt the first binding interface. The results of the alanine scanning analysis agree with the data reported in the literature. From the alanine scanning analysis, we identified three possible single-point mutations to histidine that could be exploited to allow milder conditions for the desorption of the antibodies during the elution stage. The mutated residues are GLN835, THR836, and ALA837 and belong to the second beta strand of PpL. These mutations can be tested experimentally to validate the molecular model presented here.
4. Methods
4.1. Molecular Models
Molecular models of the interaction between PpL and Fab fragments were built starting from two crystal structures available in the Protein Data Bank (PDB ID: 1HEZ(21) and 1MHH(27)). The 1HEZ crystal is composed by one C* domain of PpL33 in complex with two Fab fragments of human IgM. This structure was used to model the interaction between PpL and Fab fragments via both binding interfaces: binding site 1 interaction was modeled using chains A, B, and E, whereas binding site 2 was modeled using chains C, D, and E. The 1MHH crystal structure includes two complexes formed by PpLD55A domains with murine Fab with a VLκ9 region. We used one of the two complexes (chains A, B, and E) to model the binding site 1 interaction.
The heavy chains of the Fab fragments in both crystal structures have missing residues. They were rebuilt by homology modeling using the MODELLER interface in UCSF Chimera 1.6.1.34 Chain F from crystal structure 1DEE(8) and chain D from crystal structure 1YMH(35) were used as templates to build the homology model of the heavy chains of structures 1HEZ and 1MHH, respectively.
4.2. Free Energy Calculations
Interaction free energies between PpL and Fab were evaluated by means of two computational methodologies. The first approach is MMPBSA,36 and the other one is the WHAM, which was used to reconstruct the PMF from US simulations.37
4.2.1. MD Simulations
All MD simulations were performed in explicit water and ions with an ionic strength of 150 mM. Periodic boundary conditions were applied, and long range electrostatic interactions were evaluated with the particle mesh Ewald method38 with a nonbonded cutoff of 10 Å. All MD simulations were performed at 300 K and 1 bar. The temperature was controlled using the v-rescale algorithm.39 Protein and nonprotein molecules have been controlled separately to avoid the hot solvent/cold solute effect.40 The pressure has been controlled using the Parrinello–Rahman algorithm.41 All bond lengths have been constrained using LINCS,42 which allowed a time step of 2.0 fs. MD simulations have been performed using the GROMACS 4.5.5 package.43 Proteins and ligands were modeled with the AMBER03 force field,44 and the TIP3P force field45 was used to model water molecules. MD simulations have been prepared following a two-step protocol: 1000 steps of energy minimization with the steepest descent algorithm to remove unfavorable contacts between the solvent and the solute, followed by 100 ps of position-restrained dynamics to let water molecules distribute themselves around the solute at a constant volume and a constant temperature, using a position restraint on the heavy atoms of the solute with a harmonic constant of 2.4 kcal mol–1 Å–2.
4.2.2. Molecular Mechanics Poisson–Boltzmann Surface Area
The MMPBSA approach allows us to evaluate the free energy of binding ΔGbind for a protein–ligand complex as the sum of three terms:
| 1 |
where ΔEMM is the molecular mechanics contribution in the gas phase, calculated as the sum of electrostatic and van der Waals energies. The entropic term, TΔSgas, was evaluated as the difference of rotational and translational entropy in the gas phase between the complex, Fab, and PpL. This term was computed through statistical thermodynamics referring to the corresponding molecular partition functions. The vibrational contribution to TΔSgas has been neglected, mainly because of the difficulty of estimation for large protein molecules. Not taking into account, this term is likely to introduce an uncertainty of few kcal/mol in the calculated binding free energy. For the Fab–PpL complexes, the TΔSgas contribution is about 34 kcal/mol. Finally, ΔGsol is the free energy of solvation, evaluated as the sum of polar and nonpolar terms. The polar term is calculated by solving the Poisson–Boltzmann equation, whereas the nonpolar term is evaluated as a function of the change in SASA of the proteins
| 2 |
where γ = 5 cal mol–1 Å–2 and b = 860 cal mol–1.46 All the right-side terms in eq 1 are evaluated as the difference of the value for the complex and the value for Fab and PpL.
The g_energy program in GROMACS 4.5.5 was used to determine the molecular mechanics energy contribution. The g_sasa program was used to evaluate the SASA for complex, protein, and ligand configurations. The APBS 1.3 program47 was used to determine the polar contribution to free energies of solvation. The pdb2pqr program48 was used to create the input files for APBS. Configurations of the Fab–PpL complexes for the MMPBSA calculations were generated with 20–25 ns of MD simulations in a 10 × 10 × 10 Å simulation box. Structures of Fab–PpL complexes have been collected every 10 ps. Structures of Fab and PpL have been obtained from the structures of the complexes, following the single-trajectory approach.49
4.2.3. Potential of Mean Force
The PMF relative to the unbinding process of the second interface has been recovered from US simulations using the WHAM. The starting configuration of the complex was extracted from the last frame of the MD simulation of the 1HEZ model. The complex was then rotated to align the COMs of PpL and Fab along the y-axis of the solvation box. Simulations were performed in a box of 10 × 13 × 10 Å. PpL was progressively removed from the Fab fragment through a series of MD simulations where the distance between the COM of PpL and Fab have been constantly increased with steps of 0.5 Å by applying a 24 kcal mol–1 Å–2 harmonic potential along the y-axis. The last snapshot of each simulation was used as the starting point for US simulations where the distance of COMs of PpL and Fab was restrained by applying a 19 kcal mol–1 Å–2 harmonic potential. The values of the distance between the COMs of PpL and Fab have been saved every 100 fs for WHAM analysis. WHAM equations were solved using our in-house code50 until the difference between two successive values of the PMF differs by less than 10–5 kcal/mol.
4.2.4. Computational Alanine Scanning
An alanine scanning analysis of the first interface was performed to determine the amino acidic contribution to the free energy of binding using the 1MHH molecular model. Nonalanine and nonglycine residues in the Fab–PpL interface were mutated one by one to alanine, and the free energies of binding for the mutated systems were then evaluated following the MMPBSA approach36 described in section 4.2.2. Because the side chain of alanine is constituted only by a methyl group, mutations of the residues to alanine were done by deleting all the atoms of the side chain but the Cβ. Hydrogens of the mutated side chain were then added with the pdb2gmx program. Binding free energy for the mutated system was compared with the value obtained for the wild type protein to identify the residues that contribute to affinity binding. The structures of the complex used for the analysis have been extracted from the last 5 ns of the trajectory of the 1MHH model.
4.2.5. Mutational Study
The strong affinity between antibodies and Ig binding proteins, such as PpL, protein G, and protein A, has the drawback of requiring harsh conditions during the elution phase, like pH well under 4.0, to disrupt the binding and recover the purified antibody. The very low pH can induce agglomeration and loss of the native conformation of the product. A possible way to circumvent this problem is to engineer the affinity ligand to allow the desorption under milder conditions. This is done by mutating one or more residues in the binding interface. A notable approach is the mutation of residues to histidine to obtain a pH-dependent binding. In fact, histidine residues have an imidazole side chain that switches between protonated and unprotonated states at slightly acidic pH, near its pKa. Point mutations to histidine have been performed on protein G and PpL allowing higher pH during the elution phase.51,52 To find possible mutations to histidine that could allow an easier desorption of antibodies from PpL during the elution phase, we identified three residues belonging to the first binding interface of PpLD55A that do not contribute to the binding affinity. These residues were mutated to histidine using the rotamers tool available in the UCSF Chimera 1.6 software.53 The protonation state of the mutated histidine was then selected with the pdb2gmx program in GROMACS 4.5.5. For each structure, two models have been created: one with a neutral histidine (HISE), to simulate the adsorption stage of the affinity chromatography cycle, and the other with a charged histidine (HISP), to mimic the low pH conditions of the elution stage. MD simulations (20 ns) have been carried out, and the relative binding free energies with respect to the 1MHH model were evaluated by means of the MMPBSA approach described above.
Author Present Address
† Centre de Biochimie Structurale, CNRS UMR 5048, UM, INSERM U 1054, 29 Rue de Navacelles, FR-34090 Montpellier, France.
The authors declare no competing financial interest.
References
- Chon J. H.; Zarbis-Papastoitsis G. Advances in the Production and Downstream Processing of Antibodies. New Biotechnol. 2011, 28, 458–463. 10.1016/j.nbt.2011.03.015. [DOI] [PubMed] [Google Scholar]
- Ecker D. M.; Jones S. D.; Levine H. L. The Therapeutic Monoclonal Antibody Market. mAbs 2015, 7, 9–14. 10.4161/19420862.2015.989042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chames P.; Van Regenmortel M.; Weiss E.; Baty D. Therapeutic Antibodies: Successes, Limitations and Hopes for the Future. Br. J. Pharmacol. 2009, 157, 220–233. 10.1111/j.1476-5381.2009.00190.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Low D.; O’Leary R.; Pujar N. S. Future of Antibody Purification. J. Chromatogr. B: Anal. Technol. Biomed. Life Sci. 2007, 848, 48–63. 10.1016/j.jchromb.2006.10.033. [DOI] [PubMed] [Google Scholar]
- Jansson B.; Uhlén M.; Nygren P.-Å. All Individual Domains of Staphylococcal Protein A Show Fab Binding. FEMS Immunol. Med. Microbiol. 2006, 20, 69–78. 10.1111/j.1574-695x.1998.tb01112.x. [DOI] [PubMed] [Google Scholar]
- Hober S.; Nord K.; Linhult M. Protein A Chromatography for Antibody Purification. J. Chromatogr. B: Anal. Technol. Biomed. Life Sci. 2007, 848, 40–47. 10.1016/j.jchromb.2006.09.030. [DOI] [PubMed] [Google Scholar]
- Salvalaglio M.; Zamolo L.; Busini V.; Moscatelli D.; Cavallotti C. Molecular Modeling of Protein A Affinity Chromatography. J. Chromatogr. A 2009, 1216, 8678–8686. 10.1016/j.chroma.2009.04.035. [DOI] [PubMed] [Google Scholar]
- Graille M.; Stura E. A.; Corper A. L.; Sutton B. J.; Taussig M. J.; Charbonnier J.-B. B.; Silverman G. J. Crystal Structure of a Staphylococcus Aureus Protein A Domain Complexed with the Fab Fragment of a Human IgM Antibody: Structural Basis for Recognition of B-Cell Receptors and Superantigen Activity. Proc. Natl. Acad. Sci. U.S.A. 2000, 97, 5399–5404. 10.1073/pnas.97.10.5399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cedergren L.; Andersson R.; Jansson B.; Uhlén M.; Nilsson B. Mutational Analysis of the Interaction between Staphylococcal Protein A and Human IgG1. Protein Eng. 1993, 6, 441–448. 10.1093/protein/6.4.441. [DOI] [PubMed] [Google Scholar]
- Tashiro M.; Montelione G. T. Structures of Bacterial Immunoglobulin-Binding Domains and Their Complexes with Immunoglobulins. Curr. Opin. Struct. Biol. 1995, 5, 471–481. 10.1016/0959-440x(95)80031-x. [DOI] [PubMed] [Google Scholar]
- Deisenhofer J. Crystallographic Refinement and Atomic Models of a Human Fc Fragment and Its Complex with Fragment B of Protein A from Staphylococcus Aureus at 2.9- and 2.8-.Ang. Resolution. Biochemistry 1981, 20, 2361–2370. 10.1021/bi00512a001. [DOI] [PubMed] [Google Scholar]
- Ljungberg U. K.; Jansson B.; Niss U.; Nilsson R.; Sandberg B. E. B.; Nilsson B. The Interaction between Different Domains of Staphylococcal Protein a and Human Polyclonal IgG, IgA, IgM and F(ab’)2: Separation of Affinity from Specificity. Mol. Immunol. 1993, 30, 1279–1285. 10.1016/0161-5890(93)90044-c. [DOI] [PubMed] [Google Scholar]
- Li R.; Dowd V.; Stewart D. J.; Burton S. J.; Lowe C. R. Design, Synthesis, and Application of a Protein A Mimetic. Nat. Biotechnol. 1998, 16, 190–195. 10.1038/nbt0298-190. [DOI] [PubMed] [Google Scholar]
- Sengupta J.; Sinha P.; Mukhopadhyay C.; Ray P. K. Molecular Modeling and Experimental Approaches toward Designing a Minimalist Protein Having Fc-Binding Activity of Staphylococcal Protein A. Biochem. Biophys. Res. Commun. 1999, 256, 6–12. 10.1006/bbrc.1999.0198. [DOI] [PubMed] [Google Scholar]
- Jendeberg L.; Tashiro M.; Tejero R.; Lyons B. A.; Uhlén M.; Montelione G. T.; Nilsson B. The Mechanism of Binding Staphylococcal Protein A to Immunoglobin G Does Not Involve Helix Unwinding. Biochemistry 1996, 35, 22–31. 10.1021/bi9512814. [DOI] [PubMed] [Google Scholar]
- Rodrigo G.; Gruvegård M.; Van Alstine J. Antibody Fragments and Their Purification by Protein L Affinity Chromatography. Antibodies 2015, 4, 259–277. 10.3390/antib4030259. [DOI] [Google Scholar]
- Björck L. Protein-L. A Novel Bacterial-Cell Wall Protein with Affinity for Ig L-Chains. J. Immunol. 1988, 140, 1194–1197. [PubMed] [Google Scholar]
- Sidorin E. V.; Solov’eva T. F. IgG-Binding Proteins of Bacteria. Biochemistry 2011, 76, 295–308. 10.1134/s0006297911030023. [DOI] [PubMed] [Google Scholar]
- Akerström B.; Björck L. Protein-L: An Immunoglobulin Light Chain-Binding Bacterial Protein. Characterization of Binding and Physicochemical Properties. J. Biol. Chem. 1989, 264, 19740–19746. [PubMed] [Google Scholar]
- Wikstroem M.; Drakenberg T.; Forsen S.; Sjoebring U.; Bjoerck L. Three-Dimensional Solution Structure of an Immunoglobulin Light Chain-Binding Domain of Protein L. Comparison with the IgG-Binding Domains of Protein G. Biochemistry 1994, 33, 14011–14017. 10.1021/bi00251a008. [DOI] [PubMed] [Google Scholar]
- Graille M.; Stura E. A.; Housden N. G.; Beckingham J. A.; Bottomley S. P.; Beale D.; Taussig M. J.; Sutton B. J.; Gore M. G.; Charbonnier J.-B. Complex between Peptostreptococcus Magnus Protein L and a Human Antibody Reveals Structural Convergence in the Interaction Modes of Fab Binding Proteins. Structure 2001, 9, 679–687. 10.1016/s0969-2126(01)00630-x. [DOI] [PubMed] [Google Scholar]
- Muzard J.; Adi-Bessalem S.; Juste M.; Laraba-Djebari F.; Aubrey N.; Billiald P. Grafting of Protein L-Binding Activity onto Recombinant Antibody Fragments. Anal. Biochem. 2009, 388, 331–338. 10.1016/j.ab.2009.02.035. [DOI] [PubMed] [Google Scholar]
- Boes A.; Spiegel H.; Delbrück H.; Fischer R.; Schillberg S.; Sack M. Affinity Purification of a Framework 1 Engineered Mouse/Human Chimeric IgA2 Antibody From Tobacco. Biotechnol. Bioeng. 2011, 108, 2804–2814. 10.1002/bit.23262. [DOI] [PubMed] [Google Scholar]
- Choe W.; Durgannavar T.; Chung S. Fc-Binding Ligands of Immunoglobulin G: An Overview of High Affinity Proteins and Peptides. Materials 2016, 9, 994. 10.3390/ma9120994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shukla A. A.; Gupta P.; Han X. Protein Aggregation Kinetics during Protein A Chromatography. J. Chromatogr. A 2007, 1171, 22–28. 10.1016/j.chroma.2007.09.040. [DOI] [PubMed] [Google Scholar]
- Calmettes P.; Cser L.; Rajnavölgyi É. Temperature and pH Dependence of Immunoglobulin G Conformation. Arch. Biochem. Biophys. 1991, 291, 277–283. 10.1016/0003-9861(91)90135-6. [DOI] [PubMed] [Google Scholar]
- Graille M.; Harrison S.; Crump M. P.; Findlow S. C.; Housden N. G.; Muller B. H.; Battail-Poirot N.; Sibaï G.; Sutton B. J.; Taussig M. J.; et al. Evidence for Plasticity and Structural Mimicry at the Immunoglobulin Light Chain-Protein L Interface. J. Biol. Chem. 2002, 277, 47500–47506. 10.1074/jbc.m206105200. [DOI] [PubMed] [Google Scholar]
- Beckingham J. A.; Housden N. G.; Muir N. M.; Bottomley S. P.; Gore M. G. Studies on a Single Immunoglobulin-Binding Domain of Protein L from Peptostreptococcus Magnus: The Role of Tyrosine-53 in the Reaction with Human IgG. Biochem. J. 2001, 353, 395–401. 10.1042/bj3530395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckingham J. A.; Bottomley S. P.; Hinton R.; Sutton B. J.; Gore M. G. Interactions between a Single Immunoglobulin-Binding Domain of Protein L from Peptostreptococcus Magnus and a Human κ Light Chain. Biochem. J. 1999, 340, 193–199. 10.1042/bj3400193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roque A. C. A.; Taipa M. Â.; Lowe C. R. Synthesis and Screening of a Rationally Designed Combinatorial Library of Affinity Ligands Mimicking Protein L from Peptostreptococcus Magnus. J. Mol. Recognit. 2005, 18, 213–224. 10.1002/jmr.733. [DOI] [PubMed] [Google Scholar]
- Svensson H. G.; Wedemeyer W. J.; Ekstrom J. L.; Callender D. R.; Kortemme T.; Kim D. E.; Sjöbring U.; Baker D. Contributions of Amino Acid Side Chains to the Kinetics and Thermodynamics of the Bivalent Binding of Protein L to Ig κ Light Chain. Biochemistry 2004, 43, 2445–2457. 10.1021/bi034873s. [DOI] [PubMed] [Google Scholar]
- Marichal-Gallardo P. A.; Álvarez M. M. State-of-the-Art in Downstream Processing of Monoclonal Antibodies: Process Trends in Design and Validation. Biotechnol. Prog. 2012, 28, 899–916. 10.1002/btpr.1567. [DOI] [PubMed] [Google Scholar]
- Bottomley S. P.; Beckingham J. A.; Murphy J. P.; Atkinson M.; Atkinson T.; Hinton R. J.; Gore M. G. Cloning, Expression and Purification of Ppl-1, a Kappa-Chain Binding Protein, Based upon Protein L from Peptostreptococcus Magnus. Bioseparation 1995, 5, 359–367. [PubMed] [Google Scholar]
- Yang Z.; Lasker K.; Schneidman-Duhovny D.; Webb B.; Huang C. C.; Pettersen E. F.; Goddard T. D.; Meng E. C.; Sali A.; Ferrin T. E. UCSF Chimera, MODELLER, and IMP: An Integrated Modeling System. J. Struct. Biol. 2012, 179, 269–278. 10.1016/j.jsb.2011.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Granata V.; Housden N. G.; Harrison S.; Jolivet-Reynaud C.; Gore M. G.; Stura E. A. Comparison of the Crystallization and Crystal Packing of Two Fab Single-Site Mutant Protein L Complexes. Acta Crystallogr., Sect. D: Biol. Crystallogr. 2005, 61, 750–754. 10.1107/s0907444905007110. [DOI] [PubMed] [Google Scholar]
- Massova I.; Kollman P. A. Combined Molecular Mechanical and Continuum Solvent Approach (MM-PBSA/GBSA) to Predict Ligand Binding. Perspect. Drug Discovery Des. 2000, 18, 113–135. 10.1023/a:1008763014207. [DOI] [Google Scholar]
- Souaille M.; Roux B. Extension to the Weighted Histogram Analysis Method: Combining Umbrella Sampling with Free Energy Calculations. Comput. Phys. Commun. 2001, 135, 40–57. 10.1016/s0010-4655(00)00215-0. [DOI] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle Mesh Ewald: An N·Log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. Canonical Sampling through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Lingenheil M.; Denschlag R.; Reichold R.; Tavan P. The “Hot-Solvent/Cold-Solute” Problem Revisited. J. Chem. Theory Comput. 2008, 4, 1293–1306. 10.1021/ct8000365. [DOI] [PubMed] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
- Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18, 1463–1472. . [DOI] [Google Scholar]
- Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- Duan Y.; Wu C.; Chowdhury S.; Lee M. C.; Xiong G.; Zhang W.; Yang R.; Cieplak P.; Luo R.; Lee T.; et al. A Point-Charge Force Field for Molecular Mechanics Simulations of Proteins Based on Condensed-Phase Quantum Mechanical Calculations. J. Comput. Chem. 2003, 24, 1999–2012. 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926. 10.1063/1.445869. [DOI] [Google Scholar]
- Sitkoff D.; Sharp K. A.; Honig B. Accurate Calculation of Hydration Free Energies Using Macroscopic Solvent Models. J. Phys. Chem. 1994, 98, 1978–1988. 10.1021/j100058a043. [DOI] [Google Scholar]
- Baker N. A.; Sept D.; Joseph S.; Holst M. J.; McCammon J. A. Electrostatics of Nanosystems: Application to Microtubules and the Ribosome. Proc. Natl. Acad. Sci. U.S.A. 2001, 98, 10037–10041. 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dolinsky T. J.; Nielsen J. E.; McCammon J. A.; Baker N. A. PDB2PQR: An Automated Pipeline for the Setup of Poisson-Boltzmann Electrostatics Calculations. Nucleic Acids Res. 2004, 32, W665–W667. 10.1093/nar/gkh381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou T.; Wang J.; Li Y.; Wang W. Assessing the Performance of the MM/PBSA and MM/GBSA Methods. 1. The Accuracy of Binding Free Energy Calculations Based on Molecular Dynamics Simulations. J. Chem. Inf. Model. 2011, 51, 69–82. 10.1021/ci100275a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salvalaglio M.; Muscionico I.; Cavallotti C. Determination of Energies and Sites of Binding of PFOA and PFOS to Human Serum Albumin. J. Phys. Chem. B 2010, 114, 14860–14874. 10.1021/jp106584b. [DOI] [PubMed] [Google Scholar]
- Watanabe H.; Matsumaru H.; Ooishi A.; Feng Y.; Odahara T.; Suto K.; Honda S. Optimizing pH Response of Affinity between Protein G and IgG Fc: How Electrostatic Modulations Affect Protein-Protein Interactions. J. Biol. Chem. 2009, 284, 12373–12383. 10.1074/jbc.m809236200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe H.; Matsumaru H.; Ooishi A.; Honda S. Structure-Based Histidine Substitution for Optimizing pH-Sensitive Staphylococcus Protein A. J. Chromatogr. B: Anal. Technol. Biomed. Life Sci. 2013, 929, 155–160. 10.1016/j.jchromb.2013.04.029. [DOI] [PubMed] [Google Scholar]
- Pettersen E. F.; Goddard T. D.; Huang C. C.; Couch G. S.; Greenblatt D. M.; Meng E. C.; Ferrin T. E. UCSF Chimera? A Visualization System for Exploratory Research and Analysis. J. Comput. Chem. 2004, 25, 1605–1612. 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]