Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2017 Nov 16;2(11):8027–8032. doi: 10.1021/acsomega.7b01271

Propagating Precipitation Waves in Disordered Media

Takahiko Ban †,*, Masaru Kaji ‡,§, Yuichiro Nagatsu ∥, Hideaki Tokuyama ∥
PMCID: PMC6645417  PMID: 31457353

Abstract

graphic file with name ao-2017-01271c_0005.jpg

The study presented in this paper investigates form changes of propagating waves generated through precipitation reactions in a gel matrix that possesses an inhomogeneous microstructure. The waves demonstrate form changes from a single ring-like pattern to multiple target-like waves. Subsequently, the waves take up a spiral form and ultimately manifest themselves in the form of a turbulence pattern that intensifies with increasing fluctuations within the gel structure. An investigation into the dynamics of the precipitation waves reveals the existence of an anomalous diffusion. The effective diffusion coefficients are found to increase linearly with the quenching temperature. Further, it is revealed through the analysis of the anomalous diffusion dynamics that precipitation patterns could be adequately controlled by adjusting the permeability fluctuations within the gel structure. The findings of this study lead to a greater understanding of the spontaneous creation of precipitation patterns by a system driven by disorder.

Introduction

Particle transport in porous media or disordered systems does not follow the classical laws that describe motion in ordered media. Transport of particles in porous media, thus, exhibits many anomalous physical properties. Precipitation reactions that occur in a gel matrix may result in the creation of a range of patterns for particle transport. These include static patterns with spatial regularities, such as the Liesegang pattern1−4 and tree-like patterns,5,6 and dynamic patterns that involve propagating waves, such as those generated by the Belousov–Zhabotinsky (BZ) reaction.7,8 The creation of these patterns is an important phenomenon that can be exploited for implementation in diverse applications that include determination of the onset of patterning in reaction–diffusion systems,3,9−11 material synthesis through the use of the self-organization approach,12−14 diagnosis of Japanese encephalitis, microscopic examination of mucocutaneous lesions, calcification of epithelial odontogenic tumors, and fine-needle aspiration of breast cysts.15−18

In contrast to the familiar BZ reactions that result in the formation of reaction–diffusion waves, precipitation reactions that result in pattern formation do not exhibit the apparent autocatalytic reactions. The primary cause of the formation of various patterns, therefore, remains unknown. It was previously believed that the gel matrix merely acts to prevent the convection of current from disturbing the formation of the spatiotemporal patterns. However, studies performed over the last decade have provided a deeper insight into the role of the gel matrix. For example, modifying the gel concentration or adding other gels to the configuration and changing the precipitation reaction temperature leads to thinning of the Liesegang bands4 and changes the precipitation pattern from the Liesegang-type to a tree-like one.5,6 It has been proposed that variations in the diffusion coefficient, supersaturation, and pore size of the gel are probable causes of the above pattern transition phenomenon. However, changes in the gel concentration and type as well as precipitation reaction temperature lead to changes in multiple physicochemical properties of the gel matrix. These undesirable changes, which occur simultaneously, represent a significant obstacle in elucidating the exact properties of the gel that play a crucial role in pattern formation. This prevents us from fully exploiting the benefits of this phenomenon for use in technical applications. As such, the study proposed in this paper evaluates the effect of only a specific property—gel microstructure—on the formation of precipitation patterns in the absence of changes in other properties of the gel matrix.

Results and Discussion

The method based on quenching of an agar solution was used in this study to prepare gels. The magnitude of compositional fluctuations in the structure was altered by controlling the quenching temperature, Tq, while maintaining a constant agar concentration. Agar was specifically used as the gel matrix because agarose is a major component of agar and its solution undergoes phase separation at temperatures below 45 °C.19 The correlation length of compositional fluctuations in the agarose gel increases from 0.5 to 1.5 μm corresponding to an increase in Tq.19 The diffusion coefficient of the outer electrolyte in the gel, shear modulus, and compressive strength of the gel were monitored as functions of Tq (as depicted in Figures S1 and S2). The resulting gel structure exhibited an increase of 20.3% in the diffusion coefficient and respective decrements of 29.6 and 32.8% in the shear modulus and compressive strength corresponding to an increase in Tq from 10 to 40 °C. Although the macroscopic properties demonstrated an increase by only 20–30% corresponding to the above increase in Tq, the correlation length of compositional fluctuations was found to have increased by a factor of 3. The quenching method allows for significant changes caused exclusively to the gel microstructure, while the macroscopic properties remain largely unaffected.

The precipitation system used in this study consisted of AlCl3/NaOH. The precipitation and complex formations that occur can be explained by the following reactions:

graphic file with name ao-2017-01271c_m001.jpg
graphic file with name ao-2017-01271c_m002.jpg
graphic file with name ao-2017-01271c_m003.jpg

When AlCl3 and NaOH are used as inner and outer electrolytes, respectively, a single traveling precipitation band appears when the gel is viewed from the side. The band is seen to propagate downward in accordance with the diffusion law.20 However, when the gel is viewed from a point directly above the setup, precipitation waves in the form of a single ring-like wave, counter-rotating spiral wave, and turbulence wave are observed. These waves are found to travel at a rate much higher than that suggested by the diffusion law. The measured time scale of the traveling precipitation waves (10–1000 s) is much smaller than that of the single traveling precipitation band (1–100 h). While patterns of the traveling precipitation waves are known to depend upon the AlCl3 concentration, the effect of the gel matrix remains unknown. We investigated the effect of changes in Tq on the patterns of the traveling precipitation waves. In these investigations, the precipitation temperature (T = 25 °C) and the gel and outer electrolyte concentrations (Cgel = 4 w/w % and COH = 2.5 M) were maintained constant.

Typical patterns corresponding to the precipitation reaction are shown in Figure 1, which corresponds to the case wherein AlCl3 is homogeneously distributed at various concentrations (CAl) in the agar solution. During the initial phase of the precipitation reaction, a light region forms over the entire image, corresponding to a precipitation band. Subsequently, the thinning region of the precipitation band appears in the form of a dark region that covers the light region. The thinning phenomenon transforms the precipitation band into a diagonal precipitation feature owing to redissolution of the precipitate.8 The dark region creates various patterns. Corresponding to AlCl3 concentrations below 0.23 M, no pattern is observed. With the increase in CAl, the precipitation patterns are seen to change from an initial single ring-like wave to a target-type waveform. Subsequently, the waves take up a spiral form, which later evolves into a collapsing pattern. Finally, the precipitation waves manifest themselves in the form of a turbulence pattern (see Movies S1–S5). The complexity of the precipitation patterns increases with the increase in CAl.

Figure 1.

Figure 1

Open in a new tab

Typical precipitation waves in 4 w/w % agar gel at Tq = 25 °C. (a) Single ring-like wave at CAl = 0.24 M, (b) target-like waves at CAl = 0.28 M, (c) spiral-like waves at CAl = 0.30 M, (d) collapsing pattern at CAl = 0.32 M, and (e) turbulence pattern at CAl = 0.40 M. T = 25 °C, Cgel = 4 w/w %, and COH = 2.5 M. Scale bars are 2 mm.

The formation mechanism of target-like waves observed during precipitation reactions is different from that of similar waves observed during BZ reactions.21−23Figure S3 depicts the formation process of target-like waves and their subsequent transition into the spiral form (see Movie S3). The target-like waves observed during precipitation reactions originate owing to collisions between two counter-rotating arms of precipitation waves (see the Supporting Information). The experimental results indicate that in contrast to BZ reaction mechanisms, the gel matrix in a precipitation system does not behave like an oscillatory medium. The spiral-like waves are generated from collisions that occur between asymmetric curled arms (see Movie S4 and the Supporting Information).

With CAl > 0.3 M, a collapsing pattern appears. At this point, the traveling spiral or target-like waves break spontaneously, and many defects are generated. This process continues until the entire system is filled with defects and becomes darker. With further increase in CAl, a turbulence pattern is formed. The turbulence pattern develops following an inverse sequence when compared to the collapsing pattern. This implies that during the development of the turbulence pattern, the entire system is first filled with a dark region, and subsequently, a light region, which continues to increase in size, is generated randomly. Volford et al. demonstrated that the turbulence pattern increases in size in a self-similar manner, and its characteristic length scale increases in proportion to the square root of the elapsed time (t1/2).24

The precipitation pattern, as a function of Tq and CAl, was evaluated five times for each measurement. Table 1 lists the phase diagram of the precipitation pattern in the Tq–CAl space. In the case where two or more patterns coexist in the same vessel, the more dominant of the two was defined as the typical pattern. The dominant pattern existing at 60 min from the start of the precipitation reaction for the five measurements is included in Table 1. Interestingly, the patterns demonstrate a change from simple to complex forms with an increase in Tq, although CAl is maintained constant. For example, at Tq = 10 °C and CAl = 0.28 M, a single expanding ring-like wave is observed. Upon increasing Tq, the target-like waveform becomes dominant, and upon further increasing Tq, the spiral wave and collapsing patterns are observed. We observed that with the increase in Tq, the symmetry of the precipitation pattern is broken, and the pattern becomes complex at different concentrations. It must be noted here that the precipitation reaction temperature has no bearing on the pattern formation at constant quenching temperature (see Table S1).

Table 1. Phase Diagram of Precipitation Pattern Formed at 60 min from the Start of the Precipitation Reaction in the Tq–CAl Spacea.

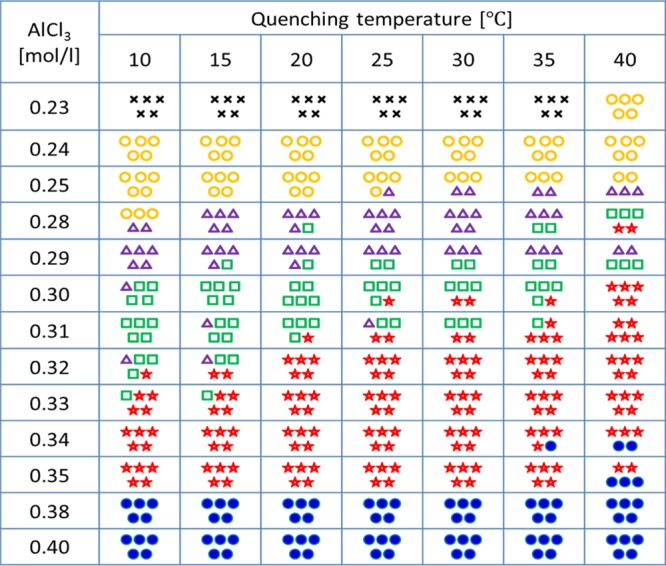
graphic file with name ao-2017-01271c_0004.jpg

Open in a new tab
a

×: no pattern, yellow circle: single ring-like wave, violet triangle: target-like waves, green square: spiral waves, red star: collapsing pattern, and blue circle: turbulence pattern.

The tendency of the complexity of precipitation patterns to increase with the increase in CAl is consistent with the study reported by Ayass et al.25 They have demonstrated that the wavelength of precipitation waves decreases monotonically with the increase in CAl regardless of the dominant precipitation patterns. The effect of CAl on the pattern formation is discussed later in this paper, and an in-depth quantitative analysis of the effect of quenching temperature on pattern formation is discussed in the following passages.

The dynamics of the single ring-like and target-like waves were evaluated corresponding to an increase in Tq. The dynamics of the single ring-like wave follow the laws of the diffusion process, that is, 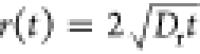Inline graphic, where r(t) and Dr are, respectively, the radius and effective diffusion coefficient of the single ring-like wave (see Figure S4). The effective diffusion coefficient is found to increase by a factor of 3 corresponding to an increase in Tq when the precipitation reaction temperature and the gel and outer electrolyte concentrations are maintained constant (Figure 2a). On the other hand, as Tq increases, the dynamics of the target-like waves deviate from the laws of the diffusion process, and an anomalous diffusion is found to occur according to the relationship, r ∝ tα (see Figure S5). The exponent α in this relation increases from 0.5 to approximately 0.75 with an increase in Tq. In addition, we investigated the dispersion relationship between the angular frequency, ω, and the wavenumber, k, for target-like waves with CAl = 0.28 M. Because a simple polynomial form (ω = a0 + a1k + a2k2 + a3k3...) cannot be used, we propose the following empirical expression to evaluate the above dispersion relationship (see the Supporting Information).

graphic file with name ao-2017-01271c_m005.jpg 1

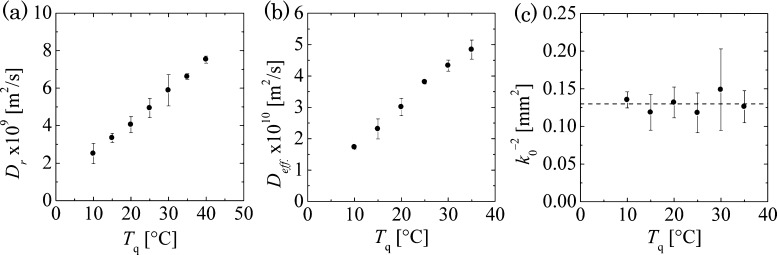
Here, Deff and k0 refer to fitting parameters having dimensions of the diffusion coefficient and the wavenumber, respectively. Corresponding to each value of Tq, a linear relationship was obtained allowing for the calculation of Deff and k0 from eq 1 (see Figure S6). Figure 2b,c demonstrates the relationship between the two fitting parameters and Tq. Deff increases linearly by a factor of 3.3 with an increase in Tq from 10 to 35 °C, whereas k0, by-and-large, remains constant (k0–2 = 0.13 ± 0.03 mm2).

Figure 2.

Figure 2

Open in a new tab

(a) Effect of Tq on the effective diffusion coefficient of the single ring-like wave calculated using 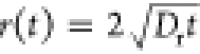Inline graphic at CAl = 0.25 M; (b,c) effect of Tq on the effective diffusion coefficient and wavenumber of the target-like waves calculated using eq 1 at CAl = 0.28 M.

There exist many different reasons, which could lead to anomalous diffusion in porous media.26,27 The anomalous diffusion observed in the gel may be related to its geometrical factors. Matheron and de Marsily28 proposed a model of a two-dimensional stratified porous medium, wherein the transport of particles in the vertical direction follows the diffusion law; the transverse velocity V(z), however, is constant at the layer and is a function of the elevation z of the layer, thereby realizing a non-Fickian type of transport. Permeability fluctuations cause the local flow velocity to exhibit a random distribution in each layer. The velocity distribution, considered to be white noise, can be described in terms of the relationship—⟨V(z)⟩ = 0,⟨V(z)V(z′)⟩ = σVδ(z – z′)—where σV represents the variance of the velocity distribution related to the permeability fluctuations and δ is the Dirac delta function. The average-squared displacement of the particles along the horizontal direction can be expressed as follows:26,28

graphic file with name ao-2017-01271c_m006.jpg 2

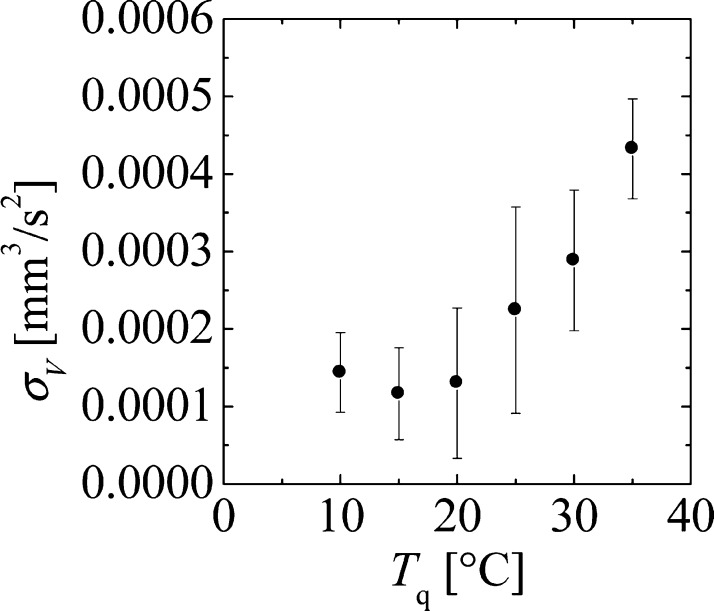
Here, D⊥ represents the vertical diffusion coefficient. The precipitation system investigated in this study resembles the model proposed by Matheron and de Marsily because transport of the precipitate in the vertical direction occurs through a diffusion process;20 on the other hand, the precipitation wave in the horizontal direction propagates in the form of a chemical wave.7,8 Thus, ⟨X2⟩ in the above model corresponds to r(t)2 in the precipitation system. The value for σV can be determined from eq 2 using the value of D⊥ determined in a previous study.20Figure 3 shows the relationship between σV and Tq, in which the value of σV increases by 3.7 times corresponding to an increase in Tq from 10 to 35 °C.

Figure 3.

Figure 3

Open in a new tab

Relationship between the variance of velocity distribution σV and Tq at CAl = 0.28 M. σV was calculated from eq 2 . For Tq = 10 °C, even though the value of α was approximately 0.5, we calculated σV using eq 1.

Localized impacts on the surface of excitable media or defects formed in the media can initiate chemical waves.29,30 It was confirmed during the experiments that scratching of the gel matrix with tweezers during the precipitation reaction and insertion of a polytetrafluoroethylene plate prior to the precipitation reaction demonstrated no effect on the pattern formation of precipitation waves.

As previously described, the increase in Tq increases the complexity of the precipitation patterns. Because macroscopic properties increase by only 20–30% with an increase in Tq, the corresponding increase in the effective diffusion coefficients of the single ring-like and target-like waves reflects a change in the gel microstructure. The increase in Tq leads to an increase in the correlation length of compositional fluctuations,19 which in turn alters the permeability of the gel and leads to an improvement in the mobility of precipitation reaction waves. The correlation length of compositional fluctuations in the agarose gel was found to have increased from 0.5 to 1.5 μm with an increase in Tq.19 The particle size of the precipitate was measured using an electron microscope (see Figure S7). The imaging results revealed that the particles grew up to 1–5 μm, and their size was comparable to the correlation length of compositional fluctuations in the agarose gel. The effective diffusion coefficients of the single ring-like and target-like patterns were found to have increased by a factor of 3. At the same time, the increase in Tq was accompanied by a coarsening of the gel matrix and an increase in the correlation length of compositional fluctuations. The rate of increase of σV was found to coincide with that of the effective diffusion coefficients of the single ring-like and target-like patterns.

From the above observations, it could be inferred that a change in the microstructure of the gel results in changes in the pattern dynamics of precipitation waves. For low values of Tq, the precipitation waves grow symmetrically because the variance in permeability fluctuations is small. This leads to the formation of highly symmetric precipitation patterns, such as the observed single ring-like and target-like waves. With increase in Tq, precipitation waves pass through an inhomogeneous gel microstructure, and each arm of these precipitation waves undergoes a different degree of hysteresis in terms of permeability fluctuations. This causes an asymmetric development of each arm of the precipitation waves. As a result, the symmetric precipitation patterns are broken spontaneously, thereby leading to asymmetrical patterns. Correspondingly, the single ring-like and target-like waves transform to the spiral-like waveform. On the basis of reaction–diffusion equations, Tinsley et al.31 demonstrated that the occurrence of spiral waves is based on the assumption of the existence of the second precipitate that exhibits directional growth at the wave front. It is also assumed that further formation of spiral waves ceases when the concentration of the second precipitate exceeds a certain threshold value. The study claimed that the directional growth plays an essential role in the dynamics of propagating waves. Changes in the microstructure of the gel may also cause suppression of the formation of the second precipitate. However, the phenomenon of anomalous diffusion requires the existence of disordered media. Therefore, theoretical models of propagating precipitation waves must account for the effect of the gel matrix.

An increase in CAl results in an increase in the value of the exponent α, as shown in Figure S5, and the complexity of the precipitation patterns. For CAl = 0.25 M, the single ring-like wave follows the diffusion law, whereas for CAl = 0.28 M the target-like waves exhibit anomalous diffusion. Ayass et al. reported that for the HgCl2/KI system, the exponent α was found to have increased with an increase in the concentration of Hg2+ ions.32,33 The results indicate that an increase in the concentration of the internal electrolyte serves to alter the gel microstructure, thereby leading to increased compositional fluctuations. This increase in compositional fluctuations may manifest itself as noise. As shown in Figure 1, the number density of precipitation patterns increases with an increase in CAl. This increase in number density corresponds to an increase in the number of nucleation. When the noise becomes large in excitable media, breakup and spontaneous nucleation of spirals are found to occur; simultaneously, a pattern curvature is also found to have increased.34 The higher the pattern curvature, the shorter is the wavelength. This tendency is consistent with the findings reported by Ayass et al.25 The increase in noise caused by changes in the gel microstructure may result in more complex precipitation patterns, such as collapsing and turbulence patterns.

Conclusions

The effects of compositional inhomogeneity of the gel matrix on morphological changes in the precipitation wave pattern have been experimentally demonstrated in this study by using a gel prepared by the quenching method. Because even a gel quenched to 25 °C exhibits phase separation, the inhomogeneous gel used here is not specific. Many researchers in the past may have subconsciously carried out experiments concerning precipitation waves using inhomogeneous gel matrices. This could perhaps be attributed to the fact that heated gel solutions require to be allowed to set and return to room temperature for gelation. In this study, we have made an effective use of an inhomogeneous gel to elucidate the quantitative relationship between its microstructure and the dynamics of pattern formation of precipitation waves based on an analysis of anomalous diffusion dynamics. It has been inferred that an increase in permeability fluctuations of the gel induces superdiffusion of precipitation waves, thereby increasing the complexity of precipitation patterns. The inhomogeneous gel reported in this study could be prepared with ease and is expected to be useful for studying the pattern formation of precipitation waves induced by other electrolytes as well as that of chemical waves in gel media.35−37 Adjusting permeability fluctuations of the gel may enable users to exercise control over precipitation patterns.

Experimental Section

Preparation Method of Agar Gel

Agar (Wako, guaranteed grade) was added to pure water at 4 w/w % on a hot plate maintained at 80 °C under gentle stirring to prevent bubble generation. The solution was removed from the hot plate, and a predetermined amount of AlCl3·6H2O (Wako, guaranteed grade) was added to the solution and completely dissolved by stirring for 5 min. This mixture (20 mL) was transferred to a Petri dish, covered with a lid, sealed, and left in a thermostatic bath at different quenching temperatures (10–40 °C) for 24 h. After gelation, the Petri dish was removed from the bath. A 2.5 M NaOH solution (20 mL) was poured into the formed gel, and the reaction was observed at room temperature (25 °C). The pattern formation of the propagating precipitation band was recorded by a digital camera (PENTAX, Optio WG-2) at 1 min intervals for 1.5 h or by a digital video camera (Panasonic, HDC-TM30) with a main light source positioned above the dish. A light region in images corresponds to a precipitation band because this illumination configuration is opposed to that of the Tinsley’s experiment.8 The recorded movies were analyzed by an image processing software (ImageJ).

Acknowledgments

This study was financially supported by the Hosokawa Powder Technology Foundation.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.7b01271.

  • Characterization of the agar gel, mechanical properties of the agar gel, pattern formation of target- and spiral-like waves, phase diagram of the precipitation pattern in the precipitation reaction temperature and Al concentration space, dynamics of single ring-like wave, dynamics of target-like waves, dispersion relationship of target-like waves, and scanning electron microscopy observation (PDF)

  • Single ring-like wave of the precipitation reaction for CAl = 0.24 M and Tq = 25 °C (MPG)

  • Target-like waves of the precipitation reaction for CAl = 0.28 M and Tq = 25 °C (MPG)

  • Spiral-like waves of the precipitation reaction for CAl = 0.30 M and Tq = 25 °C (MPG)

  • Collapsing pattern of the precipitation reaction for CAl = 0.32 M and Tq = 25 °C (MPG)

  • Turbulence pattern of the precipitation reaction for CAl = 0.40 M and Tq = 25 °C (MPG)

  • Two transition processes of the precipitation reaction for CAl = 0.29 M and Tq = 25 °C (MPG)

The authors declare no competing financial interest.

Supplementary Material

ao7b01271_si_001.pdf (1.5MB, pdf)
ao7b01271_si_002.mpg (8.9MB, mpg)
ao7b01271_si_003.mpg (11.6MB, mpg)
ao7b01271_si_004.mpg (5.2MB, mpg)
ao7b01271_si_005.mpg (3.3MB, mpg)
ao7b01271_si_006.mpg (7.7MB, mpg)
ao7b01271_si_007.mpg (5MB, mpg)

References

  1. Liesegang R. E. Uber einige Eigenschaften von Gallerten. Naturwiss. Wochenschr. 1896, 11, 353–362. [Google Scholar]
  2. Matalon R.; Packter A. The Liesegang Phenomenon. I. Sol Protection and Diffusion. J. Colloid Sci. 1955, 10, 46–62. 10.1016/0095-8522(55)90076-3. [DOI] [Google Scholar]
  3. Antal T.; Droz M.; Magnin J.; Rácz Z. Formation of Liesegang Patterns: A Spinodal Decomposition Scenario. Phys. Rev. Lett. 1999, 83, 2880–2883. 10.1103/physrevlett.83.2880. [DOI] [Google Scholar]
  4. Lagzi I. Controlling and Engineering Precipitation Patterns. Langmuir 2012, 28, 3350–3354. 10.1021/la2049025. [DOI] [PubMed] [Google Scholar]
  5. Toramaru A.; Harada T.; Okamura T. Experimental Pattern Transitions in a Liesegang system. Physica D: Nonlinear Phenomena 2003, 183, 133–140. 10.1016/s0167-2789(03)00139-8. [DOI] [Google Scholar]
  6. Lagzi I.; Ueyama D. Pattern transition between periodic Liesegang pattern and crystal growth regime in reaction–diffusion systems. Chem. Phys. Lett. 2009, 468, 188–192. 10.1016/j.cplett.2008.12.020. [DOI] [Google Scholar]
  7. Volford A.; Izsák F.; Ripszám M.; Lagzi I. Pattern Formation and Self-Organization in a Simple Precipitation System. Langmuir 2007, 23, 961–964. 10.1021/la0623432. [DOI] [PubMed] [Google Scholar]
  8. Tinsley M. R.; Collison D.; Showalter K. Propagating Precipitation Waves: Experiments and Modeling. J. Phys. Chem. A 2013, 117, 12719–12725. 10.1021/jp4095479. [DOI] [PubMed] [Google Scholar]
  9. Lee G. T. Patterns Produced by Precipitation at a Moving Reaction Front. Phys. Rev. Lett. 1986, 57, 275–278. 10.1103/physrevlett.57.275. [DOI] [PubMed] [Google Scholar]
  10. Lebedeva M. I.; Vlachos D. G.; Tsapatsis M. Phys. Rev. Lett. 2004, 92, 088301. 10.1103/physrevlett.92.088301. [DOI] [PubMed] [Google Scholar]
  11. Ueyama D.; Mimura M. RIMS Kokyuroku 2006, 1522, 136–143. [Google Scholar]
  12. Giraldo O.; Brock S. L.; Marquez M.; Suib S. L.; Hillhouse H.; Tsapatsis M. Spontaneous Formation of Inorganic Helices. Nature 2000, 405, 38. 10.1038/35011139. [DOI] [PubMed] [Google Scholar]
  13. Yamanaka J.; Murai M.; Iwayama Y.; Yonese M.; Ito K.; Sawada T. One-Directional Crystal Growth in Charged Colloidal Silica Dispersions Driven by Diffusion of Base. J. Am. Chem. Soc. 2004, 126, 7156–7157. 10.1021/ja049164w. [DOI] [PubMed] [Google Scholar]
  14. Lagzi I.; Kowalczyk B.; Grzybowski B. A. Liesegang Rings Engineered from Charged Nanoparticles. J. Am. Chem. Soc. 2010, 132, 58–60. 10.1021/ja906890v. [DOI] [PubMed] [Google Scholar]
  15. Akashi A. Sci. Bull. Fac. Agric., Kyushu 1953, 14, 185–187. [Google Scholar]
  16. Gilchrist H. M.; Wick M. R.; Patterson J. W. Liesegang rings in an apocrine hydrocystoma: A Case Report and Review of Literature. J. Cutaneous Pathol. 2010, 37, 1064–1066. 10.1111/j.1600-0560.2010.01559.x. [DOI] [PubMed] [Google Scholar]
  17. Wang Y.-P.; Lee J.-J.; Wang J.-T.; Liu B.-Y.; Yu C.-H.; Kuo R.-C.; Chiang C.-P. Non-calcifying Variant of Calcifying Epithelial Odontogenic Tumor with Langerhans Cells. J. Oral Pathol. Med. 2007, 36, 436–439. 10.1111/j.1600-0714.2007.00533.x. [DOI] [PubMed] [Google Scholar]
  18. Gupta R. K. Liesegang Rings in Fine Needle Aspirate of Breast Cysts With Predominance of Apocrine Cells: A Study of 14 Cases. Diagn. Cytopathol. 2008, 36, 701–704. 10.1002/dc.20902. [DOI] [PubMed] [Google Scholar]
  19. Morita T.; Narita T.; Mukai S.-a.; Yanagisawa M.; Tokita M. Phase Behavior of Agarose Gel. AIP Adv. 2013, 3, 042128. 10.1063/1.4802968. [DOI] [Google Scholar]
  20. Ban T.; Nagatsu Y.; Tokuyama H. Propagation Properties of the Precipitation Band in an AlCl3/NaOH System. Langmuir 2016, 32, 604–610. 10.1021/acs.langmuir.5b03571. [DOI] [PubMed] [Google Scholar]
  21. Tyson J. J.; Fife P. C. Target Patterns in a Realistic Model of the Belousov–Zhabotinskii reaction. J. Chem. Phys. 1980, 73, 2224–2237. 10.1063/1.440418. [DOI] [Google Scholar]
  22. Meron E. Pattern Formation in Excitable Media. Phys. Rep 1992, 218, 1–66. 10.1016/0370-1573(92)90098-k. [DOI] [Google Scholar]
  23. Mikhailov A. S.; Showalter K. Control of Waves, Patterns and Turbulence in Chemical Systems. Phys. Rep. 2006, 425, 79–194. 10.1016/j.physrep.2005.11.003. [DOI] [Google Scholar]
  24. Volford A.; Lagzi I.; Molnár F. Jr.; Rácz Z. Coarsening of Precipitation Patterns in a Moving Reaction-Diffusion Front. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2009, 80, 055102. 10.1103/PhysRevE.80.055102. [DOI] [PubMed] [Google Scholar]
  25. Ayass M. M.; Al-Ghoul M.; Lagzi I. Chemical Waves in Heterogeneous Media. J. Phys. Chem. A 2014, 118, 11678–11682. 10.1021/jp509246s. [DOI] [PubMed] [Google Scholar]
  26. Bouchaud J.-P.; Georges A. Anomalous Diffusion in Disordered Media: Statistical Mechanisms, Models and Physical Applications. Phys. Rep. 1990, 195, 127–293. 10.1016/0370-1573(90)90099-n. [DOI] [Google Scholar]
  27. Koch D. L.; Brady J. B. Dispersion in Fixed Beds. J. Fluid Mech. 1985, 154, 399–427. 10.1017/s0022112085001598. [DOI] [Google Scholar]
  28. Matheron G.; de Marsily G. Is Transport in Porous Media Always Diffusive. Water Resour. Res. 1980, 16, 901–917. 10.1029/wr016i005p00901. [DOI] [Google Scholar]
  29. Bishop K. J. M.; Grzybowski B. A. Localized Chemical Wave Emission and Mode Switching in a Patterned Excitable Medium. Phys. Rev. Lett. 2006, 97, 128702. 10.1103/physrevlett.97.128702. [DOI] [PubMed] [Google Scholar]
  30. Kuksenok O.; Yashin V. V.; Balazs A. C. Global Signaling of Localized Impact in Chemo-responsive Gels. Soft Matter 2009, 5, 1835–1839. 10.1039/b821838b. [DOI] [Google Scholar]
  31. Tinsley M. R.; Collison D.; Showalter K. Three-dimensional Modeling of Propagating Precipitation Waves. Chaos 2015, 25, 064306. 10.1063/1.4921695. [DOI] [PubMed] [Google Scholar]
  32. Ayass M. M.; Lagzi I.; Al-Ghoul M. Three-dimensional superdiffusive chemical waves in a precipitation system. Phys. Chem. Chem. Phys. 2014, 16, 24656–24660. 10.1039/c4cp02587c. [DOI] [PubMed] [Google Scholar]
  33. Ayass M. M.; Lagzi I.; Al-Ghoul M. Targets, Ripples and Spirals in a Precipitation System with Anomalous Dispersion. Phys. Chem. Chem. Phys. 2015, 17, 19806–19814. 10.1039/c5cp01879j. [DOI] [PubMed] [Google Scholar]
  34. Jung P.; Mayer-kress G. Spatiotemporal Stochastic Resonance in Excitable Media. Phys. Rev. Lett. 1995, 74, 2130–2133. 10.1103/physrevlett.74.2130. [DOI] [PubMed] [Google Scholar]
  35. Pertsov A. M.; Aliev R. R.; Krinsky V. I. Three-dimensional Twisted Vortices in an Excitable Chemical Medium. Nature 1990, 345, 419–421. 10.1038/345419a0. [DOI] [Google Scholar]
  36. Amemiya T.; Kádár S.; Kettunen P.; Showalter K. Spiral Wave Formation in Three-Dimensional Excitable Media. Phys. Rev. Lett. 1996, 77, 3244–3247. 10.1103/physrevlett.77.3244. [DOI] [PubMed] [Google Scholar]
  37. Yoshida R. Self-Oscillating Gels Driven by the Belousov–Zhabotinsky Reaction as Novel Smart Materials. Adv. Mater. 2010, 22, 3463–3483. 10.1002/adma.200904075. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao7b01271_si_001.pdf (1.5MB, pdf)
ao7b01271_si_002.mpg (8.9MB, mpg)
ao7b01271_si_003.mpg (11.6MB, mpg)
ao7b01271_si_004.mpg (5.2MB, mpg)
ao7b01271_si_005.mpg (3.3MB, mpg)
ao7b01271_si_006.mpg (7.7MB, mpg)
ao7b01271_si_007.mpg (5MB, mpg)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES