Generalized Born Implicit Solvent Models for Biomolecules

Abstract

It would often be useful in computer simulations to use an implicit description of solvation effects, instead of explicitly representing the individual solvent molecules. Continuum dielectric models often work well in describing the thermodynamic aspects of aqueous solvation, and can be very efficient compared to the explicit treatment of the solvent. Here we review a particular class of “fast” implicit solvent models, generalized Born (GB) models, which are widely used for molecular dynamics simulations of proteins and nucleic acids. These approaches model hydration effects and provide solvent-dependent forces with efficiencies comparable to molecular mechanics calculations on the solute alone; as such, they can be incorporated into molecular dynamics or other conformational searching strategies in a straightforward manner. The foundations of the GB model are reviewed, followed by examples of newer, emerging models and examples of important applications. We discuss their strengths and weaknesses, both for fidelity to the underlying continuum model and for the ability to replace explicit consideration of solvent molecules in macromolecular simulations.

1. INTRODUCTION

Biochemical processes often depend strongly on their environment, often consisting of water plus mobile ions, whose main thermodynamic impact is to stabilize charges or polar groups, and to screen charge–charge interactions. Computer simulations, based on molecular dynamics or Monte Carlo sampling techniques, can represent these and other solvation effects by including explicit water molecules and ions as a part of the simulation setup(88). This approach is generally straightforward, but can be both expensive and inconvenient for studies where the behavior of the biomolecular system (the ”solute”) is of primary interest. The basic idea of implicit solvation is to integrate out explicit solvent degrees of freedom, incorporating their thermodynamic effects into a solvation free energy ΔG_solv. This leads to a simulation setup where the only explicit degrees of freedom are the coordinates of the solute, and where the effects of the solvent environment adjust instantaneously as the solute configuration changes.

By its very nature, implicit solvent models only describe a thermodynamic equilibrium state; sampling of the equilibrium states can be greatly enhanced, but at the expense of disregarding the kinetics. Of greater concern is a seemingly inevitable loss of accuracy and generality of “fast” implicit solvation: the complex ways in which collections of water molecules interact with biomolecules are greatly simplified to achieve computational efficiency, to the detriment of physical realism. Furthermore, explicit solvent simulations can be very general: it is relatively straightforward to explore changes in temperature and pressure, to incorporate heterogeneous environments (such as lipid bilayers), to deal with multivalent ions, or mixtures of monovalent and divalent ions, and so on. In contrast, the implicit solvent models discussed here are mostly specific to a fairly homogeneous water/ion environment in a narrow temperature range. Given these limitations, it may be useful to sum up reasons that implicit solvent models are still of wide interest:

1. There is no need for the lengthy equilibration of water that is typically necessary in explicit water simulations; implicit solvent models correspond to instantaneous solvent dielectric response.

2. Continuum simulations generally give improved sampling, due to the absence of viscosity associated with the explicit water environment; hence, the macromolecule can more quickly explore the available conformational space.

3. There are no artifacts of periodic boundary conditions; the continuum model corresponds to solvation in an infinite volume of solvent.

4. New (and simpler) ways to estimate free energies become feasible; since solvent degrees of freedom are taken into account implicitly, estimating free energies of solvated structures is much more straightforward than with explicit water models (106, 57).

5. Implicit models provide a high degree of algorithm flexibility. For instance, a Monte-Carlo move involving a solvent exposed side-chain would require non-trivial re-arrangement of the nearby water molecules if they were treated explicitly. With an implicit solvent model this complication does not arise. Similar considerations (discussed below) arise when protonation changes are sampled in constant pH simulations.

6. Last but not least: implicit solvation approach is very useful at guiding physical reasoning(125).

In this review, we focus our discussion on the generalized Born implicit solvent model, whose computational speed is roughly comparable to that of molecular mechanics (force field) calculations for biomolecules in the absence of solvent, and which provides both solvation energies and the solvent contribution to forces on the solute atoms. The forces enable molecular dynamics simulations, and the speed make possible the sorts of extensive explorations of conformational space that are needed for computational design, docking calculations and free energy estimates. We build upon earlier reviews,(9, 8, 123, 82, 88) but will try to cover some of the most recent developments while also keeping this account reasonably self-contained.

2. POLAR SOLVATION: THE GENERALIZED BORN MODEL

One of the conceptually simplest models treats the solute as a low-dielectric region, embedded in a continuous medium characterized by a macroscopic dielectric constant ϵ_out, applying macroscopic concepts at a level of atomic detail.(99, 10) There are many reasons to be suspicious of this model, not least of which is the difficulty of assigning a single dielectric constant to the structurally diverse interior of a protein or other macromolecule.(98) Still, this represents a well-specified physical model, whose properties can be systematically explored, and whose defects might be ameliorated through empirical parameterization or adjustment. Early explorations, before the development of digital computers, treated the solute molecule as a sphere; this still provides useful insights, and we begin there.

2.1. Electrostatic interactions in spherical geometries

The Born equation(12) describes the transfer free energy of a single spherical ion (with a single charge at its center) from the gas phase to a (water) environment characterized by a continuum dielectric ϵ_out:

$$\Delta G_{\text{solv}}\left(R_i\right)=-\left(1-\frac{1}{{ϵ}_{\text{out}}}\right)\frac{q^2}{2A}$$ (1)

where A is the ion radius, q is its charge, and Gaussian units are used; a derivation is given below at Eq. 10. The complex effects of water-ion and water-water interactions across multiple water shells surrounding the ion, and including both the entropic and enthalpic contributions, are distilled into the functional dependence of ΔG_solv on the key parameters of the model: in this case the solvent dielectric and the ion charge and size.

The Born formula(12) Eq. 1 is the simplest of several models(54, 55, 112) that share the same underling physics – they are exact solutions of the Poisson equation of continuum electrostatics for a spherical solute. These ”spherical cow” models still serve to illustrate some of the key features of electrostatic interactions in biomolecules. The ”Tanford-Kirkwood” model, for example, was used for many years to rationalize the pH behavior of proteins.(112, 113, 39)

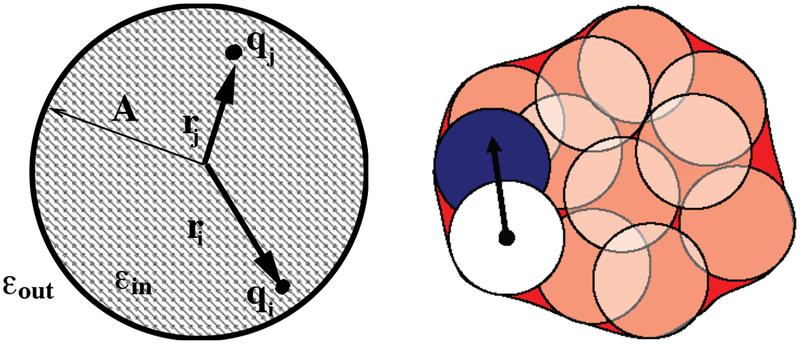
Some simple and interesting limits arise when ϵ_out becomes very large.(56) In particular, one can show that for an arbitrary charge distribution inside a spherical solute, Fig. 1 left, the exact solution of the Poisson equation (in the limit ϵ_out → ∞) gives the solvation free energy of the following simple form(38, 101):

$$\Delta G_{\text{solv}}=-\frac{1}{2}\left(\frac{1}{{ϵ}_{\text{in}}}-\frac{1}{{ϵ}_{\text{out}}}\right)\sum _{i,j}\frac{q_i{q}_j}{\sqrt{r_{ij}^2+R_i{R}_j}}$$ (2)

$$R_i=A-r_i^2/A$$ (3)

Figure 1.

Left: A spherical solute of radius A. Two point charges q_i and q_j are placed at distances r_i and r_j respectively from the sphere center. Right: Representation of a molecule as a set of overlapping spheres. The integral needed in Eq. 12 can be approximately written as a sum over all of the spheres except for the white one.

This result is very similar to the generalized Born idea introduced in the next section; note that the double summation in Eq. 2 includes ”self-energy” terms where i = j, (representing stabilization of charges via polarization of the external medium) as well as cross-terms that represent charge-charge interactions screened by the surrounding high dielectric solvent.

2.2. Treating molecules as collections of atoms

Spherical models are appealing due to their simplicity and clear physical foundation, but have obvious limitations for realistic molecules, which have multiple charge centers and are non-spherical. Attempts to generalize Eq. 1 to the multi-atom case are at least seventy years old(42), and began to be applied in earnest to biomolecular problems about three decades ago.(107, 9) If we imagine a “molecule” consisting of charges q₁ … q_N embedded in spheres of radii, a₁ … a_N, and if the separation r_ij between any two spheres is sufficiently large in comparison to the radii, then the solvation free energy can be given by a sum of individual Born terms, and pairwise Coulombic terms:

$$\Delta G_{\text{solv}}\simeq \sum _i^N-\frac{q_i^2}{2a_i}\left(1-\frac{1}{{ϵ}_{\text{out}}}\right)+\frac{1}{2}\sum _i^N\sum _{j\ne i}^N\frac{q_i{q}_j}{r_{ij}}\left(\frac{1}{{ϵ}_{\text{out}}}-1\right)$$ (4)

where the factor (1/ϵ_out −1) appears in the pairwise terms because the Coulombic interactions are re-scaled by the change of dielectric constant upon going from vacuum to solvent. Of course, in real molecules the atomic spheres are not necessarily far from each other, so one needs to go a step further.

The project of generalized Born theory can be thought of as an effort to find a relatively simple analytical formula, resembling Eq. 4, which for realistic molecular geometries will capture as much as possible, the physics of the Poisson equation. The linearity of the Poisson equation (or the linearized Poisson–Boltzmann equation) assures that ΔG_solv will indeed be quadratic in the source charges, and so it is natural to generalize Eq. 4 to

$$\Delta G_{\text{solv}}\simeq \left(1-\frac{1}{{ϵ}_{\text{out}}}\right)\frac{1}{2}\sum _{ij}\frac{q_i{q}_j}{f_{ij}^{GB}}$$ (5)

where f^GB is some reasonably simple function. Here the self (i = j) f^GB terms can be thought of as “effective Born radii,” whereas for the off-diagonal terms, it becomes an effective interaction distance. Befittingly, the collective name for the resulting models is “the generalized Born” (GB). A particularly successful version of the GB kernel $f_{ij}^{GB}$ in Eq. 5 was proposed in 1990(107):

$$f_{ij}^{GB}\left(r_{ij}\right)={\left[r_{ij}^2+R_i{R}_j\text{exp}\left(-r_{ij}^2/4R_i{R}_j\right)\right]}^{1/2},$$ (6)

Here the R_i are the effective Born radii of the atoms, which generally depend not only on a_i, the ”intrinsic” radius of atom i, but on on the radii and relative positions of all other atoms. Qualitatively, the effective Born radius of an atom corresponds to its degree of shielding from solvent by the surrounding atoms. In what follows, we call the GB model based on equations 5 and 6 the canonical GB model.

While historically the GB model was not conceived as a direct approximation to the Poisson model, and alternative interpretations exist(17), a number of arguments(88) can be made to support this viewpoint, including the very similar structure of the canonical GB and that of Eq. 2 – exact solution of the Poisson problem for a sphere. One can further argue(89) that the $\text{exp}\left(-r_{ij}^2/4R_i{R}_j\right)$ factor in Eq. 6 attempts to account, in some average sense, for the “non-sphericity” of realistic molecules, by attenuating charge-charge interactions along the ”long” dimension of the molecule. The view of the GB as an approximation to the Poisson model has been instrumental in the development of the GB for macromolecular applications, and continues to help reasoning in developing new GB-like theories.

2.3. The Coulomb field approximation

In the classical electrostatics of a linearly polarizable media (49) the work required to assemble a charge distribution can be formulated either in terms of a product of the charge distribution with the electric potential, or in terms of the scalar product of the electric field E and the electric displacement D:

$$G=\frac{1}{2}{\int }_{\Omega }\rho (x)\psi (x)dx=\frac{1}{8\pi }{\int }_{\Omega }E\cdot Ddx$$ (7)

We now introduce the essential approximation used in most early forms of generalized Born theory: that the electric displacement is Coulombic in form, and remains so even as the exterior dielectric is altered from 1 to ϵ_out in the solvation process. In other words, the displacement due to the charge of atom i (which is here presumed to lie on the origin) is,

$$D_i\approx \frac{q_{i}r}{r^3}.$$ (8)

This is called the Coulomb field approximation (CFA). It is exact for a charge at the center of a sphere, but substantial deviations arise in more complex geometries. The work of placing assembling a charge at the origin within a “molecule” whose interior dielectric constant is ϵ_in, surrounded by a medium of dielectric constant ϵ_out and in which no other charges have yet been placed is then,

$$G_i=\frac{1}{8\pi }\int (D/ϵ)\cdot Ddx\approx \frac{1}{8\pi }{\int }_{\text{in}}\frac{q_i}{r^4{ϵ}_{\text{in}}}dx+\frac{1}{8\pi }{\int }_{\text{out}}\frac{q_i}{r^4{ϵ}_{\text{out}}}dx.$$ (9)

The electrostatic component of the solvation free energy is found by taking the difference as the exterior dielectric is changed from 1.0 to ϵ_out,

$$\Delta G_{solv,i}=\frac{1}{8\pi }\left(\frac{1}{{ϵ}_{\text{out}}}-1\right){\int }_{\text{ex}}\frac{q_i}{r_4}dx$$ (10)

where the contribution due to the interior region has canceled in the subtraction. Comparing Eq. 10 to Eqs. 4 or 5, we conclude that the effective Born radius should be,

$$R_i^{-1}=\frac{1}{4\pi }{\int }_{\text{ex}}\frac{q_i}{r_4}dx$$ (11)

It is convenient to re-write this in terms of integration over the interior region, excluding a radius a_i around the origin,

$$R_i^{-1}=a_i^{-1}-\frac{1}{4\pi }{\int }_{\text{in},r>a_i}\frac{1}{r_4}dx.$$ (12)

Note that in the case of a monatomic ion, where the molecular boundary is simply the sphere of radius a_i, this equation becomes R_i = a_i and the Born formula is recovered exactly. However, in general, the CFA overestimates the effective Born radii, this problem is partially alleviated by some of the approximations used to compute them, as discussed below.

With these approximations, the original two-dielectric Poisson equation, which implies the need for a (numerical) solution of a three-dimensional partial differential equation, has been replaced by the much simpler task of estimating the three-dimensional integral over a molecular volume in Eq. 12. In the next section, we survey some of the approaches used to do this, which often involve further approximations.

2.4. Estimating effective Born radii

2.4.1. The notion of ”perfect radii”.

In principle, R_i could be chosen so that if one were to solve the Poisson equation for a charge q_i at the position of atom i, and no other charges, and a dielectric boundary determined by the molecular shape, then the self energy of charge i in its reaction field would be equal to − (q²/2R_i)(1 − 1/ϵ_out). This self energy could be computed by solving the Poisson equation numerically, and the resulting values of R_i have been called “perfect” radii; these are known to give a reasonably good approximation to Poisson theory when used in conjunction with Eqs. 5 and 6 (85). Obviously, this procedure would have no practical advantage over a direct calculations ΔG_solv using numerical a solution of the Poisson equation, but comparisons to ”perfect” radii are useful in testing more approximate (and more rapid) models. In some applications, e.g. coarse-grained DNA models(94, 95), the perfect radii are computed once and then kept constant throughout the simulation.

2.4.2. Volume integration via quadrature.

Perhaps the most straightforward approach to Eq. 12 is to make use of quadrature schemes, often loosely adapted from quantum chemistry calculations. For example, GBSW (“simple switching”) model(44, 7) uses a spherical quadrature model to sample the atomic density surrounding each atom to determine its contribution to the effective Born radius. A switching function is used to blur the sharp boundary between high and low-dielectric regions, which fills in many of the small voids shown as red regions in Fig. 1. (A correction to the Coulomb field approximation, discussed below, is also applied.) The use of quadratures results in a method that is not fully rotationally invariant, but the errors can be small, and a version optimized for GPUs provides performance on par with the non-quadrature models, depending on system size.(7)

The GBMV (“molecular volume”) models work harder to evaluate Eq. 12 over the true molecular volume, generally trading speed for accuracy.(62) The use of an analytical molecular volume (AMV) model,(35) with some heuristics to speed up table lookups, allows Born radii to be obtained that are quite close to the “exact” radii.

The Gaussian generalized Born model (GGB) (37, 36) mimics GBSW in abandoning the model of a sharp division between high- and low-dielectric regions, and estimates the integrals needed to obtain Born radii by adopting a Gaussian shape model. This approach has the advantage of providing analytical derivatives without the need for numerical grids.

2.4.3. Volume integrations over collections of overlapping spheres.

A separate path to Eq. 12 treats molecules as collections of overlapping spheres with sharp boundaries, as illustrated in Fig. 1. If the molecule consisted of a set of non-overlapping spheres of radius a_j at positions, r_ij relative to atom i, then Eq. 12 could be written as a sum of integrals over spherical volumes, which can be computed analytically (96):

$$R_i^{-1}=a_i^{-1}-\sum _j\frac{a_j}{2\left(r_{ij}^2-a_j^2\right)}-\frac{1}{4r_{ij}}\text{log}\frac{r_{ij}-a_j}{r_{ij}+a_j}.$$ (13)

An analytical expression is also available for the case of atom j overlapping with the central atom, i, provided j does not overlap any other atom j′ (96). Although in practice, the atoms j do overlap on another to some extent, these overlaps can be neglected to a first approximation, and empirical corrections can be introduced to compensate for neglect of overlap. This is referred to as the pairwise descreening approximation (40). Hawkins et al. (40, 41) have introduced such a scheme based on re-scaling the van der Waals radii by factors S_j. The expression for the generalized Born radii takes the form,

$$R_i^{-1}=a_i^{-1}-\sum _{j}H\left(r_{ij},S_j{a}_j\right),$$ (14)

where H is a rather complex expression which, apart from rescaling, is essentially Eq. 13 if i and j do not overlap, and having different functional forms in overlapping cases (41). In the AGBNP model of Gallicchio and Levy, (28) the scaling factors S_ij are not independent constants, but are computed on the fly from a Gaussian-based decomposition of the molecular volume into atomic contributions.

A serious problem with representing molecular volume as a set of overlapping atomic spheres is the neglect of interstitial spaces between the atomic spheres in the interior of the molecule, red spaces in Fig.1. In the approximation these crevices are treated as if they belonged to the solvent space, that is filled with high dielectric, which is unphysical for many types of calculations(87); the corresponding effective radii are underestimated. (The use of the CFA leads to a certain cancellation of errors in this case since the CFA tends to overestimate the effective radii.) For biopolymers, this neglect of interstitial space leads to appreciable underestimation of the effective radii, compared to the “perfect” radii introduced above.(85)

Efforts to correct this deficiency while preserving computational efficiency of the pairwise approximation have led to a series of GB flavors. In one of them, GB^OBC (now available in many modeling packages), an empirical correction is introduced(83, 84) that modifies the pairwise integration method to reduce the effect of interstitial high dielectrics. However, by design, GB^OBC approach compensates for missing interstitial volume only on average, in a geometry-independent manner. To further improve the GB accuracy, an additional correction to the pair-wise procedure was introduced(74) that brings in elements of molecular volume, in a pair-wise sense: an additional term is added to Eq. 14 that re-introduces the molecular volume between each pair of atoms missed by the original approximation. The integral over this neck-shaped region can be approximated by a simple analytical function with a negligible additional computational expense relative to GB^OBC. It took a significant re-parametrization effort to make the original “GB-neck” model a success for both proteins(81) and the DNA(80) – all of these models are now available in Amber.

2.5. Beyond the Coulomb field approximation

As mentioned above, the Coulomb field approximation can lead to significant errors in the effective Born radii. In fact, even for a perfectly spherical solute the CFA is exact only for a charge located in the center of the sphere, while for a charge near the boundary it overestimates(9) the effective radius by a factor of 2. Consequently, CFA overestimates effective radii for realistic molecular geometries as well(62). This problem has been well-known for quite some time, and varioius empirical corrections to the CFA have been proposed(62, 61, 44). These typically take the form of a simple linear or a rational combination of correction terms such as

$$\alpha N={\left(\frac{1}{4\pi }(N-3)\underset{ex}{\int }\frac{dV}{{\left|r-r_i\right|}^N}\right)}^{\frac{1}{N-3}}$$ (15)

where N ≥4. Specifically, Lee et al. were the first to propose an alternative to the CFA along these lines, namely an expression involving α₄ and α₅(62), and later an even more accurate expression based on α₄ and α₇ respectively(61). These corrections are utilized in the GBSW and GBMV models discussed above.

2.5.1. Expressions based on exact spherical limits.

The canonical GB model becomes exact for a perfect sphere in the conductor limit ϵ_out →, assuming exact effective Born radii. However, the effective radii computed via the CFA, and via other, more complex integral forms mentioned above, are not exact even for a sphere, leading to hard-to-control inaccuracies for realistic shapes.

An alternative expression to compute the effective, ”R6”, was proposed by Svrcek-Seiler(108) and independently by Grycuk(38):

$$R_i^{-1}={\left(\frac{3}{4\pi }{\int }_{ex}\frac{dV}{{\left|r-r_i\right|}^6}\right)}^{1/3}={\left(a_i^{-3}-\frac{3}{4\pi }{\int }_{r>a_i}^{solute}|r{|}^{-6}dV\right)}^{1/3}$$ (16)

where in the first expression the integral (ex) is taken over the region outside the molecule, and in the second integral, the origin is moved to the center of atom i. The above expression in an integral equivalent of Eq. 3, that is it gives the effective Born radii that are exact for any charge location within a perfect spherical solute in the conductor limit.

The potential advantage of Eq. 16 over the CFA and its extensions for practical computational became clear when it was shown(75) that the corresponding “R6” radii can be very close to the perfect radii for realistic biomolecular shapes, resulting in solvation energies in close agreement with perfect radii. It was also demonstrated(101) that the use of ϵ_out → limit in computing the effective Born radii results in more accurate estimates of ΔG_solv via canonical GB, at least for single globular molecules. Implementations of the R6 GB model in which Eq. 16 is integrated analytically over the van der Waals (VDW) volume of the solute are available(124, 58). Performing the integral analytically over the molecular volume, which has traditionally been the target for GB models intended for use in MD simulations, proved difficult, and a number of approximations had to be made to produce a fully analytical expression(2); pilot implementations in MD produced mixed results. Compared to the CFA, the R6 model is apparently less forgiving to approximations to the molecular volume, and there is no fortuitous cancellation of error (see above) that helps the CFA.

Surface-based R6 formulations have also been developed, in which the effective Born radii are calculated via:

$$R_i^{-3}=\left(-\frac{1}{4\pi }{\oint }_{\partial V}\frac{r-r_{\text{i}}}{{\left|r-r_{\text{i}}\right|}^6}\cdot dS\right)$$ (17)

where ∂V represents the molecular surface of the molecule, dS is the infinitesimal surface element vector, r_i is the position of atom i, and r represents the position of the infinitesimal surface element. [This follows the lead of earlier work to turn volume integrals into surface ones. (32)] A version of the model, GBNSR6(1, 27) (“Numerical Surface R6 GB”), is available in Amber. It has been tested in calculation of small molecule hydration energies(1) and in protein ligand binding(45), where its accuracy is noteworthy(47).

2.6. Alternative forms for charge-charge interactions

The canonical form of the GB kernel, $f_{ij}^{GB}$ in Eq. 6, is not the only one proposed and tested. For example, values of the empirical factor other than 4 in $\text{exp}\left(-r_{ij}^2/4R_i{R}_j\right)$ have been been considered(51, 38, 69, 37, 61), in the range from 1 to 8. That the canonical value of 4 remains the most widely used indicates that it is close to a “general purpose” optimum, and that further accuracy improvements may require a different functional from of the GB equation.

A substantially different form of the GB kernel $f_{ij}^{GB}$ was recently proposed(59), based on a carefully examined connection between the GB and conductor-like polarizable continuum models(117):

$$f_{ij}=r_{ij}+{\left(1+\frac{1.028r_{ij}}{16\sqrt{R_i{R}_j}}\right)}^{-16}$$ (18)

Noticeable improvements over the canonical GB in both accuracy and speed were reported(59), however the testing was so far limited to either the perfect or R6 effective Born radii.

GB-like models also exist that go beyond the canonical GB Green function itself, that is Eq. 5. One such model is ALPB(101, 100):

$$\Delta G_{el}=-\frac{1}{2}\left(\frac{1}{{ϵ}_{in}}-\frac{1}{{ϵ}_{out}}\right)\frac{1}{1+\beta \alpha }\sum _{ij}{q}_i{q}_j\left(\frac{1}{f^{GB}}+\frac{\alpha \beta }{A}\right),$$ (19)

where β= ϵ_in/ϵ_out, α= 0.571412, and A is the electrostatic size of the molecule, which is essentially the overall size of the structure. In practice, the value of A can be estimated analytically(100). Moreover, it was shown that keeping the value of A constant in MD simulation is acceptable(100). In the limit $\frac{{ϵ}_{\text{in}}}{{ϵ}_{\text{out}}}\to 0$ the canonical GB and ALPB coincide, but outside of this limit the latter model shows a closer agreement with the Poisson theory. For the case of aqueous solvation the model provides a small but consistent improvement over the canonical GB.

Going beyond the spherical shape as the basis for derivation of “beyond GB” models led to a model that accounted for the existence of two “modes” in the solution of the Poisson equation for non-spherical shapes: longitudinal and transverse(86). The former more or less corresponds to the canonical GB, while the letter is very different; the over-all Green function interpolates between the two modes based on the values of the local gradients of the effective Born radii. Compared to the canonical GB, the new model resulted in significantly fewer gross errors in pairwise charge-charge interactions, with the numerical Poisson solution taken as reference. However, the testing was so far limited to R6 effective Born radii estimated numerically.

GB-like theories can also explicitly incorporate effects that go even beyond the linear-response Poisson theory. For example, an extension of Born model was proposed(77) that explicitly accounts for charge hydration asymmetry (CHA) – strong dependence of the hydration free energy on the sign of the solute charge:

$$\Delta G\simeq -\left(1-\frac{1}{ϵ}\right)\frac{q^2}{2\left(R+R_s\right)}\left(1-sgn[q]\frac{\delta }{R+R_w}\right).$$ (20)

Here, ϵ is the dielectric constant of water, R_w is the radius of water molecule, q and R are the ion charge and ionic radius, respectively, R_s = 0.52 Å is a constant shift to the dielectric boundary (77), and δ is the symmetry breaking parameter(78). The “charge-asymmetric Born equation”, Eq. 20, contains no fitting parameters, yet describes experimental ion hydration energies to within 5% of experiment(77). The CHA effects can be introduced into the effective Born radii by analogy with Eq. 20, leading to a charge-asymmetric GB-like model CHA-GB(76), implemented in AmberTools. The introduction of CHA into the GB has improved its ability to predict hydration free energies of small molecules and amino-acids simultaneously, including the charged ones.

2.7. Effects of ionic screening

Mobile ions in the solvent can be very effective at screening charge-charge interactions, augmenting the dielectric effect itself. The linearized (or Debye-Huckel) model can be solved analytically for a sphere, (54, 112) and an extension made to general shapes in a way that done for the salt-free case discussed above. This leads to the simple ansatz:

$$\left(1-\frac{1}{\epsilon }\right)\to \left(1-\frac{\text{exp}\left(-\kappa f_{GB}\right)}{\epsilon }\right)$$ (21)

where κ is the Debye-Huckel inverse screening length.

Both the canonical GB (and the PB for that matter) utilize a mean-field description of ions, which does not account for ion-ion correlations or discreteness of ions near the charged solute surface. While in the case of monovalent ions the correlation effects are small and can often be neglected, the correlations between multivalent ions can introduce significant corrections to ion distributions and electrostatic potentials around solutes. Recently, a GB-like model was constructed(116) to handle ions explicitly. Modifications to the canonical model were required, including modifications to account for multiple interacting solutes – disconnected dielectric boundary around the solute-ion or ion-ion pairs. For a duplex DNA example, the monovalent (Na⁺) and trivalent (CoHex³⁺) counterion distributions produced by the model are in close agreement with all-atom explicit water molecular dynamics simulations used as reference.

2.8. Adopting GB for membrane environments

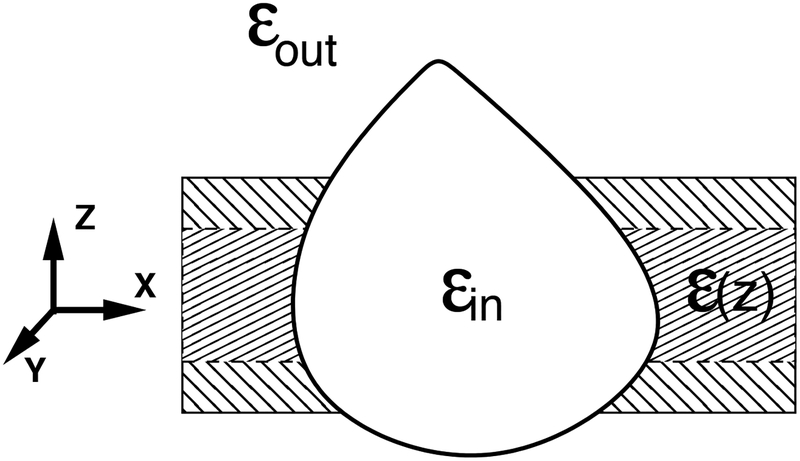
A specific challenge arises if one wants to use the GB to describe the effects of essentially heterogeneous dielectric environment of biological membranes and water/membrane interface. Several empirical modifications(103, 119, 115, 24) to the canonical GB have been proposed that so far utilize the same general idea: keep the main GB formalism intact, and use the effective Born radii to account for the presence of additional dielectric boundaries. For example, the Heterogeneous Dielectric generalized Born (HDGB) flavor is an extension of the GBMV approach, where the original expression for the effective Born radii now includes an explicit dependence on ϵ_in and ϵ_out via an analytical formula for R_i: R_i = R_i(ϵ_in, ϵ_out). The model(115) partitions the membrane “slab” into several regions of constant dielectric, Fig. 2, approximating a realistic scenario in which the dielectric properties of the membrane ϵ(z) vary continuously across the bi-layer.

Figure 2.

A schematic of an idealized, multi-dielectric membrane environment mimicked by some of the GB models.

A recent extension of HDGB model, HDGBvdW(21), provides more accurate description of the non-polar components of the free energy of solvation. Compared to the original HDGB, the extension improves free energy estimates in the hydrophobic interior of the membrane, where non-polar interactions are significant.

2.9. Speeding it up for large systems

Although the GB equations are more complex than simple molecular-mechanics force fields, they often perform well in parallel CPU architectures, and adaptations to GPUs are available in several popular packages.(22, 33, 7) However, until recently, available GB implementations were poorly suited to handle very large structures, because traditional implementations scale as O(N²) with the number of solute atoms N. A certain amount of speed-up, up to a factor of three or so for a 25,000 atom system, can be achieved by using a ”soft” cut-off in the calculation of the effective Born radii(82), but the Ewald-based procedures that addresses the O(N²) problem for explicit solvent simulations can not be readily adapted to the non-periodic geometries used in implicit solvent models. On the other hand, cut-offs applied to charge-charge interaction can lead to artifacts, especially for highly charged systems(46).

To overcome the problem, a method of hierarchical charge partitioning (HCP) was proposed(6, 3,4), which bears some similarity with the fast multipole approach, but is better suited for biomolecular simulations. Specifically, HCP is a multi-scale, yet fully atomistic, approach to perform MD simulations based on the generalized Born model, mainly intended for very large structures. HCP employs a charge coarse-graining scheme that takes advantage of the natural hierarchical partitioning of large biomolecules into smaller structural components, e.g. amino-acids, chains, etc. The charge coarse-graining is performed via a rigorous mathematical procedure, and no re-parametrization of the original atomistic force-field is needed. Molecular Dynamics simulations based on HCP (GB-HCPO(46), available in Amber), scale as NlogN with the number of atoms in the solute, which means that conformations of very large (millions of atoms) fully atomistic systems can be sampled efficiently, without cut-offs.

3. APPROACHES TO NON-POLAR SOLVATION

The electrostatic component of solvation, including stabilization of polar and charged groups, and the screeening of charge-charge interactions, are generally the most influential terms for biomolecules in (salt)-water. The electrostatic component corresponds to the free energy of discharging the solute, i.e. of setting all its charges to zero. What remains is a very non-polar object (something like an alkane) that has the same shape as the original solute. This remaining (hypothetical) object has a non-zero solvation free energy, which is generally smaller than the electrostatic component in absolute terms, but which can have a significant influence on conformational equilibria.

These interactions have proved to be hard to model in a simple fashion, primarily because one must consider two competing effects: there is an (unfavorable) free energy change required to create an empty cavity in the solute to accommodate the solute; this is partially offset by a (favorable) dispersion interaction between the solute (once it is inserted into the cavity) and the surrounding solvent molecules. The simplest, and still most widely used, approach is to assume that the non-polar contribution is proportional to the solvent-exposed surface area, even though non-polar contributions are known to depend upon the solute size and shape in a more complex fashion.(65, 14, 30, 31, 60, 48) To the extent that they “work”, simple surface area terms may capture changes in solvation over narrow ranges of conformations, and experience suggests that the relatively smooth changes associated with solvent accessible surface areas can avoid pitfalls that arise with more complex models.(111)

Even within this model, one has the additional challenge of estimating surface areas in an efficient fashion. The Amber programs use the Linear Combination of Pairwise Overlaps (LCPO) model,(122) which uses parameters characteristic of common combinations of neighboring atoms to a molecule surface area. Gallicchio and Levy have adapted a earlier model based on a superposition of Gaussian functions representing atomic volumes (34) to compute a surface area estimate (and its derivatives) in an efficient manner.(28) In this AGBNP model, they also base the solute-solvent dispersion estimates on already-computed Born radii.

4. APPLICATION EXAMPLES

Implicit solvent models have been in use in biomolecular simulations for a long time, and it is not feasible to attempt any fair overview of applications. Instead, we list here a few examples, chosen from those we are familiar with, to illustrate a range of applications where particular aspects of implicit solvation are key to eh application.

4.1. The MM-GBSA approach to free energies

The free energy of solvation estimates provided by implicit solvent models include both enthalpy and entropy contributions, and this opens up a novel end-point approach to free energy calculations(105) where the free energy of a given state (”A”) is written as

$$G(A)=\langle E_{MM}\rangle (A)-T{S}_{config}(A)+\langle \Delta G_{\text{solv}}\rangle$$ (22)

Here E_MM is the molecular mechanics estimate of the average energy of the solute in the absence of the solvent, S_config is a configurational entropy arising from the solute degrees of freedom and ΔG_solv gives the free energy contributions from the solvent. The average energy and ΔG_solv values are generally computed over the configurations sampled by an MD trajectory, since no single configuration can represent thermal motion in a given basin. The configurational entropy of the solute can be estimated by normal mode or quasiharmonic analysis for fairly rigid molecules,(70, 52) and by a variety of approaches for floppier systems.(26) Free energy differences for conformational transitions (say between bound and free states in ligand–receptor interactions) are made simply by subtracting the free energy estimates of the two end states.

This approach (in its modern incarnation for biomolecules) was first applied to study the A to B helix transtion in DNA and RNA,(105), and was rather quickly extended to study ligand binding events.(57) It has since been widely applied, with varying levels of agreement with observed data.(29, 121) One obvious limitation lies in the inability of available implicit solvent models to capture subtle changes in ΔG_solv as a function of conformation. But obtaining good estimates of configurational entropies can be equally troubling, especially as the extent of disorder increases; in fact, the reason that this end point approach is nearly useless of explicit solvent models arises from the difficulty of extracting entropy estimates for the solvent in explicit MD simulations.

4.2. Second derivatives and normal modes

Many of the GB flavors discussed above are fully analytical, and higher-order derivatives can be computed by straightforward (if tedious) applications of the chain rule. This has been implemented for the original Hawkins-Cramer-Truhlar model(40) in the Amber suite of programs.(13) One can then compute normal modes (as with isolated molecules) but where solvent electrostatic effects are incorporated. This can be a very useful model, for example, in studying mechanical properties of biopolymers, such as the stretching and bending rigidity of DNA, with varying degrees of salt.(11) Normal mode analysis also provides estimates of configurational entropies, which are useful for end-point analyses like MM-GBSA.

4.3. Large scale motions, very large structures.

One of the key advantages of the implicit solvation approach is that the effective viscosity of water can be set to a much lower value than that of real water, which can speeds-up conformational transitions significantly(5). The speed-up is particularly impressive for transitions that involve large parts of the biomolecule moving essentially unimpeded in the solvent, in which case 100-fold speed-up of conformational sampling compared to the explicit solvent is easily within reach(5), in addition to any algorithmic speed-ups that the GB can offer for the system in question. The first atomistic simulation of a long (150 base-pairs) DNA fragment free in solution is an example that illustrates the point: only several nanoseconds of the simulation(92) had revealed significant, unexpected flexibility of the double-helix. Note that even setting up a traditional explicit solvent simulation box of the appropriate size would be quite cumbersome, as the contour length of the nucleosomal DNA is ~ 500 Å.

Atomistic simulation of large biomolecular systems, especially those with flexible parts, is another area where GB-based simulations can be useful. The nucleosome – a complex of eight histone proteins and 147 base-pairs of DNA wrapped around it – is a relevant example here. GB-based MD simulations(67,23) were utilized to study highly flexible N-terminal tail regions of the histone proteins, implicated in chromatin remodeling. Recently, partially assembled intermediate states of the nucleosome, unavailable from experiment, were constructed(93) through GB-based simulations followed by refinement in the explicit solvent.

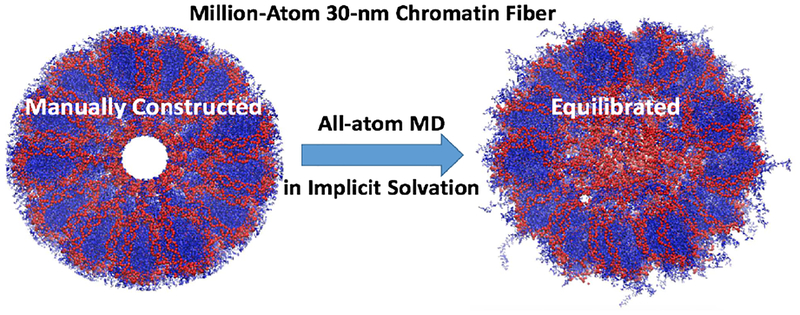
Multi-million atom systems require special multi-scale treatment. One such GB-based model (GB-HCPO(46), described above) was used to refine the atomistic structure of a chromatin fiber fragment consisting of 40 nucleosomes, starting from a low-resolution Cryo-EM input(90), Fig. 3.

Figure 3.

Atomistic simulation(46) of a Cryo-EM consistent model of 30-nm chromatin fiber reveals important details consistent with experiment: the linker DNA fills the core region, the H3 histone tails interact with the linker DNA.

4.4. Protein folding

Protein folding at the atomic resolution – once called “the grand challenge of computational science” – is arguably one of the most illustrious success stories of the GB. While intermediate states resembling the native were observed in a pioneering simulation of the folding process in explicit solvent(18), it was not until later that a complete folding of a small protein from a fully unfolded state to the native was achieved in a GB-based MD simulation(102). Many other GB-based folding studies followed(15, 50, 64), including those aimed at protein design(68, 25). Recent comparisons of the Amber GB model to Rosetta scoring functions have shown GB results that match or exceed those from Rosetta in terms of protein loop modeling or folding landscape characterization.(91)

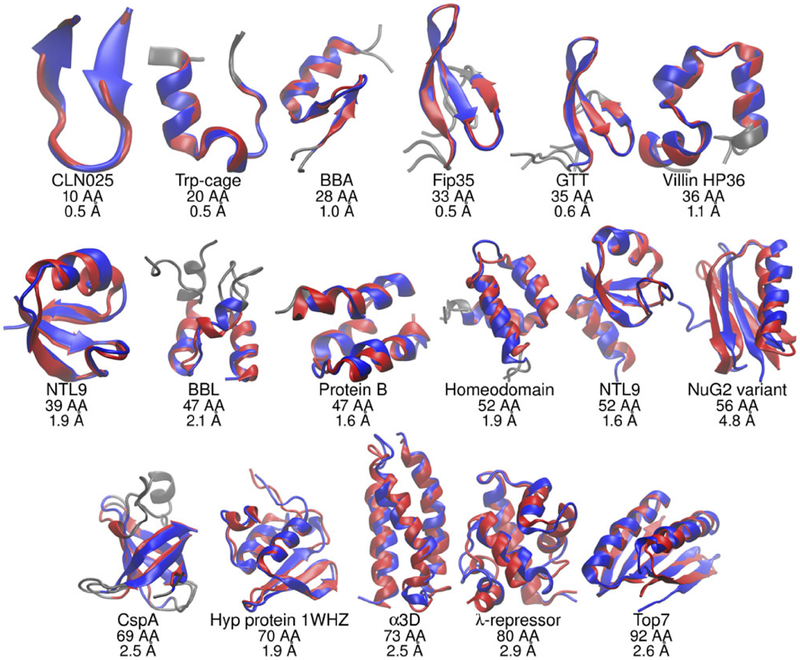
In a recent landmark study(79), folding simulations of 17 proteins, Fig. 4, were performed on a commodity PC within days(79). In implicit solvent, correct native states of small proteins can be easily identified as minimum energy snapshots(102, 5), in straightforward simulations starting from completely extended conformations – the task that is not nearly as straightforward in explicit solvent. For example, a recent study(66) of folding-unfolding transitions of 12 of the fastest folding proteins required extremely long simulations on one-of-a-kind specialized supercomputer, and the use of significantly elevated temperature to overcome kinetic traps. It is unclear for how many of the same proteins a truly de-novo (e.g. from a linear peptide) prediction of the native structure could have been made at 300K.

Figure 4.

GB-based molecular dynamics simulations (GB-neck2(81), Amber) of a number of proteins starting from completely unfolded states sample conformations (blue) that are close to the experimental native structures (red). Lowest RMSD distance to the experimental native structure, in Å, is indicated under each protein. Adapted from Ref.(79), courtesy of Carlos Simmerling.

4.5. Biomolecules in the presence of biological membranes

Translocation of molecular structures through membranes may involve significant molecular movements and conformational changes; membranes are generally large structures. These qualities make membrane systems good candidates for implicit solvent simulations, such as simulation of whole membrane proteins(104, 115, 119, 114). Recent applications include predicting the hydrophobic length of membrane proteins(19), and protein structure refinement(20).

4.6. Acid-base and redox transitions

One application area that illustrates the potential power of implicit solvent models are ”constant pH” simulations. In an early (but still popular) approach,(73, 72, 109, 110) conventional MD simulations are interupted at intervals by Monte Carlo attempts to transfer protons between the solute and a hypothetical reservoir maintained at a given pH. An attempted move like this would almost always fail in an explicit solvent simulation, since waters arranged around a charged titration site (e.g. a protein side chain) would be in a high-energy configuration for a site that suddenly neutralized, and vice-versa. In an implicit solvent model, on the other hand, the solvent model can instantaneously respond to a change in charge, and Monte Carlo move attempts can have reasonable acceptance rates. A similar use of this instantaneous response is active in models that treat the transition between charged and neutral sites in term of a continuous auxiliary variable.(63, 53, 120)

A key problem with the implicit solvent models is that results are often in poorer agreement with experiment than one would like. Such errors might arise from limitations of solute force fields, or from incomplete sampling, as well as from deficiencies in the solvent model itself. There have been quite a few Efforts to extend the constant pH idea to explicit solvent simulations (including approaches that use a hybrid explicit/implicit model), and this continues to be an active area of current research(43).

5. CONCLUSIONS

We have reviewed the over-all physical foundations and specific implementations of one of the most widely used “fast” implicit solvation model – the generalized Born (GB) approximation. Implementations are available in a variety of molecular modeling packages, and many thousands of applications have been reported.

The specific choice of GB “flavor” depends on one’s needs: a protein folding simulation may call for one flavor of the GB model(84, 79), while a study of a protein in a membrane environment will need quite another(71, 20). The model one may prefer for estimates of ligand binding energies(47), can be different from GB flavors one may recommend for simulations of the DNA(118, 16, 80). Yet a different approach is needed if the molecular charge distribution is described by (polarizable) multipoles, rather than by fixed point charges.(97) Some recent updates in parameters have led to significant improvements in the quality of GB models applied to proteins and their complexes with nucleic acids,(81, 80). This diversity of approaches reflects a lack of generality: no single implicit model works well everywhere. This is hardly surprising, given the complexity of solvent effects that one is trying to fold into a simple and fast model. Furthermore, some of the success of GB models certainly arises from fortuitous cancellation of errors, and from parameterization schemes that hide defects in the solvation model or in the underlying solute force field. In spite of these limitations, we have described a number of advantages of such schemes, and have documented some of the recent and novel ideas that continue to drive research in this area. We expect that there will be continue to be an important place for implicit solvent models in biomolecular simulation for some time to come.