Abstract
Adaptive deep brain stimulation (aDBS) is an emerging method to alleviate the side effects and improve the efficacy of conventional open-loop stimulation for movement disorders. However, current adaptive DBS techniques are primarily based on single-feature thresholding, precluding an optimized delivery of stimulation for precise control of motor symptoms. Here, we propose to use a machine learning approach for resting-state tremor detection from local field potentials (LFPs) recorded from subthalamic nucleus (STN) in 12 Parkinson’s patients. We compare the performance of state-of-the-art classifiers and LFP-based biomarkers for tremor detection, showing that the high-frequency oscillations and Hjorth parameters achieve a high discriminative performance. In addition, using Kalman filtering in the feature space, we show that the tremor detection performance significantly improves (F(1,15)=32.16, p<0.0001). The proposed method holds great promise for efficient on-demand delivery of stimulation in Parkinson’s disease.
Index Terms: Parkinson’s disease (PD), deep brain stimulation (DBS), tremor, adaptive DBS, machine learning, Kalman filtering
I. Introduction
Parkinson’s disease (PD) is one of the most prevalent neurodegenerative diseases, affecting over 6 million patients worldwide. PD is characterized by both motor and non-motor symptoms [1], with the former mainly consisting of resting tremor, muscle rigidity, and akinesia. Such disabling symptoms in advanced Parkinson’s disease can be partially alleviated by the use of deep brain stimulation technology [2], through delivering a constant high-frequency stimulation (~130Hz) to either subthalamic nucleus (STN) or internal globus pallidus (GPi) [3].
However, due to the continuous and open-loop delivery of stimulation, PD patients treated by the conventional DBS exhibit side effects such as speech impairment and psychiatric symptoms [3]. Furthermore, constant stimulation increases the energy consumption of the battery-powered DBS device, which may require a surgical replacement when running out of power. To overcome these limitations, the concept of adaptive DBS (aDBS) promises an effective alternative, by transforming the open-loop DBS to a closed-loop approach [3], [4]. In the adaptive DBS system, stimulation is dynamically controlled by the state of a patient’s motor symptoms, such as bradykinesia or tremor. Through the measurement of relevant biomarkers, adaptive DBS can deliver the stimuli only when needed, thus reducing the duration of stimulation, alleviating the side effects, and saving power. One of the pioneering studies on aDBS in humans [4] has reported promising results such as reduction of stimulation time and energy consumption by 56%, improving the UPDRS (Unified Parkinson’s Disease Rating Scale) motor score by 27%, and a better speech intelligibility compared to conventional DBS [4], [5].
Despite the promising advantages of aDBS, it is still facing many challenges on its way to clinical therapy [3]. Particularly, the lack of chronic trials and sufficient data for performance evaluation, the need for optimal feedback signals and efficient control algorithms, and the hardware integration of recording and control circuits into DBS system are among the major bottlenecks. For instance, the majority of feedback signals used for aDBS control so far have been overly simplistic and unidimensional [3], such as beta power (13–30 Hz) in local field potentials, or the tremor severity measured by accelerometer sensors. For tremor detection in Parkinson’s disease, however, the beta power in STN may not be sufficient or optimal, as it does not correlate with tremor but well correlates with bradykinesia and rigidity [3]. The potential usage of tremor acceleration or EMG as alternative feedback signals would lead to excessive energy consumption, due to the wireless communication between the implanted DBS and wearable motion or EMG sensors. Therefore, to implement aDBS for Parkinson’s disease, additional correlating biomarkers directly extracted from the brain activity (i.e., LFPs in STN, or alternatively, from motor cortex [6]) should be explored to better predict the tremor state.
In this work, we investigate the state-of-the-art machine learning algorithms previously applied to neural data [7], combined with multiple time and frequency-domain features, to detect the Parkinson’s tremor periods. Specifically, Kalman filtering in the feature space is proposed to enhance the tremor detection performance. Our results suggest that a multi-feature classification approach combined with Kalman filtering would potentially provide a more effective control of DBS.
II. Materials and Methods
All the data analysis and classification process in this work has been done offline, with the goal of translation to an online setting for closed-loop suppression of Parkinson’s tremor.
A. Subjects and Data
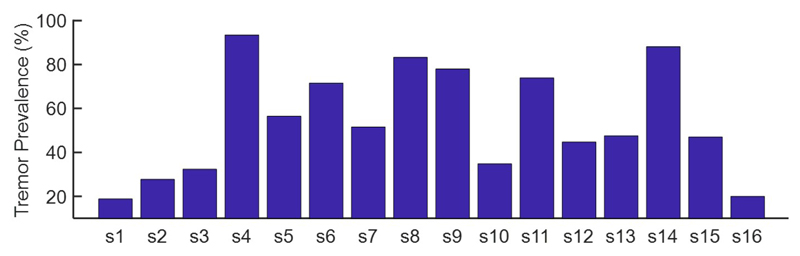
We studied 12 patients with Parkinson’s disease recruited by the University of Oxford. All patients gave their informed consent to take part in this study, which was approved by the local research ethics committee of the University of Oxford. The data includes 16 LFPs, as patients who experienced bilateral symptoms were recorded from both sides (the individual recordings are named as s1 to s16). The LFPs were recorded from STN when the stimulation was off, and the acceleration of the contralateral limb was simultaneously measured. The LFPs vary from 1.5 to 10 minutes in duration, recorded at a sampling rate of 2048 Hz using four channels at different depths. A notch filter at 50 Hz and its harmonics was applied to remove the powerline noise. To measure the bipolar LFPs, we use the difference between adjacent contacts. In total, seven channels are included in our analysis, i.e., four monopolar and three bipolar. The prevalence of tremor in the LFP recordings is shown in Fig. 1. On average, 56.3±24.4% of the total recording time is accompanied by tremor.
Fig. 1.
The tremor prevalence distribution across LFP recordings.
B. Tremor Labeling
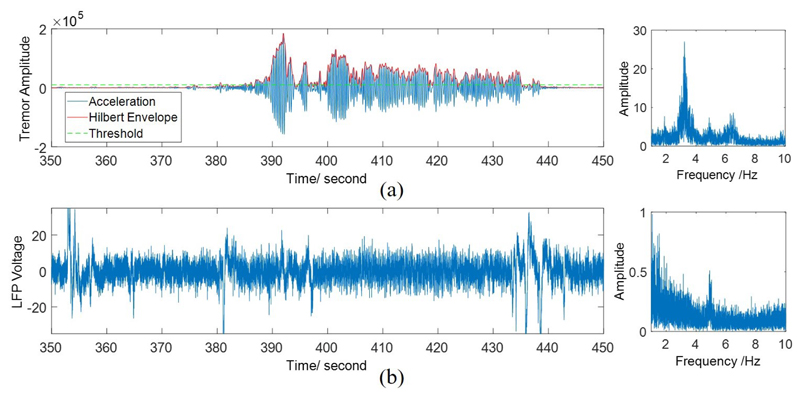
The peak frequency of tremor was determined by computing the Fast Fourier Transform of the measured acceleration and finding the frequency with maximum amplitude in (1–10 Hz) range. A second-order Butterworth band-pass filter was used to filter the acceleration data, with the determined tremor frequency as the center and a bandwidth of 2 Hz. Then, the envelope of the filtered signal was extracted using Hilbert transform, and was subsequently used for labeling the tremors. A threshold method was utilized to differentiate the tremor from non-tremor state. The threshold was determined by finding the resting non-tremor period first (the amplitude of the measured acceleration signal and the corresponding envelope was small when there was no tremor). Then, the mean value of the non-tremor period plus five standard deviation of that period was used as the threshold. The amplitude above the threshold was labeled as tremor, otherwise as non-tremor.
The labeling process is illustrated in Fig. 2(a). The threshold method can reasonably distinguish the tremor from non-tremor state, while very small tremor is considered as non-tremor. Moreover, it is impossible to differentiate the two states simply by eye, as shown in the corresponding LFP signal in Fig. 2(b).
Fig. 2.
(a) Threshold method for tremor labeling. The left figure represents the time-domain acceleration, its envelope after band-pass filtering, and applied threshold, while the figure on the right shows the power spectrum of acceleration. (b) One channel of the raw LFP signal (left), and its power spectrum (right).
C. Feature Computation
In order to extract the electrophysiological biomarkers of tremor, the LFP recordings are continuously segmented into 2-second epochs without overlapping. Then, twelve features are extracted from each epoch in seven channels as summarized in Table I. These features are carefully selected from previous studies on Parkinson’s disease and other widely explored neurological disorders such as epilepsy [7]–[14], and include: Beta power (13–30 Hz) [4]; Phase–amplitude coupling (PAC) between the phase of beta and the amplitude of high-frequency oscillations (150–400 Hz) [9]; High-frequency oscillation (HFO) power ratio between (200–300 Hz) and (300–400 Hz) [10]; HFO power (200–350 Hz); Tremor power (3–7 Hz); Maximum peak power in (3–18 Hz); Hjorth activity, mobility, and complexity [8]; Wavelet entropy [14]; Low gamma power (31–45 Hz) [11], and Gamma power (60–90 Hz).
Table I. Extracted Features.
| Feature | Description |
|---|---|
| 1. Beta Power | Spectral power in (13–30 Hz) [4] |
| 2. PAC | Phase-amplitude coupling between the phase of beta and the amplitude of high-frequency oscillations (150–400 Hz) [9] |
| 3. HFO Ratio | Power ratio of the HFO in (200–300 Hz) and (300–400 Hz) [10] |
| 4. HFO Power | Spectral power in (200–350 Hz) |
| 5. Tremor Power | Spectral power in (3–7 Hz) |
| 6. Max Power | Peak power in (3–18 Hz) |
| 7. Wavelet Entropy | Wavelet entropy [14] |
| 8. Hjo Act | Hjorth activity [8] |
| 9. Hjo Mob | Hjorth mobility [8] |
| 10. Hjo Com | Hjorth complexity [8] |
| 11. Low Gamma Power | Spectral power in (31–45 Hz) [11] |
| 12. Gamma Power | Spectral power in (60–90 Hz) |
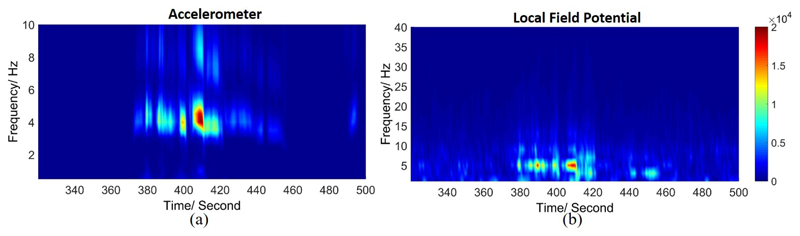
The time-frequency transforms of both LFP and acceleration measure for a sample patient are shown in Fig. 3. The peripheral acceleration exhibits a strong energy within the tremor frequency band of (3–7 Hz). Correspondingly, we also observe a power increase within the tremor band in LFP, indicating that the spectral power of tremor band in local field potentials would be a good candidate for tremor prediction.
Fig. 3.
The time-frequency distribution of power in (a) the acceleration measure of tremor, and (b) in the corresponding LFP recording.
We use a biserial correlation coefficient [15] to assess the discriminative power of each feature in tremor detection. It is defined as the difference of the mean value between the tremor and non-tremor features, divided by the pooled standard deviation of the two groups:
where N1 and N2 represent the number of samples in the X1 and X2 classes, respectively. For the on-chip integration of closed-loop DBS in our future work, we will select a feature set with high discriminative accuracy and low hardware cost from the current pool of features.
D. Kalman Filtering in Feature Space
The noisy fluctuations in the LFP time series, and consequently, in the extracted features, degrade the tremor detection accuracy. Kalman filtering has been shown to be very effective in smoothing the undesired fluctuations of the data [12], [16] by minimizing the variance of the estimation error. In this paper, we utilize a second-order Kalman filter as described below. A detailed description of Kalman filtering process can be found in [16].
Let represent the state vector sk, where denotes the rate of change in fk (first-order derivative). The extracted feature zk can be represented by the following state-space model:
| (2) |
where Tp is the prediction interval and wk is the process disturbance assumed as a zero-mean white noise with a covariance of:
| (3) |
A Kalman filter can be applied to the second-order state-space model in (2) in order to recursively provide a filtered estimate of fk. The resulting smoother variable is then used in place of zk in the classification process. The standard deviations σw of wk and σv of vk are the only design parameters of Kalman filter, and the Kalman gain depends on the ratio of σ = σw/σv, which is set to 5 × 10−5 according to [12], [16]. It should be noted that the hardware complexity of a second-order Kalman filter is negligible, compared to the feature computation and classification tasks.
E. Classification and Performance Evaluation
We study the performance of various classifiers for tremor detection, using the scikit-learn package in Python. A hyperparameter tuning of classifier parameters was performed to find optimum settings for each patient. These classifiers include: Linear Discriminant Analysis (LDA); Logistic Regression (LR); k-Nearest Neighbor (k-NN); Support Vector Machines with Linear (SVM-L) and Radial Basis kernels (SVM-R); Multilayer Perceptron Neural Network (MLP); Random Forest (RF); and Extreme Gradient-Boosted Decision Trees (XGB).
Ensembles of decision trees such as gradient boosting and random forests have been among the most useful and highly competitive methods in machine learning recently [7], particularly in the regime of limited training data, little training time, and little need for parameter tuning. In particular, the XGBoost implementation has been a winning solution in many machine learning competitions such as the intracranial EEG-based seizure prediction contest on Kaggle, and has been included in our analysis.
Dealing with a time series classification problem, we opted for a block-wise data partitioning method to fairly assess the performance of classifiers and avoid data leakage [7]. For each recording, we first divide the continuous LFP data into 20 equal-sized blocks. We then apply a 5-fold cross validation to the blocks of LFP data, by using 20% of blocks (i.e., four) for testing the model, and the remaining for training. This process is then repeated for 5 times and the results are averaged to produce a single estimation. As the tremor and non-tremor in the current dataset are highly unbalanced across subjects, the classifier performance is measured by AUC rather than accuracy. The AUC represents the area under the ROC curve (the true positive rate vs. false positive rate).
III. Tremor Detection Performance
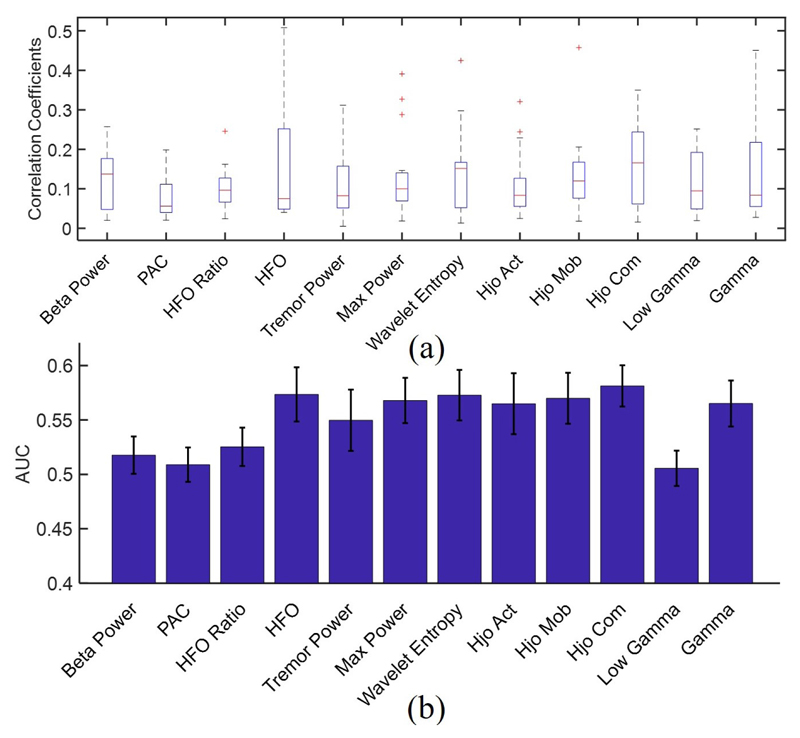
The biserial correlation coefficients of the examined features are averaged across channels and depicted in Fig. 4(a), indicating how informative each feature is in discriminating the two classes of tremor and non-tremor. We can see that the HFO and Hjorth complexity perform the best. Moreover, the overall classification performance of each feature using XGB and seven input channels is shown in Fig. 4(b). It is evident that the Hjorth complexity and HFO achieve the highest performance.
Fig. 4.
(a) Boxplot of biserial correlation coefficient for the studied features, (b) feature importance measured by AUC for XGB classifier.
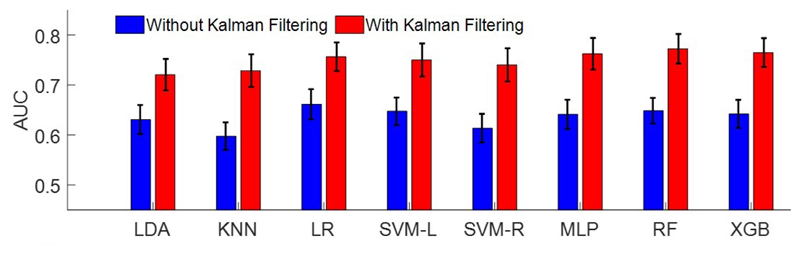
Figure 5 shows the performance of classifiers using the feature set in Table I, with and without Kalman filtering. For AUC measure, the two-way ANOVA with repeated measures shows a significant main effect on Kalman filtering (F(1,15)=32.16, p<0.0001), and on classifiers (F(7,105)=4.59, p<0.0001), with no significant interaction. The post-hoc comparison shows that Kalman filtering results in 11.42% superior performance compared to the case with no filtering. The performance of XGB, RF and MLP classifiers is significantly higher than that of k-NN. No significant difference is shown among MLP, RF, and XGB, while XGB is computationally less expensive. LR performs 3.3% better than LDA, while no significant difference is shown among LR, MLP, RF, SVM-L, SVM-R and XGB, on this dataset. Using only beta power, the performance significantly degrades (AUC: 53.79%±33.22% for LDA).
Fig. 5.
Comparison of average predictive ability of all classifiers measured by AUC, with and without Kalman filter.
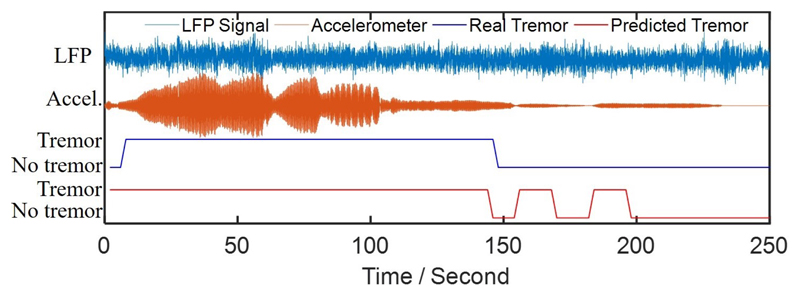
Our results suggest a careful selection of features with high detection performance for on-chip integration of aDBS, while choosing a classifier with low hardware complexity (e.g., XGB or LR), to maintain low power and small form factor of the implantable system. For XGB or RF, we can use an architecture similar to [7]. Our analysis shows that an ensemble of 10 trees with a maximum depth of 2 is sufficient to achieve an average AUC of above 70% with XGB. Moreover, RF with 10 trees and a maximum depth of 3, and MLP with one hidden layer and 20 neurons, similarly achieve AUCs of above 70%. A detailed discussion on hardware complexity of different classifiers can be found in [7]. The tremor detection results for a sample patient is shown in Fig. 6. We can see that the proposed Kalman filtering combined with XGB classifier can reasonably track the measured tremor during resting state.
Fig. 6.
Example of tremor detection using the XGB classifier and selected feature set for an arbitrary patient.
IV. Conclusion
In this work, machine learning combined with Kalman filtering is systematically studied for resting tremor detection in Parkinson’s disease. We find that Kalman filtering in feature space can significantly improve the classification performance. Furthermore, hardware-friendly machine learning models such as gradient-boosting decision trees and logistic regression, combined with HFO and Hjorth complexity features, achieve a high performance in tremor detection. This study has the potential to transform the conventional adaptive DBS to a more efficient machine learning-based closed-loop control.
Contributor Information
Lin Yao, Email: lin.yao@cornell.edu.
Peter Brown, Email: peter.brown@ndcn.ox.ac.uk.
Mahsa Shoaran, Email: shoaran@cornell.edu.
References
- [1].Rosin B, Slovik M, Mitelman R, Rivlin-Etzion M, Haber SN, Israel Z, Vaadia E, Bergman H. Closed-loop deep brain stimulation is superior in ameliorating parkinsonism. Neuron. 2011;72(2):370–384. doi: 10.1016/j.neuron.2011.08.023. [DOI] [PubMed] [Google Scholar]
- [2].Vidailhet M, Vercueil L, Houeto J-L, Krystkowiak P, Benabid A-L, Cornu P, Lagrange C, Tézenas du Montcel S, Dormont D, Grand S, et al. Bilateral deep-brain stimulation of the globus pallidus in primary generalized dystonia. New England Journal of Medicine. 2005;352(5):459–467. doi: 10.1056/NEJMoa042187. [DOI] [PubMed] [Google Scholar]
- [3].Meidahl AC, Tinkhauser G, Herz DM, Cagnan H, Debarros J, Brown P. Adaptive deep brain stimulation for movement disorders: the long road to clinical therapy. Movement disorders. 2017;32(6):810–819. doi: 10.1002/mds.27022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Little S, Pogosyan A, Neal S, Zavala B, Zrinzo L, Hariz M, Foltynie T, Limousin P, Ashkan K, FitzGerald J, et al. Adaptive deep brain stimulation in advanced Parkinson disease. Annals of neurology. 2013;74(3):449–457. doi: 10.1002/ana.23951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Little S, Tripoliti E, Beudel M, Pogosyan A, Cagnan H, Herz D, Bestmann S, Aziz T, Cheeran B, Zrinzo L, et al. Adaptive deep brain stimulation for Parkinson’s disease demonstrates reduced speech side effects compared to conventional stimulation in the acute setting. J Neurol Neurosurg Psychiatry. 2016 doi: 10.1136/jnnp-2016-313518. pp. jnnp–2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].De Hemptinne C, Ryapolova-Webb ES, Air EL, Garcia PA, Miller KJ, Ojemann JG, Ostrem JL, Galifianakis NB, Starr PA. Exaggerated phase–amplitude coupling in the primary motor cortex in parkinson’s disease. Proceedings of the National Academy of Sciences. 2013;110(12):4780–4785. doi: 10.1073/pnas.1214546110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Shoaran M, Haghi BA, Taghavi M, Farivar M, Emami A. Energy-Efficient Classification for Resource-Constrained Biomedical Applications. IEEE Journal on Emerging and Selected Topics in Circuits and Systems (JETCAS) 2018 [Google Scholar]
- [8].Hjorth B. EEG analysis based on time domain properties. Electroencephalography and clinical neurophysiology. 1970;29(3) doi: 10.1016/0013-4694(70)90143-4. [DOI] [PubMed] [Google Scholar]
- [9].van Wijk BC, Beudel M, Jha A, Oswal A, Foltynie T, Hariz MI, Limousin P, Zrinzo L, Aziz TZ, Green AL, et al. Subthalamic nucleus phase–amplitude coupling correlates with motor impairment in Parkinsons disease. Clinical Neurophysiology. 2016;127(4):2010–2019. doi: 10.1016/j.clinph.2016.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Hirschmann J, Butz M, Hartmann CJ, Hoogenboom N, Özkurt TE, Vesper J, Wojtecki L, Schnitzler A. Parkinsonian Rest Tremor Is Associated With Modulations of Subthalamic High-Frequency Oscillations. Movement Disorders. 2016;31(10):1551–59. doi: 10.1002/mds.26663. [DOI] [PubMed] [Google Scholar]
- [11].Weinberger M, Hutchison WD, Lozano AM, Hodaie M, Dostrovsky JO. Increased gamma oscillatory activity in the subthalamic nucleus during tremor in Parkinson’s disease patients. Journal of Neurophysiology. 2009;101(2):789–802. doi: 10.1152/jn.90837.2008. [DOI] [PubMed] [Google Scholar]
- [12].Zhang Z, Parhi KK. Low-complexity seizure prediction from iEEG/sEEG using spectral power and ratios of spectral power. IEEE Transactions on Biomedical Circuits and Systems. 2016;10(3):693–706. doi: 10.1109/TBCAS.2015.2477264. [DOI] [PubMed] [Google Scholar]
- [13].Wang T, Shoaran M, Emami A. Toward Adaptive Deep Brain Stimulation in Parkinson’s Disease: LFP-based Feature Analysis and Classification. IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP); 2018. [Google Scholar]
- [14].Rosso OA, Blanco S, Yordanova J, Kolev V, Figliola A, Schürmann M, Başar E. Wavelet entropy: a new tool for analysis of short duration brain electrical signals. Journal of neuroscience methods. 2001;105(1):65–75. doi: 10.1016/s0165-0270(00)00356-3. [DOI] [PubMed] [Google Scholar]
- [15].Müller K-R, Krauledat M, Dornhege G, Curio G, Blankertz B. Machine learning techniques for brain-computer interfaces. 2nd Int. BCI Workshop Training Course; 2004. [DOI] [PubMed] [Google Scholar]
- [16].Chisci L, Mavino A, Perferi G, Sciandrone M, Anile C, Colicchio G, Fuggetta F. Real-time epileptic seizure prediction using AR models and support vector machines. IEEE Transactions on Biomedical Engineering. 2010;57(5):1124–1132. doi: 10.1109/TBME.2009.2038990. [DOI] [PubMed] [Google Scholar]