Abstract
In Mitchell's chemiosmotic theory, membrane potential was given as the electric potential difference across the membrane. However, its physical origin for membrane potential was not well explained. Using the Lee proton electrostatic localization model with a newly formulated equation for protonic motive force (pmf) that takes electrostatically localized protons into account, membrane potential has now been better understood as the voltage difference contributed by the localized surface charge density at the liquid-membrane interface as in an electrostatically localized protons/cations-membrane-anions capacitor. That is, the origin of membrane potential is now better understood as the electrostatic formation of the localized surface charge density that is the sum of the electrostatically localized proton concentration and the localized non-proton cations density at the liquid membrane interface. The total localized surface charge density equals to the ideal localized proton population density before the cation-proton exchange process; since the cation-proton exchange process does not change the total localized charges density, neither does it change to the membrane potential . The localized proton concentration represents the dominant component, which accounts about 78% of the total localized surface charge density at the cation-proton exchange equilibrium state in animal mitochondria. Liquid water as a protonic conductor may play a significant role in the biological activities of membrane potential formation and utilization.
Keywords: Biochemistry, Biophysics, Biotechnology, Cell biology, Computational biology, Microbiology, Structural biology, Protonic capacitor, Bioenergetics, Mitochondria, Membrane potential, Electrostatically localized protons, ATP synthesis, Liquid-membrane interface, Localized surface charge density
1. Introduction
What really defines the origin for the membrane potential in proton-coupling bioenergetics systems? In Peter Mitchell's chemiosmotic theory [1, 2, 3] that won the 1978 Nobel Prize in chemistry, the term, membrane potential , was somewhat vaguely given as the electric potential difference across the membrane. However, its physical origin for membrane potential was not very well explained. In 1969, Mitchell and his coworker stated “ can be equated to the Donnan potential” [4]. That is, based on the Mitchellian view of delocalized proton coupling bioenergetics, membrane potential would be a delocalized parameter somehow contributed by delocalized protons and ions in the two bulk liquid phases [5].
Mitchell's central bioenergetics equation has been incorporated into many textbooks [5, 6, 7, 8], which is expressed as the protonic motive force (pmf) across a biological membrane that drives protons through the ATP synthase; It is:
| (1) |
where is the electrical potential difference (which is defined as positive (p)-phase minus negative (n)-phase and is usually positive [5]) across the membrane; R is the gas constant; T is the absolute temperature; F is Faraday's constant; and ΔpH is defined as the pH in the p-phase (e.g., the intermembrane space of mitochondria) minus the pH in the n-phase (e.g., matrix) [5, 8]. In that chemiosmotic framework, the protons are considered to be solutes, similar to sugar molecules in water that are delocalized staying everywhere in the liquid; thus whose electrochemical gradient was thought to be delocalized between the two bulk aqueous phases. Consequently, the Mitchellian view of bioenergetics is that the ATP synthase is coupled to the redox-driven proton pumps via bulk phase-to-bulk phase proton electrochemical potential gradients generated across the biological membrane. The chemiosmotic theory was a major milestone in the history of bioenergetics; its significance to the field could hardly be overstated.
However, we now know that the textbook Mitchellian pmf Eq. (1) is not entirely correct and thus must be revised [9, 10, 11, 12]. The most well-established observations that disagree with Eq. (1) are in alkalophilic bacteria, such as Bacillus pseuodofirmus [13, 14, 15]. The alkalophilic bacteria keep their internal pH about 2.3 units more acidic than the ambient bulk liquid pH while Δψ is about 180 mV [16, 17, 18]. The use of Mitchellian Eq. (1) in this case yields a pmf value so small (44 mV at T = 298 K) that has eluded mechanistic explanation for decades as to how these organisms are able to synthesize ATP [19, 20, 21].
Meanwhile, the question as to what extent the proton coupling pathway for producing ATP is delocalized throughout the bulk aqueous volume or localized at the membrane surface has remained open since it was first raised in 1961 by Williams [22, 23, 24, 25, 26, 27, 28, 29]. A number of well-documented observations, such as the localized proton coupling characteristics observed in the “low salt” treated thylakoids of the Chiang-Dilley experiment [30] and the ΔpH surface component of pmf in ATP synthesis of mitochondria [31] could not be explained by Mitchell's delocalized proton view. The newly reported lateral pH gradient between the OXPHOS complex IV and the F0F1 ATP-synthase in folded mitochondrial membranes [32] also indicates a need for “a modification to Peter Mitchell's chemiosmotic proposal.” A recent biomimetic study [33] appears to point to a similar localized proton phenomenon [34]. Furthermore, it has been noticed that the use of Mitchell's chemiosmotic theory was not even able to satisfactorily explain the bioenergetics in mitochondria and E. coli under certain conditions without considering the localized protons [35].
Recently, the author developed an electrostatic proton localization model [9, 36] that explains how free excess protons in an aqueous medium separated by an impermeable membrane alone can be localized spontaneously at the liquid-membrane interface. Moreover, a newly developed pmf equation to account for localized protons at a liquid-membrane interface was introduced and shown to result in a large enough pmf to synthesize ATP in alkalophilic bacteria [9, 37].
Our recent study [12] has also clarified that neither the Gouy-Chapman theory [38] nor the Debye length concept could be applied to estimate the thickness of the localized excess proton layer here, because the equations used in calculating the Debye length can be applied only to charge-balanced solutions including 1:1 electrolyte solutions such as NaCl [39]. Since the membrane is just an insulator layer (not an electrode), the excess proton layer at the water-membrane interface is likely to be a special monolayer (with a thickness probably of about 1 nm), but definitely not an “electric double layer” as that of a typical electrode as expected by the Gouy-Chapman theory [38]. The conclusion that there is an excess proton monolayer is also consistent with the known “electric double layer” phenomenon since the excess proton layer can be treated as an extension from the second (proton) layer of the anode's “electric double layer” around the proton-conductive water body surface as illustrated in Fig. 1a [12].
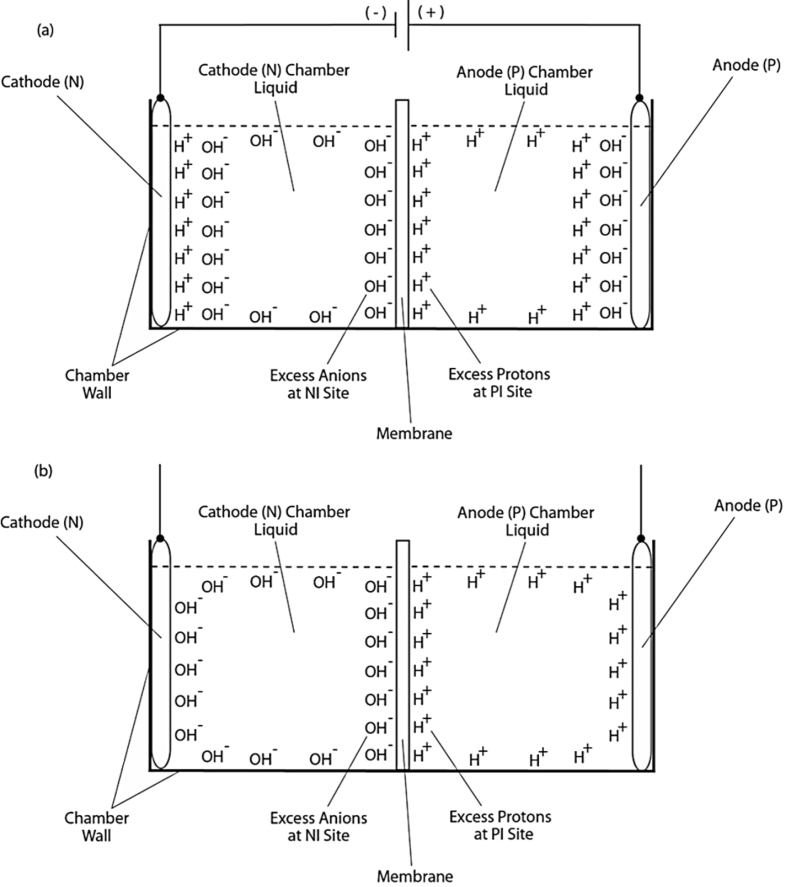
Fig. 1.
Schematic diagram showing experimental demonstration of an electrostatically localized excess protons layer at the water-membrane interface in an “anode water-membrane-water cathode” system. Top (a): showing the excess proton monolayer is extended from a secondary proton layer of the “electric double layer” that covers the anode surface when electrolysis voltage is applied; Bottom (b): showing the likely distribution of excess protons and excess hydroxyl anions in the two water chambers separated by a membrane when electrolysis voltage is turned off. Adapted from Saeed and Lee 2018 WATER Journal: Multidisciplinary Research Journal 9:116–140.
Previously, we demonstrated the formation of an electrostatically localized layer of excess protons at the water-membrane interface in biomimetic experiments using an anode water-membrane-water cathode system [10], where excess protons were generated by water electrolysis in an anode electrode chamber and excess hydroxyl anions were created in a cathode chamber. When a positive voltage is applied to the anode electrode in water, it first attracts the hydroxyl anions to the anode electrode surface and then counter-ions (protons) distribute themselves near the anions layer, forming a typical “electric double layer” on the anode surface (Fig. 1a) [12]. When a significant number of excess protons are produced by water electrolysis in the anode chamber, the excess protons electrostatically distribute themselves at the water-surface interface around the water body including a part of the “electric double layer” at the anode surface. From here, it can be seen that the excess proton layer at the water-membrane interface is apparently extended away from the secondary (proton) layer of the “electric double layer” at the anode. The excess proton layer at the water-membrane interface electrostatically attracts the excess hydroxyl anions in the cathode chamber at the other side of the membrane, forming an “excess anions-membrane-excess protons” capacitor structure (Fig. 1a) [12]. When the electrolysis voltage is turned off, the electric polarization at both anode and cathode disappears and so does the “electric double layer”, leaving only the excess proton layer around the anode chamber water body and the similarly formed excess hydroxyl (anions) layer around the cathode chamber water body (Fig. 1b) [12]. The resulting excess anions-membrane-excess protons capacitor may represent a proof-of-principle mimicking of an energized biological membrane such as a mitochondrial membrane system at its energized resting state [12].
In this article for addressing the fundamental question on the origin for the membrane potential, the localized proton bioenergetics analysis [9] is now extended and further employed to calculate the concentrations for both localized protons and localized cations at the liquid-membrane interface, using the newly determined cation-proton exchange equilibrium constants for sodium, potassium and magnesium cations from our recent experimental study [12] and using the experimental data from the well-documented animal mitochondria study [40]. This enables much better understanding of the membrane potential in proton coupling bioenergetics.
2. Theory/calculation
2.1. Theory
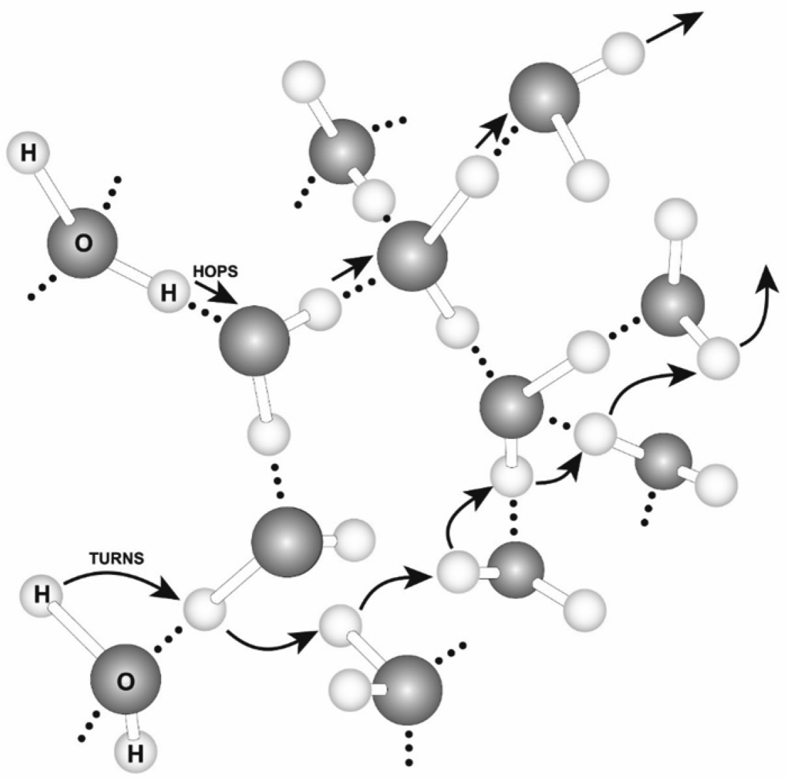
According to the electrostatic proton localization model [9, 11, 36], excess positively charged protons in an aqueous medium on one side of a membrane will electrostatically repel each other to become localized at the membrane surface, attracting an equal number of excess negatively charged hydroxyl anions to the other side of the membrane to form a “protonic capacitor structure”. This theory rests on the premise that a water body acts as a protonic conductor as illustrated in Fig. 2, which is consistent with the well-established knowledge that protons quickly transfer among water molecules by the “hops and turns” mechanism first outlined by Grotthuss [41, 42, 43]. That is, liquid water can act as a protonic conductor since protons can quickly transfer among water molecules by the “hops and turns” mechanism. Notice also that, from the negative charge point of view, hydroxyl anions are transferred in the opposite direction of proton conduction.
Fig. 2.
Protons can quickly transfer among water molecules by the “hops and turns” mechanism so that a microscopic water body may be thought of as a protonic conductor. Adapted from Lee 2012 Bioenergetics1: 104, 1–8.
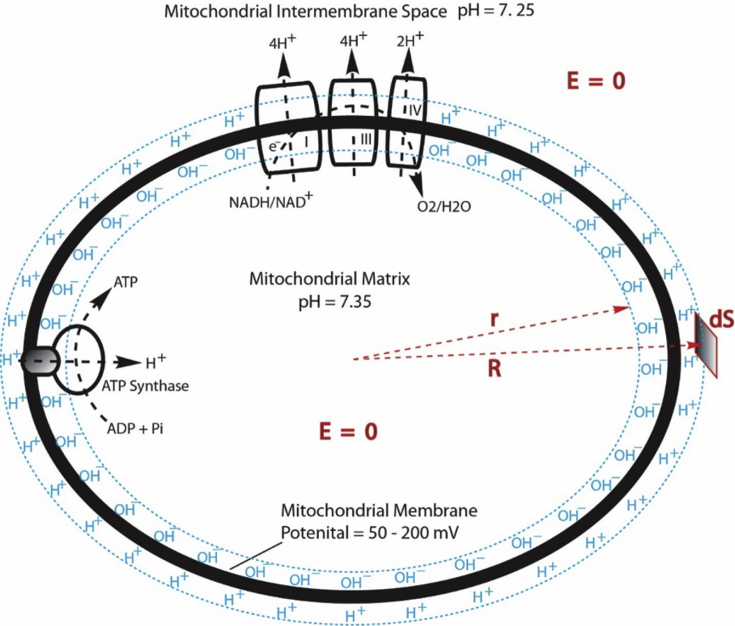
In mitochondria such as the animal mitochondria [40], as illustrated in Fig. 3, the mitochondrial intermembrane space contains liquid water (pH = 7.25) which is a protonic conductor (Fig. 2); the mitochondrial inner membrane is an insulator which is largely impermeable to ions; and the mitochondrial matrix contains liquid water (pH = 7.35) which is also a protonic conductor. Therefore, the intermembrane space liquid-inner membrane-matrix liquid system (Fig. 3) constitutes a protonic “conductor-insulator-conductor” system, which by definition naturally is a protonic capacitor.
Fig. 3.
Proton-electrostatic localization model illustrating how excess protons (H+) and hydroxyl ions (OH–) could be electrostatically localized at the water-membrane interfaces along the two sides of the mitochondrial inner membrane before proton-cation exchange as it would be in a theoretically pure water-membrane-water system.
Consequently, as shown in Fig. 3, when the redox-driven proton pumps (which, for an example, comprises the oxidative membrane protein complexes I, III and IV, using NADH as the source of electrons and O2 as the terminal electron acceptor) transport protons from the matrix into the mitochondrial intermembrane space across the mitochondrial inner membrane, it will create excess protons in the intermembrane space and leave excess hydroxyl anions in the matrix. The excess hydroxyl anions in the matrix will not stay in the bulk water phase because of their mutual repulsion and consequently they go to the water-membrane interface at the matrix side of the membrane where they then attract the excess protons at the intermembrane space side of the inner membrane, forming an “excess protons-membrane-excess anions” capacitor system (Fig. 3). Therefore, the excess protons are localized at the water-membrane interface at the intermembrane space side of the inner membrane by the electrostatic attraction from the excess anions at the other side of the membrane.
This proton-electrostatic localization theory [9, 36] suggests that excess free protons in a microscopic water body behave like electrons in a typical conductor. It is well known that for a charged electrical conductor at static equilibrium, all the (extra) electrons reside on the conducting body's surface [44]. It is reasonable to expect this since electrons repel each other, and, being free to move, they will spread out to the surface. By the same token, it is reasonable to expect that free excess protons (or conversely the excess hydroxyl anions) in a microscopic water body will move to its surface. Adapting this view to excess free hydroxyl anions in the mitochondrial matrix (created by pumping protons across the mitochondrial inner membrane into the intermembrane space through the electron-transport-coupled proton-transfer system), they will be electrostatically localized along the water-membrane interface at the matrix (n) side of the mitochondrial inner membrane. In addition, their negative charges (OH–), will attract the positively charged species, namely the excess protons (H+) in the intermembrane space to the membrane-water interface at the p-side of the membrane, as illustrated in Fig. 3.
This theoretical prediction for electrostatic proton localization at liquid-membrane interface can be mathematically justified by using the Gauss Law equation of electrostatics and the fact that there can be no electric field E inside a protonic conductor (Fig. 2). Gauss's Law relates the net charge Q within a volume to the flux of electric field lines through the closed surface surrounding the volume in the following equation, as shown in Ref. [44],
| (2) |
where εo is the electric permittivity constant and dS is a differential surface element. Here the small circle on the integral sign indicates that the integration is performed over the closed surface. Consider then a series of integration applications, where a small volume at the center of the mitochondrial matrix liquid is gradually increased until it is just inside the matrix liquid surface, indicated by r in Fig. 3. By definition, the electric field E is zero everywhere in a conductive body. Thus, in each case the left side of Eq. (2) vanishes and therefore the right side must also vanish, which means that no net charge (Q = 0) is within the volume; the excess hydroxyl anions in this case must therefore be at the matrix water-body surface, i.e. at the water-membrane interface along the n side of mitochondrial inner membrane surface.
Similarly, considering the proton-conductive water at the mitochondrial intermembrane space, the electric field E = 0 holds true everywhere in the water body of the intermembrane space. Applying Gauss's Law to a series of volumes enclosing the entire mitochondrial system and decreasing them to be just outside the mitochondrial inner membrane surface (indicated by R in Fig. 3), the surface integrals of Eq. (2) vanish and so no net excess charge is found. Since the excess hydroxyl anions are at the matrix side, the positive charges (excess protons) must be at the membrane-water interface along the membrane surface at the intermembrane space (p) side, precisely balancing the excess hydroxyl anions of the matrix (n) side, making the total net charge of the entire system zero.
In addition to the theoretical development [9, 36], the predicted formation of an “excess protons-membrane-excess anions” protonic capacitor has recently been experimentally demonstrated in the Lee laboratory using biomimetic “water-membrane-water” systems [10, 11, 12, 45].
2.2. Newly formulated protonic motive force equation with electrostatically localized protons
With both the new theory on electrostatically localized protons [9, 36, 46] and the successful experimental demonstration of a protonic capacitor using biomimetic “water-membrane-water” systems [10, 11, 12, 45], it is now very clear that the textbook Mitchellian pmf equation (Eq. 1) is not entirely correct since it misses the contribution from the electrostatically localized protons at the liquid-membrane interface that is rightly at the protonic inlet mouth of the ATP synthase (Fig. 3). Therefore, according to the proton-electrostatics localization theory [9, 36, 46], the Mitchellian protonic motive force Eq. (1), which has been in many textbooks for nearly a half century, must now be revised. First of all, it is important to note that the proton-electrostatics localization (Fig. 3) clearly indicates that the excess protons and hydroxyl ions may directly contribute to the trans-membrane potential difference Δψ. In addition, the localized excess protons (their population density) will increase the probability for protons to be available at the ATP synthase, independently from that implied by the bulk liquid pH value. To account for this effect, the author has generalized the protonic motive force equation for ATP synthesis as
| (3) |
where is the mitochondrial matrix (n) bulk liquid phase pH; is the effective concentration of electrostatically localized protons at the liquid-membrane interface along the p-side of mitochondrial inner membrane; and is the p-side bulk liquid phase proton concentration in the intermembrane space.
Note, the newly formulated pmf equation (Eq. 3) described above shows that the total effective proton concentration is the sum of both the localized proton concentration and the delocalized proton concentration proton . This is consistent with the proton-electrostatic localization model (Fig. 3) showing that both the localized protons at the liquid-membrane interface and the delocalized protons in the bulk liquid phase can enter the protonic inlet mouth of the ATP synthase. This well fits with the proton-electrostatic localization model (Fig. 3) that can explain both the proton localization and delocalization phenomena without requiring any of the “localized proton microcircuits”, or physical barrier including the hypothetical protein-based “occluded space” [47] and/or the putative interfacial potential barrier models [34, 48, 49, 50, 51]. Based on the experimental observation that the excess protons created in a bulk liquid phase can readily enter into the liquid-membrane interface forming an “excess protons-membrane-excess anions” capacitor, it is now quite clear that the putative interfacial potential barrier [34, 49, 50, 51] is either probably not real or not required to form the protonic capacitor.
To better isolate and show the contribution of the localized protons, the newly formulated pmf equation (Eq. 3) is now reorganized as follows:
| (4) |
The first two terms of Eq. (4) comprise the “classic” bulk phase-to-bulk phase proton electrochemical potential gradients expression for the pmf as noted in Eq. (1); whereas the last term accounts for the “local” pmf from the electrostatically localized protons. Here again is the concentration of electrostatically localized protons at the liquid-membrane interface on the positive (p) side of the membrane, is the proton concentration in the bulk liquid p-phase (intermembrane space in the case of mitochondria), and is the proton concentration in the bulk liquid n-phase (matrix in mitochondria).
For an idealized protonic capacitor, the concentration of the ideal localized protons at the water–membrane interface on the p-side is related to the transmembrane electrical potential difference by
| (5) |
where is the specific membrane capacitance per unit surface area, is the thickness of the localized proton layer. Note, the novel use of (the thickness of the localized proton layer) and (Faraday constant) in this equation converts the capacitor surface charge density into a quantity of localized proton concentration in the units of molarity compatible with the modern thermodynamic parameters that are now useful to pmf calculation.
In actual biological systems such as mitochondria, non-proton cations such as Na+, K+, and Mg++ in the aqueous media may exchange with the localized protons at the liquid-membrane interface and thereby reduce their concentration. For example, a non-proton cation such as a sodium cation of the bulk liquid p-phase may exchange with a localized proton at the liquid-membrane interface (Fig. 3) as expressed in the following cation-proton exchange reaction:
| (6) |
where represents a sodium cation exchanged into the localized proton layer at the liquid-membrane interface and is a proton in bulk liquid p-phase (intermembrane space). Consequently, the sodium-proton exchange equilibrium constant is defined as
| (7) |
where the localized sodium cation concentration is the difference between the initial localized proton concentration before cation exchange and the localized proton concentration after the sodium-proton exchange as shown in the following equation.
| (8) |
Through the use of Eq. (8) to substitute in Eq. (7), the sodium-proton exchange equilibrium constant can now be expressed as
| (9) |
From Eq. (9), we can solve for the localized proton concentration at the sodium-proton exchange equilibrium as
| (10) |
Note, the denominator in Eq. (10) is the “reduction factor” owing to the effect of sodium cation exchange with the localized protons.
After the sodium-proton exchange that results in as expressed in Eq. (10), let's now further consider to add K+ in the bulk liquid p-phase. Based on author's analysis using a way similar to that of Eqs. 6, 7, 8, 9 and 10, the localized proton concentration after exchange with both Na+ and K+ may be expressed in the following equation.
| (11) |
By use of Eq. (10) to substitute in Eq. (11), it can now show:
| (12) |
That is, the localized proton concentration after exchange with both Na+ and K+ is reduced from the initial localized proton concentration by a factor that is a product (multiplication rather than summation) of the two reduction factors associated with each of Na+ and K+ as shown in the following equation.
| (13) |
Therefore, for any number (n) of different non-proton cation species such as Na+, K+, and Mg++ present in the bulk liquid p-phase, the localized proton concentration (at the equilibrium state) after exchange with all of the cation species may be generalized as follows
| (14) |
Here is the concentration of any non-proton cation in the p-phase and is the equilibrium constant for each of the cation species to exchange with the localized protons. Note, the denominator in Eq. (14) is the reduction factor owing to the effect of cation exchange with the localized protons. The total contribution of the non-proton cations to this reduction factor surprisingly is a product (multiplication not summation) of the reduction factors associated with each of the non-proton cation species in the bulk liquid p-phase such as Na+, K+, and Mg++.
It is noteworthy that all the physical quantities appearing in Eqs. (3), (4), (5), (6), (7), (8), (9), (10), (11), (12), (13) and (14) may, in principle, be determined through experimental measurements. There are no freely adjustable parameters. For the membrane and protonic capacitor parameters in Eq. (5), the calculations reported in this article have taken C/S = 13.2 mf/m2 as an averaged membrane capacitance based on measured experimental data [52] and = 1 nm, which, as discussed in Ref. [9, 10], is a reasonable thickness of the localized proton layer. It is also noteworthy that the thickness of the localized proton layer is an important parameter that is not well known. It may govern the magnitude of the localized proton concentration.
Note, in some of the literature, the membrane potential might have been reported as a “negative” number [16, 17, 18] because of using an opposite reference orientation (from n-side to p-side) [53, 54] in contrast to that of the defined in Eq. (4) from the p-side to the n-side as defined by Mitchell [55, 56], Nicholls and Ferguson [5, 8]. In that case, special care must be taken to correct (remove) the negative sign for such membrane potential data with the opposite orientation such as that of ref [18, 40, 57] before applying it to the pmf Eq. (4). By using Eqs. (5) and (14), the population densities (concentrations) of electrostatically localized protons and localized non-proton cations at the liquid-membrane interface were analyzed as a function of membrane potential in animal mitochondria.
3. Results and discussion
3.1. The origin of membrane potential as a function of electrostatically localized protons and cations
According to the Lee model [9, 11] of electrostatically localized protons as shown in Eq (5), exists precisely because of the excess cations (including H+) and the excess anions (such as OH−) charge layers localized on the two sides of the membrane in a protons-membrane-anions capacitor structure (Fig. 3). This also explains the origin of and its relation with the concentration of electrostatically localized protons as expressed in Eqs (5) and (14). Consequently, the membrane potential (difference) created by the localized proton concentration before cation exchange with the localized protons may be expressed as in the following equation:
| (15) |
where is the specific membrane capacitance per unit surface area, is the thickness of the localized proton layer, and F is the Faraday constant.
From the protonic capacitor-based membrane potential equation (Eq. 15), we can now clearly understand that the membrane potential (difference) is a function of the ideal localized proton concentration . This now also explains the physical origin of membrane potential as a function of the localized excess proton concentration under the idealized condition such as in an idealized pure water-membrane-water system.
In a real biological system, the cation-proton exchange will reduce the localized proton concentration from to ; but it typically does not change the membrane potential. Therefore, the relationship between and may be expressed with the product of cation exchange reduction factors as
| (16) |
Consequently, by combining Eqs. (15) and (16), the membrane potential difference at the cation-proton exchange equilibrium may be expressed as
| (17) |
Since the cation-proton exchange typically does not change the total localized (positive) charge density at the liquid-membrane interface, the ideal localized protons equals to the sum of the localized proton concentration and the localized cation concentrations at the cation-proton exchange equilibrium as shown in the following equation.
| (18) |
where is the concentration for each of the localized non-proton cations such as sodium and potassium cations in cation-proton exchange equilibrium at a liquid-membrane interface. Therefore, the membrane potential difference can also be expressed as
| (19) |
This protonic/cationic capacitor-based equation (Eq. 19) now also explains the physical origin of membrane potential (difference) as a function of the localized proton concentration and localized cation concentrations in a real biological membrane system at cation-proton exchange equilibrium. That is, the membrane potential in proton-coupling bioenergetics represents a localized protonic/cationic membrane capacitor behavior.
From this membrane potential equation (Eq. 19), it is now also quite clear that the protons and ions in a permanent “electric double layer” formed as a result of membrane surface's fixed-charges such as the negatively-charged phosphate groups of phospholipids that permanently attract protons and cations are not relevant to the membrane potential in the proton-coupling bioenergetics. This is consistent with the conclusion made in the previous study [46] that the membrane surface-fixed-charges-attracted protons are not relevant to the pmf that drives ATP synthesis.
This protonic/cationic capacitor-based equation (Eq. 19) may also help clarifying that the “intrinsic membrane dipole potential” contributed by the intrinsic membrane properties such as phospholipid carbonyl groups and lipids-bound water molecules [58, 59] is not part of the membrane potential in proton-coupling bioenergetics. Similarly, the property of water orientation at hydrophobic interfaces [60] and the putative energy barrier for protons at hydrophobic liquid interfaces [34] are not immediately relevant to the membrane potential . Our previous study [12] also found no support for the putative interfacial potential barrier model [48] that anyhow is not really required to explain the localized proton coupling bioenergetics [9].
3.2. Nernst equation applicable as a way to estimate membrane potential
In the field of bioenergetics, the Nernst equation (Eq. 20) [5] has been widely used to estimate the membrane potential
| (20) |
where and are the concentration of a special membrane-potential probing cation (with its valance charge m) in the two bulk liquid phases: one at the positive (p) side of the membrane and the other at the negative (n) side of the membrane, respectively.
According to the Lee model of electrostatically localized protons (Fig. 3) [9], the Nernst equation (Eq. 20) is still applicable as a practical way to estimate the membrane potential . This is true as long as the concentration of the membrane-potential probing cation (with its valance charge ) such as Rb+ or K+ is not too high (for example by comparing the gradients of K+ and the cation across the inner membrane of mitochondria in the presence of the K+ ionophore valinomycin and varying low K+ concentrations) [61], so that its use would not significantly perturb the total localized surface charge density at the liquid-membrane interface and thus the true membrane potential . Under this condition, the membrane potential can also be expressed as
| (21) |
3.3. Effect of cation exchange with electrostatically localized protons as calculated in animal mitochondria
Concentrations of the major cations Na+, K+, and Mg++ in the mitochondria are presented in Table 1. They were calculated from the composition of the reaction medium reported in Ref. [40]. Also shown in Table 1 are the cation-proton exchange equilibrium constants used in this study. The values for Na+ and K+ were experimentally determined to be 5.07 × 10−8 and 6.93 × 10−8, respectively [12]. The value of 5.42 × 10−6 for Mg++ was determined from the latest experimental data of divalent cation Mg++ exchange with electrostatically localized protons at a membrane-liquid interface in the Lee laboratory through a study similar to that reported in Ref. [12].
Table 1.
Experimental cation concentrations in the mitochondria reaction medium (as reported in ref. [40]), estimated cation-proton exchange equilibrium constants, and calculated cation exchange reduction factors of the surface proton concentration at the reaction medium = 7.25.
| Cation species | Cation species concentration | Exchange equilibrium constant | |
|---|---|---|---|
| Na+ | 10 mM | 5.07 × 10−8 | 1.01 |
| K+ | 128 mM | 6.93 × 10−8 | 1.16 |
| Mg++ | 1.0 mM | 5.42 × 10−6 | 1.10 |
| Total product of cation exchange reduction factors: | 1.29 | ||
In the assay of mitochondrial ATP-ADP exchange by Chinopoulos et al (2009) [40], mitochondrial membrane potential was measured in a range from 60 to 160 mV using fluorescence quenching of a cationic dye due to its accumulation inside energized mitochondria. Their experimental data showed ATP synthesis as measured by ATP efflux rate at a membrane potential as low as anywhere between 60 and 80 mV (Figure 7C of Ref [40]). More importantly, by measuring of matrix pH using pH-sensitive fluorescence ratio to the pH of the extracellular volume, their experimental work [40] showed that there is essentially no or little bulk-phase pH difference across the mitochondrial inner membrane: the “ΔpHmax is only ∼0.11”. That is, under the given reaction medium pH 7.25 (), mitochondria matrix pH during state three was about 7.35 (). This experimental observation is consistent with our latest experimental results from a biomimetic anode water-membrane-water cathode system where the bulk-phase liquid pH in the anode liquid chamber remains about the same as that in the cathode chamber liquid before and after energization by excess protons at one side of the membrane and excess hydroxyl anions at the other side [10, 11, 12, 45]. Therefore, the measured experimental parameters (data) of the reaction medium pH 7.25 () and mitochondria matrix pH 7.35 () during the state three as reported by Chinopoulos et al (2009) were used in the bioenergetics calculations here.
Table 1 lists the calculated cation exchange reduction factors of the localized surface proton concentration for = 7.25, which was the incubation medium pH used in the mitochondrial membrane potential () determination experiment [40]. The total product of these factors (total cation exchange reduction factor in the denominator of Eq. 14) is 1.29, which is fairly close to one, indicating a relatively minor role of cation-proton exchange at the membrane surface in modulating the electrostatically localized surface proton concentration in mitochondria.
For example, when the transmembrane electrical potential difference () is 120 mV, the localized proton population density before the cation-proton exchange process is calculated to be 16.4 mM (listed in Table 2). In this example, the localized proton concentration is reduced by the cation exchange to 16.4 mM/1.29 = 12.7 mM, which is equivalent to a localized proton layer pH of 1.90 ─ remarkably lower than the bulk liquid medium pH of 7.25.
Table 2.
The concentrations of electrostatically localized protons and localized cations at the liquid-membrane interface calculated as a function of transmembrane potential using Eqs. (5) and (14) under the given reaction medium pH 7.25 (), mitochondria matrix pH 7.35 ().
| (mV) | 0 (mM) | Exchange reduction factor |
(mM) |
(mM) |
Total localized charge density (mM) | ||
|---|---|---|---|---|---|---|---|
| 50 | 7.25 | 7.35 | 6.84 | 1.29 | 5.30 | 1.54 | 6.84 |
| 55 | 7.25 | 7.35 | 7.52 | 1.29 | 5.83 | 1.69 | 7.52 |
| 60 | 7.25 | 7.35 | 8.21 | 1.29 | 6.36 | 1.85 | 8.21 |
| 65 | 7.25 | 7.35 | 8.89 | 1.29 | 6.89 | 2.00 | 8.89 |
| 70 | 7.25 | 7.35 | 9.58 | 1.29 | 7.42 | 2.15 | 9.58 |
| 75 | 7.25 | 7.35 | 10.3 | 1.29 | 7.95 | 2.31 | 10.3 |
| 80 | 7.25 | 7.35 | 10.9 | 1.29 | 8.48 | 2.46 | 10.9 |
| 90 | 7.25 | 7.35 | 12.3 | 1.29 | 9.55 | 2.77 | 12.3 |
| 100 | 7.25 | 7.35 | 13.7 | 1.29 | 10.6 | 3.08 | 13.7 |
| 110 | 7.25 | 7.35 | 15.0 | 1.29 | 11.7 | 3.38 | 15.0 |
| 120 | 7.25 | 7.35 | 16.4 | 1.29 | 12.7 | 3.69 | 16.4 |
| 130 | 7.25 | 7.35 | 17.8 | 1.29 | 13.8 | 4.00 | 17.8 |
| 140 | 7.25 | 7.35 | 19.2 | 1.29 | 14.8 | 4.31 | 19.2 |
| 150 | 7.25 | 7.35 | 20.5 | 1.29 | 15.9 | 4.61 | 20.5 |
| 160 | 7.25 | 7.35 | 21.9 | 1.29 | 17.0 | 4.92 | 21.9 |
| 170 | 7.25 | 7.35 | 23.3 | 1.29 | 18.0 | 5.23 | 23.3 |
| 180 | 7.25 | 7.35 | 24.6 | 1.29 | 19.1 | 5.54 | 24.6 |
| 190 | 7.25 | 7.35 | 26.0 | 1.29 | 20.2 | 5.84 | 26.0 |
| 200 | 7.25 | 7.35 | 27.4 | 1.29 | 21.2 | 6.15 | 27.4 |
3.4. Electrostatically localized protons and localized cations at the liquid-membrane interface calculated as a function of membrane potential in animal mitochondria
Table 2 lists the concentrations of electrostatically localized protons and localized cations calculated as a function of transmembrane potential using Eqs. (5) and (14) under the given reaction medium pH 7.25 (), mitochondria matrix pH 7.35 () and taking cation-proton exchange into account as explained above.
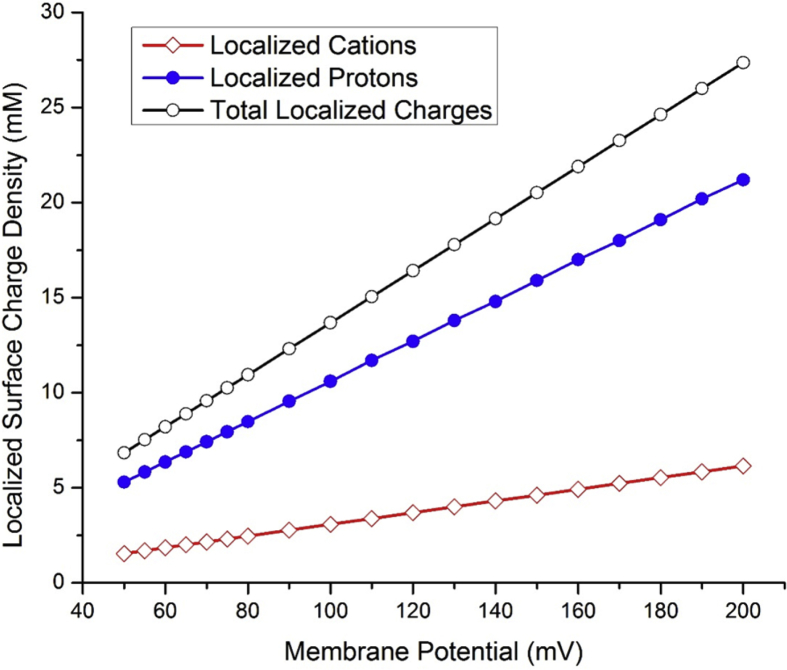
As listed in Table 2 and presented in Fig. 4, the concentration of electrostatically localized protons at the liquid-membrane interface calculated in animal mitochondria is in a range from about 5.30 to 21.2 mM depending on the membrane potential . The concentration of electrostatically localized non-proton cations including Na+, K+ and Mg++ at the liquid-membrane interface is in a range from about 1.54 to 6.15 mM. As shown in Fig. 4, both the concentration of the localized protons and that of the localized non-proton cations at the liquid-membrane interface increase with the membrane potential in animal mitochondria.
Fig. 4.
Localized surface charge density (mM) contributed by electrostatically localized protons and localized cations at the liquid-membrane interface calculated as a function of membrane potential (mV) in animal mitochondria.
The total localized surface charge density which is the sum of the localized protons and the localized non-proton cations is in a range from 6.84 to 27.4 mM. As listed Table 2, the total localized surface charge density equals to the ideal localized proton population density before the cation-proton exchange process. This is true since the cation-proton exchange process does not change the total localized charges density, neither does it change to the membrane potential .
The electrostatically localized proton concentration is the dominant component, which accounts about 78% of the total localized surface charge density at the cation-proton exchange equilibrium state in animal mitochondria (Table 2 and Fig. 4).
4. Conclusion
The origin of membrane potential is now better understood as the voltage difference across the protons/cations-membrane-anions capacitor, which is contributed by the electrostatically localized protons/cations at the liquid-membrane interface at the p side of the membrane in electrostatic balance with the surface localized anions at the n side of the membrane. That is, the membrane potential in proton-coupling bioenergetics represents a localized protonic/cationic membrane capacitor behavior.
As shown in the newly formulated protonic/cationic capacitor-based Eqs (15, 17 and 19), membrane potential can now be expressed as a function of the ideal electrostatically localized proton density or the total localized surface charge density. Therefore, the Lee proton electrostatic localization model (Fig. 3) [9, 37] with its definition of localized protons as shown in Eqs (5) and (14) adds significant clarification to the origin of membrane potential , well beyond the Mitchellian Eq. (1) that contains the term but does not clearly explain its origin. In the newly formulated pmf Eq. (4), the membrane potential that helps to drive protons through the ATP synthase is also the same factor in Eq. (5) that determines the concentration of surface localized protons which are available to the ATP synthase.
Therefore, the physical origin for membrane potential is the electrostatic formation of the localized surface charge density that is the sum of the localized proton concentration and the localized non-proton cations density at the liquid membrane interface. The total localized surface charge density equals to the ideal localized proton population density since the cation-proton exchange process does not change the total localized charges density, neither does it change to the membrane potential . The Nernst equation (Eq. 20) can still be applied here as a practical way to estimate the membrane potential as long as the concentration of the probing cation such as K+ is not too high so that its use would not significantly perturb the total localized surface charge density at the liquid-membrane interface.
In animal mitochondria, the electrostatically localized proton concentration is the dominant component, which accounts about 78% of the total localized surface charge density at the cation-proton exchange equilibrium state (data in Table 2 and Fig. 4). Therefore, liquid water as a type of protonic conductor (Fig. 2) may play a significant role in the biological activities of membrane potential formation and utilization (Fig. 3).
Declarations
Author contribution statement
James Weifu Lee: Conceived and designed the study; Performed the study; Analyzed and interpreted the data; Wrote the paper.
Funding statement
This work was supported in part with the Lee laboratory start-up research funds provided by the Department of Chemistry and Biochemistry, the College of Sciences, the Office of Research at Old Dominion University, and by the Old Dominion University Research Foundation.
Competing interest statement
The author declares no conflict of interest.
Additional information
No additional information is available for this paper.
Acknowledgements
The author wishes to thank Drs. Thomas Thundat, Paul Falkowski, Daniel Sheehan, Tobias Baskin, Todd P. Silverstein, Peter Rich, David G. Nicholls, Donald R. Ort, David S. Cafiso, Gerald H. Pollack, Peter Pohl, Patrick G. Hatcher, and William H. Schlesinger for their discussions.
Appendix A. Supplementary data
The following is the supplementary data related to this article:
References
- 1.Mitchell P. Coupling of phosphorylation to electron and hydrogen transfer by a chemi-osmotic type of mechanism. Nature. 1961;191:144–148. doi: 10.1038/191144a0. [DOI] [PubMed] [Google Scholar]
- 2.Mitchell P. Possible molecular mechanisms of the protonmotive function of cytochrome systems. J. Theor. Biol. 1976;62:327–367. doi: 10.1016/0022-5193(76)90124-7. [DOI] [PubMed] [Google Scholar]
- 3.Mitchell P. David. Keilin's respiratory chain concept and its chemiosmotic consfuences. Nobel prize lecture. 1978;1:295–330. [Google Scholar]
- 4.Mitchell P., Moyle J. Estimation of membrane potential and pH difference across the cristae membrane of rat liver mitochondria. Eur. J. Biochem. 1969;7:471–484. doi: 10.1111/j.1432-1033.1969.tb19633.x. [DOI] [PubMed] [Google Scholar]
- 5.Nicholls D.G., Ferguson S.J. Bioenergetics. fourth ed. Academic Press; 2013. pp. 27–51. [Google Scholar]
- 6.Garrett R., Grisham C. fifth edn. Brooks.; 2013. Biochemistry; pp. 644–677. [Google Scholar]
- 7.Nelson D.L., Lehninger A.L., Cox M.M. sixth edn. Macmillan; 2013. Lehninger Principles of Biochemistry; pp. 731–791. [Google Scholar]
- 8.Nicholls D.G., Ferguson S.J. In: Bioenergetics 2. Nicholls David G., Ferguson Stuart J., editors. Academic Press; 1992. pp. 38–63. [Google Scholar]
- 9.Lee J. Proton-electrostatic localization: explaining the bioenergetic conundrum in alkalophilic bacteria. Bioenergetics. 2015;4(121):1–8. [Google Scholar]
- 10.Saeed H.A., Lee J.W. Experimental demonstration of localized excess protons at a water-membrane. Int. Bioenerg. 2015;4(127):1–7. [Google Scholar]
- 11.Lee, J. Localized Excess Protons and Methods of Making and Using the Same. United States Patent Application Publication No. US 20170009357 A1, 73pp. (2017).
- 12.Saeed H., Lee J. Experimental determination of proton-cation exchange equilibrium constants at water-membrane interface fundamental to bioenergetics. WATER J.: Multidiscip. Res. J. 2018;9:116–140. [Google Scholar]
- 13.Krulwich T.A. Bioenergetics of alkalophilic bacteria. J. Membr. Biol. 1986;89:113–125. doi: 10.1007/BF01869707. [DOI] [PubMed] [Google Scholar]
- 14.Krulwich T.A., Guffanti A.A. Alkalophilic bacteria. Annu. Rev. Microbiol. 1989;43:435–463. doi: 10.1146/annurev.mi.43.100189.002251. [DOI] [PubMed] [Google Scholar]
- 15.Olsson K., Keis S., Morgan H.W., Dimroth P., Cook G.M. Bioenergetic properties of the thermoalkaliphilic Bacillus sp. strain TA2. A1. J. Bacteriol. 2003;185:461–465. doi: 10.1128/JB.185.2.461-465.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sturr M.G., Guffanti A.A., Krulwich T.A. Growth and bioenergetics of alkaliphilic Bacillus firmus OF4 in continuous culture at high pH. J. Bacteriol. 1994;176:3111–3116. doi: 10.1128/jb.176.11.3111-3116.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Krulwich T.A. Alkaliphiles:‘basic’molecular problems of pH tolerance and bioenergetics. Mol. Microbiol. 1995;15:403–410. doi: 10.1111/j.1365-2958.1995.tb02253.x. [DOI] [PubMed] [Google Scholar]
- 18.Padan E., Bibi E., Ito M., Krulwich T.A. Alkaline pH homeostasis in bacteria: new insights. Biochim. Biophys. Acta Biomembr. 2005;1717:67–88. doi: 10.1016/j.bbamem.2005.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Guffanti A., Krulwich T. Bioenergetic problems of alkalophilic bacteria. Biochem. Soc. Trans. 1984;12:411. doi: 10.1042/bst0120411. [DOI] [PubMed] [Google Scholar]
- 20.Krulwich T.A., Gilmour R., Hicks D.B., Guffanti A.A., Ito M. Energetics of alkaliphilic Bacillus species: physiology and molecules. Adv. Microb. Physiol. 1998;40:401–438. doi: 10.1016/s0065-2911(08)60136-8. [DOI] [PubMed] [Google Scholar]
- 21.Krulwich T.A. 2011. Adaptive mechanisms of extreme alkaliphiles. Extremophiles handbook; pp. 119–139. [Google Scholar]
- 22.Vinkler C., Avron M., Boyer P.D. Initial formation of ATP in photophosphorylation does not require a proton gradient. FEBS Lett. 1978;96:129–134. [Google Scholar]
- 23.Ferguson S.J. Fully delocalised chemiosmotic or localised proton flow pathways in energy coupling?: a scrutiny of experimental evidence. Biochim. Biophys. Acta Rev. Bioenerg. 1985;811:47–95. [Google Scholar]
- 24.Dilley R.A., Theg S.M., Beard W.A. Membrane-proton interactions in chloroplast bioenergetics: localized proton domains. Annu. Rev. Plant Physiol. 1987;38:347–389. [Google Scholar]
- 25.Dilley R.A. On why thylakoids energize ATP formation using either delocalized or localized proton gradients–a Ca2+ mediated role in thylakoid stress responses. Photosynth. Res. 2004;80:245–263. doi: 10.1023/B:PRES.0000030436.32486.aa. [DOI] [PubMed] [Google Scholar]
- 26.Williams R. Chemical advances in evolution by and changes in use of space during time. J. Theor. Biol. 2011;268:146–159. doi: 10.1016/j.jtbi.2010.09.021. [DOI] [PubMed] [Google Scholar]
- 27.Williams R.J.P. Multifarious couplings of energy transduction. Biochim. Biophys. Acta. 1978;505:1–44. doi: 10.1016/0304-4173(78)90007-1. [DOI] [PubMed] [Google Scholar]
- 28.Williams R.J.P. Proton-driven phosphorylation reactions in mitochondrial and chloroplast membranes. FEBS Lett. 1975;53:123–125. doi: 10.1016/0014-5793(75)80001-9. [DOI] [PubMed] [Google Scholar]
- 29.Williams R.J.P. Possible functions of chains of catalysts. J. Theor. Biol. 1961;1:1–+. doi: 10.1016/0022-5193(61)90023-6. [DOI] [PubMed] [Google Scholar]
- 30.Chiang G.G., Dilley R.A. Intact chloroplasts show Ca-2+-Gated switching between localized and delocalized proton gradient energy coupling (atp formation) Plant Physiol. 1989;90:1513–1523. doi: 10.1104/pp.90.4.1513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Xiong J.W., Zhu L.P., Jiao X.M., Liu S.S. Evidence for Delta pH surface component (Delta pH(S)) of proton motive force in ATP synthesis of mitochondria. BBA-Gen. Subj. 2010:213–222. doi: 10.1016/j.bbagen.2009.07.032. 1800. [DOI] [PubMed] [Google Scholar]
- 32.Rieger B., Junge W., Busch K.B. Lateral pH gradient between OXPHOS complex IV and F0F1 ATP-synthase in folded mitochondrial membranes. Nat. Commun. 2014;5 doi: 10.1038/ncomms4103. [DOI] [PubMed] [Google Scholar]
- 33.Weichselbaum E. Origin of proton affinity to membrane/water interfaces. Sci Rep-Uk. 2017;7 doi: 10.1038/s41598-017-04675-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhang C. Water at hydrophobic interfaces delays proton surface-to-bulk transfer and provides a pathway for lateral proton diffusion. Proc. Natl. Acad. Sci. Unit. States Am. 2012;109:9744–9749. doi: 10.1073/pnas.1121227109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Silverstein T.P. An exploration of how the thermodynamic efficiency of bioenergetic membrane systems varies with c-subunit stoichiometry of F1F0 ATP synthases. J. Bioenerg. Biomembr. 2014;46:229–241. doi: 10.1007/s10863-014-9547-y. [DOI] [PubMed] [Google Scholar]
- 36.Lee J. Proton-electrostatics hypothesis for localized proton coupling bioenergetics. Bioenergetics. 2012;1(104):1–8. [Google Scholar]
- 37.Lee, J. Localized Excess Protons and Methods of Making and Using the Same, PCT International Patent Application Publication No. WO 2017/007762 A1, 56 pages (2017).
- 38.McLaughlin S. The electrostatic properties of membranes. Annu. Rev. Biophys. Biophys. Chem. 1989;18:113–136. doi: 10.1146/annurev.bb.18.060189.000553. [DOI] [PubMed] [Google Scholar]
- 39.Grahame D.C. The electrical double layer and the theory of electrocapillarity. Chem. Rev. 1947;41:441–501. doi: 10.1021/cr60130a002. [DOI] [PubMed] [Google Scholar]
- 40.Chinopoulos C. A novel kinetic assay of mitochondrial ATP-ADP exchange rate mediated by the ANT. Biophys. J. 2009;96:2490–2504. doi: 10.1016/j.bpj.2008.12.3915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Marx D., Tuckerman M.E., Hutter J., Parrinello M. The nature of the hydrated excess proton in water. Nature. 1999;397:601–604. [Google Scholar]
- 42.Pomès R., Roux B. Molecular mechanism of H+ conduction in the single-file water chain of the gramicidin channel. Biophys. J. 2002;82:2304–2316. doi: 10.1016/S0006-3495(02)75576-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Marx D. Proton transfer 200 years after von Grotthuss: insights from ab initio simulations. ChemPhysChem. 2006;7:1848–1870. doi: 10.1002/cphc.200600128. [DOI] [PubMed] [Google Scholar]
- 44.Ohanian H.C. Vol. 24. W. W. Norton & Company; 1985. pp. 565–573. (Physics Ch). [Google Scholar]
- 45.Saeed H. Old Dominion University; Norfolk, VA 23529 USA: 2016. Bioenergetics: Experimental Demonstration of Excess Protons and Related Features. PhD Thesis. [Google Scholar]
- 46.Lee J.W. Membrane surface charges attracted protons are not relevant to proton motive force. Bioenergetics. 2013;2:e114. [Google Scholar]
- 47.Dilley R.A. On why thylakoids energize ATP formation using either delocalized or localized proton gradients - a Ca2+ mediated role in thylakoid stress responses. Photosynth. Res. 2004;80:245–263. doi: 10.1023/B:PRES.0000030436.32486.aa. [DOI] [PubMed] [Google Scholar]
- 48.Mulkidjanian A.Y., Cherepanov D.A., Heberle J., Junge W. Proton transfer dynamics at membrane/water interface and mechanism of biological energy conversion. Biochemistry-Moscow+ 2005;70:251–256. doi: 10.1007/s10541-005-0108-1. [DOI] [PubMed] [Google Scholar]
- 49.Mulkidjanian A.Y., Heberle J., Cherepanov D.A. Protons @ interfaces: implications for biological energy conversion. Bba-Bioenergetics. 2006;1757:913–930. doi: 10.1016/j.bbabio.2006.02.015. [DOI] [PubMed] [Google Scholar]
- 50.Cherepanov D.A., Feniouk B.A., Junge W., Mulkidjanian A.Y. Low dielectric permittivity of water at the membrane interface: effect on the energy coupling mechanism in biological membranes. Biophys. J. 2003;85:1307–1316. doi: 10.1016/S0006-3495(03)74565-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Weichselbaum E. Origin of proton affinity to membrane/water interfaces. Sci Rep-Uk. 2017;7:4553. doi: 10.1038/s41598-017-04675-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zheng Y., Shojaei-Baghini E., Wang C., Sun Y. Microfluidic characterization of specific membrane capacitance and cytoplasm conductivity of single cells. Biosens. Bioelectron. 2013;42:496–502. doi: 10.1016/j.bios.2012.10.081. [DOI] [PubMed] [Google Scholar]
- 53.Azzone G. Transmembrane measurements across bioenergetic membranes. Biochim. Biophys. Acta. 1993;1183:1–3. [Google Scholar]
- 54.Bertl A. Electrical measurements on endomembranes. Science. 1992;258:873–874. doi: 10.1126/science.1439795. [DOI] [PubMed] [Google Scholar]
- 55.Mitchell P., Moyle J. Estimation of membrane potential and ph difference across cristae membrane of rat liver mitochondria. Eur. J. Biochem. 1969;7:471. doi: 10.1111/j.1432-1033.1969.tb19633.x. [DOI] [PubMed] [Google Scholar]
- 56.Mitchell P. The correlation of chemical and osmotic forces in Biochemistry. J. Biochem. 1985;97:1–18. doi: 10.1093/oxfordjournals.jbchem.a135033. [DOI] [PubMed] [Google Scholar]
- 57.Zhang H. Assessment of membrane potential's of mitochondrial populations in living cells. Anal. Biochem. 2001;298:170–180. doi: 10.1006/abio.2001.5348. [DOI] [PubMed] [Google Scholar]
- 58.Peterson U. Origin of membrane dipole potential: contribution of the phospholipid fatty acid chains. Chem. Phys. Lipids. 2002;117:19–27. doi: 10.1016/s0009-3084(02)00013-0. [DOI] [PubMed] [Google Scholar]
- 59.Chen X., Hua W., Huang Z., Allen H.C. Interfacial water structure associated with phospholipid membranes studied by phase-sensitive vibrational sum frequency generation spectroscopy. J. Am. Chem. Soc. 2010;132:11336–11342. doi: 10.1021/ja1048237. [DOI] [PubMed] [Google Scholar]
- 60.Strazdaite S., Versluis J., Bakker H.J. Water orientation at hydrophobic interfaces. J. Chem. Phys. 2015;143 doi: 10.1063/1.4929905. [DOI] [PubMed] [Google Scholar]
- 61.Nicholls D.G., Ferguson S.J. Bioenergetics. fourth ed. Academic Press; 2013. pp. 53–87. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.