Charge Distributions of Nitro Groups Within Organic Explosive Crystals: Effects on Sensitivity and Modeling

Abstract

The charge distribution of NO₂ groups within the crystalline polymorphs of energetic materials strongly affects their explosive properties. We use the recently introduced basis-space iterated stockholder atom partitioning of high-quality charge distributions to examine the approximations that can be made in modeling polymorphs and their physical properties, using 1,3,5-trinitroperhydro-1,3,5-triazine, trinitrotoluene, 1-3-5-trinitrobenzene, and hexanitrobenzene as exemplars. The NO₂ charge distribution is strongly affected by the neighboring atoms, the rest of the molecules, and also significantly by the NO₂ torsion angle within the possible variations found in observed crystal structures. Thus, the proposed correlations between the molecular electrostatic properties, such as trigger-bond potential or maxima in the electrostatic potential, and impact sensitivity will be affected by the changes in conformation that occur on crystallization. We establish the relationship between the NO₂ torsion angle and the likelihood of occurrence in observed crystal structures, the conformational energy, and the charge and dipole magnitude on each atom, and how this varies with the neighboring groups. We examine the effect of analytically rotating the atomic multipole moments to model changes in torsion angle and establish that this is a viable approach for crystal structures but is not accurate enough to model the relative lattice energies. This establishes the basis of transferability of the NO₂ charge distribution for realistic nonempirical model intermolecular potentials for simulating energetic materials.

Introduction

Energetic materials, which decompose explosively under various external stimuli, are intrinsically difficult to study experimentally, and hence, the design of new materials with desirable property combinations such as low sensitivity but high detonation performance can benefit from accurate molecular modeling.¹⁻³ The explosive properties are sensitive to the arrangement of molecules in the crystal and hence to the polymorph formed.^1,4−6 Consequently, crystal structure prediction (CSP) methods may be used to determine whether an energetic molecule can crystallize in a dense structure with good energetic properties, helping to focus synthetic efforts. There have been extensive quantum mechanical studies⁷ seeking to find correlations with the experimental impact sensitivity of the materials,^1,3,8−18 but these are on the intrinsic sensitivity or stability of the isolated molecule as opposed to the measured sensitivity of the condensed phase.⁷ It has been recognized that the crystal structure will also affect energetic properties, as the intermolecular interactions in the solid are linked to dissociation processes essential to detonation, such as defect formation. Correlations have been found between the heat of fusion of the crystal and the N–N bond dissociation energy¹⁹ or crystalline void space,²⁰ but the prediction of impact sensitivity and other processes is clearly a complex combination of molecular and crystalline properties.²¹⁻²³ In particular, the crystalline conformation can differ from the isolated molecule conformation and vary between polymorphs and with temperature and pressure. We examine how changes in NO₂ torsion angles that can occur on crystallization can affect the molecular charge distribution and associated electrostatic properties. This is a preliminary and necessary step toward the goal of developing methods of predicting impact sensitivity and other explosive properties, using CSP-generated crystal structures.

Computing energetic material properties requires accurately modeling regions of the repulsive wall. These regions of the potential energy surface are not adequately sampled by empirical intermolecular potentials as they have been fitted to crystals at ambient conditions. Thus, developing nonempirical methods for modeling the intermolecular forces between energetic molecules, suitable for molecular dynamics (MD) simulations, has been the subject of a considerable body of recent research.²⁴⁻²⁶ However, such methodologies have usually treated the molecules as rigid. A distributed multipole model of the molecular charge distribution provides both a method of examining the transferability of the local charge distribution and a model for calculating the electrostatic contribution to the intermolecular energy. This study only examines the conformation dependence of the electrostatic term. However, other contributions to the intermolecular energy, such as the induction, dispersion, and anisotropic short-range repulsive terms, are very closely related to the molecular charge distribution and therefore are expected to show similar transferability properties. The electrostatic term tends to be the most dominant, orientation-dependent determinant of intermolecular interactions between molecules in van der Waals contact. It is arguably²⁷ the dominant contribution to the interactions, which are often described by crystal engineers as hydrogen bonding, π···π stacking, N···O interactions, etc. Presently, accurate nonempirical models for intermolecular forces derived from the molecular charge distribution have tended to focus on rigid molecules²⁸ because of the difficulty of modeling the changes in charge distribution with conformation.

This study of NO₂ group charge distributions and the modeling of energetic crystals is aided by the recently introduced basis-space iterated stockholder atom (BS-ISA) analysis of the molecular charge distributions.^29,30 This partitioning of the molecular charge distribution produces atomic electron densities that decay from the atomic center almost exponentially. Additionally, the ISA scheme produces maximally spherical and so transferable atomic charge distributions, which are relatively insensitive to basis set yet fast at converging, and allows the use of high-quality molecular wave functions.³¹ The high degree of sphericity of the ISA atoms reduces the importance of higher atomic multipole moments enabling the truncation of the multipole moment expansion at lower-order terms.

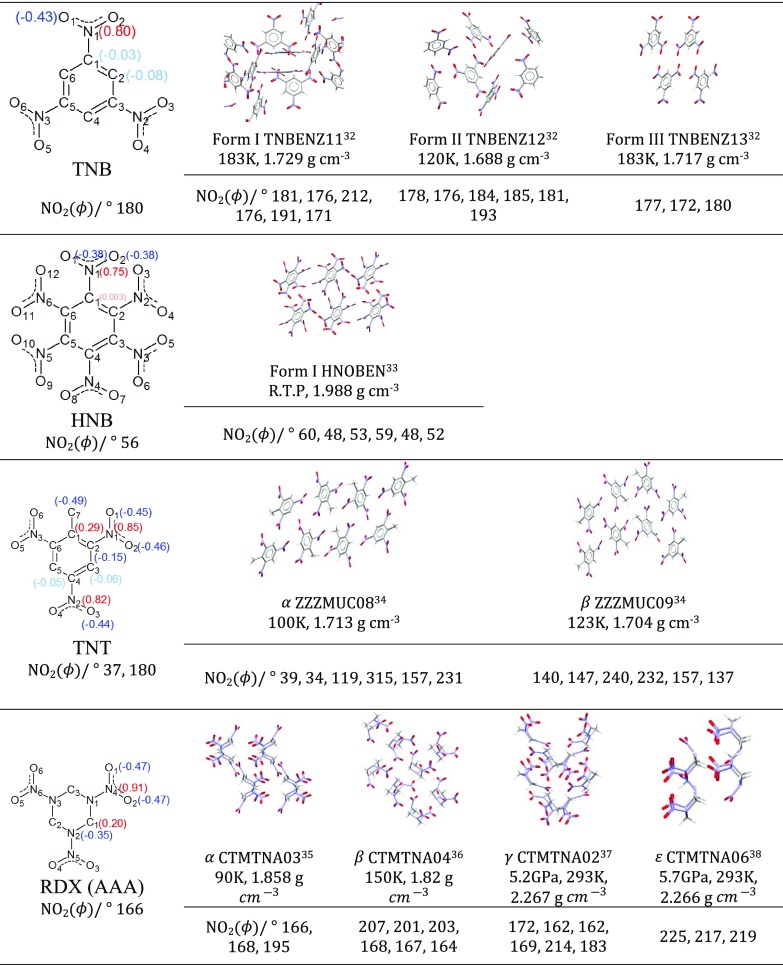
The atomic multipole moments of the nitro groups can be examined for both transferability between molecules and conformations, and used in models for impact sensitivity. This study is based on the nitro explosives 1-3-5-trinitrobenzene (TNB), hexanitrobenzene (HNB), trinitrotoluene (TNT), and 1,3,5-trinitroperhydro-1,3,5-triazine (RDX) whose structurally characterized polymorphs are shown in Figure 1. From the variation in nitro torsion angles (and axial/equatorial conformation in RDX) between polymorphs, it is clear that the crystalline structure has a significant effect on the molecular conformation. This, in turn, will affect the charge distribution by changing the orbital overlaps in π and σ bonding.

Figure 1.

Crystal structures of the energetic polymorphic crystals TNB,³² HNB,³³ TNT,³⁴ and RDX.³⁵⁻³⁸ The form, Cambridge Structural Database (CSD) reference code, determination conditions (at ambient pressure unless stated otherwise), density, and NO₂ torsion angles (deg) are given below each crystal structure. These were obtained from their experimental Cambridge Structural Database³⁹⁻⁴¹ entries and visual representations of the structures constructed using CCDC Mercury 3.6.^42,43 The iterated stockholder atom (ISA) atomic charges for the optimized structures, computed at the PBE0/aug-cc-pVTZ level, are given in parentheses in red or blue for positively or negatively charge nuclei, respectively. The NO₂ torsion angles for the optimized molecules are given below the structural diagrams.

While there are currently a few reliable methods for predicting the detonation pressures and velocities of CHNO energetics,¹ there has been less progress made toward predicting the sensitivity of an explosive compound to the different stimuli that can initiate detonation.⁴⁴ This reflects the intricacies of initiation leading to detonation; for example, the explosive molecule LLM-119 is sensitive to impact but moderately insensitive to friction and electrical sparks.⁴⁵ A widely studied and important measure of sensitivity is impact sensitivity, which is the vulnerability of the material to explosion after sudden compression due to impact.⁷ This is a complex process, dominated by the chemistry of the chemical reaction that takes place,² chemical bonding, and molecular interactions within the crystal. The impact sensitivity of an energetic material is normally determined using a drop-weight test,⁴⁶ being inversely proportional to h_50%, the height at which 50% of the experiments produce a reaction on dropping a weight onto the material. The impact sensitivity of material is heavily dependent on the particle size,¹ the shape and hardness of the crystals, the roughness of its surfaces, the purity and the presence of lattice defects, as well as the intrinsic differences in polymorph packing,^6,47−49 the surrounding temperature during experiment, and the weight used. Hence, the observed impact sensitivities (h_50%) for TNT vary from around 100 cm to over 250 cm.^4,5 We use the experimental impact sensitivities obtained in 1990 by Wilson and Bliss⁵ as they are a consistent set of experiments under consistent conditions, for TNB, HNB, and TNT, though these do not have separate values for the different polymorphs. RDX is a comparatively new explosive and its impact sensitivities were measured later.^44,50

Correlations between the molecular electrostatic potential (a molecular property) and the impact sensitivity (a crystal property) of CHNO energetic materials were investigated decades ago,⁹⁻¹³ based on the crude electrostatic models^9,14−18 available at the time. One approach focuses on the charge distribution at the trigger bonds (the bond likely to break during initiation).^46,51 The trigger bonds are typically X–NO₂ functional groups, and the strengths of C–NO₂ and N–NO₂ bonds are found to be inversely proportional to the magnitudes of the positive electrostatic potentials in the C–N and N–N internuclear regions (V_mid).^15,16,52,53 A more impact sensitive (low h_50%) conformer would be one where the charge gradient in the X–NO₂ bonds is the largest. The electrostatic potential at the longest C–NO₂ bond is often used,^16,18,54 as calculated by the equation first proposed by Owens in 1985¹⁸

1

where R is the longest bond length between C and N in the C–NO₂ bonds, while Q_C and Q_N are the atomic charges. The above equation is based on the assumption that the longest X–NO₂ bond will be the first bond to break during the initiation process. The initial correlations between V_mid and impact sensitivity computed using the Mulliken point charges⁵⁵ with an HF/STO-3G level of theory¹⁸ on each atom were only observed within a specific group of poly-nitroaromatics, which at least partly reflects the limitations of the partitioned charges in early ab initio calculations. Alternatively, to incorporate the response of the other trigger bonds in the molecule, the averaged V_mid

2

has been used⁴ to derive empirical correlation models for reproducing impact sensitivities of CHNO explosives. A more general but complex correlation has been suggested between the electrostatic potential surface of the isolated molecule and crystal impact sensitivities, with the sensitivity of the explosive to impact being exponentially related to the average positive and negative potentials across the molecular electrostatic potential surface⁴

3

where a_n are best-fit parameters, and V̅_S⁺ and V̅_S are the average positive and negative electrostatic potentials on the isosurface. This is an example of the more intricate correlations that have been investigated. However, the goal of finding an adequate predictive correlation of impact sensitivity with molecular properties across all chemical families of explosives is still elusive. This could well be because sensitivity to initiation causing detonation is not limited to a molecular property but also the crystal environment. Now that CSP could, in principle, be used in the design of new explosives, the likely crystallization environment of a molecule prior to its synthesis is no longer unknown. Given that the empirical correlations of molecular properties with impact sensitivity have focused on electrostatic properties yet ignored the conformational change on crystallization, it is appropriate to ask whether these changes in NO₂ torsion angle would affect the impact sensitivity.

In this study, we focus on the electrostatic potential surface maximum (V_max) and minimum (V_min), as many studies have focused on the correlation of impact sensitivity with these molecular properties.^{1,3,7,21,51−53,56−59} The electrostatic maxima and minima in molecules have been used in a method of estimating the likelihood of cocrystal formation,⁶⁰ i.e., as a simple and approximate surrogate for likely relative crystal energies. Analysis of the electrostatic potential of isolated TNT and CL-20 molecules and their hetero/homodimers³ was able to correlate their electrostatic potential maxima (V_max), minima (V_min), and the range of the minima and maxima (V_tot), to justify cocrystal formation and observed sensitivities to impact. Though not explicitly discussed in the paper,³ it showed that the change in conformation of CL-20 and TNT from pure crystal to cocrystal changes the charge distribution of the isolated molecules and thus the electrostatic potential, which may help rationalize the reduced impact sensitivity of the cocrystal.

Thus, this paper uses state-of-the-art electrostatic models to examine the role of conformational change on the charge distributions of NO₂ groups. We use iterated stockholder atom (ISA)²⁹ partitioned distributed multipoles to determine whether changes in torsion angle due to crystallization affect some proposed correlations with impact sensitivity. We also investigate whether this change is important to the molecular modeling of nitroenergetics, specifically for crystal structure prediction (CSP) studies and the development of nonempirical anisotropic atom–atom intermolecular potentials.

Methods

The static isolated molecular structures of RDX, TNT, TNB, and HNB were optimized using the Perdew–Burke–Ernzerhof (PBE) general gradient approximation combined with a portion of exact exchange to form the PBE0 functional⁶¹⁻⁶³ and the aug-cc-pVTZ Dunning basis⁶⁴ using the Gaussian 09 program.⁶⁵ This level of theory was also used for conformational analysis (unless stated otherwise), as augmentation is required for a better description of the higher multipole moments. In addition, for calculating the molecular charge densities in the experimental crystal conformations, hydrogen atom positions were corrected to standard bond lengths (C_aromatic–H = 1.08 Å, C_sp3–H = 1.06 Å)⁶⁶ to account for the systematic error in X-ray structure determinations. The “ISA” distributed multipoles (Q_lmⁱ) of each conformation were calculated in the molecular axis frame (Figure S1) and derived using the most recent iterated stockholder atom algorithm implemented in CAMCASP 6.0,⁶⁷ the ISA-A algorithm.⁶⁸ The ISA-A method develops on the previous BS-ISA method in CAMCASP 5.9, which includes a method for refitting the atomic electron density tails,³¹ by including another independent atomic basis set. Therefore, the ISA-A algorithm in CAMCASP 6.0 contains three bases:

• The main basis to calculate the molecular orbitals. In this study, an aug-cc-pVTZ basis set is used.

• An auxiliary basis for refitting the atomic electron density tails. This basis can take both Cartesian and spherical Gaussian-type orbitals (GTOs). In this study, we use Cartesian GTOs of aug-cc-pVTZ size.

• And an atomic basis to determine the ISA atomic expansions. In this study, an aug-cc-pVQZ basis set is used as it is independent of the main and auxiliary basis sets. However, the spherical coordinate system for the GTOs must always be used.

The distributed multipole expansion is evaluated to hexadecapole level (rank l = 4) so that the potential and energies could be evaluated including all terms up to R^–5 and so include the electrostatic effects due to lone-pair and π atomic anisotropies. To test the transferability of the multipole moments with changes in the NO₂ torsion angle, Z matrices of these structures were created and the NO₂ functional groups were rotated through 180° in 20° increments, while the rest of the molecule was held rigid at the optimized structure. The extent to which the nitro group torsion angles can change in the condensed phase was investigated using histograms of the frequency a O–N–X–C torsion angle (rounded to nearest degree) occurred in the relevant organic crystal structures found in the Cambridge Structural Database (CSD).⁶⁹ The histograms were constructed for the four unique chemical environments found in the four energetic molecules, with the most commonly observed environment being a C–NO₂ on an aromatic ring with two adjacent hydrogen atoms (Table S1).

The ISA distributed multipoles can be analytically rotated from the molecular axes into the atomic local axes of the molecule, with the z-axis along the X–N plane (along the bond) and the x-axis into X–N=O plane (perpendicular to the z-axis but in the plane of the molecule) (Figure S1). Analytically rotating the local axis-defined multipoles to a different X–NO₂ torsion angle provides an electrostatic model that includes the geometric effects of conformational change but does not explicitly account for changes in the molecular charge distribution. Provided that the non-NO₂ torsion angles, bond lengths, and angles are identical, it is possible to analytically rotate the multipoles to represent the geometric change in torsion angles, using ORIENT 4.9.08,⁷⁰ a methodology previously used to study the transferability of electrostatic models between polypeptides.⁷¹

To focus solely on the effects of changing NO₂ torsion angles and compare experimentally observed and optimized conformations, the experimentally observed NO₂ torsion angles were used, while all of the bond lengths and angles and non-NO₂ torsion angles were kept rigid at their optimized values. These structures and charge distributions calculated in this conformation are referred to as the optexptNO₂. In addition, multipole moments calculated in the optimized conformation were analytically rotated into the optexptNO₂ conformation. Charge distributions obtained this way are referred to as anarot (analytically rotated). The electrostatic properties obtained from the analytically rotated distributed multipoles can then be contrasted with those acquired from calculating the charge distribution in the optexptNO₂ conformation, which also accounts for the rearrangement of charge within the molecule, e.g., from changes in π conjugation. Analytical rotation can only be applied to the nitroaromatic molecules, as the aromatic ring is rigid and undergoes negligible changes when the molecules are optimized and the nitro group rotates. Only the NO₂ torsion angles change between the optimized and observed conformations (Figure S2). However, for nitramines, like RDX, there is a notable difference in the conformation of the aliphatic ring in the experimental crystalline conformers and the optimized conformation. The difference also results in a change in non-NO₂ torsion angles upon optimization. Thus, changing only the NO₂ torsion angle in the optimized structure using the standard Z-matrix definition (the optexptNO₂ methodology) gives a structure that is different from the experimental structure. Hence, it is not possible, let alone appropriate, to test transferability by analytically rotating the multipoles of RDX (Figure S2 and Table S4).

Using the various sets of distributed multipole moments, the electrostatic potential was computed and mapped onto an isodensity surface of 10^–3 electron/bohr³, using CAMCASP 6.0,⁶⁷ which was visualized on the isolated molecular structures using the ORIENT 4.9.08⁷⁰ program. This isodensity surface was chosen as the majority of electrostatic potential studies on energetic materials and their sensitivities use this surface, following the suggestion by Bader,^72,73 as it can include more than 95% of a molecule’s true electronic density. This surface has recently been used to define the molecular volume for use in estimating the density of energetic materials.⁷⁴ The electrostatic potential on this isodensity surface is approximately 3 Å from the nearest nucleus in the molecule and so gives the electrostatic potential sampled by the nonhydrogenic nuclei that would be in van der Waals contact with the molecule in the crystal. Lattice energies were calculated using a combination of the ISA distributed multipoles, to obtain the electrostatic energy, and the exp-6 FIT potential, for all other contributions using DMACRYS.⁷⁵

Crystal structure analysis and visual representations used the analysis software of the Cambridge Crystallographic Data Centre, mainly Mercury 3.6.^42,43 Root-mean-square deviation (RMSD_n) calculations, the optimum overlay of n (n ≤ 15 for crystal structures, n = 1 for molecular conformation comparisons) molecules in two crystal structures excluding the hydrogen atoms, were also done using Mercury.

Results

Molecular Electrostatic Properties and Correlation with Impact Sensitivity

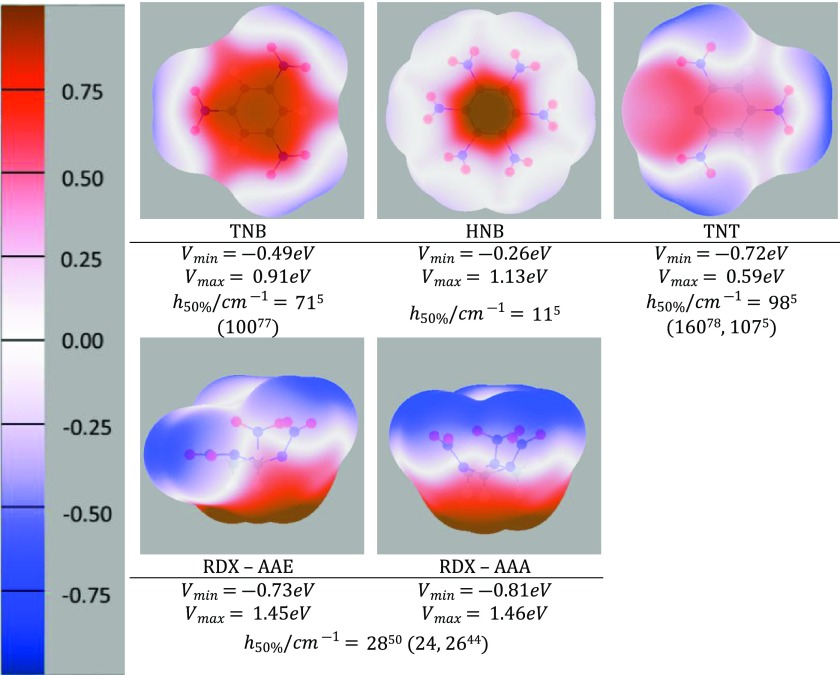
The electrostatic potential around the static optimized conformations of the four energetic molecules (Figure 2) clearly shows that the electrostatic term will greatly influence intermolecular interactions and hence explosive properties. Potential extrema (V_max and V_min) are influenced by the molecular symmetry and not necessarily centralized around the NO₂ groups, in contrast to the measure of the local NO₂ charge distribution V_mid. The AAE and AAA crystalline conformations of RDX optimize to very different geometries and therefore are conformational polymorphs.⁷⁶ The AAE conformation, with one equatorial NO₂ group, is the lower-symmetry, higher-energy conformation of RDX and occurs in the most stable α polymorph and one of the two independent molecules in the high-pressure γ form. It has a different surface shape and potential minimum (V_min), but the potential maximum for this bowl-shaped molecule is virtually unaffected. The nitramine RDX has a significantly larger gradient in the electrostatic potential around the molecule than any of the flatter nitroaromatics.

Figure 2.

Electrostatic potential (eV) computed using the ISA distributed multipole analysis (ISA-DMA) on the isodensity surface of 10^–3 electron/bohr³ around the static optimized isolated molecular structures of TNB, HNB, TNT, and RDX. Note that for some of the above molecules the maximum, V_max is greater than the potential scale, which is +1 eV (red) to −1 eV (blue). Alternative h_50%/cm measurements^5,44,77,78 have been included in parentheses.

The variations in charges on the X and N atoms in the X–NO₂ groups of the optimized conformations are contrasted with X–NO₂ groups in the experimentally observed condensed-phase conformations that have the most unique structures (Table S2). This clearly shows that the nitrogen atoms in the N–NO₂ groups in RDX are more positively charged (0.882–0.945e) than any nitrogen in the aromatic C–NO₂ groups (0.749–0.852e), and even within the C–NO₂ groups, the charge distributions are far from transferable (as seen in the atomic charges in Figure 1). Changes in conformation result in variations in the trigger-bond parameter V_mid (both longest and average) that can be comparable to the conformational differences between molecules (Table S2). The values of V_mid differ more between the molecules but also vary between the different crystalline conformations.

On comparing the molecular electrostatic properties V_max and V_mid against experimental impact sensitivity (Figure 3), one observes that conformational changes due to crystallization do affect these properties. There is a notable spread in V_max and V_mid of the optimized and observed conformations in the nitrobenzenes TNB and TNT. This will significantly affect any correlation with impact sensitivity for the nitrobenzenes. Furthermore, for RDX, the spread of values for either V_max and V_mid is not substantially larger than that for TNB despite RDX having many large conformational changes (Figures 1 and S1).

Figure 3.

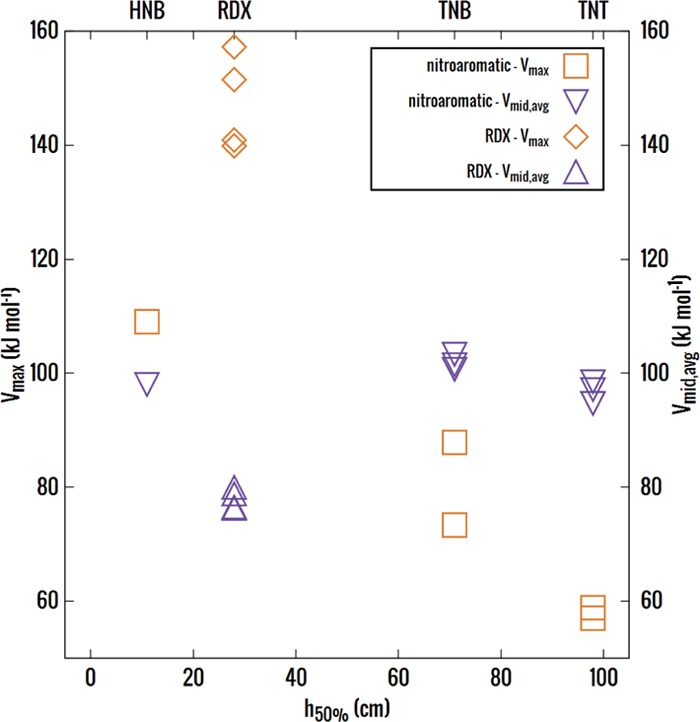
Calculated trigger-bond potential, V_mid,avg, and molecular electrostatic potential surface maximum, V_max, plotted against the experimentally observed impact sensitivities (h_50%) for the three nitroaromatic explosives.⁵ RDX has a different symbol as it is from a different chemical family, nitramines, and its observed h_50% has been obtained from a different source.⁵⁰ The variations between the optimized and the most different crystalline conformations, HNB(opt ≈ expt), TNB(opt ≈ form III, molecule 1 in form I, molecule 2 in form II), TNT(opt, α), and RDX(opt(AAA), opt (AAE), α(AAE), and ε(AAA)), are shown. The atomic charge variations and other electrostatic properties (including V_mid,longest, V_min) are given in Table S3, along with the plotted values.

Modeling the Electrostatic Contribution to Lattice Energies

How much variation is likely within the crystalline state and how does this affect atomic charges? Analysis of the NO₂ torsion angles in the crystal structures in the Cambridge Structural Database (CSD) shows that an aromatic NO₂ group adjacent to two hydrogen substituents is almost always planar, to within 20°, which corresponds to a fairly small change in conformational energy, as shown for the para-nitro group in TNT in Figure 4. There is a large barrier of about 25 kJ/mol for rotating the nitro group, presumably from changes in π electron conjugation. The atomic charge on C4 (the carbon bound to the para-NO₂) rises, while those on the neighboring C3 and C5 fall. We find that the atomic charge on N2 is mainly responsible for the charge balance. Additionally, the dipole moments on the nitro O atoms change significantly with rotation. A similar picture is seen for the NO₂ groups in TNB (Figure S3a), which are also adjacent to aromatic C–H groups. The picture is very different for the ortho-nitro groups in TNT (Figure 4), where a large range of torsion angles are observed for the NO₂ between a methyl and hydrogen substituents on an aromatic ring. Here, the planar conformation is the most commonly observed in the crystal structures, but this corresponds to a maximum in the intramolecular energy. There is a known preference for planar, extended conformations of molecules in the crystalline state as this often allows a denser packing.⁷⁹ The height of the energy barrier is probably overestimated because of the methyl group being fixed in the calculation and hence sterically clashing with the NO₂ group, whereas in the crystal structure, the methyl could rotate out of the way. However, one should note that the crystallographic angle in the CSD is an average over the torsional vibrations of the methyl and nitro groups. In the ortho case, the charges and dipoles change on many more atoms, though again the dipoles change most on the nitro-oxygen atoms. While this effect is probably exaggerated by the steric clash, it highlights the effects of changing π conjugation between the nitro groups and the aromatic ring.

Figure 4.

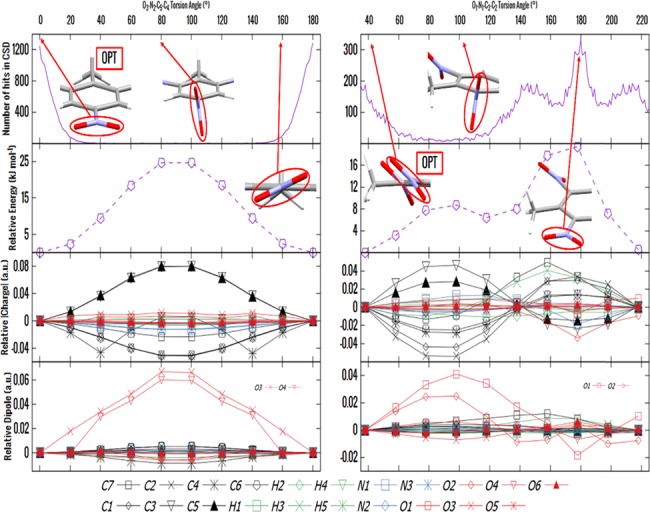
Conformational behavior of the para-nitro (left) and ortho-nitro (right) groups in TNT. The behavior as a function of torsion angle is given for (top to bottom) the distribution of the observed angles in the CSD for each environment; the change in PBE0/aug-cc-VTZ energy relative to the optimized molecule as the nitro group torsion angle is changed; and the relative changes in the magnitude of ISA charge and dipole on each atom. The oxygens that undergo the most significant changes in dipole moment have been indicated, and the optimized NO₂ torsion angles are also illustrated, alongside other more notable NO₂ torsion angles.

There is far sparser CSD data for an aromatic NO₂ between two other NO₂ groups (HNB), suggesting that any angle could be observed (Figure S3b). Nonetheless, the height of the conformational energy barrier is so great that without allowing for a concerted and highly correlated change in the other NO₂ torsion angles the range of angles seen in other crystalline conformations would not occur in HNB. There is even less CSD data for N–NO₂ groups (Figure S3c), as seen in the analysis of the AAE conformer of RDX. We find that there are significant variations in some of the atomic charges and dipoles for the ring nitrogen and the attached NO₂ atoms. Overall, from Figure 4, it is clear that the nitro group can adopt a range of conformations, as a compromise between the intramolecular steric hindrance and the crystal packing forces, and that these changes in conformation do affect the nitro group charge distribution, resulting in very different charge distributions for various NO₂ environments.

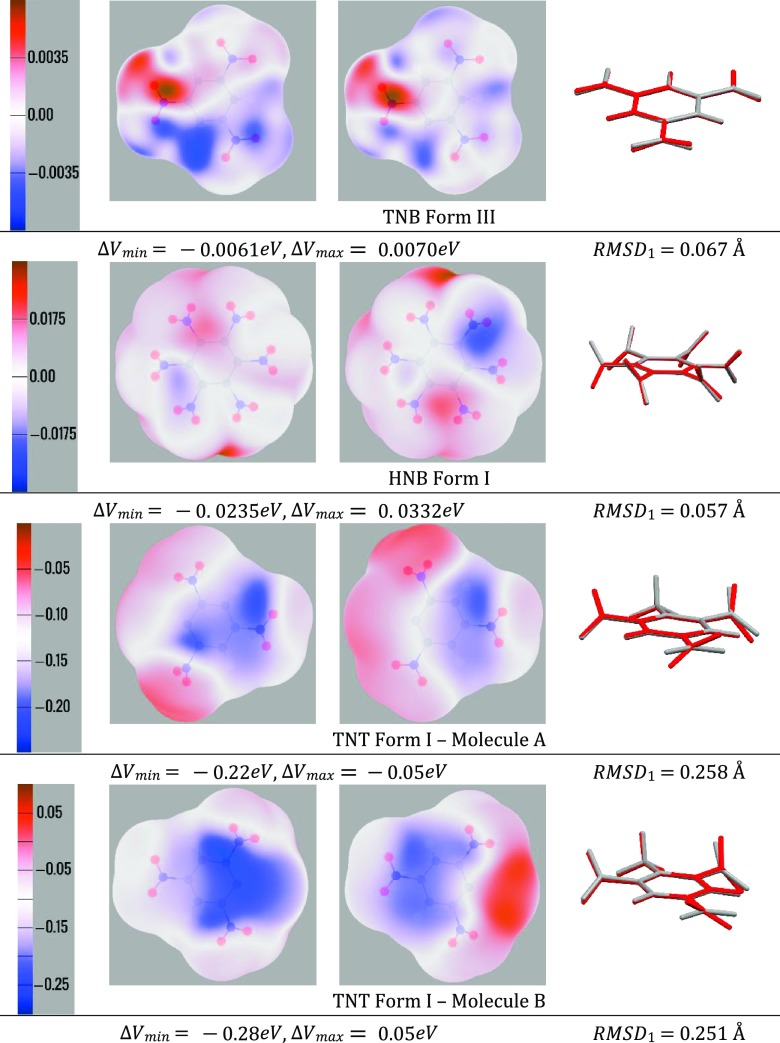
The difference maps in Figure 5 show the extent to which the changes in charge distribution, from the rearrangement of the valence electrons, affect the electrostatic potential around each nitroaromatic molecule. The difference between the potential calculated for optexptNO₂ and anarot multipole moments is shown. The differences are very dependent on the extent to which the torsion angles differ between the optimized and experimental structures, ranging from being negligible for TNB to underestimating V_min by nearly 0.3 eV for TNT.

Figure 5.

Difference in electrostatic potential around the nitroaromatic molecules for charge distributions calculated with the NO₂ groups in their experimentally observed torsion angles (optexptNO₂) and those analytically rotated from the PBE0/aug-cc-pVTZ optimized molecular structure (anarot) viewed from above and below. The potential is mapped onto an isodensity surface of 10^–3 electron/bohr³ in electron-volts (eV), and the scale varies from molecule to molecule. The RMSD₁ for the overlays of the optimized (gray) and optimized with experimental NO₂ torsion angles, optexptNO₂ (red), molecular conformations, for each nitroaromatic are included for comparison and given in Å.

Table 1 illustrates how analytically rotating the atomic multipole moments affects the intermolecular lattice energy (U_INT). For TNT, which has the largest NO₂ torsion angle difference between experimental and optimized structures, there is a significant change in the lattice energies of TNT (Table 1). However, the effect of anarot multipoles on the minimized lattice parameters and hence potential energy surface minima is negligible. The small change in the lattice energy of TNB reflects the very small differences in the torsion angles upon crystallization. The lattice energy differences are mainly due to variation in the electrostatic contributions (U_elst) as changes in the dispersion–repulsion terms (U_disp–rep) arise only from the change in the lattice structure. Even though the relative lattice energies are not well reproduced when rotated multipole moments are employed, the low RMSD₁₅ values indicate that the crystal geometries differ insignificantly. This is also illustrated by the overlays in Figure S3. Hence, the anarot distributed multipole model, which assumes that the atomic charge distributions can be analytically rotated with changes in the NO₂ torsion angle, reproduces the experimental polymorph structures satisfactorily enough to be used in CSP for initial analysis of the potential energy landscape.

Table 1. Effect of Multipole Moment Rotation on Lattice Energy Minima^a.

	TNT			TNB			HNB
REFCODE	ZZZMUC08			TNBENZ13			HNOBEN
	UINT	Uelst	Udisp–rep	UINT	Uelst	Udisp–rep	UINT	Uelst	Udisp–rep
EoptexptNO2–ISA /kJ mol–1	–121.0	–46.4	–74.6	–104.7	–34.4	–70.3	–150.1	–45.1	–105.1
Eanarot–ISA/kJ mol–1	–123.2	–48.3	–74.9	–104.4	–34.2	–70.2	–150.8	–46.0	–104.9
ΔE/kJ mol–1	2.177	1.820	0.367	–0.334	–0.262	–0.073	0.710	0.910	–0.200
%↑ in a	0.270			–0.015			0.060
%↑ in b	0.259			–0.244			–0.050
%↑ in c	–0.333			0.190			0.058
RMSD15/(optexptNO2)	0.246			0.166			0.235
RMSD15/(anarot)	0.218			0.162			0.237

^aA comparison of the effect of ISA multipole moments calculated in the optexptNO₂ conformation and those analytically rotated into the optexptNO₂ conformation (anarot), using ORIENT.⁷⁰ Each experimental crystal structure has been minimized holding the molecules rigid in their optextNO₂ observed conformation, using the FIT potential⁸⁰ and the defined set of atomic multipole moments to calculate the intermolecular forces. The changes in each intermolecular energy contribution and % change in cell parameters are compared. The RMSD₁₅ comparisons are with the experimental crystal structure. More details on the effect of conformation on lattice energy minimizations, including using the optimized molecular conformation and the experimental conformation, can be found in Tables S3 and S4.

Discussion

We find that the crystalline and isolated (optimized) conformations of most molecular explosive materials differ significantly, providing a challenge in evaluating the thermodynamic stability of their polymorphs even at ambient conditions,⁸¹ let alone at the high temperatures and pressures sampled during detonation. This study highlights the effects of the changes in the NO₂ torsion angles that can occur upon crystallization, how these can differ between polymorphs, and its importance in accurate predictive modeling.

The experimental polymorphs studied show a range of crystalline conformations that are fairly typical of those seen in all of the other nitroaromatic and nitramines in the Cambridge Structural Database (CSD). When the adjacent functional groups on the aromatic ring (or C–N–NO₂ chain, e.g., RDX) are hydrogen atoms, then the NO₂ torsion angles vary by about ±20° and the nitro groups are relatively planar (Figures 4 and S3a). On the other hand, when the adjacent functional groups are larger, any angle may be observed (Figures 4 and S3b). In the isolated molecule, the interactions with the specific neighboring substituents can have a major effect on the charge distribution and torsion angle of a nitro group; however, in the condensed phase, correlated changes in substituent conformation are more affected by crystal packing. On comparing NO₂ torsion in Figure 1, the nitroaromatics show differing degrees of conformational adjustment due to the packing forces within the crystal lattice. HNB has only one crystal structure, but the six nitro groups have different torsion angles ranging between 48 and 60°, losing its molecular symmetry and reflecting the compromises between the intramolecular steric forces and the adaption to intermolecular interactions to give a dense crystal. The TNT polymorphs have rather similar crystalline conformations as they are polytypic, comprising of different stacks of comparable layers of molecules.^6,82 Nonetheless, the two independent molecules in each polymorph show variations in the torsion angles of the ortho-NO₂ groups that sterically interact with the methyl, and the para-NO₂ groups are not coplanar. The optimized TNB molecule is planar, but the four crystalline conformations in the two polymorphs have torsion angles that are up to 32° from planar. Thus, crystal packing forces can easily overcome intramolecular stabilization from conjugation, shifting nitro groups from their preferred planar conformation.

Using an improved novel method of partitioning the isolated molecular charge distribution (ISA) and a high level of theory (PBE0/aug-cc-VTZ) to obtain realistic atomic charges and higher-order multipole moments for an X–NO₂ group shows that the NO₂ charge density differs considerably between N–NO₂ and C–NO₂ (Figure 1 and Table S2). Moreover, the charge density varies significantly with the neighboring functional groups (e.g., ortho- and para-groups in TNT, Figure 1) and also with the NO₂ torsion angle. This is to be expected as the atomic charges, in particular, reflect the changes in valence electron distribution, which also determine the molecular reactivity. Our study shows that the published empirical correlations of local electrostatic properties around the NO₂ “trigger bond”, such as V_mid, or the molecular property V_max with the crystal property, impact sensitivity (h_50%),^1,59,83 will be significantly affected by the neglect of the conformational change (Figure 3 and Table S2).

The packing arrangement of the reactive groups in the crystal will also strongly affect the energetic properties. The early correlation between detonation properties and density led to the development of MOLPAK,⁸⁴ one of the first crystal structure prediction (CSP) codes, which sought to establish the possible density of a crystal from the molecular structure. Since then, CSP methods have evolved to help predict possible polymorphs and help support their structural characterization from powder X-ray diffraction and other analytical techniques. While these techniques are being extensively developed for the pharmaceutical industry,^85,86 the much-needed extension to energetic materials requires fundamentally different modeling of specific functional groups under the extreme conditions unique to explosives. For example, periodic density functional calculations on crystalline nitroguanidine required the development of a specific dispersion correction.⁸⁷ This paper has established the care required in CSP studies of nitroaromatic explosives to ensure that the large variations in possible NO₂ torsion angles, shown by the CSD distributions (Figures 4 and S3), are effectively considered. It is the balance between the molecular cost for the conformational change (ΔE_intra) and the improved intermolecular lattice energy (U_INT) from a denser packing, which determine the total lattice energy (E_latt = ΔE_intra + U_INT). Ab initio calculations on the molecule (Ψ_mol) can be used to obtain ΔE_intra and analyzed to obtain the atomic multipoles, polarizabilities, and dispersion coefficients that determine the long-range intermolecular forces. In this study, the ISA analysis of Ψ_mol provides an anisotropic intermolecular potential with the atomic multipole moments being used to calculate the electrostatic contribution to the intermolecular energy. It seems that cell geometries can be obtained relatively accurately and very quickly without recalculating the charge density as the nitro groups rotate (Table 1), by analytically rotating the multipole moments. This suggests that the anarot methodology could be used to determine the range of low-energy crystal structures that could be adopted by a nitroaromatic energetic molecule within the Ψ_mol approach to crystal structure prediction⁸⁸ and thus could improve the prediction of crystal packing from the molecular diagram of new energetic molecules.⁷⁴ This method is suitable as an initial approximation of the potential energy landscape, but the relative energy differences in Table 1 are large in comparison with the lattice energy differences between polymorphs, which are usually much less than 5 kJ mol^–1 for small molecules.⁸⁹ The conclusion that analytical rotation does not reproduce relative electrostatic energies well was also reached in the study on the transferability of electrostatic models between polypeptides.⁷¹ Thus, Table 1 shows that in the Ψ_mol approach, it is necessary to use an accurate molecular charge distribution for the refinement of CSP-generated crystal structures, or a sufficiently accurate periodic electronic structure calculation, to determine the relative lattice energies reliably and accurately enough to know which of the generated crystal structures are thermodynamically plausible polymorphs.⁸⁸

The complexity of the processes that determine the impact sensitivity and other key properties of the polymorphs of energetic materials⁴⁸ implies that multiscale modeling, involving both periodic electronic structure calculations and MD simulations, will be required. The MD codes will need to use the best nonempirical models for the inter- and intramolecular forces derived directly from the molecular charge distribution. These models will be specific to the molecule, as the charge distribution around the nitro groups is clearly affected by changes in the rest of the molecule, particularly the adjacent functional groups or with the presence of an aromatic ring. This study implies that there will be a significant loss in accuracy if novel intermolecular potentials do not include a NO₂ torsion angle dependence. It could be possible to fit analytical models to changes in atomic multipoles,⁹⁰ as Figure 4 shows that the ISA atomic multipoles change smoothly with NO₂ torsion angle and therefore can be modeled using splines, or other functions of low complexity. However, while it is clear how these changes can be modeled as a function of a single degree of freedom (single torsion), the correlated conformational adjustments of neighboring groups on the aromatic ring may pose a challenge. The changes in multipole moments during the rotation of the methyl group in TNT, let alone with changes in the aliphatic ring seen for RDX (Figure S2), will not be represented by a simple Fourier series term, and this will also apply to the conformational energy penalty.⁹¹ Considering the polymorphs of energetic molecules and CSP studies provide a good starting point for developing the next generation of molecule-specific flexible force fields. This, in turn, will help contribute to the development of predictive computational modeling of their key physical properties such as free energies, thermal expansion, and other nonreactive properties.

Conclusions

The charge distributions of the nitro groups in TNB, TNT, HNB, and RDX vary considerably depending on the bonded and neighboring functional groups and also with the conformational differences between their polymorphs and their isolated molecular structures. The rigorous ISA partitioning of high-quality molecular charge distributions allows us to obtain the distributed multipole representation of the atomic charge distribution, which has minimal sensitivity to basis set, and hence, artifacts of conformational change are minimized. We have shown, using ISA partitioning, that variations in NO₂ conformations that occur in crystal structures cause sufficient changes in the molecular charge to affect previously proposed empirical correlations between impact sensitivity and molecular electrostatic properties.

The condensed-phase torsion angles observed for nitro groups are a subtle balance between inter- and intramolecular interactions. The charge distributions of the nitro groups, and some neighboring atoms, can change significantly with the NO₂ torsion angle, reflecting the change in the bonding and molecular charge distribution. This change is sufficiently large that distributed multipole models, which form the basis of nonempirical model intermolecular potentials, should be calculated for each conformation if the potential is to be accurate enough to model lattice energies to the accuracy needed to predict polymorph relative stability. However, analytically rotating the multipoles to reflect the change in aromatic NO₂ torsion angles is a reasonable approximation that may be useful in performing fast crystal structure prediction calculations. This study utilizes old and new computational methodologies in a novel way to establish the necessary assumptions about the transferability of charge distribution in nitroaromatic explosives. These assumptions will be instrumental in producing reliable nonempirical potentials suitable for modeling possible polymorphs, particularly those crystallized under pressure.⁹²

Glossary

Abbreviations

TNB

1-3-5 trinitrobenzene

HNB

hexanitrobenezene

TNT

trinitrotoluene

RDX

1,3,5-trinitroperhydro-1,3,5-triazine

ISA

iterated stockholder atoms

DMA

distributed multipole analysis

CSP

crystal structure prediction

CSD

Cambridge Structural Database

CCDC

Cambridge Crystallographic Data Centre

h_50%

impact sensitivity

V_mid

trigger-bond (NO₂) polarity

V_max

electrostatic potential surface maximum

V_min

electrostatic potential surface minimum

anarot

multipole moments analytically rotated from the optimized structure’s local axis into the local axis of the experimental conformation

optexptNO₂

multipole moments calculated in for the optimized structure with all nitro groups in their experimentally observed torsion angles

RMSD_n

the root-mean-square deviation, the optimum overlay of n molecules in two crystal structures excluding the hydrogen atoms

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.9b00648.

• Method of analytical rotation of multipole moments; contrasting optimized and experimental conformations of RDX and TNT; method of surveying Cambridge Structural Database; changes in electrostatic properties with conformation; additional figures showing effects of rotating nitro groups in TNT, HNB, and RDX (AAE); and lattice energy minima (PDF)

The authors declare no competing financial interest.