Abstract
Noncoding RNA molecules are composed of a large variety of noncanonical base pairs that shape up their functionally competent folded structures. Each base pair is composed of at least two interbase hydrogen bonds (H-bonds). It is expected that the characteristic geometry and stability of different noncanonical base pairs are determined collectively by the properties of these interbase H-bonds. We have studied the ground-state electronic properties [using density functional theory (DFT) and DFT-D3-based methods] of all the 118 normal base pairs and 36 modified base pairs, belonging to 12 different geometric families (cis and trans of WW, WH, HH, WS, HS, and SS) that occur in a nonredundant set of high-resolution RNA crystal structures. Having addressed some of the limitations of the earlier approaches, we provide here a comprehensive compilation of the average energies of different types of interbase H-bonds (EHB). We have also characterized each interbase H-bond using 13 different parameters that describe its geometry, charge distribution at its bond critical point (BCP), and n → σ*-type charge transfer from filled π orbitals of the H-bond acceptor to the empty antibonding orbital of the H-bond donor. On the basis of the extent of their linear correlation with the H-bonding energy, we have shortlisted five parameters to model linear equations for predicting EHB values. They are (i) electron density at the BCP: ρ, (ii) its Laplacian: ∇2ρ, (iii) stabilization energy due to n → σ*-type charge transfer: E(2), (iv) donor–hydrogen distance, and (v) hydrogen–acceptor distance. We have performed single variable and multivariable linear regression analysis over the normal base pairs and have modeled sets of linear relationships between these five parameters and EHB. Performance testing of our model over the set of modified base pairs shows promising results, at least for the moderately strong H-bonds.
1. Introduction
Until recently, the functional roles of RNA were thought to be limited mainly because of its participation in gene expression in the form of the messenger RNAs, ribosomal RNAs, and transfer RNAs.1 However, in the past 2 decades, the ever-increasing discoveries of the catalytic2 and regulatory3 roles of non (protein)coding RNAs (ncRNA) have trashed the established rules to make way for new ones (see the Supporting Information).4,5 Recent discoveries of CRISPRs (clusters of regularly interspersed short palindromic repeats6) and scanRNAs (small conjugation-specific RNA7) suggest that ncRNAs can even intervene at the genome itself and modify DNA. To participate in these diverse cellular functions, RNA molecules have to fold into functionally competent structures, which are inherently complex. The understanding of how RNA, having essentially only four types of nucleobases [adenine (A), guanine (G), cytosine (C), and uracil (U)], can display such a variety and complexity is still far from complete. A detailed analysis of base pairing interactions, however, may provide significant points toward this understanding.
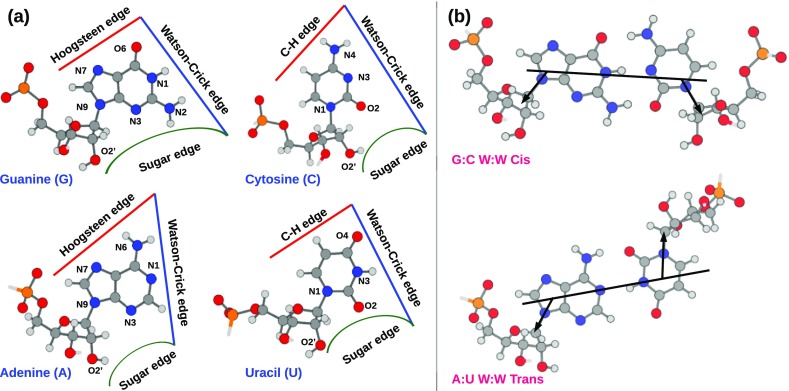
As shown in Figure 1, each nucleobase can be characterized by three edges—Watson–Crick (W), Hoogsteen (H), and Sugar (S). A base pair is formed when two bases interact noncovalently, each respectively involving one of these three edges, and form a considerably planar geometry with at least two interbase hydrogen bonds (H-bonds). Depending on the mutual orientation of the glycosidic bonds within a base pair, it can be annotated as either cis or trans.8 The cis-type interactions between the Watson–Crick edges of two complementary bases (G:C and A:U/T) are known as canonical base pairs, as they are predominantly found within the double helical stretches of both DNA and RNA. All other possible base pairs are categorized as noncanonical base pairs. Unlike the double-stranded DNA, the single-stranded RNA folds onto itself to form a large repertoire of noncanonical base pairs.8 On the basis of the identities of the interacting edges, Leontis and Westhof have organized all these base pairs into 12 geometric classes, viz., WW, WH, HH, HS, WS, and SS (cis and trans).8 It is theoretically possible to have a total of 144 different types of base pairing geometries. However, because of lack of complementary H-bonding network and other structural and functional constraints, only 118 types of base pairs are actually observed in available RNA crystal structures.9 These base pairing interactions lead to the formation of double helical stem regions (dominated by canonical base pairs) and loop regions (characterized by unpaired bases and noncanonical base pairs) in RNA. In a folded RNA, such stem and loop regions further interact with each other via tertiary interactions. Combination of such interconnected structural components is often observed recurrently as a conserved (in terms of both sequence and structure) modular unit in various RNA molecules and is known as an RNA motif.10 In this context, a reasonable hypothesis could be that different sets of noncanonical base pairs due to their characteristic geometry, stability, and physicochemical properties provide the diversity required to shape up the structure and dynamics of these RNA motifs and thereby the folding of the overall RNA molecule.11
Figure 1.
(a) RNA bases have been characterized by three edges—Watson–Crick, Hoogsteen (C–H edge for pyrimidines), and Sugar. (b) In principle, any edge of a base can interact with any other edge of a second base. Depending on the mutual orientation of the two glycosidic bonds, the base pair can be annotated as either cis or trans.
Given that variations in the properties of the constituent interbase H-bonds collectively determine the variations in geometry and stability of noncanonical base pairs, it is important to analyze the properties of individual interbase H-bonds to delineate the role of noncanonical base pairs in RNA folding. It is important to note here that in addition to interbase H-bonds, other inter-residue H-bonds (viz., base–phosphate12 and base–sugar13 interactions) are also important for shaping up the complex folded structure of RNA. However, in this work, we have only focused on the interbase H-bonds. On the basis of the identity of H-bond donor and acceptor atoms, all the interbase H-bonds present in RNA base pairs can be classified into six different types, viz., N–H···N, N–H···O, O–H···N, O–H···O, C–H···N, and C–H···O.11 Energetically, such interbase H-bonds are either weak (H-bonding energy (EHB) < 4 kcal mol–1) or moderately strong (EHB = 4–15 kcal mol–1).14 However, evaluation of the geometry and energetics of H-bonds in base pairing systems continue to pose a formidable challenge for both experimental and theoretical investigations. As discussed in earlier reviews,15−17 most of the experimental methods provide only qualitative details about individual H-bonds, especially in complex biological molecules. In practice, very few methods are available for the quantitative estimation of the H-bond strengths via experiments, for example, (a) studying the modulations in the IR spectra as a result of H-bond formation such as red shift of D–H stretching vibration frequency, increase in IR intensity, and so forth,18 (b) using experimental tools such as temperature-dependent field ionization mass spectrometry,19 calorimetry,20−22 or vibrational predissociation spectroscopy23 in order to calculate the dissociation energy of the hydrogen-bonded complex, and (c) studying the alteration in magnetic properties of the system owing to hydrogen bonding.24 Also, unlike covalent bonds, the correlation between the geometry of a H-bond (say, H-bond length) and its strength is not straightforward.14
To overcome the limitations of the experimental methods and to evaluate the strength of individual H-bonds, numerous theoretical approaches have been implemented till date.25 Among them, the quantum theory of atoms in molecules (QTAIM) approach is arguably the most widely used theoretical tool to understand the H-bonding interaction.26,27 Several efforts have also been made to relate the QTAIM-based parameters with the strength of individual hydrogen bonds. For example, (a) the complex-derived Grabowski parameters relating geometric and topological parameters to the H-bonding strength,28 (b) the relationship given by Espinosa et al.29 providing H-bond dissociation energy (De) using the virial density (Vel), and (c) the linear relationship between intermolecular complex stabilization energy and electronic charge density (ρ) or it’s Laplacian (∇2ρ) at the bond critical point (BCP) (where ∇ρ = 0) have been proposed for different H-bonded molecular systems,30−34 including base pairs.35−38 Although extensively used,13,39−42 the QTAIM-based approaches have their limitations as discussed in the Supporting Information. However, it is to be noted that the theoretical basis of QTAIM is based on electron density which is an experimentally measurable quantity. Another such approach, based on experimentally measurable quantity, is the use of vibrational spectroscopy. Advanced quantum mechanics-based methods can replicate the experimentally observed vibrational spectroscopy to a reasonable extent, at least for the nucleobases.43−47 Using the empirical Iogansen’s relationship,18 the H-bond (D–H···A) formation enthalpy (EHB) can be measured from the red shift in the D–H bond stretching frequency, which takes place because of H-bond formation. For intramolecular hydrogen bonds in a wide variety of biological systems, Nikolaienko and co-workers have established the correlation between these two theoretical approaches (QTAIM and vibrational spectroscopy) for estimating the H-bonding energy of individual H-bonds.48 Later, Hovorun and co-workers have implemented Iogansen’s relationship to study the H-bonding energy of the intermolecular H-bonds present in unconventional DNA base pairs.49−52 Another effective and widely used53−58 approach is provided by natural bond orbital (NBO) analysis,59,60 which calculates the stabilization energy associated with the charge transfer from the filled π orbital of the H-bond acceptor (A) to the corresponding empty antibonding orbital of the H-bond donor (D–H). In addition to these, estimating H-bonding energies using different properties of the compliance matrix is another less frequently used, but promising, theoretical approach.61,62 Interestingly, all these different theoretical techniques have been implemented to extensively study the canonical base pairs in DNA (A:T/G:C)51,63−67 because they are the so-called “heterogeneous” systems, where different categories of interbase H-bonds (N–H···N, N–H···O, C–H···O, etc.) are present in a single base pair. However, a consensus between these different computational approaches is lacking in the present literature. Here, we attempt to study the interrelations between these different computational approaches for interbase H-bonds present in RNA base pairs.
In this work, we have selected all the 118 types of RNA base pairs and analyzed the H-bonding energy of all their interbase H-bonds using Iogansen’s relationship.18 Each of the interbase H-bonds has been characterized by a total of 13 parameters, among which 6 are geometry-based (i.e., based on the relative positions of the H-bond donor, H-bond acceptor, and the hydrogen atom), 6 are topology- or QTAIM-based, and 1 is charge-transfer-based. All calculations have been performed using appropriate hybrid-generalized gradient approximation (GGA) density functional theory (DFT) functional, and the effect of dispersion interactions has been incorporated using DFT-D3 formalism. We have shortlisted the parameters that display significantly good linear correlation with the H-bonding energy (EHB) of all types of H-bonds (N–H···O, N–H···N, etc.). For these short-listed parameters, different sets of linear relationships between them and the H-bonding energies have been modeled using single variable and multivariable linear regression analyses. We have tested the performance of our models over a set of 36 modified base pairs (base pairs where the participating bases undergo post-transcriptional modifications), which are found in a nonredundant set of high-resolution RNA crystal structures. We have been able to achieve a root-mean-square error (RMSE) as low as 0.3 kcal mol–1 between the expected and predicted set of EHB values. Because, compared to the calculation of QTAIM or NBO parameters, calculation of vibrational spectroscopy is computationally expensive (and practically not feasible to perform for larger systems at a high level of theory), these sets of linear equations will provide a useful basis for obtaining reasonably accurate EHB values without performing expensive Hessian calculations.
2. Methods
2.1. Geometry Optimization of Selected RNA Base Pairs
We have studied all the 118 different geometries of normal base pairs and 36 modified base pairs that occur in the nonredundant set of high-resolution (resolution cutoff = 3.5 Å) RNA crystal structures provided by the HD-RNAS68 database. Gas-phase optimized geometries [B3LYP/6-31+G(d,p) level] of all the normal RNA base pairs are curated in the RNABP COGEST9 database. The hybrid GGA functional B3LYP69−71 is arguably the most widely used DFT functional for studying DNA and RNA base pairs37,72−80 and similar systems.81,82 Therefore, for the initial calculations, we have collected the B3LYP/6-31+G(d,p) level optimized geometries of different normal base pairs from the RNABP COGEST database. Gas-phase optimized geometry of modified base pairs, at the same level of theory, has been taken from the supporting information of the recent article by Seelam et al.83 Hessian calculation has been performed over the optimized geometries of all the normal and modified base pairs. For some of the normal base pairs, Hessian calculation results in imaginary frequencies because the corresponding optimized geometries present in RNABP COGEST are obtained from constrained optimization. These systems have been reoptimized. We have found that some of the reoptimized geometries are also associated with imaginary frequencies (as listed in the Supporting Information), and we have removed those cases from our study. The remaining systems are composed of 17 WW, 17 WH, 12 HH, 22 WS, 22 HS, and 13 SS pairs. Out of this final set of 103 base pairs, optimized geometries of 96 base pairs are the same as the one given in the RNABP COGEST database and geometries of rest 7 base pairs are obtained after reoptimization. They are G:C W:W Trans, A:G H:H Cis, A:U(II) H:H Trans, C:U H:H Trans, G:G H:H Trans, A:A W:H Trans, and G:rA H:S Cis. In order to incorporate the effects of dispersion interaction, they are further optimized using the B3LYP-D3(BJ) functional and the same basis set. In B3LYP-D3(BJ), the dispersion correction has been added explicitly by Grimme’s method (3rd order) with Becke–Johnson damping.84,85 All real frequencies were observed for B3LYP-D3(BJ) optimized systems on Hessian calculation. Similarly, for all the monomers, geometry optimization and subsequent Hessian calculation have been performed using both B3LYP and B3LYP-D3(BJ) functionals with the 6-31+G(d,p) basis set, respectively. Note that B3LYP and its dispersion-corrected version B3LYP-D3(BJ) are arguably the most universally used DFT functionals to study the nucleic acid-based systems.86,87 All the calculations were performed using Gaussian03 software.88
2.2. Interaction Energy of a Base Pair
Interaction energy of a base pair AB has been calculated as the difference between the electronic energy of the base pair AB (EAB) and sum of the electronic energies of the individual bases (EA and EB). All the interaction energies are further corrected for zero-point vibrational energy (ZPVE), basis set superposition error (BSSE) (EBSSE), and deformation energy (Edef), that is, Eint = EAB – (EA + EB) + Edef + EBSSE + EZPVE. Further details on the method of interaction energy calculation are discussed in the Supporting Information.
2.3. Different Types of Interbase H-Bonds
Potential H-bond donor groups present in the nucleobases are primary amino groups (NI–H), secondary amino groups (NII–H), hydroxyl group (Oh–H), and C–H group. On the other hand, potential H-bond acceptor groups present in the nucleobases are imino nitrogens (NIII), carbonyl oxygen (Oc), and hydroxyl oxygen (Oh). Table 1 shows the count of different types of H-bonds studied in this work. Note that amino acceptor interactions77,79 observed in Hoogsteen–Sugar base pairs are not included in this study as they occur only in a specific set of RNA base pairs.
Table 1. Count of Different Types of H-Bonds Studied in This Work.
| sl. | H-bond type | donor | acceptor | notation | count |
|---|---|---|---|---|---|
| 1 | N–H···N | primary N | imino N | NI–H···NIII | 42 |
| 2 | N–H···N | secondary N | imino N | NII–H···NIII | 17 |
| 3 | N–H···O | primary N | carbonyl O | NI–H···Oc | 38 |
| 4 | N–H···O | secondary N | carbonyl O | NII–H···Oc | 23 |
| 5 | N–H···O | primary N | hydroxyl O | NI–H···Oh | 17 |
| 6 | O–H···N | hydroxyl O | imino N | Oh–H···NIII | 18 |
| 7 | O–H···O | hydroxyl O | carbonyl O | Oh–H···Oc | 4 |
| 8 | O–H···O | hydroxyl O | hydroxyl O | Oh–H···Oh | 9 |
| 9 | C–H···N | C–H | imino N | C–H···NIII | 11 |
| 10 | C–H···O | C–H | carbonyl O | C–H···Oc | 14 |
2.4. H-Bonding Energy from Iogansen’s Relationship
For all the D–H···A-type interbase H-bonds, we have calculated the red shift (ΔνD–H) of the D–H stretching vibrational frequency as ΔνD–H = νD–Hfree – νD–H, where νD–Hfree and νD–H are the vibrational frequencies corresponding to the D–H bond stretching in the isolated monomer and in the H-bonded base pair, respectively. As prescribed in the Gaussian03 manual, all the vibrational frequencies are scaled by a factor 0.96 to obtain the values consistent with experimental results. We have calculated the H-bonding energy (EHB) from Iogansen’s relationship,18 which is
| 1 |
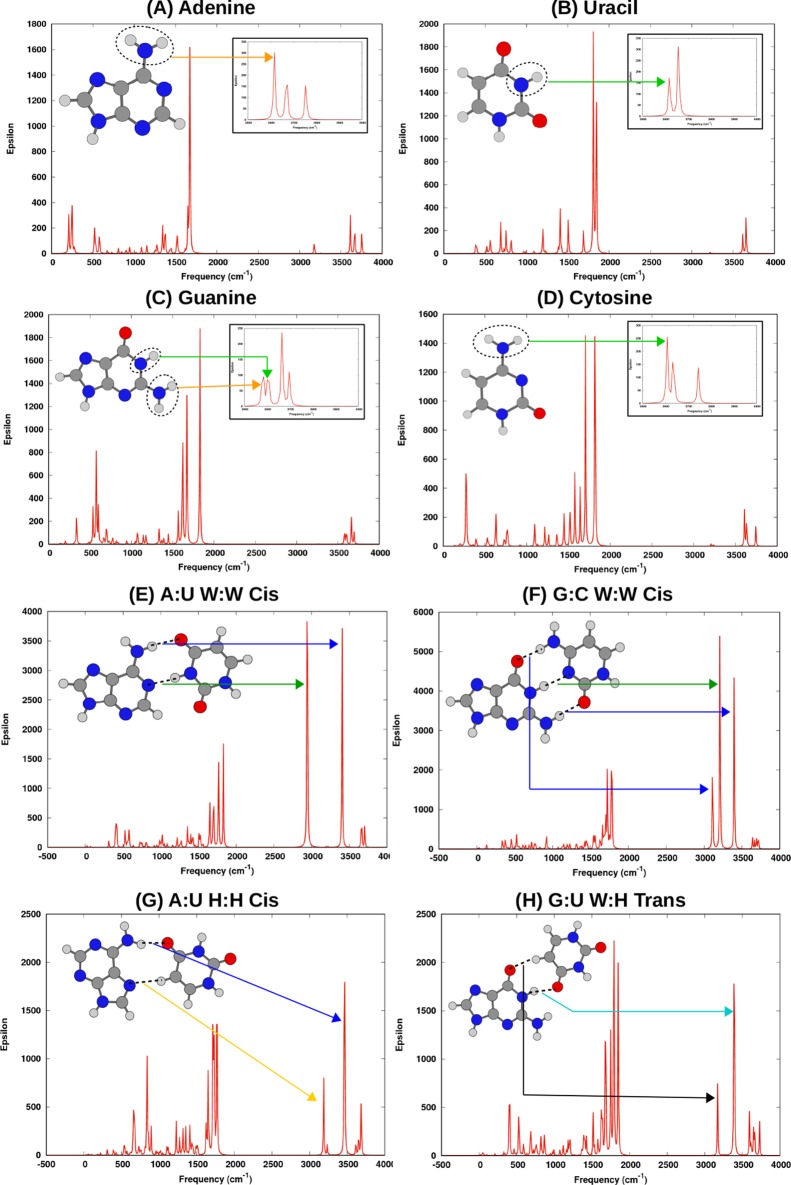
Note that Iogansen’s relationship allows us to estimate the H-bonding energy only for the red-shifted H-bonds with ΔνD–H > 40 cm–1. In this context, it is also important to mention that earlier works that implement Iogansen’s relationship to evaluate the strength of interbase H-bonds49−52 have taken special care (partial deuteration of the O–H, N–H, and NH2 groups involved in the interbase H-bonding) to minimize the effect of vibrational resonances. In this work, we have not taken any such measure. However, we confirm that in the numerically calculated IR spectra of all the base pairs, the symmetric stretching of each N–H, O–H, and C–H bond (that form interbase H-bonds) corresponds to a unique peak having high intensity (see Figure 3). Therefore, we can safely assume that the influences of vibrational resonance on our results are negligible.
Figure 3.
IR spectra (calculated at the B3LYP-D3(BJ)/6-31+G(d,p) level) of four nucleobases (A) adenine, (B) uracil, (C) guanine, and (D) cytosine; two canonical base pairs (E) A:U W:W Cis and (F) G:C W:W Cis; and two noncanonical base pairs (G) A:U H:H Cis and (H) G:U W:H Trans. For the nucleobases, the orange arrow and the green arrow point to the frequencies corresponding to symmetric stretching of the N–H bonds of the primary amino and secondary amino groups, respectively. Interbase H-bonds of the base pairs are shown in broken line. Frequencies corresponding to symmetric stretching of the N–H (or C–H) bond in interbase H-bonds are pointed using different colored arrows for different types of H-bonds: NI–H···Oc (blue), NII–H···NIII (green), NII–H···Oc (cyan), C–H···N (orange), and C–H···O (black).
2.5. Characterization of Interbase H-Bonds Using QTAIM Analysis
The QTAIM analysis has been performed over the wave functions corresponding to the ground-state optimized geometry of the base pairs obtained at both B3LYP/6-31+g(d,p) and B3LYP-D3(BJ)/6-31+g(d,p) levels of theory. We have found that all the interbase H-bonds are associated with a bond path such that at the BCP, the slope of the gradient of the electron density distribution is positive (∇2ρ > 0). We have calculated the following six topological parameters at the BCPs corresponding to the interbase H-bonds. They are (i) electron density (ρ), (ii) slope of the gradient of the electron density distribution (∇2ρ), (iii) potential energy density (V), (iv) kinetic energy density (G), (v) total energy density (Htot = V + G), and (vi) ellipticity (ε).a These topological parameters are frequently used in the literature to estimate H-bonding strength. QTAIM calculations have been performed using standalone AIMALL package.89
2.6. Characterization of Interbase H-Bonds Using NBO Analysis
NBO analysis has been performed on the optimized geometries obtained using both B3LYP/6-31G+(d,p) and B3LYP-D3/6-31G+(d,p) levels of theory. These calculations have been done using the NBO package90 as implemented in Gaussian03.88 The second-order perturbative energy has been estimated between the different Lewis-type “filled” (donor) and non-Lewis-type “empty” (acceptor) orbitals. These interactions are also referred to as “delocalization interactions” as they are a result of the donation of occupancy from the localized NBOs of the idealized Lewis structure into the empty non-Lewis orbitals, thereby showing a departure from the idealized Lewis structure description. The second-order perturbative energy (E(2)) resulting due to delocalization can be estimated for a donor NBO (i) and acceptor NBO (j) as
| 2 |
where qi is the donor orbital occupancy, εi, and εj are diagonal elements (orbital energies), and F(i,j) is the off-diagonal NBO Fock matrix element. A higher value of E(2) represents a stronger H-bonding interaction. In this work, we will refer to the E(2) parameter as “charge-transfer-based parameter”.
2.7. Characterization of the Geometry of an Interbase H-Bond
We have considered the geometry of a hydrogen bond as a triangle between the three atoms—donor (D), hydrogen (H), and acceptor (A) (see the Supporting Information). We have selected three distances (lengths of the three sides of the triangle DA, AH, and DH), the donor–hydrogen–acceptor angle (∠DHA), and the area (ΔDHA) of the DHA triangle and its perimeter (SDHA) to explore how the strength of the corresponding H-bonds depends on them.
2.8. Linear Regression Analysis
For different H-bonds, we have calculated the Pearson correlation coefficient (r) between the EHB values (say, dataset {y1, ..., yn}) and six topological parameters, six geometric parameters, and the stabilization energy E(2) obtained from NBO analysis (say, dataset {x1, ..., xn}). The Pearson correlation coefficient (r) between the two data sets {x1, ..., xn} and {y1, ..., yn} (having the average values x̅ and y®, respectively) is defined as
| 3 |
We have further performed single variable and multivariable linear regression analysis to establish linear relationships between the EHB and other topology-based, geometry-based, or charge-transfer-based parameters, following the standard least-square fit-based approach. All the interbase H-bonds studied here contribute toward the stabilization of the base pairs containing them, and hence, their energies must be represented as a negative value. However, for the ease of discussion, in the following text, all the H-bonding energies are reported in terms of their magnitude and hence have the positive sign.
3. Results and Discussion
It may be reiterated here at the outset that this approach toward estimating the average energy of a particular type of interbase H-bond has a limitation. It can be applied only to the H-bonds where the red shift in D–H bond stretching is >40 cm–1. As discussed elaborately in the following sections, C–H···O and C–H···N bonds found in RNA base pairs are usually associated with a small red shift or blue shift of the C–H bond stretching. Therefore, though improper C–H···O/N-type H-bonds are important factors that govern the geometries and stabilities of nucleic acid base pairs,91,92 we are not able to analyze their properties in detail. It may be noted that out of the remaining eight types of interbase H-bonds listed in Table 1, there are four bonds (serial numbers 5–8) that involve the sugar O2′ (either as donor or as acceptor, or both). Hence, they are found only in Sugar edge-mediated base pairs, that is, in the base pairs belonging to the WS, HS, or SS families. As shown later, EHB values of these four types of H-bonds do not show strong correlation with any of the topology-based, charge-transfer-based, or geometry-based parameters. In contrast, the other four types of H-bonds (serial numbers 1–4 in Table 1) are found in all types of base pairs and their EHB correlate well with some specific parameters studied in this work. Hence, majority of our discussions are focused on these four interbase H-bonds. They are as follows: NI–H···NIII, NII–H···NIII, NI–H···Oc, and NII–H···Oc.
3.1. Average H-Bonding Energy of Different Types of Interbase H-Bonds
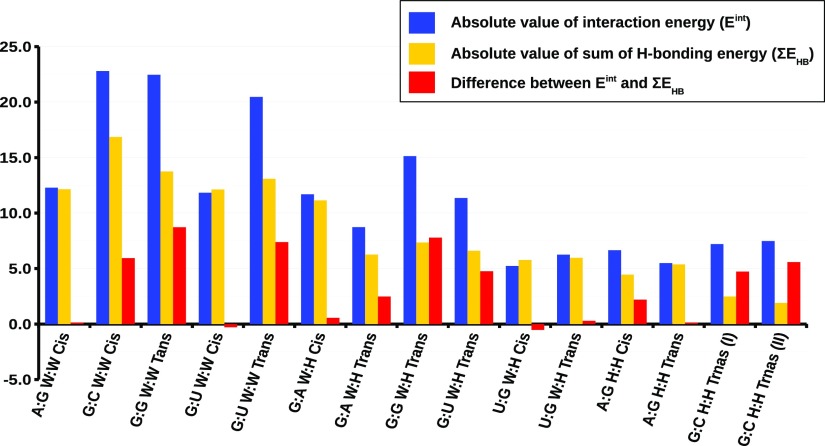
Calculating the average H-bonding energy (E®HB) for different types of interbase H-bonds that shape up the geometry and stability of noncanonical base pairs has been attempted earlier.93 There it has been assumed that the total interaction energy (Eint) of a base pair is solely contributed by the interbase H-bonds present in them, that is, Eint = ∑i=1nEHB, where n is the number of H-bonds present between the two bases and EHBi is the H-bonding energy of the interbase H-bond i. Therefore, calculations of Eint values of different base pairs give rise to a set of linear equations, which can further be solved to get the energetic contribution of each type of H-bonds (N–H···N, N–H···O, etc.). Another similar approach reported the H-bonding energies of the interbase H-bonds present in DNA base pairs.94 However, later investigations95,96 in this area have highlighted that in addition to interbase H-bonds, other factors, mainly charge delocalization, dipole–dipole interaction, London dispersion forces, and so forth, also contribute to the stability of base pairs. This means that for an RNA base pair, Ediff = Eint – ΣEHB is a nonzero quantity, which varies with its composition. To illustrate this systematically, we have calculated the EHB values of individual interbase H-bonds using the Iogansen’s relationship as discussed in the Methods section and obtained the Ediff values for all the base pairs belonging to the WW, WH, and HH families and containing guanine. Note that out of all the four nucleobases, guanine has the highest dipole moment.97Figure 2 clearly shows that Ediff values (the red bars) are significantly high, especially for high dipole moment base pairs such as G:C W:W Cis and G:G W:W Trans. For example, the interaction energy of the canonical G:C W:W cis base pairs is −22.8 kcal mol–1 and the sum of the EHB values of three interbase H-bonds present in it is −16.9 kcal mol–1 at the B3LYP/6-31+G(d,p) level (where negative signs indicate stabilization because of bond formation). These observations underline the need to revisit the problem with a different approach.
Figure 2.
Comparison of ZPVE- and BSSE-corrected interaction energy (Eint) of a base pair and the sum of the H-bonding energies of the interbase H-bonds present in it. Comparisons are made on the basis of the magnitude of the energies (in kcal mol–1) for 15 guanine-containing base pairs.
In this work, instead of calculating the interaction energy of a base pair for estimating the sum of all the interbase H-bonds present in it, we have calculated the H-bonding strength of individual H-bonds themselves (EHB) using Iogansen’s relationship. Therefore, the average H-bonding energy of a particular type of H-bond is given by the arithmetic mean of the EHB values of all its instances. Figure 3 illustrates the red shift in the D–H bond stretching frequency (ΔνD–H) because of D–H···A-type interbase H-bond formation in two canonical (A:U W:W Cis and G:C W:W Cis) and two noncanonical (A:U H:H Cis and G:U W:H Trans) base pairs. From these red shifts, the EHB values of individual H-bonds are calculated using Iogansen’s relationship, as discussed in the Methods section. Table 2 shows the average H-bonding energy (E®HB) for different types of interbase H-bonds calculated using this approach. Note that earlier attempts toward calculating E®HB values have not discriminated N–H···N (or N–H···O)-type H-bonds on the basis of the chemical identity of the donor N–H group. Our approach allows us to explore these varieties of interbase H-bonds. Interestingly, we have found that the average energy for N–H···N type H-bonds strongly depends on the hybridization state of the donor nitrogen. For NII–H···NIII-type H-bonds (see Table 1 for the annotation of different H-bonds), the average H-bonding energy is 6.42 kcal mol–1, which is 2.11 kcal mol–1 higher than the average energy of the NI–H···NIII-type H-bonds (4.31 kcal mol–1). Similarly, the average H-bonding strength of the N–H···O hydrogen bonds depends on the hybridization states of both the donor nitrogen and acceptor oxygen atoms. The average energies of the NI–H···Oc, NII–H···Oc, and NI–H···Oh H-bonds are 2.85, 5.13, and 2.56 kcal mol–1, respectively. The order of the mutual strengths of different interbase H-bonds can be explained on the basis of the mutual strengths of the corresponding H-bond donors and acceptors. The gas-phase acidity of the H-bond donor sites and gas-phase basicity (or proton affinity) of the H-bond acceptor sites of different nucleobases provide an overall estimate for their mutual H-bonding strengths. For nucleobases, a detailed and accurate estimation of the gas-phase acidity and gas-phase basicity of different polar sites has been reported by Lee and co-workers.98,99 It suggests that secondary amino groups (NII–H) are usually more acidic and hence stronger H-bond donors than primary amino groups (NI–H). Similarly, the exocyclic carboxylic oxygen groups (Oc) are usually less basic and hence weaker H-bond acceptors, compared to the imino nitrogen (NIII) atoms of the purine/pyrimidine rings. This explains why the average H-bonding energy of NII–H···NIII bonds is higher than that of NII–H···Oc and NI–H···NIII bonds (Table 2). Also, it justifies the trend that E®HB(NI–H···NIII) > E®HB(NI–H···Oc). Now, given the trends observed in Table 2 that (a) E®HB(NII–H···NIII) > E®HB(Oh–H···NIII) > E®HB(NI–H···NIII) and (b) E®HB(NII–H···Oc) > E®HB(Oh–H···Oc) > E®HB(NI–H···Oc), we can extend our argument to predict that the sugar O2′–H is a stronger H-bond donor than the primary amino group but weaker than the secondary amino group.
Table 2. Average Hydrogen Bonding Energy (EHB) of Different Interbase Hydrogen Bonds Obtained Using B3LYP and B3LYP-D3 Functionals Is Reported in kcal mol–1a.
| name | type of base pairb | B3LYP | B3LYP-D3(BJ) |
|---|---|---|---|
| NI–H···NIII | all | 4.31 (1.23) | 4.24 (1.35) |
| NS | 4.35 (1.38) | 4.40 (1.52) | |
| S | 4.26 (1.02) | 4.00 (1.04) | |
| NII–H···NIII | all | 6.42 (0.94) | 6.37 (1.16) |
| NS | 6.74 (0.84) | 6.81 (0.92) | |
| S | 5.66 (0.76) | 5.26 (1.01) | |
| NI–H···Oc | all | 2.85 (1.52) | 3.09 (1.46) |
| NS | 3.52 (1.51) | 3.75 (1.48) | |
| S | 2.25 (1.28) | 2.57 (1.25) | |
| NII–H···Oc | all | 5.13 (1.50) | 5.29 (1.39) |
| NS | 5.56 (0.81) | 5.80 (0.83) | |
| S | 4.33 (2.16) | 4.40 (1.74) | |
| NI–H···Oh | all | 2.56 (1.62) | 2.65 (1.38) |
| Oh–H···NIII | all | 5.24 (1.24) | 5.34 (1.19) |
| Oh–H···Oc | all | 4.09 (0.75) | 4.79 (1.01) |
| Oh–H···Oh | all | 3.33 (1.34) | 2.76 (1.1) |
Values reported within parenthesis represent corresponding standard deviation.
“All”: all base pairs studied, “S”: base pairs of the WS, HS, and SS families, “NS”: base pairs of the WW, WH, and HH families.
Nevertheless, our approach is not suitable for studying C–H···O and C–H···N bonds because the red shifts in the C–H bonds are usually less than 40 cm–1. In our dataset, only 3 out of total 11 C–H···N-type H-bonds and 1 out of total 14 C–H···O-type H-bonds show a red shift ΔνC–H, which is greater than 40 cm–1. Out of the C–H···N bonds, the maximum red shift (87.36 cm–1) is observed for the U(C5–H)···(N7)A H-bond in the A:U H:H Cis pair (Figure 3G). Again, out of the C–H···O bonds, the U(C5–H)···(O6)G H-bond in G:U W:H Trans pair (Figure 3H) is associated with a significant red shift (86.92 cm–1). Interestingly, six C–H···O H-bonds and one C–H···N H-bond in our dataset are also associated with a blue shift in the C–H bond stretching (ΔνC–H < 0). The origin of such a blue shift in the so-called improper hydrogen bonds such as C–H···O/N has been explained earlier.100 For any D–H···A-type H-bond, the change in the D–H bond length and hence in its symmetric stretching frequency is determined by two competing forces: —(a) the electron affinity of D, which causes increased electron density at the D–H bond region in the presence of A and thus promotes D–H bond contraction and (b) the attractive force between the electron-rich A and positively charged H that promotes D–H bond elongation. It has been found that the latter almost always dominates in polar D–H bonds, whereas the effect of the former is noticeable only in the nonpolar D–H bonds (C–H in our case) with relatively weaker H-bond acceptors.100 Therefore, a plausible justification for the observation that blue shifts in the C–H bond stretching are more abundant in C–H···O bonds than in C–H···N bonds can be obtained from the fact that compared to the imino nitrogen groups (NIII), the exocyclic carboxylic oxygen groups (Oc) are usually weaker H-bond acceptors.98,99
On the basis of the average EHB values, three out of the eight types of H-bonds listed in Table 2 (NI–H···Oc, NI–H···Oh, and Oh–H···Oh) can be categorized as weak H-bond (EHB < 4 kcal mol–1), and the rest five types can be characterized as moderately strong H-bonds (4 kcal mol–1 < EHB < 15 kcal mol–1). Interestingly, the weak H-bonds are associated with large standard deviation (Table 2), which is indicative of their flexible nature. Among the moderately strong H-bonds, NII–H···Oc and NI–H···NIII show significantly high standard deviation compared to other H-bonds and are therefore expected to have higher flexibility. Therefore, it is expected that noncanonical base pairs composed of these two H-bonds will have flexible geometry. Two such base pairing geometries are G:C W:W Trans and G:G W:H Cis. Each of them is composed of only two H-bonds: one NII–H···Oc and one NI–H···NIII, and their native geometries are indeed flexible.101 They are known to deviate significantly from their respective native geometries under gas-phase geometry optimization at different levels of theory.102 On gas-phase geometry optimization, the G:C W:W Trans base pair deviates from the reverse Watson–Crick geometry to form a bifurcated geometry, whereas the G:G W:H Cis base pair converges to a G:G W:W Trans geometry. Further studies show that they require support either from the formation of higher-order interactions103 or from the buildup of positive charge environment at the Hoogsteen edge of the guanine residue to stabilize their respective native geometries. The positive charge buildup may take place in the form of metal ion coordination,104−106 post-transcriptional modification,107 or even nucleobase protonation.108 These observations demonstrate how the geometries and stabilities of different noncanonical base pairs are determined by their constituent interbase H-bonds.
Another important trend, as shown in Table 2, is that the average H-bonding energy of the interbase H-bonds of WS, HS, and SS base pairs is smaller than the same present in WW, WH, and HH base pairs. This trend is consistent with the fact that the base pairing interactions forming via the sugar edge are comparatively flexible than others and are therefore unstable under QM-based gas-phase geometry optimization.73−75,77,79 We have also found that the influences of the dispersion interactions on the individual H-bonding energies are small (|EHB(B3LYP) – EHB(B3LYP-D3(BJ))| < 0.25 kcal mol–1), except the sugar O2′-mediated H-bonds. For the sugar O2′-mediated H-bonds, the average H-bonding energies calculated in the presence and absence of dispersion corrections are significantly different. Our results are in line with the earlier literature studies, which underscore the importance of dispersion interactions in stabilizing the base pairs of WS,74,75 HS,77,79 and SS73 families. As mentioned in the Methods section, for each of the interbase H-bonds, we have calculated 13 different parameters based on their geometry, topology of the corresponding BCP, and associated charge transfer. We have tried to find out the correlation between the H-bonding energy and these 13 parameters.
3.2. How Well Do the Topology-Based, Geometry–Based, and Charge-Transfer-Based Parameters Correlate with the H-Bonding Energies?
Pearson correlation coefficients (r) calculated between the H-bonding energies obtained from vibrational spectroscopy (EHB) and different geometry-based, topology-based, and charge-transfer-based parameters are shown in Table 3. It may be noted that though the trends observed are similar, there are noticeable differences between the values obtained using B3LYP and B3LYP-D3(BJ) functionals. In most of the cases, the Pearson correlation coefficient (r) is better with the values obtained using the dispersion-corrected B3LYP-D3(BJ) functional and has hence been used for our detailed analysis. Further to note is that we have limited our discussion below to the H-bond types 1–4 as listed in Table 3. As explained at the beginning of the section, H-bond types 5–8 are excluded from the discussion because they show poor correlation between EHB and other parameters.
Table 3. Pearson Correlation Coefficients between EHB and Different QTAIM, NBO, and Geometric Parameters (at B3LYP/6-31+G(d,p) Level) for Eight Different Types of Interbase H-Bonds Studied in This Worka.
| QTAIM
parameters |
NBO | geometrical
parameters |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sl. | type of HB | type of BP | ρ | ∇2ρ | V | G | Htot | E(2) | D–A | H–A | D–H | ∠D–H–A | SDHA | ΔDHA |
| 1 | NI–H···NIII | all | 0.89 (0.91) | 0.85 (0.90) | –0.88 (−0.89) | 0.87 (0.89) | –0.89 (−0.79) | 0.90 (0.92) | –0.74 (−0.78) | –0.88 (−0.82) | 0.92 (0.95) | 0.75 (0.73) | –0.85 (−0.81) | –0.77 (−0.74) |
| NS | 0.96 (0.96) | 0.93 (0.92) | –0.95 (−0.94) | 0.94 (0.93) | –0.89 (−0.88) | 0.97 (0.94) | –0.82 (−0.81) | –0.94 (−0.91) | 0.97 (0.97) | 0.87 (0.82) | –0.91 (−0.88) | –0.88 (−0.84) | ||
| S | 0.76 (0.89) | 0.74 (0.91) | –0.75 (−0.89) | 0.75 (0.90) | –0.63 (−0.76) | 0.80 (0.93) | –0.69 (−0.83) | –0.64 (−0.78) | 0.80 (0.91) | 0.52 (0.60) | –0.66 (−0.80) | –0.54 (−0.63) | ||
| 2 | NII–H···NIII | all | 0.83 (0.88) | 0.72 (0.80) | –0.79 (−0.84) | 0.76 (0.82) | –0.86 (−0.86) | 0.87 (0.91) | –0.77 (−0.84) | –0.82 (−0.88) | 0.99 (0.99) | 0.70 (0.65) | –0.78 (−0.85) | –0.71 (−0.66) |
| NS | 0.76 (0.79) | 0.56 (0.60) | –0.71 (−0.74) | 0.65 (0.67) | –0.92 (−0.92) | 0.79 (0.82) | –0.61 (−0.66) | –0.69 (−0.73) | 0.99 (0.99) | 0.66 (0.67) | –0.63 (−0.67) | –0.66 (−0.66) | ||
| S | 0.98 (0.96) | 0.97 (0.93) | –0.96 (−0.92) | 0.97 (0.93) | –0.86 (−0.88) | 0.93 (0.95) | –0.98 (−0.89) | –0.98 (−0.94) | 0.99 (0.99) | 0.53 (0.46) | –0.98 (−0.92) | –0.56 (−0.51) | ||
| 3 | NI–H···Oc | all | 0.93 (0.95) | 0.84 (0.83) | –0.91 (−0.91) | 0.88 (0.88) | –0.24 (−0.17) | 0.93 (0.93) | –0.62 (−0.56) | –0.83 (−0.89) | 0.94 (0.95) | 0.62 (0.74) | –0.80 (−0.81) | –0.63 (−0.76) |
| NS | 0.95 (0.97) | 0.96 (0.89) | –0.94 (−0.91) | 0.95 (0.90) | 0.12 (0.41) | 0.95 (0.93) | –0.91 (−0.89) | –0.90 (−0.97) | 0.95 (0.95) | 0.95 (0.75) | –0.92 (−0.94) | –0.73 (−0.77) | ||
| S | 0.94 (0.93) | 0.87 (0.85) | –0.93 (−0.92) | 0.91 (0.89) | –0.07 (−0.04) | 0.87 (0.91) | –0.57 (−0.47) | –0.88 (−0.89) | 0.96 (0.97) | 0.47 (0.71) | –0.87 (−0.84) | –0.48 (−0.73) | ||
| 4 | NII–H···Oc | all | 0.84 (0.89) | 0.78 (0.83) | –0.78 (−0.83) | 0.78 (0.83) | –0.16 (−0.18) | 0.90 (0.94) | –0.62 (−0.71) | –0.81 (−0.86) | 0.96 (0.98) | 0.76 (0.79) | –0.73 (−0.79) | –0.78 (−0.82) |
| NS | 0.74 (0.75) | 0.68 (0.71) | –0.66 (−0.67) | 0.67 (0.69) | –0.38 (−0.35) | 0.85 (0.85) | –0.69 (−0.72) | –0.79 (−0.81) | 0.98 (0.97) | 0.23 (0.11) | –0.71 (−0.74) | –0.26 (−0.15) | ||
| S | 0.87 (0.93) | 0.87 (0.93) | –0.84 (−0.91) | 0.86 (0.92) | 0.42 (0.45) | 0.93 (0.97) | –0.69 (−0.77) | –0.81 (−0.88) | 0.98 (0.99) | 0.84 (0.91) | –0.76 (−0.84) | –0.86 (−0.94) | ||
| 5 | NI–H···Oh | all | 0.39 (0.17) | 0.48 (0.31) | –0.41 (−0.17) | 0.44 (0.23) | –0.25 (−0.20) | 0.31 (0.10) | –0.80 (−0.63) | –0.41 (−0.12) | 0.18 (0.21) | 0.04 (−0.15) | –0.55 (−0.34) | –0.08 (0.12) |
| 6 | Oh–H···NIII | all | 0.54 (0.60) | 0.43 (0.49) | –0.55 (−0.60) | 0.51 (0.57) | –0.61 (−0.65) | 0.55 (0.63) | –0.48 (−0.49) | –0.46 (−0.55) | 0.63 (0.64) | –0.10 (0.26) | –0.46 (−0.52) | 0.08 (−0.27) |
| 7 | Oh–H···Oc | all | 0.46 (0.64) | 0.38 (0.61) | –0.43 (−0.65) | 0.40 (0.63) | –0.67 (−0.60) | 0.64 (0.60) | –0.44 (−0.58) | –0.47 (−0.59) | 0.41 (0.66) | 0.73 (0.66) | –0.46 (−0.58) | –0.65 (−0.63) |
| 8 | Oh–H···Oh | all | –0.45 (0.04) | –0.51 (0.07) | 0.49 (−0.01) | –0.50 (−0.04) | 0.34 (0.35) | –0.34 (−0.06) | 0.64 (0.04) | 0.50 (−0.01) | –0.01 (0.07) | –0.09 (−0.02) | 0.58 (−0.01) | 0.22 (0.05) |
Values given in parenthesis represent the Pearson correlation coefficients calculated at the B3LYP-D3/6-31+G(d,p) level of theory.
For these four types of hydrogen bonds, some of the parameters show remarkably good linear correlation (|r| ≥ 0.9). Out of them, the best correlation with the EHB values is displayed by the E(2) values obtained from NBO calculations. E(2) values correspond to the stabilization energy because of n → σ*-type charge transfer from the π orbital of the H-bond acceptor to the corresponding antibonding orbital of the H-bond donor (N–H, O–H, or C–H bond). Therefore, our results suggest that for H-bonds with red-shifted D–H bonds, the extent of n → σ* charger transfer determines the H-bonding strength. This is in line with the justification for the electronic basis of H-bonding given by Alabugin and co-workers.109 We further observe that correlation between E(2) and EHB is the maximum for the two strongest H-bonds found in the studied RNA base pairs (Table 2). They are (i) NI–H···NIII bonds (r = 0.94 for H-bonds observed in base pairs of the WW, WH, and HH families) and (ii) NII–H···Oc bonds (r = 0.97 for H-bonds observed in the base pairs of the WS, HS, and SS families).
The set of geometry-based parameters consists of three interatomic distances (D–A, D–H, and H–A); the angle described by H-bond donor, hydrogen, and H-bond acceptor (∠DHA); the perimeter of the DHA triangle (SDHA) and its area (ΔDHA). As discussed earlier,100,109 n → σ*-type charge transfer from the π orbital of the H-bond acceptor to the antibonding orbital of the H-bond donor results into elongation of the corresponding σ bond (N–H, O–H, or C–H). Therefore, the change in D–H distance due to H-bonding is inherently connected to the concomitant red shift. This rationalizes the observation that out of the three interatomic distances, D–H shows exceptionally good correlation (|r| ≥ 0.95) with the H-bonding strength of all the four types of H-bonds (Table 3). Such weakening of the D–H σ bonds is linked to the attractive interaction between the acceptor and hydrogen atoms. Consequently, we have found that the extent of weakening of the N–H/O–H bonds is also strongly correlated with the H-bonding energies calculated from Iogansen’s relationship (r = 0.95 for all the H-bonds present in all the base pairs of the WW family).b Hence, the H–A distances are significantly well correlated (|r| ≥ 0.85) with the H-bonding strength of all the four types of H-bonds. This also explains why the perimeter of the DHA triangle SDHA shows reasonably good correlation with the corresponding H-bonding strengths. We further note that consistent with the recent reports,110 the correlations between EHB and D–A distances are comparatively poor (|r| < 0.8) for all kinds of H-bonds. It is therefore intuitive that the strength of an interbase H-bond (D–H···A) does not depend strongly on the corresponding ∠DHA and the geometry-based parameters derived from that (e.g., the area of the DHA triangle, ΔDHA). Hence, as shown in Table 3, ∠DHA and ΔDHA display comparatively poor correlation (|r| < 0.8) with the corresponding H-bonding strengths (EHB).
Unlike the charge-transfer-based and geometry-based parameters, the physical origin of the relationship between the H-bonding energies and topological parameters calculated at the corresponding BCPs is not well understood. Out of the six topological parameters thus for each interbase H-bond, the electron density (ρ) shows good correlation (0.95 ≥ |r| ≥ 0.88) with the EHB values for all the four interbase H-bonds. On the other hand, the ellipticity (ε) shows poor correlation with EHB for all kinds of interbase H-bonds studied and has therefore not been included in Table 3. Performances of the other four topological parameters depend on the nature of the H-bond. For example, the Laplacian of the electron density (∇2ρ) is well correlated with the EHB values corresponding to the H-bonds having primary amino group as the donor (N6 of adenine, N4 of cytosine, and N2 of guanine), but for the H-bonds having secondary amino groups as the donor (N1 of guanine and N3 of uracil) the correlation is comparatively poor. Similar trend is also observed for the potential energy density (V) and kinetic energy density (G). Table 3 suggests that the poor correlation is explicitly due to those NII–H···NIII and NII–H···Oc bonds which are present exclusively in the base pairs belonging to the WW, WH, and HH families. Interestingly, the Pearson correlation coefficient between EHB and the total energy density (Htot) shows remarkably different trends for N–H···N and N–H···O H-bonds, respectively. The correlation is good for the N–H···N bonds (r = −0.89 and −0.86 for NI–H···NIII and NII–H···NIII bonds, respectively), whereas it is extremely poor for N–H···O bonds (r = −0.24 and −0.16 for NI–H···Oc and NII–H···Oc bonds, respectively).
On the basis of the above analysis, we may infer that the three parameters E(2), ρ, and D–H, covering three different aspects (charge transfer, topology, and geometry, respectively) display remarkably good (|r| > 0.9) correlation with the H-bonding energy of all the four different types of H-bonds, especially when the dispersion corrections are taken into consideration. Among the remaining 10 parameters, only ∇2ρ and H–A are the two parameters, which show good correlation (0.9 < |r| < 0.85) with EHB for all the four different types of H-bonds. Therefore, these five parameters are shortlisted as potential candidates for modeling linear relationships with EHB. These models will be useful to estimate the H-bonding energy of individual H-bonds.
3.3. Modeling Linear Relationship between EHB and Other Topology-Based, Charge-Transfer–Based, and Geometry-Based Parameters
We have modeled linear equations linking the above-mentioned topology-based, charge-transfer-based, and geometry-based parameters with the H-bonding energy calculated from vibrational spectroscopy (EHB). To benchmark the efficiency of our models, we have selected a set of 36 modified base pairs. They occur naturally in a nonredundant set of high-resolution RNA crystal structures (HDRNAS68). Their occurrence contexts, structures, and possible contribution in the structural dynamics of functional RNAs have been analyzed recently by Seelam et al.83 The modified base pairs constitute an ideal test set for our model because their overall physicochemical properties are reasonably close to our training set (normal base pairs), but at the same time, they possess a significant amount of chemical variations. Both the bases are modified in 2 of these 36 modified base pairs (m2G:Um W:WC and Cm:Gm W:WC), whereas the rest of the base pairs are composed of one normal base and one modified base. Among these 36 base pairs, 12 base pairs have modification in the sugar moiety in the form of methylation at O2′ position. Others display different nucleobase modifications, such as m2G (2 base pairs), s4U (3 base pairs), m5C (3 base pairs), m5U(3 base pairs), m7G (2 base pairs), D (3 base pairs), m22G (2 base pairs), m62A (1 base pair), and Ψ (5 base pairs). Note that we have removed the base pairs containing m7G modification as they are charged systems. In the rest 34 base pairs, we have identified 56 hydrogen bonds which are associated with a red shift greater than 40 cm–1, and therefore, the corresponding hydrogen bonding energies can be calculated using Iogansen’s relationship. Among them, 6 are of NI–H···NIII type, 16 are of NII–H···NIII type, 21 are of NI–H···Oc type, and 13 are of NII–H···Oc type.
First, we have performed a single variable linear regression for all the four hydrogen bonds and modeled the equations (y = Ax + B) relating EHB with each of the five parameters (ρ, ∇2ρ, E(2), D–H, and H–A), respectively, following the conventional least-square fit approach. The slope (A) and the y-intercept (B) of the modeled equations are listed in Table 4. Similar linear equations for other seven parameters (V, G, H, D–A, ∠DHA, SDHA, and ΔDHA) are shown in Table S3 of the Supporting Information. We have implemented these single variable equations to predict the EHB values of the interbase H-bonds of the modified base pairs. Mean square error (MSE) and RMSE values (Table 5) calculated between the predicted EHB and expected EHB values (as calculated from the vibrational spectra of modified base pairs) show that all the RMSE of all the single variable models varies between 0.4 and 0.8 kcal mol–1. As expected, the model based on D–H distance gives the best result (RMSE = 0.41 kcal mol–1), followed by the models based on E(2) and ρ. It is important to note that the MSE and RMSE values of these single variable models are independent of the strength of the H-bonds (Table 5). Hence, in the worst-case scenario (EHB ≈ 2.0 kcal mol–1), the mean error in predicting the H-bonding energies will be as high as 20%. On the other hand, in the best-case scenario (EHB ≈ 8.0 kcal mol–1), the mean error will be only 5%.
Table 4. Linear Relationships (y = Ax + B) between H-Bonding Strength and the Individual Parameters, Which Have High Pearson Correlation Coefficient (r) for All the Four Types of H-Bonds in Table 3, Were Derived from Single Variable Linear Regression Analysisa.
| H-bond type | independent variable (x) | slope (A) | intercept (B) |
|---|---|---|---|
| NI–H···NIII | ρ | 190.34 ± 14.68 | –0.60 ± 0.38 |
| ∇2ρ | 90.09 ± 7.60 | –1.35 ± 0.48 | |
| E(2) | 0.22 ± 0.02 | 1.33 ± 0.22 | |
| H–A | –6.90 ± 0.81 | 18.44 ± 1.67 | |
| D–H | 210.20 ± 11.88 | –210.78 ± 12.16 | |
| NII–H···NIII | ρ | 135.45 ± 21.24 | 1.89 ± 0.72 |
| ▽2ρ | 57.20 ± 12.58 | 1.98 ± 0.99 | |
| E(2) | 0.13 ± 0.02 | 3.65 ± 0.39 | |
| H–A | –9.90 ± 1.58 | 25.42 ± 3.04 | |
| D–H | 150.20 ± 5.17 | –149.41 ± 5.36 | |
| NI–H···Oc | E(2) | 0.26 ± 0.02 | –0.14 ± 0.24 |
| ρ | 251.43 ± 13.83 | –3.42 ± 0.37 | |
| ∇2ρ | 75.03 ± 8.71 | –2.71 ± 0.69 | |
| H–A | –12.32 ± 1.10 | 27.04 ± 2.14 | |
| D–H | 253.08 ± 13.98 | –254.87 ± 14.25 | |
| NII–H···Oc | E(2) | 0.18 ± 0.01 | 1.88 ± 0.27 |
| ρ | 145.50 ± 16.13 | 0.60 ± 0.54 | |
| ▽2ρ | 46.48 ± 6.76 | 0.88 ± 0.66 | |
| H–A | –8.57 ± 1.17 | 21.28 ± 2.21 | |
| D–H | 212.44 ± 9.71 | –213.70 ± 10.01 |
For this, two topological parameters (ρ, ∇2ρ), one charge-transfer-based parameter (E(2)), and two geometry-based parameters (H–A distance and D–H distance) were considered as independent variables (x) and EHB was considered as the scalar dependent variable (y). The values for the slope (A) and y-intercept (B), along with their respective standard deviations, are tabulated here. Units of different parameters are as follows: EHB [kcal mol–1], ρ [a.u., 1 a.u. = ea0–3, where e is the elementary charge and a0 is the Bohr radius], ∇2ρ [a.u., 1 a.u. = ea0–5], E(2) [kcal mol–1], H–A [Å] and D–H [Å].
Table 5. MSE and RMSE Values (in kcal mol–1) between the Set of Expected EHB Values and Set of Predicted EHB Values from Different Single Parameter and Multiparameter Modelsa.
| MSE |
RMSE |
|||||
|---|---|---|---|---|---|---|
| parameter | weak | strong | all | weak | strong | all |
| ρ | 0.32 | 0.33 | 0.33 | 0.56 | 0.58 | 0.58 |
| ∇2ρ | 0.59 | 0.63 | 0.62 | 0.77 | 0.79 | 0.79 |
| E(2) | 0.20 | 0.25 | 0.23 | 0.45 | 0.50 | 0.49 |
| H–A | 0.44 | 0.49 | 0.47 | 0.66 | 0.7 | 0.69 |
| D–H | 0.17 | 0.16 | 0.17 | 0.41 | 0.4 | 0.41 |
| 3-P model | 0.54 | 0.20 | 0.30 | 0.74 | 0.45 | 0.55 |
| 5-P model | 0.12 | 0.07 | 0.09 | 0.34 | 0.28 | 0.30 |
“Weak” and “strong” correspond to H-bonds with EHB < 4 and 15 kcal mol–1 ≥ EHB ≥ 4 kcal mol–1, respectively.
To improve the performance of our model, we have performed multiple linear regression analysis with the three parameters ρ, E(2), and D–H (we call it a three-parameter model) and with all the five parameters (we call it a five-parameter model). Using a similar least-square fit approach, we model the following two sets of linear equations;
Three-parameter model: EHB = C0 + C1 × ρ + C2 × E(2) + C3 × DH
NI–H···NIII: EHB = −135.1 + 11.2ρ + 0.08E(2) + 135.0DH
NII–H···NIII: EHB = −121.9 – 15.5ρ + 0.04E(2) + 123.3DH
NI–H···Oc: EHB = −112.6 + 103.6ρ + 0.05E(2) + 110.2DH
NII–H···Oc: EHB = −142.4 + 27.6ρ + 0.04E(2) + 141.7DH
Five-parameter model: EHB = C0 + C1 × ρ + C2 × ∇2ρ + C3 × E(2) + C4 × HA + C5 × DH
NI–H···NIII: EHB = −110.2 + 227.8ρ – 27.9∇2ρ + 0.06E(2) + 4.4HA + 98.3DH
NII–H···NIII: EHB = −87.4 + 4.5ρ – 37.2∇2ρ + 0.03E(2) – 6.7HA + 104.9DH
NI–H···Oc: EHB = −107.95 + 108.0ρ – 13.9∇2ρ + 0.05E(2) – 2.2HA + 110.8DH
NII–H···Oc: EHB = −143.2 + 44.3ρ – 10.0∇2ρ + 0.03E(2) – 1.26HA + 145.4DH
Comparison of the performance of the five-parameter model (5-P model) and the three-parameter model (3-P model) is illustrated in Figure 4. Interestingly, our analyses show that the performance of the three-parameter model (RMSE = 0.55 kcal mol–1) is better than all the single parameter models, except the D–H-based model (RMSE = 0.41 kcal mol–1). At the same time, performance of the five-parameter model (RMSE = 0.3 kcal mol–1) is even better than that of the D-H-based single parameter model. It is also noteworthy that the corresponding MSE and RMSE values of the 3-P and 5-P models are dependent on the strength of the H-bonds. Table 5 shows that in comparison to the weak H-bonds (EHB < 4 kcal mol–1), their performance is significantly better for the moderately strong H-bonds (15 ≥ EHB ≥ 4 kcal mol–1). Therefore, for the worst-case scenario (for H-bonds with EHB ≈ 2 kcal mol–1), the 5-P model is expected to predict the H-bonding energies with an average error of 17.5%. On the other hand, for the best-case scenario (for H-bonds with EHB ≈ 8 kcal mol–1), the 5-P model is expected to predict the H-bonding energies with an average error of only 3.5%. Importantly, in an average case scenario (EHB ≈ 5 kcal mol–1), the 5-P model is expected to perform reasonably well with an average error of only 6%.
Figure 4.
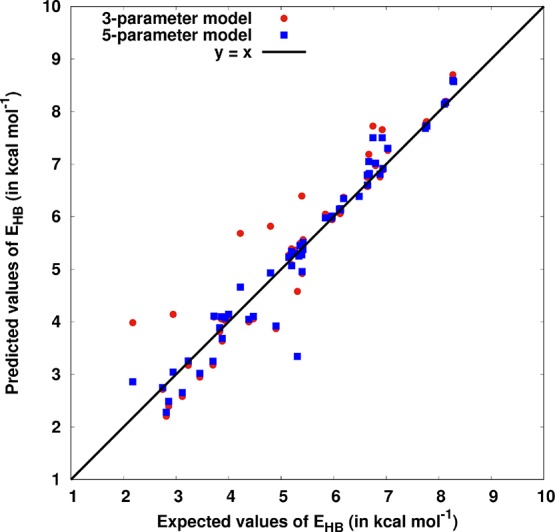
Comparison of the three-parameter (in red circle) and five-parameter (in blue square) models for interbase H-bonds present in modified base pairs. The predicted values of EHB are plotted with respect to their corresponding expected values. To illustrate the performance of the two models, the y = x straight line is shown as a reference.
We have also analyzed the performances of these two multivariable linear regression models for different types of H-bonds separately (Tables S5 and S6 in the Supporting Information) and found that performances of both the models are reasonably good (variance score or R2 > 0.9) for all the four types of interbase H-bonds (NI–H···NIII, NII–H···NIII, NI–H···Oc, and NII–H···Oc). Consistent with the trends discussed above, their performances are exceptionally good (R2 = 1) for the strongest NII–H···NIII bonds. To understand the relative significance of the individual parameters in these two models, importance analysis(111) was carried out. In keeping with the usual procedure,112 the importance value is estimated as the difference in the corresponding R2 values, when the corresponding variable is replaced with its average value (see Tables S5 and S6). As expected, the distance between donor and hydrogen atoms (D–H) turns out to be the most significant parameter (importance ∼0.5), specially for NII–H···Oc-type H-bonds.
There are several earlier reports attempting to express H-bonding energies as linear functions of different individual parameters, such as E(2), ρ, ∇2ρ, and so forth. The novelty in our multivariable models lies in the inclusion of additional parameters, belonging to different domains such as charge transfer, topology, and geometry, which may be capturing additional information regarding system properties. While the respective reliabilities of earlier and our models can be seen in terms of the extent of correlation between predicted values and experimental data, there are problems when it comes to rating or comparing them. That is because none of the earlier approaches have considered the subclassification of the different H-bond classes, in terms of the bonding contexts of the donor and acceptor atoms. However, despite the demonstrated reliability of our multivariable models, caution must be exercised before applying them universally to any system of interest. Rather, it is advisable to validate the approach for other H-bonded systems before carrying out any predictive applications.
4. Conclusions
In this work, we have come up with a comprehensive estimate of the average H-bonding energies (EHB) of different interbase hydrogen bonds that constitute the canonical and noncanonical RNA base pairs. Depending on the chemical identity of the H-bond donor and acceptor atoms, all these interbase hydrogen bonds can be classified into 10 categories, out of which 2 are associated with a small red shift (<40 cm–1) of the D–H bond stretching and hence are not part of the detailed analysis (C–H···O and C–H···N). EHB values for these eight types of interbase H-bonds have been calculated from their vibrational spectra obtained from computationally expensive Hessian calculation. The average EHB values fall within the range of 2.5–7 kcal mol–1 and follow the order: NII–H···NIII > NII–H···Oc ≳ OII–H···NIII > NI–H···NIII ≳ Oh–H···Oc > NI–H···Oc ≳ Oh–H···Oh > NI–H···Oh. We have studied the linear correlation of EHB with 13 other frequently used H-bond strength descriptors that can be obtained from computationally inexpensive methods (QTAIM, NBO, etc.). The four H-bonds, which occur exclusively within the Sugar edge-mediated base pairs, do not show strong correlation with any of the parameters studied in this work. For the other four interbase H-bonds (also they are the strongest four interbase H-bonds), we have found (a) three parameters E(2), ρ, and D–H that belong to three different domains (charge transfer, topology, and geometry, respectively) and display remarkably good (|r| > 0.9) linear correlation and (b) two parameters ∇2ρ and H–A that show reasonably good linear correlation (0.9 < |r| < 0.85), especially when the dispersion corrections are taken into consideration. Therefore, we have performed single variable and multiple variable regression analysis to establish linear relationships between the H-bond strength descriptors obtained from computationally inexpensive methods with the EHB values obtained from accurate but computationally expensive methods. We have tested the performance of our linear models over an independent set of base pairs having modified nucleobases. We have obtained promising results, at least with the model composed of five parameters (the 5-P model). In an average case scenario (H-bonds with EHB ≈ 5 kcal mol–1), it can predict the strength of an interbase H-bond with a 94% accuracy. At the same time, in the best-case scenario (H-bonds with EHB ≈ 8 kcal mol–1), the accuracy is as good as 96.5%. These predictive models show relatively poor accuracy for the weak H-bonds (EHB < 4.0 kcal mol–1). In this regard, it may be noted that depending on the chemical identity of the donor (D) and acceptor (A) groups of a H-bond (D–H···A), the shift in D–H symmetric stretching frequency leads to a continuum of behavior (red shift to no shift to blue shift), where the zero shift occurs around EHB ≤ 4.0 kcal mol–1.100,113 Therefore, any interpretation at this energy range is bound to be error-prone. Overall, these linear models provide the scope to calculate the EHB values of any individual interbase H-bond.
We expect that our efforts will be useful in exploring the intriguing world of H-bonding as our predictive models provide reliable estimates for H-bond strengths with computationally inexpensive calculations. On the other hand, our analysis of the strengths of individual interbase H-bonds provides effective inputs for designing coarse-grain-based force fields for RNA and other nucleic acid-based systems. These consolidated information are also helpful in analyzing the trajectories obtained from molecular dynamics simulations of DNA/RNA and similar systems.
Acknowledgments
A.H. acknowledges CSIR for SRF support. A.M. and A.H. thank DBT, Government of India, project BT/PR-14715/PBD/16/903/2010 for partial funding and financial support. A.M. and D.B. thank DBT, Government of India, project BT/PR-11429/BID/07/271/2008 for supporting computational infrastructure.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b03689.
Limitations of different computational approaches proposed for estimating the H-bonding energy, computational details of interaction energy calculation, list of RNA base pairs studied in this work, details of EHB calculation from Iogansen’s relationship (range of observed red shifts), average values of different parameters (AIM, NBO, geometry-based), and details about the performances of the single variable and multivariable linear regression-based models (PDF)
Cartesian coordinates of the optimized geometries of the natural and modified base pairs and optimized geometries (ZIP)
Author Present Address
§ Solid State and Structural Chemistry Unit (SSCU), Indian Institute of Science (IISc), Bangalore 560012, India.
Author Present Address
∥ Department of Chemistry and Biochemistry, University of Lethbridge, 4401 University Drive West, Lethbridge, Alberta, Canada T1K 3M4.
The authors declare no competing financial interest.
Footnotes
ε = (λ1/λ2) – 1, where λ1, λ2, and λ3 are the eigenvectors of the Hessian matrix.
One can
estimate the change in energy
of the N–H/O–H bond because of H-bond formation by evaluating 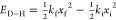 . Here, ki and xi represent the force constant and bond length
of the D–H bond of the isolated nucleobase, respectively. On
base pairing and consequent H-bond formation, the force constant and
bond length of the D–H bond change to kf and xf, respectively.
. Here, ki and xi represent the force constant and bond length
of the D–H bond of the isolated nucleobase, respectively. On
base pairing and consequent H-bond formation, the force constant and
bond length of the D–H bond change to kf and xf, respectively.
Supplementary Material
References
- Nelson D. L.; Lehninger A. L.; Cox M. M.. Lehninger principles of biochemistry, 5th ed.; W. H. Freeman: New York, 2008. [Google Scholar]
- Kruger K.; Grabowski P. J.; Zaug A. J.; Sands J.; Gottschling D. E.; Cech T. R. Self-splicing RNA: autoexcision and autocyclization of the ribosomal RNA intervening sequence of Tetrahymena. Cell 1982, 31, 147–157. 10.1016/0092-8674(82)90414-7. [DOI] [PubMed] [Google Scholar]
- RNA and the Regulation of gene expression: A hidden layer of complexity, 1st ed.; Morris K. V., Ed.; Caister Academic Press: Norfolk, U.K., 2008. [Google Scholar]
- Eddy S. R. Non-coding RNA genes and the modern RNA world. Nat. Rev. Genet. 2001, 2, 919–929. 10.1038/35103511. [DOI] [PubMed] [Google Scholar]
- Cech T. R.; Steitz J. A. The Noncoding RNA Revolution-Trashing Old Rules to Forge New Ones. Cell 2014, 157, 77–94. 10.1016/j.cell.2014.03.008. [DOI] [PubMed] [Google Scholar]
- Barrangou R.; Fremaux C.; Deveau H.; Richards M.; Boyaval P.; Moineau S.; Romero D. A.; Horvath P. CRISPR provides acquired resistance against viruses in prokaryotes. Science 2007, 315, 1709–1712. 10.1126/science.1138140. [DOI] [PubMed] [Google Scholar]
- Nowacki M.; Vijayan V.; Zhou Y.; Schotanus K.; Doak T. G.; Landweber L. F. RNA-mediated epigenetic programming of a genome-rearrangement pathway. Nature 2007, 451, 153–158. 10.1038/nature06452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leontis N. B.; Westhof E. Geometric nomenclature and classification of RNA base pairs. RNA 2001, 7, 499–512. 10.1017/s1355838201002515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhattacharya S.; Mittal S.; Panigrahi S.; Sharma P.; P P. S.; Paul R.; Halder S.; Halder A.; Bhattacharyya D.; Mitra A. RNABP COGEST: a resource for investigating functional RNAs. Database 2015, 2015, bav011. 10.1093/database/bav011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hendrix D. K.; Brenner S. E.; Holbrook S. R. RNA structural motifs: building blocks of a modular biomolecule. Q. Rev. Biophys. 2005, 38, 221–243. 10.1017/s0033583506004215. [DOI] [PubMed] [Google Scholar]
- Halder S.; Bhattacharyya D. RNA structure and dynamics: a base pairing perspective. Prog. Biophys. Mol. Biol. 2013, 113, 264–283. 10.1016/j.pbiomolbio.2013.07.003. [DOI] [PubMed] [Google Scholar]
- Zirbel C. L.; Šponer J. E.; Šponer J.; Stombaugh J.; Leontis N. B. Classification and energetics of the base-phosphate interactions in RNA. Nucleic Acids Res. 2009, 37, 4898–4918. 10.1093/nar/gkp468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yurenko Y. P.; Zhurakivsky R. O.; Samijlenko S. P.; Hovorun D. M. Intramolecular CH...O Hydrogen Bonds in the AI and BI DNA-like Conformers of Canonical Nucleosides and their Watson-Crick Pairs. Quantum Chemical and AIM Analysis. J. Biomol. Struct. Dyn. 2011, 29, 51–65. 10.1080/07391102.2011.10507374. [DOI] [PubMed] [Google Scholar]
- Jeffrey G. A.; Saenger W.. Hydrogen Bonding in Biological Structures, 1st ed.; Springer-Verlag: Berlin, Heidelberg, 1991. [Google Scholar]
- Müller-Dethlefs K.; Hobza P. Noncovalent interactions: a challenge for experiment and theory. Chem. Rev. 2000, 100, 143–168. 10.1021/cr9900331. [DOI] [PubMed] [Google Scholar]
- Buck U.; Huisken F. Infrared spectroscopy of size-selected water and methanol clusters. Chem. Rev. 2000, 100, 3863–3890. 10.1021/cr990054v. [DOI] [PubMed] [Google Scholar]
- Neusser H. J.; Siglow K. High-resolution ultraviolet spectroscopy of neutral and ionic clusters: hydrogen bonding and the external heavy atom effect. Chem. Rev. 2000, 100, 3921–3942. 10.1021/cr9900578. [DOI] [PubMed] [Google Scholar]
- Iogansen A. V. Direct proportionality of the hydrogen bonding energy and the intensification of the stretching ν(XH) vibration in infrared spectra. Spectrochim. Acta, Part A 1999, 55, 1585–1612. 10.1016/s1386-1425(98)00348-5. [DOI] [Google Scholar]
- Sukhodub L. F. Interactions and hydration of nucleic acid bases in a vacuum. Experimental study. Chem. Rev. 1987, 87, 589–606. 10.1021/cr00079a006. [DOI] [Google Scholar]
- Arnett E. M.; Joris L.; Mitchell E.; Murty T. S. S. R.; Gorrie T. M.; Schleyer P. v. R. Hydrogen-bonded complex formation. III. Thermodynamics of complexing by infrared spectroscopy and calorimetry. J. Am. Chem. Soc. 1970, 92, 2365–2377. 10.1021/ja00711a029. [DOI] [Google Scholar]
- Jelesarov I.; Bosshard H. R. Isothermal titration calorimetry and differential scanning calorimetry as complementary tools to investigate the energetics of biomolecular recognition. J. Mol. Recognit. 1999, 12, 3–18. . [DOI] [PubMed] [Google Scholar]
- Solomonov B. N.; Novikov V. B.; Varfolomeev M. A.; Klimovitskii A. E. Calorimetric determination of hydrogen-bonding enthalpy for neat aliphatic alcohols. J. Phys. Org. Chem. 2005, 18, 1132–1137. 10.1002/poc.977. [DOI] [Google Scholar]
- Rocher-Casterline B. E.; Ch’ng L. C.; Mollner A. K.; Reisler H. Communication: Determination of the bond dissociation energy (D0) of the water dimer, (H2O)2, by velocity map imaging. J. Chem. Phys. 2011, 134, 211101. 10.1063/1.3598339. [DOI] [PubMed] [Google Scholar]
- Fliegl H.; Lehtonen O.; Sundholm D.; Kaila V. R. I. Hydrogen-bond strengths by magnetically induced currents. Phys. Chem. Chem. Phys. 2011, 13, 434–437. 10.1039/c0cp00622j. [DOI] [PubMed] [Google Scholar]
- Parthasarathi R.; Subramanian V.. Hydrogen Bonding–New Insights, 1st ed.; Grabowski S. J., Ed.; Springer: Dordrecht, The Netherlands, 2006; Chapter 1, pp 1–50. [Google Scholar]
- Bader R. F. W.Atoms in Molecules: A Quantum Theory, 1st ed.; Oxford Science: Oxford, 1990. [Google Scholar]
- Bader R. F. W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. 10.1021/cr00005a013. [DOI] [Google Scholar]
- Grabowski S. J. A new measure of hydrogen bonding strength - ab initio and atoms in molecules studies. Chem. Phys. Lett. 2001, 338, 361–366. 10.1016/s0009-2614(01)00265-2. [DOI] [Google Scholar]
- Espinosa E.; Molins E.; Lecomte C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. 10.1016/s0009-2614(98)00036-0. [DOI] [Google Scholar]
- Parthasarathi R.; Subramanian V.; Sathyamurthy N. Electron Density Topography, NMR, and NBO Analysis of Water Clusters. Synth. React. Inorg., Met.-Org., Nano-Met. Chem. 2008, 38, 18–27. 10.1080/15533170701851250. [DOI] [Google Scholar]
- Parthasarathi R.; Subramanian V.; Sathyamurthy N. Hydrogen Bonding in Phenol, Water, and Phenol–Water Clusters. J. Phys. Chem. A 2005, 109, 843–850. 10.1021/jp046499r. [DOI] [PubMed] [Google Scholar]
- Parthasarathi R.; Subramanian V.; Sathyamurthy N. Hydrogen bonding in protonated water clusters: an atoms-in-molecules perspective. J. Phys. Chem. A 2007, 111, 13287–13290. 10.1021/jp0775909. [DOI] [PubMed] [Google Scholar]
- Parthasarathi R.; Subramanian V.; Sathyamurthy N. Hydrogen bonding without borders: an atoms-in-molecules perspective. J. Phys. Chem. A 2006, 110, 3349–3351. 10.1021/jp060571z. [DOI] [PubMed] [Google Scholar]
- Rai S.; Singh H. Electronic structure theory based study of proline interacting with gold nano clusters. J. Mol. Model. 2013, 19, 4099–4109. 10.1007/s00894-012-1711-x. [DOI] [PubMed] [Google Scholar]
- Parthasarathi R.; Amutha R.; Subramanian V.; Nair B. U.; Ramasami T. Bader’s and Reactivity Descriptors’ Analysis of DNA Base Pairs. J. Phys. Chem. A 2004, 108, 3817–3828. 10.1021/jp031285f. [DOI] [Google Scholar]
- Grabowski S. J. ?-Electron delocalisation for intramolecular resonance assisted hydrogen bonds. J. Phys. Org. Chem. 2003, 16, 797–802. 10.1002/poc.675. [DOI] [Google Scholar]
- Sharma P.; Mitra A.; Sharma S.; Singh H.; Bhattacharyya D. Quantum Chemical Studies of Structures and Binding in Noncanonical RNA Base pairs: The Trans Watson-Crick:Watson-Crick Family. J. Biomol. Struct. Dyn. 2008, 25, 709–732. 10.1080/07391102.2008.10507216. [DOI] [PubMed] [Google Scholar]
- Ebrahimi A.; Habibi Khorassani S. M.; Delarami H. Estimation of individual binding energies in some dimers involving multiple hydrogen bonds using topological properties of electron charge density. Chem. Phys. 2009, 365, 18–23. 10.1016/j.chemphys.2009.09.013. [DOI] [Google Scholar]
- Mata I.; Molins E.; Alkorta I.; Espinosa E. The Paradox of Hydrogen-Bonded Anion-Anion Aggregates in Oxoanions: A Fundamental Electrostatic Problem Explained in Terms of Electrophilic···Nucleophilic Interactions. J. Phys. Chem. A 2014, 119, 183–194. 10.1021/jp510198g. [DOI] [PubMed] [Google Scholar]
- Rai S.; Singh H.; Priyakumar U. D. Binding to gold nanoclusters alters the hydrogen bonding interactions and electronic properties of canonical and size-expanded DNA base pairs. RSC Adv. 2015, 5, 49408–49419. 10.1039/c5ra04668h. [DOI] [Google Scholar]
- Alkorta I.; Mata I.; Molins E.; Espinosa E. Charged versus Neutral Hydrogen-Bonded Complexes: Is There a Difference in the Nature of the Hydrogen Bonds?. Chem. - Eur. J. 2016, 22, 9226–9234. 10.1002/chem.201600788. [DOI] [PubMed] [Google Scholar]
- Balamurugan K.; Prakash M.; Subramanian V. Theoretical Insights into the Role of Water Molecules in the Guanidinium-Based Protein Denaturation Process in Specific to Aromatic Amino Acids. J. Phys. Chem. B 2019, 123, 2191–2202. 10.1021/acs.jpcb.8b08968. [DOI] [PubMed] [Google Scholar]
- Gould I. R.; Vincent M. A.; Hillier I. H. A theoretical study of the infrared spectrum of uracil. J. Chem. Soc., Perkin Trans. 2 1992, 69–71. 10.1039/p29920000069. [DOI] [Google Scholar]
- Kwiatkowski J. S.; Leszczyński J. Molecular structure and vibrational IR spectra of cytosine and its thio and seleno analogues by density functional theory and conventional ab initio calculations. J. Phys. Chem. 1996, 100, 941–953. 10.1021/jp9514640. [DOI] [Google Scholar]
- Nowak M. J.; Lapinski L.; Kwiatkowski J. S.; Leszczyński J. Molecular Structure and Infrared Spectra of Adenine. Experimental Matrix Isolation and Density Functional Theory Study of Adenine15N Isotopomers. J. Phys. Chem. 1996, 100, 3527–3534. 10.1021/jp9530008. [DOI] [Google Scholar]
- Lopes R. P.; Valero R.; Tomkinson J.; Marques M. P. M.; Batista de Carvalho L. A. E. Applying vibrational spectroscopy to the study of nucleobases - adenine as a case-study. New J. Chem. 2013, 37, 2691–2699. 10.1039/c3nj00445g. [DOI] [Google Scholar]
- Lopes R. P.; Marques M. P. M.; Valero R.; Tomkinson J.; de Carvalho L. A. E. B. Guanine: a combined study using vibrational spectroscopy and theoretical methods. Spectroscopy 2012, 27, 273–292. 10.1155/2012/168286. [DOI] [Google Scholar]
- Nikolaienko T. Y.; Bulavin L. A.; Hovorun D. M. Bridging QTAIM with vibrational spectroscopy: The energy of intramolecular hydrogen bonds in DNA-related biomolecules. Phys. Chem. Chem. Phys. 2012, 14, 7441–7447. 10.1039/c2cp40176b. [DOI] [PubMed] [Google Scholar]
- Brovarets’ O. O.; Hovorun D. M. Does the G G*syn DNA mismatch containing canonical and rare tautomers of the guanine tautomerise through the DPT? A QM/QTAIM microstructural study. Mol. Phys. 2014, 112, 3033–3046. 10.1080/00268976.2014.927079. [DOI] [Google Scholar]
- Brovarets’ O. O.; Tsiupa K. S.; Hovorun D. M. Unexpected A·T(WC)↔A·T(rWC)/A·T(rH) and A·T(H)↔A·T(rH)/A·T(rWC) conformational transitions between the classical A·T DNA base pairs: A QM/QTAIM comprehensive study. Int. J. Quantum Chem. 2018, 118, e25674 10.1002/qua.25692. [DOI] [Google Scholar]
- Brovarets’ O. O.; Tsiupa K. S.; Hovorun D. M. Non-dissociative structural transitions of the Watson-Crick and reverse Watson-Crick A·T DNA base pairs into the Hoogsteen and reverse Hoogsteen forms. Sci. Rep. 2018, 8, 10371. 10.1038/s41598-018-28636-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brovarets’ O. O.; Tsiupa K. S.; Hovorun D. M. Novel pathway for mutagenic tautomerization of classical A·T DNA base pairs via sequential proton transfer through quasi-orthogonal transition states: A QM/QTAIM investigation. PLoS One 2018, 13, e0199044 10.1371/journal.pone.0199044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinhold F. Nature of H-bonding in clusters, liquids, and enzymes: an ab initio, natural bond orbital perspective. J. Mol. Struct. 1997, 398–399, 181–197. 10.1016/s0166-1280(96)04936-6. [DOI] [Google Scholar]
- Szatyłowicz H.; Sadlej-Sosnowska N. Characterizing the Strength of Individual Hydrogen Bonds in DNA Base Pairs. J. Chem. Inf. Model. 2010, 50, 2151–2161. 10.1021/ci100288h. [DOI] [PubMed] [Google Scholar]
- Halder A.; Datta A.; Bhattacharyya D.; Mitra A. Why Does Substitution of Thymine by 6-Ethynylpyridone Increase the Thermostability of DNA Double Helices?. J. Phys. Chem. B 2014, 118, 6586–6596. 10.1021/jp412416p. [DOI] [PubMed] [Google Scholar]
- Li L.; Wu C.; Wang Z.; Zhao L.; Li Z.; Sun C.; Sun T. Density functional theory (DFT) and natural bond orbital (NBO) study of vibrational spectra and intramolecular hydrogen bond interaction of l-ornithine-l-aspartate. Spectrochim. Acta, Part A 2015, 136, 338–346. 10.1016/j.saa.2014.08.153. [DOI] [PubMed] [Google Scholar]
- Khatuntseva E. A.; Krest’yaninov M. A.; Fedorova I. V.; Kiselev M. G.; Safonova L. P. Hydrogen bonds in complexes of phosphonic and metylphosphonic acids with dimethylformamide. Russ. J. Phys. Chem. A 2015, 89, 2248–2253. 10.1134/s003602441512016x. [DOI] [Google Scholar]
- Szatylowicz H.; Jezierska A.; Sadlej-Sosnowska N. Correlations of NBO energies of individual hydrogen bonds in nucleic acid base pairs with some QTAIM parameters. Struct. Chem. 2016, 27, 367–376. 10.1007/s11224-015-0724-3. [DOI] [Google Scholar]
- Foster J. P.; Weinhold F. Natural hybrid orbitals. J. Am. Chem. Soc. 1980, 102, 7211–7218. 10.1021/ja00544a007. [DOI] [Google Scholar]
- Weinhold F.; Landis C. R. Natural Bond Orbitals and Extensions of Localized Bonding Concepts. Chem. Educ. Res. Pract. 2001, 2, 91–104. 10.1039/b1rp90011k. [DOI] [Google Scholar]
- Grunenberg J. Direct Assessment of Interresidue Forces in Watson–Crick Base Pairs Using Theoretical Compliance Constants. J. Am. Chem. Soc. 2004, 126, 16310–16311. 10.1021/ja046282a. [DOI] [PubMed] [Google Scholar]
- Pandey S. K.; Manogaran D.; Manogaran S.; Schaefer H. F. Quantification of Hydrogen Bond Strength Based on Interaction Coordinates: A New Approach. J. Phys. Chem. A 2017, 121, 6090–6103. 10.1021/acs.jpca.7b04752. [DOI] [PubMed] [Google Scholar]
- Gould I. R.; Kollman P. A. Theoretical investigation of the hydrogen bond strengths in guanine-cytosine and adenine-thymine base pairs. J. Am. Chem. Soc. 1994, 116, 2493–2499. 10.1021/ja00085a033. [DOI] [Google Scholar]
- Asensio A.; Kobko N.; Dannenberg J. J. Cooperative Hydrogen-Bonding in Adenine–Thymine and Guanine–Cytosine Base Pairs. Density Functional Theory and Møller–Plesset Molecular Orbital Study. J. Phys. Chem. A 2003, 107, 6441–6443. 10.1021/jp0344646. [DOI] [Google Scholar]
- Matta C. F.; Castillo N.; Boyd R. J. Extended Weak Bonding Interactions in DNA: π-Stacking (Base–Base), Base–Backbone, and Backbone–Backbone Interactions†. J. Phys. Chem. B 2006, 110, 563–578. 10.1021/jp054986g. [DOI] [PubMed] [Google Scholar]
- Brovarets’ O. O.; Hovorun D. M. New structural hypostases of the A·T and G·C Watson-Crick DNA base pairs caused by their mutagenic tautomerisation in a wobble manner: a QM/QTAIM prediction. RSC Adv. 2015, 5, 99594–99605. 10.1039/c5ra19971a. [DOI] [Google Scholar]
- Alkorta I.; Mata I.; Molins E.; Espinosa E. Energetic, Topological and Electric Field Analyses of Cation-Cation Nucleic Acid Interactions in Watson-Crick Disposition. ChemPhysChem 2019, 20, 148–158. 10.1002/cphc.201800878. [DOI] [PubMed] [Google Scholar]
- Ray S. S.; Halder S.; Kaypee S.; Bhattacharyya D. HD-RNAS: An automated hierarchical database of RNA structures. Front. Genet. 2012, 3, 59. 10.3389/fgene.2012.00059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becke A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- Miehlich B.; Savin A.; Stoll H.; Preuss H. Results obtained with the correlation energy density functionals of Becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989, 157, 200–206. 10.1016/0009-2614(89)87234-3. [DOI] [Google Scholar]
- Swart M.; Fonseca Guerra C.; Bickelhaupt F. M. Hydrogen bonds of RNA are stronger than those of DNA, but NMR monitors only presence of methyl substituent in uracil/thymine. J. Am. Chem. Soc. 2004, 126, 16718–16719. 10.1021/ja045276b. [DOI] [PubMed] [Google Scholar]
- Šponer J. E.; Leszczynski J.; Sychrovský V.; Šponer J. Sugar Edge/Sugar Edge Base Pairs in RNA: Stabilities and Structures from Quantum Chemical Calculations. J. Phys. Chem. B 2005, 109, 18680–18689. 10.1021/jp053379q. [DOI] [PubMed] [Google Scholar]
- Šponer J. E.; Špačková N.; Kulhánek P.; Leszczynski J.; Šponer J. Non-Watson-Crick base pairing in RNA. quantum chemical analysis of the cis Watson-Crick/sugar edge base pair family. J. Phys. Chem. A 2005, 109, 2292–2301. 10.1021/jp050132k. [DOI] [PubMed] [Google Scholar]
- Šponer J. E.; Špačková N.; Leszczynski J.; Šponer J. Principles of RNA base pairing: structures and energies of the trans Watson-Crick/sugar edge base pairs. J. Phys. Chem. B 2005, 109, 11399–11410. 10.1021/jp051126r. [DOI] [PubMed] [Google Scholar]
- Bhattacharyya D.; Koripella S. C.; Mitra A.; Rajendran V. B.; Sinha B. Theoretical analysis of noncanonical base pairing interactions in RNA molecules. J. Biosci. 2007, 32, 809–825. 10.1007/s12038-007-0082-4. [DOI] [PubMed] [Google Scholar]
- Mládek A.; Sharma P.; Mitra A.; Bhattacharyya D.; Šponer J.; Šponer J. E. Trans Hoogsteen/Sugar Edge Base Pairing in RNA. Structures, Energies, and Stabilities from Quantum Chemical Calculations. J. Phys. Chem. B 2009, 113, 1743–1755. 10.1021/jp808357m. [DOI] [PubMed] [Google Scholar]
- Sharma P.; Chawla M.; Sharma S.; Mitra A. On the role of Hoogsteen:Hoogsteen interactions in RNA: Ab initio investigations of structures and energies. RNA 2010, 16, 942–957. 10.1261/rna.1919010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma P.; Šponer J. E.; Šponer J.; Sharma S.; Bhattacharyya D.; Mitra A. On the Role of the cis Hoogsteen:Sugar-Edge Family of Base Pairs in Platforms and Triplets-Quantum Chemical Insights into RNA Structural Biology. J. Phys. Chem. B 2010, 114, 3307–3320. 10.1021/jp910226e. [DOI] [PubMed] [Google Scholar]
- Mládek A.; Šponer J. E.; Kulhánek P.; Lu X.-J.; Olson W. K.; Šponer J. Understanding the sequence preference of recurrent RNA building blocks using quantum chemistry: the intrastrand RNA dinucleotide platform. J. Chem. Theory Comput. 2011, 8, 335–347. 10.1021/ct200712b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma P.; Lait L. A.; Wetmore S. D. Exploring the limits of nucleobase expansion: computational design of naphthohomologated (xx-) purines and comparison to the natural and xDNA purines. Phys. Chem. Chem. Phys. 2013, 15, 15538–15549. 10.1039/c3cp52656a. [DOI] [PubMed] [Google Scholar]
- Sharma P.; Lait L. A.; Wetmore S. D. yDNA versus yyDNA pyrimidines: computational analysis of the effects of unidirectional ring expansion on the preferred sugar-base orientation, hydrogen-bonding interactions and stacking abilities. Phys. Chem. Chem. Phys. 2013, 15, 2435–2448. 10.1039/c2cp43910g. [DOI] [PubMed] [Google Scholar]
- Seelam P. P.; Sharma P.; Mitra A. Structural landscape of base pairs containing post-transcriptional modifications in RNA. RNA 2017, 23, 847–859. 10.1261/rna.060749.117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Azarhazin E.; Izadyar M.; Housaindokht M. R. Molecular dynamic simulation and DFT study on the Drug-DNA interaction; Crocetin as an anti-cancer and DNA nanostructure model. J. Biomol. Struct. Dyn. 2018, 36, 1063–1074. 10.1080/07391102.2017.1310060. [DOI] [PubMed] [Google Scholar]
- Kaur S.; Sharma P. Cyanoacetaldehyde as a building block for prebiotic formation of pyrimidines. Int. J. Quantum Chem. 2019, e25886 10.1002/qua.25886. [DOI] [Google Scholar]
- Frisch M. J.; et al. Gaussian 03, Revision E.01; Gaussian, Inc.: Wallingford, CT, 2004.
- Keith T.AIMAll, Version 11.12.19, 2011.
- Reed A. E.; Carpenter J. E.; Glendening E. D.; Weinhold F.. NBO, Version 3.1; Gaussian, Inc.: Wallingford, CT, 2004.
- Brovarets’ O. O.; Yurenko Y. P.; Hovorun D. M. The significant role of the intermolecular CH···O/N hydrogen bonds in governing the biologically important pairs of the DNA and RNA modified bases: a comprehensive theoretical investigation. J. Biomol. Struct. Dyn. 2015, 33, 1624–1652. 10.1080/07391102.2014.968623. [DOI] [PubMed] [Google Scholar]
- Brovarets’ O. O.; Yurenko Y. P.; Hovorun D. M. Intermolecular CH···O/N H-bonds in the biologically important pairs of natural nucleobases: a thorough quantum-chemical study. J. Biomol. Struct. Dyn. 2014, 32, 993–1022. 10.1080/07391102.2013.799439. [DOI] [PubMed] [Google Scholar]
- Roy A.; Panigrahi S.; Bhattacharyya M.; Bhattacharyya D. Structure, stability, and dynamics of canonical and noncanonical base pairs: quantum chemical studies. J. Phys. Chem. B 2008, 112, 3786–3796. 10.1021/jp076921e. [DOI] [PubMed] [Google Scholar]
- Dong H.; Hua W.; Li S. Estimation on the Individual Hydrogen-Bond Strength in Molecules with Multiple Hydrogen Bonds. J. Phys. Chem. A 2007, 111, 2941–2945. 10.1021/jp0709860. [DOI] [PubMed] [Google Scholar]
- Anatole von Lilienfeld O.; Tkatchenko A. Two- and three-body interatomic dispersion energy contributions to binding in molecules and solids. J. Chem. Phys. 2010, 132, 234109. 10.1063/1.3432765. [DOI] [PubMed] [Google Scholar]
- Hobza P. Calculations on Noncovalent Interactions and Databases of Benchmark Interaction Energies. Acc. Chem. Res. 2012, 45, 663–672. 10.1021/ar200255p. [DOI] [PubMed] [Google Scholar]
- Halder A.; Halder S.; Bhattacharyya D.; Mitra A. Feasibility of occurrence of different types of protonated base pairs in RNA: a quantum chemical study. Phys. Chem. Chem. Phys. 2014, 16, 18383–18396. 10.1039/c4cp02541e. [DOI] [PubMed] [Google Scholar]
- Liu M.; Li T.; Amegayibor F. S.; Cardoso D. S.; Fu Y.; Lee J. K. Gas-phase thermochemical properties of pyrimidine nucleobases. J. Org. Chem. 2008, 73, 9283–9291. 10.1021/jo801822s. [DOI] [PubMed] [Google Scholar]
- Zhachkina A.; Liu M.; Sun X.; Amegayibor F. S.; Lee J. K. Gas-Phase Thermochemical Properties of the Damaged BaseO6-Methylguanine versus Adenine and Guanine. J. Org. Chem. 2009, 74, 7429–7440. 10.1021/jo901479m. [DOI] [PubMed] [Google Scholar]
- Joseph J.; Jemmis E. D. Red-, Blue-, or No-Shift in Hydrogen Bonds: A Unified Explanation. J. Am. Chem. Soc. 2007, 129, 4620–4632. 10.1021/ja067545z. [DOI] [PubMed] [Google Scholar]
- Panigrahi S.; Pal R.; Bhattacharyya D. Structure and Energy of Non-Canonical Basepairs: Comparison of Various Computational Chemistry Methods with Crystallographic Ensembles. J. Biomol. Struct. Dyn. 2011, 29, 541–556. 10.1080/07391102.2011.10507404. [DOI] [PubMed] [Google Scholar]
- Halder A.; Vemuri S.; Roy R.; Katuri J.; Bhattacharyya D.; Mitra A. Evidence for Hidden Involvement of N3-Protonated Guanine in RNA Structure and Function. ACS Omega 2019, 4, 699–709. 10.1021/acsomega.8b02908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chawla M.; Abdel-Azeim S.; Oliva R.; Cavallo L. Higher order structural effects stabilizing the reverse Watson–Crick Guanine-Cytosine base pair in functional RNAs. Nucleic Acids Res. 2014, 42, 714. 10.1093/nar/gkt800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oliva R.; Cavallo L. Frequency and Effect of the Binding of Mg2+, Mn2+, and Co2+Ions on the Guanine Base in Watson–Crick and Reverse Watson–Crick Base Pairs. J. Phys. Chem. B 2009, 113, 15670–15678. 10.1021/jp906847p. [DOI] [PubMed] [Google Scholar]
- Halder A.; Roy R.; Bhattacharyya D.; Mitra A. How Does Mg 2+ Modulate the RNA Folding Mechanism: A Case Study of the G:C W:W Trans Basepair. Biophys. J. 2017, 113, 277–289. 10.1016/j.bpj.2017.04.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halder A.; Roy R.; Bhattacharyya D.; Mitra A. Consequences of Mg2+ binding on the geometry and stability of RNA base pairs. Phys. Chem. Chem. Phys. 2018, 20, 21934–21948. 10.1039/c8cp03602k. [DOI] [PubMed] [Google Scholar]
- Oliva R.; Tramontano A.; Cavallo L. Mg2+ binding and archaeosine modification stabilize the G15 C48 Levitt base pair in tRNAs. RNA 2007, 13, 1427–1436. 10.1261/rna.574407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halder A.; Bhattacharya S.; Datta A.; Bhattacharyya D.; Mitra A. The role of N7 protonation of guanine in determining the structure, stability and function of RNA base pairs. Phys. Chem. Chem. Phys. 2015, 17, 26249–26263. 10.1039/c5cp04894j. [DOI] [PubMed] [Google Scholar]
- Alabugin I. V.; Manoharan M.; Peabody S.; Weinhold F. Electronic Basis of Improper Hydrogen Bonding: A Subtle Balance of Hyperconjugation and Rehybridization. J. Am. Chem. Soc. 2003, 125, 5973–5987. 10.1021/ja034656e. [DOI] [PubMed] [Google Scholar]
- Hansen P. E.; Spanget-Larsen J. NMR and IR investigations of strong intramolecular hydrogen bonds. Molecules 2017, 22, 552. 10.3390/molecules22040552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tonidandel S.; LeBreton J. M. Relative Importance Analysis: A Useful Supplement to Regression Analysis. J. Bus. Psychol. 2011, 26, 1–9. 10.1007/s10869-010-9204-3. [DOI] [Google Scholar]
- Bothra N.; Rai S.; Pati S. K. Tailoring Ca2Mn2O5 Based Perovskites for Improved Oxygen Evolution Reaction. ACS Appl. Energy Mater. 2018, 1, 6312–6319. 10.1021/acsaem.8b01301. [DOI] [Google Scholar]
- Sen S.; Patwari G. N. Electrostatics and Dispersion in X-H···Y (X = C, N, O; Y = N, O) Hydrogen Bonds and Their Role in X-H Vibrational Frequency Shifts. ACS Omega 2018, 3, 18518–18527. 10.1021/acsomega.8b01802. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.