Abstract
We report accurate optical measurements of tubulin polarizability in aqueous suspensions. We determined the dependence of polarizability on tubulin concentration and on the suspension’s pH, providing benchmark numbers for quantifying the optical response of this protein in various artificial and cellular environments. We compare our measurement data with a few estimates found in the previous literature and also with our simplified model estimations.
1. Introduction
The interactions between electromagnetic (EM) fields in the optical regime and biological structures are important because they can lead to a better understanding of both the optical properties of biological matter (passive sensing) as well as the mechanisms involved to actively influence biological processes using light. In order to quantitatively describe this interaction, the optical response of the biological structures involved must be known first. In this work, we aim at describing the optical response of individual proteins in aqueous environments; more specifically, we focus our attention on tubulin because of its biological importance.
Tubulin is a globular cellular protein that self-assembles from α–β heterodimers to form cylindrical polymers termed microtubules that are responsible for a variety of key roles in the cell, including maintenance of cell shape, force generation required to segregate chromosomes in cell division, and transport of macromolecular cargo.
Whereas the biochemical properties such as tubulin’s ligand binding sites, microtubule polymerization dynamics, and post-translational modifications are well researched, the optical properties of tubulin and microtubules have recently gained interest because of the reported large dipole moment ≈ 1740 D1 and net negative charge of 47e2 that this protein heterodimer possesses. Besides the relevant roles of tubulin in biological processes, these characteristics, which ultimately determine the outcome of its interactions with optical fields, make tubulin unusual among all proteins.
Microtubules and unpolymerized tubulin dimers have recently been computationally modeled to shed light on the mechanisms by which they play electrically relevant roles, such as acting as targets of tumor-treating electric fields,3 acting as cables for ionic transport across the cell,4 and morphologically responding to electrostatic changes in the cellular environment using negatively charged C-termini tails.5 Experimentally, microtubules have been shown to re-orient in the presence of externally applied ac electric fields6 and increase electrical conductance of the buffer solution containing them.7
2. Materials and Methods
The tubulin samples were prepared mainly by following the standard protocol from Cytoskeleton, Inc., similarly to previous reports.8 Briefly, the sample is prepared with tubulin powder (porcine brain, >99% pure, T240, Cytoskeleton, Inc.), 1 mM GTP, and prefiltered BRB80 buffer (pore size 0.22 μM), which contains 80 mM PIPES, 2 mM MgCl2, and 0.5 mM EGTA. Samples with different tubulin concentrations were prepared in the range from 2.5 to 5 mg/mL.
Even though these systems have concentrations below the critical level (5 mg/mL), spontaneous polymerization can still occur.9 Unlike other studies, we implemented preventive mechanisms in our preparation procedure to avoid protein aggregation. Briefly, the tubulin buffer suspension was reconstituted in ice by using a so-called cushion buffer solution containing glycerol and colchicine. These steps are critical for preventing aggregation and polymerization of tubulin dimers and creating cluster- and microtubule-free suspensions of tubulin dimers, which could affect the interpretation of the refractometric measurements. More details on the sample preparation procedure and the errors associated with this process can be found in Appendices A and B, respectively.
3. Tubulin Polarizability
The response of material systems, especially biological, to EM fields is quite complex. The specific manifestations of a material’s reaction to an EM field can be described by different parameters such as the refractive index (RI), permittivity, polarizability, or dipole moment, depending upon the scale of the light–matter interaction. For instance, the size of a tubulin dimer is about 2 orders of magnitude smaller (4 nm × 5 nm × 8 nm) than the optical wavelength; thus, it acts as a dipole when interacting with visible light. Microtubules, on the other hand, are multidimer polymers with a well-defined cylindrical geometry (with a 25 nm diameter) and can be significantly larger (up to 100’s of μm) than the optical wavelength along one dimension, namely, the MT axis. Thus, the EM response of the two systems (polymerized and unpolymerized tubulin ensemble) must be described differently.
Characterizing the polarizability of a single tubulin dimer is practically very difficult to achieve because it requires localizing and performing measurements on a single dipole. Designing procedures and noninvasive probes may be an extremely challenging task.10 Alternatively, one can examine a large collection of dimers suspended in a solvent that can act as an optically homogeneous medium. Tubulin’s optical properties are then inferred using appropriate effective media descriptions. Because the measurement constraints are significantly relaxed, this macroscopic approach is usually the preferred solution. It is also worth pointing out that this approach provides, in fact, only a measure of the average speed of light through the medium and cannot account for possible specific characteristics of the microscopic structures.
A variety of EM mixing theories (EMTs), including Maxwell Garnett,11 Lorentz–Lorenz,12 Wiener,13 and Arago-Biot,14 have been proposed and used in different situations. Some of them are based on more or less rigorous coupling of dipolar responses, whereas the others are empirical. Essentially, all these mixing rules are developed under the assumption of weak and local electric fields, which practically requires a small volume fraction of inclusions, low permittivity contrast between host and inclusions, as well as spatially uncorrelated dipoles. In the limit of high dilution and weak scattering, all EMTs predict essentially similar results. The discrepancies appear when the models’ premises start to be gradually infringed. In such situations, more sophisticated homogenization approaches are necessary to account, for instance, for anisotropic or structured inclusions, for spatially correlated arrangements of scattering centers, and so forth.11 Nevertheless, regardless of the model used for homogenization, the process of retrieving the electric permittivity εd of the dipolar inclusions requires knowing the effective permittivity εeff of the composite medium, that of the host material, εs, and also the volume fraction f of dipoles in the medium.
4. New Technique for Measuring RI: Optical Fiber-Based Reflectometry
Here, we report on using a spatio-temporal coherence-gated dynamic light scattering (DLS) technique15 to determine the effective polarizability of tubulin in suspension. The method, schematically depicted in Figure 1, permits performing simultaneously an optical fiber-based refractometric measurement and dynamic scattering examination of the medium under test. In general, when a composite medium such as a suspension of scattering centers is illuminated through a partially transmitting interface, part of the illuminating field, Er, is backscattered at the interface because of inherent Fresnel reflections. At the same time, a portion of the transmitted field, Es(t), that is usually time-dependent, is scattered back through the interface. Here, this scattering is weak, that is |Er|2 ≫ |Es|2, and the time averaged detected intensity is ⟨I(t)⟩ ≈ |Er|2. In these conditions, one can use differential measurements of reflectivity to estimate an effective RI of the tubulin suspension and then safely use the abovementioned EMTs to retrieve the polarizability of tubulin dimers.
Figure 1.
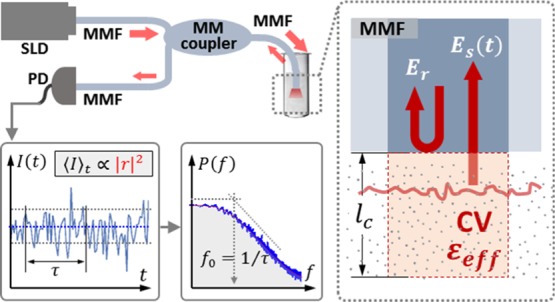
Schematic of the spatio-temporal coherence-gated DLS. A fiber-based common-path multimode interferometer allows performing simultaneously optical fiber-based refractometric measurements and sensing dynamic scattering. Light from a super-luminescent diode (SLD) is launched to and collected from the sample through multimode fibers (MMFs) and measured with a photodetector (PD). The bottom panels indicate the time-fluctuating signal measured at the detector, I(t), which results from the interference between Er and Es(t), both in the time- and frequency-domain, P(f). In weak scattering conditions, the picoliter-sized coherence volume (CV) at the distal end of the fiber probe, which is determined by the size of the core of the MMF and the coherence length (lc) of the broadband light source, can be interpreted as a medium with effective optical properties, εeff, as indicated in the inset. The time-averaged total intensity detected, ⟨I(t)⟩, can be used to retrieve information on the effective reflectivity of the fiber−medium interface, ⟨I(t)⟩ ∝ |r|2, and, therefore, on the effective polarizability of the suspended protein, α̅. The simultaneous measurement of dynamic scattering ensures that the information retrieval is properly framed within effective medium theories.
At the same time, the system records the interference between Er and Es(t) originating within a volume determined by the temporal coherence of the radiation used. Effectively, this interference originates in a picoliter-sized volume determined by the core size of the optical fiber and the spectral properties of the light source. The heterodyne amplification of Es(t), permits a direct and quantitative assessment of the scattering contributions and therefore provides means for validating and correcting the effective medium description usually invoked in these situations. In the presence of scattering, the effective medium depiction should comprise a complex RI.16
In our experiments, light from the low-coherence source, an SLD of 7 nm bandwidth centered at 670 nm (Superlum BLM-S-670-G-I-4; coherence length of about 30 μm in aqueous media) was launched in a multimode fiber (62.5 μm core) and then coupled to a 50/50 multimode coupler. It is important to note that the choice of wavelength is irrelevant for our methodology. Our choice of wavelength is simply to diminish as much as possible any thermal influences generated by absorption. In fact, our technique was specifically designed to operate in biologically relevant environments where one would prefer to operate far from vis/NIR absorption bands for water or UV for biological structures.
5. Tubulin Measurements
Panel (a) in Figure 2 shows the raw measurement
of reflectivity in the form of the time-averaged
voltage measured by the photo-receiver (New Focus 2001-FC) as a function
of tubulin concentration. Given the RI n1 of the optical fiber and that of the solvent alone, n2, one can calculate the Δn2 necessary to produce a change ΔR in
the measured reflectivity. The calculation uses the change in the
normal incidence Fresnel reflection coefficient 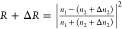 , where
, where 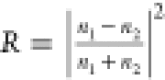 is the baseline reflectivity measured from
the solvent alone. Once Δn2 is found,
a first estimate for the value of the effective RI of the composite
can be evaluated simply as neff(0) = n2 + Δn2, as shown in panel
(c).
is the baseline reflectivity measured from
the solvent alone. Once Δn2 is found,
a first estimate for the value of the effective RI of the composite
can be evaluated simply as neff(0) = n2 + Δn2, as shown in panel
(c).
Figure 2.
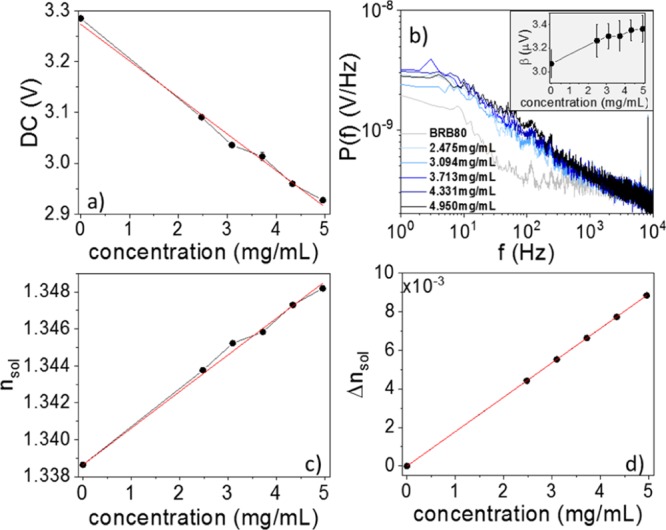
(a) Reflectivity measured as the time-averaged signal recorded by the PD. (b) Averaged power spectra of the light intensity fluctuations recorded for different tubulin concentrations, as indicated. The inset shows the total scattered power β. (c) Effective RI of the tubulin suspension inferred from measured reflectivity in (a). (d) Glycerol-correction to the RI of tubulin suspension in (c); this must be subtracted before using EMTs to retrieve the polarizability of individual tubulin dimers.
Estimating the tubulin polarizability from this effective RI must account for contributions from all the components: BRB80 + glycerol, tubulin, and colchicine. Because of the small amount used, the influence of colchicine is negligible. Figure 2d shows the actual contribution of glycerol to the change in RI measured for the tubulin suspensions.17 The effective RI of the BRB80–tubulin system can then be calculated as neff = neff(0) – Δngly. Because of the linearity of the effective RI in aqueous solutions of glycerol, a similar result can be obtained by using a multiphase mixture model (BRB80–glycerol–tubulin).11
Along with the average reflectivity, we also recorded the power spectra of the intensity fluctuations of the light scattered from the tubulin suspensions (Figure 2b). The power spectra P(f) were recorded in the frequency range from 1 Hz to 10 kHz with 1 Hz resolution and an integration time of 30 s over a total duration of 5 min (10 spectra per measurement). The total scattering power slightly increases with tubulin concentration but remains close to that of the buffer alone at all times (inset of Figure 2b).
The small differences can be due to residual aggregates, which were found to be negligible from independent DLS measurements performed with a commercial equipment (Malvern Zetasizer; see Appendix B). Overall, these measurements verify that our results can be framed within an effective medium interpretation.
The
variability in the measurements of reflected power is smaller
than 5 mV at all times. This corresponds to an instrumental precision
of about 5 × 10–4 for our RI measurement (see Appendix C for details). From this experiment,
the refractive index increment (slope of neff vs concentration) obtained is 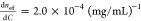 . The effective RI of tubulin suspensions
measured for different concentrations can now be used in an appropriate
EMT to retrieve the average polarizability of tubulin dimers. Here,
we used the Maxwell Garnett mixing model; more details on the applicability
of different mixing rules can be found in Appendix B. The effective permittivity of the suspensions was estimated
by assuming a baseline RI of the solvent of 1.3386, which is equal
to that of water at a temperature of 21 °C and for a wavelength
of 670 nm.18 This retrieves a permittivity
of the tubulin dimers of εtub = 3.5251 ± 0.861
(ntub = 1.8765 ± 0.227), where the
standard deviation was obtained from the raw values of εtub retrieved across the different suspensions. The relatively
large error is inherent to the EMTs in the dilute limit used here
(see Appendix B). This value of εtub as well as the slope in the concentration experiment
. The effective RI of tubulin suspensions
measured for different concentrations can now be used in an appropriate
EMT to retrieve the average polarizability of tubulin dimers. Here,
we used the Maxwell Garnett mixing model; more details on the applicability
of different mixing rules can be found in Appendix B. The effective permittivity of the suspensions was estimated
by assuming a baseline RI of the solvent of 1.3386, which is equal
to that of water at a temperature of 21 °C and for a wavelength
of 670 nm.18 This retrieves a permittivity
of the tubulin dimers of εtub = 3.5251 ± 0.861
(ntub = 1.8765 ± 0.227), where the
standard deviation was obtained from the raw values of εtub retrieved across the different suspensions. The relatively
large error is inherent to the EMTs in the dilute limit used here
(see Appendix B). This value of εtub as well as the slope in the concentration experiment 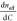 are comparable
to those obtained from experiments
performed with commercial refractometers not only on the same protein,8 but also on many other molecular species.19
are comparable
to those obtained from experiments
performed with commercial refractometers not only on the same protein,8 but also on many other molecular species.19
By using the standard Clausius–Mossotti
formulation,11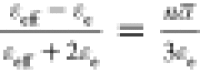 , the average polarizability of
the tubulin
dimers can be estimated by using the effective permittivity measured,
εeff, and the number density of dipoles, n = NAC, where NA is Avogadro’s number and C is the concentration in mol/m3. For the concentration
range explored here, and using the molecular weight of a tubulin dimer
(110 kDa), this results in an average permittivity α̅
in the range from 3.30 to 9.10 × 10–34 cm2 V–1, at a wavelength of 670 nm and in aqueous
media.
, the average polarizability of
the tubulin
dimers can be estimated by using the effective permittivity measured,
εeff, and the number density of dipoles, n = NAC, where NA is Avogadro’s number and C is the concentration in mol/m3. For the concentration
range explored here, and using the molecular weight of a tubulin dimer
(110 kDa), this results in an average permittivity α̅
in the range from 3.30 to 9.10 × 10–34 cm2 V–1, at a wavelength of 670 nm and in aqueous
media.
6. Effect of pH on Tubulin Polarizability
In a first stage of our experiments, the pH of the tubulin suspension was adjusted in the range from 7 to 7.5. The pH of a baseline sample (tubulin 33.75 μM, pH 7) was increased by progressively adding drops of an aqueous solution of KOH (1 μM; 5 μL/drop). Similarly, in a second stage, the pH was decreased to 6.5 starting from a similar baseline sample by progressively adding drops of an aqueous solution of HCl (1 μM; 5 μL/drop). For reference, the same procedures were applied to the buffer solutions (solutions of BRB80 alone); the pH was varied in the same range. In all cases, the initial sample volume was 250 μL. At the final condition of dilution, the concentration of tubulin is 18.0 μM. BRB80 remains a stable buffer within the range of our experiments.20 For the case of the buffers, we did not observe a significant change, or a monotonic trend, with increasing concentration of salt or acid; the reflectivity was practically constant in the range of pH explored (less than 0.1% variability for both salt and acid).
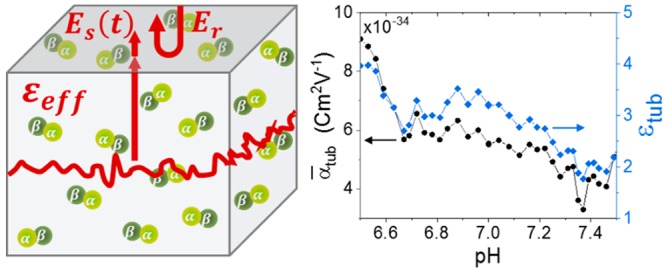
The fluctuation spectra were verified at all times during our experiments; no changes with the pH levels were detected. Similarly to the previous experiment, the effective RI of the suspension was first corrected for the amount of glycerol present at each point before using the EMTs. Figure 3 shows the RI of tubulin retrieved as a function of pH. The value reported by Krivosudský et al.,8 which was re-calculated here for an aqueous solvent, and using the same protein density and concentration as in our case, is plotted for reference.
Figure 3.
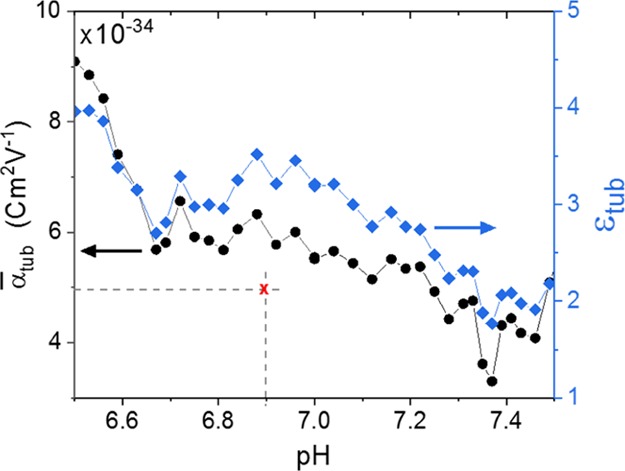
Effective permittivity, εtub (right axis), and average polarizability, α̅tub (left axis), of tubulin dimers in suspension as a function of the environmental pH. The red cross indicates the value reported in ref (8), after being re-calculated for an aqueous solvent, and using the same protein density and concentration as is our case.
The strong dependence of the response of tubulin to the environment is in accordance to that observed at lower frequencies.6a
7. Discussion
A quantitative estimation of the tubulin polarizability at optical wavelengths and the influence of its structural composition is a challenging task. Even modeling the effect of a static electric field must account for various contributions from the stretch of permanent dipole moments, displacements of mobile positive and negative charges, displacement of counter ions at C-terminals, and the organization of water molecules within the solvation shell. Nevertheless, we simulated the structure of tubulin21 at different pH levels and then computed the permanent dipole moment at protonation states across a pH range between 6.5 and 7.5. Details of the modeling procedure are included in Appendix D and the results are summarized in Figure 4.
Figure 4.
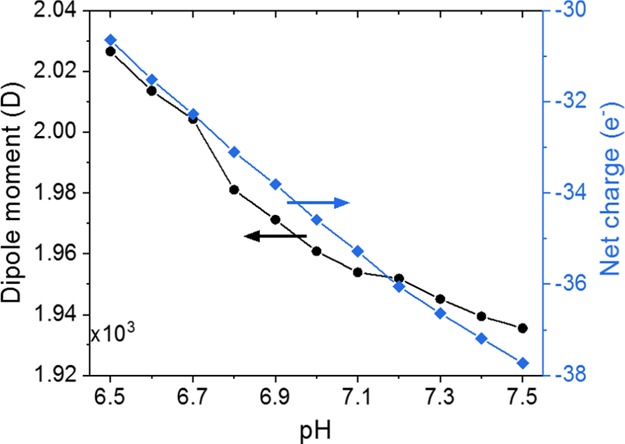
Computed magnitude of the molecular dipole moment (left axis) and the net charge (right axis) of the tubulin monomer as a function of the pH.
As can be seen, the evaluated variation of the dipole moment has a trend similar to the functional dependence seen experimentally. This indicates that there is a correlation between the effects of pH-dependent protonation that affects the net charge and dipole moments of tubulin on its dynamic response to the external EM fields, as can be expected.
Also shown in Figure 4 is the fact that the net charge increases significantly across the pH range examined. Note that, for tubulin, about 40% of this charge is associated with the C-termini.22 This observation together with the fact that a higher pH value leads to increase of the effective protein size could allow one to consider the tubulin monomer as a charged nanosized particle with a varying surface potential and placed in an oscillatory field.23 At a higher pH, the excess charge is practically distributed across an effectively larger area, leading to a decay of the dielectric function and the corresponding monomer polarizability. A quantitative assessment of the permittivity at the experimental frequency of 440 THz should involve a detailed description of the surface conductivity24 and will be the focus of a separate communication.
To put our present results in perspective, we should discuss them in the context of available literature reports, namely those from Mershin et al.1a,25 and Krivosudský et al.8 In Mershin,1a,25 the reported RI value for tubulin is ntub = 2.9, which is obtained in two independent measurements of refractometry and surface plasmon resonance. More recently, the refractometric measurements performed by Krivosudský8 indicate a value around ntub = 1.6, which is somewhat closer to the values retrieved in our experiments. The actual effects causing the retrieval of high values of the measured RI in earlier experimental works1a,25,26 are unclear. However, we found a number of reasons for the rather large discrepancies that range from sample preparation to data analysis and interpretation.
When operating around the critical concentration for protein polymerization (5 mg/mL in the case of tubulin), considerable care should be exerted for the sample preparation. In the experiments reported in refs (1a and 25), the concentration of tubulin goes as high as 8 mg/mL, whereas in ref (8) it is kept below the critical value at all times. However, neither of those works involved corrective measures to avoid the spontaneous polymerization of tubulin, which is prone to occur, even at room temperature.9 A related issue is the purity of the tubulin samples themselves, which may influence the presence of tubulin aggregates. A detailed description of our procedure and the systematic measures to prevent aggregation are included in Appendix A.
Regarding the data processing, we note that the correct formulation of the EMTs is in terms of volume fractions of the components. However, to avoid using the mass density of tubulin dimers, the previous works conducted their analysis in terms of mass fractions. An approximately density-matched condition is assumed based on the reported density of ρsol = 1.4 mg/mL for the solvent, which is rather high for an aqueous solution. In fact, we measured this density to be ρsol = 1.0085 mg/mL for similar solvents. Moreover, using the molecular weight and the approximate volume of a monomer, we estimated the mass density of tubulin to be ρtub = 2.08 g/mL, which is about twice larger than ρsol. Consequently, in this type of measurements the retrieval of tubulin polarizability must involve the rigorous formulation of the EMTs in terms of volume fractions. Further details can be found in Appendix B.
We also noticed that the RI
increment expected for a large number
of protein species is around 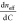 = 1.9 × 10−4 (mg/mL)−1.19 Although there are
reports on species with dn/dC larger
than that, the value of dn/dC remains
very far from the value used in refs (1a and 25), which
is one order of magnitude off.
= 1.9 × 10−4 (mg/mL)−1.19 Although there are
reports on species with dn/dC larger
than that, the value of dn/dC remains
very far from the value used in refs (1a and 25), which
is one order of magnitude off.
Lastly, we would like to stress that the dielectric properties of various components can be estimated using such mixing rules only if the suspension is optically homogeneous. Scattering of light outside the measurement volume represents a loss that is not accounted for in conventional EMTs. Nevertheless, this approach has been used indiscriminately in the previous literature reports to interpret measurements on suspensions of both tubulin and microtubules.1a,8 Surprisingly, the latter papers report similar RI values for both tubulin dimers and for much larger MT structures. In the current experiments, we ensured a minimal and constant level of scattering by continuously monitoring the strength of the dynamic scattering. The measurement of an effective polarizability of MT constructs will be the subject of a separate report.
8. Biological Relevance
Cancer cells have been shown to have higher intracellular pH and lower extracellular pH opposed to healthy cells.27 More specifically, despite the large diversity of diseases that cancer comprises, cancer cells share common features such as a typical “reversed” pH gradient with a constitutively increased intracellular pH that is higher than the extracellular pH, which makes them more acidic.28 The pH changes in cancer cells alter the metabolic rates and aid in cell proliferation, thus promoting cancer progression.27b,29 For microtubules specifically, an alkaline pH leads to disassembly and reduces the critical concentration required for nucleation.30 Additionally, microtubule interactions with taxol weaken in the presence of alkaline pH,31 and the net charge on the tubulin dimer increases.6a Computational models also show that as the pH increases, the C-termini tails extend outwards.5b,32 Here, we show that at higher pH, the RI of tubulin dimers decreases, which can provide a measure of the physical state of the tubulin dimer.
Whereas cell growth is well-known to be attenuated by the pH of the growth culture, the pH inside a cell itself has been hypothesized to act as a “clock for mitosis”,33 with the maximum pH being observed as mitosis initiates, and falling as it progresses. Our findings show that as mitosis progresses, the RI of tubulin increases. Therefore, measurements of subtle variations of tubulin’s RI can be used as a proxy for probing the dynamical state of the cell. With the methodology presented in this paper, new avenues can be opened for probing internal cell dynamics via optical properties of one of the most important and abundant proteins in eukaryotic cells, tubulin.
Acknowledgments
This research was partially supported by funding from DARPA and NSERC (Canada).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.9b00137.
Detailed sample preparation; errors, error propagation, and detailed discussion and contextualization of the results; procedural details for the refractometric measurements; and procedural details for the numerical computations (PDF)
Author Contributions
A.D. and J.A.T. conceived and designed the research. J.R.G.-S. and R.W. conducted the experiments, and performed the processing and analysis of the data. A.P.K. and M.A. performed the numerical calculations. The results were discussed by all authors. The paper was written and revised by all the authors.
The authors declare no competing financial interest.
Supplementary Material
References
- a Mershin A.; Kolomenski A. A.; Schuessler H. A.; Nanopoulos D. V. Tubulin dipole moment, dielectric constant and quantum behavior: computer simulations, experimental results and suggestions. BioSystems 2004, 77, 73–85. 10.1016/j.biosystems.2004.04.003. [DOI] [PubMed] [Google Scholar]; b Sanabria H.; Miller J. H. Jr.; Mershin A.; Luduena R. F.; Kolomenski A. A.; Schuessler H. A.; Nanopoulos D. V. Impedance spectroscopy of α-β tubulin heterodimer suspensions. Biophys. J. 2006, 90, 4644–4650. 10.1529/biophysj.106.069427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuszynski J. A.; Luchko T.; Carpenter E. J.; Crawford E. Results of molecular dynamics computations of the structural and electrostatic properties of tubulin and their consequences for microtubules. J. Comput. Theor. Nanosci. 2004, 1, 392–397. 10.1166/jctn.2004.042. [DOI] [Google Scholar]
- Tuszynski J.; Wenger C.; Friesen D.; Preto J. An overview of sub-cellular mechanisms involved in the action of TTFields. Int. J. Environ. Res. Public Health 2016, 13, 1128. 10.3390/ijerph13111128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sekulić D. L.; Satarić B. M.; Tuszynski J. A.; Satarić M. V. Nonlinear ionic pulses along microtubules. Eur. Phys. J. E: Soft Matter Biol. Phys. 2011, 34, 49. 10.1140/epje/i2011-11049-0. [DOI] [PubMed] [Google Scholar]
- a Priel A.; Tuszynski J. A.; Woolf N. J. Transitions in microtubule C-termini conformations as a possible dendritic signaling phenomenon. Eur. Biophys. J. 2005, 35, 40. 10.1007/s00249-005-0003-0. [DOI] [PubMed] [Google Scholar]; b Satarić M.; Ilić D.; Ralević N.; Tuszynski J. A. A nonlinear model of ionic wave propagation along microtubules. Eur. Biophys. J. 2009, 38, 637–647. 10.1007/s00249-009-0421-5. [DOI] [PubMed] [Google Scholar]
- a Minoura I.; Muto E. Dielectric measurement of individual microtubules using the electroorientation method. Biophys. J. 2006, 90, 3739–3748. 10.1529/biophysj.105.071324. [DOI] [PMC free article] [PubMed] [Google Scholar]; b Uppalapati M.; Huang Y.-M.; Jackson T. N.; Hancock W. O. Microtubule alignment and manipulation using AC electrokinetics. Small 2008, 4, 1371–1381. 10.1002/smll.200701088. [DOI] [PubMed] [Google Scholar]
- Santelices I. B.; Friesen D. E.; Bell C.; Hough C. M.; Xiao J.; Kalra A.; Kar P.; Freedman H.; Rezania V.; Lewis J. D. Response to Alternating Electric Fields of Tubulin Dimers and Microtubule Ensembles in Electrolytic Solutions. Sci. Rep. 2017, 7, 9594. 10.1038/s41598-017-09323-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krivosudský O.; Dráber P.; Cifra M. Resolving controversy of unusually high refractive index of a tubulin. Europhys. Lett. 2017, 117, 38003. 10.1209/0295-5075/117/38003. [DOI] [Google Scholar]
- Engelborghs Y.; Heremans K. A. H.; DE MAEYER L. C. M.; HOEBEKE J. Effect of temperature and pressure on polymerisation equilibrium of neuronal microtubules. Nature 1976, 259, 686. 10.1038/259686a0. [DOI] [PubMed] [Google Scholar]
- Cuervo A.; Dans P. D.; Carrascosa J. L.; Orozco M.; Gomila G.; Fumagalli L. Direct measurement of the dielectric polarization properties of DNA. Proc. Natl. Acad. Sci. U.S.A. 2014, 111, E3624–E3630. 10.1073/pnas.1405702111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sihvola A. Mixing rules with complex dielectric coefficients. Subsurf. Sens. Technol. Appl. 2000, 1, 393–415. 10.1023/a:1026511515005. [DOI] [Google Scholar]
- Lorentz H. A. Ueber die Anwendung des Satzes vom Virial in der kinetischen Theorie der Gase. Ann. Phys. 1881, 248, 127–136. 10.1002/andp.18812480110. [DOI] [Google Scholar]
- Wiener O. Mathematisch-Physikalische Klasse. Leipziger Berichte 1910, 62, 256. [Google Scholar]
- Heller W. Remarks on refractive index mixture rules. J. Phys. Chem. 1965, 69, 1123–1129. 10.1021/j100888a006. [DOI] [Google Scholar]
- a Popescu G.; Dogariu A. Dynamic light scattering in localized coherence volumes. Opt. Lett. 2001, 26, 551–553. 10.1364/ol.26.000551. [DOI] [PubMed] [Google Scholar]; b Popescu G.; Dogariu A.; Rajagopalan R. Spatially resolved microrheology using localized coherence volumes. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2002, 65, 041504. 10.1103/physreve.65.041504. [DOI] [PubMed] [Google Scholar]; c Popescu G.; Dogariu A. Scattering of low coherence radiation and applications. Eur. Phys. J. Appl. Phys. 2005, 32, 73–93. 10.1051/epjap:2005082. [DOI] [Google Scholar]; d Guzman-Sepulveda J. R.; Dogariu A. Probing complex dynamics with spatiotemporal coherence-gated DLS. Appl. Opt. 2019, 58, D76–D90. 10.1364/AO.58.000D76. [DOI] [PubMed] [Google Scholar]
- Hulst H. C.; van de Hulst H. C.. Light Scattering by Small Particles; Courier Corporation, 1981. [Google Scholar]
- a Haynes W. M.CRC Handbook of Chemistry and Physics; CRC press, 2014. [Google Scholar]; b Rheims J.; Köser J.; Wriedt T. Refractive-index measurements in the near-IR using an Abbe refractometer. Meas. Sci. Technol. 1997, 8, 601. 10.1088/0957-0233/8/6/003. [DOI] [Google Scholar]
- Daimon M.; Masumura A. Measurement of the refractive index of distilled water from the near-infrared region to the ultraviolet region. Appl. Opt. 2007, 46, 3811–3820. 10.1364/ao.46.003811. [DOI] [PubMed] [Google Scholar]
- a Harding S.Refractive Increment Data-Book for Polymer and Biomolecular Scientists; Nottingham University Press: Nottingham U.K., 2000. [Google Scholar]; b Zhao H.; Brown P. H.; Schuck P. On the distribution of protein refractive index increments. Biophys. J. 2011, 100, 2309–2317. 10.1016/j.bpj.2011.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferreira C. M. H.; Pinto I. S. S.; Soares E. V.; Soares H. M. V. M. (Un) suitability of the use of pH buffers in biological, biochemical and environmental studies and their interaction with metal ions–a review. RSC Adv. 2015, 5, 30989–31003. 10.1039/c4ra15453c. [DOI] [Google Scholar]
- Löwe J.; Li H.; Downing K. H.; Nogales E. Refined structure of αβ-tubulin at 3.5 Å resolution1. J. Mol. Biol. 2001, 313, 1045–1057. 10.1006/jmbi.2001.5077. [DOI] [PubMed] [Google Scholar]
- Tuszynski J. A.; Carpenter E. J.; Huzil J. T.; Malinski W.; Luchko T.; Luduena R. F. The evolution of the structure of tubulin and its potential consequences for the role and function of microtubules in cells and embryos. Int. J. Dev Biol 2006, 50, 341–358. 10.1387/ijdb.052063jt. [DOI] [PubMed] [Google Scholar]
- Bohren C. F.; Hunt A. J. Scattering of electromagnetic waves by a charged sphere. Can. J. Phys. 1977, 55, 1930–1935. 10.1139/p77-235. [DOI] [Google Scholar]
- a Heinisch R. L.; Bronold F. X.; Fehske H. Mie scattering by a charged dielectric particle. Phys. Rev. Lett. 2012, 109, 243903. 10.1103/physrevlett.109.243903. [DOI] [PubMed] [Google Scholar]; b Klačka J.; Kocifaj M.; Kundracik F.; Videen G.; Kohút I. Generalization of electromagnetic scattering by charged grains through incorporation of interband and intraband effects. Opt. Lett. 2015, 40, 5070–5073. 10.1364/ol.40.005070. [DOI] [PubMed] [Google Scholar]
- Schuessler H. A.; Mershin A.; Kolomenskii A. A.; Nanopoulos D. V. Surface plasmon resonance study of the actin-myosin sarcomeric complex and tubulin dimers. J. Mod. Opt. 2003, 50, 2381–2391. 10.1080/09500340308233570. [DOI] [Google Scholar]
- Bon P.; Lécart S.; Fort E.; Lévêque-Fort S. Fast label-free cytoskeletal network imaging in living mammalian cells. Biophys. J. 2014, 106, 1588–1595. 10.1016/j.bpj.2014.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- a Gallagher F. A.; Kettunen M. I.; Day S. E.; Hu D.-E.; Ardenkjær-Larsen J. H.; Zandt R. i. t.; Jensen P. R.; Karlsson M.; Golman K.; Lerche M. H.; Brindle K. M. Magnetic resonance imaging of pH in vivo using hyperpolarized 13 C-labelled bicarbonate. Nature 2008, 453, 940. 10.1038/nature07017. [DOI] [PubMed] [Google Scholar]; b Webb B. A.; Chimenti M.; Jacobson M. P.; Barber D. L. Dysregulated pH: a perfect storm for cancer progression. Nat. Rev. Cancer 2011, 11, 671. 10.1038/nrc3110. [DOI] [PubMed] [Google Scholar]
- Griffiths J. Are cancer cells acidic?. Br. J. Cancer 1991, 64, 425. 10.1038/bjc.1991.326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parks S. K.; Chiche J.; Pouysségur J. Disrupting proton dynamics and energy metabolism for cancer therapy. Nat. Rev. Cancer 2013, 13, 611. 10.1038/nrc3579. [DOI] [PubMed] [Google Scholar]
- a Regula C.; Berlin R. Microtubule assembly and disassembly at alkaline pH. J. Cell Biol. 1981, 89, 45–53. 10.1083/jcb.89.1.45. [DOI] [PMC free article] [PubMed] [Google Scholar]; b Schatten G.; Bestor T.; Balczon R.; Henson J.; Schatten H. Intracellular pH shift leads to microtubule assembly and microtubule-mediated motility during sea urchin fertilization: correlations between elevated intracellular pH and microtubule activity and depressed intracellular pH and microtubule disassembly. Eur. J. Cell Biol. 1985, 36, 116–127. [PubMed] [Google Scholar]
- Ringel I.; Horwitz S. B. Effect of alkaline pH on taxol-microtubule interactions. J. Pharmacol. Exp. Ther. 1991, 259, 855–860. [PubMed] [Google Scholar]
- Tuszyński J. A.; Brown J.; Crawford E.; Carpenter E.; Nip M.; Dixon J.; Satarić M. Molecular dynamics simulations of tubulin structure and calculations of electrostatic properties of microtubules. Math. Comput. Model. 2005, 41, 1055–1070. 10.1016/j.mcm.2005.05.002. [DOI] [Google Scholar]
- Gagliardi L. J.; Shain D. H. Is intracellular pH a clock for mitosis?. Theor. Biol. Med. Modell. 2013, 10, 8. 10.1186/1742-4682-10-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


