Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2019 Jan 14;4(1):1178–1184. doi: 10.1021/acsomega.8b02813

Roles of Closed- and Open-Loop Conformations in Large-Scale Structural Transitions of l-Lactate Dehydrogenase

Kimichi Suzuki †,‡,*, Satoshi Maeda †,§,∥,*, Keiji Morokuma ‡
PMCID: PMC6648161  PMID: 31459393

Abstract

graphic file with name ao-2018-02813w_0007.jpg

The mechanism of l-lactate generation from pyruvate by l-lactate dehydrogenase (LDH) from the rabbit muscle was studied theoretically by the multistructural microiteration (MSM) method combined with the quantum mechanics/molecular mechanics (QM/MM)–ONIOM method, where the MSM method describes the MM environment as a weighted average of multiple different structures that are fully relaxed during geometry optimization or a reaction path calculation for the QM part. The results showed that the substrate binding and product states were stabilized only in the open-loop conformation of LDH and the reaction occurred in the closed-loop conformation. In other words, before and after the chemical reaction, a large-scale structural transition from the open-loop conformation to the closed-loop conformation and vice versa occurred. The closed-loop conformation stabilized the transition state of the reaction. In contrast, the open-loop conformation stabilized the substrate binding and final states. In other words, the closed- to open-loop transition at the substrate binding state urges capture of the substrate molecule, the subsequent open- to closed-loop transition promotes the product generation, and the final closed- to open-loop transition at the final state prevents the reverse reaction going back to the substrate binding state. It is thus suggested that the exchange of stability between the closed- and open-loop conformations at different states promotes the catalytic cycle.

1. Introduction

Enzyme catalysis generally proceeds under moderate conditions and is fast and highly selective.1,2 Enzyme catalysis has therefore been applied to syntheses of various organic compounds.2−4 In general, the entire process of an enzyme-catalyzed reaction consists of three steps; that is, substrate binding, catalytic reaction in the active site, and product release.5 It has been shown experimentally that some catalytic reactions proceed with a large-scale structural transition in the surrounding protein.6−9 In such cases, one needs to take into account the large structural change in the surrounding protein before and after the chemical reaction that occurs at a local active site. However, revealing the roles of such a large structural change either experimentally or theoretically is challenging.2,4

l-Lactate dehydrogenase (LDH) exists in various organisms, and its catalytic mechanism has been the topic of many experimental and computational studies.10−23 LDH catalyzes a reversible transformation of pyruvate to l-lactate in the presence of NADH/NAD+ as a cofactor. Holbrook and co-workers proposed that the mechanism of this transformation consists of the five steps shown in Figure 1.7 In this mechanism, substrate binding occurs while LDH is in the open-loop conformation. Then, LDH changes its form to the closed-loop conformation. The transformation of pyruvate to l-lactate occurs while LDH is in the closed-loop conformation. The product is released with LDH in the open-loop conformation. This proposed mechanism involves large-scale structural transitions from the closed-loop conformation to the open-loop conformation and vice versa. The closure of the open loop over the active site after substrate binding is considered to be the rate-limiting step in the LDH catalytic process of wild-type Bacillus stearothermophilus.22

Figure 1.

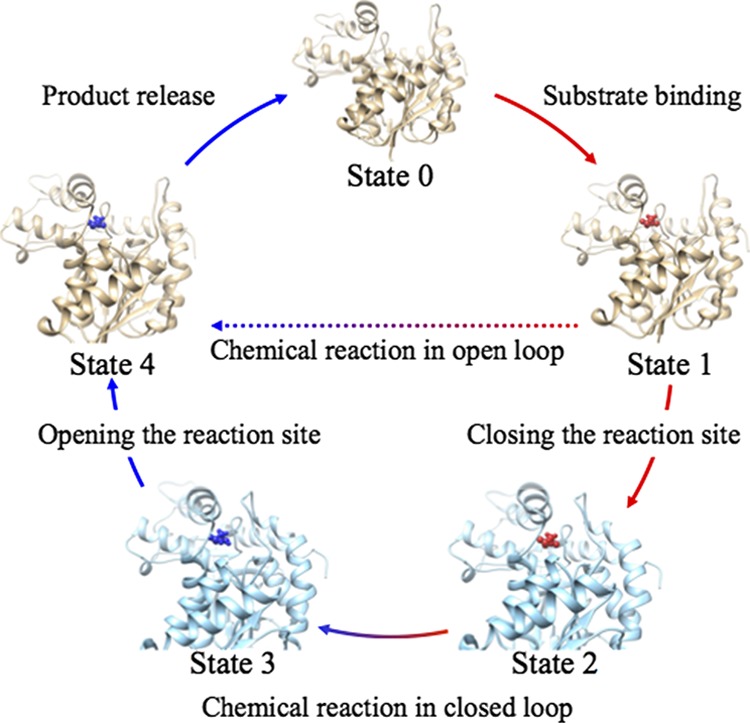
Figure 1

Open in a new tab

Schematic illustration of the full LDH catalytic process.7

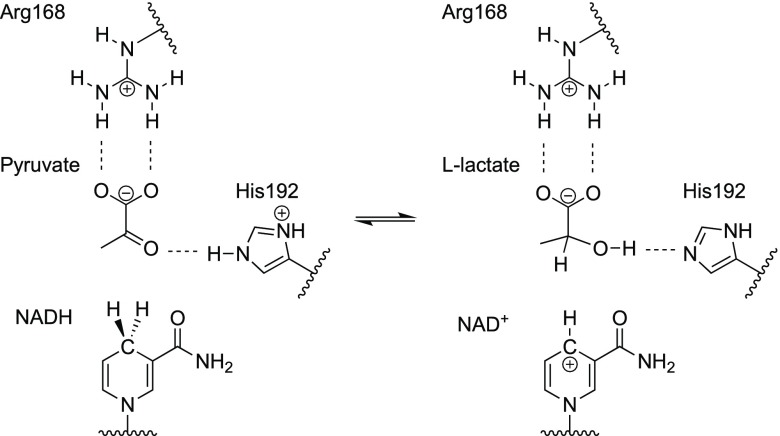
Figure 2 illustrates the transformation of pyruvate to l-lactate in the LDH active site. In early theoretical studies, quantum mechanics/molecular mechanics (QM/MM) molecular dynamics (MD) calculations were performed to examine whether these events occur in a concerted or stepwise manner.18−20 Recently, free energy surfaces were calculated for two collective variables through QM/MM MD simulations using the AM1 and RM1 methods for the QM part.21 After making a correction based on density functional theory calculations, these free energy surfaces showed that proton and hydride transfers were concerted in LDH from the rabbit muscle. This theoretical result is supported experimentally by a recent spectroscopic study.10

Figure 2.

Figure 2

Open in a new tab

Reversible reaction in the LDH active site.

The roles of closed- and open-loop conformations of LDH are not yet well understood theoretically. In principle, their behavior can be studied if MD trajectories over a long timescale can be computed at a QM or QM/MM level.24 The QM/MM free energy perturbation method coupled with geometry optimization calculations is another approach to study this topic.25−29 However, these calculations could be practically difficult because of the high computational cost to achieve converged statistical sampling describing the slow structural transition between open- and closed-loop conformations. We therefore use an alternative approach in which both open- and closed-loop conformations are prepared beforehand and then the entire structure is expressed as a weighted sum of these conformations. The weight changes depending on the stage of the reaction cycle and the transition between the two conformations are described as changes in weight. Such a calculation can be performed easily in the framework of our recently proposed multistructural microiteration (MSM) method.30

2. Theoretical Background

In this study, the structures of two conformations of LDH are prepared by replica-exchange MD simulations.31 Then, twelve initial structures are prepared. Among the twelve structures, six have an open-loop conformation and the other six have a closed-loop conformation. To distinguish between the two conformations, we introduced four distance parameters which are Cα-Glu103 and Cα-Tyr238, O3-pyruvate and CZ-Arg105, O1-pyruvate and CZ-Arg105, and CZ-Arg105 and CZ-Arg168 (see Figure S1). The structures with distances between Cα-Glu103 and Cα-Tyr238, O3-pyruvate and CZ-Arg105, O1-pyruvate and CZ-Arg105, and CZ-Arg105 and CZ-Arg168 of longer than 13, 8, 10, and 13 Å are regarded as open-loop conformation. Experimental values for these distances for open-loop conformations are 17.9, 12.0, 15.2, and 18.6 Å, while those for closed-loop ones are 8.0, 3.9, 4.5, and 7.2 Å.32 Details of the structural preparation are described in the Computational Details section. In the conventional QM/MM, our own N-layer integrated molecular orbital molecular mechanics (ONIOM) method,33,34 the total energy E is expressed as

2. 1

where Emodel-QM, Emodel-MM, and Ereal-MM correspond to the QM energy of the model system, MM energy of the model system, and MM energy of the real system, respectively. In contrast, in the QM/MM–ONIOM–MSM method, E is expressed as

2. 2

where N is the number of structures considered and Ereal-MM(i) corresponds to the energy of the ith structure. The weight ωi is given as

2. 3

where β = 1/kBTMSM, in which kB is the Boltzmann constant and TMSM is a model temperature parameter (see Computational Details section).30 During geometry optimization, all the N structures in the real system were optimized one-by-one with the atoms fixed in the model system (reaction-center region) before changing the positions of atoms in the model system. In other words, the optimization of the model system was performed in the geometrical subspace in which the gradient of the region not involved in the reaction (part of the real system excluding the model system) was zero.

The minimum energy path (MEP) for the abovementioned reaction process was computed. The MEP was obtained by optimizing an initial path using the locally updated plane (LUP) method.35 Initial paths were obtained as described below. During the path optimization, energy peaks (maxima) were directly optimized to transition states (TSs) using the quasi-Newton method. Three different calculations were performed: (i) a mixed calculation in which all twelve structures were used, (ii) an open-only calculation in which only the six structures with the open-loop conformation were used, and (iii) a closed-only calculation in which only the six structures with the closed-loop conformation were used. In calculations (ii) and (iii), the system adopts either an open- or closed-loop conformation throughout the calculation. The open- to closed-loop conformational transition or vice versa could only take place in calculation (i). The results of these three calculations are compared below. In calculation (i), the initial path was generated by the artificial force-induced reaction (AFIR) method.36 In contrast, in calculations (ii) and (iii), the MEP of the mixed calculation was used as the initial path, and then the six surrounding structures with the nontarget conformation were deleted before performing the LUP path optimization.

3. Results and Discussion

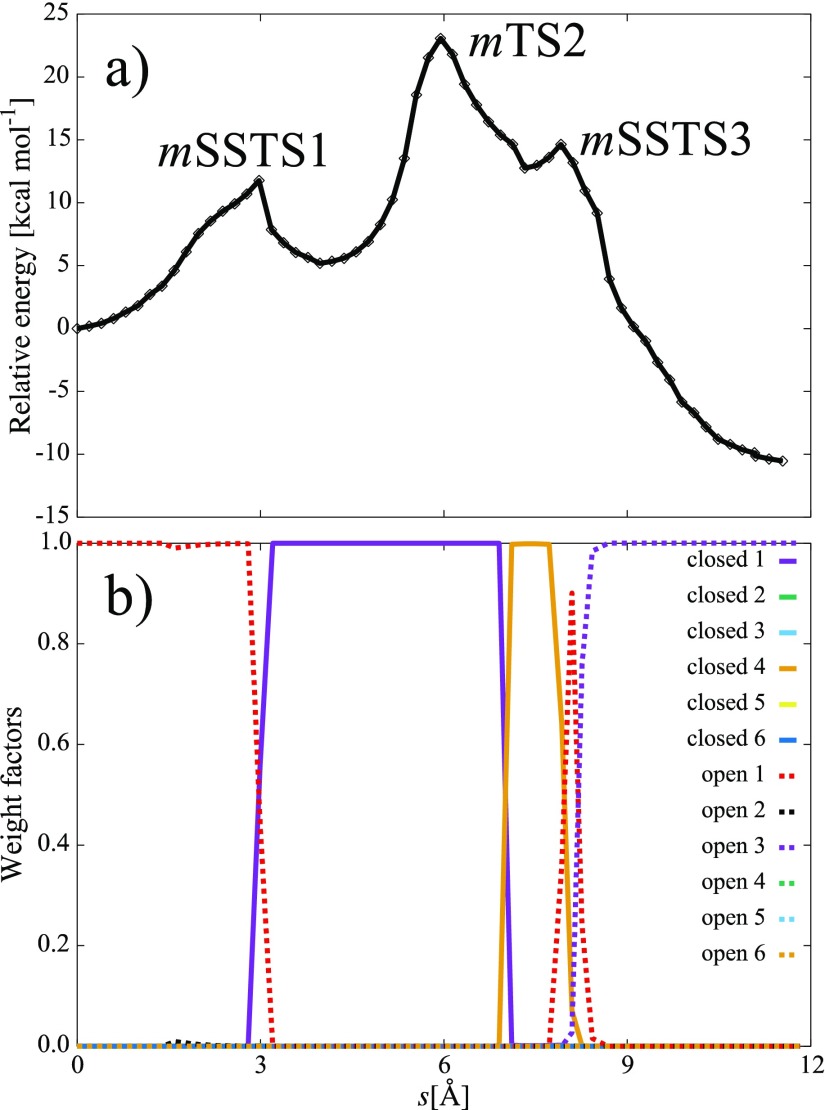
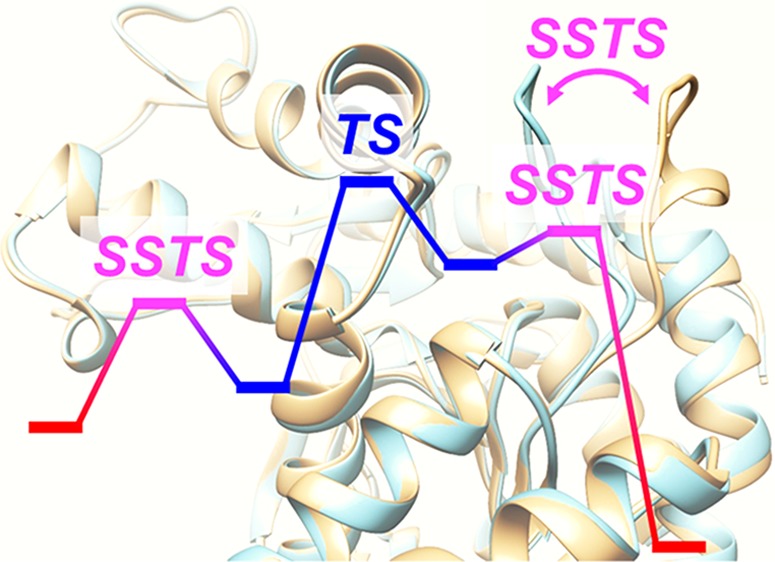
An energy profile and variations of ωi along the MEP obtained by the mixed calculation are shown in Figure 3a,b, respectively. Three energy peaks were observed in the MEP, where the highest peak corresponds to the TS of concerted proton and hydride transfers. In Figure 3b, ωi changed around the first and third peaks. The first and third peaks therefore describe the open- to closed-loop and closed- to open-loop structural transitions, respectively. Among the three peaks, the highest peak corresponds to the TS. The other two peaks were arisen through the dramatical change in ωi; we therefore call these energy maxima as surrounding structural TSs (SSTSs). For coordinates of the reaction-center atoms (atoms in the QM model system plus those bonded to the QM model system), each SSTS is a local maximum along the MEP of the potential energy surface calculated by the MSM method. We note that each SSTS also corresponds to a local minimum in the geometrical subspace in which the two main contributing surrounding structures have the same energy. Therefore, assuming immediate thermal equilibration for the surrounding structure, each SSTS corresponds to the energetically most preferred structure at which the population moves from one surrounding structure to the other. Figure 3b shows that the system adopts the open-loop conformation before SSTS1, the closed-loop conformation between SSTS1 and SSTS3, and the open-loop conformation again after SSTS3. This behavior is consistent with the mechanism in Figure 1 proposed from experimental results.

Figure 3.

Figure 3

Open in a new tab

(a) Energy profile and (b) variation of weight factors ωi along the MEP obtained by the mixed calculation. The s-coordinates are defined as a distance between discretized structures along the MEP.

Figure 4 compares energy profiles of the corresponding paths obtained from the open-only (denoted o) and closed-only (denoted c) calculations with the path of the mixed (denoted m) calculation. On the energy profile, surrounding structural features in open- or closed-loop conformations are clearly distinguishable (see Table S1). At the substrate binding equilibrium state EQ1, the open-loop conformation m(o)EQ1 is more stable than the closed-loop conformation cEQ1. Therefore, the substrate binding is likely to take place in the open-loop conformation. The mSSTS1, which describes the structural transition from the open-loop conformation to the closed-loop conformation, leads to intermediate state m(c)EQ2. Then, the concerted proton and hydride transfers occur from m(c)EQ2 through m(c)TS2. Meanwhile, oEQ1 is directly connected to oTS2. After passing oTS2, the system again directly reaches the most stable state m(o)EQ4. In contrast, the EQs in the closed-loop conformation, m(c)EQ3 and cEQ4, are both less stable than m(o)EQ4. From m(c)EQ3, the system can also reach m(o)EQ4 accompanying the surrounding structural transition through mSSTS3. Figure 4 clearly shows that the path obtained by the mixed calculation is the most energetically favorable path, and the surrounding structural transitions through mSSTS1 and mSSTS3 are necessary for the system to follow this path. In addition, the energy landscape was not largely affected (only ∼2.0 kcal mol–1) by the polarization effects taken by the electronic embedding scheme as shown in Figure 4. The calculated activation energy 22.3 kcal mol–1 is larger than an experimental value 14.0 kcal mol–1 obtained by taking a logarithm of observed kcat (= 245 s–1) at 295 K.37,38 Taking account of the free-energy correction at 295 K estimated based on the harmonic vibrational analysis, the activation energy for this step decreased from 22.3 to 19.4 kcal mol–1 showing a better agreement with the experimental value, although the value still is larger than the experimental one. One reason would be because initial surrounding structures were prepared at the reactant state. This treatment may significantly overestimate relative stability of the reactant state and consequently the barrier height. However, we believe that the relative stability between open- and closed-loop conformations at each state, which is the main focus of this study, can be discussed from the results in Figure 4. There are many other factors that may affect the computational barrier height such as QM computational level, size of the QM part, parameters of the MM force field, efficiency of quantum tunneling, and dynamical fluctuation in the surrounding part, although taking these into account is beyond the scope of this study.

Figure 4.

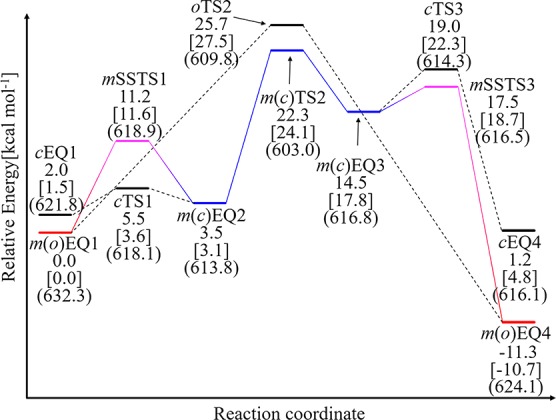
Figure 4

Open in a new tab

Energy diagram of the LDH catalytic process obtained from the mixed (m), open-only (o), and closed-only (c) calculations. EQ, TS, and SSTS are denoted as EQn, TSm, and SSTSl, respectively, where mEQ, mTS, and mSSTS are those obtained from the m calculation; oEQ and oTS are those obtained from the o calculation; and cEQ and cTS are those obtained from the c calculation. It should be noted that mEQ1, mEQ2, mEQ3, mEQ4, and mTS2 are identical to oEQ1, cEQ2, cEQ3, oEQ4, and cTS2, respectively. The volume, which is estimated with assuming that each atom is a sphere with 1.5 times of the corresponding van der Waals radius, and single point energies estimated by the electronic embedding scheme are shown in parentheses and square bracket, respectively.

Interestingly, the profile in Figure 4 reveals that the reaction does not only proceed in the closed-loop conformation. Without the surrounding structural transition to the open-loop conformation through mSSTS3, the reaction is reversible because the stability of cEQ4 is similar to that of cEQ1. The surrounding structural transition from the open-loop conformation to the closed-loop conformation through mSSTS1 shifts the reaction bottleneck from oTS2 to the lower energy m(c)TS2 and also promotes the reaction. We therefore conclude that the exchanges between the two conformations play roles in facilitating the reaction in the present system.

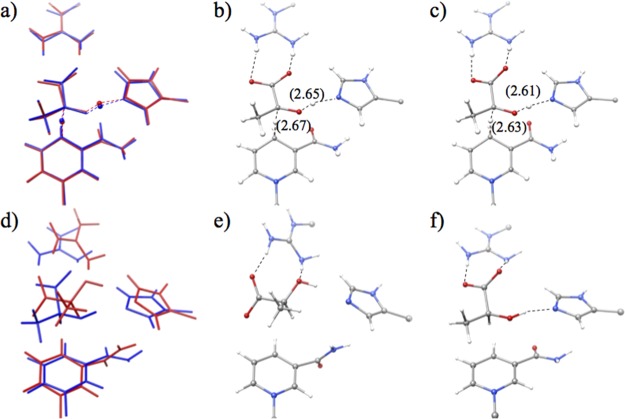
Next, we discuss reaction-center structures along the MEPs. At all the EQs and TSs in Figure 4, the volume which is estimated with assuming that each atom is a sphere with 1.5 times of the corresponding van der Waals radius is smaller in the closed-loop conformation than in the open-loop conformation throughout the process. This indicates that the open-loop conformation provides a larger reaction space than the closed-loop conformation. At TS2, the substrate must approach both His192 and NADH to transfer the proton and hydride. It is known in hydrogen-bonded cluster systems that a tight reaction space accelerates proton transfers.39,40 Consequently, the volume is the smallest at TS2 in the entire energy profile. Figure 5a–c compares structures of oTS2 and cTS2. The distances between the proton/hydride donor and acceptor are shorter in cTS2 than in oTS2 because of the tighter reaction space in the closed-loop conformation than in the open-loop conformation. In contrast, the greater space is available in the substrate binding state EQ1 and the final product state EQ4 than in TS2. In EQ4, the open-loop conformation allows the product to rotate in the reaction space and adopt a more stable configuration, as shown in Figure 5d–f. Because the substrate can move easily in the open-loop conformation, the system can reach the more stable configurations EQ1 and EQ4 directly without being captured at the tighter configurations EQ2 and EQ3. In short, the volume is small in the closed-loop conformation but is large in the open-loop conformation, while the volume is small at TS2 but is large at EQ1 and EQ4. In other words, the closed-loop conformation fits well to TS2, while the open-loop conformation fits well to EQ1 and EQ4. We thus propose that the volume matching is one factor controlling the variation of relative stability between the two conformations along the reaction path. The volume matching would strengthen some attractive interactions such as electrostatic interactions between the QM and MM parts and enhance stability of one of conformations at each state.

Figure 5.

Figure 5

Open in a new tab

Reaction-center structures: (a) superposition of oTS2 (red) and cTS2 (blue), (b) oTS2, (c) cTS2, (d) superposition of oEQ4 (red) and cEQ4 (blue), (e) oEQ4, and (f) cEQ4. Distances (in Å) between the proton/hydride donor and acceptor at TS2 are shown in parentheses.

Figure 6 shows structural differences between EQ1 and EQ2 and between EQ3 and EQ4. The difference between cEQ1 and m(o)EQ1 is in the interaction form between pyruvate and His192. The cEQ1 becomes m(c)EQ2 via cTS1 through the reorientation of His192 as highlighted in Figure 6a by an arrow. Although structures of m(c)EQ3 and cEQ4 resemble each other as shown in Figure 6b, changes occur in the surrounding structure through the movement of acetamide group in NAD via cTS3 as highlighted in Figure 6b by an arrow. The energy difference between m(c)EQ3 and cEQ4 is 13.4 kcal mol–1. The energy lowering of cEQ4 is due to the surrounding structural difference between m(c)EQ3 and cEQ4, where QM and MM components of the energy difference in m(c)EQ3 and cEQ4 (l-lactate) were 3.7 and −17.1 kcal mol–1, respectively.

Figure 6.

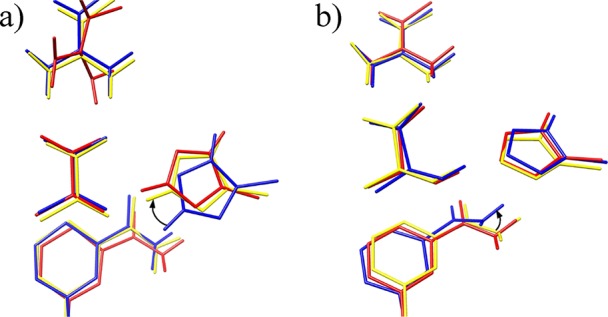
Figure 6

Open in a new tab

Reaction-center structures: (a) superposition of m(o)EQ1 (red), cEQ1 (blue), and cEQ2 (yellow), and (b) superposition of m(c)EQ3 (red), cTS3 (blue), and cEQ4 (yellow).

Finally, we discuss about four issues in the model adopted in this study. First, a previous study showed that formation of the tetramer structure of LDH affects the active site structure and the binding energy of the substrate.41 Because interactions between different chains were not considered in our model, it is expected that the energy profile in Figure 4 changes when the tetramer structure is used. Second, the dynamic fluctuation of the entire molecule that affects the entropic term of the free energy barrier is not taken into account by the MSM method. Third, it was shown that the transition between open- and closed-loop configurations was the slowest process among several reaction steps in the entire reaction.22 On the other hand, the MSM method describes the open to closed transition just as the weight change occurring along the reaction coordinate for the reaction-center part. In other words, actual atomic motions as well as the time required in the transition are not considered explicitly by the MSM method. Nevertheless, the MSM method is useful for predicting the sequence of stability changes in the surrounding structure part occurring along the reaction coordinate for the reaction-center part. Beyond this model, couplings between motions in the reaction-center part and the surrounding structure must be taken into account through QM/MM-MD simulations in the future. Fourth, we used twelve surrounding structures with six open- and six closed-loop conformations in this study. As shown in Figure 3b, the entire catalytic process was represented only with four surrounding structures, that is, “open 1”, “open 3”, “closed 1”, and “closed 4”. From this fact, we concluded that twelve were enough in this system. It should be noted that the number of structures required to describe an entire process would change depending on systems. It is thus recommended to prepare twice or more of structures than those required to describe the system.

4. Conclusions

We studied the roles of the open- and closed-loop conformations in the transformation reaction of pyruvate to l-lactate in LDH. The substrate binding state and final product binding state are more stable in the open-loop conformation than in the closed-loop conformation. In contrast, the TS for the concerted proton and hydride transfers is more stable in the closed-loop conformation. These stability differences at different states are found to correlate with the variation of the volume of the reaction center along the MEP, where the initial and final binding states are stabilized in the larger reaction space of the open-loop conformation and the TS is stabilized in the smaller reaction space of the closed-loop conformation. We suggest that the exchanges of the stability between the open- and closed-loop conformations at the different states play the central role in promoting the present reaction in one direction.

5. Computational Details

The initial structure was obtained from the protein data bank (PDB code: 3H3F).32 The structure of LDH from the rabbit muscle consists of two independent tetramers, each of which has four active sites; that is, two with the open-loop conformation and the other two with the closed-loop conformation. The model structure was built using chain C (closed loop) and D (open loop), where oxamate in the PDB structure was replaced by the reactant pyruvate. Hydrogen atoms were added assuming the normal protonation states at a pH of 7.0 using the PROPKA program,42,43 and His192 was manually protonated. The charged protein was neutralized with chlorine ions and fully solvated in the octahedron water box. To prepare the surrounding structures in the open- and closed-loop conformations, two replica exchange MD simulations with fixing of reaction-center atoms were performed: one for the open-loop conformation and the other for the closed-loop conformation. In each MD simulation, 20 replicas for the temperature range of 300 to 400 K were used and 5 000 000 steps were computed for each replica.31 Time step size and cutoff radius were set to 0.1 (fs) and 12.0 Å, respectively. Structures were printed every 10 000 MD steps, and among the 10 000 printed structures (500 for each replica), the six with the lowest energies were chosen as the initial surrounding structures of the open- and closed-loop conformations. Distance parameters defined at the theoretical back ground and distances between CZ-Arg168 and O1-pyruvate, and CZ-Arg168 and O3-pyruvate during MD simulations were shown in Figure S2. Afterward, aqueous environment molecules more than 50 Å away from the center of protein coordinates and counterions were removed for the reaction path calculations, where total charge of the protein was +2. From open- and closed-loop conformations, both six initial structures were merged for the mixed-loop calculations. Among the twelve structures, six have an open-loop conformation and the other six have a closed-loop conformation. It should be noted that our model structure constructs from a single reaction-center and twelve different surrounding structures.

The B3LYP/6-31+G(d,p) level of theory and general AMBER force field44 were used as the high-level QM and low-level MM methods, respectively. The mechanical embedding scheme33,34 was employed in all calculations, while the electronic embedding scheme45,46 was used for single-point calculations. AMBER force field parameters of NADH cofactor and pyruvate were obtained from generalized AMBER force field files (gaff.dat). The reaction center consisted of 46 atoms including the three link atoms placed at the QM/MM boundary indicated by wavy lines in Figure 2. All molecular structures were depicted by the UCSF Chimera package.47 The MEP calculations were performed by the MSM method using the GRRM program combined with the Gaussian 09 program.30,48,49 The initial path of the mixed calculation was obtained by the AFIR method with the model collision energy parameter of the AFIR method set to γ = 150 kJ/mol and the model temperature parameter of the MSM method set to TMSM = 50 000 K; these settings are discussed in our previous papers.30,36 The artificial force was applied to two atom pairs: between the shifting proton and acceptor oxygen and between the shifting hydride and acceptor carbon. The initial path was further optimized by the LUP path optimization method,35 where the model temperature parameter of the MSM method was set to TMSM = 300 K. Three different LUP calculations were performed (as discussed in the main text): (i) a mixed calculation, (ii) an open-only calculation, and (iii) a closed-only calculation. During the LUP calculations, all energy maxima were directly optimized to actual TSs using the quasi-Newton algorithm.

Acknowledgments

This work was supported by a grant from the Japan Science and Technology Agency with a Core Research for Evolutional Science and Technology (CREST) grant in the area of “Establishment of Molecular Technology towards the Creation of New Functions” at Hokkaido University (grant no. JPMJCR14L5). Calculations were performed at the Research Center Computational Science (RCCS), Okazaki, Japan. We thank Natasha Lundin, PhD, from Edanz Group (www.edanzediting.com/ac) for editing a draft of this manuscript.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b02813.

  • Illustration of distances between key residues defined in the section of the theoretical background, variations in MD simulations, and optimized structures, full reference of the Gaussian 09 program and Cartesian coordinates of the reaction center for all structures described in Figure 4 (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao8b02813_si_001.pdf (419.8KB, pdf)

References

  1. Wolfenden R.; Snider M. J. The Depth of Chemical Time and the Power of Enzymes as Catalysts. Acc. Chem. Res. 2001, 34, 938–945. 10.1021/ar000058i. [DOI] [PubMed] [Google Scholar]
  2. Nestl B. M.; Hammer S. C.; Nebel B. A.; Hauer B. New Generation of Biocatalysts for Organic Synthesis. Angew. Chem., Int. Ed. 2014, 53, 3070–3095. 10.1002/anie.201302195. [DOI] [PubMed] [Google Scholar]
  3. Rasor J. P.; Voss E. Enzyme-Catalyzed Processes in Pharmaceutical Industry. Appl. Catal., A 2001, 221, 145–158. 10.1016/s0926-860x(01)00804-3. [DOI] [Google Scholar]
  4. Laurent N.; Haddoub R.; Flitsch S. L. Enzyme Catalysis on Solid Surfaces. Trends Biotechnol. 2008, 26, 328–337. 10.1016/j.tibtech.2008.03.003. [DOI] [PubMed] [Google Scholar]
  5. Fersht A.Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding; W.H. Freeman: New York, 1999. [Google Scholar]
  6. Yasuda R.; Noji H.; Yoshida M.; Kinosita K.; Itoh H. Resolution of Distinct Rotational Substeps by Submillisecond Kinetic Analysis of F1-ATPase. Nature 2001, 410, 898–904. 10.1038/35073513. [DOI] [PubMed] [Google Scholar]
  7. Kȩdziernski P.; Moreton K.; Clarke A. R.; Holbrook J. J. The A245K Mutation Exposes Another Stage of the Bacterial L -Lactate Dehydrogenase Reaction Mechanism. Biochemistry 2001, 40, 7247–7252. 10.1021/bi0026775. [DOI] [PubMed] [Google Scholar]
  8. Boehr D. D.; McElheny D.; Dyson H. J.; Wright P. E. The Dynamic Energy Landscape of Dihydrofolate Reductase Catalysis. Science 2006, 313, 1638–1642. 10.1126/science.1130258. [DOI] [PubMed] [Google Scholar]
  9. Henzler-Wildman K. A.; Thai V.; Lei M.; Ott M.; Wolf-Watz M.; Fenn T.; Pozharski E.; Wilson M. A.; Petsko G. A.; Karplus M.; et al. Intrinsic Motions along an Enzymatic Reaction Trajectory. Nature 2007, 450, 838–844. 10.1038/nature06410. [DOI] [PubMed] [Google Scholar]
  10. Wang Z.; Chang E. P.; Schramm V. L. Triple Isotope Effects Support Concerted Hydride and Proton Transfer and Promoting Vibrations in Human Heart Lactate Dehydrogenase. J. Am. Chem. Soc. 2016, 138, 15004–15010. 10.1021/jacs.6b09049. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Basner J. E.; Schwartz S. D. How Enzyme Dynamics Helps Catalyze a Reaction in Atomic Detail: A Transition Path Sampling Study. J. Am. Chem. Soc. 2005, 127, 13822–13831. 10.1021/ja043320h. [DOI] [PubMed] [Google Scholar]
  12. Quaytman S. L.; Schwartz S. D. Reaction Coordinate of an Enzymatic Reaction Revealed by Transition Path Sampling. Proc. Natl. Acad. Sci. U.S.A. 2007, 104, 12253–12258. 10.1073/pnas.0704304104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Deng H.; Vu D. V.; Clinch K.; Desamero R.; Dyer R. B.; Callender R. Conformational Heterogeneity within the Michaelis Complex of Lactate Dehydrogenase. J. Phys. Chem. B 2011, 115, 7670–7678. 10.1021/jp2015929. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Quaytman S. L.; Schwartz S. D. Comparison Studies of the Human Heart andBacillus stearothermophilusLactate Dehydrogreanse by Transition Path Sampling†. J. Phys. Chem. A 2009, 113, 1892–1897. 10.1021/jp804874p. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Pineda J. R. E. T.; Antoniou D.; Schwartz S. D. Slow Conformational Motions That Favor Sub-Picosecond Motions Important for Catalysis. J. Phys. Chem. B 2010, 114, 15985–15990. 10.1021/jp1071296. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Pan X.; Schwartz S. D. Free Energy Surface of the Michaelis Complex of Lactate Dehydrogenase: A Network Analysis of Microsecond Simulations. J. Phys. Chem. B 2015, 119, 5430–5436. 10.1021/acs.jpcb.5b01840. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Pan X.; Schwartz S. D. Conformational Heterogeneity in the Michaelis Complex of Lactate Dehydrogenase: An Analysis of Vibrational Spectroscopy Using Markov and Hidden Markov Models. J. Phys. Chem. B 2016, 120, 6612–6620. 10.1021/acs.jpcb.6b05119. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Yadav A.; Jackson R. M.; Holbrook J. J.; Warshel A. Role of Solvent Reorganization Energies in the Catalytic Activity of Enzymes. J. Am. Chem. Soc. 1991, 113, 4800–4805. 10.1021/ja00013a013. [DOI] [Google Scholar]
  19. Ranganathan S.; Gready J. E. Hybrid Quantum and Molecular Mechanical (QM/MM) Studies on the Pyruvate tol-Lactate Interconversion inl-Lactate Dehydrogenase. J. Phys. Chem. B 1997, 101, 5614–5618. 10.1021/jp971051u. [DOI] [Google Scholar]
  20. Moliner V.; Williams I. H. Flexible QM/MM Modelling Embraces Alternative Mechanisms for Lactate Dehydrogenase. Chem. Commun. 2000, 19, 1843–1844. 10.1039/b005549m. [DOI] [Google Scholar]
  21. Świderek K.; Tuñón I.; Martí S.; Moliner V. Protein Conformational Landscapes and Catalysis. Influence of Active Site Conformations in the Reaction Catalyzed by L-Lactate Dehydrogenase. ACS Catal. 2015, 5, 1172–1185. 10.1021/cs501704f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Dunn C. R.; Wilks H. M.; Halsall D. J.; Atkinson T.; Clarke A. R.; Muirhead H.; Holbrook J. J. Design and synthesis of new enzymes based on the lactate dehydrogenase framework. Philos Trans R Soc Lond, B, Biol Sci 1991, 332, 177–84. 10.1098/rstb.1991.0047. [DOI] [PubMed] [Google Scholar]
  23. Ferrer S.; Tuñón I.; Martí S.; Moliner V.; Garcia-Viloca M.; González-Lafont À.; Lluch J. M. A Theoretical Analysis of Rate Constants and Kinetic Isotope Effects Corresponding to Different Reactant Valleys in Lactate Dehydrogenase. J. Am. Chem. Soc. 2006, 128, 16851–16863. 10.1021/ja0653977. [DOI] [PubMed] [Google Scholar]
  24. Nishihara Y.; Kato S.; Hayashi S. Protein Collective Motions Coupled to Ligand Migration in Myoglobin. Biophys. J. 2010, 98, 1649–1657. 10.1016/j.bpj.2009.12.4318. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Jorgensen W. L. Free Energy Calculations: A Breakthrough for Modeling Organic Chemistry in Solution. Acc. Chem. Res. 1989, 22, 184–189. 10.1021/ar00161a004. [DOI] [Google Scholar]
  26. Štrajbl M.; Hong G.; Warshel A. Ab Initio QM/MM Simulation with Proper Sampling: “First Principle” Calculations of the Free Energy of the Autodissociation of Water in Aqueous Solution. J. Phys. Chem. B 2002, 106, 13333–13343. 10.1021/jp021625h. [DOI] [Google Scholar]
  27. Rod T. H.; Ryde U. Accurate QM/MM Free Energy Calculations of Enzyme Reactions: Methylation by CatecholO-Methyltransferase. J. Chem. Theory Comput. 2005, 1, 1240–1251. 10.1021/ct0501102. [DOI] [PubMed] [Google Scholar]
  28. Hu H.; Yang W. Free Energies of Chemical Reactions in Solution and in Enzymes with Ab Initio Quantum Mechanics/Molecular Mechanics Methods. Annu. Rev. Phys. Chem. 2008, 59, 573–601. 10.1146/annurev.physchem.59.032607.093618. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Kosugi T.; Hayashi S. QM/MM Reweighting Free Energy SCF for Geometry Optimization on Extensive Free Energy Surface of Enzymatic Reaction. J. Chem. Theory Comput. 2011, 8, 322–334. 10.1021/ct2005837. [DOI] [PubMed] [Google Scholar]
  30. Suzuki K.; Morokuma K.; Maeda S. Multistructural Microiteration Technique for Geometry Optimization and Reaction Path Calculation in Large Systems. J. Comput. Chem. 2017, 38, 2213–2221. 10.1002/jcc.24857. [DOI] [PubMed] [Google Scholar]
  31. Case D. A.; Cheatham T. E.; Darden T.; Gohlke H.; Luo R.; Merz K. M. Jr.; Onufriev A.; Simmerling C.; Wang B.; Woods R. J. The Amber Biomolecular Simulation Programs. J. Comput. Chem. 2005, 26, 1668–1688. 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Šwiderek K.; Panczakiewicz A.; Bujacz A.; Bujacz G.; Paneth P. Modeling of Isotope Effects on Binding Oxamate to Lactic Dehydrogenase. J. Phys. Chem. B 2009, 113, 12782–12789. 10.1021/jp903579x. [DOI] [PubMed] [Google Scholar]
  33. Vreven T.; Morokuma K.; Farkas Ö.; Schlegel H. B.; Frisch M. J. Geometry optimization with QM/MM, ONIOM, and other combined methods. I. Microiterations and constraints. J. Comput. Chem. 2003, 24, 760–769. 10.1002/jcc.10156. [DOI] [PubMed] [Google Scholar]
  34. Chung L. W.; Sameera W. M. C.; Ramozzi R.; Page A. J.; Hatanaka M.; Petrova G. P.; Harris T. V.; Li X.; Ke Z.; Liu F.; et al. The ONIOM Method and Its Applications. Chem. Rev. 2015, 115, 5678–5796. 10.1021/cr5004419. [DOI] [PubMed] [Google Scholar]
  35. Choi C.; Elber R. Reaction Path Study of Helix Formation in Tetrapeptides: Effect of Side Chains. J. Chem. Phys. 1991, 94, 751–760. 10.1063/1.460343. [DOI] [Google Scholar]
  36. Maeda S.; Morokuma K. Communications: A systematic method for locating transition structures of A+B→X type reactions. J. Chem. Phys. 2010, 132, 241102. 10.1063/1.3457903. [DOI] [PubMed] [Google Scholar]
  37. Peng H.-L.; Deng H.; Dyer R. B.; Callender R. Energy Landscape of the Michaelis Complex of Lactate Dehydrogenase: Relationship to Catalytic Mechanism. Biochemistry 2014, 53, 1849–1857. 10.1021/bi500215a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Peng H.-L.; Egawa T.; Chang E.; Deng H.; Callender R. Mechanism of Thermal Adaptation in the Lactate Dehydrogenases. J. Phys. Chem. B 2015, 119, 15256–15262. 10.1021/acs.jpcb.5b09909. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Marx D. Proton Transfer 200 Years after Von Grotthuss: Insights from Ab Initio Simulations. ChemPhysChem 2006, 7, 1849–1870. 10.1002/cphc.200600128. [DOI] [PubMed] [Google Scholar]
  40. Suzuki K.; Shiga M.; Tachikawa M. Temperature and Isotope Effects on Water Cluster Ions with Path Integral Molecular Dynamics Based on the Fourth Order Trotter Expansion. J. Chem. Phys. 2008, 129, 144310. 10.1063/1.2987445. [DOI] [PubMed] [Google Scholar]
  41. Šwiderek K.; Paneth P. Importance of the Lactate Dehydrogenase Quaternary Structure in Theoretical Calculations. J. Phys. Chem. B 2010, 114, 3393–3397. 10.1021/jp100026z. [DOI] [PubMed] [Google Scholar]
  42. Li H.; Robertson A. D.; Jensen J. H. Very fast empirical prediction and rationalization of protein pKa values. Proteins: Struct., Funct., Genet. 2005, 61, 704–721. 10.1002/prot.20660. [DOI] [PubMed] [Google Scholar]
  43. Bas D. C.; Rogers D. M.; Jensen J. H. Very fast prediction and rationalization of pKa values for protein-ligand complexes. Proteins: Struct., Funct., Genet. 2008, 73, 765–783. 10.1002/prot.22102. [DOI] [PubMed] [Google Scholar]
  44. Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
  45. Bakowies D.; Thiel W. Hybrid Models for Combined Quantum Mechanical and Molecular Mechanical Approaches. J. Phys. Chem. 1996, 100, 10580–10594. 10.1021/jp9536514. [DOI] [Google Scholar]
  46. Vereven T.; Byun K. S.; Komáromi I.; Dapprich S.; Montgomery J. A. Jr.; Morokuma K.; Frisch M. J. Combining Quantum Mechanics Methods with Molecular Mechanics Methods in ONIOM. J. Chem. Theory Comput. 2006, 2, 815–826. 10.1021/ct050289g. [DOI] [PubMed] [Google Scholar]
  47. Pettersen E. F.; Goddard T. D.; Huang C. C.; Couch G. S.; Greenblatt D. M.; Meng E. C.; Ferrin T. E. UCSF Chimera?A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
  48. Maeda S.; Harabuchi Y.; Sumiya Y.; Takagi M.; Suzuki K.; Hatanaka M.; Osada Y.; Taketsugu T.; Morokuma K.; Ohno K.. GRRM, a developmental version, see http://iqce.jp/index_e.shtml (accessed date June 19, 2018).
  49. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; et al. Gaussian 09, Revision E01; Gaussian, Inc.: Wallingford, CT, 2016.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao8b02813_si_001.pdf (419.8KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES