Accurate prediction of boundaries of high resolution topologically associated domains (TADs) in fruit flies using deep learning

Abstract

Genomes are organized into self-interacting chromatin regions called topologically associated domains (TADs). A significant number of TAD boundaries are shared across multiple cell types and conserved across species. Disruption of TAD boundaries may affect the expression of nearby genes and could lead to several diseases. Even though detection of TAD boundaries is important and useful, there are experimental challenges in obtaining high resolution TAD locations. Here, we present computational prediction of TAD boundaries from high resolution Hi-C data in fruit flies. By extensive exploration and testing of several deep learning model architectures with hyperparameter optimization, we show that a unique deep learning model consisting of three convolution layers followed by a long short-term-memory layer achieves an accuracy of 96%. This outperforms feature-based models’ accuracy of 91% and an existing method's accuracy of 73–78% based on motif TRAP scores. Our method also detects previously reported motifs such as Beaf-32 that are enriched in TAD boundaries in fruit flies and also several unreported motifs.

INTRODUCTION

Genomes of different organisms are organized into domains called topologically associated domains (TADs), which consist of self-interacting chromatin regions. Recent studies have shown that boundaries of TADs are conserved across different cell types and related species (1). Disruption of TAD boundaries affects the expression of nearby genes and is associated with diseases including neuroblastoma (2,3), medulloblastoma (4) and leukemia (5,6). The boundaries show distinct deviation from regions within the TADs because they harbor binding sites for insulator proteins such as CTCF (7) in mammals and Beaf-32 in insects (8).

To study TADs and to understand how chromatin is organized in the nucleus, chromosome conformation capture experiments such as Hi-C are usually performed. However, these experiments are costly and time consuming. For larger genomes such as those found in mammals, achieving TAD boundaries with a resolution of a few hundred bases is still a challenge and most of the Hi-C experiments done on humans achieve 10–40 kb resolution (1). High sub-kb resolution TAD boundaries are much easier to achieve with smaller genomes such as insects (8). These experimental challenges appeal for computational approaches to predict the boundaries of TADs from DNA sequence information.

In predictive analytics of DNA sequences, there are primarily two approaches: feature-based models, which use k-mers as features, and deep learning models, which rely on convolutional neural networks (CNNs). Recently, CNNs have proven to perform better than the k-mer-based models in the context of classifying genomic sequences (9–11). There is also another kind of deep learning model known as a recurrent neural network (RNN) or long short-term memory network (LSTM), which has not been widely applied in classifying DNA sequences. CNN focuses on learning local sequence patterns, RNN or LSTM relies on long-range correlation across the entire sequence.

In this study, we focused on 500-bp resolution Hi-C data obtained from the fruit flies cell line kc167 (8). This data consist of ∼5400 TAD boundaries, each boundary of length 1000 bp. Equal number of intervals were randomly selected from within the TADs to be used as the background set. To perform prediction of the boundaries, genomic sequences were extracted for the boundaries and background set and were numerically represented with one-hot encoding. We explored 12 different deep learning model architectures which contained CNN, LSTM and dense layers in different permutations. Each of these 12 architectures also went through hyperparameter tuning to achieve the best set of hyperparameters. We found that a deep learning model with three CNN layers followed by a bidirectional LSTM layer performed the best by achieving an accuracy of 96%, outperforming a previous study with an accuracy of 73–78% (8). In comparison, feature-based models were able to achieve an accuracy of 91%. For unbiased metrics such as the Matthews correlation coefficient, the deep learning models performed at least 10% or better than feature-based models. Better performance of a model with both CNN and LSTM layers indicates that TAD boundaries are characterized by local sequence motifs with long-range dependencies. These sequences were ‘learned’ and embedded by the 64 kernels in the first CNN layer of the best deep learning model. Out of the 64 motifs, only 12 matched known annotated motifs of fruit flies. Interestingly, the Beaf-32 motif was detected as the second highest scoring motif by our model resonating with previous reports of strong enrichment of Beaf-32 motif in TAD boundaries of fruit flies. Previously reported insulator proteins associated with TAD boundaries in insects such as Trl and Z4 were also detected. Factors involved in the development and chromatin modeling such as Byn, Ovo and Pho were also detected but not previously reported in the context of TAD boundaries. This indicates that there are several other motifs, which may be binding sites of uncharacterized insulator factors important to the formation of TAD boundaries.

MATERIALS AND METHODS

First, we describe the different layers of the deep learning models for classifying DNA sequences: input layer, convolution layer, LSTM layer and output layer.

Input layer

The input layer to a deep learning model represents the input data and should be numerically encoded. Because the input sequences consist of a series of bases (A, T, G or C), each of the four letters was one-hot encoded by a binary vector of four entries with all 0s except for the matching letter entry being a 1. A, T, C and G were encoded as [1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0] and [0, 0, 0, 1], respectively. If the length of each sequence is L, each sequence was converted to a matrix of shape (L, 4). This encoded matrix was used as the input layer to the deep learning models.

Convolution and pooling layer

A DNA sequence of length L with the bases as one-hot encoded is a matrix X of shape (L, 4). This can be treated as a one-dimensional image with length = L, and four channels. Instead of applying a two-dimensional CNN layer, a 1D CNN layer can be applied to a DNA sequence. A one-dimensional CNN layer for the case of one-hot encoded DNA sequence consists of a collection (let's say N) of filters or kernels of shape (k, 4), where k is the length of the kernel. Each of the kernels, when convolved with the input DNA matrix X followed by an activation function, yields an activation map of size ((L + 2(p – d)(k – 1) – 1)/s, 4), where p is the padding length, d is the dilation, and s is the stride. In our case, we set p = 0, d = 1 and s = 1. Hence, for N kernels, it yields N activation maps, each activation map of size (L + (k – 1), 4). Each of these kernels represents a sequence pattern and is designed to locate a particular pattern or motif along the sequence. High values in the activation map indicate the existence of that sequence pattern represented by the kernel. In this study, the ReLU (rectified linear unit) activation function was used in each CNN layer.

Bidirectional LSTM

The LSTM layer consists of a sequence of LSTM ‘blocks,’ each ‘block’ containing the same number of hidden LSTM units. An LSTM unit is the basic building unit for the LSTM layer. Unlike a traditional RNN unit, an LSTM unit contains four gates: input gate, forget gate, output gate and input modulation gate. Using these gates, the LSTM unit captures both long- and short-range dependencies. LSTM units are widely used and well documented. We refer to these papers for further details (12,13). The length of the LSTM layer is equal to the number of ‘time’ steps (T) in the input data sequence. The input to an LSTM layer is a sequence of vectors h^t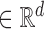, where t = 1, 2, …, T, and d is an integer > 0. We used a many-to-many architecture where the output at each time step is ‘remembered.’ We used a bidirectional version consisting of two LSTMs running in parallel: one on the input sequence and the other on the reverse of the input data sequence. The outputs of the two parallel LSTMs were concatenated to capture the forward and backward information in the DNA sequence. LSTM architecture has been used to solve the problem of exploding or vanishing gradients in traditional sequence models such as RNNs.

Deep learning model architectures

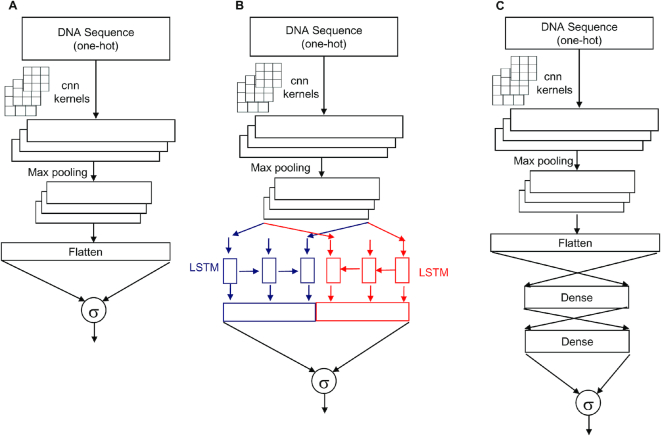
Table 1 summarizes the different deep learning model architectures explored in this study. We first explored models (1layerCNN, 2layerCNN, 3layerCNN, 4layerCNN and 8layerCNN) which consist primarily of 1D CNN layers only. The number of CNN layers in the model is indicated by the prefix before the word ‘CNN’ in the model name. For example, the 4layerCNN model had four CNN layers, where each CNN layer was followed by a max-pooling layer (Table 1). In the case of 8layerCNN, only the third, sixth and eighth CNN layers were followed by max-pooling layers of size = 5 and stride = 2. To prevent overfitting, the dropout technique of removing 30% of the nodes in a CNN layer during each training epoch was used. An illustration of a 1layerCNN is shown in Figure 1A.

Table 1.

Deep learning models. The table shows the deep learning model architectures explored in this study with model name and hidden layers shown in columns 1 and 2, respectively. A repeated layer is indicated as ‘N × {layer},' where N is the number of repetitions. For example, 4 × {CNN, Maxpooling} means a CNN – Maxpooling layer repeated four times. The respective hyperparameters that were tuned for each model are shown in column 3. For example, for the 1layerCNN model, the hyperparameter ‘Batch Size’ was tested for two permutations: 50 and 100

Model	Hidden layers	Parameters/hyper-parameters
1layerCNN	1 x {CNN, Maxpooling}	Number of kernels (16, 32, 64, 96)
2layerCNN	2 x {CNN, MaxPooling}	Length of kernel (9, 15)
3layerCNN	3 x {CNN, MaxPooling}	Learning Rate (0.001, 0.005, 0.01)
4layerCNN	4 x {CNN, MaxPooling}	Batch Size (50, 100)
8layerCNN	2xCNN, {CNN, pooling}, 2xCNN, {CNN,pooling}, CNN, {CNN,pooling}
1layerCNN_LSTM	1 x {CNN, Maxpooling}, 1 bidirectional LSTM layer	Number of kernels (16, 32, 64, 96)
2layerCNN_LSTM	2 x {CNN, Maxpooling}, 1 bidirectional LSTM layer	Length of kernel (9, 15)
3layerCNN_LSTM	3 x {CNN, Maxpooling}, 1 bidirectional LSTM layer	Learning Rate (0.001, 0.005, 0.01)
4layerCNN_LSTM	4 x {CNN, Maxpooling}, 1 bidirectional LSTM layer	Number of LSTM units (10, 20, 30, 40) ) Batch Size (50, 100)
1layerCNN_Dense	1 x {CNN, Maxpooling}, Dense layers	Number of kernels (16, 32, 64, 96)
2layerCNN_Dense	2 x {CNN, Maxpooling}, Dense layers	Length of kernel (9, 15)
3layerCNN_Dense	3 x {CNN, Maxpooling}, Dense layers	Learning Rate (0.001, 0.005, 0.01)
4layerCNN_Dense	4 x {CNN, Maxpooling}, Dense layers	Number of Dense Layers (1, 2, 3, 4) Batch Size (50, 100)

Figure 1.

Three representative deep learning models. Panel (A) shows the 1layerCNN model, which consists of an input layer, CNN layer, pooling layer, flatten layer and output layer. Panel (B) shows the 1layerCNN_LSTM model, which is comprised of an input layer, CNN layer, pooling layer, bidirectional LSTM layer, and output layer. Panel (C) shows the 1layerCNN_Dense consisting of an input layer, CNN layer, pooling layer, two dense layers and output layer. The output layer has one neuron with sigmoid activation function indicated by σ.

The second set of four models had a series of CNN-pooling layers and a bidirectional LSTM layer following the final max-pooling layer. 1layerCNN_LSTM, 2layerCNN_LSTM, 3layerCNN_LSTM, and 4layerCNN_LSTM had 1, 2, 3 and 4 CNN layers, respectively. Every CNN layer was immediately followed by a max-pooling layer with pool size = 5 and stride = 2. The final pooling layer was followed by a bidirectional LSTM layer. To prevent overfitting, the dropout technique of removing 30% of the nodes in the CNN layer was used. An illustration of a 1layerCNN_LSTM is shown in Figure 1B.

The third set of models (1layerCNN_Dense, 2layerCNN_Dense, 3layerCNN_Dense and 4layerCNN_Dense) had a series of CNN-pooling layers followed by a series of fully connected dense layers after the final max-pooling layer (Table 1). Each dense layer had 100 neurons with ReLU activation functions. To prevent overfitting, we added a dropout layer with 30% nodes removed during each epoch of training. An illustration of a 1layerCNN_Dense with two dense layers is shown in Figure 1C.

Output layer

For all the models, the output layer had only one node with sigmoid activation function. If the value of the activation function was >0.5, the input sequence was classified as a TAD boundary, otherwise not.

Training

The dataset was split into three nonoverlapping sets for training, validation and testing with a ratio of 0.80:0.10:0.10. The training set was used to train the weights of the model, the validation set was used to avoid overfitting, and the testing set was used to ‘validate’ the predicting ability of the trained model. The deep learning networks were implemented using Keras with TensorFlow as the backend. During the training process, we used the ‘Adam’ optimization algorithm to minimize the binary cross-entropy loss function. The training period was set for 150 epochs but an early stopping criterion was introduced in the optimization process when the loss function on the validation set failed to decrease for five consecutive epochs. This was done to prevent overfitting.

Within each model architecture, we also varied the values for a set of hyperparameters as shown in Table 1. This included number of kernels and kernel length in each hidden CNN layer, learning rate of the optimizer, batch size, number of hidden units in the LSTM layer, and number of dense layers (Table 1). Finally, the models were evaluated using six different metrics: area under the curve (AUC), accuracy, Matthews's correlation coefficient, precision, recall, and f1 score/measure. We used these different metrics to view the model performance from different perspectives. AUC measures the overall performance of the model across the entire prediction probability threshold.

Motif analysis

The N filters or kernels from the first CNN layer of the best deep learning model (3layersCNN_LSTM) are matrices of shape (9, 4). For each kernel (k), the subsequence in each positive testing sequence (DNA_n, where n = 1 to T/2, T represents the total number of testing sequences) which maximally matched the kernel were collected. Specifically, for each kernel of length 9, the subsequence S_n (of length 9) within each sequence DNA_n which yielded the maximal activation (A_kn, n = 1 to T/2 and k = 1 to N) from the first CNN layer were collected. From these collected subsequences, only those were retained with activations greater than 0.5 of the maximum activation of the kernel across all positive sequences, i.e., A_kn > 0.5 × max_n(A_kn). These retained subsequences were aligned and visualized as sequence logos using WebLogo and the corresponding position weight matrix (PWM_k) was computed.

To compute the importance score of each kernel, we used two different techniques. In the first approach (or the ‘activation-ratio’ approach), the sums of the maximal activity score across positive testing sequences and negative testing sequences were computed. The ratio of the former to the latter was used as the importance score of the kernel. The higher the value of this ratio, the higher the importance score of the motif. The PWMs were compared with known fruit fly motifs in the JASPAR database using TOMTOM with a q-value threshold of <0.05. In the second approach, we used a method based on ‘gradients’ similar to a previous work (14). In this approach, the gradient contributed by the motif (kernel) to the model output was measured. The gradient of the model prediction with respect to each kernel in the first CNN layer was computed. A dot product was taken between the gradient and representation of the kernel followed by summing across the vector to aggregate the effect into one single value which represents the motif or kernel importance. The higher the value of this aggregate value, the higher the importance of the motif represented by the kernel.

To group similar motifs together, the PWMs were clustered using the STAMP tool with column comparison metric as Pearson Correlation Coefficient, Ungapped Smith–Waterman as the alignment algorithm, UPGMA as the hierarchical tree-building algorithm, and Iterative Refinement as the multiple alignment strategy. For a better grouping of the PWMs, motif edges with an information content of <0.4 were trimmed. After trimming, the motifs of length >4 were retained.

Feature-based models

To apply traditional feature-based models, we first split each DNA sequence into k-mers using a sliding window approach. We extracted all subsequences of length k with stride = 1 from all the training sequences. A unique set of k-mers was obtained and their frequencies in the training sequences served as the features. We then trained Random Forest, K-nearest neighbor, Decision Trees, elastic-net logistic regression, dense neural network with two hidden layers, and Boosted Trees by tuning the appropriate model parameters (Supplementary Table S1) using 10-fold cross-validation. We also trained gkmSVM, which applies support vector machines to gapped k-mer features. For each of these feature-based models, three different k-mer lengths (6, 9 and 12) were tested using 10-fold cross-validation.

RESULTS

Training

We implemented the deep learning models shown in Table 1 using Keras and Tensorflow as backend. During the training process, we used ‘binary cross-entropy’ as the loss function to be minimized and ‘Adam’ as the optimization algorithm. To prevent overfitting, we applied an early stopping criterion to stop the optimization iterations during training after five epochs of unimproved loss on the validation set. Different values for hyperparameters such as batch size and learning rate were tested as indicated in Table 1. The maximum number of epochs was set to 100. The models were evaluated using six different metrics: AUC, accuracy, Matthews correlation coefficient (MCC), precision, recall, and f1 score/measure. We used these different metrics to view the model performance from different perspectives. AUC measures the overall performance of the model across the entire prediction probability threshold. Precision and recall focus on the model performance in one specific ‘class label’; the f1 score combines precision and recall scores. MCC is a balanced metric and can indicate a model's performance compared with a random model. The deep learning models in python code are available in this GitHub page https://github.com/lincshunter/TADBoundaryDectector.

The choice of hyperparameters can affect model performance

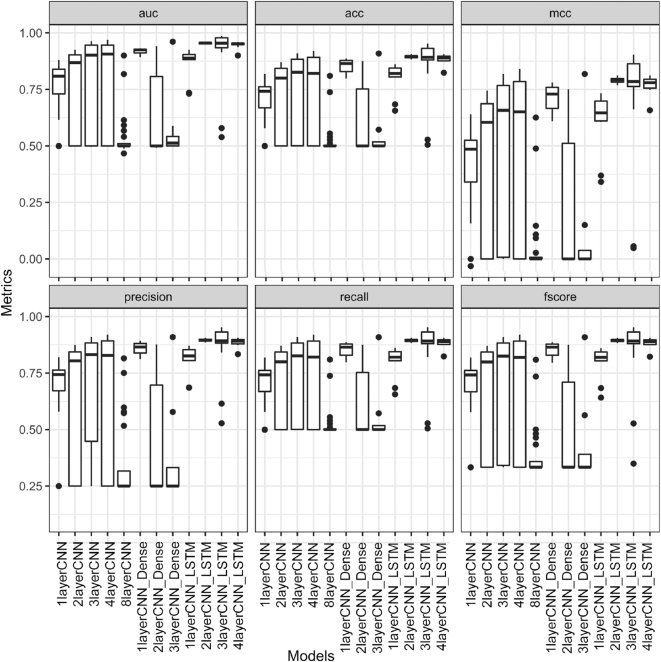
We found that the performance of deep learning models depends on the choice of hyperparameters (Figure 1). A wrong choice of hyperparameters yielded very poor performance (Figure 2). Depending on the hyperparameters, models such as 2layerCNN, 3layerCNN, 4layerCNN and 8layerCNN gave low accuracy and AUC (Figure 2). The more balanced metric MCC also exhibited very low values close to zero for some values of hyperparameters indicating no better performance than a random model. The models consisting of CNN layers only and ones with both CNN and dense layers displayed large variance in their performance across the different permutations of hyperparameters (Figure 2). However, models that contained both CNN and LSTM (Figure 1) showed lower variance (Figure 2). These observations indicate that different values of hyperparameters should be tested when evaluating deep learning models. Focusing on one single set of hyperparameters might lead to wrong conclusions.

Figure 2.

Deep learning model's performance metrics versus hyperparameters. The figure shows boxplots for six different performance metrics (auc: area under the curve, acc: accuracy, mcc: Matthews correlation coefficient, precision, recall, and f1 score) of 12 different deep learning architectures for different permutations of hyperparameter set tested. The annotations of the models are provided in Table 1. There are six sub-panels distributed in two rows and three columns to accommodate all the metrics. The model labels at the bottom are for both the rows.

Deep learning accurately predicts boundaries of TADs

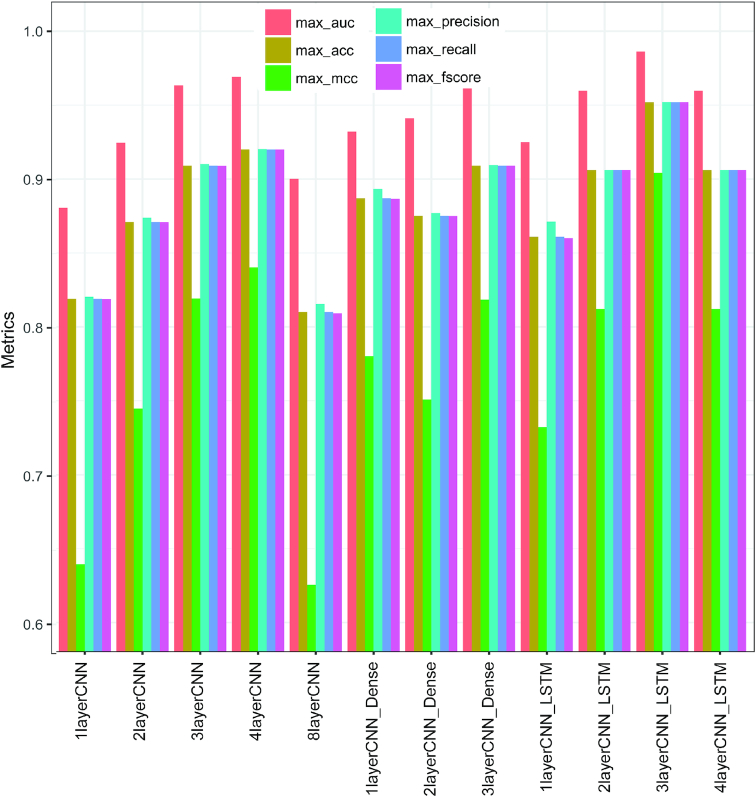
Because of the dependence of model performance on hyperparameters, several permutations of hyperparameters were tested and the best set was obtained for each of the 12 architectures shown in Table 1. Among the models that contained only CNN layers, we noted that performance increased with an increase in the number of CNN layers from 1 (1layerCNN: AUC of 0.881, accuracy of 0.819) to 4 (4layerCNN: AUC of 0.969, accuracy of 0.910) (Figure 3). However, increasing the number of layers to eight decreased the performance (8layerCNN model: AUC of 0.900, accuracy of 0.810) (Figure 3) indicating that adding more hidden CNN layers does not necessarily improve model performance. The first CNN layer captures individual local patterns or motifs in the sequences. An additional hidden CNN layer captures higher-order interactions between patterns learned by the previous CNN layers. Our results suggest that individual local sequence patterns with some dependencies between each other distinguish the TAD boundaries and nonboundary sequences.

Figure 3.

Best performance by 12 different deep learning model architectures. The figure shows the best performance achieved by each of the 12 different deep learning model architectures. Six different metrics were used (auc: area under the curve, acc: accuracy, mcc: Matthews correlation coefficient, precision, recall and f1 score) and the model annotations are provided in Table 1.

Unlike a CNN layer, which captures local patterns or motifs and local interactions between these patterns, LSTM or dense layer can capture the long-range dependencies or more complicated interactions between these patterns. In our study, we found that adding a bidirectional LSTM layer or dense layer improved the performance from the corresponding model that contained only CNN layers. For example, 1layerCNN_LSTM and 1layerCNN_Dense achieved AUCs of 0.925 and 0.932, respectively, compared with 1layerCNN with AUC of 0.881. In addition, 2layerCNN_LSTM and 2layerCNN_Dense achieved AUCs of 0.960 and 0.941, respectively, compared with 2layerCNN with AUC of 0.925. However, adding LSTM layers to CNN models proved better than adding dense (Figure 3). It should be noted that the number of dense layers (1, 2, 3 or 4) to be added was a part of the hyperparameter optimization process.

Among all the models explored, the 3layerCNN_LSTM model that contained three CNN layers (64 kernels in each layer, each kernel of length 9) followed by a bidirectional LSTM layer (40 LSTM units) performed the best (Figure 3). This model achieved AUC, accuracy, MCC, precision, recall, and f1 score of 0.986, 0.955, 0.904, 0.952, 0.952 and 0.952, respectively (Figure 3). It is interesting to note that adding an LSTM layer after three CNN layers performed better than adding an LSTM layer after four CNN layers (AUC = 0.96, accuracy = 0.906, MCC = 0.812, precision = 0.906, recall = 0.906, f1 score = 0.906) (Figure 3). This indicates that an appropriate number of CNN layers is necessary for an LSTM layer to work. We also noted that the top five best performing permutations of hyperparameters for the 3layerCNN_LSTM model indicate that the number of kernels of at least 64 was used in each CNN layer (Table 2). This means multiple short sequence signals contribute to the discrimination between the boundaries and the other sequences.

Table 2.

Performance of 3layersCNN_LSTM. Five different permutation sets of hyperparameters for the 3layersCNN_LSTM model that yielded the top five performances are shown. The first six columns indicate the value of six different performance metrics. The standard deviation in the metrics value from 10-fold cross validation are indicated within parentheses. The remaining columns indicate the hyperparameters

AUC	Accuracy	MCC	Precision	Recall	F1 score	Learning rate	Kernel size	number of kernels	LSTM units
0.9829 (0.0026)	0.9503 (0.0044)	0.8916 (0.0091)	0.9515 (0.0046)	0.9502 (0.0045)	0.9502 (0.0045)	0.001	9	64	40
0.9795 (0.0034)	0.9358 (0.0122)	0.8643 (0.0235)	0.9385 (0.0113)	0.9358 (0.0122)	0.9357 (0.0122)	0.001	9	64	60
0.9768 (0.0114)	0.9352 (0.0145)	0.8609 (0.0291)	0.9358 (0.0146)	0.9352 (0.0145)	0.9352 (0.0145)	0.001	9	120	40
0.9892 (0.0061)	0.9360 (0.0061)	0.8641 (0.0130)	0.9381 (0.0070)	0.936 (0.0061)	0.9359 (0.0061)	0.001	9	64	20
0.9752 (0.0037)	0.9230 (0.0053)	0.8370 (0.0104)	0.9240 (0.0052)	0.9230 (0.0053)	0.9229 (0.0053)	0.001	9	96	20

To validate further the superior performance of 3layerCNN_LSTM and to estimate the effect of sampling on the performance, we chose the top five permutation sets of hyperparameters (Table 2) that yielded the best results for 3layerCNN_LSTM. Then, we separately performed a 10-fold cross-validation analysis of the 3layerCNN_LSTM model for these five sets of hyperparameters. The standard deviation in most of the performance metrics resulting from using different ‘folds’ is <0.5% (Table 2). To compare with the 3layerCNN model, which is the counterpart model without the LSTM layer, similar 10-fold cross-validation analysis was performed (Supplementary Table S2). The results showed a standard deviation of less than 0.6% in most of the performance metrics (Supplementary Table S2). The results showed that adding an LSTM layer improved the performance. For example, the 3layerCNN_LSTM had an average performance accuracy of 95.03 ± 0.44% compared with 90.50 ± 0.64% in 3layerCNN (Supplementary Table S2 and Table 2A). This shows that even after taking into account the effect of sampling variance, 3layerCNN_LSTM still performed better than its counterpart model without the LSTM layer.

Overall, our results indicate that a deep learning model, when appropriately optimized, can accurately differentiate between TAD boundaries and internal regions of TADs. Because of the best performance by a model with three CNN layers and one LSTM layer, it can be qualitatively concluded that there may exist both higher-order and long-range dependencies between sequence motifs in the TAD boundaries.

Deep Learning performs better than feature-based models

Next, we compared the ability of deep learning models in predicting TAD boundaries to traditional feature-based models. First, we used the frequencies of all possible k-mers in the sequences as the features (Methods and Materials). The top 500 k-mers with the highest count in the training sequences were retained and used for training purposes. This was done for k = 6, 9 and 12. Using a 10-fold cross-validation technique, we trained traditional feature-based models: Random Forest, K-nearest neighbor, Decision Trees, elastic-net logistic regression, dense neural network with two hidden layers, and Boosted Trees by varying the appropriate model parameters (Supplementary Table S1). We also trained the gkmSVM model (15) that has been used as a benchmark feature-based method to compare with deep learning models in genomics (9,11). This model applies support vector machines to gapped k-mers. In our case, we used k = 6, 9 and 12. Boosted Trees performed the best in the AUC metric (0.974 when k = 6) (Supplementary Table S3). In the remaining five metrics, Random Forest performed the best with k-mer length of 6 (accuracy = 0.912, MCC = 0.825, precision = 0.898, recall = 0.933, f1 score = 0.914). (Supplementary Table S3). GkmSVM’s performance was a little lower than Random Forest with k = 9 (AUC = 0.945, accuracy = 0.906, MCC = 0.813, precision = 0.886, recall = 0.932, f1 score = 0.908) (Figure 2B). However, the feature-based models did not outperform the best deep learning model (Figure 3 and Table 2). These results show that deep learning models, when appropriately tuned, outperform feature-based models in predicting TAD boundaries.

Motifs enriched in TAD boundaries

There has been an indication that TAD boundaries are enriched in binding sites of insulator proteins. Related to this context, the deep learning model not only can accurately predict the boundaries but can also be used to decipher the sequence motifs that differentiate the boundaries from the ‘nonboundary’ sequences. The 64 filters or kernels from the first CNN layer in the best deep learning model (3layerCNN-LSTM with the optimal hyperparameters) are matrices of shape (9, 4) and recognize sequence motifs of length 9 in similar ways to traditional position weight matrices (PWMs). To generate the sequence logos, the subsequences that maximally matched the filter were collected and aligned to generate sequence logos and their corresponding PWMs. The PWMs were clustered using STAMP with column comparison metric as the Pearson Correlation Coefficient. The PWMs were compared with known fruit fly motifs in the JASPAR database. To obtain the importance score of each kernel, we used two approaches: ‘activation-ratio’ and gradient based (Materials and Methods). In the ‘activation-ratio’ approach, the sums of the maximal activity score across positive testing sequences and negative testing sequences were computed. The ratio of the former to the latter was used as the importance score of the kernel. In the second approach (Materials and Methods), we used a gradient-based approach similar to a previous study (14).

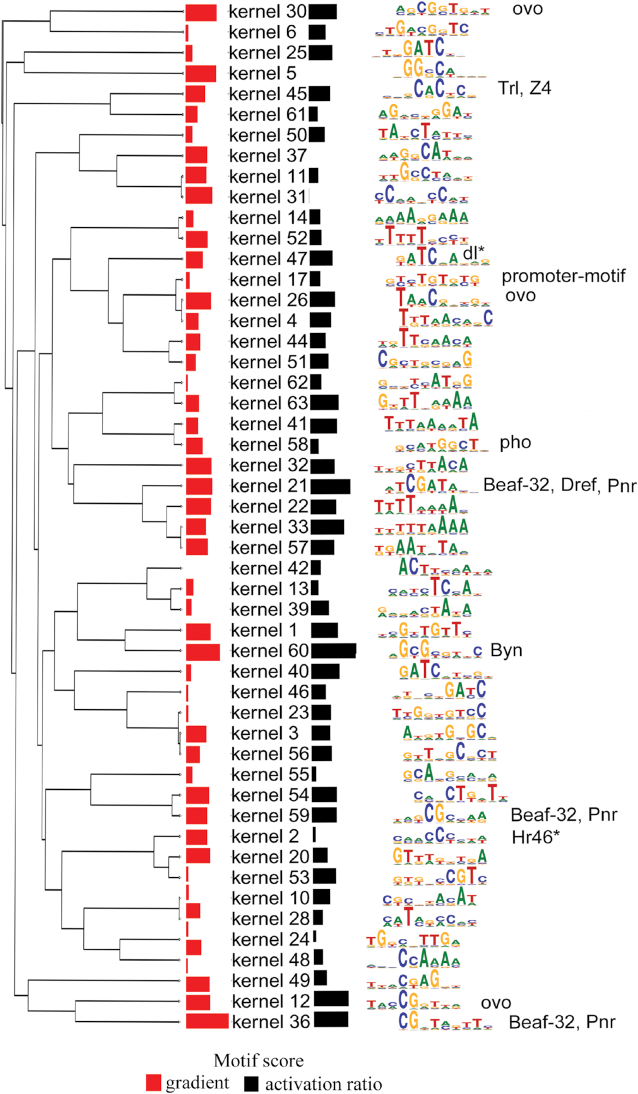
We found that out of 64 kernels, 12 matched annotated motifs in the JASPAR fly database (16). The Beaf-32 motif, previously detected as highly enriched in the TAD boundary motif (8), matched to two top kernels: 21 and 36, ranked second and sixth, respectively, based on the ‘activation-ratio’ approach (Figure 4), and ranked sixth and first by the gradient-based approach (Figure 4). Another two motifs, Pnr and Dref, which are very similar to the Beaf-32 motif, matched to the same kernels (Figure 4). Trl (or GAF) elements which frequently co-occur with housekeeping transcriptional regulatory elements or TREs at TAD boundaries (17) was also detected as a motif (Figure 4). Embryonic development factors such as Byn or brachyenteron and Ovo, which is involved in development specification in fruit flies (18) and expression of germline genes, respectively, were also detected as the top scoring motifs (Figure 4). However, CTCF was not detected by the first CNN layer, most likely because of its weak enrichment in TAD boundaries of fruit flies (8). The motifs detected by the first CNN layer resonate with previous studies reporting similar motifs in TAD boundaries. However, our study shows several other unannotated motifs that contribute to the discrimination between TAD boundaries and nonboundary regions. This means the biological rules that characterize TAD boundaries are complex and encompass not just a few factors.

Figure 4.

Deep learning identifies motifs enriched in TAD boundaries. The kernels along with their scores, sequence logos, and the matched motifs in fruit flies are shown. The scores are indicated by ‘black colored’ bar graphs (using ‘activation-ratio’) and ‘red colored’ bar graphs (using a gradient-based approach). A longer bar graph indicates a higher score. The matched motif in fruit flies is indicated next to the sequence logo.

DISCUSSION

In this paper, we explore several deep learning architectures containing dense, CNN and LSTM layers to predict boundaries of TADs from sub-kb high resolution chromatin capture experiments. One bottleneck that comes with deep learning models is that the choice of hyperparameters can drastically affect the weights and performance of the models. To obtain the appropriate set of hyperparameters, we performed hyperparameter tuning for a set of parameters such as learning rate of the optimizer, batch size, kernels’ length, and number of kernels. We found that a model that contains three CNN layers followed by a bidirectional LSTM layer performed the best with a high accuracy of 96%. This outperformed the best feature-based model with 91% accuracy and a previous study of 75% accuracy on the same data set.

We did not create a background set by shuffling the boundary sequences by maintaining the same dinucleotide frequency because such method has been reported to overestimate the performance of predictive models (19). The background set was chosen to represent actual DNA sequences from the genome but restricted to regions inside the TADs. Our goal was to design a deep learning model that can accurately predict TAD boundaries but also allow the model to learn ‘features/motifs’ that can differentiate the boundaries from internal sequences. That is why the background set was restricted to internal regions of TADs.

Besides accuracy, we used five other metrics to capture the performance of the models from different perspectives. AUC captures how a model generally performs across different thresholds applied to the probability of prediction. The accuracy metric does not take into account a model's differential performance (if it exists) between the two classes. Hence, other metrics such as precision, recall, and f1 score provide supplemental information on whether the model performance is biased toward a specific class. Matthew's correlation coefficient compares the model's performance with that of a random model. In our case, we found that some of the metrics are almost identical to the accuracy metric (Figures 2 and 3) indicating that the model's performance is not biased toward one specific class.

Deep learning models require a large training set and can overfit easily. To address this issue, we added three main techniques: ‘drop out,’ ‘data augmentation,’ and ‘early stopping.’ Dropout is a technique that has been proven to prevent overfitting in deep learning models. It randomly removes a fraction of nodes during each epoch of the training process allowing ‘learning’ from randomly chosen units. In general, we added a ‘drop out’ layer after every hidden layer. Data augmentation was also applied to increase the size of the training set by creating additional ‘TAD boundaries.’ These artificial ‘TAD boundaries’ were created by shifting the actual TAD boundary intervals to the left or right randomly by some base pairs of length between 0 and 100. The data augmentation was only applied to the training set and not to the testing set. We also applied ‘early stopping’ criteria by terminating the optimization process when the value of the loss function on the validation set did not improve after five consecutive epochs.

Our model focused on high resolution TAD boundary intervals of 1 kb in length. For mammalian genomes, there are other Hi-C data that have achieved TAD boundary resolution in a range of 10–40 kb. For example, for 10 kb resolution Hi-C data, traditional analysis of Hi-C data divides the genome into intervals or bins of 10 kb and generates contact counts between these bins. In such a case, each TAD boundary will be 20 kb in length. First, the models explored in this study will be impractical on these large length boundary sequences. Second, this kind of resolution introduces some ‘uncertainty’ to that reported by these experiments. In the future, we plan to develop deep learning models that are ‘time-distributed’ and/or contain k-mer embedding features to address long TAD boundaries. In a ‘time-distributed’ model, instead of analyzing the entire sequence, it can be divided into several nonoverlapping intervals. A deep learning layer can be applied to these intervals independently and can be integrated subsequently. In a k-mer embedding technique, the DNA sequence can be treated as a sequence of k-mers instead of a sequence of single letter bases. The k-mers can be translated to numerical vectors in a higher dimension using techniques such as GloVe. Nevertheless, we have demonstrated that deep learning, when optimized to the right architecture and hyperparameters, can accurately predict TAD boundaries and can extract motifs that differentiate the boundaries from other nonboundary sequences.

We also found that out of 64 kernels represented in the first CNN layer, only 11 matched annotated motifs in the JASPAR fly database. The Beaf-32 motif, previously detected as highly enriched in the TAD boundaries, was one of the top scoring motifs detected by our method. Because elimination of Beaf-32 binding sequences has been shown not to alter Hi-C interaction data in fruit flies (8) and our study reveals motifs Dref and Pnr matched the same kernels representing Beaf-32, it is possible that Dref and Pnr have more important roles in TAD boundary formation. Interestingly, CTCF was not detected by the first CNN layer in the model, most likely because of its weak enrichment in TAD boundaries of fruit flies. Besides, other TAD boundary associated motifs such as Trl (or GAF) were detected. Some of the motifs detected by the first CNN layer resonate with previous studies reporting similar motifs in TAD boundaries. This validates the methodology used in this study to predict TAD boundaries and identification of motifs. Our study also revealed embryonic development factors such as Byn or brachyenteron and Ovo, which are involved in development specification in fruit flies and expression of germline genes, respectively, as high scoring motifs in TAD boundaries. We also detected Pho as a motif in the TADs (not previously detected). Pho is known to play a role in DNA binding and stabilization of Polycomb complexes in fruit flies (20). It is possible that these factors are required for TAD formation or that their binding is just a product of formation of TADs. Overall, there were more than 50 unannotated motifs that contributed to the differentiation between TAD boundaries and nonboundary sequences. One should note that each of these motifs collectively or combinatorically contributes to the prediction power of the deep learning model. To decipher fully the nature of the interactions between these motifs is beyond the scope of this paper and will be addressed in future studies.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

American Heart Association [181PA34170360 to Y.L.] (in part); Organized Research and Creative Activities (ORCA) awards [University of Houston-Downtown to B.S.]. Funding for open access charge: University of Houston-Downtown University of Houston.

Conflict of interest statement. None declared.