Abstract
The binding between two biomolecules is one of the most critical factors controlling many bioprocesses. Therefore, it is of great interest to derive a reliable method to calculate the free binding energy between two biomolecules. In this work, we have demonstrated that the binding affinity of ligands to proteins can be determined through biased sampling simulations. The umbrella sampling (US) method was applied on 20 protein–ligand complexes, including the cathepsin K (CTSK), type II dehydroquinase (DHQase), heat shock protein 90 (HSP90), and factor Xa (FXa) systems. The ligand-binding affinity was evaluated as the difference between the largest and smallest values of the free-energy curve, which was obtained via a potential of mean force analysis. The calculated affinities differ sizably from the previously reported experimental values, with an average difference of ∼3.14 kcal/mol. However, the calculated results are in good correlation with the experimental data, with correlation coefficients of 0.76, 0.87, 0.96, and 0.97 for CTSK, DHQase, HSP90, and FXa, respectively. Thus, the binding free energy of a new ligand can be reliably estimated using our US approach. Furthermore, the root-mean-square errors (RMSEs) of binding affinity of these systems are 1.13, 0.90, 0.37, and 0.25 kcal/mol, for CTSK, DHQase, HSP90, and FXa, respectively. The small RMSE values indicate the good precision of the biased sampling method that can distinguish the ligands exhibiting similar binding affinities.
Introduction
A large number of biological processes involve the binding of two or more biomolecules, which is often evaluated through Gibbs free-energy difference.1 The accurate determination or ranking of the binding affinity is a prerequisite for the synthesis of potential inhibitors that would allow for the reduction of therapeutic development and medication cost.2 Several schemes have been developed, including molecular docking,3−6 quantitative structure–activity relationship,7−10 linear interaction energy,11,12 molecular mechanism/Poisson–Boltzmann surface area (MM-PBSA),13−15 fast pulling of ligand,16,17 free-energy perturbation,18,19 thermodynamic integration,20,21 and nonequilibrium molecular dynamics (MD) simulations.22 Many studies in this area have been published in recent years.23−26 Nevertheless, precise prediction of binding affinity yet remains elusive.
The biased sampling method has emerged as a promising approach for the determination of the binding free energy of protein–ligand complexes27−29 or protein–protein complexes.23,30 Furthermore, the free-energy permeation of an ion across a channel has been also investigated using this approach.31 The ligand is normally forced to move out of an enzyme active site by an external force. The movement of the ligand is tracked and recorded along the reaction coordinate (ξ), and then the obtained conformations were subjected to umbrella sampling (US) simulations. The free-energy barrier between smallest and largest values extracted from the potential of mean force (PMF) during US simulations can be used for the prediction of the binding affinity.30 Here, the PMF values are determined using the weighted histogram analysis method (WHAM)32 calculation.
In this work, the US method was applied to 20 protein–ligand complexes with solvent-exposed binding sites, including cathepsin K (CTSK), type II dehydroquinase (DHQase), heat shock protein 90 (HSP90), and factor Xa (FXa) systems. CTSK is a protease associating with a number of biological problems. The weakening of bone and cartilage is related to the action of CTSK on the catabolization of collagen, elastin, and gelatin. The CTSK inhibitors have thus been developed to prevent osteoporosis.33 Moreover, the enzyme was also shown to be involved in human breast cancers34 and overexpressed in glioblastoma.35 DHQase is known to be linked with the shikimic acid pathway. Inhibiting DHQase is a potential method to treat malaria, a parasitic infection causing more than a million deaths every year.36 HSP90 is a chaperone protein that helps to stabilize other proteins under the effect of irregular temperature.37 The protein also aids the protein folding and degradation processes.37 As HSP90 stabilizes proteins needed for tumor growth, HSP90 inhibitors have been screened for anticancer therapy development.38 FXa is an enzyme involved in the coagulation cascade.39 FXa inhibitors have been developed to prevent the venous thromboembolism.40 Our obtained results are well correlated with previously reported experimental data with high relation coefficients, on the basis of which the experimental binding free energy of a new ligand can be reliably calculated. The method is also demonstrated to be precise with a relatively small root-mean-square error (RMSE).
Results and Discussion
Selected Model and Generated Conformation for Umbrella Sampling Simulation
Many enzymes and proteins contain sophisticated ligand-binding sites, which require significant protein conformational changes upon ligand binding or dissociation. The binding affinity estimation for these proteins requires simultaneous calculations of both free energy and the kinetics of protein folding, which requires a tremendous amount of computational processing time. The biased sampling method used in our work may not be suitable for these proteins. Many other proteins, however, contain solvent-exposed ligand-binding sites, which allows their ligands to easily move in/out without substantial protein conformational changes. Thus, for the complexes of these proteins, the ligand-binding affinity can be rapidly determined through US computation, as mentioned in Materials and Methods section. The structure of the protein could be restrained using a harmonic potential applied on the Cα atoms during the simulations. In this work, initially, the compound is forced to mobilize out of the binding site onward the unbinding pathway by an external harmonic force with a constant velocity as described above, according to a previous work.16 Although the slower pulling speeds provided better results, the efficient gain is not significant.16,30 The forms of recorded pulling forces are consistent with the previous works (Figure S1).41 The coordination of the ligand center of mass and applied force value is recorded every 0.1 ps over FPL simulations, as shown in Figure S2. The value was employed to estimate the initial conformations of biasing sampling simulations, as mentioned above.
Free-Energy Calculation
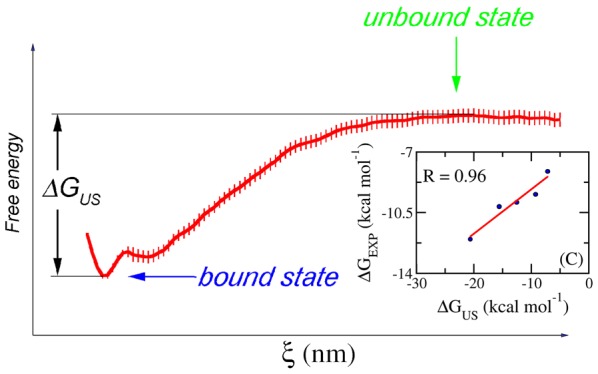
The free-energy profile along the reaction coordinate (ξ) was analyzed using the “gmx wham” tools. The obtained PMF value of each studied system is shown as a function of the reaction coordinates (ξ) in Figure 1. These PMF curves show similar trends and are in good agreement with a previous study.42 The free energy starts at zero value, then drops to a minimum value, and finally increases to a stable value when ξ reaches 1.0–1.2 nm (Figure 1). This range corresponds to the state where the noncovalent interaction between the protein and the ligand is broken. The calculated binding free energy ΔGUS can be determined as the difference between the largest and smallest values of PMF curves, which is described in Figure 4C. The binding affinities calculated for the complexes of CTSK, DHQ, HSP90, and FXa are provided in Table 1. The computational error of the binding free energy was estimated using bootstrapping analysis with 100 rounds of computations.43
Figure 1.
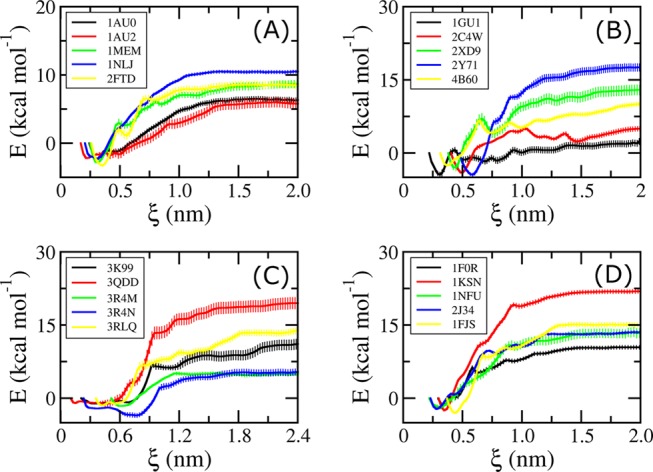
PMF curves obtained from WHAM analysis for CTSK systems (A), DHQase complexes (B), HSP90 systems (C), and FXa systems (D). The errors were evaluated over 100 rounds of bootstrapping analysis.43
Figure 4.
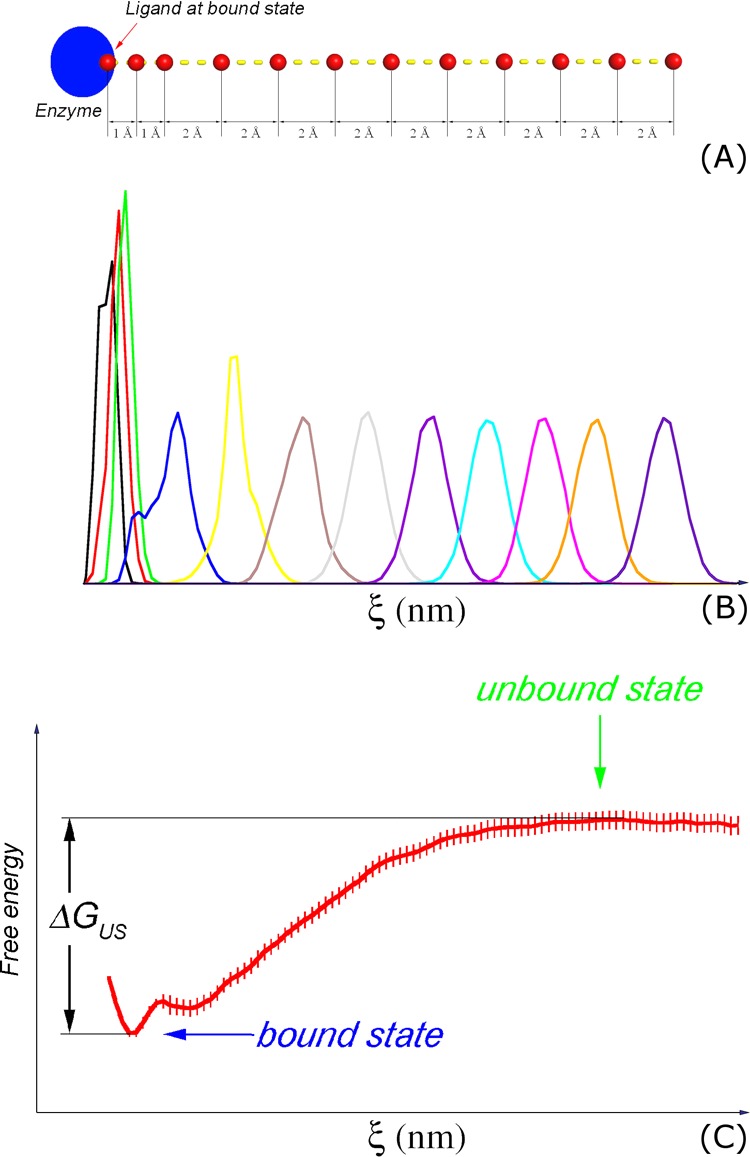
Computational scheme. (A) Initial windows of US simulations with indications of displacement of the center of mass of the ligand; (B) the representative histograms of US simulations; (C) the binding free energy is estimated as the difference between the maximum and minimum values of the PMF curve provided from the US simulations.30 Shown in (C) is the calculation result of the 1AUO system. The error of computations was evaluated over 100 rounds of bootstrapping analysis.43
Table 1. Free-Energy Values Obtained from US Simulationsa.
| complexes | protein | ΔGUS | ΔGEXP |
|---|---|---|---|
| 1AU0 | CTSK | –9.05 ± 0.36 | –10.51 |
| 1AU2 | CTSK | –8.47 ± 0.70 | –10.82 |
| 1MEM | CTSK | –11.54 ± 0.57 | –10.90 |
| 1NLJ | CTSK | –12.74 ± 0.23 | –13.45 |
| 2FTD | CTSK | –11.91 ± 0.69 | –14.26 |
| 1GU1 | DHQase | –6.83 ± 0.63 | –6.21 |
| 2C4W | DHQase | –9.84 ± 0.51 | –6.45 |
| 2XD9 | DHQase | –16.21 ± 1.07 | –8.86 |
| 2Y71 | DHQase | –22.25 ± 0.77 | –10.12 |
| 4B6O | DHQase | –12.96 ± 0.55 | –9.61 |
| 3K99 | HSP90 | –12.56 ± 1.01 | –9.91 |
| 3QDD | HSP90 | –20.62 ± 1.38 | –12.04 |
| 3R4M | HSP90 | –7.17 ± 0.44 | –8.13 |
| 3R4N | HSP90 | –9.27 ± 0.66 | –9.45 |
| 3RLQ | HSP90 | –15.61 ± 0.94 | –10.15 |
| 1F0R | FXa | –12.65 ± 0.55 | –10.51 |
| 1KSN | FXa | –24.45 ± 0.52 | –12.90 |
| 1NFU | FXa | –15.43 ± 0.97 | –10.63 |
| 2J34 | FXa | –16.06 ± 0.28 | –10.74 |
| 1FJS | FXa | –13.48 ± 0.77 | –10.14 |
The errors were evaluated over 100 rounds of bootstrapping analysis.43 The unit of free energy is kcal/mol.
The calculated binding free energies (ΔGUS) of the HSP90, DHQase, and FXa systems are larger than the corresponding experimental values (ΔGEXP), with average differences of ∼3.11, 5.37, and 5.43 kcal/mol, respectively. In contrast, the average ΔGUS of the CTSK system is slightly (1.24 kcal/mol) smaller than the experimental value. The larger calculated binding free energy likely resulted from the inaccuracy of mimicking the interaction among constituent molecules, including protein, ligand, and water molecules.44,45 The differences ΔGUS and ΔGEXP are similar to the difference obtained with an alchemical binding free-energy calculation described in previous studies.46,47 In some cases, the difference is more than 10 kcal/mol (Table 1). Nevertheless, there is a good correlation between ΔGUS and ΔGEXP in each studied system, especially in the case of HSP90 and FXa (Figure 2). The regression equations obtained for the studied systems are
| 1 |
| 2 |
| 3 |
| 4 |
Using these equations and our US approach described herein, the binding affinity of a new ligand to these proteins can be reliably calculated.
Figure 2.
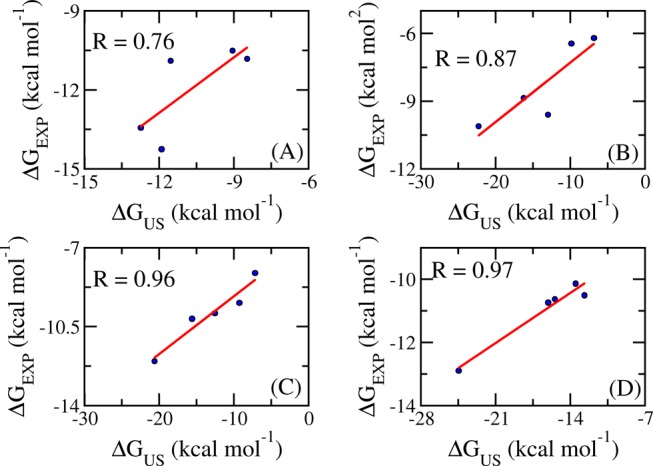
Correlation between computed and experimental binding free energies of CTSK complexes (A), DHQase complexes (B), HSP90 complexes (C), and FXa complexes (D).
In addition, the errors of calculations are small (Table 1). The computed errors (δ) obtained for CTSK, DHQase, HSP90, and FXa systems are ca. 5, 5, 7, and 4%, respectively. These values are significantly smaller than those obtained from other methods, such as FPL (∼7–15%16,48) and MM-PBSA (∼20%49,50). It is generally difficult to select the dielectric constant for polar solvation calculation as the ligand is partially solvent-exposed, resulting in poor precision in the MM-PBSA method.50 Furthermore, the polar solvation free energy is also dependent on the calculating approach, which are Poisson–Boltzmann (PB) or generalized Born (GB) schemes. Many studies indicated that the obtained results strongly depend on the studied system.50 The PB method provides better results in some cases,51 whereas the GB method is more accurate/precise in some other cases.52 In addition, the lower precision of the FPL method in comparison with the US method is probably caused by the fewer number of ligand samples over the unbinding pathway. Furthermore, the binding affinity estimation using the FPL method is relatively simple wherein it scores the ligand affinity using recorded rupture force41 or pulling work.16 Absolutely, these metrics do not consider the contribution of entropic conformation, resulting in reducing the precision of the calculation. Moreover, the RMSE analysis indicates that the computational study would predict the experimental value with the precisions of RMSECTSK = 1.13, RMSEDHQase = 0.90, RMSEHSP90 = 0.37, and RMSEFXa = 0.25 kcal/mol. The estimation with high precision would definitely distinguish the ligands with similar binding affinities.
The better results obtained with the US method compared with the FPL scheme16,48 come at the cost of computational resources, although. In the FPL scheme, one calculation requires ca. 0.7 ns whereas the total molecular dynamics (MD) simulation time in the US method is ca. 120.7 ns (including FPL simulation as well). Fortunately, recent developments in GPU computing help remarkably speeding up the US simulation studies. One compute node with dual Xeon E5-2670V3 and GTX 1070 GPU can approximately produce one US calculation per day. It is noteworthy that the computing resource required for US calculation is similar to that found for the MM-PBSA method, which required several nanoseconds of MD simulation to generate equilibrium snapshots for the free-energy calculation.50 The MM-PBSA method would take a much longer CPU time to evaluate the contribution of conformational entropy for a large complex consisting of more than 4000 atoms. Hence, for large systems, the US computation has great advantages over the MM-PBSA method.
Conclusions
In this work, we have demonstrated that biased sampling simulation is a highly appropriate approach for ranking the affinity between ligand and enzyme for the CTSK, DHQase, HSP90, and FXa complexes. The computational binding affinity of the inhibitor was evaluated as the difference between the largest and smallest values of the free-energy curve obtained with PMF calculation. The calculated binding affinities sizably differ from the corresponding experimental values, with an average difference of of 3.14 kcal/mol (some values >10 kcal/mol).53 To decrease the difference, more advanced methods, such as the combination of free-energy perturbation and US simulations, should be employed.53 However, it is very time consuming to evaluate the absolute binding free energy of a ligand. The calculated binding free energy highly correlates with the experimental values, with correlation coefficients ranging from R = 0.76–0.97, which allows for the reliable estimation of the binding affinity of new ligands. Furthermore, the high precision, which is observed with the values ranging from RMSE = 1.13–0.25 kcal/mol, would easily categorize the ligands with similar binding affinities. Using the US method, both the accuracy and precision are significantly increased in comparison with FPL and MM-PBSA methods.16,48−50 Besides, the computational processing time required in the US method is acceptable, compared to that in the MM-PBSA method. Especially, when simulating large systems, the US computation would require much lesser CPU time than the MM-PBSA method.
Materials and Methods
Target Complexes
Three-dimensional structures of complexes were obtained from the protein data bank (PDB). The PDB IDs of the CTSK complexes are 1AU0,541AU2,541MEM,551NLJ,56 and 2FTD.57 The IDs of the DHQase complexes are 1GU1,582C4W,592XD9,602Y71,61 and 4B6O.62 The IDs of HSP90 complexes are 3K99,633QDD,643R4M,653R4N,65 and 3RLQ.66 The IDs of FXa complexes are 1F0R,671FJS,681KSN,691NFU,70 and 2J34.71 The structures of the ligands are described in Table S1. The ligand was forced to move out of the cavity of the enzyme along an unbinding pathway, which was predicted using the Caver program,72 as described in previous works.16 The complexes were rotated to fit the unbinding pathway along Z axis. A representative model with the unbinding direction is shown in Figure 3.
Figure 3.
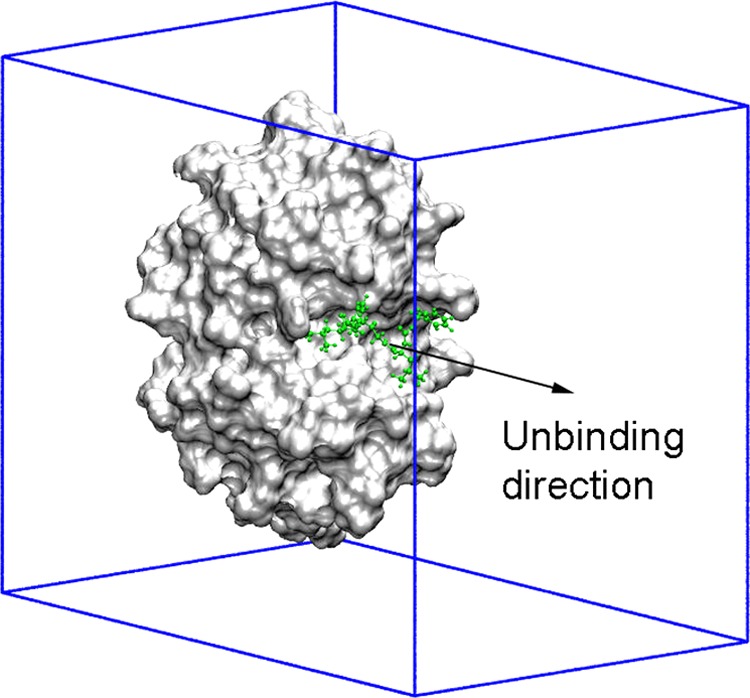
Representation of the initial simulation setup. The ligand (green) is pulled along the unbinding direction (Z axis) using a harmonic force with a cantilever spring constant of 600 kJ/mol/nm2 and a pulling speed of ν = 0.005 nm/ps, as described in previous studies.73,74
Atomistic Simulations
GROMACS 5.1.3 was used to simulate the soluble complexes.75 The proteins were parameterized using the Amber99SB-ILDN force field.76 The ligands were represented using the general Amber force field.77 Charges were obtained by employing the restrained electrostatic potential method78 using quantum chemical calculation at MP2 level with 6-31G(d,p) basis set. Each protein–ligand complex was inserted into a rectangular box with periodic boundary conditions (Figure 3). The dimensions of the boxes for CTSK, DHQase, HSP90, and FXa are 4.92 × 5.67 × 7.19, 5.23 × 6.68 × 8.02, 5.52 × 6.13 × 8.72, and 6.08 × 6.40 × 8.50 nm3, respectively. The simulation parameters were referred from previous studies.79 van der Waals interaction cutoff was set at 0.9 nm, and the particle mesh Ewald method80 is used to treat the electrostatic interaction with a radius of 0.9 nm. Initially, the solvated systems were energy-minimized using the steepest descent method. The complexes were then relaxed during NVT and NPT simulations at 300 K for 100 ps. During relaxed simulations, the Cα atoms of the proteins were restrained by a small harmonic force.
The last conformations of NPT simulations were used as the starting structures of ligand unbinding simulation using the FPL method.16,17 An external harmonic force was applied to dissociate the ligands along the pulling orientation (Figure 3). The Cα atoms of the proteins were restrained over the steered-molecular dynamic (SMD) simulations by a small harmonic potential. The ligands were thus dissociated utilizing a harmonic force with the cantilever spring constant of k = 600 kJ/mol/nm2 along the reaction coordinate (ξ). The pulling speed was chosen as ν = 0.005 nm/ps according to previous studies.16,48 The length of the SMD simulations was ca. 500 ps. During the FPL process, the pulling force and the coordination of the ligand center of mass were recorded every 0.1 ps.
The initial structures of biased sampling simulations were extracted from the unbinding trajectory with the spacing of the center of mass of the ligand shown in Figure 4A. During the FPL process, the conformation of the solvated complexes was recorded at every step of ∼0.2 nm and then used as the initial conformation for the US simulations.30 Eleven snapshots were extracted from bound to unbound states along the reaction coordinate (ξ). However, because the ligand narrowly diffuses in the bound state, as shown in the histograms of simulations (Figure 4B), an additional conformation was taken, resulting in the spacing of 0.1 nm between the first three windows (Figure 4A). Totally, 12 conformations along the reaction coordinate were obtained during FPL simulations. These conformations were subjected to US simulations over 10 ns. Therefore, there are totally 120 ns of MD simulations used for US simulations. To avoid initial fluctuation, the first 0.5 ns duration was removed from the analysis. The weighted histogram analysis method (WHAM)32 was used to evaluate a potential of the mean force (PMF) along the reaction coordinate (ξ), following the gmx wham protocol.81 The WHAM equations can be expressed as follows81
| 5 |
where
| 6 |
in which 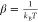 with temperature T and Boltzmann constant kB, hj is the histogram with total number
of values nj, gi = 1 + 2τi is the statistical inefficiency with autocorrelated
time τi corresponding to umbrella
sampling i; and P(ξ) corresponds
to the unbiased probability distribution relating to PMF through
with temperature T and Boltzmann constant kB, hj is the histogram with total number
of values nj, gi = 1 + 2τi is the statistical inefficiency with autocorrelated
time τi corresponding to umbrella
sampling i; and P(ξ) corresponds
to the unbiased probability distribution relating to PMF through 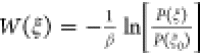 where ξ0 corresponds
to W(ξ0) = 0. The binding free energy
ΔG is simply evaluated as the difference between
the largest and smallest values of the PMF curve (Figure 4C).30 The error of computations was evaluated over 100 rounds of bootstrapping
analysis.43
where ξ0 corresponds
to W(ξ0) = 0. The binding free energy
ΔG is simply evaluated as the difference between
the largest and smallest values of the PMF curve (Figure 4C).30 The error of computations was evaluated over 100 rounds of bootstrapping
analysis.43
Acknowledgments
This work was supported by Vietnam National Foundation for Science & Technology Development (NAFOSTED) grant #103.01-2016.48.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.8b03258.
List of ligands and their structure; recorded values of pulling force and the displacement of the ligand center of mass (PDF)
Author Contributions
All authors designed the studies, collected, analyzed data, and wrote the manuscript.
The authors declare no competing financial interest.
Supplementary Material
References
- Marshall G. R. Computer-Aided Drug Design. Annu. Rev. Pharmacol. Toxicol. 1987, 27, 193–213. 10.1146/annurev.pa.27.040187.001205. [DOI] [PubMed] [Google Scholar]
- Homeyer N.; Stoll F.; Hillisch A.; Gohlke H. Binding Free Energy Calculations for Lead Optimization: Assessment of Their Accuracy in an Industrial Drug Design Context. J. Chem. Theory Comput. 2014, 10, 3331–3344. 10.1021/ct5000296. [DOI] [PubMed] [Google Scholar]
- Morris G. M.; Huey R.; Lindstrom W.; Sanner M. F.; Belew R. K.; Goodsell D. S.; Olson A. J. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009, 30, 2785–2791. 10.1002/jcc.21256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang M. W.; Ayeni C.; Breuer S.; Torbett B. E. Virtual Screening for HIV Protease Inhibitors: A Comparison of AutoDock 4 and Vina. PLoS One 2010, 5, e11955 10.1371/journal.pone.0011955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukherjee S.; Balius T. E.; Rizzo R. C. Docking Validation Resources: Protein Family and Ligand Flexibility Experiments. J. Chem. Inf. Model. 2010, 50, 1986–2000. 10.1021/ci1001982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lang P. T.; Brozell S. R.; Mukherjee S.; Pettersen E. F.; Meng E. C.; Thomas V.; Rizzo R. C.; Case D. A.; James T. L.; Kuntz I. D. DOCK 6: Combining Techniques to Model RNA–Small Molecule Complexes. RNA 2009, 15, 1219–1230. 10.1261/rna.1563609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maw H. H.; Hall L. H. E-State Modeling of HIV-1 Protease Inhibitor Binding Independent of 3D Information. J. Chem. Inf. Comput. Sci. 2002, 42, 290–298. 10.1021/ci010091z. [DOI] [PubMed] [Google Scholar]
- Coderch C.; Tang Y.; Klett J.; Zhang S.-E.; Ma Y.-T.; Shaorong W.; Matesanz R.; Pera B.; Canales A.; Jimenez-Barbero J.; Morreale A.; Diaz J. F.; Fang W.-S.; Gago F. A Structure-Based Design of New C2- and C13-Substituted Taxanes: Tubulin Binding Affinities and Extended Quantitative Structure-Activity Relationships using Comparative Binding Energy (COMBINE) Analysis. Org. Biomol. Chem. 2013, 11, 3046–3056. 10.1039/c3ob40407b. [DOI] [PubMed] [Google Scholar]
- Gil-Redondo R.; Klett J.; Gago F.; Morreale A. gCOMBINE: A Graphical User Interface to Perform Structure-Based Comparative Binding Energy (COMBINE) Analysis on a Set of Ligand-Receptor Complexes. Proteins 2010, 78, 162–172. 10.1002/prot.22543. [DOI] [PubMed] [Google Scholar]
- Nakamura S.; Nakanishi I.; Kitaura K. Binding Affinity Prediction of Non-Peptide Inhibitors of HIV-1 Protease using COMBINE Model Introduced from Peptide Inhibitors. Bioorg. Med. Chem. Lett. 2006, 16, 6334–6337. 10.1016/j.bmcl.2006.09.006. [DOI] [PubMed] [Google Scholar]
- Åqvist J.; Medina C.; Samuelsson J.-E. A New Method for Predicting Binding Affinity in Computer-Aidded Drug Design. Protein Eng., Des. Sel. 1994, 7, 385–391. 10.1093/protein/7.3.385. [DOI] [PubMed] [Google Scholar]
- Jones-Hertzog D. K.; Jorgensen W. L. Binding Affinities for Sulfonamide Inhibitors with Human Thrombin Using Monte Carlo Simulations with a Linear Response Method. J. Med. Chem. 1997, 40, 1539–1549. 10.1021/jm960684e. [DOI] [PubMed] [Google Scholar]
- Kollman P. A.; Massova I.; Reyes C.; Kuhn B.; Huo S.; Chong L.; Lee M.; Lee T.; Duan Y.; Wang W.; Donini O.; Cieplak P.; Srinivasan J.; Case D. A.; Cheatham T. E. Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Acc. Chem. Res. 2000, 33, 889–897. 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- Kuhn B.; Kollman P. A. Binding of a siverse set of ligands to avidin and streptavidin: an accurate quantitative prediction of their relative affinities by a combination of molecular mechanics and continuum solvent models. J. Med. Chem. 2000, 43, 3786–3791. 10.1021/jm000241h. [DOI] [PubMed] [Google Scholar]
- Wang W.; Kollman P. A. Computational study of protein specificity: the molecular basis of HIV-1 protease drug resistance. Proc. Natl. Acad. Sci. U.S.A. 2001, 98, 14937–14942. 10.1073/pnas.251265598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ngo S. T.; Hung H. M.; Nguyen M. T. Fast and accurate determination of the relative binding affinities of small compounds to HIV-1 protease using non-equilibrium work. J. Comput. Chem. 2016, 37, 2734–2742. 10.1002/jcc.24502. [DOI] [PubMed] [Google Scholar]
- Ngo S. T.; Nguyen M. T.; Nguyen M. T. Determination of the absolute binding free energies of HIV-1 protease inhibitors using non-equilibrium molecular dynamics simulations. Chem. Phys. Lett. 2017, 676, 12–17. 10.1016/j.cplett.2017.03.034. [DOI] [Google Scholar]
- Zwanzig R. W. High-temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys. 1954, 22, 1420–1426. 10.1063/1.1740409. [DOI] [Google Scholar]
- Beveridge D. L.; DiCapua F. M. Free energy via molecular simulation: applications to chemical and biomolecular systems. Annu. Rev. Biophys. Biophys. Chem. 1989, 18, 431–492. 10.1146/annurev.bb.18.060189.002243. [DOI] [PubMed] [Google Scholar]
- Kirkwood J. G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3, 300–313. 10.1063/1.1749657. [DOI] [Google Scholar]
- Kollman P. Free energy calculations: applications to chemical and biochemical phenomena. Chem. Rev. 1993, 93, 2395–2417. 10.1021/cr00023a004. [DOI] [Google Scholar]
- Jarzynski C. Equilibrium free-energy differences from nonequilibrium measurements: A master-equation approach. Phys. Rev. E 1997, 56, 5018–5035. 10.1103/PhysRevE.56.5018. [DOI] [Google Scholar]
- Domański J.; Hedger G.; Best R. B.; Stansfeld P. J.; Sansom M. S. P. Convergence and Sampling in Determining Free Energy Landscapes for Membrane Protein Association. J. Phys. Chem. B 2017, 121, 3364–3375. 10.1021/acs.jpcb.6b08445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryde U.; Soderhjelm P. Ligand-Binding Affinity Estimates Supported by Quantum-Mechanical Methods. Chem. Rev. 2016, 116, 5520–5566. 10.1021/acs.chemrev.5b00630. [DOI] [PubMed] [Google Scholar]
- Dahan A.; Markovic M.; Keinan S.; Kurnikov I.; Aponick A.; Zimmermann E. M.; Ben-Shabat S. Computational modeling and in-vitro/in-silico correlation of phospholipid-based prodrugs for targeted drug delivery in inflammatory bowel disease. J. Comput.-Aided Mol. Des. 2017, 31, 1021–1028. 10.1007/s10822-017-0079-5. [DOI] [PubMed] [Google Scholar]
- de Ruiter A.; Polyansky A. A.; Zagrovic B. Dependence of Binding Free Energies between RNA Nucleobases and Protein Side Chains on Local Dielectric Properties. J. Chem. Theory Comput. 2017, 13, 4504–4513. 10.1021/acs.jctc.6b01202. [DOI] [PubMed] [Google Scholar]
- Miao Y.; Huang Y.-m. M.; Walker R. C.; McCammon J. A.; Chang C.-e. A. Ligand Binding Pathways and Conformational Transitions of the HIV Protease. Biochemistry 2018, 57, 1533–1541. 10.1021/acs.biochem.7b01248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang M.; Huang W.; Wen F.; Larson Ronald G. Efficient estimation of binding free energies between peptides and an MHC class II molecule using coarse-grained molecular dynamics simulations with a weighted histogram analysis method. J. Comput. Chem. 2017, 38, 2007–2019. 10.1002/jcc.24845. [DOI] [PubMed] [Google Scholar]
- Mu H.; Geacintov N. E.; Min J.-H.; Zhang Y.; Broyde S. Nucleotide Excision Repair Lesion-Recognition Protein Rad4 Captures a Pre-Flipped Partner Base in a Benzo[a]pyrene-Derived DNA Lesion: How Structure Impacts the Binding Pathway. Chem. Res. Toxicol. 2017, 30, 1344–1354. 10.1021/acs.chemrestox.7b00074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemkul J. A.; Bevan D. R. Assessing the Stability of Alzheimer’s Amyloid Protofibrils Using Molecular Dynamics. J. Phys. Chem. B 2010, 114, 1652–1660. 10.1021/jp9110794. [DOI] [PubMed] [Google Scholar]
- Guardiani C.; Rodger P. M.; Fedorenko O. A.; Roberts S. K.; Khovanov I. A. Sodium Binding Sites and Permeation Mechanism in the NaChBac Channel: A Molecular Dynamics Study. J. Chem. Theory Comput. 2017, 13, 1389–1400. 10.1021/acs.jctc.6b01035. [DOI] [PubMed] [Google Scholar]
- Ferrenberg A. M.; Swendsen R. H. Optimized Monte Carlo data analysis. Phys. Rev. Lett. 1989, 63, 1195–1198. 10.1103/PhysRevLett.63.1195. [DOI] [PubMed] [Google Scholar]
- Brömme D.; Lecaille F. Cathepsin K inhibitors for osteoporosis and potential off-target effects. Expert Opin. Invest. Drugs 2009, 18, 585–600. 10.1517/13543780902832661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duong L. T.; Wesolowski G. A.; Leung P.; Oballa R.; Pickarski M. Efficacy of a Cathepsin K Inhibitor in a Preclinical Model for Prevention and Treatment of Breast Cancer Bone Metastasis. Mol. Cancer Ther. 2014, 13, 2898–2909. 10.1158/1535-7163.MCT-14-0253. [DOI] [PubMed] [Google Scholar]
- Verbovšek U.; Motaln H.; Rotter A.; Atai N. A.; Gruden K.; Van Noorden C. J. F.; Lah T. T. Expression Analysis of All Protease Genes Reveals Cathepsin K to Be Overexpressed in Glioblastoma. PLoS One 2014, 9, e111819 10.1371/journal.pone.0111819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Concepción G.-B.; Luis C. Progress in type II dehydroquinase inhibitors: From concept to practice. Med. Res. Rev 2007, 27, 177–208. 10.1002/med.20076. [DOI] [PubMed] [Google Scholar]
- Zuehlke A. D.; Moses M. A.; Neckers L., Heat shock protein 90: its inhibition and function. Philos. Trans. R. Soc., B 2018, 372 (). 10.1098/rstb.2016.0527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neckers L.; Ivy S. P. Heat shock protein 90. Curr. Opin. Oncol. 2003, 15, 419–424. 10.1097/00001622-200311000-00003. [DOI] [PubMed] [Google Scholar]
- Xie Z. L.; Tian Y. B.; Lv X.; Xiao X.; Zhan M. M.; Cheng K.; Li S. Y.; Liao C. Z. The selectivity and bioavailability improvement of novel oral anticoagulants: An overview. Eur. J. Med. Chem. 2018, 146, 299–317. 10.1016/j.ejmech.2018.01.067. [DOI] [PubMed] [Google Scholar]
- Patel N. R.; Patel D. V.; Murumkar P. R.; Yadav M. R. Contemporary developments in the discovery of selective factor Xa inhibitors: A review. Eur. J. Med. Chem. 2016, 121, 671–698. 10.1016/j.ejmech.2016.05.039. [DOI] [PubMed] [Google Scholar]
- Mai B. K.; Viet M. H.; Li M. S. Top-Leads for Swine Influenza A/H1N1 Virus Revealed by Steered Molecular Dynamics Approach. J. Chem. Inf. Model. 2010, 50, 2236–2247. 10.1021/ci100346s. [DOI] [PubMed] [Google Scholar]
- Zeller F.; Zacharias M. Efficient calculation of relative binding free energies by umbrella sampling perturbation. J. Comput. Chem. 2014, 35, 2256–2262. 10.1002/jcc.23744. [DOI] [PubMed] [Google Scholar]
- Efron B. Bootstrap methods: Another look at the Jackknife. Ann. Stat. 1979, 7, 1–26. 10.1214/aos/1176344552. [DOI] [Google Scholar]
- Zhang H.; Yin C.; Jiang Y.; van der Spoel D. Force Field Benchmark of Amino Acids: I. Hydration and Diffusion in Different Water Models. J. Chem. Inf. Model. 2018, 58, 1037–1052. 10.1021/acs.jcim.8b00026. [DOI] [PubMed] [Google Scholar]
- Zhang H.; Jiang Y.; Cui Z.; Yin C. Force Field Benchmark of Amino Acids. 2. Partition Coefficients between Water and Organic Solvents. J. Chem. Inf. Model. 2018, 58, 1669–1681. 10.1021/acs.jcim.8b00493. [DOI] [PubMed] [Google Scholar]
- Ngo S. T.; Mai B. K.; Hiep D. M.; Li M. S. Estimation of the binding free energy of AC1NX476 to HIV-1 protease wild type and mutations using free energy perturbation method. Chem. Biol. Drug. Des. 2015, 86, 546–558. 10.1111/cbdd.12518. [DOI] [PubMed] [Google Scholar]
- Steinbrecher T. B.; Dahlgren M.; Cappel D.; Lin T.; Wang L.; Krilov G.; Abel R.; Friesner R.; Sherman W. Accurate Binding Free Energy Predictions in Fragment Optimization. J. Chem. Inf. Model. 2015, 55, 2411–2420. 10.1021/acs.jcim.5b00538. [DOI] [PubMed] [Google Scholar]
- Tam N. M.; Vu K. B.; Vu V. V.; Ngo S. T. Influence of various force fields in estimating the binding affinity of acetylcholinesterase inhibitors using fast pulling of ligand scheme. Chem. Phys. Lett. 2018, 701, 65–71. 10.1016/j.cplett.2018.04.024. [DOI] [Google Scholar]
- Chen J.; Wang J.; Lai F.; Wang W.; Pang L.; Zhu W. Dynamics revelation of conformational changes and binding modes of heat shock protein 90 induced by inhibitor associations. RSC Adv. 2018, 8, 25456–25467. 10.1039/C8RA05042B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genheden S.; Ryde U. The MM/PBSA and MM/GBSA Methods to Estimate Ligand-Binding Affinities. Expert Opin. Drug Discovery 2015, 10, 449–461. 10.1517/17460441.2015.1032936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weis A.; Katebzadeh K.; Söderhjelm P.; Nilsson I.; Ryde U. Ligand Affinities Predicted with the MM/PBSA Method: Dependence on the Simulation Method and the Force Field. J. Med. Chem. 2006, 49, 6596–6606. 10.1021/jm0608210. [DOI] [PubMed] [Google Scholar]
- Hou T.; Wang J.; Li Y.; Wang W. Assessing the Performance of the MM/PBSA and MM/GBSA Methods. 1. The Accuracy of Binding Free Energy Calculations Based on Molecular Dynamics Simulations. J. Chem. Inf. Model. 2011, 51, 69–82. 10.1021/ci100275a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woo H.-J.; Roux B. Calculation of absolute protein–ligand binding free energy from computer simulations. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 6825–6830. 10.1073/pnas.0409005102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamashita D. S.; Smith W. W.; Zhao B.; Janson C. A.; Tomaszek T. A.; Bossard M. J.; Levy M. A.; Oh H.-J.; Carr T. J.; Thompson S. K.; Ijames C. F.; Carr S. A.; McQueney M.; D’Alessio K. J.; Amegadzie B. Y.; Hanning C. R.; Abdel-Meguid S.; DesJarlais R. L.; Gleason J. G.; Veber D. F. Structure and Design of Potent and Selective Cathepsin K Inhibitors. J. Am. Chem. Soc. 1997, 119, 11351–11352. 10.1021/ja972204u. [DOI] [Google Scholar]
- McGrath M. E.; Klaus J. L.; Barnes M. G.; Brömme D. Crystal structure of human cathepsin K complexed with a potent inhibitor. Nat. Struct. Biol. 1997, 4, 105. 10.1038/nsb0297-105. [DOI] [PubMed] [Google Scholar]
- Marquis R. W.; Ru Y.; LoCastro S. M.; Zeng J.; Yamashita D. S.; Oh H.-J.; Erhard K. F.; Davis L. D.; Tomaszek T. A.; Tew D.; Salyers K.; Proksch J.; Ward K.; Smith B.; Levy M.; Cummings M. D.; Haltiwanger R. C.; Trescher G.; Wang B.; Hemling M. E.; Quinn C. J.; Cheng H. Y.; Lin F.; Smith W. W.; Janson C. A.; Zhao B.; McQueney M. S.; D’Alessio K.; Lee C.-P.; Marzulli A.; Dodds R. A.; Blake S.; James I. E.; Gress C. J.; Bradley B. R.; Lark M. W.; Gowen M.; Veber D. F. Azepanone-Based Inhibitors of Human and Rat Cathepsin K. J. Med. Chem. 2001, 44, 1380–1395. 10.1021/jm000481x. [DOI] [PubMed] [Google Scholar]
- Yamashita D. S.; Marquis R. W.; Xie R.; Nidamarthy S. D.; Oh H.-J.; Jeong J. U.; Erhard K. F.; Ward K. W.; Roethke T. J.; Smith B. R.; Cheng H. Y.; Geng X.; Lin F.; Offen P. H.; Wang B.; Nevins N.; Head M. S.; Haltiwanger R. C.; Narducci Sarjeant A. A.; Liable-Sands L. M.; Zhao B.; Smith W. W.; Janson C. A.; Gao E.; Tomaszek T.; McQueney M.; James I. E.; Gress C. J.; Zembryki D. L.; Lark M. W.; Veber D. F. Structure Activity Relationships of 5-, 6-, and 7-Methyl-Substituted Azepan-3-one Cathepsin K Inhibitors. J. Med. Chem. 2006, 49, 1597–1612. 10.1021/jm050915u. [DOI] [PubMed] [Google Scholar]
- Roszak A. W.; Robinson D. A.; Krell T.; Hunter I. S.; Fredrickson M.; Abell C.; Coggins J. R.; Lapthorn A. J. The Structure and Mechanism of the Type II Dehydroquinase from Streptomyces coelicolor. Structure 2002, 10, 493–503. 10.1016/S0969-2126(02)00747-5. [DOI] [PubMed] [Google Scholar]
- Robinson D. A.; Stewart K. A.; Price N. C.; Chalk P. A.; Coggins J. R.; Lapthorn A. J. Crystal Structures of Helicobacter pylori Type II Dehydroquinase Inhibitor Complexes: New Directions for Inhibitor Design. J. Med. Chem. 2006, 49, 1282–1290. 10.1021/jm0505361. [DOI] [PubMed] [Google Scholar]
- Paz S.; Tizón L.; Otero J. M.; Llamas-Saiz A. L.; Fox G. C.; van Raaij M. J.; Lamb H.; Hawkins A. R.; Lapthorn A. J.; Castedo L.; González-Bello C. Tetrahydrobenzothiophene Derivatives: Conformationally Restricted Inhibitors of Type II Dehydroquinase. ChemMedChem 2011, 6, 266–272. 10.1002/cmdc.201000343. [DOI] [PubMed] [Google Scholar]
- Tizón L.; Otero J. M.; Prazeres V. F. V.; Llamas-Saiz A. L.; Fox G. C.; van Raaij M. J.; Lamb H.; Hawkins A. R.; Ainsa J. A.; Castedo L.; González-Bello C. A Prodrug Approach for Improving Antituberculosis Activity of Potent Mycobacterium tuberculosis Type II Dehydroquinase Inhibitors. J. Med. Chem. 2011, 54, 6063–6084. 10.1021/jm2006063. [DOI] [PubMed] [Google Scholar]
- Lence E.; Tizón L.; Otero J. M.; Peón A.; Prazeres V. F. V.; Llamas-Saiz A. L.; Fox G. C.; van Raaij M. J.; Lamb H.; Hawkins A. R.; González-Bello C. Mechanistic Basis of the Inhibition of Type II Dehydroquinase by (2S)- and (2R)-2-Benzyl-3-dehydroquinic Acids. ACS Chem. Biol. 2013, 8, 568–577. 10.1021/cb300493s. [DOI] [PubMed] [Google Scholar]
- Kung P.-P.; Huang B.; Zhang G.; Zhou J. Z.; Wang J.; Digits J. A.; Skaptason J.; Yamazaki S.; Neul D.; Zientek M.; Elleraas J.; Mehta P.; Yin M.-J.; Hickey M. J.; Gajiwala K. S.; Rodgers C.; Davies J. F.; Gehring M. R. Dihydroxyphenylisoindoline Amides as Orally Bioavailable Inhibitors of the Heat Shock Protein 90 (Hsp90) Molecular Chaperone. J. Med. Chem. 2010, 53, 499–503. 10.1021/jm901209q. [DOI] [PubMed] [Google Scholar]
- Shi J.; Van de Water R.; Hong K.; Lamer R. B.; Weichert K. W.; Sandoval C. M.; Kasibhatla S. R.; Boehm M. F.; Chao J.; Lundgren K.; Timple N.; Lough R.; Ibanez G.; Boykin C.; Burrows F. J.; Kehry M. R.; Yun T. J.; Harning E. K.; Ambrose C.; Thompson J.; Bixler S. A.; Dunah A.; Snodgrass-Belt P.; Arndt J.; Enyedy I. J.; Li P.; Hong V. S.; McKenzie A.; Biamonte M. A. EC144 Is a Potent Inhibitor of the Heat Shock Protein 90. J. Med. Chem. 2012, 55, 7786–7795. 10.1021/jm300810x. [DOI] [PubMed] [Google Scholar]
- Zehnder L.; Bennett M.; Meng J.; Huang B.; Ninkovic S.; Wang F.; Braganza J.; Tatlock J.; Jewell T.; Zhou J. Z.; Burke B.; Wang J.; Maegley K.; Mehta P. P.; Yin M.-J.; Gajiwala K. S.; Hickey M. J.; Yamazaki S.; Smith E.; Kang P.; Sistla A.; Dovalsantos E.; Gehring M. R.; Kania R.; Wythes M.; Kung P.-P. Optimization of Potent, Selective, and Orally Bioavailable Pyrrolodinopyrimidine-Containing Inhibitors of Heat Shock Protein 90. Identification of Development Candidate 2-Amino-4-{4-chloro-2-[2-(4-fluoro-1H-pyrazol-1-yl)ethoxy]-6-methylphenyl}-N-(2,2-difluoropropyl)-5,7-dihydro-6H-pyrrolo[3,4-d]pyrimidine-6-carboxamide. J. Med. Chem. 2011, 54, 3368–3385. 10.1021/jm200128m. [DOI] [PubMed] [Google Scholar]
- Kung P.-P.; Sinnema P.-J.; Richardson P.; Hickey M. J.; Gajiwala K. S.; Wang F.; Huang B.; McClellan G.; Wang J.; Maegley K.; Bergqvist S.; Mehta P. P.; Kania R. Design strategies to target crystallographic waters applied to the Hsp90 molecular chaperone. Bioorg. Med. Chem. Lett. 2011, 21, 3557–3562. 10.1016/j.bmcl.2011.04.130. [DOI] [PubMed] [Google Scholar]
- Maignan S.; Guilloteau J.-P.; Pouzieux S.; Choi-Sledeski Y. M.; Becker M. R.; Klein S. I.; Ewing W. R.; Pauls H. W.; Spada A. P.; Mikol V. Crystal Structures of Human Factor Xa Complexed with Potent Inhibitors. J. Med. Chem. 2000, 43, 3226–3232. 10.1021/jm000940u. [DOI] [PubMed] [Google Scholar]
- Adler M.; Davey D. D.; Phillips G. B.; Kim S.-H.; Jancarik J.; Rumennik G.; Light D. R.; Whitlow M. Preparation, Characterization, and the Crystal Structure of the Inhibitor ZK-807834 (CI-1031) Complexed with Factor Xa. Biochemistry 2000, 39, 12534–12542. 10.1021/bi001477q. [DOI] [PubMed] [Google Scholar]
- Guertin K. R.; Gardner C. J.; Klein S. I.; Zulli A. L.; Czekaj M.; Gong Y.; Spada A. P.; Cheney D. L.; Maignan S.; Guilloteau J.-P.; Brown K. D.; Colussi D. J.; Chu V.; Heran C. L.; Morgan S. R.; Bentley R. G.; Dunwiddie C. T.; Leadley R. J.; Pauls H. W. Optimization of the β-Aminoester class of factor Xa inhibitors. part 2: Identification of FXV673 as a potent and selective inhibitor with excellent In vivo anticoagulant activity. Bioorg. Med. Chem. Lett 2002, 12, 1671–1674. 10.1016/S0960-894X(02)00213-5. [DOI] [PubMed] [Google Scholar]
- Maignan S.; Guilloteau J.-P.; Choi-Sledeski Y. M.; Becker M. R.; Ewing W. R.; Pauls H. W.; Spada A. P.; Mikol V. Molecular Structures of Human Factor Xa Complexed with Ketopiperazine Inhibitors: Preference for a Neutral Group in the S1 Pocket. J. Med. Chem. 2003, 46, 685–690. 10.1021/jm0203837. [DOI] [PubMed] [Google Scholar]
- Senger S.; Convery M. A.; Chan C.; Watson N. S. Arylsulfonamides: A study of the relationship between activity and conformational preferences for a series of factor Xa inhibitors. Bioorg. Med. Chem. Lett. 2006, 16, 5731–5735. 10.1016/j.bmcl.2006.08.092. [DOI] [PubMed] [Google Scholar]
- Chovancova E.; Pavelka A.; Benes P.; Strnad O.; Brezovsky J.; Kozlikova B.; Gora A.; Sustr V.; Klvana M.; Medek P.; Biedermannova L.; Sochor J.; Damborsky J. CAVER 3.0: a tool for the analysis of transport pathways in dynamic protein structures. PLoS Comput. Biol. 2012, 8, e1002708 10.1371/journal.pcbi.1002708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Truong D. T.; Nguyen M. T.; Vu V. V.; Ngo S. T. Fast Pulling of Ligand Approach for the Design of β-Secretase 1 Inhibitors. Chem. Phys. Lett. 2017, 671, 142–146. 10.1016/j.cplett.2017.01.032. [DOI] [Google Scholar]
- Tam N. M.; Nguyen M. T.; Ngo S. T. Evaluation of the absolute affinity of neuraminidase inhibitor using steered molecular dynamics simulations. J. Mol. Graphics Modell. 2017, 77, 137–142. 10.1016/j.jmgm.2017.08.018. [DOI] [PubMed] [Google Scholar]
- Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Aliev A. E.; Kulke M.; Khaneja H. S.; Chudasama V.; Sheppard T. D.; Lanigan R. M. Motional timescale predictions by molecular dynamics simulations: case study using proline and hydroxyproline sidechain dynamics. Proteins: Struct., Funct., Bioinf. 2014, 82, 195–215. 10.1002/prot.24350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Bayly C. I.; Cieplak P.; Cornell W.; Kollman P. A. A Well-Behaved Electrostatic Potential Based Method using Charge Restraints for Deriving Atomic Charges: the RESP Model. J. Phys. Chem. 1993, 97, 10269–10280. 10.1021/j100142a004. [DOI] [Google Scholar]
- Ngo S. T.; Luu X.-C.; Nguyen M. T.; Le C. N.; Vu V. V. In silico studies of solvated F19W amyloid β (11-40) trimer. RSC Adv. 2017, 7, 42379–42386. 10.1039/C7RA07187F. [DOI] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Hub J. S.; de Groot B. L.; van der Spoel D. g_wham—A Free Weighted Histogram Analysis Implementation Including Robust Error and Autocorrelation Estimates. J. Chem. Theory Comput. 2010, 6, 3713–3720. 10.1021/ct100494z. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


