Abstract
The etiology of many complex diseases involves both environmental exposures and inherited genetic predisposition as well as interactions between them. Gene-environment-wide interaction studies (GEWIS) provide a means to identify the interactions between genetic variation and environmental exposures that underlie disease risk. However, current GEWIS methods lack the capability to adjust for the potentially complex correlations in studies with varying degrees of relationships (both known and unknown) among individuals in admixed populations. We developed novel generalized estimating equation (GEE) based methods - GEE-adaptive and GEE-joint - to account for phenotypic correlations due to kinship while accounting for covariates, including measures of genome-wide ancestry. In simulation studies of admixed individuals, both methods controlled family-wise error rates, an advantage over the case-only approach. They demonstrated higher power than traditional case-control methods across a wide range of underlying alternative hypotheses, especially where both marginal and interaction effects were present. We applied the proposed method to conduct a GEWIS of a known sarcoidosis risk factor (insecticide exposure) and risk of sarcoidosis in African Americans and identified two novel loci with suggestive evidence of GxE interaction.
Keywords: gene by environment interaction, Sarcoidosis, GWIS, GEE, admixture
Introduction
The presence of gene-by-environment interactions (GxE) has been confirmed for several traits (Hunter, 2005; Rothman et al., 2010), and gene-environment-wide interaction studies (GEWIS) are considered an important approach to identify GxE (Khoury & Wacholder, 2009; D. Thomas, 2010). For example, insecticide exposure has been previously shown to be associated with sarcoidosis risk both independently (Newman et al., 2004; Rossman et al., 2008) and through G×E (J. Li et al., 2014) in the Ancestry Mapping of African genes of Sarcoidosis Susceptibility (AMASS) study (Rybicki et al., 2011). The AMASS study consists of samples from both unrelated case-control and family-based study designs. Such samples present analytic challenges due to varying degrees of correlation between individuals. In addition to the complexity of genetic relatedness, African Americans are an admixed population, with genetic contributions from two ancestral populations. Therefore, it is also necessary to be able to adequately account for potential differences in population substructure between those with and without the disease in GxE interaction studies. Despite the recent development of methods to improve power to identify GxE interactions, current methods for GEWIS have not adequately addressed the analysis of studies with admixed and related individuals.
Generally, GxE methods have been largely limited to case-control designs of unrelated individuals and motivated by the known low power attributable to modeling the interaction with a multiplicative GxE term in logistic regression (Mukherjee, Ahn, Gruber, & Chatterjee, 2012). The case-only approach (Piegorsch, Weinberg, & Taylor, 1994) can provide substantial improvements in power (Yang, Khoury, & Flanders, 1997), but it can have an unacceptably high false positive rate if the independence assumption between the genetic and environmental factors are violated (Mukherjee et al., 2012). To address these challenges, researchers have proposed different approaches to provide greater power than the conventional methods for a standard case-control study of unrelated individuals, while controlling the type-1 error. These approaches fall into two main groups. The first is the two-step method, which combines both screening and testing steps (Hsu et al., 2012; Kooperberg & LeBlanc, 2008; Murcray, Lewinger, & Gauderman, 2009). This method improves power through the independence between the two-steps and the resulting reduction in the number of GxE tests in the second step. The second is Bayesian that includes empirical Bayes (Mukherjee & Chatterjee, 2008) and Bayes model averaging(Li & Conti, 2009) approaches. However, current methods have not identified optimal GEWIS strategies in studies with varying degrees of relatedness among individuals.
Additionally, it has been well established that differences in population substructure between those with and without a disease can lead to a biased finding in both genetic association (Freedman et al., 2004; Marchini, Cardon, Phillips, & Donnelly, 2004; D. C. Thomas, Haile, & Duggan, 2005) and GxE (Dudbridge & Fletcher, 2014; Sul et al., 2016; Wang, Localio, & Rebbeck, 2006) studies. However, methods for GEWIS with admixed individuals in the presence of familial relationships have largely not been developed. To test for genetic association while accounting for the relatedness in families, several methods exist that employ generalized estimating equation (GEE) or mixed effect models. Wang et al. (2013) developed the GEE–based–kernel association (GSKAT) test with a working covariance matrix that reflects the cluster dependencies within known pedigree structures(Wang, Lee, Zhu, Redline, & Lin, 2013). Lin et al. (2014) proposed a weighted version of GEE (W-PS), to account for unequal inclusion probabilities and family relationships(Lin et al., 2014). The generalized mixed model association test (GMMAT)(Chen et al., 2016) utilized logistic mixed models which can properly account for the sample relatedness and population structure. Zhou et al. (2018) provided a more accurate p-value calculation to control for case-control imbalance using the saddlepoint approximation method on the score statistic (SAIGE)(Zhou et al., 2018). However, these methods have not been extended for testing GxE interactions. Previously, we (Li et al., 2014) developed an extended generalized least squares (GLX) approach by incorporating empirical kinship in the covariance matrix to perform GEWIS of individuals with varying degrees of relatedness. However, this method was intended for categorical data and cannot adjust for other continuous covariates, including genetic ancestry. To address these additional complexities, we developed two strategies utilizing GEEbased methods for GEWIS, GEE-adaptive and GEE-joint. These methods integrate the p-values for testing marginal genetic and/or GxE interaction effects sequentially or simultaneously. These GEE models use the empirical kinship matrix to account for correlation between known or cryptically related individuals and allow for adjustment for population substructure that may bias GxE estimates in admixed populations. We first detail the theoretical development of the GEE-adaptive and GEE-joint methods. We also present simulation results comparing findings from these extended methods with those from the GEE model using standard case-control and case-only analysis approaches. Finally, we apply the proposed methods to genetic and environmental data from combined family and case-control studies of sarcoidosis (Rybicki et al., 2011).
Methods
Conceptual Models
Figure 1 shows several conceptual models for the interaction of genetic and environmental factors to demonstrate the rationale of our proposed methods. Figure 1A – 1C identify scenarios where carrying a particular genotype is associated with a higher trait value. The scenario in Figure 1A indicates that both genetic and environmental main effects exist, but there is no interaction between them. On the other hand, a quantitative interaction is depicted in Figures 1B and 1C. Figures 1D and 1E represent opposite genetic effects in the context of environmental exposures. However, the scenario in Figure 1D demonstrates underlying marginal effects while the scenario in Figure 1E does not. These five GxE interaction scenarios represent a wide range of possible GxE. Genetic variants or single-nucleotide polymorphisms (SNPs) with an interaction effect and/or a marginal effect are of particular interest for the GxE analysis. Therefore, we propose GEE-adaptive and GEE-joint methods to determine SNPs that have a marginal effect, an interaction effect with an environmental exposure, or both.
Figure 1:
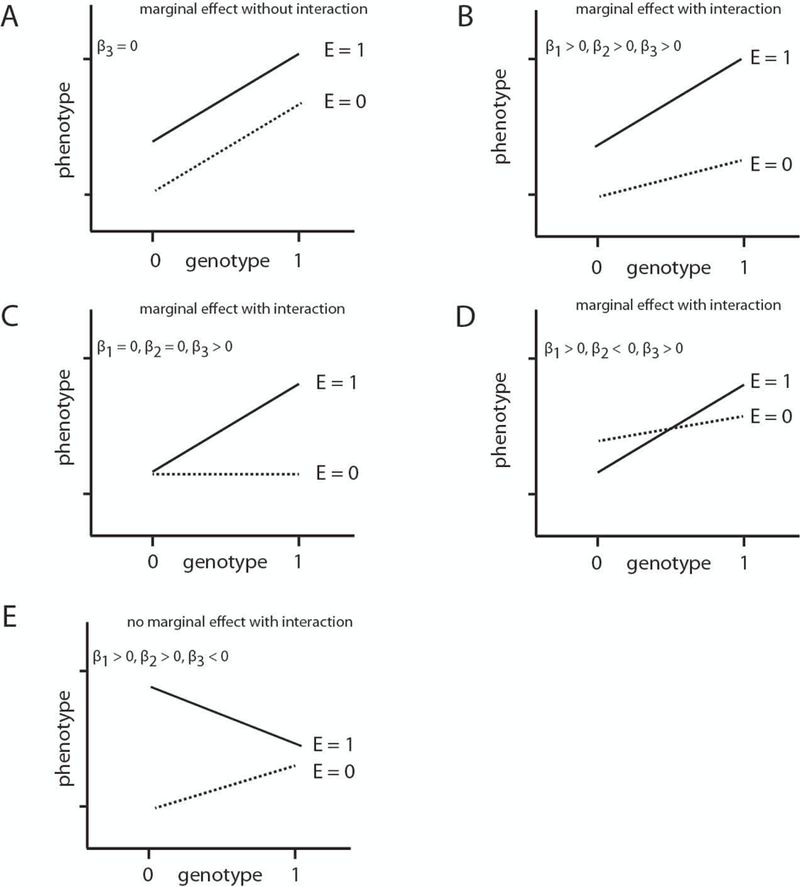
Five conceptual models of gene-environment interactions: (A) genetic marginal effects, but no GxE interaction; (B-D), marginal effects and GxE interaction; (E) no marginal effect for gene but GxE interaction exists. β1, β2, β3 are as shown in model (2), where β1 is the main effect for genetic factors, β2 is the main effect for environmental factors and β3 stands for interaction effects of the two.
General Model Notation
To model GxE interactions in studies containing familial relationships, a modeling framework is arranged where j and i indicate the jth individual in the ith family, and q is the total sample size. Different matrices are then set up for the phenotype , genetic variant , environmental variable , and q×1 vector of confounding variables . Yij is a binary phenotype for each sample, is the genotype of a SNP in a sample (coded as additive, dominant, or recessive), and is the environmental exposure, either binary or continuous measures. To detect a GxE effect, the following two logistic regression models for a given SNP are considered:
| (1) |
where is the population mean and is the marginal effect of G, and
| (2) |
where is the population mean, is the additive effect for a SNP, is the environmental main effect, and is the interaction effect between and The parameters and are estimated by GEE:
| (3) |
where is the total number of families, and , and is the working covariance matrix of . can be expressed in terms of a working correlation matrix , where is a diagonal marginal variance matrix, and accounts for relatedness between individuals. can be further parameterized into , where is the empirical kinship between individuals j and s in the ith family, and is a scale parameter. The empirical kinship is calculated using the genome-wide SNP genotype data and has been shown to be robust in the estimation of relatedness for both family-based studies and in structured populations with genetic contributions from two or more ancestral populations (Manichaikul et al., 2010; Thornton et al., 2012). The covariance matrix of can be estimated by a “sandwich estimator” (Huber, 1967):
| (4) |
The quantity of from model (2) is the natural logarithm of the GxE interaction odds ratio (OR). Testing the null hypothesis for each SNP is a common practice to test GxE effects; however, this approach suffers from low power in the context of GEWIS (Mukherjee et al., 2012). We propose two additional methods based on models (1) and (2): GEE-adaptive and GEE-joint. Let represent the p-value for testing and indicates the p-value for testing
GEE-adaptive
The GEE-adaptive method consists of two steps. In Step 1, is used at a significance level to screen genetic associations with the outcome. In Step 2, is utilized for the subset of SNPs advancing from Step 1, with a Bonferroni-corrected significance level of , as proposed by Kooperberg and LeBlanc (Kooperberg & LeBlanc, 2008).
Assuming that the working correlation matrix is correctly specified, and can be shown to be asymptotically independent (see Appendix). Therefore, for the proposed method, the theorem presented by Dai et al (Dai, Kooperberg, Leblanc, & Prentice, 2012) guarantees control of the family-wise type I error. If the correlation is misspecified, will not be asymptotically independent of In simulation studies, this dependence between and is sufficiently small that the proposed adaptive method reasonably controlled the family-wise error rate (FWER).
GEE-joint
In contrast, GEE-joint combines both and to derive a joint test statistic: Assuming the independence of these p-values, the test statistic T follows a Chi-square distribution with four degrees of freedom under the null hypothesis of no marginal and no interaction effects. In reality, the statistics are not independent, and the test based on the Chi-square distribution with four degrees of freedom tends to be liberal. Brown (Brown, 1975) and Yang (Yang, 2010) have shown that if these p-values are correlated, the distribution of the T statistic approximates a gamma distribution with the shape parameter and the scale parameter under the null hypothesis. Yang et al. (Yang, Li, Williams, & Buu, 2016) further extended the statistic to a two-sided test for testing pleiotropic effects. For the proposed GEE-joint test, the statistic follows a gamma distribution with a mean of 4 and a variance of , where is a function of the correlation between and Therefore, it can be approximated by a tenth-order polynomial of is estimated by the bias-corrected sample correlation between and (Yang et al., 2016).
Note that rejecting the null hypothesis indicates a marginal and/or an interaction effect. As indicated in Figure 1, some of the interaction effects are accompanied by a marginal gene effect. The test is more powerful than testing the interaction effect alone when the marginal effect is present. The individual p-values, and , can be parsed out of the T test statistic to separate out marginal gene and GxE effects.
Simulation Studies
The FWER and power of the proposed estimators were evaluated in simulated pedigrees with simple and complex structures to mimic the AMASS study (Rybicki et al., 2011) and the Framingham Heart Study (Govindaraju et al., 2008), respectively. For the simple pedigrees, we simulated 1,877 individuals. A total of 1,283 individuals were part of 475 pedigrees that comprised 277 sibships, from size two to six. The remaining 594 individuals were singleton cases and controls. For the complex pedigree structure, we randomly generated 570 families of differing size and number of generations and singletons, with the largest family size of 15 individuals with pedigree sizes ranging from 2 to 296 individuals.
Using each pedigree structure, we simulated 1,000 datasets of genotype “G” data through gene dropping from simulated admixed founders, varying the minor allele frequency from 0.1 to 0.5. Admixed founders were simulated based on the Balding-Nichols model (Balding & Nichols, 2008) with two admixed populations. The ancestral minor allele frequency at a SNP, , followed a uniform distribution from 0.1 to 0.5. The allele frequency of SNPs in subpopulation is denoted as and:
| (5) |
where fK can be treated as Wright’s standardized measure of variation (Weir & Cockerham, 1984) and set at 0.01. The ancestral proportion for an admixed individual j is , where The expected allele frequency at SNPs of admixed individual j is:
| (6) |
Each dataset consisted of 10,000 SNPs (M=10,000) in linkage equilibrium and assumed to be evenly distributed across the genome. For each dataset, a single SNP was chosen to be a disease locus interacting with E, with a minor allele frequency of 0.3. The probability of each SNP associated with E at the population level was denoted as and the simulated values were 0.0001, 0.001 and 0.01. The environmental exposure of individual j in family was generated by where is a SNP for individual j that is associated with represents the natural logarithm of the OR for the association of each SNP with E, which was randomly generated from the Beta distribution. To allow for correlation between phenotypes within each family, is a random family effect that follows a multivariate normal distribution where the elements of denote the correlation coefficient between individuals in family . Dichotomous E were then generated from the Bernoulli distribution with probability . The phenotype of individual j in family has the following linear relationship to underlying genetic () and environmental (E) factors,
where is the population mean, is the additive effect for a SNP, is the environmental main effect, and is the interaction effect between and . Dichotomous phenotypes were generated from the Bernoulli distribution with . The baseline disease prevalence and the exposure prevalence for , pe, were both set at 10%. Finally, three possible values for , and corresponding to GxE scenarios in Figure 1 were considered. First, , and were set to 0, 0, and log (3), respectively, yielding an OR of 1 for the genetic main effect, 1 for the environmental main effect, and 3 for the interaction effect (i.e. Figure 1C). Second,, and were set to log (1.5), log (1.5), and log (3), respectively, resulting in an OR of 1.5 for the genetic main effect, 1.5 for the environmental main effect and 3 for the interaction effect (i.e. Figure 1B). Third, , and were set to log (2), log (1.5), and log (0.25), respectively, resulting in an OR of 2 for the genetic main effect, 1.5 for the environmental main effect and 0.25 for the interaction effect (i.e. Figure 1E).
The GEE-adaptive and GEE-joint were compared to the standard practice of testing using model (3) on cases and controls, namely the GEE-case-control (GEE-CC). The nominal FWER was set at 0.05 and 0.01 respectively. For GEE-joint, when assuming the independence between and the T statistic under a Chi-square distribution with four degrees of freedom (GEE-joint-chisq) was utilized, and when assuming the dependence between and , a Gamma distribution with shape parameter of 4 and scale parameter equal to (GEE-joint-gamma) was used. The strategy using a case-only analysis (GEE-CO) was examined where the interaction effect is identified by fitting the logistic regression model: on cases. Based on the simulated data, empirical kinship coefficients were calculated using KING (Manichaikul et al., 2010).
Application to the AMASS Sarcoidosis Study
To evaluate the utilization of the proposed methods in a real dataset, a GEWIS was performed using the insecticide exposure variable and GWAS autosomal data available for the AMASS study comprising 1073 African-American sarcoidosis cases and 804 controls collected from family and unrelated case-control studies (Rybicki et al., 2011). Genotyping was conducted using the Illumina Human Omni1-Quad for 1.1 million SNPs across the genome as described in Adrianto et al. (Adrianto et al., 2012). The final SNP dataset consisted of 887,296 autosomal SNPs after applying quality control measures. The first two principal components of genetic data (calculated using EIGENSOFT 3.0 (Galinsky et al., 2016)) and sex were included as covariates in the GEWIS analysis.
Results
Simulation Results
Figure 2 displays the FWER for each of the four methods tested on the nine simulation settings based on both the simple and complex pedigree structures. For the simple structure, the FWER of GEE-CO method (FWERCO) increased dramatically as the proportion of SNPs associated with E () increased, and the FWERCO were severely inflated, with the exception of the lowest of 10−4 (Figure 2A). The FWER of GEE-CC (FWERCC), GEE-adaptive (FWERadaptive), and GEE-joint (FWERjoint-chisq and FWERjoint-gamma) methods were similar and controlled near the nominal level of 0.05 (Figure 2A). For simulations based on the complex structure with larger pedigrees (Figure 2B), FWER displayed a similar pattern across methods and simulation conditions as that of the simple structure.
Figure 2:
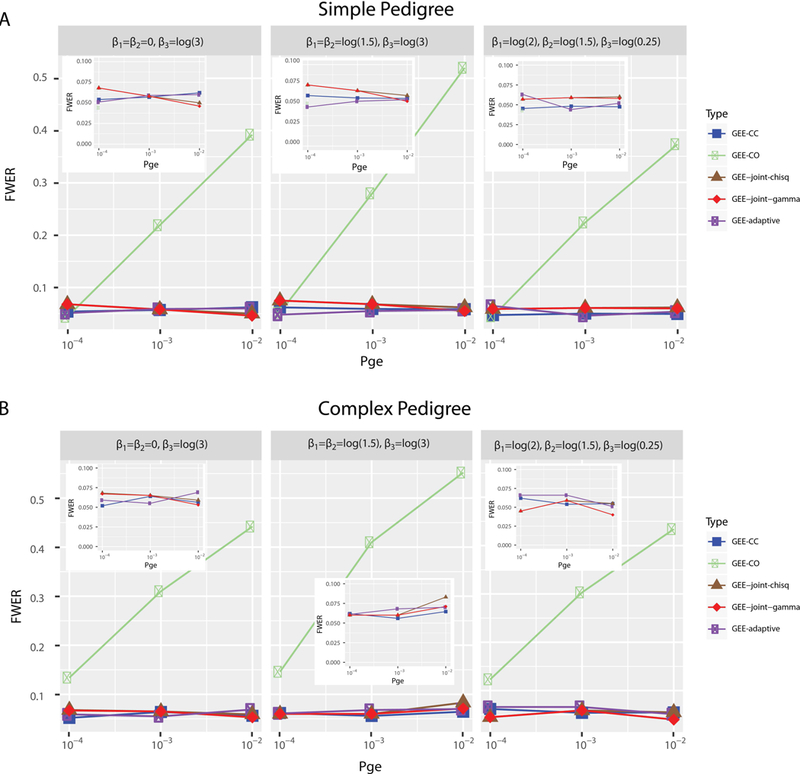
Family-wise error rate (FWER) from simulation results. (A) for simple pedigree structure simulations and (B) for complex pedigree structure simulations. Y-axis represents FWER and x-axis shows the probability of SNPs associated with environment (Pge) in simulation. The simulation parameters are listed on top of each panel. Left panel: β1 = β2 = 0, and β3 = log(3); middle panel: β1 = β2 = log(1.5), and β3 = log(3); β1 = log(2), β2 = log(1.5), and β3 = log(0.25). Five methods are tested: GEE-CC, GEE-CO, GEE-joint-chisq, GEE-joint-gamma, and GEE-adaptive. The insert plots are zoom-in on the FWER range of 0 to 0.1.
Figure 3 shows the corresponding power from the nine simulations shown. The left and middle panels in Figures 3A and B resembled the conceptual models with both marginal and interaction effects in Figures 1B and C, respectively. The right panel in Figures 3A and B represented the conceptual model without marginal but with interaction effects in Figure 1E. Both GEE-joint-chisq and GEE-joint-gamma demonstrated consistently high power across all simulations. When a moderate marginal effect was present (Figure 3A, left and middle panels), the power of GEE-joint-chisq and GEE-joint-gamma increased and were the highest of all four methods tested. GEE-adaptive demonstrated superior power over GEE-CC when there was a marginal effect (Figure 3A, left and middle panels). When there was a GxE effect without a marginal effect (Figure 3A, right panel), GEE-CC showed superior power to GEE-joint. GEE-joint tends to be more powerful relative to the other methods when the probability of each SNP associated with the environmental factor is higher. As SNPs with small marginal effects were filtered at the first step of GEE-adaptive, GEE-adaptive had lower power compared to GEE-CC as expected. In this scenario, GEE-CO had the lowest power. The patterns of the power estimates of the four methods in the complex structure (Figure 3B) were similar to those observed in the simple structure.
Figure 3:
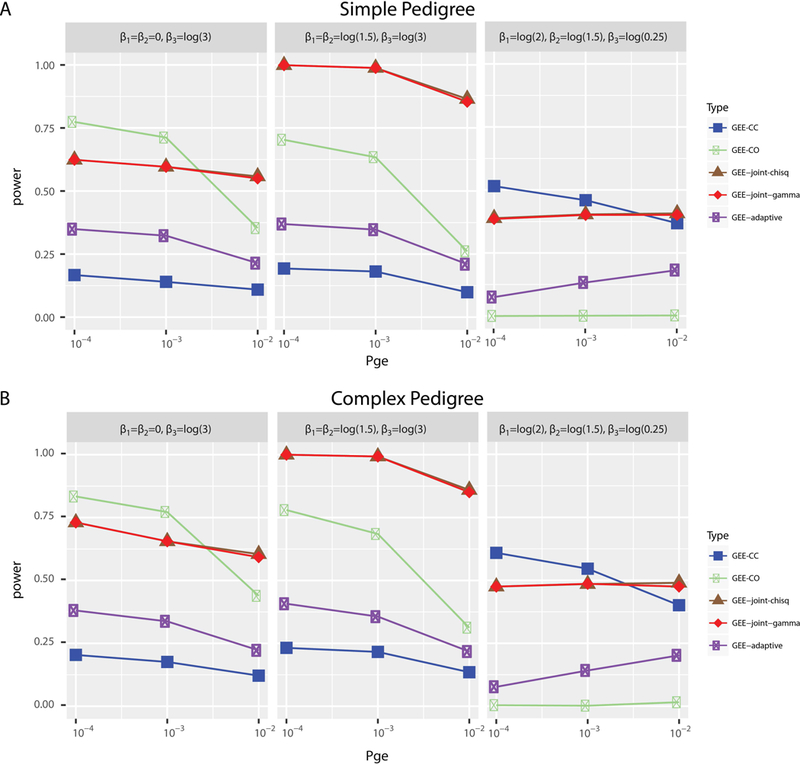
Power from simulation results. (A) for simple pedigree structure simulations and (B) for complex pedigree structure simulations. The plots are arranged in the same order as in Figure 2 for easy comparison.
Sarcoidosis insecticide GEWIS application
For GEE-adaptive, 43,131 SNPs passed Step 1 significance level α1 of 0.05. There was no indication of an inflated type-1 error as suggested by quantile-quantile plot for both GEE-adaptive (Supplemental Figure S1) and GEE-joint-gamma (Figure 4A). No SNP associations passed the step2 significance threshold (0.05/43,131 = 1.16*10−6) in GEE-adaptive (Supplemental Figure S1). Further, no GEE-joint-gamma tests reached genome-wide significance (p-value less than 5×10−8 - Figure 4B).
Figure 4:
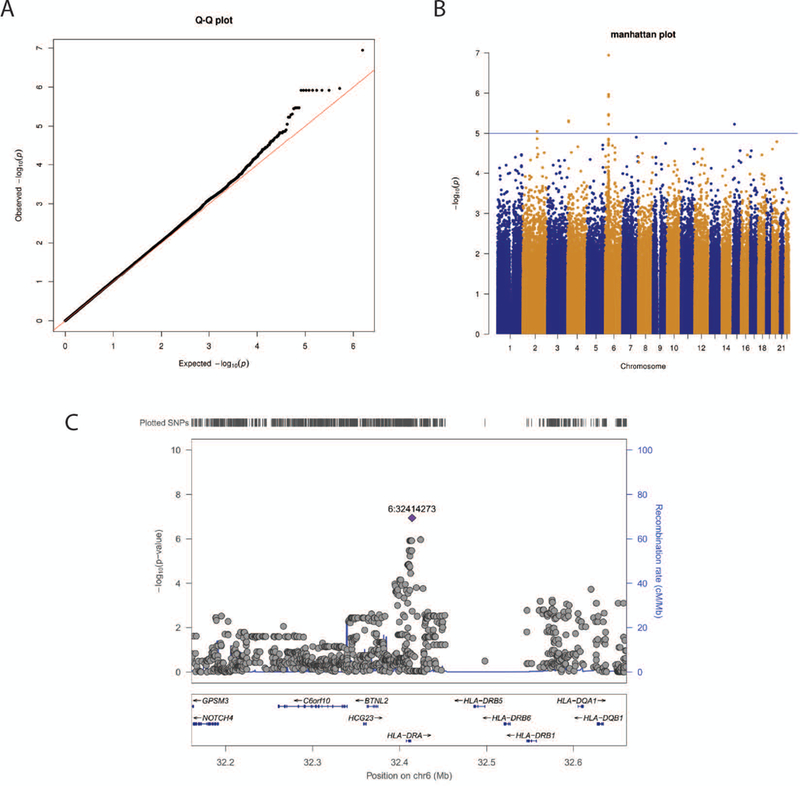
The SNP and insecticide interaction scan using genotyped AMASS data using GEE-joint-gamma method. (a) QQ plot of p-values from the joint test. (b) the Manhattan plot of p-values across autosomes, where the suggestive significance line is drawn at p value of 10−5. (c) LocusZoom plot of the peak region on chromosome 6 as identified in Manhattan plot. Each SNP is represented by a circle except the lead variant as diamond and labeled as chr:position in hg19.
Nineteen SNPs from GEE-joint-gamma reached a suggestive level of association (p-value < 1*10−5) and are displayed in Table 1. The corresponding and values provide a convenient basis to categorize identified SNPs into the following three categories: category 1 SNPs are those with a significant (p<0.05) marginal effect but without significant interaction with insecticide exposure; category 2 SNPs are those with both a significant marginal effect and interaction with insecticide exposure; and category 3 SNPs have a significant interaction effect with insecticide exposure without a significant marginal effect. Using these categories, twelve of the 19 SNPs identified by GEE-joint-gamma had marginal effects without a significant interaction(Category 1); seven SNPs had both marginal and interaction effects (Category 2); and no SNPs were found for Category 3. Category 2 and 3 SNPs were of particular interest for this analysis. Of the seven Category 2 SNPs, Six were located on chromosome 6, clustered closely in the human leukocyte antigen (HLA) region, either around or within HLA-DRA. Among these six, SNP rs3129890 had the most significant GEE-joint-gamma test (iOR =1.62, 95% CI: 1.06 – 2.49). Among those exposed to insecticides, the effect of the SNP was higher (OR=2.32, 95%CI 1.61 – 3.36) relative to the unexposed (OR=1.43, 95%CI 1.15 – 1.79). The effects of the remaining five SNPs in the region reflected these same iOR and stratum specific ORs, likely due to their moderate to high linkage disequilibrium with SNP rs3129890 (r2>0.33; Table 1). The SNP rs1347729 on chromosome 2 was the only Category 2 SNP with an interaction OR (iOR) less than 1 (iOR = 0.56, 95% CI: 0.35 – 0.90), where insecticide exposure leads to a larger reduction in sarcoidosis risk for individuals carrying the minor allele (unexposed OR 0.75, 95% CI: 0.58 – 0.96; exposed OR 0.42, 95% CI: 0.28 – 0.63). No genes were found close to rs1347729; with the closest genes, LRP1B, NXPH2, and SPOPL about 1 Mb away (Supplemental Figure S2). At the cutoff of 5*10−5, we found additional 68 SNPs (Supplemental Table S1). The SNPs rs10499003 and rs7745248 in gene FUT9 that have interaction effects alone have been identified and discussed in our previous study (Li et al., 2014). As these two markers have low marginal effects and moderate interaction effects, they are ranked lower compared to those with both moderate marginal effects and low interaction effects in general using the GEE-joint method.
Table1:
Suggestive level associations of SNP-insecticide interaction with sarcoidosis risk in AMASS study.
| SNP | CHR | BP | MAF | Alleles (mino/maj) |
Pmarginal | Pinteraction | PGEEjoint | Category | Interaction | Insecticide Exposure | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Unexposed | Exposed | |||||||||||||
| OR | 95% CI | OR | 95% CI | OR | 95% CI | |||||||||
| rs1347729 | 2 | 140323265 | 0.110 | A/C | 3.26*10−5 | 0.018 | 8.94*10−6 | 2 | 0.559 | 0.345 – 0.904 | 0.746 | 0.579 – 0.961 | 0.417 | 0.277 – 0.627 |
| rs7660096 | 4 | 10903005 | 0.176 | G/A | 4.17*10−7 | 0.773 | 5.13*10−6 | 1 | 1.069 | 0.678 – 1.686 | 1.632 | 1.298 – 2.053 | 1.745 | 1.181 – 2.580 |
| rs2904192 | 4 | 10904684 | 0.175 | G/T | 3.37*10−7 | 0.910 | 4.89*10−6 | 1 | 1.027 | 0.650 – 1.621 | 1.662 | 1.320 – 2.092 | 1.706 | 1.154 – 2.524 |
| rs2227139* | 6 | 32413459 | 0.478 | G/A | 1.26*10−6 | 0.053 | 1.21*10−6 | 1 | 1.561 | 0.994 – 2.451 | 1.445 | 1.141 – 1.829 | 2.256 | 1.539 – 3.305 |
| rs9268668 | 6 | 32413889 | 0.427 | C/A | 3.84*10−6 | 0.053 | 3.41*10−6 | 1 | 1.522 | 0.995 – 2.327 | 1.378 | 1.107 – 1.715 | 2.097 | 1.460 – 3.011 |
| rs3129890* | 6 | 32414273 | 0.431 | C/T | 2.01*10−7 | 0.027 | 1.14*10−7 | 2 | 1.622 | 1.056 – 2.493 | 1.432 | 1.149 – 1.785 | 2.324 | 1.606 – 3.362 |
| rs7180475 | 15 | 36701276 | 0.056 | T/C | 2.28*10−6 | 0.162 | 5.91*10−6 | 1 | 0.636 | 0.338 – 1.199 | 0.602 | 0.443 – 0.818 | 0.383 | 0.224 – 0.655 |
category 2 SNPs rs8084 (r2 = 0.64), rs9268659 (r2 = 0.64), rs2239802 (r2 = 0.33), rs7196 (r2 = 0.33) and rs7776297 (r2 = 0.47) are in close linkage disequilibrium (LD) with rs3129890. Similarly, rs7192 (r2 = 0.997), rs4935354 (r2 = 0.998), rs7195 (r2 = 1), rs2213586 (r2 = 1), rs2213585 (r2 = 1), rs2213584 (r2 = 1) and rs3763327 (r2 = 0.987) are in close LD with rs2227139.
Discussion
Strategies for efficient analyses in GEWIS in the context of data containing related individuals from admixed populations is an understudied area. We developed two GEE-based methods – GEE-joint and GEE-adaptive – to assess the association between disease and GxE interactions while accounting for correlations among related and admixed individuals. To our knowledge, this is the first systematic investigation in this area. Our methods can robustly identify GxE with different combinations of marginal and interaction effects. The GEE-joint and GEE-adaptive methods are also flexible as many response functions under varying model assumptions can be used, and covariates can be included in the model. Using data from simulations and a previously reported sarcoidosis study (Adrianto et al., 2012), we demonstrate their improved performance over traditional case-control and case-only GxE analyses. We also compared GEE-joint with the 2 degrees of freedom test (2DF) which jointly test the main effects of gene and the GxE interaction in model (2) (Kraft, Yen, Stram, Morrison, & Gauderman, 2007) using simulations based on complex pedigree structures. Both tests have similar power. The advantage of the proposed GEE-joint test is that it provides a more flexible and meaningful interpretation of the findings, because the test combines GWAS and GEWIS simultaneously.
The GEE-joint and GEE-adaptive methods were written in C++ using the linear algebra library Armadillo (Sanderson & Curtin, 2016) and integrated into the R programming language through RCPP package (Eddelbuettel & Francois, 2011). The C++ implementation makes the program more computationally efficient. When utilizing 40 threads of a Linux node equipped with 12 CPUs (the Intel(R) Xeon(R) CPU E5–2695 v2 @ 2.40GHz) and 256 GB of random access memory, it took less than 1 hour to finish scans on 1 million SNPs for the sarcoidosis dataset.
In the sarcoidosis study, the most significant GEE-joint test in the GEWIS of insecticide exposure and sarcoidosis risk in African Americans was SNP rs3129890, located within the HLA class II region on chromosome 6. Consistent with its strong marginal genetic effect, SNP rs3129890 is in high linkage disequilibrium (r2=0.78) in African Americans with SNP rs2227139, which was identified in our previously published GWAS of sarcoidosis risk in African Americans (Adrianto et al., 2012). Further, SNP rs2227139 shows a similar GxE effect as rs3129890 (Table 1), with the minor allele associated with higher risk of sarcoidosis in those individuals reporting insecticide exposure relative to those who did not. SNP rs2227139 has been identified as a cis-acting expression quantitative trait locus (eQTL) in lymphoblastoid cells for multiple HLA class II genes including HLA-DRB1, -DQB1, -DQA1, -DRB5, and -DRA (Houldcroft et al., 2014). Alleles in these genes have been associated with risk of sarcoidosis and are thought to mechanistically alter risk through antigen presentation to CD4+ T-cells. In the Genotype-Tissue Expression (GTEx) project (Consortium, 2013), SNP rs2227139 has also been implicated as a cross-tissue eQTL for HLA class II genes (www.gtexportal.org).
The validity of this sarcoidosis risk associated GxE effect between SNP rs2227139 and insecticide exposure is supported by a similar, recent finding in Parkinson’s disease (PD). Similar to the sarcoidosis data above, SNP rs3129882 in HLA-DRA has been associated with increased risk of PD in multiple GWAS studies (Hamza et al., 2010; Wissemann et al., 2013), and PD-associated risk of rs3129882 appears to be mediated by its function as an eQTL for HLA class II genes. Further, a recent study by Kannarkat et al. also described that the association between SNP rs3129882 and PD risk was dependent upon insecticide exposure, with increased risk associated with the minor “G” allele restricted to those exposed to the insecticide pyrethroid (Kannarkat et al., 2015). While the PD risk SNP rs3129882 is in low linkage disequilibrium (r2=0.18 in the African Americans from the Southwest 1000 genomes subjects) with the sarcoidosis risk SNP rs2227139, the SNP-by-insecticide interactions are remarkably similar across the two diseases, and both appear to function through a broad effect on the expression of multiple HLA class II genes. Taken together with this parallel finding in PD, this sarcoidosis GxE finding is provocative and requires further study within African Americans, a population with a nearly four-fold higher risk of disease in comparison to European Americans (Rybicki, Major, Popovich, Maliarik, & Iannuzzi, 1997).
As with any analytic method, limitations exist which could be addressed by future extensions. First, the GEE-joint test has limited power when there is no marginal effect. The joint test is the Fisher’s combination of p-values, which has been shown to be admissible, providing good power for a wide range of alternative hypotheses (Li & Tseng, 2011). Furthermore, in this study, we used individual p-values (pmarginal and pinteraction) to group the detected markers into three categories (Category 1: SNPs with significant marginal effect but insignificant interaction effect; Category 2: SNPs with both significant marginal and interaction effect; and Category 3: SNPs with insignificant marginal effect but significant interaction effect). In future work, we intend to extend the adaptive weighted method developed by Li et al. (Li & Tseng, 2011) to address these restrictions. Second, as with other 2-step approaches developed for independent samples, the choice of the first step threshold in GEE-adaptive can impact its power. In general, GEE-adaptive is preferred over GEE-CC and GEE-CO. However, GEE-adaptive suffers from low power if the gene has no marginal effect. The hybrid strategy proposed by Murcray et al. (2011) may be adapted to improve upon the current method in the absence of marginal effects. Finally, our proposed method may be extended for gene-set based testing summary measures of multiple SNPs with subtle effects by taking into account the linkage disequilibrium among them (Wang et al., 2013). Through differential weighting, this extension could accommodate additional known functional data, including tissue-specific expression quantitative trait loci information from resources such as GTEx (Consortium, 2013).
In conclusion, recent methods to improve power for GEWIS have focused primarily on studies of unrelated individuals. The methods we have developed add to the GEWIS approaches available for the analysis of data from studies containing known and unknown relationships of any degree, while allowing for the inclusion of potential confounding variables including genetic ancestry. Further, the GEE framework upon which these methods are based also open the possibility of extension to other outcomes, including time-to-event and longitudinal analyses. The R code for GEE-adaptive and GEE-joint is available on GitHub https://github.com/ndtkinesin/GxE_GEEKin_Joint).
Supplementary Material
Acknowledgments
This work was supported by R21-HL129023–01 (AML); R56-AI072727, R01-HL092576 (BAR); R01-HL54306, U01-HL060263(MCI); 1RC2HL101499, R01HL113326 (CGM); P20GM103456 (IA).
References
- Adrianto I, Lin CP, Hale JJ, Levin AM, Datta I, Parker R, … Montgomery CG (2012). Genome-wide association study of African and European Americans implicates multiple shared and ethnic specific loci in sarcoidosis susceptibility. PLoS One, 7(8), e43907. doi:10.1371/journal.pone.0043907 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balding DJ, & Nichols RA (2008). A method for quantifying differentiation between populations at multi-allelic loci and its implications for investigating identity and paternity (vol 96, pg 3, 1995). Genetica, 133(1), 107–107. doi:10.1007/s10709–007-9181–2 [DOI] [PubMed] [Google Scholar]
- Brown MB (1975). 400: A Method for Combining Non-Independent, One-Sided Tests of Significance. Biometrics, 31(4), 987–992. doi:10.2307/2529826 [Google Scholar]
- Chen H, Wang C, Conomos MP, Stilp AM, Li Z, Sofer T, … Lin X (2016). Control for Population Structure and Relatedness for Binary Traits in Genetic Association Studies via Logistic Mixed Models. Am J Hum Genet, 98(4), 653–666. doi:10.1016/j.ajhg.2016.02.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Consortium GT (2013). The Genotype-Tissue Expression (GTEx) project. Nat Genet, 45(6), 580–585. doi:10.1038/ng.2653 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai JY, Kooperberg C, Leblanc M, & Prentice RL (2012). Two-stage testing procedures with independent filtering for genome-wide gene-environment interaction. Biometrika, 99(4), 929–944. doi:10.1093/biomet/ass044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudbridge F, & Fletcher O (2014). Gene-Environment Dependence Creates Spurious Gene-Environment Interaction. American Journal of Human Genetics, 95(3), 301–307. doi:10.1016/j.ajhg.2014.07.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eddelbuettel D, & Francois R (2011). Rcpp: Seamless R and C++ Integration. 2011, 40(8), 18. doi:10.18637/jss.v040.i08 [Google Scholar]
- Freedman ML, Reich D, Penney KL, McDonald GJ, Mignault AA, Patterson N, … Altshuler D (2004). Assessing the impact of population stratification on genetic association studies. Nature Genetics, 36(4), 388–393. doi:10.1038/ng1333 [DOI] [PubMed] [Google Scholar]
- Galinsky KJ, Bhatia G, Loh PR, Georgiev S, Mukherjee S, Patterson NJ, & Price AL (2016). Fast Principal-Component Analysis Reveals Convergent Evolution of ADH1B in Europe and East Asia. American Journal of Human Genetics, 98(3), 456–472. doi:10.1016/j.ajhg.2015.12.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Govindaraju DR, Cupples LA, Kannel WB, O’Donnell CJ, Atwood LD, D’Agostino RB, … Benjamin EJ (2008). Genetics of the Framingham Heart Study Population. Advances in Genetics, Vol 62, 62, 33–65. doi:10.1016/S0065–2660(08)00602–0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamza TH, Zabetian CP, Tenesa A, Laederach A, Montimurro J, Yearout D, … Payami H (2010). Common genetic variation in the HLA region is associated with late-onset sporadic Parkinson’s disease. Nat Genet, 42(9), 781–785. doi:10.1038/ng.642 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houldcroft CJ, Petrova V, Liu JZ, Frampton D, Anderson CA, Gall A, & Kellam P (2014). Host genetic variants and gene expression patterns associated with Epstein-Barr virus copy number in lymphoblastoid cell lines. PLoS One, 9(10), e108384. doi:10.1371/journal.pone.0108384 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu L, Jiao S, Dai JY, Hutter C, Peters U, & Kooperberg C (2012). Powerful Cocktail Methods for Detecting Genome-Wide Gene-Environment Interaction. Genetic Epidemiology, 36(3), 183–194. doi:10.1002/gepi.21610 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber PJ (1967, 1967). The behavior of maximum likelihood estimates under nonstandard conditions. Paper presented at the Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics, Berkeley, Calif. [Google Scholar]
- Hunter DJ (2005). Gene-environment interactions in human diseases. Nat Rev Genet, 6(4), 287–298. doi:10.1038/nrg1578 [DOI] [PubMed] [Google Scholar]
- Kannarkat GT, Cook DA, Lee JK, Chang J, Chung J, Sandy E, … Tansey MG (2015). Common Genetic Variant Association with Altered HLA Expression, Synergy with Pyrethroid Exposure, and Risk for Parkinson’s Disease: An Observational and Case-Control Study. NPJ Parkinsons Dis, 1. doi:10.1038/npjparkd.2015.2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khoury MJ, & Wacholder S (2009). Invited commentary: from genome-wide association studies to gene-environment-wide interaction studies--challenges and opportunities. Am J Epidemiol, 169(2), 227–230; discussion 234–225. doi:10.1093/aje/kwn351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kooperberg C, & LeBlanc M (2008). Increasing the power of identifying gene x gene interactions in genome-wide association studies. Genetic Epidemiology, 32(3), 255–263. doi:10.1002/gepi.20300 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraft P, Yen YC, Stram DO, Morrison J, & Gauderman WJ (2007). Exploiting gene-environment interaction to detect genetic associations. Human Heredity, 63(2), 111–119. doi:10.1159/000099183 [DOI] [PubMed] [Google Scholar]
- Li DL, & Conti DV (2009). Detecting Gene-Environment Interactions Using a Combined Case-Only and Case-Control Approach. American Journal of Epidemiology, 169(4), 497–504. doi:10.1093/aje/kwn339 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, & Tseng GC (2011). An Adaptively Weighted Statistic for Detecting Differential Gene Expression When Combining Multiple Transcriptomic Studies. Annals of Applied Statistics, 5(2a), 994–1019. doi:10.1214/10-Aoas393 [Google Scholar]
- Li J, Yang J, Levin AM, Montgomery CG, Datta I, Trudeau S, … Rybicki BA (2014). Efficient generalized least squares method for mixed population and family-based samples in genome-wide association studies. Genet Epidemiol, 38(5), 430–438. doi:10.1002/gepi.21811 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin DY, Tao R, Kalsbeek WD, Zeng D, Gonzalez F 2nd, Fernandez-Rhodes L, … Heiss G (2014). Genetic association analysis under complex survey sampling: the Hispanic Community Health Study/Study of Latinos. Am J Hum Genet, 95(6), 675–688. doi:10.1016/j.ajhg.2014.11.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manichaikul A, Mychaleckyj JC, Rich SS, Daly K, Sale M, & Chen WM (2010). Robust relationship inference in genome-wide association studies. Bioinformatics, 26(22), 2867–2873. doi:10.1093/bioinformatics/btq559 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchini J, Cardon LR, Phillips MS, & Donnelly P (2004). The effects of human population structure on large genetic association studies. Nature Genetics, 36(5), 512–517. doi:10.1038/ng1337 [DOI] [PubMed] [Google Scholar]
- Mukherjee B, Ahn J, Gruber SB, & Chatterjee N (2012). Testing Gene-Environment Interaction in Large-Scale Case-Control Association Studies: Possible Choices and Comparisons. American Journal of Epidemiology, 175(3), 177–190. doi:10.1093/aje/kwr367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukherjee B, & Chatterjee N (2008). Exploiting gene-environment independence for analysis of case-control studies: an empirical Bayes-type shrinkage estimator to trade-off between bias and efficiency. Biometrics, 64(3), 685–694. doi:10.1111/j.1541–0420.2007.00953.x [DOI] [PubMed] [Google Scholar]
- Murcray CE, Lewinger JP, Conti DV, Thomas DC, & Gauderman WJ (2011). Sample Size Requirements to Detect Gene-Environment Interactions in Genome-Wide Association Studies. Genetic Epidemiology, 35(3), 201–210. doi:10.1002/gepi.20569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murcray CE, Lewinger JP, & Gauderman WJ (2009). Gene-environment interaction in genome-wide association studies. Am J Epidemiol, 169(2), 219–226. doi:10.1093/aje/kwn353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman LS, Rose CS, Bresnitz EA, Rossman MD, Barnard J, Frederick M, … Group AR (2004). A case control etiologic study of sarcoidosis: environmental and occupational risk factors. Am J Respir Crit Care Med, 170(12), 1324–1330. doi:10.1164/rccm.200402–249OC [DOI] [PubMed] [Google Scholar]
- Piegorsch WW, Weinberg CR, & Taylor JA (1994). Non-hierarchical logistic models and case-only designs for assessing susceptibility in population-based case-control studies. Stat Med, 13(2), 153–162. [DOI] [PubMed] [Google Scholar]
- Rossman MD, Thompson B, Frederick M, Iannuzzi MC, Rybicki BA, Pander JP, … Group, A. (2008). HLA and environmental interactions in sarcoidosis. Sarcoidosis Vasc Diffuse Lung Dis, 25(2), 125–132. [PubMed] [Google Scholar]
- Rothman N, Garcia-Closas M, Chatterjee N, Malats N, Wu X, Figueroa JD, … Chanock SJ (2010). A multi-stage genome-wide association study of bladder cancer identifies multiple susceptibility loci. Nat Genet, 42(11), 978–984. doi:10.1038/ng.687 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rybicki BA, Levin AM, McKeigue P, Datta I, Gray-McGuire C, Colombo M, … Iannuzzi MC (2011). A genome-wide admixture scan for ancestry-linked genes predisposing to sarcoidosis in African-Americans. Genes Immun, 12(2), 67–77. doi:10.1038/gene.2010.56 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rybicki BA, Major M, Popovich J, Maliarik MJ, & Iannuzzi MC (1997). Racial differences in sarcoidosis incidence: a 5-year study in a health maintenance organization. Am J Epidemiol, 145(3), 234–241. [DOI] [PubMed] [Google Scholar]
- Sanderson C, & Curtin R (2016). Armadillo: a template-based C++ library for linear algebra. Journal of Open Source Software, 1(26). doi:10.21105/joss.00026 [Google Scholar]
- Sul JH, Bilow M, Yang WY, Kostem E, Furlotte N, He D, & Eskin E (2016). Accounting for Population Structure in Gene-by-Environment Interactions in Genome-Wide Association Studies Using Mixed Models. PLoS genetics, 12(3). doi:ARTN e100584910.1371/journal.pgen.1005849 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas D (2010). Gene-environment-wide association studies: emerging approaches. Nature Reviews Genetics, 11(4), 259–272. doi:10.1038/nrg2764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas DC, Haile RW, & Duggan D (2005). Recent developments in genomewide association scans: A workshop summary and review. American Journal of Human Genetics, 77(3), 337–345. doi:Doi.10.1086/432962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton T, Tang H, Hoffmann TJ, Ochs-Balcom HM, Caan BJ, & Risch N (2012). Estimating kinship in admixed populations. Am J Hum Genet, 91(1), 122–138. doi:10.1016/j.ajhg.2012.05.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XF, Lee S, Zhu XF, Redline S, & Lin XH (2013). GEE-Based SNP Set Association Test for Continuous and Discrete Traits in Family-Based Association Studies. Genetic Epidemiology, 37(8), 778–786. doi:10.1002/gepi.21763 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang YT, Localio R, & Rebbeck TR (2006). Evaluating bias due to population stratification in epidemiologic studies of gene-gene or gene-environment interactions. Cancer Epidemiology Biomarkers & Prevention, 15(1), 124–132. doi:10.1158/1055–9965.Epi-05–0304 [DOI] [PubMed] [Google Scholar]
- Weir BS, & Cockerham CC (1984). Estimating F-Statistics for the Analysis of Population Structure. Evolution, 38(6), 1358–1370. doi:10.1111/j.1558–5646.1984.tb05657.x [DOI] [PubMed] [Google Scholar]
- Wissemann WT, Hill-Burns EM, Zabetian CP, Factor SA, Patsopoulos N, Hoglund B, … Payami H (2013). Association of Parkinson disease with structural and regulatory variants in the HLA region. Am J Hum Genet, 93(5), 984–993. doi:10.1016/j.ajhg.2013.10.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang JJ (2010). Distribution of Fisher’s combination statistic when the tests are dependent. Journal of Statistical Computation and Simulation, 80(1–2), 1–12. doi:10.1080/00949650802412607 [Google Scholar]
- Yang JJ, Li J, Williams LK, & Buu A (2016). An efficient genome-wide association test for multivariate phenotypes based on the Fisher combination function. BMC Bioinformatics, 17, 19. doi:10.1186/s12859–015-0868–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Q, Khoury MJ, & Flanders WD (1997). Sample size requirements in case-only designs to detect gene-environment interaction. Am J Epidemiol, 146(9), 713–720. [DOI] [PubMed] [Google Scholar]
- Zhou W, Nielsen JB, Fritsche LG, Dey R, Gabrielsen ME, Wolford BN, … Lee S (2018). Efficiently controlling for case-control imbalance and sample relatedness in large-scale genetic association studies. Nature Genetics, 50(9), 1335-+. doi:10.1038/s41588–018-0184-y [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


