Interaction Forces on Polyampholytic Hydrogel Gradient Surfaces

Abstract

Rational design and informed development of nontoxic antifouling coatings requires a thorough understanding of the interactions between surfaces and fouling species. With more complex antifouling materials, such as composites or zwitterionic polymers, there follows also a need for better characterization of the materials as such. To further the understanding of the antifouling properties of charge-balanced polymers, we explore the properties of layered polyelectrolytes and their interactions with charged surfaces. These polymers were prepared via self-initiated photografting and photopolymerization (SIPGP); on top of a uniform bottom layer of anionic poly(methacrylic acid) (PMAA), a cationic poly(2-dimethylaminoethyl methacrylate) (PDMAEMA) thickness gradient was formed. Infrared microscopy and imaging spectroscopic ellipsometry were used to characterize chemical composition and swelling of the combined layer. Direct force measurements by colloidal probe atomic force microscopy were performed to investigate the forces between the polymer gradients and charged probes. The swelling of PMAA and PDMAEMA are very different, with steric and electrostatic forces varying in a nontrivial manner along the gradient. The gradients can be tuned to form a protein-resistant charge-neutral region, and we demonstrate that this region, where both electrostatic and steric forces are small, is highly compressed and the origin of the protein resistance of this region is most likely an effect of strong hydration of charged residues at the surface, rather than swelling or bulk hydration of the polymer. In the highly swollen regions far from charge-neutrality, steric forces dominate the interactions between the probe and the polymer. In these regions, the SIPGP polymer has qualitative similarities with brushes, but we were unable to quantitatively describe the polymer as a brush, supporting previous data suggesting that these polymers are cross-linked.

Introduction

Hydrogels are water-soluble polymers with a certain degree of crosslinking. Their potentially large water content and structural properties similar to those of tissue frequently yield high biocompatibility, and they are therefore widely developed for biomedical and biomaterial applications.¹⁻⁵ By applying hydrogel-like thin-film coatings onto substrates or supporting materials, the interfacial advantages of hydrogels can be preserved, whereas the geometry or dimensions can be adapted and structural properties also improved. Thus, they may be designed to meet many different needs in biologically oriented surface and interfacial science. In particular, surface-bound hydrogels which provide a permanent surface modification to various substrates are commonly utilized in cell adhesion applications,⁶⁻⁸ tissue engineering,⁹ and as models for extracellular matrices.¹⁰ Hydrogels resistant to nonspecific adsorption are of particular interest in antifouling applications for biomedical^6,11 or marine^12,13 applications. End-grafted polymer brushes have been widely studied and used for the latter purposes^14,15 and have certain similarities with hydrogels, though they are not cross-linked. Furthermore, it has been observed that charge-balanced systems, such as zwitterionic materials¹⁶⁻²⁰ and other polyampholytes²¹⁻²³ can also show good fouling resistance. Although steric or structural repulsion is the dominating mechanisms maintaining the protein resistance of neutral polymers or brushes,^{11,12,24−26} charge-balanced systems may interact with bio-objects in more complex ways. Electrostatic interactions with the surface are likely to attract proteins, but under charge-balanced conditions, this attraction is minimized, and the strong hydration due to the presence of many ionizable groups could add considerably to the steric contributions through much enhanced surface hydration, providing additional resistance to protein adsorption. At high salt concentrations, antipolyelectrolyte behavior contributes to increased hydration, with ensuing improvements in fouling resistance.²⁷ Most charge-balanced polymers are prepared via polymerization of zwitterionic monomers²⁸ or by copolymerization of anionic and cationic monomers,²² but we have reported that charge-balanced hydrogels can be created also by polymerizing two polyelectrolyte layers with opposite charges on top of each other.^21,29 P(AEMA−CEA) hydrogel films, composed of a thickness gradient of anionic poly(2-carboxyethyl acrylate), PCEA, on top of a uniform layer of cationic poly(2-aminoethyl methacrylate hydrochloride), PAEMA, had a region of near-zero protein adsorption, as monitored by imaging surface plasmon resonance.²¹ In these gradients, the net charge was balanced in the protein-resistant region, whereas proteins adsorbed to the oppositely charged regions on either side of the charge-balanced portion of the gradient. Later, we also demonstrated that the location of this charge-balanced region, and hence also the protein adsorption, can be controlled via the pH of the surrounding solution.²⁹ The mechanisms behind the antifouling properties of these systems are thought to be similar to fouling-resistant zwitterionic polyelectrolytes.¹⁸ Direct force measurements by colloidal probe atomic force microscopy (AFM) to determine the surface charge distribution on these films revealed a charge-balanced area around the zero protein adsorption region and opposite surface charge on either side of this region.^21,29 These gradient structures are useful in the exploration of materials and surfaces suitable for pH-controllable adsorption and/or desorption, and can be used to further our understanding of protein adhesion processes, and also to clarify protein resistance mechanisms in zwitterionic polymers. In these hydrogel film architectures, the charges from the thickness gradient layer are distributed on top of a homogeneous background of opposite charge. However, the resulting surface charge, and specifically, the charge perceived by an AFM probe or an approaching protein will be affected by several parameters, among these are the volume distribution of charges between the two sequentially polymerized layers, any association between oppositely charged groups, and screening by the intervening electrolyte. A complication in the characterization of the charge distribution on these gradients is that the swelling of the two materials can be very different. In the case of P(AEMA−CEA), the swelling of the anionic component is much greater than that of the cationic component,²⁹ with the result that unambiguous interpretation of the direct force measurement results in terms of electrostatic interactions becomes problematic since steric contributions to the total interaction will be difficult to separate from the electrostatic interactions. From this follows that correlations between surface properties and, for example, protein resistance or other phenomena along the gradient become uncertain, and this motivates more detailed studies of the surface properties on these gradients, in particular, a clarification of how steric and electrostatic interactions contribute to the total force acting on a particle approaching different parts of the gradient.

To the extent that zwitterionic materials rely on charge-neutrality for antifouling efficiency, these materials will also be more susceptible to variations in environmental properties for their continued fouling resistance than nominally uncharged materials, such as poly(ethylene glycol) (PEG)-based polymers. Most surfaces acquire some charge upon immersion in aqueous environments due to preferential adsorption of ions. This can be very difficult to control or predict in complex physiological, marine, or freshwater environments with low, but highly variable, concentrations of metal ions. The adsorption of, for example, multivalent ions, with potentially high affinity to the surface, and possibly causing charge reversal, might alter the interfacial properties of the material, as well as interactions between charged residues within the polyelectrolyte. Furthermore, zwitterionic materials will have acidic and basic groups with different strengths, resulting in a pH-dependent net charge, with additional secondary effects from the exact composition of the ionic environment. Thus, understanding charging, as well as electrostatic and steric interactions at polyelectrolyte interfaces, is of immediate relevance to the understanding of all charge-balanced materials.

The properties of adsorbed and dissolved polyelectrolytes have been investigated by direct force measurements using a number of methods and in a multitude of systems.^30,31 After the pioneering work by Luckham using poly-l-lysine adsorbed from solution,³² have followed a multitude of reports on forces in systems with adsorbed polymers,^33,34 multilayers,^35,36 brushes,³⁷⁻⁴⁰ comb-type,⁴¹ bottle-brush,⁴² or more complex⁴³ polyelectrolytes. This interest stems from, for example, the widespread industrial use of polyelectrolytes for control of colloidal stability and the importance of charged biopolymers such as DNA and polysaccharides. For weak polyelectrolytes, pH and ionic strength can significantly change the charge distribution and swelling,⁴⁴⁻⁴⁶ which is ultimately the reason why in charge-balanced hydrogels formed from weak electrolytes, the surface charge distribution, and thus also the protein resistance, can be controlled.²⁹ Among weak polyelectrolytes, poly(methacrylic acid) (PMAA) and poly(2-dimethylaminoethyl methacrylate) (PDMAEMA) are frequently used and well-studied materials.⁴⁷⁻⁵¹ The self-initiated photografting and photopolymerization (SIPGP) fabrication method can be used to grow polymer films on a wide range of organic materials,^12,52 and works well with many different monomers, including MAA and DMAEMA. The characteristics and performance of hydrogels formed from these materials are described in the literature,⁴⁶⁻⁴⁸ and this also makes them interesting candidates for further studies as components in two-layer hydrogel gradients.

In this work, we extend the previous work on P(AEMA−CEA) hydrogel gradient films to other combinations of anionic and cationic polyelectrolytes, in this case, P(MAA–DMAEMA). To improve our understanding of the mechanisms governing the protein resistance around the charge-neutral region and to clarify the contributions from steric and electrostatic forces to the interactions with an approaching particle, we carry out direct force measurements using colloidal probe AFM to study the interaction forces between such gradients and both charged and (nominally) uncharged probes, to better understand how electrostatic and steric forces, swelling, and polymer composition are related along these thickness gradients. Ultimately, we anticipate that better understanding of these parameters will enable the rational design of more efficient and robust fouling-resistant polymers.

Results and Discussion

Infrared Spectra

Long gradients on gold substrates were characterized by infrared microspectroscopy for chemical identification in a nitrogen-purged dry state. IR spectra were collected along the gradient and subsequently reassembled into three-dimensional (3D)-representations of the absorbance over the sample surface. Figure 1a,b shows 3D spectra of a long P(MAA–DMAEMA) gradient and a PDMAEMA gradient (without the PMAA bottom layer), respectively (see the Supporting Information for detailed spectra and peak assignments). In both panes of Figure 1, the peak at 1733 cm^–1 is identified as the carbonyl C=O stretching band, to which both the PMAA and PDMAEMA layers contribute. Since the PMAA layer is uniform, the increasing intensity is assigned to the thickness/mass increase of PDMAEMA,⁵⁰ as is evident in Figure 1b, in particular. The band near 1266 cm^–1 is assigned to C–C–O stretching and the band around 1184 cm^–1 is C–O stretching coupled with O–H in-plane bending.⁵³ Contributions from COO^– groups, expected to appear approximately in the range of 1580–1590 cm^–1 (asymmetric stretching) or near 1400 cm^–1 (symmetric stretching) are absent from the spectra in Figure 1, indicating that the PMAA layer was not ionized in the dry state under N₂ purging. Tertiary ammonium groups are difficult to resolve in IR spectra, so the same cannot be stated with certainty about the PDMAEMA layer, though the absence of carboxylates nevertheless indicates that the association of amines with carboxylates in the dry film is limited. In general, the IR spectra of both P(MAA–DMAEMA) and PDMAEMA gradients confirm that gradients with continuously changing mass and chemical composition are formed during polymerization.

Figure 1.

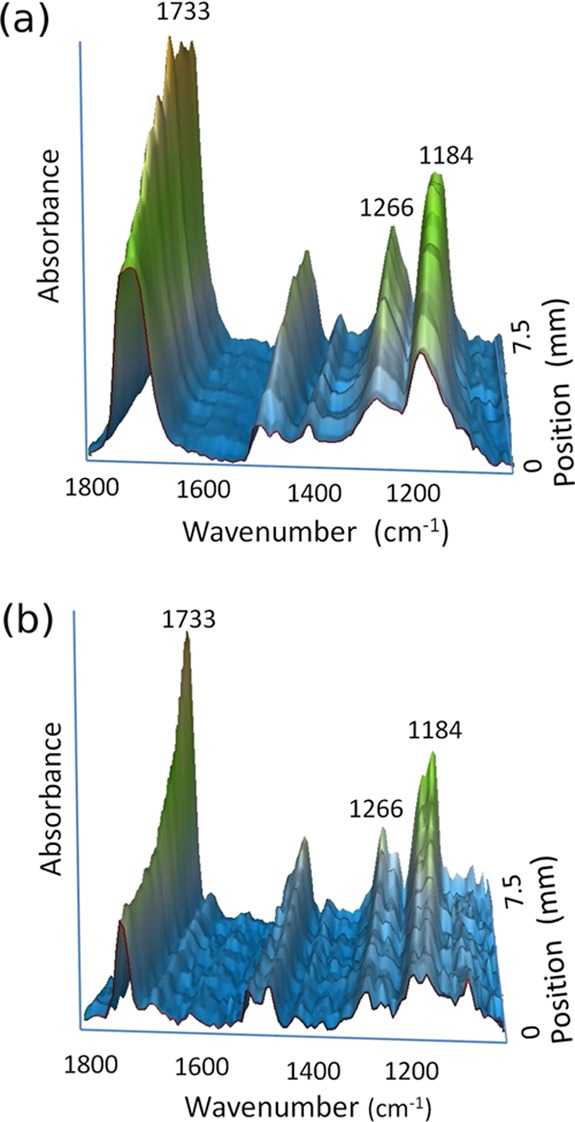
IR spectra of long gradients of (a) P(MAA–DMAEMA) and (b) PDMAEMA. Increasing carbonyl peak near 1733 cm^–1 indicates the presence of the PDMAEMA gradient.

Swelling Profiles

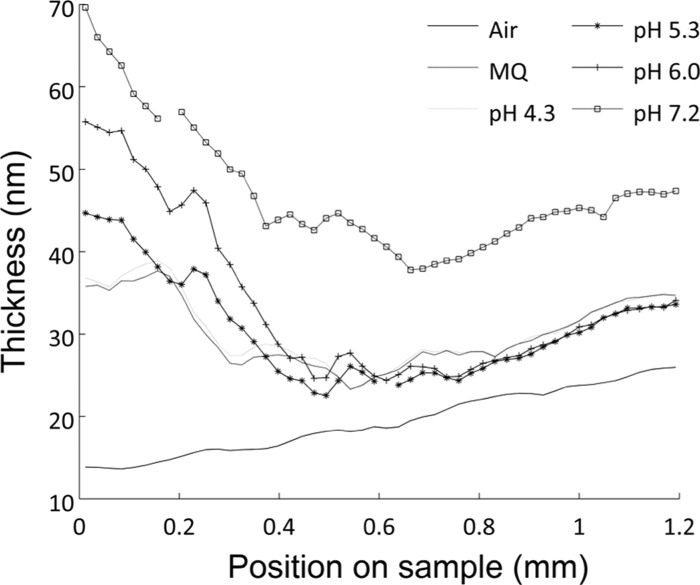
Imaging ellipsometry offers a nondestructive optical method to monitor the swelling of surface-grafted polymers under various conditions, notably as the pH is varied in this case. Figure 2 shows the swelling profile of P(MAA–DMAEMA), plotted as thickness against the surface position along a short gradient, in water as well as in buffers over a pH range from 4.3 to 7.2. The thickness profile in air shows a monotonous thickness increase with position, confirming the presence of a polymer thickness gradient. When changing the medium from air to water, the contrast between the polymer and the medium decreases. For the swollen film, this is particularly important, and the water content affects the refractive index of the hydrogel which also varies in the direction of the surface normal. The degrees of crosslinking or interpenetration in these SIPGP hydrogels are unknown, although there is evidence that crosslinking does occur.^52,54 Since the degree of crosslinking influences both the polymer architecture and the charge distribution,^21,55−57 the interpretation of results from highly swollen polymer films should be made with care. Based on previous work,^21,29 we hypothesize that the reduction of the total thickness of around 0.6 mm on the sample position as shown in Figure 2 is a charge-balanced region where the two layers are interpenetrated and the opposite charges in the two polymers neutralize each other, resulting in reduced electrostatic repulsion within the film.

Figure 2.

Swelling profiles of a short gradient of P(MAA–DMAEMA) in air, water (Milli-Q (MQ)), and in buffers with various pH values. PMAA forms a bottom uniform layer and PDMAEMA is the gradient on top of PMAA. From the left to the right there is a gradual increase in PDMAEMA thickness.

The swelling in the thicker region of the PDMAEMA gradient does not respond to variations in pH as much as the region dominated by PMAA, on the left side of Figure 2. The strong dependence of pH in the thin region of the gradient can be understood in terms of protonation of the carboxylic groups. First, the thickness of the PDMAEMA layer is thin here, and the properties of the polymer film can safely be assumed to be dominated by the PMAA layer. At low pH, carboxylic groups are protonated (neutralized) to a greater extent, resulting in less electrostatic repulsion within the polymer film, permitting the chains to adopt an entropically more favorable, relaxed state. As the pH is increased, more carboxylic groups are deprotonated and the electrostatic repulsion within the film results in swelling and an increase in the total thickness of the hydrogel.

The swelling up to pH 6 is considerably smaller at the thicker end of the gradient (to the right in Figure 2) as the amount of PDMAEMA increases along the gradient. This may be explained either by increased crosslinking between the PMAA and PDMAEMA layers or by attractive electrostatic interactions between the ionized carboxylic and amine groups. Crosslinking induces a higher elastic resistance to expansion, and the charge neutralization effect minimizes the amount of counterions in the film which lowers the osmotic pressure; both effects would result in less swelling. The whole gradient swells significantly at pH 7.2 and uniformly in the region of high PDMAEMA content. This is probably due to a high degree of deprotonation of the carboxylic groups in the PMAA layer, in combination with a low ionization of the PDMAEMA layer. However, we emphasize that the thicknesses obtained from spectroscopic ellipsometry measurements on highly swollen polymers must be considered with care and the uncertainties in absolute terms increase with layer thickness, as described above.

The pK_a values of the charged residues in polyelectrolytes are strongly dependent on the local environment, and the exact pK_a values in the SIPGP-prepared layers remain unknown.

The pK_a values of PMAA have been estimated to be ca. 5–6,^58,59 and the pK_a values of DMAEMA have been found to decrease from ca. 8.3–8.6 to 7.4 in PDMAEMA,^60,61 but these values will all be modified in the presence of counterions. Taking the pK_a data at face value, it would appear that from pH 4.3 up to 7.2, the charging of the PMAA layer is more affected than that of the PDMAEMA layer, in agreement with the observations in Figure 2.

Direct Force Measurements

Figure 3 shows force curves obtained on seven different positions along a P(MAA–DMAEMA) gradient, using an 11-mecaptoundecanoic acid (MUA)-coated colloidal probe in 10 mM phosphate buffer (PB) at pH 6.0. The data are plotted as force/radius versus separation. Data for long and short gradients are qualitatively comparable to each other (not shown), indicating that the polymer structure and charge distribution does not change significantly when the fabrication protocols are applied to different gradient lengths. The Debye screening length in 10 mM mono-PB is 3.04 nm, which is due to the bulk ionic atmosphere, and thus depends solely on the liquid. The surface potential of the MUA probe in the symmetric MUA–MUA system, as measured in 10 mM PB was found to be −91 mV, resulting in a surface charge density of −0.0323 C m^–2 or 4.7 nm² per surface charge (the corresponding results for experiments in 10 mM NaCl are −88 mV, −0.0319 C m^–2, or 4.8 nm² per charge). These are higher charge densities than were obtained in previous studies,⁶² though the experimental conditions were not identical, so the comparison should not be taken too far.

Figure 3.

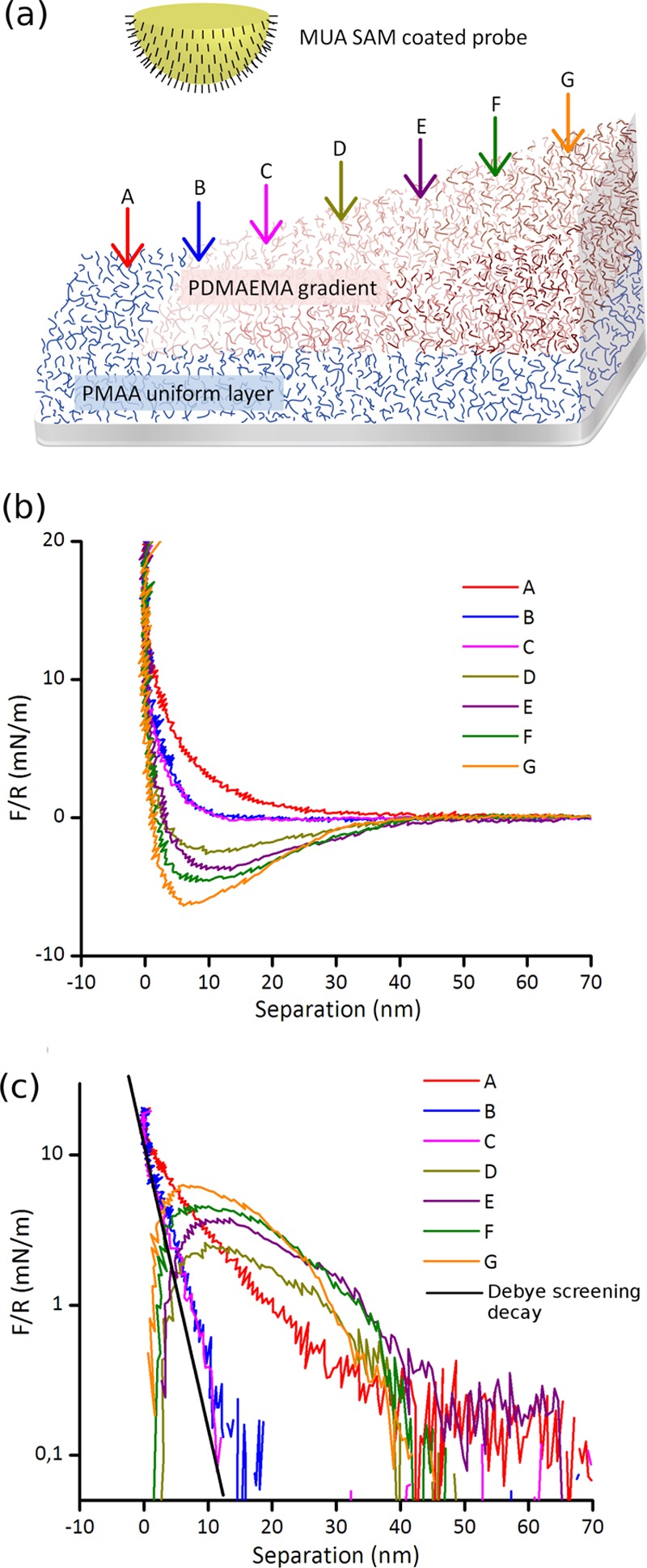
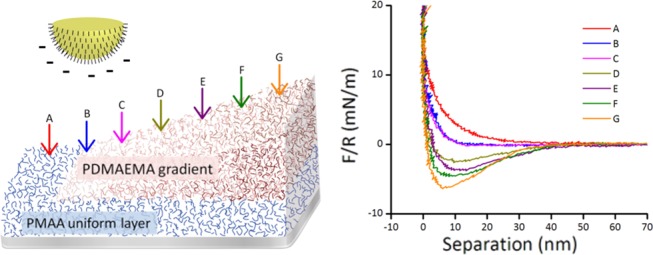
(a) Cartoon showing the geometry of the experiment (not to scale; note that in reality, some degree of interpenetration of the two polymer layers occurs). The P(MAA–DAMEMA) gradient is probed by an MUA self-assembled monolayer (SAM)-coated probe and arrows indicate the positions of the obtained force curves at 500 μm intervals. Position A is bare PMAA and the PDMAEMA gradient starts from curve B, increasing in thickness toward G. (b) Force curves on a P(MAA–DMAEMA) gradient, obtained in 10 mM PB buffer at pH 6.0, upon approach. (c) shows the same data as in (b), plotted on a log scale (curves D–G with an opposite sign). Solid black line in (c) is the decay of the electrostatic repulsion for the used buffer ionic strength, adjusted to coincide with curves B and C at short separation.

In Figure 3, the curve at position A was obtained on the uniform PMAA layer and the PDMAEMA gradient starts at position B, with the increasing thickness toward curve G. Figure 3b,c shows the same data but plotted on a log scale in Figure 3c. In the latter, the curves showing net attraction (D–G) were plotted with an opposite sign. The solid black line in (c) indicates an exponential decay with a Debye length of the used electrolyte, showing the expected contribution from electrostatic repulsion to the total interaction in curves B and C.

Considering first the qualitative changes in the curves in Figure 3b, curve A obtained on the negatively charged PMAA is repulsive over the whole range of interaction, as expected for an MUA SAM probe interacting with a negatively charged surface. The reduced repulsion for B and C and the switch to increasing net attraction from curves D to G reflect the presence of increasing amounts of PDMAEMA, making the polymer film net positive as the gradient of PDMAEMA becomes thicker. Due to the transition from net repulsion to net attraction between positions C and D, it is also clear that the results are consistent with the presence of a charge-balanced region with a low net surface charge, as has been suggested previously.^21,29

In Figure 3c, the force curves are plotted on a log scale and the attractive force curves (D–G) are plotted with an opposite sign. The two force contributions dominating the total interaction are the electrostatic forces and steric repulsion arising from the interaction of the probe with the swollen polymer networks. If we consider the force profile at position A, it is seen in Figure 3c that the repulsion decays nearly exponentially with separation but the decay exceeds by far the Debye screening length (indicated as the solid black line adjusted to coincide with the data at close separation). Thus, the repulsion in position A is dominated by steric interaction with the swollen PMAA layer. There may well be an electrostatic contribution to the repulsion, but considering the highly swollen conditions of the PMAA film at pH 6 (see Figure 2), even if the carboxylic groups in the PMAA layer are fully deprotonated, most of the charges in the film would be much further from the probe than the Debye screening length (approximately 3 nm), and thus not directly affecting the probe as it interacts sterically with the polymer layer. Thus, the effective charge of the film which is probed by the MUA SAM-coated particle is only a fraction of the total number of ionizable groups in the PMAA layer. However, there may be an indirect contribution to the steric force from electrostatic interactions within the polymer layer, as charges are brought closer together upon compression of the hydrogel film.

The functional form of the attractive interaction in curves D–G is difficult to establish; at separations around 40 nm, the decay of the force with the distance has a slope which is similar to the Debye length observed for the repulsive curves B and C but the reduced noise level at shorter separations suggests that the probe is hydrodynamically damped and that the approach rate here is limited by the viscosity of the intervening buffer during jump-in of the probe, in a range where the stiffness of the cantilever is smaller than the force gradient. Hence, the range of distances over which the electrostatic attraction dominates the interaction and the separation where steric forces start contributing significantly, cannot be determined in the attractive regime from these data.

In an effort to simplify the interpretation of the interaction of the MUA probe with the PDMAEMA gradient and to clarify the steric contribution to the interaction, a single PDMAEMA gradient was investigated using an MUA probe without interference from a PMAA bottom layer (see the Supporting information). However, little useful information could be extracted from the data, and instead, it was decided to study how an uncharged probe interacts with the hydrogel gradient, to understand the role of steric contributions to the total forces. We chose a 16-thiohexadecanol (C16OH) SAM to represent a neutral probe for studying the steric interaction of the probe with the P(MAA–DMAEMA) gradient.

However, a surface rarely stays completely charge neutral in aqueous solution, for example, as a result of preferential adsorption of ions from the solution, and the charge of the C16OH probe was thus characterized in a symmetric system, using a C16OH SAM also as the substrate. In 10 mM PB, the surface potential was found to be −22 mV and the surface charge density was −0.00514 C m^–2, equivalent to an area of 29.5 nm² per charge, which is considerably lower than what is observed on the carboxyl-terminated SAM. The absence of pH-dependence in the interactions of hydroxylated surfaces (and notably the difference between hydroxylated and carboxylated surfaces in this respect) has been demonstrated by others.⁶³ In Figure 4 (as in Figure 3), curve A represents probing on PMAA only and points B–G represent probing on increasingly thicker portions of the P(MAA–DMAEMA) gradient. In Figure 4b, the long-range attraction seen in Figure 3b is considerably reduced and appears only very weakly for curves C–F, which is explained by the much weaker negative surface charge on the C16OH probe compared to the MUA probe. The electrostatic contribution to the Derjaguin–Landau–Verwey–Overbeek (DLVO) force (again using the 3.04 nm Debye screening length in 10 mM monophosphatic PB buffer) fits the decay of the repulsion very well for the curves B, E, and F (Figure 4c). Since the Debye length sets an upper limit for the range of electrostatic forces, we conclude that curves A and G represent cases where the long-range interaction is dominated by steric repulsion. Similarly, in the force profiles obtained on C and D, the total force is very weak, and then also by necessity the electrostatic contributions, and in C, the jump into contact due to the van der Waals attraction indicates that both electrostatic and steric contributions are weak and/or short-ranged, and the fact that the van der Waals attraction is not present further along the gradient (at point D, for example) also confirms the presence of a little-swollen charge-balanced region at C, surrounded by more swollen domains on either side. Comparing the results from A and G with the swelling characteristics in Figure 2, we also note that the swelling is greatest at either end of the gradient sample, in full agreement with the observation that long-range steric repulsion dominates A and G. The data in Figures 3 and 4 also clearly confirm that there is a region of charge neutralization between a positively and a negatively charged end of the gradient.

Figure 4.

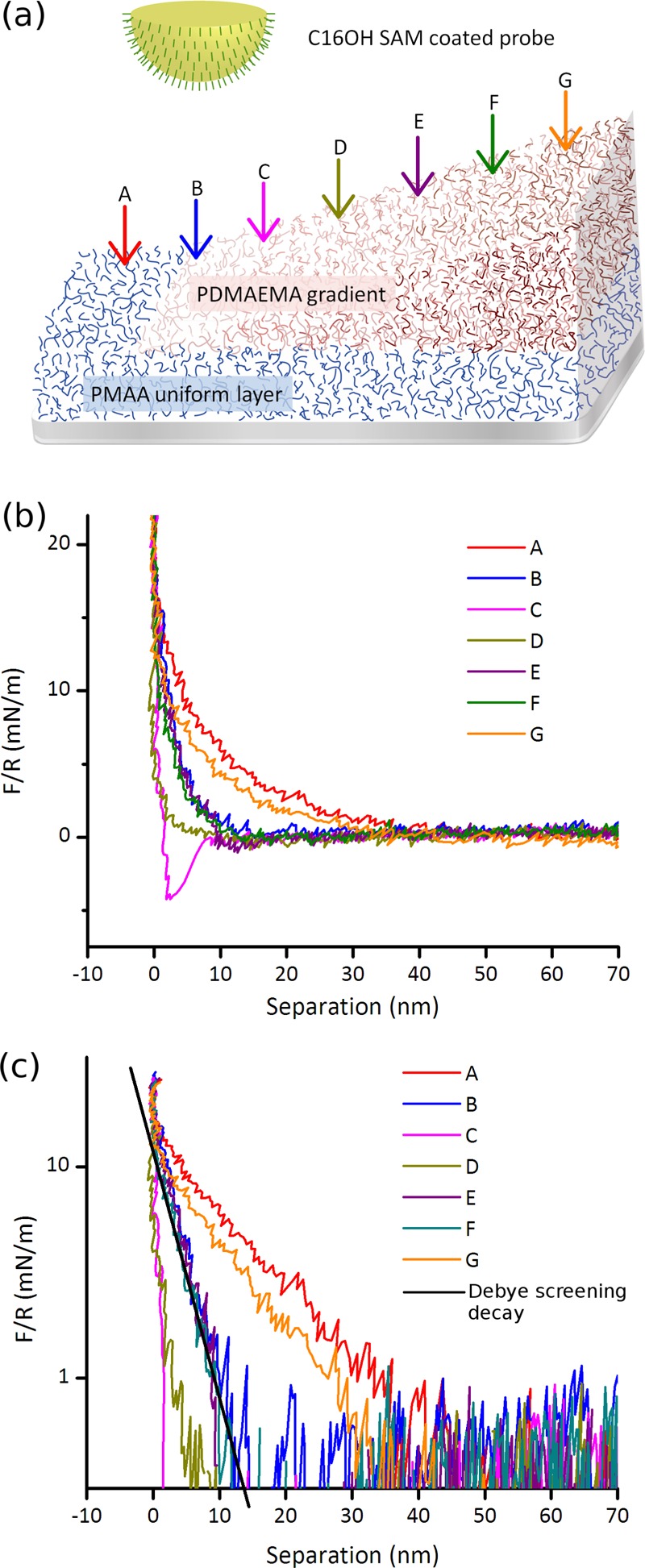
(a) Experimental geometry. P(MAA–DAMEMA) gradient is probed by a C16OH SAM-coated probe and the arrows indicate the positions where the force curves were obtained. Position A is bare PMAA, and the PDMAEMA gradient starts from curve B, increasing in thickness toward G. (b) Force curves obtained in 10 mM PB buffer at pH 6.0, and (c) the same data plotted on a log scale, and the solid line in (c) is the exponential decay obtained from the Debye length of the buffer, adjusted to coincide with curves B, E, and F at short separations.

Modeling the Steric Interaction

Numerous force studies in polymer systems describe the behavior of the adsorbed polymers as well as grafted polymer brushes on surfaces.^{45,56,64−66} Dilute polymer systems, either polyelectrolytes or neutral polymers, may be modeled as brushes with reasonable accuracy. This, however, will not work for densely grafted or cross-linked, branched systems.^21,52 The classic Alexander–de Gennes (AdG) model^67,68 is a good model for neutral polymer brushes,⁶⁹ it has been successfully applied, developed, and expanded to many related systems.^{44,45,64,65,70} As a first approximation, we assume that our systems can be modeled as salted neutral polymer brushes.⁶⁵ When the bulk ionic strength is high and the thickness of the polymer layer exceeds the Debye length, charged polymer brushes can behave in a way similar to that of neutral brushes.⁶⁵ Within the AdG model, Butt et al.⁶⁴ demonstrate that the force between two brushes can be written as F = A e^–D/λ, where the two fit parameters A and λ are the amplitude (dependent on the grafting density and the molecular weight) and the decay length, respectively, and D is the separation between the surfaces. This relation is valid when 0.2 < D/L < 0.9, where L is the polymer thickness in equilibrium. However, when this model was applied to the P(MAA–DAMEMA) gradient interacting with neutral C16OH (see Figure 5), good fits could be obtained, but these did not result in physically reasonable parameters: the total thickness of the polymer layer in the gradient will be reduced due to intra- and interchain interactions between the oppositely charged groups at the interface between the two polymer layers and thus not directly comparable to the brush height as yielded from the model. Also, if the brush height as obtained from the ellipsometric swelling profile is used together with any molecular weight chosen in the range permitted by the model, the obtained grafting density will be far too small to fall in the brush regime, which is not in agreement with structural investigations of SIPGP hydrogels by other methods.^54,71

Figure 5.

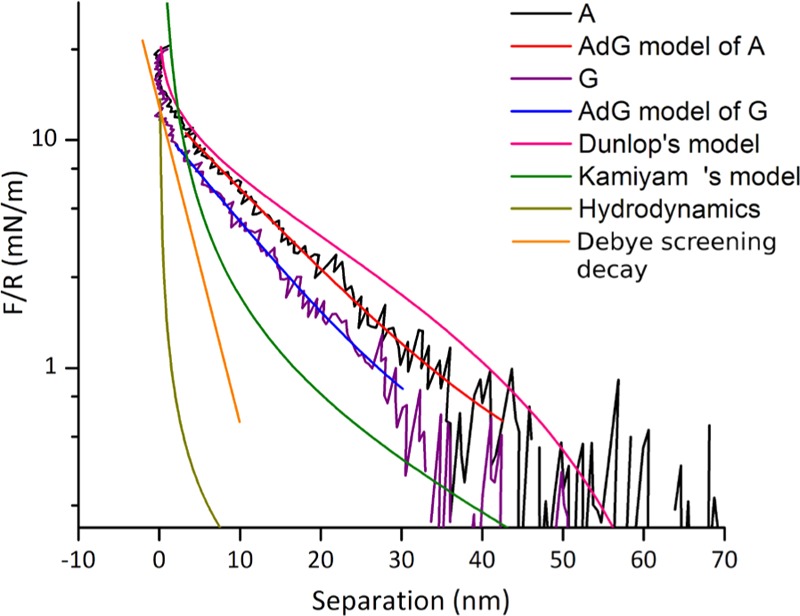
Force curves A and G of P(MAA–DMAEMA) gradient are probed by a C16OH-SAM-modified probe, which fitted by single exponential decay curves (red and blue) according to the Alexander–de Gennes model. Pink curve is Dunlop’s model and the green curve is Kamiyama’s model. Both the expected electrostatic contributions determined by the Debye length (orange) and the hydrodynamic force at the used approach rate (dark yellow) are considerably smaller than the measured forces.

The shortcomings of the AdG model in our systems are related to the range of the steric forces. For the AdG model to yield reasonable parameters from the fitting, the range of steric interaction needs to be considerably shorter than that in our data. To account for such discrepancies in polyelectrolyte systems, the AdG model has been extended by, for example, Kamiyama and Israelachvili,⁴⁵ and later also modified by Dunlop et al.⁶⁵ The two major contributions to the force as discussed by Kamiyama, are steric interactions of the brushes in the “overlap region” at D < 2L, where L is the brush height and electrostatic forces for D > 2L. The total force was

where s is the mean distance between the molecules and D is the separation. Dunlop et al. described surface-grafted brushes as a Pincus brush^72,73 which cannot quantitatively fit; therefore, the effective charges on the polyelectrolytes were relocated on a nominal plane, which was at a distance δL_charge = (1/2k) ln(A/A_max) above the substrates, where A_max is the constant of the linear Poisson–Boltzmann equation: 128πk_BTρ₀/k. In Dunlop’s work, the forces between the surfaces F(D) were eventually reconstructed by applying five parameters into the total free energy and using the Derjaguin approximation, the force is

γ₁ and γ₂ are constants of order unity and B = 2παk_BTN/s². L₀ is the uncompressed brush height that contains all its counterions and given by L₀ ≅ α^1/2Na, where N is the degree of polymerization, a is the Kuhn step length, α is the fraction of charged monomers, and s is the distance between the adjacent polymer chain anchor points. For the above formula to be physical, it must be ensured that γ₂ ≥ 2γ₁.

The fitting parameters of both Dunlop’s and Kamiyama’s models were constrained to remain physically realistic. The fit to Dunlop’s model shown in Figure 5 was performed using these parameters: N = 110, s = 9, α = 0.09, γ₁ = 0.75, γ₂ = 1.5, and L₀ = 70 nm, which we deem realistic, from our previous knowledge of these types of polymer films, viz. the largest measured thickness of the film and estimates based on our available information on the structure and density of SIPGP-prepared polymers.^21,74 The (mathematical) agreement between the model and the data could be further improved, however, this would lead to very low grafting densities. Also, variations in γ₁ and γ₂ could be used to adjust the fitting, though the physical implications of this are unclear.

The qualitative agreement indicates that our hydrogel gradient may have similarities to the polymers used by Dunlop et al. in terms of polymer structures and charge distribution. However, when we tried to fit our data to Kamiyama’s model, using s = 5 to bring the fitted curve close to data sets A and G (see Figure 5), the force predicted by the model at small separations is 1 order of magnitude larger than the data, which indicates that the decay of this model is rather fast and probably due to smaller steric forces in dense polymers (low s value), but the slope of the long electrostatic tail appears to fit better than in Dunlop’s model. Dunlop’s system was a grafted strong polyelectrolyte brush containing quaternary amine, whereas Kamiyama’s system was gelatin adsorbed onto mica, presumably exposing loops and tails of the polymer chains, containing both positive and negative charges. Even though SIPGP does not produce well-defined brushes in the way atom transfer radical polymerization does, it seems probable that our P(MAA–DAMEMA) films are closer to Dunlop’s system, in terms of the way the steric and electrostatic forces contribute to the interaction.

The similarities between the force curves at position A as obtained with the different probes (curves A in Figures 3 and 4, respectively, as probed by MUA and C16OH probes) demonstrate that the interaction at this point is dominated by steric forces. As inferred from the fits to the AdG model, the range of the steric forces exceeds those expected for a neutral brush. This may be because of branching or crosslinking of the polymer during polymerization, but we would also expect an intrachain contribution from the ionizable groups in the polymer. The curves at position A as obtained with the MUA and C16OH probes are of similar magnitude but differ in that the former has a clearly distinguishable tail extending to farther separations, perhaps as a result of electrostatic interactions between the charged probe and charges on polymer chains extending into the solution. This contribution to the total force is small and only significant at large separations where the net force is small.

Curves A and G are of similar magnitude as probed with the neutral probe. This does neither imply that the compressibility of the polymer at these positions are similar nor that the range of steric forces is similar. The amount of dry material is very different at these positions, and with the AFM the point of zero separation is not absolute, and at point G there will be a much thicker layer of compressed polymer remaining at high compressive load, effectively offsetting the separation scale, with an amount approximately equal to the difference in dry thicknesses of the polymer at these two positions. Comparing the forces at points A and G, as obtained with the negatively charged probe, MUA, it is clear that the negative PMAA layer has very few charges contributing to electrostatic repulsion. The PMAA has a very thin dry thickness, but when it swells in wet-state the thickness can increase up to 3–5 times, distributing the negative charges into a large volume, whose thickness by far exceeds the Debye length, and few of the charges on the PMAA chains will be sensed by an approaching probe before steric forces dominate the interaction.

In summary, failure to fit the obtained data with a number of polyelectrolyte brush models in the highly swollen regions, far from the charge-balanced region, provides some support to the view that the polymer in these regions are not brushes, in agreement with previous data suggesting that crosslinking occurs in the preparation of these hydrogel films.^21,52

Bulk and Surface Charge, Structure, and Swelling

The swelling profiles of P(MAA–DMAEMA) in Figure 2, in combination with the force profiles in Figures 3 and 4 (and, additionally, in Figure S3) provide excellent complementary information that informs us about the polymer structure. Figures 3 and 4 (and Figure S3) show that PDMAEMA effectively adds a continuously increasing density of positive charges along the gradients. However, the swelling of PDMAEMA did not respond much to pH changes and was overall very small, indicating that PDMAEMA has a rather dense structure compared to the highly swollen PMAA, so that the MUA probe interacts with a greater net charge density at the surface of PDMAEMA, compared to the more dilute distribution of negative charges (see curve A in Figure 3) in the more swollen PMAA. In PMAA, the charges in the polymer will, on average, be farther from the probe at a given probe–polymer distance due to the swelling. This may also explain that in the AdG model, we cannot obtain reasonable grafting densities that satisfy neutral brushes: the elasticity of PDMAEMA appears to be significantly lower than that of neutral brushes, therefore, the total mean grafting density is much underestimated, whereas the stiffness is beyond the range expected for brushes. Dunlop’s and Kamiyama’s models both describe their systems as salted brushes by modified AdG models, however, from the swelling profiles of our gradient P(MAA–DMAEAM), we recognize that the polymer structure in our case is much more complex. In principle, PMAA, which is highly swollen, may be described as a salted brush, but PDMAEMA with its ionizable groups confined within a dense distribution, particularly at the thicker end of the gradient (see Figures 2 and S3), cannot be described as a brush, but more likely as a branched or cross-linked polymer. This can also be seen as a low elasticity of PDMAEMA where the attractive electrostatic forces are not present (compare curves A and G in Figure 4). In addition to this, the charge neutralization between PMAA and PDMAEMA is significant in that the total thickness of the gradient reduces at the charge-balanced area, and which limits the swelling at the interface.

The complex swelling profiles and the nontrivial variation of the force curves of P(MAA–DMAEMA) gradients are the combined result of steric and electrostatic interactions both within the polymer and between the probes and the gradients. We have not been able to quantitatively describe the interactions within a model of swollen polyelectrolytes, but are able to qualitatively describe how swelling and charging of the polymer contribute both to the structural properties and to the formation of a charge-neutral region. We anticipate that ongoing and future work using neutron reflectometry will reveal further details about the swollen state of such SIPGP-grafted layers.^54,71,75 Although it is of great interest how both the surface potential (and charge density) and the steric contributions vary along the gradient, this information cannot be unambiguously extracted from the current AFM data but will require further work, also involving other methods. Previous work has demonstrated that protein fouling onto the hydrogel gradients occur primarily outside the charge-neutral region.^21,29 The data presented here demonstrate that these charged regions are the most swollen and that the interactions with charged and neutral probes are very similar in these areas, suggesting that the surface charge is weak and that the swelling is caused by electrostatic interactions within the polymer layers. This implies that, to the extent that electrostatic interactions are responsible for the nonspecific adsorption of proteins, this might be a result of proteins diffusing into the swollen polymer, rather than adsorption onto the polymer surface. Considering the interesting antifouling properties of these hydrogel gradients, and in particular, the ability to control surface charge and protein resistance via pH,²⁹ we are convinced that further studies of these materials have the potential to provide fundamental and general information about the antifouling properties of charge-balanced and/or zwitterionic polymers.

Conclusions

Samples fabricated by SIPGP with a PDMAEMA gradient on top of a PMAA uniform bottom layer were characterized by infrared microscopy and imaging ellipsometry to verify the chemical composition and swelling along the gradients under different pH conditions. Colloidal probe AFM, with probes chemically modified by SAMs of either 11-mercaptoundecanoic acid or 16-thiohexadecanol, was used to measure the interaction forces with the gradient surfaces, at several positions along the gradients, to facilitate separation of electrostatic and steric contributions to the total interaction.

Combining these methods, we confirm the presence of a charge-balanced and less swollen region in the thin hydrogel gradient. The PDMAEMA gradient layer adds a continuously increasing positive charge contribution, resulting in a shift from the net negative surface charge where the PDMAEMA layer is thin, over the charge-neutral region where electrostatic forces are canceled, or small, due to charge neutralization and where also steric forces are small due to the reduction of internal electrostatic repulsion between ionizable groups within the polymers. Further along the gradient, the interaction is dominated by a positive surface charge, which is attractive when probed by MUA. However, as the film becomes thicker, the electrostatic attraction is reduced in favor of increasing steric repulsion, where the range of the measured repulsive forces extends far beyond the projected range of electrostatic interaction. We conclude that the charge-neutral region is highly condensed with virtually no long-range steric contribution to the interaction. Previous work has shown that this region is highly protein-resistant,^21,29 and our current findings of its structure stands in sharp contrast to protein-resistant neutral polymer brushes, such as PEG, which are generally highly compressible and whose fouling resistance is conferred via strong hydration, causing swelling of the layer and considerable chain flexibility.⁷⁶ Thus, the protein resistance of this charge-neutral region appears to stem from short-range steric repulsion provided by strong hydration of charged residues. Furthermore, the weak surface charge of the swollen ends of the gradient suggests that charge-driven protein adsorption in these regions, that was observed previously,²⁹ occurs by diffusion of proteins into the swollen polymer, rather than by adsorption on top of the polymer film. However, the inconclusive modeling of the polymer structure precludes quantitative separation of steric and electrostatic forces, and thus neither diffuse layer potentials nor steric contributions versus position or composition along the gradients can be provided.

These results are useful for understanding the effects of, for example, pH-dependent charging and responses of zwitterionic, or otherwise charge-balanced, polymers, and their interactions with proteins. In view of the current interest in this class of polymers for potential antifouling properties, it will also contribute to supporting knowledge-driven development of coatings for marine, freshwater or biomedical uses.

Materials and Methods

Materials

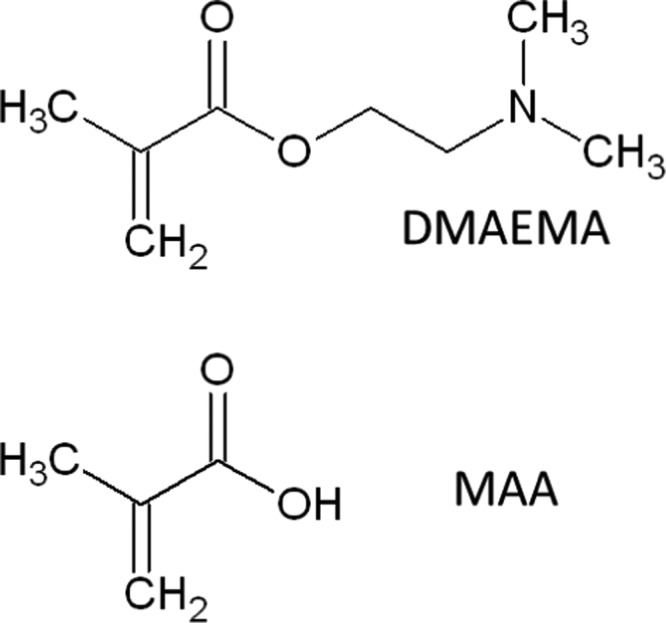
The monomers methacrylic acid (MAA, 99%) and 2-dimethylaminoethyl methacrylate (DMAEMA 98%) were purchased from Sigma-Aldrich and used without further purification, their structures are shown in Scheme 1. MAA monomers were polymerized in phosphate-buffered saline (PBS: 10 mM sodium hydrogen phosphate, 10 mM potassium dihydrogen phosphate, 150 mM NaCl) and adjusted to pH 6.0 with HCl. DMAEMA monomers were polymerized in 10 mM acetate buffer at pH 4.5. 0.1–10 mM monophosphate buffers (PBs), adjusted from pH 8.0 to 6.1 with HCl, 10 mM 2-(N-morpholino)ethanesulfonic acid (Calbiochem) buffer from pH 5.3 to 7.2 adjusted by NaOH, and 10 mM acetate buffer at pH 4.5 were used in all wet-state measurements to cover a wide pH range. 11-Mecaptoundecanoic acid (MUA) (99%, Sigma-Aldrich) and 16-thiohexadecanol (C16OH) (99.5%, gift from Biacore AB, Uppsala (now GE Healthcare)) were used for probe modification.

Scheme 1.

Gradient Fabrication

Due to experimental constraints, the gradients were prepared in two different dimensions. Short gradients, with a total length of 2 mm, were prepared to fit into the field of view of the imaging ellipsometer, which was used to investigate the swelling behavior of the thin films under different solution conditions, and 15 mm long gradients were prepared to provide sufficient spatial resolution along the length of the gradient in the infrared microscope, which was used to verify the chemical composition of the gradients. The samples for infrared microscopy were prepared on gold-coated substrates to increase the total reflectivity of the samples. Both gradient types were characterized by the colloidal probe atomic force measurements to confirm that they had similar properties.

Short Gradients

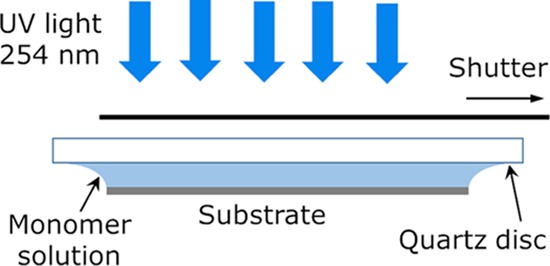
Short P(MAA–DMAEMA) gradient samples (2 mm gradient length), with a homogeneous PMAA bottom layer and a PDMAEMA gradient on top,⁷⁷ were made for imaging ellipsometry and for colloidal probe AFM force measurements. Before grafting the hydrogels, a silane monolayer was formed on a silicon substrate (Si(110), Topsil Semiconductor Materials A/S, Denmark) by incubation in a mixture of 5 mL 95% ethanol, 5 mL Milli-Q (MQ) water (Millipore), 4 μL acetic acid, and 40 μL methacryloxypropyltrimethoxysilane (PlusOne Bind-Silane, Amersham Bioscience) for 5 min. The surface was then dried in N₂ gas and baked at 115 °C for 10 min, ultrasonicated for 10 s in 95% ethanol and then stored in 95% ethanol. To form the first uniform anionic layer, The MAA monomer was diluted in PBS buffer to a concentration of 5% (v/v). The monomer solution was placed between a UV-transparent quartz disc and the sample surface, which is suspended beneath the disc and held in place by the surface tension, as described by Larsson et al.,⁵² and then polymerized for 5 min under a UV lamp (Philips TUV PL-L, 18 W) with the main emission peak at 254 nm (see Scheme 2). The surface was then sonicated for 1 min in PBS. The cationic PDMAEMA gradient was created in a similar manner, but by using a moving shutter above the sample. The monomers were diluted in 10 mM acetate buffer at pH 4.5 to a concentration of 15% (v/v). The moving speed of the shutter was 0.5 mm min^–1 with 4 min exposure time, which results in a 2 mm long gradient. Finally, the surface was rinsed by ultrasonication in a mixture of MQ water and 95% ethanol for 1 min and finally rinsed and stored in MQ water.

Scheme 2.

Long Gradients

Long P(MAA–DMAEMA) gradients (15 mm gradient length) were made primarily for infrared microscopy but were also subjected to AFM measurements. Pieces of silicon were coated with 25 Å chromium (99.9%, Balzers, Liechtenstein) followed by 200 nm gold (99.99%, Nordic High Vacuum AB, Sweden) in a custom-made resistive evaporation system. The clean gold substrates were then spin-coated by 0.25% polystyrene in xylene at 1250 rpm for 30 s using a spin-coater (WS-400B-6NPP/Lite, Laurell Technologies Corp.). PMAA and PDMAEMA layers were polymerized as described above, but the irradiation time and speed of the shutter were adjusted to provide a longer gradient with the same total maximum thickness: PMAA was polymerized for 3 min and PDMAEMA was polymerized for 5 min with the shutter moving at a speed of 3 mm min^–1. To study the properties of the PDMAEMA thickness gradient alone, PDMAEMA was also polymerized directly onto polystyrene-coated gold without a PMAA layer, but otherwise according to the protocol above.

Infrared Microscopy

A Bruker Hyperion 3000 IR microscope, with light supplied from a Tensor 27 IR spectrometer (Bruker) and equipped with a motorized and computer-controlled sample stage for accurate positioning of the sample was used for collecting the infrared reflection–absorption spectra. The objective used double surface reflection with angles between 52 and 80° relative to the surface normal. A nitrogen-cooled single-element mercury cadmium telluride detector was used and the resolution was 4 cm^–1. Two-hundred interferograms were recorded at each measurement point through a 100 × 200 μm² aperture window with the longer side perpendicular to the gradient direction when mapping the samples by 250 μm intervals. Thirty spectra were taken under N₂ purging and all spectra were background corrected by a concave rubberband method with 64 baseline points. This procedure was used for the characterization of long P(MAA–DMAEMA) and PDMAEMA gradients, as has also been described in more detail previously.^21,78

Imaging Null Ellipsometry

An EP3 imaging spectroscopic ellipsometer (Nanofilm Surface Analysis, Germany) equipped with a flow cell having windows at an angle of 60° from the sample surface normal was assembled to carry out the in situ ellipsometric measurements. The data were collected at 40 wavelengths between 350 and 850 nm, whereas the buffer exchange was made with a peristaltic pump operating at a flow rate of 0.78 mL min^–1. The total liquid volume in the system was approximately 3 mL, including the cell and pipe tubing. The pump was running for 12 min at each buffer exchange, but during the measurements, the flow was halted. The total area of simultaneous measurement was 1.2 × 0.8 mm², and Δ and Ψ pairs were averaged over 50 regions along the gradients. The measurements were carried out in the following order: air, MQ, and then in buffers starting from low toward high pH.

A four-zone measurement was made to collect data, under the assumption that the system did not change significantly during the 50 min required to carry out the measurement. This stability was confirmed by both ellipsometry and QCM-D (data not shown).⁷⁷ The obtained Δ and Ψ pairs at different wavelengths were used to model the thickness profiles by EP3.3 View software (supplied with the ellipsometer), where dispersion functions for silicon, silica, and water were taken from an internal database. The refractive indices of the polymers were evaluated on the dry films using a Cauchy function,⁷⁷ finally, the standard deviations for modeled film thicknesses were obtained by the software. In air, these ranged between 0.1 and 0.2 nm. In water, and for the swollen film, this was increased to 3–5 nm. A Bruggeman effective medium approximation, which models the medium as consisting of randomly arranged spherical particles of different compositions,⁷⁹ was used to account for the refractive index change due to the mixing of liquid with the polymer.

Force Measurement by Colloidal Probe AFM

The force measurements were performed with a NanoScope IVa Dimension 3100 SPM (Veeco Instruments, Inc., now Bruker) equipped with a liquid cell. The gold-coated glass colloidal probes with 10 μm diameter were purchased from NovaScan, individually calibrated with the Sader method, and all with spring constants near 0.19 N m^–1 (exact values for each probe were used in the data processing). The probes were modified to be either negatively charged, using an 11-mercaptoundecanoic acid (MUA) self-assembled monolayer (SAM) or nearly neutral by 16-thiohexadecanol (C16OH) SAMs. SAMs were formed by incubation in 1 mM thiol solutions in ethanol, for at least 24 h at room temperature. To determine the surface potential and the surface charge of the MUA and C16OH probes, force curves were obtained in symmetric systems with MUA or C16OH SAMs covering both the probe and the flat substrate. These measurements were carried out in monophosphate buffer (PB) solutions from 0.1 to 10 mM, and the results averaged over four probes and eight flat substrates for each SAM. Force data were fitted to DLVO theory using numerical solutions to the nonlinear Poisson–Boltzmann equation under both constant potential and constant charge conditions, according to the procedure described by Chan,⁸⁰ and using a Hamaker constant of 4 × 10^–20 J (ignoring retardation⁸¹). The surface charge was calculated using the Grahame equation.⁸² The presented force measurements were obtained in 10 mM PB buffers; the choice of a 10 mM electrolyte is a compromise between conflicting requirements. Ultimately, we are interested in the behavior and properties of these coatings under physiological and/or marine conditions, in which the total electrolyte concentrations are much higher than 10 mM. However, at relevant physiological or marine electrolyte levels, the Debye screening lengths become extremely short, and the measurement of electrostatic forces, and thus also the determination of surface charge, becomes very difficult. Ten millimolar was deemed the highest concentration, where the relevant features of the electrostatic properties are still reproduced and measurable with reasonable accuracy and was also used in our previous study.²⁹ In the force measurements, the probe was approaching the gradient surface, whereas the cantilever deflection was recorded as a function of the piezoelectric actuator displacement (in total 2 μm), with a frequency of 0.1 Hz per cycle. Force curves were converted from deflection-position to force/radius-separation data by assuming a zero separation in the constant compliance region. Forces are shown as normalized by the probe radius according to the Derjaguin approximation⁸² which yields F/R = 2πG, where G is the total free energy of interaction for planar surfaces. At least five approaches (force curves) were recorded at every point; the gradients were very robust, with the curves acquired at the same point consistently being similar, as would be expected with the large (10 μm) probe particle. When probing the short gradients (data not shown), force curves were collected and averaged at 10 positions with 200 μm pitch along the gradient. When probing the long gradients, force curves were recorded and averaged at each position, with 500 μm separation at 10 positions along the gradients. Force measurements on short and long gradients were consistent throughout the experiments. For clarity in presentation, results from only seven adjacent positions are shown in the following; the excluded data obtained at the peripheries of the gradients are similar and provide no additional information. In total, three MUA and two C16OH probes were used to investigate 10 different gradients.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.9b00339.

• Infrared spectra and peak assignments for MAA–DMAEMA and DMAEMA gradients; interaction forces between a negatively charged probe and a single cationic gradient layer (PDF)

Author Present Address

^∥ Present address: MariboHilleshög Research AB, 261 23 Landskrona, Sweden (T.E.).

Author Present Address

^§ Present address: Insplorion AB, Medicinaregatan 8A, 413 90 Göteborg, Sweden (O.A.).

Author Present Address

^‡ Present address: Susos AG, Lagerstrasse 14, 8600 Dübendorf, Switzerland (O.S.).

Author Present Address

^† Present address: Kagaku Analys AB, Sven Hultins gata 9A, 412 88 Göteborg, Sweden (F.-I.T.).

The authors declare no competing financial interest.